A New Method to Retrieve the Three-Dimensional Refractive Index and Specimen Size Using the Transport Intensity Equation, Taking Diffraction into Account
Abstract
1. Introduction
2. Materials and Methods
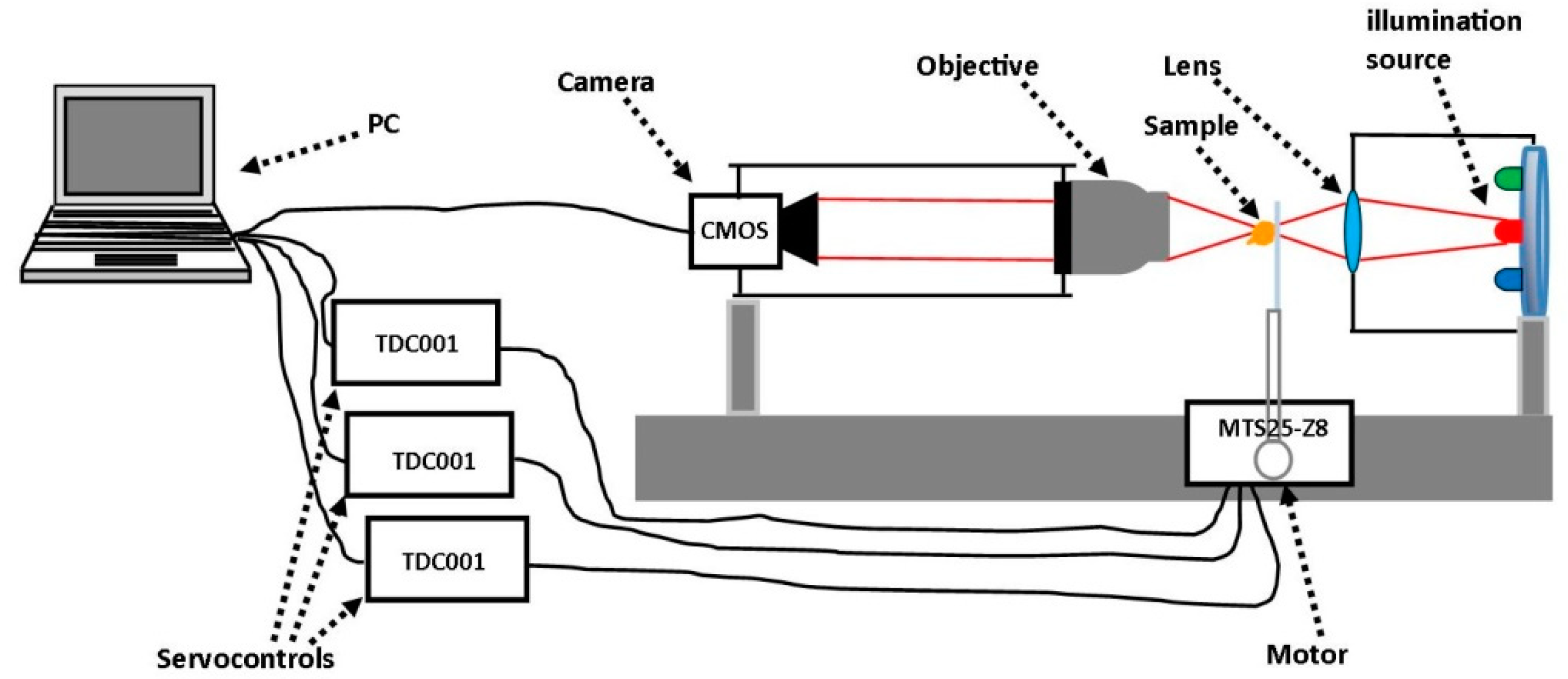
2.1. Experimental Set-Up
2.2. Sample Preparation
2.3. Measurement Procedure
- -
- image Td, the contribution of the background and the dark current in the detector; it was achieved with nothing in the microscope and with the source illumination turned off;
- -
- image Tb, the bright reference; it was achieved with an empty slide in the microscope;
- -
- image Ts, the raw image of the sample, it was achieved with the sample in the microscope.
2.4. Analysis Methods
- -
- computed from the optical properties of the microscope system,
- -
- estimated from the measurements of the microspheres.
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Barer, R.; Joseph, S. Refractometry of Living Cells Part I. Basic Principles. Q. J. Microsc. Sci. 1954, 95, 399–423. [Google Scholar]
- Zhuo, W.; Krishnara, T.; Balla, A.; Popescu, G. Tissue refractive index as marker of disease. J. Biomed. Opt. 2011, 16, 116017. [Google Scholar]
- YongKeun, P.; Monica, D.S.; Popescu, G.; Lykotrafitis, G.; Wonshik, C.; Feld, S.M.; Subra, S. Refractive index maps and membrane dynamics of human red blood cells parasitized by Plasmodium falciparum. Proc. Natl. Acad. Sci. USA 2008, 105, 13730–13735. [Google Scholar]
- Florian, C.; Anca, M.; Frédéric, M.; Jonas, K.; Tristan, C.; Etienne, C.; Pierre, M.; Christian, D. Cell refractive index tomography by digital holographic microscopy. Opt. Lett. 2006, 31, 178–180. [Google Scholar]
- Chao, Z.; Qian, C.; Anand, A. Transport of intensity equation: A new approach to phase and light field. Proc. SPIE 2014, 9271, 92710H. [Google Scholar]
- Teague, M.R. Deterministic phase retrieval: A Green’s function solution. J. Opt. Soc. Am. 1983, 73, 1434–1441. [Google Scholar] [CrossRef]
- Laura, W.; Lei, T.; Barbastathis, G. Transport of Intensity phase-amplitude imaging with higher order intensity derivatives. Opt. Express 2010, 18, 12552–12561. [Google Scholar]
- Kevin, G.P.; Steven, L.J.; Owen, J.T.M. Measurement of Single Cell Refractive Index, Dry Mass, Volume, and Density Using a Transillumination Microscope. Phys. Rev. Lett. 2012, 109, 118105. [Google Scholar]
- Ivan, D.N.; Christo, D.I. Optical plastic refractive measurements in the visible and the near-infrared regions. Appl. Opt. 2000, 39, 2067–2070. [Google Scholar]
- Tadrous, P.J. A method of PSF generation for 3D brightfield deconvolution. J. Microsc. 2009, 237, 192–199. [Google Scholar] [CrossRef] [PubMed]
- Brydegaard, M.; Merdasa, A.; Jayaweera, H.; Ålebring, J.; Svanberg, S. Versatile multispectral microscope based on light emitting diodes. Rev. Sci. Instrum. 2011, 82, 123106. [Google Scholar] [CrossRef] [PubMed]
- Agnero, M.A.; Zoueu, J.T.; Konan, K. Characterization of a Multimodal and Multispectral Led Imager: Application to Organic Polymer’s Microspheres with Diameter Φ=10.2μm. Opt. Photonics J. 2016, 6, 171–183. [Google Scholar] [CrossRef]
- Laura, W. Computational Phase Imaging Based on Intensity Transport. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2010. [Google Scholar]
- McNally, J.G.; Karpova, T.; Cooper, J.; Conchello, J.A. Three-dimensional imaging by deconvolution microscopy. Methods 1999, 19, 373–385. [Google Scholar] [CrossRef] [PubMed]
- Swedlow, J.R. Quantitative fluorescence microscopy and image deconvolution. Methods Cell Biol. 2007, 81, 447–465. [Google Scholar] [PubMed]
- Hernandez, C.N.; Gutierrez-Medina, B. Direct Imaging of Phase Objects Enables Conventional Deconvolution in Bright Field Light Microscopy. PLoS ONE 2014, 9, e89106. [Google Scholar] [CrossRef] [PubMed]
- Chrysanthe, P.; Michael, I.M.; Lewis, J.T.; James, G.M. Regularized linear method for reconstruction of three-dimensional microscopic objects from optical sections. J. Opt. Soc. Am. 1992, 9, 209–228. [Google Scholar]
- Streibl, N. Three-dimensional imaging by a microscope. J. Opt. Soc. Am. A 1985, 2, 121–127. [Google Scholar] [CrossRef]
- Laasmaa, M.; Vendelin, M.; Peterson, P. Application of regularized Richardson-Lucy algorithm for deconvolution of confocal microscopy images. J. Microsc. 2011, 243, 124–140. [Google Scholar] [CrossRef] [PubMed]
- Yasushi, H.; John, W.S.; Agard, D.A. Determination of three-dimensional imaging properties of a light microscope system Partial confocal behavior in epifluorescence microscopy. Biophys. Soc. 1990, 57, 325–333. [Google Scholar]
- Haeberlé, O.; Bcha, F.; Simler, C.; Dieterlen, A.; Xu, C.; Colicchio, B.; Jacquey, S.; Gramain, M.P. Identification of acquisition parameters from the point spread function of a fluorescence microscope. Opt. Commun. 2001, 196, 109–117. [Google Scholar] [CrossRef]
- Lai, X.; Lin, Z.; Ward, E.S.; Ober, R.J. Noise suppression of point spread functions and its influence on deconvolution of three-dimensional fluorescence microscopy image sets. J. Microsc. 2005, 217, 93–108. [Google Scholar] [CrossRef] [PubMed]
- Gibson, S.F.; Lanni, F. Experimental test of an analytical model of aberration in an oil-immersion objective lens used in three-dimensional light microscopy. J. Opt. Soc. Am. 1991, 8, 1601–1613. [Google Scholar] [CrossRef]
- Besson, P.; Vonesch, C.; Aguet, F. PSF Gibson generator plug-in for Image-J. v.1.0. 2005. Available online: http://bigwww.epfl.ch/demo/deconvolution3D/ (accessed on May 2009).
- Aguet, F.; Dimitri, D.V.; Unser, M. An accurate PSF model with few parameters for axially shift-variant déconvolution. In Proceedings of the 2008 5th IEEE International Symposium on Biomedical Imaging: From Nano to Macro, Paris, France, 14–17 May 2008; pp. 157–160. [Google Scholar]
- Chao, Z.; Qian, C.; Anand, A. Comparison of Digital Holography and Transport of Intensity for Quantitative Phase Contrast Imaging. In Fringe; Osten, W., Ed.; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar] [CrossRef]
- Gureyev, T.; Nugent, K. Rapid quantitative phase imaging using the transport of intensity equation. Opt. Commun. 1997, 133, 339–346. [Google Scholar] [CrossRef]
- Allen, L.J.; Oxley, M.P. Phase retrieval from series of images obtained by defocus variation. Opt. Commun. 2001, 199, 65–75. [Google Scholar] [CrossRef]
- Ishimaru, A. Wave Propagation and Scattering in Random Media, Part II; Academic: New York, NY, USA, 1978; Chapter 7. [Google Scholar]
- Liu, P.Y.; Chin, L.K.; Ser, W.; Chen, H.F.; Hsieh, C.M.; Lee, C.H.; Sung, K.B.; Ayi, T.C.; Yap, P.H.; Liedberg, B.; et al. Cell refractive index for cell biology and disease diagnosis: past, present and future. R. Soc. Chem. 2016, 16, 634–644. [Google Scholar] [CrossRef] [PubMed]
- Zhong, J.; Claus, A.R.; Dauwels, J.; Lei, T.; Laura, W. Transport of Intensity phase imaging by intensity spectrum fitting of exponentially spaced defocus planes. Opt. Express 2014, 22, 10662–10674. [Google Scholar]
- Rodrigo, J.A.; Alieva, T. Rapid quantitative phase imaging for partially coherent light microscopy. Opt. Express 2014, 22, 13472–13483. [Google Scholar] [CrossRef] [PubMed]
- James, C.O. Optical Refractive Index of Air: Dependence on Pressure, Temperature and Composition. Appl. Opt. 1967, 6, 51–59. [Google Scholar]
- Garrel, V. Réalisation d’un instrument d’imagerie visible à la limite de diffraction pour un grand télescope. Ph.D. Thesis, École doctorale d’Astronomie et d’Astrophysique, Ile de France, Meudon, France, 2012; pp. 1–11. [Google Scholar]
- Richardson, W.H. Bayesian-Based Iterative Method of Image Restoration. J. Opt. Soc. Am. 1970, 62, 55–59. [Google Scholar] [CrossRef]
- Lucy, L.B. An iterative technique for the rectification of observed distributions. Astron. J. 1974, 79, 745–749. [Google Scholar] [CrossRef]
- Wonshik, C.; Fang-Yen, C.; Badizadegan, K.; Dasari, R.R.; Feld, M.S. Extended depth of focus in tomographic phase microscopy using a propagation algorithm. Opt. Lett. 2008, 33, 171–173. [Google Scholar]

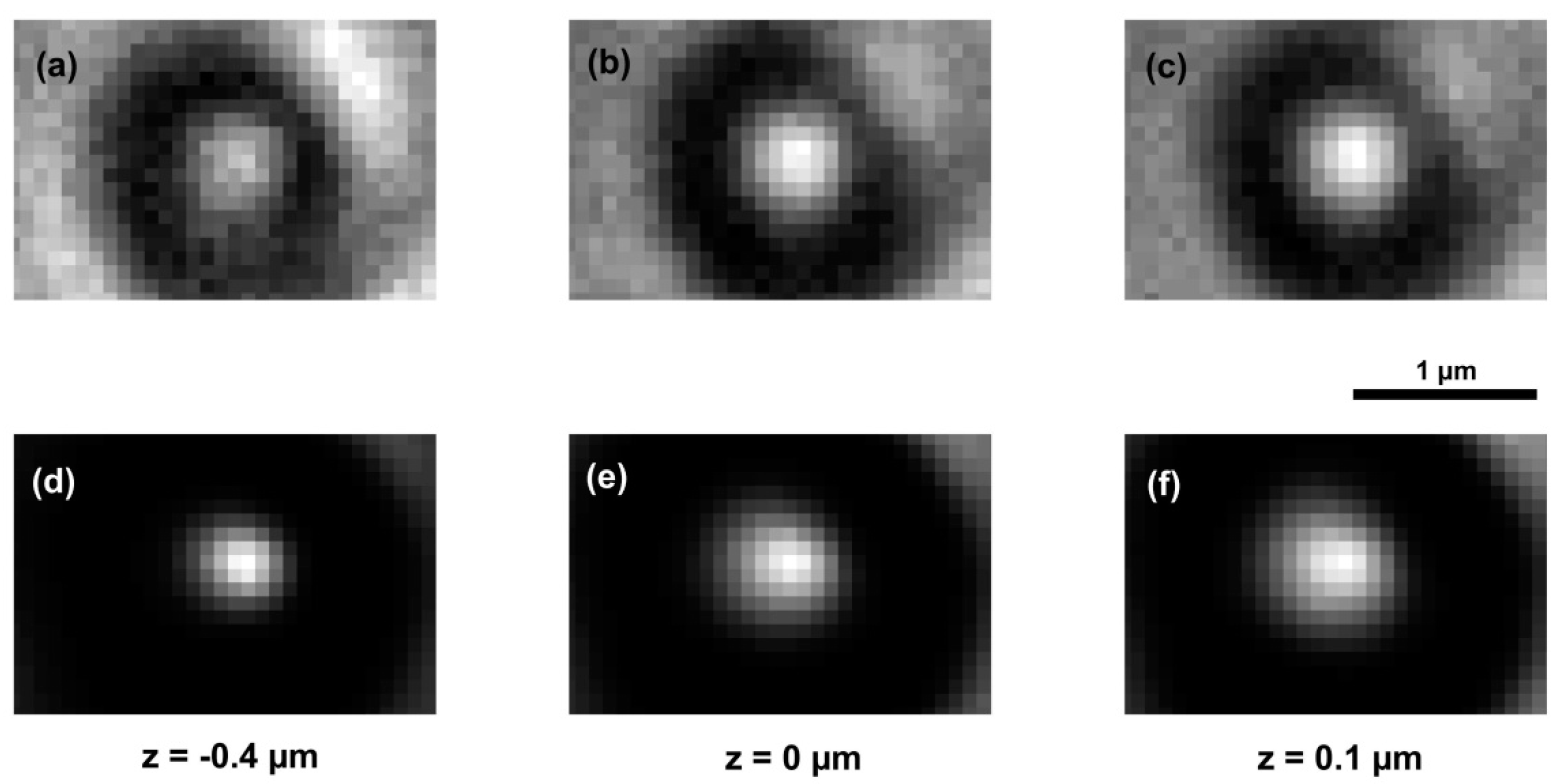
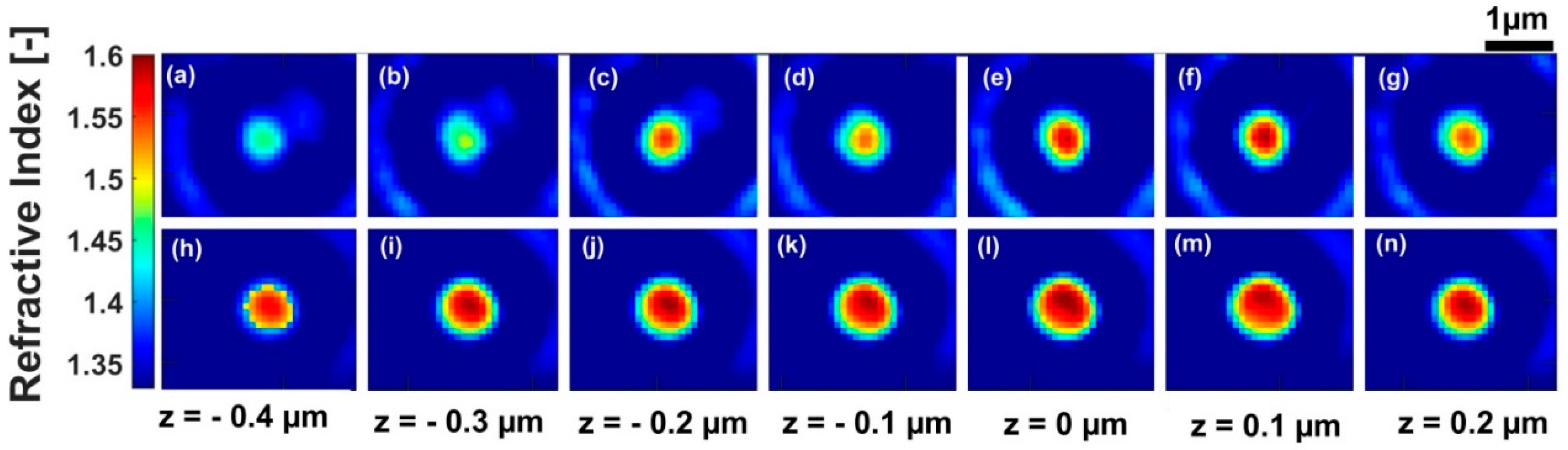

| Z = −0.4 | Z = −0.3 | Z = −0.2 | Z = −0.1 | Z = 0 | Z = 0.1 | Z = 0.2 | |
|---|---|---|---|---|---|---|---|
| Refractive index before deconvolution | 1.444 | 1.460 | 1.526 | 1.512 | 1.556 | 1.558 | 1.515 |
| Refractive index after deconvolution | 1.584 | 1.585 | 1.587 | 1.586 | 1.587 | 1.585 | 1.586 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Agnero, M.A.; Konan, K.; Kossonou, A.T.; Bagui, O.K.; Zoueu, J.T. A New Method to Retrieve the Three-Dimensional Refractive Index and Specimen Size Using the Transport Intensity Equation, Taking Diffraction into Account. Appl. Sci. 2018, 8, 1649. https://doi.org/10.3390/app8091649
Agnero MA, Konan K, Kossonou AT, Bagui OK, Zoueu JT. A New Method to Retrieve the Three-Dimensional Refractive Index and Specimen Size Using the Transport Intensity Equation, Taking Diffraction into Account. Applied Sciences. 2018; 8(9):1649. https://doi.org/10.3390/app8091649
Chicago/Turabian StyleAgnero, Marcel A., Kouakou Konan, Alvarez T. Kossonou, Olivier K. Bagui, and Jérémie T. Zoueu. 2018. "A New Method to Retrieve the Three-Dimensional Refractive Index and Specimen Size Using the Transport Intensity Equation, Taking Diffraction into Account" Applied Sciences 8, no. 9: 1649. https://doi.org/10.3390/app8091649
APA StyleAgnero, M. A., Konan, K., Kossonou, A. T., Bagui, O. K., & Zoueu, J. T. (2018). A New Method to Retrieve the Three-Dimensional Refractive Index and Specimen Size Using the Transport Intensity Equation, Taking Diffraction into Account. Applied Sciences, 8(9), 1649. https://doi.org/10.3390/app8091649






