Figure 1.
Four Neewer lapel microphones above Langstroth landing pad. The four microphones (two on each side of the pad) are placed approximately 10 cm above the Langstroth landing pad; four microphones are connected to the microphone hub inside the box with the BeePi hardware components placed on top of the hive; the microphones are not affected by rain or snow.
Figure 1.
Four Neewer lapel microphones above Langstroth landing pad. The four microphones (two on each side of the pad) are placed approximately 10 cm above the Langstroth landing pad; four microphones are connected to the microphone hub inside the box with the BeePi hardware components placed on top of the hive; the microphones are not affected by rain or snow.
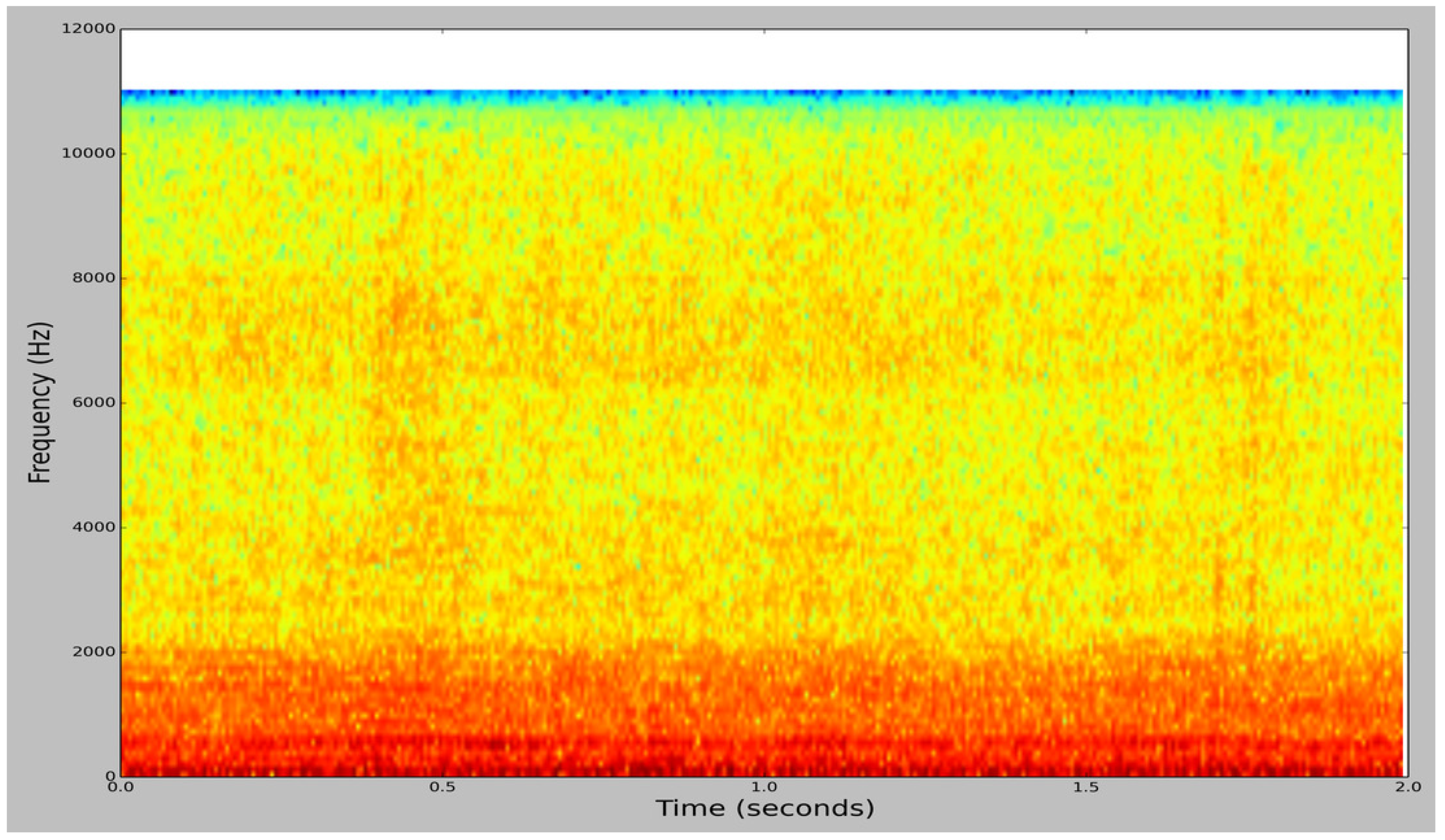
Figure 2.
Spectrogram image of a bee buzzing audio sample from BUZZ1.
Figure 2.
Spectrogram image of a bee buzzing audio sample from BUZZ1.
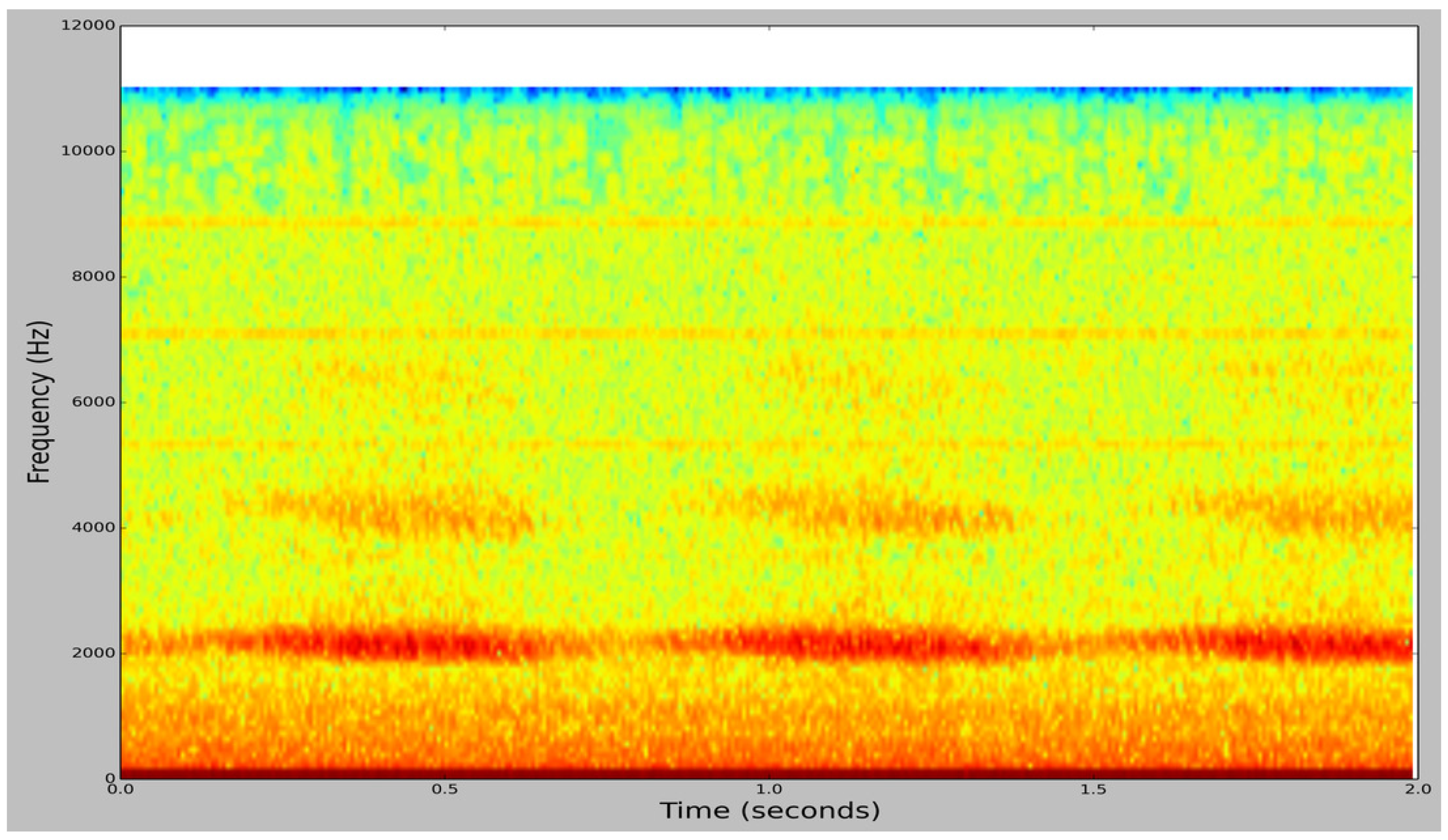
Figure 3.
Spectrogram image of a cricket chirping audio sample from BUZZ1.
Figure 3.
Spectrogram image of a cricket chirping audio sample from BUZZ1.
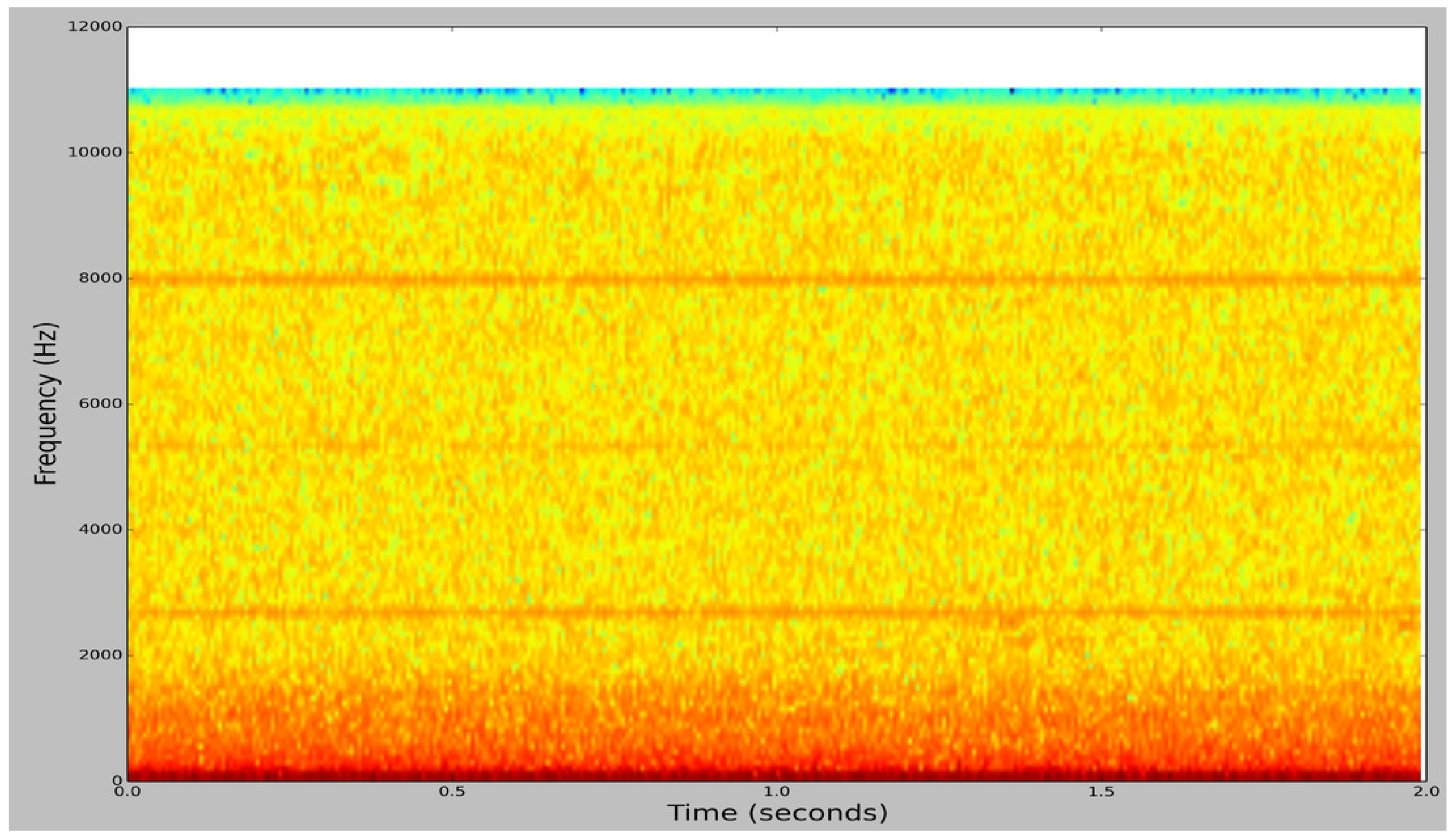
Figure 4.
Spectrogram image of an ambient noise audio sample from BUZZ1.
Figure 4.
Spectrogram image of an ambient noise audio sample from BUZZ1.
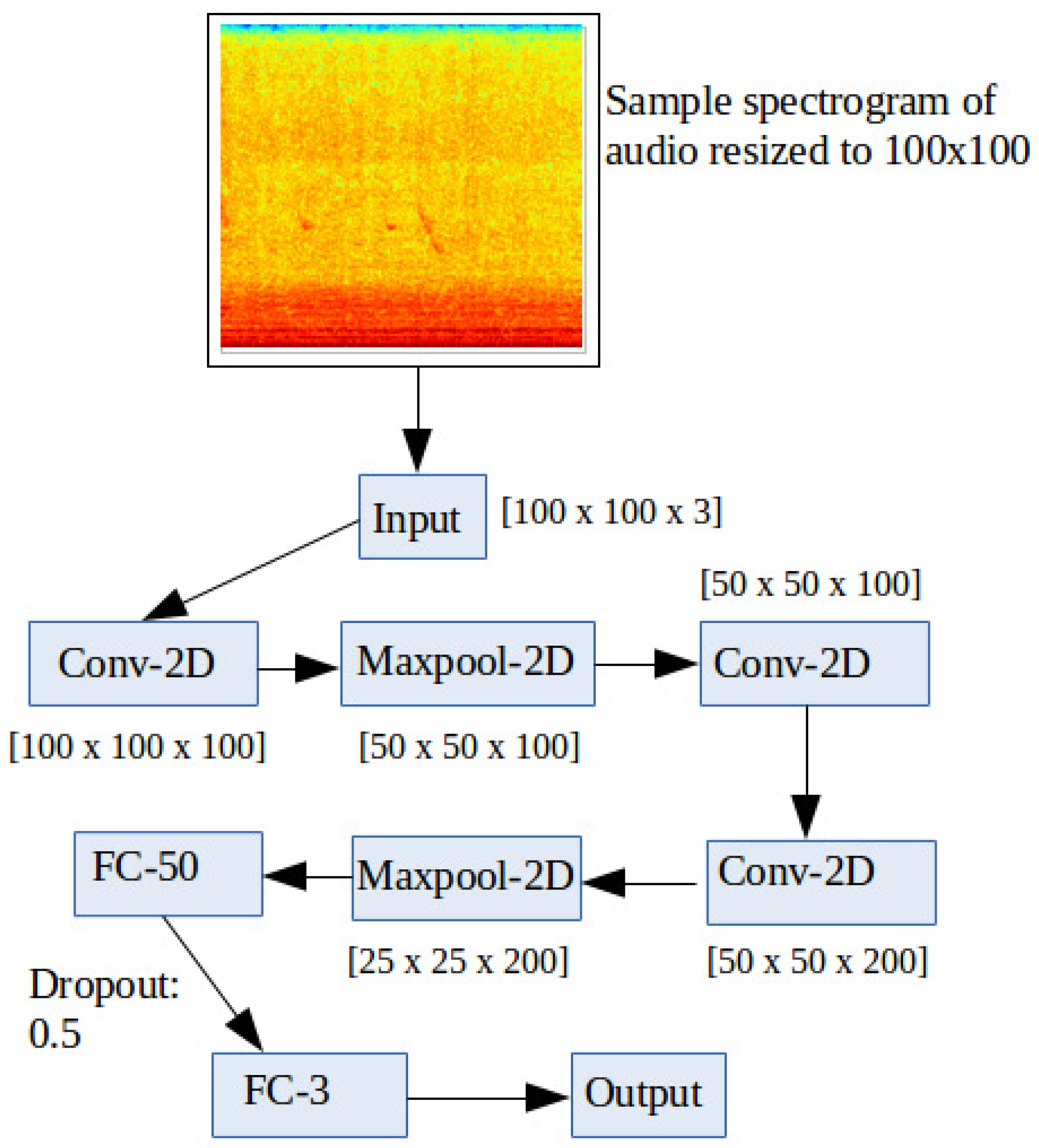
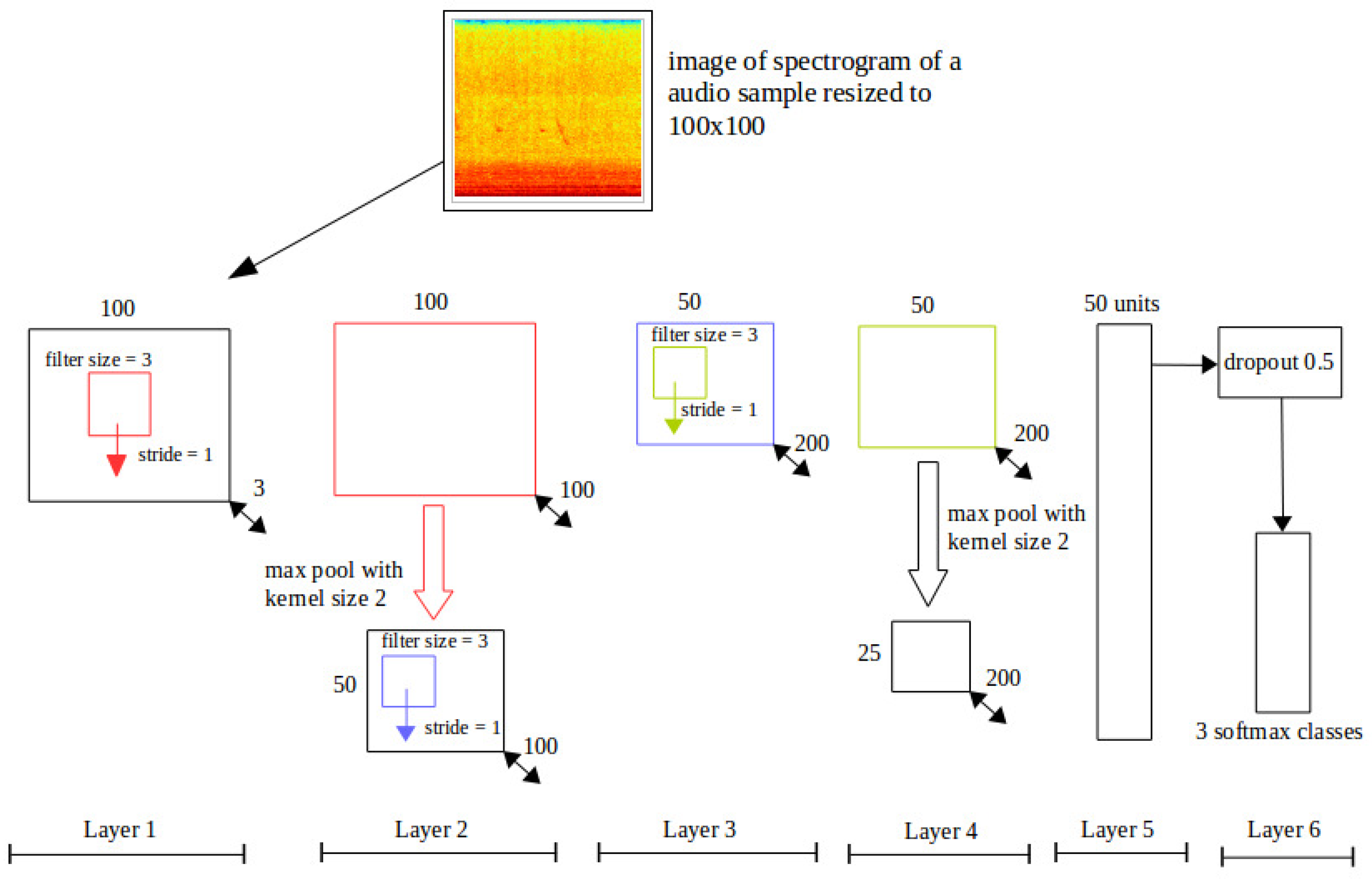
Figure 5.
SpectConvNet Architecture. The numbers below each box, except for the input, denote the dimensions of the resultant feature map following the corresponding operation in the box.
Figure 5.
SpectConvNet Architecture. The numbers below each box, except for the input, denote the dimensions of the resultant feature map following the corresponding operation in the box.
Figure 6.
SpectConvNet Control Flow. Layer by layer control flow of SpectConvNet; the numbers at the corners of each rectangle represent the corresponding dimensions.
Figure 6.
SpectConvNet Control Flow. Layer by layer control flow of SpectConvNet; the numbers at the corners of each rectangle represent the corresponding dimensions.
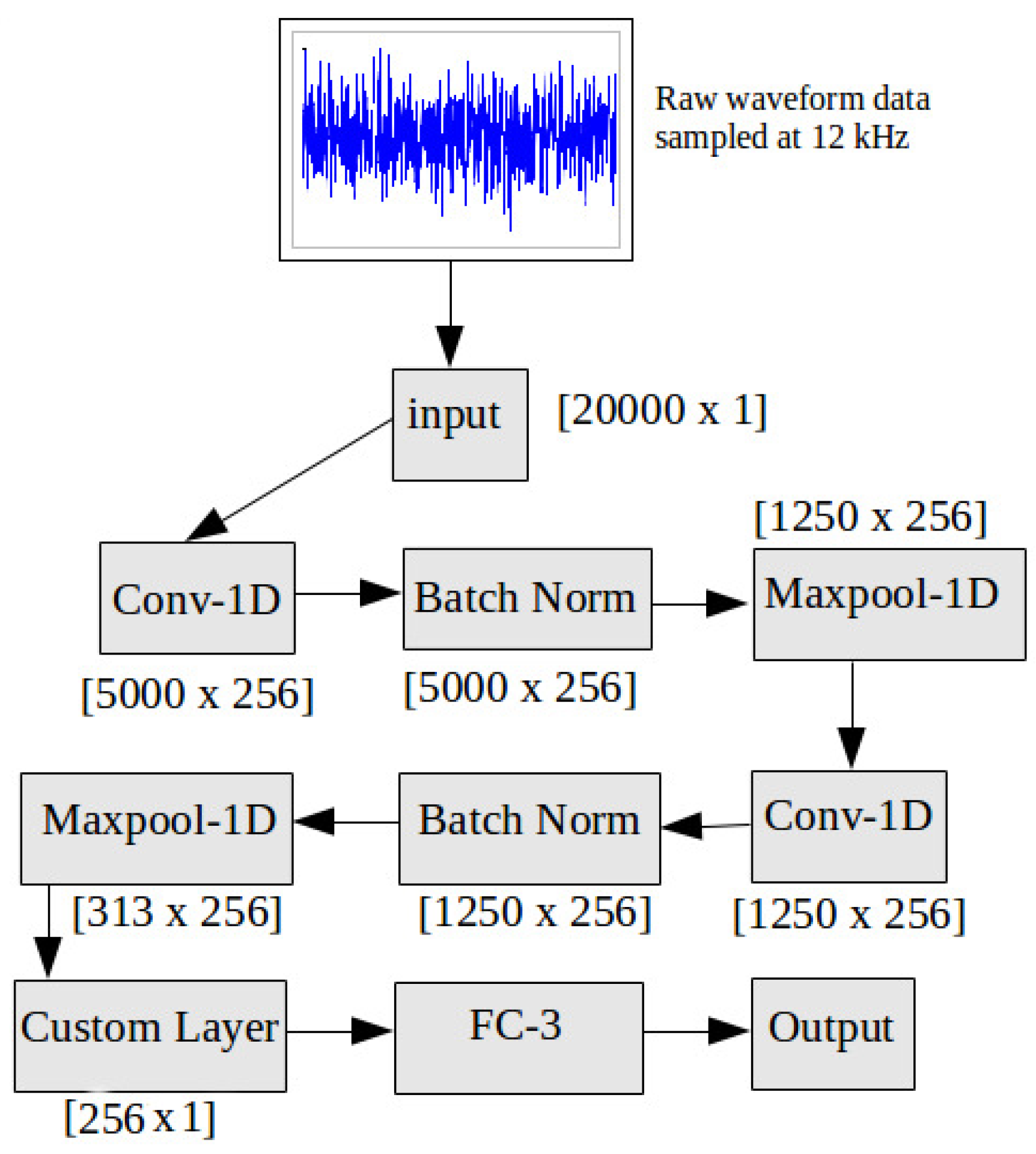
Figure 7.
RawConvNet Architecture. The numbers below each box, except for the input, are the dimensions of the resultant feature map following the corresponding operation in the box.
Figure 7.
RawConvNet Architecture. The numbers below each box, except for the input, are the dimensions of the resultant feature map following the corresponding operation in the box.
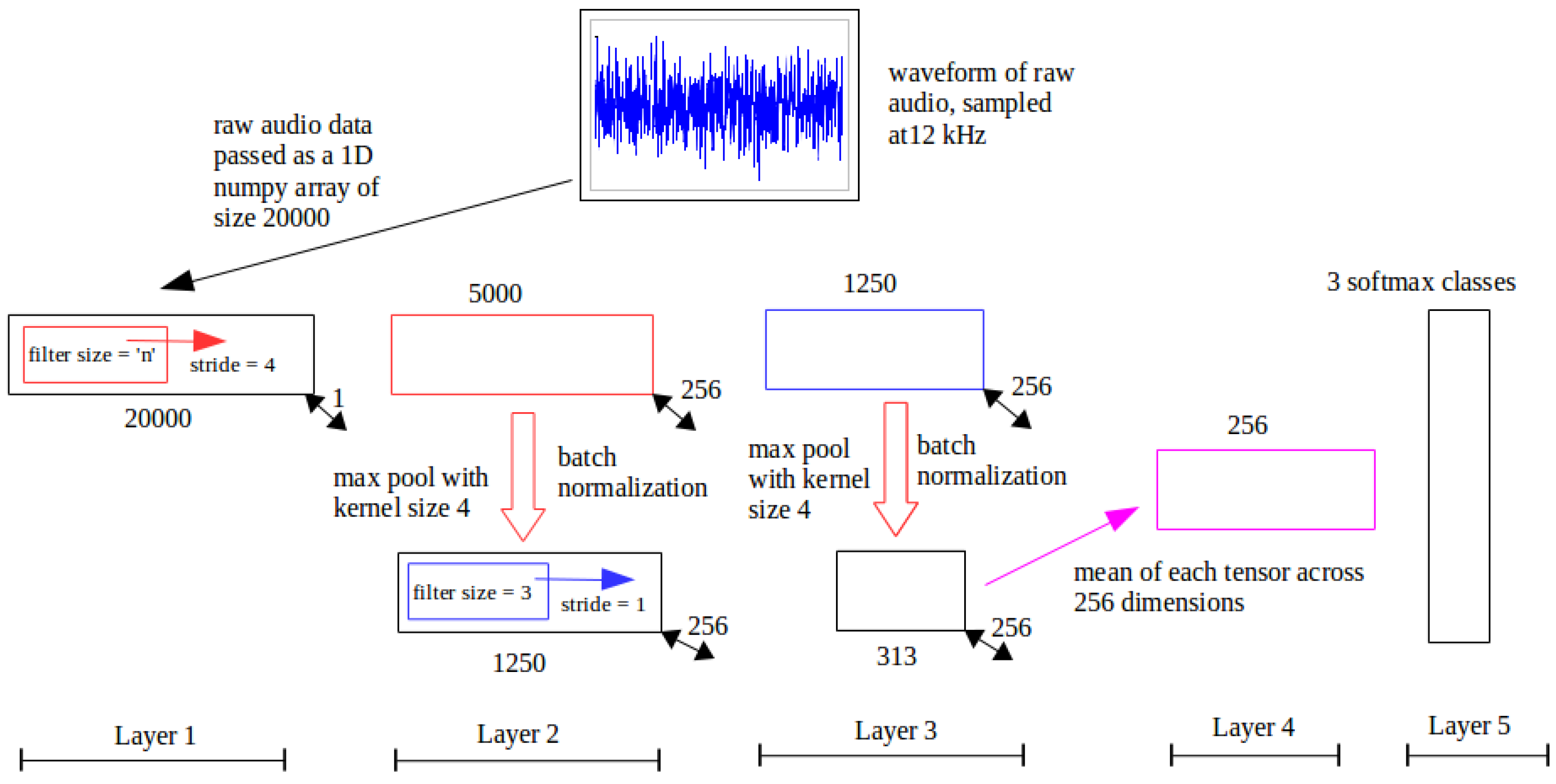
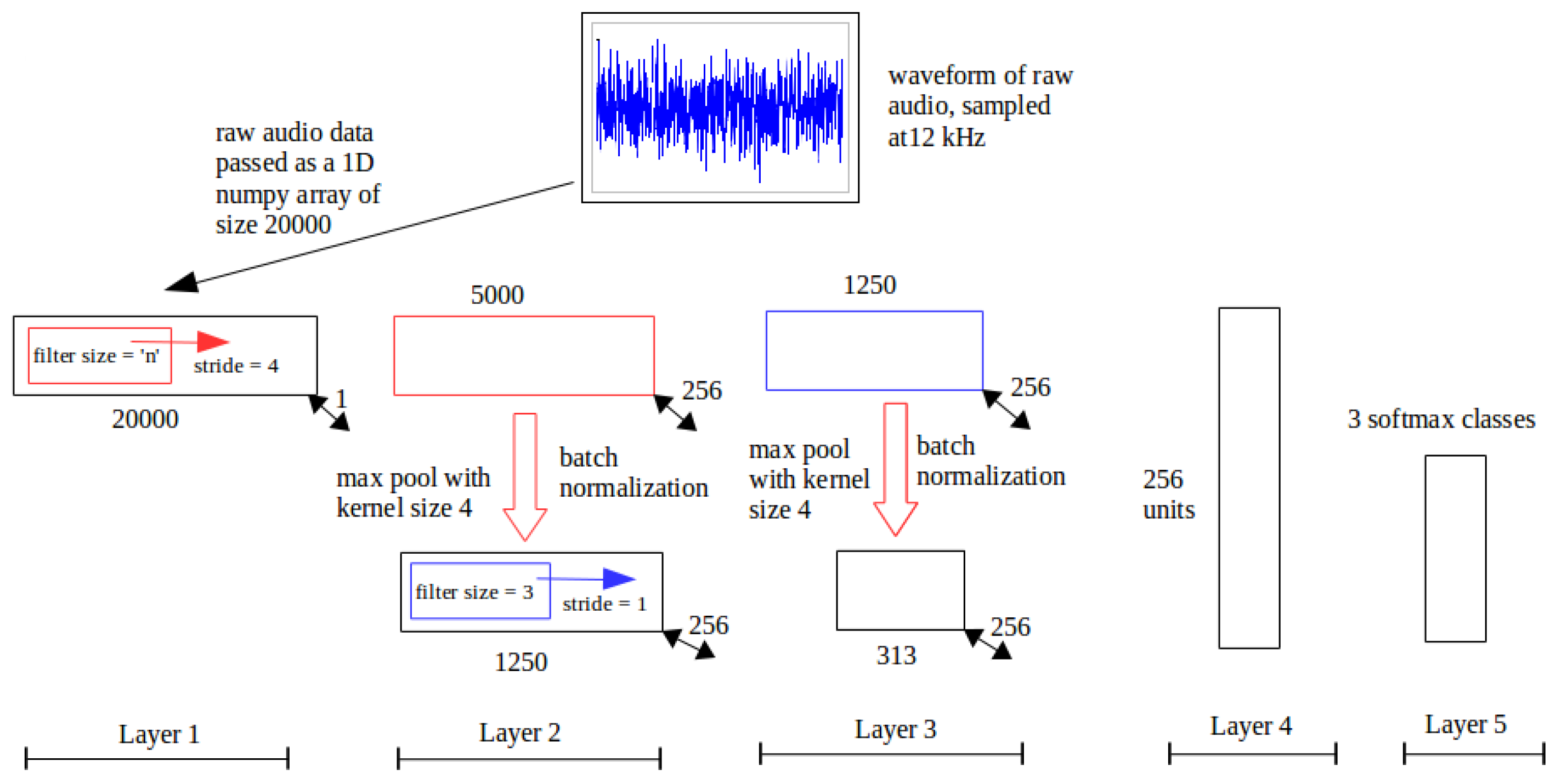
Figure 8.
RawConvNet Control Flow. Layer by layer control flow in RawConvNet trained to classify raw audio samples; the numbers below each box at the corners of each rectangle represent the corresponding dimensions; all filters and feature maps are rectangular in shape with a breadth of one unit.
Figure 8.
RawConvNet Control Flow. Layer by layer control flow in RawConvNet trained to classify raw audio samples; the numbers below each box at the corners of each rectangle represent the corresponding dimensions; all filters and feature maps are rectangular in shape with a breadth of one unit.
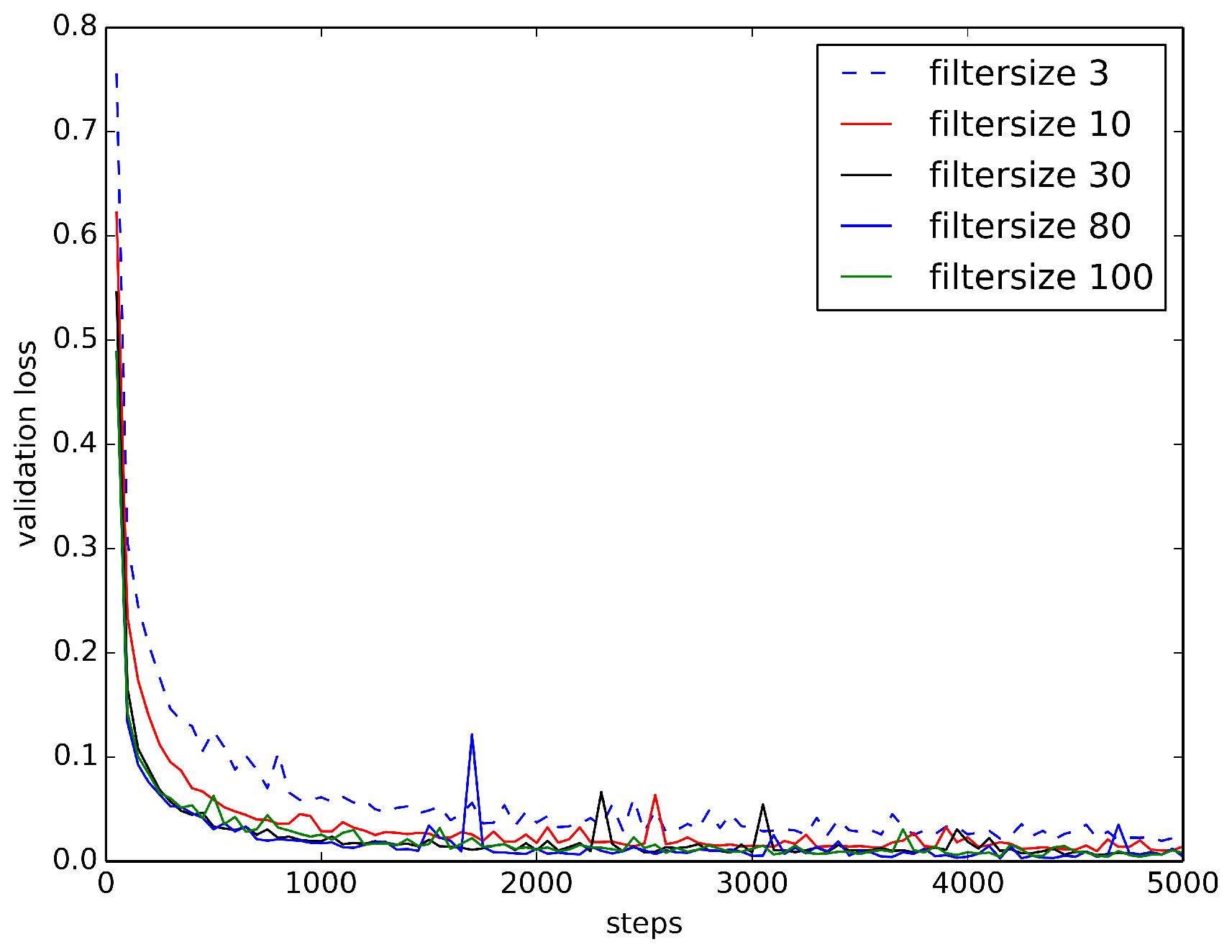
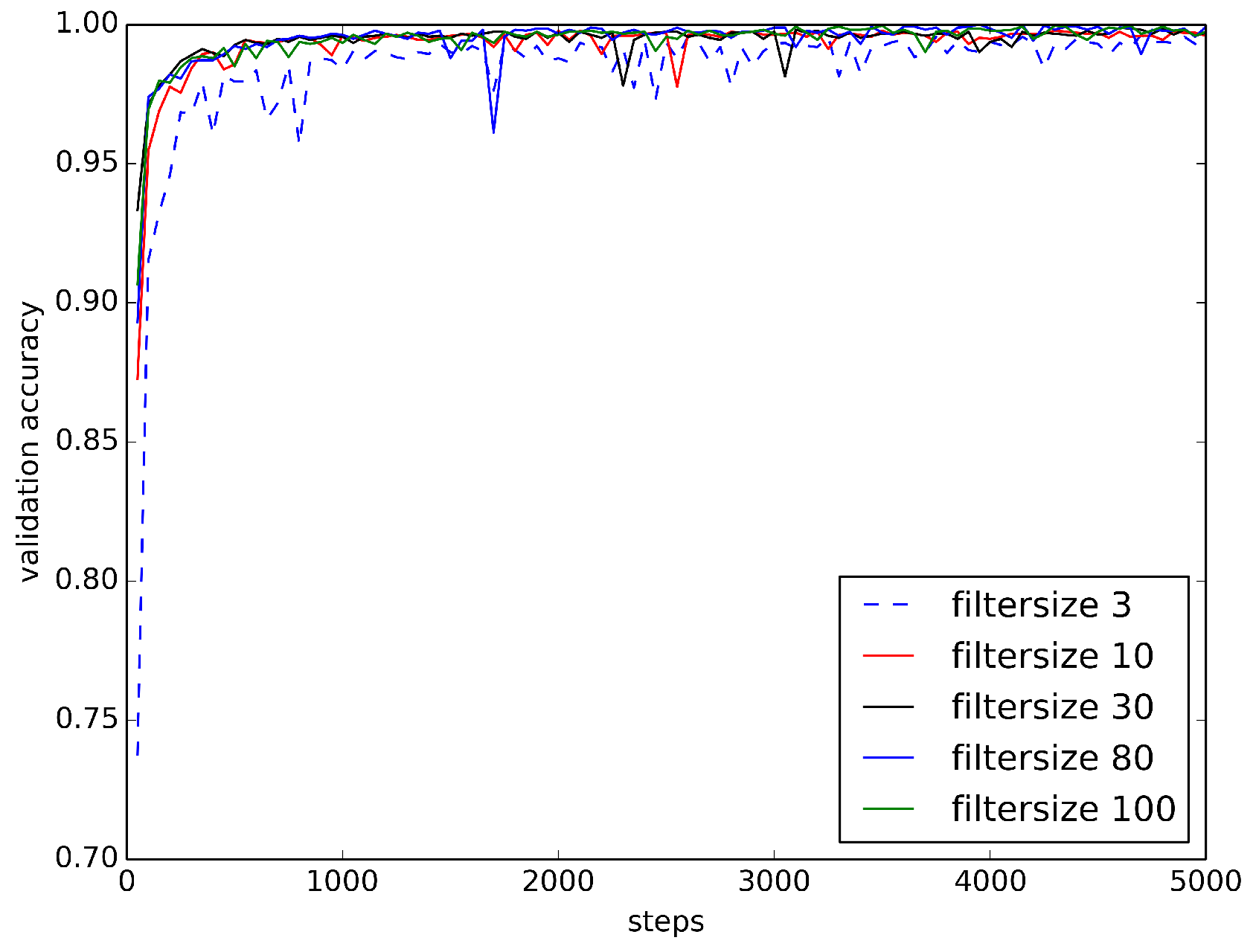
Figure 9.
Loss Curves of RawConvNet on BUZZ1 Train/Test Dataset. As the size of the receptive field increases, loss curves become smoother and decrease faster.
Figure 9.
Loss Curves of RawConvNet on BUZZ1 Train/Test Dataset. As the size of the receptive field increases, loss curves become smoother and decrease faster.
Figure 10.
Accuracy Curves of RawConvNet on BUZZ1 Train/Test Dataset. As the size of the receptive field increases, accuracy curves become smoother and increase faster.
Figure 10.
Accuracy Curves of RawConvNet on BUZZ1 Train/Test Dataset. As the size of the receptive field increases, accuracy curves become smoother and increase faster.
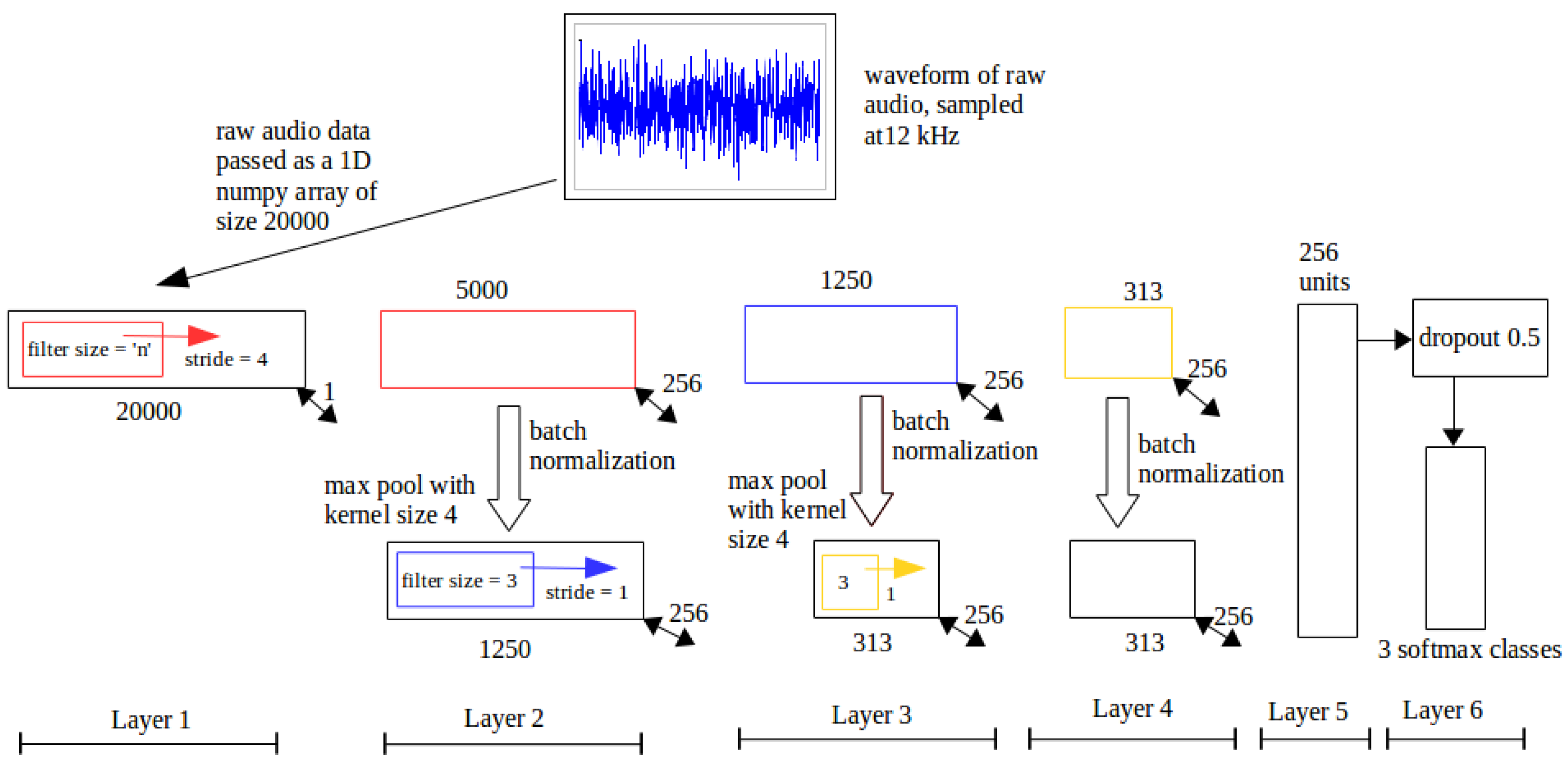
Figure 11.
ConvNet 1. This ConvNet is similar to RawConvNet, but the custom layer (layer 4) of RawConvNet is replaced with an FC layer with 256 neurons.
Figure 11.
ConvNet 1. This ConvNet is similar to RawConvNet, but the custom layer (layer 4) of RawConvNet is replaced with an FC layer with 256 neurons.
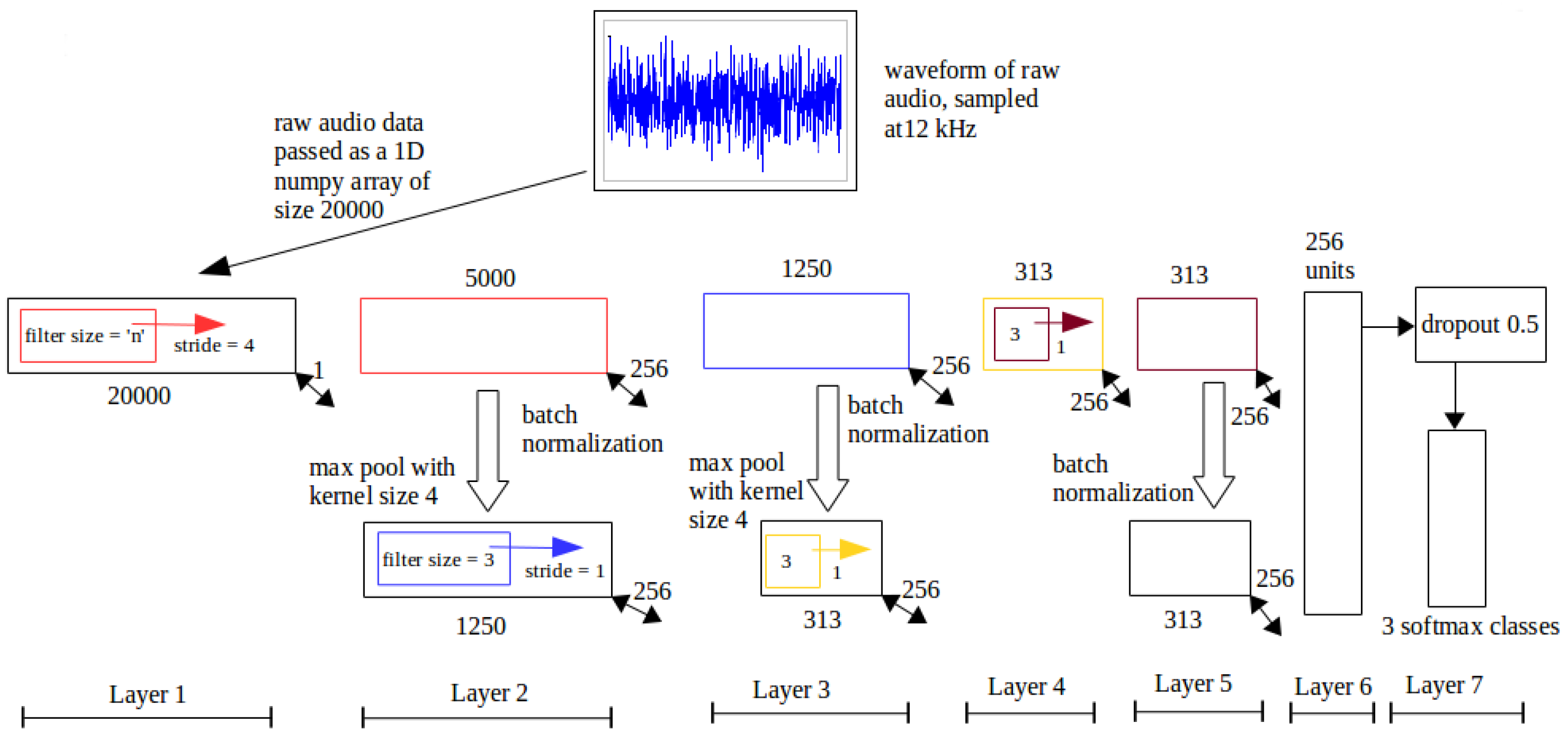
Figure 12.
ConvNet 2. Layers 1 and 2 are identical to ConvNet 1; in layer 3, maxpooling output is convolved with 256 filters and batch normalization is used.
Figure 12.
ConvNet 2. Layers 1 and 2 are identical to ConvNet 1; in layer 3, maxpooling output is convolved with 256 filters and batch normalization is used.
Figure 13.
ConvNet 3. Layers 1, 2, and 3 are identical to the same layers in ConvNet 2; in layer 4, the output is convolved with 256 filters and batch normalization is performed in layer 5.
Figure 13.
ConvNet 3. Layers 1, 2, and 3 are identical to the same layers in ConvNet 2; in layer 4, the output is convolved with 256 filters and batch normalization is performed in layer 5.
Table 1.
SpectConvNet’s Layer Specification.
Table 1.
SpectConvNet’s Layer Specification.
| Configuration of the Best Performing Model |
|---|
| Layers | Specification |
|---|
| Layer 1 | Conv-2D | filters = 100, filterSize = 3, strides = 1, activation = relu, bias = True, biasInit = zeros, weightsInit = uniform scaling, regularizer = none, weightDecay = 0.001 |
| Layer 2 | Maxpool-2D | kernelSize = 2, strides = none |
| Conv-2D | filters = 200, filterSize = 3, strides = 1, activation = relu, bias = True, biasInit = zeros, weightsInit = uniform scaling, regularizer = none, weightDecay = 0.001 |
| Layer 3 | Conv-2D | filters = 200, filterSize = 3, strides = 1, activation = relu, bias = True, biasInit = zeros, weightsInit = uniform scaling, regularizer = none, weightDecay = 0.001 |
| Layer 4 | Maxpool-2D | kernelSize = 2, strides = none |
| Layer 5 | FC | number of units = 50, activation = relu |
| Layer 6 | Dropout | keep probability = 0.5 |
| FC | number of units = 3, activation = softmax |
Table 2.
RawConvNet’s layer specification.
Table 2.
RawConvNet’s layer specification.
| Layers | Specification |
|---|
| Layer 1 | Conv-1D | filters = 256, filterSize = n ∈ {3, 10, 30, 80, 100}, strides = 4, activation = relu, bias = True, weightsInit = xavier, biasInit = zeros, regularizer = L2, weightDecay = 0.0001 |
| Layer 2 | Batch Normalization | gamma = 1.0, epsilon = 1e − 05, decay = 0.9, stddev = 0.002 |
| Maxpool-1D | kernelSize = 4, strides = none |
| Conv-1D | filters = 256, filterSize = 3, strides = 1, activation = relu, bias = True, weightsInit = xavier, biasInit = zeros, regularizer = L2, weightDecay = 0.0001 |
| Layer 3 | Batch Normalization | gamma = 1.0, epsilon = 1e − 05, decay = 0.9, stddev = 0.002 |
| Maxpool-1D | kernelSize = 4, strides = none |
| Layer 4 | Custom Layer | calculates the mean of each feature map |
| Layer 5 | FC | number of units = 3, activation = softmax |
Table 3.
SpectConvNet vs. RawConvNet on BUZZ1 train/test dataset with 70–30 train/test split. The parameter n denotes the size of the receptive field in the first layer of RawConvNet.
Table 3.
SpectConvNet vs. RawConvNet on BUZZ1 train/test dataset with 70–30 train/test split. The parameter n denotes the size of the receptive field in the first layer of RawConvNet.
| Number of Training Samples: 6377; Number of Testing Samples: 2733 |
|---|
| Model Name | Training Loss | Training Accuracy | Testing Loss | Testing Accuracy | Runtime per Epoch |
|---|
| SpectConvNet | 0.00619 | 99.04% | 0.00702 | 99.13% | 690 s |
| RawConvNet (n = 3) | 0.02759 | 99.24% | 0.03046 | 98.87% | 460 s |
| RawConvNet (n = 10) | 0.01369 | 99.74% | 0.01429 | 99.60% | 462 s |
| RawConvNet (n = 30) | 0.00827 | 99.91% | 0.00679 | 99.71% | 465 s |
| RawConvNet (n = 80) | 0.00692 | 99.85% | 0.00432 | 99.93% | 462 s |
| RawConvNet (n = 100) | 0.00456 | 99.97% | 0.00785 | 99.74% | 505 s |
Table 4.
Contribution of Custom Layer. RawConvNet is compared with ConvNets 1, 2, and 3 after 100 epochs of training with a 70–30 train/test split of the BUZZ1 train/test dataset. The receptive field size n is set to 80 for all ConvNets.
Table 4.
Contribution of Custom Layer. RawConvNet is compared with ConvNets 1, 2, and 3 after 100 epochs of training with a 70–30 train/test split of the BUZZ1 train/test dataset. The receptive field size n is set to 80 for all ConvNets.
| Training Samples: 6377, Testing Samples: 2733 |
|---|
| Model Name | Training Loss | Training Accuracy | Testing Loss | Testing Accuracy | Runtime per Epoch |
|---|
| RawConvNet | 0.00692 | 99.85% | 0.00432 | 99.93% | 462 s |
| ConvNet 1 | 0.55387 | 99.77% | 0.57427 | 97.59% | 545 s |
| ConvNet 2 | 0.67686 | 68.07% | 0.59022 | 98.21% | 532 s |
| ConvNet 3 | 0.68694 | 66.81% | 0.59429 | 98.02% | 610 s |
Table 5.
Classification accuracy of M1 (Logistic Regression) on BUZZ1 train/test dataset.
Table 5.
Classification accuracy of M1 (Logistic Regression) on BUZZ1 train/test dataset.
| Test No. | Test Type | Scaling Type | Testing Accuracy |
|---|
| 1 | train/test | none (S1) | 99.83% |
| 2 | train/test | standard (S2) | 99.86% |
| 3 | train/test | min max (S3) | 99.34% |
| 4 | train/test | L1 (S4) | 90.64% |
| 5 | train/test | L2 (S5) | 93.11% |
| 6 | k-fold, k = 10 | none (S1) | 99.91% |
| 7 | k-fold, k = 10 | standard (S2) | 99.89% |
| 8 | k-fold, k = 10 | min max (S3) | 99.63% |
| 9 | k-fold, k = 10 | L1 (S4) | 92.34% |
| 10 | k-fold, k = 10 | L2 (S5) | 93.77% |
Table 6.
Confusion matrix for M1 (Logistic Regression) with train/test and no scaling (S1) on BUZZ1 train/test dataset with 60-40 train/test split.
Table 6.
Confusion matrix for M1 (Logistic Regression) with train/test and no scaling (S1) on BUZZ1 train/test dataset with 60-40 train/test split.
| True | Predicted |
|---|
| Bee | Noise | Cricket | Total | Testing Accuracy |
|---|
| Bee | 1174 | 4 | 0 | 1178 | 99.66% |
| Noise | 2 | 1243 | 0 | 1245 | 99.83% |
| Cricket | 0 | 0 | 1221 | 1221 | 100% |
| Total Accuracy | | 99.00% |
Table 7.
Confusion matrix for M1 (Logistic Regression) with train/test and L2 scaling (S5) on BUZZ1 train/test dataset with 60-40 train/test split.
Table 7.
Confusion matrix for M1 (Logistic Regression) with train/test and L2 scaling (S5) on BUZZ1 train/test dataset with 60-40 train/test split.
| True | Predicted |
|---|
| Bee | Noise | Cricket | Total | Testing Accuracy |
|---|
| Bee | 1176 | 2 | 0 | 1178 | 99.83% |
| Noise | 57 | 1038 | 150 | 1245 | 83.37% |
| Cricket | 41 | 1 | 1179 | 1221 | 96.56% |
| Total Accuracy | | 93.00% |
Table 8.
Classification accuracy for M2 KNN on BUZZ1 train/test dataset. The accuracy is the mean accuracy computed over n ∈ [1, 25], where n is the number of nearest neighbors.
Table 8.
Classification accuracy for M2 KNN on BUZZ1 train/test dataset. The accuracy is the mean accuracy computed over n ∈ [1, 25], where n is the number of nearest neighbors.
| Test No. | Testing Type | Scaling Type | Testing Accuracy |
|---|
| 1 | train/test | none (S1) | 99.86% |
| 2 | train/test | standard (S2) | 99.87% |
| 3 | train/test | min max (S3) | 99.91% |
| 4 | train/test | L1 (S4) | 99.84% |
| 5 | train/test | L2 (S5) | 99.89% |
| 6 | k-fold, k = 10 | none (S1) | 99.93% |
| 7 | k-fold, k = 10 | standard (S2) | 99.94% |
| 8 | k-fold, k = 10 | min max (S3) | 99.96% |
| 9 | k-fold, k = 10 | L1 (S4) | 99.95% |
| 10 | k-fold, k = 10 | L2 (S5) | 99.96% |
Table 9.
Classification accuracy for M3 SVM OVR on BUZZ1 train/test dataset.
Table 9.
Classification accuracy for M3 SVM OVR on BUZZ1 train/test dataset.
| Test No. | Testing Type | Scaling Type | Testing Accuracy |
|---|
| 1 | train/test | none (S1) | 99.83% |
| 2 | train/test | standard (S2) | 99.91% |
| 3 | train/test | min max (S3) | 99.86% |
| 4 | train/test | L1 (S4) | 91.19% |
| 5 | train/test | L2 (S5) | 93.08% |
| 6 | k-fold, k = 10 | none (S1) | 99.89% |
| 7 | k-fold, k = 10 | standard (S2) | 99.78% |
| 8 | k-fold, k = 10 | min max (S3) | 99.67% |
| 9 | k-fold, k = 10 | L1 (S4) | 92.20% |
| 10 | k-fold, k = 10 | L2 (S5) | 95.06% |
Table 10.
Classification accuracy for M4 (Random Forests) on BUZZ1 train/test dataset.
Table 10.
Classification accuracy for M4 (Random Forests) on BUZZ1 train/test dataset.
| Test No. | Testing Type | Scaling Type | Testing Accuracy |
|---|
| 1 | train/test | none | 99.97% |
| 2 | k-fold, k = 10 | none | 99.94% |
Table 11.
Confusion matrix for RawConvNet with receptive field size n = 80 on BUZZ1 validation dataset.
Table 11.
Confusion matrix for RawConvNet with receptive field size n = 80 on BUZZ1 validation dataset.
| True | Predicted |
|---|
| Bee | Noise | Cricket | Total | Validation Accuracy |
|---|
| Bee | 300 | 0 | 0 | 300 | 100% |
| Noise | 7 | 343 | 0 | 350 | 97.71% |
| Cricket | 0 | 48 | 452 | 500 | 90.04% |
| Total Accuracy | | 95.21% |
Table 12.
Confusion matrix for M1 (logistic regression) on BUZZ1 validation dataset.
Table 12.
Confusion matrix for M1 (logistic regression) on BUZZ1 validation dataset.
| True | Predicted |
|---|
| Bee | Noise | Cricket | Total | Validation Accuracy |
|---|
| Bee | 299 | 1 | 0 | 300 | 99.66% |
| Noise | 41 | 309 | 0 | 350 | 95.42% |
| Cricket | 1 | 19 | 480 | 500 | 96.00% |
| Total Accuracy | | 94.60% |
Table 13.
Performance summary for DL and ML models on BUZZ1 validation dataset.
Table 13.
Performance summary for DL and ML models on BUZZ1 validation dataset.
| Model | Validation Accuracy |
|---|
| RawConvNet (n = 80) | 95.21% |
| ConvNet 1 (n = 80) | 74.00% |
| ConvNet 2 (n = 80) | 78.08% |
| ConvNet 3 (n = 80) | 75.04% |
| Logistic regression | 94.60% |
| Random forests | 93.21% |
| KNN (n = 5) | 85.47% |
| SVM OVR | 83.91% |
Table 14.
Raw audio ConvNets on BUZZ2 train/test dataset.
Table 14.
Raw audio ConvNets on BUZZ2 train/test dataset.
| Training Samples: 7582, Testing Samples: 2332 |
|---|
| Model Name | Training Loss | Training Accuracy | Testing Loss | Testing Accuracy |
|---|
| RawConvNet | 0.00348 | 99.98% | 0.14259 | 95.67% |
| ConvNet 1 | 0.47997 | 99.99% | 0.55976 | 94.85% |
| ConvNet 2 | 0.64610 | 69.11% | 0.57461 | 95.50% |
| ConvNet 3 | 0.65013 | 69.62% | 0.58836 | 94.64% |
Table 15.
Confusion matrix for logistic regression on BUZZ2 testing dataset.
Table 15.
Confusion matrix for logistic regression on BUZZ2 testing dataset.
| True | Predicted |
|---|
| Bee | Noise | Cricket | Total | Testing Accuracy |
|---|
| Bee | 673 | 221 | 0 | 898 | 74.94% |
| Noise | 2 | 932 | 0 | 934 | 99.78% |
| Cricket | 0 | 26 | 474 | 500 | 94.80% |
| Total Accuracy | | 89.15% |
Table 16.
Confusion matrix for KNN (n = 5) on BUZZ2 testing dataset.
Table 16.
Confusion matrix for KNN (n = 5) on BUZZ2 testing dataset.
| True | Predicted |
|---|
| Bee | Noise | Cricket | Total | Testing Accuracy |
|---|
| Bee | 895 | 3 | 0 | 898 | 99.66% |
| Noise | 5 | 929 | 0 | 934 | 99.46% |
| Cricket | 0 | 26 | 474 | 500 | 94.80% |
| Total Accuracy | | 98.54% |
Table 17.
Confusion matrix for SVM OVR on BUZZ2 testing dataset.
Table 17.
Confusion matrix for SVM OVR on BUZZ2 testing dataset.
| True | Predicted |
|---|
| Bee | Noise | Cricket | Total | Testing Accuracy |
|---|
| Bee | 623 | 275 | 0 | 898 | 69.37% |
| Noise | 9 | 925 | 0 | 934 | 99.03% |
| Cricket | 20 | 132 | 348 | 500 | 69.60% |
| Total Accuracy | | 81.30% |
Table 18.
Confusion matrix for random forests on BUZZ2 testing dataset.
Table 18.
Confusion matrix for random forests on BUZZ2 testing dataset.
| True | Predicted |
|---|
| Bee | Noise | Cricket | Total | Testing Accuracy |
|---|
| Bee | 892 | 6 | 0 | 898 | 99.33% |
| Noise | 3 | 931 | 0 | 934 | 99.67% |
| Cricket | 0 | 70 | 430 | 500 | 86.00% |
| Total Accuracy | | 96.61% |
Table 19.
Performance summary of raw audio ConvNets and ML models on BUZZ2 validation dataset.
Table 19.
Performance summary of raw audio ConvNets and ML models on BUZZ2 validation dataset.
| Model | Validation Accuracy |
|---|
| RawConvNet (n = 80) | 96.53% |
| ConvNet 1 (n = 80) | 82.96% |
| ConvNet 2 (n = 80) | 83.53% |
| ConvNet 3 (n = 80) | 83.40% |
| Logistic regression | 68.53% |
| Random forests | 65.80% |
| KNN (n = 5) | 37.42% |
| SVM OVR | 56.60% |
Table 20.
Confusion matrix for RawConvNet with receptive field n = 80 on BUZZ2 validation dataset.
Table 20.
Confusion matrix for RawConvNet with receptive field n = 80 on BUZZ2 validation dataset.
| True | Predicted |
|---|
| Bee | Noise | Cricket | Total | Validation Accuracy |
|---|
| Bee | 969 | 31 | 0 | 1000 | 96.9% |
| Noise | 6 | 994 | 0 | 1000 | 99.4% |
| Cricket | 0 | 67 | 933 | 1000 | 94.8% |
| Total Accuracy | | 96.53% |
Table 21.
Confusion matrix for logistic regression on BUZZ2 validation dataset.
Table 21.
Confusion matrix for logistic regression on BUZZ2 validation dataset.
| True | Predicted |
|---|
| Bee | Noise | Cricket | Total | Validation Accuracy |
|---|
| Bee | 515 | 485 | 0 | 1000 | 51.50% |
| Noise | 405 | 594 | 1 | 1000 | 59.40% |
| Cricket | 0 | 53 | 947 | 1000 | 94.70% |
| Total Accuracy | | 68.53% |
Table 22.
Confusion matrix for SpectConvNet on BUZZ2 validation dataset.
Table 22.
Confusion matrix for SpectConvNet on BUZZ2 validation dataset.
| True | Predicted |
|---|
| Bee | Noise | Cricket | Total | Validation Accuracy |
|---|
| Bee | 544 | 445 | 1 | 1000 | 55.40% |
| Noise | 182 | 818 | 0 | 1000 | 81.80% |
| Cricket | 0 | 42 | 958 | 1000 | 95.80% |
| Total Accuracy | | 77.33% |
Table 23.
Summary of validation accuracies on BUZZ1 and BUZZ2 validation datasets.
Table 23.
Summary of validation accuracies on BUZZ1 and BUZZ2 validation datasets.
| Model | BUZZ1 | BUZZ2 |
|---|
| RawConvNet (n = 80) | 95.21% | 96.53% |
| ConvNet 1 (n = 80) | 74.00% | 82.96% |
| ConvNet 2 (n = 80) | 78.08% | 83.53% |
| ConvNet 3 (n = 80) | 75.04% | 83.40% |
| Logistic regression | 94.60% | 68.53% |
| Random forests | 93.21% | 65.80% |
| KNN (n = 5) | 85.47% | 37.42% |
| SVM OVR | 83.91% | 56.60% |
Table 24.
Classification accuracy summary on BUZZ1 validation dataset by category.
Table 24.
Classification accuracy summary on BUZZ1 validation dataset by category.
| Method vs. Category | Bee | Cricket | Noise |
|---|
| RawConvNet (n = 80) | 100% | 90.04% | 97.71% |
| ConvNet 1 (n = 80) | 99% | 90.08% | 28.57% |
| ConvNet 2 (n = 80) | 99% | 87.8% | 46.28% |
| ConvNet 3 (n = 80) | 100% | 88% | 35.14% |
| Logistic regression | 99.66% | 96% | 95.42% |
| KNN (n = 5) | 100% | 93.8% | 61.14% |
| SVM OVR | 100% | 73.8% | 84.57% |
| Random forests | 100% | 87.6% | 95.42% |
Table 25.
Classification accuracy summary on BUZZ2 validation dataset by category.
Table 25.
Classification accuracy summary on BUZZ2 validation dataset by category.
| Method vs. Category | Bee | Cricket | Noise |
|---|
| RawConvNet (n = 80) | 96.90% | 94.80% | 99.40% |
| ConvNet 1 (n = 80) | 86.50% | 95.70% | 66.70% |
| ConvNet 2 (n = 80) | 76.60% | 96.40% | 77.60% |
| ConvNet 3 (n = 80) | 86.40% | 96.40% | 67.40% |
| Logistic regression | 51.50% | 94.70% | 59.40% |
| KNN (n = 5) | 19.40% | 90.80% | 87.20% |
| SVM OVR | 51.80% | 11.10% | 49.40% |
| Random forests | 29.20% | 48.80% | 79.80% |