Abstract
One of the major concerns in photoacoustic computed tomography (PACT) is obtaining a high-quality image using the minimum number of ultrasound transducers/view angles. This issue is of importance when a cost-effective PACT system is needed. On the other hand, analytical reconstruction algorithms such as back projection (BP) and time reversal, when a limited number of view angles is used, cause artifacts in the reconstructed image. Iterative algorithms provide a higher image quality, compared to BP, due to a model used for image reconstruction. The performance of the model can be further improved using the sparsity concept. In this paper, we propose using a novel sparse dictionary to capture important features of the photoacoustic signal and eliminate the artifacts while few transducers is used. Our dictionary is an optimum combination of Wavelet Transform (WT), Discrete Cosine Transform (DCT), and Total Variation (TV). We utilize two quality assessment metrics including peak signal-to-noise ratio and edge preservation index to quantitatively evaluate the reconstructed images. The results show that the proposed method can generate high-quality images having fewer artifacts and preserved edges, when fewer view angles are used for reconstruction in PACT.
1. Introduction
In a photoacoustic computed tomography (PACT) configuration, the ultrasonic waves are collected using ultrasonic transducers placed all around the tissue. The waves are then processed through a reconstruction algorithm, and an image is generated [1,2,3,4]. The number of transducers/view angles in PACT is directly proportional to the quality of the reconstructed image. In the past several years, researchers in the field of PACT have focused on two main topics: the design of the imaging system and image reconstruction algorithms [5,6,7,8,9]. In the case of system design, most of the attention has been on the arrangement of the transducers. The simplest proposed configuration has been using a single transducer swiping around the targeted object, and a more complicated one is to use a transducer array that covers either 360 degrees around the object (ring shape) or some parts of it. The type of transducers used in the configuration of PACT can be spherical, cylindrical, or flat [10,11,12,13]. The expansion of this concept is beyond the scope of this study. The literature cited here is a limited amount of PACT work. For a more complete list, please read [14]. Readers are referred to Figure 1 of [15] and Figure 11 of [16] for further explanation of PACT imaging systems.
Several reconstruction algorithms have been designed for PACT, where a circular or linear array has been used for data acquisition [17,18,19]. Back-Projection (BP) and its derivations e.g., filtered back projection (FBP), could be considered as the most eminent PACT reconstruction algorithm due to their simple implementation [20]. They use the fact that pressures propagating from an acoustic source reach the detectors at different time delays, which depends on the speed of sound, as well as the distance between the source and the detectors [6,8,21].
The requirement in the BP algorithm is to input a large number of signals collected from different view angles. As mentioned, for a circular detection, the signals can be collected either using a single transducer rotating around the object or a ring shape transducer array. Such systems are either too expensive (due to the transducer ring array) or have a poor temporal resolution (due to using single transducer). To address theses problems, iterative image reconstruction algorithms (known as model-based algorithms too) can be used where there is a model used for the reconstruction [22]. In other words, iterative algorithms build up a model to describe the relationship between the detected photoacoustic (PA) signals and the optical absorption distribution and iteratively reduce the artifacts [23,24,25].
One of the concepts which can be combined with the model-based algorithms is compressed sensing (CS) and sparsity [26]. Over the past few years, it has been shown that using sparsity with model-based image reconstruction algorithms can mitigate the artifacts caused by the limited view angles and improve the quality of the reconstructed PA images [24,27,28,29]. Donoho et al. proposed the CS theory in 2006, for the first time, which is based on a prior knowledge of unknowns [30]. This method can be used in data acquisition procedure of PACT [31], which leads to information reconstruction based on the convex optimization from some observations that seem highly incomplete [28]. This concept has been used in the reconstruction of magnetic resonance imaging (MRI) and Computed Tomography (CT)-MRI in order to reduce the scan time and have an inherent registration in space and time [32]. In addition, CS has been used for thermoacoustic imaging (TAI) [33].
Provost and Lesage [28] have used CS for PACT image reconstruction, where due to the advantages of sparse characteristic of a sample, fewer projections were used to reconstruct the optical absorption distribution map of the tissue [34]. Signal sparsification can be done in two different ways: (i) applying a dictionary learning and (ii) using standard transform functions. Even though dictionary learning-based methods outperform the standard transform functions, in order to make the signal sparser, they impose a higher complexity for reconstruction [35,36]. On the other hand, standard transform functions can simply translate the signal to a sparse shape. The Wavelet Transform (WT), Discrete Cosine Transform (DCT), and Total Variation (TV) are some of the popular sparsifying transforms. Such transformations result different sparse representations of the original signal. Similar to compression algorithms, the combination of the original signal in different transformation domains, can provide an image with an improved quality.
In this paper, we introduce a novel dictionary for sparse representation of PA signals in order to improve the quality of the reconstructed PA image. The proposed method consists of three sparsifying transformation functions: WT, DCT, and TV. Using the proposed method, users are able to highlight information provided by each of the functions. We compared the performance of the proposed algorithm with the performance of BP and sparse reconstruction based on different methods when the same number of view angles is used. We use two established quality assessment metrics—peak signal-to-noise ratio (PSNR) and edge preservation index (EPI)—for quantitative evaluation of the results. Quantitative and qualitative results indicate that the proposed method can be a proper option when we face a limited number of angle views.
2. Methods
2.1. Analytical Reconstruction
In a PACT system, after laser excitation, acoustic waves are generated. The waves are collected by ultrasonic transducers all around the imaging target, stored in a computer by a data acquisition (DAQ) card, and processed in a reconstruction algorithm. The acoustic wave generation is based on thermoelastic expansion effect. Based on the principle of acoustic theories, in a homogeneous medium, the pressure at position r and time t, , follows the thermoacoustic equation shown in Equation (1). In this equation, the initial pressure, , is generated by a short pulse, which can be mathematically considered as a delta function ((t)) [20].
where c indicates the speed of sound. The pressure at , generated from the initial pressure at , is given in Equation (2), known as the Forward Problem.
In PACT, we look for initial pressure () calculation using the pressure measured at different view angles/times (). To this end, Equation (3), known as the Backward Problem, would be used [27].
where , and denotes the weight that must be allocated to the detected pressures by transducers [27]. A favorite reconstruction algorithm for the PACT system could be the one that generates a high-quality image with fewer number of view angles. Analytical algorithms such as BP and TV-based have an inherent limitation (necessity of a large number of view angles around the target object) for accurate estimation of the optical absorption. In other words, such algorithms cause artifacts in the reconstructed images when a limited number of view angles is available in the PACT system. One solution to address this problem is a model-based algorithm in which artifacts and noise are iteratively degraded using a model. It should be noted that reconstruction algorithms are mostly simplified, and the effects of transducer size, imaging noise, and directivity of sensors are not considered in the reconstruction procedure. All these assumptions lead to negative effects called artifacts in this paper.
2.2. The Proposed Method
We model the procedure of PACT using , where A is the measurement matrix, and x is the assumed phantom in the forward problem and the reconstructed image in the backward problem. b is the detected signals by the ultrasound transducers. When the number of unknowns (number of pixels of the PA image) is greater than the number of equations (number of recorded samples), which usually happens in PACT, especially when a low number of view angles is used for decreasing the data acquisition time, we have an underdetermined system. In this case, there is no exact solution.
One commonly used method to solve an underdetermined problem is the least square technique, giving . The least square method uses the error minimization to obtain a solution, but the answer is not the best and the most accurate one that can be obtained. The sparse component analysis and sparse representation of signals can be used to solve the underdetermined problem of the PA image reconstruction. Having a prior knowledge, we can promote sparsity using , , and () norms to obtain a more accurate solution [30]. In other words, we can improve the image quality by assuming that the imaging target is sparse.
Targets in PA imaging are composed of many singularities. A singularity is the point of an exceptional set where it fails to be well-behaved in differentiability. These singularities can be considered as non-zero values of x. Such an assumption in the procedure of the backward problem leads to a more accurate solution in comparison with algorithms that use error minimization. The representation of the backward problem is given in Equation (4).
where is the prior knowledge function that is used to promote sparsity. The basis pursuit method uses the -norm to sparsify the problem and transfers it into a linear or quadratic equation (see Equation (5)).
where is the scalar regularization parameter, and and indicate the -norm and -norm, respectively. The first and second terms of Equation (5) represent the error of estimation and level of sparsity of estimated x, respectively. An effective sparsity method should represent all of the most important features of the PA images. Considering the diagnostically relevant features in a PA image, significant features can be edges, singular points, and homogenous texture.
A standard transform function can be used for signal sparsification. A single transformation, however, can well represent only one of the major features. In order to obtain an image having all these features, we propose combining some of the well-known standard transform functions. Although WT’s magnitude will not oscillate around singularities, and it uses continuous transform to characterize the oscillations and discontinuities, the images generated by WT are blurred. DCT helps separate the image into spectral sub-bands of differing importance. In addition, it preserves homogeneous textures better than WT. However, it provides some blocking artifacts in the image. The blocking artifact is a distortion that appears as abnormally large pixel blocks. Therefore, WT and DCT cannot capture two-dimensional singularities, i.e., curves and edges in an image. On the other hand, the TV is an operator that works based on the local variations in a signal. It well preserves the edges in the image. However, the artifacts in the initial image introduced by limited view angles significantly affect the performance of TV [37]. As illustrated, all the three mentioned transformation functions have some benefits and disadvantages. We therefore propose to optimally use the combination of basis functions of WT, DCT, and TV, where WT captures point-like features, DCT captures homogeneous texture components, and TV sharpens the edges and reduces other artifacts without eliminating essential information of the image. In this way, due to the properties of the imaging target, which directly affect the PA reconstructed image generated in the first attempt, the reconstruction procedure is updated, moving toward a high image quality. The procedure of the proposed method can be seen in Figure 1.
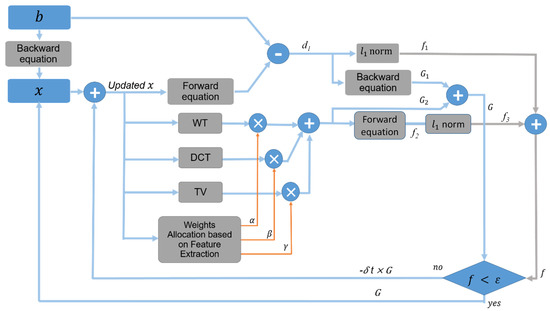
Figure 1.
Block diagram of the proposed method. All the italic letters have been described in the text.
The signal (b) can be decomposed to three sub-signals (, , and ), each emphasizing a feature in the image, utilizing the morphological component analyses (MCA). Having three sub-signal and three sparse representation methods, MCA assumes that, for each sub-signal, there is a corresponding sparse representation which makes the sub-signal sparser than others. The proposed method is described in Equations (6) and (7), which are the expansion of Equation (5) for the MCA concept.
where x is an initial image, obtained from BP algorithm, and and are WT and DCT transform operators, respectively. D is the gradient operator. , , and are the weight factors for WT, DCT, and TV transform operators, respectively. It should be noted that, in each basis, the emphasis is on one major feature and other features are less signified. These features are preserved as shown in Equation (6).
Paradigm of the Proposed Method
The proposed reconstruction method, demonstrated in Figure 1, is an iterative algorithm with the raw data acquired by transducer/s as the input and the reconstructed image as the output. The principle of the algorithm is as follows. First, we reconstruct an image (x) using the traditional BP method (considered as the initial image). The image reconstructed by the BP algorithm and the signal used within the BP algorithm (for reconstruction) are considered as the input of the proposed method. Here, b indicates the raw data, detected by the US transducer/s. Using the forward problem, shown in Equation (2), and the initial image (x), we calculate the raw data that could be used to obtain the initial image x. It should be noted that the initial image is obtained by the recorded signals using US transducer/s, but using the forward equation presented in Figure 1, we calculate the signal which could be as the initial signal, ignoring the recorded data. As the next step, we differentiate the recorded signals by the calculated signals. The result of differentiation is called . By applying -norm to , is generated. The indicates the power of the error signal. In addition, we calculate an error image, , from the error signal by applying the backward problem illustrated in Equation (3). Simultaneously, the system applies the proposed combinational sparsifying method on x to obtain an image. This image is called , as shown in Figure 1. At this step, the signals that could be used for generation of is calculated using the forward problem, called . By applying -norm to , is generated as the power of . Therefore, summation of and (i.e., f ) is a parameter that shows the difference between the real image and what we have estimated. If f does not meet the desired margin error, x should be updated. The updating process can be done by subtracting a portion of G from x, i.e., , iteration step.
Big step accelerates the speed of the program and reduces the execution time, but it may increase the error and lead to an unstable loop. If f meets the desired margin error, the last updated x would be the final image at this first step. The number of the steps is selected based on the trade-off between the execution time and the performance of the final reconstructed image. In our algorithm, we set the number of steps to 50. By allocating appropriate weights to each basis function, coefficients corresponding to dominant features will receive higher gain and those corresponding to less critical features will receive a lower gain.
It should be noted that the weighting factors are determined based on what diagnostically relevant features need to be emphasized in the image, i.e., edges, singular points, and homogeneous textures. A statistical texture analysis method, the Gray-Level Co-Occurrence Matrix (GLCM) technique, has been used to measure the homogeneous texture components [38]. GLCM is used in 0, 45, 90, and 135 degree directions. Singular points are small local areas that the signal values in these areas are changed in two dimensions. The Harris operator, by providing an analytical autocorrelation, considering the local intensity changes in different directions, has been used to detect singular points [39]. We used the canny filter, a first-order image edge detector, to determine the weighting factor TV (which signifies the edges). It should be noted that the main justification for the proposed method is to utilize the advantages of the overlapping methods to improve the image quality in limited view PACT systems. As mentioned, using only one sparsifying function leads to information loss. By combining the three basis, all the information loss in one of them can be mitigated using another one, leading to a higher image quality, compared to using any one of them.
3. Results
To evaluate the performance of the reconstruction algorithms, we made a gel phantom with imaging target inside. The phantom was made by 3% Agar powder in water. Eight straight graphite pencil leads with a 0.5 mm diameter were placed co-centered in the same plane embedded in the gel. The size of the phantom was 30 × 30 mm (Figure 2b). The phantom was imaged using a single-transducer PACT system (Figure 2a). A Quanta-Ray PRO-Series Nd:YAG laser (Spectra-Physics Inc., Santa Clara, CA, USA) pumped a VersaScan V1.7 optical parametric oscillator (OPO) (Spectra-Physics Inc., USA), generating wavelengths in the range of 398–708 nm, with a pulse width of 7 ns and a repetition rate of 30 Hz. In this experiment, the illumination wavelength was 532 nm. A large graded index plastic optical fiber with a diameter of 10 mm and a numerical aperture of 0.55 was used on the top of the ring, 5 cm away from the sample, forming an uniform illumination. A cylindrically focused ultrasound transducer, V326-SU (Olympus Inc., Center Valley, PA, USA) with the element size of 0.375 inch, central frequency of 5 MHz and the focal length of 0.625 inch was positioned on a cylindrical construct. The position of the transducer was in the same plane as the pencil leads were. The diameter of the construct was 75 mm. The cylinder was rotated using a stepper motor (Applied Motion Products Inc., Watsonville, CA, USA) with a driver controlled by LabVIEW. The transducer was smoothly rotated around the phantom with the speed of 0.0125 round/s to collect the PA signal in 360 degrees. The data acquisition is performed using our FPGA based National Instrument (NI) system. Specification of the experiment is presented in Table 1. A photograph of the PAI system is shown in Figure 3. The system was placed on a 12 ft × 4 ft optical table (New Port, Inc., Irvine, CA, USA).

Figure 2.
(a) Schematic of our PACT system; (b) gel phantom with eight 0.5 mm pencil leads.

Table 1.
Specification of the experimental setup presented in Figure 2.

Figure 3.
Low-cost photoacoustic computed tomography (LC-PACT) system diagram comprised of an Nd:YAG 30Hz Spectra Physics laser, an optical parametric oscillator (OPO), a circular ring, a DC supply for the motor driver, an NI DAQ, an NI trigger, a servo motor, a motor gear, a three-axis translation stage for phantom, and a transducer-amplifier unit.
For image reconstruction, we used a laptop with i7 core, 2.3 GHz CPU, and 8 GB Memory. Figure 4 demonstrates a set of results of different reconstruction algorithms on the phantom data acquired by our PACT system. They are C-scan images with their dimensions annotated in the right image. The reconstructed images with BP and CS with different sparsifying methods for different numbers of views (30, 60, 90, and 120) have been presented. As seen in the first column, BP generates images with a high level of artifacts and imaging noise. Even though increasing the number of angles improves the image quality with lower imaging noise and reconstruction artifacts, the images are still affected. The CS-based WT removes a considerable amount of artifacts presented in the BP image (initial image). However, it blurs the edges of the reconstructed image. Even for a low number of angles, the real structure of the imaging target is compromised. It can be seen that adding the TV sparsifying method to the WT sharpens the edges, especially for 90 and 120 angles. While improvement is obtained, it removes the artifacts in the image along with useful information, lowering the accuracy of the reconstructed image. Finally, the proposed method removes the artifacts effectively and more accurately by sharpening the edges while retaining the significant information in the image. It should be noted that, in all the reconstruction implementations, investigated in this study, the media is assumed to be acoustically homogeneous. It should be noted that some algorithms produce more artifacts and decrease the visibility of the details in reconstructed images. The contrast of the image concerned with the proposed method is not changed, but the amount of artifact is, leading to a better visibility.

Figure 4.
Results of reconstruction algorithms on the phantom data acquired from our PACT system. Different rows show different number of views, 30, 60, 90, and 120, and columns show different reconstruction methods, BP, sparse with basis WT, sparse with basis WT+TV, and sparse with the proposed sparsifying method.
The simulation results performed on Shepp–Logan synthetic phantom with 60 view angles confirm the superiority of the proposed method to other reconstruction algorithms (see Figure 5).
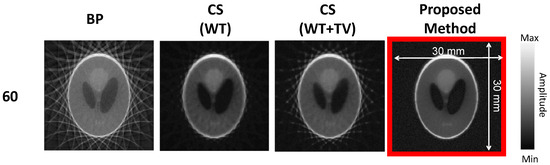
Figure 5.
Results of reconstruction algorithms on the Shepp–Logan synthetic phantom for 60 view angles and different reconstruction algorithms.
For evaluation of the edge preservation capability of the proposed algorithm, we used the edge preservation index (EPI) [40]. This metric indicates the edge preservation capability in horizontal and perpendicular directions, after applying filters such as the Laplacian operator on the image. The EPI values for different methods/angle views are reported in Figure 6a. Each experiment was repeated 10 times. The values of deviation are shown by error bars in this figure. The value of EPI changes from 0 to 1. A higher value suggests a better ability to preserve the edges. Statistical analysis shows that, for a number of view angles lower than 45, the proposed algorithm outperforms other methods. This indicates that, with lower data acquisition time (a lower number of angles), the proposed method provides a higher image quality, compared to other methods. In addition, Figure 6a shows that the proposed method provides better preserved edges for numbers of angles between 80 and 92. The PSNR is calculated for different methods/angle views, and the results are presented in Figure 6b. PSNR is calculated using the formula presented in [23]. To calculate the minimum square error (MSE), the result of sparse reconstruction with WT basis at the maximum possible number of views, i.e., 600, has been considered as the Gold standard image.
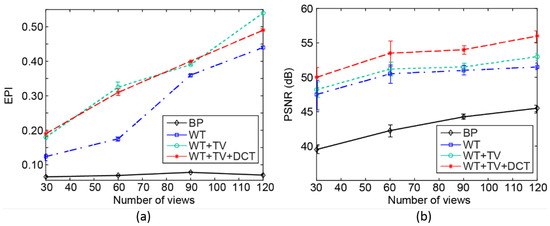
Figure 6.
Quantitative evaluation, (a) EPI and (b) PSNR, of the performance of four reconstruction algorithms with different number of view angles.
From the quantitative assessment of the results presented in Figure 6b, it can be seen that, for all numbers of angles, the proposed method results in a higher PSNR. For instance, for 60 angles, BP, WT, WT+TV, and the proposed method lead to PSNR values of about 42.5 dB, 49.5 dB, 50.5 dB, and 54.2 dB, respectively. In other words, PSNR is improved by about 27%, 9%, and 7%, in comparison to BP, WT, and WT+TV, respectively. Considering all the quantitative evaluation, it can be concluded that our proposed algorithm works effectively with a limited number of view angles, outperforming other algorithms. We performed statistical analysis on the PSNR values using SPSS®. At every view angle, the improvement obtained by the proposed method compared to other aforementioned methods was statistically significant (p-value < 0.001).
Table 2 shows the execution time for BP, sparse reconstruction with basis WT, sparse reconstruction with bases WT+TV, and the proposed reconstruction algorithms. The proposed method provides a higher image quality at the expense of a higher processing time, compared to other algorithms. The higher processing time of the proposed algorithm is due to the fact that it should use all the information of the three used sparsifying functions in order to reconstruct a photoacoustic image with a higher image quality. In addition, the feature measurement of the proposed algorithm increases the processing time as well.

Table 2.
Execution time for different reconstruction algorithms with 120 view angles.
4. Conclusions
In this paper, we propose a novel dictionary-based image reconstruction algorithm in which the desired information of the images is shown more accurately. The proposed method uses a combination of WT, DCT, and TV in order to preserve the necessary information within the reconstruction procedure. The algorithm was evaluated experimentally (using a single-element PACT system). EPI and PSNR were used as the quantitative metrics of evaluation. The qualitative and quantitative results presented here show that the proposed algorithm can generate images with specific emphasis on a desired feature, defined by the user. Quantitative analysis of EPI showed that, for a number of angles lower than 45, the proposed algorithm preserves the edges better than other methods. In addition, the calculated PSNR at 60 angles indicated that the proposed method improves PSNR by about 27%, 9%, and 7%, compared with BP, WT, and WT+TV, respectively. At every view angle, the improvement obtained by the proposed method compared to the above-mentioned methods was statistically significant (p-value < 0.001). The proposed technique is particularly useful when a low-cost PACT system (limited number of view angles) with a fine temporal resolution is required. However, all the improvements are obtained at the expense of a higher computational burden. As a feature work, we will evaluate the proposed method in an in vivo study. Accelerating the algorithm as well as reducing its computational complexity is the next major step.
Author Contributions
Conceptualization, P.O. and M.M.; Methodology, P.O., M.M. and A.H.; Software, P.O., A.H., M.Z., M.M. and X.H.; Validation, P.O., M.M., A.H., M.Z. and X.H.; Formal Analysis, P.O., A.H., M.M., X.H.; Investigation, P.O., M.M.; Resources, P.O., M.M., A.H., M.Z. and X.H.; Data Curation, P.O., A.H., M.Z. and X.H.; Writing—Original Draft Preparation, P.O., M.M., A.H., M.Z. and X.H.; Writing—Review & Editing, P.O., M.M., M.N., M.O.; Visualization, M.N. and M.O.; Supervision, M.N. and M.O.; Project Administration, M.N.; Funding Acquisition, M.N.
Funding
This project has been partially supported by a WSU startup fund and the Andersen Institute fund.
Acknowledgments
We thank Jun Xia from Buffalo University for his constructive discussion and help in image reconstruction.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| PACT | Photoacoustic Computed Tomography |
| BP | Back Projection |
| WT | Wavelet Transform |
| DCT | Discrete Cosine Transform |
| TV | Total Variation |
| EPI | Edge Preservation Index |
| PSNR | Peak Signal-to-Noise Ratio |
| FBP | Filtered Back Projection |
| PA | Photoacoustic |
| CS | Compressed Sensing |
| MRI | Magnetic Resonance Imaging |
| TAI | Theracoustic Imaging |
| DAQ | Data Acquisition |
| MCA | Morphological Component Analysis |
| GLCM | Gray-Level Co-occurrence Matrix |
| OPO | Optical Parametric Oscillator |
| NI | National Instrument |
| MSE | Minimum Square Error |
References
- Xu, M.; Wang, L.V. Photoacoustic imaging in biomedicine. Rev. Sci. Instrum. 2006, 77, 041101. [Google Scholar] [CrossRef]
- Nasiriavanaki, M.; Xia, J.; Wan, H.; Bauer, A.Q.; Culver, J.P.; Wang, L.V. High-resolution photoacoustic tomography of resting-state functional connectivity in the mouse brain. Proc. Natl. Acad. Sci. USA 2014, 111, 21–26. [Google Scholar] [CrossRef] [PubMed]
- Jeon, M.; Song, W.; Huynh, E.; Kim, J.; Kim, J.; Helfield, B.L.; Leung, B.Y.; Geortz, D.E.; Zheng, G.; Oh, J.; et al. Methylene blue microbubbles as a model dual-modality contrast agent for ultrasound and activatable photoacoustic imaging. J. Biomed. Opt. 2014, 19, 016005. [Google Scholar] [CrossRef] [PubMed]
- Mohammadi-Nejad, A.R.; Mahmoudzadeh, M.; Hassanpour, M.S.; Wallois, F.; Muzik, O.; Papadelis, C.; Hansen, A.; Soltanian-Zadeh, H.; Gelovani, J.; Nasiriavanaki, M. Neonatal brain resting-state functional connectivity imaging modalities. Photoacoustics 2018, 10, 1–19. [Google Scholar] [CrossRef] [PubMed]
- Mahmoodkalayeh, S.; Lu, X.; Ansari, M.A.; Li, H.; Nasiriavanaki, M. Optimization of light illumination for photoacoustic computed tomography of human infant brain. In Proceedings of the Photons Plus Ultrasound: Imaging and Sensing 2018, International Society for Optics and Photonics, San Francisco, CA, USA, 27 January–1 February 2018; Volume 10494, p. 104946U. [Google Scholar]
- Mozaffarzadeh, M.; Mahloojifar, A.; Orooji, M.; Kratkiewicz, K.; Adabi, S.; Nasiriavanaki, M. Linear-array photoacoustic imaging using minimum variance-based delay multiply and sum adaptive beamforming algorithm. J. Biomed. Opt. 2018, 23, 026002. [Google Scholar] [CrossRef] [PubMed]
- Hariri, A.; Fatima, A.; Mohammadian, N.; Mahmoodkalayeh, S.; Ansari, M.A.; Bely, N.; Avanaki, M.R. Development of low-cost photoacoustic imaging systems using very low-energy pulsed laser diodes. J. Biomed. Opt. 2017, 22, 075001. [Google Scholar] [CrossRef] [PubMed]
- Mozaffarzadeh, M.; Mahloojifar, A.; Orooji, M.; Adabi, S.; Nasiriavanaki, M. Double-Stage Delay Multiply and Sum Beamforming Algorithm: Application to Linear-Array Photoacoustic Imaging. IEEE Trans. Biomed. Eng. 2018, 65, 31–42. [Google Scholar] [CrossRef] [PubMed]
- Mozaffarzadeh, M.; Mahloojifar, A.; Periyasamy, V.; Pramanik, M.; Orooji, M. Eigenspace-Based Minimum Variance Combined with Delay Multiply and Sum Beamformer: Application to Linear-Array Photoacoustic Imaging. IEEE J. Sel. Top. Quantum Electron. 2019, 25, 1–8. [Google Scholar] [CrossRef]
- Yeh, C.; Li, L.; Zhu, L.; Xia, J.; Li, C.; Chen, W.; Garcia-Uribe, A.; Maslov, K.I.; Wang, L.V. Dry coupling for whole-body small-animal photoacoustic computed tomography. J. Biomed. Opt. 2017, 22, 041017. [Google Scholar] [CrossRef] [PubMed]
- Cho, Y.; Chang, C.C.; Yu, J.; Jeon, M.; Kim, C.; Wang, L.V.; Zou, J. Handheld photoacoustic tomography probe built using optical-fiber parallel acoustic delay lines. J. Biomed. Opt. 2014, 19, 086007. [Google Scholar] [CrossRef] [PubMed]
- Li, G.; Li, L.; Zhu, L.; Xia, J.; Wang, L.V. Multiview Hilbert transformation for full-view photoacoustic computed tomography using a linear array. J. Biomed. Opt. 2015, 20, 066010. [Google Scholar] [CrossRef] [PubMed]
- Zhang, P.; Li, L.; Lin, L.; Hu, P.; Shi, J.; He, Y.; Zhu, L.; Zhou, Y.; Wang, L.V. High-resolution deep functional imaging of the whole mouse brain by photoacoustic computed tomography in vivo. J. Biophotonics 2018, 11, e201700024. [Google Scholar] [CrossRef] [PubMed]
- Jo, J.; Tian, C.; Xu, G.; Sarazin, J.; Schiopu, E.; Gandikota, G.; Wang, X. Photoacoustic tomography for human musculoskeletal imaging and inflammatory arthritis detection. Photoacoustics 2018, in press. [Google Scholar] [CrossRef]
- Lin, L.; Xia, J.; Wong, T.T.; Li, L.; Wang, L.V. In vivo deep brain imaging of rats using oral-cavity illuminated photoacoustic computed tomography. J. Biomed. Opt. 2015, 20, 016019. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Wang, Y. An Efficient Compensation Method for Limited-View Photoacoustic Imaging Reconstruction Based on Gerchberg–Papoulis Extrapolation. Appl. Sci. 2017, 7, 505. [Google Scholar] [CrossRef]
- Li, L.; Zhu, L.; Ma, C.; Lin, L.; Yao, J.; Wang, L.; Maslov, K.; Zhang, R.; Chen, W.; Shi, J.; et al. Single-impulse panoramic photoacoustic computed tomography of small-animal whole-body dynamics at high spatiotemporal resolution. Nat. Biomed. Eng. 2017, 1, 0071. [Google Scholar] [CrossRef] [PubMed]
- Matthews, T.P.; Anastasio, M.A. Joint reconstruction of the initial pressure and speed of sound distributions from combined photoacoustic and ultrasound tomography measurements. Inverse Probl. 2017, 33, 124002. [Google Scholar] [CrossRef] [PubMed]
- Matthews, T.P.; Wang, K.; Li, C.; Duric, N.; Anastasio, M.A. Regularized dual averaging image reconstruction for full-wave ultrasound computed tomography. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2017, 64, 811–825. [Google Scholar] [CrossRef] [PubMed]
- Xu, M.; Wang, L.V. Universal back-projection algorithm for photoacoustic computed tomography. Phys. Rev. E 2005, 71, 016706. [Google Scholar] [CrossRef] [PubMed]
- Egolf, D.M.; Chee, R.K.; Zemp, R.J. Sparsity-based reconstruction for super-resolved limited-view photoacoustic computed tomography deep in a scattering medium. Opt. Lett. 2018, 43, 2221–2224. [Google Scholar] [CrossRef] [PubMed]
- Dean-Ben, X.L.; Buehler, A.; Ntziachristos, V.; Razansky, D. Accurate model-based reconstruction algorithm for three-dimensional optoacoustic tomography. IEEE Trans. Med. Imaging 2012, 31, 1922–1928. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Wang, Y.; Zhang, C. Total variation based gradient descent algorithm for sparse-view photoacoustic image reconstruction. Ultrasonics 2012, 52, 1046–1055. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Wang, Y.; Zhang, C. Efficient discrete cosine transform model–based algorithm for photoacoustic image reconstruction. J. Biomed. Opt. 2013, 18, 066008. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Zhang, Y.; Wang, Y. A photoacoustic image reconstruction method using total variation and nonconvex optimization. Biomed. Eng. Online 2014, 13, 117. [Google Scholar] [CrossRef] [PubMed]
- Mozaffarzadeh, M.; Mahloojifar, A.; Nasiriavanaki, M.; Orooji, M. Model-based photoacoustic image reconstruction using compressed sensing and smoothed L0 norm. In Proceedings of the Photons Plus Ultrasound: Imaging and Sensing 2018, International Society for Optics and Photonics, San Francisco, CA, USA, 27 January–1 February 2018; Volume 10494, p. 104943Z. [Google Scholar]
- Guo, Z.; Li, C.; Song, L.; Wang, L.V. Compressed sensing in photoacoustic tomography in vivo. J. Biomed. Opt. 2010, 15, 021311. [Google Scholar] [CrossRef] [PubMed]
- Provost, J.; Lesage, F. The application of compressed sensing for photo-acoustic tomography. IEEE Trans. Med. Imaging 2009, 28, 585–594. [Google Scholar] [CrossRef] [PubMed]
- Rosenthal, A.; Razansky, D.; Ntziachristos, V. Quantitative optoacoustic signal extraction using sparse signal representation. IEEE Trans. Med. Imaging 2009, 28, 1997–2006. [Google Scholar] [CrossRef] [PubMed]
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Ramirez-Giraldo, J.; Trzasko, J.; Leng, S.; Yu, L.; Manduca, A.; McCollough, C.H. Nonconvex prior image constrained compressed sensing (NCPICCS): Theory and simulations on perfusion CT. Med. Phys. 2011, 38, 2157–2167. [Google Scholar] [CrossRef] [PubMed]
- Xi, Y.; Zhao, J.; Bennett, J.R.; Stacy, M.R.; Sinusas, A.J.; Wang, G. Simultaneous CT-MRI reconstruction for constrained imaging geometries using structural coupling and compressive sensing. IEEE Trans. Biomed. Eng. 2016, 63, 1301–1309. [Google Scholar] [CrossRef] [PubMed]
- Qin, T.; Wang, X.; Qin, Y.; Wan, G.; Witte, R.S.; Xin, H. Quality improvement of thermoacoustic imaging based on compressive sensing. IEEE Antennas Wirel. Propag. Lett. 2015, 14, 1200–1203. [Google Scholar] [CrossRef]
- Meng, J.; Wang, L.V.; Liang, D.; Song, L. In vivo optical-resolution photoacoustic computed tomography with compressed sensing. Opt. Lett. 2012, 37, 4573–4575. [Google Scholar] [CrossRef] [PubMed]
- Liu, Q.; Wang, S.; Ying, L.; Peng, X.; Zhu, Y.; Liang, D. Adaptive dictionary learning in sparse gradient domain for image recovery. IEEE Trans. Image Process. 2013, 22, 4652–4663. [Google Scholar] [CrossRef] [PubMed]
- Zhou, W.; Cai, J.F.; Gao, H. Adaptive tight frame based medical image reconstruction: a proof-of-concept study for computed tomography. Inverse Probl. 2013, 29, 125006. [Google Scholar] [CrossRef]
- Duarte-Carvajalino, J.M.; Sapiro, G. Learning to sense sparse signals: Simultaneous sensing matrix and sparsifying dictionary optimization. IEEE Trans. Image Process. 2009, 18, 1395–1408. [Google Scholar] [CrossRef] [PubMed]
- Haralick, R.M. Statistical and structural approaches to texture. Proc. IEEE 1979, 67, 786–804. [Google Scholar] [CrossRef]
- Harris, C.; Stephens, M. A combined corner and edge detector. In Proceedings of the Alvey Vision Conference, Manchester, UK, 31 August–2 September 1988; Volume 15, pp. 10–5244. [Google Scholar]
- Adabi, S.; Mohebbikarkhoran, H.; Mehregan, D.; Conforto, S.; Nasiriavanaki, M. An intelligent despeckling method for swept source optical coherence tomography images of skin. In Proceedings of the Medical Imaging 2017: Biomedical Applications in Molecular, Structural, and Functional Imaging, International Society for Optics and Photonics, Orlando, FL, USA, 13 March 2017; Volume 10137, p. 101372B. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).