HELL: High-Energy Electrons by Laser Light, a User-Oriented Experimental Platform at ELI Beamlines
Abstract
:1. Introduction
2. The Experimental Platform HELL: High-Energy Electrons by Laser Light
2.1. The 10 Hz, 1 PW Laser Driver “L3”
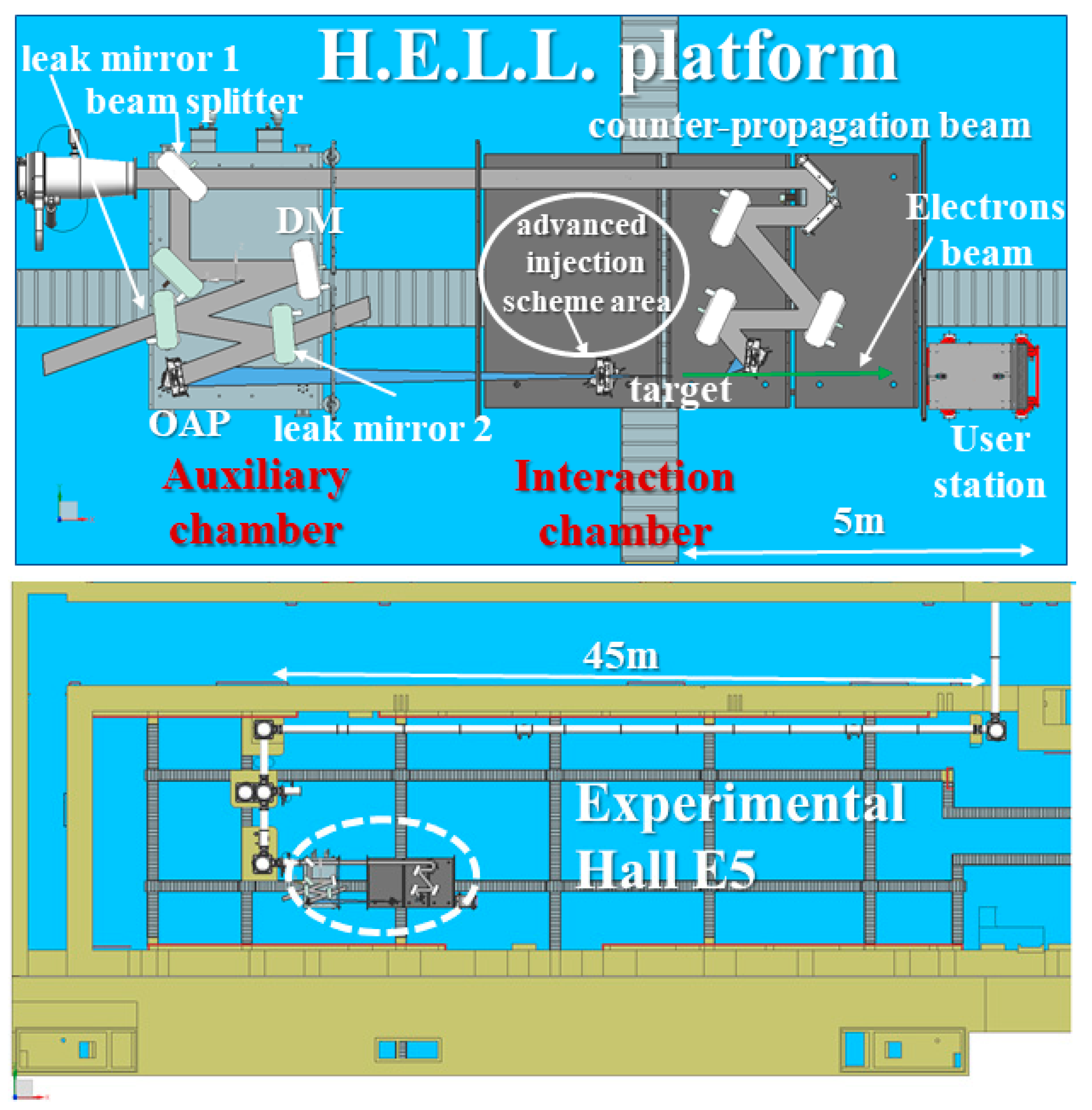
2.2. The HELL Platform
2.3. Diagnostics for the Driver Laser Pulse
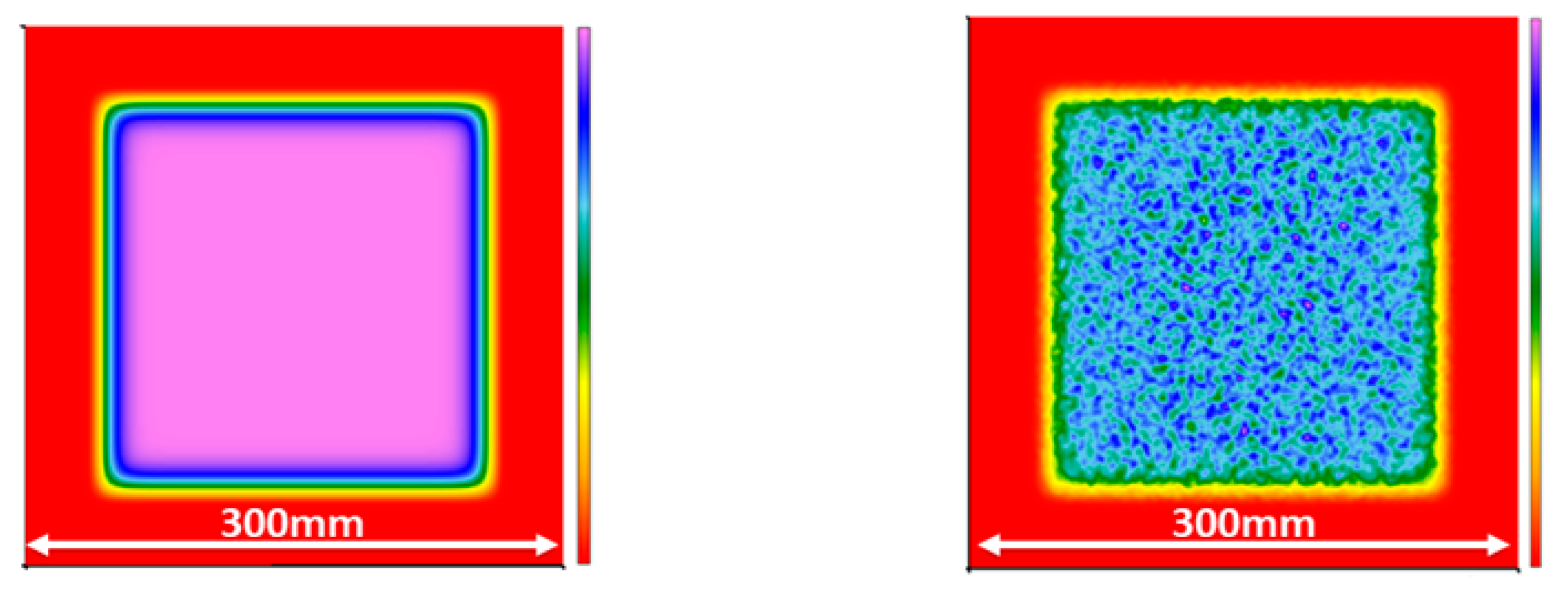
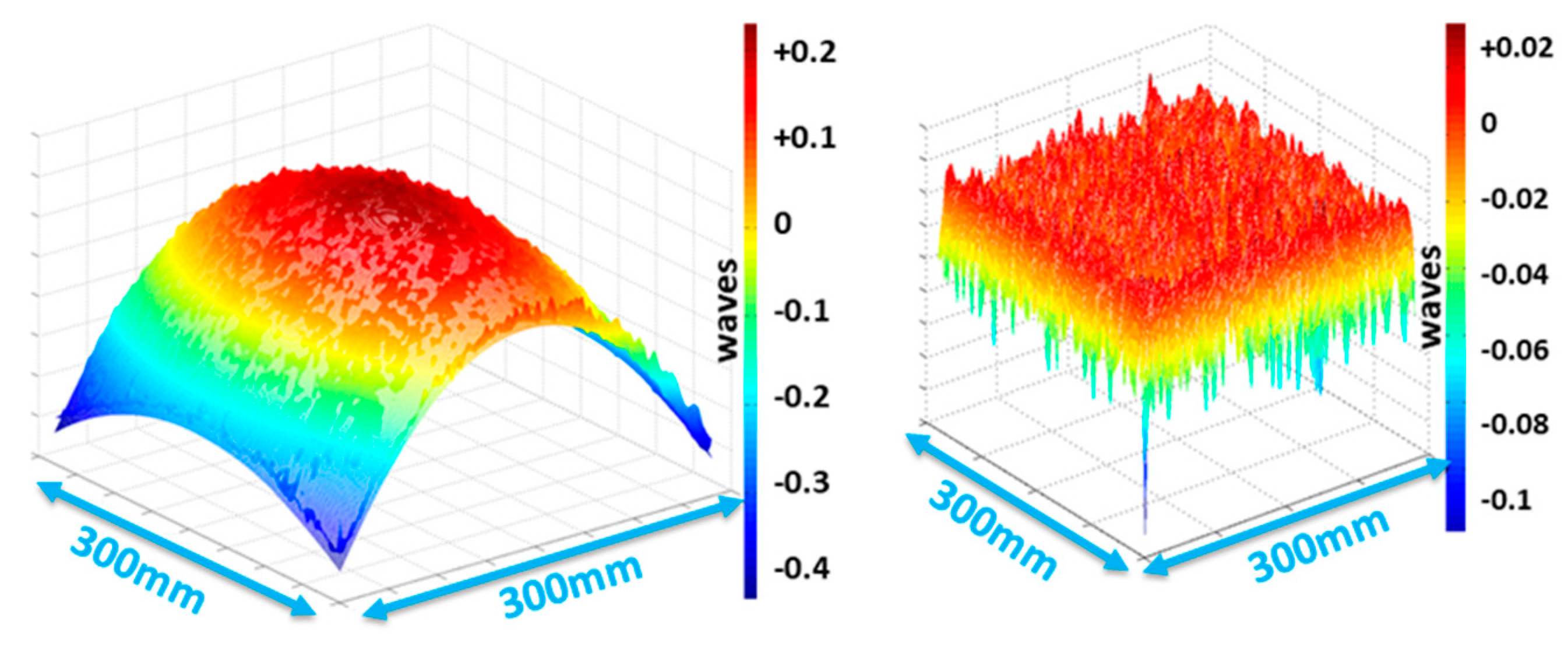
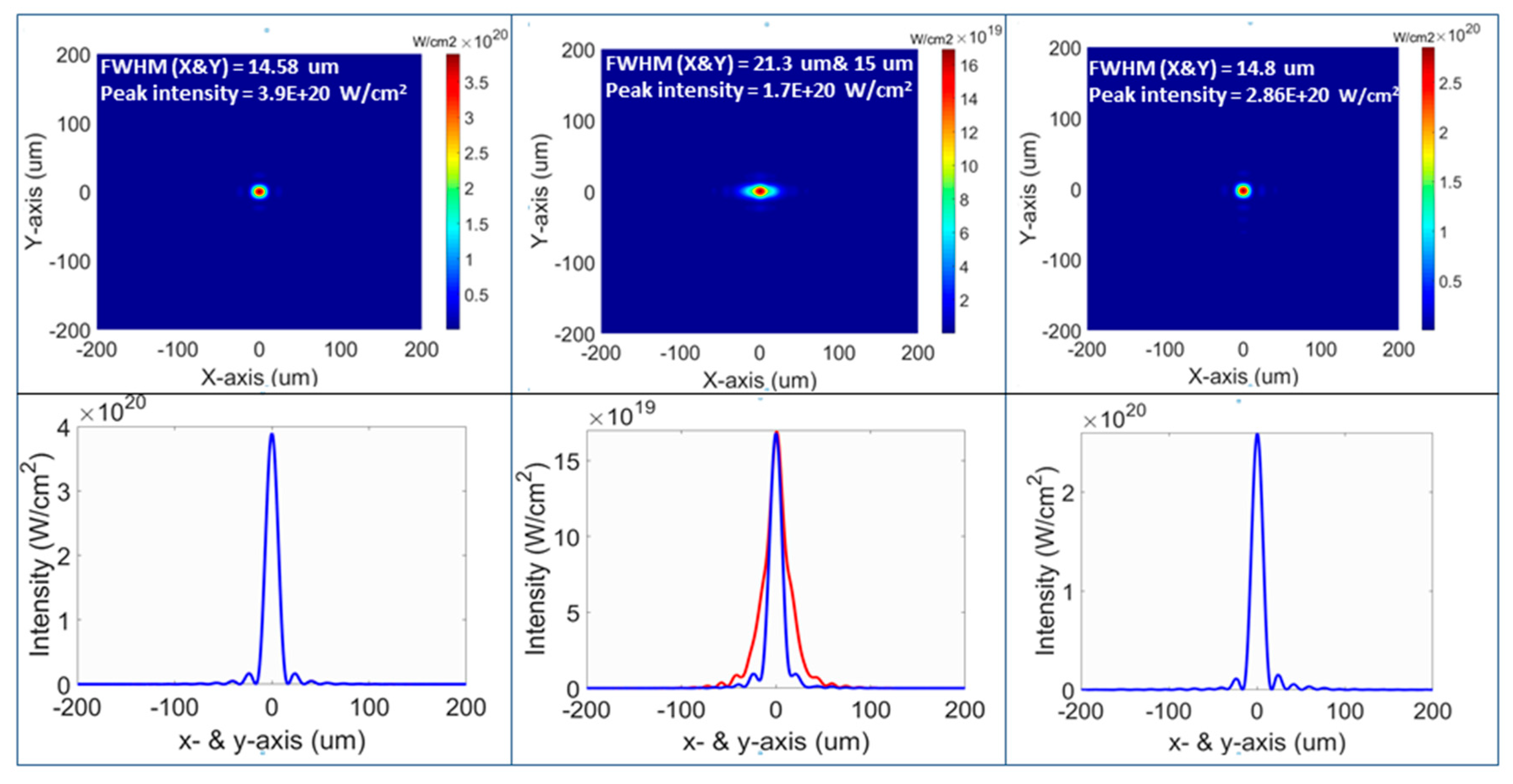
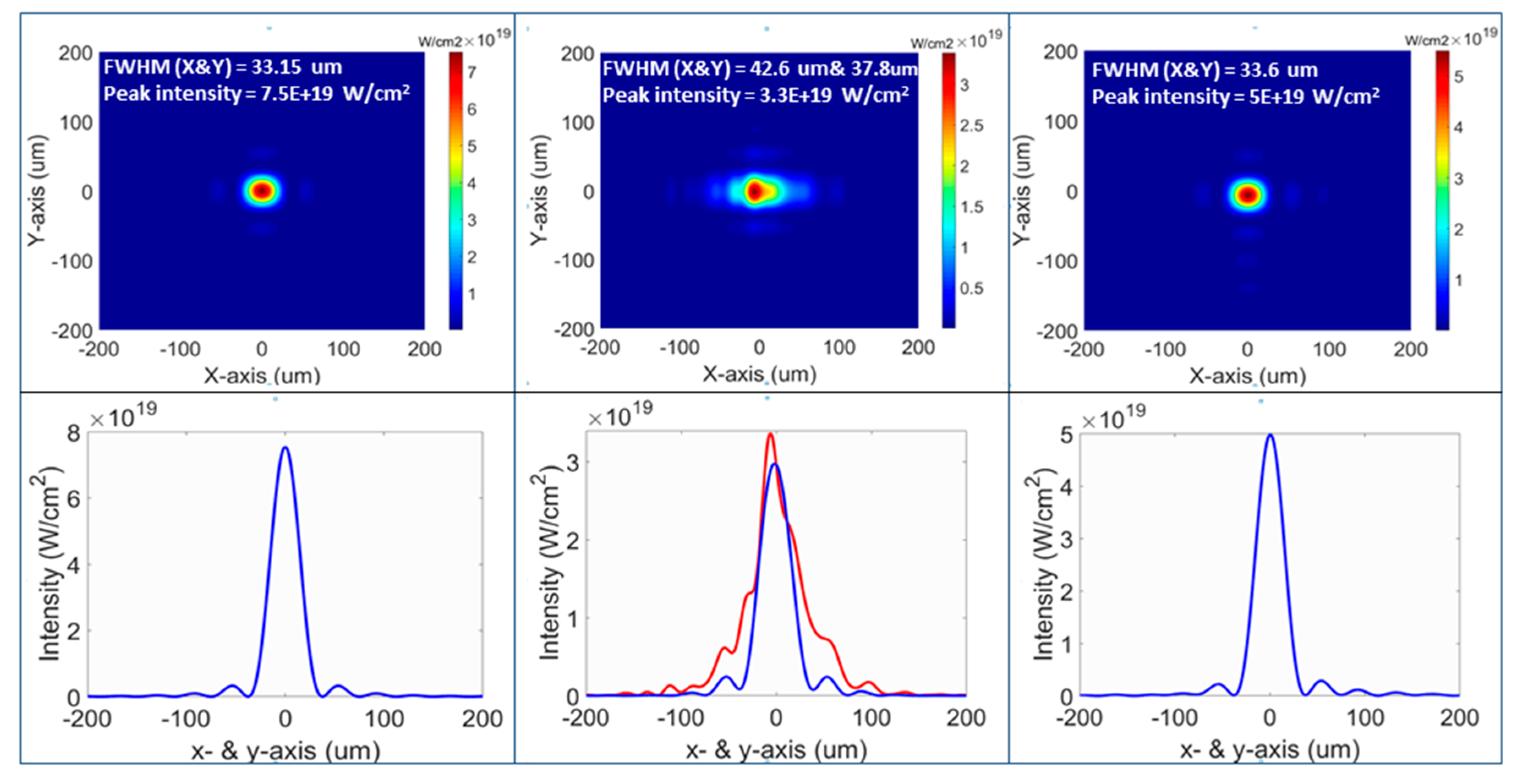
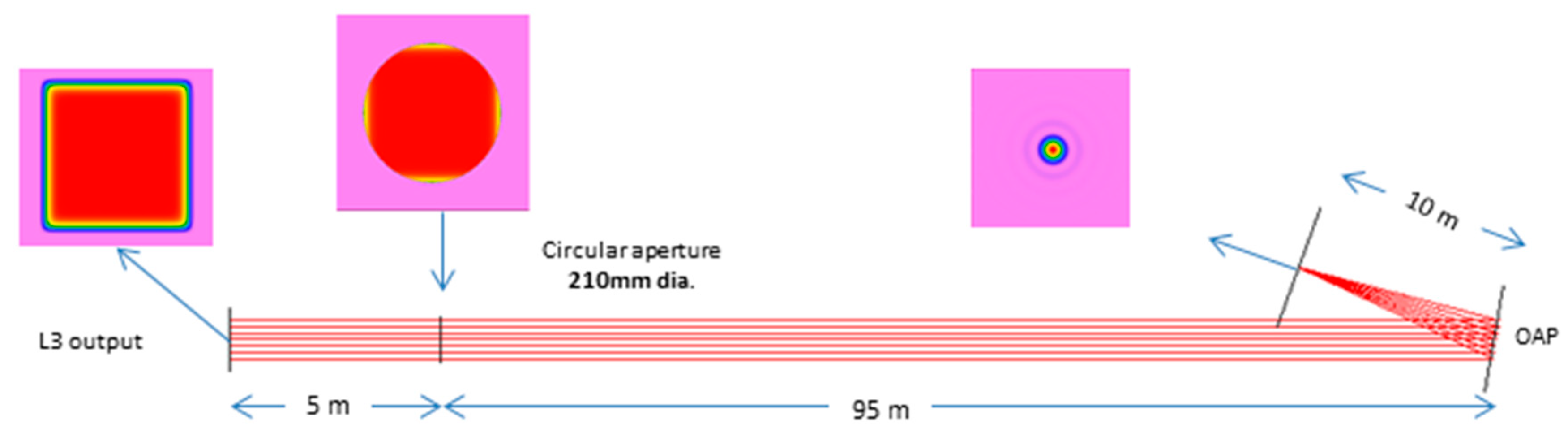
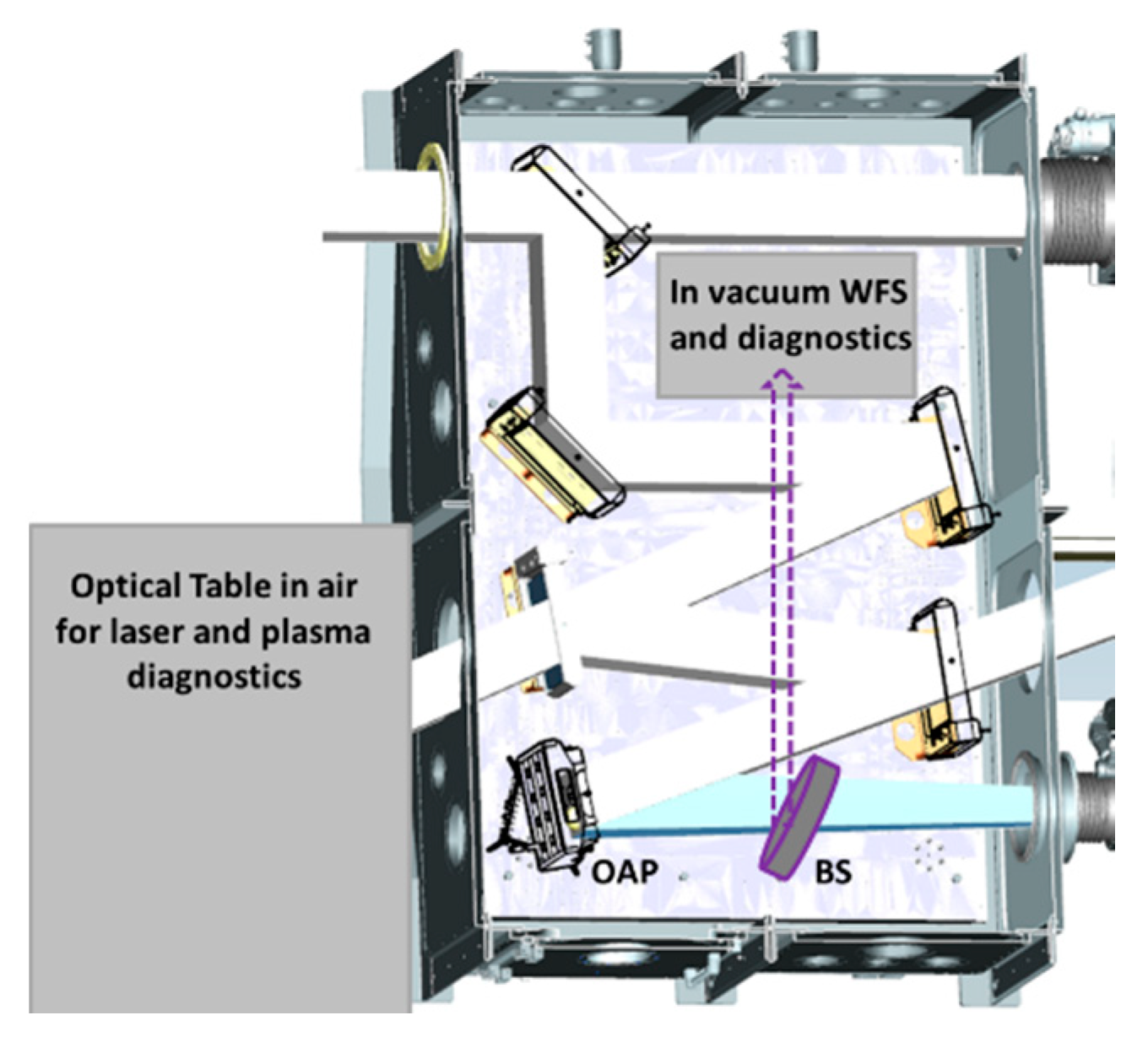
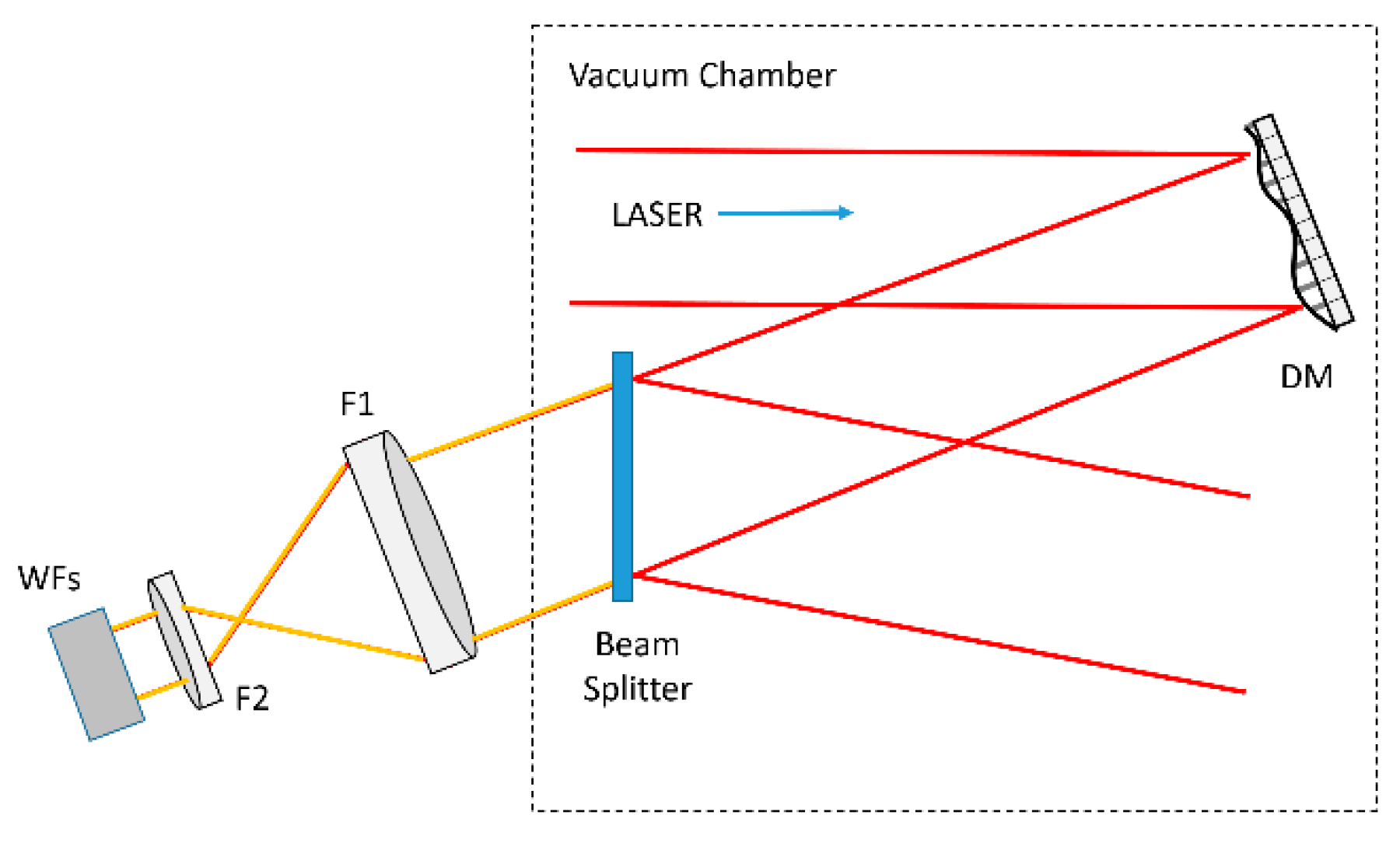
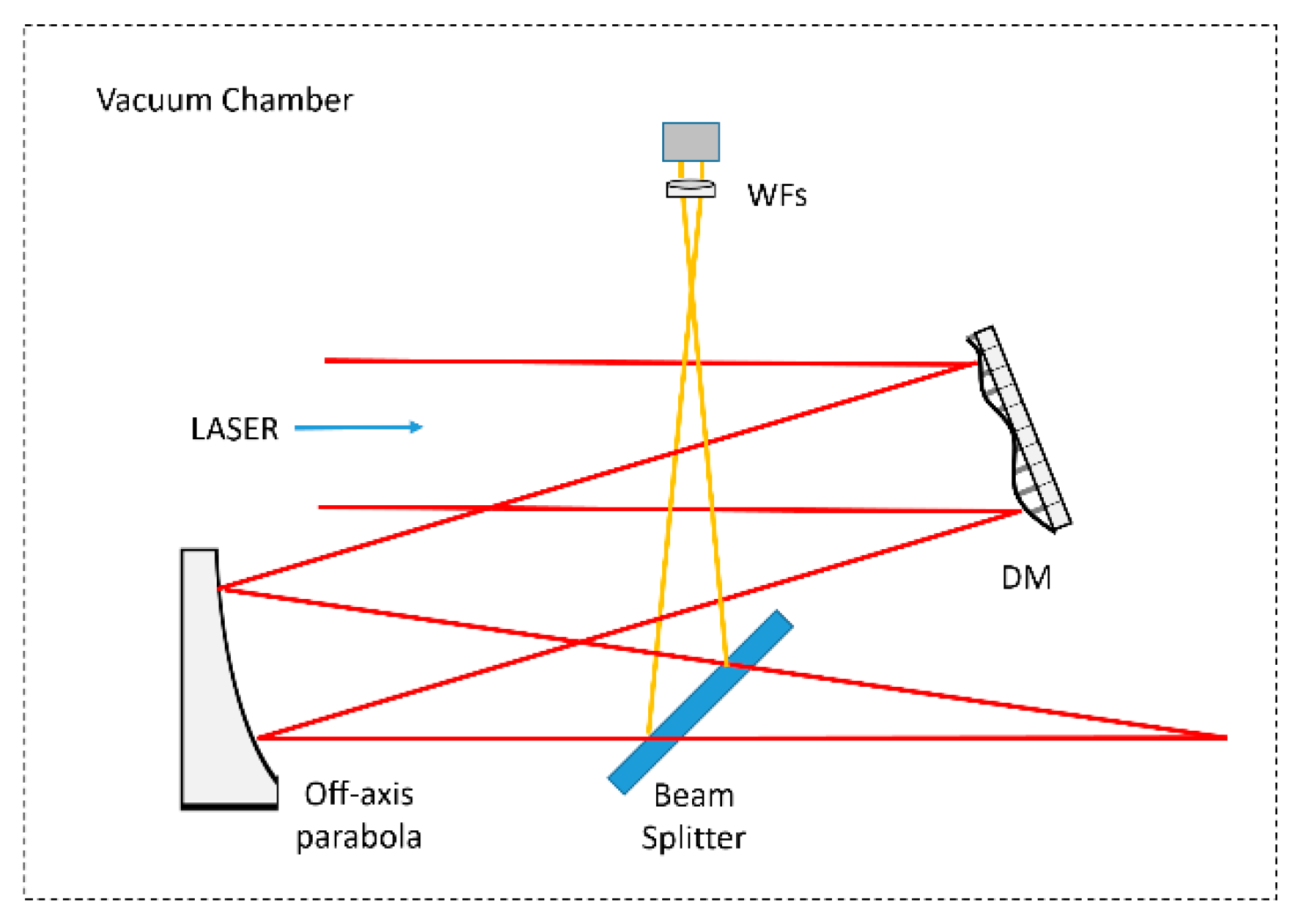
2.3.1. Wavefront Diagnostics; Examples and Tests “in Air” and “in-Vacuum”
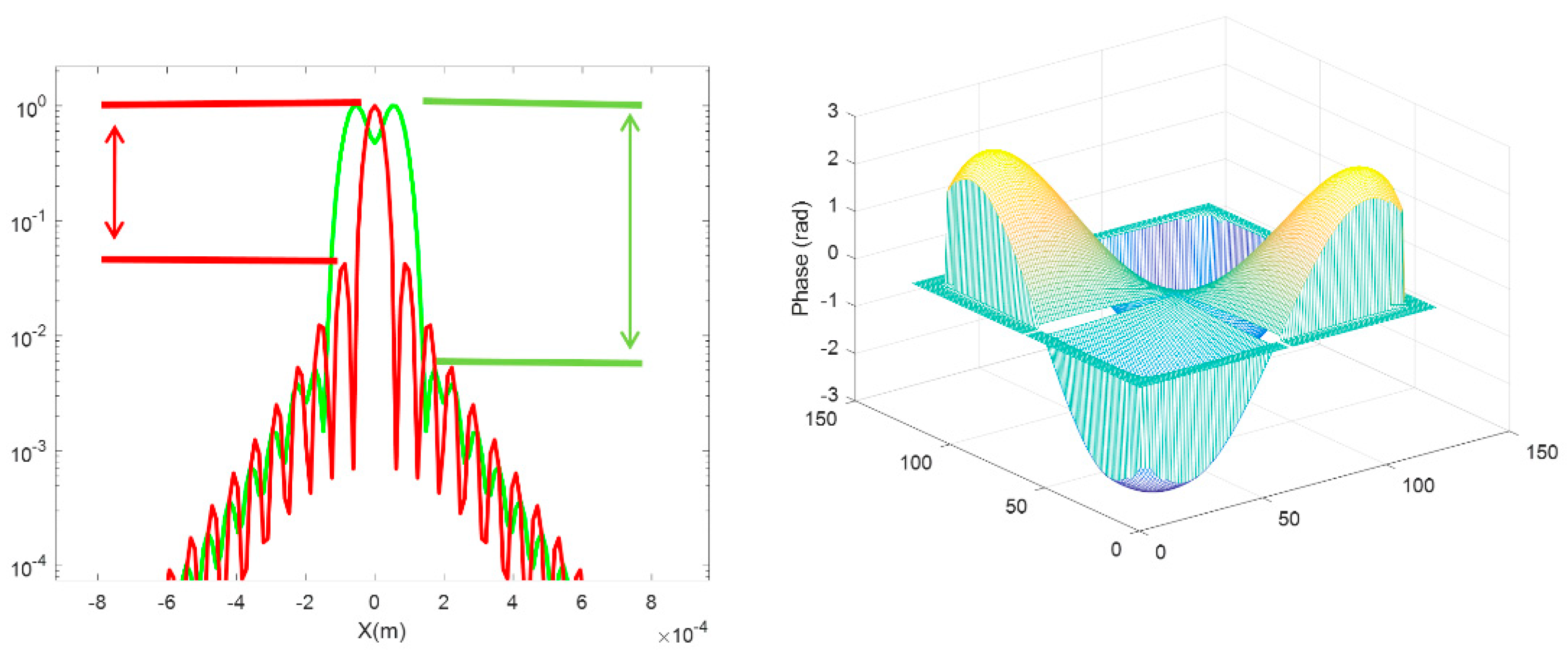
2.3.2. Correction of Non Common Path Aberrations
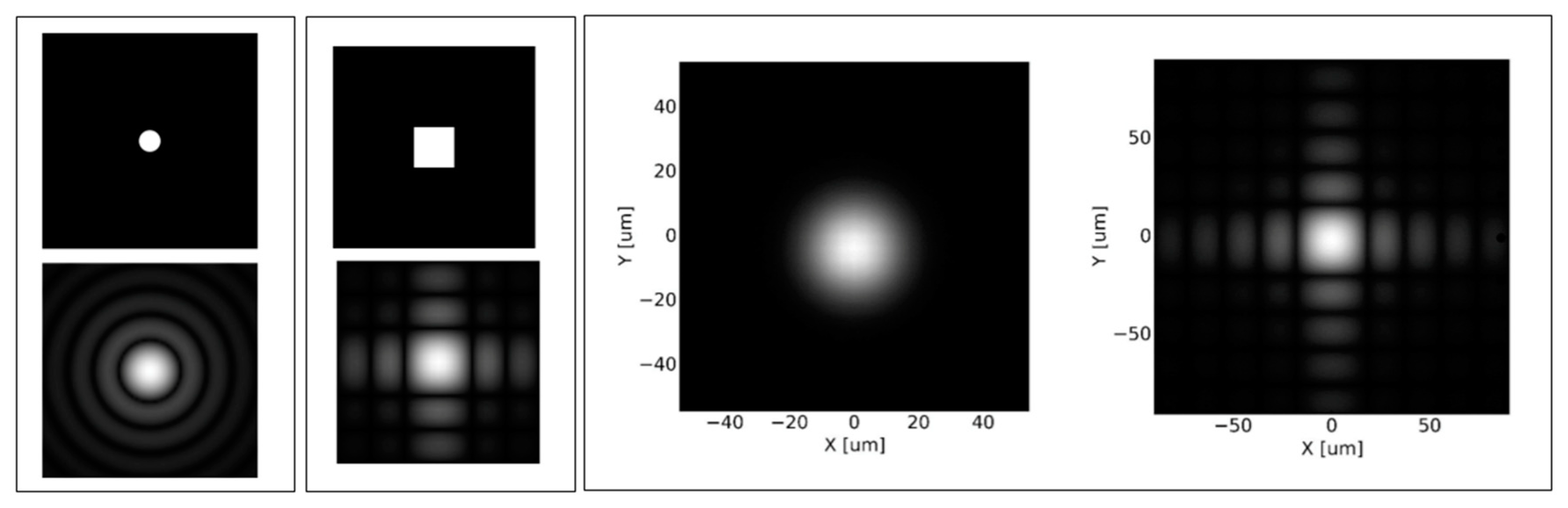
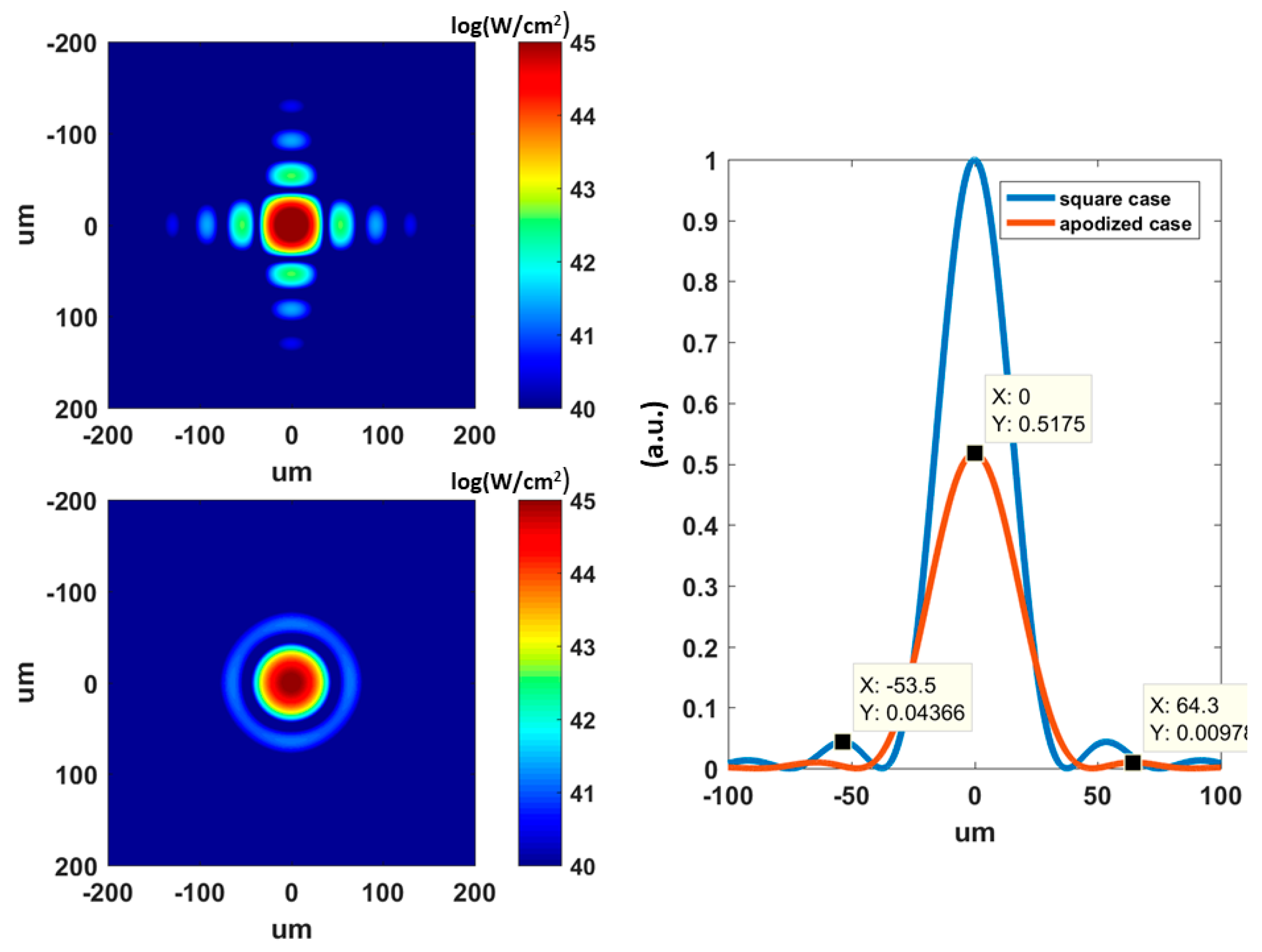
2.3.3. Beam Shaping with the Deformable Mirror
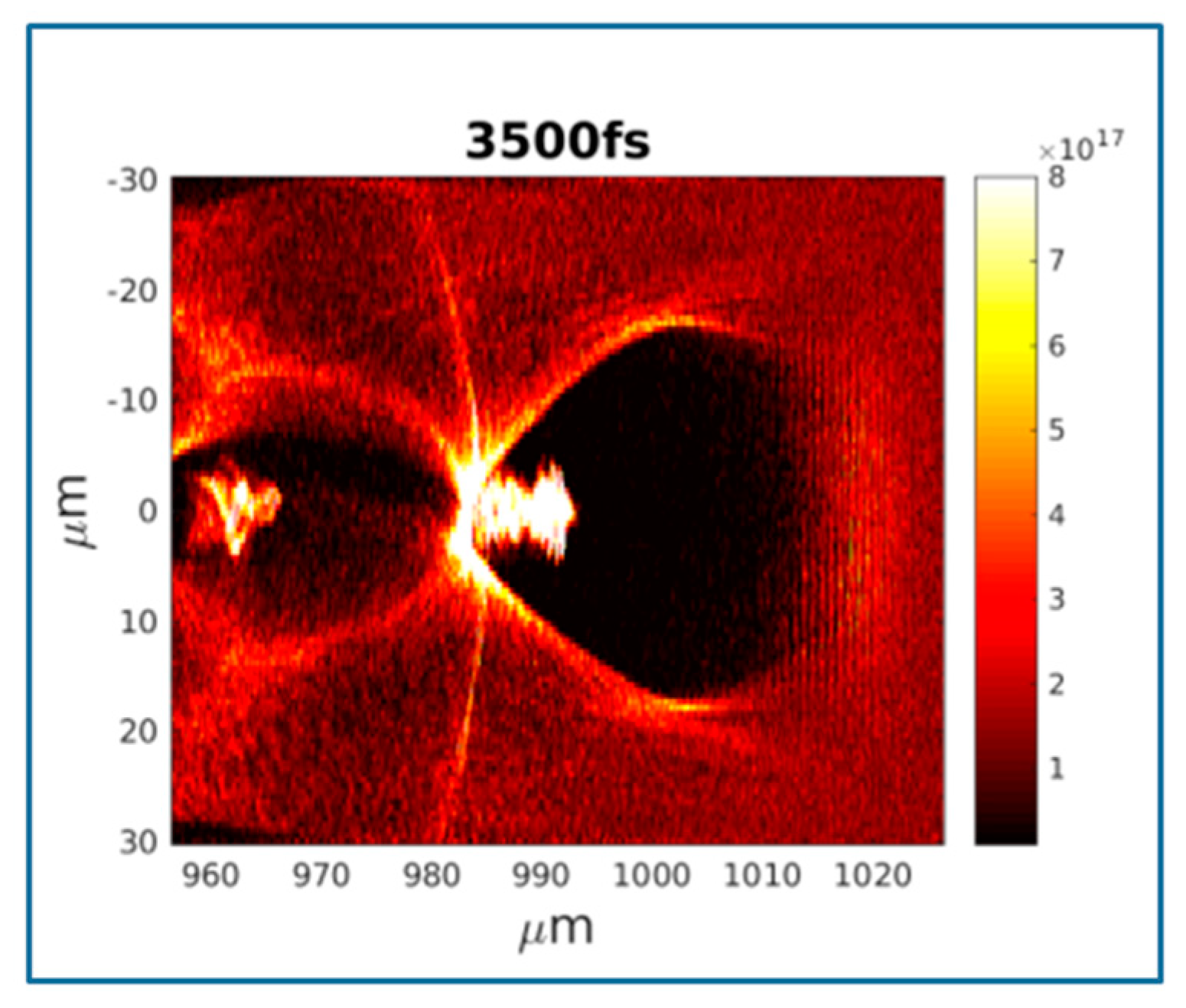
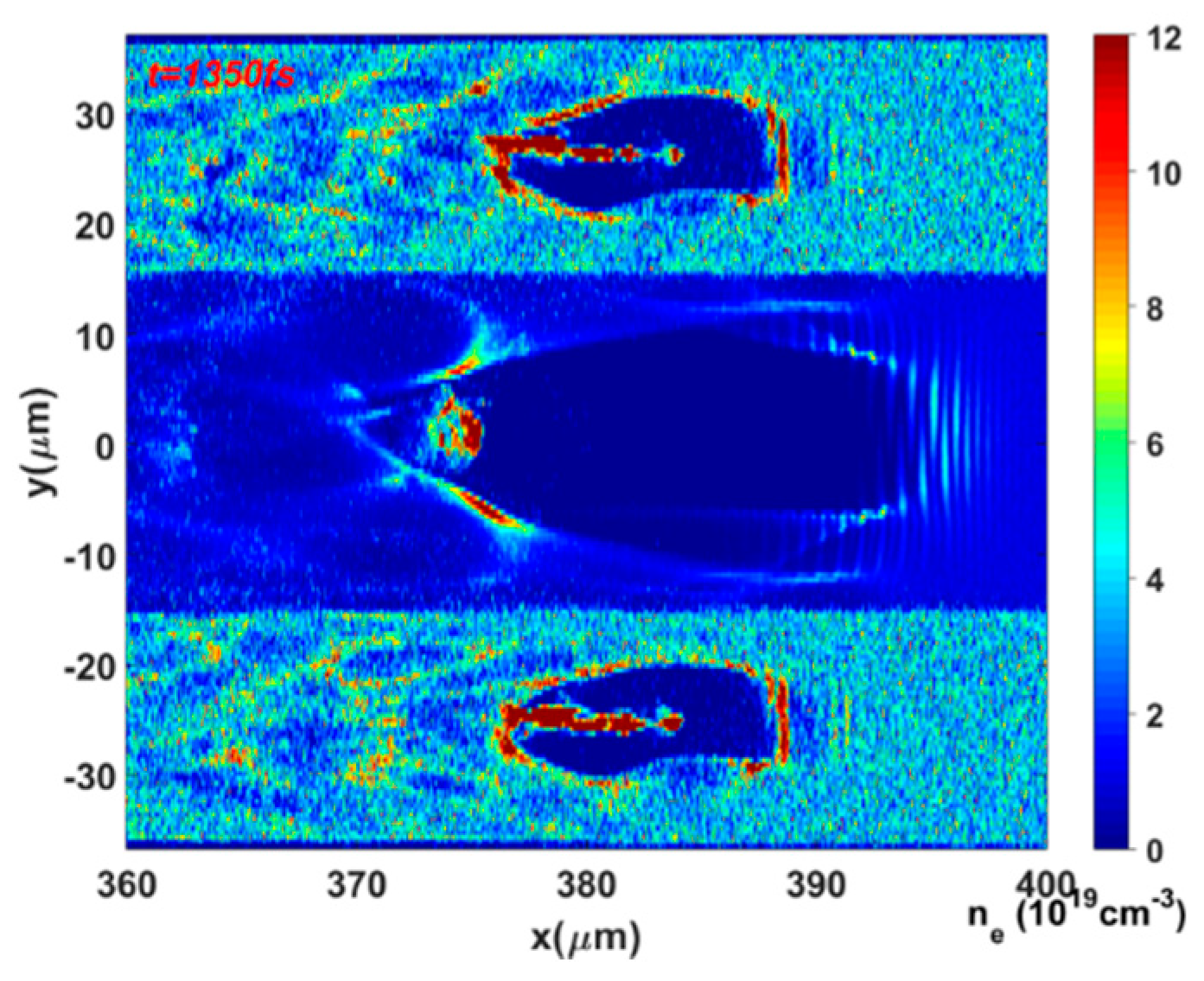
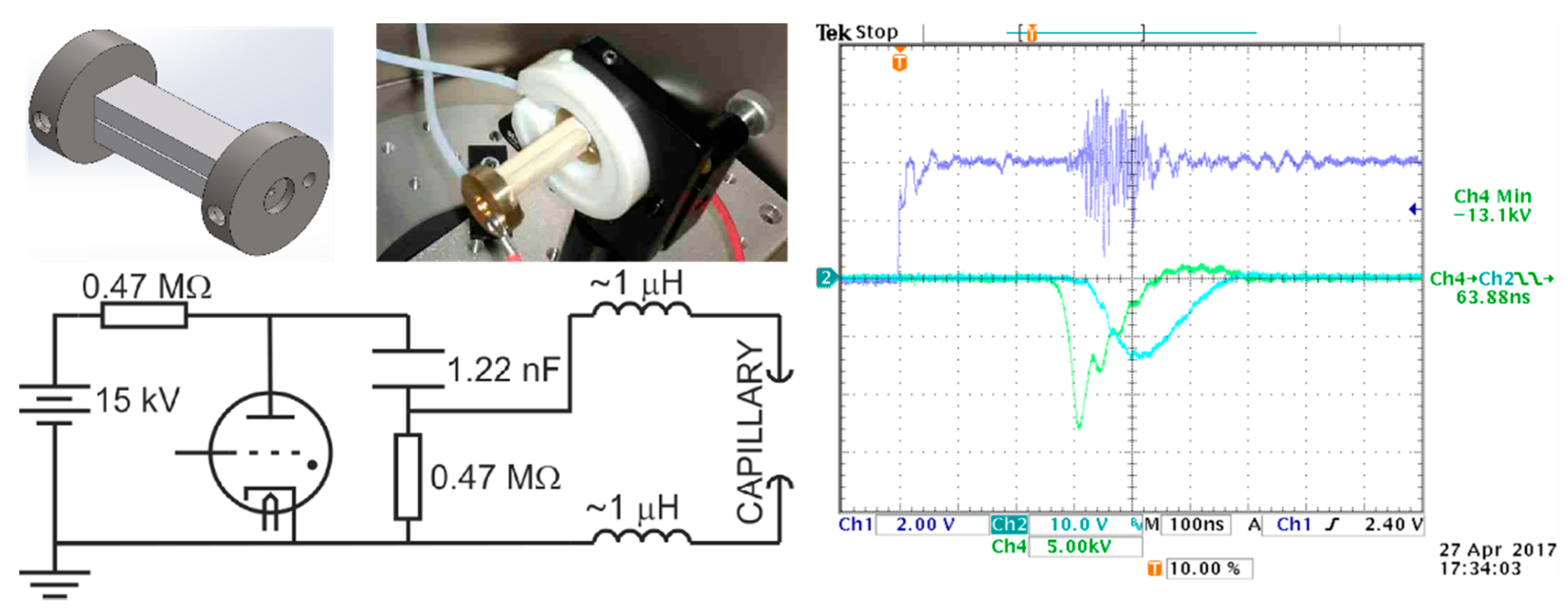
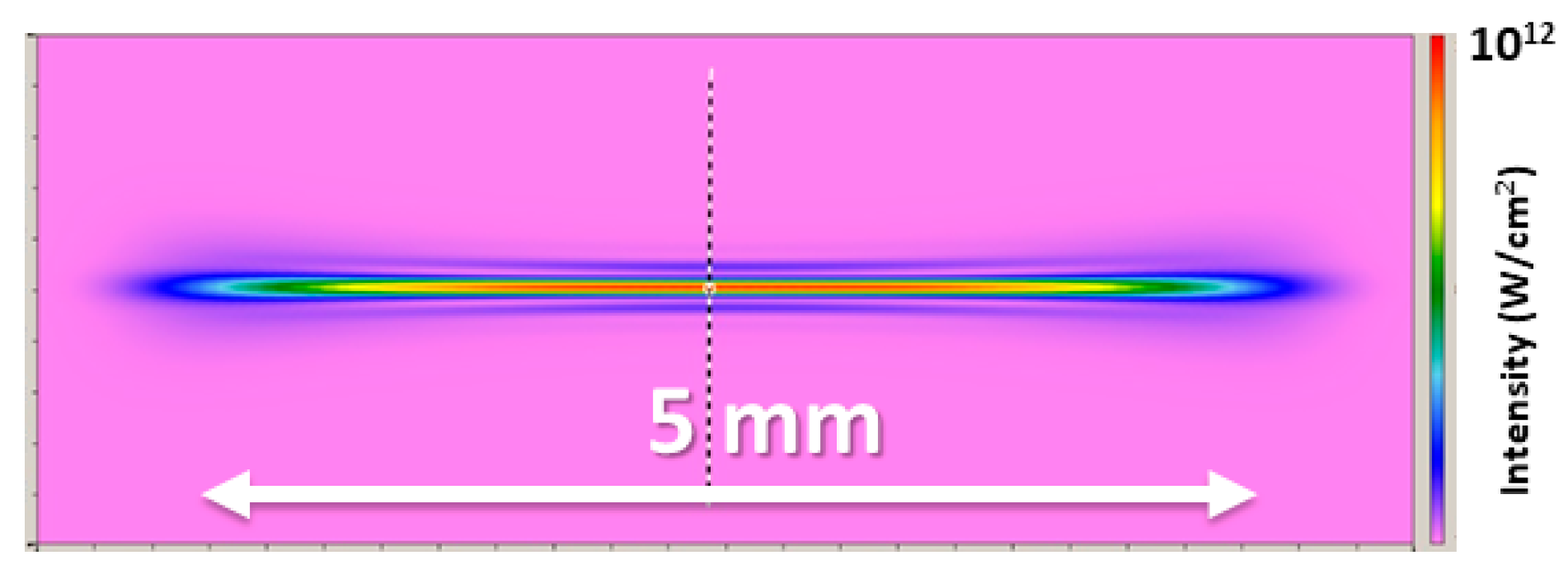
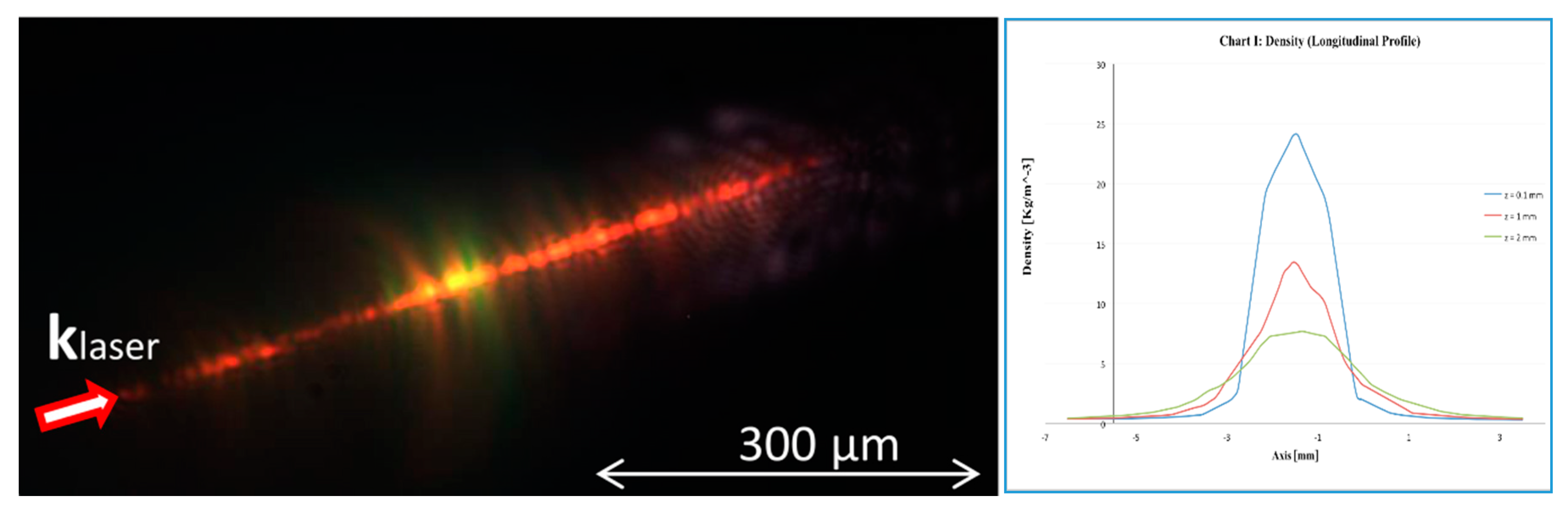
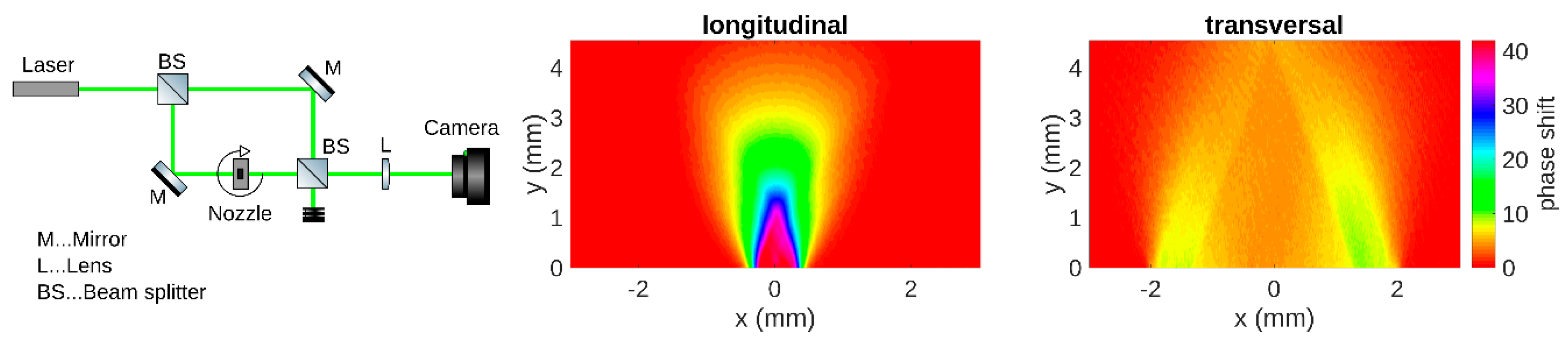
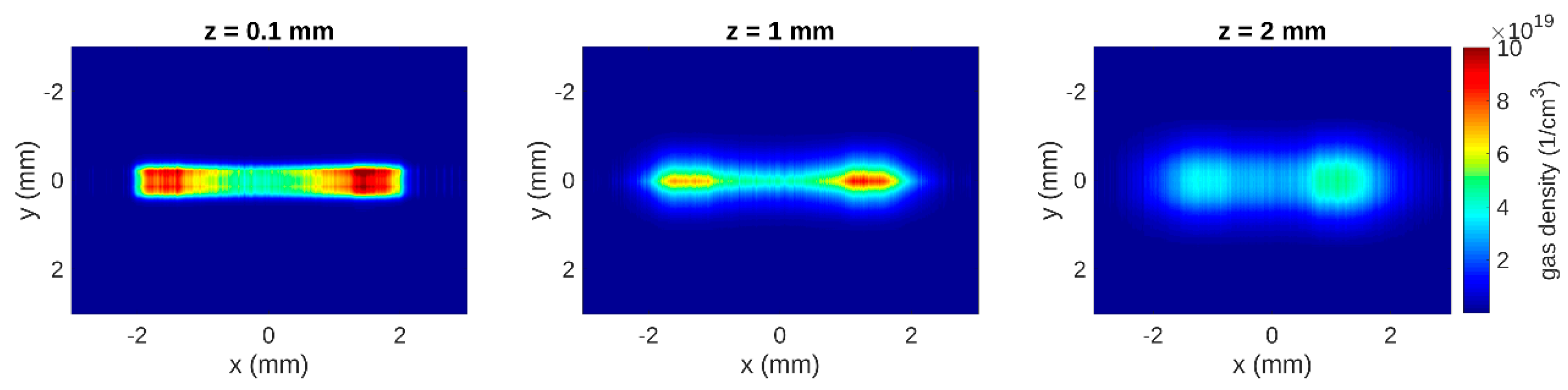
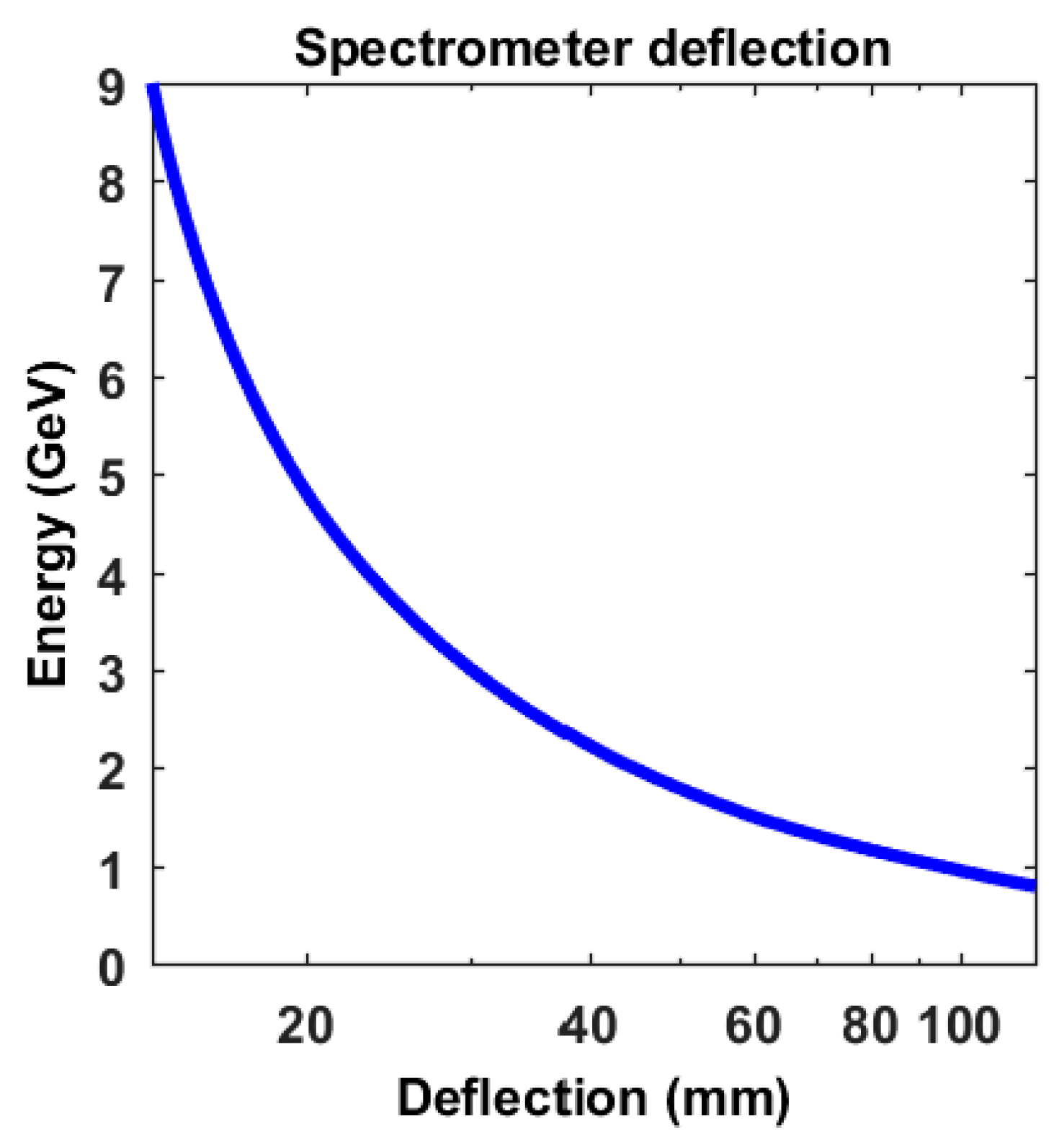
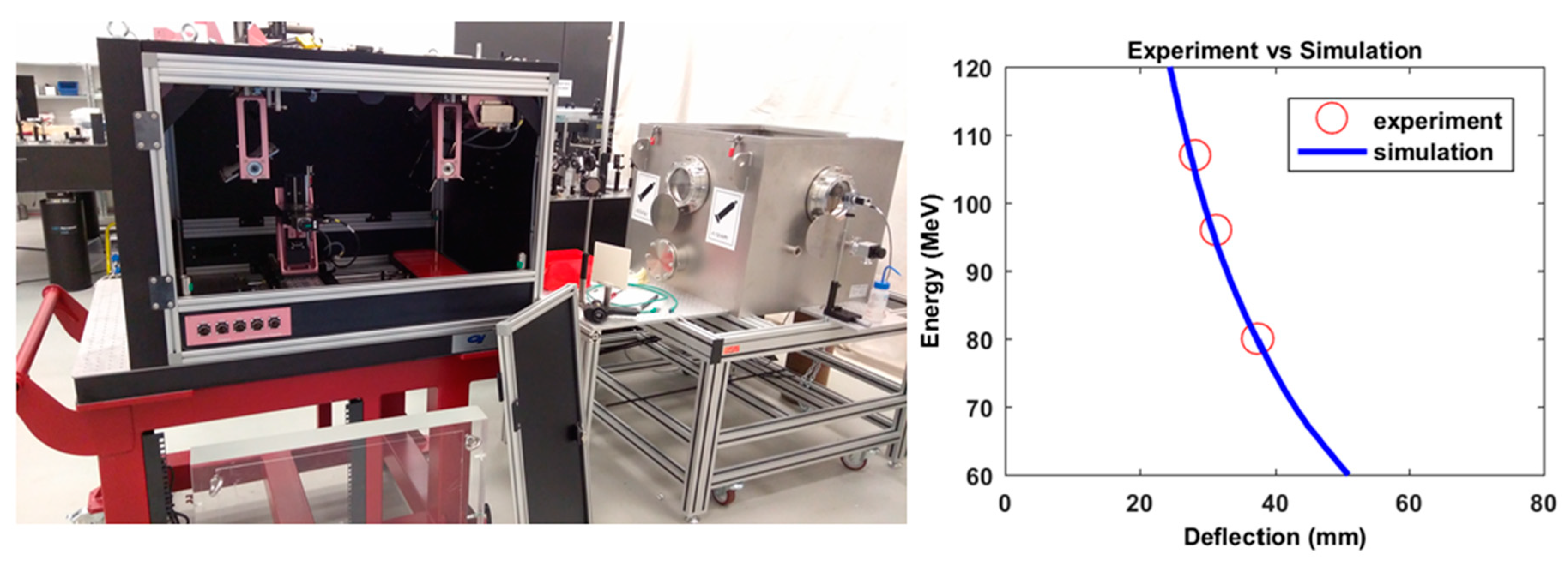
2.4. Diagnostics for Plasma Interaction and Electron Beams
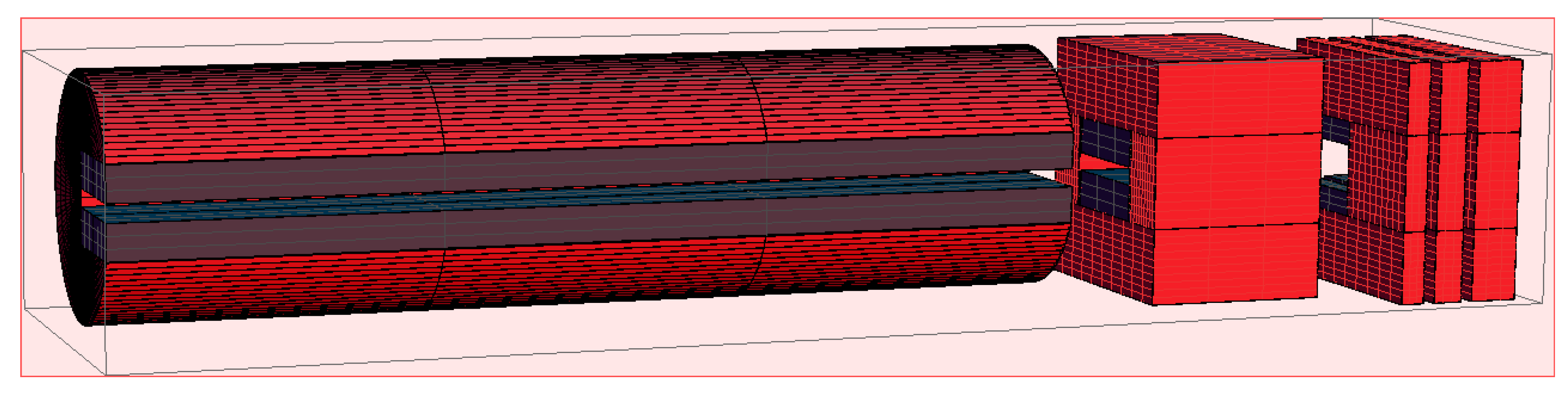
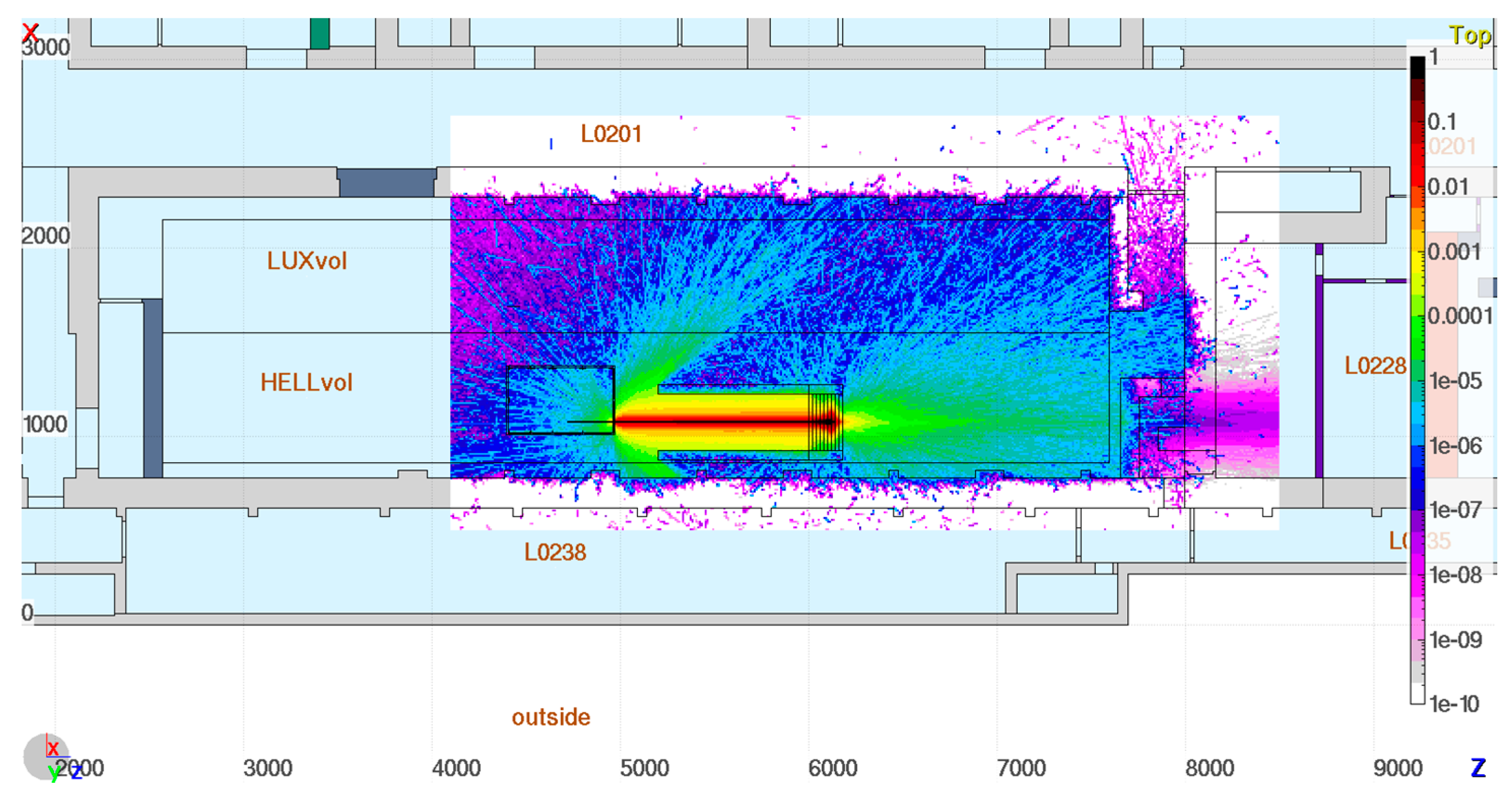
2.5. Radioprotection Analysis and Shielding Design
3. Conclusions
Acknowledgments
Conflicts of Interest
References
- Tajima, T.; Dawson, J.M. Laser electron accelerator. Phys. Rev. Lett. 1979, 43, 267. [Google Scholar] [CrossRef]
- Mourou, G.A.; Korn, G.; Sandner, W.; Collier, J.L. ELI—Extreme Light Infrastructure Whitebook, Science and Technology with Ultra-Intense Lasers; THOSS Media GmbH: Berlin, Germany, 2011. [Google Scholar]
- The ELI Beamline Project Website. Available online: https://www.eli-beams.eu/ (accessed on 29 August 2018).
- Rus, B.; Bakule, P.; Kramer, D.; Naylon, J.; Thoma, J.; Fibrich, M.; Green, J.T.; Lagron, J.C.; Antipenkov, R.; Bartoníček, J.; et al. ELI-beamlines: Progress in development of next generation short-pulse laser systems. In Proceedings of the SPIE 10241, Research Using Extreme Light: Entering New Frontiers with Petawatt-Class Lasers III, Prague, Czech Republic, 24–27 April 2017. [Google Scholar]
- HELL platform project. Available online: https://www.eli-beams.eu/en/facility/experimental-halls/e5-electron-accelaration-laser-undulator-x-ray-source/hell-experiment/ (accessed on 4 September 2018).
- Geddes, C.G.; Toth, C.; Van Tilborg, J.; Esarey, E.; Schroeder, C.B.; Bruhwiler, D.; Nieter, C.; Cary, J.; Leemans, W.P. High-quality electron beams from a laser wakefield accelerator using plasma-channel guiding. Nature 2004, 431, 538. [Google Scholar] [CrossRef] [PubMed]
- Mangles, S.P.; Murphy, C.D.; Najmudin, Z.; Thomas, A.G.; Collier, J.L.; Dangor, A.E.; Divall, E.J.; Foster, P.S.; Gallacher, J.G.; Hooker, C.J.; et al. Monoenergetic beams of relativistic electrons from intense laser–plasma interactions. Nature 2004, 431, 535. [Google Scholar] [CrossRef] [PubMed]
- Faure, J.; Glinec, Y.; Pukhov, A.; Kiselev, S.; Gordienko, S.; Lefebvre, E.; Rousseau, J.P.; Burgy, F.; Malka, V. A laser-plasma accelerator producing monoenergetic electron beams. Nature 2004, 431, 541. [Google Scholar] [CrossRef] [PubMed]
- Leemans, W.P.; Nagler, B.; Gonsalves, A.J.; Toth, C.; Nakamura, K.; Geddes, C.G.; Esarey, E.; Schroeder, C.B.; Hooker, S.M. GeV electron beams from a centimetre-scale accelerator. Nat. Phys. 2006, 2, 696–699. [Google Scholar] [CrossRef]
- Wang, X.; Zgadzaj, R.; Fazel, N.; Li, Z.; Yi, S.A.; Zhang, X.; Henderson, W.; Chang, Y.Y.; Korzekwa, R.; Tsai, H.E.; et al. Quasi-monoenergetic laser-plasma acceleration of electrons to 2 GeV. Nat. Commun. 2013, 4, 1988. [Google Scholar] [CrossRef] [PubMed]
- Leemans, W.P.; Gonsalves, A.J.; Mao, H.S.; Nakamura, K.; Benedetti, C.; Schroeder, C.B.; Tóth, C.; Daniels, J.; Mittelberger, D.E.; Bulanov, S.S.; et al. Multi-GeV Electron Beams from Capillary-Discharge-Guided Subpetawatt Laser Pulses in the Self-Trapping Regime. Phys. Rev. Lett. 2014, 113, 245002. [Google Scholar] [CrossRef] [PubMed]
- HELL Detailed User Workshop. Available online: https://www.eli-beams.eu/en/media/events/hell-dur-2014/ (accessed on 4 September 2018).
- Faure, J.; Rechatin, C.; Norlin, A.; Lifschitz, A.; Glinec, Y.; Malka, V. Controlled injection and acceleration of electrons in plasma wakefields by colliding laser pulses. Nature 2006, 444, 737. [Google Scholar] [CrossRef] [PubMed]
- Lu, W.; Tzoufras, M.; Joshi, C.; Tsung, F.S.; Mori, W.B.; Vieira, J.; Fonseca, R.A.; Silva, L.O. Generating multi-GeV electron bunches using single stage laser wakefield acceleration in a 3D nonlinear regime. Phys. Rev. Spéc. Top. Accelerators Beams 2007, 10, 061301. [Google Scholar] [CrossRef]
- Bulanov, S.V.; Esirkepov, T.Z.; Hayashi, Y.; Kando, M.; Kiriyama, H.; Koga, J.K.; Kondo, K.; Kotaki, H.; Pirozhkov, A.S.; Bulanov, S.S.; et al. On the design of experiments for the study of extreme field limits in the interaction of laser with ultrarelativistic electron beam. Nucl. Instrum. Methods Phys. Res. Sect. A 2011, 660, 31–42. [Google Scholar] [CrossRef] [Green Version]
- Arber, T.D.; Bennett, K.; Brady, C.S.; Lawrence-Douglas, A.; Ramsay, M.G.; Sircombe, N.J.; Gillies, P.; Evans, R.G.; Schmitz, H.; Bell, A.R.; et al. Contemporary particle-in-cell approach to laser-plasma modelling. Plasma Phys. Control. Fusion 2015, 57, 113001. [Google Scholar] [CrossRef]
- Di Piazza, A.; Müller, C.; Hatsagortsyan, K.Z.; Keitel, C.H. Extremely high-intensity laser interactions with fundamental quantum systems. Rev. Mod. Phys. 2012, 84, 1177. [Google Scholar] [CrossRef]
- Silva, L.O.; Fiúza, F.; Fonseca, R.A.; Martins, J.L.; Martins, S.F.; Vieira, J.; Huang, C.; Lu, W.; Tsung, F.; Tzoufras, M.; et al. Laser electron acceleration with 10 PW lasers. C. R. Phys. 2009, 10, 167–175. [Google Scholar] [CrossRef]
- Martins, S.F.; Fonseca, R.A.; Lu, W.; Mori, W.B.; Silva, L.O. Exploring laser-wakefield-accelerator regimes for near-term lasers using particle-in-cell simulation in Lorentz-boosted frames. Nat. Phys. 2010, 6, 311–316. [Google Scholar] [CrossRef]
- Bulanov, S.V.; Inovenkov, I.N.; Kirsanov, V.I.; Naumova, N.M.; Sakharov, A.S. Ultra fast depletion of ultra-short and relativistically strong laser pulses in an underdense plasma. Phys. Fluids B 1992, 4, 1935. [Google Scholar] [CrossRef]
- Pukhov, A.; Meyer-ter-Vehn, J. Laser wake field acceleration: The highly non-linear broken-wave regime. Appl. Phys. B 2002, 74, 355–361. [Google Scholar] [CrossRef]
- Lu, W.; Huang, C.; Zhou, M.; Mori, W.B.; Katsouleas, T. Nonlinear Theory for Relativistic Plasma Wakefields in the Blowout Regime. Phys. Rev. Lett. 2006, 96, 165002. [Google Scholar] [CrossRef] [PubMed]
- Thomas, A.G.R.; Ridgers, C.P.; Bulanov, S.S.; Griffin, B.J.; Mangles, S.P.D. Strong Radiation-Damping Effects in a Gamma-Ray Source Generated by the Interaction of a High-Intensity Laser with a Wakefield-Accelerated Electron Beam. Phys. Rev. X 2012, 2, 041004. [Google Scholar] [CrossRef]
- Cole, J.M.; Behm, K.T.; Gerstmayr, E.; Blackburn, T.G.; Wood, J.C.; Baird, C.D.; Duff, M.J.; Harvey, C.; Ilderton, A.; Joglekar, A.S.; et al. Experimental evidence of radiation reaction in the collision of a high-intensity laser pulse with a laser-wakefield accelerated electron beam. Phys. Rev. X 2018, 8, 011020. [Google Scholar] [CrossRef]
- Bulanov, S.V.; Esirkepov, T.; Tajima, T. Light intensification towards the Schwinger limit. Phys. Rev. Lett. 2003, 91, 085001. [Google Scholar] [CrossRef] [PubMed]
- Bulanov, S.V.; Esirkepov, T.Z.; Kando, M.; Pirozhkov, A.S.; Rosanov, N.N. Relativistic Mirrors in Plasmas–Novel Results and Perspectives. Phys. Uspekhi 2013, 56, 429–464. [Google Scholar] [CrossRef]
- Kando, M.; Esirkepov, T.Z.; Koga, J.K.; Pirozhkov, A.S.; Bulanov, S.V. Coherent, Short X-ray Generation via Relativistic Flying Mirrors. Quantum Beam Sci. 2018, 2, 7. [Google Scholar] [CrossRef]
- Ehrlich, Y.; Cohen, C.; Zigler, A.; Krall, J.; Sprangle, P.; Esarey, E. Guiding of High Intensity Laser Pulses in Straight and Curved Plasma Channel Experiments. Phys. Rev. Lett. 1996, 77, 4186. [Google Scholar] [CrossRef] [PubMed]
- Hooker, S.M.; Spence, D.J.; Smith, R.A. Guiding of high-intensity picosecond laser pulses in a discharge-ablated capillary waveguide. Opt. Soc. Am. B 2000, 17, 90–98. [Google Scholar] [CrossRef]
- Bobrova, N.A.; Esaulov, A.A.; Sakai, J.I.; Sasorov, P.V.; Spence, D.J.; Butler, A.; Hooker, S.M.; Bulanov, S.V. Simulations of a hydrogen-filled capillary discharge waveguide. Phys. Rev. E 2001, 65, 016407. [Google Scholar] [CrossRef] [PubMed]
- Sasorov, P.V.; Bobrova, N.A.; Olkhovskaya, O.G.; Bagdasarov, G.A.; Boldarev, A.S.; Gasilov, V.A.; Bulanov, S.S.; Gonsalves, A.J.; Schroeder, C.B.; Esarey, E.; et al. Simulations of Plasma Channel Formation by Knife-Like Nanosecond Laser Beam; KIAM RAS: Moscow, Russia, 2018. [Google Scholar]
- Bagdasarov, G.A.; Sasorov, P.V.; Gasilov, V.A.; Boldarev, A.S.; Olkhovskaya, O.G.; Benedetti, C.; Bulanov, S.S.; Gonsalves, A.; Mao, H.S.; Schroeder, C.B.; et al. Laser beam coupling with capillary discharge plasma for laser wakefield acceleration applications. Phys. Plasmas 2017, 24, 083109. [Google Scholar] [CrossRef] [Green Version]
- Bagdasarov, G.A.; Bobrova, N.A.; Boldarev, A.S.; Olkhovskaya, O.G.; Sasorov, P.V.; Gasilov, V.A.; Barber, S.K.; Bulanov, S.S.; Gonsalves, A.J.; Schroeder, C.B.; et al. On production and asymmetric focusing of flat electron beams using rectangular capillary discharge plasmas. Phys. Plasmas 2017, 24, 123120. [Google Scholar] [CrossRef] [Green Version]
- Bagdasarov, G.; Sasorov, P.; Boldarev, A.; Olkhovskaya, O.; Gasilov, V.; Gonsalves, A.J.; Barber, S.; Bulanov, S.S.; Schroeder, C.B.; van Tilborg, J.; et al. Plasma equilibrium inside various cross-section capillary discharges. Phys. Plasmas 2017, 24, 053111. [Google Scholar] [CrossRef] [Green Version]
- Nevrkla, M. Proceedings of the 1st Annual HiLASE Wokrshop.
- Gasilov, V.; Boldarev, A.; Dyachenko, S.; Olkhovskaya, O.; Kartasheva, E.; Bagdasarov, G.; Boldyrev, S.; Gasilova, I.; Shmyrov, V.; Tkachenko, S.; et al. Applications, Tools and Techniques on the Road to Exascale Computing, Advances in Parallel Computing; de Bosschere, K., D’Hollander, E.H., Joubert, G.R., Padua, D., Peters, F., Eds.; IOS Press: Amsterdam, The Netherlands, 2012; Volume 22, p. 235. [Google Scholar]
- Negro, M.; Quintavalla, M.; Mocci, J.; Ciriolo, A.G.; Devetta, M.; Muradore, R.; Stagira, S.; Vozzi, C.; Bonora, S. High-speed adaptive deformable lens for boosting an high-energy optical parametric amplifier. In Proceedings of the 2017 European Conference on Lasers and Electro-Optics and European Quantum Electronics Conference, Munich, Germany, 25–29 June 2017. [Google Scholar]
- Mocci, J.; Quintavalla, M.; Trestino, C.; Bonora, S.; Muradore, R. A multi-platform CPU-based architecture for cost-effective adaptive optics systems. IEEE Trans. Ind. Inform. 2018. [Google Scholar] [CrossRef]
- Gu, Y.J.; Klimo, O.; Kumar, D.; Liu, Y.; Singh, S.K.; Esirkepov TZh Bulanov, S.V.; Weber, S.; Korn, G. Fast magnetic-field annihilation in the relativistic collisionless regime driven by two ultrashort high-intensity laser pulses. Phys. Rev. E 2016, 93, 103203. [Google Scholar] [CrossRef] [PubMed]
- Gizzi, L.A.; Cecchetti, C.A.; Giulietti, A.; Giulietti, D.; Koester, P.; Labate, L.; Levato, T.; Pathak, N. Thomson Scattering Imaging From Ultrashort Ultraintense Laser Interaction With Gas. IEEE Trans. Plasma Sci. 2011, 39, 2954–2955. [Google Scholar] [CrossRef]
- Jaroszynski, D.A.; Bingham, R.A.; Cairns, R.A. Laser Plasma Interactions; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Guillaume, E.; Döpp, A.; Thaury, C.; Phuoc, K.T.; Lifschitz, A.; Grittani, G.; Goddet, J.-P.; Tafzi, A.; Chou, S.; Veisz, L.; et al. Electron rephasing in a laser-wakefield accelerator. Phys. Rev. Lett. 2015, 115, 155002. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Grittani, G.M.; Levato, T.; Krus, M.; Fasso, A.; Jeong, T.M.; Kim, H.T.; Margarone, D.; Mocek, T.; Precek, M.; Versaci, R.; et al. Design and development of the HELL user station: Beam transport, characterization, and shielding. In Proceedings of the SPIE 9515K, Prague, Czech Republic, 13–16 April 2015. [Google Scholar] [CrossRef]
- Grittani, G.M.; Levato, T.; Korn, G. Design and development of the HELL User Station for multi-disciplinary experiments. In Proceedings of the SPIE 102410E, Prague, Czech Republic, 24–27 April 2017. [Google Scholar] [CrossRef]
- Synchrotron and free electron laser radiation and their applications in materials and life sciences. Available online: http://www.elettra.eu/ (accessed on 4 September 2018).
- Battistoni, G.; Boehlen, T.; Cerutti, F.; Chin, P.W.; Esposito, L.S.; Fassò, A.; Ferrari, A.; Lechner, A.; Empl, A.; Mairani, A.; et al. Overview of the FLUKA code. Ann. Nucl. Energy 2015, 82, 10–18. [Google Scholar] [CrossRef] [Green Version]
- Ferrari, A.; Sala, P.R.; Fasso, A.; Ranft, J. FLUKA: A Multi-Particle Transport Code; CERN-2005-10; U.S. Department of Energy: Washington, DC, USA, 2015.
- Vlachoudis, V. Flair: A Powerful But User Friendly Graphical Interface for FLUKA. In Proceedings of the International Conference on Mathematics, Computational Methods & Reactor Physics (M&C 2009), Saratoga Springs, NY, USA, 3–7 May 2009. [Google Scholar]
- Sasorov, P.V.; Bobrova, N.A.; Olkhovskaya, O.G.; Bagdasarov, G.A.; Boldarev, A.S.; Gasilov, V.A.; Bulanov, S.S.; Gonsalves, A.J.; Schroeder, C.B.; Esarey, E.; et al. Radiation shielding of electron beamlines at ELI Beamlines. In Proceedings of the Shielding aspects of Accelerators, Target and Irradiation Facilities (SATIF-13), Dresden, Germany, 10–12 October 2016. [Google Scholar]


© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Levato, T.; Bonora, S.; Grittani, G.M.; Lazzarini, C.M.; Nawaz, M.F.; Nevrkla, M.; Villanova, L.; Ziano, R.; Bassanese, S.; Bobrova, N.; et al. HELL: High-Energy Electrons by Laser Light, a User-Oriented Experimental Platform at ELI Beamlines. Appl. Sci. 2018, 8, 1565. https://doi.org/10.3390/app8091565
Levato T, Bonora S, Grittani GM, Lazzarini CM, Nawaz MF, Nevrkla M, Villanova L, Ziano R, Bassanese S, Bobrova N, et al. HELL: High-Energy Electrons by Laser Light, a User-Oriented Experimental Platform at ELI Beamlines. Applied Sciences. 2018; 8(9):1565. https://doi.org/10.3390/app8091565
Chicago/Turabian StyleLevato, Tadzio, Stefano Bonora, Gabriele Maria Grittani, Carlo Maria Lazzarini, Muhammad Fahad Nawaz, Michal Nevrkla, Leonardo Villanova, Roberto Ziano, Silvano Bassanese, Nadezhda Bobrova, and et al. 2018. "HELL: High-Energy Electrons by Laser Light, a User-Oriented Experimental Platform at ELI Beamlines" Applied Sciences 8, no. 9: 1565. https://doi.org/10.3390/app8091565
APA StyleLevato, T., Bonora, S., Grittani, G. M., Lazzarini, C. M., Nawaz, M. F., Nevrkla, M., Villanova, L., Ziano, R., Bassanese, S., Bobrova, N., Casarin, K., Chacon-Golcher, E., Gu, Y., Khikhlukha, D., Kramer, D., Lonza, M., Margarone, D., Olšovcová, V., Rosinski, M., ... Korn, G. (2018). HELL: High-Energy Electrons by Laser Light, a User-Oriented Experimental Platform at ELI Beamlines. Applied Sciences, 8(9), 1565. https://doi.org/10.3390/app8091565





