Swarm Intelligence Algorithms for Feature Selection: A Review
Abstract
Featured Application
Abstract
1. Introduction
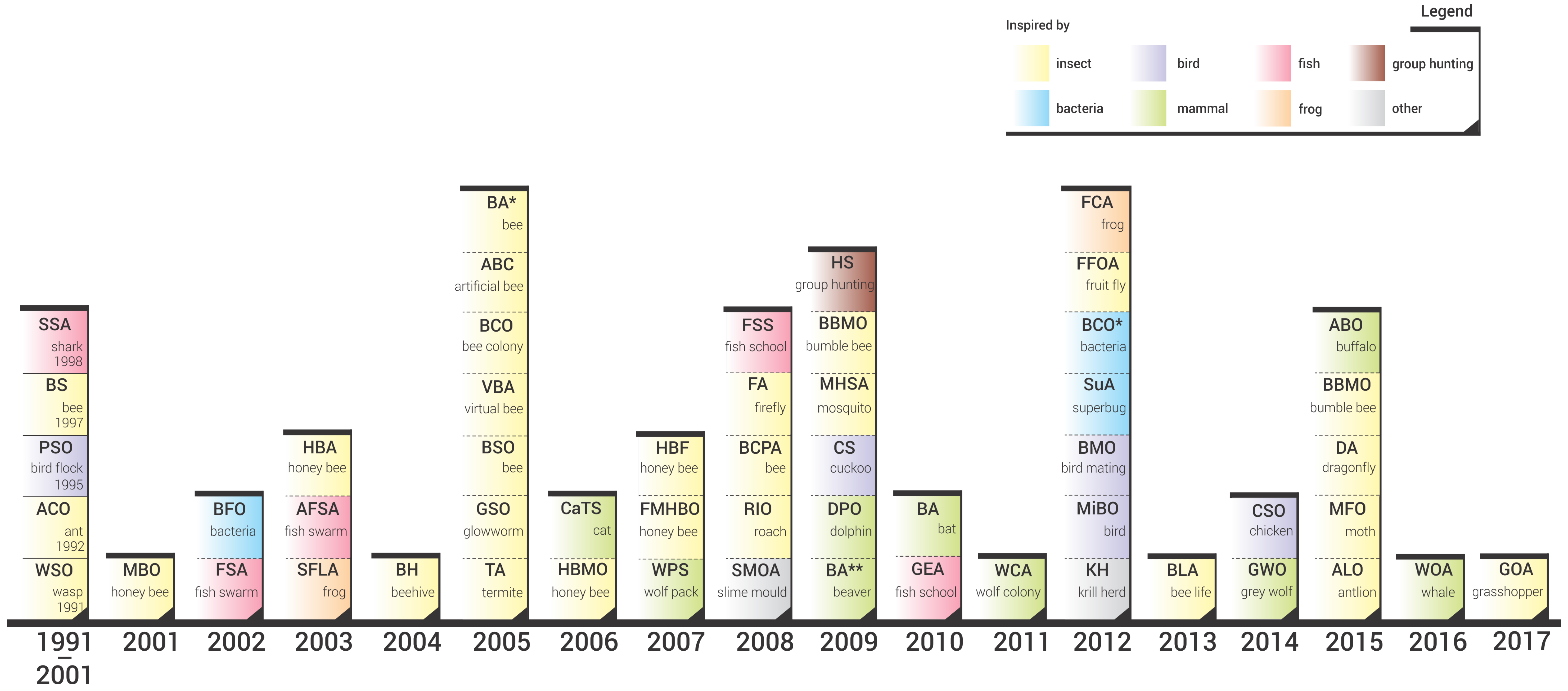
- We performed a comprehensive literature review of swarm intelligence algorithms and propose an SI taxonomy based on the algorithms’ biological inspiration. For all the reviewed algorithms we provide the year of its first appearance in scientific literature; the chronological perspective of SI evolution is presented in this manner.
- We provide unified SI framework, which consists of five fundamental phases. Although the algorithms use different mechanisms, these five phases are common for all of them. The SI framework is used to explain different approaches to FS.
- We provide a comprehensive overview of SI algorithms for FS. Using the proposed SI framework, different approaches, techniques, methods, their settings and implications for use are explained for various FS aspects. Furthermore, the most frequent datasets used for the evaluation of SI algorithms for FS are presented, as well as the most common application areas. Differences among EA approaches against SI approaches are also outlined.
- We systematically outline guidelines for researchers who would like to use SI approaches for FS tasks in real-world.
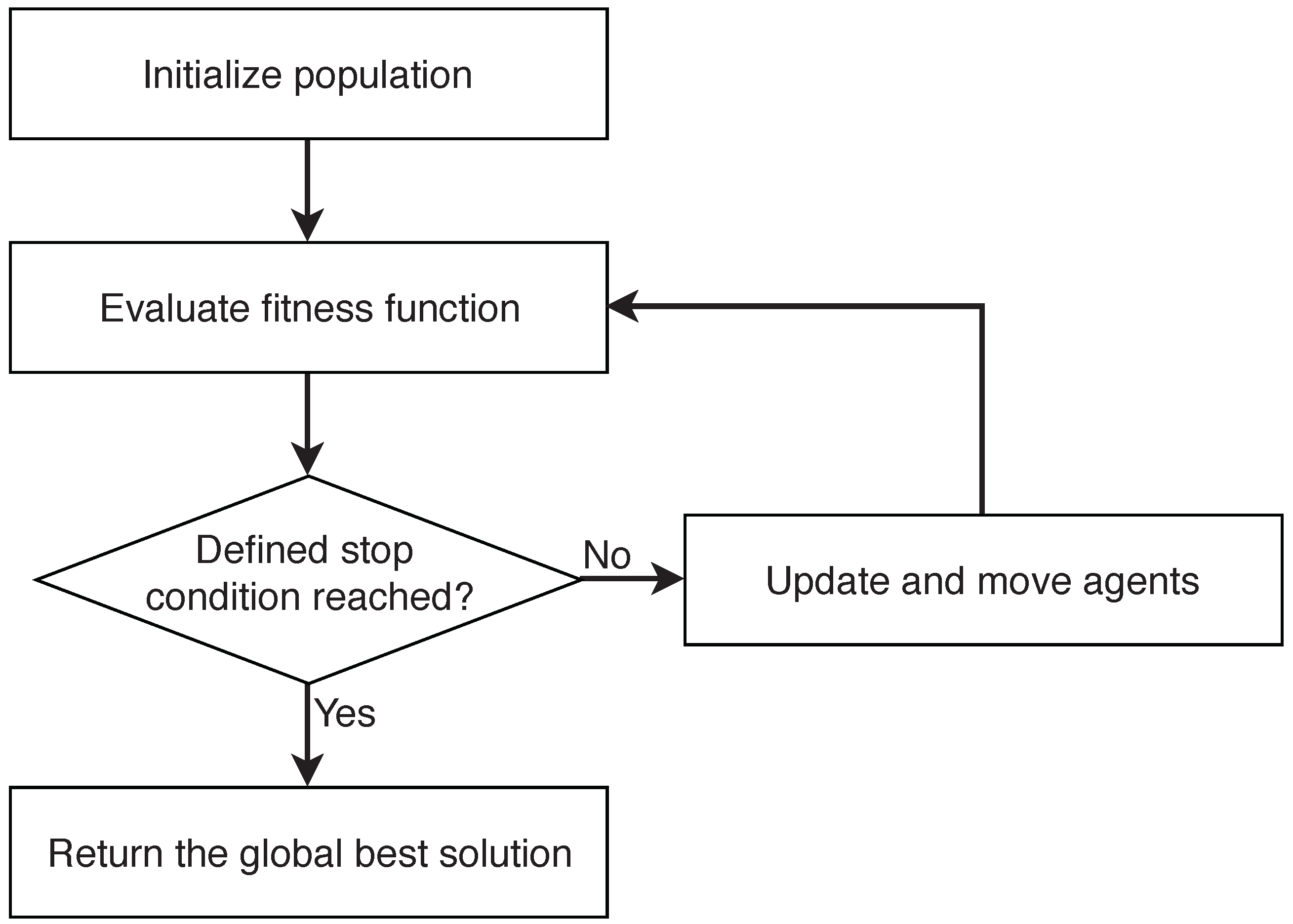
2. Swarm Intelligence
- Initialize population
- Define stop condition
- Evaluate fitness function
- Update and move agents
- Return the global best solution
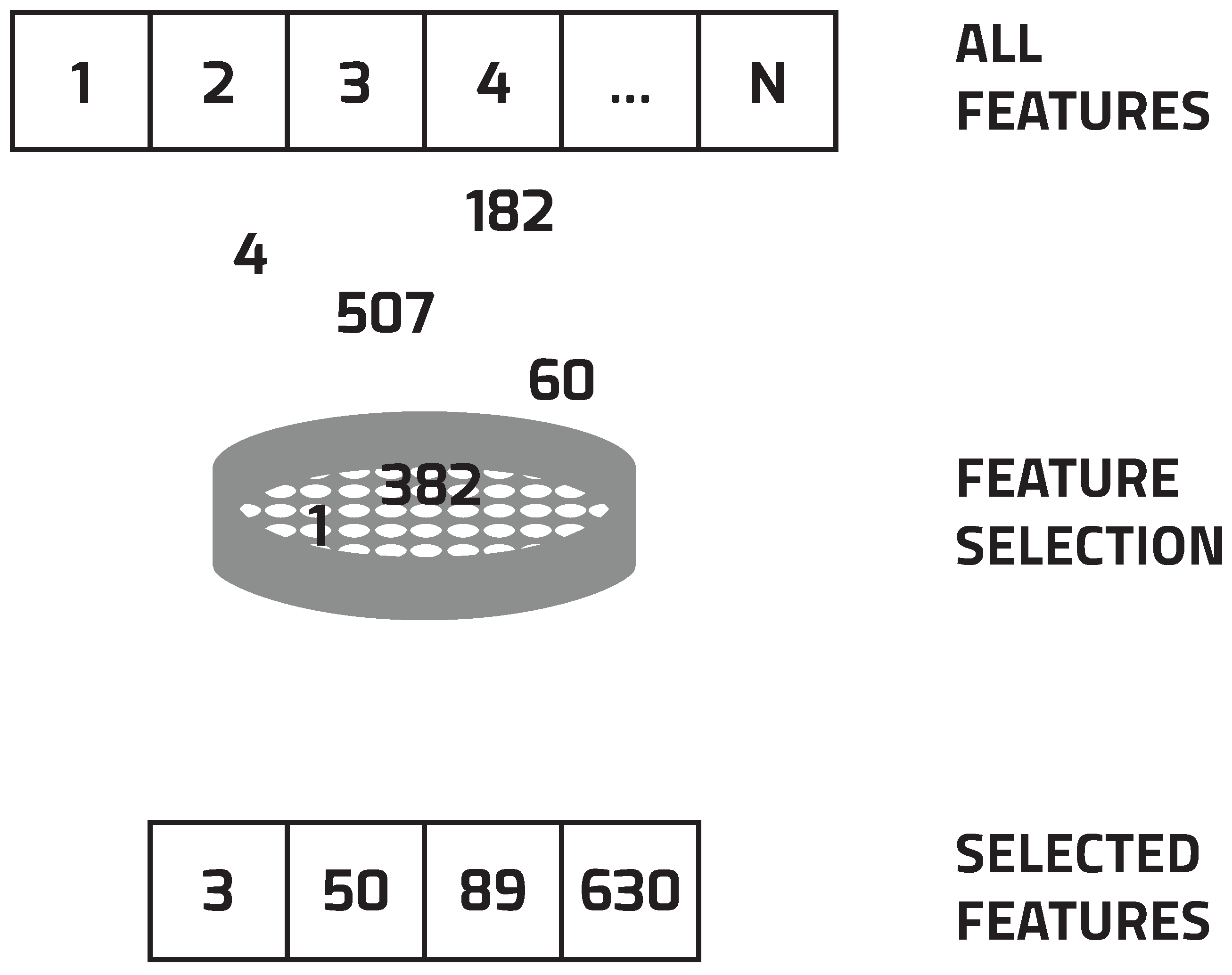
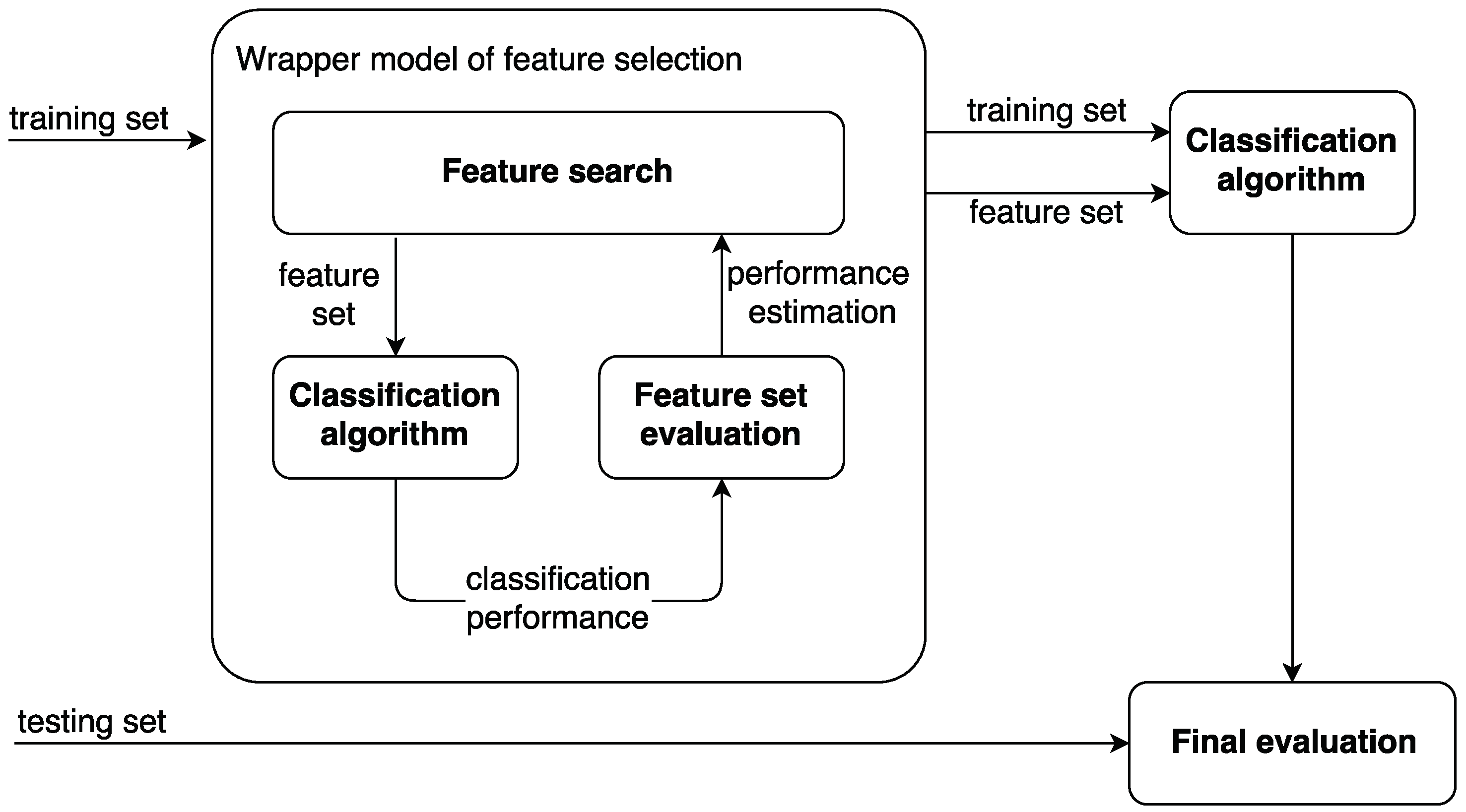
3. Feature Selection
- filter models;
- wrapper models; and
- embedded models.
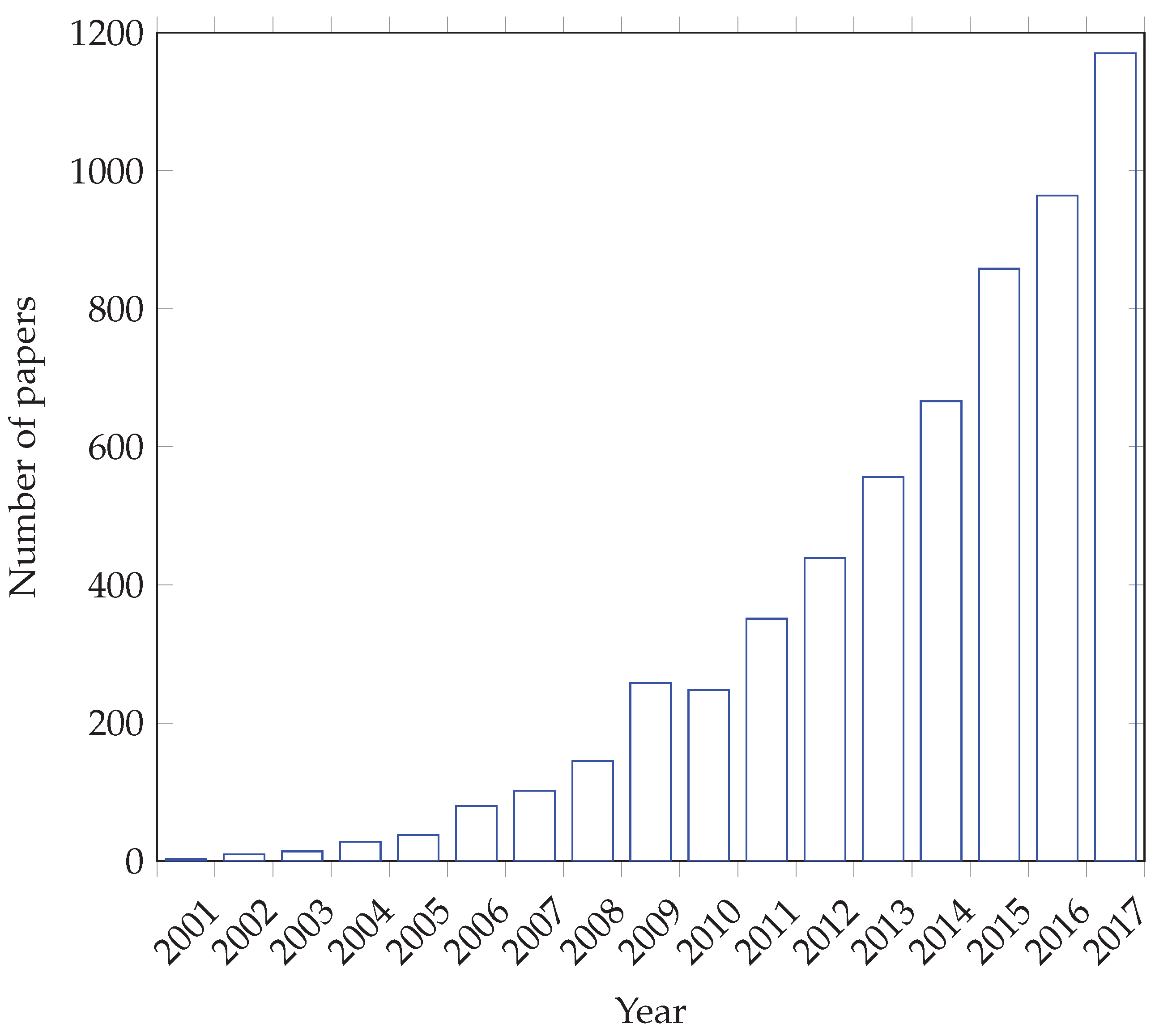
4. Methodology
5. Swarm Intelligence for Feature Selection
- Select a subset of features.
- Evaluate the selected subset by performing the selected classification algorithm.
5.1. Agent Representation
5.2. Initialize Population
5.3. Defined Stopping Condition
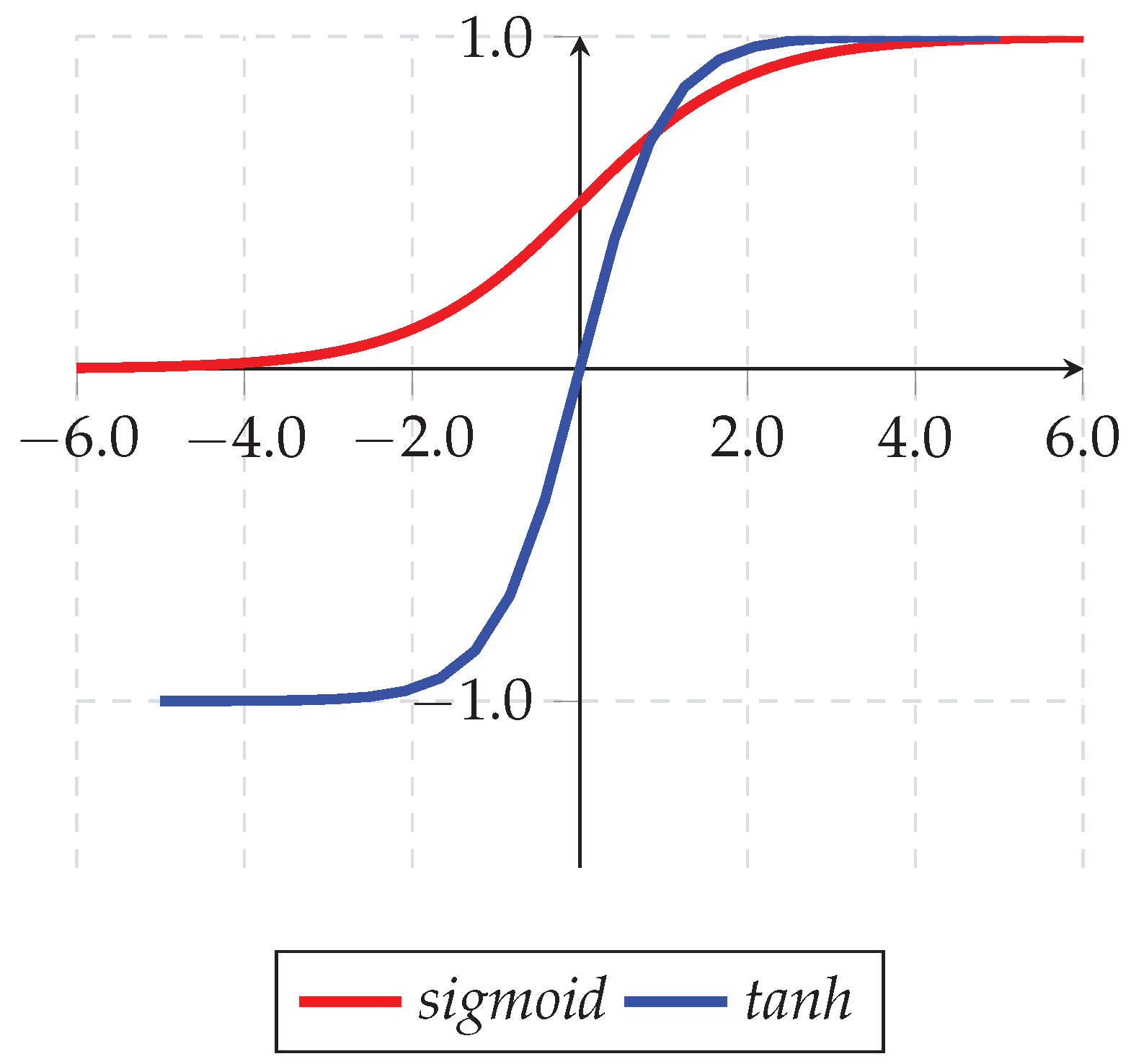
5.4. Fitness Function
| n | is the number of selected features, |
| N | is the number of all features, |
| is the weight for classification accuracy, | |
| is the weight for selected features. |
5.5. Update and Move Agents
6. Applications of Feature Selection with Swarm Intelligence
6.1. Datasets
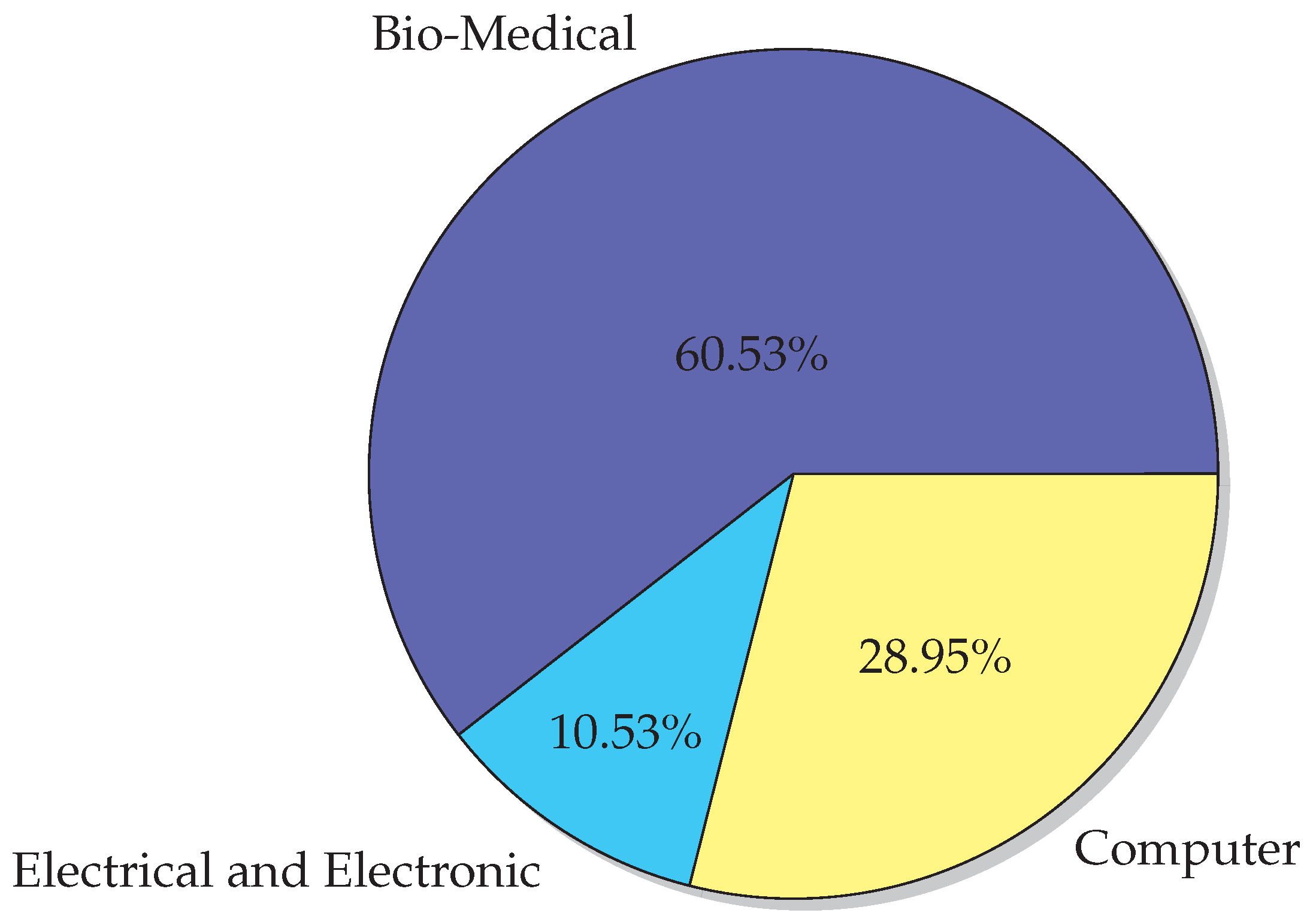
6.2. Application Areas
- Bio-Medical Engineering
- Electrical and Electronic Engineering
- Computer Engineering
7. Discussion
7.1. Issues and Open Questions
7.2. Guidelines for SI Researchers
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Swarm Intelligence Algorithms Sorted by Name
| Algorithm | Full Name | Reference |
|---|---|---|
| ABC | Artificial Bee Colony Algorithm | [112] |
| ABO | African Buffalo Optimization | [113] |
| ACO | Ant Colony Optimization | [8] |
| AFSA | Artificial Fish Swarm Algorithm | [114] |
| ALO | Antlion Optimizer | [115] |
| BA | Bat Algorithm | [116] |
| BA* | Bees Algorithm | [117] |
| BA** | Beaver Algorithm | [118] |
| BBMO | Bumble Bees Mating Optimization | [119] |
| BCO | Bee Colony Optimisation | [120] |
| BCO* | Bacterial Colony Optimization | [121] |
| BCPA | Bee Collecting Pollen Algorithm | [122] |
| BFO | Bacterial Foraging Optimization | [123] |
| BH | BeeHive | [124] |
| BLA | Bees Life Algorithm | [125] |
| BMO | Bird Mating Optimizer | [126] |
| BS | Bee System | [127] |
| BSO | Bees Swarm Optimization | [128] |
| CaTS | The Cat Swarm Optimization | [129] |
| CS | Cuckoo Search | [130] |
| CSO | Chicken Swarm Optimization | [131] |
| DA | Dragonfly Algorithm | [132] |
| DPO | Dolphin Partner Optimization | [133] |
| FA | Firefly Algorithm | [134] |
| FCA | Frog Calling Algorithm | [135] |
| FFOA | Fruit Fly Optimization Algorithm | [136] |
| FMHBO | Fast Marriage in Honey Bees Optimization | [137] |
| FSA | Fish-Swarm Algorithm | [138] |
| FSS | Fish School Search | [139] |
| GEA | Group Escaping Algorithm | [140] |
| GOA | Grasshopper Optimisation Algorithm | [141] |
| GSO | Glow-worm Swarm Optimization | [142] |
| GWO | Grey Wolf Optimizer | [143] |
| HBA | Honey Bee Algorithm | [144] |
| HBF | Honey Bee Foraging | [145] |
| HBMO | Honey Bees Mating Optimization | [146] |
| HS | Hunting Search Algorithm | [147] |
| KH | Krill Herd Algorithm | [148] |
| MBO | Marriage in Honey Bees Optimization | [149] |
| MFO | Moth-Flame Optimization | [150] |
| MHSA | Mosquito Host-Seeking Algorithm | [151] |
| MiBO | Migrating Birds Optimization | [152] |
| PSO | Particle Swam Optimization | [7] |
| RIO | Roach Infestation Optimization | [153] |
| SFLA | Shuffled Frog Leaping Algorithm | [154] |
| SMOA | Slime Mould Optimization Algorithm | [155] |
| SSA | Shark-Search Algorithm | [156] |
| SuA | Superbug Algorithm | [157] |
| TA | Termite Algorithm | [158] |
| VBA | Virtual Bee Algorithm | [159] |
| WCA | Wolf Colony Algorithm | [160] |
| WOA | Whale Optimization Algorithm | [161] |
| WPS | Wolf Pack Search Algorithm | [162] |
| WSO | Wasp Swarm Optimization | [163] |
References
- Cao, J.; Cui, H.; Shi, H.; Jiao, L. Big Data: A Parallel Particle Swarm Optimization-Back-Propagation Neural Network Algorithm Based on MapReduce. PLoS ONE 2016, 11, e157551. [Google Scholar] [CrossRef] [PubMed]
- Cheng, S.; Shi, Y.; Qin, Q.; Bai, R. Swarm Intelligence in Big Data Analytics. In Intelligent Data Engineering and Automated Learning—IDEAL 2013; Yin, H., Tang, K., Gao, Y., Klawonn, F., Lee, M., Weise, T., Li, B., Yao, X., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 417–426. [Google Scholar]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction, 2nd ed.; Springer: New York, NY, USA, 2009; p. 745. [Google Scholar] [CrossRef]
- Blum, C.; Li, X. Swarm Intelligence in Optimization. In Swarm Intelligence; Springer: Berlin/Heidelberg, Germany, 2008; pp. 43–85. [Google Scholar] [CrossRef]
- Hassanien, A.E.; Emary, E. Swarm Intelligence: Principles, Advances, and Applications; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Garey, M.R.; Johnson, D.S. Computers and Intractability, a Guide to the Theory of NP-Completness; W. H. Freeman & Co.: New York, NY, USA, 1979. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the IEEE International Conference on Neural Networks (ICNN ’95), Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar] [CrossRef]
- Dorigo, M. Learning and Natural Algorithms. Ph.D. Thesis, Politecnico di Milano, Milano, Italy, 1992. [Google Scholar]
- Parpinelli, R.; Lopes, H. New inspirations in swarm intelligence: A survey. Int. J. Bio-Inspir. Comput. 2011, 3, 1–16. [Google Scholar] [CrossRef]
- Kar, A.K. Bio inspired computing—A review of algorithms and scope of applications. Expert Syst. Appl. 2016, 59, 20–32. [Google Scholar] [CrossRef]
- Fong, S.; Deb, S.; Yang, X.S.; Li, J. Feature Selection in Life Science Classification: Metaheuristic Swarm Search. IT Prof. 2014, 16, 24–29. [Google Scholar] [CrossRef]
- Basir, M.A.; Ahmad, F. Comparison on Swarm Algorithms for Feature Selections Reductions. Int. J. Sci. Eng. Res. 2014, 5, 479–486. [Google Scholar]
- Xue, B.; Zhang, M.; Browne, W.N.; Yao, X. A Survey on Evolutionary Computation Approaches to Feature Selection. IEEE Trans. Evol. Comput. 2016, 20, 606–626. [Google Scholar] [CrossRef]
- Beni, G.; Wang, J. Swarm Intelligence in Cellular Robotic Systems. In Robots and Biological Systems: Towards a New Bionics? Dario, P., Sandini, G., Aebischer, P., Eds.; Springer: Berlin/Heidelberg, Germany, 1993; pp. 703–712. [Google Scholar] [CrossRef]
- Engelbrecht, A.P. Computational Intelligence: An introduction; Wiley: Hoboken, NJ, USA, 2007. [Google Scholar]
- Millonas, M.M. Swarms, Phase Transitions, and Collective Intelligence. arXiv, 1993; arXiv:adap-org/9306002. [Google Scholar]
- Olariu, S.; Zomaya, A.Y. Handbook of Bioinspired Algorithms and Applications; Chapman and Hall/CRC: London, UK, 2005; Volume 5, p. 704. [Google Scholar] [CrossRef]
- Fister, I., Jr.; Yang, X.S.; Fister, I.; Brest, J.; Fister, D. A Brief Review of Nature-Inspired Algorithms for Optimization. Elektroteh. Vestn. 2013, 80, 116–122. [Google Scholar]
- Mucherino, A.; Seref, O. Monkey search: A novel metaheuristic search for global optimization. AIP Conf. Proc. 2007, 953, 162–173. [Google Scholar] [CrossRef]
- Kaveh, A.; Farhoudi, N. A new optimization method: Dolphin echolocation. Adv. Eng. Softw. 2013, 59, 53–70. [Google Scholar] [CrossRef]
- Chen, C.C.; Tsai, Y.C.; Liu, I.I.; Lai, C.C.; Yeh, Y.T.; Kuo, S.Y.; Chou, Y.H. A Novel Metaheuristic: Jaguar Algorithm with Learning Behavior. In Proceedings of the 2015 IEEE International Conference on Systems, Man, and Cybernetics, Kowloon, China, 9–12 October 2015; pp. 1595–1600. [Google Scholar] [CrossRef]
- Montalvo, I.; Izquierdo, J. Agent Swarm Optimization: Exploding the search space. In Machine Learning for Cyber Physical Systems; Beyerer, J., Niggemann, O., Kühnert, C., Eds.; Springer: Berlin/Heidelberg, Germany, 2017; pp. 55–64. [Google Scholar]
- Montalvo, I.; Izquierdo, J.; Pérez-García, R.; Herrera, M. Water Distribution System Computer-Aided Design by Agent Swarm Optimization. Comput.-Aided Civ. Infrastruct. Eng. 2014, 29, 433–448. [Google Scholar] [CrossRef]
- Liu, H.; Yu, L. Toward integrating feature selection algorithms for classification and clustering. IEEE Trans. Knowl. Data Eng. 2005, 17, 491–502. [Google Scholar]
- Tang, J.; Alelyani, S.; Liu, H. Feature selection for classification: A review. In Data Classification: Algorithms and Applications; CRC Press: Boca Raton, FL, USA, 2014; p. 37. [Google Scholar]
- Liu, H.; Motoda, H. Computational Methods of Feature Selection; CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar]
- Kohavi, R.; John, G.H. Wrappers for feature subset selection. Artif. Intell. 1997, 97, 273–324. [Google Scholar] [CrossRef]
- Brezočnik, L. Feature Selection for Classification Using Particle Swarm Optimization. In Proceedings of the 17th IEEE International Conference on Smart Technologies (IEEE EUROCON 2017), Ohrid, Macedonia, 6–8 July 2017; pp. 966–971. [Google Scholar]
- Lin, S.W.; Ying, K.C.; Chen, S.C.; Lee, Z.J. Particle swarm optimization for parameter determination and feature selection of support vector machines. Expert Syst. Appl. 2008, 35, 1817–1824. [Google Scholar] [CrossRef]
- Vieira, S.M.; Mendonça, L.F.; Farinha, G.J.; Sousa, J.M. Modified binary PSO for feature selection using SVM applied to mortality prediction of septic patients. Appl. Soft Comput. 2013, 13, 3494–3504. [Google Scholar] [CrossRef]
- Boubezoul, A.; Paris, S. Application of global optimization methods to model and feature selection. Pattern Recognit. 2012, 45, 3676–3686. [Google Scholar] [CrossRef]
- Xue, B.; Zhang, M.; Browne, W.N. Novel Initialisation and Updating Mechanisms in PSO for Feature Selection in Classification. In Applications of Evolutionary Computation: 16th European Conference, EvoApplications 2013; Springer: Vienna, Austria, 2013; pp. 428–438. [Google Scholar] [CrossRef]
- Mohammadi, F.G.; Abadeh, M.S. Image steganalysis using a bee colony based feature selection algorithm. Eng. Appl. Artif. Intell. 2014, 31, 35–43. [Google Scholar] [CrossRef]
- Emary, E.; Zawbaa, H.M.; Hassanien, A.E. Binary grey wolf optimization approaches for feature selection. Neurocomputing 2016, 172, 371–381. [Google Scholar] [CrossRef]
- Kashef, S.; Nezamabadi-pour, H. An advanced ACO algorithm for feature subset selection. Neurocomputing 2015, 147, 271–279. [Google Scholar] [CrossRef]
- Kanan, H.R.; Faez, K.; Taheri, S.M. Feature Selection Using Ant Colony Optimization (ACO): A New Method and Comparative Study in the Application of Face Recognition System. In Advances in Data Mining. Theoretical Aspects and Applications: 7th Industrial Conference, ICDM 2007; Perner, P., Ed.; Springer: Leipzig, Germany, 2007; Volume 4597, pp. 63–76. [Google Scholar] [CrossRef]
- Yu, H.; Gu, G.; Liu, H.; Shen, J.; Zhao, J. A Modified Ant Colony Optimization Algorithm for Tumor Marker Gene Selection. Genom. Proteom. Bioinform. 2009, 7, 200–208. [Google Scholar] [CrossRef]
- Schiezaro, M.; Pedrini, H. Data feature selection based on Artificial Bee Colony algorithm. EURASIP J. Image Video Process. 2013, 2013, 47. [Google Scholar] [CrossRef]
- Emary, E.; Zawbaa, H.M.; Grosan, C.; Hassenian, A.E. Feature Subset Selection Approach by Gray-Wolf Optimization. In Afro-European Conference for Industrial Advancement: Proceedings of the First International Afro-European Conference for Industrial Advancement AECIA 2014; Abraham, A., Krömer, P., Snasel, V., Eds.; Springer: Cham, Switzerland, 2015; pp. 1–13. [Google Scholar] [CrossRef]
- Emary, E.; Zawbaa, H.M.; Grosan, C. Experienced Gray Wolf Optimization Through Reinforcement Learning and Neural Networks. IEEE Trans. Neural Netw. Learn. Syst. 2017, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Marinakis, Y.; Marinaki, M.; Matsatsinis, N. A hybrid discrete Artificial Bee Colony—GRASP algorithm for clustering. In Proceedings of the 2009 International Conference on Computers & Industrial Engineering, Troyes, France, 6–9 July 2009; pp. 548–553. [Google Scholar] [CrossRef]
- Zhang, L.; Shan, L.; Wang, J. Optimal feature selection using distance-based discrete firefly algorithm with mutual information criterion. Neural Comput. Appl. 2016, 28, 2795–2808. [Google Scholar] [CrossRef]
- Medjahed, S.A.; Ait Saadi, T.; Benyettou, A.; Ouali, M. Gray Wolf Optimizer for hyperspectral band selection. Appl. Soft Comput. J. 2016, 40, 178–186. [Google Scholar] [CrossRef]
- Marinaki, M.; Marinakis, Y. A bumble bees mating optimization algorithm for the feature selection problem. Handb. Swarm Intell. 2016, 7, 519–538. [Google Scholar] [CrossRef]
- Hu, B.; Dai, Y.; Su, Y.; Moore, P.; Zhang, X.; Mao, C.; Chen, J.; Xu, L. Feature Selection for Optimized High-dimensional Biomedical Data using the Improved Shuffled Frog Leaping Algorithm. IEEE/ACM Trans. Comput. Biol. Bioinform. 2016. [Google Scholar] [CrossRef] [PubMed]
- Medjahed, S.A.; Saadi, T.A.; Benyettou, A.; Ouali, M. Kernel-based learning and feature selection analysis for cancer diagnosis. Appl. Soft Comput. 2017, 51, 39–48. [Google Scholar] [CrossRef]
- Enache, A.C.; Sgarciu, V.; Petrescu-Nita, A. Intelligent feature selection method rooted in Binary Bat Algorithm for intrusion detection. In Proceedings of the 10th Jubilee IEEE International Symposium on Applied Computational Intelligence and Informatics, Proceedings (SACI 2015), Timisoara, Romania, 21–23 May 2015; pp. 517–521. [Google Scholar] [CrossRef]
- Packianather, M.S.; Kapoor, B. A wrapper-based feature selection approach using Bees Algorithm for a wood defect classification system. In Proceedings of the 10th System of Systems Engineering Conference, SoSE 2015, San Antonio, TX, USA, 17–20 May 2015; pp. 498–503. [Google Scholar] [CrossRef]
- Hendrawan, Y.; Murase, H. Neural-Discrete Hungry Roach Infestation Optimization to Select Informative Textural Features for Determining Water Content of Cultured Sunagoke Moss. Environ. Control Biol. 2011, 49, 1–21. [Google Scholar] [CrossRef]
- Gurav, A.; Nair, V.; Gupta, U.; Valadi, J. Glowworm Swarm Based Informative Attribute Selection Using Support Vector Machines for Simultaneous Feature Selection and Classification. In 5th International Conference Swarm, Evolutionary, and Memetic Computing; Springer: Cham, Switzerland, 2015; Volume 8947, pp. 27–37. [Google Scholar] [CrossRef]
- Lin, K.C.; Chen, S.Y.; Hung, J.C. Feature Selection for Support Vector Machines Base on Modified Artificial Fish Swarm Algorithm. In Ubiquitous Computing Application and Wireless Sensor, Lecture Notes in Electrical Engineering 331; Springer: Dordrecht, The Netherlands, 2015. [Google Scholar] [CrossRef]
- Lin, K.C.; Chen, S.Y.; Hung, J.C. Feature Selection and Parameter Optimization of Support Vector Machines Based on Modified Artificial Fish Swarm Algorithms. Math. Probl. Eng. 2015, 2015, 604108. [Google Scholar] [CrossRef]
- Chhikara, R.R.; Sharma, P.; Singh, L. An improved dynamic discrete firefly algorithm for blind image steganalysis. Int. J. Mach. Learn. Cybern. 2016, 9, 821–835. [Google Scholar] [CrossRef]
- Hancer, E.; Xue, B.; Karaboga, D.; Zhang, M. A binary ABC algorithm based on advanced similarity scheme for feature selection. Appl. Soft Comput. J. 2015, 36, 334–348. [Google Scholar] [CrossRef]
- Nakamura, R.Y.M.; Pereira, L.A.M.; Costa, K.A.; Rodrigues, D.; Papa, J.P.; Yang, X.S. BBA: A binary bat algorithm for feature selection. In Proceedings of the Brazilian Symposium of Computer Graphic and Image Processing, Ouro Preto, Brazil, 22–25 August 2012; pp. 291–297. [Google Scholar] [CrossRef]
- Goodarzi, M.; dos Santos Coelho, L. Firefly as a novel swarm intelligence variable selection method in spectroscopy. Anal. Chim. Acta 2014, 852, 20–27. [Google Scholar] [CrossRef] [PubMed]
- Erguzel, T.T.; Ozekes, S.; Gultekin, S.; Tarhan, N. Ant Colony Optimization Based Feature Selection Method for QEEG Data Classification. Psychiatry Investig. 2014, 11, 243–250. [Google Scholar] [CrossRef] [PubMed]
- Long, N.C.; Meesad, P.; Unger, H. A highly accurate firefly based algorithm for heart disease prediction. Expert Syst. Appl. 2015, 42, 8221–8231. [Google Scholar] [CrossRef]
- Jensen, R.; Jensen, R.; Shen, Q. Finding Rough Set Reducts with Ant Colony Optimization. In Proceedings of the 2003 UK Workshop on Computational Intelligence, Guilford, UK, 9–11 September 2003; pp. 15–22. [Google Scholar]
- Lee, S.; Soak, S.; Oh, S.; Pedrycz, W.; Jeon, M. Modified binary particle swarm optimization. Prog. Nat. Sci. 2008, 18, 1161–1166. [Google Scholar] [CrossRef]
- Khanesar, M.A.; Teshnehlab, M.; Shoorehdeli, M.A. A novel binary particle swarm optimization. In Proceedings of the IEEE 2007 Mediterranean Conference on Control & Automation, Athens, Greece, 27–29 June 2007; pp. 1–6. [Google Scholar] [CrossRef]
- Kabir, M.M.; Shahjahan, M.; Murase, K. A new hybrid ant colony optimization algorithm for feature selection. Expert Syst. Appl. 2012, 39, 3747–3763. [Google Scholar] [CrossRef]
- Marinakis, Y.; Marinaki, M.; Matsatsinis, N. A Hybrid Bumble Bees Mating Optimization—GRASP Algorithm for Clustering. In Hybrid Artificial Intelligence Systems, Proceedings of the 4th International Conference, HAIS 2009, Salamanca, Spain, 10–12 June 2009; Corchado, E., Wu, X., Oja, E., Herrero, Á., Baruque, B., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 549–556. [Google Scholar] [CrossRef]
- Wang, H.; Jing, X.; Niu, B. Bacterial-inspired feature selection algorithm and its application in fault diagnosis of complex structures. In Proceedings of the 2016 IEEE Congress on Evolutionary Computation (CEC), Vancouver, BC, Canada, 24–29 July 2016; pp. 3809–3816. [Google Scholar] [CrossRef]
- Lin, K.C.; Zhang, K.Y.; Huang, Y.H.; Hung, J.C.; Yen, N. Feature selection based on an improved cat swarm optimization algorithm for big data classification. J. Supercomput. 2016, 72, 3210–3221. [Google Scholar] [CrossRef]
- Dara, S.; Banka, H. A Binary PSO Feature Selection Algorithm for Gene Expression Data. In Proceedings of the 2014 International Conference on Advances in Communication and Computing Technologies, Mumbai, India, 10–11 August 2014; pp. 1–6. [Google Scholar]
- Mafarja, M.M.; Mirjalili, S. Hybrid Whale Optimization Algorithm with simulated annealing for feature selection. Neurocomputing 2017, 260, 302–312. [Google Scholar] [CrossRef]
- Rodrigues, D.; Pereira, L.A.M.; Papa, J.P.; Weber, S.A.T. A binary krill herd approach for feature selection. Proc. Int. Conf. Pattern Recognit. 2014, 1407, 1407–1412. [Google Scholar] [CrossRef]
- Dheeru, D.; Karra Taniskidou, E. UCI Machine Learning Repository. University of California, Irvine, School of Information and Computer Sciences, 2017. Available online: http://archive.ics.uci.edu/ml. (accessed on 20 June 2018).
- Statnikov, A.; Tsamardinos, I.; Dosbayev, Y.; Aliferis, C.F. GEMS: A system for automated cancer diagnosis and biomarker discovery from microarray gene expression data. Int. J. Med. Inform. 2005, 74, 491–503. [Google Scholar] [CrossRef] [PubMed]
- Chang, C.-C.; Lin, C.-J. LIBSVM: A library for support vector machines. ACM Trans. Intell. Syst. Technol. 2011, 2, 27:1–27:27. [Google Scholar] [CrossRef]
- Li, J. Kent Ridge Bio-medical Dataset. Available online: http://leo.ugr.es/elvira/DBCRepository/ (accessed on 20 June 2018).
- Fan, H.; Zhong, Y. A Rough Set Approach to Feature Selection Based on Wasp Swarm Optimization. J. Comput. Inf. Syst. 2012, 8, 1037–1045. [Google Scholar]
- Chen, K.H.; Wang, K.J.; Tsai, M.L.; Wang, K.M.; Adrian, A.M.; Cheng, W.C.; Yang, T.S.; Teng, N.C.; Tan, K.P.; Chang, K.S. Gene selection for cancer identification: A decision tree model empowered by particle swarm optimization algorithm. BMC Bioinform. 2014, 15, 49. [Google Scholar] [CrossRef] [PubMed]
- Kar, S.; Das Sharma, K.; Maitra, M. Gene selection from microarray gene expression data for classification of cancer subgroups employing PSO and adaptive K-nearest neighborhood technique. Expert Syst. Appl. 2015, 42, 612–627. [Google Scholar] [CrossRef]
- Pashaei, E.; Ozen, M.; Aydin, N. Improving medical diagnosis reliability using Boosted C5.0 decision tree empowered by Particle Swarm Optimization. In Proceedings of the 2015 37th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Milan, Italy, 25–29 Ausgut 2015; pp. 7230–7233. [Google Scholar] [CrossRef]
- Fong, S.; Wong, R.; Vasilakos, A. Accelerated PSO Swarm Search Feature Selection for Data Stream Mining Big Data. IEEE Trans. Serv. Comput. 2015, 33–45. [Google Scholar] [CrossRef]
- Tran, B.; Xue, B.; Zhang, M. A New Representation in PSO for Discretization-Based Feature Selection. IEEE Trans. Cybern. 2017. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Zhu, Q.; Xu, H. Finding rough set reducts with fish swarm algorithm. Knowl.-Based Syst. 2015, 81, 22–29. [Google Scholar] [CrossRef]
- Shahana, A.H.; Preeja, V. A binary krill herd approach based feature selection for high dimensional data. In Proceedings of the IEEE 2016 International Conference on Inventive Computation Technologies (ICICT), Coimbatore, India, 26–27 August 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Thamaraichelvi, B.; Yamuna, G. Hybrid Firefly Swarm Intelligence Based Feature Selection for Medical Data Classification and Segmentation in SVD—NSCT Domain. Int. J. Adv. Res. 2016, 4, 744–760. [Google Scholar] [CrossRef]
- Wan, Y.; Wang, M.; Ye, Z.; Lai, X. A feature selection method based on modified binary coded ant colony optimization algorithm. Appl. Soft Comput. 2016, 49, 248–258. [Google Scholar] [CrossRef]
- Saraç, E.; Özel, S.A. An ant colony optimization based feature selection for web page classification. Sci. World J. 2014, 2014, 649260. [Google Scholar] [CrossRef] [PubMed]
- Pal, M.; Bhattacharyya, S.; Roy, S.; Konar, A.; Tibarewala, D.; Janarthanan, R. A bacterial foraging optimization and learning automata based feature selection for motor imagery EEG classification. In Proceedings of the IEEE 2014 International Conference on Signal Processing and Communications (SPCOM), Bangalore, India, 22–25 July 2014; pp. 1–5. [Google Scholar] [CrossRef]
- Zhou, D.; Fang, Y.; Botzheim, J.; Kubota, N.; Liu, H. Bacterial Memetic Algorithm based Feature Selection for Surface EMG based Hand Motion Recognition in Long-term Use. In Proceedings of the 2016 IEEE Symposium Series on Computational Intelligence, Athens, Greece, 6–9 December 2016; pp. 1–7. [Google Scholar]
- Wang, M.; Wang, X.; Li, G. A improved speech synthesis system utilizing BPSO-based lip feature selection. In Proceedings of the IEEE 2011 4th International Conference on Biomedical Engineering and Informatics (BMEI), Shanghai, China; 2011; pp. 1292–1295. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, W.; Li, Y.; Jiao, L. PSO-based automatic relevance determination and feature selection system for hyperspectral image classification. Electron. Lett. 2012, 48, 1263–1265. [Google Scholar] [CrossRef]
- Hu, Z.; Chiong, R.; Pranata, I.; Susilo, W.; Bao, Y. Identifying malicious web domains using machine learning techniques with online credibility and performance data. In Proceedings of the 2016 IEEE Congress on Evolutionary Computation (CEC), Vancouver, BC, Canada, 24–29 July 2016; pp. 5186–5194. [Google Scholar] [CrossRef]
- Sattiraju, M.; Manikandan, M.V.; Manikantan, K.; Ramachandran, S. Adaptive BPSO based feature selection and skin detection based background removal for enhanced face recognition. In Proceedings of the 2013 IEEE Fourth National Conference on Computer Vision, Pattern Recognition, Image Processing and Graphics (NCVPRIPG), Jodhpur, India, 18–21 December 2013; pp. 1–4. [Google Scholar] [CrossRef]
- Dehuri, S.; Roy, R.; Cho, S.B. An adaptive binary PSO to learn bayesian classifier for prognostic modeling of metabolic syndrome. In Proceedings of the 13th annual conference companion on Genetic and evolutionary computation (GECCO ’11), Dublin, Ireland, 12–16 July 2011; ACM Press: New York, NY, USA, 2011; pp. 495–502. [Google Scholar] [CrossRef]
- Chen, K.H.; Wang, K.J.; Wang, K.M.; Angelia, M.A. Applying particle swarm optimization-based decision tree classifier for cancer classification on gene expression data. Appl. Soft Comput. 2014, 24, 773–780. [Google Scholar] [CrossRef]
- Li, Q.; Chen, H.; Huang, H.; Zhao, X.; Cai, Z.; Tong, C.; Liu, W.; Tian, X. An Enhanced Grey Wolf Optimization Based Feature Selection Wrapped Kernel Extreme Learning Machine for Medical Diagnosis. Comput. Math. Methods Med. 2017, 2017, 9512741. [Google Scholar] [CrossRef] [PubMed]
- Manikandan, S.; Manimegalai, R.; Hariharan, M. Gene Selection from Microarray Data Using Binary Grey Wolf Algorithm for Classifying Acute Leukemia. Curr. Signal Transduct. Ther. 2016, 11, 76–78. [Google Scholar] [CrossRef]
- Seth, J.K.; Chandra, S. Intrusion detection based on key feature selection using binary GWO. In Proceedings of the IEEE 3rd International Conference on Computing for Sustainable Global Development (INDIACom), New Delhi, India, 16–18 March 2016; pp. 3735–3740. [Google Scholar]
- Sargo, J.A.G.; Vieira, S.M.; Sousa, J.M.C.; Filho, C.J.B. Binary Fish School Search applied to feature selection: Application to ICU readmissions. In Proceedings of the 2014 IEEE International Conference on Fuzzy Systems (FUZZ-IEEE), Beijing, China, 6–11 July 2014; pp. 1366–1373. [Google Scholar] [CrossRef]
- Wang, G.; Dai, D. Network Intrusion Detection Based on the Improved Artificial Fish Swarm Algorithm. J. Comput. 2013, 8, 2990–2996. [Google Scholar] [CrossRef]
- Dai, Y.; Hu, B.; Su, Y.; Mao, C.; Chen, J.; Zhang, X.; Moore, P.; Xu, L.; Cai, H. Feature selection of high-dimensional biomedical data using improved SFLA for disease diagnosis. In Proceedings of the 2015 IEEE International Conference on Bioinformatics and Biomedicine (BIBM), Washington, DC, USA, 9–12 November 2015; pp. 458–463. [Google Scholar] [CrossRef]
- Ladgham, A.; Torkhani, G.; Sakly, A.; Mtibaa, A. Modified support vector machines for MR brain images recognition. In Proceedings of the 2013 IEEE International Conference on Control, Decision and Information Technologies (CoDIT), Hammamet, Tunisia, 6–8 May 2013; pp. 32–35. [Google Scholar] [CrossRef]
- Baranidharan, T.; Sumathi, T.; Shekar, V. Weight Optimized Neural Network Using Metaheuristics for the Classification of Large Cell Carcinoma and Adenocarcinoma from Lung Imaging. Curr. Signal Transduct. Ther. 2016, 11, 91–97. [Google Scholar] [CrossRef]
- Wang, L.; Jia, P.; Huang, T.; Duan, S.; Yan, J.; Wang, L. A Novel Optimization Technique to Improve Gas Recognition by Electronic Noses Based on the Enhanced Krill Herd Algorithm. Sensors 2016, 16, 1275. [Google Scholar] [CrossRef] [PubMed]
- Gunavathi, C.; Premalatha, K. A comparative analysis of swarm intelligence techniques for feature selection in cancer classification. Sci. World J. 2014, 2014, 693831. [Google Scholar] [CrossRef] [PubMed]
- Chuang, L.Y.; Yang, C.H.; Yang, C.H. Tabu Search and Binary Particle Swarm Optimization for Feature Selection Using Microarray Data. J. Comput. Biol. 2009, 16, 1689–1703. [Google Scholar] [CrossRef] [PubMed]
- Hafez, A.I.; Hassanien, A.E.; Zawbaa, H.M. Hybrid Swarm Intelligence Algorithms for Feature Selection: Monkey and Krill Herd Algorithms. In Proceedings of the IEEE International Computer Engineering Conference—ICENCO, Cairo, Egypt, 29–30 December 2015. [Google Scholar]
- Monteiro, S.T.; Kosugi, Y. Applying Particle Swarm Intelligence for Feature Selection of Spectral Imagery. In Proceedings of the IEEE Seventh International Conference on Intelligent Systems Design and Applications (ISDA 2007), Rio de Janeiro, Brazil, 20–24 October 2007; pp. 933–938. [Google Scholar] [CrossRef]
- Martinez, E.; Alvarez, M.M.; Trevino, V. Compact cancer biomarkers discovery using a swarm intelligence feature selection algorithm. Comput. Biol. Chem. 2010, 34, 244–250. [Google Scholar] [CrossRef] [PubMed]
- Fister, I., Jr.; Tepeh, A.; Brest, J.; Fister, I. Population Size Reduction in Particle Swarm Optimization Using Product Graphs. In Mendel 2015; Springer: Cham, Switzerland, 2015; pp. 77–87. [Google Scholar]
- Črepinšek, M.; Liu, S.H.; Mernik, M. Replication and comparison of computational experiments in applied evolutionary computing: common pitfalls and guidelines to avoid them. Appl. Soft Comput. 2014, 19, 161–170. [Google Scholar] [CrossRef]
- Sörensen, K. Metaheuristics—The metaphor exposed. Int. Trans. Oper. Res. 2013, 3–18. [Google Scholar] [CrossRef]
- Vrbančič, G.; Brezočnik, L.; Mlakar, U.; Fister, D.; Fister, I., Jr. NiaPy: Python microframework for building nature-inspired algorithms. J. Open Source Softw. 2018, 3. [Google Scholar] [CrossRef]
- Wolpert, D.H.; Macready, W.G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef]
- Ho, Y.C.; Pepyne, D.L. Simple explanation of the no-free-lunch theorem and its implications. J. Optim. Theory Appl. 2002, 115, 549–570. [Google Scholar] [CrossRef]
- Karaboga, D. An Idea Based on Honey Bee Swarm for Numerical Optimization; Technical Report; Erciyes University, Engineering Faculty, Computer Engineering Department: Kayseri, Turkey, 2005. [Google Scholar]
- Odili, J.B.; Kahar, M.N.M.; Anwar, S. African Buffalo Optimization: A Swarm-Intelligence Technique. Procedia Comput. Sci. 2015, 76, 443–448. [Google Scholar] [CrossRef]
- Li, X.L. A New Intelligent Optimization-Artificial Fish Swarm Algorithm. Ph.D. Thesis, Zhejiang University, Hangzhou, China, 2003. [Google Scholar]
- Mirjalili, S. The Ant Lion Optimizer. Adv. Eng. Softw. 2015, 83, 80–98. [Google Scholar] [CrossRef]
- Yang, X.S. A New Metaheuristic Bat-Inspired Algorithm. In Nature Inspired Cooperative Strategies for Optimization (NICSO 2010); Springer: Berlin/Heidelberg, Germany, 2010; Volume 284, pp. 65–74. [Google Scholar]
- Pham, D.; Ghanbarzadeh, A.; Koc, E.; Otri, S.; Rahim, S.; Zaidi, M. The Bees Algorithm. Technical Note; Technical Report; Manufacturing Engineering Centre, Cardiff University: Cardiff, UK, 2005. [Google Scholar]
- Ayesh, A. Beaver algorithm for network security and optimization: Preliminary report. In Proceedings of the 2009 IEEE International Conference on Systems, Man and Cybernetics, San Antonio, TX, USA, 11–14 October 2009; pp. 3657–3662. [Google Scholar] [CrossRef]
- Marinakis, Y.; Marinaki, M.; Matsatsinis, N. A Bumble Bees Mating Optimization Algorithm for Global Unconstrained Optimization Problems. In Nature Inspired Cooperative Strategies for Optimization (NICSO 2010); González, J.R., Pelta, D.A., Cruz, C., Terrazas, G., Krasnogor, N., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 305–318. [Google Scholar]
- Teodorović, D.; Dell’Orco, M. Bee colony optimization—A cooperative learning approach to complex transportation problems. Adv. OR AI Methods Transp. 2005, 51, 60. [Google Scholar]
- Niu, B.; Wang, H. Bacterial Colony Optimization. Discret. Dyn. Nat. Soc. 2012, 2012, 698057. [Google Scholar] [CrossRef]
- Lu, X.; Zhou, Y. A Novel Global Convergence Algorithm: Bee Collecting Pollen Algorithm. In Advanced Intelligent Computing Theories and Applications. With Aspects of Artificial Intelligence; Springer: Berlin/Heidelberg, Germany, 2008; pp. 518–525. [Google Scholar]
- Passino, K. Biomimicry of bacterial foraging for distributed optimization and control. IEEE Control Syst. Mag. 2002, 22, 52–67. [Google Scholar] [CrossRef]
- Wedde, H.F.; Farooq, M.; Zhang, Y. BeeHive: An Efficient Fault-Tolerant Routing Algorithm Inspired by Honey Bee Behavior. In Ant Colony Optimization and Swarm Intelligence; Dorigo, M., Birattari, M., Blum, C., Gambardella, L.M., Mondada, F., Stützle, T., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; pp. 83–94. [Google Scholar] [CrossRef]
- Bitam, S.; Mellouk, A. Bee life-based multi constraints multicast routing optimization for vehicular ad hoc networks. J. Netw. Comput. Appl. 2013, 36, 981–991. [Google Scholar] [CrossRef]
- Askarzadeh, A.; Rezazadeh, A. A new heuristic optimization algorithm for modeling of proton exchange membrane fuel cell: bird mating optimizer. Int. J. Energy Res. 2012, 37, 1196–1204. [Google Scholar] [CrossRef]
- Sato, T.; Hagiwara, M. Bee System: finding solution by a concentrated search. In Proceedings of the 1997 IEEE International Conference on Systems, Man, and Cybernetics, Orlando, FL, USA, 12–15 October 1997; Volume 4, pp. 3954–3959. [Google Scholar] [CrossRef]
- Drias, H.; Sadeg, S.; Yahi, S. Cooperative Bees Swarm for Solving the Maximum Weighted Satisfiability Problem. In International Work-Conference on Artificial Neural Networks (IWANN); Springer: Berlin/Heidelberg, Germany, 2005; pp. 318–325. [Google Scholar] [CrossRef]
- Chu, S.C.; Tsai, P.w.; Pan, J.S. Cat Swarm Optimization. In Pacific Rim International Conference on Artificial Intelligence; Springer: Berlin/Heidelberg, Germany, 2006; pp. 854–858. [Google Scholar] [CrossRef]
- Yang, X.S.; Suash, D. Cuckoo Search via Lévy flights. In Proceedings of the 2009 IEEE World Congress on Nature & Biologically Inspired Computing (NaBIC), Coimbatore, India, 9–11 December 2009; pp. 210–214. [Google Scholar] [CrossRef]
- Meng, X.; Liu, Y.; Gao, X.; Zhang, H. A New Bio-inspired Algorithm: Chicken Swarm Optimization. In Advances in Swarm Intelligence; Springer: Cham, Switzerland, 2014; pp. 86–94. [Google Scholar]
- Mirjalili, S. Dragonfly algorithm: A new meta-heuristic optimization technique for solving single-objective, discrete, and multi-objective problems. Neural Comput. Appl. 2015, 27, 1053–1073. [Google Scholar] [CrossRef]
- Shiqin, Y.; Jianjun, J.; Guangxing, Y. A Dolphin Partner Optimization. In Proceedings of the 2009 IEEE WRI Global Congress on Intelligent Systems, Xiamen, China, 19–21 May 2009; pp. 124–128. [Google Scholar] [CrossRef]
- Yang, X.S. Firefly Algorithm. In Nature-Inspired Metaheuristic Algorithms; Luniver Press: Beckington, UK, 2008; p. 128. [Google Scholar]
- Mutazono, A.; Sugano, M.; Murata, M. Energy efficient self-organizing control for wireless sensor networks inspired by calling behavior of frogs. Comput. Commun. 2012, 35, 661–669. [Google Scholar] [CrossRef]
- Pan, W.T. A new Fruit Fly Optimization Algorithm: Taking the financial distress model as an example. Knowl.-Based Syst. 2012, 26, 69–74. [Google Scholar] [CrossRef]
- Yang, C.; Chen, J.; Tu, X. Algorithm of Fast Marriage in Honey Bees Optimization and Convergence Analysis. In Proceedings of the 2007 IEEE International Conference on Automation and Logistics, Jinan, China, 18–21 August 2007; pp. 1794–1799. [Google Scholar] [CrossRef]
- Li, X.L.; Shao, Z.J.; Qian, J.X. An Optimizing Method based on Autonomous Animate: Fish Swarm Algorithm. Syst. Eng. Theory Pract. 2002, 22, 32–38. [Google Scholar]
- Bastos Filho, C.J.A.; de Lima Neto, F.B.; Lins, A.J.C.C.; Nascimento, A.I.S.; Lima, M.P. A novel search algorithm based on fish school behavior. In Proceedings of the 2008 IEEE International Conference on Systems, Man and Cybernetics, Singapore, 12–15 October 2008; pp. 2646–2651. [Google Scholar] [CrossRef]
- Min, H.; Wang, Z. Group escape behavior of multiple mobile robot system by mimicking fish schools. In Proceedings of the IEEE International Conference on Robotics and Biometrics (ROBIO), Tianjin, China, 14–18 December 2010; pp. 320–326. [Google Scholar]
- Saremi, S.; Mirjalili, S.; Lewis, A. Grasshopper Optimisation Algorithm: Theory and application. Adv. Eng. Softw. 2017, 105, 30–47. [Google Scholar] [CrossRef]
- Krishnanand, K.; Ghose, D. Detection of multiple source locations using a glowworm metaphor with applications to collective robotics. In Proceedings of the IEEE Swarm Intelligence Symposium, Pasadena, CA, USA, 8–10 June 2005; pp. 84–91. [Google Scholar]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Nakrani, S.; Tovey, C. On Honey Bees and Dynamic Allocation in an Internet Server Colony. In Proceedings of the 2nd International Workshop on The Mathematics and Algorithms of Social Insects, Atlanta, GA, USA, 15–17 December 2003; pp. 1–8. [Google Scholar]
- Baig, A.R.; Rashid, M. Honey bee foraging algorithm for multimodal & dynamic optimization problems. In Proceedings of the 9th Annual Conference on Genetic and Evolutionary Computation (GECCO ’07), London, UK, 7–11 July 2007; ACM Press: New York, NY, USA, 2007; p. 169. [Google Scholar] [CrossRef]
- Haddad, O.B.; Afshar, A.; Mariño, M.A. Honey-Bees Mating Optimization (HBMO) Algorithm: A New Heuristic Approach for Water Resources Optimization. Water Resour. Manag. 2006, 20, 661–680. [Google Scholar] [CrossRef]
- Oftadeh, R.; Mahjoob, M.J. A new meta-heuristic optimization algorithm: Hunting Search. In Proceedings of the 2009 IEEE Fifth International Conference on Soft Computing, Computing with Words and Perceptions in System Analysis, Decision and Control, Famagusta, Cyprus, 2–4 September 2009; pp. 1–5. [Google Scholar] [CrossRef]
- Gandomi, A.H.; Alavi, A.H. Krill herd: A new bio-inspired optimization algorithm. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 4831–4845. [Google Scholar] [CrossRef]
- Abbass, H. MBO: marriage in honey bees optimization-a Haplometrosis polygynous swarming approach. In Proceedings of the 2001 IEEE Congress on Evolutionary Computation (IEEE Cat. No.01TH8546), Seoul, Korea, 27–30 May 2001; Volume 1, pp. 207–214. [Google Scholar] [CrossRef]
- Mirjalili, S. Moth-flame optimization algorithm: A novel nature-inspired heuristic paradigm. Knowl.-Based Syst. 2015, 89, 228–249. [Google Scholar] [CrossRef]
- Feng, X.; Lau, F.C.M.; Gao, D. A New Bio-inspired Approach to the Traveling Salesman Problem. In International Conference on Complex Sciences; Springer: Berlin/Heidelberg, Germany, 2009; pp. 1310–1321. [Google Scholar] [CrossRef]
- Duman, E.; Uysal, M.; Alkaya, A.F. Migrating Birds Optimization: A new metaheuristic approach and its performance on quadratic assignment problem. Inf. Sci. 2012, 217, 65–77. [Google Scholar] [CrossRef]
- Havens, T.C.; Spain, C.J.; Salmon, N.G.; Keller, J.M. Roach Infestation Optimization. In Proceedings of the 2008 IEEE Swarm Intelligence Symposium, St. Louis, MO, USA, 21–23 September 2008; pp. 1–7. [Google Scholar] [CrossRef]
- Eusuff, M.M.; Lansey, K.E. Optimization of Water Distribution Network Design Using the Shuffled Frog Leaping Algorithm. J. Water Resour. Plan. Manag. 2003, 129, 210–225. [Google Scholar] [CrossRef]
- Monismith, D.R.; Mayfield, B.E. Slime Mold as a model for numerical optimization. In Proceedings of the 2008 IEEE Swarm Intelligence Symposium, St. Louis, MO, USA, 21–23 September 2008; pp. 1–8. [Google Scholar] [CrossRef]
- Hersovici, M.; Jacovi, M.; Maarek, Y.S.; Pelleg, D.; Shtalhaim, M.; Ur, S. The shark-search algorithm. An application: Tailored Web site mapping. Comput. Netw. ISDN Syst. 1998, 30, 317–326. [Google Scholar] [CrossRef]
- Anandaraman, C.; Madurai Sankar, A.V.; Natarajan, R. A New Evolutionary Algorithm Based on Bacterial Evolution and Its Application for Scheduling A Flexible Manufacturing System. J. Tek. Ind. 2012, 14, 1–12. [Google Scholar] [CrossRef]
- Roth, M.H. Termite: A Swarm Intelligent Routing Algorithm for Mobile Wireless Ad-Hoc Networks. Ph.D. Thesis, Cornell University, Ithaca, NY, USA, 2005. [Google Scholar]
- Yang, X.S. Engineering Optimizations via Nature-Inspired Virtual Bee Algorithms. In International Work-Conference on the Interplay Between Natural and Artificial Computation; Springer: Berlin/Heidelberg, Germany, 2005; pp. 317–323. [Google Scholar]
- Liu, C.; Yan, X.; Liu, C.; Wu, H. The Wolf Colony Algorithm and Its Application. Chin. J. Electron. 2011, 20, 664–667. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Yang, C.; Tu, X.; Chen, J. Algorithm of Marriage in Honey Bees Optimization Based on the Wolf Pack Search. In Proceedings of the 2007 IEEE International Conference on Intelligent Pervasive Computing (IPC 2007), Jeju City, Korea, 11–13 October 2007; pp. 462–467. [Google Scholar] [CrossRef]
- Theraulaz, G.; Goss, S.; Gervet, J.; Deneubourg, J.L. Task differentiation in Polistes wasp colonies: A model for self-organizing groups of robots. In Proceedings of the First international Conference on Simulation of Adaptive Behavior on from Animals to Animats, Paris, France, 24–28 September 1991; pp. 346–355. [Google Scholar]
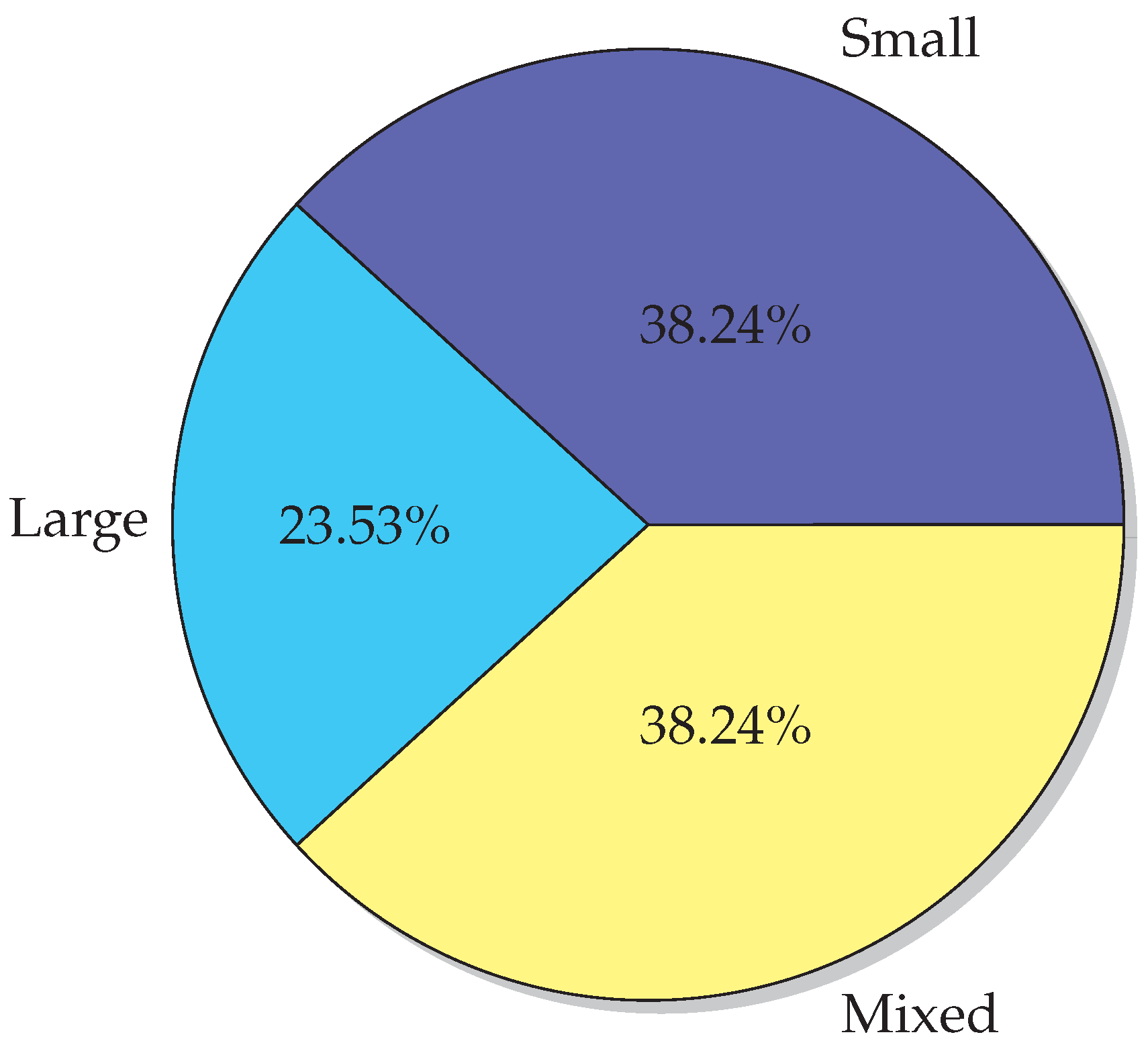
| Academic Online Database | Hits |
|---|---|
| ACM Digital Library | 61 |
| IEEE Xplore | 52 |
| ScienceDirect | 409 |
| SpringerLink | 603 |
| Web of Science | 98 |
| Small | Large | Mixed | ∑ | |
|---|---|---|---|---|
| Insect | ABC [38,41] | DA [46] | ABC [54] | 11 |
| BBMO [44,63] | GSO [50] | FA [42] | ||
| ACO [35] | ACO [62] | |||
| WSO [73] | ||||
| Bacteria | BFO and BCO [64] | 1 | ||
| Bird | PSO [29,31] | PSO [66,74,75] | PSO [28,30,76] | 10 |
| [77] | [78] | |||
| Mammal | GWO [39] | GWO [34,40] | 6 | |
| CaTS [65] | BA [55] | |||
| WOA [67] | ||||
| Fish | AFSA [51,52] | 3 | ||
| FSA [79] | ||||
| Frog | SFLA [45] | 1 | ||
| Other | KH [68,80] | 2 |
| Bio-Medical Engineering | Electrical and Electronic Engineering | Computer Engineering | ∑ | |
|---|---|---|---|---|
| Insects | DA [46] RIO [49] | FA [56] | ABC [33,41] | 13 |
| GSO [50] | FA [53] | |||
| FA [58,81] | ACO [82] | ACO [83] | ||
| ACO [37,57] | ||||
| Bacteria | BFO [84] | BFO and BCO [64] | 3 | |
| BMA [85] | ||||
| Bird | PSO [66,74,75,86] | PSO [87] | PSO [88,89] | 10 |
| [76,90,91] | ||||
| Mammal | GWO [92,93] | GWO [43] | BA [47] | 5 |
| GWO [94] | ||||
| Fish | FSS [95] | AFSA [96] | 2 | |
| Frog | SFLA [45,97,98] | 3 | ||
| Other | KH [99] | KH [100] | 2 |
| Algorithm | Publications | Citations | Share |
|---|---|---|---|
| PSO | 16 | 766 | 46.62% |
| ACO | 6 | 226 | 13.76% |
| BA | 2 | 154 | 9.37% |
| ABC | 4 | 152 | 9.25% |
| GWO | 7 | 123 | 7.49% |
| FA | 5 | 49 | 2.98% |
| WSO | 1 | 26 | 1.58% |
| Others | 23 | 147 | 8.95% |
| Algorithm | Presentation; Initialization | Definition of Stop Condition | Evaluation | Move | Validation | Advantages |
|---|---|---|---|---|---|---|
| ABC [38] | binary; forward search strategy | 100 iterations | acc (SVM) | with the pertubation frequency | 10-fold CV | + outperforms PSO, ACO, and GA + on average smaller number of selected features |
| ABC [54] | binary; random | 50 iterations | classification error rate (5NN) | use of mutation, recombination and selection | 70% training set, 30% test set, 10-fold CV on training set | + introduced DE based neighborhood mechanism for FS + method removes redundant features effectively and is the most stable and consistent |
| ACO [35] | graph | 50 iterations | acc (1NN) | graph search with the probabilistic transition rule | 60% training set, 40% test set | + ants have the authority to select or deselect visiting features; + method permits ants to explore all features; + ants can see all of the unvisited features simultaneously |
| PSO [75] | continuous; random | different tests | combined function with acc(adaptive KNN) and number of selected features | based on inertia weight, social and cognitive component | different CV techniques | + high classification accuracy, small muber of selected features, and lower computing time |
| GWO [92] | binary; random | 100 iterations | combined function with acc(KELM) and number of selected features | based on alpha, beta, and delta wolves | 10-fold CV | + method adaptively converges more quickly, produces much better solution quality, but also gains less number of selected features, achieving high classification performance |
| WOA [67] | binary; random | 100 iterations | combined function with acc (5NN) and number of selected features | based on neighbours | CV | + method combined with the Simulated annealing following two hybrid models: LTH and HRH |
| AFSA [52] | binary; random | lack of changes in the optimal features subset for a period of 1 h | acc (SVM) | execution of the three search steps (follow, swarm, and prey) | 10-fold CV | + experiment with and without parameter optimization + dynamic vision proposed to assign an appropriate search space for each fish |
| SFLA [45] | binary; random with two equations | 50 iterations | combined function with acc (1NN) and number of selected features | with equations containing adaptive transition factor | 10-fold CV | + provided three improvement strategies |
| KH [68] | binary; random | 100 iterations | acc (OPF) | with Sigmoid function | 5-fold CV | + fast method |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brezočnik, L.; Fister, I.; Podgorelec, V. Swarm Intelligence Algorithms for Feature Selection: A Review. Appl. Sci. 2018, 8, 1521. https://doi.org/10.3390/app8091521
Brezočnik L, Fister I, Podgorelec V. Swarm Intelligence Algorithms for Feature Selection: A Review. Applied Sciences. 2018; 8(9):1521. https://doi.org/10.3390/app8091521
Chicago/Turabian StyleBrezočnik, Lucija, Iztok Fister, and Vili Podgorelec. 2018. "Swarm Intelligence Algorithms for Feature Selection: A Review" Applied Sciences 8, no. 9: 1521. https://doi.org/10.3390/app8091521
APA StyleBrezočnik, L., Fister, I., & Podgorelec, V. (2018). Swarm Intelligence Algorithms for Feature Selection: A Review. Applied Sciences, 8(9), 1521. https://doi.org/10.3390/app8091521






