Sizing Hybrid Energy Storage Systems for Distributed Power Systems under Multi-Time Scales
Abstract
1. Introduction
2. Modeling of Distributed Power System
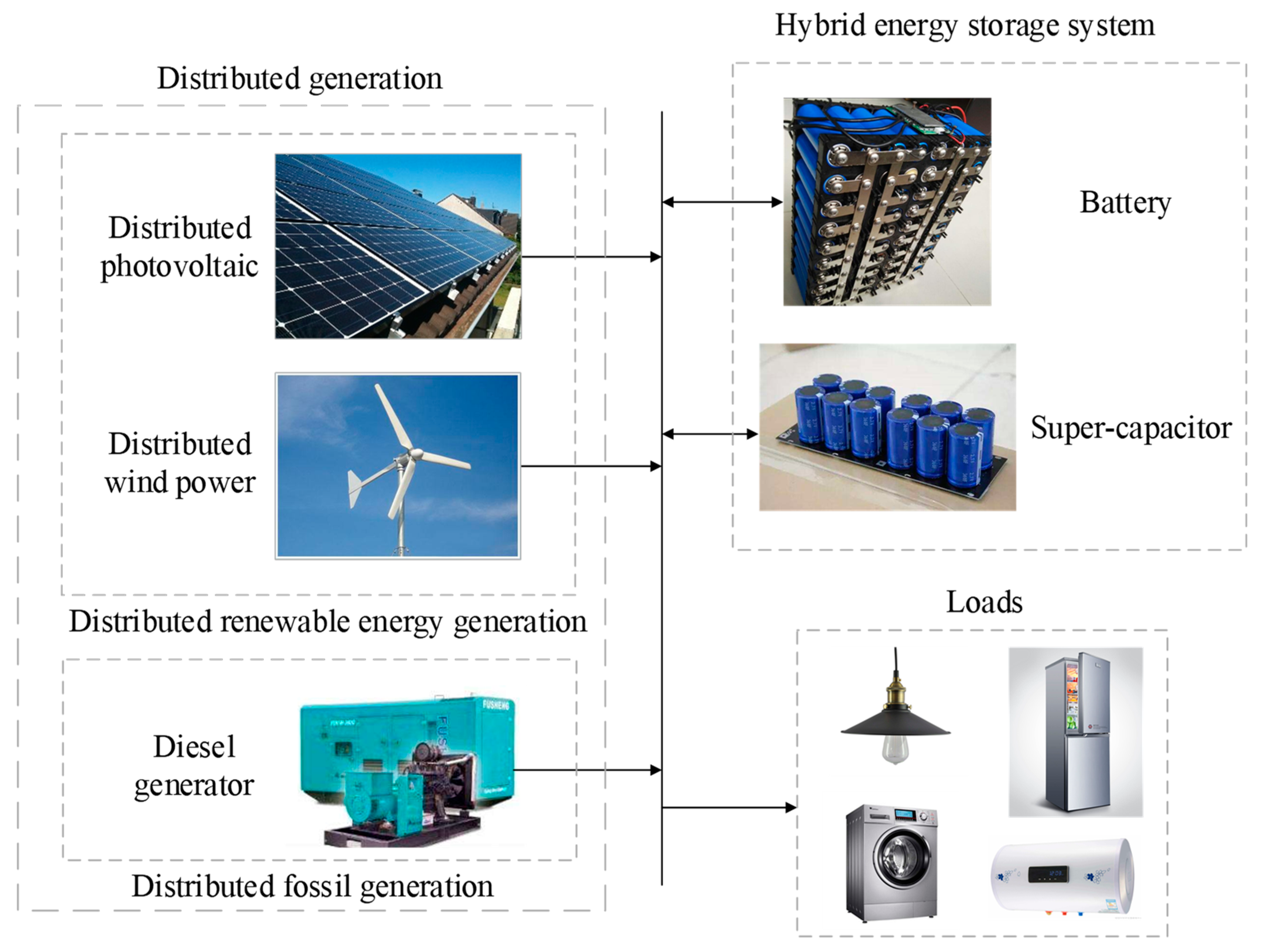
2.1. The Structure of a Typical Distributed Power System
2.2. Modelling of Distributed Energy Carriers
2.2.1. Distributed Renewable Power Generation System
2.2.2. Distributed Diesel Generator System
2.2.3. Distributed Energy Storage System
3. System Optimization
3.1. Objective Function
3.2. Constraints
3.2.1. Equality Constraints
3.2.2. Inequality Constraints
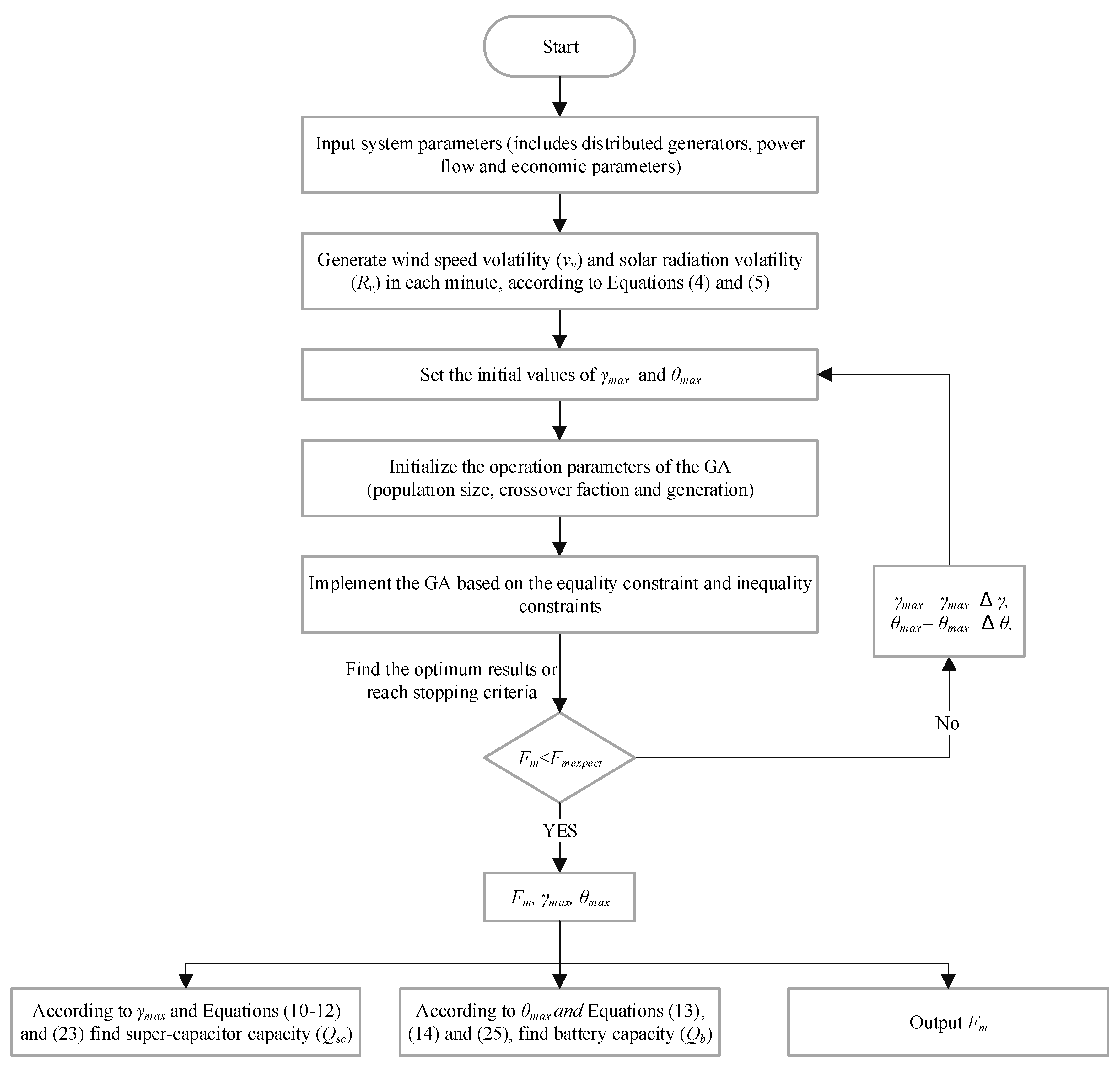
3.3. Optimization Algorithm
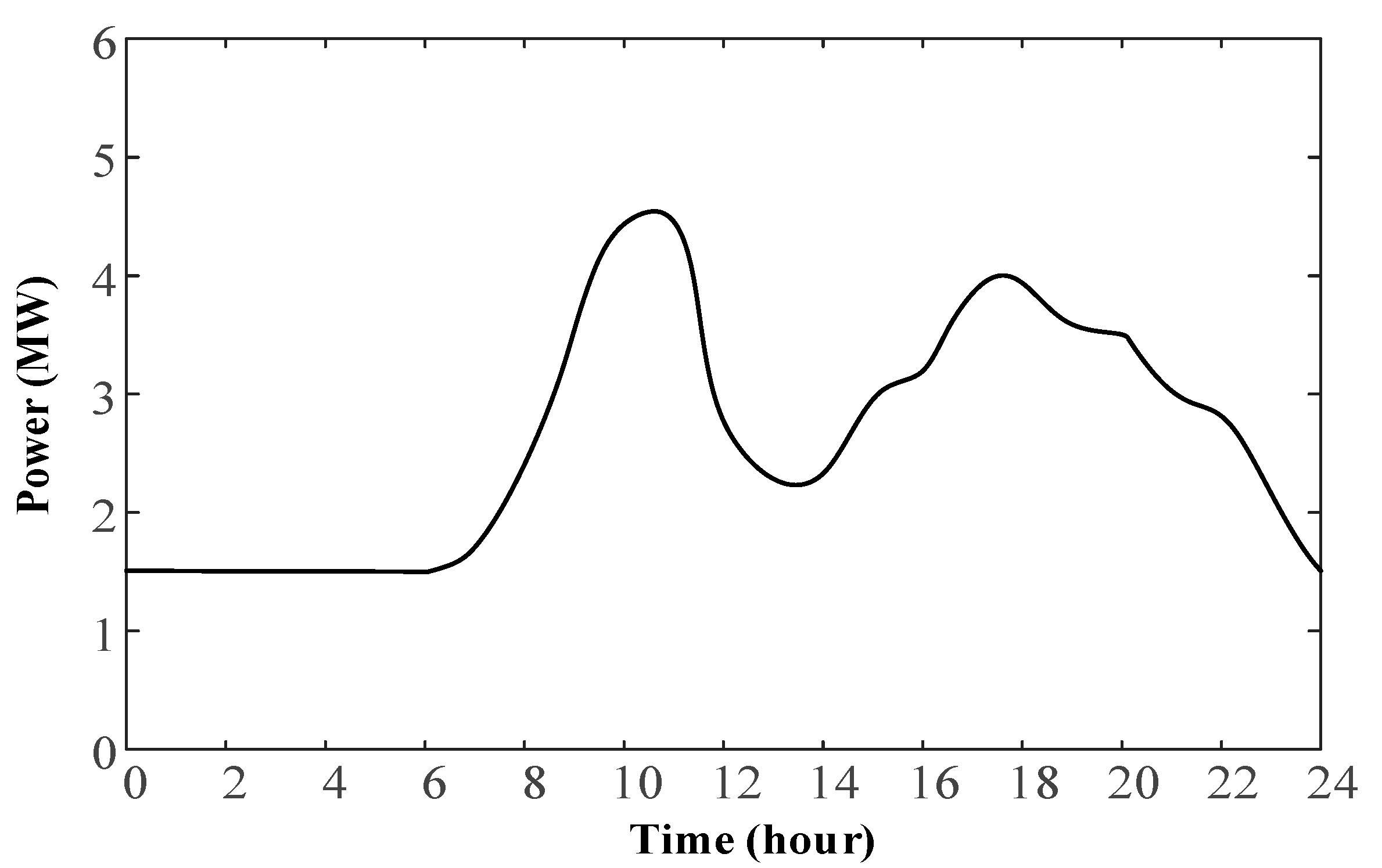
4. Case Study
5. Results and Analysis
5.1. Optimization Results of Battery Super-Capacitor Installation Capacity
5.2. System Optimal Operation Strategy of Point P
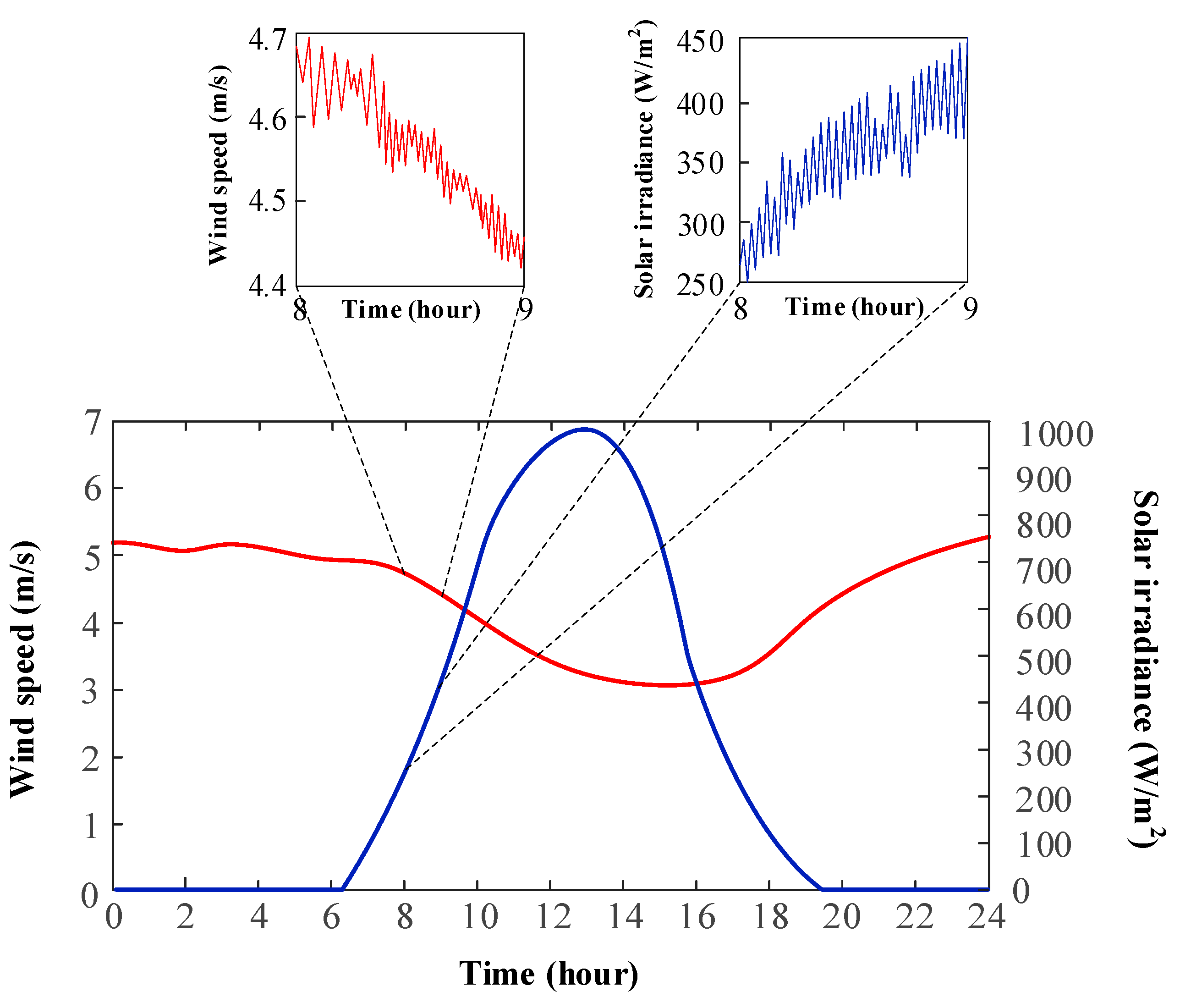
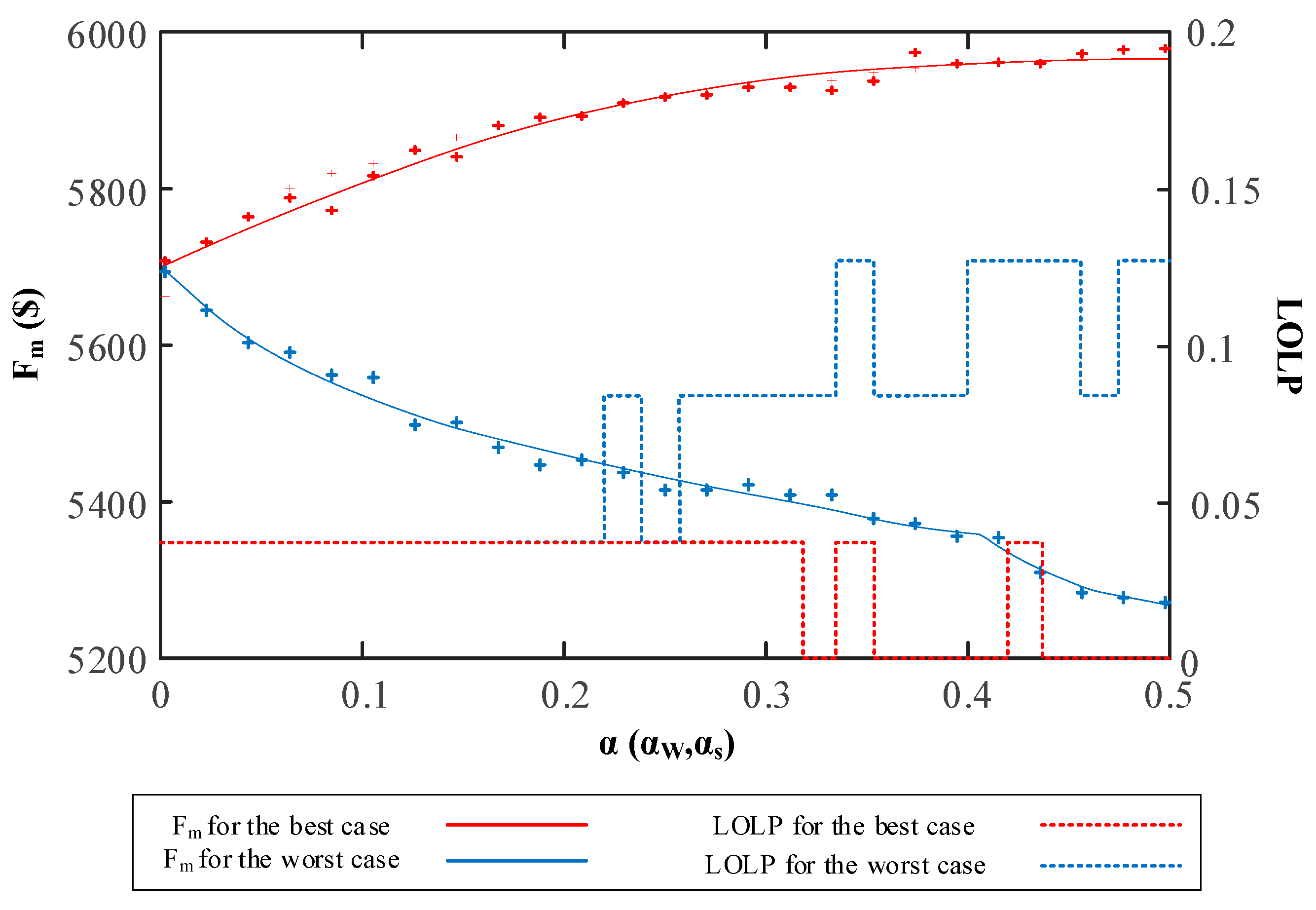
5.3. The Influence of Renewable Energy Volatility on the Proposed Energy Storage System
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Daliento, S.; Chouder, A.; Guerriero, P.; Pavan, A.M.; Mellit, A.; Moeini, R.; Tricoli, P. Monitoring, diagnosis, and power forecasting for photovoltaic fields: A review. Int. J. Photoenergy 2017, 2017, 1–13. [Google Scholar] [CrossRef]
- Hansen, A.D.; Altin, M.; Iov, F. Provision of enhanced ancillary services from wind power plants–examples and challenges. Renew. Energy 2016, 97, 8–18. [Google Scholar] [CrossRef]
- Abedini, M.; Nasiri, A. Output power smoothing for wind turbine permanent magnet synchronous generators using rotor inertia. Electr. Mach. Power Syst. 2008, 37, 1–19. [Google Scholar] [CrossRef]
- Abeywardana, D.B.W.; Hredzak, B.; Agelidis, V.G. A fixed-frequency sliding mode controller for a boost-inverter-based battery-supercapacitor hybrid energy storage system. IEEE Trans. Power Electron. 2017, 32, 668–680. [Google Scholar] [CrossRef]
- Ciccarelli, F.; Iannuzzi, D.; Kondo, K.; Fratelli, L. Line-voltage control based on wayside energy storage systems for tramway networks. IEEE Trans. Power Electron. 2016, 31, 884–899. [Google Scholar] [CrossRef]
- Hall, P.J. Energy storage: The route to liberation from the fossil fuel economy? Energy Policy 2008, 36, 4363–4367. [Google Scholar] [CrossRef]
- Xu, Y.; Singh, C. Adequacy and economy analysis of distribution systems integrated with electric energy storage and renewable energy resources. IEEE Trans. Power Syst. 2012, 27, 2332–2341. [Google Scholar] [CrossRef]
- Le, H.T.; Nguyen, T.Q. Sizing energy storage systems for wind power firming: An analytical approach and a cost-benefit analysis. In Proceedings of the IEEE Power and Energy Society General Meeting–Conversion and Delivery of Electrical Energy in the 21st Century, Pittsburgh, PA, USA, 20–24 July 2008; pp. 1–8. [Google Scholar]
- Kaldellis, J.K.; Zafirakis, D.; Kondili, E. Optimum sizing of photovoltaic-energy storage systems for autonomous small islands. Int. J. Electr. Power Energy Syst. 2010, 32, 24–36. [Google Scholar] [CrossRef]
- Chen, S.X.; Gooi, H.B.; Wang, M.Q. Sizing of energy storage for microgrids. IEEE Trans. Smart Grid 2012, 3, 142–151. [Google Scholar] [CrossRef]
- Lee, T.Y.; Chen, N. Determination of optimal contract capacities and optimal sizes of battery energy storage systems for time-of-use rates industrial customers. IEEE Trans. Energy Convers. 1995, 10, 562–568. [Google Scholar]
- Chen, S.X.; Gooi, H.B. Scheduling of energy storage in a grid-connected PV/battery system via SIMPLORER. In Proceedings of the TENCON 2009—2009 IEEE Region 10 Conference, Singapore, 23–26 November 2009; pp. 1–5. [Google Scholar]
- Barelli, L.; Bidini, G.; Bonucci, F.; Castellini, L.; Castellini, S.; Ottaviano, A.; Pelosi, D.; Zuccari, A. Dynamic analysis of a hybrid energy storage system (H-ESS) coupled to a photovoltaic (PV) plant. Energies 2018, 11, 396. [Google Scholar] [CrossRef]
- Rueda-Medina, A.C.; Franco, J.F.; Rider, M.J.; Padilha-Feltrin, A.; Romero, R. A mixed-integer linear programming approach for optimal type, size and allocation of distributed generation in radial distribution systems. Electr. Power Syst. Res. 2013, 97, 133–143. [Google Scholar] [CrossRef]
- Nguyen, T.A.; Crow, M.L.; Elmore, A.C. Optimal sizing of a vanadium redox battery system for microgrid Ssystems. IEEE Trans. Sustain. Energy 2015, 6, 729–737. [Google Scholar] [CrossRef]
- Schneider, M.; Biel, K.; Pfaller, S.; Schaede, H.; Rinderknecht, S.; Glock, C.H. Optimal sizing of electrical energy storage systems using inventory models. Energy Procedia 2015, 73, 48–58. [Google Scholar] [CrossRef]
- Mohammadi, S.; Mohammadi, A. Stochastic scenario-based model and investigating size of battery energy storage and thermal energy storage for micro-grid. Int. J. Electr. Power Energy Syst. 2014, 61, 531–546. [Google Scholar] [CrossRef]
- Liu, W.; Guo, D.; Xu, Y.; Cheng, R.; Wang, Z.; Li, Y. Reliability assessment of power systems with photovoltaic power stations based on intelligent state space reduction and pseudo-sequential Monte Carlo simulation. Energies 2018, 11, 1431. [Google Scholar] [CrossRef]
- Bakkiyaraj, R.A.; Kumarappan, N. Optimal reliability planning for a composite electric power system based on Monte Carlo simulation using particle swarm optimization. Int. J. Electr. Power Energy Syst. 2013, 47, 109–116. [Google Scholar] [CrossRef]
- Arshad, A.; Püvi, V.; Lehtonen, M. Monte Carlo-based comprehensive assessment of PV hosting capacity and energy storage impact in realistic finnish low-voltage networks. Energies 2018, 11, 1467. [Google Scholar] [CrossRef]
- Jiang, Z.; Han, X.; Li, Z.; Wang, M.; Liu, G.; Wang, M.; Li, W.; Ollis, T.B. Capacity optimization of a centralized charging station in joint operation with a wind farm. Energies 2018, 11, 1164. [Google Scholar] [CrossRef]
- Seyedmahmoudian, M.; Jamei, E.; Thirunavukkarasu, G.S.; Soon, T.K.; Mortimer, M.; Horan, B.; Stojcevski, A.; Mekhilef, S. Short-term forecasting of the output power of a building-integrated photovoltaic system using a metaheuristic approach. Energies 2018, 11, 1260. [Google Scholar] [CrossRef]
- Sadamato, T.; Chakraborty, A.; Ishizaki, T.; Imura, J.I. Retrofit control of wind-integrated power systems. IEEE Trans. Power Syst. 2018, 33, 2804–2815. [Google Scholar] [CrossRef]
- Chakraborty, T.; Watson, D.; Rodgers, M. Automatic generation control using an energy storage system in a wind park. IEEE Trans. Power Syst. 2018, 33, 198–205. [Google Scholar] [CrossRef]
- Dui, X.; Zhu, G.; Yao, L. Two-stage optimization of battery energy storage capacity to decrease wind power curtailment in grid-connected wind farms. IEEE Trans. Power Syst. 2018, 33, 3296–3305. [Google Scholar] [CrossRef]
- Hashemi, S.; Østergaard, J.; Yang, G. A scenario-based approach for energy storage capacity determination in LV grids with high PV penetration. IEEE Trans. Smart Grid 2014, 5, 1514–1522. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, Q.; Gong, T.; Sun, H.; Su, X. Peak load regulation and cost optimization for microgrids by installing a heat storage tank and a portable energy system. Appl. Sci. 2018, 8, 567. [Google Scholar] [CrossRef]
- Riffonneau, Y.; Bacha, S.; Barruel, F.; Ploix, S. Optimal power flow management for grid connected PV systems with batteries. IEEE Trans. Sustain. Energy 2011, 2, 309–320. [Google Scholar] [CrossRef]
- Hong, Y.; Lai, Y.; Chang, Y.; Lee, Y.; Liu, P. Optimizing capacities of distributed generation and energy storage in a small autonomous power system considering uncertainty in renewables. Energies 2015, 8, 2473–2492. [Google Scholar] [CrossRef]
- Gee, A.M.; Robinson, F.V.P.; Dunn, R.W. Analysis of battery lifetime extension in a small-scale wind-energy system using supercapacitors. IEEE Trans. Energy Convers. 2013, 28, 24–33. [Google Scholar] [CrossRef]
- Linzen, D.; Buller, S.; Karden, E.; de Doncker, R.W. Analysis and evaluation of charge-balancing circuits on performance, reliability, and lifetime of supercapacitor systems. IEEE Trans. Ind. Appl. 2005, 41, 1135–1141. [Google Scholar] [CrossRef]
- Asghar, F.; Talha, M.; Kim, S.H. Robust frequency and voltage stability control strategy for standalone AC/DC hybrid microgrid. Energies 2017, 10, 760. [Google Scholar] [CrossRef]
- Yu, D.; Liu, H.; Yan, G.; Jiang, J.; Le Blond, S. Optimization of hybrid energy storage systems at the building level with combined heat and power generation. Energies 2017, 10, 606. [Google Scholar] [CrossRef]
- Marchi, B.; Pasetti, M.; Zanoni, S. Life cycle cost analysis for BESS optimal sizing. Energy Procedia 2017, 113, 127–134. [Google Scholar] [CrossRef]
- Yu, D.; Meng, Y.; Yan, G.; Mu, G.; Li, D.; Blond, S.L. Sizing combined heat and power units and domestic building energy cost optimisation. Energies 2017, 10, 771. [Google Scholar] [CrossRef]
- State Electricity Regulatory Commission. 2010 Annual Implementation Electricity Price and Electricity Bill Settlement Report. Available online: https://wenku.baidu.com/view/f9625b2e2af90242a895e575.html (accessed on 13 June 2018).
- SUNRUN. Product Handbook. Available online: https://www.alibaba.com/product-detail/75kw-china-yuchai-japanese-used-desiel_60603876154.html?spm=a2700.7724857.main07.12.1dc37c5fp6riH7&s=p (accessed on 13 June 2018).
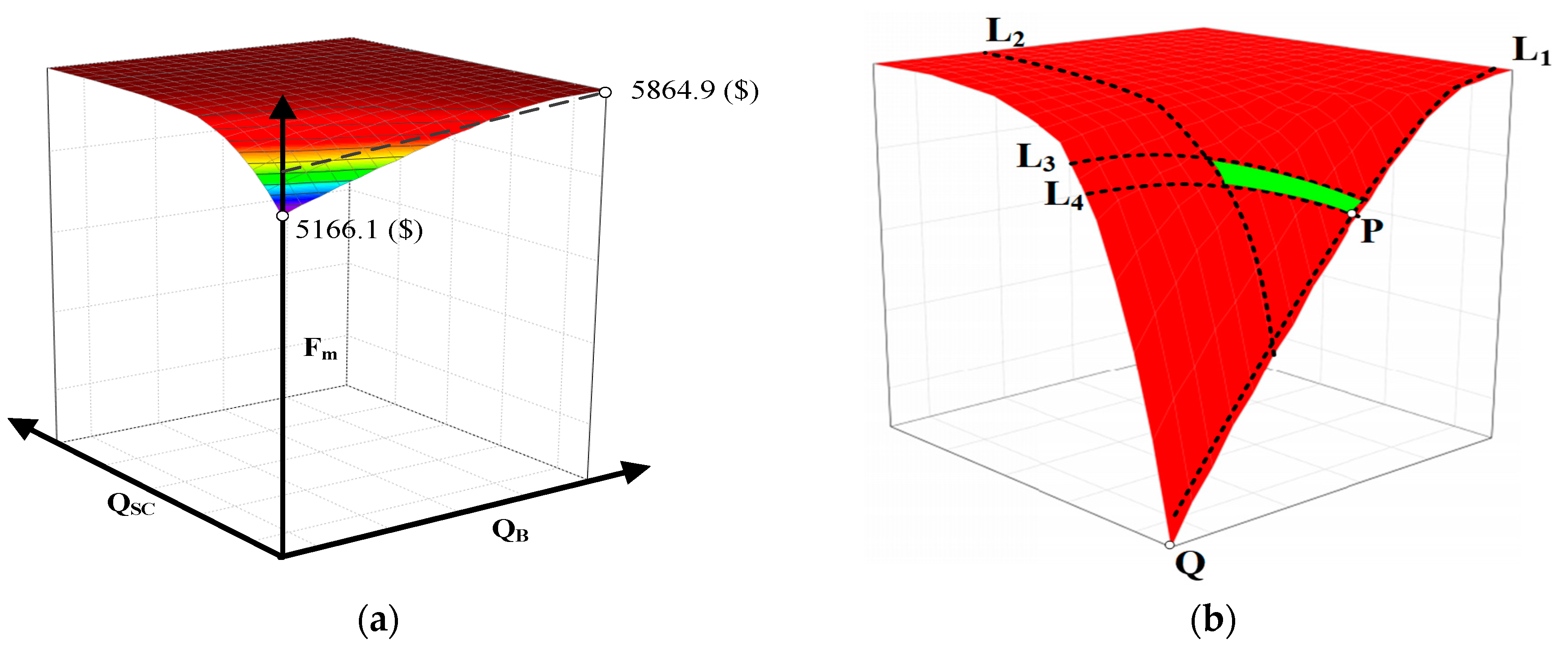


| Battery Capacity (kAh) | Super-Capacitor Capacity (F) | Average Daily Generation Cost ($) | Carbon Emissions (t) |
|---|---|---|---|
| 10.92 | 495.87 | 5708.4 | 1.67 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, H.; Li, D.; Liu, Y.; Dong, M.; Liu, X.; Zhang, H. Sizing Hybrid Energy Storage Systems for Distributed Power Systems under Multi-Time Scales. Appl. Sci. 2018, 8, 1453. https://doi.org/10.3390/app8091453
Liu H, Li D, Liu Y, Dong M, Liu X, Zhang H. Sizing Hybrid Energy Storage Systems for Distributed Power Systems under Multi-Time Scales. Applied Sciences. 2018; 8(9):1453. https://doi.org/10.3390/app8091453
Chicago/Turabian StyleLiu, Huanan, Dezhi Li, Yuting Liu, Mingyu Dong, Xiangnan Liu, and Hong Zhang. 2018. "Sizing Hybrid Energy Storage Systems for Distributed Power Systems under Multi-Time Scales" Applied Sciences 8, no. 9: 1453. https://doi.org/10.3390/app8091453
APA StyleLiu, H., Li, D., Liu, Y., Dong, M., Liu, X., & Zhang, H. (2018). Sizing Hybrid Energy Storage Systems for Distributed Power Systems under Multi-Time Scales. Applied Sciences, 8(9), 1453. https://doi.org/10.3390/app8091453





