Optimisation of the Structure of a Wind Farm—Kinetic Energy Storage for Improving the Reliability of Electricity Supplies
Abstract
1. Introduction
2. Characteristics of a Wind Farm—Kinetic Energy Storage System
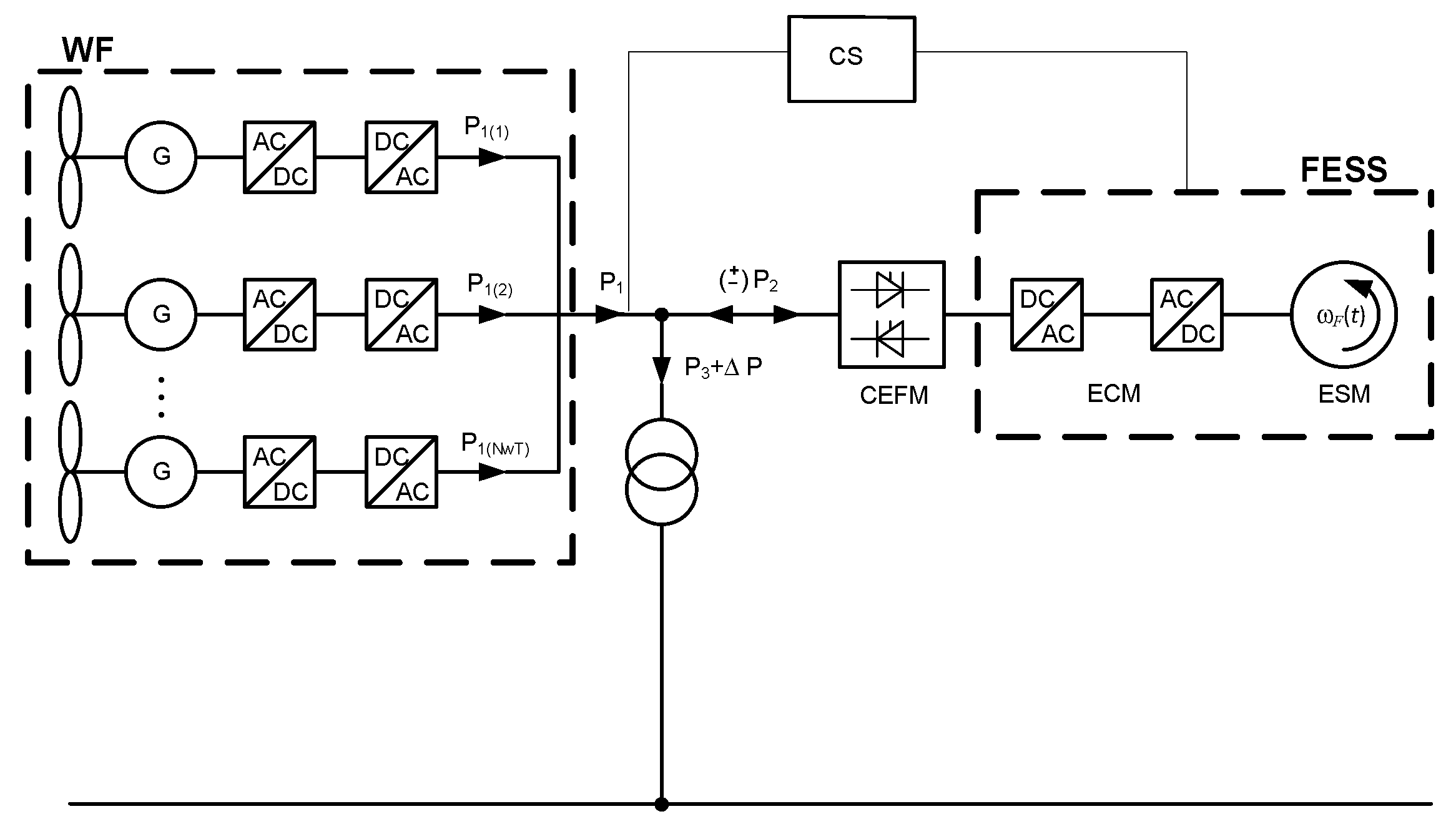
2.1. Description of the System, Power Flow Algorithm
2.2. Wind Speed Measurement Data
3. Mathematical Model of the System
3.1. Turbine and Wind Farm
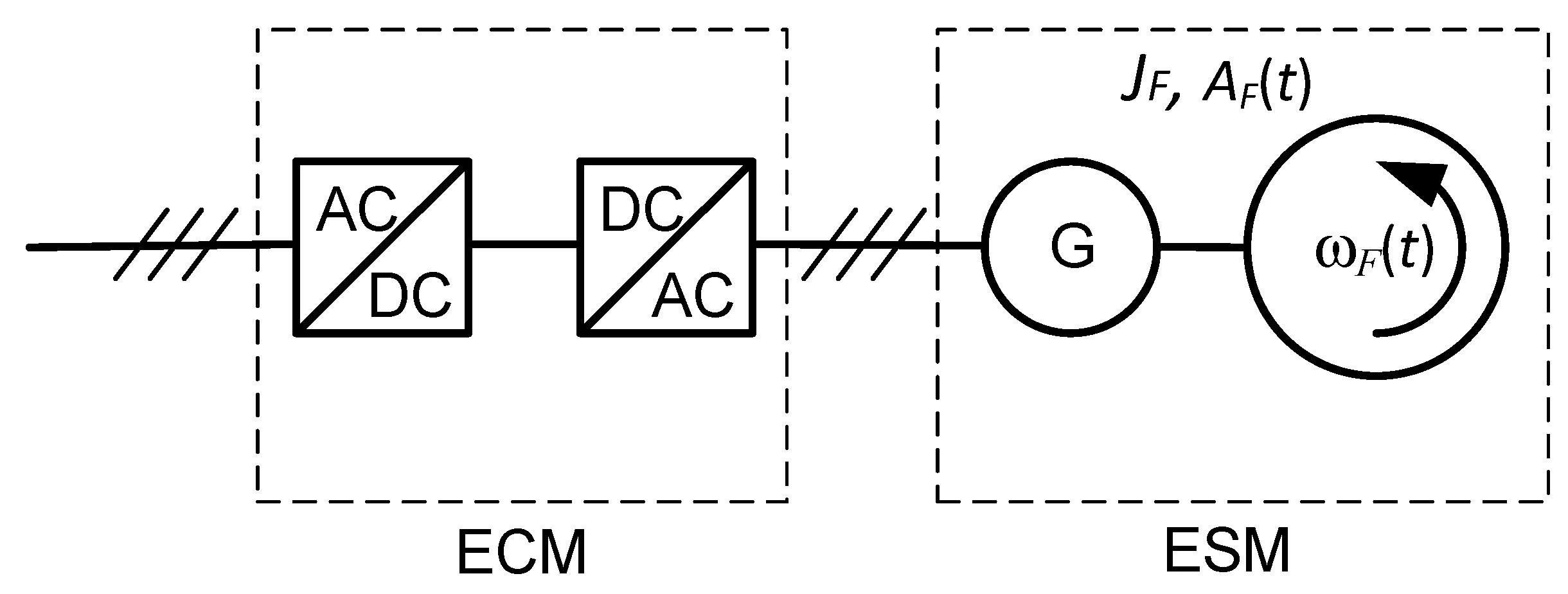
3.2. Kinetic Energy Storage
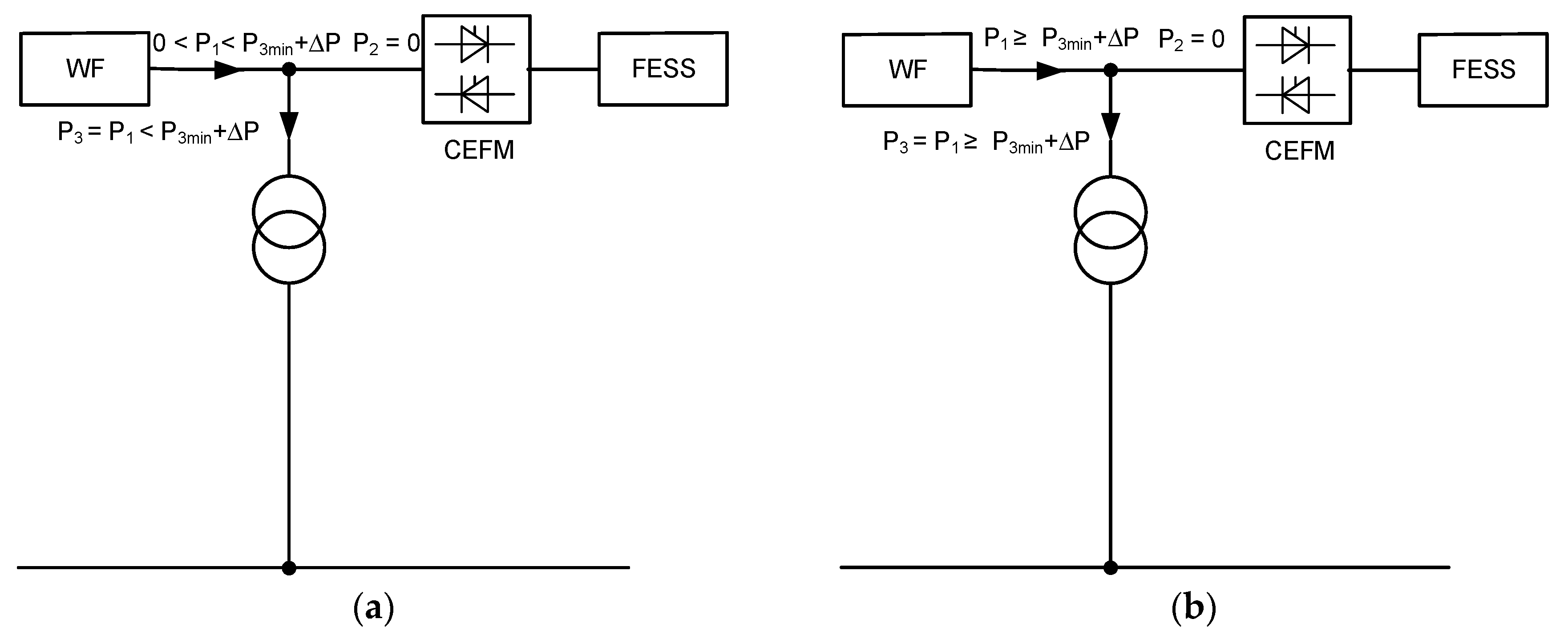
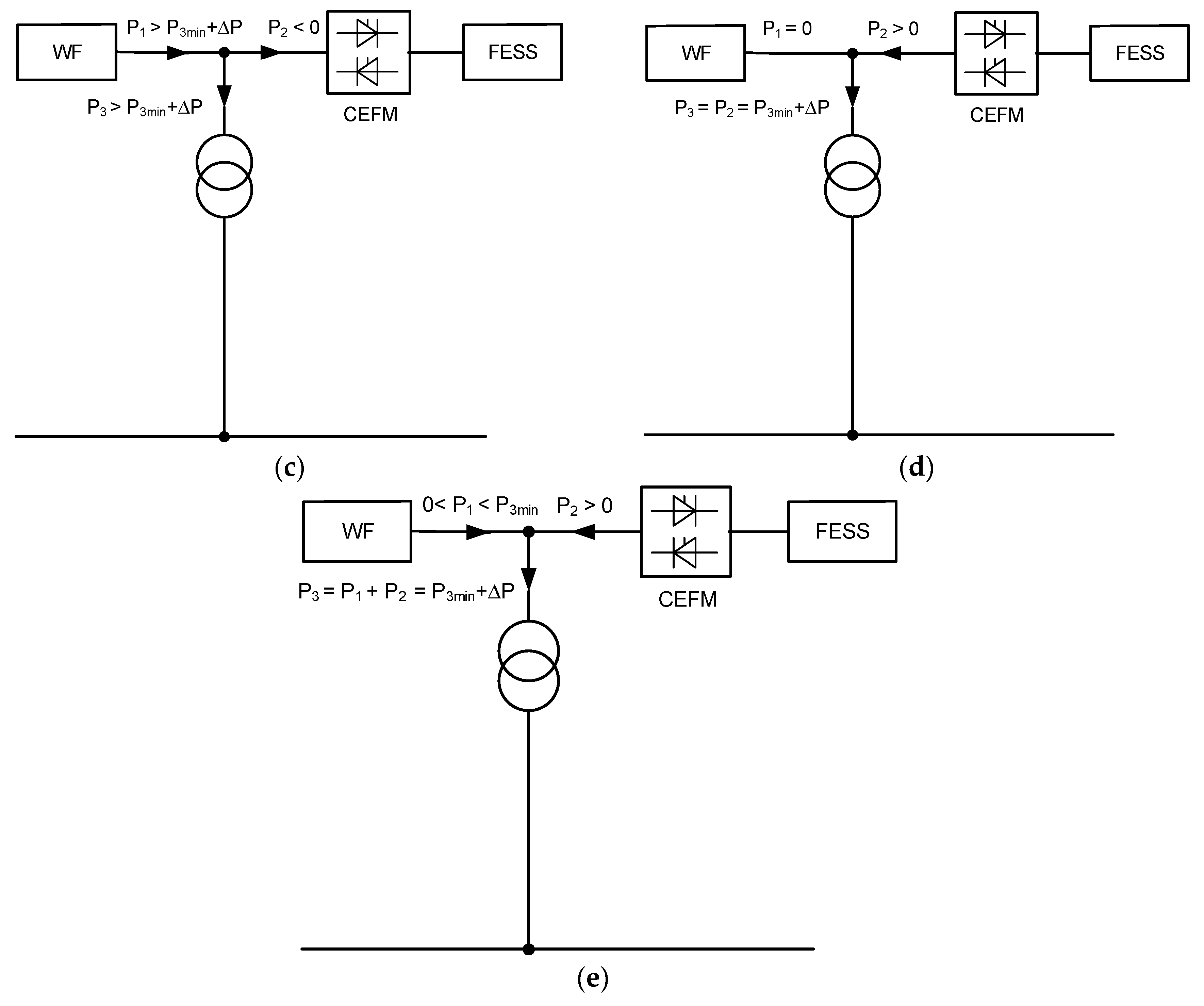
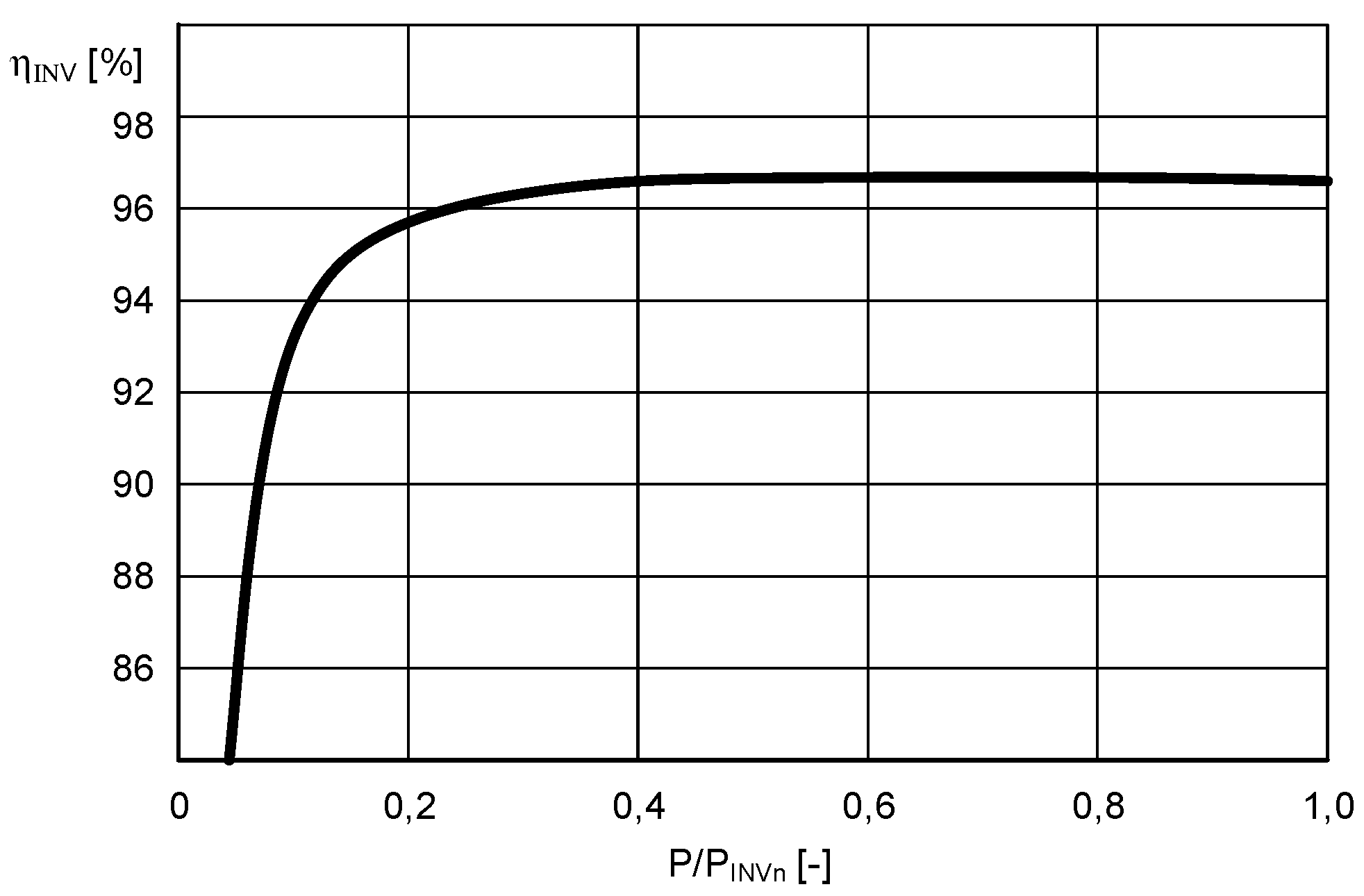
3.4. Power Electronics Systems Controlling the Flow of Power
4. Indicators of Electrical Energy Supplies from a Wind Farm—Kinetic Energy Storage System to the Power Grid
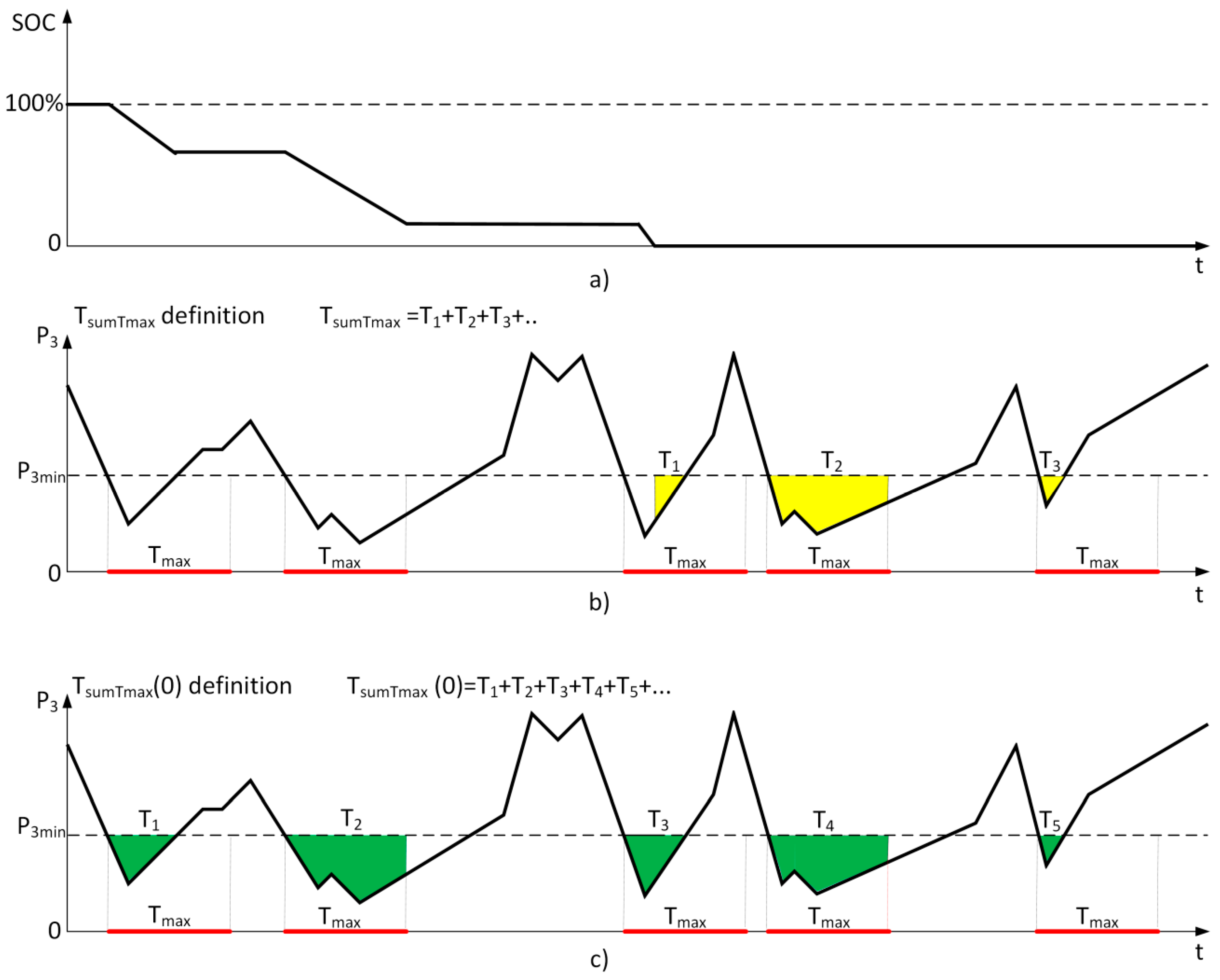
- total annual time of power generation with a value lower than P3min, covering only the periods lasting up to Tmax (according to the system operation algorithm, the generated power deficit is replenished by the energy from the storage) at the storage capacity AFESS:where: TTmax(i) is the duration of the ith interval which is shorter than or equal to Tmax in which the power supplied to the grid P3 is lower than the assumed minimum power P3min, and M is the number of intervals TTmax in which power deficit occurs,
- percentage coefficient of elimination of periods when the generated power value is lower than P3min, considering only the periods which last up to Tmax:where: TsumTmax(0) is time TsumTmax identified for a system without storage, TsumTmax(AFESSn) is the time TsumTmax identified for a system with energy storage with a rated capacity AFESS (the diagram explaining the difference between Tmax, TsumTmax and TsumTmax(0) was presented in Figure 5),
- power deficit accounting only for periods lasting up to Tmax:where: P3avg(i) is the mean power supplied to the grid from the wind farm—kinetic energy storage system in the ith interval shorter than or equal to Tmax, in which the power released to the grid P3 is lower than the assumed minimum power P3min.
5. Optimisation of a Wind Farm—Kinetic Energy Storage System
5.1. Purpose of Optimisation, Function and Constraints
- True power of the farm PWFr(x):
- Size of turbine database (number of designs and turbine heights) and kinetic storage units (number of energy storage types).
- time TsumTmax(x) − Equation (6):where: TsumTmaxY is the total annual boundary time of power generation below P3min assumed in the optimisation task, covering only the periods lasting up to Tmax;
- maximum power of kinetic storage PFESSMax(x):
5.2. Selection of Optimisation Method, Description of Application Developed
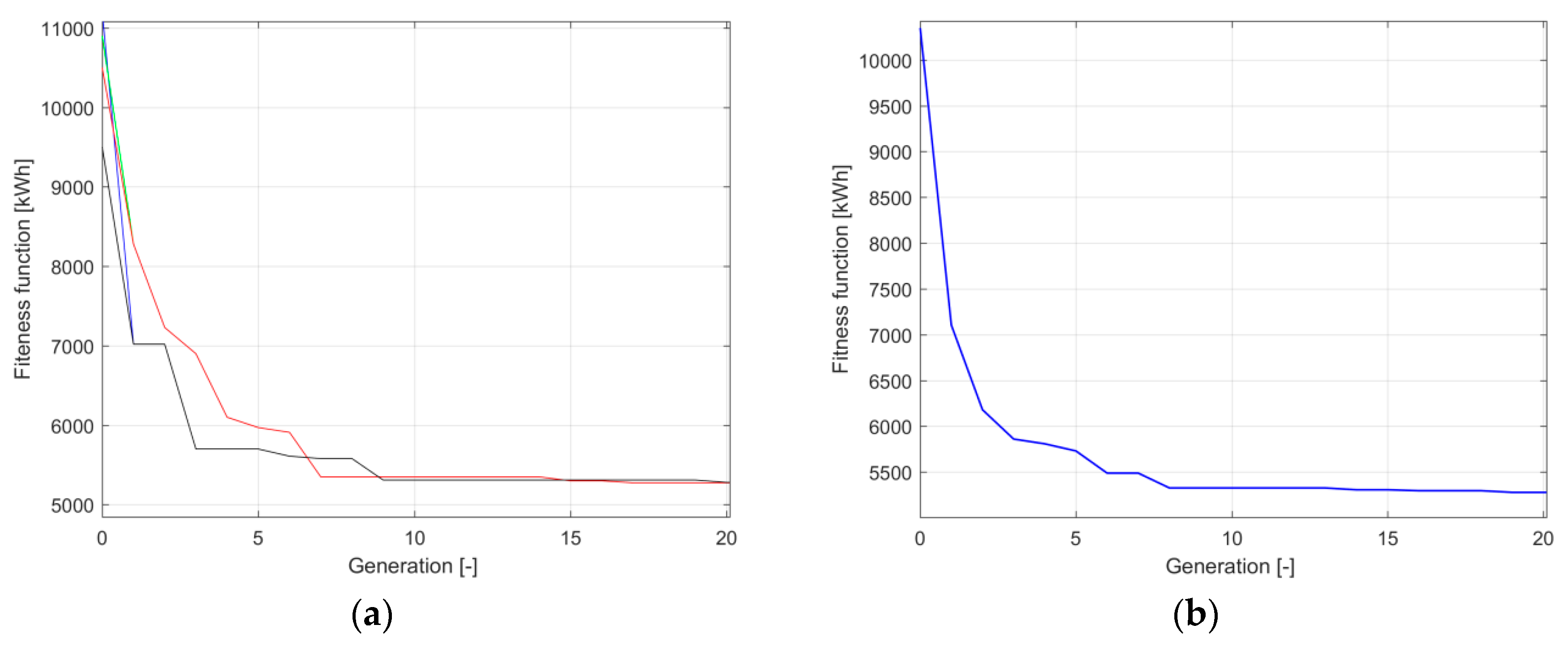
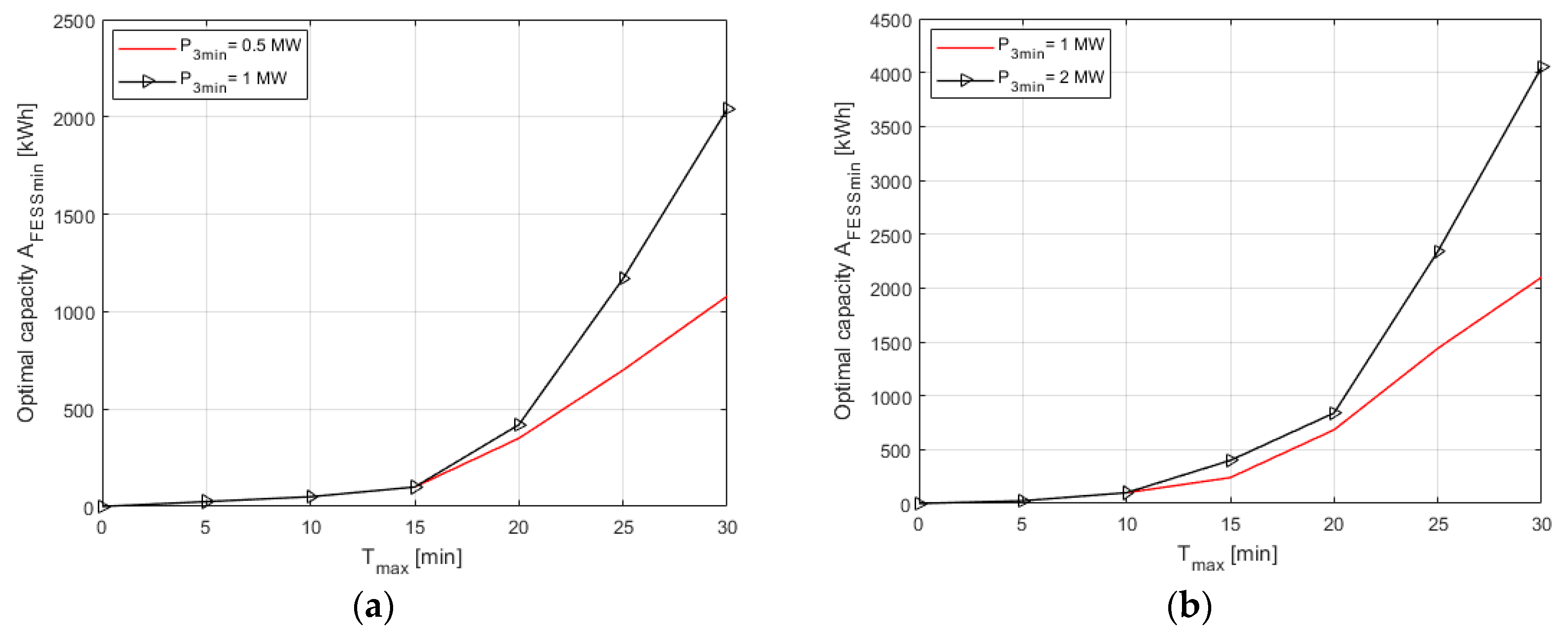
5.3. Optimisation Calculations
5.4. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Trzmiel, G. Determination of a mathematical model of the thin-film photovoltaic panel (CiS) based on measurement data. Eksploat. Niezawodn. 2017, 19, 516–521. [Google Scholar] [CrossRef]
- Koh, L.H.; Peng, W.; Tseng, K.J.; Gao, Z. Reliability evaluation of electric power systems with solar photovoltaic & energy storage. In Proceedings of the 2014 International Conference on Probabilistic Methods Applied to Power Systems, Durham, UK, 7–10 July 2014; pp. 1–5. [Google Scholar]
- Renewables 2016 Global Status Report. Available online: http://www.ren21.net (accessed on 15 May 2018).
- Renewable Energy in Europe—2017 Update. Recent Growth and Knock-on Effects; EEA Report, No 23/2017; European Environment Agency (EEA): Copenhagen, Denmark, 2017. [CrossRef]
- Europe 2020 Indicators. Available online: http://ec.europa.eu/eurostat/portal/page/portal/europe_2020_indicators/ (accessed on 15 May 2018).
- Kasprzyk, L. Modelling and analysis of dynamic states of the lead-acid batteries in electric vehicles. Eksploat. Niezawodn. 2017, 19, 229–236. [Google Scholar] [CrossRef]
- Price, J.E.; Sheffrin, A. Adapting California’s energy markets to growth in renewable resources. In Proceedings of the 2010 IEEE PES General Meeting, Providence, RI, USA, 25–29 July 2010; pp. 1–8. [Google Scholar]
- Komarnicki, P.; Lombardi, P.; Styczynski, Z. Economics of Electric Energy Storage Systems. In Electric Energy Storage Systems; Springer: Berlin/Heidelberg, Germany, 2017; pp. 181–194. [Google Scholar]
- Amiryar, M.E.; Pullen, K.R.; Nankoo, D. Development of a High-Fidelity Model for an Electrically Driven Energy Storage Flywheel Suitable for Small Scale Residential Applications. Appl. Sci. 2018, 8, 453. [Google Scholar] [CrossRef]
- Baghaee, H.R.; Mirsalim, M.; Gharehpetian, G.B.; Talebi, H.A. Fuzzy unscented transform for uncertainty quantification of correlated wind/PV microgrids: Possibilistic–probabilistic power flow based on RBFNNs. IET Renew. Power Gener. 2017, 11, 867–877. [Google Scholar] [CrossRef]
- Zheng, D.; Semero, Y.K.; Zhang, J.; Wei, D. Short-term wind power prediction in microgrids using a hybrid approach integrating genetic algorithm, particle swarm optimization, and adaptive neuro-fuzzy inference systems. IEEJ Trans. Electr. Electron. Eng. 2018. [Google Scholar] [CrossRef]
- Ding, Y.; Wang, P.; Chang, L.P. Reliability evaluation of electric power systems with high wind power penetration. In Proceedings of the 2009 8th International Conference on Reliability, Maintainability and Safety, Chengdu, China, 20–24 July 2009; pp. 24–26. [Google Scholar]
- Sideratos, G.; Hatziargyriou, N. An advanced statistical method for wind power forecasting. IEEE Trans. Power Syst. 2007, 22, 258–265. [Google Scholar] [CrossRef]
- Chang, W.Y. A literature review of wind forecasting methods. J. Power Energy Eng. 2014, 2, 161–168. [Google Scholar] [CrossRef]
- Kassa, Y.; Zhang, J.H.; Zheng, D.H.; Wei, D. Short term wind power prediction using ANFIS. In Proceedings of the 2016 1st IEEE International Conference on Power and Renewable Energy, Shanghai, China, 21–23 October 2016; pp. 388–393. [Google Scholar]
- Zhu, Y.; Zang, H.; Cheng, L.; Gao, S. Output Power Smoothing Control for a Wind Farm Based on the Allocation of Wind Turbines. Appl. Sci. 2018, 8, 980. [Google Scholar] [CrossRef]
- Mazzeo, D.; Oliveti, G.; Baglivo, C.; Congedo, P.M. Energy reliability-constrained method for the multi-objective optimization of a photovoltaic-wind hybrid system with battery storage. Energy 2018, 156, 688–708. [Google Scholar] [CrossRef]
- Alemany, J.; Kasprzyk, L.; Magnago, F. Effects of binary variables in mixed integer linear programming based unit commitment in large-scale electricity markets. Electr. Power Syst. Res. 2018, 160, 429–438. [Google Scholar] [CrossRef]
- Lombardi, P.; Röhrig, C.; Rudion, K.; Marquardt, R.; Müller-Mienack, M.; Estermann, A.S.; Voropai, N.I. An A-CAES pilot installation in the distribution system: A technical study for RES integration. Energy Sci. Eng. 2014, 2, 116–127. [Google Scholar] [CrossRef]
- Baghaee, H.R.; Mirsalim, M.; Gharehpetian, G.B. Multi-objective optimal power management and sizing of a reliable wind/PV microgrid with hydrogen energy storage using MOPSO. J. Intell. Fuzzy Syst. 2017, 32, 1753–1773. [Google Scholar] [CrossRef]
- Kaviani, A.; Baghaee, H.R.; Riahy, G.H. Optimal sizing of a stand-alone wind/photovoltaic generation unit using particle swarm optimization. Simul. Trans. Soc. Model. Simul. 2009, 85, 89–99. [Google Scholar]
- Acuña, L.G.; Padilla, R.V.; Mercado, A.S. Measuring reliability of hybrid photovoltaic-wind energy systems: A new indicator. Renew. Energy 2017, 106, 68–77. [Google Scholar] [CrossRef]
- Jiang, X.; Zhang, Z.; Wang, J. Studies on the reliability and reserve capacity of electric power system with wind power integration. In Proceedings of the 2012 Power Engineering and Automation Conference, Wuhan, China, 18–20 September 2012; pp. 1–4. [Google Scholar]
- Tomczewski, A. Operation of a Wind Turbine-Flywheel Energy Storage System under Conditions of Stochastic Change of Wind Energy. Sci. World J. 2014, 2014, 643769. [Google Scholar] [CrossRef] [PubMed]
- Kaabeche, A.; Belhamel, M.; Ibtiouen, R. Techno-economic valuation and optimization of integrated photovoltaic/wind energy conversion system. Sol. Energy 2011, 85, 2407–2420. [Google Scholar] [CrossRef]
- Díaz-Gonzáleza, F.; Sumpera, A.; Gomis-Bellmunta, O.; Villafáfila-Roblesb, R. A review of energy storage technologies for wind power applications. Renew. Sustain. Energy Rev. 2012, 16, 2154–2171. [Google Scholar] [CrossRef]
- Fuchs, G.; Lunz, B.; Leuthold, M.; Sauer, D.U. Technology Overview on Electricity Storage; Overview on the Potential and on the Deployment Perspectives of Electricity Storage Technologies; Institute for Power Electronics and Electrical Drives: Aachen, Germany, 2012. [Google Scholar]
- Amiryar, M.E.; Pullen, K.R. A Review of Flywheel Energy Storage System Technologies and Their Applications. Appl. Sci. 2017, 7, 286. [Google Scholar] [CrossRef]
- Paska, J. Reliability Issues in Electric Power Systems with Distributed Generation. Rynek Energii 2008, 5, 18–28. (In Polish) [Google Scholar]
- Glossary of Terms Used in Reliability Standards; NERC: Swindon, UK, 2008.
- Power System Reliability Analysis; Application Guide; CIGRE WG 03 of SC 38 (Power System Analysis and Techniques); e-cigre: Paris, France, 1987.
- Power System Reliability Analysis; Composite Power System Reliability Evaluation; CIGRE Task Force 38-03-10; e-cigre: Paris, France, 1992.
- Reliability Assessment Guidebook, version 2.1; NERC: Swindon, UK, 2010.
- Castro Mora, J.; Calero Baro, J.M.; Riquelme Santos, J.M.; Burgos Payan, M. An evolutive algorithm for wind farm optimal design. Neurocomputing 2007, 70, 2651–2658. [Google Scholar] [CrossRef]
- Goldberg, D.E. Genetic Algorithms in Search, Optimization and Machine Learning; Addison-Wesley Longman Publishing: Boston, MA, USA, 1988. [Google Scholar]
- Michalewicz, Z.; Fogel, D.B. How to Solve It: Modern Heuristics, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Kasprzyk, L.; Tomczewski, A.; Bednarek, K.; Bugała, A. Minimisation of the LCOE for the hybrid power supply system with the lead-acid battery. In Proceedings of the 2017 International Conference Energy, Enviroment and Material Systems, Polanica-Zdroj, Poland, 13–15 September 2017. [Google Scholar]
- Ismail, M.S.; Moghavvemi, M.; Mahlia, T.M.I. Genetic algorithm based optimization on modeling and design of hybrid renewable energy systems. Energy Convers. Manag. 2014, 85, 120–130. [Google Scholar] [CrossRef]
- Al-Shamma’a, A.A.; Addoweesh, K.E. Techno-economic optimization of hybrid power system using genetic algorithm. Int. J. Energy Res. 2014, 38, 1608–1623. [Google Scholar] [CrossRef]
- Bednarek, K. Electrodynamic calculations and optimal designing of heavy-current lines. Prz. Elektrotech. 2008, 84, 138–141. [Google Scholar]
- Bednarek, K.; Nawrowski, R.; Tomczewski, A. An application of genetic algorithm for three phases screened conductors optimization. In Proceedings of the 2000 International Conference on Parallel Computing in Electrical Engineering, Trois-Rivieres, QC, Canada, 27–30 August 2000; pp. 218–222. [Google Scholar]
- Bednarek, K.; Jajczyk, J. Effectiveness of optimization methods in heavy-current equipment designing. Prz. Elektrotech. 2009, 85, 29–32. [Google Scholar]
- Kasprzyk, L.; Tomczewski, A.; Bednarek, K. Efficiency and economic aspects in electromagnetic and optimization calculations of electrical systems. Prz. Elektrotech. 2010, 86, 57–60. [Google Scholar]
- Kasprzyk, L.; Nawrowski, R.; Tomczewski, A. Optimization of Complex Lighting Systems in Interiors with use of Genetic Algorithm and Elements of Paralleling of the Computation Process. In Intelligent Computer Techniques in Applied Electromagnetics, Studies in Computational Intelligence; Wiak, S., Krawczyk, A., Dolezel, I., Eds.; Springer: Berlin/Heilderberg, Germany; New York, NY, USA, 2008; Volume 116, pp. 21–29. [Google Scholar]
- Nawrowski, R.; Tomczewski, A. Optimization of overall costs in designing complex lighting systems. Acta Techn. CSAV 2008, 53, 65–79. [Google Scholar]
- Conn, A.R.; Gould, N.I.M.; Toint, P.L. A Globally Convergent Augmented Lagrangian Barrier Algorithm for Optimization with General Inequality Constraints and Simple Bounds. Math. Comput. 1997, 66, 261–288. [Google Scholar] [CrossRef]
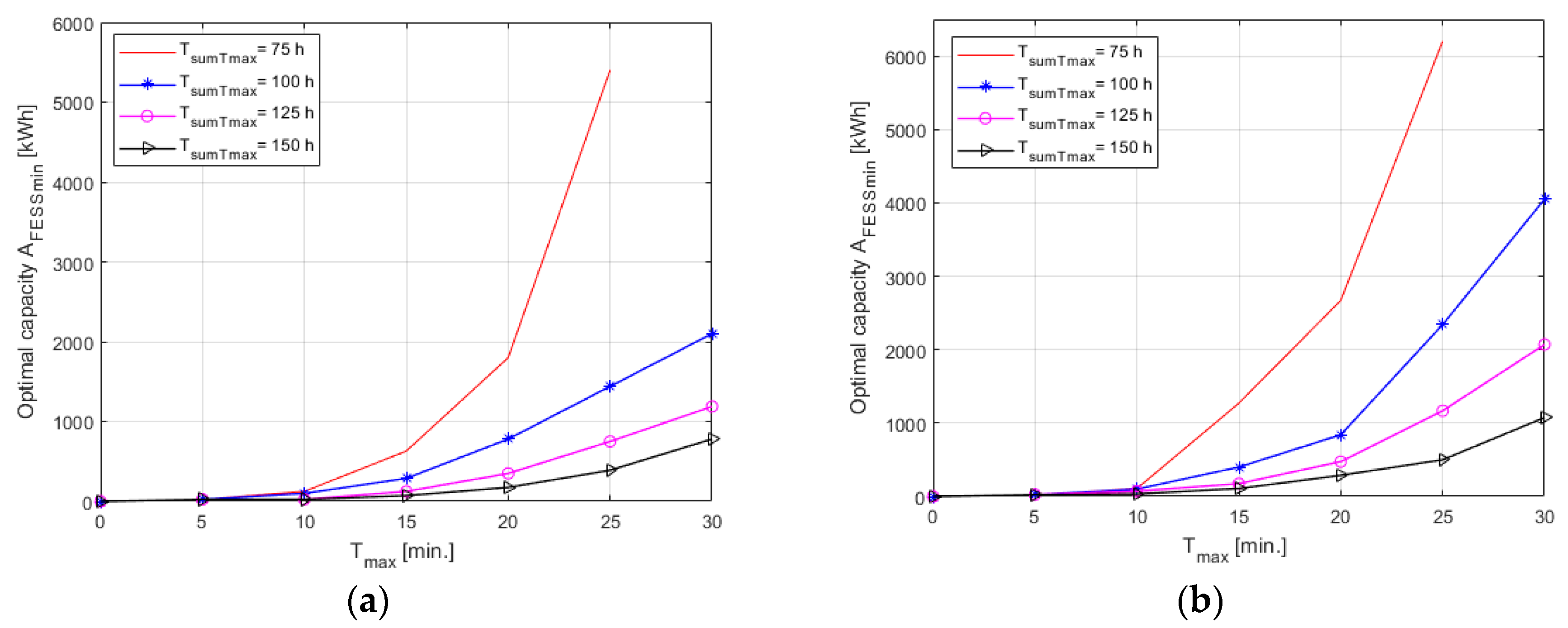
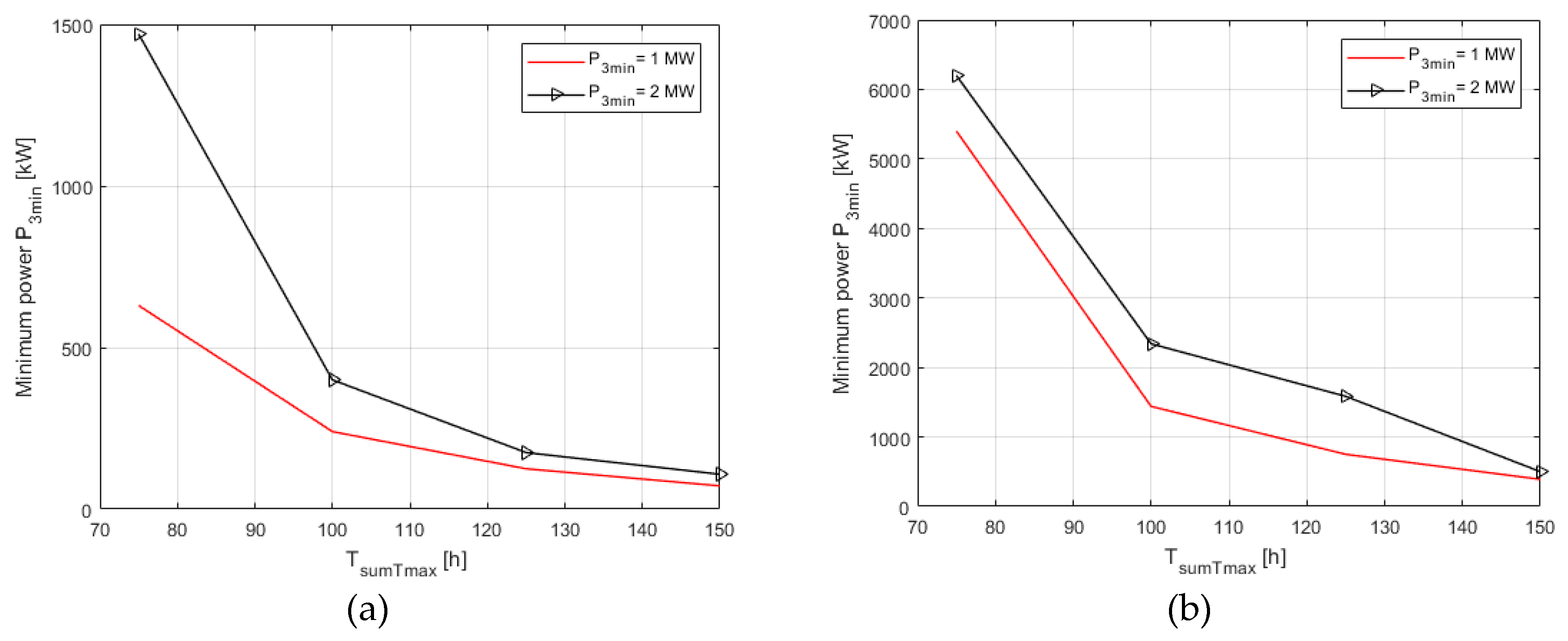
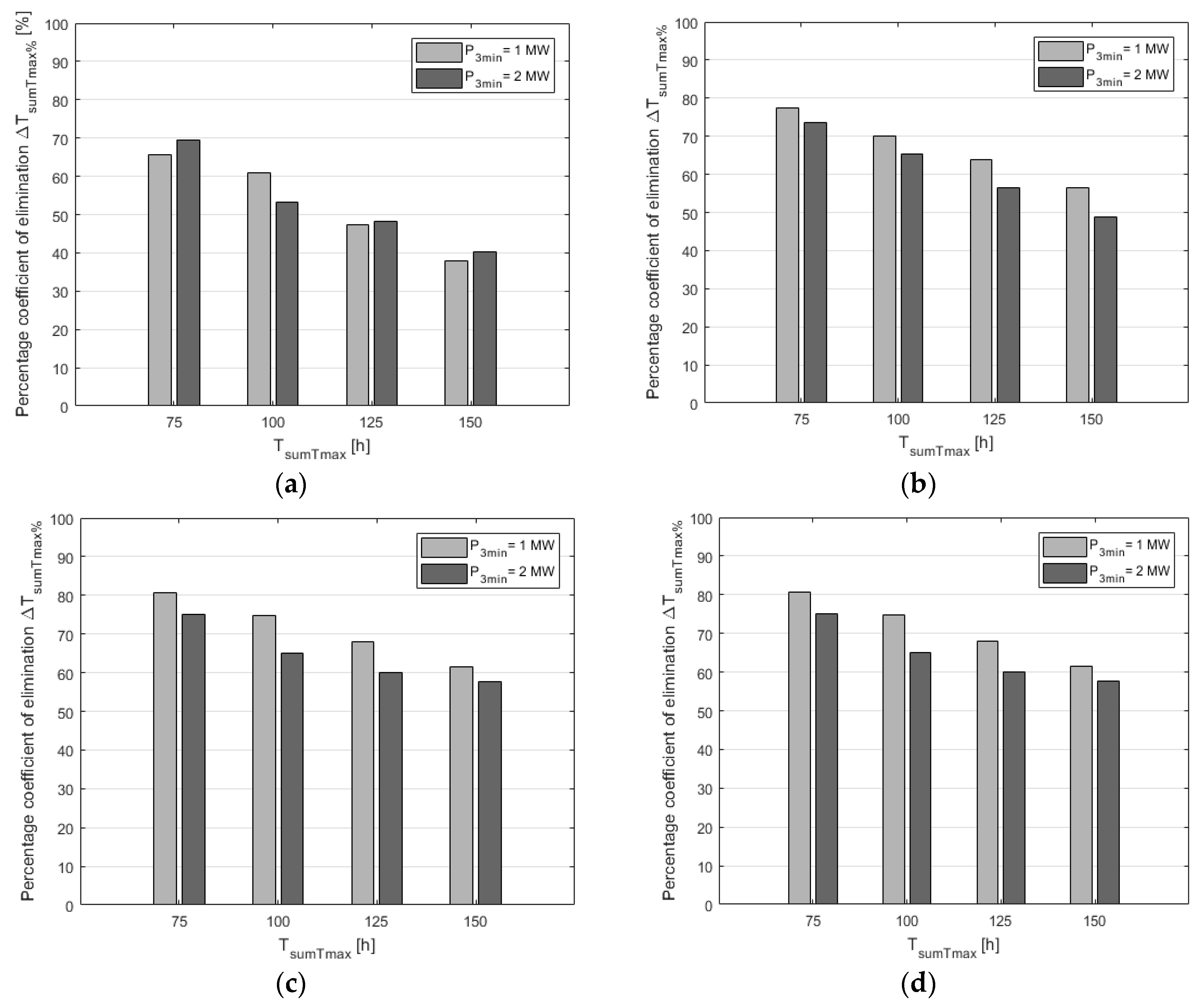
| No. | P3min (MW) | Tmax (min) | TsumTmax (h) | TsumTmax (AFESSmin) (h) | TsumTmax(0) (h) | ΔTsumTmax (%) | AFESSmin (kWh) | Turbine’s Number/Power(−)/(MW) | PWFnr (MW) | ΔA (MWh) |
|---|---|---|---|---|---|---|---|---|---|---|
| Tmax(2) = 10 min | ||||||||||
| 1 | 1 | 10 | 75 | 73.7 | 214.3 | 65.6 | 125 | 10/0.9 | 9 | 21.1 |
| 2 | 1 | 10 | 100 | 96.2 | 247.1 | 61.0 | 72 | 5/1.8 | 9 | 31.6 |
| 3 | 1 | 10 | 125 | 122.5 | 232.1 | 47.2 | 36 | 4/2.3 | 9.2 | 38.5 |
| 4 | 1 | 10 | 150 | 144.8 | 225.5 | 37.8 | 25 | 6/1.8 | 10.8 | 47.6 |
| 5 | 2 | 10 | 75 | 73.4 | 241.6 | 69.6 | 108 | 10 0.9 | 9 | 37.3 |
| 6 | 2 | 10 | 100 | 92.7 | 198.0 | 53.2 | 100 | 4/2.3 | 9.2 | 49.3 |
| 7 | 2 | 10 | 125 | 120.5 | 231.2 | 48.1 | 72 | 3/3 | 9 | 60.4 |
| 8 | 2 | 10 | 150 | 144.2 | 241.5 | 40.2 | 36 | 6/1.8 | 10.8 | 72.0 |
| Tmax(3) = 15 min | ||||||||||
| 9 | 1 | 15 | 75 | 74.9 | 329.8 | 77.3 | 630 | 12/0.9 | 10.8 | 25.7 |
| 10 | 1 | 15 | 100 | 93.3 | 312.2 | 70.1 | 240 | 10/0.9 | 9 | 30.0 |
| 11 | 1 | 15 | 125 | 118.1 | 327.6 | 63.9 | 125 | 4/2.3 | 9.2 | 36.9 |
| 12 | 1 | 15 | 150 | 142.7 | 327.6 | 56.4 | 72 | 4/2.3 | 9.2 | 42.8 |
| 13 | 2 | 15 | 75 | 74.9 | 283.9 | 73.6 | 1470 | 4/2.3 | 9.2 | 50.9 |
| 14 | 2 | 15 | 100 | 98.2 | 283.9 | 65.4 | 400 | 4/2.3 | 9.2 | 63.4 |
| 15 | 2 | 15 | 125 | 123.6 | 283.9 | 56.4 | 175 | 4/2.3 | 9.2 | 75.6 |
| 16 | 2 | 15 | 150 | 145.2 | 283.9 | 48.9 | 108 | 4/2.3 | 9.2 | 84.5 |
| Tmax(4) = 20 min | ||||||||||
| 17 | 1 | 20 | 75 | 74.7 | 384.9 | 80.6 | 1800 | 12/0.9 | 10.8 | 37.8 |
| 18 | 1 | 20 | 100 | 99.5 | 397.7 | 74.9 | 684 | 12/0.9 | 10.8 | 34.1 |
| 19 | 1 | 20 | 125 | 123.3 | 384.9 | 67.9 | 350 | 10/0.9 | 9 | 40.3 |
| 20 | 1 | 20 | 150 | 147.9 | 384.9 | 61.6 | 175 | 10/0.9 | 9 | 46.7 |
| 21 | 2 | 20 | 75 | 74.9 | 302.8 | 75.3 | 2670 | 11/0.9 | 9.9 | 52.0 |
| 22 | 2 | 20 | 100 | 98.8 | 285.6 | 65.4 | 840 | 10/0.9 | 9 | 62.9 |
| 23 | 2 | 20 | 125 | 124.9 | 314.2 | 60.2 | 474 | 12/0.9 | 10.8 | 76.5 |
| 24 | 2 | 20 | 150 | 149.5 | 353.0 | 57.7 | 288 | 4/2.3 | 9.2 | 96.7 |
| Tmax(5) = 25 min | ||||||||||
| 25 | 1 | 25 | 75 | 74.9 | 447.2 | 83.3 | 5400 | 10/0.9 | 9 | 29.3 |
| 26 | 1 | 25 | 100 | 99.3 | 482.8 | 79.4 | 1440 | 4/2.3 | 9.2 | 39.2 |
| 27 | 1 | 25 | 125 | 124.9 | 447.2 | 72.1 | 750 | 10/0.9 | 9 | 44.0 |
| 28 | 1 | 25 | 150 | 148.7 | 447.2 | 66.8 | 390 | 10/0.9 | 9 | 54.6 |
| 29 | 2 | 25 | 75 | 74.9 | 355.5 | 78.9 | 6200 | 11/0.9 | 9.9 | 54.4 |
| 30 | 2 | 25 | 100 | 99.8 | 355.5 | 71.9 | 2340 | 11/0.9 | 9.9 | 70.3 |
| 31 | 2 | 25 | 125 | 124.7 | 334.1 | 62.7 | 1584 | 10/0.9 | 9 | 87.3 |
| 32 | 2 | 25 | 150 | 148.9 | 334.1 | 55.5 | 500 | 10/0.9 | 9 | 95.8 |
| Tmax(6) = 30 min | ||||||||||
| 33 | 1 | 30 | 75 | - | - | - | - | - | - | - |
| 34 | 1 | 30 | 100 | 99.3 | 552.0 | 82.1 | 2100 | 6/1.8 | 10.8 | 54.0 |
| 35 | 1 | 30 | 125 | 124.3 | 552.0 | 77.5 | 1188 | 6/1.8 | 10.8 | 65.0 |
| 36 | 1 | 30 | 150 | 148.9 | 552.0 | 73.0 | 780 | 6/1.8 | 10.8 | 75.9 |
| 37 | 2 | 30 | 75 | - | - | - | - | - | - | - |
| 38 | 2 | 30 | 100 | 99.8 | 426.9 | 76.6 | 4050 | 12/0.9 | 10.8 | 70.9 |
| 39 | 2 | 30 | 125 | 124.9 | 398.8 | 68.7 | 2070 | 11/0.9 | 9.9 | 88.3 |
| 40 | 2 | 30 | 150 | 149.7 | 378.9 | 60.5 | 1075 | 11/0.9 | 9 | 103.0 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tomczewski, A.; Kasprzyk, L. Optimisation of the Structure of a Wind Farm—Kinetic Energy Storage for Improving the Reliability of Electricity Supplies. Appl. Sci. 2018, 8, 1439. https://doi.org/10.3390/app8091439
Tomczewski A, Kasprzyk L. Optimisation of the Structure of a Wind Farm—Kinetic Energy Storage for Improving the Reliability of Electricity Supplies. Applied Sciences. 2018; 8(9):1439. https://doi.org/10.3390/app8091439
Chicago/Turabian StyleTomczewski, Andrzej, and Leszek Kasprzyk. 2018. "Optimisation of the Structure of a Wind Farm—Kinetic Energy Storage for Improving the Reliability of Electricity Supplies" Applied Sciences 8, no. 9: 1439. https://doi.org/10.3390/app8091439
APA StyleTomczewski, A., & Kasprzyk, L. (2018). Optimisation of the Structure of a Wind Farm—Kinetic Energy Storage for Improving the Reliability of Electricity Supplies. Applied Sciences, 8(9), 1439. https://doi.org/10.3390/app8091439





