Effect of Sinusoidal Corrugated Geometries on the Vibrational Response of Viscoelastic Nanoplates
Abstract
:1. Introduction
2. Modeling Assumptions
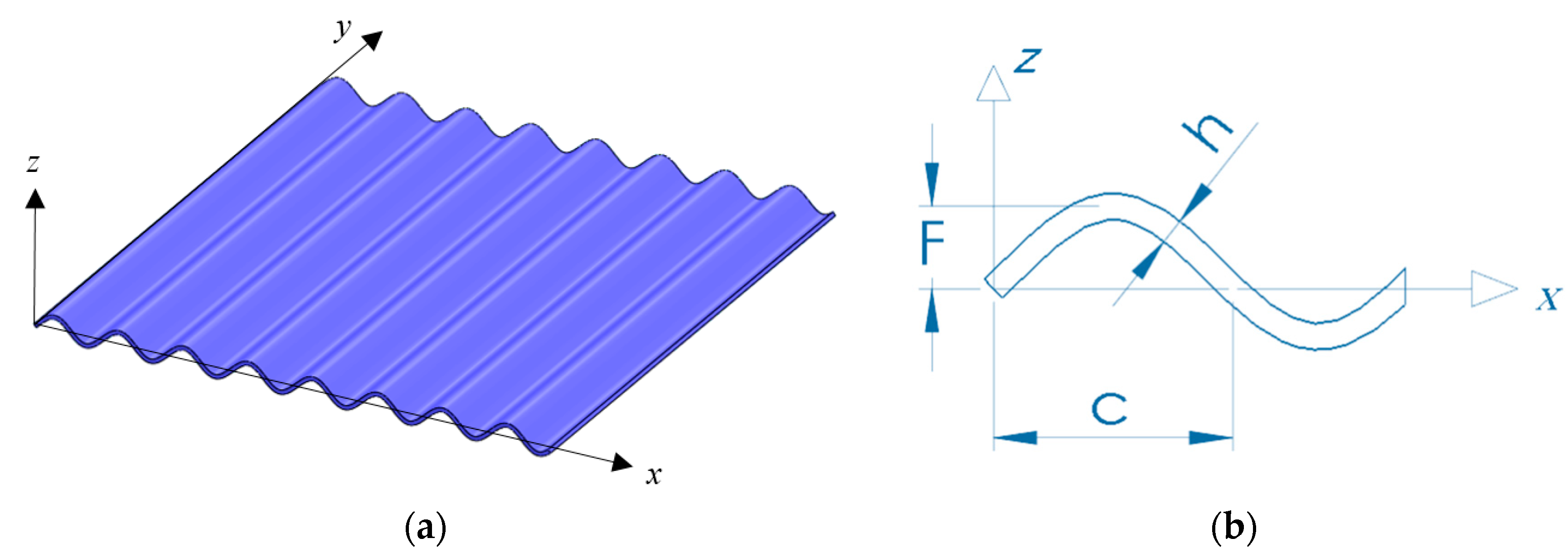
2.1. Problem Definition
2.2. Non-Local Strain Gradient Theory
2.3. The Linear Viscoelastic Model
3. Analytical Approach
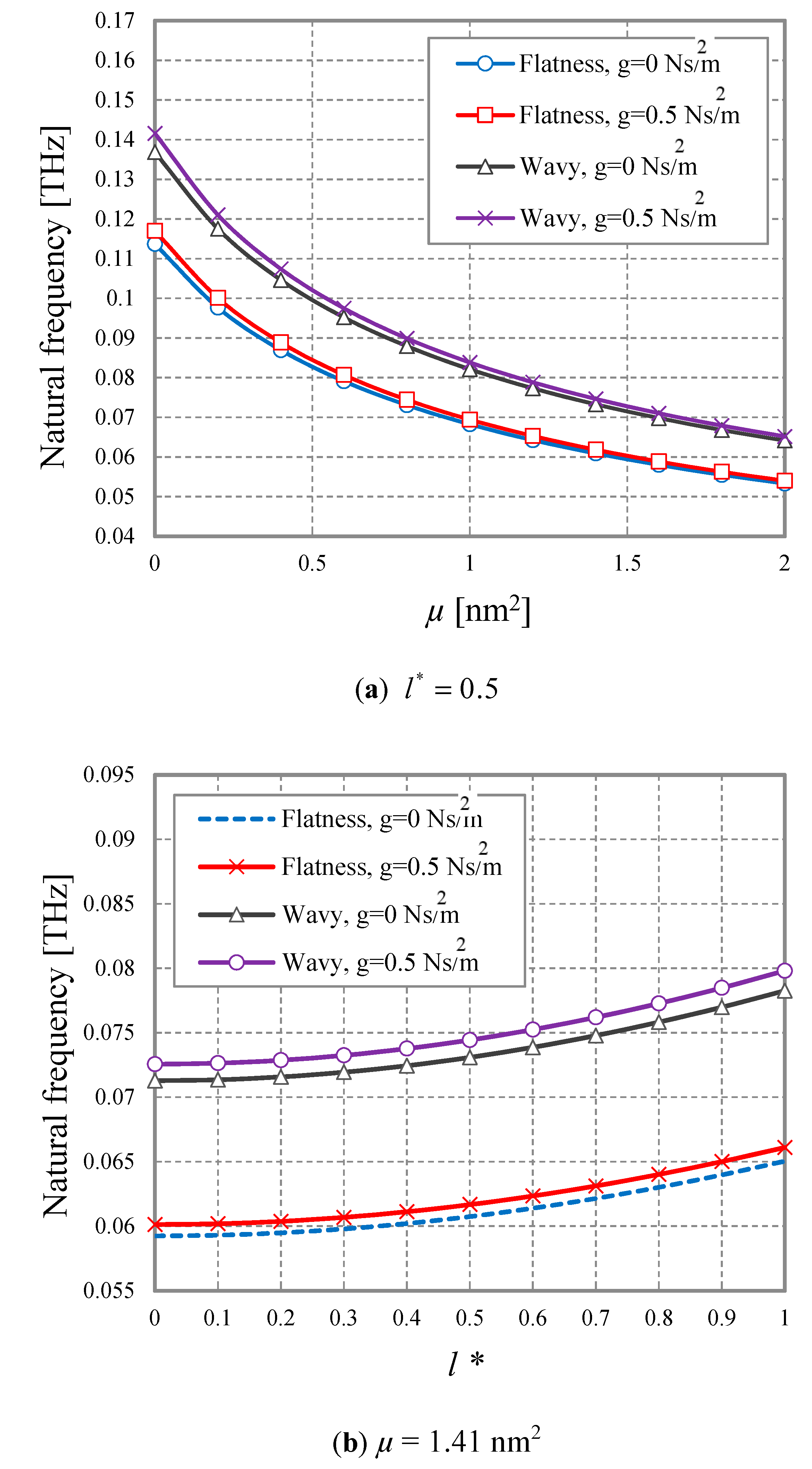
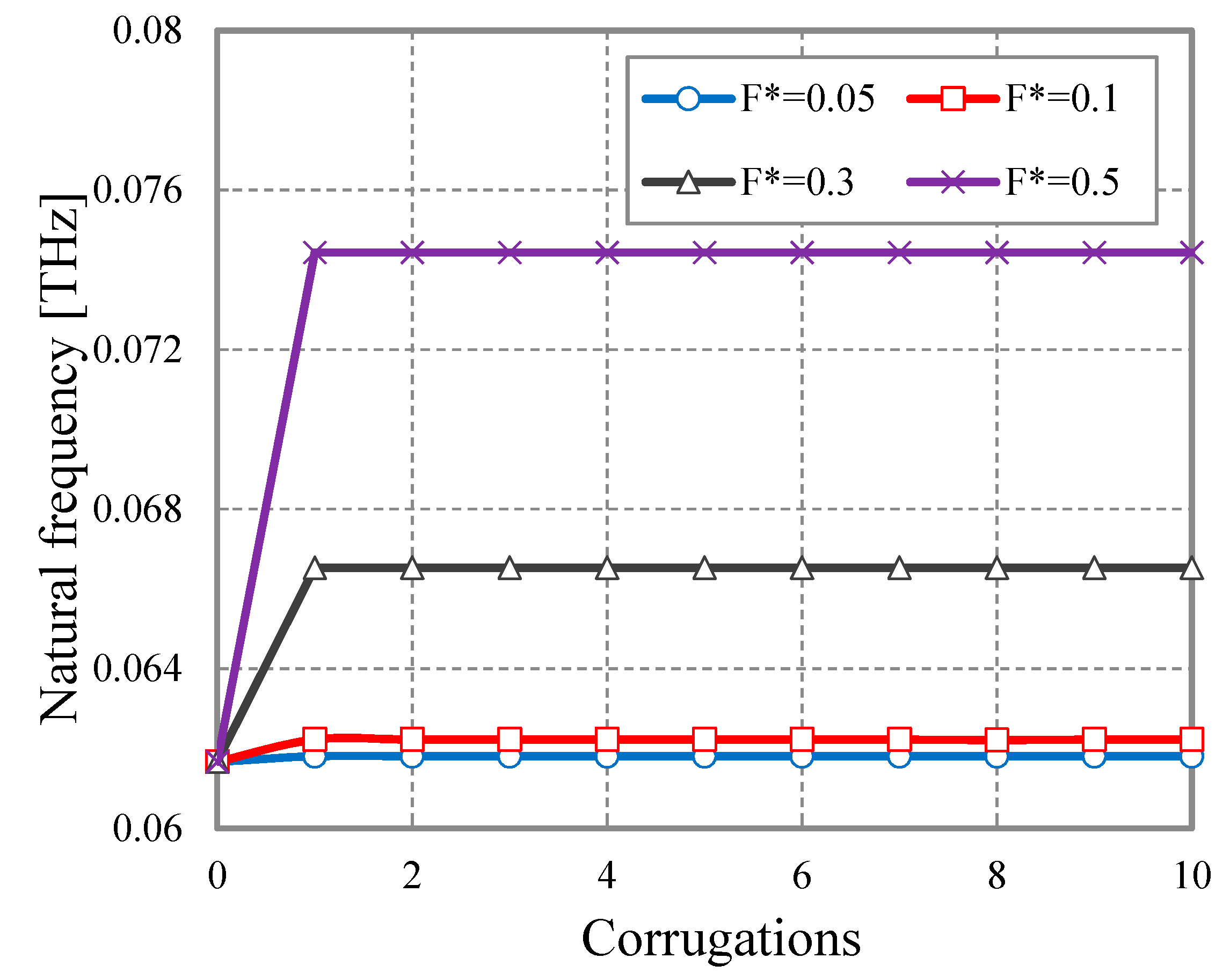
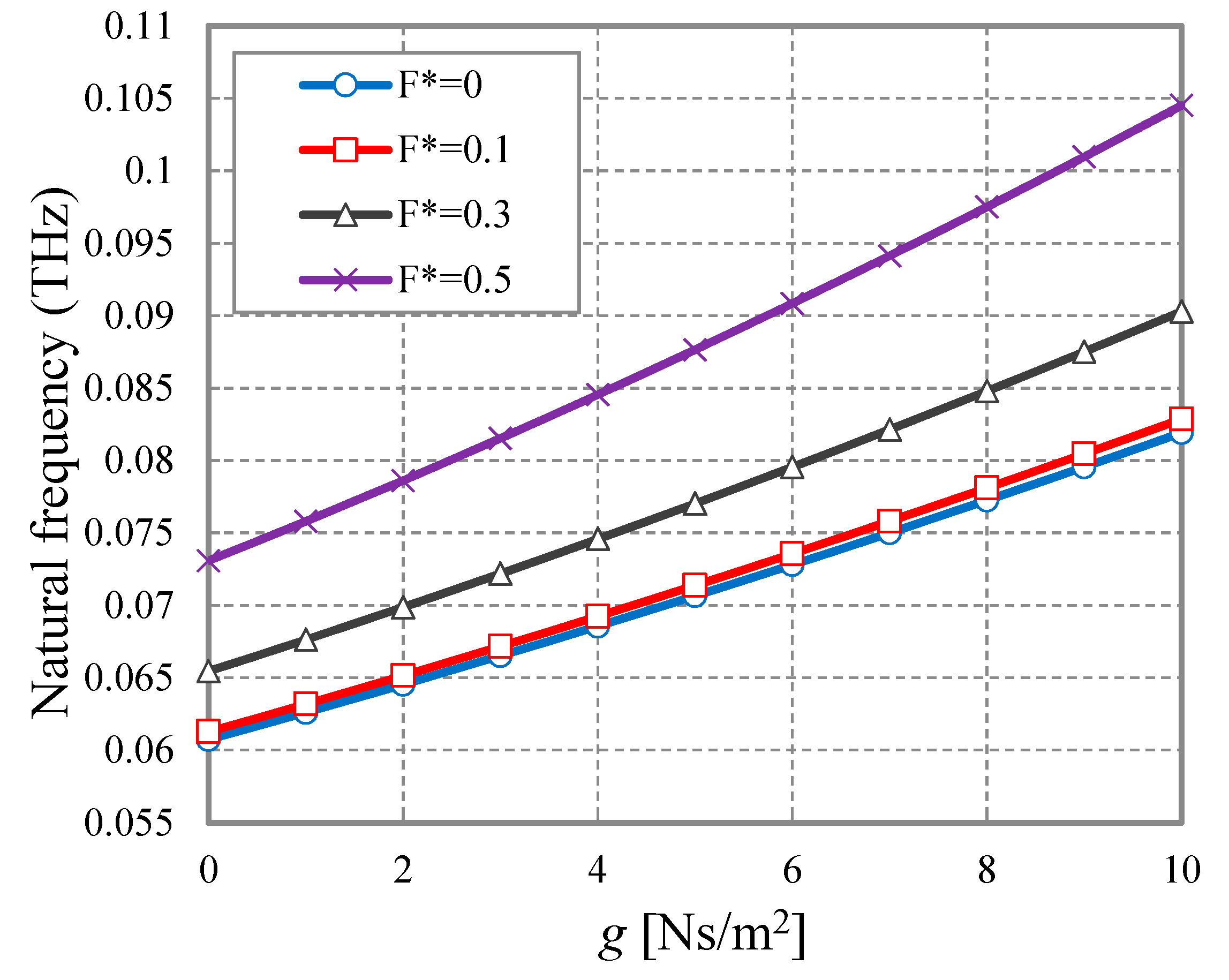
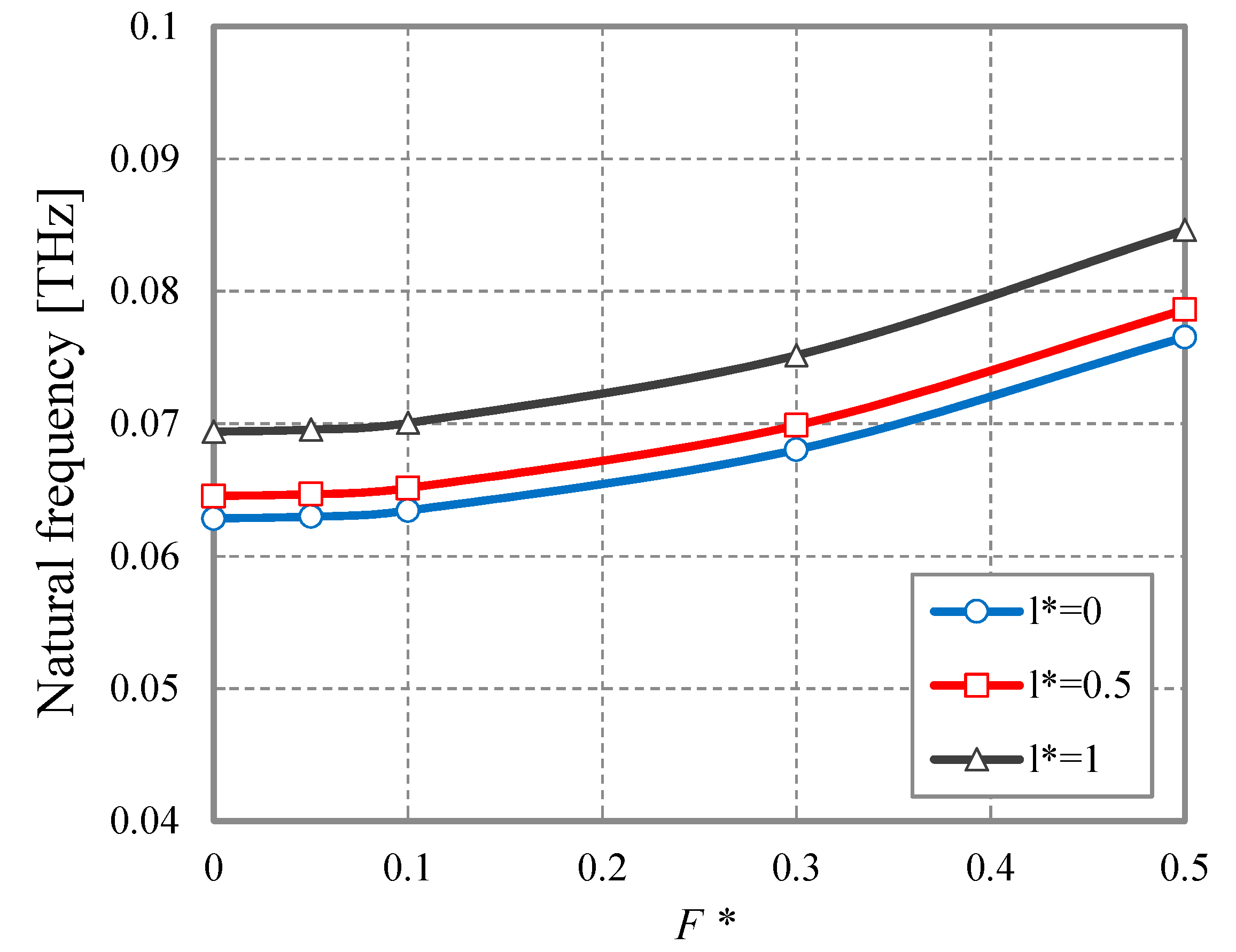
4. Numerical Results and Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Sunthorn, S.; Kittiphat, R. The effect on rolling mill of waviness in hot rolled steel, World academy of sciences, Engineering and technology. Int. J. Metall. Mater. Eng. 2014, 8, 2077–2082. [Google Scholar]
- Kamarian, S.; Salim, M.; Dimitri, R.; Tornabene, F. Free vibration analysis of conical shells reinforced with agglomerated carbon nanotubes. Int. J. Mech. Sci. 2016, 108–109, 157–165. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M.; Viola, E. Effect of agglomeration on the natural frequencies of functionally graded carbon nanotube-reinforced laminated composite doubly-curved shells. Compos. Part B-Eng. 2016, 89, 187–218. [Google Scholar] [CrossRef]
- Banić, D.; Bacciocchi, M.; Tornabene, F.; Ferreira, A.J.M. Influence of Winkler-Pasternak foundation on the vibrational behavior of plates and shells reinforced by agglomerated carbon nanotubes. Appl. Sci. 2017, 7, 1228. [Google Scholar] [CrossRef]
- Nejati, M.; Dimitri, R.; Tornabene, F.; Hossein, Y.M. Thermal buckling of nanocomposite stiffened cylindrical shells reinforced by functionally graded wavy carbon nano-tubes with temperature-dependent properties. Appl. Sci. 2017, 7, 1223. [Google Scholar] [CrossRef]
- Malikan, M.; Jabbarzadeh, M.; Dastjerdi, S. Non-linear Static stability of bi-layer carbon nanosheets resting on an elastic matrix under various types of in-plane shearing loads in thermo-elasticity using nonlocal continuum. Microsyst. Technol. 2017, 23, 2973–2991. [Google Scholar] [CrossRef]
- Malikan, M. Electro-mechanical shear buckling of piezoelectric nanoplate using modified couple stress theory based on simplified first order shear deformation theory. Appl. Math. Model. 2017, 48, 196–207. [Google Scholar] [CrossRef]
- Malikan, M. Analytical predictions for the buckling of a nanoplate subjected to nonuniform compression based on the four-variable plate theory. J. Appl. Comput. Mech. 2017, 3, 218–228. [Google Scholar]
- Malikan, M. Buckling analysis of a micro composite plate with nano coating based on the modified couple stress theory. J. Appl. Comput. Mech. 2018, 4, 1–15. [Google Scholar]
- Malikan, M.; Nguyen, V.B. Buckling analysis of piezo-magnetoelectric nanoplates in hygrothermal environment based on a novel one variable plate theory combining with higher-order nonlocal strain gradient theory. Phys. E Low-Dimens. Syst. Nanostruct. 2018, 102, 8–28. [Google Scholar] [CrossRef]
- Malikan, M. Temperature influences on shear stability of a nanosize plate with piezoelectricity effect. Multidiscip. Model. Mater. Struct. 2018, 14, 125–142. [Google Scholar] [CrossRef]
- Golmakani, M.E.; Malikan, M.; Far, M.N.S.; Majidi, H.R. Bending and buckling formulation of graphene sheets based on nonlocal simple first order shear deformation theory. Mater. Res. Express 2018, 5, 065010. [Google Scholar] [CrossRef]
- Malikan, M.; Far, M.N.S. Differential quadrature method for dynamic buckling of graphene sheet coupled by a viscoelastic medium using neperian frequency based on nonlocal elasticity theory. J. Appl. Comput. Mech. 2018, 4, 147–160. [Google Scholar]
- Malikan, M.; Dastjerdi, S. Analytical buckling of FG nanobeams on the basis of a new one variable first-order shear deformation beam theory. Int. J. Eng. Appl. Sci. 2018, 10, 21–34. [Google Scholar] [CrossRef]
- Malikan, M. On the buckling response of axially pressurized nanotubes based on a novel nonlocal beam theory. J. Appl. Comput. Mech. 2018. [Google Scholar] [CrossRef]
- Fantuzzi, N.; Tornabene, F.; Bacciocchi, M.; Dimitri, R. Free vibration analysis of arbitrarily shaped Functionally Graded Carbon Nanotube-reinforced plates. Compos. Part B-Eng. 2017, 115, 384–408. [Google Scholar] [CrossRef]
- Nejati, M.; Asanjarani, A.; Dimitri, R.; Tornabene, F. Static and free vibration analysis of functionally graded conical shells reinforced by carbon nanotubes. Int. J. Mech. Sci. 2017, 130, 383–398. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M. Linear static response of nanocomposite plates and shells reinforced by agglomerated carbon nanotubes. Compos. Part B-Eng. 2017, 115, 449–476. [Google Scholar] [CrossRef]
- Tornabene, F.; Bacciocchi, M.; Fantuzzi, N.; Reddy, J.N. Multiscale approach for three-Phase CNT/Polymer/Fiber laminated nanocomposite structures. Polym. Compos. 2017, in press. [Google Scholar] [CrossRef]
- Hashemi, S.H.; Mehrabani, H.; Ahmadi-Savadkoohi, A. Forced vibration of nanoplate on viscoelastic substrate with consideration of structural damping: An analytical solution. Compos. Struct. 2015, 133, 8–15. [Google Scholar] [CrossRef]
- Wang, Y.; Li, F.; Wang, Y. Nonlinear vibration of double layered viscoelastic nanoplates based on nonlocal theory. Physica E 2015, 67, 65–76. [Google Scholar] [CrossRef]
- Zenkour, A.M.; Sobhy, M. Nonlocal piezo-hygrothermal analysis for vibration characteristics of a piezoelectric Kelvin–Voigt viscoelastic nanoplate embedded in a viscoelastic medium. Acta Mech. 2018, 229, 3–19. [Google Scholar] [CrossRef]
- Aghababaei, R.; Reddy, J.N. Nonlocal third-order shear deformation plate theory with application to bending and vibration of plates. J. Sound Vib. 2009, 326, 277–289. [Google Scholar] [CrossRef]
- Malikan, M.; Tornabene, F.; Dimitri, R. Nonlocal three-dimensional theory of elasticity for buckling behavior of functionally graded porous nanoplates using volume integrals. Mater. Res. Express 2018, 5, 095006. [Google Scholar] [CrossRef]
- Malikan, M.; Nguyen, V.B.; Tornabene, F. Damped forced vibration analysis of single-walled carbon nanotubes resting on viscoelastic foundation in thermal environment using nonlocal strain gradient theory. Eng. Sci. Technol. Int. J. 2018, 21, 778–786. [Google Scholar] [CrossRef]
- Malikan, M.; Nguyen, V.B.; Tornabene, F. Electromagnetic forced vibrations of composite nanoplates using nonlocal strain gradient theory. Mater. Res. Express 2018, 5, 075031. [Google Scholar] [CrossRef]
- Malikan, M. Electro-thermal buckling of elastically supported double-layered piezoelectric nanoplates affected by an external electric voltage. Multidiscip. Model. Mater. Struct. 2018. [Google Scholar] [CrossRef]
- She, G.-L.; Yuan, F.-G.; Ren, Y.-R.; Xiao, W.-S. On buckling and postbuckling behavior of nanotubes. Int. J. Eng. Sci. 2017, 121, 130–142. [Google Scholar] [CrossRef]
- She, G.-L.; Yuan, F.-G.; Ren, Y.-R. Thermal buckling and post-buckling analysis of functionally graded beams based on a general higher-order shear deformation theory. Appl. Math. Model. 2017, 47, 340–357. [Google Scholar] [CrossRef]
- She, G.-L.; Yuan, F.-G.; Ren, Y.-R.; Liu, H.-B.; Xiao, W.-S. Nonlinear bending and vibration analysis of functionally graded porous tubes via a nonlocal strain gradient theory. Compos. Struct. 2018, 203, 614–623. [Google Scholar] [CrossRef]
- Lim, C.W.; Zhang, G.; Reddy, J.N. A Higher-order nonlocal elasticity and strain gradient theory and Its Applications in wave propagation. J. Mech. Phys. Solids 2015, 78, 298–313. [Google Scholar] [CrossRef]
- Barati, M.R.; Shahverdi, H. Hygro-thermal vibration analysis of graded double-refined-nanoplate systems using hybrid nonlocal stress-strain gradient theory. Compos. Struct. 2017, 176, 982–995. [Google Scholar] [CrossRef]
- Briassoulis, D. Equivalent orthotropic properties of corrugated sheets. Comput. Struct. 1986, 23, 129–138. [Google Scholar] [CrossRef]
- Liew, K.M.; Peng, L.X.; Kitipornchai, S. Buckling analysis of corrugated plates using a mesh-free Galerkin method based on the first-order shear deformation theory. Comput. Mech. 2006, 38, 61–75. [Google Scholar] [CrossRef]
- Liew, K.M.; Peng, L.X.; Kitipornchai, S. Vibration analysis of corrugated Reissner–Mindlin plates using a mesh-free Galerkin method. Int. J. Mech. Sci. 2009, 51, 642–652. [Google Scholar] [CrossRef]
- Ansari, R.; Sahmani, S.; Arash, B. Nonlocal plate model for free vibrations of single-layered graphene sheets. Phys. Lett. A 2010, 375, 53–62. [Google Scholar] [CrossRef]
- Wu, C.; Li, W. Free vibration analysis of embedded single-layered nanoplates and graphene sheets by using the multiple time scale method. Comput. Math. Appl. 2017, 73, 838–854. [Google Scholar] [CrossRef]
- Malekzadeh, P.; Shojaee, M. Free vibration of nanoplates based on a nonlocal two-variable refined plate theory. Compos. Struct. 2013, 95, 443–452. [Google Scholar] [CrossRef]
| Natural Frequency (THz) | |||
|---|---|---|---|
| Present-Non-Local, Navier | Non-Local-FSDT, GDQ [36] | Zigzag Graphene, MD [36] | |
| OVFSDT | |||
| 0.0592339 | 0.0584221 | 0.0587725 | 10 |
| 0.0287035 | 0.0282888 | 0.0273881 | 15 |
| 0.0153208 | 0.0164593 | 0.0157524 | 20 |
| 0.0103514 | 0.0107085 | 0.0099480 | 25 |
| 0.0074258 | 0.0075049 | 0.0070655 | 30 |
| 0.0055703 | 0.0055447 | 0.0052982 | 35 |
| 0.0043250 | 0.0042608 | 0.0040985 | 40 |
| 0.0034512 | 0.0033751 | 0.0032609 | 45 |
| 0.0028157 | 0.0027388 | 0.0026194 | 50 |
| Natural Frequency (THz) | |||
|---|---|---|---|
| Present-Non-Local, Navier | Non-Local-FSDT, GDQ [36] | Armchair Graphene, MD [36] | |
| OVFSDT | |||
| 0.0603135 | 0.0592359 | 0.0595014 | 10 |
| 0.0290542 | 0.0284945 | 0.0277928 | 15 |
| 0.0154374 | 0.0165309 | 0.0158141 | 20 |
| 0.0104078 | 0.0107393 | 0.0099975 | 25 |
| 0.0074558 | 0.0075201 | 0.0070712 | 30 |
| 0.0055876 | 0.0055531 | 0.0052993 | 35 |
| 0.0043356 | 0.0042657 | 0.0041017 | 40 |
| 0.0034580 | 0.0033782 | 0.0032614 | 45 |
| 0.0028202 | 0.0027408 | 0.0026197 | 50 |
| Theories | Non-Dimensional Natural Frequency () | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| nm2 | nm2 | nm2 | nm2 | nm2 | nm2 | nm2 | nm2 | nm2 | nm2 | nm2 | nm2 | |
| [37]-case 1 | 0.0955 | 0.0873 | 0.0809 | 0.0240 | 0.0220 | 0.0203 | 0.0599 | 0.0565 | 0.0536 | 0.0150 | 0.0142 | 0.0135 |
| [37]-case 2 | 0.0931 | 0.0850 | 0.0788 | 0.0239 | 0.0218 | 0.0202 | 0.0589 | 0.0556 | 0.0528 | 0.0150 | 0.0141 | 0.0134 |
| [37]-case 3 | 0.0931 | 0.0851 | 0.0789 | 0.0239 | 0.0218 | 0.0202 | 0.0589 | 0.0556 | 0.0528 | 0.0150 | 0.0141 | 0.0134 |
| [37]-case 4 | 0.0931 | 0.0851 | 0.0789 | 0.0239 | 0.0218 | 0.0202 | 0.0589 | 0.0556 | 0.0528 | 0.0150 | 0.0141 | 0.0134 |
| Non-local-CPT [23] | 0.0963 | 0.0880 | 0.0816 | 0.0241 | 0.0220 | 0.0204 | 0.0602 | 0.0568 | 0.0539 | 0.0150 | 0.0142 | 0.0135 |
| Non-local-FSDT [23] | 0.0930 | 0.0850 | 0.0788 | 0.0239 | 0.0218 | 0.0202 | 0.0589 | 0.0556 | 0.0527 | 0.0150 | 0.0141 | 0.0134 |
| Non-local-TSDT [23] | 0.0935 | 0.0854 | 0.0791 | 0.0239 | 0.0218 | 0.0202 | 0.0591 | 0.0557 | 0.0529 | 0.0150 | 0.0141 | 0.0134 |
| Non-local-S-FSDT [38] | 0.0930 | 0.0850 | 0.0787 | 0.02386 | 0.0218 | 0.0202 | 0.0588 | 0.0555 | 0.0527 | 0.0149 | 0.0141 | 0.0134 |
| Non-local-Present, OVFSDT | 0.0928 | 0.0849 | 0.0780 | 0.02337 | 0.0217 | 0.02019 | 0.0589 | 0.0552 | 0.0521 | 0.0145 | 0.0140 | 0.0134 |
| Elastic properties |
| , |
| Density |
| kg/m3 |
| Dimensional values |
| , |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Malikan, M.; Dimitri, R.; Tornabene, F. Effect of Sinusoidal Corrugated Geometries on the Vibrational Response of Viscoelastic Nanoplates. Appl. Sci. 2018, 8, 1432. https://doi.org/10.3390/app8091432
Malikan M, Dimitri R, Tornabene F. Effect of Sinusoidal Corrugated Geometries on the Vibrational Response of Viscoelastic Nanoplates. Applied Sciences. 2018; 8(9):1432. https://doi.org/10.3390/app8091432
Chicago/Turabian StyleMalikan, Mohammad, Rossana Dimitri, and Francesco Tornabene. 2018. "Effect of Sinusoidal Corrugated Geometries on the Vibrational Response of Viscoelastic Nanoplates" Applied Sciences 8, no. 9: 1432. https://doi.org/10.3390/app8091432
APA StyleMalikan, M., Dimitri, R., & Tornabene, F. (2018). Effect of Sinusoidal Corrugated Geometries on the Vibrational Response of Viscoelastic Nanoplates. Applied Sciences, 8(9), 1432. https://doi.org/10.3390/app8091432








