Double-Consensus Based Distributed Optimal Energy Management for Multiple Energy Hubs
Abstract
:1. Introduction
- (1)
- The centralized approaches rely on a powerful central controller to process a huge mass of data and require two-way and high-bandwidth communication to work on the information gathered for the whole system [20,21]. Thus, solutions based on centralized approaches are costly to implement and are prone to single-point failures and modeling errors.
- (2)
- (1)
- By making use of some change of variables, the strongly coupled form between variables in global equality constraints are transformed to the local function and inequality constraints. With this effort, the EMP is formulated as a kind of distributed coupled optimization problem.
- (2)
- The proposed DDC algorithm, which does not require a price coordinator or a leader to collect global parameters, can solve the EMP in a fully distributed fashion. In contrast to centralized algorithms, the proposed algorithm is more flexible, reliable and robust, etc. To the best knowledge of the authors, there still exist very few papers concerned about solving the EMP for multiple energy hubs in a fully distributed fashion.
- (3)
- The strong coupling problem, existing in the objective function and constraint limits, can be effectively solved by implementing the proposed DDC algorithm. Moreover, the rigorous optimality and convergence analysis are presented only under strong connectivity conditions, which is more reasonable and general, and possesses less conservatism.
2. Problem Formulation
2.1. Energy Hub Model
2.2. EMP of Multiple Energy Hubs
- (1)
- Objective: The total objective function is to cooperatively minimize the aggregated energy costs (i.e., the electricity and natural gas consumption costs associated with the individual energy hub) and the emissions penalty from electricity and heat power generation. The mathematical expression of this objective function can be seen in Appendix A-(b).
- (2)
- Constraints: Energy hubs collectively make decisions on their own subject to global and local constraints. Accordingly, the set of local constraints for each energy hub is listed in Appendix A-(c). Moreover, the global constraints imply the supply–demand balance constraints. Specifically, the total electricity and heat power generation, i.e., and , should be equal to the total respective electricity and heat load demands, i.e., and , respectively. In terms of the defined coupling matrix, we can further establish the relationship between the input variables and load demands as follows:
3. Distributed Algorithm
3.1. Basic Knowledge
- (1)
- Graph theory: We consider a directed graph with a set of vertices , a set of edges and an adjacency matrix . The in-neighbors and out-neighbors of ith node are denoted by with cardinality and with cardinality , respectively. Each node can receive information from its in-neighbors and send information to its out-neighbors; meanwhile, it can be also assumed to communicate with itself.
- (2)
- Basic definitions: With regard to problem Equations (3)–(6), there are three variables that need to be calculated. To this aim, we define two strongly regular graphs G1 and G2. The first consists of nodes, where each node represents the statement related to . The second is built by dividing each node of graph G1 into two nodes which represent the statements related to and , respectively. Furthermore, we define two matrices and associated with ; meanwhile, let if , if , and if , if . It is not difficult to verify that is row stochastic and is column stochastic. Similarly, we define two matrices and for ; meanwhile, let if , if , and if , if .
- (3)
- Consensus algorithm: Based on the definitions discussed above, we consider two different discrete-time systems—shown in Appendix B-(a)—which will be employed in the design of our proposed algorithm.
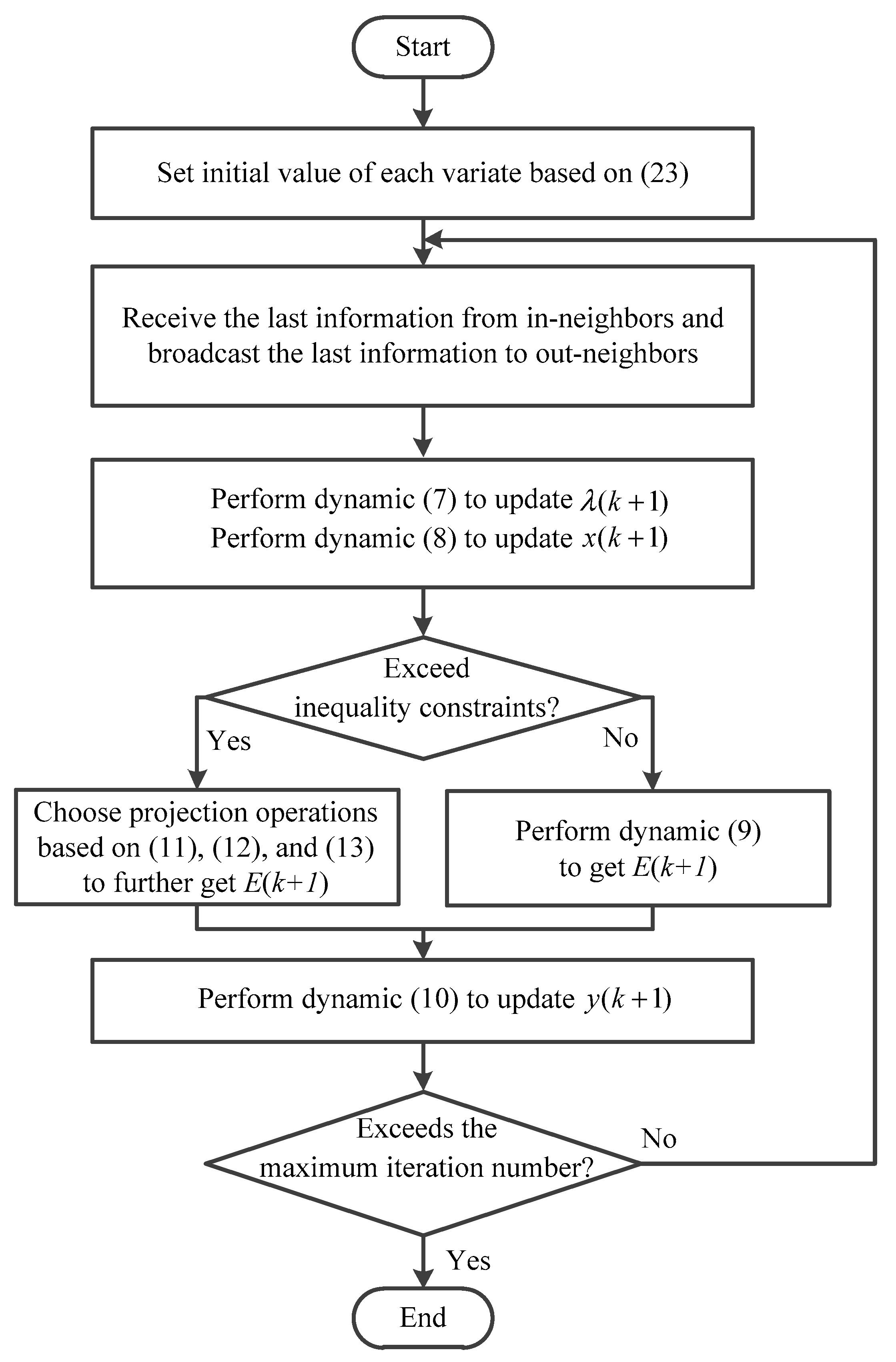
3.2. DDC Algorithm without Inequality Constraints
- (1)
- The united updating rules for energy hubs’ coordination to estimate the electricity and heat multipliers are designed forwhere and .
- (2)
- Based on the relationship between the optimal solutions and Lagrange multipliers, the updating rules for energy hubs to estimate the optimal , and are designed forwhere , and . Therein, , , , , , , and .
- (3)
- Please note that the electricity and heat power supply–demand balance constraints, i.e., Equations (4a) and (4b), are global constraints. Similar to the solving method for λe and λg, the concept of local estimation of the mismatch between demand and total generations, obtained by using only neighbors’ information, is used to solve the two global constraints in a distributed manner. Inspired by the features of (P2), the updating rules for the energy hubs’ coordination to estimate the electricity and heat power mismatches are designed as follows:whereWith regard to the determination of initializations, they are shown in detail in Appendix B-(c).
3.3. DDC Algorithm with Inequality Constraints
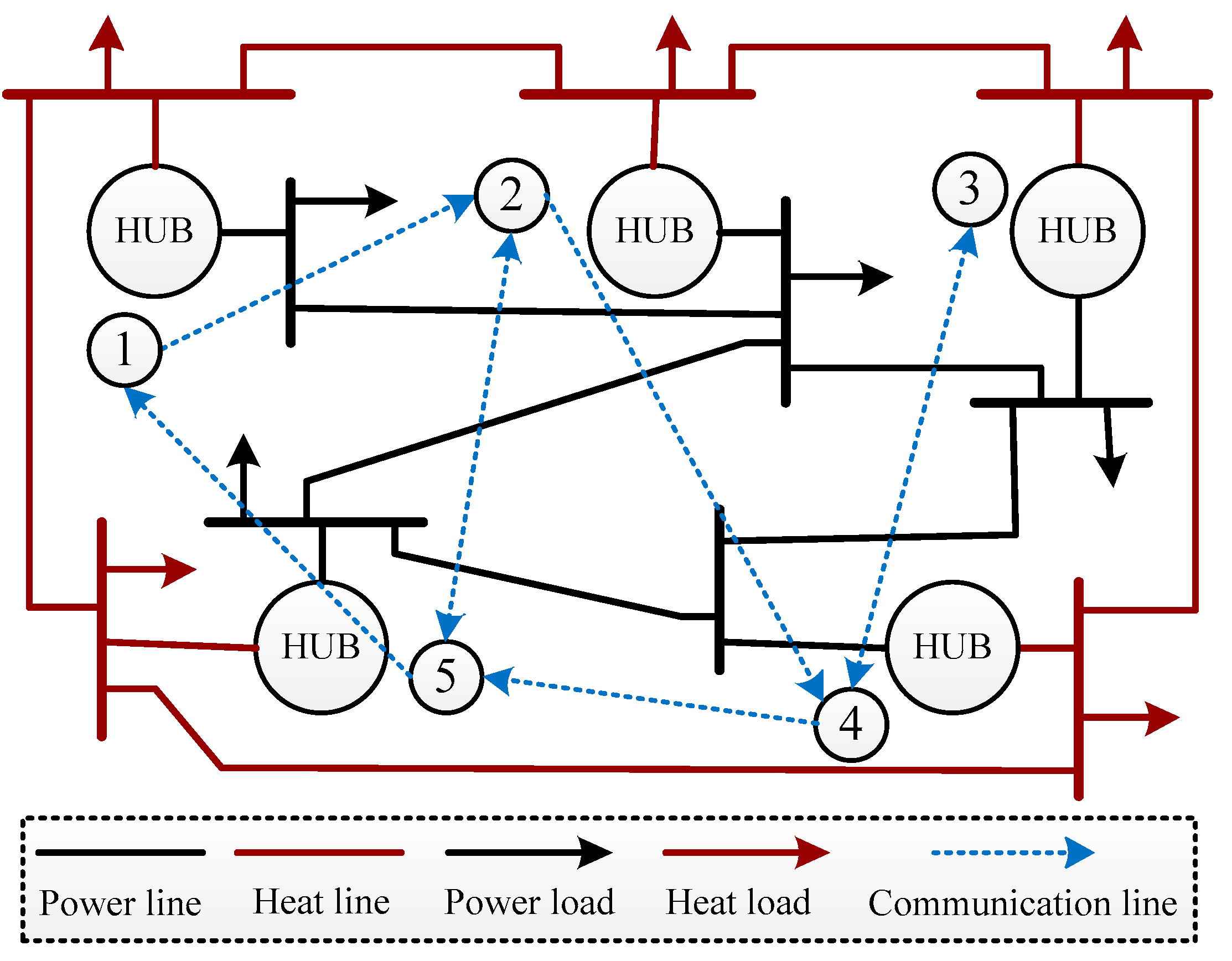
4. Application Examples
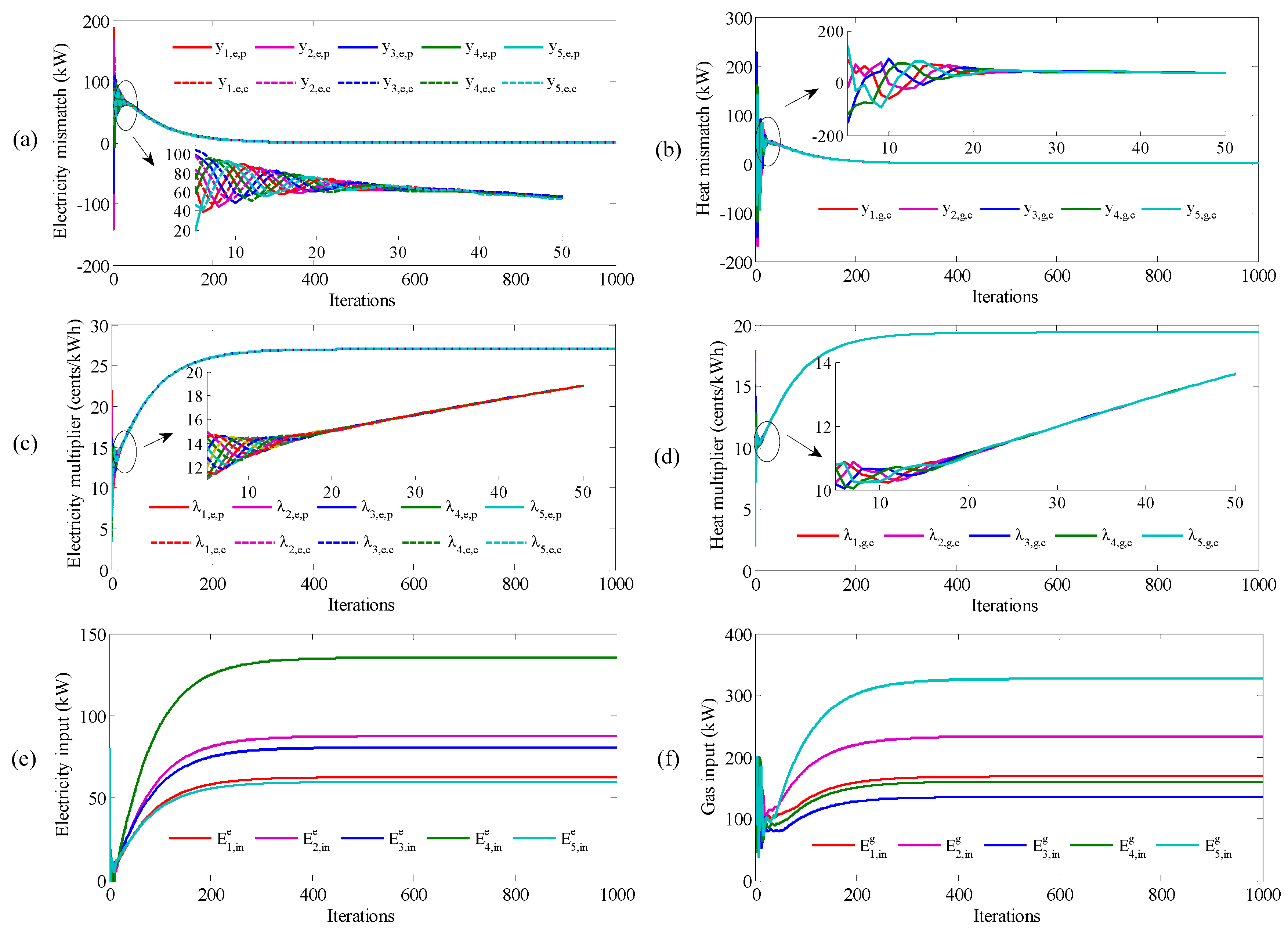
4.1. Comparison with Centralized Algorithm
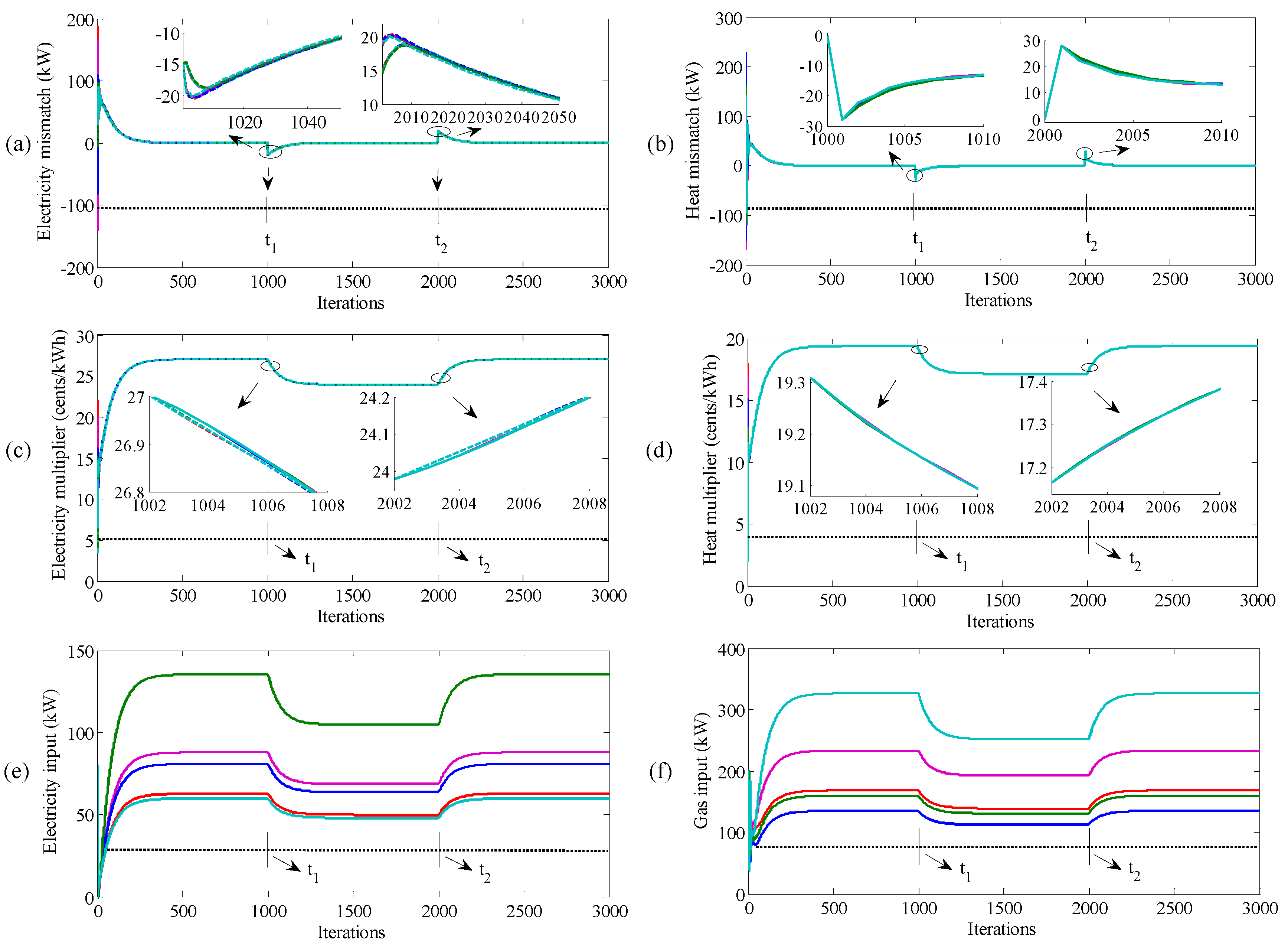
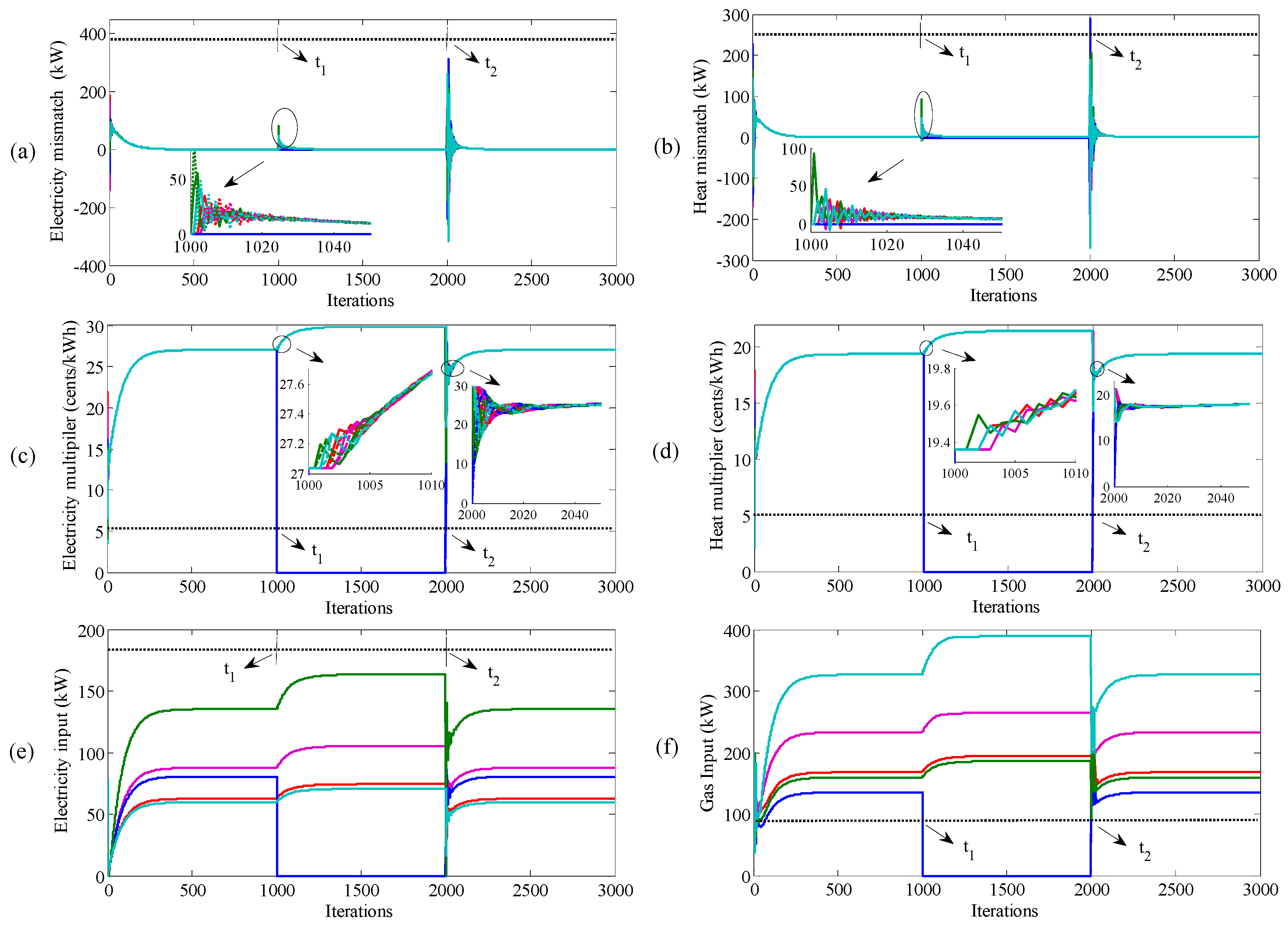
4.2. Time-Varying Demand
4.3. Plug and Play Capability
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| EMP | Energy management problem |
| DDC | Distributed double-consensus |
| CHP | Combined heat and power |
| KKT | Karush-Kuhn-Tucker |
| , | energy hub indices |
| n | Number of energy hubs |
| m | Linear inequality constraint indices |
| , | Inputs of electricity and natural gas powers |
| , | Lower and upper bounds of |
| , | Lower and upper bounds of |
| , | Outputs of electricity and heat powers |
| , | The transformer efficiencies of transformer, CHP unit from gas to electricity, CHP unit from gas to heat and boiler |
| Dispatch factor | |
| , | Electricity and natural gas cost functions |
| Penalty function | |
| , | Cost coefficients |
| , | penalty coefficients |
| , | Local electricity and natural gas loads connected to ith energy hub |
| , , | Coefficients of mth linear inequality constraint for variables and |
| and | Electricity and heat multipliers for the equality constraints |
| , , | Lagrangian multiplier for inequality constraints |
| , | State variables of agent |
| Normalized left eigenvector of associated with the eigenvalue 1 | |
| Column stack vector of | |
| , | Estimated electricity multipliers |
| Estimated heat multiplier | |
| , | Estimated electricity power mismatches |
| Estimated heat power mismatch | |
| , , | Estimated of optimal , and |
| , , , , , | Column stack vectors form of , , , , and |
| , , , , , | Column stack vectors of , , , , and |
Appendix A. Constraints and Optimality Conditions
- (a)
- The conversion relationship between inputs and outputs can be expressed as the following coupling matrix form,where the dispatch factor is introduced to specify the share of natural gas by the CHP unit and boiler.
- (b)
- The total objective function of the EMP for multiple energy hubs is modeled as the following form,where
- (c)
- The local constraints arise from the limitations of the energy hubs’ capability and the dispatch factors, which are expressed as
- (d)
- The Lagrange function for problem (3)–(6) is expressed as the following equation:
Appendix B. Consensus Algorithm, Initializations and Projection Conditions
- (a)
- The two different discrete-time systems considered are as follows:Since R is row stochastic, P1 forms the first-order consensus protocol. Each node reaches the final common value . Since S is column stochastic, the summation of all state variables is a constant, i.e., .
- (b)
- We let . Then, according to the first three equations of Equation (12), the optimal solution of , and of each energy hub can be determined by the unique Lagrange multipliers λe and λe, given bywhere , , , , , , , , , and .
- (c)
- , and can be designed as any admissible values, and the other variables are initialized as
- (d)
- To map the infeasible values into the feasible operating region, the cases for no active constraints, one active constraint and two active constraints are separately discussed to further give the corresponding identification conditions as follows:
- (1)
- None of the constraints are active constraints, i.e., the optimal solutions before and after considering the inequality constraints have the same values. The identification condition of this case is if and satisfythen there are no active constraints; otherwise, the optimal solution belongs to another case.
- (2)
- Only one inequality constraint is an active constraint. Let represent any one inequality equation. The identification condition of this case is that if there exist solutions , and satisfyingthen is the only active constraint; otherwise, the optimal solution belongs to another case.
- (3)
- Two inequality constraints are active constraints. In this case, let and represent two adjacent constraints (e.g., 2 and 3) and the corner point determined by them be defined as . The identification condition of this case is that if there exist solutions and satisfyingthen, and are the two active constraints; otherwise, the optimal solution belongs to another case.
Appendix C. Proof of Theorem 1
References
- Han, R.; Meng, L.; Guerrero, J.M.; Vasquez, J.C. Distributed nonlinear control with event-triggered communication to achieve current-sharing and voltage regulation in DC microgrids. IEEE Trans. Power Electron. 2018, 33, 6416–6433. [Google Scholar] [CrossRef]
- Zhang, H.; Li, Y.; Gao, D.W.; Zhou, J. Distributed optimal energy management for energy internet. IEEE Trans. Ind. Inform. 2017, 13, 3081–3097. [Google Scholar] [CrossRef]
- Geidl, M.; Andersson, G. Optimal power flow of multiple energy carriers. IEEE Trans. Power Syst. 2007, 22, 145–155. [Google Scholar] [CrossRef]
- Krause, T.; Andersson, G.; Frohlich, K.; Alfredo, V. Multiple-energy carriers: Modeling of production, delivery, and consumption. Proc. IEEE 2011, 99, 15–27. [Google Scholar] [CrossRef]
- Tronchin, L.; Manfren, M.; Nastasi, B. Energy efficiency, demand side management and energy storage technologies—A critical analysis of possible paths of integration in the built environment. Renew. Sustain. Energy Rev. 2018, 95, 341–353. [Google Scholar] [CrossRef]
- Berardi, U.; Tronchin, L.; Manfren, M.; Nastasi, B. On the effects of variation of thermal conductivity in buildings in the italian construction sector. Energies 2018, 11, 872. [Google Scholar] [CrossRef]
- Tronchin, L.; Tommasino, M.C.; Fabbri, K. On the “cost-optimal levels” of energy performance requirements and its economic evaluation in Italy. Int. J. Sustain. Energy Plan. Manag. 2014, 3, 49–62. [Google Scholar]
- Tronchin, L.; Manfren, M.; Tagliabue, L.C. Optimization of building energy performance by means of multi-scale analysis–Lessons learned from case studies. Sustain. Cities Soc. 2016, 27, 296–306. [Google Scholar] [CrossRef]
- Paterakis, N.G.; Erdinç, O.; Catalão, J.P.S. An overview of demand response: Key-elements and international experience. Renew. Sustain. Energy Rev. 2017, 69, 871–891. [Google Scholar] [CrossRef]
- Parisio, A.; Del Vecchio, C.; Vaccaro, A. A robust optimization approach to energy hub management. Int. J. Electr. Power Energy Syst. 2012, 42, 98–104. [Google Scholar] [CrossRef]
- Rastegar, M.; Fotuhi-Firuzabad, M. Load management in a residential energy hub with renewable distributed energy resources. Energy Build. 2015, 107, 234–242. [Google Scholar] [CrossRef]
- Adamek, F.; Arnold, M.; Andersson, G. On decisive storage parameters for minimizing energy supply costs in multicarrier energy systems. IEEE Trans. Sustain. Energy 2013, 5, 102–109. [Google Scholar] [CrossRef]
- Moeini-Aghtaie, M.; Dehghanian, P.; Fotuhi-Firuzabad, M.; Ali, A. Multiagent genetic algorithm: An online probabilistic view on economic dispatch of energy hubs constrained by wind availability. IEEE Trans. Sustain. Energy 2014, 5, 699–708. [Google Scholar] [CrossRef]
- Rastegar, M.; Fotuhi-Firuzabad, M.; Zareipour, H.; Moein, M.-A. A probabilistic energy management scheme for renewable-based residential energy hubs. IEEE Trans. Smart Grid 2017, 8, 2217–2227. [Google Scholar] [CrossRef]
- Beigvand, S.D.; Abdi, H.; Scala, M.L. A general model for energy hub economic dispatch. Appl. Energy 2017, 190, 1090–1111. [Google Scholar] [CrossRef]
- Shabanpour-Haghighi, A.; Seifi, A.R. Energy flow optimization in multicarrier systems. IEEE Trans. Ind. Inform. 2015, 11, 1067–1077. [Google Scholar] [CrossRef]
- Shao, C.; Wang, X.; Shahidehpour, M.; Wang, X.; Wang, B. An MILP-based optimal power flow in multicarrier energy systems. IEEE Trans. Sustain. Energy 2017, 8, 239–248. [Google Scholar] [CrossRef]
- Moeini-Aghtaie, M.; Farzin, H.; Fotuhi-Firuzabad, M.; Reza, A. Generalized analytical approach to assess reliability of renewable-based energy hubs. IEEE Trans. Power Syst. 2017, 32, 368–377. [Google Scholar] [CrossRef]
- Zhang, X.; Che, L.; Shahidehpour, M.; Alabdulwahab, A.S. Reliability-based optimal planning of electricity and natural gas interconnections for multiple energy hubs. IEEE Trans. Smart Grid 2017, 8, 1658–1667. [Google Scholar] [CrossRef]
- Liu, N.; Wang, J. Energy sharing for interconnected microgrids with a battery storage system and renewable energy sources based on the alternating direction method of multipliers. Appl. Sci. 2018, 8, 590. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, H.; Liang, X.; Huang, B. Event-triggered based distributed cooperative energy management for multi-energy systems. IEEE Trans. Ind. Inf. 2018. [Google Scholar] [CrossRef]
- Han, R.; Meng, L.; Ferrari-Trecate, G.; Coelho, E.A.A.; Vasquez, J.C.; Guerrero, J.M. Containment and consensus-based distributed coordination control to achieve bounded voltage and precise reactive power sharing in islanded ac microgrids. IEEE Trans. Ind. Appl. 2017, 53, 5187–5199. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, H.; Han, J.; Sun, Q. Distributed multi-agent optimization via event-triggered based continuous-time newton-raphson algorithm. Neurocomputing 2018, 275, 1416–1425. [Google Scholar] [CrossRef]
- Lao, M.; Tang, J. Cooperative multi-UAV collision avoidance based on distributed dynamic optimization and causal analysis. Appl. Sci. 2017, 7, 83. [Google Scholar] [CrossRef]
- Varagnolo, D.; Zanella, F.; Cenedese, A.; Gianluigi, P.; Luca, S. Newton-raphson consensus for distributed convex optimization. IEEE Trans. Autom. Control 2016, 61, 994–1009. [Google Scholar] [CrossRef]
- Xie, X.; Yue, D.; Peng, C. Relaxed real-time scheduling stabilization of discrete-time takagi-sugeno fuzzy systems via a alterable-weights-based ranking switching mechanism. IEEE Trans. Fuzzy Syst. 2018. [Google Scholar] [CrossRef]
- Bahrami, S.; Sheikhi, A. From demand response in smart grid toward integrated demand response in smart energy hub. IEEE Trans. Smart Grid 2016, 7, 650–658. [Google Scholar] [CrossRef]
- Fan, S.; Li, Z.; Wang, J.; Piao, L.; Qian, A. Cooperative economic scheduling for multiple energy hubs: A bargaining game theoretic perspective. IEEE Access 2018, 6, 27777–27789. [Google Scholar] [CrossRef]
- Horn, R.A.; Johnson, C.R. Matrix Analysis; Cambridge University Press: Cambridge, UK, 1985. [Google Scholar]
- Roldán-Blay, C.; Escrivá-Escrivá, G.; Roldán-Porta, C.; Carlos, Á.-B. An optimisation algorithm for distributed energy resources management in micro-scale energy hubs. Energy 2017, 132, 126–135. [Google Scholar] [CrossRef]

| Number | Hub1 | Hub2 | Hub3 | Hub4 | Hub5 |
|---|---|---|---|---|---|
| 0.12 | 0.08 | 0.09 | 0.05 | 0.13 | |
| 12.0 | 13.0 | 12.5 | 13.5 | 11.5 | |
| 0.033 | 0.023 | 0.042 | 0.033 | 0.012 | |
| 5.8 | 6.0 | 5.5 | 6.3 | 8.6 | |
| 0.011 | 0.012 | 0.009 | 0.012 | 0.008 | |
| 0.021 | 0.023 | 0.031 | 0.025 | 0.026 | |
| 0 | 0 | 0 | 0 | 0 | |
| 200 | 150 | 175 | 210 | 200 | |
| 0 | 0 | 0 | 0 | 0 | |
| 200 | 275 | 150 | 175 | 375 |
| Number | DDC Algorithm | Centralized Algorithm | ||
|---|---|---|---|---|
| Hub1 | 62.6477 | 168.2670 | 62.7895 | 168.2715 |
| Hub2 | 87.7216 | 233.4601 | 87.7325 | 233.4569 |
| Hub3 | 80.7525 | 135.3102 | 80.7861 | 135.3133 |
| Hub4 | 135.3545 | 159.9385 | 135.3687 | 159.9256 |
| Hub5 | 59.7517 | 326.7947 | 59.7336 | 326.8010 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.-S.; Li, T.-Y.; Zhou, J.-G.; Huang, B.-N. Double-Consensus Based Distributed Optimal Energy Management for Multiple Energy Hubs. Appl. Sci. 2018, 8, 1412. https://doi.org/10.3390/app8091412
Li Y-S, Li T-Y, Zhou J-G, Huang B-N. Double-Consensus Based Distributed Optimal Energy Management for Multiple Energy Hubs. Applied Sciences. 2018; 8(9):1412. https://doi.org/10.3390/app8091412
Chicago/Turabian StyleLi, Yu-Shuai, Tian-Yi Li, Jian-Guo Zhou, and Bo-Nan Huang. 2018. "Double-Consensus Based Distributed Optimal Energy Management for Multiple Energy Hubs" Applied Sciences 8, no. 9: 1412. https://doi.org/10.3390/app8091412
APA StyleLi, Y.-S., Li, T.-Y., Zhou, J.-G., & Huang, B.-N. (2018). Double-Consensus Based Distributed Optimal Energy Management for Multiple Energy Hubs. Applied Sciences, 8(9), 1412. https://doi.org/10.3390/app8091412






