Single-Pixel Color Imaging Method with a Compressive Sensing Measurement Matrix
Abstract
:1. Introduction
2. Introduction to CS Theory
3. Design of Pseudo-Random Circulant Measurement Matrix Based on Chaotic Sequence
3.1. Design of Measurement Matrix Based on Chaotic Sequence
3.2. Design of Pseudo-Random Circulant Measurement Matrix Based on Chaotic Sequence
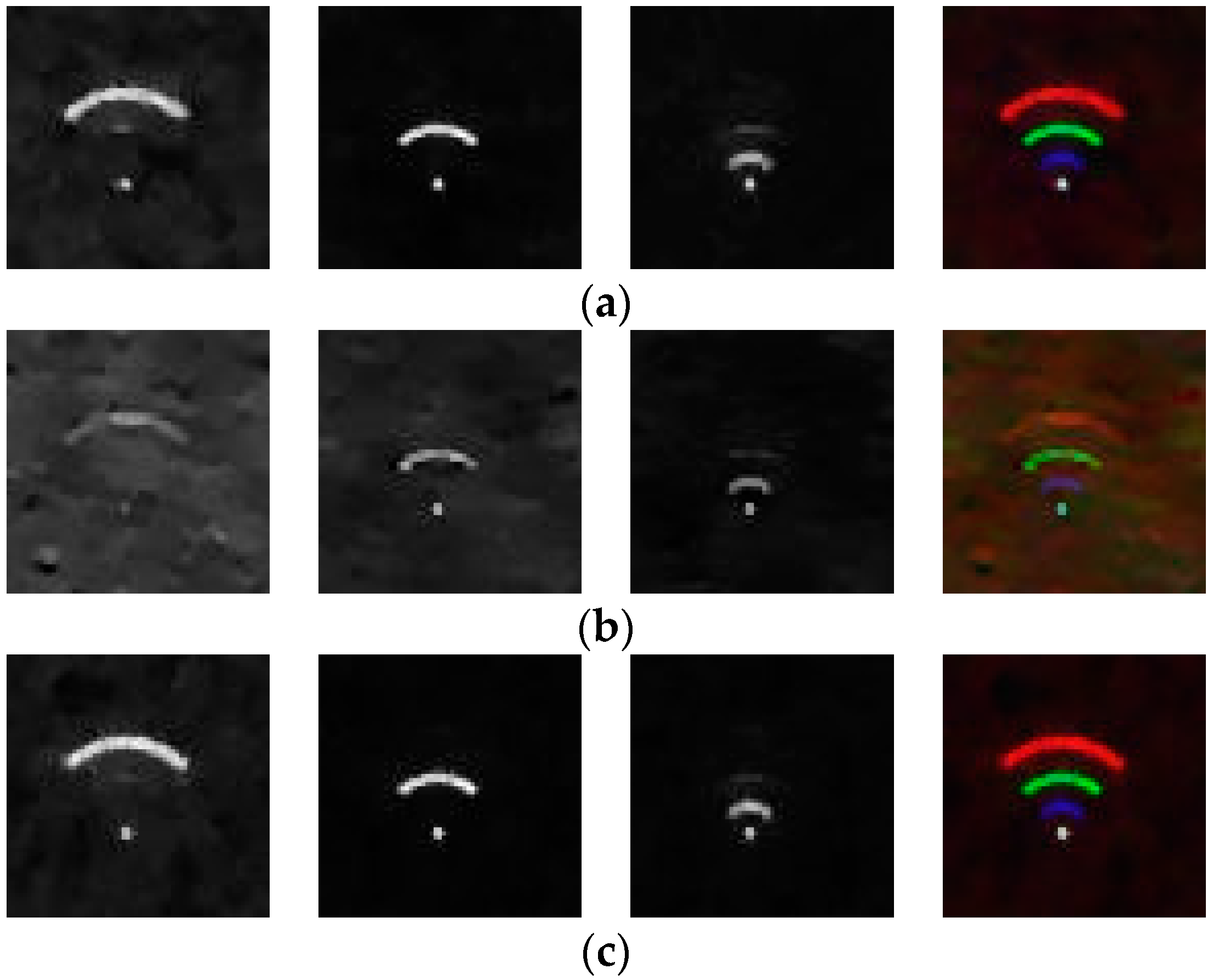
4. Experimental Results and Analysis
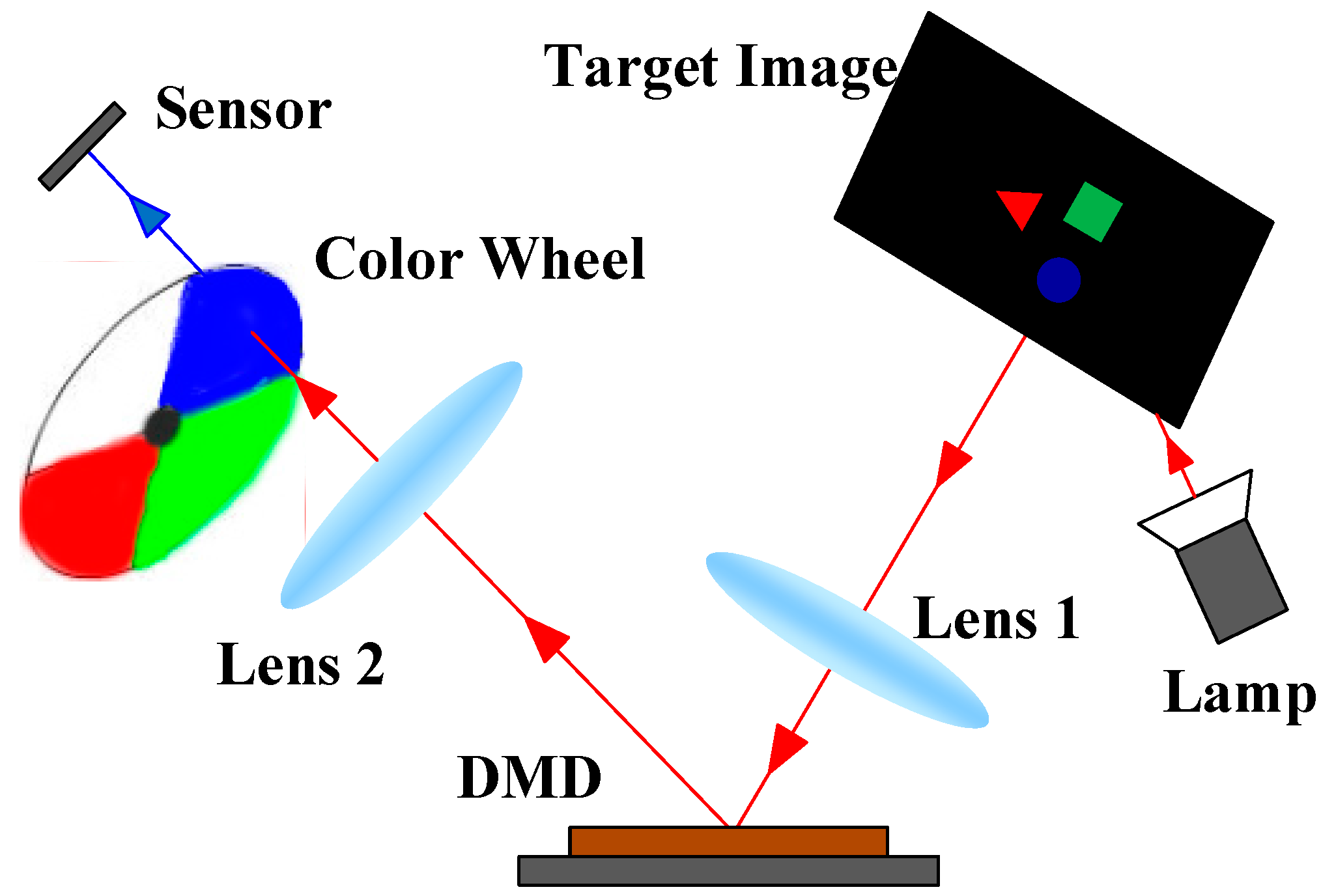
4.1. Design of Single-Pixel Color Imaging System
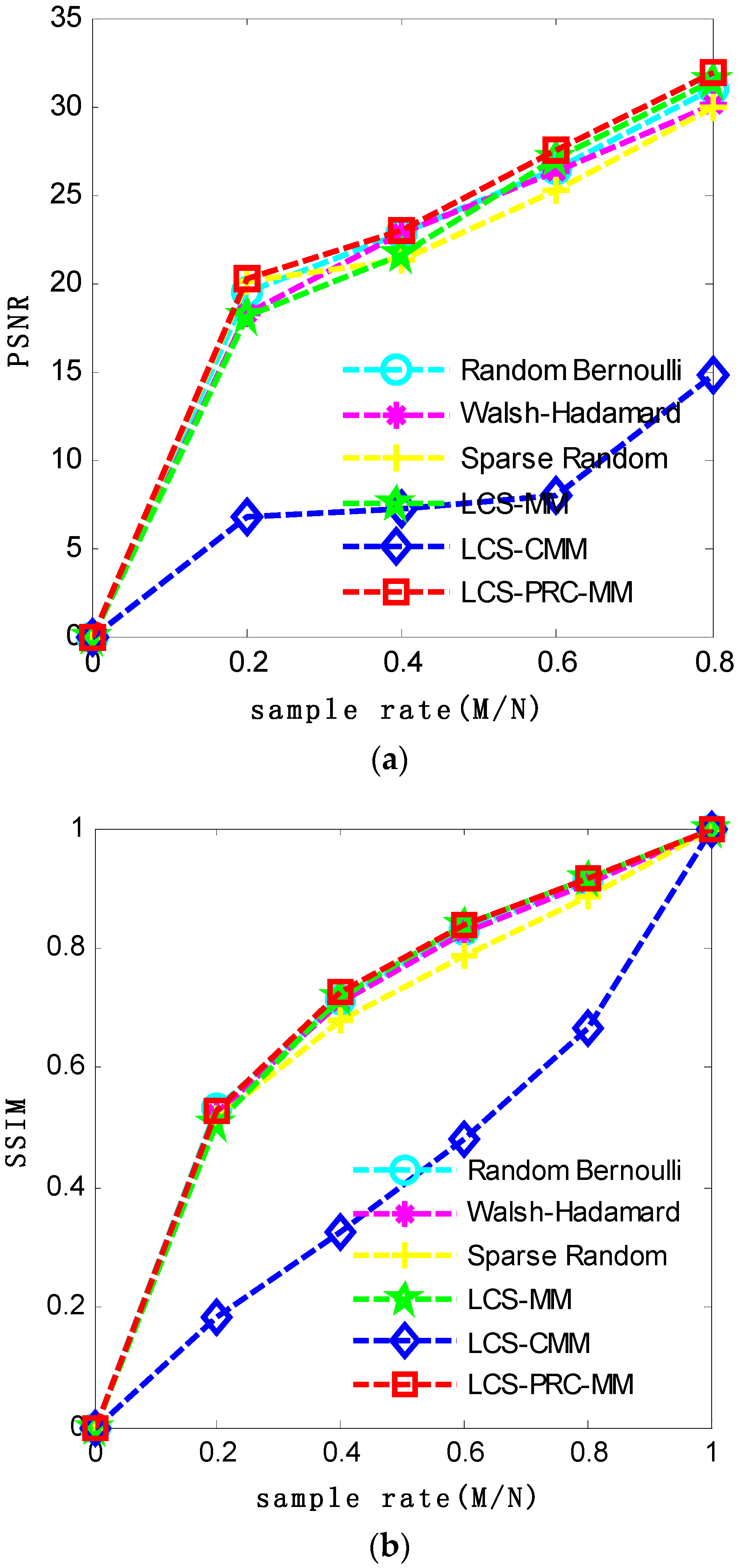
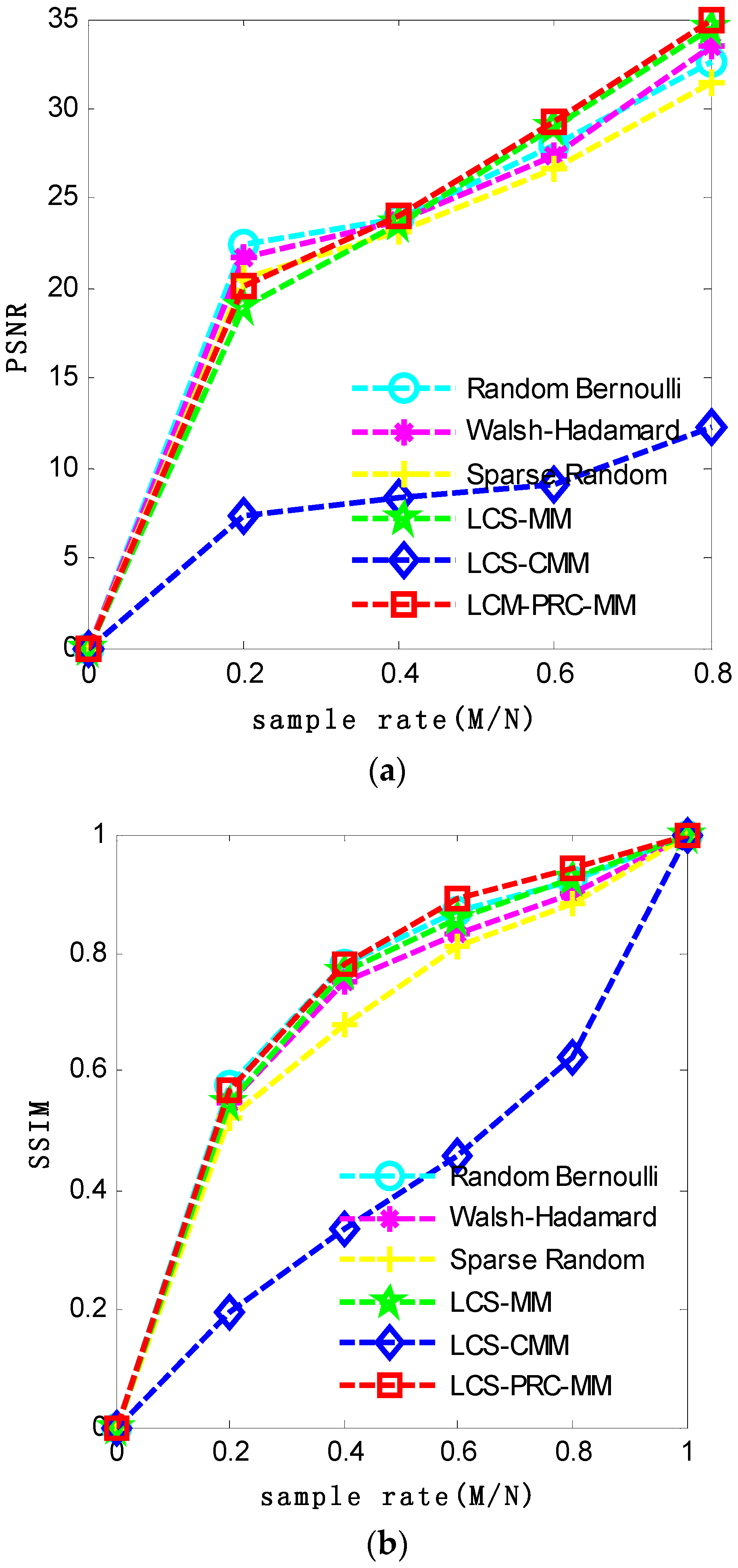
4.2. Performance Comparison of Measurement Matrices
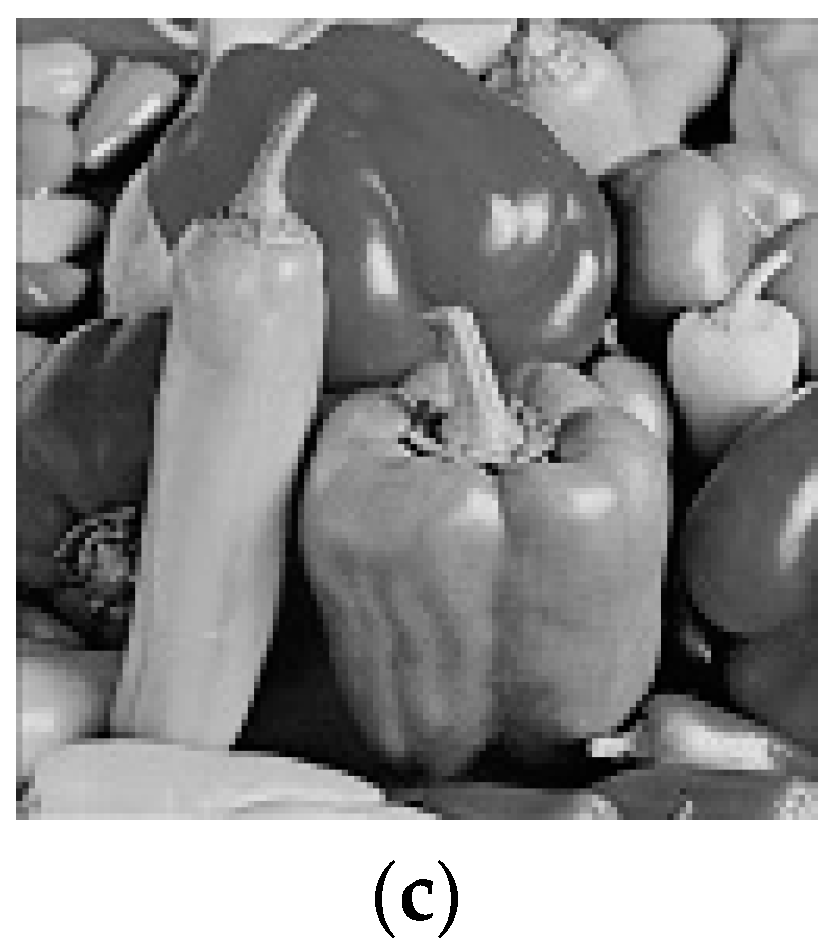
4.3. Color Camera Imaging Experiment
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Candès, E.J.; Romberg, J. Robust signal recovery from incomplete observations. In Proceedings of the IEEE International Conference on Image Processing, Atlanta, GA, USA, 8–11 October 2006; pp. 1281–1284. [Google Scholar]
- Candès, E.J. Compressive sampling. In Proceedings of the International Congress of Mathematicians, Madrid, Spain, 22–30 August 2006; pp. 1433–1452. [Google Scholar]
- Candès, E.J.; Romberg, J.K.; Tao, T. Stable signal recovery from incomplete and inaccurate measurements. Commun. Pure Appl. Math. 2006, 59, 1207–1223. [Google Scholar] [CrossRef] [Green Version]
- Yu, H.Y.; Wang, G. HYCA: A New Technique for Hyperspectral Compressive Sensing. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2819–2831. [Google Scholar]
- Ma, R.Q.; Cheng, B.; Liu, X.N.; Liu, Y.M.; Jiang, W.; Yang, C. Research on GF-1 remote sensing HIS image fusion algorithm based on compressed sensing. Remote Sens. Land Resour. 2017, 29, 26–32. [Google Scholar]
- Wang, L.; Zhou, X. Analysis of infrared remote sensing image reconstruction algorithms based on compressive sensing. Tele-Commun. Eng. 2018, 58, 332–337. [Google Scholar]
- Guariglia, E. Entropy and Fractal Antennas. Entropy 2016, 18, 84. [Google Scholar] [CrossRef]
- Berry, M.V.; Lewis, Z.V. On the Weierstrass-Mandelbrot fractal function. Proc. R. Soc. Lond. Ser. A 1980, 370, 459–484. [Google Scholar] [CrossRef]
- Fazel, F.; Fazel, M.; Stojanovic, M. Random Access Compressed Sensing over Fading and Noisy Communication Channels. IEEE Trans. Wirel. Commun. 2012, 12, 2114–2125. [Google Scholar] [CrossRef]
- Mairal, J.; Bach, F.; Ponce, J.; Sapiro, G.; Zisserman, A. Discriminative learned dictionaries for local image analysis. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Anchorage, AK, USA, 23–28 June 2008. [Google Scholar]
- Qin, J.; Guo, W.H. An efficient compressive sensing MR image reconstruction scheme. In Proceedings of the IEEE, International Symposium on Biomedical Imaging, San Francisco, CA, USA, 7–11 April 2013; pp. 306–309. [Google Scholar]
- Zhang, H.Y. Based on sparse vector and low-rank matrix compressed sensing magnetic resonance image reconstruction algorithm. J. Tianjin Univ. Technol. 2017, 33, 25–29. [Google Scholar]
- Wang, J.; Liu, J.-C. A Survey of Magnetic Resonance Imaging Based on Compressed Sensing. Electron. Qual. 2018, 373, 65–69. [Google Scholar]
- Mahyar, H.; Hasheminezhad, R. Compressive sensing of high betweenness centrality nodes in networks. Stat. Mech. Appl. 2018, 497, 166–184. [Google Scholar] [CrossRef]
- Xu, D.; Zhang, J.X.; Li, C.; Xu, R.; Zhang, Y.; Liu, S.; Wang, J. MEMS-based super-resolution remote sensing system using compressive sensing. Opt. Commun. 2018, 426, 410–417. [Google Scholar]
- Petrantonakis, P.C. Grid cell firing field detection using compressed sensing. Biomed. Signal Process. Control 2018, 44, 221–228. [Google Scholar] [CrossRef]
- Chai, X.L.; Zheng, X.Y.; Gan, Z.; Han, D.; Chen, Y. An image encryption algorithm based on chaotic system and compressive sensing. Signal Process. 2018, 148, 124–144. [Google Scholar] [CrossRef]
- Takhar, D.; Laska, J.N.; Wakin, M.B.; Duarte, M.F.; Baron, D.; Sarvotham, S.; Kelly, K.F.; Baraniuk, R.G. A new compressive imaging camera architecture using optical-domain compression. Electron. Imaging Int. Soc. Opt. Photonics 2006, 6065, 43–52. [Google Scholar]
- Duarte, M.F.; Davenport, M.A.; Takhar, D.; Laska, J.N.; Sun, T.; Kelly, K.F.; Baraniuk, R.G. Single-pixel imaging via compressive sampling. IEEE Signal Process. Mag. 2008, 25, 83–91. [Google Scholar] [CrossRef] [Green Version]
- Xiang, S.; Cai, L. Transmission Control for Compressive Sensing Video over Wireless Channel. IEEE Trans. Wirel. Commun. 2013, 3, 1429–1437. [Google Scholar] [CrossRef]
- Chen, H.; Xi, N.; Song, B.; Chen, L.; Zhao, J.; Lai, K.W.C.; Yang, R. Infrared Camera Using a Single Nano-Photodetector. IEEE Sensors J. 2013, 13, 949–958. [Google Scholar] [CrossRef]
- Withayachumnankul, W.; Abbott, D. Terahertz imaging: Compressing onto a single pixel. Nat. Photon. 2014, 8, 593–594. [Google Scholar] [CrossRef]
- Candès, E.J.; Romberg, J.; Tao, T. Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information. IEEE Trans. Inf. Theory 2006, 52, 489–509. [Google Scholar] [CrossRef]
- Kafedziski, V.; Stojanovski, T. Compressive sampling with chaotic dynamical systems. Teleconmmn. Forum 2011, 42, 495–989. [Google Scholar]
- Yu, L.; Barbot, J.P.; Zheng, G.; Sun, H. Compressive sensing with chaotic sequence. IEEE Signal Process. Lett. 2010, 17, 731–734. [Google Scholar]
- Baraniuk, R.; Davenport, M.; Devore, R.; Wakin, M. A Simple Proof of the Restricted Isometry Property for Random Matrices. Constr. Approx. 2008, 3, 253–263. [Google Scholar] [CrossRef]
- Bajwa, W.U.; Haupt, J.D.; Raz, G.M.; Wright, S.J.; Nowak, R.D. Toeplitz-structured compressed sensing matrices. In Proceedings of the 14th IEEE/SP Workshop on Statistical Signal Processing, Madison, WI, USA, 26–29 August 2007; pp. 294–298. [Google Scholar]
- Emmanuel, J.C.; Michael, B.W. An introduction to compressive sampling. IEEE Signal Process. Mag. 2008, 25, 21–30. [Google Scholar]
- Nguyen, T.L.N.; Shin, Y. Deterministic Sensing Matrices in Compressive Sensing: A Survey. Sci. World J. 2013, 2013, 192795. [Google Scholar] [CrossRef] [PubMed]
- Arjoune, Y.; Kaabouch, N.; el Ghazi, H.; Tamtaoui, A. A performance comparison of measurement matrices in compressive sensing. WILEY Int. J. Commun. Syst. 2018, 31, e3576. [Google Scholar] [CrossRef]
- Abo-Zahhad, M.M.; Hussein, A.I.; Mohamed, A.M. Compressive sensing algorithms for signal processing applications: A survey. Int. J. Commun. Netw. Syst. Sci. 2015, 8, 197–216. [Google Scholar]
- Tong, Y.B.; Zhang, Q.S.; Qi, Y.P. Image Quality Assessing by Combing PSNR with SSIM. J. Image Gr. 2006, 12, 1758–1763. [Google Scholar]
- Ji, S.; Xue, Y.; Carin, L. Bayesian compressive sensing. IEEE Trans. Signal Process. 2008, 56, 2346–2356. [Google Scholar] [CrossRef]
- Ajoune, Y.; Kaabouch, N.; el Ghazi, H.; Tamtaoui, A. Compressive sensing: A performance comparison of recovery algorithm. In Proceedings of the Computing and Communication Workshop and Conference, Las Vegas, NV, USA, 9–11 January 2017; pp. 1–7. [Google Scholar]
- Babaan, S.D.; Molina, R.; Katsaggelos, A.K. Bayesian compressive sensing using Laplace priors. IEEE Trans. Image Process. 2010, 19, 53–63. [Google Scholar] [CrossRef] [PubMed]
- Baro, D.; Sarvotham, S.; Baraniuk, R.G. Bayesian compressive sensing via belief propagation. IEEE Trans. Signal Process. 2010, 58, 269–280. [Google Scholar] [CrossRef]
- Trop, J.A.; Gilbert, A.C. Signal recovery from random measurements via orthogonal matching pursuit. IEEE Trans. Inf. Theory 2007, 53, 4655–4666. [Google Scholar] [CrossRef]
- Neeell, D.; Tropp, J.A. CoSaMP: Iterative signal recovery from incomplete and inaccurate samples. Appl. Comput. Harmon. Anal. 2009, 26, 301–321. [Google Scholar] [CrossRef]
- Li, C. An Efficient Algorithm for Total Variation Regularization with Applications to the Single Pixel Camera and Compressive Sensing. Ph.D. Thesis, Rice University, Houston, TX, USA, 2009. [Google Scholar]





© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, T.; Chen, D.; Wang, J.; Xu, D. Single-Pixel Color Imaging Method with a Compressive Sensing Measurement Matrix. Appl. Sci. 2018, 8, 1293. https://doi.org/10.3390/app8081293
Jia T, Chen D, Wang J, Xu D. Single-Pixel Color Imaging Method with a Compressive Sensing Measurement Matrix. Applied Sciences. 2018; 8(8):1293. https://doi.org/10.3390/app8081293
Chicago/Turabian StyleJia, Tong, Dongyue Chen, Ji Wang, and Dong Xu. 2018. "Single-Pixel Color Imaging Method with a Compressive Sensing Measurement Matrix" Applied Sciences 8, no. 8: 1293. https://doi.org/10.3390/app8081293
APA StyleJia, T., Chen, D., Wang, J., & Xu, D. (2018). Single-Pixel Color Imaging Method with a Compressive Sensing Measurement Matrix. Applied Sciences, 8(8), 1293. https://doi.org/10.3390/app8081293



