Effect of Surface Roughness on Ultrasonic Testing of Back-Surface Micro-Cracks
Abstract
:Featured Application
Abstract
1. Introduction
2. Background
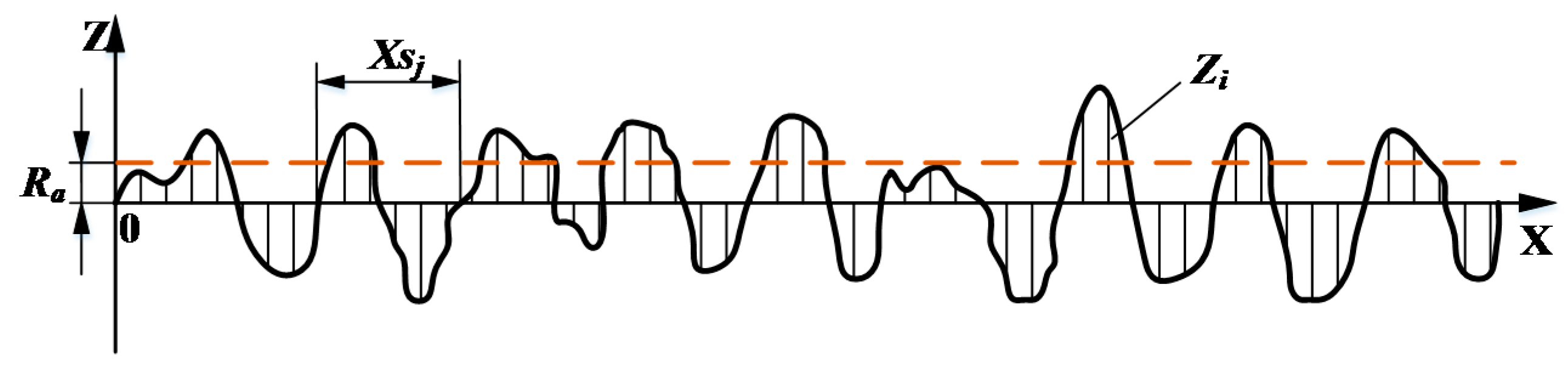
2.1. Surface Roughness
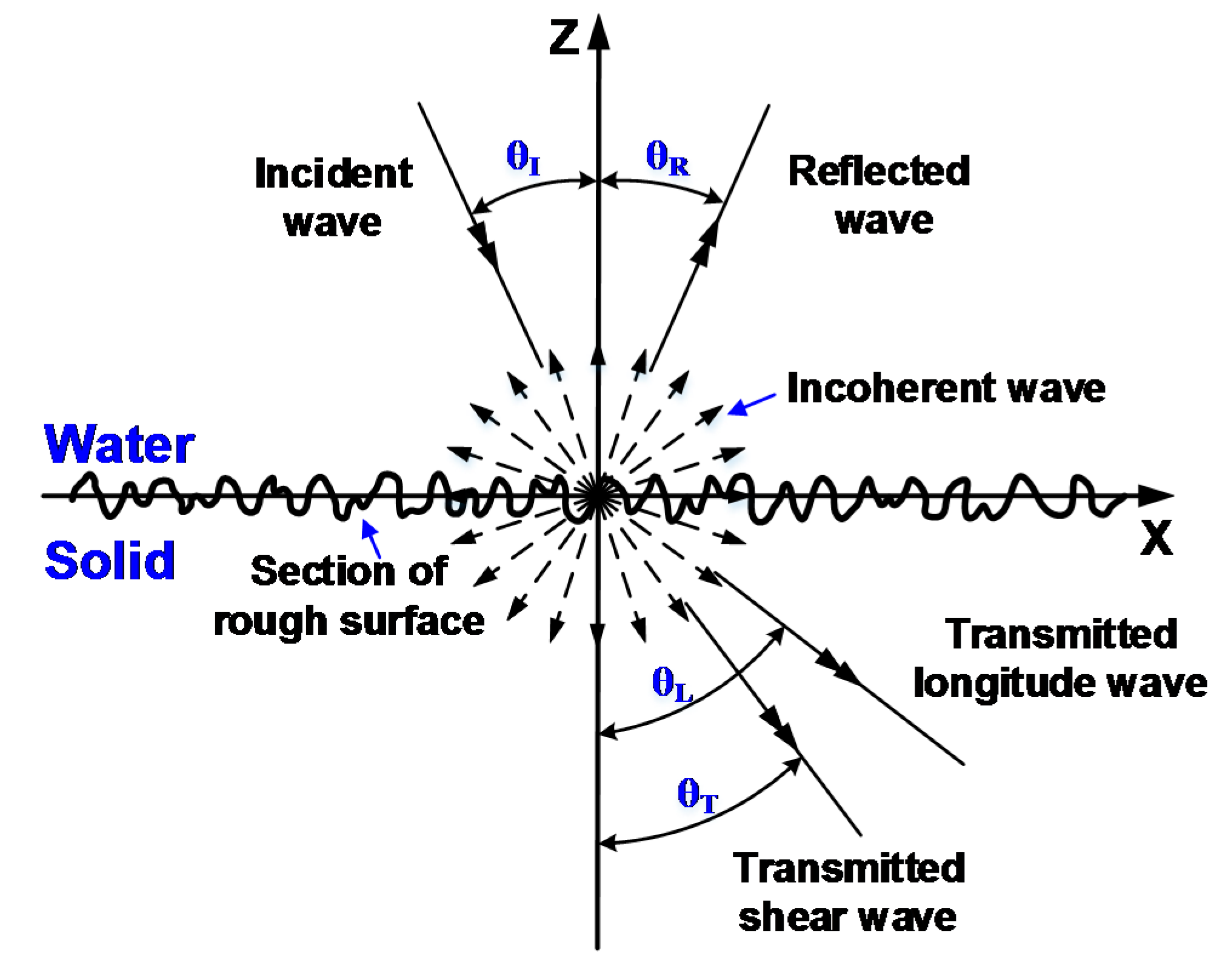
2.2. Scattering from Rough Surface
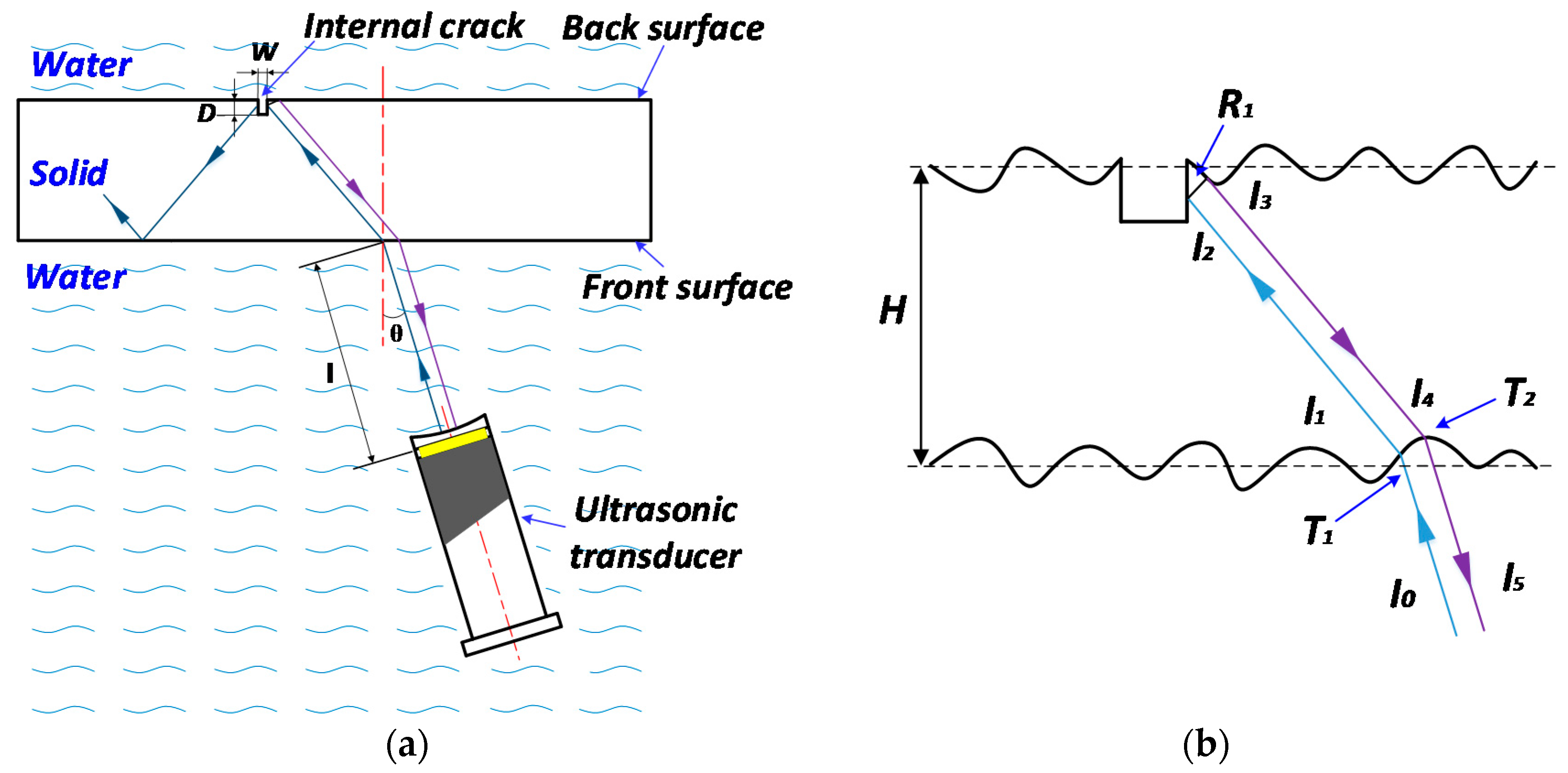
2.3. Detection of Back-Surface Crack with Rough Surface
3. Simulation and Analyses
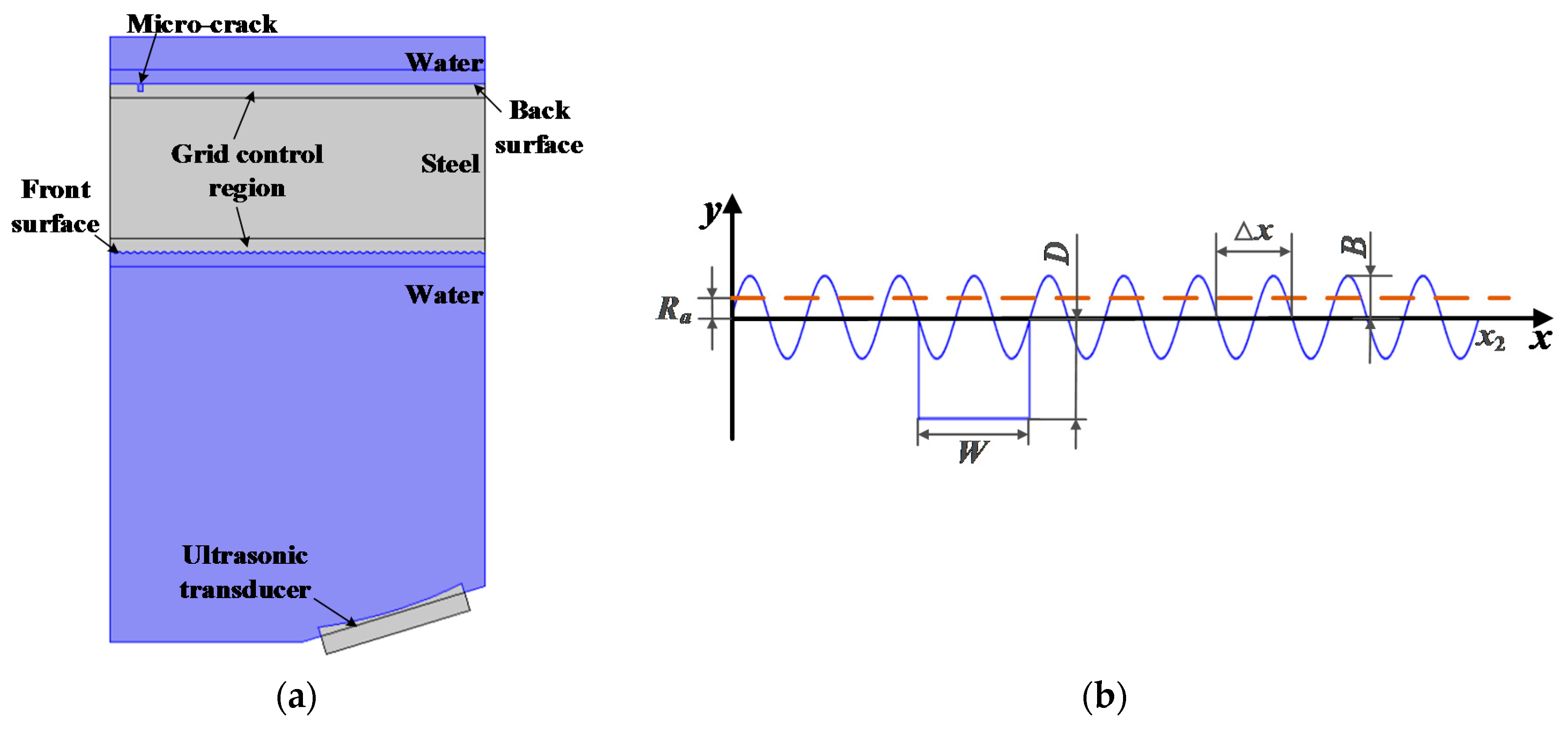
3.1. Two-Dimensional Rough Surface Model Setup
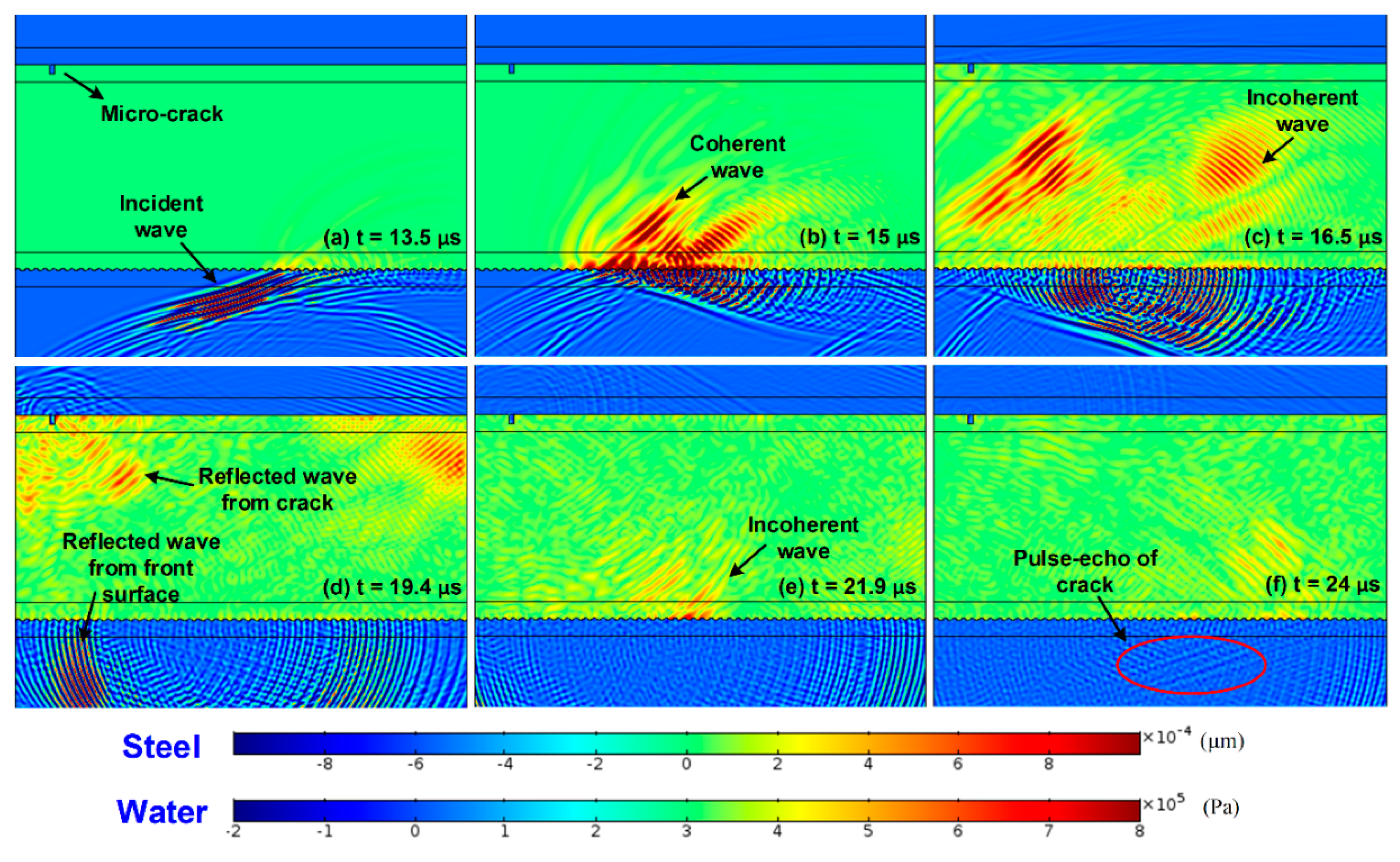
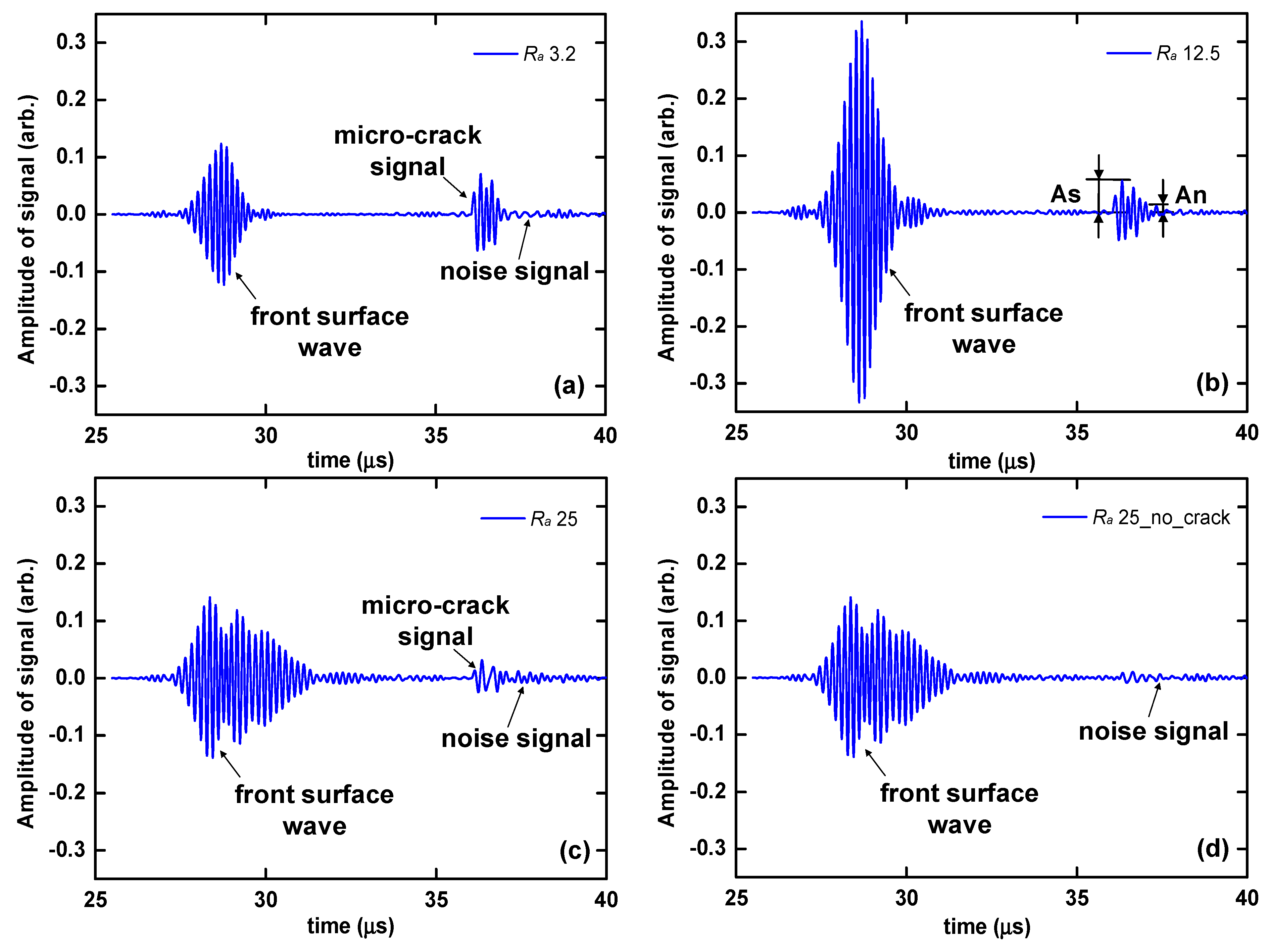
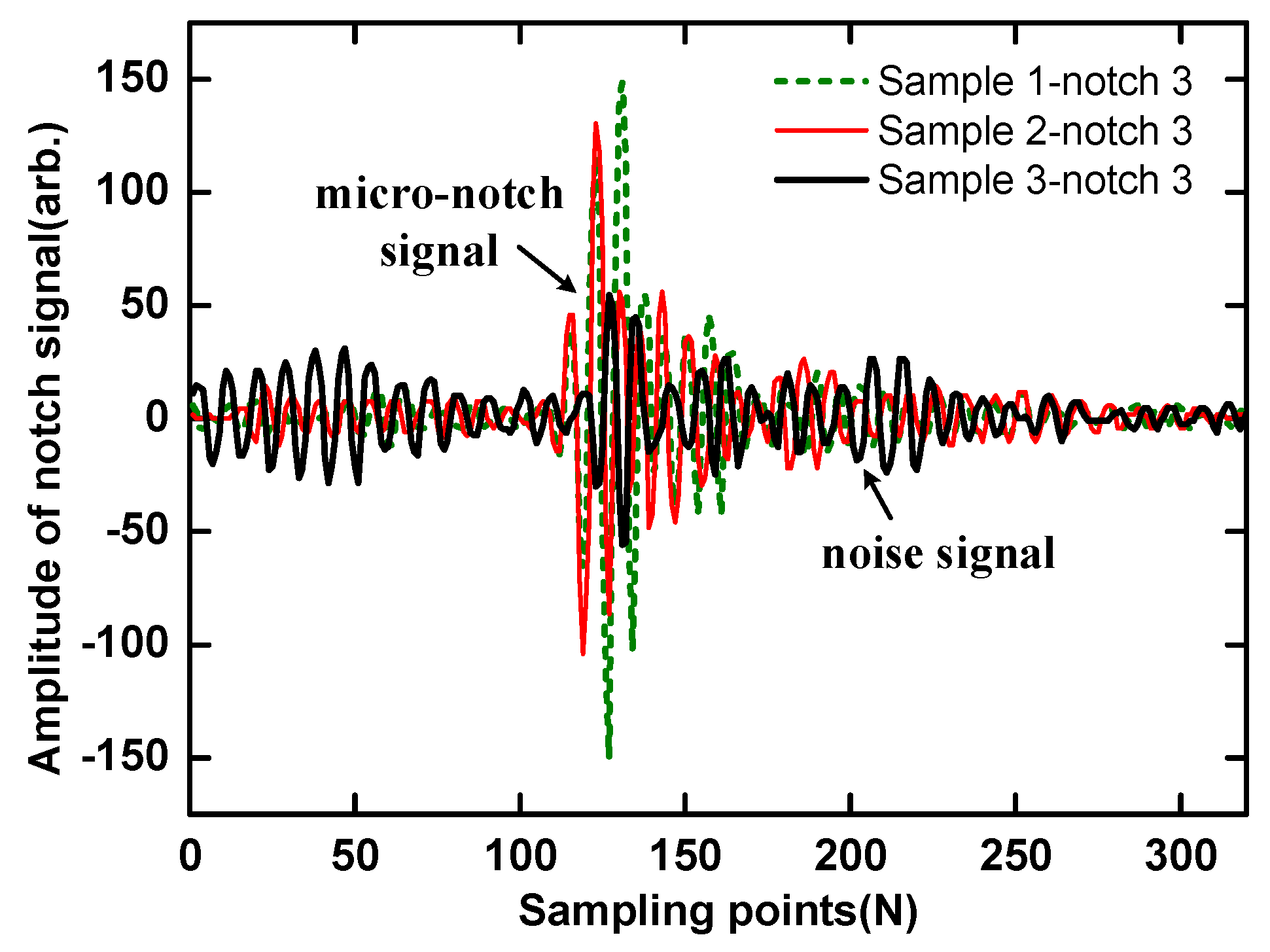
3.2. Verification of the Micro-Crack Signal on the Rough Surface
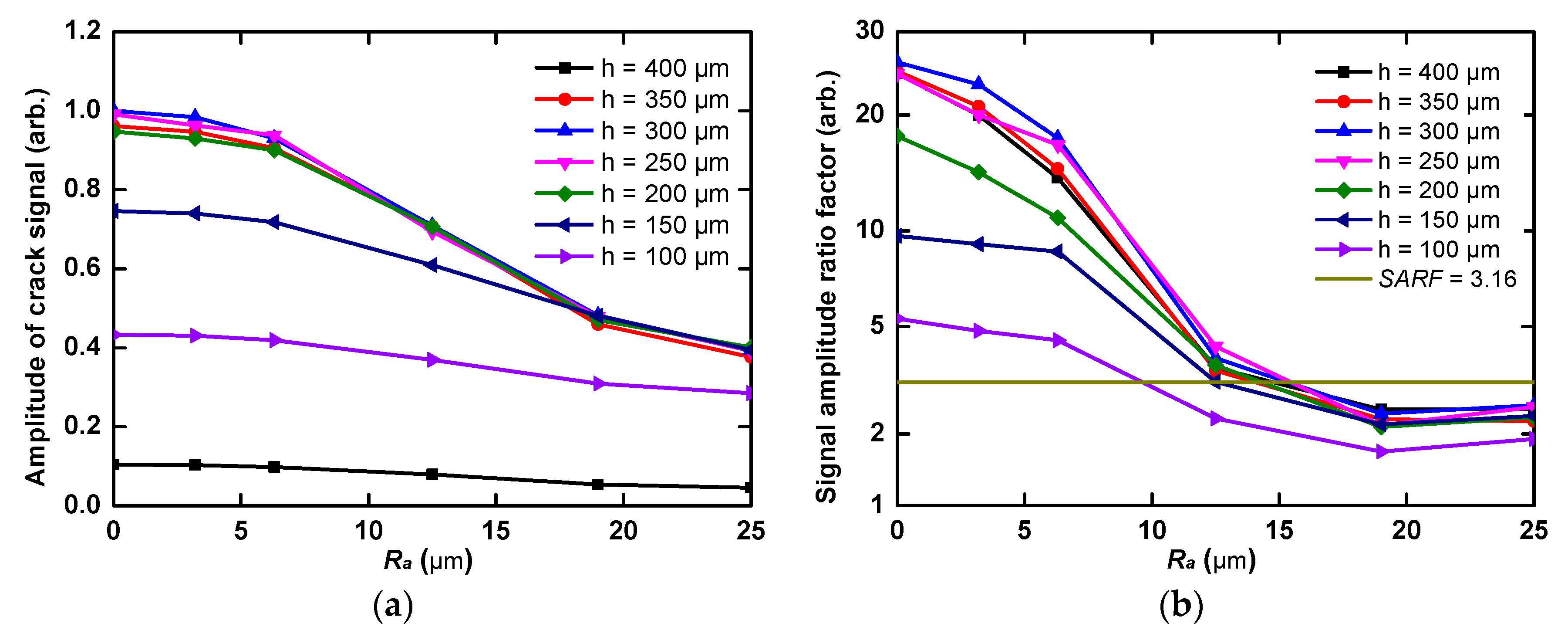
3.3. Micro-Crack Signal Assessment under the Effect of Front-Surface Ra
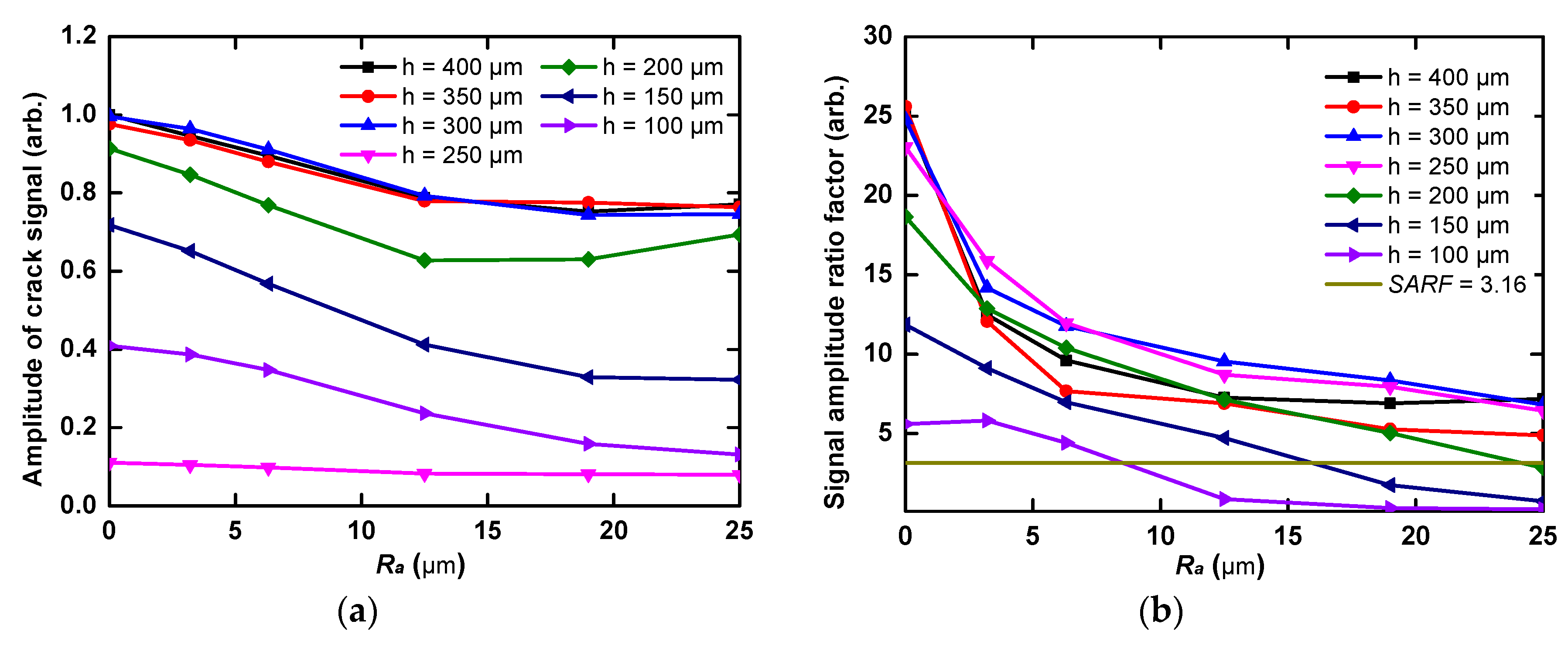
3.4. Micro-Crack Signal Assessment under the Effect of Back-Surface Ra
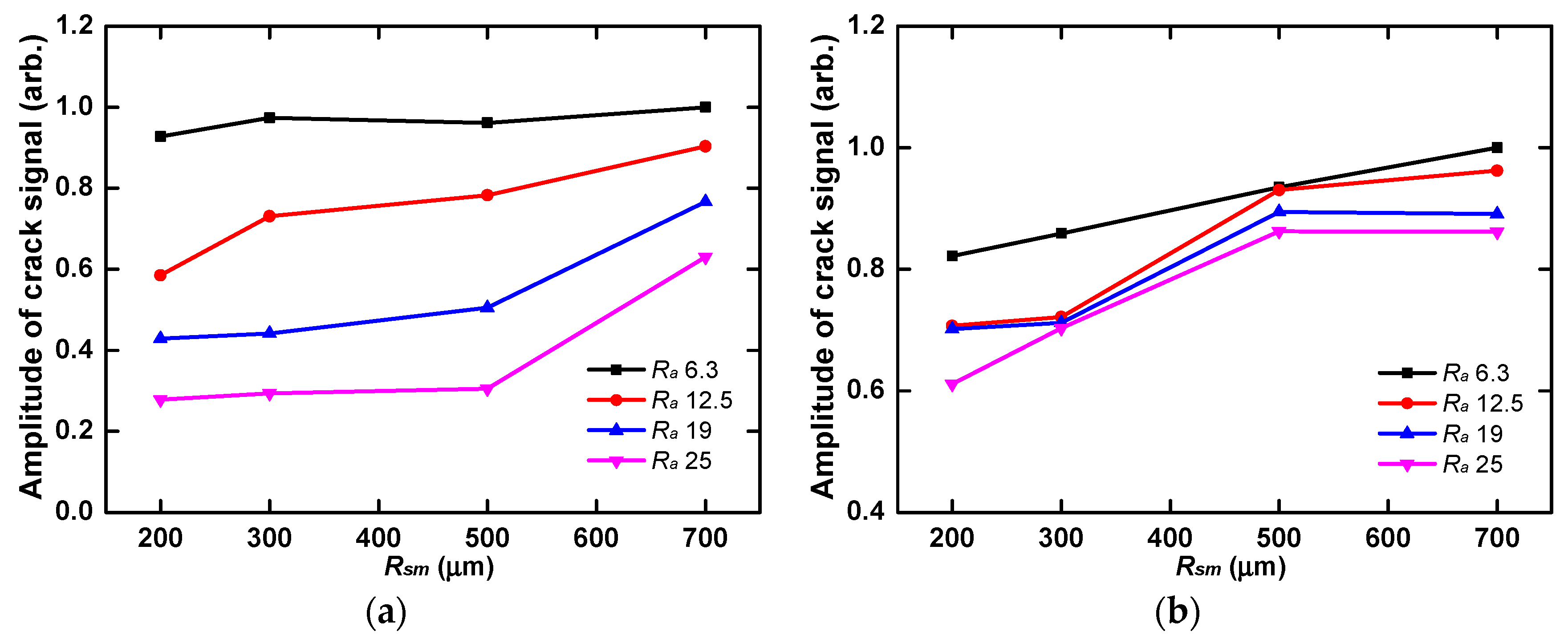
3.5. Micro-Crack Signal Assessment under the Effect of Roughness Rsm
4. Experiments and Discussion
4.1. Experimental Equipment
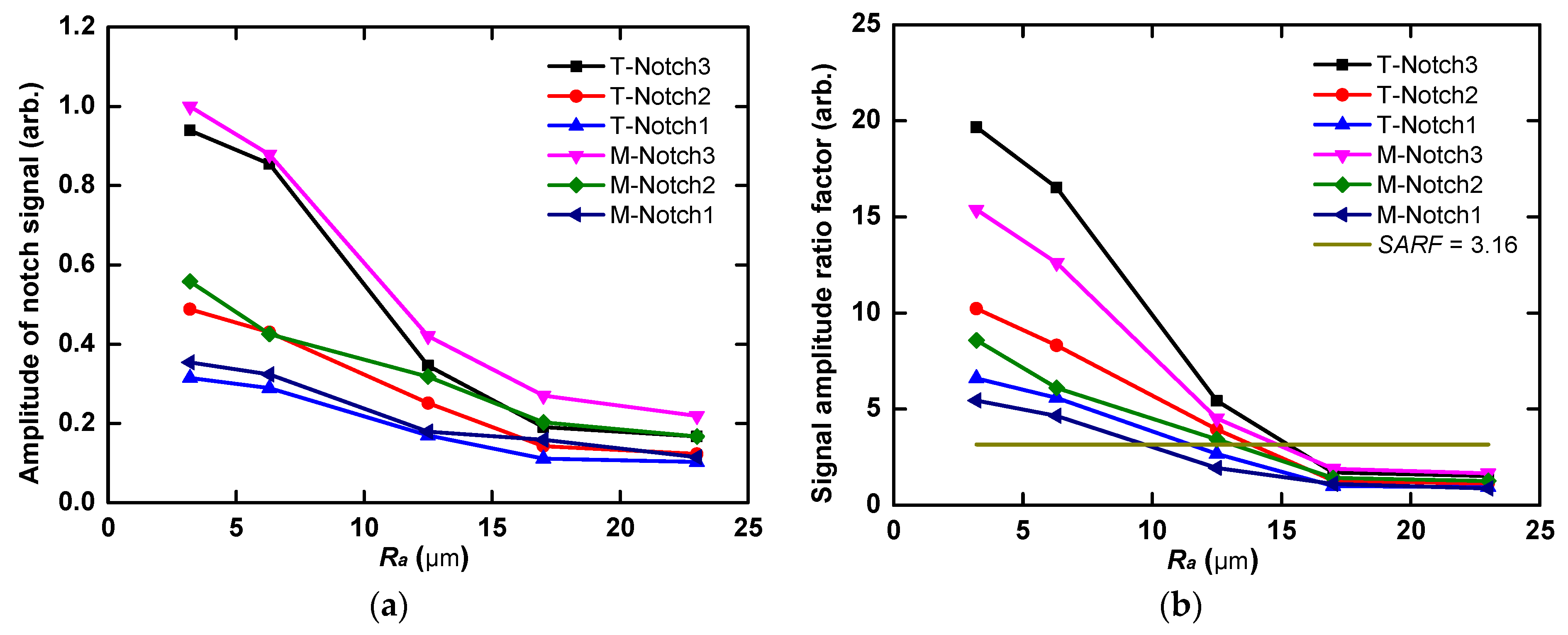
4.2. The Effect of Front-Surface Roughness on Notch Detection
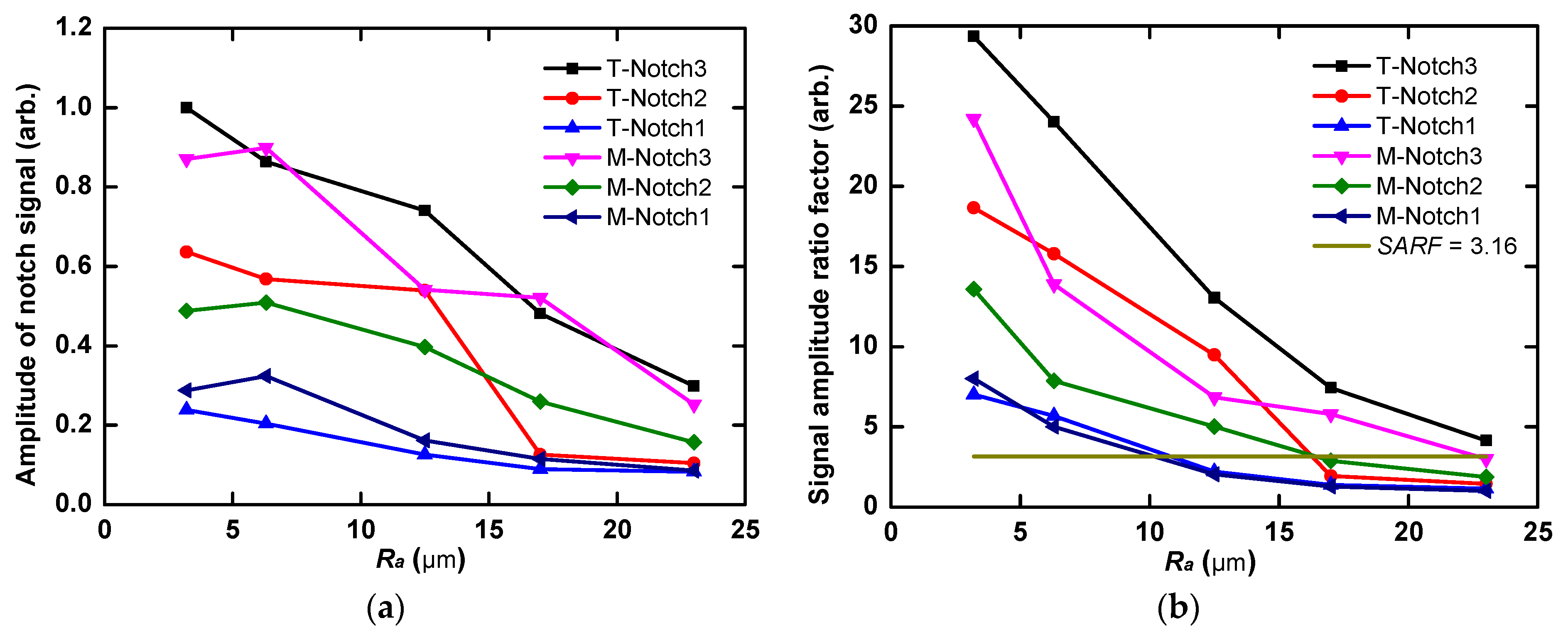
4.3. The Effect of Back-Surface Roughness on Notch Detection
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Mineo, C.; Cerniglia, D.; Pantano, A. Numerical study for a new methodology of flaws detection in train axles. Ultrasonics 2014, 54, 841–849. [Google Scholar] [CrossRef] [PubMed]
- Lee, L.H.; Rajkumar, R.; Lo, L.H.; Wan, C.H.; Isa, D. Oil and gas pipeline failure prediction system using long range ultrasonic transducers and Euclidean-Support Vector Machines classification approach. Expert Syst. Appl. 2013, 40, 1925–1934. [Google Scholar] [CrossRef]
- Carvalho, A.A.; Rebello, J.M.A.; Souza, M.P.V.; Sagrilo, L.V.S.; Soares, S.D. Reliability of non-destructive test techniques in the inspection of pipelines used in the oil industry. Int. J. Press. Vessels Pip. 2008, 85, 745–751. [Google Scholar] [CrossRef]
- Achenbach, J.D.; Adler, L.; Lewis, D.K.; McMaken, H. Diffraction of ultrasonic waves by penny-shaped cracks in metals: Theory and experiment. J. Acoust. Soc. Am. 1979, 66, 1848–1856. [Google Scholar] [CrossRef]
- Chapman, R.K. A system model for the ultrasonic inspection of smooth planar cracks. J. Nondestr. Eval. 1990, 9, 197–210. [Google Scholar] [CrossRef]
- Skjelvareid, M.H.; Birkelund, Y.; Larsen, Y. Synthetic aperture focusing of outwardly directed cylindrical ultrasound scans. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2012, 59, 2460–2469. [Google Scholar] [CrossRef] [PubMed]
- Benstock, D.; Cegla, F.; Stone, M. The influence of surface roughness on ultrasonic thickness measurements. J. Acoust. Soc. Am. 2014, 136, 3028–3039. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jarvis, A.J.C.; Cegla, F.B. Application of the distributed point source method to rough surface scattering and ultrasonic wall thickness measurement. J. Acoust. Soc. Am. 2012, 132, 1325–1335. [Google Scholar] [CrossRef] [PubMed]
- Bass, F.G.; Fuks, I.M. Wave Scattering from Statistically Rough Surfaces: International Series on Natural Philosophy; Pergamon Press: Oxford, UK, 1979; Volume 93, pp. 240–274. ISBN 0-08-019896-1. [Google Scholar]
- Ogilvy, J.A.; Merklinger, H.M. Theory of wave scattering from random rough surfaces. J. Acoust. Soc. Am. 1991, 90, 3382. [Google Scholar] [CrossRef]
- Nagy, P.B.; Adler, L. Surface roughness induced attenuation of reflected and transmitted ultrasonic waves. J. Acoust. Soc. Am. 1987, 82, 193–197. [Google Scholar] [CrossRef]
- Nagy, P.B.; Rose, J.H. Surface roughness and the ultrasonic detection of subsurface scatterers. J. Appl. Phys. 1993, 73, 566–580. [Google Scholar] [CrossRef]
- Chimenti, D.E.; Lobkis, O.I. The effect of rough surfaces on guided waves in plates. Ultrasonics 1998, 36, 155–162. [Google Scholar] [CrossRef] [Green Version]
- Lopez-Sanchez, A.L.; Kim, H.J.; Schmerr, L.W.; Sedov, A. Measurement models and scattering models for predicting the ultrasonic pulse-echo response from side-drilled holes. J. Nondestr. Eval. 2005, 24, 83–96. [Google Scholar] [CrossRef]
- Chapman, R.K. Ultrasonic Scattering from Smooth Flat Cracks—An Elastodynamic Kirchhoff Diffraction Theory; CEGB Report; Central Electricity Generating Board: Wythenshawe, UK, 1984. [Google Scholar]
- Burch, S.F.; Collett, N.; Chapman, R.K.; Toft, M.W. Experimental validation of the TRANGLE and related NDT codes for modelling the ultrasonic inspection of rough cracks. Insight Nondestr. Test. Cond. Monit. 2004, 46, 74–76. [Google Scholar] [CrossRef]
- Shi, F.; Lowe, M.J.S.; Xi, X.; Craster, R.V. Diffuse scattered field of elastic waves from randomly rough surfaces using an analytical Kirchhoff theory. J. Mech. Phys. Solids 2016, 92, 260–277. [Google Scholar] [CrossRef] [Green Version]
- Dacol, D.K. The Kirchhoff approximation for acoustic scattering from a rough fluid-elastic solid interface. J. Acoust. Soc. Am. 1990, 88, 978–983. [Google Scholar] [CrossRef]
- Thorsos, E.I. The validity of the perturbation approximation for rough surface scattering using a Gaussian roughness spectrum. J. Acoust. Soc. Am. 1988, 83, 78–92. [Google Scholar] [CrossRef]
- Ogilvy, J.A. Theoretical comparison of ultrasonic signal amplitudes from smooth and rough defects. NDT Int. 1986, 19, 371–385. [Google Scholar] [CrossRef]
- Ogilvy, J.A. Computer simulation of acoustic wave scattering from rough surfaces. J. Phys. D Appl. Phys. 1988, 21, 260–277. [Google Scholar] [CrossRef]
- Ogilvy, J.A. Wave scattering from rough surfaces. Rep. Prog. Phys. 1987, 50, 1553–1608. [Google Scholar] [CrossRef]
- Shi, F.; Lowe, M.; Craster, R. Diffusely scattered and transmitted elastic waves by random rough solid-solid interfaces using an elastodynamic Kirchhoff approximation. Phys. Rev. B 2017, 95, 1–13. [Google Scholar] [CrossRef]
- Castaings, M.; Bacon, C. Finite element modeling of torsional wave modes along pipes with absorbing materials. J. Acoust. Soc. Am. 2006, 119, 3741–3751. [Google Scholar] [CrossRef]
- Rajagopal, P.; Drozdz, M.; Skelton, E.A.; Lowe, M.J.S.; Craster, R.V. On the use of absorbing layers to simulate the propagation of elastic waves in unbounded isotropic media using commercially available Finite Element packages. NDT E Int. 2012, 51, 30–40. [Google Scholar] [CrossRef]
- Mahaut, S.; Leymarie, N.; Poidevin, C.; Fouquet, T.; Dupond, O. Study of complex ultrasonic NDT cases using hybrid simulation method and experimental validations. Insight Nondestr. Test. Cond. Monit. 2011, 53, 664–667. [Google Scholar] [CrossRef]
- Pettit, J.R.; Walker, A.; Cawley, P.; Lowe, M.J.S. A Stiffness Reduction Method for efficient absorption of waves at boundaries for use in commercial Finite Element codes. Ultrasonics 2014, 54, 1868–1879. [Google Scholar] [CrossRef] [PubMed]
- Jarvis, A.; Cegla, F. Scattering of near normal incidence SH waves by sinusoidal and rough surfaces in 3-D: Comparison to the scalar wave approximation. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2014, 61, 1179–1190. [Google Scholar] [CrossRef] [PubMed]
- Cegla, F.; Jarvis, A. Modeling the effect of roughness on ultrasonic scattering in 2D and 3D. AIP Conf. Proc. 2014, 1581, 595–601. [Google Scholar]
- Zhang, J.; Drinkwater, B.W.; Wilcox, P.D. Longitudinal wave scattering from rough crack-like defects. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2011, 58, 2171–2180. [Google Scholar] [CrossRef] [PubMed]
- Pettit, J.R.; Walker, A.E.; Lowe, M.J.S. Improved detection of rough defects for ultrasonic nondestructive evaluation inspections based on finite element modeling of elastic wave scattering. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2015, 62, 1797–1808. [Google Scholar] [CrossRef] [PubMed]
- Standard ASME B46.1-2009. Surface Text (Surface Roughness, Waviness, and Lay); American Scociety of Mechanical Engineerings: New York, NY, USA, 2009; pp. 1–107.
- Gadelmawla, E.S.; Koura, M.M.; Maksoud, T.; Elewa, I.M.; Soliman, H.H. Roughness parameters. J. Mater. Process. Technol. 2002, 123, 133–145. [Google Scholar] [CrossRef]
- Deng, Z.; Sun, Y.; Yang, Y.; Kang, Y. Effects of surface roughness on magnetic flux leakage testing of micro-cracks. Meas. Sci. Technol. 2017, 28. [Google Scholar] [CrossRef]
- Zhang, Y.; Shi, T.; Su, L.; Wang, X.; Hong, Y.; Chen, K.; Liao, G. Sparse reconstruction for micro defect detection in acoustic micro imaging. Sensors 2016, 16. [Google Scholar] [CrossRef] [PubMed]


| Processing Method | Sample No. | Ra (µm) | Rsm (µm) | Notch Depth D (µm) | Notch Width W (µm) | Material | ||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||||
| CNC turning (Rough surface) | 1 | 3.2 | 1320 | 250 | 150 | 100 | 100 | Q235A Steel |
| 2 | 6.3 | |||||||
| 3 | 12.5 | |||||||
| 4 | 17.0 | |||||||
| 5 | 23.0 | |||||||
| Vertical CNC milling (Rough surface) | 6 | 3.2 | 900 | 250 | 150 | 100 | ||
| 7 | 6.3 | |||||||
| 8 | 12.5 | |||||||
| 9 | 17.0 | |||||||
| 10 | 23.0 | |||||||
| Grinding (Smooth surface) | All samples | 1.6 | 85 | 250 | 150 | 100 | ||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Cui, X.; Ma, H.; Kang, Y.; Deng, Z. Effect of Surface Roughness on Ultrasonic Testing of Back-Surface Micro-Cracks. Appl. Sci. 2018, 8, 1233. https://doi.org/10.3390/app8081233
Wang Z, Cui X, Ma H, Kang Y, Deng Z. Effect of Surface Roughness on Ultrasonic Testing of Back-Surface Micro-Cracks. Applied Sciences. 2018; 8(8):1233. https://doi.org/10.3390/app8081233
Chicago/Turabian StyleWang, Zhe, Ximing Cui, Hongbao Ma, Yihua Kang, and Zhiyang Deng. 2018. "Effect of Surface Roughness on Ultrasonic Testing of Back-Surface Micro-Cracks" Applied Sciences 8, no. 8: 1233. https://doi.org/10.3390/app8081233
APA StyleWang, Z., Cui, X., Ma, H., Kang, Y., & Deng, Z. (2018). Effect of Surface Roughness on Ultrasonic Testing of Back-Surface Micro-Cracks. Applied Sciences, 8(8), 1233. https://doi.org/10.3390/app8081233





