Investigation of the Dynamic Buckling of Spherical Shell Structures Due to Subsea Collisions
Abstract
1. Introduction
2. Static Buckling Criteria
2.1. Static Buckling Criteria
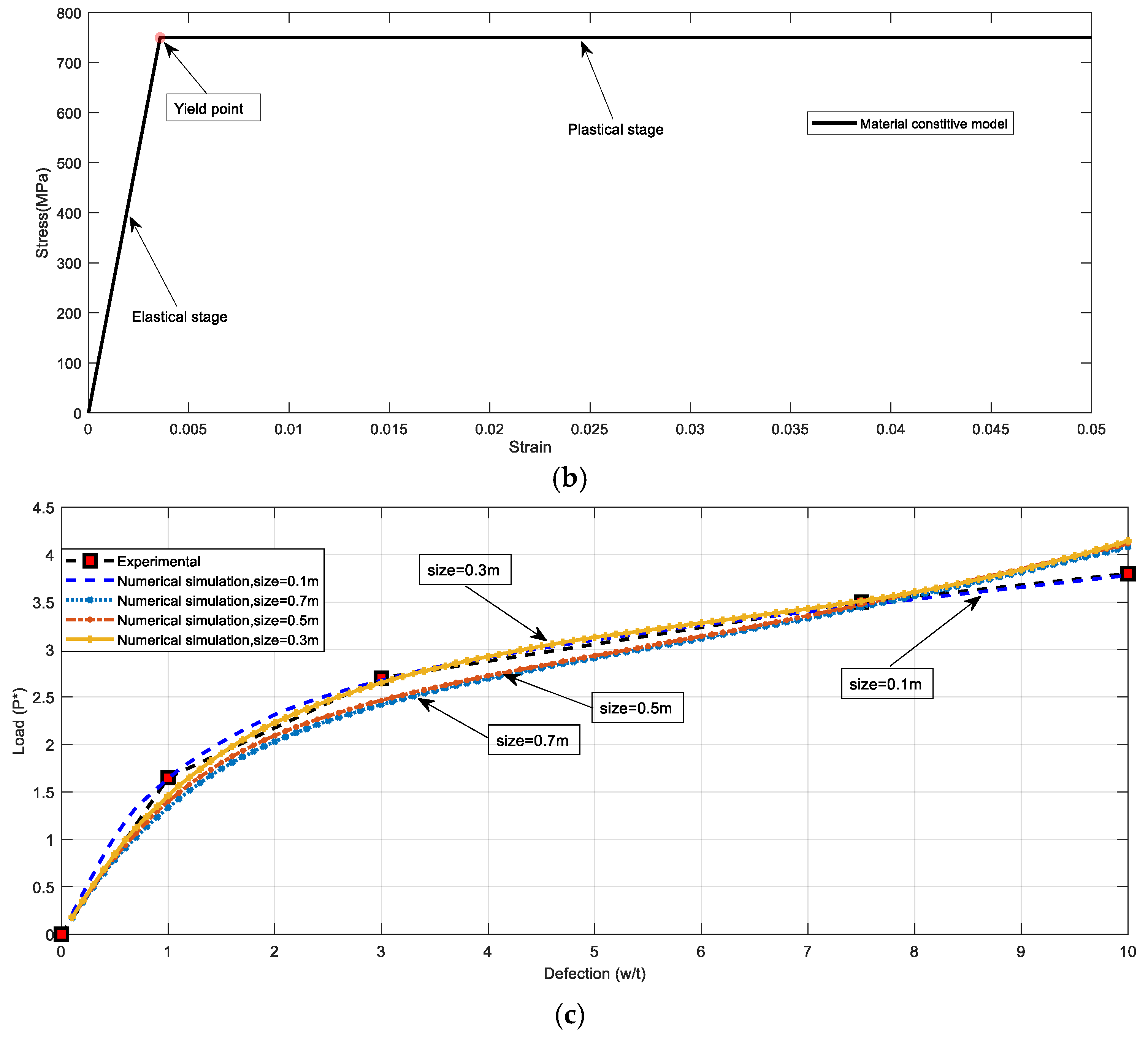
2.2. Verification of FEM Model
2.3. Static Simulations
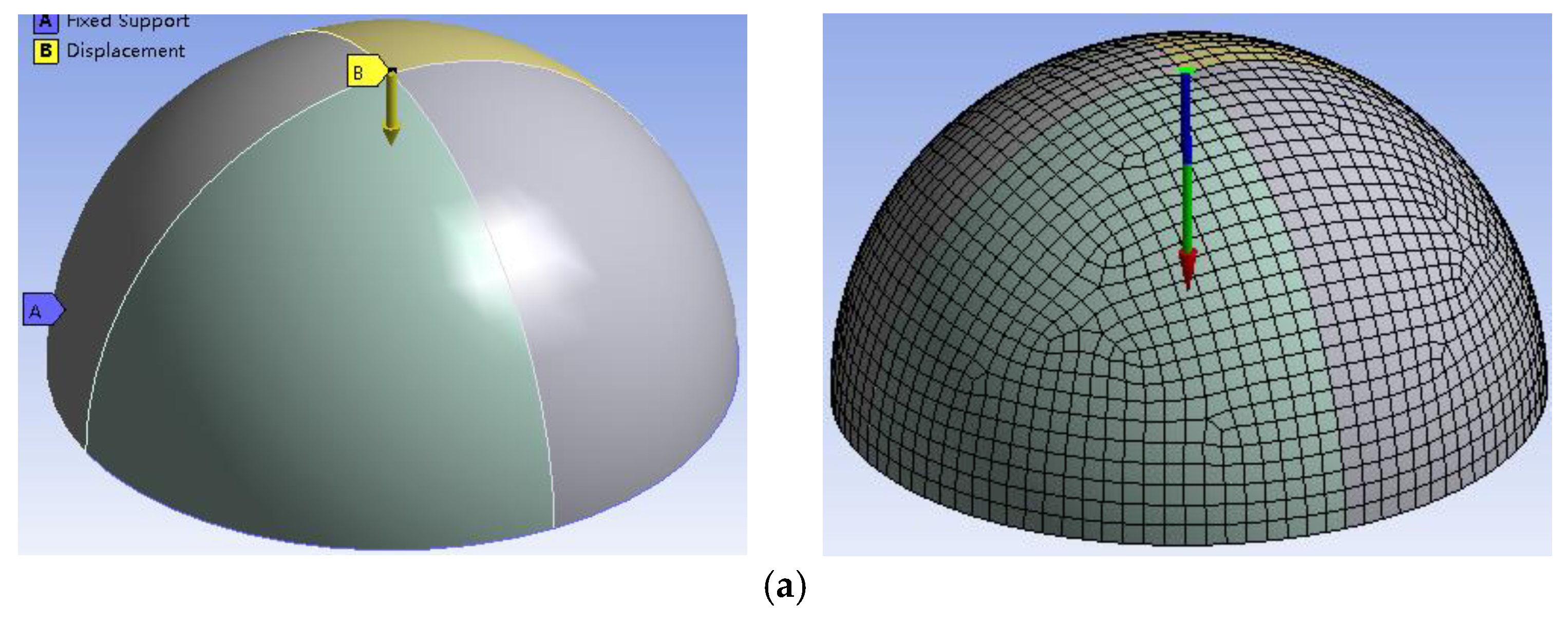
2.3.1. Model
2.3.2. Results
2.3.3. Regression Analysis
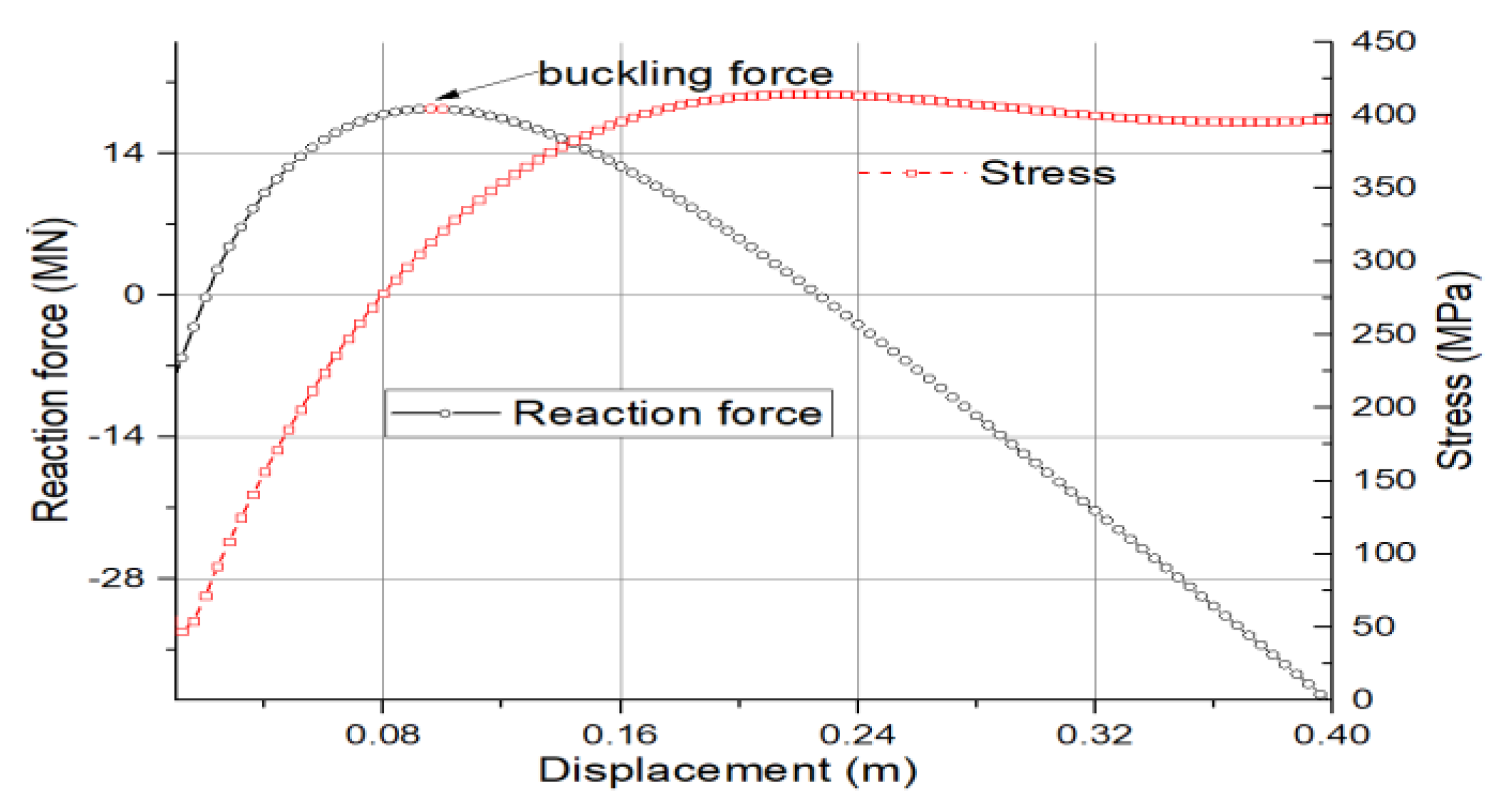
2.4. Buckling Criteria Analysis
2.5. Discussion on Static Buckling
3. Dynamic Buckling Criteria
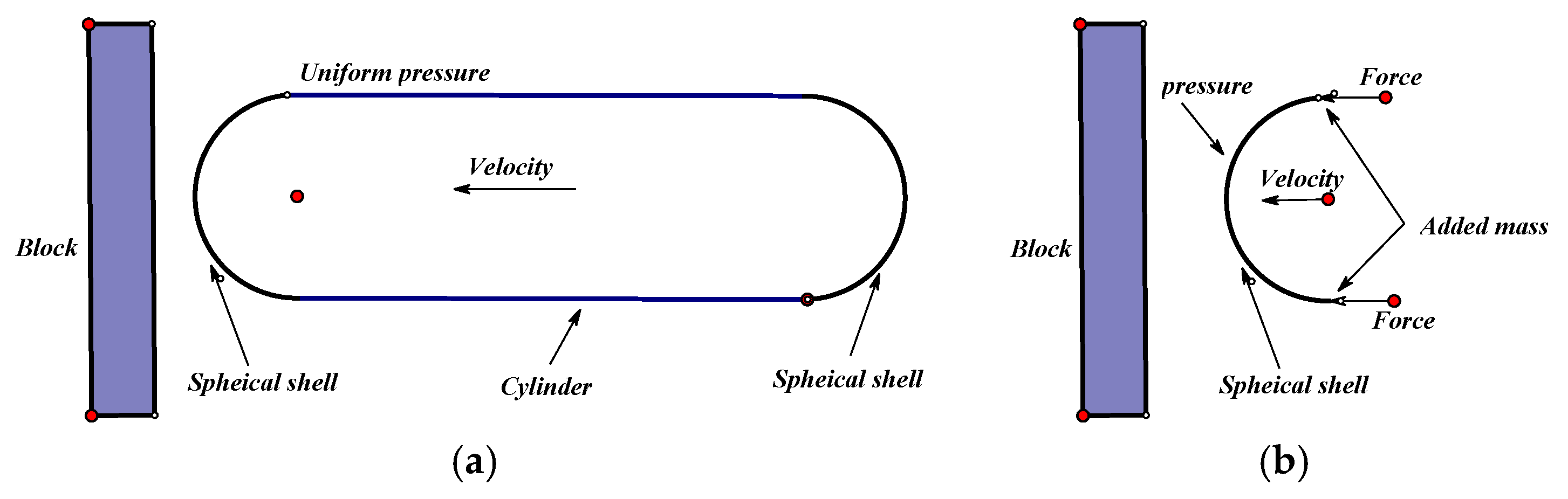
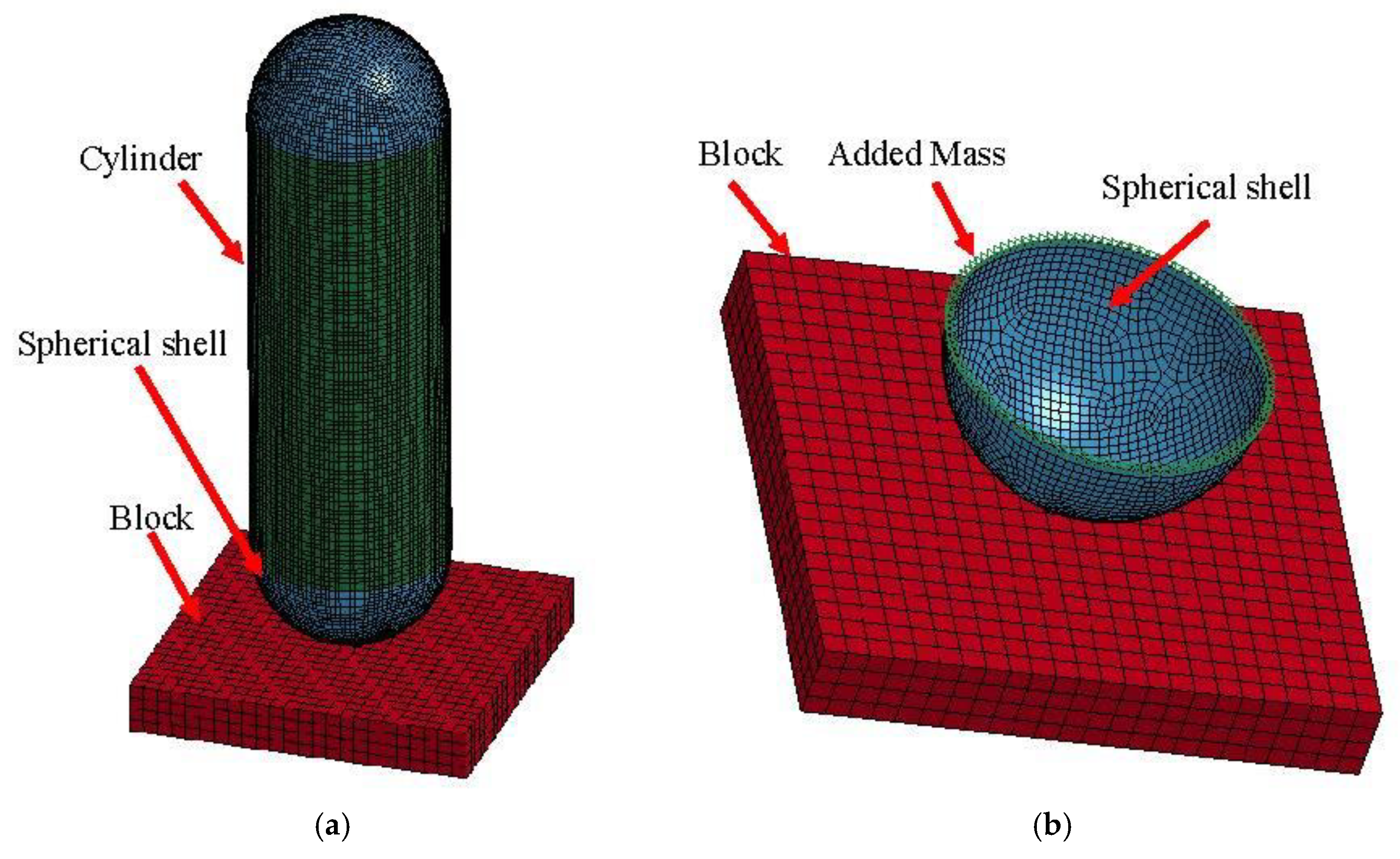
3.1. Model
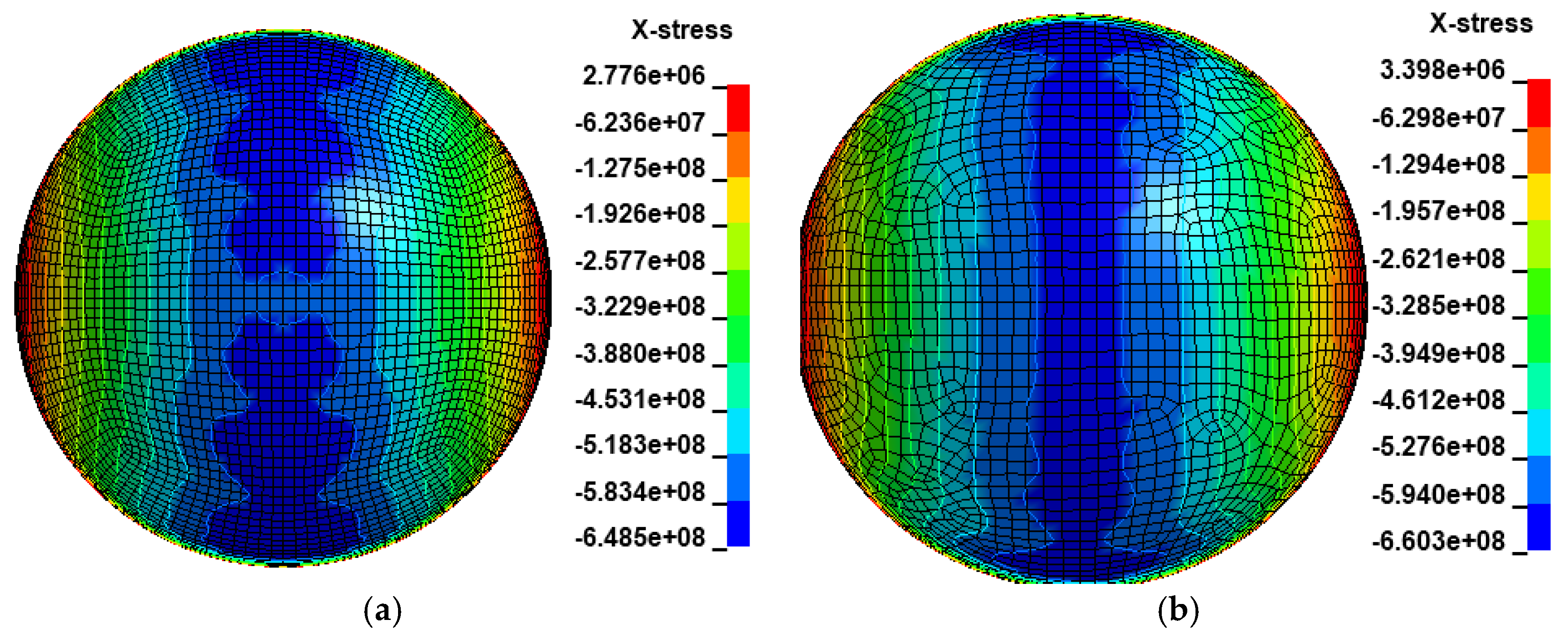
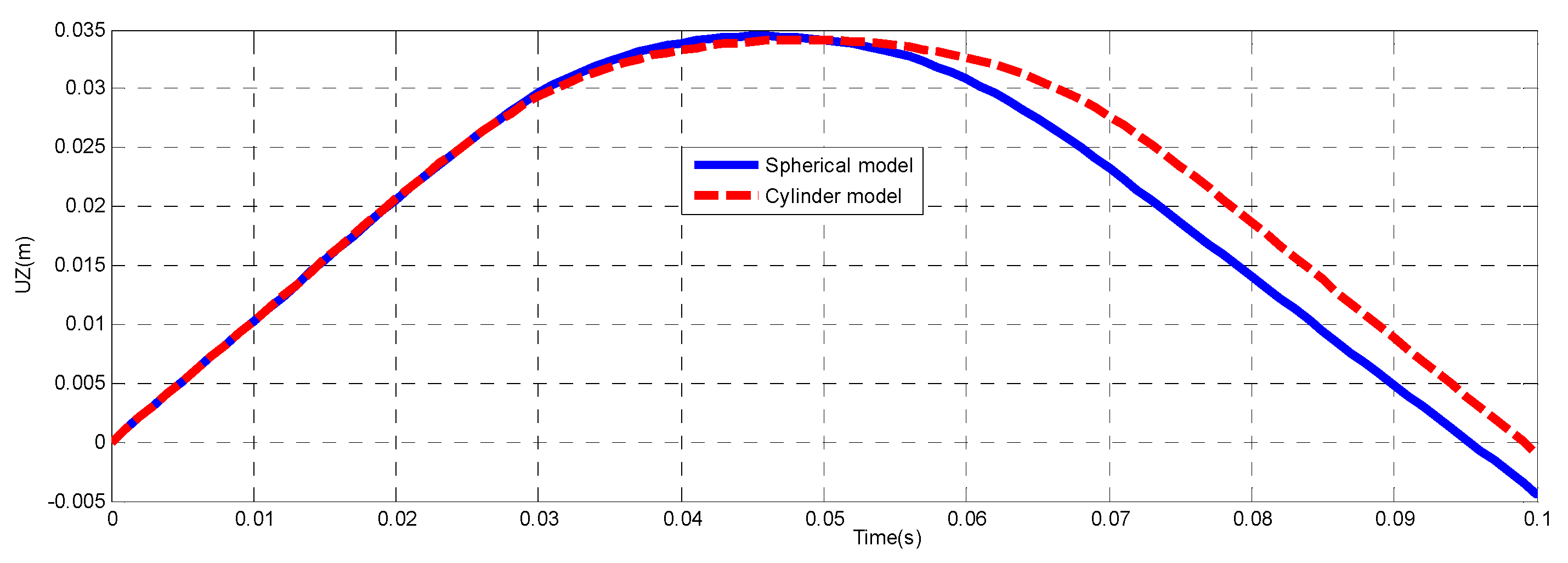
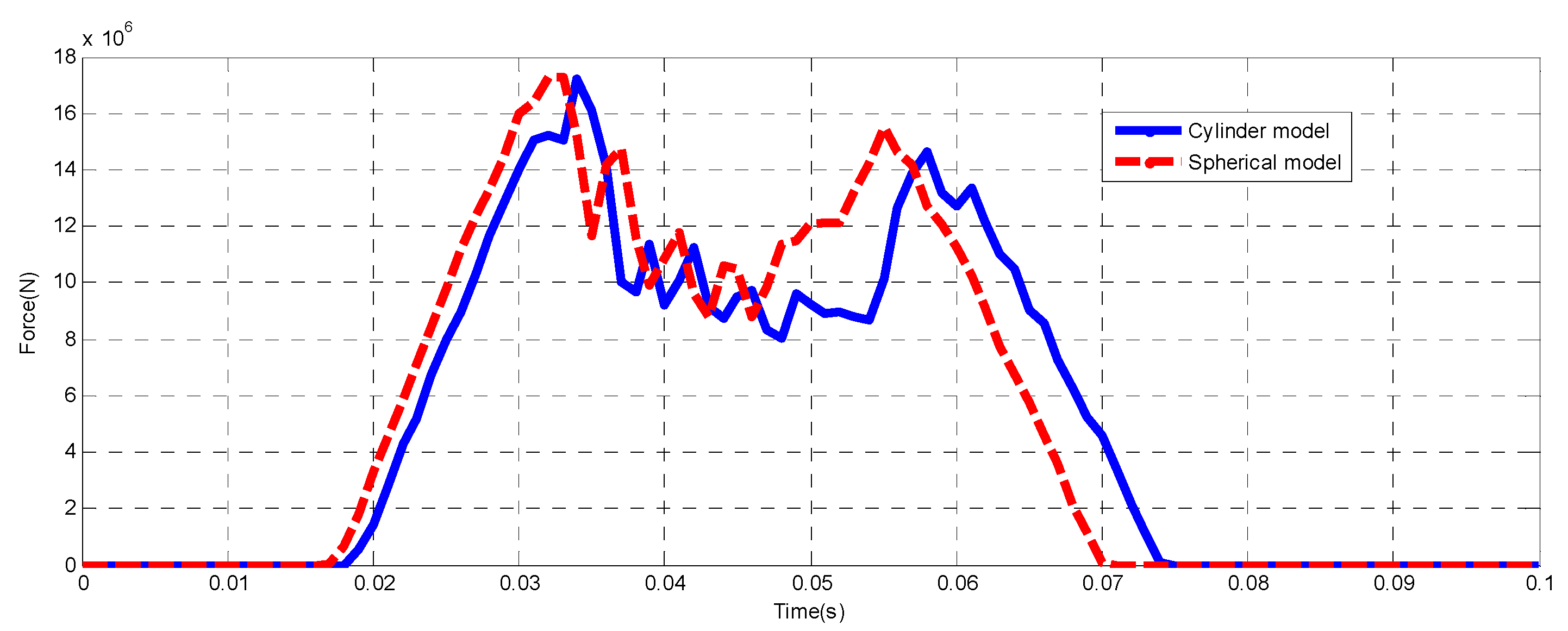
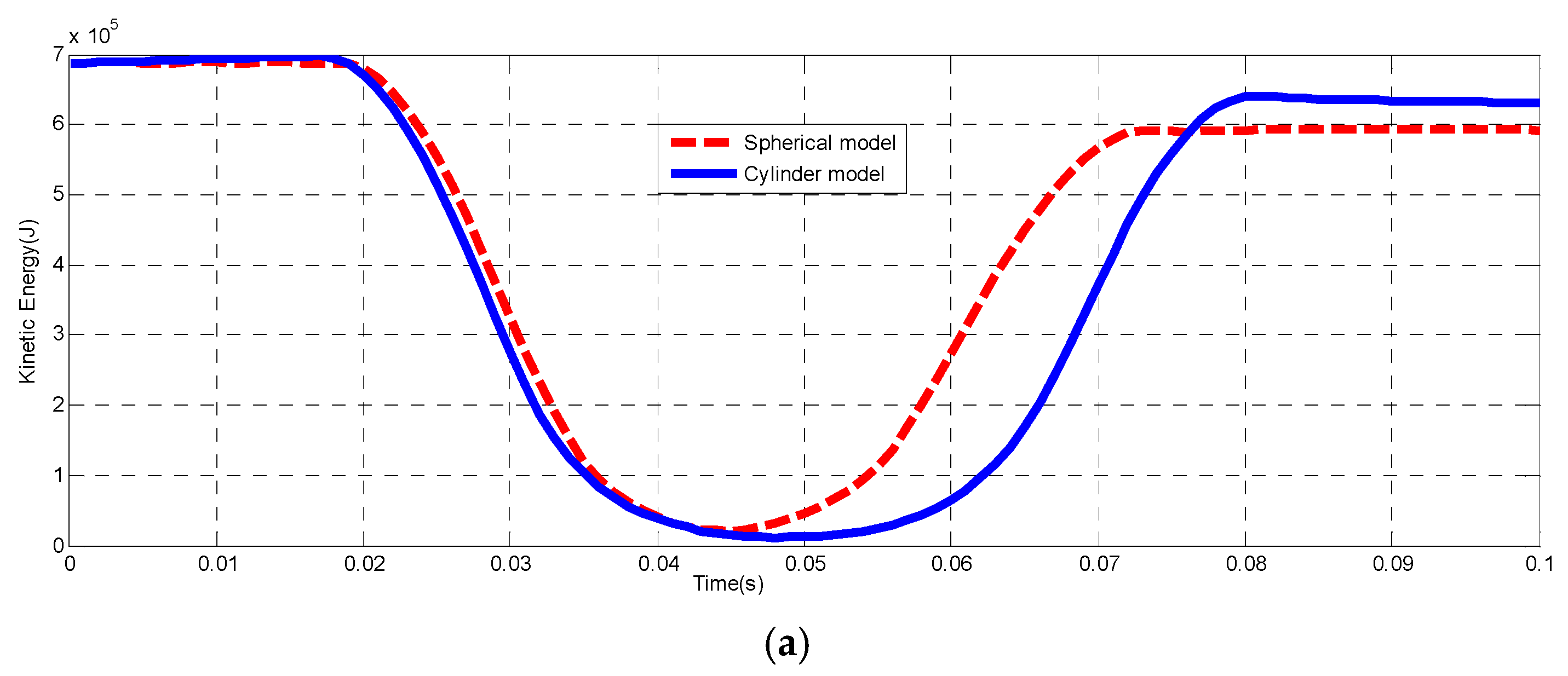
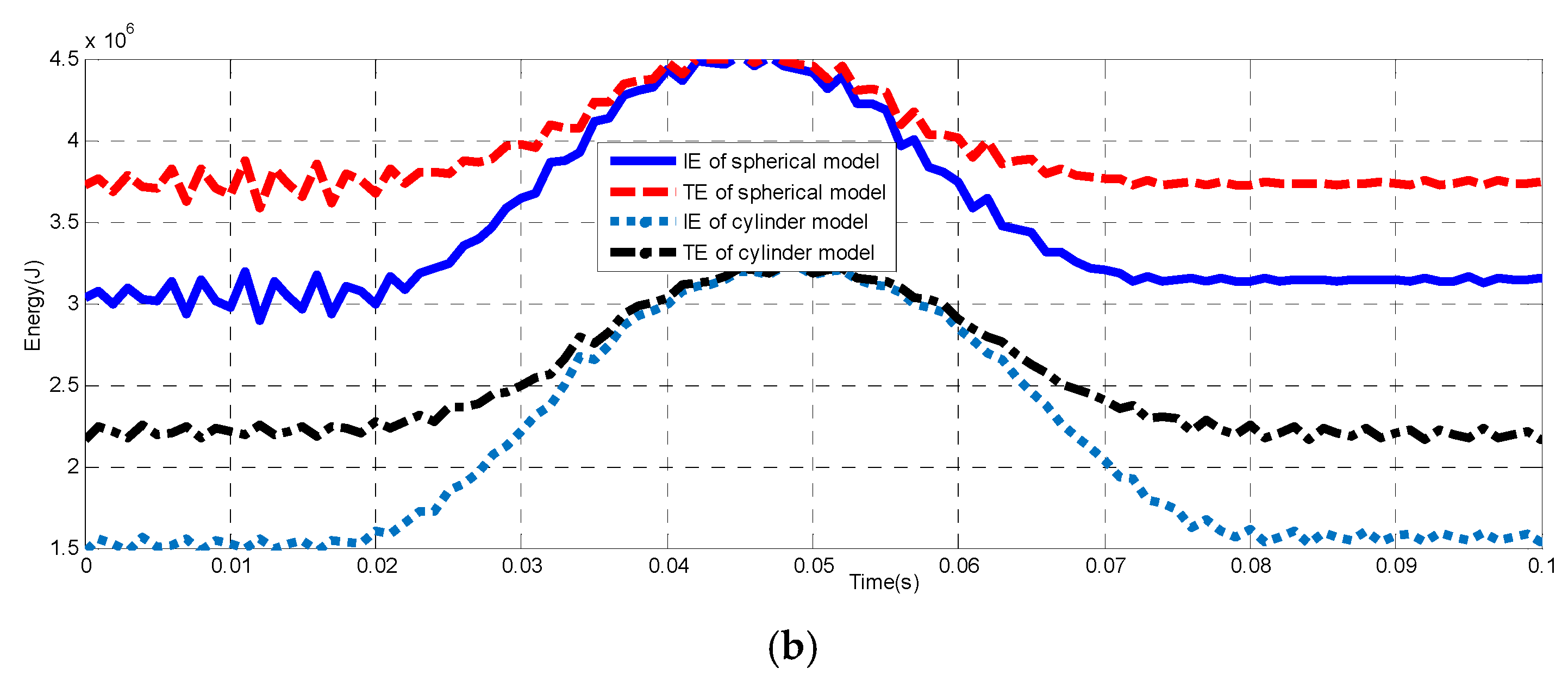
3.2. Comparison of Two Models
3.3. Relationship between Static Force and Dynamic Force
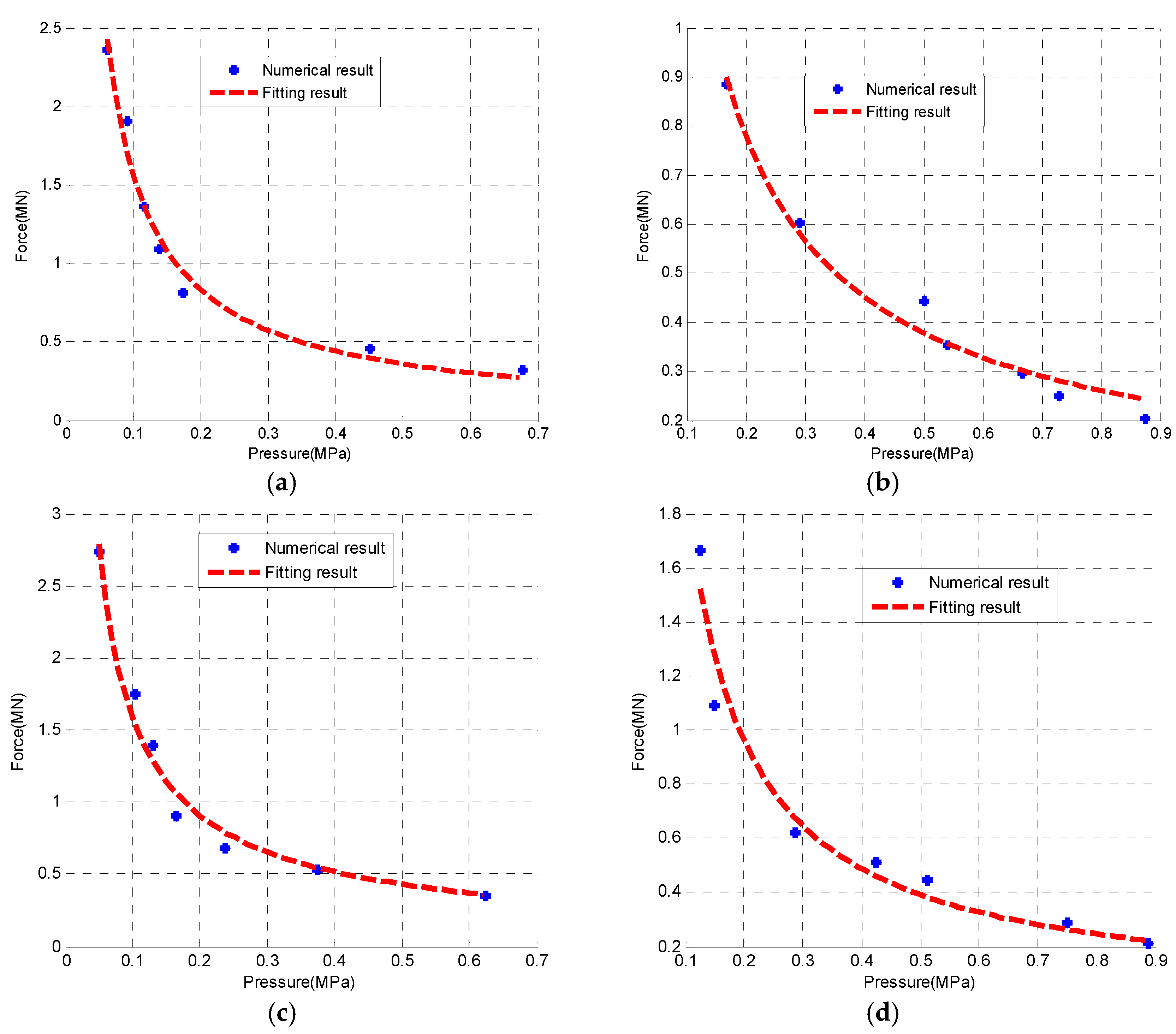
3.3.1. Methodology
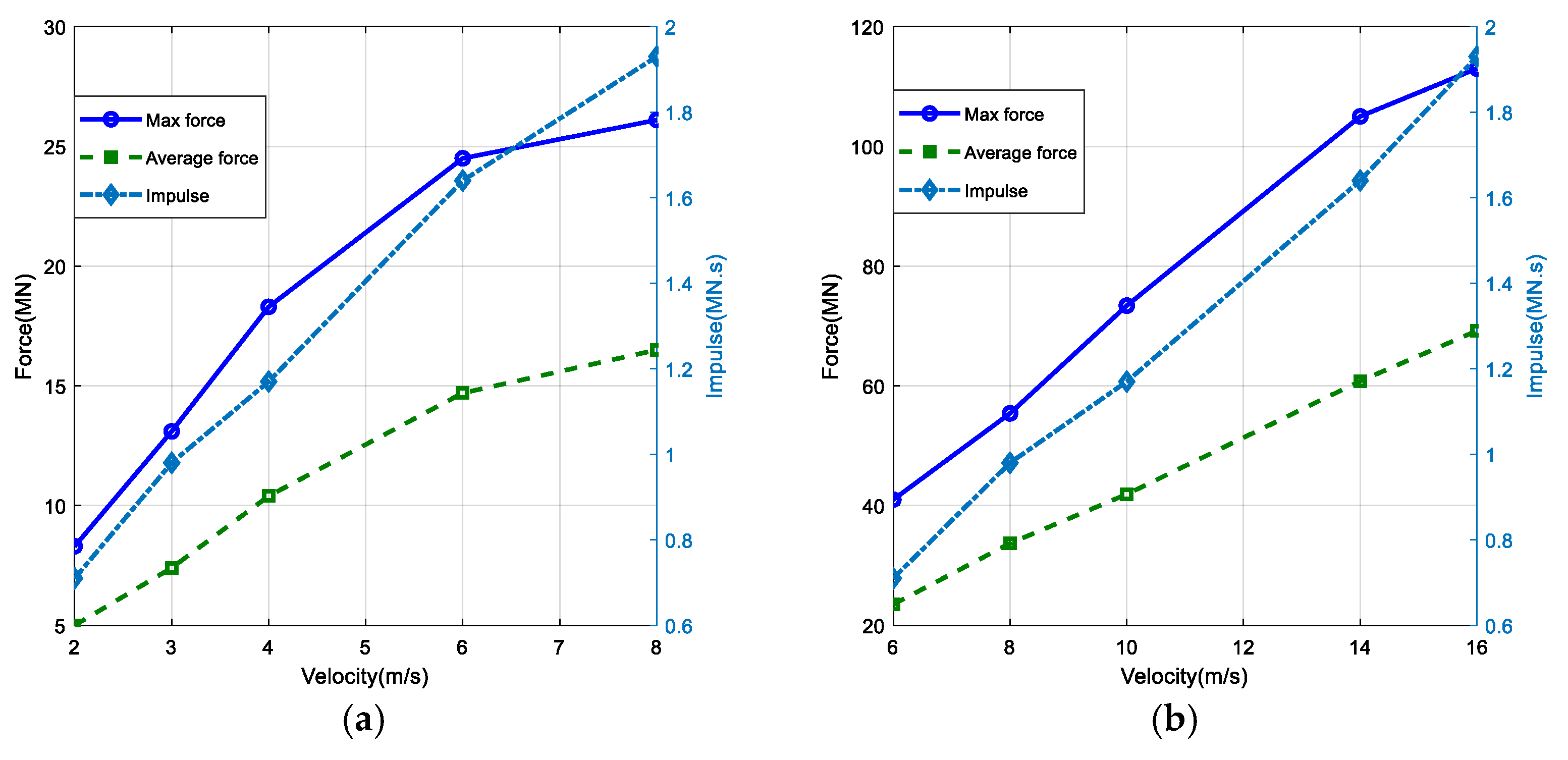
3.3.2. Parametric Effect Due to Velocity
3.3.3. Parametric Effect Due to Thickness
3.3.4. Effect of Elastic Modulus and External Pressure
3.3.5. Parametric Effect of Added Mass
3.3.6. Contact Force Principle
3.4. Dynamic Buckling Criteria
3.5. Dynamic Buckling Force
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Yang, C.; Weller, S.D.; Wang, Y.X.; Ning, D.Z.; Johanning, L. Hydrodynamic response of a submerged tunnel element suspended from a twin-barge under random waves. Ocean Eng. 2017, 135, 63–75. [Google Scholar] [CrossRef]
- Figeys, W.; Ignoul, S.; Van Gemert, D. Strengthening of an industrial cylindrical shell damaged by a collision. In Structural Analysis of Historic Construction: Preserving Safety and Significance, Proceedings of the 6th International Conference on Structural Analysis of Historic Construction (SAHC08), Bath, UK, 2–4 July 2008; Taylor & Francis: London, UK, 2008. [Google Scholar]
- Kaewunruen, S.; Pompeo, G.; Bartoli, G. Blast simulations and transient responses of longspan glass roof structures: A case of London’s railway station. In Proceedings of the 25th UKACM Conference on Computational Mechanics, Birmingham, UK, 12–13 April 2017. [Google Scholar]
- Savićević, S.; Jovanović, Ž.I.J. Experimental research on machine elements of helicoidal shell shape. Tehnicki Vjesnik 2017, 24, 167–175. [Google Scholar]
- Wang, L.P.; Ayala, O.; Kasprzak, S.E.; Grabowski, W.W. Theoretical Formulation of Collision Rate and Collision Efficiency of Hydrodynamically Interacting Cloud Droplets in Turbulent Atmosphere. Am. Meteorol. Soc. 2005, 62, 2433–2450. [Google Scholar] [CrossRef]
- Ida, D.; Nakao, K. Collision of Time-Like Shells in Spherically Symmetric Spacetime. Prog. Theor. Phys. 1999, 101, 989–1000. [Google Scholar] [CrossRef]
- Thompson, J.M.T. Advances in Shell Buckling: Theory and Experiments. Int. J. Bifurc. Chaos 2015, 25, 1530001. [Google Scholar] [CrossRef]
- Bauer, S.M.; Tovstik, P.E. Buckling of Spherical Shells under Concentrated Load and Internal Pressure. Tech. Mech. 1998, 18, 135–139. [Google Scholar]
- Nash, T.J.; McDaniel, D.H.; Leeper, R.J.; Deeney, C.D.; Sanford, T.W.; Struve, K.; DeGroot, J.S. Design, simulation, and application of quasi-spherical 100 ns z-pinch implosions driven by tens of mega-amperes. Phys. Plasmas 2005, 12, 052705. [Google Scholar] [CrossRef]
- Ahn, S.S.; Ruzzene, M. Optimal design of cylindrical shells for enhanced buckling stability: Application to supercavitating underwater vehicles. Finite Elem. Anal. Des. 2006, 42, 967–976. [Google Scholar] [CrossRef]
- Chung, M.; Lee, H.J.; Kang, Y.C.; Lim, W.B.; Kim, J.H.; Cho, J.Y.; Byun, W.; Kim, S.J.; Park, S.H. Experimental study on dynamic buckling phenomena for supercavitating underwater vehicle. Int. J. Naval Archit. Ocean Eng. 2012, 4, 183–198. [Google Scholar] [CrossRef]
- Tan, C.S.; Sutton, R.; Chudley, J. An integrated collision avoidance system for autonomous underwater vehicles. Int. J. Control 2008, 7, 1027–1049. [Google Scholar] [CrossRef]
- McPhail, S.; Furlong, M.; Pebody, M. Low-Altitude Terrain following and Collision Avoidance in a Flight-Class Autonomous Underwater Vehicle. Proc. Inst. Mech. Eng. Part M J. Eng. Maritime Environ. 2010, 224, 279–292. [Google Scholar] [CrossRef]
- Qin, Q.H.; Wang, T.J. Low-velocity heavy-mass impact response of slender metal foam core sandwich beam. Compos. Struct. 2011, 93, 1526–1537. [Google Scholar] [CrossRef]
- Zhang, M.; Tang, W.; Wang, F.; Zhang, J.; Cui, W.; Chen, Y. Buckling of bi-segment spherical shells under hydrostatic external pressure. Thin-Walled Struct. 2017, 120, 1–8. [Google Scholar] [CrossRef]
- Pan, B.B.; Cui, W.C.; Shen, Y.S.; Liu, T. Further study on the ultimate strength analysis of spherical pressure hulls. Mar. Struct. 2010, 23, 444–461. [Google Scholar] [CrossRef]
- Helfer, E.; Harlepp, S.; Bourdieu, L.; Robert, J.; MacKintosh, F.C.; Chatenay, D. Buckling of actin-coated membranes under application of a local force. Phys. Rev. Lett. 2001, 87, 088103. [Google Scholar] [CrossRef] [PubMed]
- Seaman, L. The Nature of Buckling in Thin Spherical Shells. PhD Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1962. [Google Scholar]
- Kaplan, A.; Fung, Y.C. A Nonlinear Theory of Bending and Buckling of Tein Elastic Shallow Spherical Shells; National Advisory Committee for Aeronautics: Washington, DC, USA, 1954.
- Vető, D. Analysis of Quasi-Isometric Polygonal Buckling Shapes of Spherical Shells. Ph.D. Thesis, Budapest University of Technology and Economics, Department of Mechanics, Materials and Structures, Budapest, Hungary, 2016. [Google Scholar]
- Timoshenko, S.; Gere, J.M. Theory of Elastic Stability; McGraw-Hill International Book Company: London, UK, 1963. [Google Scholar]
- Shahandeh, R.; Showkati, H. Influence of ring-stiffeners on buckling behavior of pipelines under hydrostatic pressure. J. Construct. Steel Res. 2016, 121, 237–252. [Google Scholar] [CrossRef]
- Wang, J.H.; Zhang, W.J.; Guo, X.; Koizumi, A.; Tanaka, H. Mechanism for buckling of shield tunnel linings under hydrostatic pressure. Tunn. Undergr. Space Technol. 2015, 49, 144–155. [Google Scholar] [CrossRef]
- Yan, S.T.; Shen, X.L.; Jin, Z.J.; Ye, H. On elastic-plastic collapse of subsea pipelines under external hydrostatic pressure and denting force. Appl. Ocean Res. 2016, 58, 305–321. [Google Scholar] [CrossRef]
- Błachut, J.; Smith, P. Buckling of multi-segment underwater pressure hull. Ocean Eng. 2008, 35, 247–260. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, M.; Cui, W.; Wang, F.; Hua, Z.; Tang, W. Effect of thickness on the buckling strength of egg- shaped pressure hulls. Ships Offshore Struct. 2018, 13, 375–384. [Google Scholar] [CrossRef]
- Khakina, P.N. Buckling Load of Thin Spherical Shells Based on the Theorem of Work and Energy. Int. J. Eng. Technol. 2013, 5, 392–394. [Google Scholar] [CrossRef]
- Evkin, A.Y.; Lykhachova, O.V. Energy barrier as a criterion for stability estimation of spherical shell under uniform external pressure. Int. J. Solids Struct. 2017, 118–119, 14–23. [Google Scholar] [CrossRef]
- Gish, L.A. A pseudo-coupled analytic fluid-structure interaction method for underwater implosion of cylindrical shells. Appl. Ocean Res. 2017, 66, 156–163. [Google Scholar] [CrossRef]
- Gangyi, H.; Fei, X.; Jun, L. The transient responses of two-layered cylindrical shells attacked by underwater explosive shock waves. Compos. Struct. 2010, 92, 1551–1560. [Google Scholar] [CrossRef]
- Cho, S.R.; Muttaqie, T.; Do, Q.T.; Kim, S.; Kim, S.M.; Han, D.H. Experimental investigations on the failure modes of ring-stiffened cylinders under external hydrostatic pressure. Int. J. Naval Archit. Ocean Eng. 2018. [Google Scholar] [CrossRef]
- Hutchinson, J.W.; Thompson, J.M.T. Imperfections and energy barriers in shell buckling. Int. J. Solids Struct. 2018. [Google Scholar] [CrossRef]
- Kaewunruen, S. Underpinning systems thinking in railway engineering education. Australas. J. Eng. Educ. 2017, 22, 107–114. [Google Scholar] [CrossRef]
- Huang, H.; Zhang, Y.; Han, Q. Stability of hydrostatic-pressured FGM thick rings with material nonlinearity. Appl. Math. Model. 2017, 45, 55–64. [Google Scholar] [CrossRef]
- Wang, J.H.; Koizumi, A.; Yuan, D.J. Theoretical and numerical analyses of hydrostatic buckling of a noncircular composite liner with arched invert. Thin-Walled Struct. 2016, 102, 148–157. [Google Scholar] [CrossRef]
- Yu, C.L.; Chen, Z.T.; Chen, C.; Chen, Y.T. Influence of initial imperfections on ultimate strength of spherical shells. Int. J. Naval Archit. Ocean Eng. 2017, 9, 473–483. [Google Scholar] [CrossRef]
- Lin, S.; Xie, Y.M.; Li, Q.; Huang, X.; Zhou, S. Buckling-induced retraction of spherical shells: A study on the shape of aperture. Sci. Rep. 2015, 5, 11309. [Google Scholar] [CrossRef] [PubMed]
- Liang, C.C.; Shiah, S.W.; Jen, C.Y.; Chen, H.W. Optimum design of multiple intersecting spheres deep-submerged pressure hull. Ocean Eng. 2004, 31, 177–199. [Google Scholar] [CrossRef]
- Bai, X.; Xu, W.; Ren, H.; Li, J. Analysis of the influence of stiffness reduction on the load carrying capacity of ring-stiffened cylindrical shell. Ocean Eng. 2017, 135, 52–62. [Google Scholar] [CrossRef]
- MacKay, J.R.; Smith, M.J.; van Keulen, F.; Bosman, T.N.; Pegg, N.G. Experimental investigation of the strength and stability of submarine pressure hulls with and without artificial corrosion damage. Mar. Struct. 2010, 23, 339–359. [Google Scholar] [CrossRef]
- Bich, D.H.; Dung, D.V.; Hoa, L.K. Nonlinear static and dynamic buckling analysis of functionally graded shallow spherical shells including temperature effects. Compos. Struct. 2012, 94, 2952–2960. [Google Scholar] [CrossRef]
- Shariati, M.; Allahbakhsh, H.R. Numerical and experimental investigations on the buckling of steel semi-spherical shells under various loadings. Thin-Walled Struct. 2010, 48, 620–628. [Google Scholar] [CrossRef]
- Hutchinson, J.W.; Thompson, J.M. Nonlinear buckling behaviour of spherical shells: Barriers and symmetry-breaking dimples. Philos. Trans. A Math. Phys. Eng. Sci. 2017, 375. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Zhang, M.; Cui, W.; Tang, W.; Wang, F.; Pan, B. Elastic-plastic buckling of deep sea spherical pressure hulls. Mar. Struct. 2018, 57, 38–51. [Google Scholar] [CrossRef]
- Penning, F.A.; Tburston, G.A. The Stability of Shallow Spherical Shells under Concentrated Load; National Aeronautics and Space Administration: Washington, DC, USA, 1965.
- Zhang, J.; Zhu, B.; Wang, F.; Tang, W.; Wang, W.; Zhang, M. Buckling of prolate egg-shaped domes under hydrostatic external pressure. Thin-Walled Struct. 2017, 119, 296–303. [Google Scholar] [CrossRef]
- Takla, M. Instability and axisymmetric bifurcation of elastic-plastic thick-walled cylindrical pressure vessels. Int. J. Press. Vessel. Pip. 2018, 159, 73–83. [Google Scholar] [CrossRef]
- Yan, S.; Shen, X.; Jin, Z. On instability failure of corroded rings under external hydrostatic pressure. Eng. Fail. Anal. 2015, 55, 39–54. [Google Scholar] [CrossRef]
- Sabir, A.B. Large deflection and buckling behaviour of a spherical shell with inward point load and uniform external pressure. J. Mech. Des. 1964, 6, 399–409. [Google Scholar] [CrossRef]
- Coman, C.D.; Bassom, A.P. Asymptotic limits and wrinkling patterns in a pressurised shallow spherical cap. Int. J. Non-Linear Mech. 2016, 81, 8–18. [Google Scholar] [CrossRef]
- Farhat, C.; Wang, K.G.; Main, A.; Kyriakides, S.; Lee, L.H.; Ravi-Chandar, K.; Belytschko, T. Dynamic implosion of underwater cylindrical shells: Experiments and Computations. Int. J. Solids Struct. 2013, 50, 2943–2961. [Google Scholar] [CrossRef]
- Nski, T.N.; Swiniarski, J. Numerical Calculations of Stability of Spherical Shells. Mech. Mech. Eng. 2010, 14, 325–337. [Google Scholar]
- Veto, D.; Sajtos, I. Theoretical, numerical and experimental analysis of polygonal buckling shapes of spherical shells subjected to concentrated load. J. Int. Assoc. Shell Spat. Struct. 2017, 58, 144–155. [Google Scholar] [CrossRef]
- MacKay, J.R.; van Keulen, F.; Smith, M.J. Quantifying the accuracy of numerical collapse predictions for the design of submarine pressure hulls. Thin-Walled Struct. 2011, 49, 145–156. [Google Scholar] [CrossRef]
- Livermore Software Technology Corporation (LSTC). LS-DYNA®KEYWORD USER’S MANUAL I; Livermore Software Technology Corporation: Livermore, CA, USA, 2016. [Google Scholar]
- Fan, W.; Xing, W. Deflection Solutions for Concentrated Force on Spherical Shell. In Proceedings of the 5th International Conference on Civil Engineering Transportation (ICCET 2015), Guangzhou, China, 28–29 November 2015. [Google Scholar]
- Evkin, A.Y. Large deflections of deep orthotropic spherical shells under radial concentrated load: Asymptotic solution. Int. J. Solids Struct. 2005, 42, 1173–1186. [Google Scholar] [CrossRef]
- Wunderlich, W.; Albertin, U. Buckling behaviour of imperfect spherical shells. Non-Linear Mech. 2002, 37, 589–605. [Google Scholar] [CrossRef]
- Gao, S.; Wang, X. A static spherically symmetric thin shell wormhole colliding with a spherical thin shell. Phys. Rev. D 2015, 93, 064027. [Google Scholar]
- Kaewunruen, S.; Sussman, J.M.; Matsumoto, A. Grand Challenges in Transportation and Transit Systems. Front. Built Environ. 2016, 2, 4. [Google Scholar] [CrossRef]


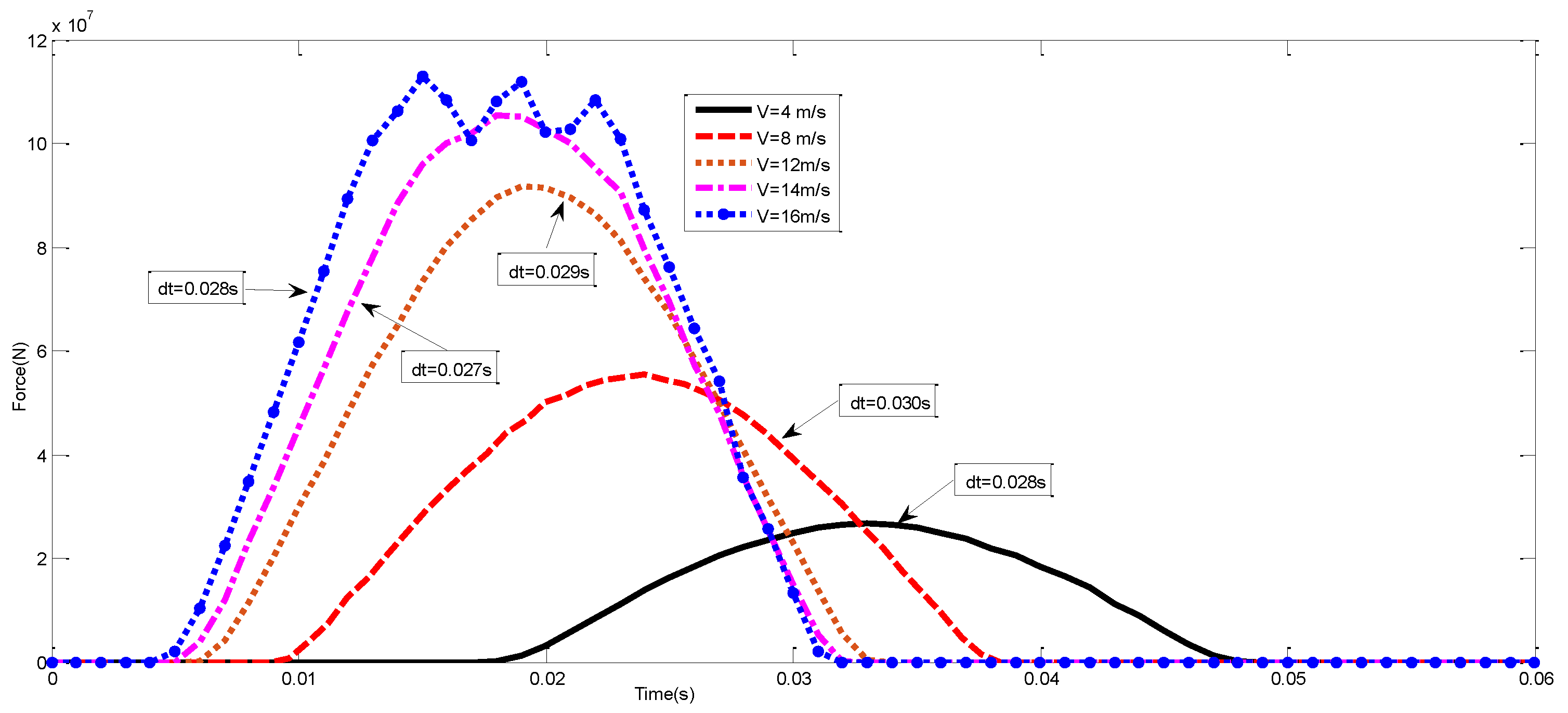
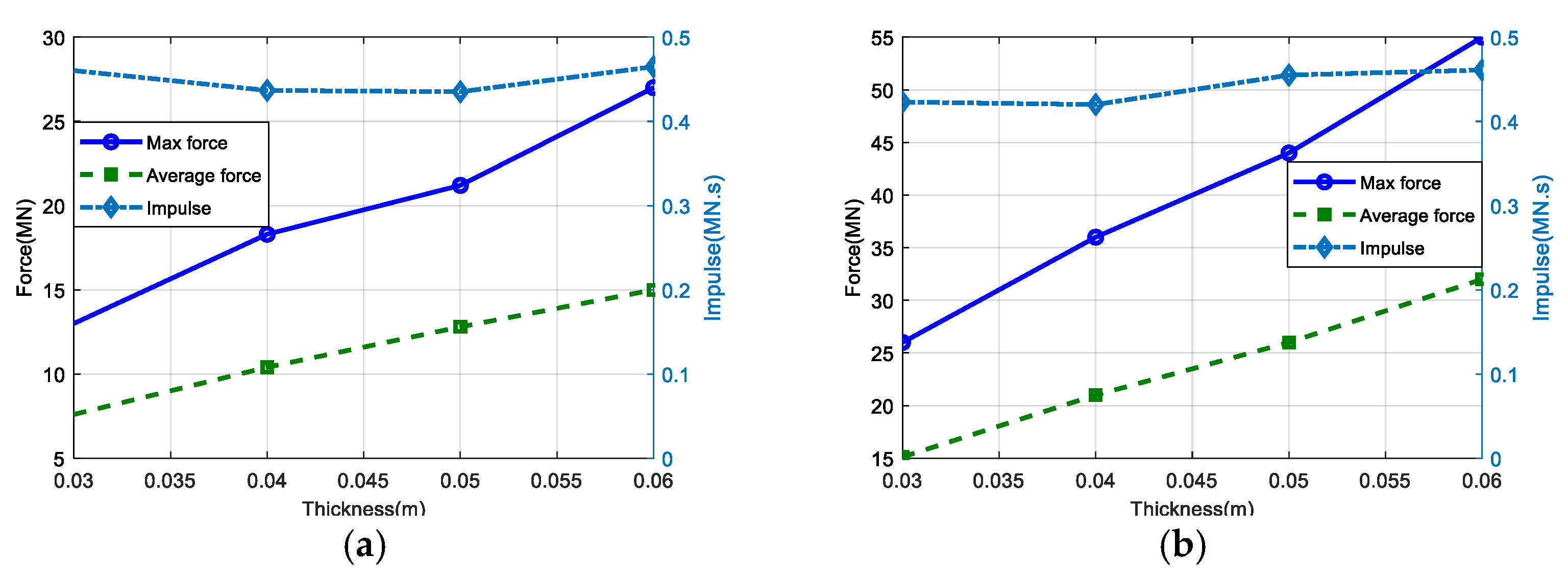
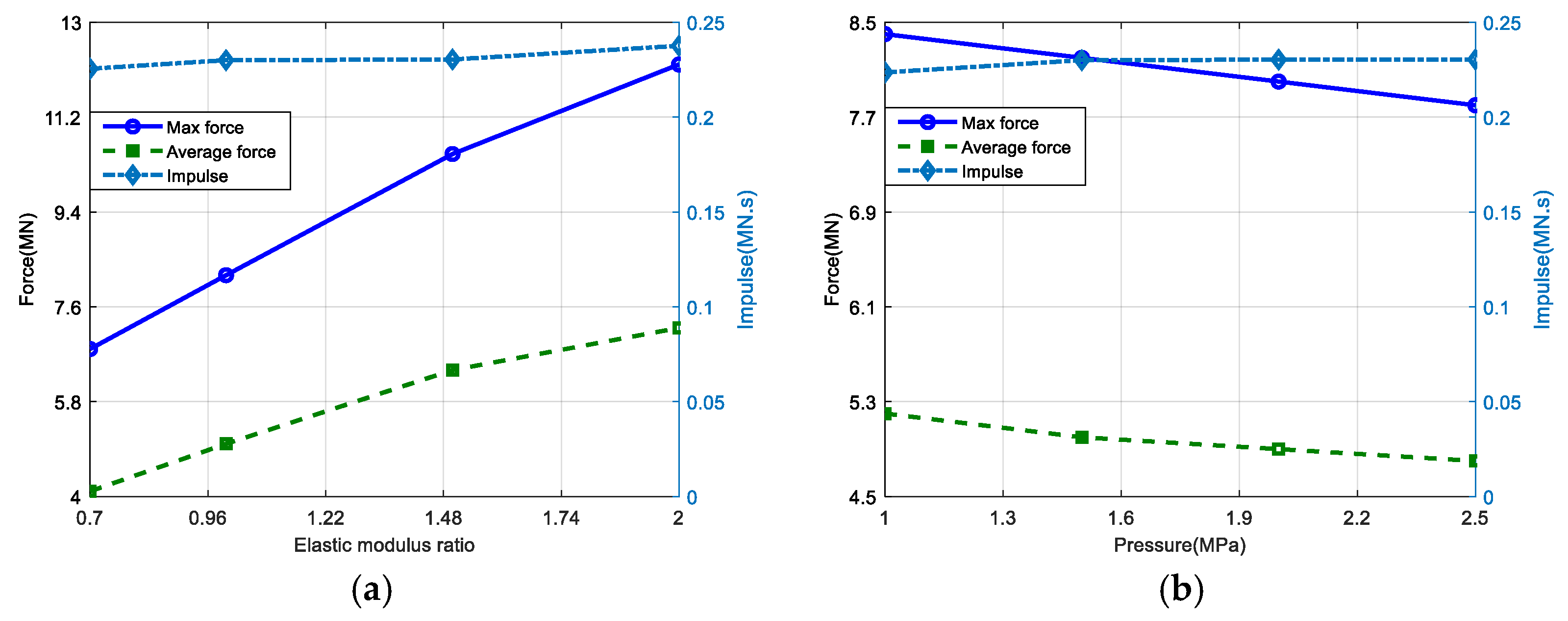
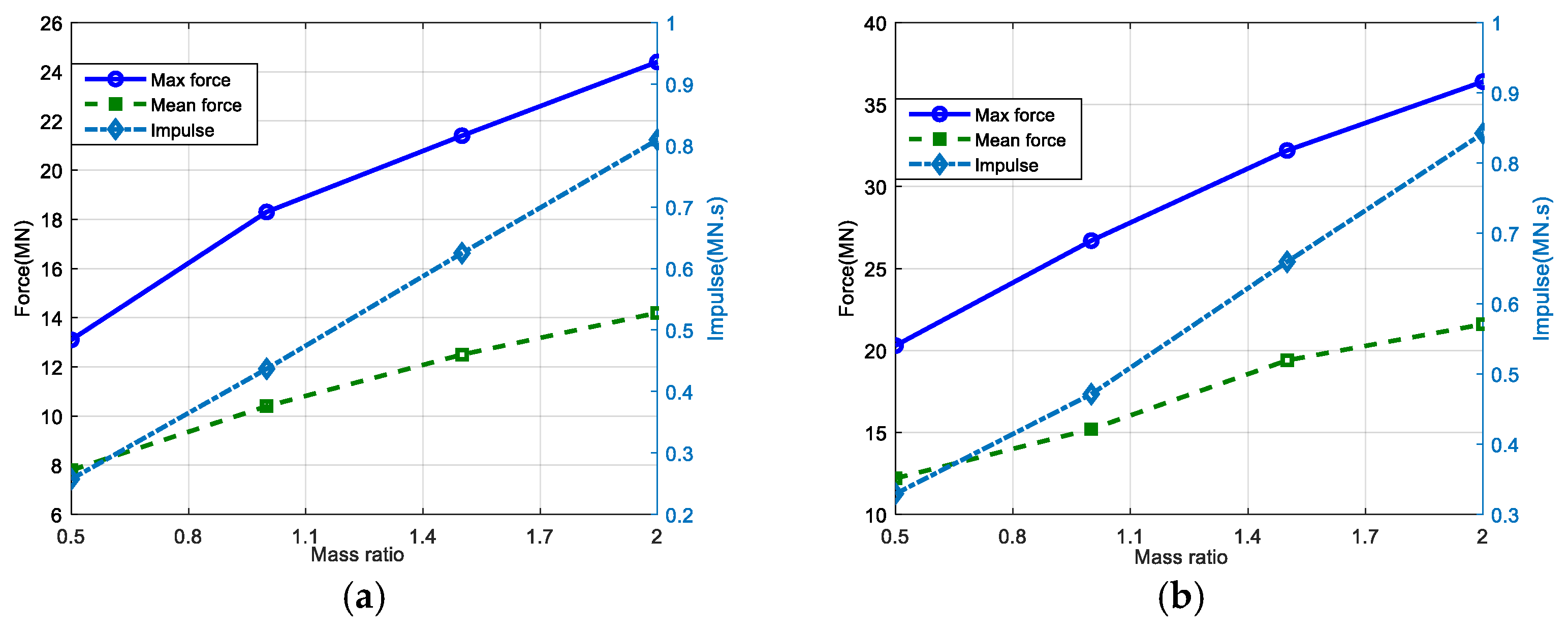
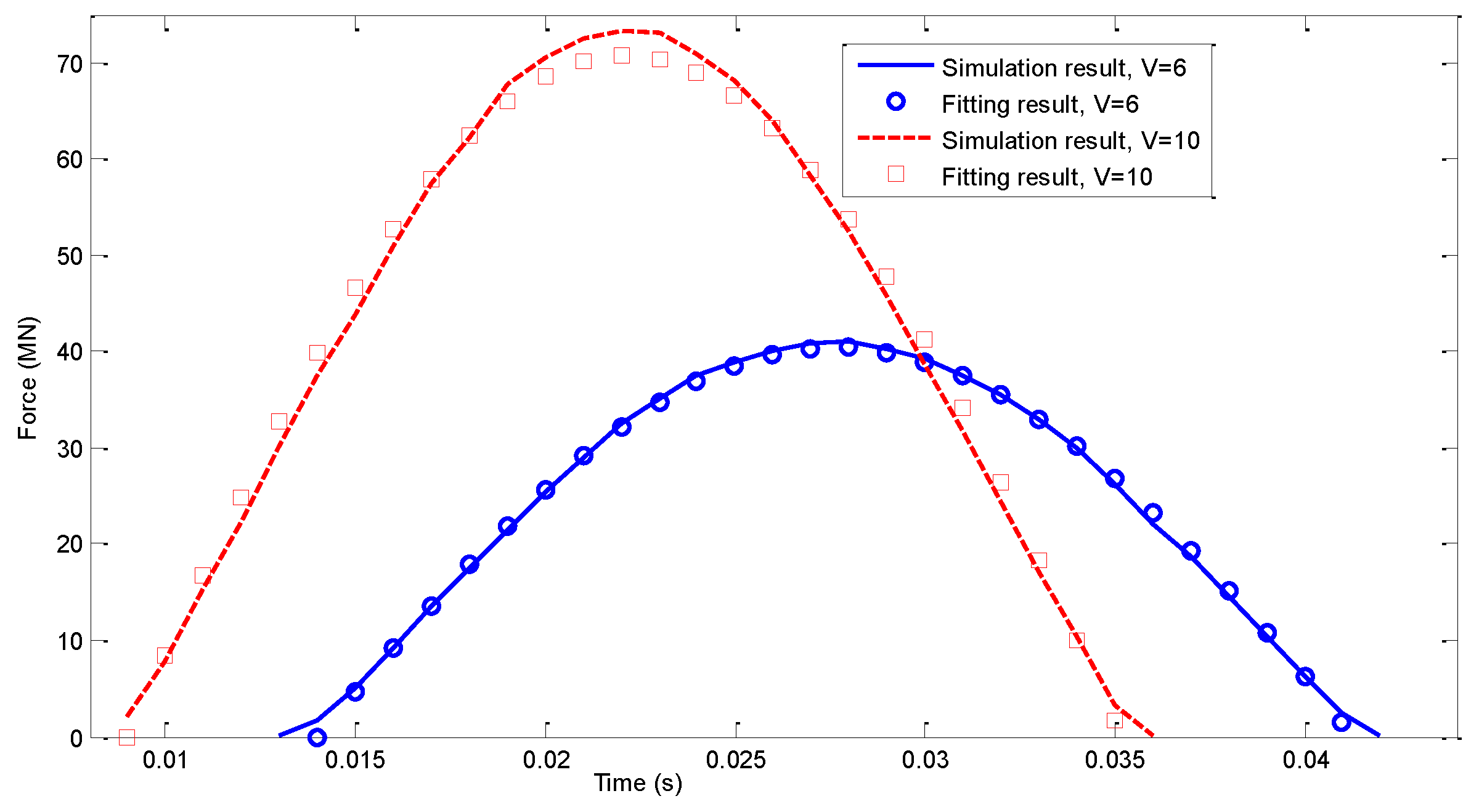
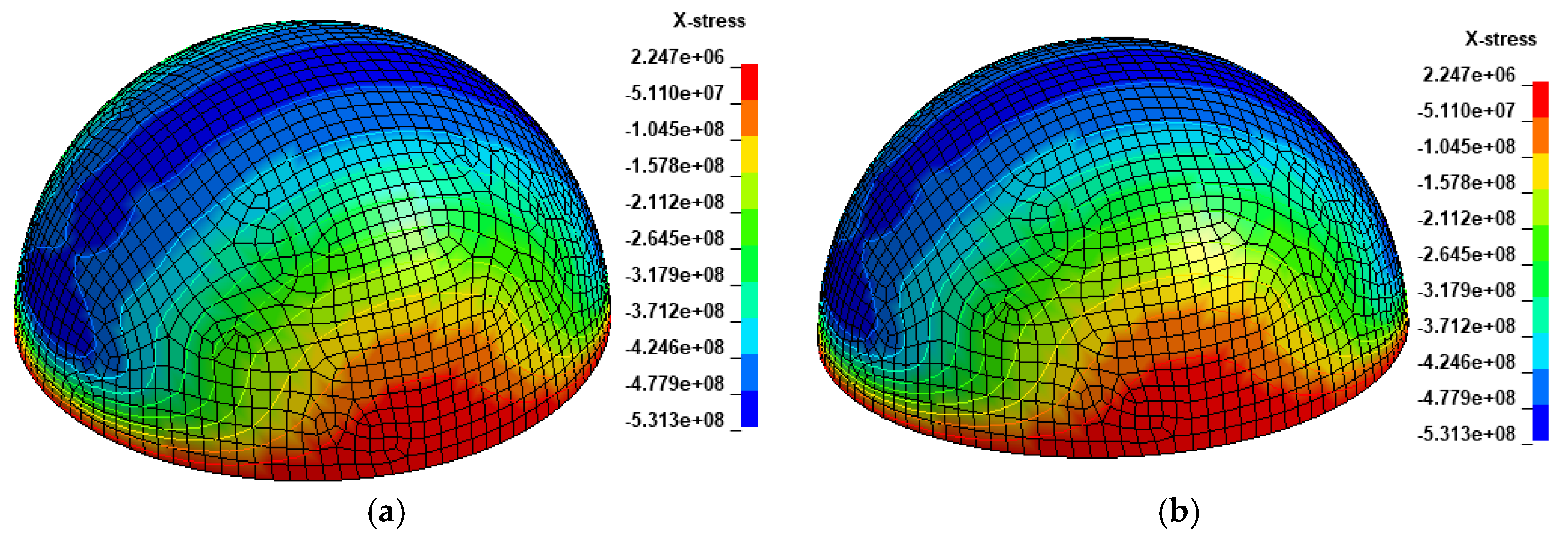
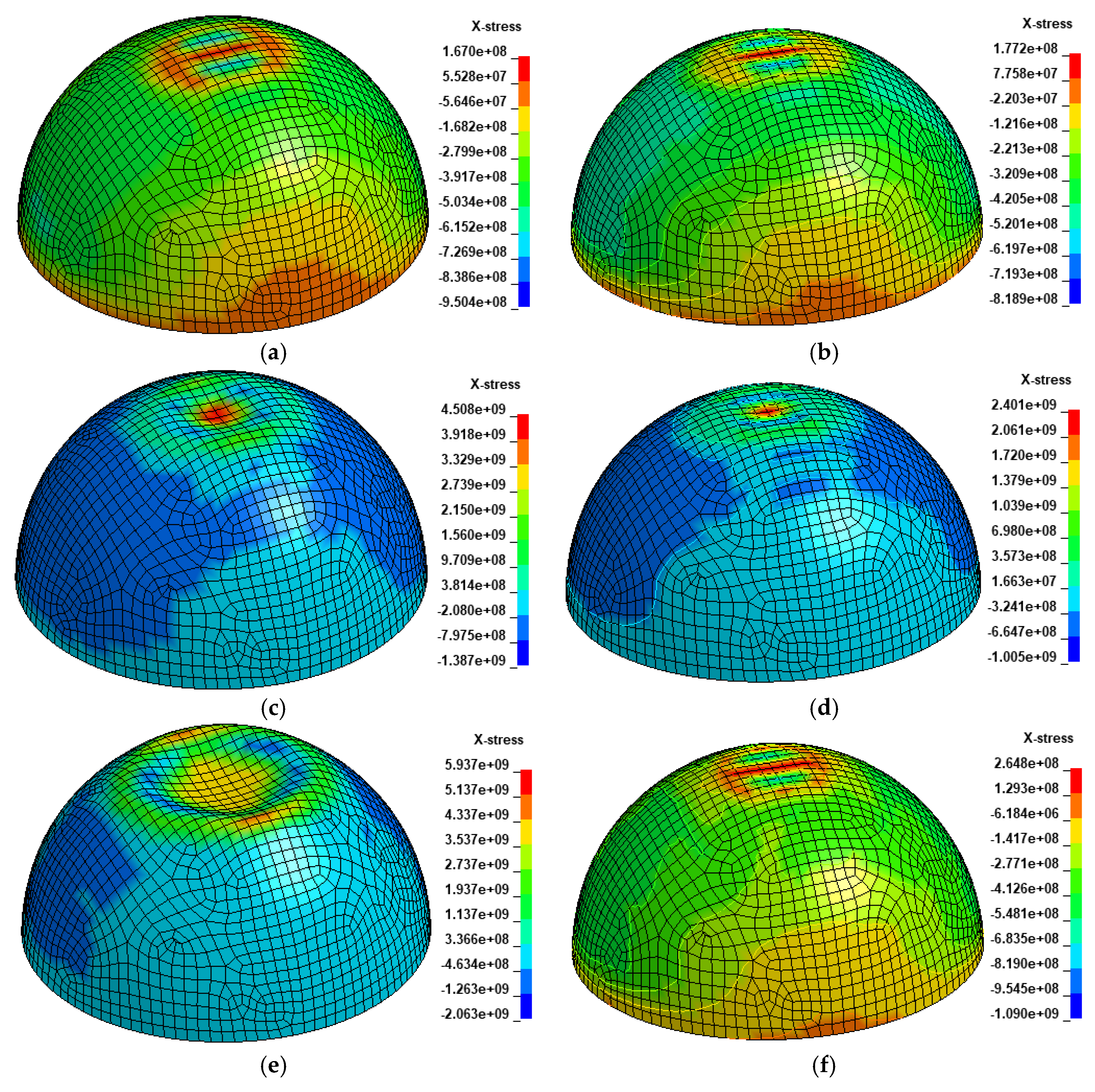
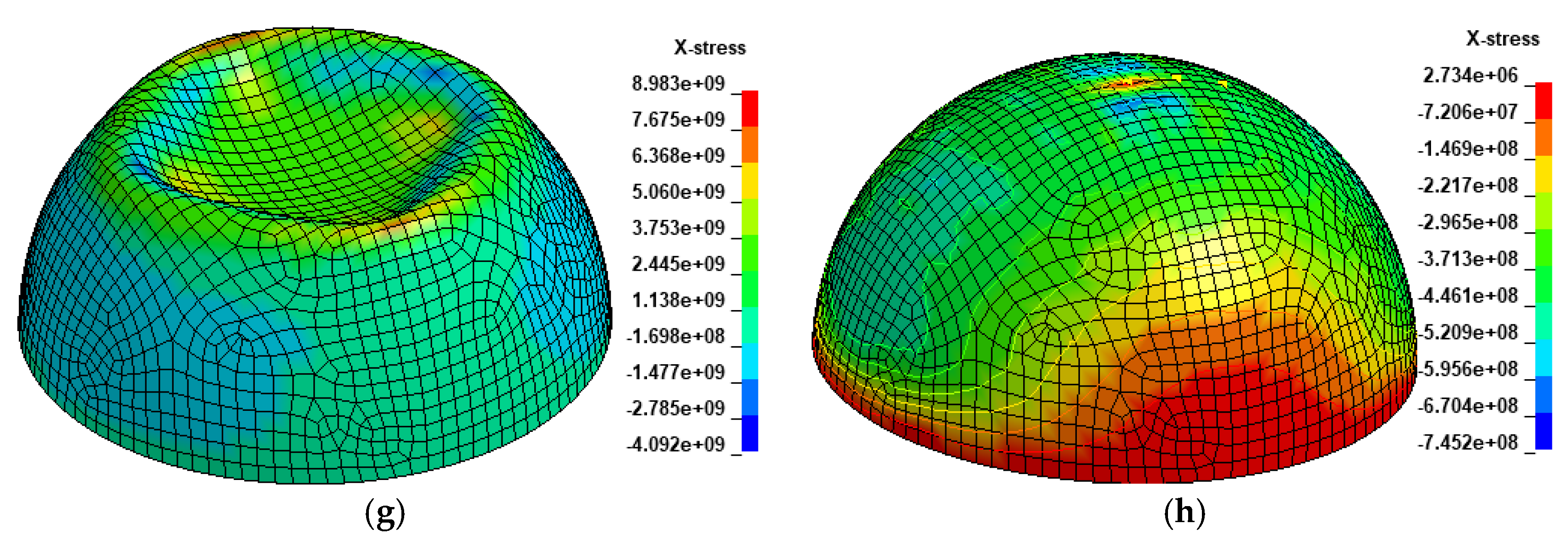
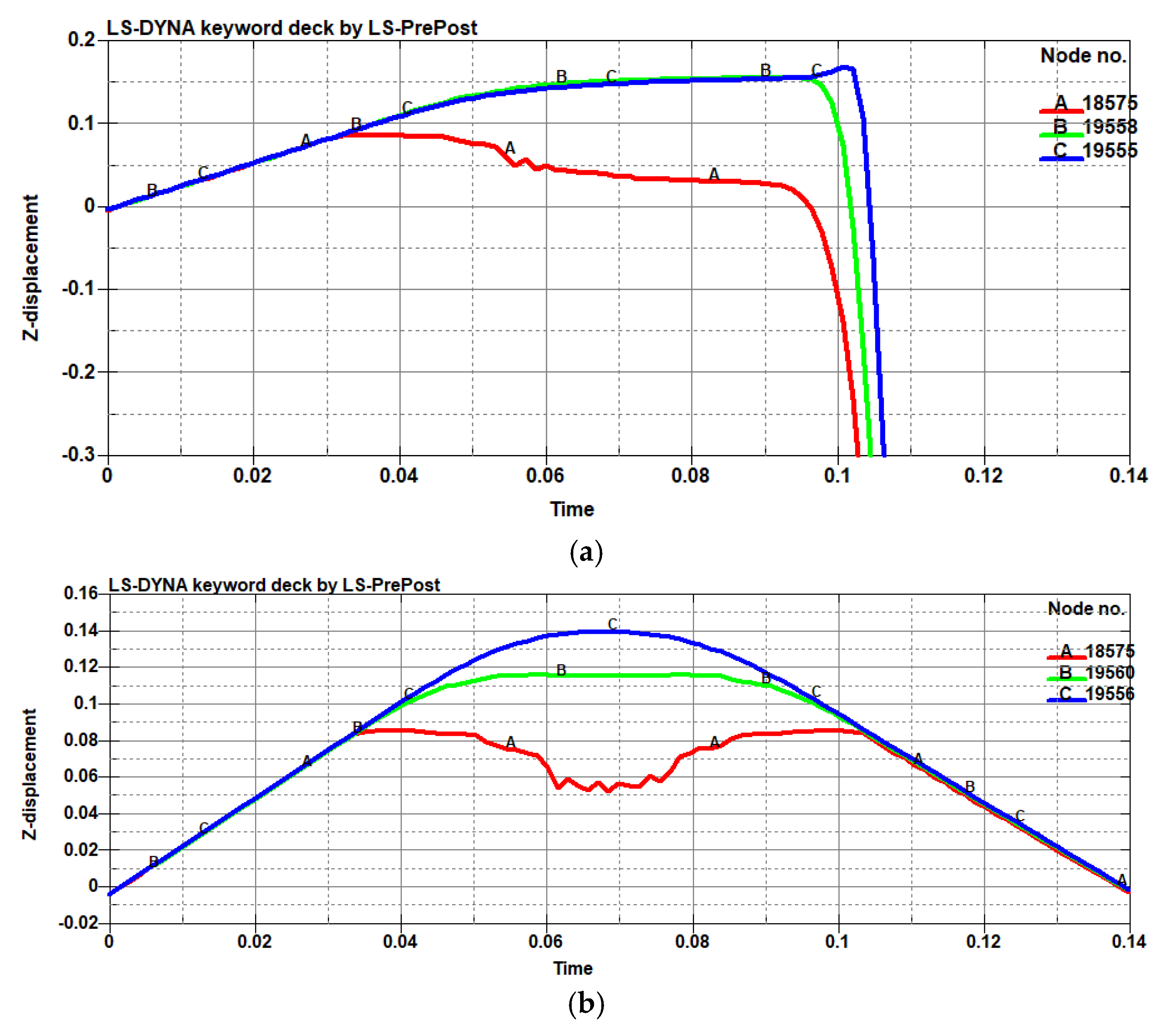
| Case 1 | p (MN) | q (MPa) | Case 2 | p (MN) | q (MPa) | ||
|---|---|---|---|---|---|---|---|
| t = 0.05 m E = 210 GPa ν = 0.3 | = 11.0 = 11.5 | 3.5 | 7.8 | t = 0.10 m E = 210 GPa ν = 0.3 | = 88 = 48 | 78 | 8.0 |
| 5.0 | 5.2 | 53 | 14 | ||||
| 8.9 | 2.0 | 39 | 24 | ||||
| 12 | 1.6 | 31 | 26 | ||||
| 15 | 1.35 | 26 | 32 | ||||
| 21 | 1.05 | 22 | 35 | ||||
| 26 | 0.72 | 18 | 42 |
| Case 3 | p (MN) | q (MPa) | Case 4 | p (MN) | q (MPa) | ||
|---|---|---|---|---|---|---|---|
| t = 0.05 m E = 200 GPa ν = 0.23 | = 18 = 32 | 49.2 | 1.6 | t = 0.05 m E = 500 GPa ν = 0.23 | = 45 = 80 | 75 | 10 |
| 31.5 | 3.3 | 49 | 12 | ||||
| 25.1 | 4.2 | 28 | 23 | ||||
| 16.2 | 5.3 | 23 | 34 | ||||
| 12.3 | 7.6 | 20 | 41 | ||||
| 9.6 | 12 | 13 | 60 | ||||
| 6.3 | 20 | 9.6 | 71 |
| Case | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| 0.190 | 0.219 | 0.226 | 0.198 | |
| −0.919 | −0.789 | −0.811 | −0.981 |
| Case | Vel | Case | Vel | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| R = 2.0 E = 210 ν = 0.15 t = 0.04 | 2 | 0.044 | 8.3 | 5.0 | 1.67 | 0.22 | R = 2.0 E = 210 ν = 0.15 t = 0.06 | 6 | 0.030 | 41.0 | 23.5 | 1.74 | 0.71 |
| 3 | 0.044 | 13.1 | 7.4 | 1.74 | 0.33 | 8 | 0.029 | 55.4 | 33.7 | 1.64 | 0.98 | ||
| 4 | 0.042 | 18.3 | 10.4 | 1.75 | 0.44 | 10 | 0.028 | 73.4 | 41.9 | 1.75 | 1.17 | ||
| 6 | 0.044 | 24.5 | 14.7 | 1.67 | 0.65 | 14 | 0.027 | 105 | 60.8 | 1.73 | 1.64 | ||
| 8 | 0.052 | 26.1 | 16.5 | 1.59 | 0.86 | 16 | 0.028 | 113 | 69.2 | 1.63 | 1.93 |
| Thickness | |||
|---|---|---|---|
| 0.06 m | 7.0 | 4.2 | 1.67 |
| 0.04 m | 4.6 | 2.6 | 1.73 |
| Case | t/v | Case | t/v | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| R = 2.0 E = 210 ν = 0.15 q = 15 | 0.03/1 | 0.063 | 3.07 | 1.91 | 0.12 | R = 2.0 E = 210 ν = 0.15 q = 15 | 0.03/2 | 0.062 | 5.7 | 3.5 | 0.22 |
| 0.04/4 | 0.042 | 18.3 | 10.4 | 0.44 | 0.04/4 | 0.042 | 18 | 10 | 0.42 | ||
| 0.05/4 | 0.034 | 21.2 | 12.8 | 0.44 | 0.05/8 | 0.035 | 44 | 26 | 0.91 | ||
| 0.06/4 | 0.031 | 27.0 | 15.0 | 0.47 | 0.06/8 | 0.029 | 55 | 32 | 0.93 |
| Velocity | ||||||
|---|---|---|---|---|---|---|
| 4 m/s | 449 | −0.33 | 265 | −0.38 | 1.69 | 1.69 |
| 8 m/s | 950 | −2.5 | 556 | −1.5 | 1.67 | 1.72 |
| Case | e | Case | q | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| R = 2.0 t = 0.04 q = 15 v = 3.0 | 0.7 | 0.055 | 6.8 | 4.1 | 0.23 | R = 2.0 t = 0.06 e = 1.0 v = 3.0 | 1.0 | 0.043 | 8.4 | 5.2 | 0.22 |
| 1.0 | 0.046 | 8.2 | 5.0 | 0.23 | 1.5 | 0.046 | 8.2 | 5.0 | 0.23 | ||
| 1.5 | 0.036 | 10.5 | 6.4 | 0.23 | 2.0 | 0.047 | 8.0 | 4.9 | 0.23 | ||
| 2.0 | 0.033 | 12.2 | 7.2 | 0.24 | 2.5 | 0.048 | 7.8 | 4.8 | 0.23 |
| Thickness | Remark | ||||||
|---|---|---|---|---|---|---|---|
| 0.04 m | 4.2 | 4.0 | 2.4 | 2.4 | 1.75 | 1.67 | Elastic |
| 0.06 m | −0.4 | 8.8 | −0.26 | 5.4 | 1.67 | 1.72 | Pressure |
| Case | Case | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| t = 0.04 R = 2.0 E = 210 v = 4.0 | 0.5 | 0.033 | 13.1 | 7.8 | 0.26 | t = 0.06 R = 2.0 E = 210 v = 4.0 | 0.5 | 0.027 | 20.3 | 12.2 | 0.33 |
| 1.0 | 0.042 | 18.3 | 10.4 | 0.44 | 1.0 | 0.031 | 26.7 | 15.2 | 0.47 | ||
| 1.5 | 0.050 | 21.4 | 12.5 | 0.63 | 1.5 | 0.034 | 32.2 | 19.4 | 0.67 | ||
| 2.0 | 0.057 | 24.4 | 14.2 | 0.81 | 2.0 | 0.039 | 36.4 | 21.6 | 0.84 |
| Thickness | ||||||
|---|---|---|---|---|---|---|
| 0.04 m | 7.4 | 10 | 4.3 | 5.9 | 1.72 | 1.69 |
| 0.06 m | 10.8 | 15.5 | 6.5 | 9.0 | 1.67 | 1.72 |
| Case | q | Vcr | Max Force | Case | q | Vcr | Max Force | Case | q | Vcr | Max force |
|---|---|---|---|---|---|---|---|---|---|---|---|
| t = 0.04 R = 2.0 E = 210 | 10 | 16 | 45/3.0 | t = 0.04 R = 1.5 E = 210 | 30 | 9.3 | 30/1.5 | t = 0.04 R = 2.5 E = 210 | 10 | 7.1 | 23/2.0 |
| 15 | 9.8 | 26/1.7 | 45 | 6.9 | 20/1.0 | 15 | 4.2 | 16/1.3 | |||
| 20 | 6.7 | 20/1.3 | 20 | 15 | 40/2.0 | 20 | 3.3 | 11/1.0 | |||
| 25 | 5.1 | 17/1.0 | 25 | 10 | 34/1.7 | 25 | 2.2 | 7.0/0.6 |
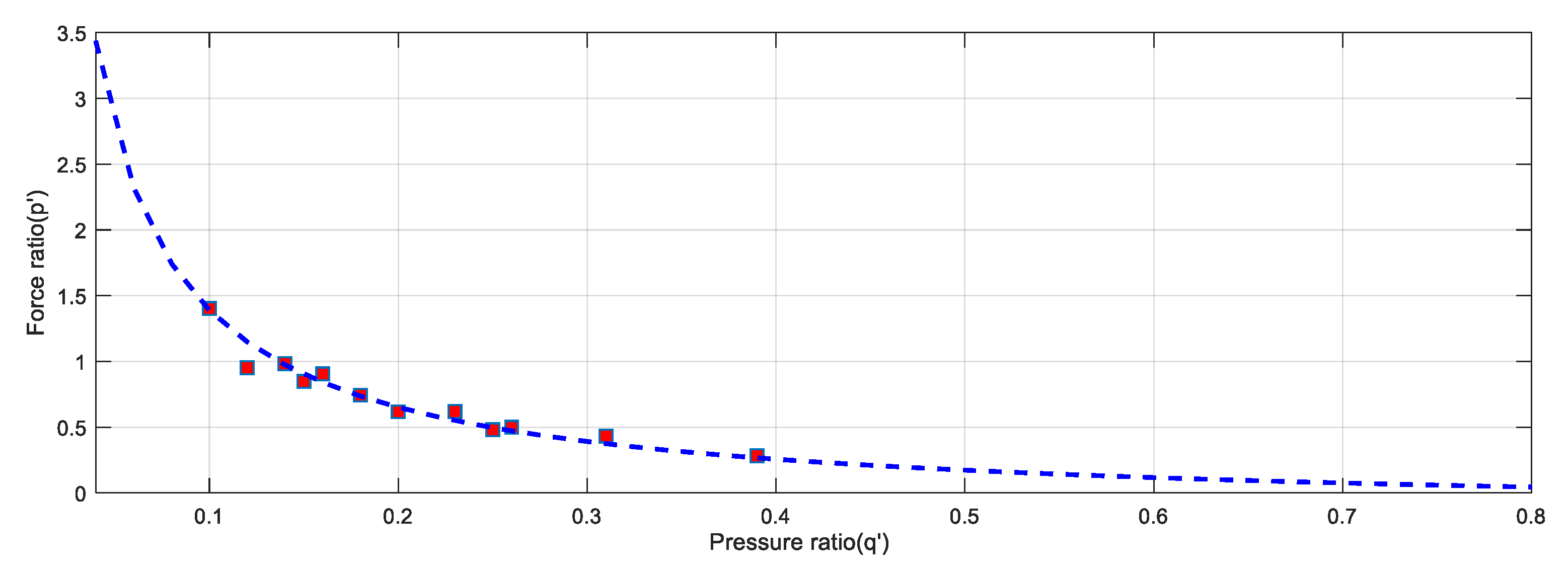
| Case | q’ | p’/pe | Ratio | Case | q’ | p’/pe | Ratio | Case | q’ | p’/pe | Ratio |
|---|---|---|---|---|---|---|---|---|---|---|---|
| t = 0.04 R = 2.0 E = 210 | 0.10 | 3.0/1.40 | 2.12 | t = 0.04 R = 1.5 E = 210 | 0.18 | 1.5/0.73 | 2.12 | t = 0.04 R = 2.5 E = 210 | 0.16 | 1.9/0.84 | 2.26 |
| 0.15 | 1.7/0.90 | 1.97 | 0.26 | 1.0/0.47 | 2.22 | 0.23 | 1.3/0.55 | 2.36 | |||
| 0.20 | 1.3/0.65 | 1.99 | 0.12 | 2.0/1.15 | 1.74 | 0.31 | 0.9/0.37 | 2.43 | |||
| 0.25 | 1.0/0.50 | 2.03 | 0.14 | 1.7/0.97 | 2.12 | 0.39 | 0.6/0.27 | 2.22 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, P.; Kaewunruen, S.; Zhou, D.; Wang, S. Investigation of the Dynamic Buckling of Spherical Shell Structures Due to Subsea Collisions. Appl. Sci. 2018, 8, 1148. https://doi.org/10.3390/app8071148
Liu P, Kaewunruen S, Zhou D, Wang S. Investigation of the Dynamic Buckling of Spherical Shell Structures Due to Subsea Collisions. Applied Sciences. 2018; 8(7):1148. https://doi.org/10.3390/app8071148
Chicago/Turabian StyleLiu, Ping, Sakdirat Kaewunruen, Daochuan Zhou, and Shanshui Wang. 2018. "Investigation of the Dynamic Buckling of Spherical Shell Structures Due to Subsea Collisions" Applied Sciences 8, no. 7: 1148. https://doi.org/10.3390/app8071148
APA StyleLiu, P., Kaewunruen, S., Zhou, D., & Wang, S. (2018). Investigation of the Dynamic Buckling of Spherical Shell Structures Due to Subsea Collisions. Applied Sciences, 8(7), 1148. https://doi.org/10.3390/app8071148






