Output Power Smoothing Control for a Wind Farm Based on the Allocation of Wind Turbines
Abstract
1. Introduction
2. Wind Energy Conversion System Description
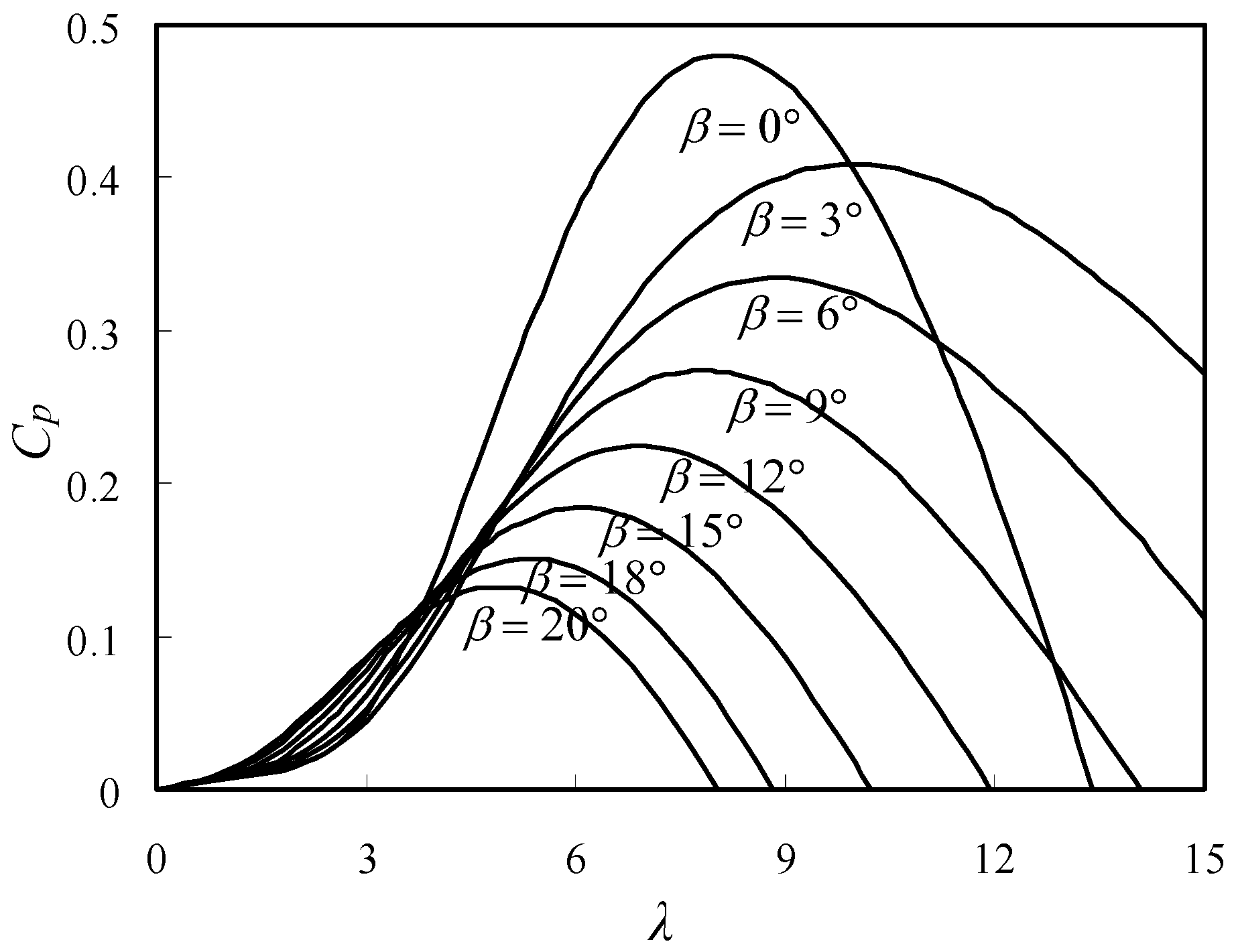
2.1. Wind Turbine Model
2.2. PMSG Model
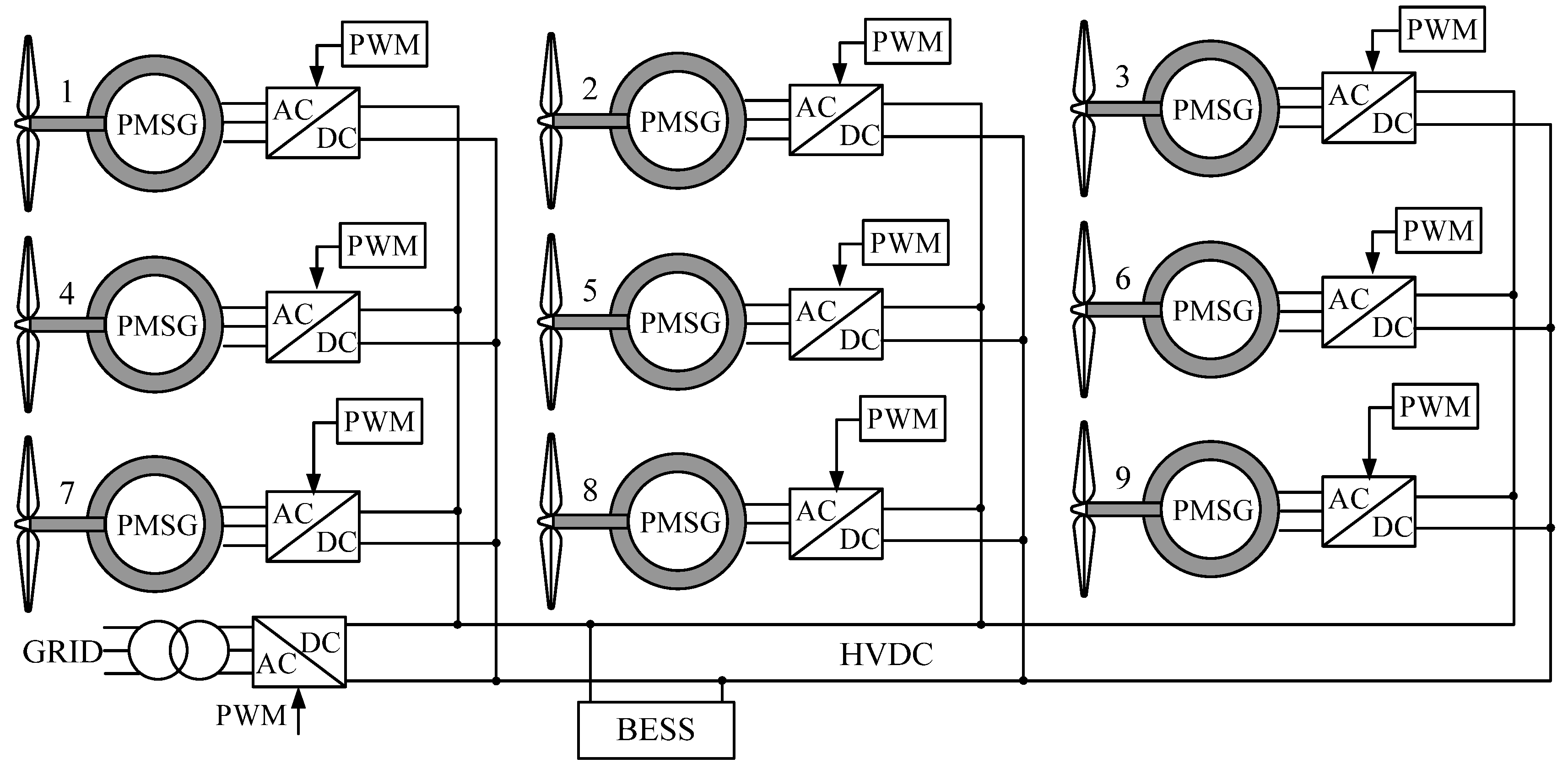
2.3. Configuration of the Wind Farm
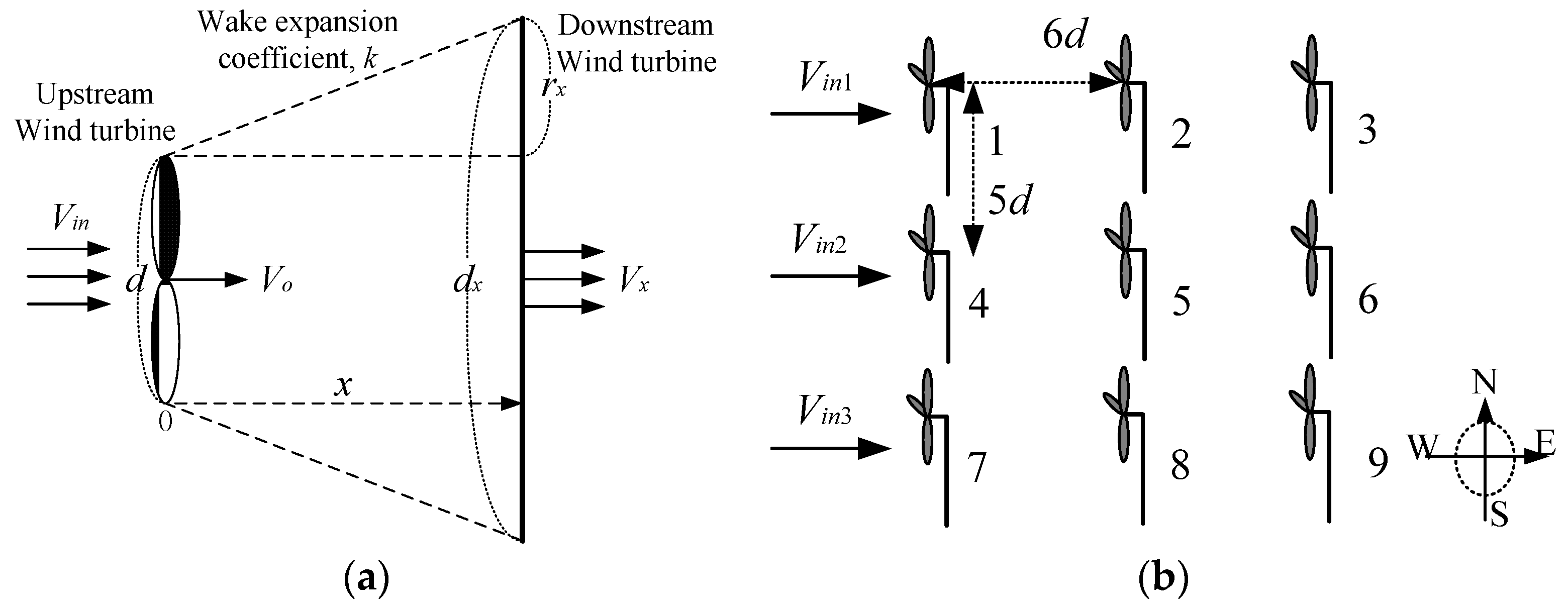
2.4. Wake Effect Model of the Wind Farm
3. Power Smoothing Control Strategy
3.1. Power Allocation of the PWTs, CWTs and the BESS
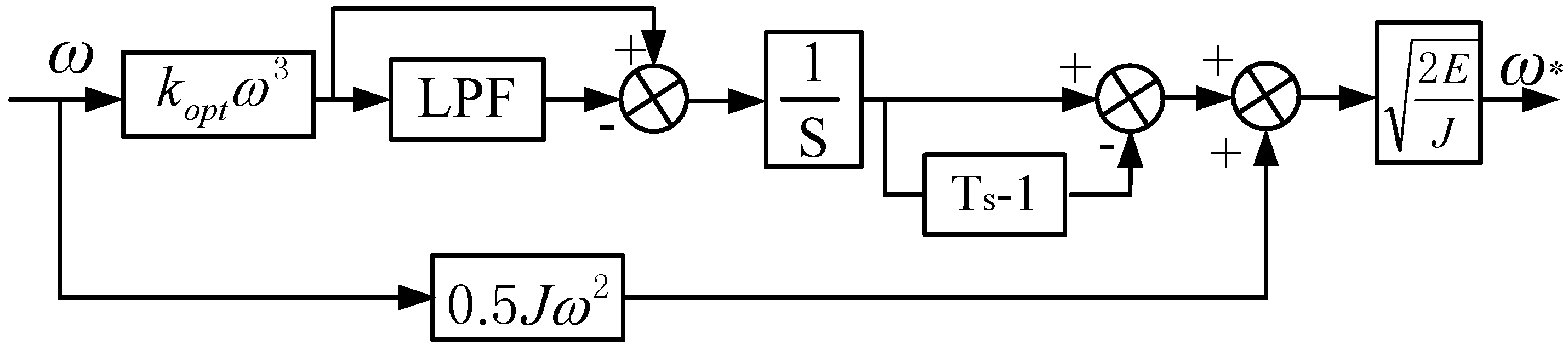
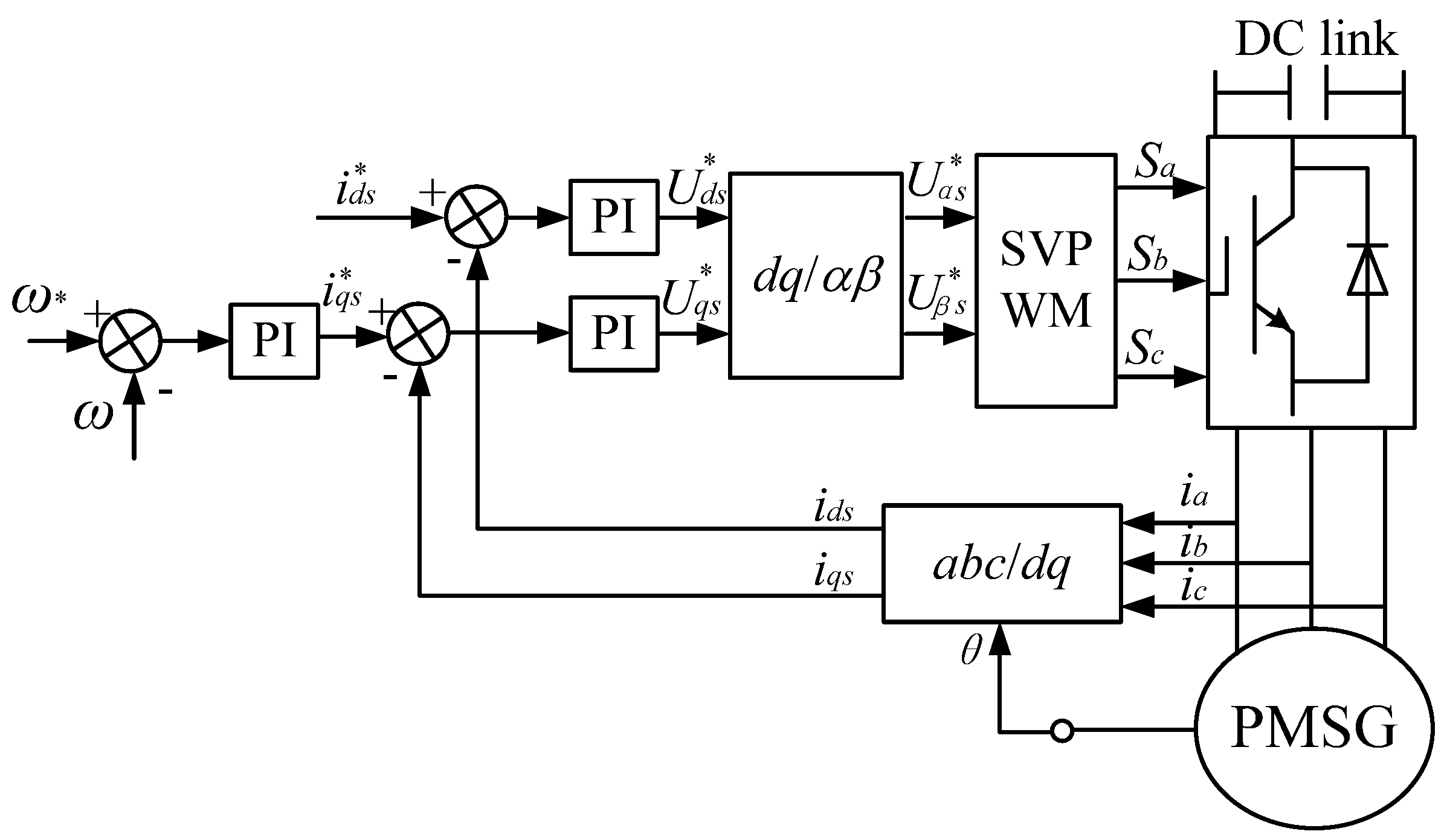
3.2. Control Strategy for the PWTs
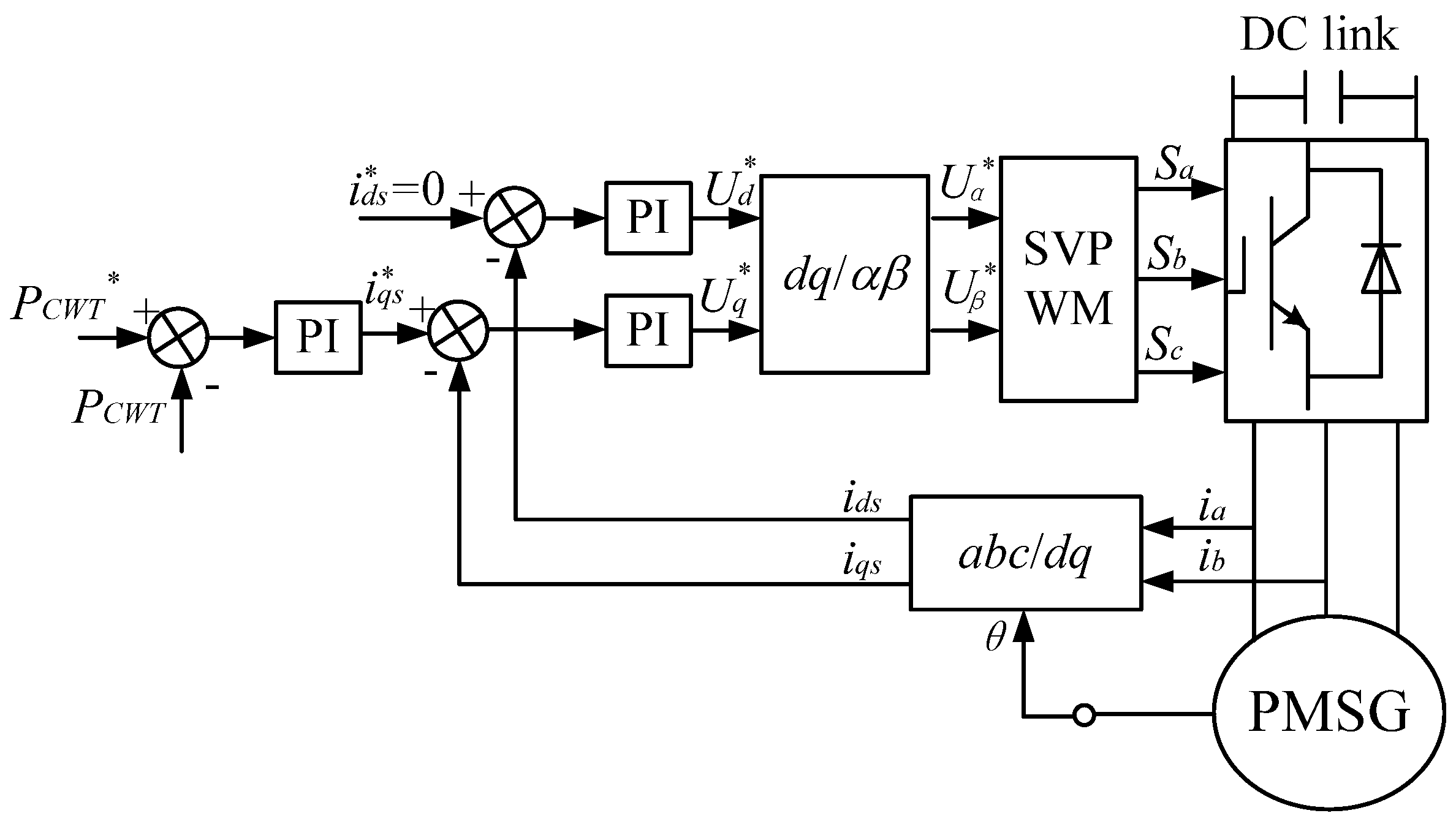
3.3. Control Strategy for the CWTs
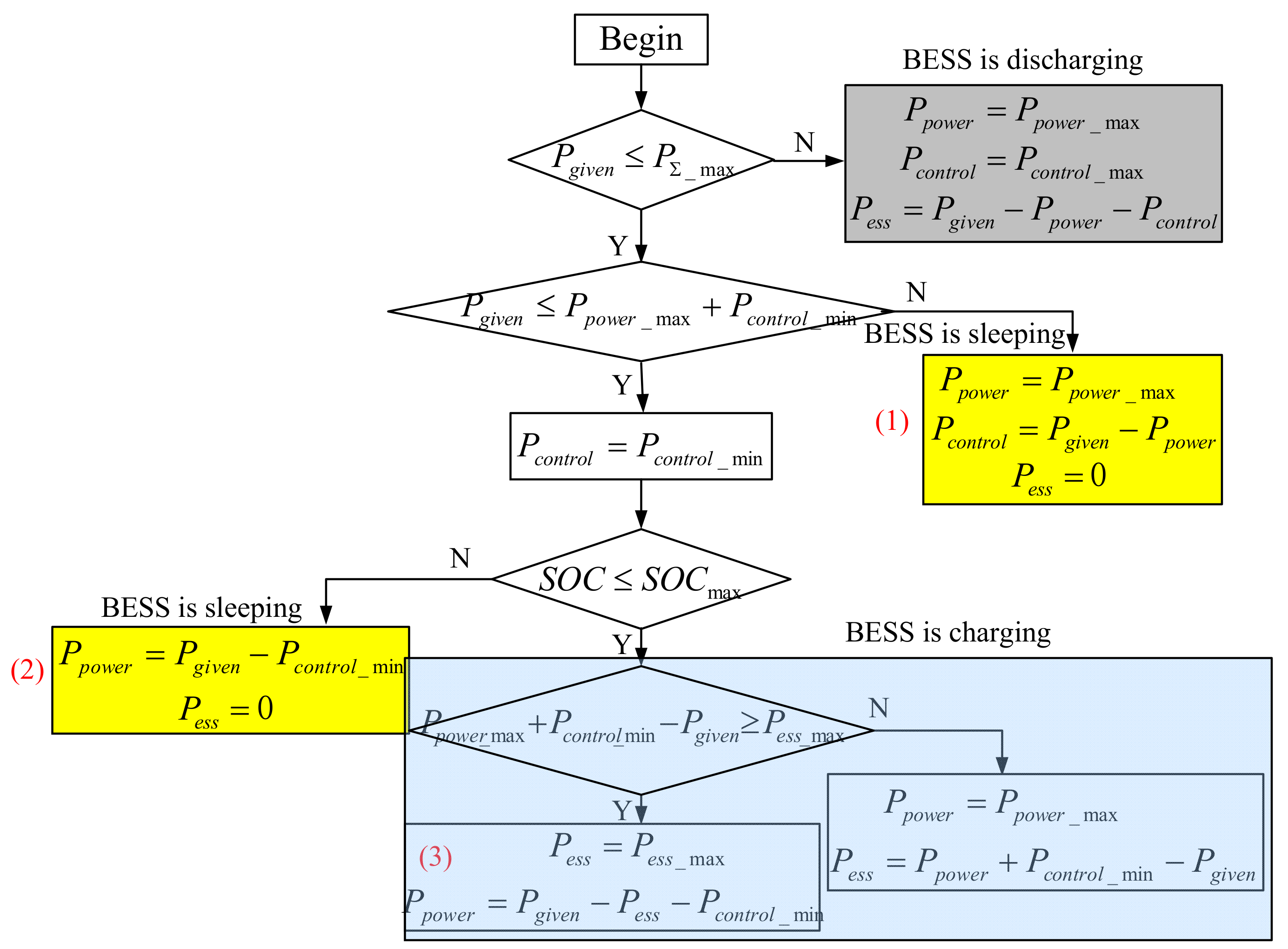
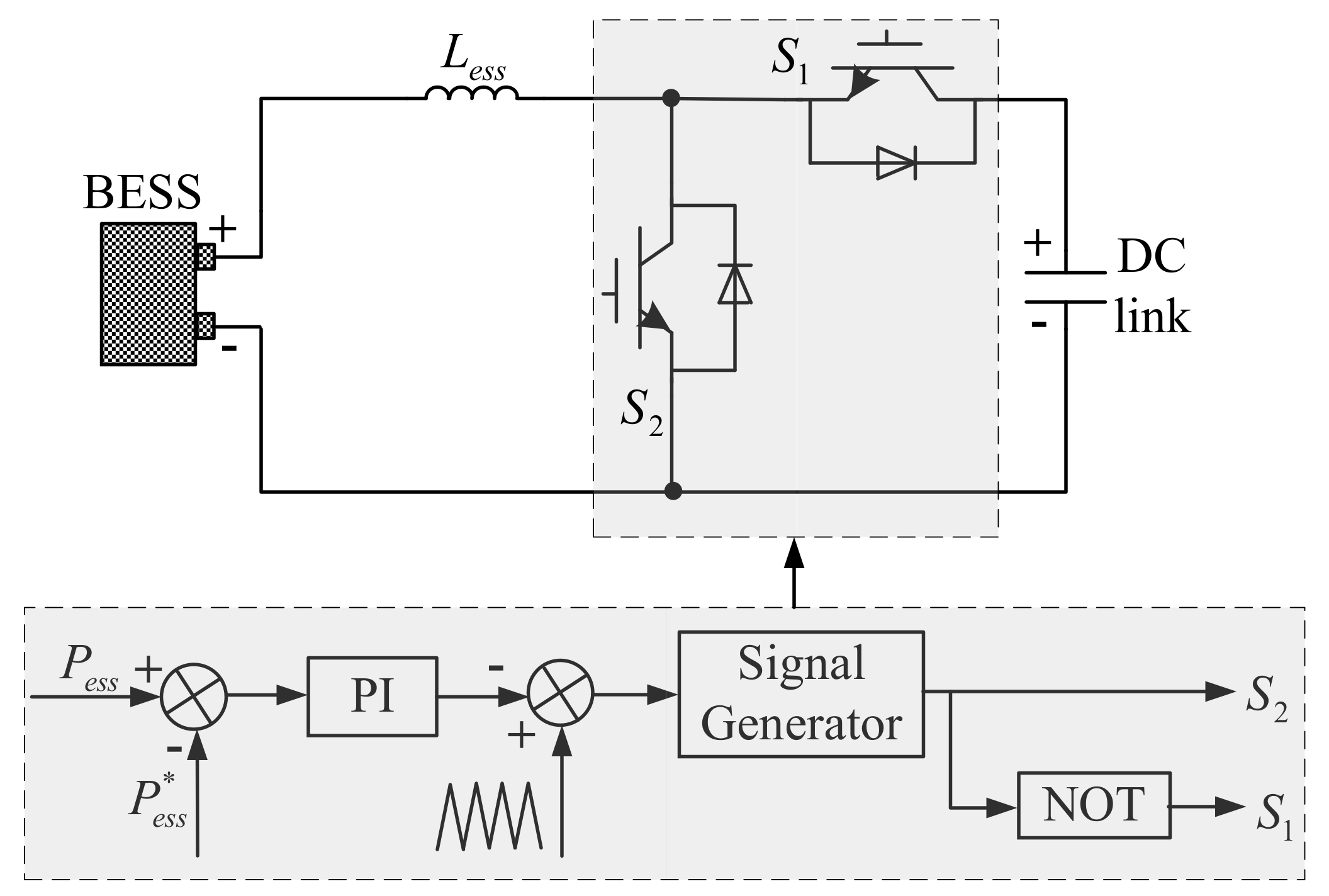
3.4. Control Strategy for the BESS
3.5. Evaluation of the Power Efficiency
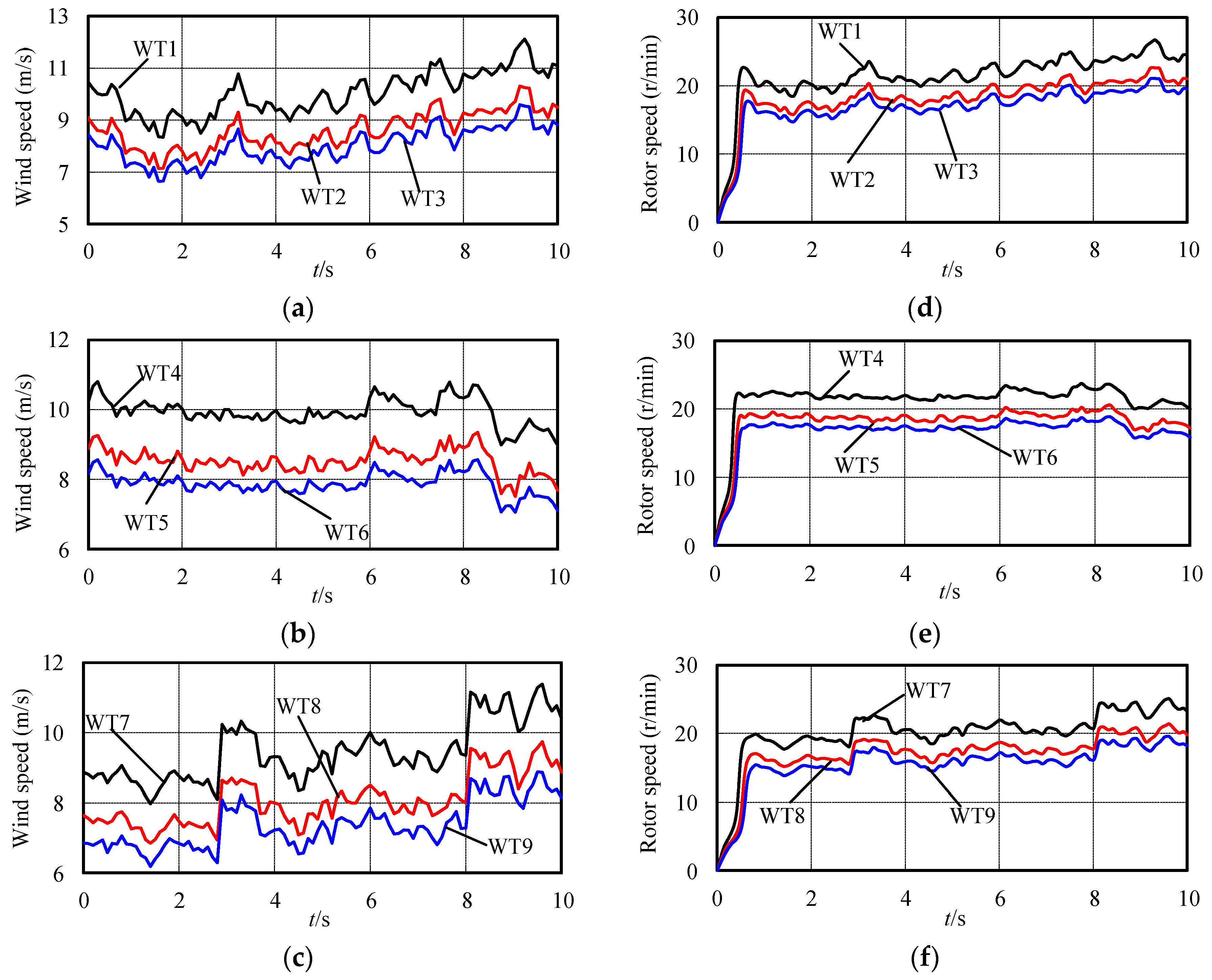
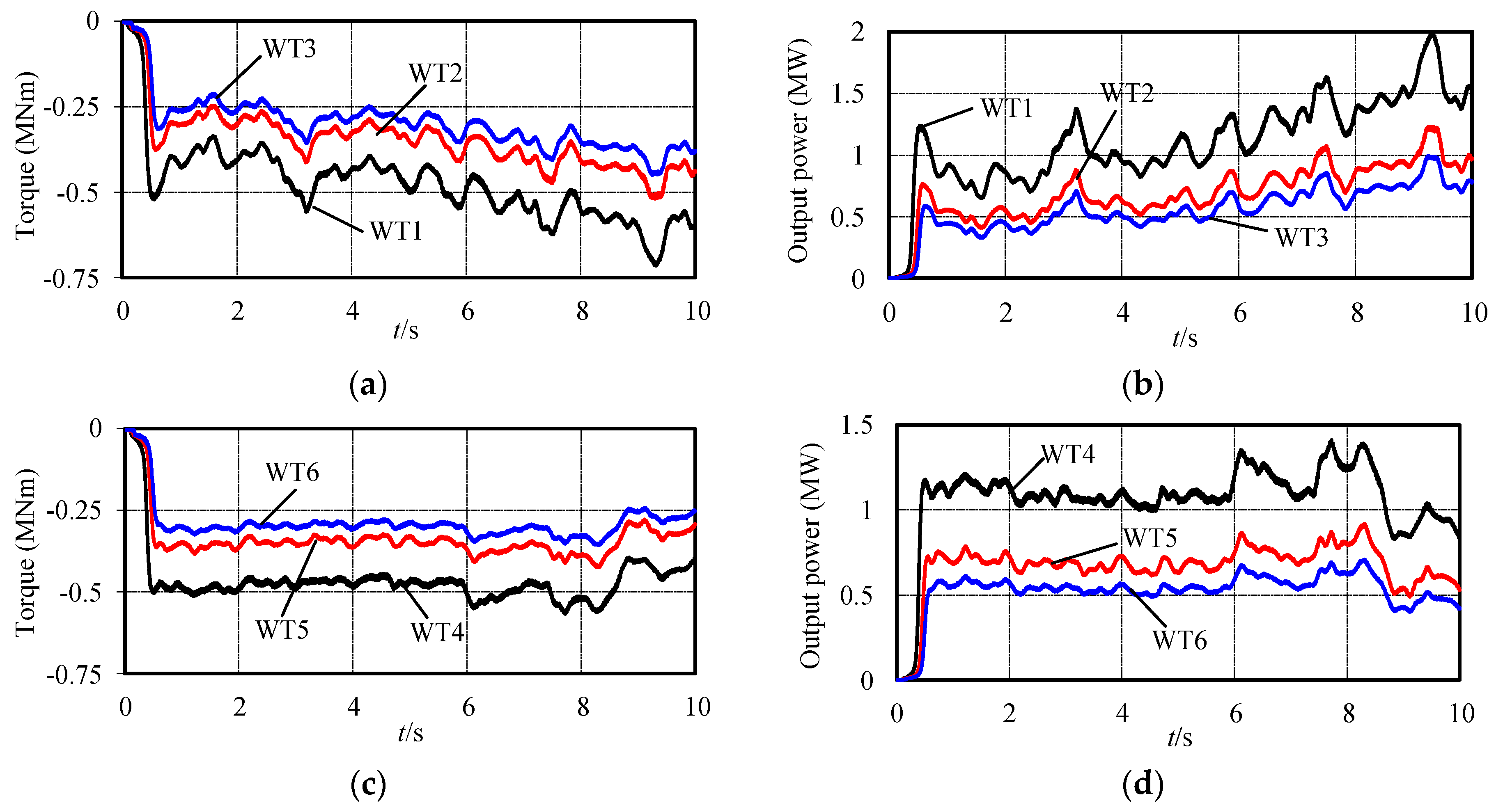
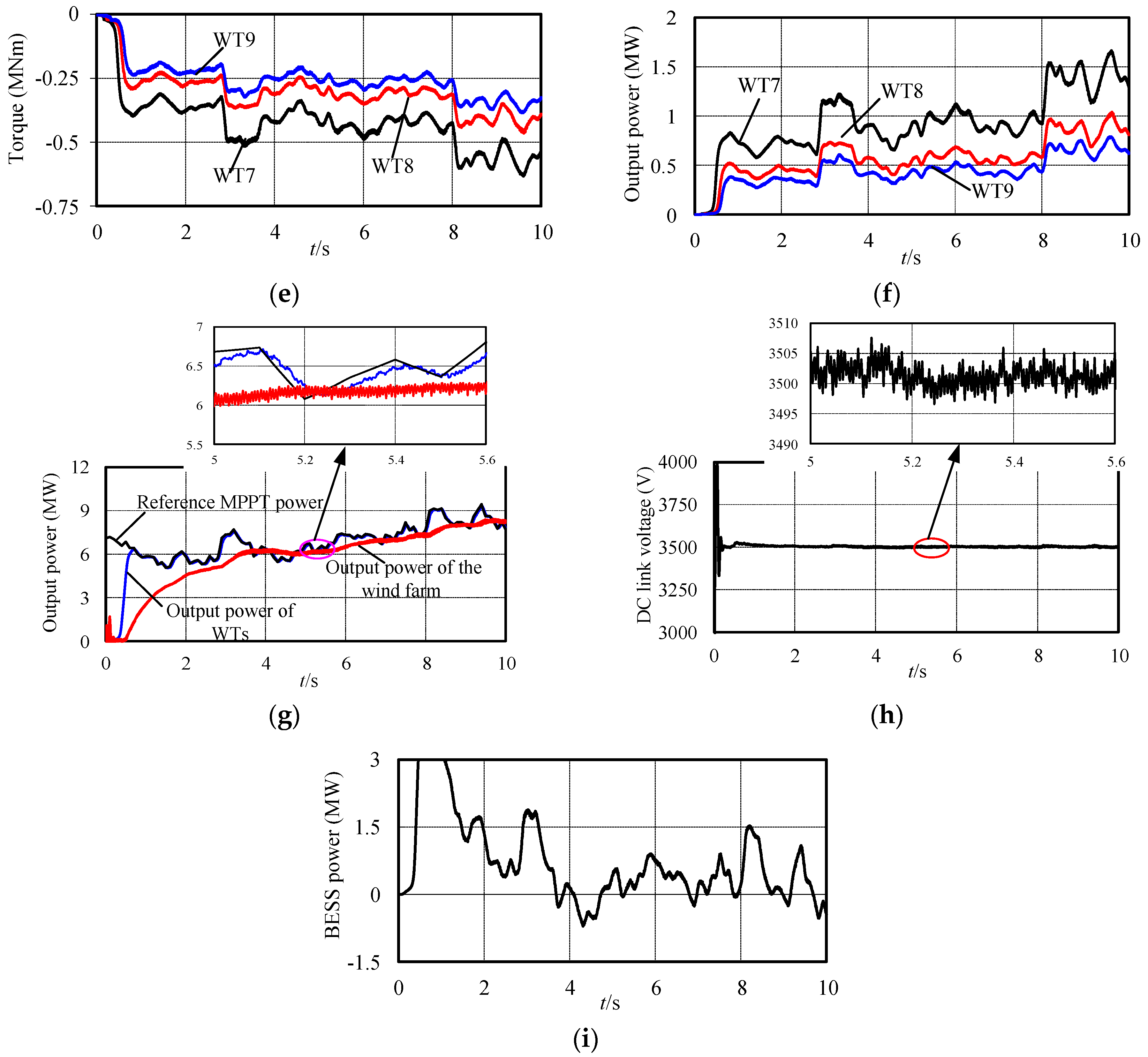
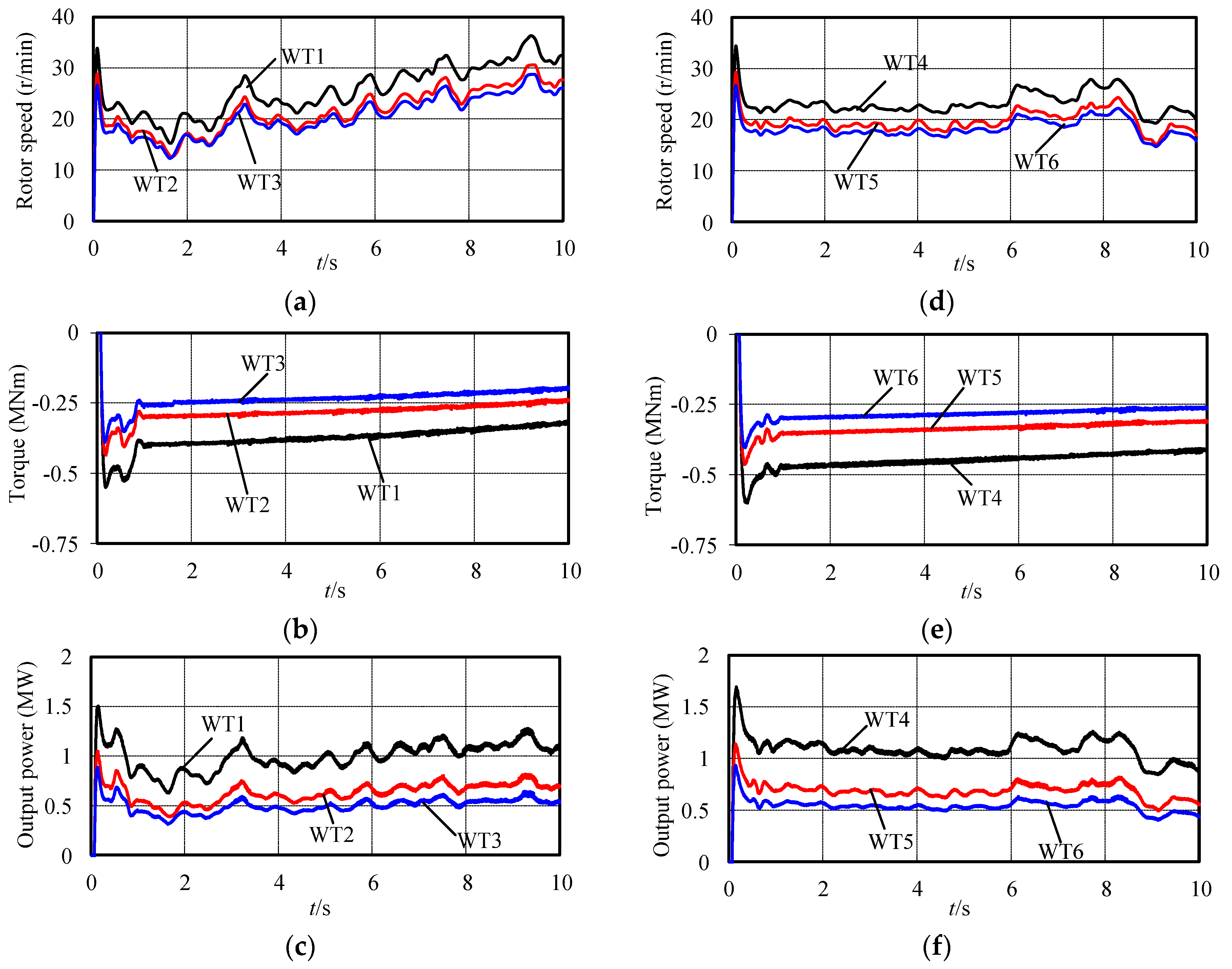
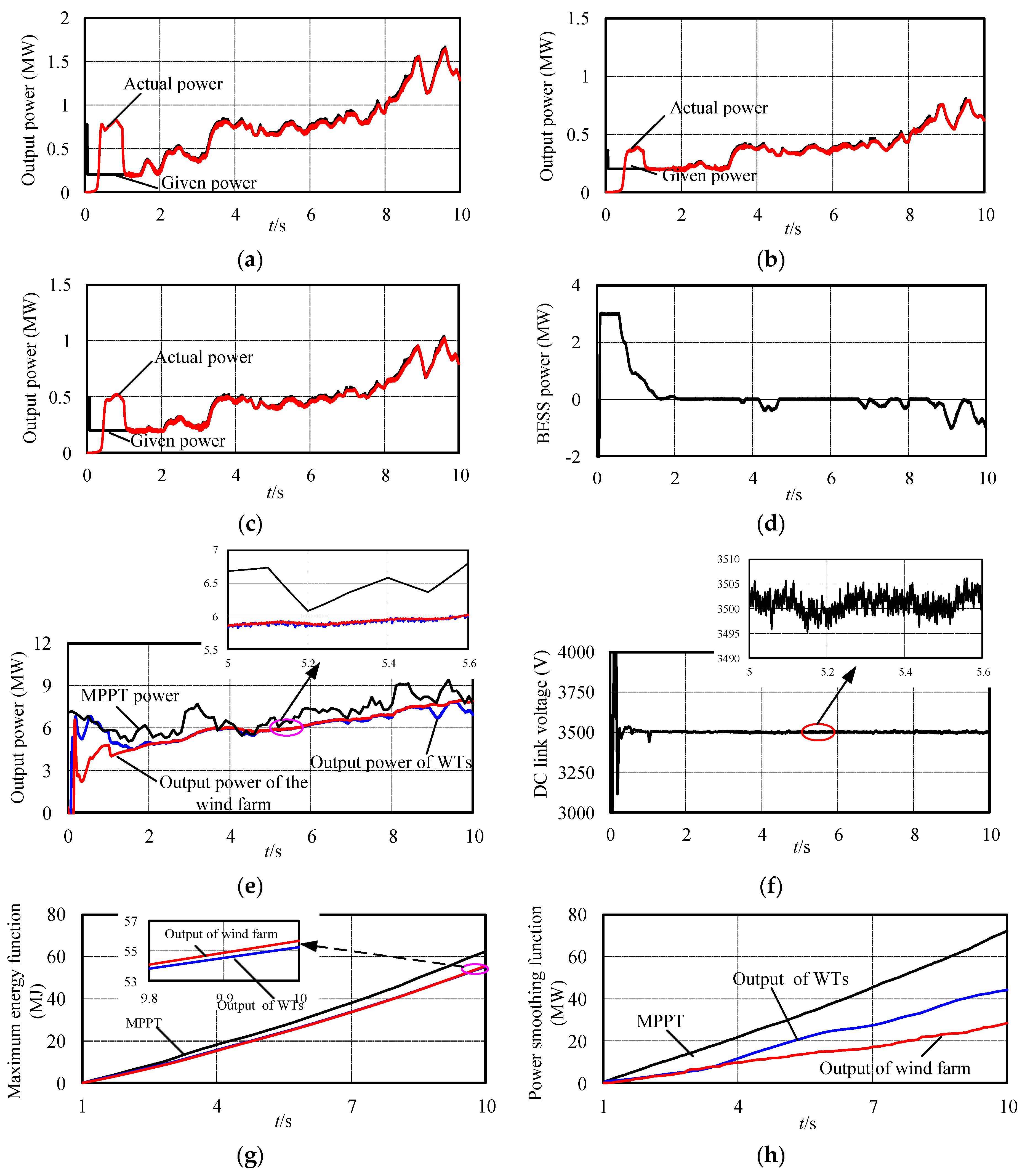
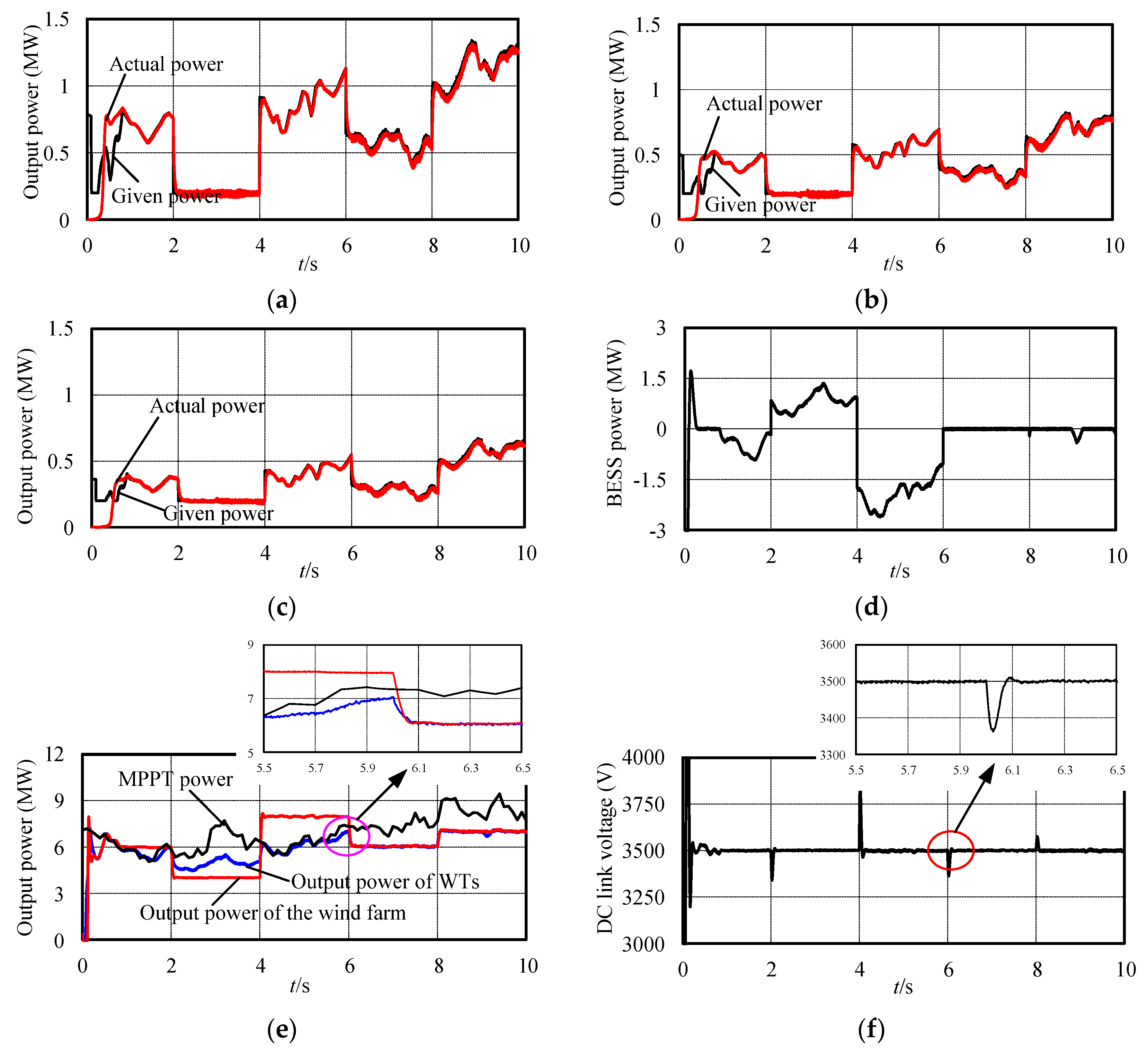
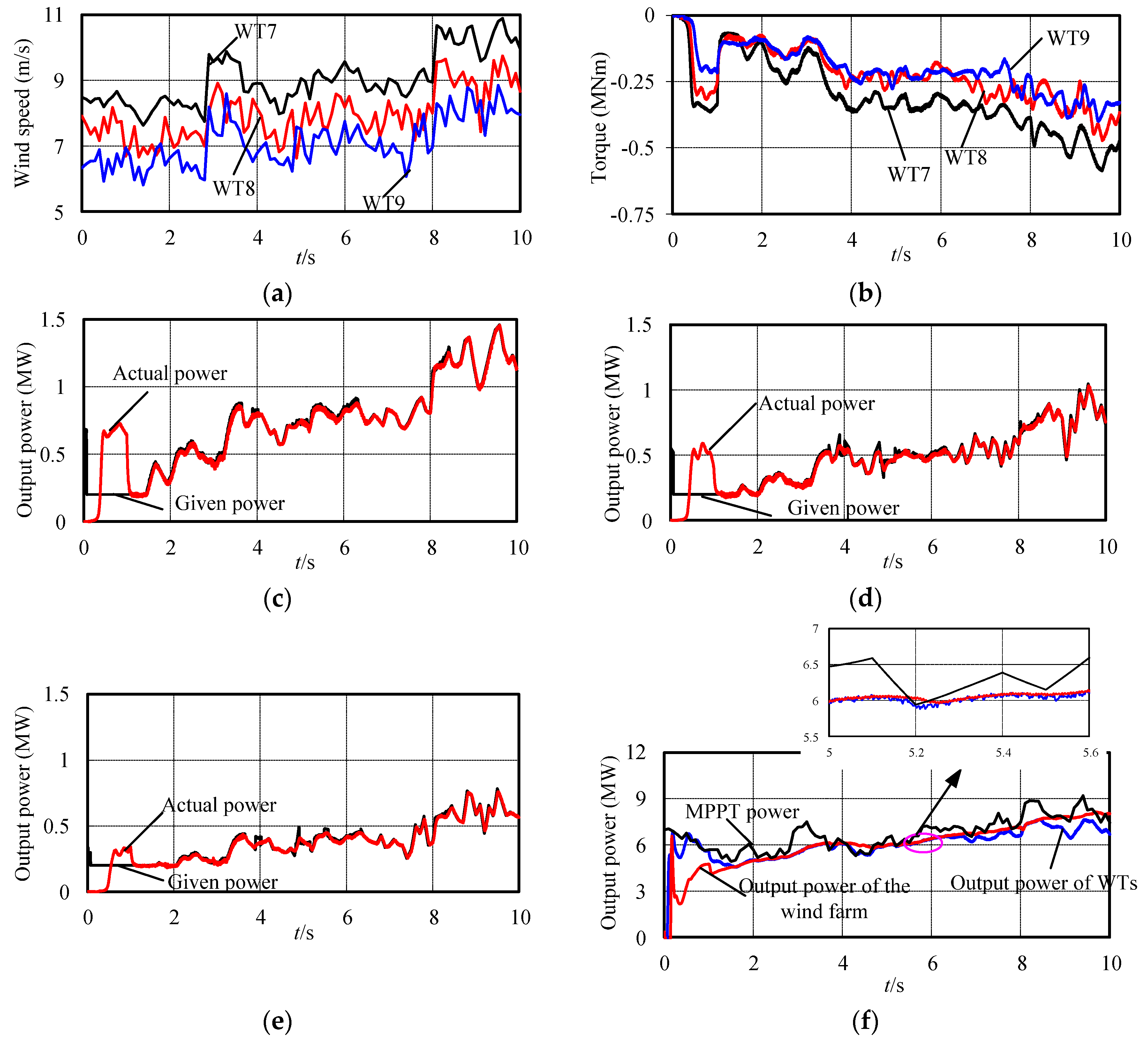
4. Simulation Results
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Cheng, M.; Zhu, Y. The state of the art of wind energy conversion systems and technologies: A review. Energy Convers. Manag. 2014, 88, 332–347. [Google Scholar] [CrossRef]
- Muyeen, S.M.; Takahashi, R.; Murata, T.; Tamura, J. A variable speed wind turbine control strategy to meet wind farm grid code requirements. IEEE Trans. Power Syst. 2010, 25, 331–340. [Google Scholar] [CrossRef]
- Uehara, A.; Pratap, A.; Goya, T.; Senjyu, T.; Yona, A.; Urasaki, N.; Funabashi, T. A coordinated control method to smooth wind power fluctuations of a PMSG-based WECS. IEEE Trans. Energy Convers. 2011, 26, 550–558. [Google Scholar] [CrossRef]
- Aigner, T.; Jaehnert, S.; Doormain, G.L.; Gjengedal, T. The effect of large-scale wind power on system balancing in Northern Europe. IEEE Trans. Sustain. Energy 2012, 3, 751–759. [Google Scholar] [CrossRef]
- Howlader, A.M.; Senjyu, T.; Saber, A.Y. An integrated power smoothing control for a grid-interactive wind farm considering wake effects. IEEE Syst. J. 2015, 9, 954–965. [Google Scholar] [CrossRef]
- Howlader, A.M.; Urasaki, N.; Yona, A.; Senjyu, T.; Saber, A.Y. A review of output power smoothing methods for wind energy conversion systems. Renew. Sustain. Energy Rev. 2013, 26, 135–146. [Google Scholar] [CrossRef]
- Simon, D.R.; Johan, D.; Johan, M. Power smoothing in large wind farms using optimal control of rotating kinetic energy reserves. Wind Energy 2015, 18, 1777–1791. [Google Scholar]
- Johan, M.; Simon, D.R.; Johan, D. Smoothing turbulence-induced power fluctuations in large wind farms by optimal control of the rotating kinetic energy of the turbines. J. Phys. Conf. Ser. 2014, 524, 012187. [Google Scholar]
- Rawn, B.G.; Lehn, P.W.; Maggiore, M. Disturbance margin for quantifying limits on power smoothing by wind turbines. IEEE Trans. Control Syst. Technol. 2013, 21, 1795–1807. [Google Scholar] [CrossRef]
- Varzaneh, S.G.; Gharehpetian, G.B.; Abedi, M. Output power smoothing of variable speed wind farms using rotor-inertia. Electr. Power Syst. Res. 2014, 116, 208–217. [Google Scholar] [CrossRef]
- Rijcke, S.D.; Tielens, P.; Rawn, B.; Hertem, D.V.; Driesen, J. Trading energy yield for frequency regulation: Optimal control of kinetic energy in wind farms. IEEE Trans. Power Syst. 2015, 30, 2469–2478. [Google Scholar] [CrossRef]
- Zou, J.; Peng, C.; Shi, J.; Xin, X.; Zhang, Z. State-of-charge optimizing control approach of battery energy storage system for wind farm. IET Renew. Power Gener. 2015, 9, 647–652. [Google Scholar] [CrossRef]
- Zhang, F.; Xu, Z.; Meng, K. Optimal sizing of substation-scale energy storage station considering seasonal variations in wind energy. IET Gener. Transm. Distrib. 2016, 10, 3241–3250. [Google Scholar] [CrossRef]
- Jayasinghe, S.D.G.; Vilathgamuwa, D.M. Flying supercapacitors as power smoothing elements in wind generation. IEEE Trans. Ind. Electron. 2013, 60, 2909–2918. [Google Scholar] [CrossRef]
- Muyeen, S.M.; Hasanien, H.M.; Al-Durra, A. Transient stability enhancement of wind farms connected to a multi-machine power system by using an adaptive ANN-controlled SMES. Energy Convers. Manag. 2014, 78, 412–420. [Google Scholar] [CrossRef]
- Hasanien, H.M. A set-membership affine projection algorithm-based adaptive-controlled SMES units for wind farms output power smoothing. IEEE Trans. Sustain. Energy 2014, 5, 1226–1233. [Google Scholar] [CrossRef]
- Diaz-Gonzalez, F.; Bianchi, F.D.; Sunper, A.; Gomis-Bellmunt, O. Control of a flywheel energy storage system for power smoothing in wind power plants. IEEE Trans. Energy Convers. 2014, 29, 204–214. [Google Scholar] [CrossRef]
- Islam, F.; Al-Durra, A.; Muyeen, S.M. Smoothing of wind farm output by prediction and supervisory-control-unit-based FESS. IEEE Trans. Sustain. Energy 2013, 4, 925–933. [Google Scholar] [CrossRef]
- Jiang, Q.; Hong, H. Wavelet-based capacity configuration and coordinated control of hybrid energy storage system for smoothing out wind power fluctuations. IEEE Trans. Power Syst. 2013, 28, 1363–1372. [Google Scholar] [CrossRef]
- Pucci, M.; Cirrincione, M. Neural MPPT control of wind generators with induction machines without speed sensors. IEEE Trans. Ind. Electron. 2011, 58, 37–47. [Google Scholar] [CrossRef]
- Rosyadi, M.; Muyeen, S.M.; Takahashi, R.; Tamura, J. A Design Fuzzy Logic Controller for a Permanent Magnet Wind Generator to Enhance the Dynamic Stability of Wind Farms. Appl. Sci. 2012, 2, 780–800. [Google Scholar] [CrossRef]
- Muyeen, S.M.; Hasanien, H.M. Operation and control of HVDC stations using continuous mixed p-norm-based adaptive fuzzy technique. IET Gener. Transm. Distrib. 2017, 11, 2275–2282. [Google Scholar] [CrossRef]
- Kim, H.; Singh, C.; Sprintson, A. Simulation and estimation of reliability in a wind farm considering the wake effect. IEEE Trans. Sustain. Energy. 2012, 3, 274–282. [Google Scholar] [CrossRef]
- Gil, M.P.; Gomis-Bellmunt, O.; Sumper, A.; Bergas-Jane, J. Power generation efficiency analysis of offshore wind farms connected to a SLPC (single large power converter) operated with variable frequencies considering wake effects. Energy 2012, 37, 455–468. [Google Scholar]
- Tian, J.; Zhou, D.; Su, C.; Soltani, M.; Chen, Z.; Blaabjerg, F. Wind turbine power curve design for optimal power generation in wind farms considering wake effect. Energies 2017, 10, 395. [Google Scholar] [CrossRef]
- Tian, J.; Zhou, D.; Su, C.; Blaabjerg, F.; Chen, Z. Optimal Control to Increase Energy Production of Wind Farm Considering Wake Effect and Lifetime Estimation. Appl. Sci. 2017, 7, 65. [Google Scholar] [CrossRef]
- Lee, J.; Muljadi, E.; Sorensen, P.; Kang, Y.C. Releasable kinetic energy-based inertial control of a DFIG wind power plant. IEEE Trans. Sustain. Energy 2016, 7, 279–288. [Google Scholar] [CrossRef]
- Hang, J.; Zhang, J.; Cheng, M.; Ding, S. Detection and discrimination of open phase fault in permanent magnet synchronous motor drive system. IEEE Trans. Power Electron. 2016, 31, 4697–4709. [Google Scholar] [CrossRef]
- Gupta, A.K.; Khambadkone, A.M. A general space vector PWM algorithm for multilevel inverters, including operation in overmodulation range. IEEE Trans. Power Electron. 2007, 22, 517–526. [Google Scholar] [CrossRef]
- Geng, H.; Yang, G. Output power control for variable-speed variable-pitch wind generation systems. IEEE Trans. Energy Convers. 2010, 25, 494–503. [Google Scholar] [CrossRef]
- Zhu, Y.; Zang, H.; Fu, Q. Grid-connected Control Strategies for a Dual Power Flow Wind Energy Conversion System. Electr. Power Compon. Syst. 2017, 45, 1–14. [Google Scholar] [CrossRef]
- Wang, Q.; Cheng, M.; Jiang, Y.; Zuo, W.; Buja, G. A simple active and reactive power control for applications of single-phase electric springs. IEEE Trans. Ind. Electron. 2018, 65, 6291–6300. [Google Scholar] [CrossRef]
| Wind Turbine | PMSG | ||
|---|---|---|---|
| Blade radius (m) | 35 | Stator resistant (Ω) | 0.01 |
| Air density (kg/m3) | 1.225 | Inductance (mH) | 0.835 |
| Optimum TSR | 8.1 | Rotor inertia (kg·m2) | 8500 |
| Optimum power coefficient | 0.48 | PM linkage (Wb) | 8.76 |
| Rated wind speed (m/s) | 12 | Pole pairs | 32 |
| Rated power (MW) | 2 | Rated power (MW) | 2 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Y.; Zang, H.; Cheng, L.; Gao, S. Output Power Smoothing Control for a Wind Farm Based on the Allocation of Wind Turbines. Appl. Sci. 2018, 8, 980. https://doi.org/10.3390/app8060980
Zhu Y, Zang H, Cheng L, Gao S. Output Power Smoothing Control for a Wind Farm Based on the Allocation of Wind Turbines. Applied Sciences. 2018; 8(6):980. https://doi.org/10.3390/app8060980
Chicago/Turabian StyleZhu, Ying, Haixiang Zang, Lexiang Cheng, and Shengyu Gao. 2018. "Output Power Smoothing Control for a Wind Farm Based on the Allocation of Wind Turbines" Applied Sciences 8, no. 6: 980. https://doi.org/10.3390/app8060980
APA StyleZhu, Y., Zang, H., Cheng, L., & Gao, S. (2018). Output Power Smoothing Control for a Wind Farm Based on the Allocation of Wind Turbines. Applied Sciences, 8(6), 980. https://doi.org/10.3390/app8060980







