Acoustic Metamaterials in Aeronautics
Abstract
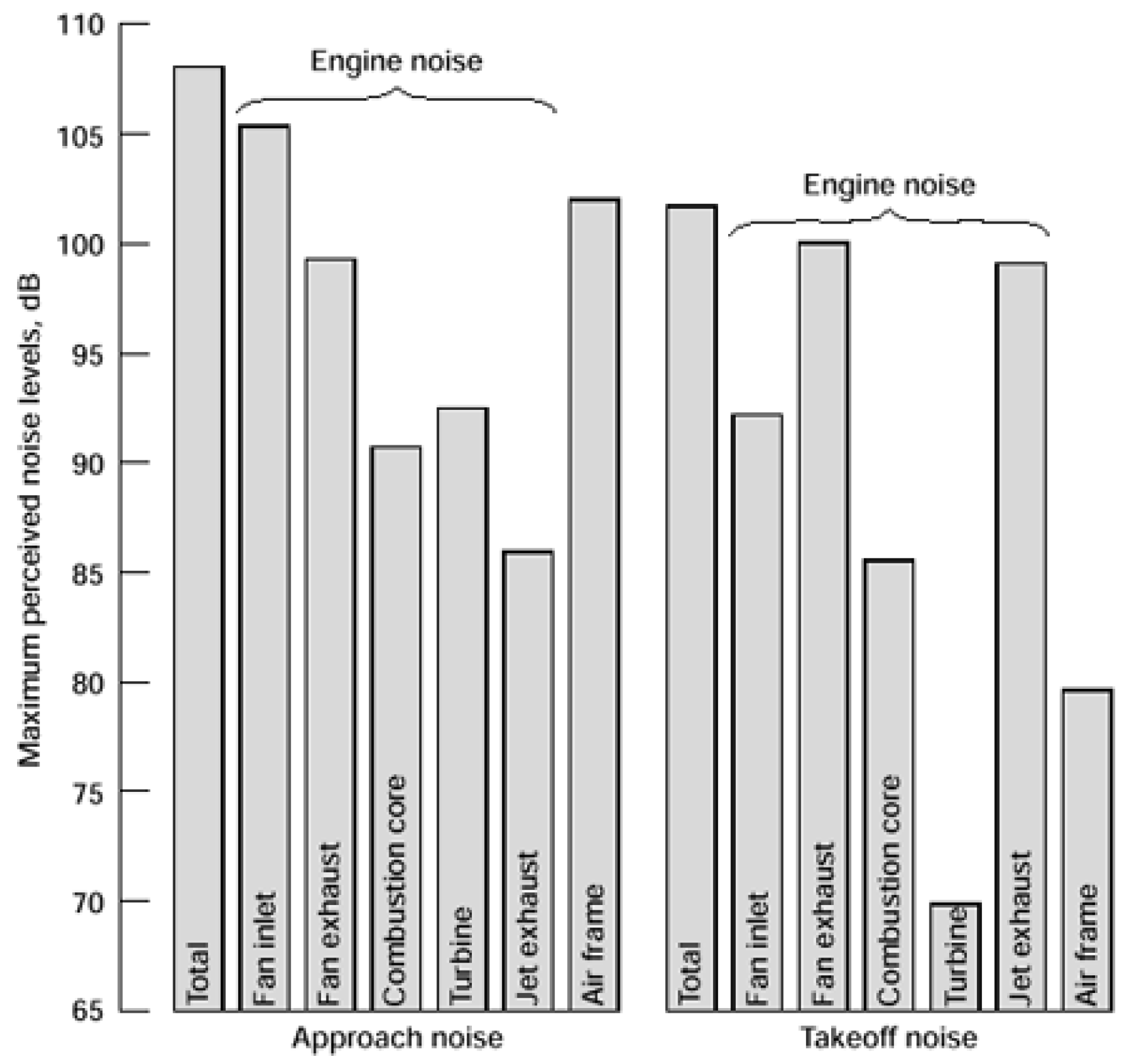
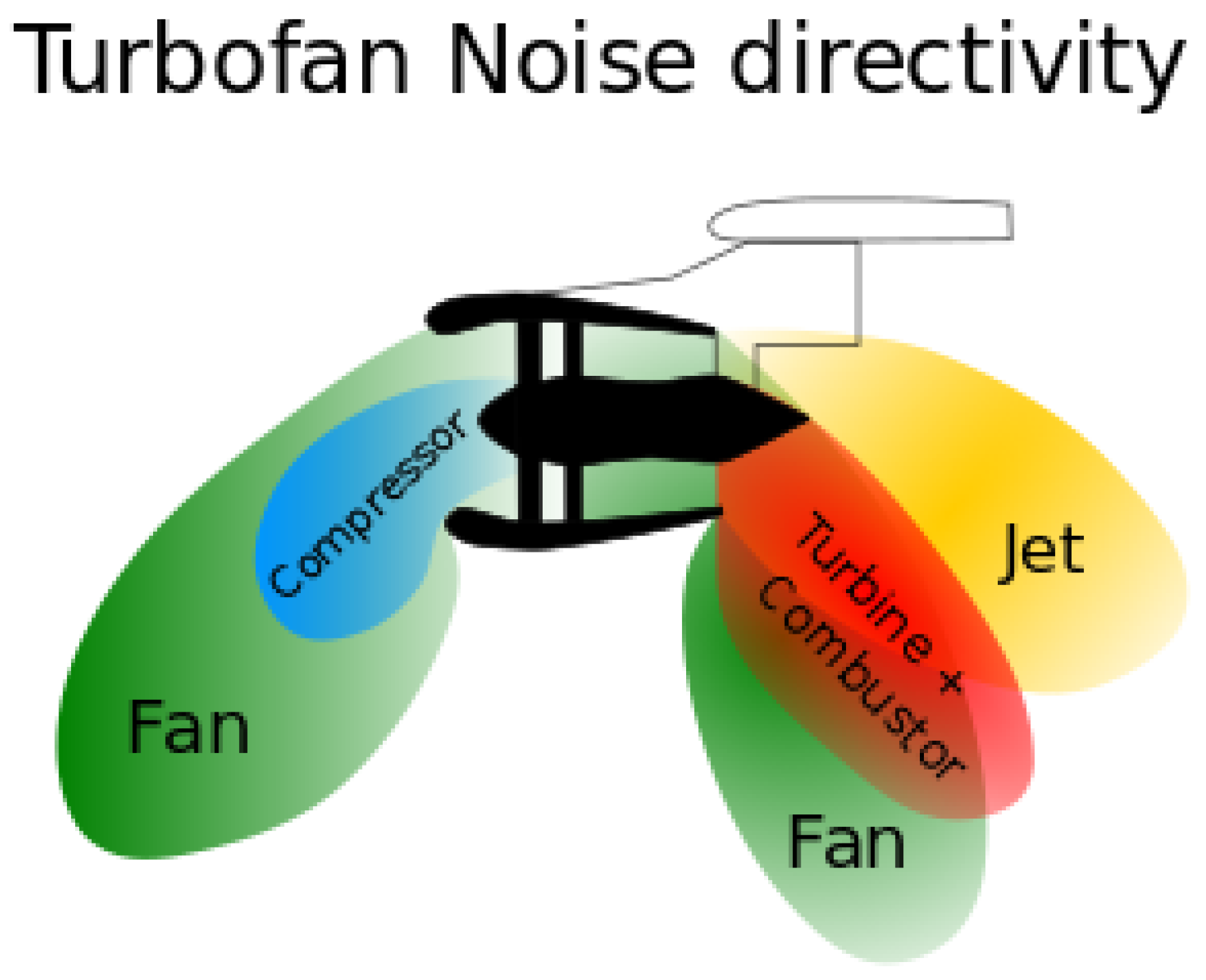
1. Introduction
2. Potential Applications of Aeroacoustic Metamaterials
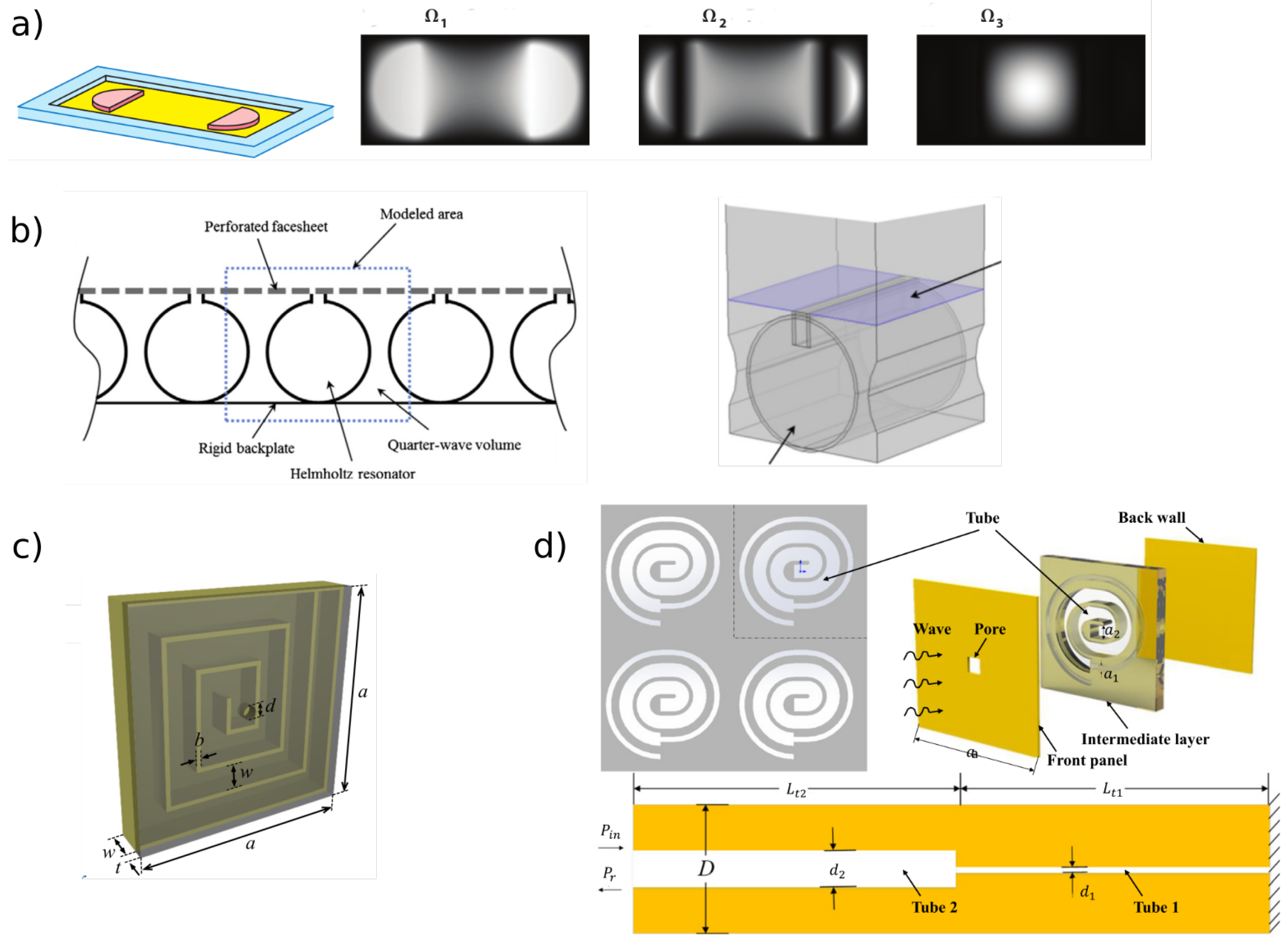
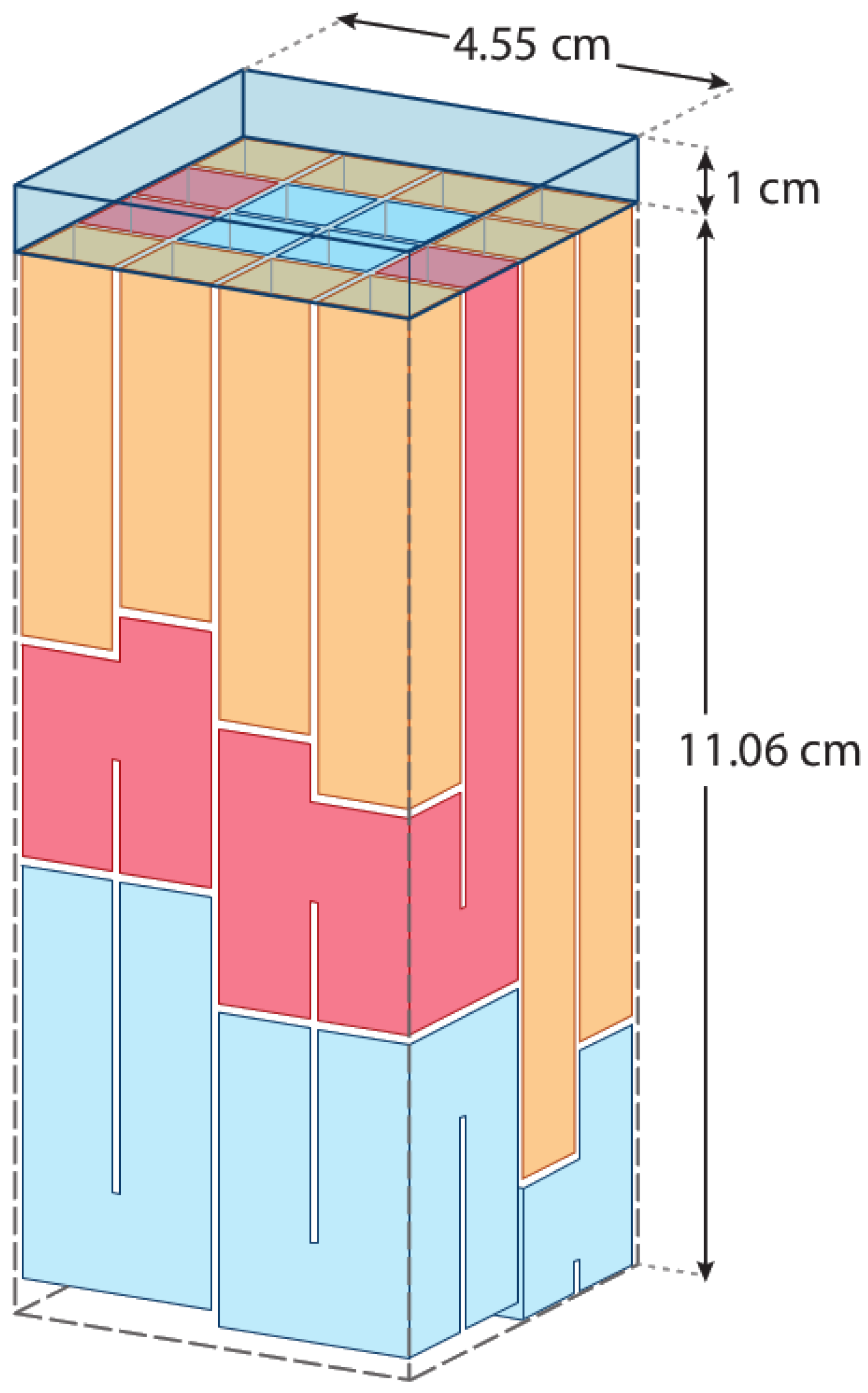
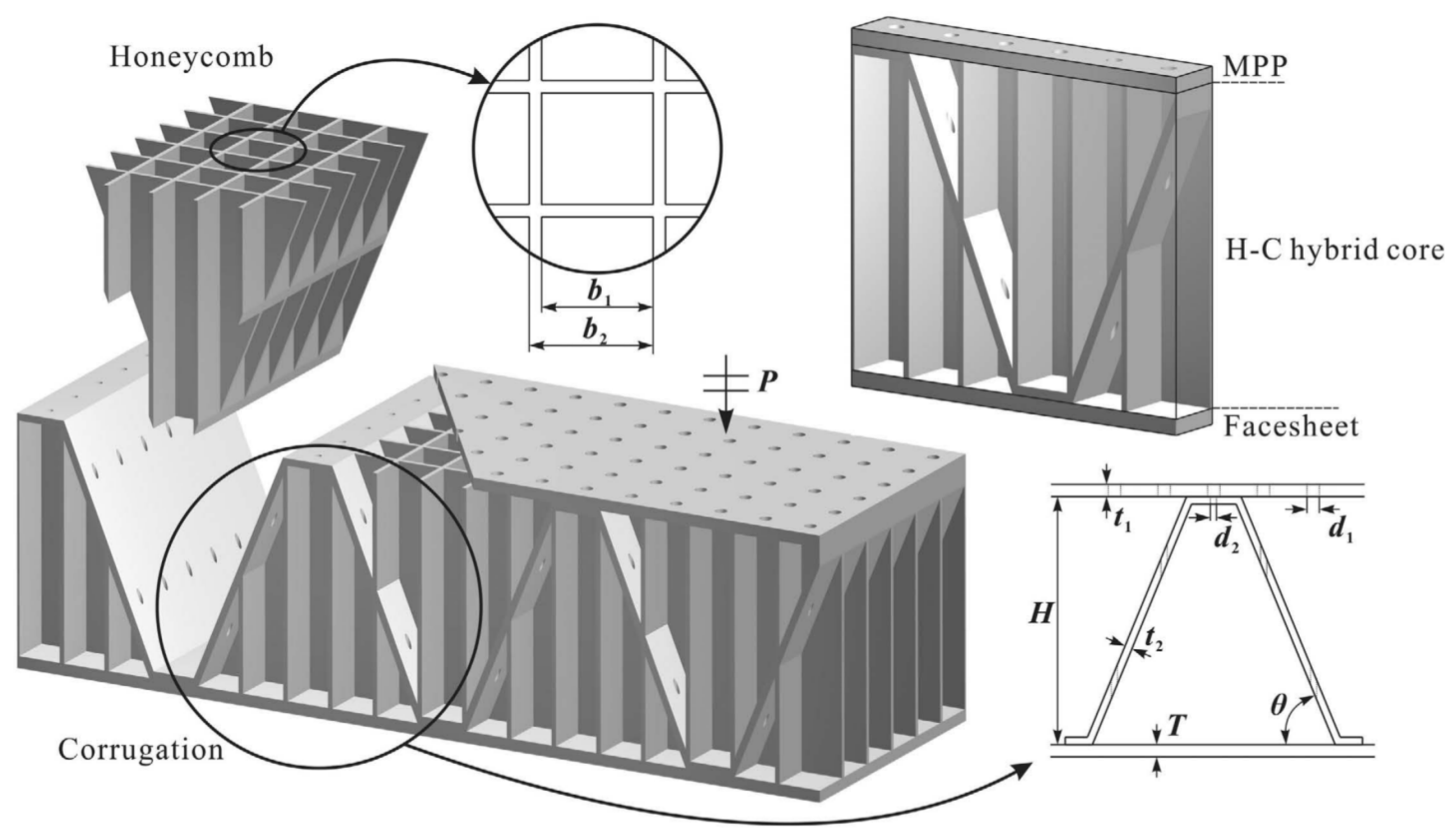
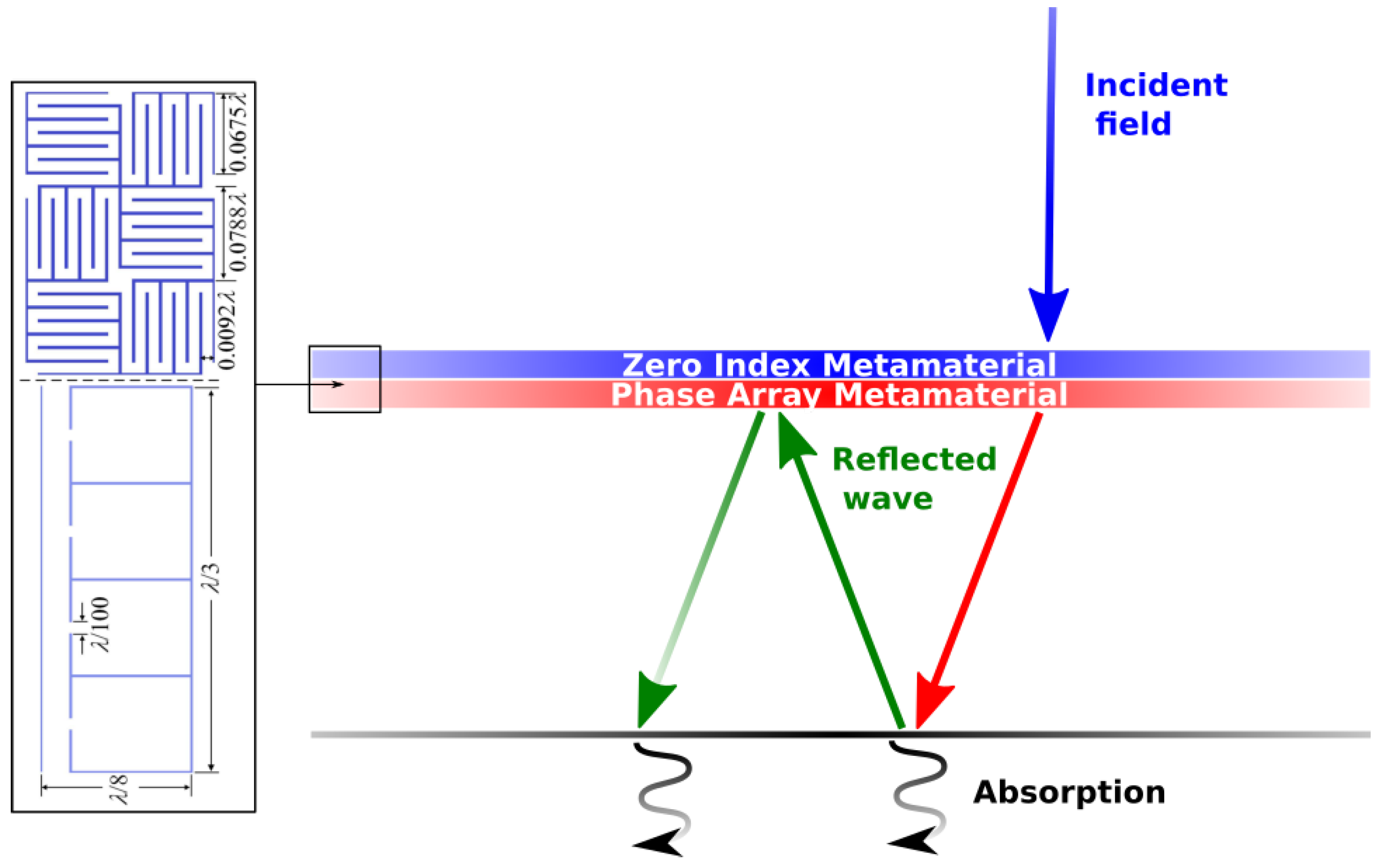
2.1. Absorption and Dissipation
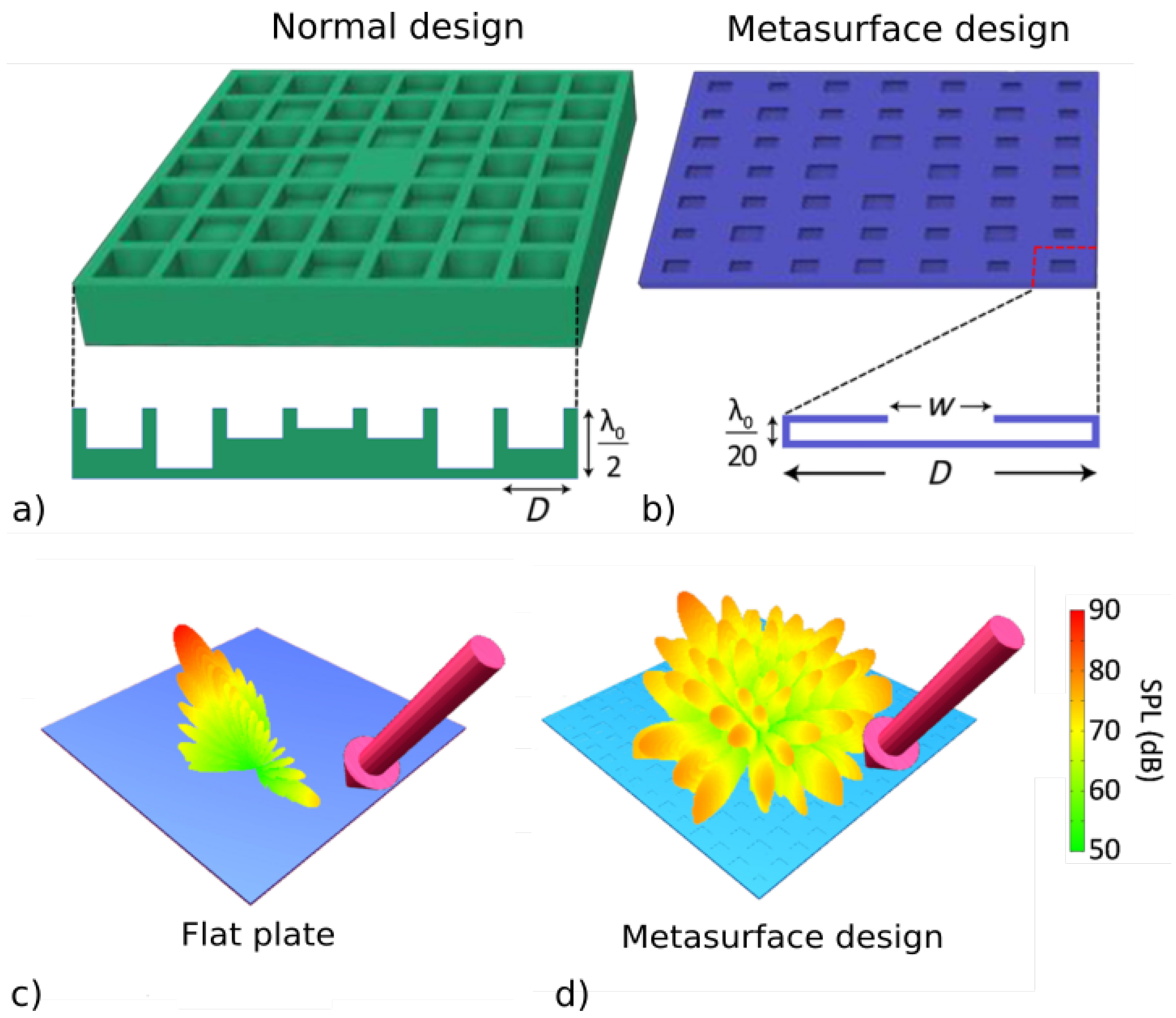
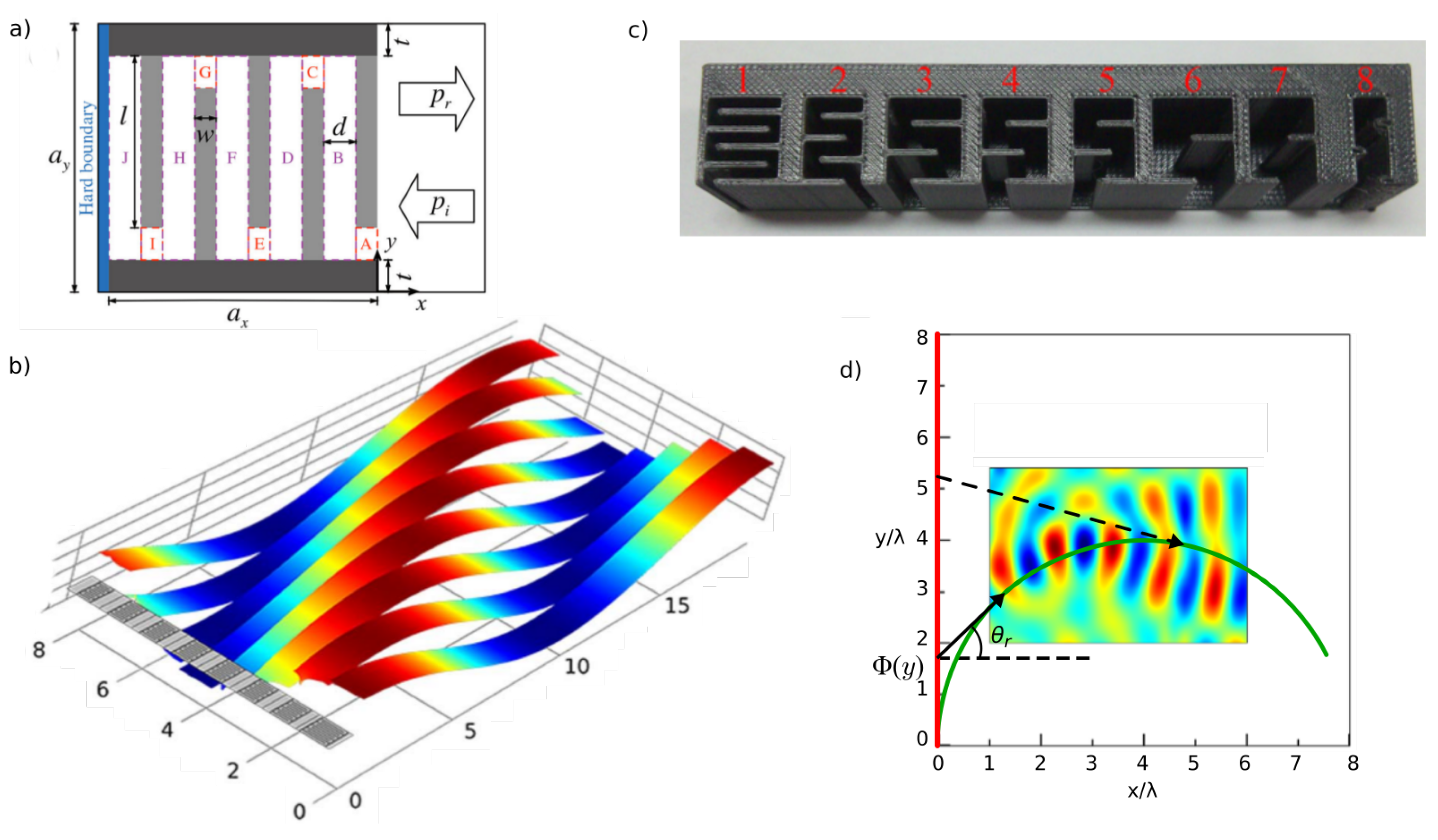
2.2. Reflection
2.3. Noise Trapping
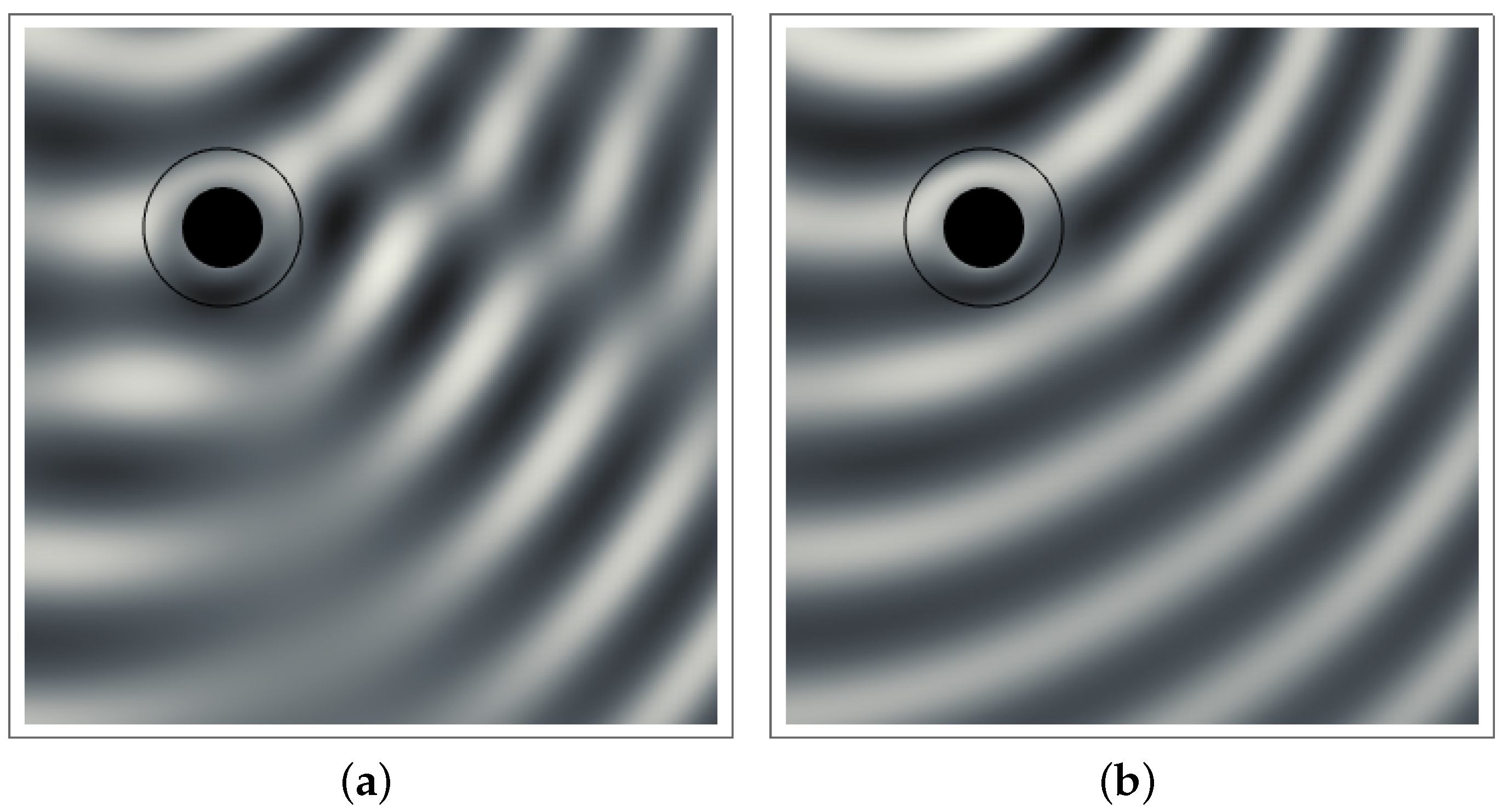
2.4. Scattering Abatement (Cloaking)
3. Challenges
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Weiglhofer, W.S.; Lakhtakia, A. Introduction to Complex Mediums for Optics and Electromagnetics; SPIE Publications: Bellingham, WA, USA, 1999. [Google Scholar]
- Cui, T.J.; Smith, D.; Liu, R. Metamaterials; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Veselago, V.G. The electrodynamics of substances with simultaneously negative values of ϵ and μ. Sov. Phys. Uspekhi 1968, 10, 509. [Google Scholar] [CrossRef]
- Pendry, J.B. Negative refraction makes a perfect lens. Phys. Rev. Lett. 2000, 85, 3966. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Zhang, X.; Mao, Y.; Zhu, Y.Y.; Yang, Z.; Chan, C.T.; Sheng, P. Locally Resonant Sonic Materials. Science 2000, 289, 1734–1736. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Chan, C.T. Double-negative acoustic metamaterial. Phys. Rev. E 2004, 70, 055602. [Google Scholar] [CrossRef] [PubMed]
- Ding, Y.; Liu, Z.; Qiu, C.; Shi, J. Metamaterial with Simultaneously Negative Bulk Modulus and Mass Density. Phys. Rev. Lett. 2007, 99, 093904. [Google Scholar] [CrossRef] [PubMed]
- Brunet, T.; Merlin, A.; Mascaro, B.; Zimny, K.; Leng, J.; Poncelet, O.; Aristégui, C.; Mondain-Monval, O. Soft 3D acoustic metamaterial with negative index. Nat. Mater. 2014, 14, 384. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.H.; Wright, O.B. Origin of negative density and modulus in acoustic metamaterials. Phys. Rev. B 2016, 93, 024302. [Google Scholar] [CrossRef]
- Ma, G.; Sheng, P. Acoustic metamaterials: From local resonances to broad horizons. Sci. Adv. 2016, 2, e1501595. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Yin, L.; Fang, N. Focusing Ultrasound with an Acoustic Metamaterial Network. Phys. Rev. Lett. 2009, 102, 194301. [Google Scholar] [CrossRef] [PubMed]
- Yang, Z.; Mei, J.; Yang, M.; Chan, N.H.; Sheng, P. Membrane-Type Acoustic Metamaterial with Negative Dynamic Mass. Phys. Rev. Lett. 2008, 101, 204301. [Google Scholar] [CrossRef] [PubMed]
- Yang, Z.; Dai, H.M.; Chan, N.H.; Ma, G.C.; Sheng, P. Acoustic metamaterial panels for sound attenuation in the 50–1000 Hz regime. Appl. Phys. Lett. 2010, 96, 041906. [Google Scholar] [CrossRef]
- Langfeldt, F.; Riecken, J.; Gleine, W.; Von Estorff, O. A membrane-type acoustic metamaterial with adjustable acoustic properties. J. Sound Vib. 2016, 373, 1–18. [Google Scholar] [CrossRef]
- Mei, J.; Ma, G.; Yang, M.; Yang, Z.; Wen, W.; Sheng, P. Dark acoustic metamaterials as super absorbers for low-frequency sound. Nat. Commun. 2012, 3, 756. [Google Scholar] [CrossRef] [PubMed]
- Cselyuszka, N.; Sečujski, M.; Crnojević-Bengin, V. Novel negative mass density resonant metamaterial unit cell. Phys. Lett. A 2015, 379, 33–36. [Google Scholar] [CrossRef]
- Sheng, P. Coupled membranes with doubly negative mass density and bulk modulus. J. Acoust. Soc. Am. 2013, 134, 4026. [Google Scholar] [CrossRef]
- Fang, N.; Xi, D.; Xu, J.; Ambati, M.; Srituravanich, W.; Sun, C.; Zhang, X. Ultrasonic metamaterials with negative modulus. Nat. Mater. 2006, 5, 452–456. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.N.; Hu, G.K.; Huang, G.L.; Sun, C.T. An elastic metamaterial with simultaneously negative mass density and bulk modulus. Appl. Phys. Lett. 2011, 98, 251907. [Google Scholar] [CrossRef]
- Graciá-Salgado, R.; García-Chocano, V.M.; Torrent, D.; Sánchez-Dehesa, J. Negative mass density and ρ-near-zero quasi-two-dimensional metamaterials: Design and applications. Phys. Rev. B 2013, 88, 224305. [Google Scholar] [CrossRef]
- Lee, S.H.; Park, C.M.; Seo, Y.M.; Wang, Z.G.; Kim, C.K. Composite Acoustic Medium with Simultaneously Negative Density and Modulus. Phys. Rev. Lett. 2010, 104, 054301. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Liang, B.; Gu, Z.M.; Zou, X.Y.; Cheng, J.C. Reflected wavefront manipulation based on ultrathin planar acoustic metasurfaces. Sci. Rep. 2013, 3, 2546. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Jiang, X.; Li, R.Q.; Liang, B.; Zou, X.Y.; Yin, L.L.; Cheng, J.C. Experimental Realization of Full Control of Reflected Waves with Subwavelength Acoustic Metasurfaces. Phys. Rev. Appl. 2014, 2, 064002. [Google Scholar] [CrossRef]
- Zhu, Y.F.; Fan, X.D.; Liang, B.; Yang, J.; Yang, J.; Yin, L.l.; Cheng, J.C. Multi-frequency acoustic metasurface for extraordinary reflection and sound focusing. AIP Adv. 2016, 6, 121702. [Google Scholar] [CrossRef]
- Gu, Z.M.; Liang, B.; Zou, X.Y.; Cheng, J.C. Broadband diffuse reflections of sound by metasurface with random phase response. EPL (Europhys. Lett.) 2015, 111, 64003. [Google Scholar] [CrossRef]
- Zhu, Y.; Fan, X.; Liang, B.; Cheng, J.; Jing, Y. Ultrathin Acoustic Metasurface-Based Schroeder Diffuser. Phys. Rev. X 2017, 7, 021034. [Google Scholar] [CrossRef]
- Wang, W.; Xie, Y.; Konneker, A.; Popa, B.I.; Cummer, S.A. Design and demonstration of broadband thin planar diffractive acoustic lenses. Appl. Phys. Lett. 2014, 105, 101904. [Google Scholar] [CrossRef]
- Xie, Y.; Wang, W.; Chen, H.; Konneker, A.; Popa, B.I.; Cummer, S.A. Wavefront modulation and subwavelength diffractive acoustics with an acoustic metasurface. Nat. Commun. 2014, 5, 5553. [Google Scholar] [CrossRef] [PubMed]
- Liang, Z.; Feng, T.; Lok, S.; Liu, F.; Ng, K.B.; Chan, C.H.; Wang, J.; Han, S.; Lee, S.; Li, J. Space-coiling metamaterials with double negativity and conical dispersion. Sci. Rep. 2013, 3, 1614. [Google Scholar] [CrossRef] [PubMed]
- Tang, K.; Qiu, C.; Ke, M.; Lu, J.; Ye, Y.; Liu, Z. Anomalous refraction of airborne sound through ultrathin metasurfaces. Sci. Rep. 2014, 4, 6517. [Google Scholar] [CrossRef] [PubMed]
- Zhai, S.; Chen, H.; Ding, C.; Shen, F.; Luo, C.; Zhao, X. Manipulation of transmitted wave front using ultrathin planar acoustic metasurfaces. Appl. Phys. A 2015, 120, 1283–1289. [Google Scholar] [CrossRef]
- Christensen, J.; Martín-Moreno, L.; García-Vidal, F.J. All-angle blockage of sound by an acoustic double-fishnet metamaterial. Appl. Phys. Lett. 2010, 97, 134106. [Google Scholar] [CrossRef]
- Zhao, J.; Li, B.; Chen, Z.N.; Qiu, C.W. Redirection of sound waves using acoustic metasurface. Appl. Phys. Lett. 2013, 103, 151604. [Google Scholar] [CrossRef]
- Zhao, S.D.; Wang, Y.S.; Zhang, C. A continuously tunable acoustic metasurface for transmitted wavefront manipulation. arXiv, 2017; arXiv:1711.09701. [Google Scholar]
- Díaz-Rubio, A.; Tretyakov, S.A. Acoustic metasurfaces for scattering-free anomalous reflection and refraction. Phys. Rev. B 2017, 96, 125409. [Google Scholar] [CrossRef]
- Leroy, V.; Strybulevych, A.; Lanoy, M.; Lemoult, F.; Tourin, A.; Page, J.H. Superabsorption of acoustic waves with bubble metascreens. Phys. Rev. B 2015, 91, 020301. [Google Scholar] [CrossRef]
- Starkey, T.A.; Smith, J.D.; Hibbins, A.P.; Sambles, J.R.; Rance, H.J. Thin structured rigid body for acoustic absorption. Appl. Phys. Lett. 2017, 110, 041902. [Google Scholar] [CrossRef]
- Cai, X.; Guo, Q.; Hu, G.; Yang, J. Ultrathin low-frequency sound absorbing panels based on coplanar spiral tubes or coplanar Helmholtz resonators. Appl. Phys. Lett. 2014, 105, 121901. [Google Scholar] [CrossRef]
- Molerón, M.; Serra-Garcia, M.; Daraio, C. Visco-thermal effects in acoustic metamaterials: From total transmission to total reflection and high absorption. New J. Phys. 2016, 18, 033003. [Google Scholar] [CrossRef]
- Lambert, J.; Champelovier, P.; Blanchet, R.; Lavandier, C.; Terroir, J.; Márki, F.; Griefahn, B.; Iemma, U.; Janssens, K.; Bisping, R. Human response to simulated airport noise scenarios in home-like environments. Appl. Acoust. 2015, 90, 116–125. [Google Scholar] [CrossRef]
- NASA Glenn Research Center. Available online: https://www.nasa.gov/centers/glenn/images/content/83522main_fs003_fig3.gif (accessed on 22 May 2018).
- Beck, B.S. Grazing incidence modeling of a metamaterial-inspired dual-resonance acoustic liner. Proc. SPIE 2014, 9064, 906421. [Google Scholar]
- Beck, B.S.; Schiller, N.H.; Jones, M.G. Impedance assessment of a dual-resonance acoustic liner. Appl. Acoust. 2015, 93, 15–22. [Google Scholar] [CrossRef]
- Mitchell, K.R.; Fuller, C.R. Design Optimization of Broadband Acoustic Liners through Finite Element Efficacy Studies. In Proceedings of the 21st AIAA/CEAS Aeroacoustics Conference, Dallas, TX, USA, 22–26 June 2015; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2015. [Google Scholar]
- Li, Y.; Assouar, B.M. Acoustic metasurface-based perfect absorber with deep subwavelength thickness. Appl. Phys. Lett. 2016, 108, 063502. [Google Scholar] [CrossRef]
- Chen, C.; Du, Z.; Hu, G.; Yang, J. A low-frequency sound absorbing material with subwavelength thickness. Appl. Phys. Lett. 2017, 110, 221903. [Google Scholar] [CrossRef]
- Yang, M.; Chen, S.; Fu, C.; Sheng, P. Optimal sound-absorbing structures. Mater. Horiz. 2017, 4, 673–680. [Google Scholar] [CrossRef]
- Tang, Y.; Ren, S.; Meng, H.; Xin, F.; Huang, L.; Chen, T.; Zhang, C.; Lu, T.J. Hybrid acoustic metamaterial as super absorber for broadband low-frequency sound. Sci. Rep. 2017, 7, 43340. [Google Scholar] [CrossRef] [PubMed]
- Diez, M.; Iemma, U.; Marchese, V. A Sound-Matching-Based Approach for Aircraft Noise Annoyance Alleviation Via MDO. In Proceedings of the 13th AIAA/CEAS Aeroacoustics Conference (28th AIAA Aeroacoustics Conference), Rome, Italy, 21–23 May 2007. [Google Scholar]
- Iemma, U.; Diez, M.; Leotardi, C.; Centracchio, F. On the use of noise annoyance as a design optimization constraint: the COSMA experience. In Proceedings of the 18th International Congress on Sound and Vibration (ICSV), Rio de Janeiro, Brazil, 10–14 July 2011. [Google Scholar]
- Diez, M.; Iemma, U. Multidisciplinary conceptual design optimization of aircraft using a sound-matching-based objective function. Eng. Optim. 2012, 44, 591–612. [Google Scholar] [CrossRef]
- Montetagaud, F.; Montoux, S. Negatively Scarfed Intake: Design and Acoustic Performances. In Proceedings of the 11th AIAA/CEAS Aeroacoustics Conference, Monterey, CA, USA, 23–25 May 2005; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2005. [Google Scholar]
- Gall, P.E.; Cros, C. Aircraft Having a Reduced Environmental Impact. U.S. Patent 2008/0258005 A1, 2008. [Google Scholar]
- Moore, M.D.; Boren, K.L.; Marques, E.C. Airplane Configuration. U.S. Patent 8,087,607 B2, 2012. [Google Scholar]
- Wang, X.; Huang, Z.; Han, F.; Feng, Z. Reduction of aircraft engine noise by covering surface acoustic metamaterials on sidewalls. In Proceedings of the 24th International Congress on Sound and Vibration (ICSV), London, UK, 23–27 July 2017. [Google Scholar]
- Naify, C.J.; Chang, C.M.; McKnight, G.; Nutt, S.R. Experimental and FEA evaluation of membrane-type locally resonant acoustic metamaterial arrays for aircraft interior sound insulation. In Proceedings of the 17th AIAA/CEAS Aeroacoustics Conference (32nd AIAA Aeroacoustics Conference), Portland, Oregon, 5–8 June 2011. [Google Scholar]
- Marinova, P.; von Estorff, O.; Lippert, S. Low–frequency air- and structure-borne sound insulation challenges for a counterrotating open–rotor aircraft. In Proceedings of the 21th International Congress on Sound and Vibration (ICSV), Beijing, China, 6–10 July 2014. [Google Scholar]
- Langfeldt, F.; Marinova, P.; Gleine, W.; Lippert, S.; von Estorff, O. Noise-shield with membrane-type metamaterials for low-frequency sound insulation. Part I: Analytical investigation of the multi-layered assembly. In Proceedings of the 40th German Annual Conference on Acoustics DAGA, Oldenburg, Germany, 10–13 March 2014. [Google Scholar]
- Marinova, P.; Langfeldt, F.; Gleine, W.; Lippert, S.; von Estorff, O. Noise-shield with membrane-type metamaterials for low-frequency sound insulation. Part II: Numerical investigation of the full-scale acoustic panel assembly. In Proceedings of the 40th German Annual Conference on Acoustics DAGA, Oldenburg, Germany, 10–13 March 2014. [Google Scholar]
- Sui, N.; Yan, X.; Huang, T.Y.; Xu, J.; Yuan, F.G.; Jing, Y. A lightweight yet sound-proof honeycomb acoustic metamaterial. Appl. Phys. Lett. 2015, 106, 171905. [Google Scholar] [CrossRef]
- Wang, X.; Zhao, H.; Luo, X.; Huang, Z. Membrane-constrained acoustic metamaterials for low frequency sound insulation. Appl. Phys. Lett. 2016, 108, 041905. [Google Scholar] [CrossRef]
- Gao, N.; Hou, H. Low frequency acoustic properties of a honeycomb-silicone rubber acoustic metamaterial. Modern Phys. Lett. B 2017, 31, 1750118. [Google Scholar] [CrossRef]
- Jiang, X.; Liang, B.; Zou, X.Y.; Yang, J.; Yin, L.L.; Yang, J.; Cheng, J.C. Acoustic one-way metasurfaces: Asymmetric Phase Modulation of Sound by Subwavelength Layer. Sci. Rep. 2016, 6, 28023. [Google Scholar] [CrossRef] [PubMed]
- Pendry, J.B.; Schurig, D.; Smith, D. Controlling electromagnetic fields. Science 2006, 312, 1780–1782. [Google Scholar] [CrossRef] [PubMed]
- Leonhardt, U. Optical conformal mapping. Science 2006, 312, 1777–1780. [Google Scholar] [CrossRef] [PubMed]
- Cummer, S.A.; Schurig, D. One path to acoustic cloaking. New J. Phys. 2007, 9, 45. [Google Scholar] [CrossRef]
- Norris, A. Acoustic cloaking theory. Proc. R. Soc. A Math. Phys. Eng. Sci. 2008, 464, 2411–2434. [Google Scholar] [CrossRef]
- Norris, A. Acoustic metafluids. J. Acoust. Soc. Am. 2009, 125, 839–849. [Google Scholar] [CrossRef] [PubMed]
- Kadic, M.; Bückmann, T.; Stenger, N.; Thiel, M.; Wegener, M. On the practicability of pentamode mechanical metamaterials. Appl. Phys. Lett. 2012, 100, 191901. [Google Scholar] [CrossRef]
- Kadic, M.; Bückmann, T.; Schittny, R.; Gumbsch, P.; Wegener, M. Pentamode Metamaterials with Independently Tailored Bulk Modulus and Mass Density. Phys. Rev. Appl. 2014, 2, 054007. [Google Scholar] [CrossRef]
- Cai, L.W.; Sánchez-Dehesa, J. Analysis of Cummer—Schurig acoustic cloaking. New J. Phys. 2007, 9, 450. [Google Scholar] [CrossRef]
- Chen, H.; Chan, C.T. Acoustic cloaking in three dimensions using acoustic metamaterials. Appl. Phys. Lett. 2007, 91, 183518. [Google Scholar] [CrossRef]
- Cheng, Y.; Yang, F.; Xu, J.Y.; Liu, X.J. A multilayer structured acoustic cloak with homogeneous isotropic materials. Appl. Phys. Lett. 2008, 92, 151913. [Google Scholar] [CrossRef]
- Torrent, D.; Sánchez-Dehesa, J. Broadband acoustic cloaks based on the homogenization of layered materials. Wave Motion 2011, 48, 497–504. [Google Scholar] [CrossRef]
- Iemma, U.; Burghignoli, L. An integral equation approach to acoustic cloaking. J. Sound Vib. 2012, 331, 4629–4643. [Google Scholar] [CrossRef]
- Scandrett, C.L.; Boisvert, J.E.; Howarth, T.R. Acoustic cloaking using layered pentamode materials. J. Acoust. Soc. Am. 2010, 127, 2856–2864. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Liu, X.; Hu, G. Latticed pentamode acoustic cloak. Sci. Rep. 2015, 5, 15745. [Google Scholar] [CrossRef] [PubMed]
- Méndez, C.G.; Podestá, J.M.; Lloberas-Valls, O.; Toro, S.; Huespe, A.E.; Oliver, J. Computational material design for acoustic cloaking. Int. J. Numer. Methods Eng. 2017, 112, 1353–1380. [Google Scholar] [CrossRef]
- Pendry, J.B.; Li, J. An acoustic metafluid: Realizing a broadband acoustic cloak. New J. Phys. 2008, 10, 115032. [Google Scholar] [CrossRef]
- Popa, B.I.; Cummer, S.A. Homogeneous and compact acoustic ground cloaks. Phys. Rev. B 2011, 83, 224304. [Google Scholar] [CrossRef]
- Popa, B.I.; Zigoneanu, L.; Cummer, S.A. Experimental acoustic ground cloak in air. Phys. Rev. Lett. 2011, 106, 253901. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.L.; Ni, X.; Lu, M.H.; Chen, Y.F. A feasible approach to achieve acoustic carpet cloak in air. Phys. Lett. A 2012, 376, 493–496. [Google Scholar] [CrossRef]
- Zigoneanu, L.; Popa, B.I.; Cummer, S.A. Three-dimensional broadband omnidirectional acoustic ground cloak. Nat. Mater. 2014, 4, 352–355. [Google Scholar] [CrossRef] [PubMed]
- Zhu, J.; Chen, T.; Liang, Q.; Wang, X.; Jiang, P. Design of a broadband ultra-large area acoustic cloak based on a fluid medium. J. Appl. Phys. 2014, 116, 164906. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, H.; Yu, F.; Xu, Z.; Chen, H. A metasurface carpet cloak for electromagnetic, acoustic and water waves. Sci. Rep. 2016, 6, 20219. [Google Scholar] [CrossRef] [PubMed]
- Esfahlani, H.; Karkar, S.; Lissek, H.; Mosig, J.R. Acoustic carpet cloak based on an ultrathin metasurface. Phys. Rev. B 2016, 94, 014302. [Google Scholar] [CrossRef]
- Faure, C.; Richoux, O.; Félix, S.; Pagneux, V. Experiments on metasurface carpet cloaking for audible acoustics. Appl. Phys. Lett. 2016, 108, 064103. [Google Scholar] [CrossRef]
- Huang, X.; Zhong, S.; Stalnov, O. Analysis of scattering from an acoustic cloak in a moving fluid. Acoust. Soc. Am. 2014, 135, 2571–2580. [Google Scholar] [CrossRef] [PubMed]
- Ryoo, H.; Jeon, W. Effect of compressibility and non-uniformity in flow on the scattering pattern of acoustic cloak. Sci. Rep. 2017, 7, 2125–2136. [Google Scholar] [CrossRef] [PubMed]
- Iemma, U.; Carley, M.; Pellegrini, R. Tailoring Acoustic Metamaterials to Aeroacoustic Applications. In Proceedings of the 43th International Congress and Exposition on Noise Control Engineering (Inter-Noise), Melbourne, Australia, 16–19 November 2014. [Google Scholar]
- Iemma, U. Theoretical and Numerical Modeling of Acoustic Metamaterials for Aeroacoustic Applications. Aerospace 2016, 3, 15. [Google Scholar] [CrossRef]
- Iemma, U.; Palma, G. Aeroacoustic Design of Metafluid Devices. In Proceedings of the 24th International Congress on Sound and Vibration (ICSV), London, UK, 23–27 July 2017. [Google Scholar]
- Huang, X.; Zhong, S.; Liu, X. Acoustic invisibility in turbulent fluids by optimised cloaking. J. Fluid Mech. 2014, 749, 460–477. [Google Scholar] [CrossRef]
- García-Meca, C.; Carloni, S.; Barceló, C.; Jannes, G.; Sánchez-Dehesa, J.; Martínez, A. Analogue transformations in physics and their application to acoustics. Sci. Rep. 2013, 3, 2009. [Google Scholar] [CrossRef] [PubMed]
- García-Meca, C.; Carloni, S.; Barceló, C.; Jannes, G.; Sánchez-Dehesa, J.; Martínez, A. Space-time transformation acoustics. Wave Motion 2014, 51, 785–797. [Google Scholar] [CrossRef]
- García-Meca, C.; Carloni, S.; Barceló, C.; Jannes, G.; Sánchez-Dehesa, J.; Martínez, A. Analogue transformation acoustics and the compression of spacetime. Photonics Nanostruct. Fundam. Appl. 2014, 4, 312–318. [Google Scholar] [CrossRef][Green Version]
- Iemma, U.; Palma, G. Analogue Transformation Acoustics in Aeronautics. In Proceedings of the 46th International Congress and Exposition on Noise Control Engineering (Inter-Noise), Hong Kong, China, 27–30 August 2017. [Google Scholar]
- Iemma, U.; Palma, G. On the Use of the Analogue Transformation Acoustics in Aeroacoustics. Math. Probl. Eng. 2017, 2017, 8981731. [Google Scholar] [CrossRef]
- Zhang, S.; Xia, C.; Fang, N. Broadband Acoustic Cloak for Ultrasound Waves. Phys. Rev. Lett. 2011, 106, 024301. [Google Scholar] [CrossRef] [PubMed]
- Yang, S.K.; Lin, J.C.; Cheng, J.W. The Experimental Realization of an Acoustic Cloak in Air with a Meta-Composite Shell. Appl. Sci. 2017, 7, 456. [Google Scholar] [CrossRef]
- Sklan, S.R.; Li, B. A Unified Approach to Nonlinear Transformation Materials. Sci. Rep. 2018, 8, 4436–4448. [Google Scholar] [CrossRef] [PubMed]
- Sklan, S.R. Splash, pop, sizzle: Information processing with phononic computing. AIP Adv. 2015, 5, 053302. [Google Scholar] [CrossRef]
- Gaborit, M.; Schwan, L.; Dazel, O.; Groby, J.P.; Weisser, T.; Göransson, P. Coupling FEM, Bloch Waves and TMM in Meta Poroelastic Laminates. Acta Acust. United Acust. 2018, 104, 220–227. [Google Scholar] [CrossRef]
- Gao, K. Multiscale Modelling of Acoustic Porous Materials. Ph.D. Thesis, Technische Universiteit Eindhoven, Eindhoven, The Netherlands, 2016. [Google Scholar]
- Roca, D.; Lloberas-Valls, O.; Cante, J.; Oliver, J. A computational multiscale homogenization framework accounting for inertial effects: Application to acoustic metamaterials modelling. Comput. Methods Appl. Mech. Eng. 2018, 330, 415–446. [Google Scholar] [CrossRef]
- Sridhar, A.; Kouznetsova, V.G.; Geers, M.G.D. Homogenization of locally resonant acoustic metamaterials towards an emergent enriched continuum. Comput. Mech. 2016, 57, 423–435. [Google Scholar] [CrossRef] [PubMed]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Palma, G.; Mao, H.; Burghignoli, L.; Göransson, P.; Iemma, U. Acoustic Metamaterials in Aeronautics. Appl. Sci. 2018, 8, 971. https://doi.org/10.3390/app8060971
Palma G, Mao H, Burghignoli L, Göransson P, Iemma U. Acoustic Metamaterials in Aeronautics. Applied Sciences. 2018; 8(6):971. https://doi.org/10.3390/app8060971
Chicago/Turabian StylePalma, Giorgio, Huina Mao, Lorenzo Burghignoli, Peter Göransson, and Umberto Iemma. 2018. "Acoustic Metamaterials in Aeronautics" Applied Sciences 8, no. 6: 971. https://doi.org/10.3390/app8060971
APA StylePalma, G., Mao, H., Burghignoli, L., Göransson, P., & Iemma, U. (2018). Acoustic Metamaterials in Aeronautics. Applied Sciences, 8(6), 971. https://doi.org/10.3390/app8060971





