Effect of Wettability on Collapsing Cavitation Bubble near Solid Surface Studied by Multi-Relaxation-Time Lattice Boltzmann Model
Abstract
1. Introduction
2. Pseudopotential MRT LB Model
3. Numerical Simulation and Analysis
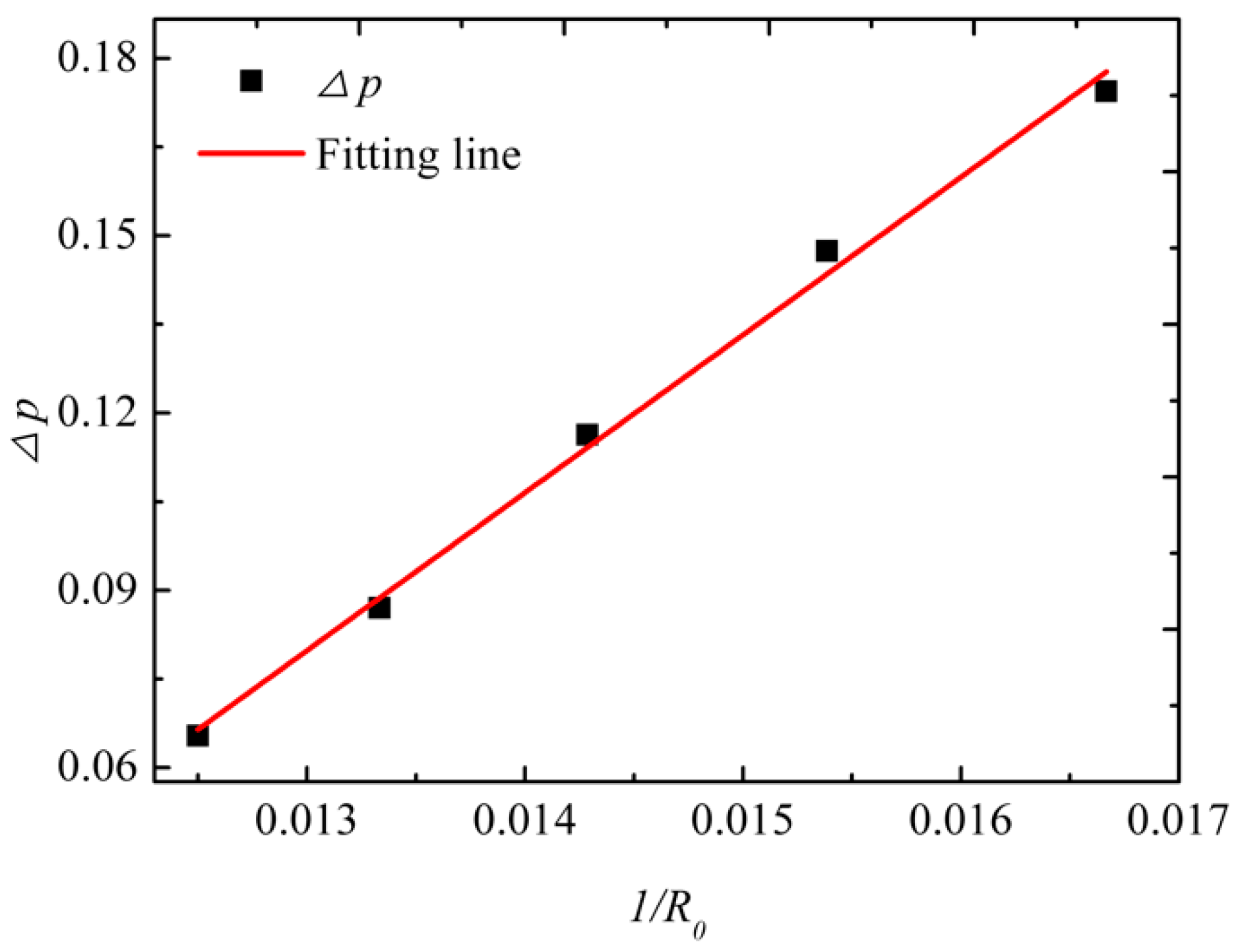
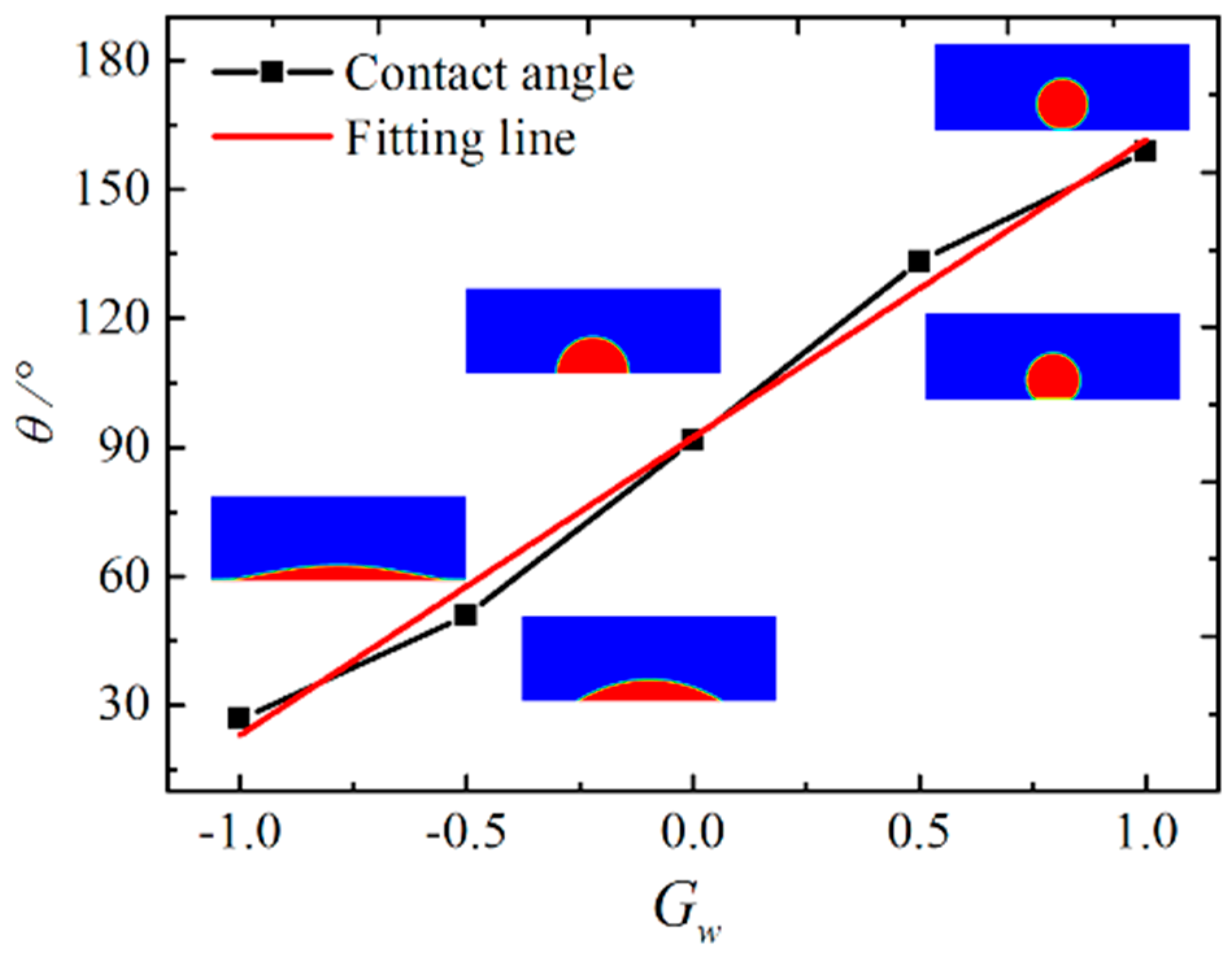
3.1. Laplace Law and the Contact Angle
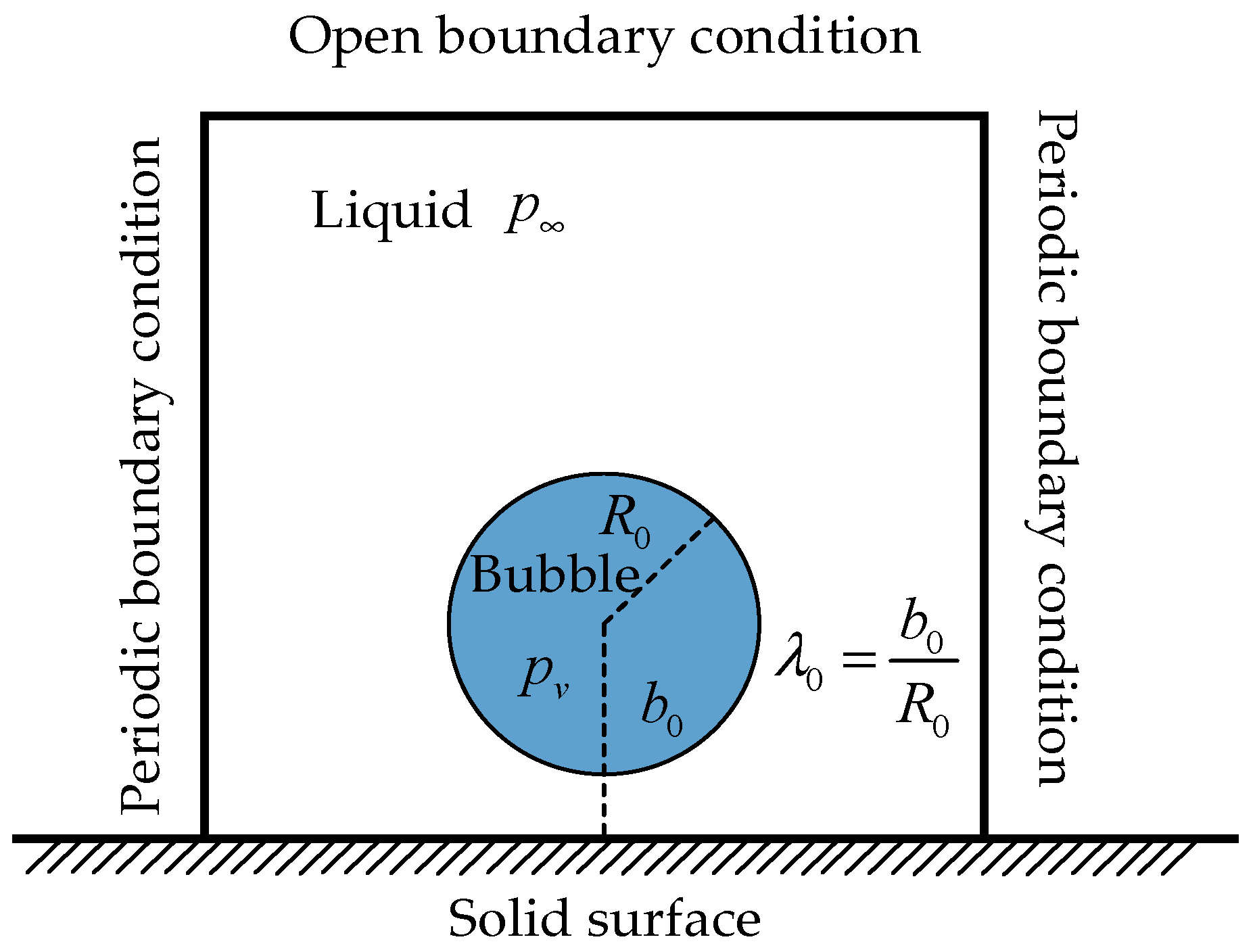
3.2. Verification of the Collapsing Bubble Near the Solid Surface
3.3. Effect of Wettability on Cavitation Inception
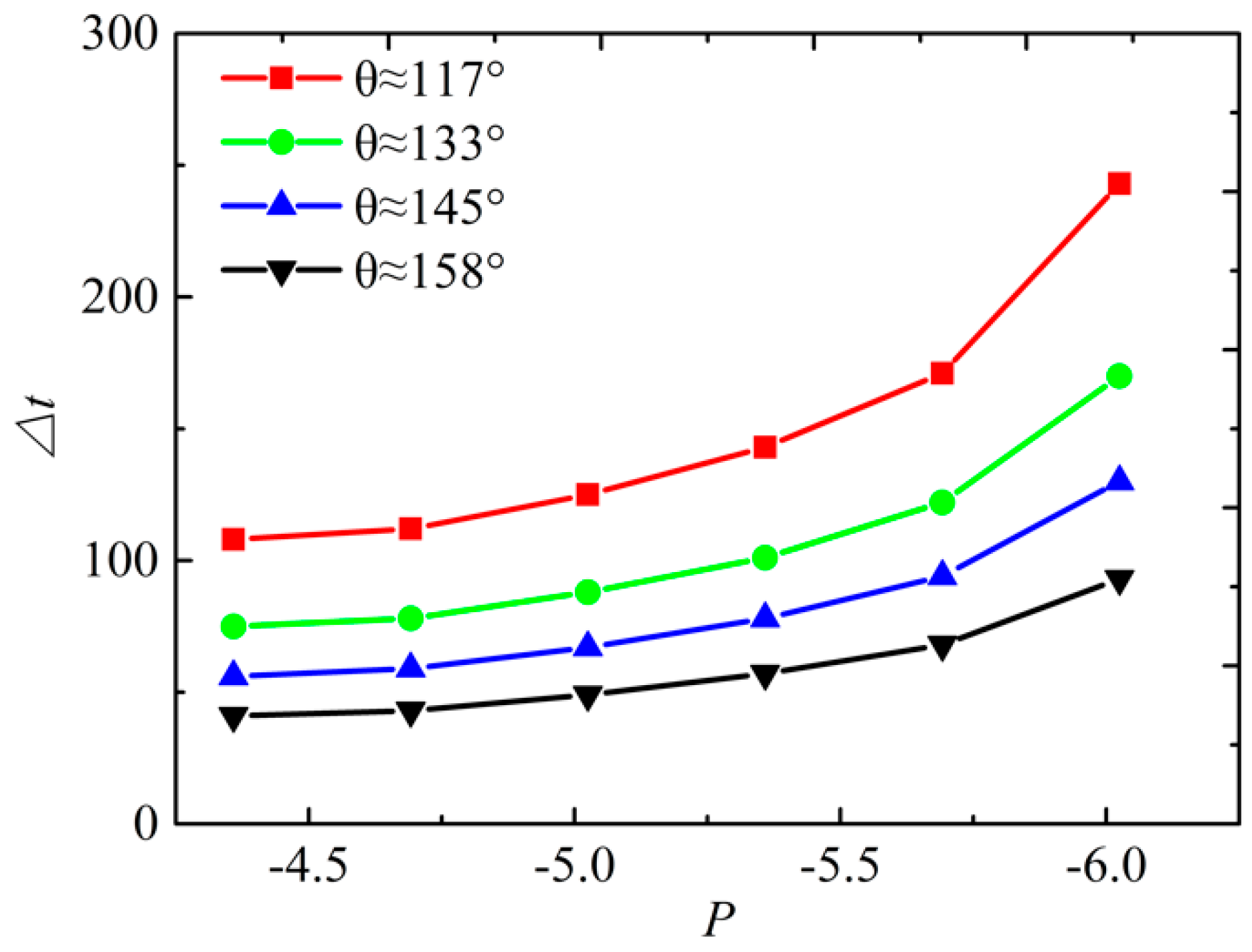
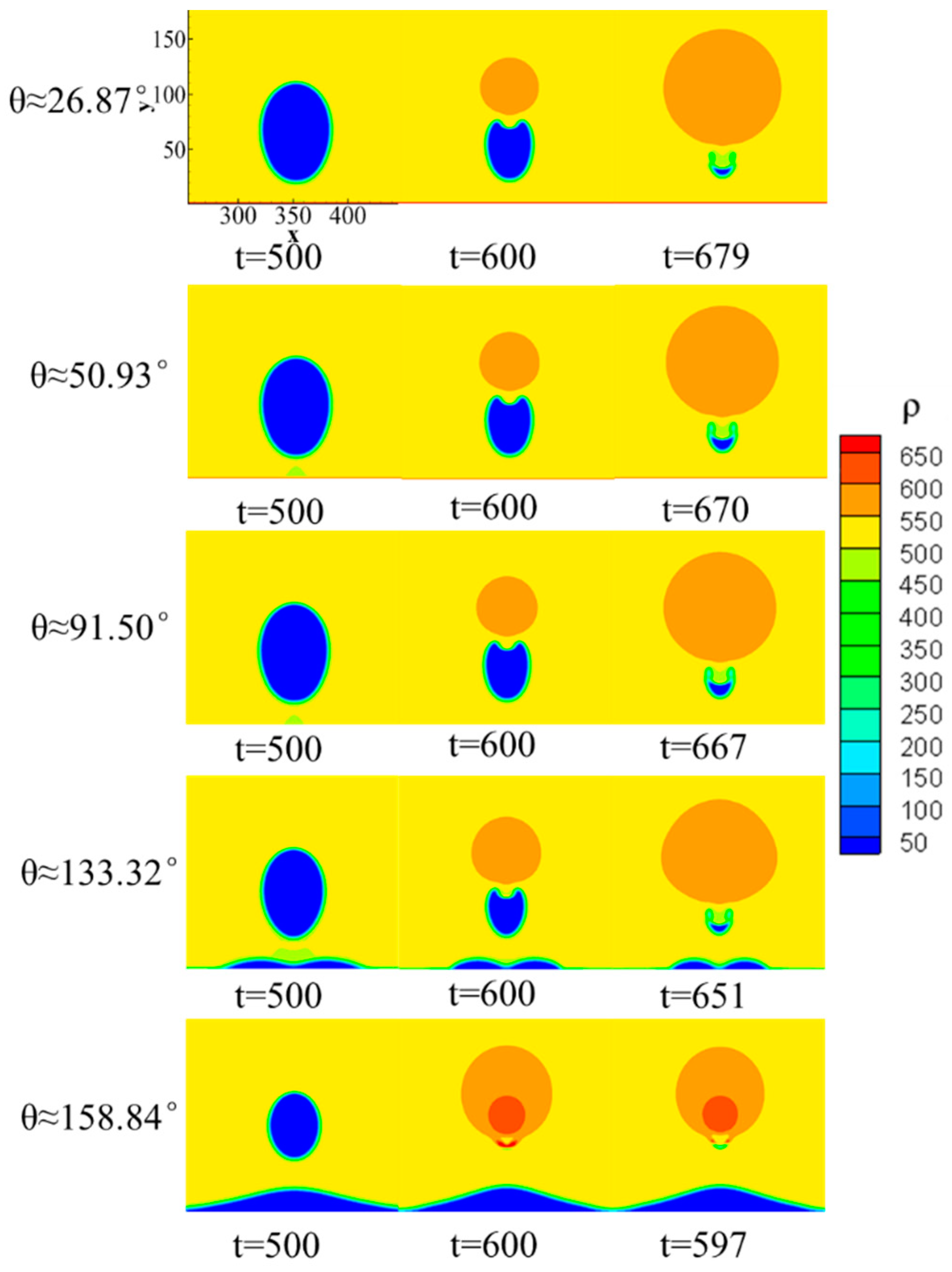
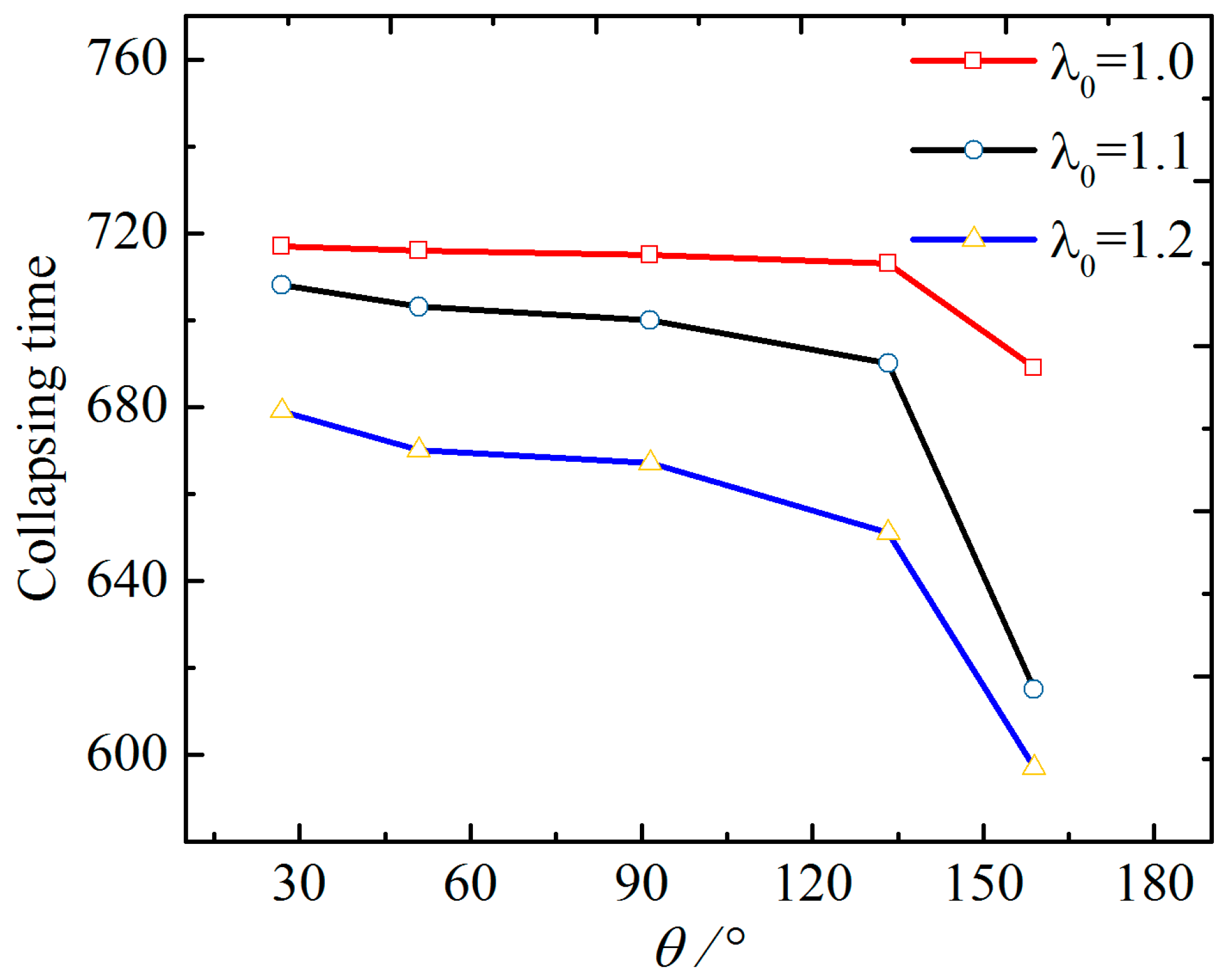
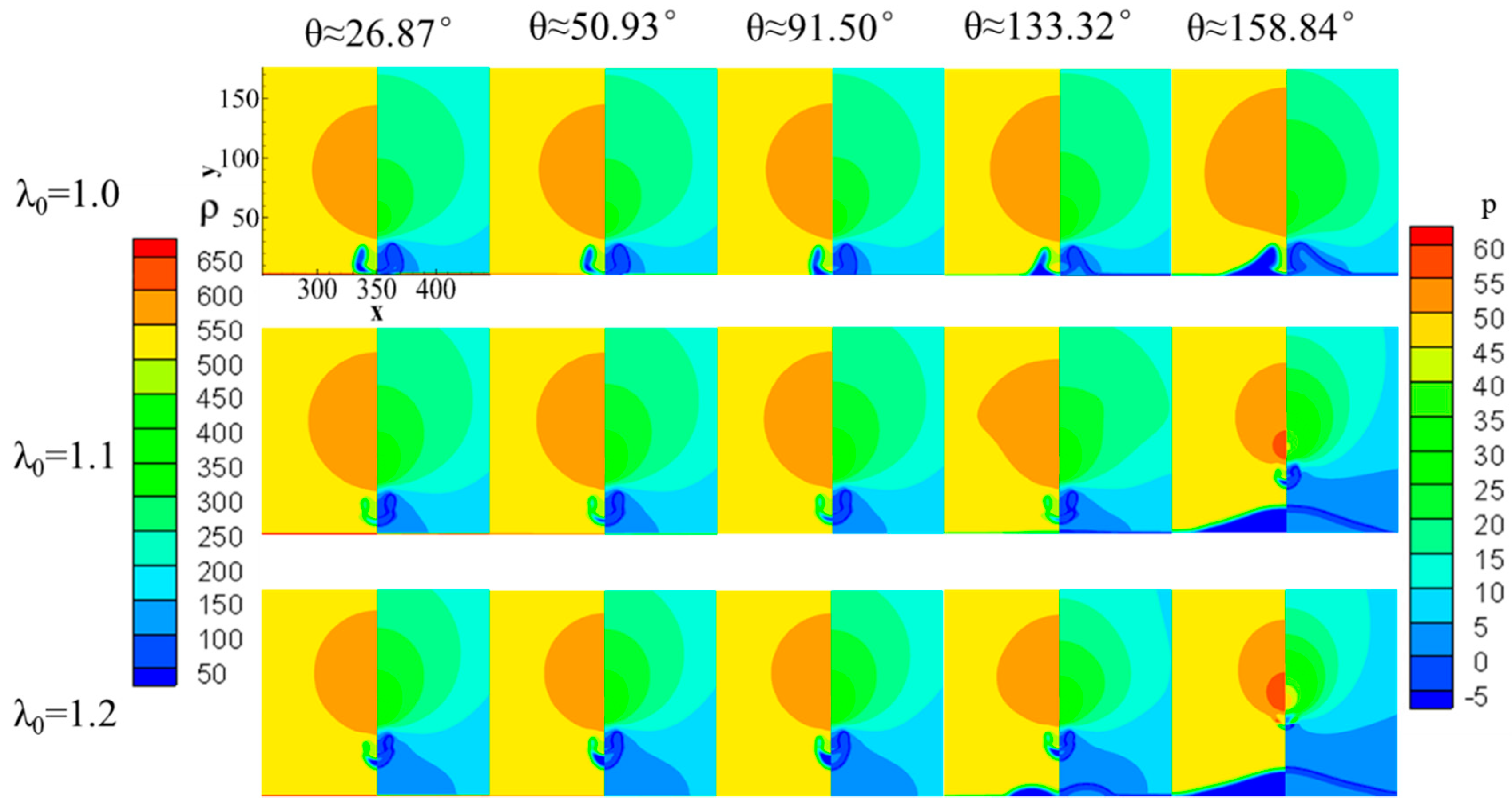
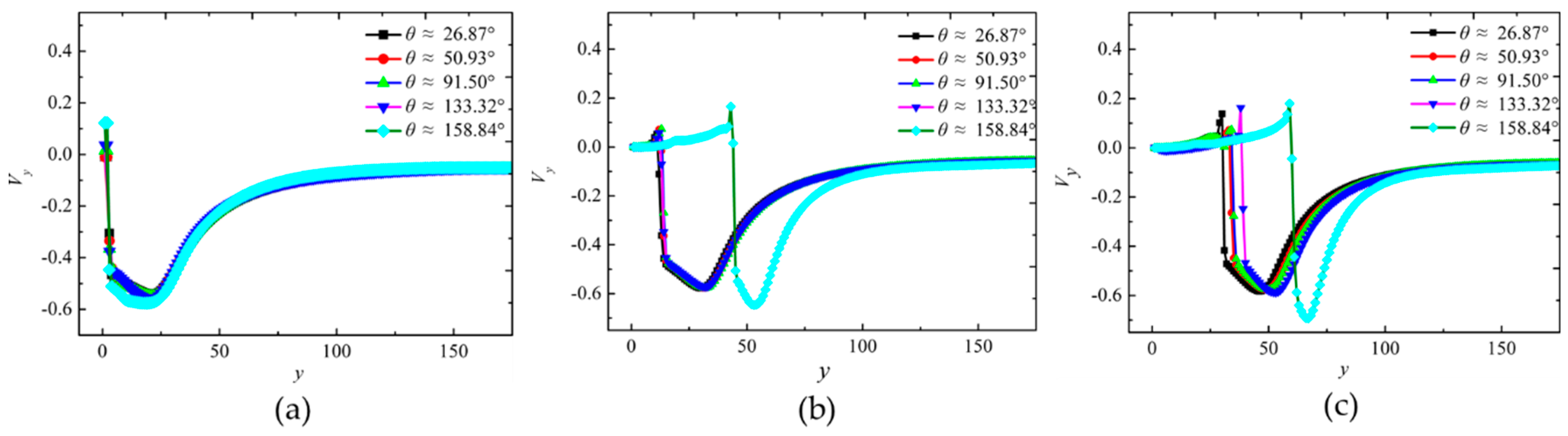
4. The Effect of Wettability on the Collapsing Bubble near the Solid Surface
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Bagal, M.V.; Gogate, P.R. Wastewater treatment using hybrid treatment schemes based on cavitation and Fenton chemistry: A review. Ultrason. Sonochem. 2014, 21, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Teran Hilares, R.; Ramos, L.; da Silva, S.S.; Dragone, G.; Mussatto, S.I.; Santos, J.C.D. Hydrodynamic cavitation as a strategy to enhance the efficiency of lignocellulosic biomass pretreatment. Crit. Rev. Biotechnol. 2017, 38, 483–493. [Google Scholar] [CrossRef]
- Kerboua, K.; Hamdaoui, O. Influence of reactions heats on variation of radius, temperature, pressure and chemical species amounts within a single acoustic cavitation bubble. Ultrason. Sonochem. 2018, 41, 449–457. [Google Scholar] [CrossRef]
- Vyas, N.; Pecheva, E.; Dehghani, H.; Sammons, R.L.; Wang, Q.X.; Leppinen, D.M.; Walmsley, A.D. High Speed Imaging of Cavitation around Dental Ultrasonic Scaler Tips. PLoS ONE 2016, 11, e0149804. [Google Scholar] [CrossRef] [PubMed]
- Vyas, N.; Dehghani, H.; Sammons, R.L.; Wang, Q.X.; Leppinen, D.M.; Walmsley, A.D. Imaging and analysis of individual cavitation microbubbles around dental ultrasonic scalers. Ultrasonics 2017, 81, 66–72. [Google Scholar] [CrossRef] [PubMed]
- Ye, L.; Zhu, X. Analysis of the effect of impact of near-wall acoustic bubble collapse micro-jet on Al 1060. Ultrason. Sonochem. 2017, 36, 507–516. [Google Scholar] [CrossRef] [PubMed]
- Fu, H.; Comer, J.; Cai, W.; Chipot, C. Sonoporation at Small and Large Length Scales: Effect of Cavitation Bubble Collapse on Membranes. J. Phys. Chem. Lett. 2015, 6, 413–418. [Google Scholar] [CrossRef] [PubMed]
- Adhikari, U.; Goliaei, A.; Berkowitz, M.L. Nanobubbles, cavitation, shock waves and traumatic brain injury. Phys. Chem. Chem. Phys. 2016, 18, 32638–32652. [Google Scholar] [CrossRef] [PubMed]
- Landhuis, E. Ultrasound for the brain. Nature 2017, 551, 257–259. [Google Scholar] [CrossRef] [PubMed]
- Li, D.; Kang, Y.; Wang, X.; Ding, X.; Fang, Z. Effects of nozzle inner surface roughness on the cavitation erosion characteristics of high speed submerged jets. Exp. Therm. Fluid Sci. 2016, 74, 444–452. [Google Scholar] [CrossRef]
- Belova, V.; Gorin, D.A.; Shchukin, D.G.; Mohwald, H. Controlled effect of ultrasonic cavitation on hydrophobic/hydrophilic surfaces. ACS Appl. Mater. Interfaces 2011, 3, 417–425. [Google Scholar] [CrossRef] [PubMed]
- Guo, Z.L.; Shu, C. Lattice Boltzmann Method and Its Applications in Engineering; World Scientific Publishing: Singapore, 2013; pp. 1–34. ISBN 978-981-4508-29-2. [Google Scholar]
- Ezzatneshan, E. Study of surface wettability effect on cavitation inception by implementation of the lattice Boltzmann method. Phys. Fluids 2017, 29, 113–304. [Google Scholar] [CrossRef]
- Li, Q.; Luo, K.H. Thermodynamic consistency of the pseudopotential lattice Boltzmann model for simulating liquid–vapor flows. Appl. Therm. Eng. 2014, 72, 56–61. [Google Scholar] [CrossRef]
- Kupershtokh, A.L.; Medvedev, D.A.; Karpov, D.I. On equations of state in a lattice Boltzmann method. Comput. Math. Appl. 2009, 58, 965–974. [Google Scholar] [CrossRef]
- Li, Q.; Luo, K.H.; Li, X.J. Forcing scheme in pseudopotential lattice Boltzmann model for multiphase flows. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2012, 86, 1–28. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Luo, K.H.; Li, X.J. Lattice Boltzmann modeling of multiphase flows at large density ratio with an improved pseudopotential model. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2013, 87, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Shan, M.L.; Zhu, C.P.; Zhou, X.; Yin, C.; Han, Q.B. Investigation of cavitation bubble collapse near rigid boundary by lattice Boltzmann method. J. Hydrodyn. Ser. B 2016, 28, 442–450. [Google Scholar] [CrossRef]
- Li, Q.; Luo, K.H. Achieving tunable surface tension in the pseudopotential lattice Boltzmann modeling of multiphase flows. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2013, 88, 05330701–05330710. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Luo, K.H.; Kang, Q.J.; Chen, Q. Contact angles in the pseudopotential lattice Boltzmann modeling of wetting. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2014, 90, 05330101–05330109. [Google Scholar] [CrossRef] [PubMed]
- Shan, X.; Chen, H. Lattice Boltzmann model for simulating flows with multiple phases and components. Phys. Rev. E 1993, 47, 1815–1819. [Google Scholar] [CrossRef]
- Shan, X.; Chen, H. Simulation of nonideal gases and liquid-gas phase transitions by the lattice Boltzmann equation. Phys. Rev. E 1994, 49, 2941–2948. [Google Scholar] [CrossRef]
- Weaver, D.P.; Shizgal, B.D. Rarefied Gas Dynamics: Theory and Simulations; The American Institute of Aeronautics and Astronautics: Reston, VA, USA, 1994; pp. 409–503. [Google Scholar]
- Shan, M.L.; Zhu, C.P.; Yao, C.; Yin, C.; Jiang, X.Y. Pseudopotential multi-relaxation-time lattice Boltzmann model for cavitation bubble collapse with high density ratio. Chin. Phys. B 2016, 25, 104–701. [Google Scholar] [CrossRef]
- Huang, H.; Sukop, M.C.; Lu, X.Y. Multiphase Lattice Boltzmann Methods: Theory and Application; John Wiley & Sons: Hoboken, NJ, USA, 2015; pp. 121–122. ISBN 978-1-118-97133-8. [Google Scholar]
- Shan, X. Pressure tensor calculation in a class of nonideal gas lattice Boltzmann models. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2008, 77, 06670201–06670206. [Google Scholar] [CrossRef] [PubMed]
- Yuan, P.; Schaefer, L. Equations of state in a lattice Boltzmann model. Phys. Fluids 2006, 18, 04210101–04210111. [Google Scholar] [CrossRef]
- Porter, M.L.; Coon, E.T.; Kang, Q.; Moulton, J.D.; Carey, J.W. Multicomponent interparticle-potential lattice Boltzmann model for fluids with large viscosity ratios. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2012, 86, 03670101–03670108. [Google Scholar] [CrossRef] [PubMed]
- Martys, N.S.; Chen, H. Simulation of multicomponent fluids in complex three-dimensional geometries by the lattice Boltzmann method. Phys. Rev. E 1996, 53, 743–750. [Google Scholar] [CrossRef]
- Zou, Q.; He, X. On pressure and velocity boundary conditions for the lattice Boltzmann BGK model. Phys. Fluids 1997, 9, 1591–1598. [Google Scholar] [CrossRef]
- Krüger, T.; Kusumaatmaja, H.; Kuzmin, A.; Shardt, O.; Silva, G.; Viggen, E.M. The Lattice Boltzmann Method; Springer: Cham, Switzerland, 2017; pp. 199–200. ISBN 978-3-319-44647-9. [Google Scholar]
- Plesset, M.S.; Chapman, R.B. Collapse of an initially spherical vapour cavity in the neighbourhood of a solid boundary. J. Fluid Mech. 1971, 47, 283–290. [Google Scholar] [CrossRef]
- Bernardin, J.D.; Mudawar, I.; Walsh, C.B.; Franses, E.I. Contact angle temperature dependence for water droplets on practical aluminum surfaces. Int. J. Heat Mass Transf. 1997, 40, 1017–1033. [Google Scholar] [CrossRef]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Y.; Shan, M.; Yang, Y.; Han, Q.; Zhu, C.; Zhang, X. Effect of Wettability on Collapsing Cavitation Bubble near Solid Surface Studied by Multi-Relaxation-Time Lattice Boltzmann Model. Appl. Sci. 2018, 8, 940. https://doi.org/10.3390/app8060940
Zhu Y, Shan M, Yang Y, Han Q, Zhu C, Zhang X. Effect of Wettability on Collapsing Cavitation Bubble near Solid Surface Studied by Multi-Relaxation-Time Lattice Boltzmann Model. Applied Sciences. 2018; 8(6):940. https://doi.org/10.3390/app8060940
Chicago/Turabian StyleZhu, Yipeng, Minglei Shan, Yu Yang, Qingbang Han, Changping Zhu, and Xuewu Zhang. 2018. "Effect of Wettability on Collapsing Cavitation Bubble near Solid Surface Studied by Multi-Relaxation-Time Lattice Boltzmann Model" Applied Sciences 8, no. 6: 940. https://doi.org/10.3390/app8060940
APA StyleZhu, Y., Shan, M., Yang, Y., Han, Q., Zhu, C., & Zhang, X. (2018). Effect of Wettability on Collapsing Cavitation Bubble near Solid Surface Studied by Multi-Relaxation-Time Lattice Boltzmann Model. Applied Sciences, 8(6), 940. https://doi.org/10.3390/app8060940




