A Comparative Study on Violent Sloshing with Complex Baffles Using the ISPH Method

Featured Application

This research aims to explore an effective baffle configuration to mitigate the sloshing effect in engineering practice for the purpose of safe navigation.

Abstract

The Smoothed Particle Hydrodynamics (SPH) method has become one of the most promising methods for violent wave impact simulations. In this paper, the incompressible SPH (ISPH) method will be used to simulate liquid sloshing in a 2D tank with complex baffles. Firstly, the numerical model is validated against the experimental results and the simulations from commercial CFD software STAR-CCM+ for a sloshing tank without any baffle. Then various sloshing tanks are simulated under different conditions to analyze the influence of the excitation frequency and baffle configuration. The results show that the complex baffles can significantly influence the impact pressures on the wall caused by the violent sloshing, and the relevant analysis can help find the engineering solutions to effectively suppress the problem. The main purpose of the paper is to study the practical importance of this effect.

1. Introduction

The phenomenon of liquid sloshing is frequently observed in marine and offshore engineering. It occurs in a partially filled container due to external excitation on the inside liquid. If the excitation frequency is close to the natural frequency of the tank, the liquid container is subject to tremendous impact load, which may cause serious damage to the hull structure. Such a consequence would be very serious in engineering practice [1]. Therefore, it is necessary to study the sloshing characteristics and analyze the influence of excitation frequency, aiming to find the solutions on damping the liquid sloshing and reducing the impact loads.

Now, the common techniques for analyzing the sloshing problem include theoretical, experimental, and numerical methods. Theoretical approaches, such as the analytical solution [2,3,4] or the potential flow theory based method [5,6], can be used to study sloshing tanks of relatively simple geometry and internal structure. Experimental works, on the other hand, have been carried out to study the sloshing behavior in tanks with more complex shapes under different external excitations [7], in spite of the high expenses of site and facility. In recent years, numerical simulations have been playing an increasingly greater role in the study of liquid sloshing, and most are carried out by using grid-based methods, such as the finite element [8] and finite difference [9] methods. However, these conventional methods cannot easily track the movement of the free-surface automatically, which undergoes large deformations in the violent sloshing. To track the moving free surface in a conventional Eulerian grid approach, additional surface tracking techniques such as the Marker-in-Cell and Volume-of-Fluids must be used. The former uses the marker particles to define the free surface while the latter solves a transport equation for the volume fraction of fluid. However, in both cases the Navier–Stokes (N–S) equations are solved on a fixed Eulerian grid and potential problems of numerical diffusion can arise due to advection terms in the N–S equations. This problem becomes serious when the deformation of the free surface is large, such as in a liquid sloshing when the treatment of the surface cells becomes extremely complicated. As one potential substitute, the mesh-free numerical modeling method has attracted a lot of attention in the last decade [10]. The Smoothed Particle Hydrodynamics (SPH) method, which originates in astrophysics, provides a promising tool to model a wide range of free surface flow problems. One of the great advantages of the SPH modeling technique is that particles move in Lagrangian coordinates and the advection term in the N–S equation is directly calculated by the particle motion through particle interaction models. Thus, free surfaces can be conveniently and accurately tracked by the particles without numerical diffusion or extra surface tracking algorithms, which is always required in the traditional Eulerian approaches. For both the grid and particle modeling techniques, the discretization scheme heavily depends on the density of points and therefore on their total numbers; i.e., spatial resolution. However, each point in the SPH can move freely, which is more suitable to treat the large deformation and discontinuous free-surfaces. The mesh-less methods have become one of the most promising approaches for simulating the violent liquid sloshing and also include the Moving Particle Semi-implicit (MPS) method [11] and Mesh-less Local Petrov–Galerkin method based on the Rankine source solution (MLPG_R) [12]. In coastal and offshore applications, the SPH method is one of the most popular particle modeling tools and has shown to provide a promising solution platform on liquid sloshing and its interaction with various complex internal baffles [13,14,15,16,17].

Currently, changing the geometric shape of the sloshing tank and installing the baffles are the two major practices to dampen the liquid sloshing. Since it is not so easy to change the geometric shape of the tank by a large margin, the installation of baffles in the tank becomes the primary way to constrain the liquid sloshing. Quite a few studies on liquid sloshing in the tank with different baffles have been documented. For example, Biswal et al. [18] studied the effect of horizontal baffles on liquid sloshing. Panigrahy et al. [19] studied liquid sloshing in a rectangular tank with ring baffles and monitored the pressure variation on the tank walls and the surface elevation. Xue and Lin [20] simulated a sloshing tank with both horizontal and vertical baffles by using a virtual boundary force (VBF) method and explored the reduction of violent sloshing. Goudarzi and Sabbagh-Yazdi [21] made various experiments to study the influence of horizontal and vertical baffles. Besides, Goudarzi and Danesh [22] also studied liquid sloshing in a rectangular tank with vertical baffles under seismic excitation. In this paper, liquid sloshing in a rectangular tank with complex baffles will be studied by using the incompressible SPH (ISPH) method. Through a comparison of different combinations of horizontal and vertical baffles, the effect of these internal structures on reducing the impact pressure is studied. The aim of this study is to identify the most effective baffle configuration to protect the container structure so as to mitigate sloshing problems in practical engineering.

2. ISPH Methodology

The standard SPH approach (i.e., weakly compressible SPH) has quite a few appealing advantages; it is easy to program and does not involve the pressure boundary problem. However, it can cause substantial spurious pressure fluctuations unless some additional correction schemes are used to overcome the issue. An alternative ISPH numerical scheme has emerged as a result. It essentially projects the intermediate velocity of particles onto a divergence-free space or their intermediate density onto a density-invariance field by solving a pressure Poisson equation based on strict hydrodynamic formulations [23]. The ISPH model is based on the semi-Lagrangian form of the continuity equation and momentum equations, in which fluid density is considered to be a constant, and thus the governing equations are written as follows:

$$\nabla ·\mathit{u}=0$$

(1)

$$\frac{D\mathit{u}}{Dt}=-\frac{1}{\rho }\nabla P+\mathit{g}+{\nu }_0{\nabla }^2\mathit{u}$$

(2)

where $\rho$ is the fluid density; $\mathit{u}$ is the particle velocity; $t$ is the time; $P$ is the particle pressure; $\mathit{g}$ is the gravitational acceleration; and ${\nu }_0$ is the kinematic viscosity. A two-step projection method is used to solve the velocity and pressure fields of Equations (1) and (2). The first step is the prediction of velocity in the time domain without considering the pressure term. The intermediate particle velocity ${\mathit{u}}^{*}$ and position ${\mathit{r}}^{*}$ are obtained by

$${\mathit{u}}^{*}={\mathit{u}}^t+\Delta {\mathit{u}}^{*},$$

(3)

$$\Delta {\mathit{u}}^{*}=\left(\mathit{g}+{\nu }_0{\nabla }^2\mathit{u}\right)\Delta t,$$

(4)

$${\mathit{r}}^{*}={\mathit{r}}^t+{\mathit{u}}^{*}\Delta t$$

(5)

where ${\mathit{u}}^t$ and ${\mathit{r}}^t$ are the velocity and position at time $t$; $\Delta t$ is the time step; $\Delta {\mathit{u}}^{*}$ is the velocity increment; and ${\mathit{u}}^{*}$ and ${\mathit{r}}^{*}$ are the intermediate velocity and position of the particle.

The second step is the correction step in which the incompressibility is imposed, and $\Delta {\mathit{u}}^{**}$ is the change of velocity in the correction step

$$\Delta {\mathit{u}}^{**}=-\frac{1}{\rho }\nabla P^{t+\Delta t}\Delta t$$

(6)

The following ${\mathit{u}}^{t+\Delta t}$ and ${\mathit{r}}^{t+\Delta t}$ represent the velocity and position of the particle at the next time step

$${\mathit{u}}^{t+\Delta t}={\mathit{u}}^{*}+\Delta {\mathit{u}}^{**}$$

(7)

$${\mathit{r}}^{t+\Delta t}={\mathit{r}}^t+\frac{{\mathit{u}}^t+{\mathit{u}}^{t+\Delta t}}{2}\Delta t$$

(8)

The key process in the second step is to solve the pressure Poisson equation (PPE) to obtain the pressure field. By combining Equations (1) and (6), the PPE is written as follows:

$${\nabla }^2{P}^{t+\Delta t}=\frac{\rho \nabla ·{\mathit{u}}^{*}}{\Delta t}$$

(9)

On the other hand, Shao and Lo [23] proposed a projection-based incompressible approach by imposing the density invariance on each fluid particle, leading to the following PPE form:

$$\nabla ·\left(\frac{1}{{\rho }^{\ast }}\nabla P^{t+\Delta t}\right)=\frac{{\rho }_0-{\rho }^{\ast }}{{\rho }_0\Delta t^2}$$

(10)

where ${\rho }^{\ast }$ is the particle density at the intermediate time step; and ${\rho }_0$ is the original density of the fluid particle, which is set at the beginning of the computation.

Due to the fact that ${\rho }^{\ast }/{\rho }_0$ is very close to unity, the difference between ${\rho }^{\ast }$ on the left and ${\rho }_0$ on the right hand side of Equation (10) can be reasonably ignored, and the alternative form of PPE incorporating the influence of both velocity divergence and density variation of the particles can be written as

$${\nabla }^2{P}^{t+\Delta t}=\alpha \frac{{\rho }_0-{\rho }^{\ast }}{\Delta t^2}+\left(1-\alpha \right)\frac{{\rho }_0\nabla ·{\mathit{u}}^{*}}{\Delta t}$$

(11)

where $\alpha$ is a tuning coefficient and a value of 0.01 is adopted in this paper based on the computational experience. More advanced PPEs with the error-compensating source term (ECS) are documented by [24,25]. The treatment of free surface and solid boundary conditions follows the study of Zheng et al. [26].

For the tuning coefficient $\alpha$, it should be noted that in the ISPH computation, if this value is too large, the left term on the RHS equation dominates. Therefore, the density-invariance effect is larger and the incompressibility of fluid is better conserved. However, this may lead to substantial pressure noises and particle randomness. On the other hand, if this tuning value is too small, the right term on the RHS of Equation (11) dominates and the flow is more controlled by the velocity divergence-free criterion. As a result, a more smooth and stable velocity and pressure field can be achieved, but the incompressibility of the fluids may be violated. A delicate balance should be found depending on a variety of influence factors such as the particle resolution and application case. We tried different values of this coefficient to achieve the best match with benchmark data in our previous work. It has been found that a value of around 0.01 is more or less suitable for violent flow processes such as dam break or liquid sloshing with a large deformation of the free surface.

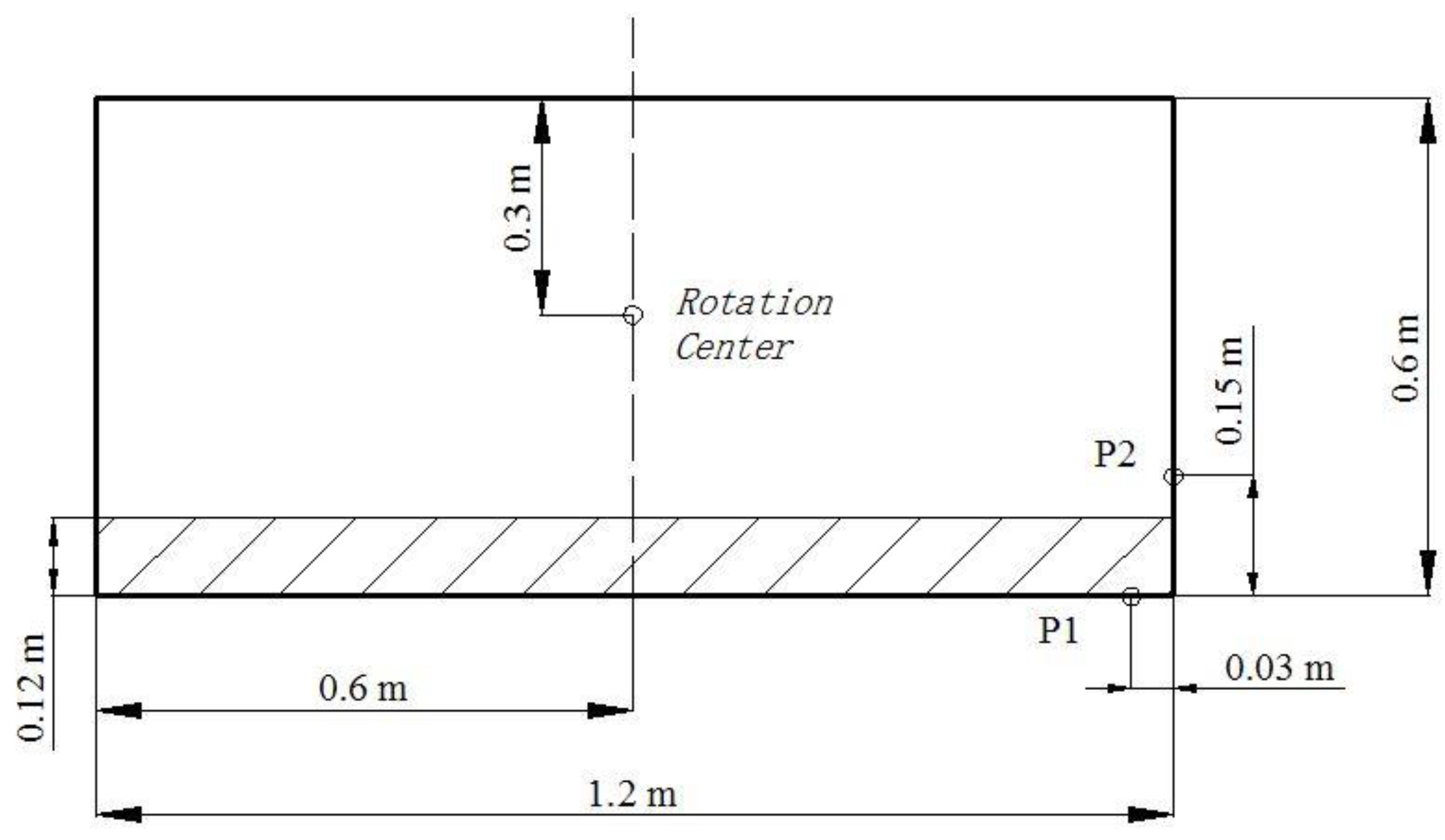
3. Model Validation and Convergence Analysis

In order to validate the accuracy of the sloshing computation by using the ISPH method, the numerical results of the sloshing tank are compared with the experimental data of Liao and Hu [27] and the computations by using the commercial CFD software, i.e., STAR-CCM+. In STAR-CCM+, the 2D viscous incompressible Navier–Stokes equations are solved. The conservation equations for the mass and momentum are based on the Reynolds averaged methods. The standard $k-\epsilon$ turbulence model and Eulerian two-phase model are used. The free surface is captured by the volume of fluid (VOF) approach.

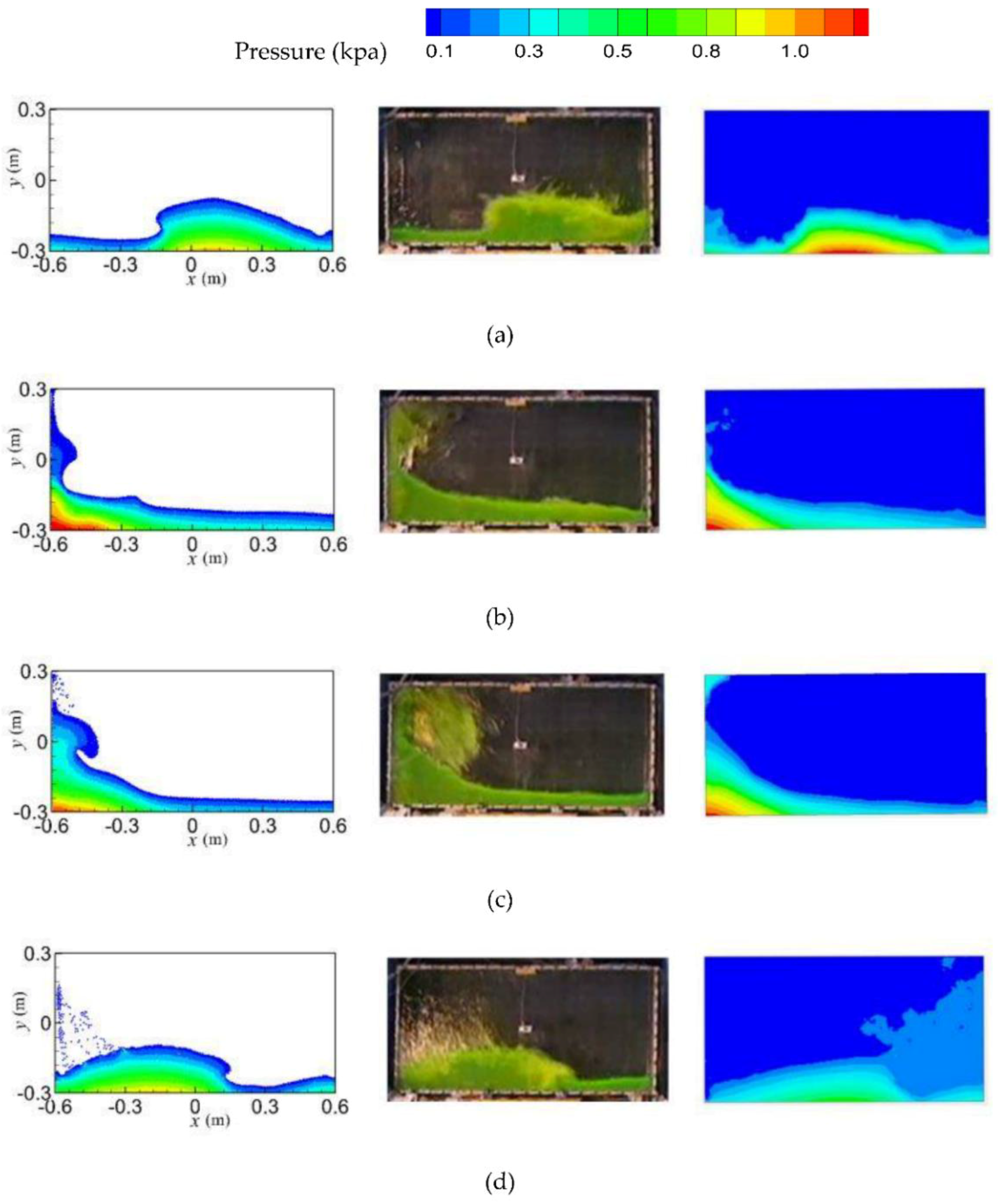
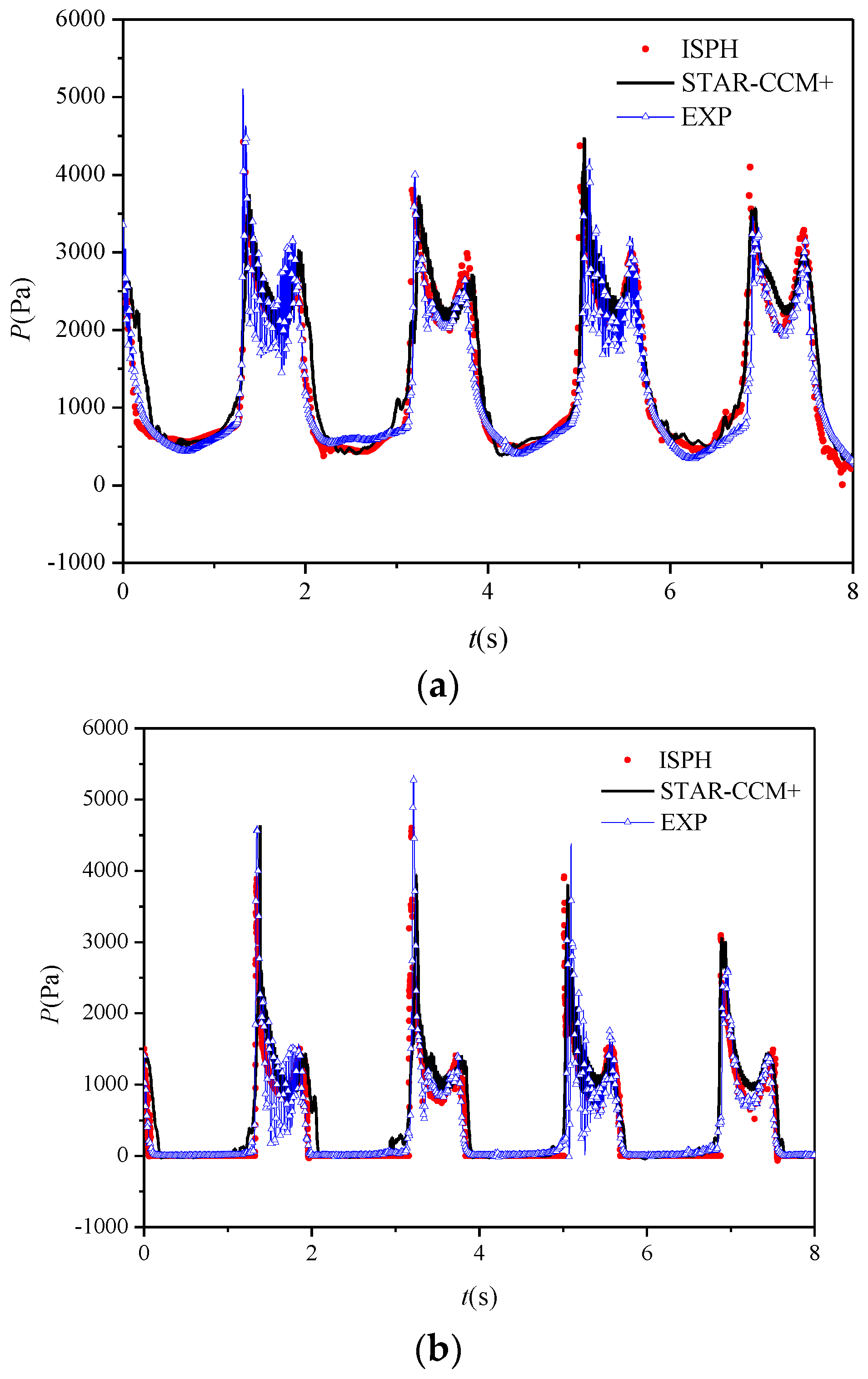
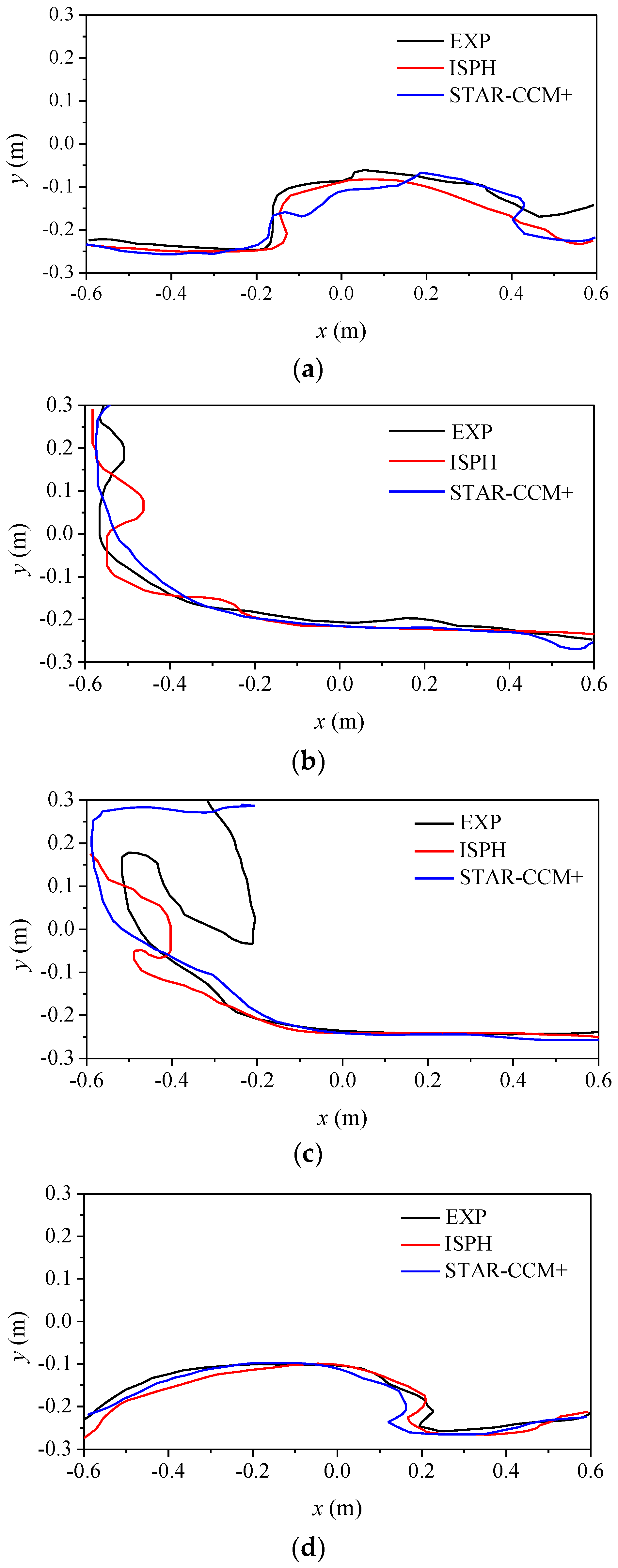
3.1. Model Validations through Experiment

In this section, a sloshing tank without any baffle is simulated by the ISPH method and the results are compared with the experimental data of Liao and Hu [27] as well as numerical computations from STAR-CCM+. A schematic view of the numerical tank is shown in Figure 1, where the geometry of the sloshing tank and the location of the pressure sensors are provided. In the experiment, the tank experienced a forced harmonic rolling motion with an amplitude 10° and an excitation period 1.85 s. The initial water depth is 0.12 m and the tank is rotated at the geometric center. Although the study of Liao and Hu [27] focused on violent flow dampening through an elastic plate, their fluid model was first validated without the existence of the plate. Generally speaking, a large deformation of the free surface and dynamic impact pressure inside the tank are the two main factors for the evaluation of sloshing hazards and these were recorded in the experiment. In the ISPH computation, a particle size dx = 0.002 m is used, corresponding to the same basic cell size in STAR-CCM+. Both models used a time step of dt = 0.0003 s for consistency. The numerical data is extracted for 8 s after the initial transient period or initial cycle, which lasts for around 1–2 times the sloshing period T, so as to include sufficient data series to illustrate the repeatability of the flow histories. There is no information available on the experimental transient phase.

Figure 2 provides the comparisons of the free surface profiles between the experimental photos and the numerical results for half of the sloshing period T. Both of the ISPH and STAR-CCM+ computations are shown for a comparison with their internal pressure contours. Overall features of the violent sloshing process have been captured by the two numerical models in a very satisfactory manner. These include the turbulent bore propagation at the time origin, running against the tank wall, plunging down and collapsing, and then propagating in the opposite direction. Generally speaking, it seems that the ISPH captured the sloshing free surface much better than STAR-CCM+ and produced closer surface profiles with the experimental recordings. Even if the flow situation is rather complex, the ISPH computed pressure contours show a very stable pattern without much noise while the particle distributions are fairly regular, even near the free surface.

For quantification of the model accuracy and the pressure time histories at two sensor points (P1 and P2) are compared between the ISPH/STAR-CCM+ computations and the experimental data of Liao and Hu in Figure 3a,b, respectively. Although both models seem to over-predict the measured peak values at P1 and under-predict them at P2, the arrival time of peak pressure, its amplitude and evolution, especially the two-peak pressure patterns, have all been captured with good accuracy. It should be noted that the impact pressure in violent flows is always a difficult parameter to forecast, but the present ISPH method provides a promising reproduction due to its mesh-free nature. Furthermore, it should also be noted that the pressure history patterns of Figure 3a,b look quite different. This is due to the fact that P1 is located on the tank bottom, which is always submerged under the liquid, while P2 is near the alternation region between the water and air; thus it experiences more pressure fluctuations and the relevant pressure peaks become much narrower. Although both of the ISPH and STAR-CCM+ computations provided a reasonable match with the experimental pressures, the former looks better in the general agreement with an averaged error of 0.4% at both pressure gauging points. On the other hand, STAR-CCM+ reached an averaged error of 0.8% at P1 and 1.5% at P2.

Further comparisons of the spatial variation of the water surface profiles are shown in Figure 4a–d, for half of the sloshing period T. Again, a generally better agreement with the experimental surface data by the ISPH computations is clearly demonstrated. Both numerical models poorly predict the overturning water column at time t = T/3 on the left wall, but the ISPH results better reproduced the practical situation and captured the overall surface shape. This is the region of complex flow with stronger turbulence and two-phase effects, so much more refined numerical resolutions would be expected to provide an accurate prediction.

3.2. Model Convergence and CPU Analyses

To study the convergence of the two numerical models and compare their CPU efficiency, three different particle spacings and grid sizes have been used by ISPH and STAR-CCM+, respectively, to examine their performance on the computation of wave impact pressures at P1 and P2 on the tank wall with a simulation time of 10 s. The numerical errors with the experimental data of Liao and Hu [27] are quantified for each simulation test by using the following formula and the results are summarized in

Table 1. Numerical error and CPU analyses of ISPH and STAR-CCM+.

Models	Grid/Particle No.	Grid/Particle Size (m)	CPU Time (h)	Er (P1)	Er (P2)
STAR-CCM+	11,589	0.01	11.1	2.42%	3.32%
	45,376	0.004	32.2	0.92%	1.69%
	88,463	0.002	72.5	0.82%	1.52%
ISPH	9000	0.004	1.3	1.77%	1.35%
	16,000	0.003	2.8	0.97%	0.93%
	49,000	0.002	7.2	0.40%	0.36%

.

$$Er=\frac{1}{M}{\displaystyle \sum }_{i=1}^M\left|\frac{\widetilde{P\left(t\right)}-P\left(t\right)}{P\left(t\right)}\right|$$

(12)

where $Er$ is the defined mean error; $\widetilde{P\left(t\right)}$ is the numerical value of pressure; $P\left(t\right)$ is the experimental value of pressure; and M is the number of sampling points.

By using the convergence evaluation of Zheng et al. [26], the ISPH numerical scheme was found to be second-order accurate while the STAR-CCM+ only achieved a first-order accuracy. Besides, the comparisons of CPU time in Table 1 further evidence that ISPH is more computationally efficient than STAR-CCM+ by saving around one order of CPU expenses due to its mesh-free solution scheme, which was achieved because it does not need to use an additional free-surface tracking technique. Also, the single-phase solution of ISPH as compared with the two-phase one of STAR-CCM+ further saved computational cost. However, it should be noted that the CPU increase in STAR-CCM+ is linearly proportional to the increase of grid resolution, while this is quadratic in ISPH. This is a result of the neighboring particle search in ISPH being a very time-consuming process, which roughly requires the computational load of N², where N is the total particle number.

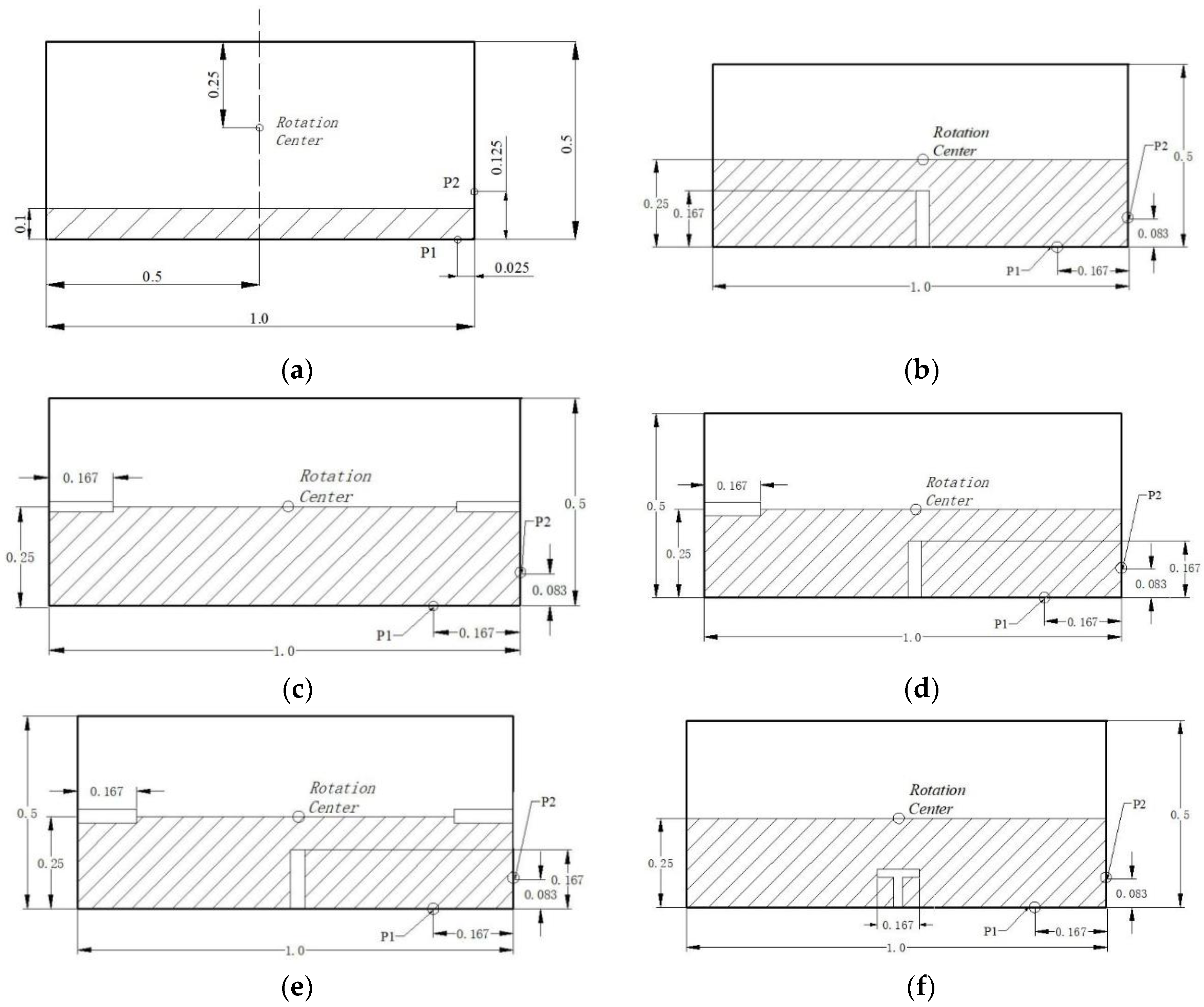
4. Configurations of Different Complex Baffles

To evaluate the influence of sloshing dampening by using different configurations of the complex baffle, a series of practical designs are illustrated in this section. For generality, the length scale of the sloshing tank, the internal baffles, and their installation positions have been normalized by the length of the sloshing tank; i.e., L = 1.2 m, as used in the previous section of model validation. In total, five different baffle configurations are investigated in the present study and the schematic view of each design scenario is shown in Figure 5a–f. These include a reference sloshing tank without any internal baffle, one vertical baffle, two horizontal baffles, one vertical and one horizontal baffle, one vertical and two horizontal baffles, and one T-shaped baffle.

To further evaluate the performance of each baffle configuration, either simple or complex, the length and installation height of these baffles are also altered to examine the collective effect on the sloshing pressure. A summary on the relevant key parameters of change is provided in

Table 2. Summary of different baffle configurations and external excitation conditions.

Baffle Type	Length	Distance from Bottom	Number of Particle	Excitation Frequency (rad/s)	Ω/Ω0
No baffle	----	----	22,500	1.5–5.0	0.3–1.2
One vertical only	0.083	----	22,275	1.5–5.0	0.3–1.2
	0.117	----	22,165
	0.167	----	22,000
	0.217	----	21,835
Two horizontal	0.167	0.117	21,825	2.0–5.0	0.5–1.2
		0.183
		0.250
One vertical and one horizontal		0.250	21,575	1.5–5.0	0.3–1.2
One vertical and two horizontal		0.250	21,275	1.5–5.0	0.3–1.2
One T-shaped only	0.083	----	21,710	1.7–4.5	0.4–1.1
	0.117	----	21,600
	0.167	----	21,435
	0.217	----	21,270

. Inside the Table, $\mathsf{\Omega }$ is the external excitation frequency and ${\mathsf{\Omega }}_0$ is the natural frequency of the sloshing tank without any baffle, calculated by

$${\mathsf{\Omega }}_0=\sqrt{(g\pi /L)\tanh (\pi d)/L}$$

(13)

where g is the gravitational acceleration, L is the length of the tank, and d is the depth of water.

During the design of the external excitation conditions as shown in Table 2, $\mathsf{\Omega }$ values have been selected in such a way that the maximum impact pressure for each baffle scenario can be captured, and also the normalized frequencies $\mathsf{\Omega }/{\mathsf{\Omega }}_0$ are more or less within a consistent range for all the design cases. In ISPH computations, the tank experiences a forced harmonic rolling motion with an amplitude of 10° and an excitation frequency as listed in Table 2. The tank is rotated at the geometric center, where P1 and P2 are the two locations of pressure monitoring. A particle size of dx = 0.004 m and a time step of dt = 0.00032 s are used for all the tests. The model is run for a sufficiently long time of 16 s to extract the stable numerical data and the repeatability of the sloshing flow condition is well achieved within the first 2–4 s, depending on the different baffle systems. The impact pressure on the tank wall due to the sloshing liquids is the main focus of the present study for the evaluation of the efficiency of various complex baffles.

The computed particle snapshots with pressure contours for the selected two cases in Figure 5d,e are shown in Figure 6, to illustrate the violent sloshing flow and strong fluid-structure interactions with the installed baffles for half of the sloshing period T. This qualitatively demonstrates the important role the baffles have played in the sloshing mitigation process, through which strong jet collisions and fluid–baffle actions dampened the flow energy. The smooth and noise-free stable pressure fields indicate the robustness of ISPH pressure solution scheme, which will support the following analyses of the impact pressures. The particle snapshots demonstrated the flow climbing up the baffles, running against the tank wall, returning back as a propagating bore, and eventually plunging down upon the water surface of the sloshing tank.

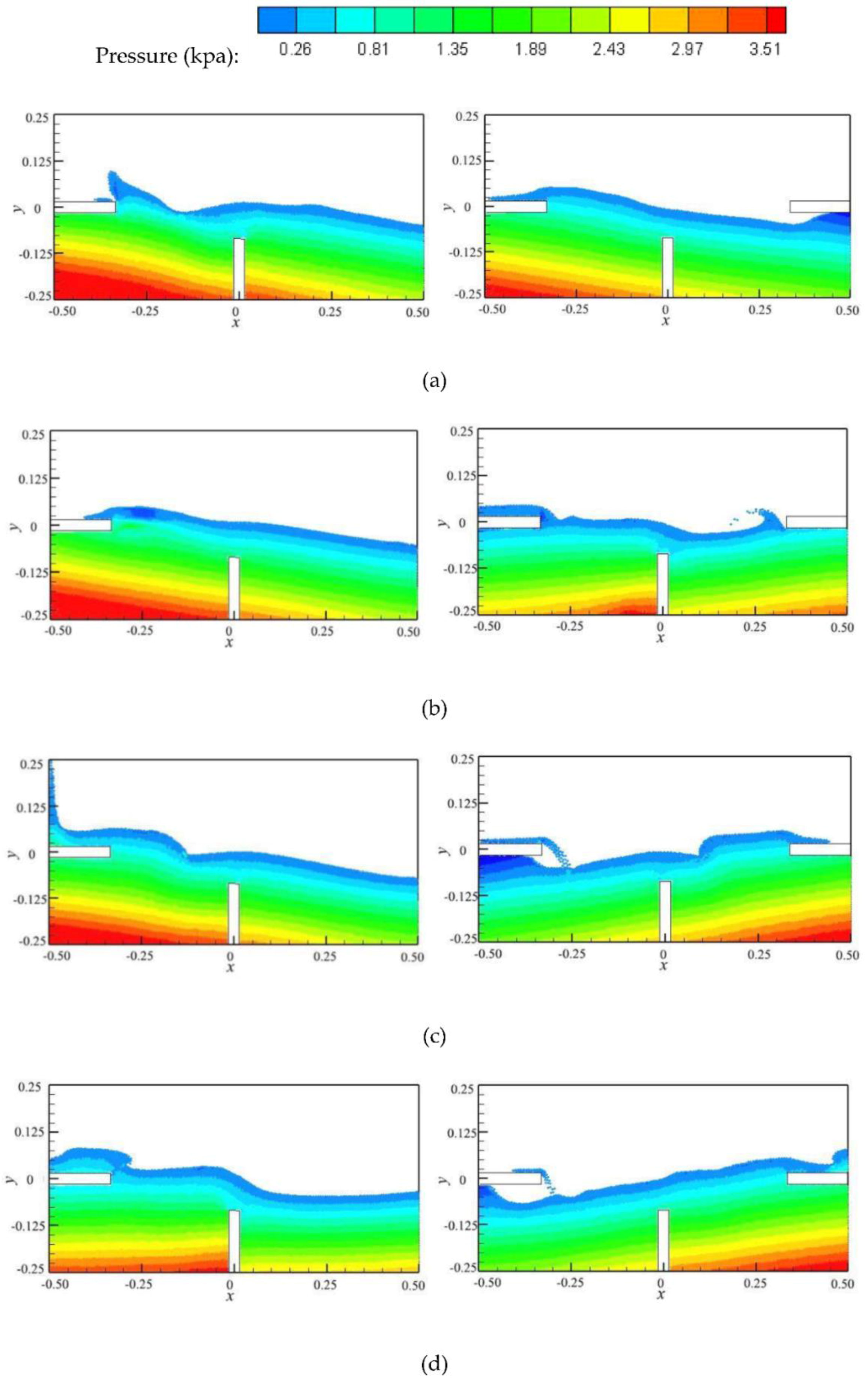
5. Analyses and Discussion

The main scientific problem discussed in this paper is the effect of different baffles on the liquid sloshing dampening, in form of the maximum impact pressure, under different external excitation frequencies.

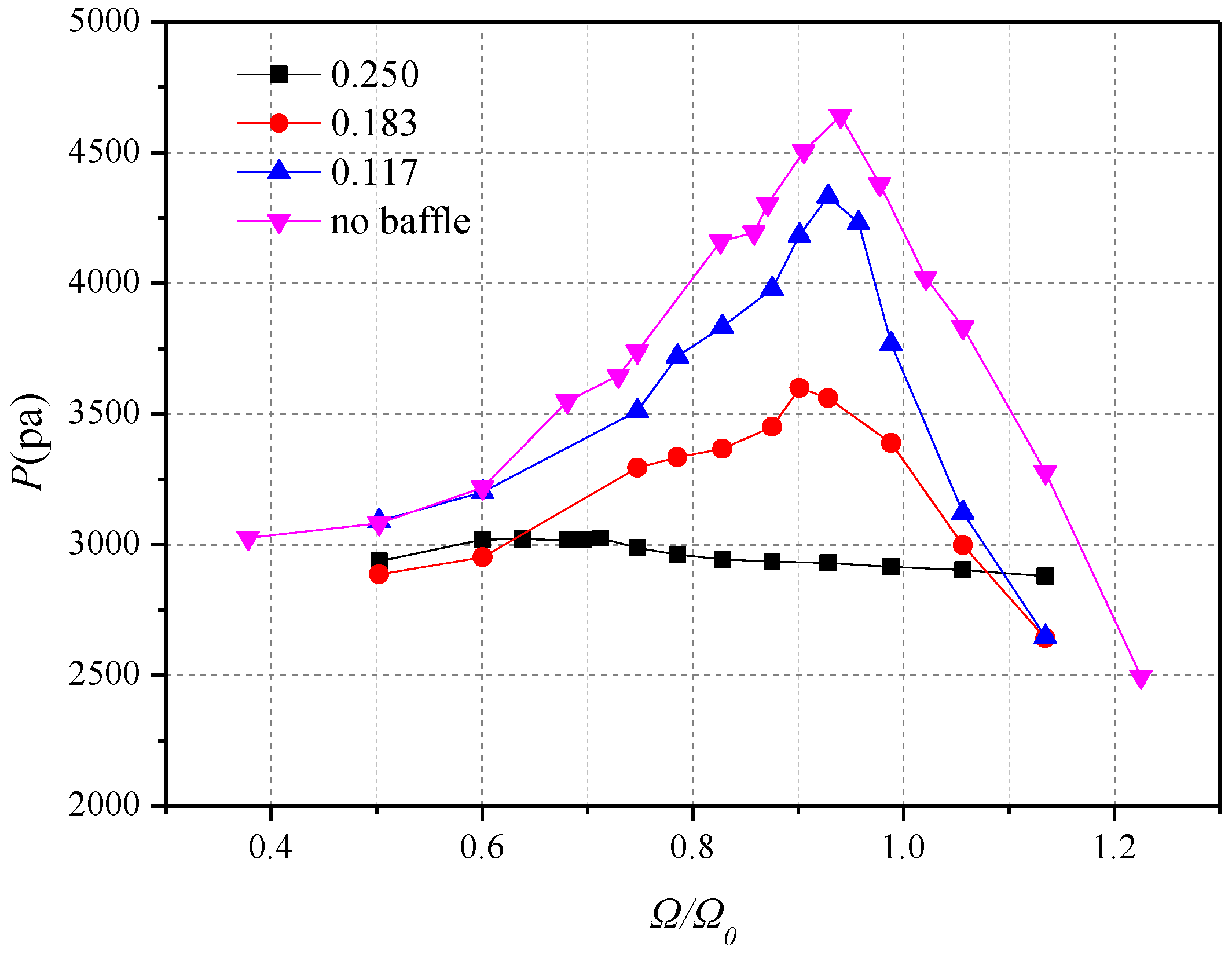
5.1. Height of Simple Vertical Baffle

In this section the liquid sloshing in a tank with a vertical baffle of various heights and under different excitation frequencies are computed and compared with the sloshing in a tank without any baffle. Using the baffle configuration in Figure 5b, a series of ISPH computations are made based on the parameters provided in Table 2. Through monitoring the impact pressures at P2 at every time step, picking up the maximum value of every sloshing period, and averaging across the frequencies, Figure 7 shows the maximum impact pressure at this location under the non-dimensional excitation frequencies of 0.3–1.2 for the normalized baffle height of 0.083–0.217. It can be seen that the pressure values decrease obviously when the sloshing tank is positioned with a vertical baffle, and also, they decrease accordingly with an increase of the baffle height. Through quantitative analysis, it is found that the maximum pressure is reduced by around 20% comparing the systems with and without a vertical baffle, and this difference reaches up to 38.2% when the highest baffle is installed. The findings demonstrate that installing a vertical baffle on the bottom of a sloshing tank is an effective way to reduce the impact load of sloshing liquids, especially when a higher baffle is installed.

5.2. Position Height of Two Horizontal Baffles

In this section, the liquid sloshing in a tank with two horizontal baffles installed on different positions under different excitation frequencies are compared. The configuration of the tank and baffles has been shown in Figure 5c, where the two horizontal baffles are installed at a normalized distance of 0.117–0.250 from the tank bottom. Figure 8 shows the maximum impact pressure at P2 computed by ISPH for the various installation heights under a range of non-dimensional frequencies. It can be seen that the effect on the liquid sloshing pressure improves obviously with an increase in the height placement of the horizontal baffles. It also shows that installing the horizontal baffles on the side wall near the water surface is the most effective way to reduce the impact pressure. This is evidenced by the fact that the evolution of the sloshing loads appears to be quite stable and the impact pressure is nearly kept at a constant, as shown in Figure 8, for the curve with normalized installation height of 0.250. Compared with the sloshing tank without any baffle, the impact pressure can be reduced by around 40%.

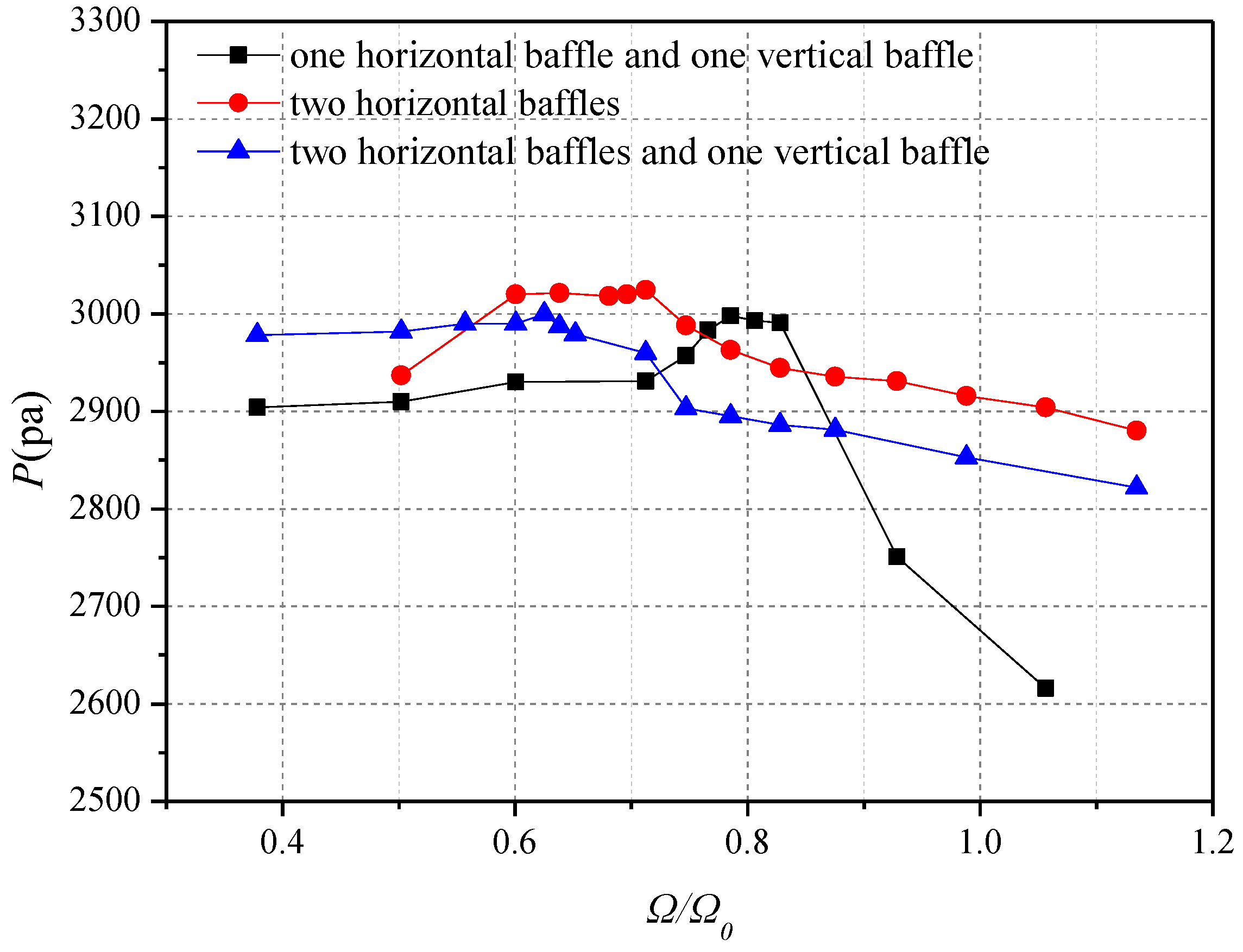
5.3. Combined Vertical and Horizontal Baffles

Now the liquid sloshing in a tank with two horizontal baffles, one horizontal, and one vertical baffle, and two horizontal and one vertical baffle, under different excitation frequencies are compared, and these correspond to the baffle configurations as shown in Figure 5c–e. As already mentioned in Section 5.1 and Section 5.2, it is considered that the horizontal baffles are installed on the tank wall with a normalized distance of 0.25 from the tank bottom, and the vertical baffle is located in the middle of the tank with a normalized height of 0.167.

Figure 9 shows the comparisons of maximum impact pressure at P2 for the three baffle configurations under non-dimensional excitation frequencies of 0.3–1.2, computed from the ISPH. Comparing the two horizontal baffles, with two horizontal and one vertical baffle, it can be seen that their performance on reducing the impact pressures is not much different, although the combined one is a little better but only by several percentages. Furthermore, the comparisons between the mixed baffles of two horizontal and one vertical baffle, and one horizontal and one vertical baffle, clearly showed that the maximum pressure value of the two is nearly the same. These imply that adding an additional horizontal baffle to the sloshing tank with an existing horizontal and vertical baffle cannot reduce the impact pressure loads beyond meager results.

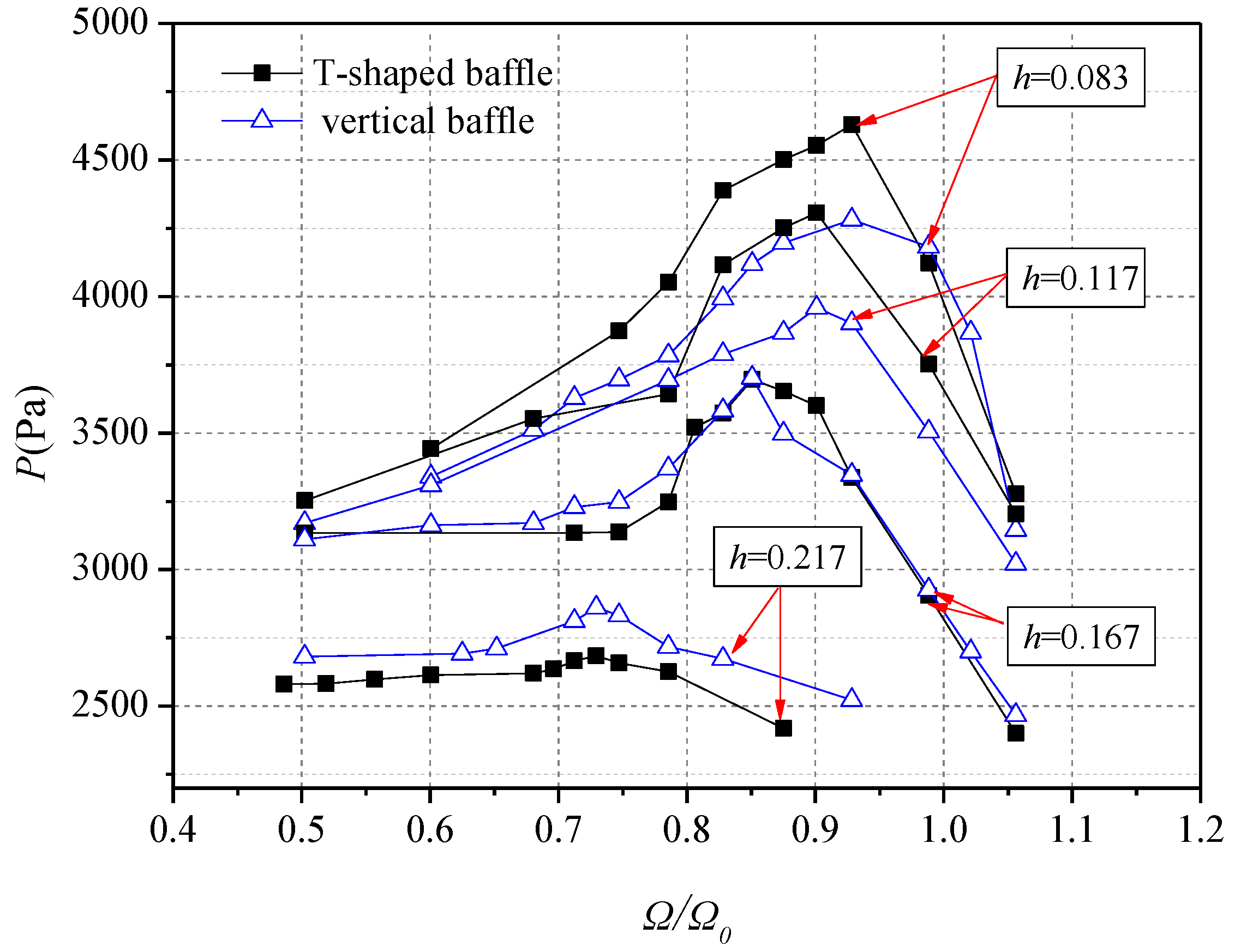
5.4. T-Shaped Baffle

Finally, a T-shaped baffle is investigated based on the configuration as shown in Figure 5f. By considering the different heights of T-shape baffle in Table 2, the maximum impact pressures at measuring point P2 with different excitation frequencies are provided in Figure 10. It shows that when the height of the baffle is lower, such as h = 0.083 and 0.117, the impact pressure of the sloshing liquid is higher than the corresponding one with only a normal vertical baffle. However, when the height of the T-shaped baffle increases to h = 0.167, its performance is similar to that of a simple vertical one. Furthermore, with the increase of the height to h = 0.217, the reduction of impact pressures through the T-shaped baffle becomes much more pronounced.

By further normalizing the designed flow depth of 0.3 m, it is found that when the ratio of the baffle height over water depth is smaller than 60%, the normal vertical baffle is better in view of reducing the impact pressure of the sloshing liquids. In between 60% and 70% of the two types of baffle have a similar performance. The T-shaped baffle demonstrates its superiority in reducing the sloshing loads when the height-to-depth ratio is greater than 70%.

6. Conclusions

The incompressible SPH method is used to simulate liquid sloshing in a tank with different configurations of the baffles, including one vertical baffle, two horizontal baffles, one vertical and one horizontal baffle, one vertical and two horizontal baffles, and one T-shape baffle. By comparison of the ISPH results with the experimental data and CFD software STAR-CCM+ computations, ISPH shows a better agreement in both the free surface profiles and the impact pressures for a sloshing tank without any baffles. Through follow-on model applications, ISPH demonstrated its great potential in predicting the fluid-structure interaction in violent sloshing flows. The main purpose of the paper is to study the practical importance of the effect.

The main conclusions of the paper are as follows. Firstly, installing baffles in the sloshing tank can dampen the liquid sloshing and reduce the impact load effectively. Secondly, increasing the length of the vertical baffle in the tank is useful for dampening the liquid sloshing surfaces and reducing impact pressures. Thirdly, the submerged depth of the horizontal baffles has a great effect on the sloshing damping and the free surface is the most effective position to place the horizontal baffles. Finally, the combination of one horizontal baffle and one vertical baffle has an excellent effect on the sloshing dampening, while adding an extra horizontal baffle to the tank shows little improvement in view of dampening the sloshing load. In summary, the maximum fluid impact pressure of the sloshing system can be controlled to some extent by effectively using a well-designed complex baffle system with optimum configurations. In reality, the baffles installed in the practical sloshing tanks are usually not rigid, so the baffles with hydro-elasticity [28,29,30] should be further studied in future works.

Moreover, the following issues should be noted as the model limitations in the present sloshing applications:

(1)

Both of the ISPH and STAR-CCM+ computations have been carried out in 2D. According to previous trials, it seems that not much difference has been generated between the 2D and 3D STAR-CCM+, at least for the water surface and impact pressure in the present sloshing flows;

(2)

The compressibility of entrapped air should have played an important role during the violent sloshing process, and a fully two-phase ISPH coupled model would provide an ultimate solution for such a process. The maximum Mach number of all the particles in the experimental validations remains nearly below 1%, which may have partially justified the use of the incompressible SPH model;

(3)

Using a full 3-D model compared with a 2-D model could lead to different flow fields when the turbulence model is employed. This could partially explain the numerical disagreement between STAR-CCM+ and ISPH in the model validations. As documented by Alberello et al. [31], the presence of turbulence produces fully three-dimensional flow structures in the breaking region at the tip of the wave crest. In the sloshing applications, the major interest would be the general free surface deformation and macro liquid impact pressure on the tank walls. Therefore, a 2D ISPH model could provide a reasonable engineering approximation;

(4)

SPH for the coastal and ocean engineering problems has been mainly used for impulsive wave impact on breakwater, and similar longer simulations are often performed with the more traditional CFD methods such as VOF;

(5)

Lastly, the existence of baffles can indeed change the resonance frequency of a sloshing tank and this effect can be quantitatively evaluated by [2,3,4]. However, under the resonance frequency, some nonlinear quantities such as impact pressure may not achieve the maximum but result in a slight phase shift, which has also been observed in [20]. In the present study, we mainly used the maximum impact pressure rather than other resonance quantities.