Stability Analysis of Mixed Convection Flow towards a Moving Thin Needle in Nanofluid
Abstract
:1. Introduction
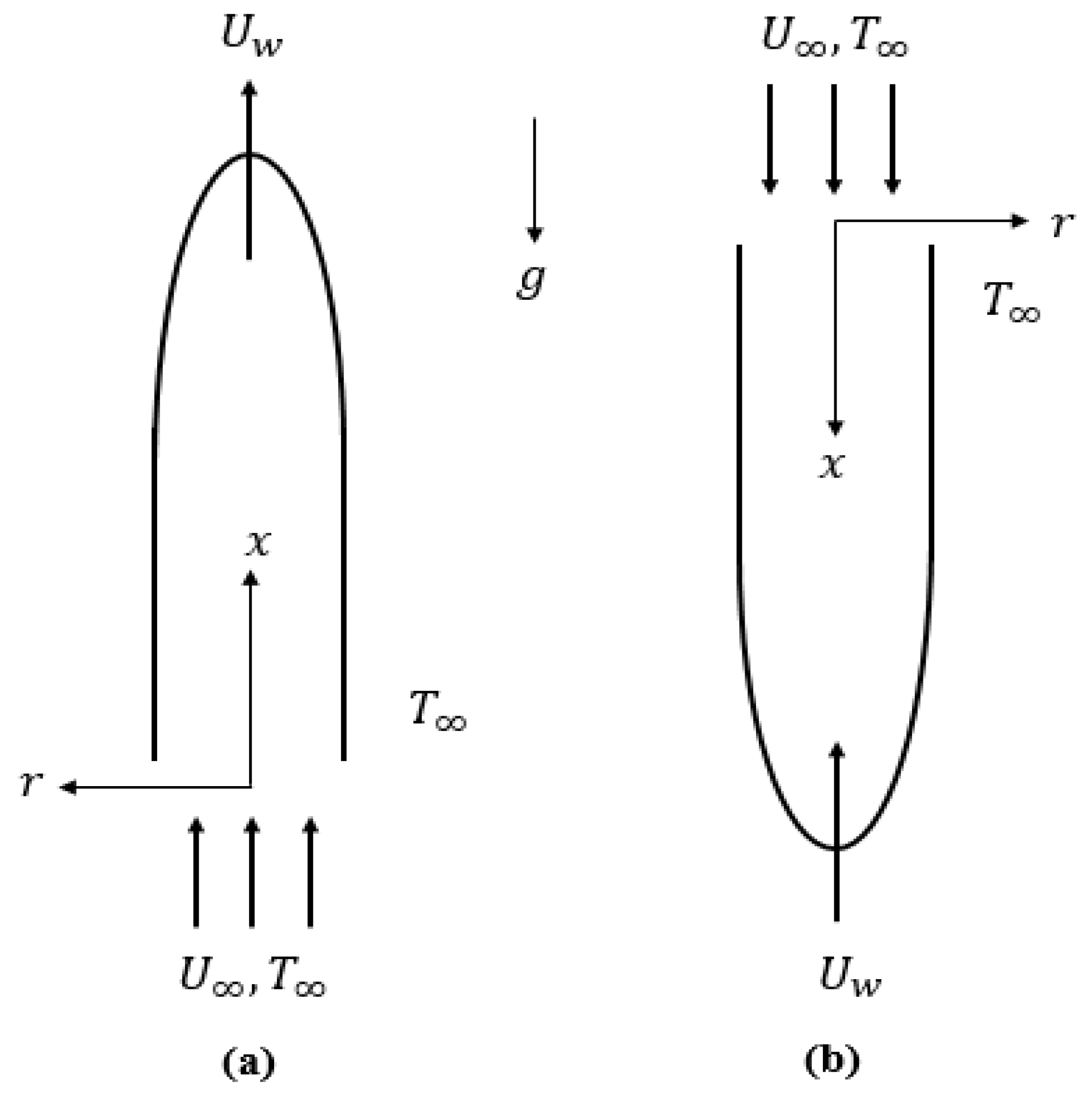
2. Problem Formulation
2.1. Basic Equation
2.2. Steady-State Solution
2.3. Stability Analysis
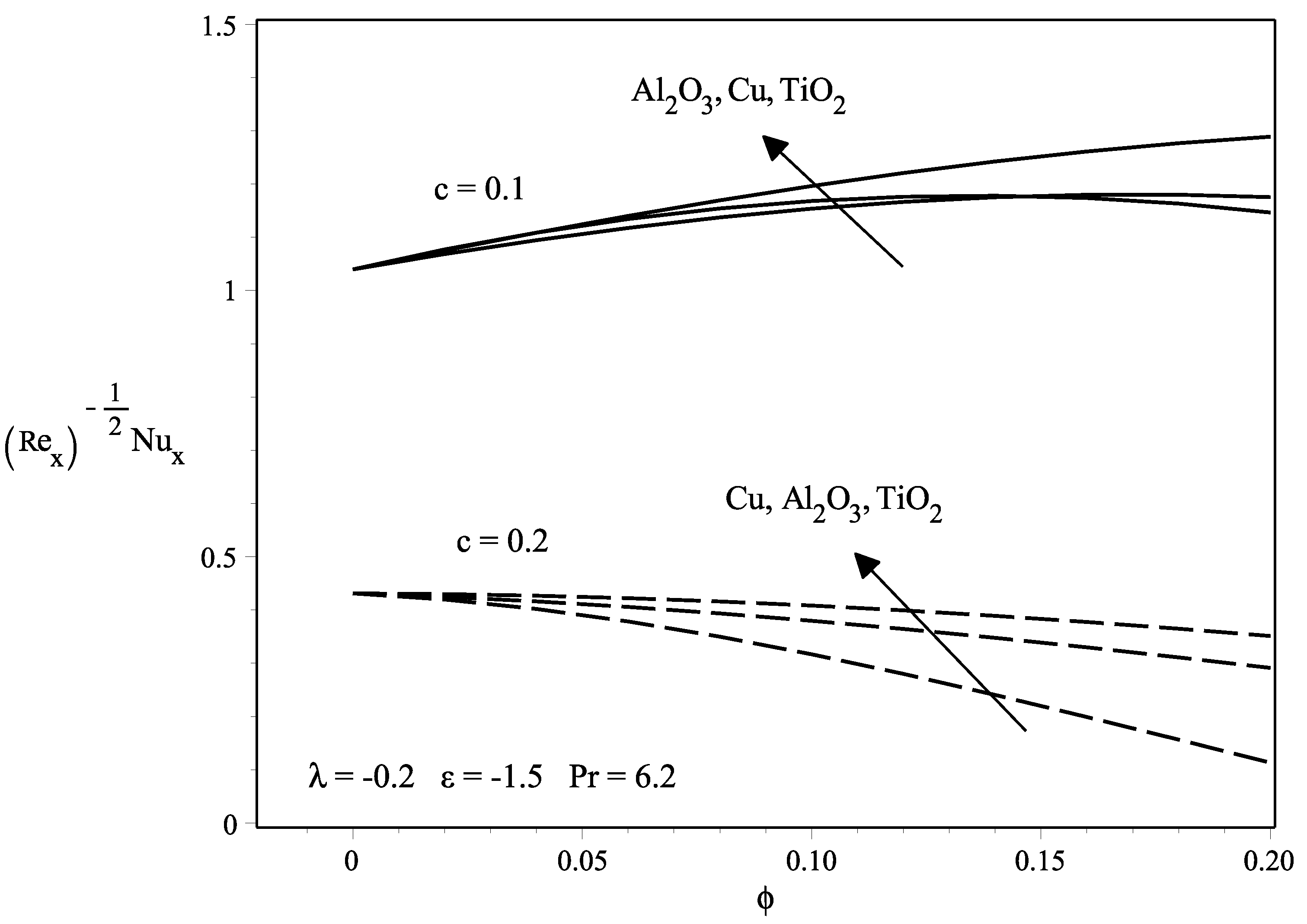
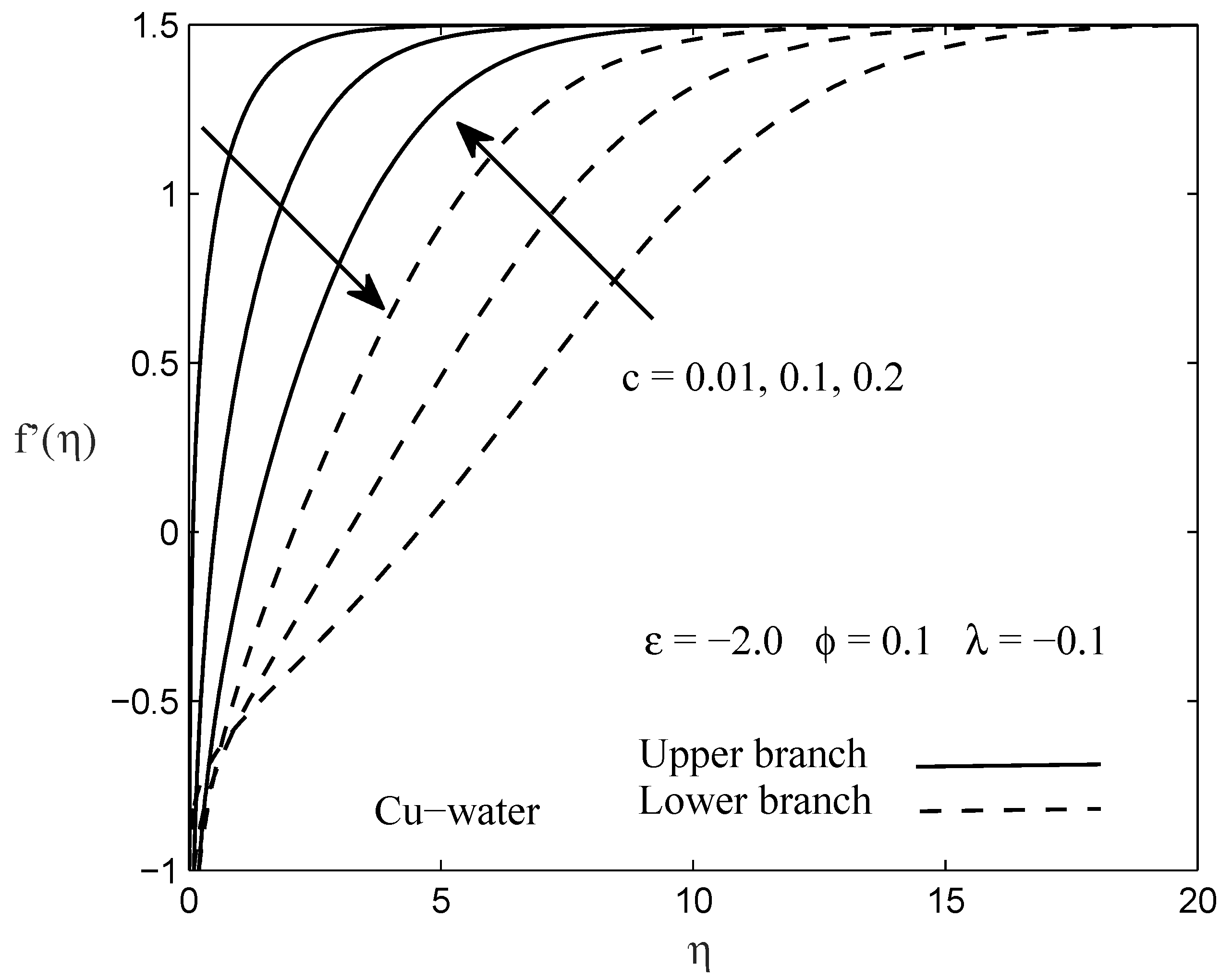
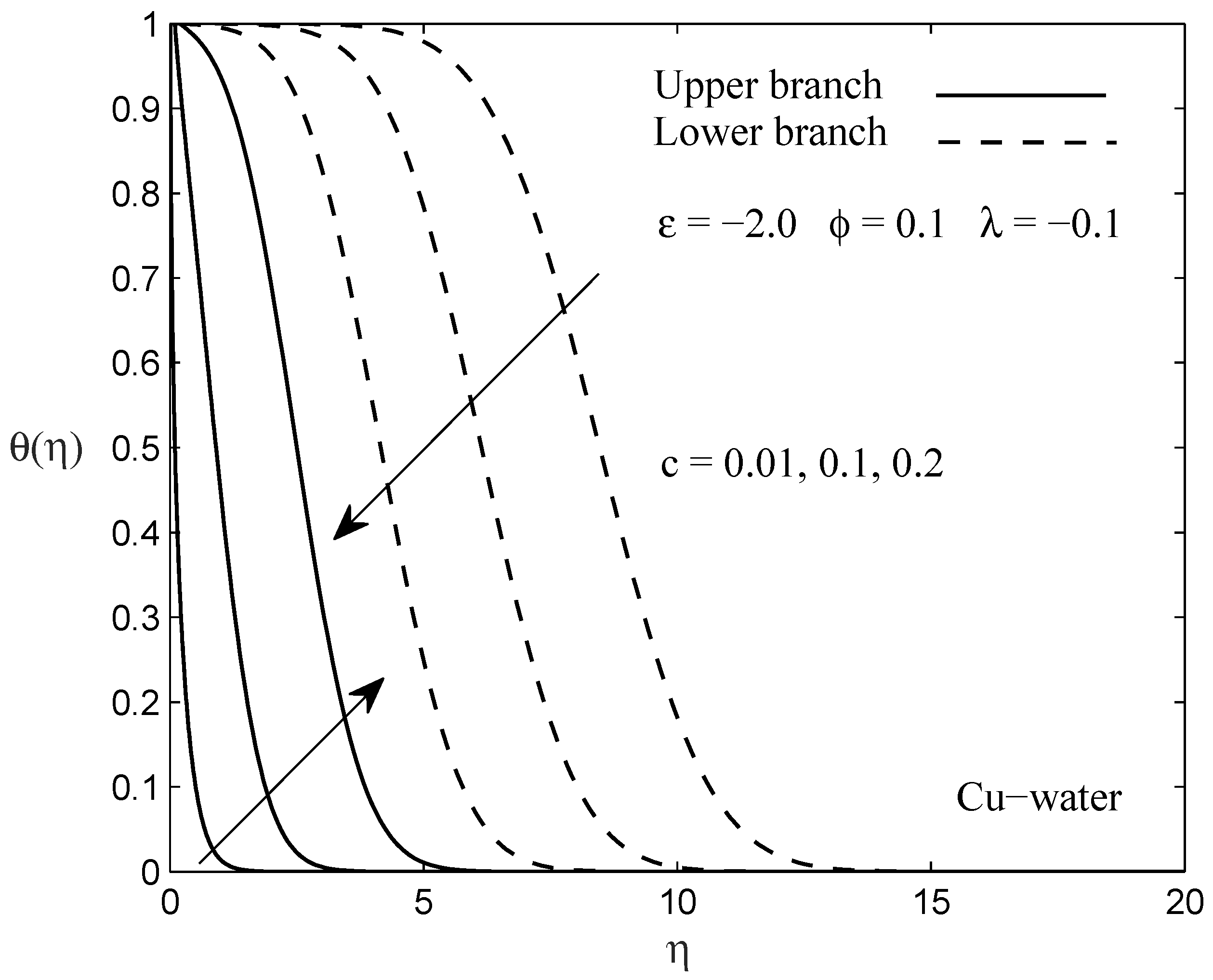
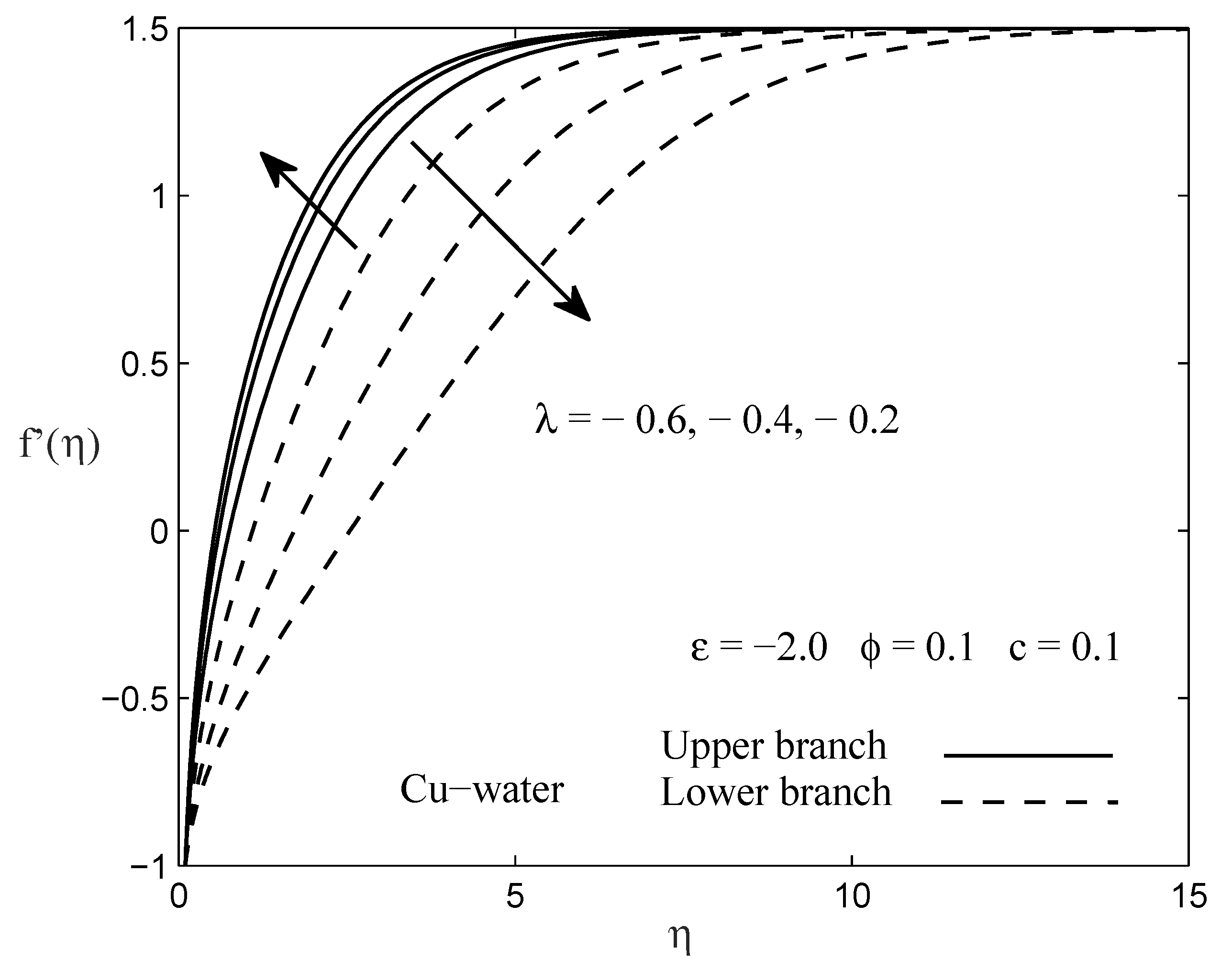
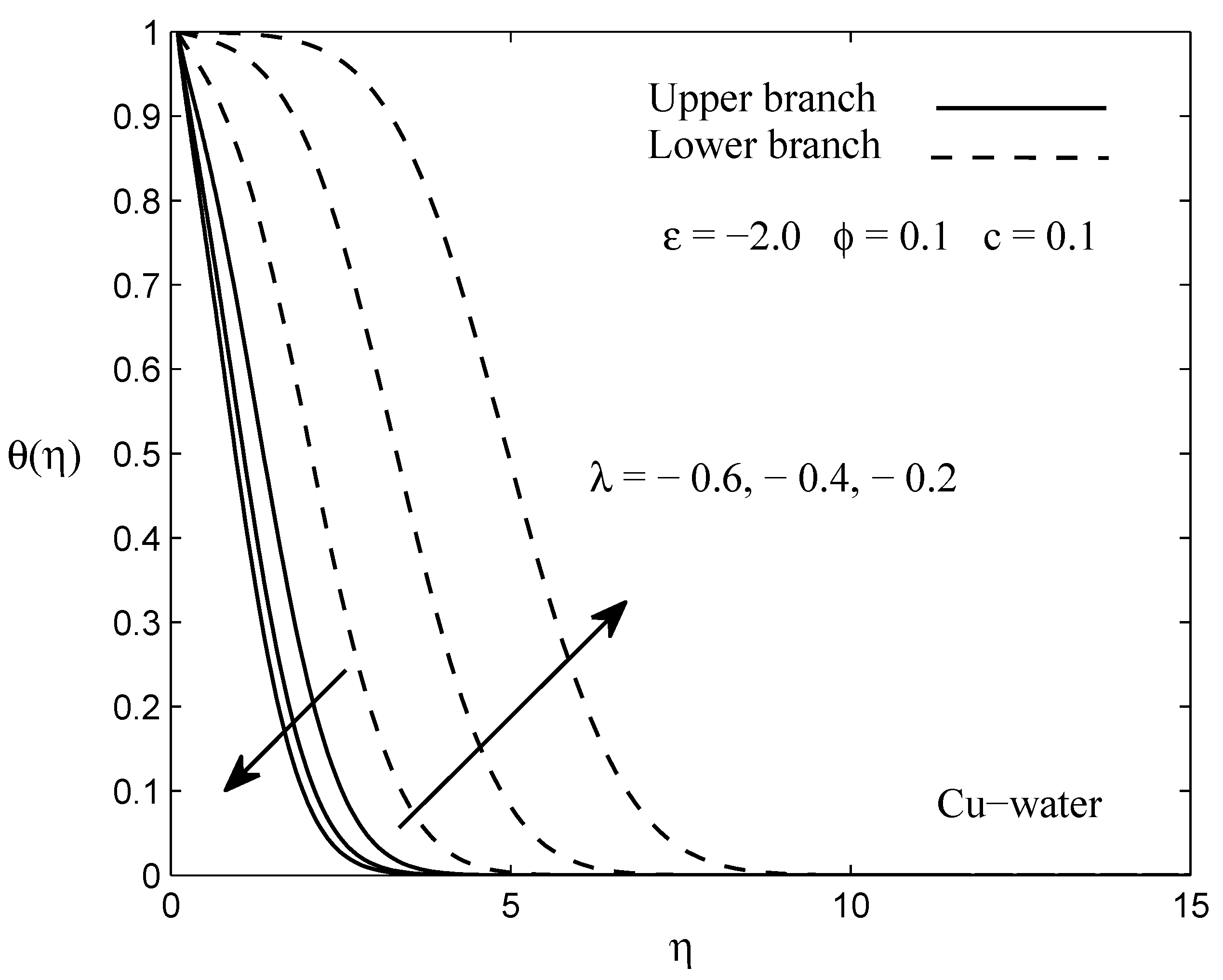
3. Results and Discussion
4. Conclusions
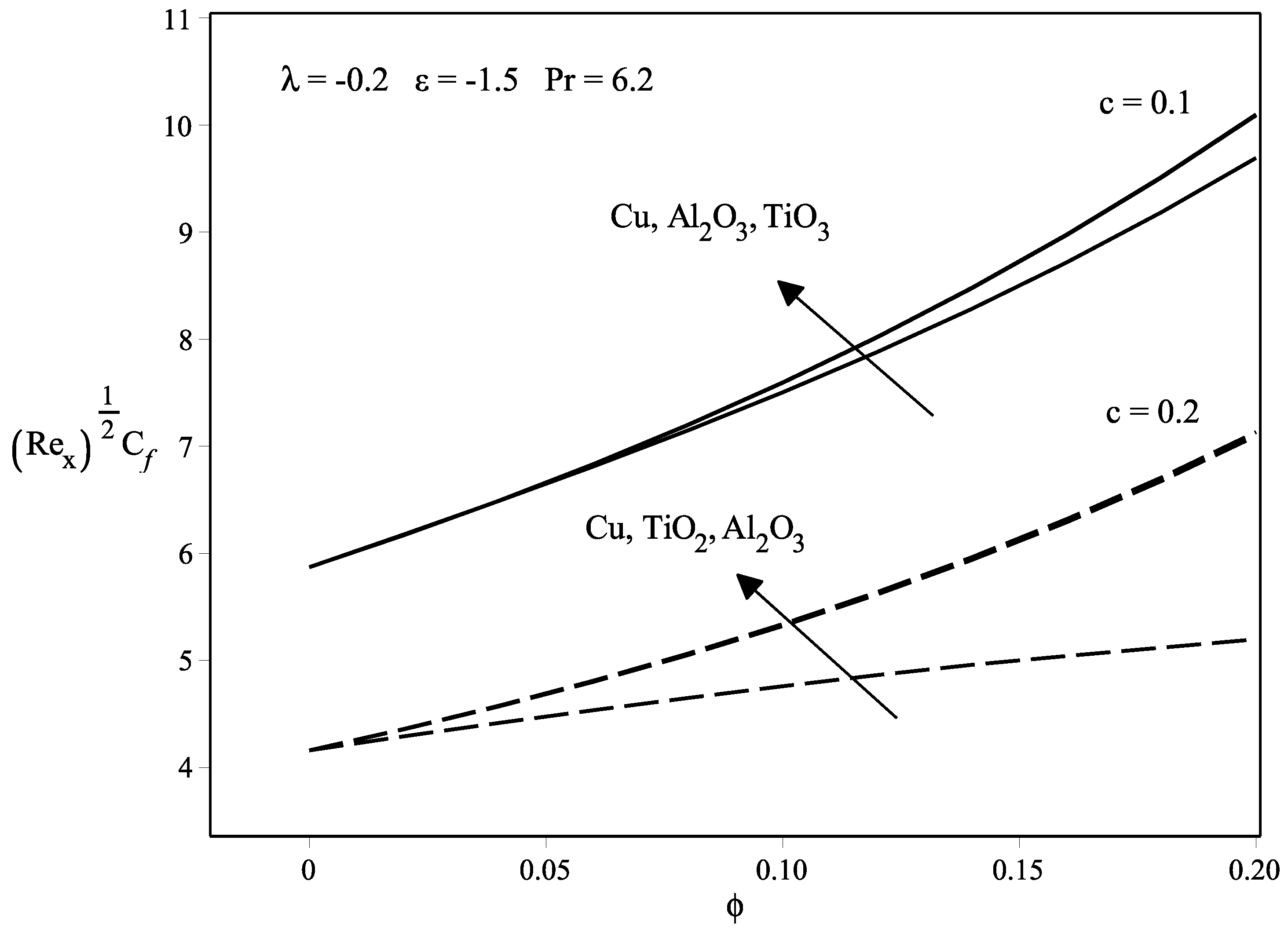
- The magnitude of the skin friction coefficient and the local Nusselt number increases as the size of the needle decreases. The thinner surface of the needle causes the heat to be easily diffused, hence reducing the drag force between the needle and the free stream.
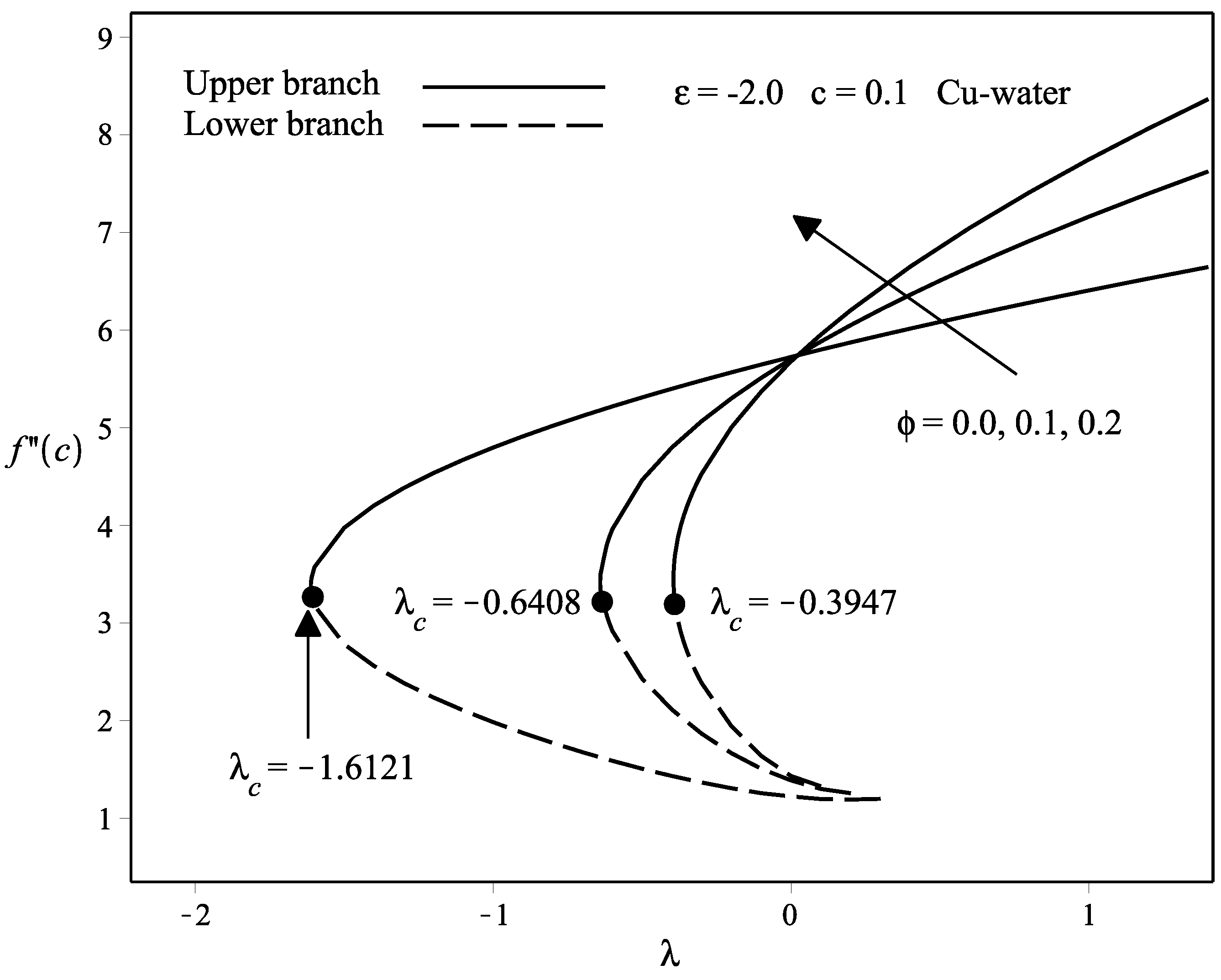
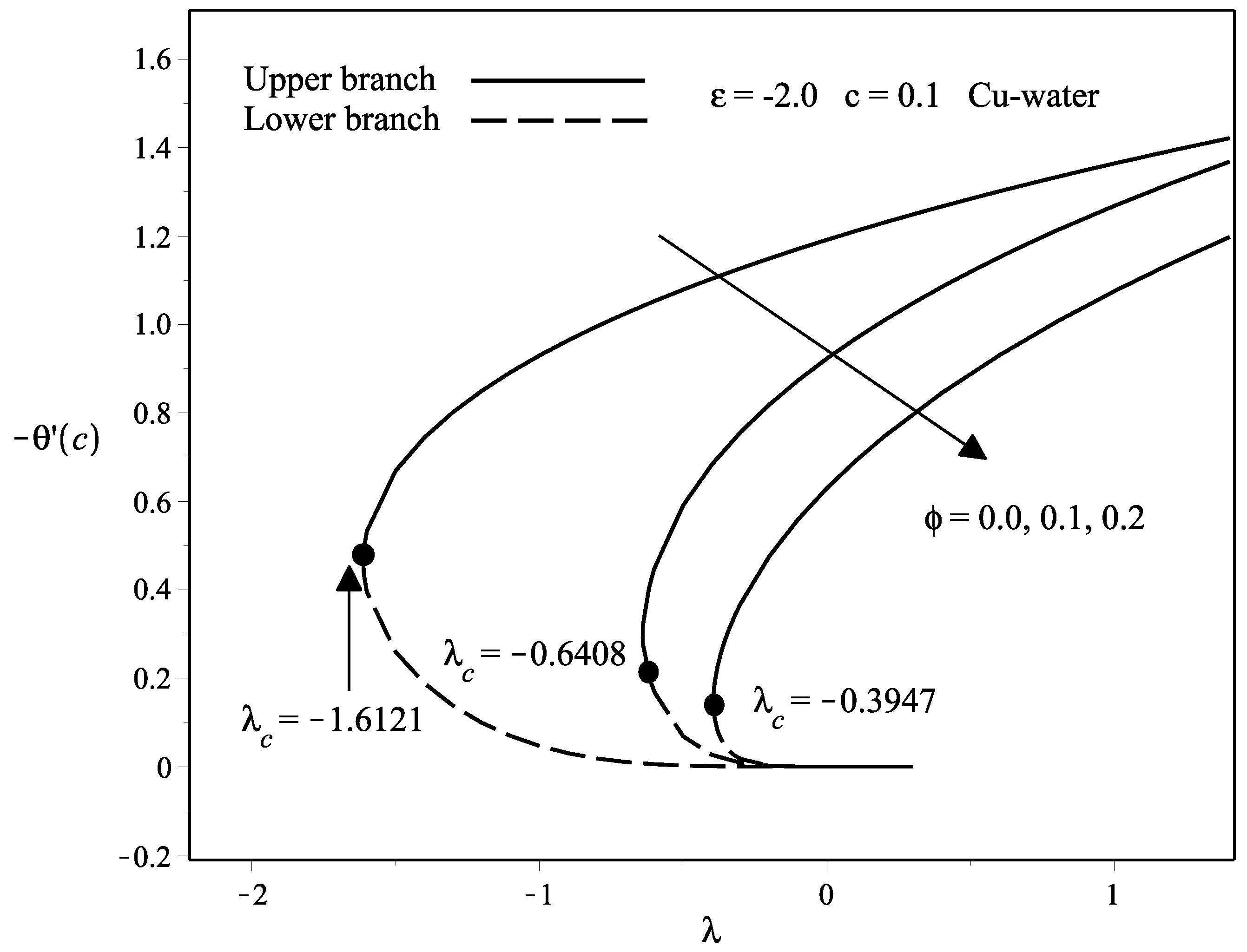
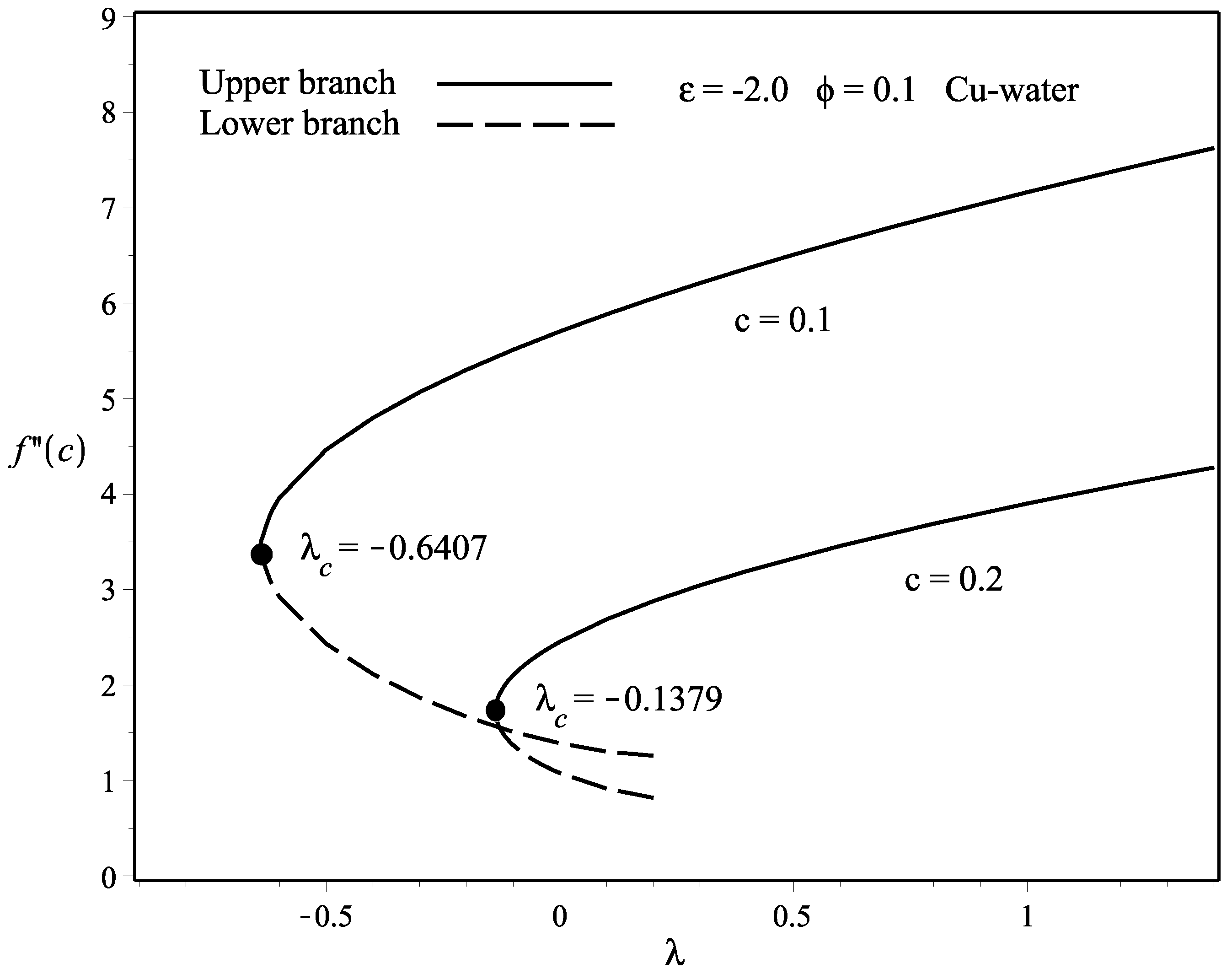
- The existence of the dual solutions occurs when the needle and the fluid move in the opposite way (), while the solution is unique when they move in the same way (). Nevertheless, the range of the dual solutions exists only in between .
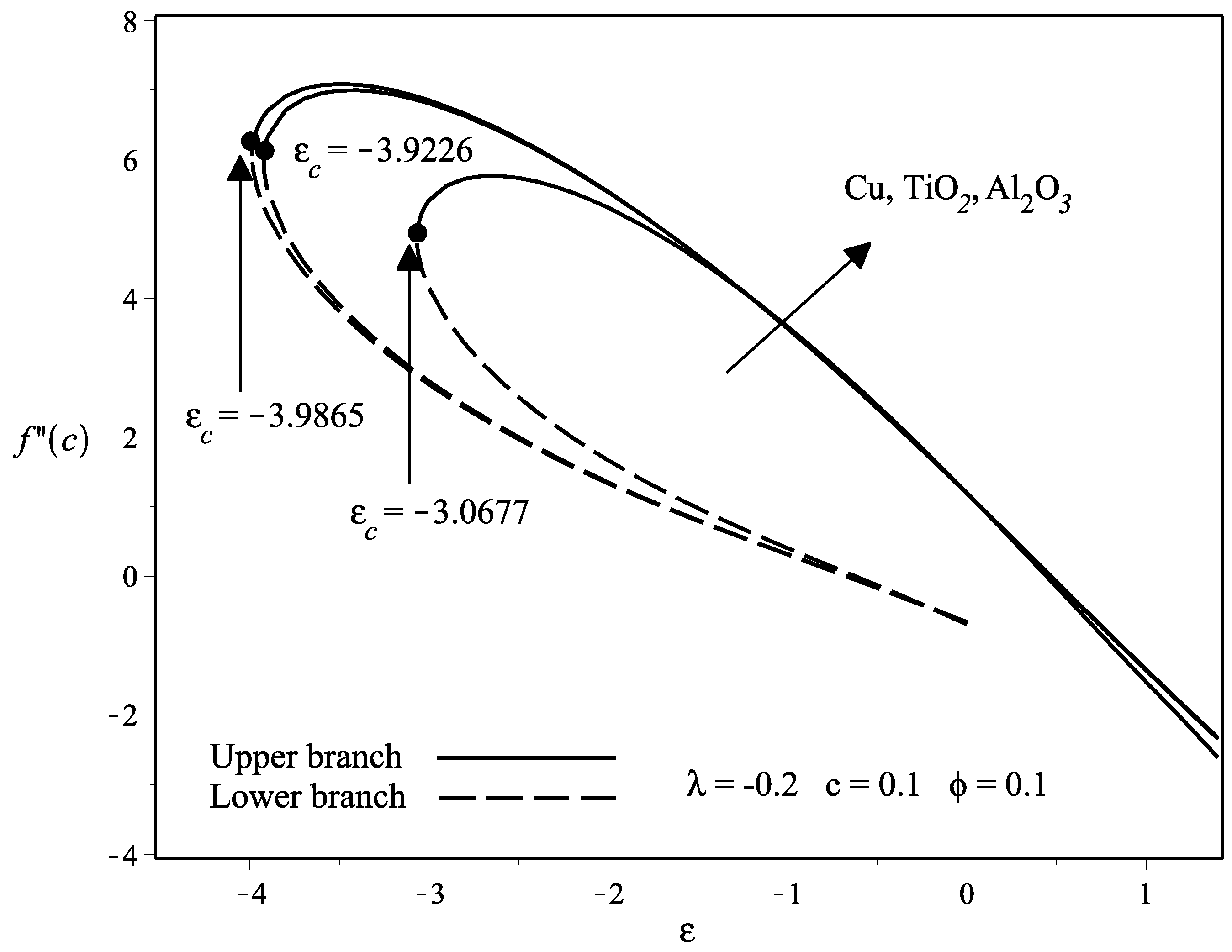
- The presence of the nanoparticles volume fraction in the flow causes the skin friction coefficient, as well as the heat transfer rate on the needle surface to increase especially for the thinner surface.
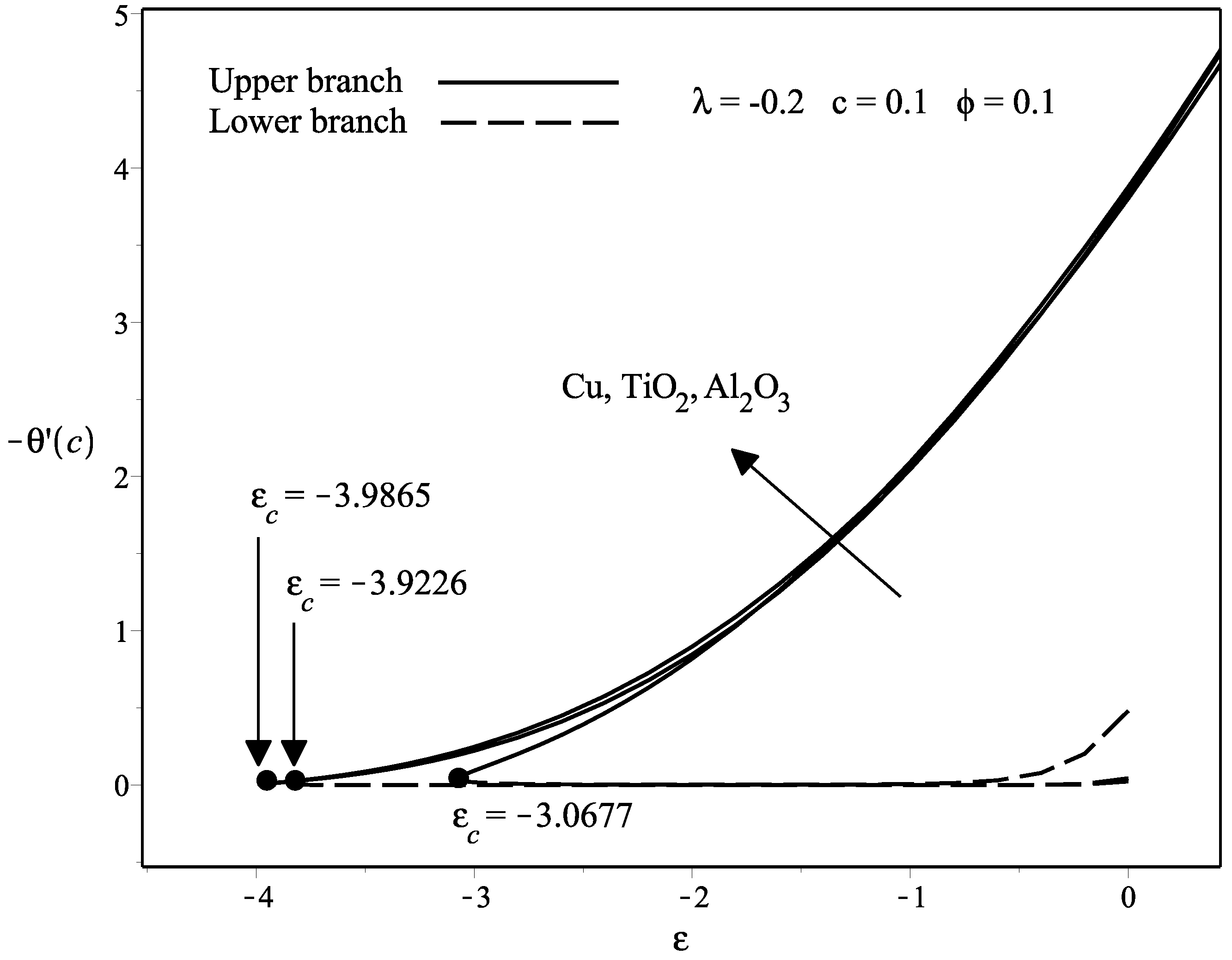
- The dual solutions are more pronounced when the flow is opposing () and the range is between . When , no solutions are obtained.
- The stability analysis has confirmed that the upper branch solution is stable, while the lower branch solution is unstable by observing the positive and negative sign of the eigenvalues obtained.
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Choi, S.U.S. Enhancing thermal conductivity of fluids with nanoparticles. Am. Soc. Mech. Eng. Fluids Eng. Div. 1995, 231, 99–105. [Google Scholar]
- Wong, K.V.; Leon, O.D. Applications of Nanofluids: Current and Future. Adv. Mech. Eng. 2010, 2010, 519659. [Google Scholar] [CrossRef]
- Saidur, R.; Leong, K.Y.; Mohammad, H.A. A review on applications and challenges of nanofluids. Renew. Sustain. Energy Rev. 2011, 15, 1646–1668. [Google Scholar] [CrossRef]
- Huminic, G.; Huminic, A. Application of nanofluids in heat exchangers: A review. Renew. Sustain. Energy Rev. 2012, 16, 5625–5638. [Google Scholar] [CrossRef]
- Khanafer, K.; Vafai, K.; Lightstone, M. Buoyancy-driven heat transfer enhancement in a two-dimensional enclosure utilizing nanofluids. Int. J. Heat Mass Trans. 2003, 46, 3639–3653. [Google Scholar] [CrossRef]
- Buongiorno, J. Convective transport in nanofluids. J. Heat Trans. 2006, 128, 240–250. [Google Scholar] [CrossRef]
- Tiwari, R.K.; Das, M.K. Heat transfer augmentation in a two-sided lid-driven differentially heated square cavity utilizing nanofluids. Int. J. Heat Mass Trans. 2007, 50, 2002–2018. [Google Scholar] [CrossRef]
- Nield, D.A.; and Kuznetsov, A.V. The Cheng–Minkowycz problem for natural convective boundary-layer flow in a porous medium saturated by a nanofluid. Int. J. Heat Mass Trans. 2009, 52, 5792–5795. [Google Scholar] [CrossRef]
- Kuznetsov, A.V.; Nield, D.A. The onset of double-diffusive nanofluid convection in a layer of a saturated porous medium. Transp. Porous Med. 2010, 85, 941–951. [Google Scholar]
- Brinkman, H.C. The viscosity of concentrated suspensions and solutions. J. Chem. Phys. 1952, 20, 571–581. [Google Scholar] [CrossRef]
- Jalilpour, B.; Jafarmadar, S.; Ganji, D.D.; Shotorban, A.B.; Taghavifar, H. Heat generation/absorption on MHD stagnation flow of nanofluid towards a porous stretching sheet with prescribed surface heat flux. J. Mol. Liq. 2004, 195, 194–204. [Google Scholar] [CrossRef]
- Bachok, N.; Ishak, A.; Pop, I. Boundary-layer flow of nanofluids over a moving surface in a flowing fluid. Int. J. Therm. Sci. 2010, 49, 1663–1668. [Google Scholar] [CrossRef]
- Reddy, C.R.; Murthy, P.V.S.N.; Chamkha, A.J.; Rashad, A.M. Soret effect on mixed convection flow in a nanofluid under convective boundary condition. Int. J. Heat Mass Trans. 2013, 64, 384–392. [Google Scholar] [CrossRef]
- Roşca, N.C.; Pop, I. Unsteady boundary layer flow of a nanofluid past a moving surface in an external uniform free stream using Buongiorno’s model. Comput. Fluids 2014, 95, 49–55. [Google Scholar] [CrossRef]
- Lee, L.L. Boundary layer over a thin needle. Phys. Fluids 1967, 10, 1820–1822. [Google Scholar] [CrossRef]
- Narain, J.P.; Uberoi, S.M. Combined forced and free-convection heat transfer from vertical thin needles in a uniform stream. Phys. Fluids 1972, 15, 1879–1882. [Google Scholar] [CrossRef]
- Narain, J.P.; Uberoi, S.M. Combined forced and free-convection over thin needles. Int. J. Heat Mass Trans. 1973, 16, 1505–1512. [Google Scholar] [CrossRef]
- Wang, C.Y. Mixed convection on a vertical needle with heated tip. Phys. Fluids 1990, 2, 622–625. [Google Scholar] [CrossRef]
- Ishak, A.; Nazar, R.; Pop, I. Boundary layer flow over a continuously moving thin needle in a parallel free stream. Chin. Phys. Lett. 2007, 24, 2895–2897. [Google Scholar] [CrossRef]
- Ahmad, S.; Arifin, N.M.; Nazar, R.; Pop, I. Mixed convection boundary layer flow along vertical thin needles: Assisting and opposing flows. Int. Commun. Heat Mass Trans. 2008, 35, 157–162. [Google Scholar] [CrossRef]
- Afridi, M.I.; Qasim, M. Entropy generation and heat transfer in boundary layer flow over a thin needle moving in a parallel stream in the presence of nonlinear Rosseland radiation. Int. J. Therm. Sci. 2018, 123, 117–128. [Google Scholar] [CrossRef]
- Grosan, T.; Pop, I. Forced Convection Boundary Layer Flow Past Nonisothermal Thin Needles in Nanofluids. J. Heat Trans. 2011, 133. [Google Scholar] [CrossRef]
- Hayat, T.; Khan, M.I.; Farooq, M.; Yasmeen, T.; Alsaedi, A. Water-carbon nanofluid flow with variable heat flux by a thin needle. J. Mol. Liq. 2016, 224, 786–791. [Google Scholar] [CrossRef]
- Soid, S.K.; Ishak, A.; Pop, I. Boundary layer flow past a continuously moving thin needle in a nanofluid. Appl. Therm. Eng. 2017, 114, 58–64. [Google Scholar] [CrossRef]
- Krishna, P.M.; Sharma, R.P.; Sandeep, N. Boundary layer analysis of persistent moving horizontal needle in Blasius and Sakiadis magnetohydrodynamic radiative nanofluid flows. Nucl. Eng. Technol. 2017, 49, 1654–1659. [Google Scholar] [CrossRef]
- Ahmad, R.; Mustafa, M.; Hina, S. Buongiorno’s model for fluid flow around a moving thin needle in a flowing nanofluid: A numerical study. Chin. J. Phys. 2017, 55, 1264–1274. [Google Scholar] [CrossRef]
- Trimbitas, R.; Grosan, T.; Pop, I. Mixed convection boundary layer flow along vertical thin needles in nanofluids. Int. J. Numer. Methods Heat Fluid Flow 2014, 24, 579–594. [Google Scholar] [CrossRef]
- Sparrow, E.M.; Abraham, J.P. Universal solutions for the streamwise variation of the temperature of a moving sheet in the presence of a moving fluid. Int. J. Heat Mass Trans. 2005, 48, 3047–3056. [Google Scholar] [CrossRef]
- Abraham, J.P.; Sparrow, E.M. Friction drag resulting from the simultaneous imposed motions of a freestream and its bounding surface. Int. J. Heat Fluid Flow 2005, 26, 289–295. [Google Scholar] [CrossRef]
- Oztop, H.F.; Abu-Nada, E. Numerical study of natural convection in partially heated rectangular enclosures filled with nanofluids. Int. J. Heat Fluid Flow 2008, 29, 1326–1336. [Google Scholar] [CrossRef]
- Weidman, P.D.; Kubitschek, D.G.; Davis, A.M.J. The effect of transpiration on self-similar boundary layer flow over moving surfaces. Int. J. Eng. Sci. 2006, 44, 730–737. [Google Scholar] [CrossRef]
- Harris, S.D.; Ingham, D.B.; Pop, I. Mixed convection boundary-layer flow near the stagnation point on a vertical surface in a porous medium: Brinkman model with slip. Transp. Porous Media 2009, 77, 267–285. [Google Scholar] [CrossRef]
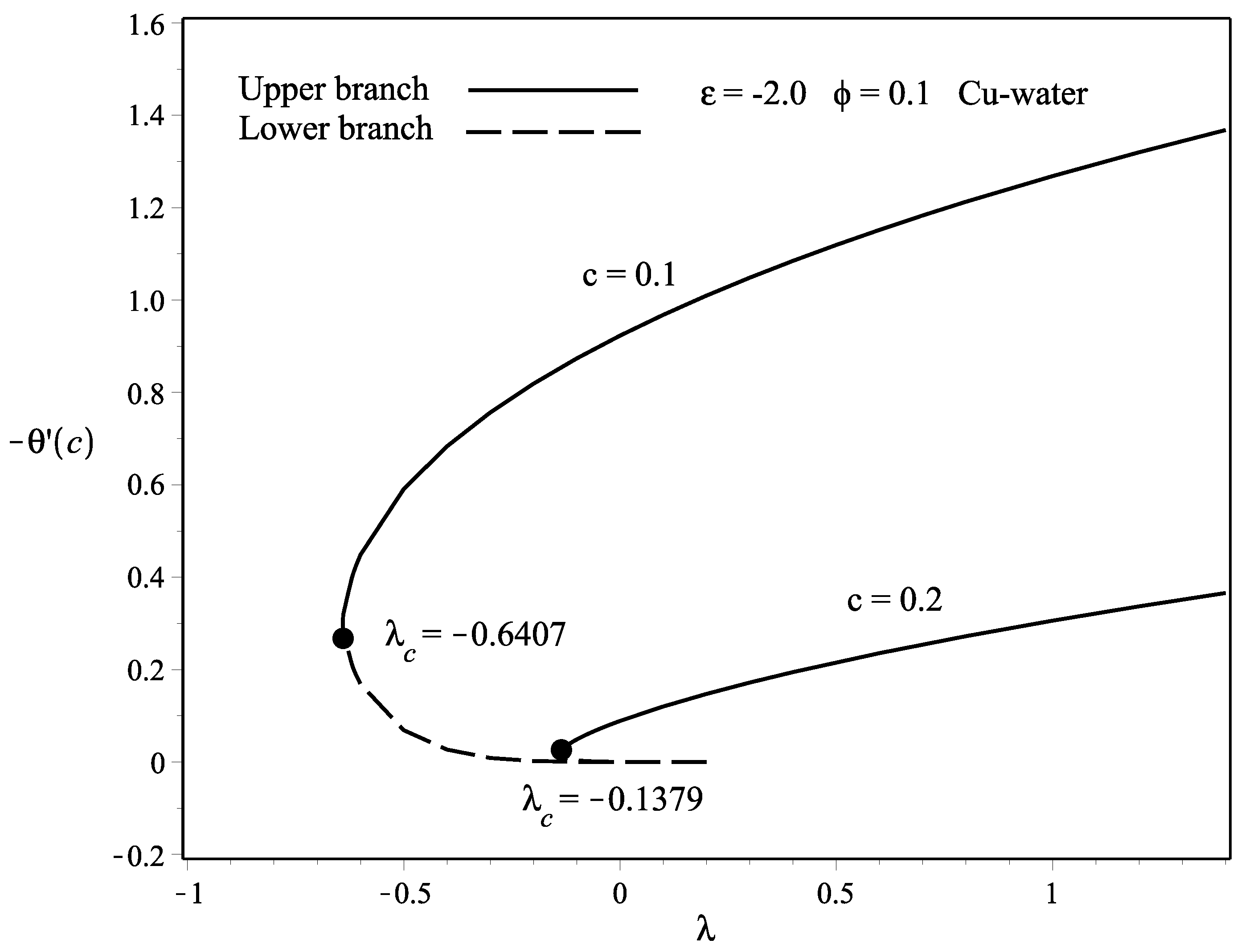
| c | Ishak et al. [19] | Soid et al. [24] | Present Results |
|---|---|---|---|
| 0.01 | 8.4924 | 8.491454 | 8.491455 |
| 0.1 | 1.2888 | 1.288778 | 1.288778 |
| 0.2 | - | 0.751665 | 0.751665 |
| c | Upper Branch | Lower Branch | ||
|---|---|---|---|---|
| 0.0 | 0.1 | −1.612 | 0.0008 | −0.0008 |
| −1.610 | 0.0029 | −0.0029 | ||
| −1.60 | 0.0202 | −0.0194 | ||
| −1.58 | 0.0354 | −0.0327 | ||
| 0.2 | −0.5998 | 0.0061 | −0.0059 | |
| −0.599 | 0.0081 | −0.0079 | ||
| −0.594 | 0.0175 | −0.0166 | ||
| −0.58 | 0.0303 | −0.0277 | ||
| 0.1 | 0.1 | −0.635 | 0.0057 | −0.0056 |
| −0.634 | 0.0103 | −0.0100 | ||
| −0.63 | 0.0165 | −0.0159 | ||
| −0.62 | 0.0326 | −0.0301 | ||
| 0.2 | −0.1378 | 0.0031 | −0.0031 | |
| −0.137 | 0.0084 | −0.0082 | ||
| −0.136 | 0.0126 | −0.0121 | ||
| −0.135 | 0.0158 | −0.0149 | ||
| 0.2 | 0.1 | −0.3946 | 0.0024 | −0.0024 |
| −0.394 | 0.0071 | −0.0070 | ||
| −0.392 | 0.0164 | −0.0157 | ||
| −0.39 | 0.0171 | −0.0163 | ||
| 0.2 | −0.066 | 0.0028 | −0.0028 | |
| −0.0655 | 0.0090 | −0.0087 | ||
| −0.0650 | 0.0110 | −0.0106 | ||
| −0.064 | 0.0162 | −0.0153 |
| Nanoparticles | Upper Branch | Lower Branch | |
|---|---|---|---|
| Cu | −3.0674 | 0.0033 | −0.0033 |
| −3.067 | 0.0045 | −0.0044 | |
| −3.06 | 0.0158 | −0.0152 | |
| −3.00 | 0.0470 | −0.0420 | |
| AlO | −3.986 | 0.0040 | −0.0040 |
| −3.984 | 0.0108 | −0.0106 | |
| −3.98 | 0.0152 | −0.0147 | |
| −3.97 | 0.0275 | −0.0260 | |
| TiO | −3.922 | 0.0042 | −0.0041 |
| −3.92 | 0.0052 | −0.0052 | |
| −3.90 | 0.0113 | −0.0111 | |
| −3.89 | 0.0401 | −0.0370 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salleh, S.N.A.; Bachok, N.; Arifin, N.M.; Ali, F.M.; Pop, I. Stability Analysis of Mixed Convection Flow towards a Moving Thin Needle in Nanofluid. Appl. Sci. 2018, 8, 842. https://doi.org/10.3390/app8060842
Salleh SNA, Bachok N, Arifin NM, Ali FM, Pop I. Stability Analysis of Mixed Convection Flow towards a Moving Thin Needle in Nanofluid. Applied Sciences. 2018; 8(6):842. https://doi.org/10.3390/app8060842
Chicago/Turabian StyleSalleh, Siti Nur Alwani, Norfifah Bachok, Norihan Md Arifin, Fadzilah Md Ali, and Ioan Pop. 2018. "Stability Analysis of Mixed Convection Flow towards a Moving Thin Needle in Nanofluid" Applied Sciences 8, no. 6: 842. https://doi.org/10.3390/app8060842
APA StyleSalleh, S. N. A., Bachok, N., Arifin, N. M., Ali, F. M., & Pop, I. (2018). Stability Analysis of Mixed Convection Flow towards a Moving Thin Needle in Nanofluid. Applied Sciences, 8(6), 842. https://doi.org/10.3390/app8060842






