Static and Dynamic Response of FG-CNT-Reinforced Rhombic Laminates
Abstract
:1. Introduction
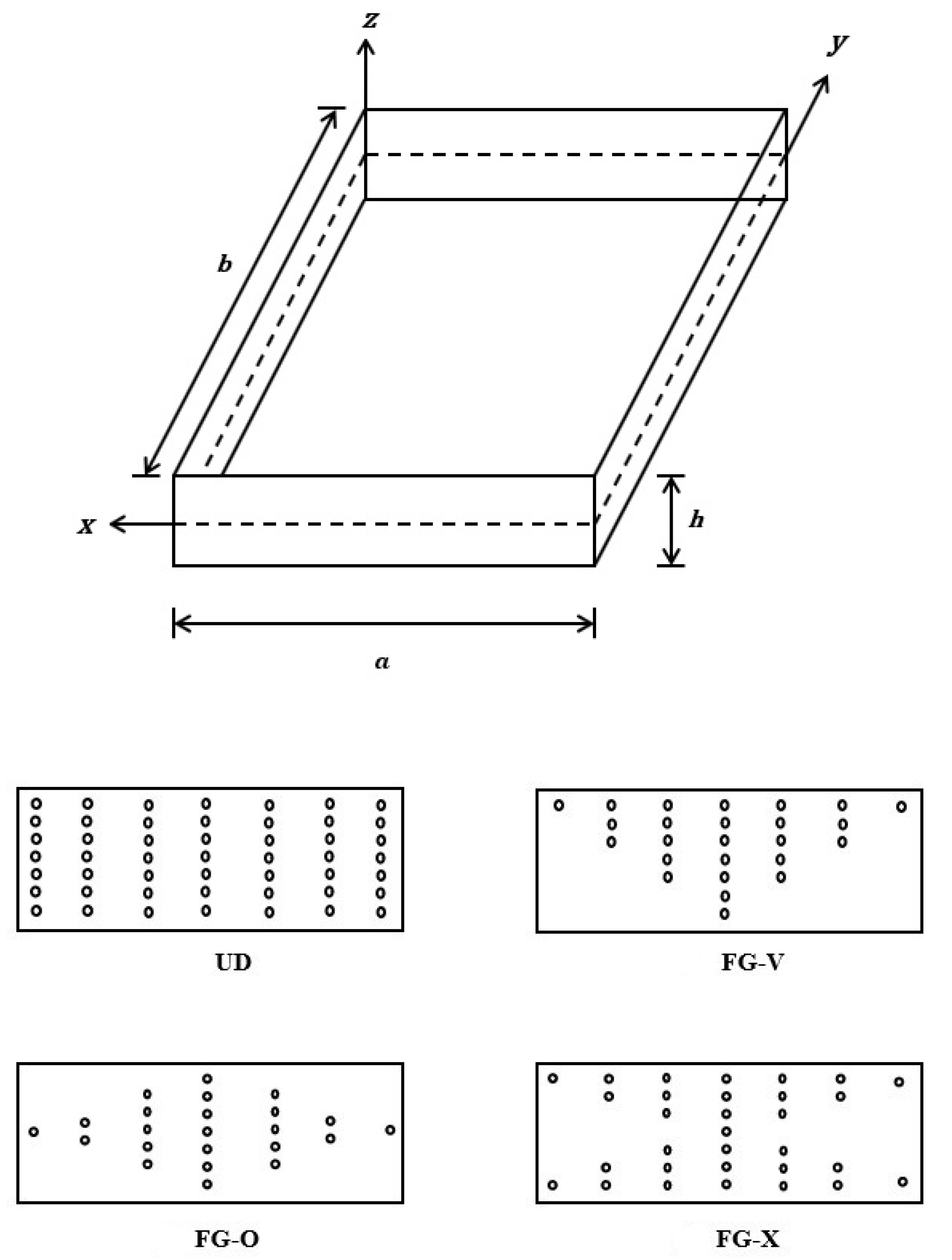
2. Carbon Nanotube-Reinforced Laminates
3. Mathematical Formulation
3.1. Displacement Fields and Strains
3.2. Constitutive Relationship
4. Finite Element Formulation
4.1. Element Description
4.2. Governing Equation for Bending Analysis
4.3. Governing Equation for Free Vibration Analysis
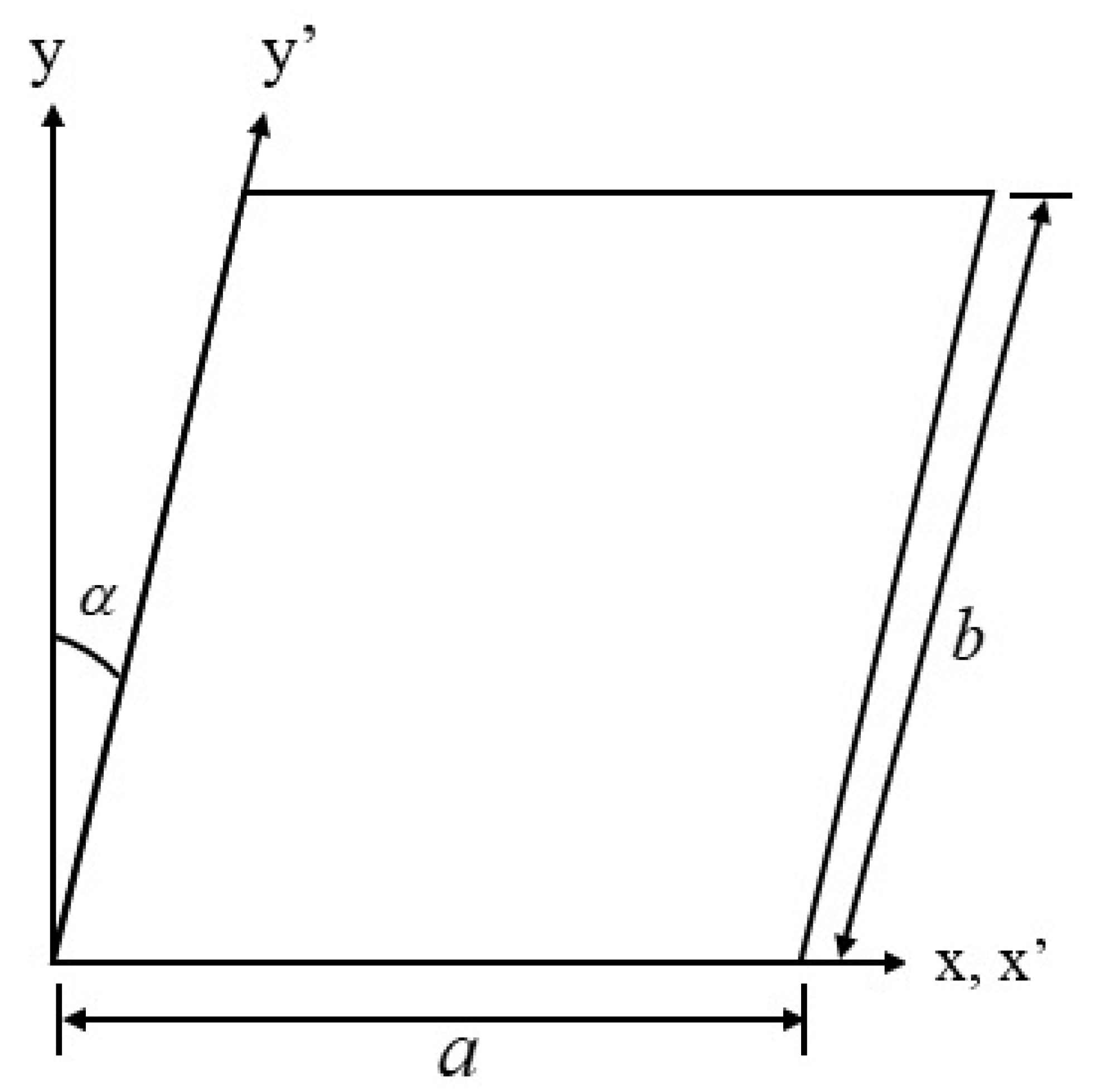
4.4. Skew Boundary Transformation
5. Numerical Results and Discussion
- For the bending analysis
- For the free vibration analysis
- Simply supported (SSSS):
- Clamped (CCCC):
- Clamped and simply supported (CCSS):
5.1. Convergence and Validation of Present Formulation
5.1.1. Free Vibration Analysis
5.1.2. Bending Analysis
5.2. Results and Discussion
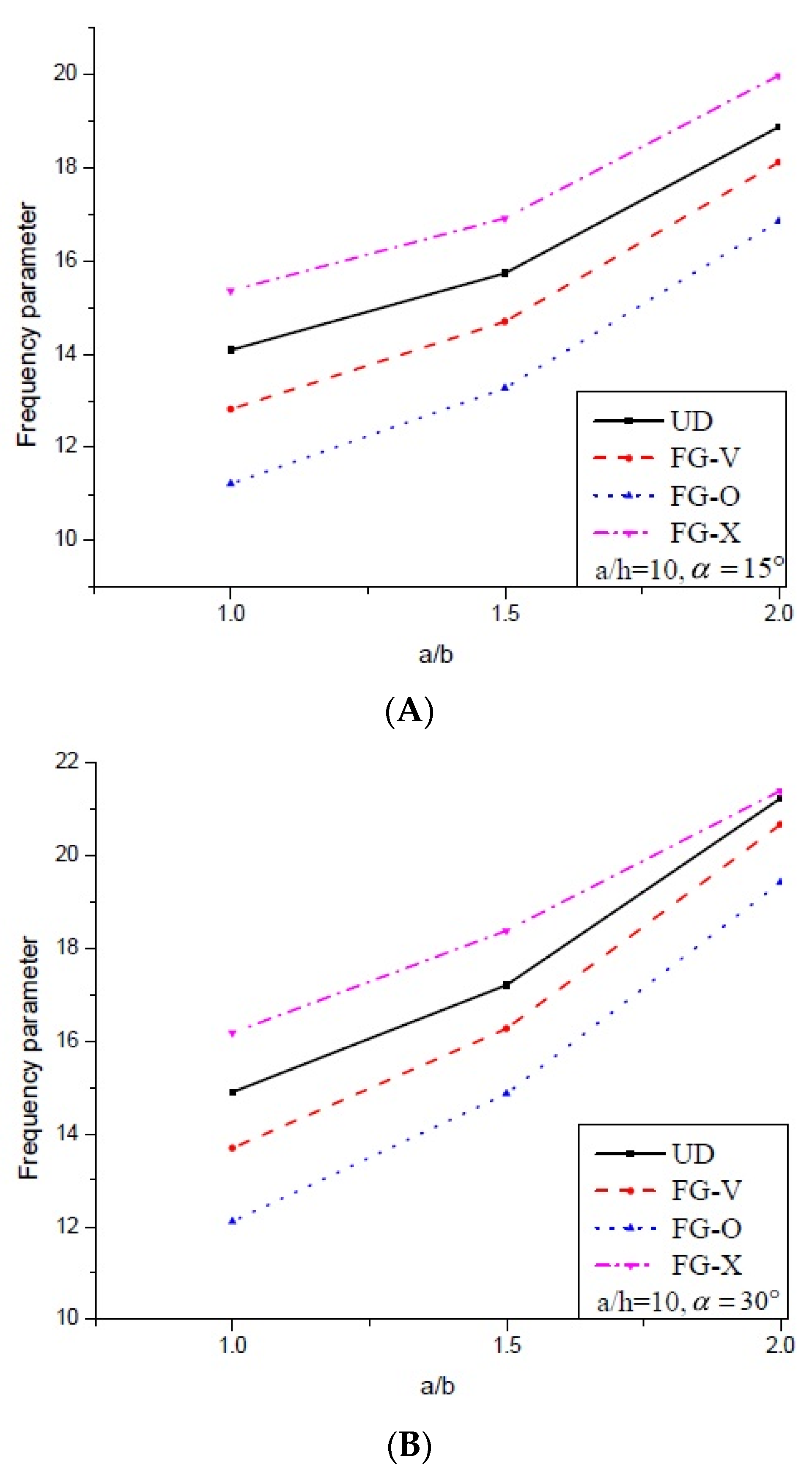
5.2.1. Free Vibration Analysis
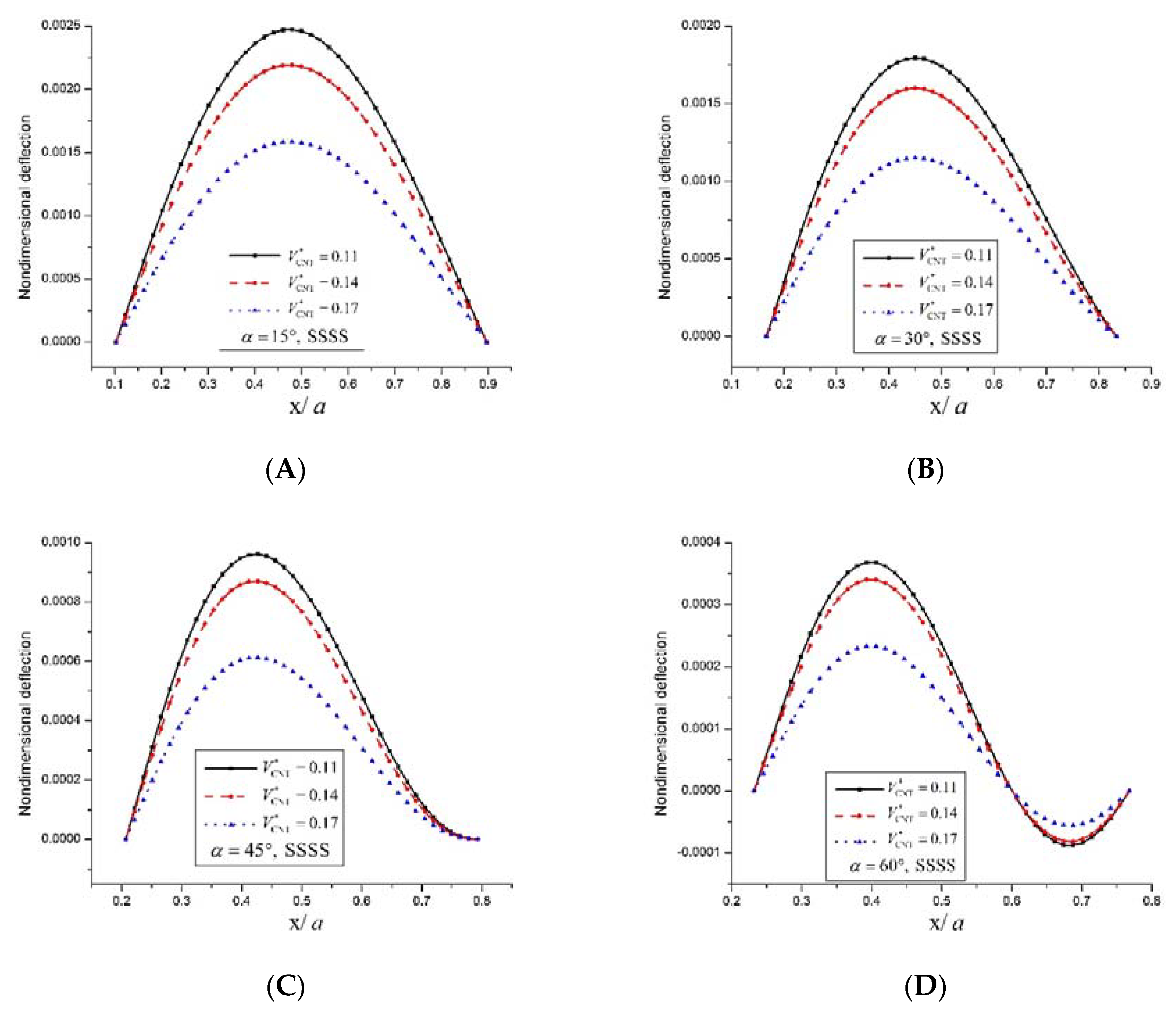
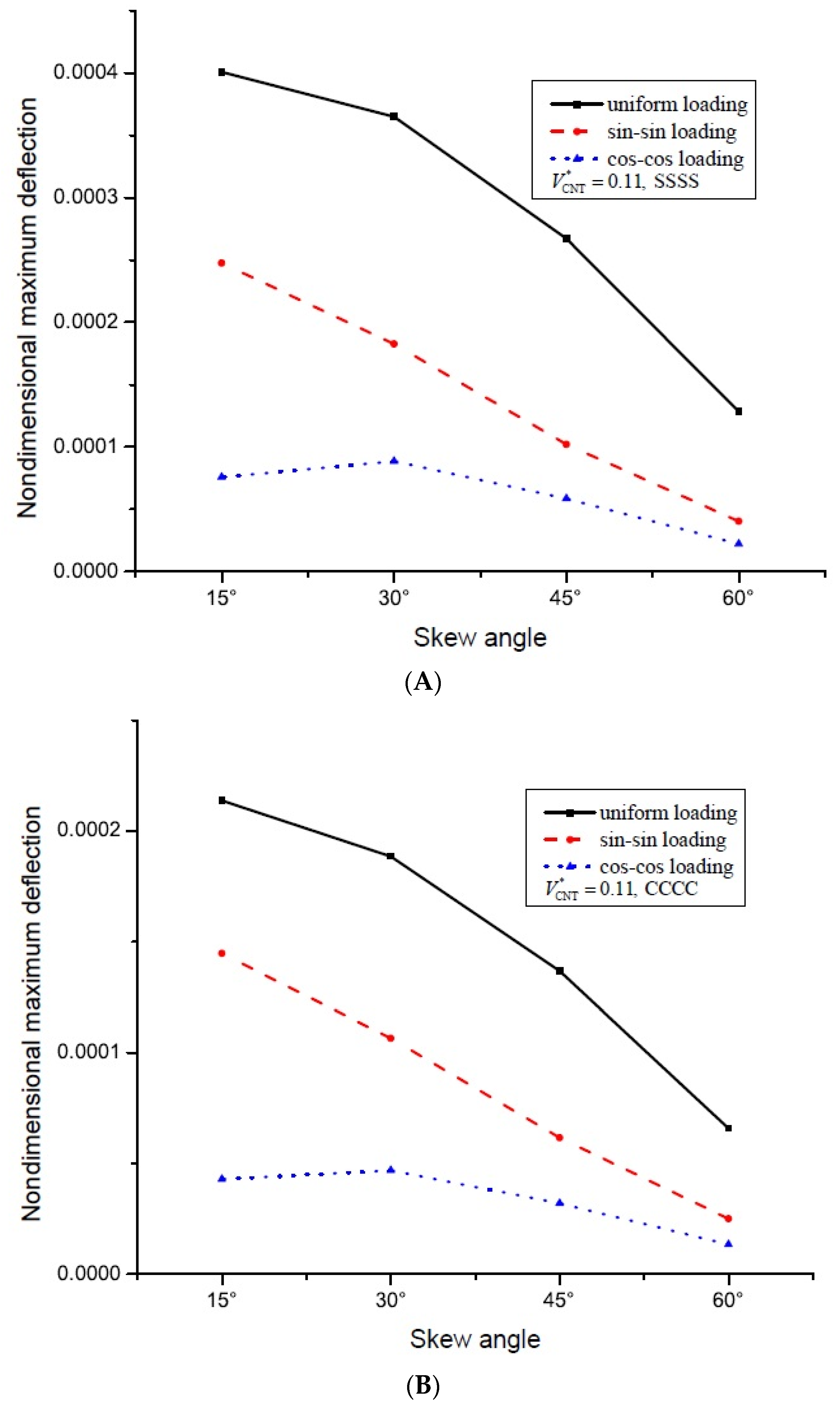
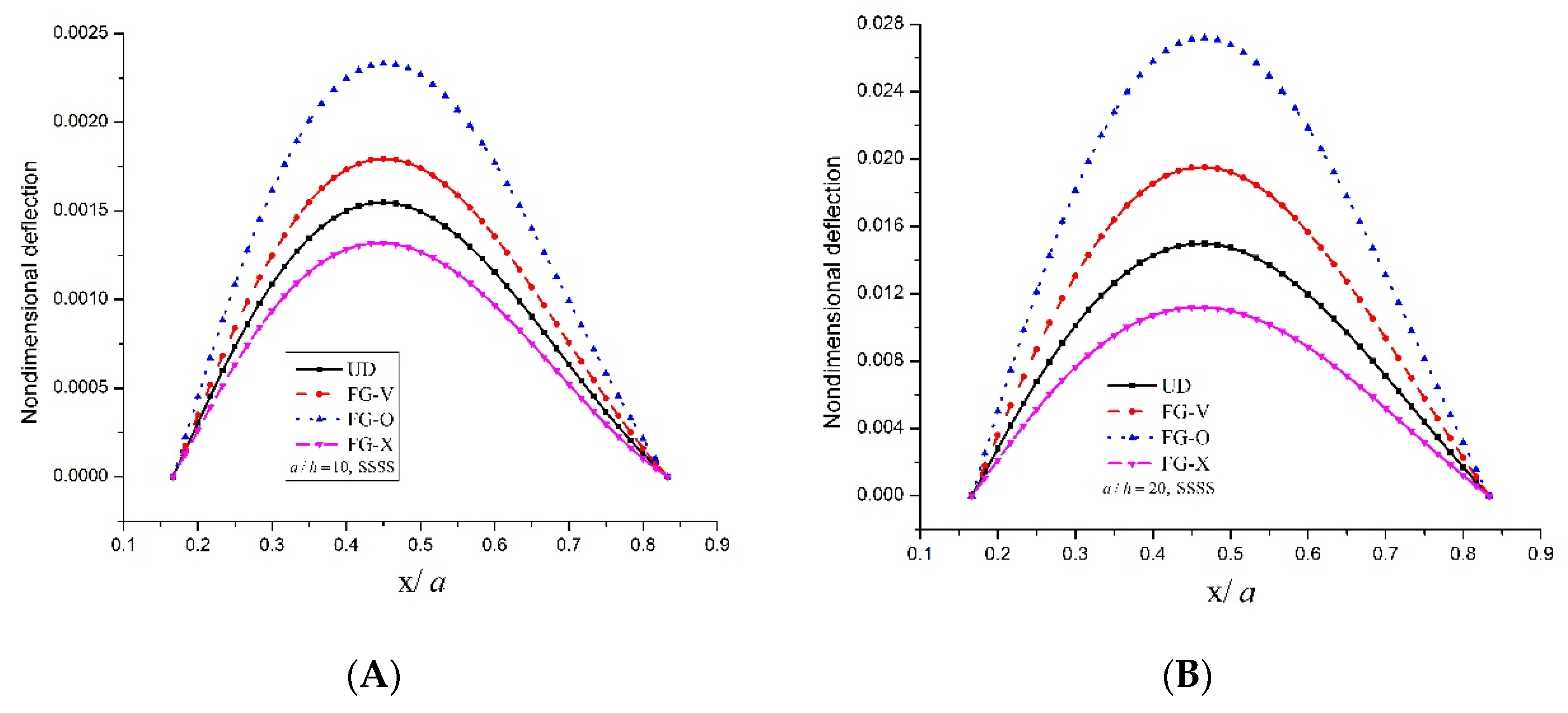
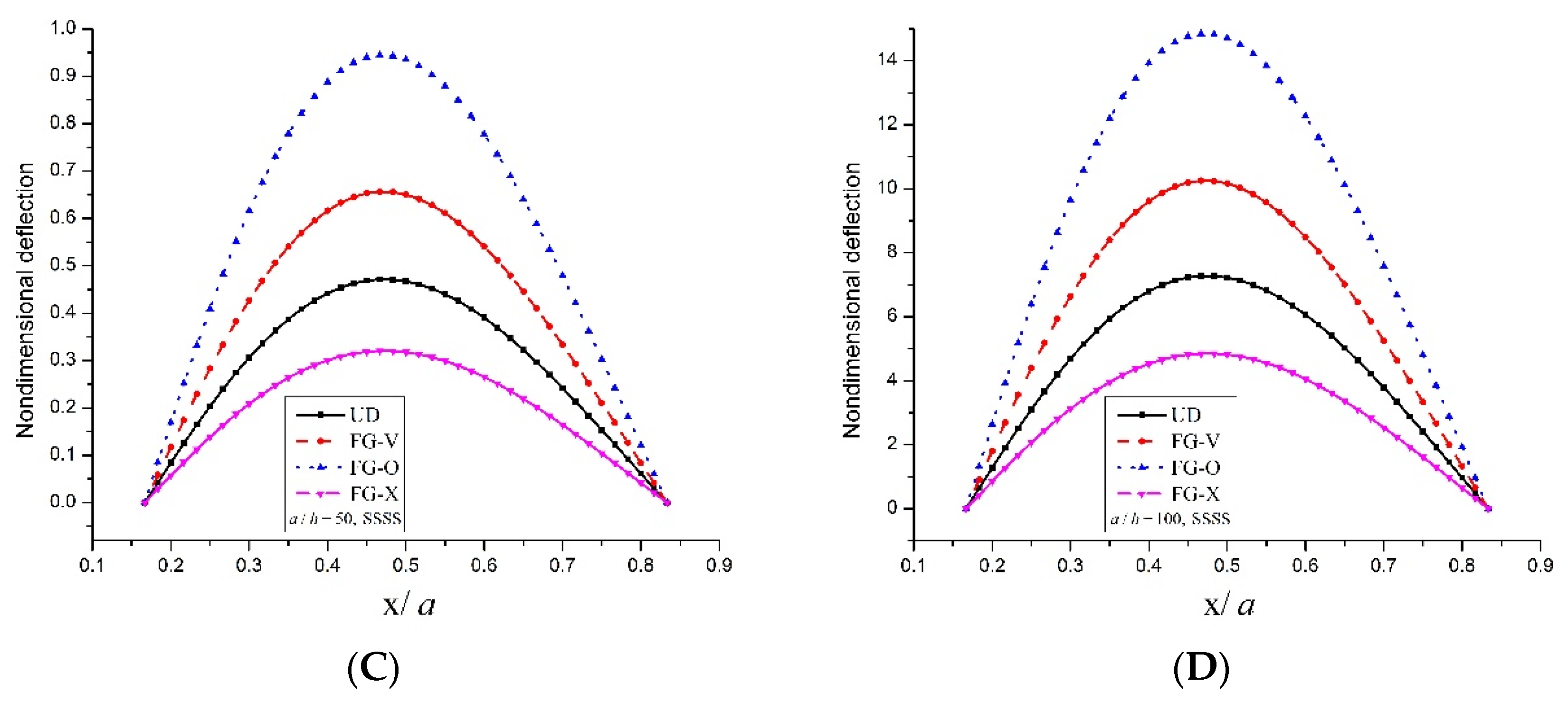
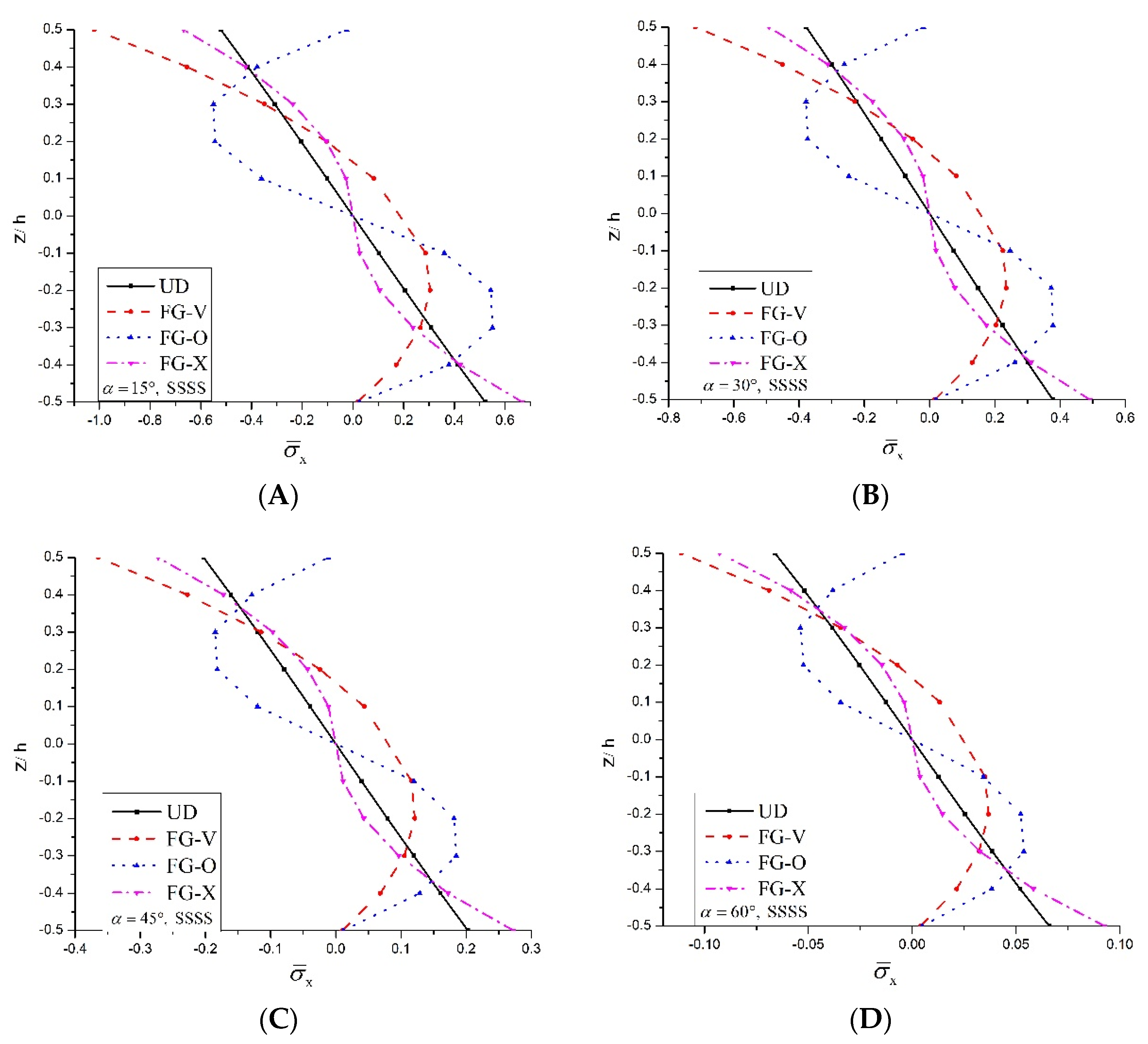
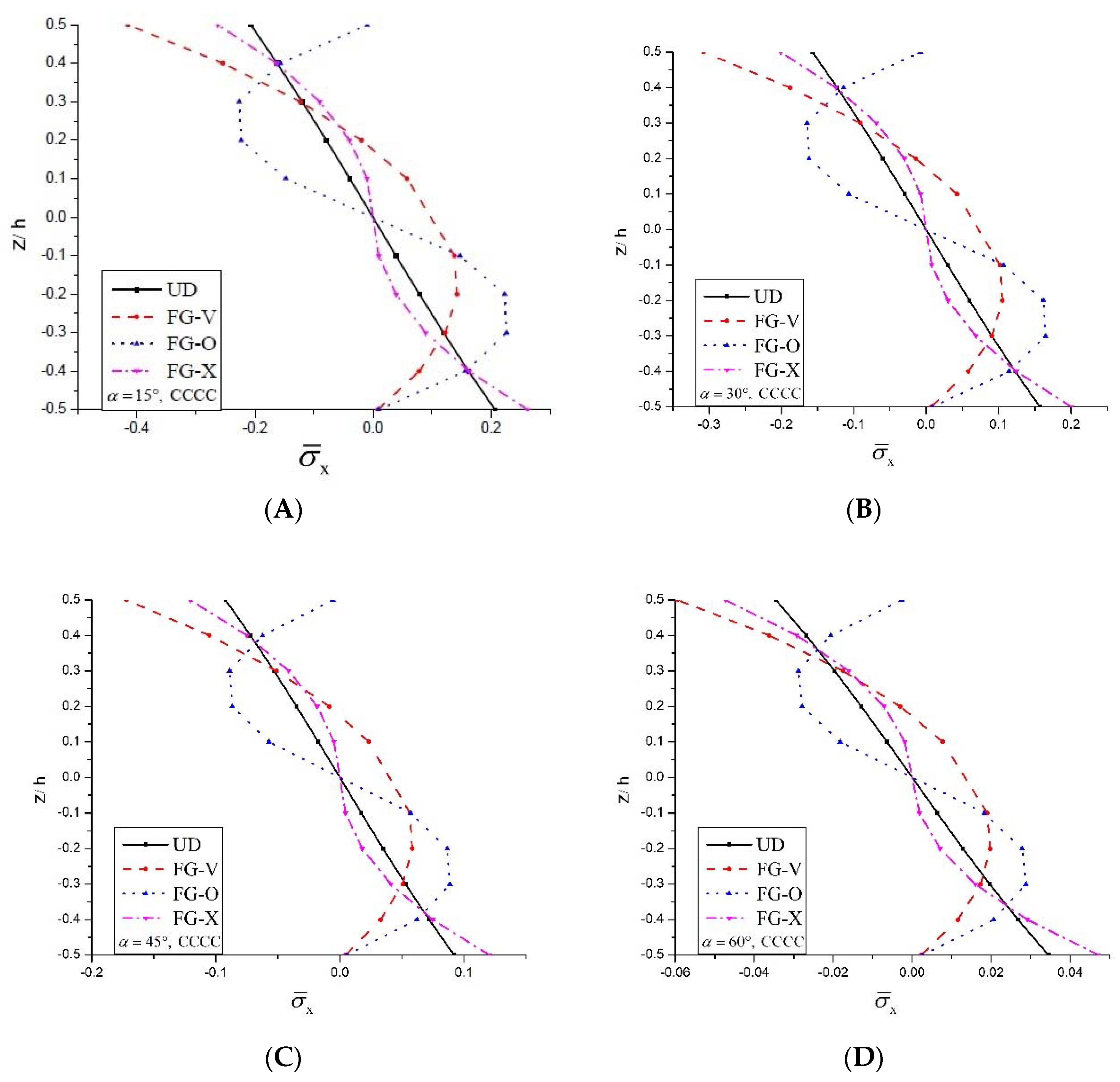
5.2.2. Static Analysis
6. Conclusions
- The FG-O and FG-X type distributions inside the CNT rhombic plates have lower and higher non-dimensional frequency parameter as well as higher and lower dimensionless deflection, respectively.
- The rise in the CNTs volume fraction results in a decrease in the deflection and an increase in the frequency parameter of the CNT-reinforced rhombic plate.
- The dimensionless frequency parameter increases along with the skew angle, irrespective of the CNT distribution and boundary condition.
- Maximum dimensionless deflection and dimensionless normal stresses decrease along with the skew angle.
- Higher values of non-dimensional fundamental frequencies and lower values of dimensionless deflection are found for greater constraints on boundaries.
Author Contributions
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Element Stiffness Matrix
Appendix A.2. Element Mass Matrix
References
- Iijima, S.; Ichihashi, T. Single-shell carbon nanotubes of 1-nm diameter. Nature 1993, 363, 603–605. [Google Scholar] [CrossRef]
- Hone, J.; Llaguno, M.C.; Biercuk, M.J.; Johnson, A.T.; Batlogg, B.; Benes, Z.; Fischer, J.E. Thermal properties of carbon nanotubes and nanotube-based materials. Appl. Phys. A Mater. Sci. Process. 2002, 74, 339–343. [Google Scholar] [CrossRef]
- Dresselhaus, M.S.; Dresselhaus, G.; Charlier, J.C.; Hernandez, E. Electronic, thermal and mechanical properties of carbon nanotubes. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2004, 362, 2065–2098. [Google Scholar] [CrossRef] [PubMed]
- Reissner, E. On the theory of transverse bending of elastic plates. Int. J. Solids Struct. 1976, 12, 545–554. [Google Scholar] [CrossRef]
- Zhu, P.; Lei, Z.X.; Liew, K.M. Static and free vibration analyses of carbon nanotube-reinforced composite plates using finite element method with first order shear deformation plate theory. Compos. Struct. 2012, 94, 1450–1460. [Google Scholar] [CrossRef]
- Lei, Z.X.; Liew, K.M.; Yu, J.L. Free vibration analysis of functionally graded carbon nanotube-reinforced composite plates using the element-free kp-Ritz method in thermal environment. Compos. Struct. 2013, 106, 128–138. [Google Scholar] [CrossRef]
- Moradi-dastjerdi, R.; Foroutan, M.; Pourasghar, A.; Sotoudeh-bahreini, R. Static analysis of functionally graded carbon nanotube-reinforced composite cylinders by a mesh-free method. J. Reinf. Plast. Compos. 2013, 32, 593–601. [Google Scholar] [CrossRef]
- Yas, M.H.; Pourasghar, A.; Kamarian, S.; Heshmati, M. Three-dimensional free vibration analysis of functionally graded nanocomposite cylindrical panels reinforced by carbon nanotube. Mater. Des. 2013, 49, 583–590. [Google Scholar] [CrossRef]
- Malekzadeh, P.; Zarei, A.R. Free vibration of quadrilateral laminated plates with carbon nanotube reinforced composite layers. Thin Walled Struct. 2014, 82, 221–232. [Google Scholar] [CrossRef]
- Nami, M.R.; Janghorban, M. Thermal buckling analysis of functionally graded rectangular nanoplates based on nonlocal third-order shear deformation theory. Adv. Compos. Mater. 2015, 24, 439–450. [Google Scholar] [CrossRef]
- Shahrbabaki, E.A.; Alibeigloo, A. Three-dimensional free vibration of carbon nanotube-reinforced composite plates with various boundary conditions using Ritz method. Compos. Struct. 2014, 111, 362–370. [Google Scholar] [CrossRef]
- Sankar, A.; Natarajan, S.; Ganapathi, M. Dynamic instability analysis of sandwich plates with CNT reinforced facesheets. Compos. Struct. 2016, 146, 187–200. [Google Scholar] [CrossRef]
- Mehar, K.; Panda, S.K. Vibration analysis of functionally graded carbon nanotube reinforced composite plate in thermal environment. J. Sandw. Struct. Mater. 2015, 18, 151–173. [Google Scholar] [CrossRef]
- Mayandi, K.; Jeyaraj, P. Bending, buckling and free vibration characteristics of FG-CNT polymer composite beam under non-uniform thermal load. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2015, 229, 13–28. [Google Scholar] [CrossRef]
- Zhang, L.W.; Cui, W.C.; Liew, K.M. Vibration analysis of functionally graded carbon nanotube reinforced composite thick plates with elastically restrained edges. Int. J. Mech. Sci. 2015, 103, 9–21. [Google Scholar] [CrossRef]
- Huang, B.; Guo, Y.; Wang, J.; Du, J.; Qian, Z.; Ma, T.; Yi, L. Bending and free vibration analyses of antisymmetrically laminated carbon nanotube-reinforced functionally graded plates. J. Compos. Mater. 2016, 51, 3111–3125. [Google Scholar] [CrossRef]
- García-macías, E.; Castro-triguero, R.; Saavedra, E.I.; Friswell, M.I.; Gallego, R. Static and free vibration analysis of functionally graded carbon nanotube reinforced skew plates. Compos. Struct. 2016, 140, 473–490. [Google Scholar] [CrossRef]
- Mirzaei, M.; Kiani, Y. Free vibration of functionally graded carbon nanotube reinforced composite cylindrical panels. Compos. Struct. 2016, 142, 45–56. [Google Scholar] [CrossRef]
- Song, Z.G.; Zhang, L.W.; Liew, K.M. Vibration analysis of CNT-reinforced functionally graded composite cylindrical shells in thermal environments. Int. J. Mech. Sci. 2016, 115–116, 339–347. [Google Scholar] [CrossRef]
- Thomas, B.; Roy, T. Vibration analysis of functionally graded carbon nanotube-reinforced composite shell structures. Acta Mech. 2016, 599, 581–599. [Google Scholar] [CrossRef]
- Duong, H.M.; Gong, F.; Liu, P.; Tran, T.Q. Advanced Fabrication and Properties of Aligned Carbon Nanotube Composites: Experiments and Modeling. In Carbon Nanotubes—Current Progress of Their Polymer Composites; Intech: Houston, TX, USA, 2016; pp. 47–72. ISBN 978-953-51-2470-2. [Google Scholar]
- Selim, B.A.; Zhang, L.W.; Liew, K.M. Vibration analysis of CNT reinforced functionally graded composite plates in a thermal environment based on Reddy’ s higher-order shear deformation theory. Compos. Struct. 2016, 156, 276–290. [Google Scholar] [CrossRef]
- Zhang, L.W.; Selim, B.A. Vibration analysis of CNT-reinforced thick laminated composite plates based on Reddy’s higher-order shear deformation theory. Compos. Struct. 2017, 160, 689–705. [Google Scholar] [CrossRef]
- Manevitch, L.I.; Smirnov, V.V.; Strozzi, M.; Pellicano, F. Nonlinear optical vibrations of single-walled carbon nanotubes. Procedia Eng. 2017, 199, 705–710. [Google Scholar] [CrossRef]
- Fantuzzi, N.; Tornabene, F.; Bacciocchi, M.; Dimitri, R. Free vibration analysis of arbitrarily shaped Functionally Graded Carbon Nanotube-reinforced plates. Compos. Part B 2017, 115, 384–408. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M. Linear static response of nanocomposite plates and shells reinforced by agglomerated carbon nanotubes. Compos. Part B 2017, 115, 449–476. [Google Scholar] [CrossRef]
- Romano, G.; Barretta, R. Nonlocal elasticity in nanobeams: The stress-driven integral model. Int. J. Eng. Sci. 2017, 115, 14–27. [Google Scholar] [CrossRef]
- Romano, G.; Barretta, R.; Diaco, M. On nonlocal integral models for elastic nano-beams. Int. J. Mech. Sci. 2017, 131–132, 490–499. [Google Scholar] [CrossRef]
- Mahmoudpour, E.; Hosseini-Hashemi, S.H.; Faghidian, S.A. Nonlinear vibration analysis of FG nano-beams resting on elastic foundation in thermal environment using stress-driven nonlocal integral model. Appl. Math. Model. 2018, 57, 302–315. [Google Scholar] [CrossRef]
- Barretta, R.; Ali Faghidian, S.; Luciano, R.; Medaglia, C.M.; Penna, R. Stress-driven two-phase integral elasticity for torsion of nano-beams. Compos. Part B Eng. 2018, 145, 62–69. [Google Scholar] [CrossRef]
- Oskouie, M.F.; Ansari, R.; Rouhi, H. Bending of Euler–Bernoulli nanobeams based on the strain-driven and stress-driven nonlocal integral models: A numerical approach. Acta Mech. Sin. 2018. [Google Scholar] [CrossRef]
- Barretta, R.; Faghidian, S.A.; Luciano, R. Longitudinal vibrations of nano-rods by stress-driven integral elasticity. Mech. Adv. Mater. Struct. 2018. [Google Scholar] [CrossRef]
- Ansari, R.; Torabi, J.; Shakouri, A.H. Vibration analysis of functionally graded carbon nanotube-reinforced composite elliptical plates using a numerical strategy. Aerospace Sci. Technol. 2017, 60, 152–161. [Google Scholar] [CrossRef]
- Tornabene, F.; Bacciocchi, M.; Fantuzzi, N.; Reddy, J.N. Multiscale Approach for Three-Phase CNT/Polymer/Fiber Laminated Nanocomposite Structures. Polym. Compos. 2017. [Google Scholar] [CrossRef]
- Ardestani, M.M.; Zhang, L.W.; Liew, K.M. Isogeometric analysis of the effect of CNT orientation on the static and vibration behaviors of CNT-reinforced skew composite plates. Comput. Methods Appl. Mech. Eng. 2017, 317, 341–379. [Google Scholar] [CrossRef]
- Esawi, A.M.K.; Farag, M.M. Carbon nanotube reinforced composites: Potential and current challenges. Mater. Des. 2007, 28, 2394–2401. [Google Scholar] [CrossRef]
- Fidelus, J.D.; Wiesel, E.; Gojny, F.H.; Schulte, K.; Wagner, H.D. Thermo-mechanical properties of randomly oriented carbon/epoxy nanocomposites. Compos. Part A Appl. Sci. Manuf. 2005, 36, 1555–1561. [Google Scholar] [CrossRef]
- Shen, H.S. Nonlinear bending of functionally graded carbon nanotube-reinforced composite plates in thermal environments. Compos. Struct. 2009, 91, 9–19. [Google Scholar] [CrossRef]
- Reddy, J.N. A simple higher-order theory for laminated composite plates. J. Appl. Mech. 1984, 51, 745–752. [Google Scholar] [CrossRef]
- Han, Y.; Elliott, J. Molecular dynamics simulations of the elastic properties of polymer/carbon nanotube composites. Comput. Mater. Sci. 2007, 39, 315–323. [Google Scholar] [CrossRef]
- Reddy, J.N. An Introduction to the Finite Element Method; McGraw-Hill: New York, NY, USA, 1993. [Google Scholar]
- Srinivas, S.; Joga Rao, C.V.; Rao, A.K. An exact analysis for vibration of simply-supported homogeneous and laminated thick rectangular plates. J. Sound Vib. 1970, 12, 187–199. [Google Scholar] [CrossRef]
- Mantari, J.L.; Oktem, A.S.; Soares, C.G. Bending and free vibration analysis of isotropic and multilayered plates and shells by using a new accurate higher-order shear deformation theory. Compos. Part B 2012, 43, 3348–3360. [Google Scholar] [CrossRef]

| Temperature (K) | (TPa) | (TPa) | (TPa) | (10−6/K) | (10−6/K) |
|---|---|---|---|---|---|
| 300 | 5.6466 | 7.0800 | 1.9445 | 3.4584 | 5.1682 |
| 500 | 5.5308 | 6.9348 | 1.9643 | 4.5361 | 5.0189 |
| 700 | 5.4744 | 6.8641 | 1.9644 | 4.6677 | 4.8943 |
| Mesh | UD | FG-V | FG-O | FG-X |
|---|---|---|---|---|
| 8 × 8 | 18.5932 | 18.0731 | 16.6424 | 19.2637 |
| 10 × 10 | 18.5915 | 18.0719 | 16.4112 | 19.2623 |
| 12 × 12 | 18.5906 | 18.0709 | 16.4093 | 19.2612 |
| 14 × 14 | 18.5894 | 18.0697 | 16.4085 | 19.2606 |
| 16 × 16 | 18.5892 | 18.0694 | 16.4084 | 19.2604 |
| a/h | Source | ||
|---|---|---|---|
| 10 | Present | 4.666 | 0.289 |
| Reddy [41] | 4.770 | 0.289 | |
| 20 | Present | 4.491 | 0.287 |
| Reddy [41] | 4.570 | 0.268 | |
| 50 | Present | 4.408 | 0.284 |
| Reddy [41] | 4.496 | 0.266 |
| Source | Mode | ||
|---|---|---|---|
| (1, 1) | (1, 2) | (1, 3) | |
| Present | 0.093 | 0.221 | 0.415 |
| Mantari et al. [43] | 0.093 | 0.222 | 0.415 |
| Srinivas et al. [42] | 0.093 | 0.223 | 0.417 |
| BC | V*CNT | Mode | a/h = 10 | a/h = 20 | a/h = 50 | |||
|---|---|---|---|---|---|---|---|---|
| Zhu et al. [5] | Present | Zhu et al. [5] | Present | Zhu et al. [5] | Present | |||
| CCCC | 0.11 | 1 | 17.625 | 18.284 | 28.400 | 29.232 | 39.730 | 41.246 |
| 2 | 23.041 | 23.793 | 33.114 | 34.108 | 43.876 | 45.501 | ||
| 3 | 33.592 | 34.188 | 44.559 | 45.456 | 54.768 | 56.313 | ||
| 4 | 33.729 | 35.188 | 59.198 | 60.708 | 74.488 | 75.080 | ||
| 5 | 37.011 | 38.536 | 61.851 | 63.003 | 98.291 | 100.577 | ||
| 6 | 37.317 | 38.738 | 63.043 | 63.553 | 100.537 | 101.437 | ||
| 0.14 | 1 | 18.127 | 18.854 | 29.911 | 30.795 | 43.583 | 45.216 | |
| 2 | 23.572 | 24.374 | 34.516 | 35.558 | 47.479 | 49.218 | ||
| 3 | 34.252 | 34.874 | 45.898 | 46.830 | 57.968 | 59.617 | ||
| 4 | 34.650 | 36.267 | 61.628 | 63.337 | 77.395 | 78.064 | ||
| 5 | 37.921 | 39.384 | 64.199 | 64.457 | 106.371 | 104.359 | ||
| 6 | 37.972 | 39.592 | 64.496 | 66.100 | 106.487 | 108.807 | ||
| SSSS | 0.11 | 1 | 13.532 | 13.885 | 17.355 | 18.014 | 19.223 | 20.124 |
| 2 | 17.700 | 18.199 | 21.511 | 22.278 | 23.408 | 24.396 | ||
| 3 | 19.449 | 19.422 | 32.399 | 33.231 | 34.669 | 35.734 | ||
| 4 | 19.449 | 19.427 | 38.898 | 38.844 | 54.043 | 54.658 | ||
| 5 | 27.569 | 28.121 | 38.898 | 38.854 | 70.811 | 73.189 | ||
| 6 | 32.563 | 33.291 | 50.199 | 50.524 | 72.900 | 75.313 | ||
| 0.14 | 1 | 14.306 | 14.668 | 18.921 | 19.618 | 21.354 | 22.359 | |
| 2 | 18.362 | 18.870 | 22.867 | 23.666 | 25.295 | 26.373 | ||
| 3 | 19.791 | 19.769 | 33.570 | 34.419 | 36.267 | 37.393 | ||
| 4 | 19.791 | 19.774 | 39.583 | 39.538 | 55.608 | 56.238 | ||
| 5 | 28.230 | 28.784 | 39.583 | 39.548 | 78.110 | 80.675 | ||
| 6 | 33.646 | 34.492 | 51.422 | 51.737 | 80.015 | 82.137 | ||
| BC | V*CNT | Mode | a/h = 10 | a/h = 20 | a/h = 50 | |||
|---|---|---|---|---|---|---|---|---|
| Zhu et al. [5] | Present | Zhu et al. [5] | Present | Zhu et al. [5] | Present | |||
| CCCC | 0.11 | 1 | 17.211 | 17.753 | 26.304 | 26.693 | 34.165 | 34.480 |
| 2 | 22.812 | 23.462 | 31.496 | 32.099 | 39.043 | 39.584 | ||
| 3 | 33.070 | 34.035 | 43.589 | 44.133 | 51.204 | 51.815 | ||
| 4 | 33.552 | 34.355 | 56.249 | 57.061 | 72.202 | 71.954 | ||
| 5 | 36.528 | 37.889 | 59.249 | 60.253 | 86.291 | 86.133 | ||
| 6 | 37.437 | 38.841 | 62.608 | 62.218 | 89.054 | 89.105 | ||
| 0.14 | 1 | 17.791 | 18.405 | 27.926 | 28.371 | 37.568 | 37.909 | |
| 2 | 23.413 | 24.113 | 32.976 | 33.629 | 42.175 | 42.733 | ||
| 3 | 34.101 | 34.792 | 44.989 | 45.573 | 53.963 | 54.590 | ||
| 4 | 34.275 | 35.553 | 58.951 | 59.968 | 74.785 | 74.546 | ||
| 5 | 37.538 | 39.053 | 61.816 | 63.051 | 94.022 | 93.911 | ||
| 6 | 38.159 | 39.574 | 64.135 | 63.758 | 96.573 | 96.680 | ||
| SSSS | 0.11 | 1 | 12.452 | 12.601 | 15.110 | 15.291 | 16.252 | 16.465 |
| 2 | 17.060 | 17.409 | 19.903 | 20.297 | 21.142 | 21.573 | ||
| 3 | 19.499 | 19.479 | 31.561 | 32.106 | 33.350 | 33.993 | ||
| 4 | 19.499 | 19.484 | 38.998 | 38.959 | 53.430 | 53.670 | ||
| 5 | 27.340 | 27.762 | 38.998 | 38.969 | 60.188 | 60.337 | ||
| 6 | 31.417 | 31.903 | 47.739 | 47.899 | 62.198 | 63.042 | ||
| 0.14 | 1 | 13.256 | 13.415 | 16.510 | 16.701 | 17.995 | 18.228 | |
| 2 | 17.734 | 18.090 | 21.087 | 21.483 | 22.643 | 23.082 | ||
| 3 | 19.879 | 19.871 | 32.617 | 33.163 | 34.660 | 35.306 | ||
| 4 | 19.879 | 19.876 | 39.759 | 39.742 | 54.833 | 55.062 | ||
| 5 | 28.021 | 28.449 | 39.759 | 39.752 | 66.552 | 66.712 | ||
| 6 | 32.678 | 33.284 | 51.078 | 51.122 | 68.940 | 69.212 | ||
| Mesh | UD | FG-V | FG-O | FG-X |
|---|---|---|---|---|
| 8 × 8 | 0.00372 | 0.00422 | 0.00588 | 0.00309 |
| 10 × 10 | 0.00361 | 0.00411 | 0.00576 | 0.00297 |
| 12 × 12 | 0.00355 | 0.00406 | 0.00568 | 0.00292 |
| 14 × 14 | 0.00349 | 0.00402 | 0.00561 | 0.00289 |
| 16 × 16 | 0.00345 | 0.00401 | 0.00557 | 0.00287 |
| BC | V*CNT | a/h = 10 | a/h = 20 | a/h = 50 | |||
|---|---|---|---|---|---|---|---|
| Zhu et al. [5] | Present | Zhu et al. [5] | Present | Zhu et al. [5] | Present | ||
| CCCC | 0.11 | 0.00222 | 0.00207 | 0.01339 | 0.01257 | 0.2618 | 0.24056 |
| 0.14 | 0.00208 | 0.00192 | 0.01188 | 0.01115 | 0.2131 | 0.19644 | |
| SSSS | 0.11 | 0.00373 | 0.00354 | 0.03628 | 0.03352 | 1.1550 | 1.04729 |
| 0.14 | 0.00330 | 0.00314 | 0.03001 | 0.02779 | 0.9175 | 0.83205 | |
| SCSC | 0.11 | 0.00332 | 0.00313 | 0.03393 | 0.03127 | 1.0990 | 0.99624 |
| 0.14 | 0.00297 | 0.00281 | 0.02852 | 0.02634 | 0.8890 | 0.80555 | |
| SFSF | 0.11 | 0.00344 | 0.00339 | 0.03341 | 0.03223 | 1.0680 | 1.01428 |
| 0.14 | 0.00302 | 0.00297 | 0.02760 | 0.02654 | 0.8505 | 0.80295 | |
| BC | V*CNT | a/h = 10 | a/h = 20 | a/h = 50 | |||
|---|---|---|---|---|---|---|---|
| Zhu et al. [5] | Present | Zhu et al. [5] | Present | Zhu et al. [5] | Present | ||
| CCCC | 0.11 | 0.00211 | 0.00191 | 0.01150 | 0.01052 | 0.18940 | 0.16721 |
| 0.14 | 0.00198 | 0.00179 | 0.01036 | 0.00954 | 0.15600 | 0.13941 | |
| SSSS | 0.11 | 0.00318 | 0.00294 | 0.02701 | 0.02398 | 0.79000 | 0.67655 |
| 0.14 | 0.00284 | 0.00266 | 0.02256 | 0.02021 | 0.62710 | 0.53777 | |
| SCSC | 0.11 | 0.00286 | 0.00264 | 0.02587 | 0.02297 | 0.77280 | 0.66351 |
| 0.14 | 0.00258 | 0.00240 | 0.02184 | 0.01955 | 0.62060 | 0.53313 | |
| SFSF | 0.11 | 0.00290 | 0.00276 | 0.02484 | 0.02281 | 0.73380 | 0.70308 |
| 0.14 | 0.00259 | 0.00248 | 0.02078 | 0.01916 | 0.58540 | 0.54605 | |
| Types | V*CNT | Skew Angle | Mode | |||||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |||
| UD | 0.11 | 15° | 14.0884 | 18.3200 | 18.8946 | 22.6183 | 29.3328 | 33.6414 |
| 30° | 14.8977 | 18.8299 | 21.3717 | 28.4322 | 33.1078 | 35.1178 | ||
| 45° | 17.1862 | 20.5115 | 26.9900 | 37.0144 | 39.6322 | 39.6568 | ||
| 60° | 22.7998 | 24.0366 | 38.2235 | 46.2487 | 47.8936 | 50.9246 | ||
| 0.14 | 15° | 14.8687 | 18.6487 | 19.5642 | 23.0233 | 30.0198 | 34.8422 | |
| 30° | 15.6755 | 19.1758 | 22.0498 | 28.9455 | 33.9035 | 36.3247 | ||
| 45° | 17.9727 | 20.9102 | 27.7332 | 37.7063 | 40.6588 | 40.8949 | ||
| 60° | 23.2808 | 24.8769 | 39.2472 | 47.5170 | 49.0156 | 52.2774 | ||
| 0.17 | 15° | 17.4811 | 22.9180 | 23.5104 | 28.2964 | 36.5676 | 41.9224 | |
| 30° | 18.4931 | 23.5450 | 26.6092 | 35.5615 | 41.2831 | 43.7657 | ||
| 45° | 21.3530 | 25.6345 | 33.6340 | 46.2801 | 49.4285 | 49.4321 | ||
| 60° | 28.4860 | 29.9161 | 47.6618 | 57.6946 | 59.7955 | 63.5234 | ||
| FG-V | 0.11 | 15° | 12.8212 | 18.1269 | 18.3759 | 22.6786 | 28.9595 | 32.2712 |
| 30° | 13.6868 | 18.8528 | 20.6993 | 28.4857 | 32.6175 | 33.8100 | ||
| 45° | 16.0825 | 20.5023 | 26.3727 | 36.9725 | 38.5706 | 38.8945 | ||
| 60° | 22.7651 | 23.1363 | 37.4158 | 45.9406 | 47.6860 | 50.0097 | ||
| 0.14 | 15° | 13.6306 | 18.7223 | 18.8344 | 23.1366 | 29.6827 | 33.6486 | |
| 30° | 14.4859 | 19.2484 | 21.3970 | 29.0713 | 33.4956 | 35.1799 | ||
| 45° | 16.8766 | 20.9596 | 27.1726 | 37.8010 | 39.9021 | 40.0565 | ||
| 60° | 23.3107 | 23.9748 | 38.5628 | 47.3845 | 48.9510 | 51.4979 | ||
| 0.17 | 15° | 15.8726 | 22.5869 | 23.1041 | 28.5207 | 36.1984 | 40.2043 | |
| 30° | 16.9639 | 23.7009 | 25.8142 | 35.8176 | 40.7628 | 42.1365 | ||
| 45° | 19.9783 | 25.7658 | 32.9286 | 46.4775 | 48.1150 | 48.5974 | ||
| 60° | 28.6027 | 28.8423 | 46.7338 | 57.6186 | 59.8787 | 62.5277 | ||
| FG-O | 0.11 | 15° | 11.2246 | 16.8568 | 18.2727 | 22.5605 | 27.7024 | 28.6900 |
| 30° | 12.1133 | 18.7752 | 19.3640 | 28.3558 | 30.3139 | 30.7798 | ||
| 45° | 14.5197 | 20.4388 | 24.7329 | 35.2696 | 36.2118 | 36.9006 | ||
| 60° | 21.5223 | 22.7001 | 34.8852 | 45.8698 | 46.6015 | 47.6229 | ||
| 0.14 | 15° | 11.9547 | 17.3832 | 18.6042 | 22.9689 | 28.2193 | 30.0605 | |
| 30° | 12.8181 | 19.1248 | 19.9022 | 28.8740 | 31.5416 | 31.6441 | ||
| 45° | 15.1892 | 20.8433 | 25.3918 | 36.4990 | 37.2763 | 37.6006 | ||
| 60° | 22.1785 | 23.1888 | 35.8993 | 47.2005 | 47.9486 | 48.7680 | ||
| 0.17 | 15° | 13.8793 | 20.7785 | 22.8791 | 22.8791 | 34.1824 | 35.9124 | |
| 30° | 14.9671 | 23.4971 | 23.8865 | 35.4973 | 37.8814 | 38.1425 | ||
| 45° | 17.9248 | 25.5652 | 30.5918 | 43.9152 | 45.0463 | 46.1779 | ||
| 60° | 26.5756 | 28.3845 | 43.3295 | 57.2497 | 58.0859 | 59.5035 | ||
| FG-X | 0.11 | 15° | 15.3579 | 18.4618 | 19.9956 | 22.7929 | 30.4082 | 35.0962 |
| 30° | 16.1745 | 18.9803 | 22.4702 | 28.6545 | 34.2453 | 36.6028 | ||
| 45° | 18.4949 | 20.6851 | 28.1124 | 37.3147 | 40.9182 | 41.2241 | ||
| 60° | 23.0073 | 25.4117 | 39.5510 | 46.7919 | 48.3756 | 52.4841 | ||
| 0.14 | 15° | 16.0673 | 18.8614 | 20.7220 | 23.2855 | 31.2995 | 36.1529 | |
| 30° | 16.9039 | 19.3980 | 23.2367 | 29.2774 | 35.2156 | 37.6988 | ||
| 45° | 19.2847 | 21.1602 | 28.9762 | 38.1470 | 42.0428 | 42.4396 | ||
| 60° | 23.5712 | 26.3605 | 40.6662 | 48.1906 | 49.6636 | 53.9309 | ||
| 0.17 | 15° | 19.0583 | 23.2864 | 25.1259 | 28.7507 | 38.4760 | 43.6385 | |
| 30° | 20.1180 | 23.9280 | 28.2892 | 36.1352 | 43.2193 | 45.5938 | ||
| 45° | 23.1055 | 26.0614 | 35.4283 | 47.0376 | 51.4225 | 51.5545 | ||
| 60° | 28.9750 | 31.9346 | 49.7188 | 58.8146 | 60.8682 | 65.8386 | ||
| Types | V*CNT | Skew Angle | Mode | |||||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |||
| UD | 0.11 | 15° | 18.5892 | 24.6235 | 35.3293 | 35.6482 | 39.8059 | 40.1566 |
| 30° | 19.7907 | 27.5192 | 37.5758 | 38.7334 | 44.7699 | 44.8668 | ||
| 45° | 23.1240 | 33.7718 | 43.5280 | 45.2188 | 54.8007 | 56.3342 | ||
| 60° | 32.8768 | 46.6645 | 58.8579 | 62.5042 | 70.8589 | 76.4394 | ||
| 0.14 | 15° | 19.1594 | 25.2162 | 36.0641 | 36.7261 | 40.8256 | 40.8465 | |
| 30° | 20.3677 | 28.1613 | 38.6503 | 39.6187 | 45.6147 | 45.7882 | ||
| 45° | 23.7315 | 34.5566 | 44.6059 | 46.2941 | 55.7146 | 57.5412 | ||
| 60° | 33.6101 | 47.7344 | 60.1998 | 63.7591 | 72.4446 | 77.7145 | ||
| 0.17 | 15° | 23.1763 | 30.7160 | 44.0894 | 44.4545 | 49.6574 | 50.1117 | |
| 30° | 24.6779 | 34.3325 | 46.8674 | 48.3332 | 55.8713 | 55.9847 | ||
| 45° | 28.8430 | 42.1399 | 54.3158 | 56.4308 | 68.3713 | 70.3186 | ||
| 60° | 41.0318 | 58.2465 | 73.4787 | 78.0518 | 88.4742 | 95.3523 | ||
| FG-V | 0.11 | 15° | 18.0694 | 24.2993 | 34.8395 | 35.1140 | 39.2444 | 40.2623 |
| 30° | 19.3073 | 27.1997 | 36.8576 | 38.3514 | 44.4246 | 44.9823 | ||
| 45° | 22.7117 | 33.3930 | 43.0375 | 44.7306 | 54.9298 | 55.8898 | ||
| 60° | 32.5888 | 46.2233 | 58.3954 | 62.3472 | 70.4436 | 76.6148 | ||
| 0.14 | 15° | 18.7213 | 24.9627 | 35.9325 | 36.0340 | 40.3826 | 41.0223 | |
| 30° | 19.9628 | 27.9173 | 38.0427 | 39.3412 | 45.5331 | 45.8315 | ||
| 45° | 23.3936 | 34.2698 | 44.2154 | 45.9247 | 55.9691 | 57.3257 | ||
| 60° | 33.3992 | 47.4078 | 59.8831 | 63.7136 | 72.2043 | 78.0564 | ||
| 0.17 | 15° | 22.5493 | 30.3816 | 43.5223 | 43.9471 | 49.0751 | 50.5020 | |
| 30° | 24.1057 | 34.0165 | 46.0643 | 47.9801 | 55.5987 | 56.4159 | ||
| 45° | 28.3819 | 41.7701 | 53.8425 | 55.9614 | 68.8770 | 69.9530 | ||
| 60° | 40.7818 | 57.8482 | 73.1009 | 78.1001 | 88.2112 | 96.0396 | ||
| FG-O | 0.11 | 15° | 16.4084 | 22.9046 | 31.6159 | 33.6029 | 36.6562 | 40.0537 |
| 30° | 17.7077 | 25.7508 | 33.8501 | 36.2830 | 42.3527 | 44.7506 | ||
| 45° | 21.2099 | 31.6586 | 40.5674 | 42.2311 | 52.8152 | 53.9899 | ||
| 60° | 31.2046 | 44.1065 | 55.5461 | 60.6186 | 66.8835 | 76.2352 | ||
| 0.14 | 15° | 17.0452 | 23.4601 | 32.8241 | 34.3062 | 37.6525 | 40.7285 | |
| 30° | 18.3275 | 26.3574 | 34.9993 | 37.1966 | 43.2631 | 45.5052 | ||
| 45° | 21.8175 | 32.4388 | 41.6106 | 43.3410 | 54.1879 | 55.1259 | ||
| 60° | 31.8862 | 45.1773 | 56.9465 | 61.7865 | 68.6013 | 77.5228 | ||
| 0.17 | 15° | 20.4935 | 28.4369 | 39.6386 | 41.7340 | 45.7071 | 50.0278 | |
| 30° | 22.0844 | 31.9798 | 42.3651 | 45.1869 | 52.6957 | 55.8895 | ||
| 45° | 26.3966 | 39.3908 | 50.6104 | 52.6850 | 65.9841 | 67.2724 | ||
| 60° | 38.8088 | 55.0062 | 69.4149 | 75.5700 | 83.7054 | 95.1822 | ||
| FG-X | 0.11 | 15° | 19.2604 | 25.3608 | 36.1914 | 36.8063 | 40.4675 | 40.9340 |
| 30° | 20.4754 | 28.2998 | 38.7220 | 39.7120 | 45.2151 | 45.8357 | ||
| 45° | 23.8434 | 34.6543 | 44.6261 | 46.3103 | 55.2276 | 57.4279 | ||
| 60° | 33.6486 | 47.6758 | 59.9923 | 63.4780 | 72.0668 | 77.0374 | ||
| 0.14 | 15° | 19.8084 | 26.0430 | 37.1106 | 37.8532 | 41.2910 | 42.0442 | |
| 30° | 21.0506 | 29.0493 | 39.8008 | 40.7351 | 46.1353 | 47.0096 | ||
| 45° | 24.4920 | 35.5521 | 45.7961 | 47.4919 | 56.3516 | 58.8017 | ||
| 60° | 34.4934 | 48.8548 | 61.4386 | 64.9465 | 73.7658 | 78.6049 | ||
| 0.17 | 15° | 24.0671 | 31.9338 | 45.6821 | 45.9560 | 50.9173 | 51.3375 | |
| 30° | 25.6288 | 35.6476 | 48.4261 | 49.9805 | 56.8856 | 57.6593 | ||
| 45° | 29.9300 | 43.6056 | 55.9981 | 58.1580 | 69.4729 | 72.2037 | ||
| 60° | 42.3389 | 59.8760 | 75.2616 | 79.8475 | 90.3762 | 96.8913 | ||
| Types | V*CNT | Skew Angle | Boundary Condition | |||
|---|---|---|---|---|---|---|
| CCSS | CSCS | CCFF | CFCF | |||
| UD | 0.11 | 15° | 17.5656 | 16.1325 | 17.1211 | 5.8025 |
| 30° | 18.3524 | 17.1106 | 17.4540 | 5.8490 | ||
| 45° | 20.7007 | 19.8447 | 18.4603 | 5.9919 | ||
| 60° | 28.2486 | 27.7948 | 21.7009 | 6.3069 | ||
| 0.14 | 15° | 18.1342 | 16.7688 | 17.7012 | 6.2424 | |
| 30° | 18.9229 | 17.7494 | 18.0355 | 6.2905 | ||
| 45° | 21.2864 | 20.5072 | 19.0480 | 6.4353 | ||
| 60° | 28.9146 | 28.5757 | 22.3161 | 6.7554 | ||
| 0.17 | 15° | 21.8982 | 20.0801 | 21.3412 | 7.1743 | |
| 30° | 22.8820 | 21.3025 | 21.7584 | 7.2326 | ||
| 45° | 25.8166 | 24.7178 | 23.0172 | 7.4116 | ||
| 60° | 35.2478 | 34.6467 | 27.0680 | 7.8059 | ||
| FG-V | 0.11 | 15° | 17.0086 | 15.3184 | 16.5114 | 5.0487 |
| 30° | 17.8273 | 16.3356 | 16.8584 | 5.0936 | ||
| 45° | 20.2441 | 19.1336 | 17.8998 | 5.2408 | ||
| 60° | 27.9303 | 27.1387 | 21.2303 | 5.5617 | ||
| 0.14 | 15° | 17.6618 | 16.0166 | 17.1825 | 5.4678 | |
| 30° | 18.4787 | 17.0329 | 17.5285 | 5.5141 | ||
| 45° | 20.9045 | 19.8505 | 18.5709 | 5.6624 | ||
| 60° | 28.6673 | 27.9750 | 21.9207 | 5.9884 | ||
| 0.17 | 15° | 21.2161 | 19.0620 | 20.5857 | 6.2207 | |
| 30° | 22.2464 | 20.3420 | 21.0234 | 6.2774 | ||
| 45° | 25.2838 | 23.8570 | 22.3339 | 6.4629 | ||
| 60° | 34.9349 | 33.9038 | 26.5208 | 6.8657 | ||
| FG-O | 0.11 | 15° | 15.2966 | 13.7187 | 14.7110 | 4.3016 |
| 30° | 16.1749 | 14.7745 | 15.0980 | 4.3467 | ||
| 45° | 18.6942 | 17.6072 | 16.2095 | 4.4929 | ||
| 60° | 26.5093 | 25.5699 | 19.6311 | 4.7975 | ||
| 0.14 | 15° | 15.9573 | 14.3811 | 15.4087 | 4.6680 | |
| 30° | 16.8163 | 15.4187 | 15.7844 | 4.7147 | ||
| 45° | 19.3078 | 18.2378 | 16.8762 | 4.8622 | ||
| 60° | 27.1313 | 26.2562 | 20.2771 | 5.1739 | ||
| 0.17 | 15° | 19.1484 | 17.0768 | 18.4438 | 5.2956 | |
| 30° | 20.2204 | 18.3681 | 18.9177 | 5.3519 | ||
| 45° | 23.3092 | 21.8497 | 20.2813 | 5.5337 | ||
| 60° | 32.9609 | 31.7016 | 24.4972 | 5.9132 | ||
| FG-X | 0.11 | 15° | 18.2140 | 17.0254 | 17.7792 | 6.5860 |
| 30° | 19.0078 | 18.0146 | 18.1123 | 6.6352 | ||
| 45° | 21.3832 | 20.7913 | 19.1261 | 6.7811 | ||
| 60° | 29.0061 | 28.8746 | 22.3997 | 7.1022 | ||
| 0.14 | 15° | 18.7355 | 17.6246 | 18.2942 | 7.0150 | |
| 30° | 19.5470 | 18.6364 | 18.6340 | 7.0670 | ||
| 45° | 21.9758 | 21.4797 | 19.6696 | 7.2180 | ||
| 60° | 29.7641 | 29.7602 | 23.0163 | 7.5489 | ||
| 0.17 | 15° | 22.7038 | 21.2134 | 22.1242 | 8.1485 | |
| 30° | 23.7285 | 22.4908 | 22.5506 | 8.2111 | ||
| 45° | 26.7784 | 26.0495 | 23.8494 | 8.3974 | ||
| 60° | 36.4902 | 36.3121 | 28.0370 | 8.8055 | ||
| Types | V*CNT | Skew Angle | a/h | |||
|---|---|---|---|---|---|---|
| 5 | 20 | 50 | 100 | |||
| UD | 0.11 | 15° | 9.0743 | 18.2012 | 20.3073 | 20.6787 |
| 30° | 9.4150 | 18.9711 | 21.0669 | 21.4408 | ||
| 45° | 10.2558 | 21.3334 | 23.4743 | 23.8687 | ||
| 60° | 11.3999 | 29.4063 | 32.2438 | 32.8085 | ||
| 0.14 | 15° | 9.3243 | 19.7973 | 22.5305 | 23.0303 | |
| 30° | 9.5879 | 20.5395 | 23.2468 | 23.7472 | ||
| 45° | 10.4551 | 22.8478 | 25.5594 | 26.0749 | ||
| 60° | 11.6404 | 30.8885 | 34.2574 | 34.9408 | ||
| 0.17 | 15° | 11.3132 | 22.4497 | 24.9546 | 25.3933 | |
| 30° | 11.7725 | 23.4173 | 25.9121 | 26.3544 | ||
| 45° | 12.8172 | 26.3808 | 28.9389 | 29.4075 | ||
| 60° | 14.2430 | 36.4827 | 39.9125 | 40.5928 | ||
| FG-V | 0.11 | 15° | 8.7986 | 15.5123 | 16.6902 | 16.8853 |
| 30° | 9.4269 | 16.4011 | 17.5995 | 17.8014 | ||
| 45° | 10.2475 | 19.0147 | 20.3313 | 20.5637 | ||
| 60° | 11.3736 | 27.4772 | 29.5441 | 29.9513 | ||
| 0.14 | 15° | 9.1228 | 16.9116 | 18.4397 | 18.6988 | |
| 30° | 9.6238 | 17.7666 | 19.3058 | 19.5706 | ||
| 45° | 10.4761 | 20.3260 | 21.9636 | 22.2570 | ||
| 60° | 11.6465 | 28.7997 | 31.1984 | 31.6713 | ||
| 0.17 | 15° | 10.9766 | 19.0705 | 20.4470 | 20.6737 | |
| 30° | 11.8498 | 20.1959 | 21.5996 | 21.8348 | ||
| 45° | 12.8769 | 23.4938 | 25.0480 | 25.3214 | ||
| 60° | 14.2886 | 34.1237 | 36.6062 | 37.0957 | ||
| FG-O | 0.11 | 15° | 8.0040 | 13.1635 | 13.9508 | 14.0776 |
| 30° | 8.7975 | 14.0945 | 14.9077 | 15.0418 | ||
| 45° | 10.2194 | 16.7496 | 17.6897 | 17.8561 | ||
| 60° | 11.3501 | 25.0679 | 26.6826 | 27.0149 | ||
| 0.14 | 15° | 8.3081 | 14.3293 | 15.3437 | 15.5098 | |
| 30° | 9.1008 | 15.2139 | 16.2464 | 16.4188 | ||
| 45° | 10.4216 | 17.7910 | 18.9359 | 19.1387 | ||
| 60° | 11.5944 | 26.0648 | 27.8938 | 28.2650 | ||
| 0.17 | 15° | 9.9887 | 16.1395 | 17.0377 | 17.1815 | |
| 30° | 10.9641 | 17.2789 | 18.2081 | 18.3607 | ||
| 45° | 12.7826 | 20.5334 | 21.6118 | 21.8026 | ||
| 60° | 14.1922 | 30.7514 | 32.6180 | 33.0048 | ||
| FG-X | 0.11 | 15° | 9.2309 | 21.2410 | 24.8589 | 25.5557 |
| 30° | 9.4901 | 21.9714 | 25.5444 | 26.2392 | ||
| 45° | 10.3425 | 24.2577 | 27.7886 | 28.4923 | ||
| 60° | 11.5036 | 32.2825 | 36.4515 | 37.3272 | ||
| 0.14 | 15° | 9.4307 | 22.9391 | 27.5913 | 28.5358 | |
| 30° | 9.6990 | 23.6674 | 28.2521 | 29.1913 | ||
| 45° | 10.5801 | 25.9622 | 30.4437 | 31.3820 | ||
| 60° | 11.7856 | 34.0782 | 39.1212 | 40.2237 | ||
| 0.17 | 15° | 11.6432 | 26.2338 | 30.6098 | 31.4489 | |
| 30° | 11.9640 | 27.1943 | 31.5188 | 32.3564 | ||
| 45° | 13.0307 | 30.1785 | 34.4733 | 35.3262 | ||
| 60° | 14.4875 | 40.5269 | 45.7146 | 46.8021 | ||
| Types | V*CNT | Skew Angle | |||
|---|---|---|---|---|---|
| 15° | 30° | 45° | 60° | ||
| UD | 0.11 | 0.00345 | 0.00311 | 0.00234 | 0.00119 |
| 0.14 | 0.00306 | 0.00278 | 0.00212 | 0.00110 | |
| 0.17 | 0.00222 | 0.00199 | 0.00150 | 0.00076 | |
| FG-V | 0.11 | 0.00401 | 0.00365 | 0.00267 | 0.00128 |
| 0.14 | 0.00354 | 0.00323 | 0.00240 | 0.00118 | |
| 0.17 | 0.00257 | 0.00234 | 0.00170 | 0.00081 | |
| FG-O | 0.11 | 0.00557 | 0.00479 | 0.00333 | 0.00149 |
| 0.14 | 0.00486 | 0.00424 | 0.00302 | 0.00140 | |
| 0.17 | 0.00360 | 0.00310 | 0.00216 | 0.00097 | |
| FG-X | 0.11 | 0.00287 | 0.00261 | 0.00201 | 0.00106 |
| 0.14 | 0.00260 | 0.00237 | 0.00183 | 0.00098 | |
| 0.17 | 0.00185 | 0.00167 | 0.00127 | 0.00066 | |
| Types | V*CNT | Skew Angle | |||
|---|---|---|---|---|---|
| 15° | 30° | 45° | 60° | ||
| UD | 0.11 | 0.00201 | 0.00178 | 0.00131 | 0.00065 |
| 0.14 | 0.00187 | 0.00167 | 0.00124 | 0.00061 | |
| 0.17 | 0.00127 | 0.00113 | 0.00083 | 0.00041 | |
| FG-V | 0.11 | 0.00214 | 0.00189 | 0.00137 | 0.00066 |
| 0.14 | 0.00197 | 0.00175 | 0.00128 | 0.00062 | |
| 0.17 | 0.00136 | 0.00120 | 0.00087 | 0.00042 | |
| FG-O | 0.11 | 0.00263 | 0.00226 | 0.00158 | 0.00072 |
| 0.14 | 0.00241 | 0.00210 | 0.00148 | 0.00069 | |
| 0.17 | 0.00166 | 0.00144 | 0.00101 | 0.00046 | |
| FG-X | 0.11 | 0.00186 | 0.00166 | 0.00123 | 0.00061 |
| 0.14 | 0.00174 | 0.00155 | 0.00116 | 0.00058 | |
| 0.17 | 0.00117 | 0.00104 | 0.00077 | 0.00038 | |
| Types | V*CNT | Skew Angle | |||
|---|---|---|---|---|---|
| 15° | 30° | 45° | 60° | ||
| UD | 0.11 | 0.00215 | 0.00158 | 0.00092 | 0.00038 |
| 0.14 | 0.00192 | 0.00142 | 0.00084 | 0.00036 | |
| 0.17 | 0.00138 | 0.00101 | 0.00059 | 0.00024 | |
| FG-V | 0.11 | 0.00248 | 0.00183 | 0.00102 | 0.00040 |
| 0.14 | 0.00220 | 0.00163 | 0.00093 | 0.00037 | |
| 0.17 | 0.00159 | 0.00117 | 0.00065 | 0.00026 | |
| FG-O | 0.11 | 0.00339 | 0.00237 | 0.00126 | 0.00047 |
| 0.14 | 0.00297 | 0.00211 | 0.00115 | 0.00044 | |
| 0.17 | 0.00219 | 0.00153 | 0.00081 | 0.00030 | |
| FG-X | 0.11 | 0.00181 | 0.00135 | 0.00081 | 0.00035 |
| 0.14 | 0.00165 | 0.00123 | 0.00074 | 0.00032 | |
| 0.17 | 0.00116 | 0.00086 | 0.00051 | 0.00022 | |
| Types | V*CNT | Skew Angle | |||
|---|---|---|---|---|---|
| 15° | 30° | 45° | 60° | ||
| UD | 0.11 | 0.00136 | 0.00101 | 0.00059 | 0.00025 |
| 0.14 | 0.00127 | 0.00095 | 0.00056 | 0.00023 | |
| 0.17 | 0.00086 | 0.00064 | 0.00038 | 0.00016 | |
| FG-V | 0.11 | 0.00145 | 0.00106 | 0.00062 | 0.00025 |
| 0.14 | 0.00134 | 0.00099 | 0.00058 | 0.00024 | |
| 0.17 | 0.00092 | 0.00067 | 0.00039 | 0.00016 | |
| FG-O | 0.11 | 0.00177 | 0.00128 | 0.00071 | 0.00027 |
| 0.14 | 0.00163 | 0.00118 | 0.00067 | 0.00026 | |
| 0.17 | 0.00112 | 0.00081 | 0.00045 | 0.00017 | |
| FG-X | 0.11 | 0.00126 | 0.00094 | 0.00056 | 0.00023 |
| 0.14 | 0.00118 | 0.00088 | 0.00052 | 0.00022 | |
| 0.17 | 0.00080 | 0.00059 | 0.00035 | 0.00015 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ansari, M.I.; Kumar, A.; Barnat-Hunek, D.; Suchorab, Z.; Andrzejuk, W.; Majerek, D. Static and Dynamic Response of FG-CNT-Reinforced Rhombic Laminates. Appl. Sci. 2018, 8, 834. https://doi.org/10.3390/app8050834
Ansari MI, Kumar A, Barnat-Hunek D, Suchorab Z, Andrzejuk W, Majerek D. Static and Dynamic Response of FG-CNT-Reinforced Rhombic Laminates. Applied Sciences. 2018; 8(5):834. https://doi.org/10.3390/app8050834
Chicago/Turabian StyleAnsari, Md Irfan, Ajay Kumar, Danuta Barnat-Hunek, Zbigniew Suchorab, Wojciech Andrzejuk, and Dariusz Majerek. 2018. "Static and Dynamic Response of FG-CNT-Reinforced Rhombic Laminates" Applied Sciences 8, no. 5: 834. https://doi.org/10.3390/app8050834
APA StyleAnsari, M. I., Kumar, A., Barnat-Hunek, D., Suchorab, Z., Andrzejuk, W., & Majerek, D. (2018). Static and Dynamic Response of FG-CNT-Reinforced Rhombic Laminates. Applied Sciences, 8(5), 834. https://doi.org/10.3390/app8050834







