Abstract
The proportion of instances belonging to each class in a data-set plays an important role in machine learning. However, the real world data often suffer from class imbalance. Dealing with multi-class tasks with different misclassification costs of classes is harder than dealing with two-class ones. Undersampling and oversampling are two of the most popular data preprocessing techniques dealing with imbalanced data-sets. Ensemble classifiers have been shown to be more effective than data sampling techniques to enhance the classification performance of imbalanced data. Moreover, the combination of ensemble learning with sampling methods to tackle the class imbalance problem has led to several proposals in the literature, with positive results. The ensemble margin is a fundamental concept in ensemble learning. Several studies have shown that the generalization performance of an ensemble classifier is related to the distribution of its margins on the training examples. In this paper, we propose a novel ensemble margin based algorithm, which handles imbalanced classification by employing more low margin examples which are more informative than high margin samples. This algorithm combines ensemble learning with undersampling, but instead of balancing classes randomly such as UnderBagging, our method pays attention to constructing higher quality balanced sets for each base classifier. In order to demonstrate the effectiveness of the proposed method in handling class imbalanced data, UnderBagging and SMOTEBagging are used in a comparative analysis. In addition, we also compare the performances of different ensemble margin definitions, including both supervised and unsupervised margins, in class imbalance learning.
1. Introduction
Class distribution, i.e., the proportion of instances belonging to each class in a data set, plays a key role in any kind of machine-learning and data-mining research. However, the real world data often suffer from class imbalance. The class imbalance case has been reported to exist in a wide variety of real-world domains, such as face recognition [1], text mining [2], software defect prediction [3], and remote sensing [4]. Binary imbalanced data classification problems occur when one class, usually the one that refers to the concept of interest (positive or minority class), is underrepresented in the data-set; in other words, the number of negative (majority) instances outnumbers the amount of positive class instances [5,6,7]. Processing minority class instances as noise can reduce classification accuracy. Dealing with multi-class tasks with different misclassification costs of classes is harder than dealing with two-class ones [8,9,10]. Some traditional classification algorithms, such as K-Nearest Neighbors (KNN), Support Vector Machines (SVM), and decision trees, which show good behavior in problems with balanced classes, do not necessarily achieve good performance in class imbalance problems. Consequently, how to classify imbalanced data effectively has emerged as one of the biggest challenges in machine learning.
The objective of imbalance learning can be generally described as obtaining a classifier that will provide high accuracy for the minority class without severely jeopardizing the accuracy of the majority class. Typically, there are four methods for imbalanced learning [11]: sampling methods [12], cost-sensitive methods [7,13], kernel-based methods [7] and active learning methods [14].
- Sampling methods: The objective of these non-heuristic methods is to provide a balanced distribution by considering the representative proportions of class examples. They are carried out before training starts. These methods will be presented in detail in Section 2.1.
- Cost-sensitive methods: These methods incorporate both data level transformations (by adding costs to instances) and algorithm level modifications (by modifying the learning process to accept costs). They generally use the cost matrix to consider the costs associated with misclassifying samples [11]. Cost-sensitive neural network [15] with threshold-moving technique was proposed to adjust the output threshold toward inexpensive classes, such that high-cost samples are unlikely to be misclassified. Three cost-sensitive methods, AdaC1, AdaC2, and AdaC3 were proposed [16] and cost items were used to weight the updating strategy in the boosting algorithm. The disadvantage of these approaches is the need to define misclassification costs, which are not usually available in the data sets [5].
- Kernel-based methods: The principles of kernel-based learning are centered on the theories of statistical learning and Vapnik-Chervonenkis dimensions [17,18]. In kernel-based methods, there have been many works to apply sampling and ensemble techniques to the support vector machine (SVM) concept [19]. Different error costs [20] were suggested for different classes to bias the SVM to shift the decision boundary away from positive instances and make positive instances more densely distributed.
- Active learning methods: Traditional active learning methods were used to solve the imbalanced training data problem. Recently, various approaches on active learning from imbalanced data sets were proposed [14]. Active learning effectively selects the instances from a random set of training data, therefore significantly reducing the computational costs when dealing with large imbalanced data sets. The major drawback of these approaches is large computation costs for large datasets [14].
Ensemble classifiers are known to increase the accuracy of single classifiers by combining several of them and have been successfully applied to imbalanced data-sets [21,22,23,24]. Ensemble learning methods have been shown to be more effective than data sampling techniques to enhance the classification performance of imbalanced data [25]. However, as the standard techniques for constructing ensembles are rather too overall accuracy oriented, they still have difficulty sufficiently recognizing the minority class [26]. So, the ensemble learning algorithms have to be designed specifically to effectively handle the class imbalance problem [5]. The combination of ensemble learning with imbalanced learning techniques (such as sampling methods presented in Section 2.1) to tackle the class imbalance problem has led to several proposals in the literature, with positive results [5]. Hence, aside from conventional categories such as kernel-based methods, ensemble-based methods can be classified into a new category in imbalanced domains [5]. In addition, the idea of combining multiple classifiers itself can reduce the probability of overfitting.
Margins, which were originally applied to explain the success of boosting [27] and to develop the Support Vector Machines (SVM) theory [17], play a crucial role in modern machine learning research. The ensemble margin [27] is a fundamental concept in ensemble learning. Several studies have shown that the generalization performance of an ensemble classifier is related to the distribution of its margins on the training examples [27]. A good margin distribution means that most examples have large margins [28]. Moreover, ensemble margin theory is a proven effective way to improve the performance of classification models [21,29]. It can be used to detect the most important instances, which have low margin values, and thus help ensemble classifiers to avoid the negative effects of redundant and noisy samples. In machine learning, the ensemble margin has been used in imbalanced data sampling [21], noise removal [30,31,32], instance selection [33], feature selection [34] and classifier design [35,36,37].
In this paper, we propose a novel ensemble margin based algorithm, which handles imbalanced classification by employing more low margin examples which are more informative than high margin samples. This algorithm combines ensemble learning with undersampling, but instead of balancing classes randomly such as UnderBagging [38], our method pays attention to constructing higher quality balanced sets for each base classifier. In order to demonstrate the effectiveness of the proposed method in handling class imbalanced data, UnderBagging [38] and SMOTEBagging [8], which will be presented in detail in the following section, are used in a comparative analysis. We also compare the performances of different ensemble margin definitions, including the new margin proposed, in class imbalance learning.
The remaining part of this paper is organized as follows. Section 2 presents an overview of the imbalanced classification domain from the two-class and multi-class perspectives. The ensemble margin definition and the effect of class imbalance on ensemble margin distribution is presented in Section 3. Section 4 describes in detail the proposed methodology. Section 5 presents the experimental study and Section 6 provides a discussion according to the analysis of the results. Finally, Section 7 presents the concluding remarks.
2. Related Works
2.1. Sampling Methods for Learning from Imbalanced Data
The sampling approach rebalances the class distribution by resampling the data space. This method avoids the modification of the learning algorithm by trying to decrease the effect caused by data imbalance with a preprocessing step, so it is usually more versatile than the other imbalance learning methods. Many works have been studying the suitability of data preprocessing techniques to deal with imbalanced data-sets [5,39]. Their studies have shown that for several base classifiers, a balanced data set provides an improved overall classification performance compared to an imbalanced data set. He [11] and Galar et al. [5] give a good overview of these sampling methods, among which random oversampling [40] and random undersampling [12] are the most popular.
2.1.1. Oversampling Techniques
Random oversampling tries to balance class distribution by randomly replicating minority class instances. However, several authors agree that this method can increase the likelihood of overfitting occuring, since it makes exact copies of existing instances [5].
Synthetic Minority Over-sampling Technique (SMOTE), the most popular over-sampling method, was proposed by Chawla et al. [40]. Its main idea is to create new minority class examples by interpolating several minority class instances that lie together. SMOTE can avoid the over fitting problem [41]. However, its procedure is inherently dangerous since it blindly generalizes the minority class without regard to the majority class and this strategy is particularly problematic in the case of highly skewed class distributions since, in such cases, the minority class is very sparse with respect to the majority class, thus resulting in a greater chance of class mixture [42].
Many improved oversampling algorithms attempt to retain SMOTE’s advantages and reduce its shortcomings. MSMOTE (Modified SMOTE) [6] is a modified version of SMOTE. The main idea of this algorithm is to divide the instances of the minority class into three groups, safe, border and latent noise instances, by the calculation of distances among all examples. When MSMOTE generates new examples, the strategy to select the nearest neighbors is changed with respect to SMOTE and depends on the group previously assigned to the instance. For safe instances, the algorithm randomly selects a data point from the K nearest neighbors; for border instances, it only selects the nearest neighbor; finally, for latent noise instances, it does nothing. This method is effective to reduce the risk of introducing artificially mislabeled instances. Hence, it can lead to more accurate classification than SMOTE. Sáez et al. try to increase the effectiveness of SMOTE by dividing the data set into four groups: safe, borderline, rare and outliers [10]. In fact, it is another version of MSMOTE which considers a fourth group in the underlying instance categorisation: rare instances. Their results show that borderline examples are usually preprocessed. The preprocessing of outliers depends on whether the safe examples are representative enough within the core of the class: if the amount of safe examples is rather low, preprocessing outliers is usually a good alternative. Finally, the preprocessing of rare examples mainly depends on the amounts of safe examples and outliers.
2.1.2. Undersampling Techniques
Random undersampling aims to balance class distribution through the random elimination of majority class examples. Its major drawback is that it can discard potentially useful data, which could be important for the induction process [5,41].
Zhang and Mani used the K-Nearest Neighbors (KNN) classifier to achieve undersampling [43]. Based on the characteristics of the given data distribution, four KNN undersampling methods were proposed in [43], namely, NearMiss-1, NearMiss-2, NearMiss-3, and the “most distant” method. Instead of using the entire set of over-represented majority training examples, a small subset of these examples is selected such that the resulting training data is less skewed. The NearMiss-1 method selects those majority examples whose average distance to the three closest minority class examples is the smallest, while the NearMiss-2 method selects the majority class examples whose average distance to the three farthest minority class examples is the smallest. NearMiss-3 selects a given number of the closest majority examples for each minority example to guarantee that every minority example is surrounded by some majority examples. Finally, the most distant method selects the majority class examples whose average distance to the three closest minority class examples is the largest. Experimental results suggest that the NearMiss-2 method can provide competitive results with respect to SMOTE and random undersampling methods for imbalanced learning. This method is effective in cleaning the decision surface by increasing the distance between minority class and majority class. In addition, it is useful to reduce class overlapping.
2.1.3. Oversampling versus Undersampling
At first glance, the oversampling and undersampling methods appear to be functionally equivalent since they both alter the size of the original data set and can actually provide the same proportion of class balance. However, this commonality is only superficial; each method introduces its own set of problematic consequences that can potentially hinder learning [44]. In the case of undersampling, the problem is relatively obvious: removing examples from the majority class may cause the classifier to miss important concepts pertaining to the majority class. In regards to oversampling, the problem is a little more opaque: the computational complexity is increased rapidly with the production of more positive samples, especially in dealing with large data such as remote sensing data. In addition, oversampling has the risk of over-fitting [41]. For example, since random oversampling simply appends replicated data to the original data set, multiple instances of certain examples become tied leading to overfitting [41]. In particular, overfitting in oversampling occurs when classifiers produce multiple clauses in a rule for multiple copies of the same example which causes the rule to become too specific; although the training accuracy will be high in this scenario, the classification performance on the unseen testing data is generally far worse. Despite some limitations, oversampling and undersampling schemes have their own strengths. For example, one of the main advantages of undersampling techniques lies in the reduction of the training time, which is especially significant in the case of highly imbalanced large data sets [45]. Oversampling can provide a balanced distribution without losing information on majority class.
2.2. Ensemble-Based Imbalanced Data Classification Methods
Ensemble learners are more robust than single classifiers and have been certificated more effective than sampling methods to deal with the imbalance problem [4,46]. According to the used ensemble method, this paper divides them into three sub-categories: boosting-based ensembles, bagging-based extended ensembles and hybrid combined ensembles.
2.2.1. Boosting Based Ensemble Learning
For multi-class imbalance problems, besides using data sampling to balance the number of samples for each class, another approach [45,47] is decomposing the multi-class problem into several binary subproblems by one-versus-one [48] or one-versus-all approaches [49]. Wang and Yao compared the performances of adaboost.NC and adaboost combined with random oversampling with or without using classes decomposition for multi-class imbalanced data sets [47]. Their results in the case of classes decomposition show adaboost. NC and adaboost have similar performance. The one-versus-all decomposition approach does not provide any advantages for both boosting ensembles in their multi-class imbalance learning experiments. The reason seems to be the loss of global information of class distributions in the process of class decomposition. Although, the results achieved without using classes decomposition show adaboost. NC outperforms adaboost; their performances are degraded as the number of imbalanced classes increases. For the data sets with more classes, despite the increased quantity of minority class examples by oversampling, the class distribution in data space is still imbalanced, which seems to be dominated by the majority class [47].
The methods consisting of first pre-processing data and then using standard ensembles on balanced data cannot absolutely avoid the shortcomings of sampling. Moreover, internal imbalance sampling based ensemble approaches should work better [50]. This technique balances the data distribution in each iteration when constructing the ensemble. It can obtain more diversity than the mere use of a sampling process before learning a model [5]. SMOTEBoost [51] proposed by Chawla et al. improves the over-sampling method SMOTE [40] by combining it with AdaBoost.M2. They used the SMOTE data preprocessing algorithm before evaluating the prediction error of the base classifier. The weights of the new instances are proportional to the total number of instances in the new data-set. Hence, their weights are always the same. Whereas the original data-set’s instances weights are normalized in such a way that they form another distribution with the new instances. After training a classifier, the weights of the original data-set instances are updated; then another sampling phase is applied (again, modifying the weight distribution). The basic idea is to let the base learners focus more and more on difficult yet rare class examples. In each round, the weights for minority class examples are increased. However, SMOTE has high risk of producing mislabeled instances in noisy environment, and boosting is very sensitive to class noise. Hence, how to increase its robustness should not be overlooked.
Thanathamathee et al. proposed a method combining synthetic boundary data generation and boosting procedures to handle imbalanced data sets [52]. They first eliminate the imbalanced error domination effect by measuring the distance between class sets with Hausdorff distance [53], and then identify all relevant class boundary data, which have minimum distance value with the instances of other classes. Then, they synthesize new boundary data using a bootstrapping re-sampling technique on original boundary instances [54]. Finally, they proceed to learning the synthesized data by a boosting neural network [55]. Their method outperforms KNN, adaboost.M1 and SMOTEBoost. However, the method relies mainly on boundary definition; if the boundary is not correctly detected, the results may be deteriorated.
Random UnderSampling Boosting (RUSBoost) [56] is an algorithm that combines data sampling and boosting. It realizes a random undersampling by removing examples from the majority class while SMOTEBoost creates synthetic examples for the minority class by using SMOTE. Compared to SMOTEBoost, this algorithm is less complex and time-consuming, and easier to operate [5]. Moreover, it is reported as the best approach in [5] with less computational complexity and higher performances than many other more complex algorithms such as BalanceCascade in dealing with binary class imbalance problems [5]. Further, it outperforms the other two best methods, SMOTEBagging and UnderBagging, in [5].
Random balance boost [57] follows the same philosophy as SMOTEBoost and RUSBoost. Each base classifier is trained with a data set obtained through random balance. The random balance is designed to be used in an ensemble and relies on randomness and repetition. It conserves the size of the original dataset but varies the class proportions in the training sample of each base classifier using a random ratio. This includes the case in which the minority class is overrepresented and the imbalance ratio is inverted. SMOTE and random undersampling (resampling without replacement) are used to respectively increase or reduce the size of the classes to achieve the desired ratios. The combination of SMOTE and undersampling provides more diversity and leads to better performance compared with other state-of-the-art combined ensemble methods such as SMOTEBoost and RUSBoost for binary-class imbalance problem [57,58] .
There are many other boosting-based algorithms designed to address imbalance problems at the data level such as Evolutionary UnderSampling Boosting (EUSBoost) [59], cost-sensitive boosting [16,60] and so on. However, most boosting-based methods face the threat of noise as the original boosting method [57]. In addition, most boosting-based imbalanced learning techniques only focus on two-class imbalance problems and are difficult to extend to multi-class imbalance problems. They generally rely on class decomposition to simplify the multi-class imbalance problem. However, each individual classifier is trained without full data knowledge. Consequently, class decomposition can cause classification ambiguity or uncovered data regions [61].
2.2.2. Bagging Based Ensemble Learning
Bagging significantly outperforms boosting over noisy and imbalanced data [62]. Moreover, bagging techniques are not only easy to develop, but also powerful when dealing with class imbalance if they are properly combined [5]. Most of the related works in the literature indicate good performance of bagging extensions versus the other ensembles [50,63]. OverBagging [8] is a method for the management of class imbalance that merges bagging and data preprocessing. It increases the cardinality of the minority class by replication of original examples (random oversampling), while the examples in the majority class can be all considered in each bag or can be resampled to increase the diversity. This method outperforms original bagging in dealing with binary imbalanced data problems [5].
SMOTEBagging has been proposed to deal with multi-class imbalance problems [8]. It creates each bag to be significantly different. A SMOTE resampling rate (a) is set in each iteration (ranging from 10% in the first iteration to 100% in the last, always being multiple of 10) and this ratio defines the number of minority class instances () randomly resampled (with replacement) from the original data-set in each iteration. The rest of the minority class instances are generated by the SMOTE algorithm. The reported results show that this method can get better performance than OverBagging for both binary class and multi-class imbalance problems [5,63].
Blaseczynski and Stefanowski proposed a Neighbourhood Balanced Bagging [26] for binary class imbalance problems. In this method, the sampling probabilities of training examples are modified according to the class distribution in their neighbourhood. Then it consists in keeping a larger size of bootstrap samples by a probability-based oversampling. Their experiments prove that their extended bagging is significantly better than OverBagging and SMOTEBagging.
UnderBagging was first proposed by Barandela et al. [38]. In this method, the number of the majority class examples in each bootstrap sample is randomly reduced to the cardinality of the minority class. Simple versions of undersampling combined with bagging are proved to work better than more complex solutions such as EasyEnsemble and BalanceCascade [26,50,64]. Another popular extended version of bagging is Roughly Balanced Bagging (RBBag) [65]. It results from the critics of the original UnderBagging algorithm and its variants which use exactly the same number of majority and minority class examples in each bootstrap sample. Instead of fixing a constant sample size, RBBag equalizes the sampling probability of each class. For each iteration, the size of the majority class in the bootstrap sample is set according to the minority class binomial distribution. The class distribution of the resulting bootstrap samples may be slightly imbalanced and it varies over iterations. This approach is more consistent with the nature of the original bagging and better uses the information about the minority examples. Both under-sampling bagging extensions outperform SMOTEBagging and OverBagging for binary class imbalance problems in [26]. However, the performances of the two methods were not tested for multi-class imbalance learning.
Neighbourhood Balanced Bagging has another version [26]. The difference with the presented method in the previous section is in reducing the sample size with a probability-based undersampling. The reported experiments prove that this method is competitive with RBBag for binary-class imbalance tasks and outperforms the first version that involved an oversampling scheme.
Qian et al. proposed a resampling bagging algorithm [22] which is another version of UnderOverBagging [8,66], a combination of UnderBagging and OverBagging. In that method, small classes are oversampled and large classes are undersampled. The resampling scale is determined by the ratio of the minimum class size and the maximum class size. The reported experimental results show that this method is more efficient than bagging, adaboost, random forests and some popular extended versions of bagging (UnderBagging, SMOTEBagging, OverBagging) and some hybrid ensembles for binary class imbalance problems [50]. However, the algorithm performance is highly related to the ratio of minority class size and features number. When this ratio is less than 3, the probability of obtaining a worse performance can increase significantly.
Classifier level approaches try to adapt existing classifier learning algorithms to bias the learning toward the minority class. Sometimes these methods require special knowledge of both the corresponding classifier and the application domain, comprehending why the classifier fails when the class distribution is uneven [5]. For example, Park et Ghosh introduce a method by bagging a novel kind of decision α-Tree for imbalanced classification problems [67]. Experimental results show that their approach has better performance than bagging C4.5 and UnderBagging C4.5 in dealing with binary imbalance problems. However, base classifier variation based approaches have a disadvantage of being difficult to carry out and improve.
2.2.3. Hybrid Combined Ensembles
EasyEnsemble [50] was proposed by Liu and Zhou in the context of imbalanced data sampling. The main motivation of this method was to keep the high efficiency of under-sampling but reduce the risk of ignoring potentially useful information contained in majority class examples. It adopts a very simple strategy. First, it randomly generates multiple subsamples from the majority class sample. The size of each subsample is the same as that of the minority class sample , i.e., = , . Then, the union of each possible pair (, ) is used to train an adaboost ensemble. The final ensemble is formed by combining all the base learners in all the adaboost ensembles. It can get better results than adaboost, bagging, random forest, SMOTEBoost and BRF for binary imbalance problems [23]. It seems that using an ensemble as base classifier is more effective (though less efficient) for imbalance classification than using a single classifier.
BalanceCascade [50] tries to use guided rather than random deletion of majority class examples. In contrast to EasyEnsemble, it works in a supervised manner. In the ith round, a subsample is randomly generated from the current majority class data set with sample size = . Then, an ensemble is trained from the union of and by adaboost. After that, the majority class data examples that are correctly classified by are removed from . Since BalanceCascade removes correctly classified majority class examples in each iteration, it should be more efficient on highly imbalanced data sets. The method outperforms adaboost and random forest combined with both random undersampling and oversampling schemes on binary-class imbalanced data sets. However, despite the underlying guided sampling procedure, the reported results are not better than those achieved by EasyEnsemble. Furthermore, some borderline instances of majority class face the risk of being removed.
3. Ensemble Margin for Imbalance Learning
Ensemble margin has great potential for classifier design by identifying important instances as demonstrated by some recent work that appeared in the literature [46]. Minority class instances having small ensemble margin values, and the effectiveness of combining ensemble learning with margin theory for imbalanced data is also an interesting research direction to explore. In this section, we first present the different ensemble margin definitions, then we analyze the effect of class imbalance on the margin distribution of training data.
3.1. Ensemble Margin Definitions
Different definitions of ensemble margin have been proposed [27,35,36,68]. The decision by an ensemble for each instance is made by voting. The ensemble margin can be calculated as a difference between the votes according to two different well-known definitions [69] in both supervised [27] and unsupervised [70] ways.
- A popular ensemble margin, which has been introduced by Shapire et al. [27], is defined by Equation (1), where is the number of votes for the true class y and is the number of votes for any other class c. This ensemble margin is in the range [, +1] and the examples which are correctly classified have positive margin values. A large positive ensemble margin can be interpreted as a confident correct classification.where L represents the number of classes.
- The ensemble margin of a sample can also be obtained by the difference between the fraction of classifiers voting correctly and incorrectly, as in Equation (2) [69]. This second popular ensemble margin definition follows the same idea introduced by Schapire [27] but instead of using a max operation, it uses a sum operation [69].This ensemble margin is also in the range [, +1]. However, correctly classified samples do not necessarily have positive margin values.
- In this paper, we propose an unsupervised ensemble margin alternative defined as Equation (4), where is the votes number of the most voted class for sample x and T represents the number of base classifiers in the ensemble. The proposed margin is an unsupervised version of the classic sum-margin referred to as Equation (2); it does not require the true class label of instance x. Hence, it is potentially more robust to class noise. This new margin will be named as unsupervised sum-margin.The proposed margin also has the advantage of being considered as a classifier evaluation function or adopted for classifier design in unsupervised or semi-supervised ensemble learning.
Naturally, for two-class problems these definitions are quite similar. However, a major concern needs to be solved in relation to multi-class problems. For example, by Equation (2), the margins can represent a lower bound, since they can assume negative values even when the correct label gets most of the votes (when there is a plurality, but not a majority) [69].
3.2. Effect of Class Imbalance on Ensemble Margin Distribution
The margin distribution of training instances effectively reflects the performance of an ensemble algorithm. In this section, we analyze the effect of class imbalance on the margin distribution of the training set. During the process of classifying a balanced multi-class data, each class has the same number of instances. However, class imbalance makes the learning task more complex. Figure 1 shows the margin distribution of correctly classified training instances by bagging involving decision tree as base learner on data set Vehicle (Table 1) in both balanced and imbalanced cases, using our ensemble margin Equation (4). The margin values should be as high as possible for correctly classified instances. From the margin plot, we can see that imbalanced data lead to more instances of obtaining high margin values and less instances with low margin values. In fact, the existence of one or more minority classes in a classification task results in majority classes obtaining more space. Thus causes a classifier bias to the classification of majority classes and an illusory optimized margin distribution for imbalance learning.
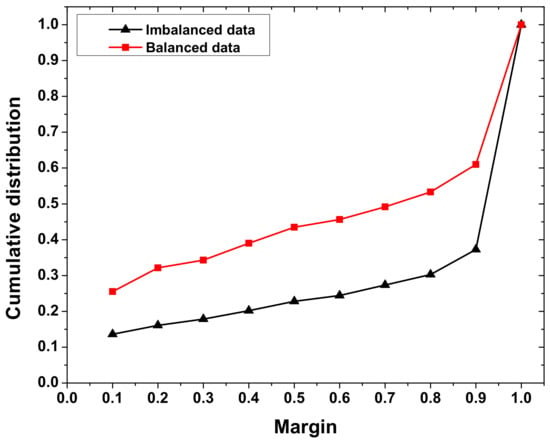
Figure 1.
Margin distribution of correctly classified training instances by bagging with both balanced and imbalanced versions of data set Vehicle using a new ensemble margin.

Table 1.
Imbalanced and balanced versions of data set Vehicle.
4. A Novel Bagging Method Based on Ensemble Margin
Compared to binary classification data imbalance problems, multi-class imbalance problems increase the data complexity and negatively affect the classification performance regardless of whether the data is imbalanced or not. Hence, multi-class imbalance problems cannot be simply solved by rebalancing the number of examples among classes in the pre-processing step. In this section, we propose a new algorithm to handle the class imbalance problem. Several methods proposed in the literature to address the problem of class imbalance as well as their strengths and weaknesses have been presented in the previous section. Ensemble classifiers have been shown to be more effective than data sampling techniques to enhance the classification performance of imbalanced data. Moreover, the combination of ensemble learning with sampling methods to tackle the class imbalance problem has led to several proposals with positive results in the literature.
In addition, as mentioned in the previous section, boosting based methods are sensitive to noise. On the contrary, bagging techniques are not only robust to noise but also easy to develop. Galar et al. pointed out that bagging ensembles would be powerful when dealing with class imbalance if they are properly combined [5,63]. Consequently, we chose to found our new imbalance ensemble learning method on bagging.
Enhancing the classification of class decision boundary instances is useful to improve the classification accuracy. Hence, for a balanced classification, focusing on the usage of the small margin instances of a global margin ordering should benefit the performance of an ensemble classifier. However, the same scheme is not suited to improve the model built from an imbalanced training set. Although most of the minority class instances have low margin values, selecting useful instances from a global margin sorting still has a risk to lose partial minority class samples, and even causes the classification performance to deteriorate. Hence, the most appropriate method for the improvement of imbalanced classification is to choose useful instances from each class independently.
4.1. Ensemble Margin Based Data Ordering
The informative instances such as class decision boundary samples and difficult class instances play an important role in classification particularly when it is imbalanced classification. These instances generally have low ensemble margins. To utilize the relationship between the importance of instances and their margins effectively in imbalance learning, we designed our class imbalance sampling algorithm based on margin ordering.
Let us consider a training set denoted as , where is a vector with feature values and is the value of the class label. The importance of a training instance could be assessed by an importance evaluation function which relies on an ensemble margin’s definition and is defined by Equation (5). The lower the margin value (in absolute value), the more informative the instance is and the more important it is to consider for our imbalance sampling scheme.
To solve the problem previously mentioned related to the margins (both supervised and unsupervised) based on a sum operation, a shift is performed before data importance calculation. The shifted margin values are achieved by subtracting the minimum margin value of the samples of the training set which are correctly classified from their original margin values. An example is used to explain the margin shift procedure in Figure 2.
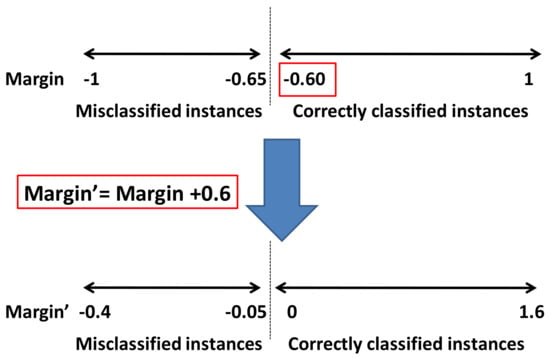
Figure 2.
Shift procedure for sum operation based margin.
4.2. A Novel Bagging Method Based on Ensemble Margin
The proposed ensemble margin based imbalance learning method is inspired by SMOTEBagging [8], a major oversampling method which has been defined in the previous section. It combines under sampling, ensemble and margin concepts. Our method pays more attention to low margin instances. It could overcome the shortcomings of both SMOTEBagging [8] and UnderBagging [38]. This method has lower computational complexity than SMOTEBagging and focuses more on important instances for classification tasks than UnderBagging.
The proposed method has three main steps:
- Computing the ensemble margin values of the training samples via an ensemble classifier.
- Constructing balanced training subsets by focusing more on small margin instances.
- Training base classifiers on balanced training subsets and constructing a new ensemble with a better capability for imbalance learning.
Denote as training samples. The first step of our method involves a robust ensemble classifier: bagging which is constructed using the whole training set. The margin value of each training instance is then calculated. In the second phase, we aim to select the most significant training samples for classification to form several new balanced training subsets. Suppose L is the number of classes and the number of training instances of the class. We sort those classes in descending order according to their number of instances. Therefore, is the training size of class L, which is the smallest, and is the training size of class 1 which is the largest. The training instances of each class, , are sorted in descending order according to the margin based importance evaluation function (Equation (5)) previously introduced. For each class c, the higher the importance value of an instance , the more important this instance is for classification decision. Then, as in SMOTEBagging [8], a resampling rate a is used to control the amount of instances which should be chosen in each class to contract a balanced data set. All the instances of the smallest class are kept. The detailed steps of our method are shown in Algorithm 1.
The range of a is set from 10 to 100 first. For each class , L representing the smallest class, instances are bootstrapped from the first of the importance ordered samples of class c to construct subset . All the subsets are balanced. When the amount of class is under , instances are bootstrapped from the first samples of class c, which is the same as in UnderBagging. Then the smallest class samples are combined with to construct the first balanced data. In the next phase, the first base classifier is built using the obtained balanced training set. Figure 3 presents the flowchart of our method with an ensemble size T and a range of 10–100% for a. The elements in the range of a could construct an arithmetic progression denoted as A. If we build classifiers as ensemble members, every 10 classifiers will be built with different resampling rates a ranging from 10% to 100%, as in SMOTEBagging. However, while SMOTEBagging uses , the training size of the largest class 1, as a standard for carrying out oversampling (SMOTE) on other relative minority classes, our method use , the training size of the smallest class L, as a standard for performing an instance importance based undersampling on other relative majority classes.
| Algorithm 1: A novel ensemble margin based bagging method (MBagging). |
Training phase Inputs:
|
| Prediction phase Inputs:
|
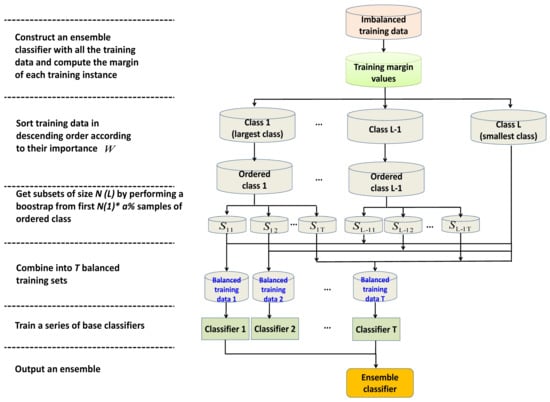
Figure 3.
Flowchart of margin based imbalanced ensemble classification (ensemble size , range of resampling rate a 10–100%).
5. Experimental Results
5.1. Data Sets
We applied our margin-based imbalance learning method on 18 UCI data sets including 17 multi-class and 1 binary data (Table 2). Among these imbalanced data, Optdigit, Pendigit and Vehicle are artificially imbalanced data. The 18 data sets are characterized by different sizes, class numbers and features. Furthermore, they differ in class imbalance ratio.

Table 2.
Imbalanced data sets.
Table 2 summaries the properties of the selected data-sets, including the number of classes (CL), the number of attributes (AT), the number of examples (EX) as well as the number of instances for each class ().
5.2. Experimental Setup
In all our experiments, Classification and Regression Trees (CART) are used as base classifiers for training all the classification models. Standard Bagging [71] is utilized to obtain the margin values of training instances. All the ensembles are implemented with 100 trees. Each data set has been randomly divided into two parts: training set and test set. In order to avoid the case that all the minority class instances are in the training set (or test set), and there are no samples of the smallest class in the test set (or training set), the percentage of the instances used for training and testing is set to 1:1, i.e., 50% original data is obtained via adopting random sampling without replacement to form a training set, and all the unselected instances compose a test set. All the reported results are mean values of a 10-time calculation. The range of sampling parameter a is set to 10–100.
5.3. Evaluation Methods
In the framework of imbalanced data-sets, standard metrics such as overall accuracy are not the most appropriate, since they do not distinguish between the classification rates of different classes, which might lead to erroneous conclusions [45]. Therefore we adopt , F-measure, and as performance measures in our experiments.
- Recall, also called per class accuracy, is the percentage of instances correctly classified in each class. [10] strongly recommends using the dedicated performance measure to evaluate classification algorithms, especially when dealing with multi class imbalance problems. Let and represent the true prediction of the ith class and the false prediction of the ith class into jth class respectively. The per class accuracy for class i can be defined as (6).where L stands for the number of classes
- Average accuracy is a performance metric that gives the same weight to each of the classes of the problem, independently of the number of examples it has. It can be calculated as the following equation:
- F-Measure is one of the most frequently used measurements to evaluate the performance of an algorithm for imbalance data classification. It is a family of metrics that attempts to measure the trade-offs between precision, which measures how often an instance that was predicted as positive is actually positive, and recalls by outputting a single value that reflects the goodness of a classifier in the presence of rare classes [72].where can be computed by .
- KW Diversity [73] is a performance metric that gives the same weight to each of the classes of the problem, independently of the number of examples it has. It can be calculated as the following equation [69]:where diversity increases with KW variance, T is the size of the ensemble of classifiers, is the number of classifiers that correctly recognize sample , and N represents the number of samples.
5.4. Imbalance Learning Performance Comparative Analysis
These experiments evaluate the classification performance of the proposed ensemble margin based imbalance learning algorithm, and its comparison to original bagging as well as state of the art algorithms UnderBagging [38] and SMOTEBagging [8]. In addition, the performances of four ensemble margin definitions in our margin based ensemble are compared. The best results are marked in bold. The values in parentheses of the Table 3, Table 4 and Table 5 represent the rank of the comparative methods.

Table 3.
Average accuracy of standard bagging, UnderBagging, SMOTEBagging and margin-based bagging with four margins.

Table 4.
F-measure of standard bagging, UnderBagging, SMOTEBagging and margin-based bagging with four margins.

Table 5.
Minimum accuracy per class of standard bagging, UnderBagging, SMOTEBagging and margin-based bagging with four margins.
5.4.1. Average Accuracy
Table 3 shows the average accuracy achieved by the proposed margin based extended bagging algorithm, bagging, UnderBagging as well as SMOTEBagging on the 18 imbalanced data sets of Table 2. The experimental results in this table show that all the imbalance learning algorithms lead to an improved classification with respect to traditional bagging. Moreover, undersampling based ensemble classifiers such as margin based bagging and UnderBagging outperform oversampling based ensemble classifiers (SMOTEBagging). This result is consistent with the state-of-the-art work presented in the previous section, where we have explained that oversampling based methods have a risk of injecting additional noise into the training set. The ensemble model based on margin achieves the best performance, especially in addressing the imbalance problem of many-majority and less-minority classes, that often occurs in the real world. These results put a clear emphasis on the importance of preprocessing the training set prior to building a base classifier by focusing on the examples with low margin values and not treating them uniformly. Although there are not obvious differences between the performances of the four ensemble margin definitions, unsupervised margins perform slightly better than supervised margins. Max margins have very similar performances as sum margins.
5.4.2. F-Measure
For F-measure results presented in Table 4, we can observe that, the best average of F-measure is still achieved by margin based bagging. The achieved improvement of our algorithm is about 6% (data set Hayer-roth) compared to UnderBagging and about 10% (data set Pendigit) with respect to SMOTEBagging. Moreover, unsupervised margins slightly outperform supervised margins in our method. In addition, for the binary data Wilt and multi-class data Page-blocks which is with the imbalance ratio of up 175, all the improved bagging methods lose effectiveness. This means that imbalance classification algorithms still face great challenges in avoiding hurting the accuracy of majority class when increasing the accuracy of minority class in the case of very high imbalance rate.
5.4.3. Minimum Accuracy Per Class
Table 5 organized as the previous table, presents the results on minimum accuracy per class obtained on the 18 imbalanced data sets of Table 2 by margin based bagging, traditional bagging, UnderBagging as well as SMOTEBagging. This table shows that our extended bagging algorithm outperforms traditional bagging on the recognition of the most difficult class. With respect to UnderBagging, the win frequency of our method is 13/18 and its improvement in per class classification accuracy is up to 15% (data set Hayes-roth). When compared with SMOTEBagging, the margin based method also obtains a win frequency of 13/18 and improves the minimum accuracy per class of up to 39% (data set Pendigit). Unlike in the previous average accuracy margin analysis, unsupervised max margin performs better than other margins in our margin based method for the classification of the smallest difficult class.
5.4.4. Statistical Analysis of Results
The above analysis of the behaviour and performance of classifiers was based on the groupings formed by considering average accuracy, F-measure and minimum accuracy per class on the datasets. In order to extend the analysis provided above, a non-parametric statistical test [74,75] is conducted for validating the effectiveness of margin based bagging method. The Friedman test is recognised as one of the best tests when multiple different datasets are used. Therefore, in our experiment, the Friedman test [74] is leveraged to verify whether there is a significant difference among the mean ranks of different alternatives when different algorithms provide varying performances on different data sets. Table 3, Table 4 and Table 5 have provided a summary of mean ranks of comparative algorithms on all datasets. The null hypothesis that we used was that the ranks of average accuracy, F-measure and minimum accuracy per class across the three reference classifiers and the proposed method with four margin definitions was the same. When the significant level is selected as 0.05, the null hypotheses in terms of all three metrics can be rejected. To verify whether our method performs better than other algorithms, we compute the critical difference (CD) chosen by the Bonferroni–Dunn post-hoc test.
Figure 4 presents the results of post-hoc tests on average accuracy, F-measure and minimum accuracy per class for comparative algorithms over all the datasets. If the difference between the mean ranks of two algorithms in terms of an evaluation metric is greater or equal to CD, then we can state that there is a statistical difference between the two algorithms. As CD = 1.900, the Table 3 and Table 4 performances of margin based method are significantly better than that of bagging, UnderBagging and SMOTEBagging. The minimum accuracy per class performance of the proposed method with first three margin definitions is significantly better than that of bagging and other state-of-the-art methods. From the above analysis, we can state that the proposed method obtains a good tradeoff between the majority class and minority class performances when tested on multi-class imbalanced data sets. Furthermore, unsupervised max margin statistically outperforms other margins especially for the improvement of the classification of the smallest class instances.
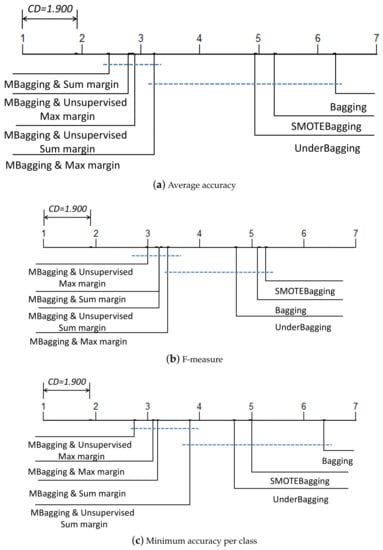
Figure 4.
Bonferroni-Dunn (95% confidence level) for the comparative methods on all data sets (ensemble size = 100).
5.4.5. Diversity
Ensemble diversity is a property of an ensemble with respect to a set of data. It has been recognized as an important characteristic in classifier combination. Ensemble methods can effectively make use of diversity to reduce the variance-error without increasing the bias-error. In other words, ensemble learning is very effective, mainly due to the phenomenon that base classifiers have different “biases”. Table 6 shows the ensemble diversity of the proposed method, original bagging, UnderBagging and SMOTEBagging. This table shows that, with respective to the traditional data sampling based methods, the margin guiding ensemble is not only more accurate for the classification of multi-class imbalanced data, but also leads to more ensemble diversity. Hence, the ability of the novel algorithm is demonstrated again.

Table 6.
Ensemble diversity of standard bagging, UnderBagging, SMOTEBagging and margin-based bagging with four margins.
5.4.6. Time Complexity and Space Complexity
Over sampling techniques such as SMOTEBagging are computationally more expensive than traditional bagging and under sampling based methods as a result of having a larger training set. The time complexity of bagging is , where N and respectively stands for the number of samples in a dataset X and the training complexity of an algorithm given a dataset X [76]. The time complexity of UnderBagging is , where R is the number of samples in a dataset Q which is a subset taken from the dataset X [76]. The time complexity of our approach arises mainly from two sources: the computing of the training instances margins using bagging and the building of the following under sampling combined bagging model. Therefore, the overall time complexity of our proposal is the sum of that of bagging and UnderBagging, , i.e., the proposed algorithm is with polynomial time complexity. Although,= compared with bagging and UnderBagging, our method is slightly more computationally consuming, the time complexity of our method will decrease with the increase in imbalance ratio, because it is based on the under sampling technique.
The space complexity of bagging and UnderBagging are all where D is the number of features. Although in the first step of the proposed approach, the margin values of the training set are computed by an ensemble, the space complexity is not increased, since the initial examples are not stored and the margin values of the training instances are not used for the base classifiers building. Hence, the space complexity of the proposed method is still linear and the same as that of UnderBagging.
5.5. Influence of Model Parameters on Classification Performance
5.5.1. Influence of the Ensemble Size
The results presented so far were about the ”final” bagging made of 100 trees. In order to study the influence of ensemble size on bagging construction, we present in Figure 5 the evaluation of the average accuracy, F-measure and minimum accuracy per class, which are average values through all the datasets, with respect to ensemble size throughout the bagging induction processes, i.e., from 1 up to 150 trees for all the bagging methods. We can observe that a larger ensemble size is beneficial to the classification improvement of the multi-class imbalance data. However, it could lead to increased computational complexity. In particular applications, the balance between the computational complexity and the performance should be considered. One of the main objectives with the design of our algorithm is to obtain a performance improvement while ensemble less trees, faster and in a more straightforward way than with traditional bagging, UnderBagging and SMOTEBagging. Although, the curves of Figure 5 have similar trends for those imbalance learning algorithms. The margin based bagging curves have a faster increase from 1 to about 30 trees. This has a practical interest since it means that designing a stopping criterion based on performance will be possible for the margin based bagging induction to achieve good performance with low time complexity. This stopping criterion has not yet been included in the process of our margin based algorithm, but it is an important mechanism to design in future work.
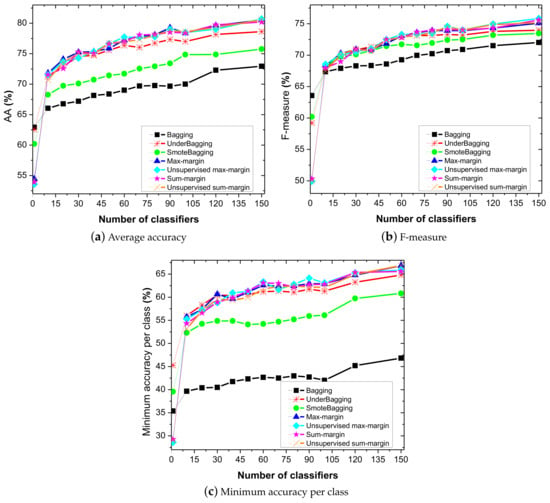
Figure 5.
Evolution of the average accuracy, F-measure and minimum accuracy per class according to the ensemble size.
5.5.2. Influence of the Resampling Rate
This section aims to study the influence of the resampling rate a on margin-based bagging performance in imbalanced classification. We first employ the following example to illustrate our experimental design. The maximum value of the resampling rate a should be equal to or less than 100. When the size of A, the associated set of a values, is set to 5, the elements of A are , i.e., the range of a is 20–100. When , our margin based method becomes similar to UnderBagging.
In this experiment, the size T of the bagging ensemble is set to 100 and the tested number of elements in A is set from 1 to 40. Figure 6, Figure 7 and Figure 8 exhibits the optimal range of a which respectively lead to the best average accuracy, F-measure and minimum accuracy per class for each of the four margin definitions, on all the data sets. Almost all the classification results are improved compared with those of Table 3, Table 4 and Table 5. The best increase in average accuracy is about 1.5% for most data. The best increase in minimum accuracy per class is about 10% for datasets Covtype, Statlog and Vehicle. Hence, it is interesting to further optimize our algorithm by the selection of an optimal resampling range.
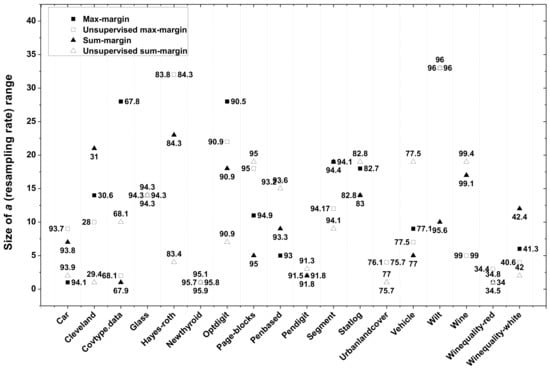
Figure 6.
Average accuracy with the optimal resampling rate a in margin based bagging involving four different margins for all the data sets.
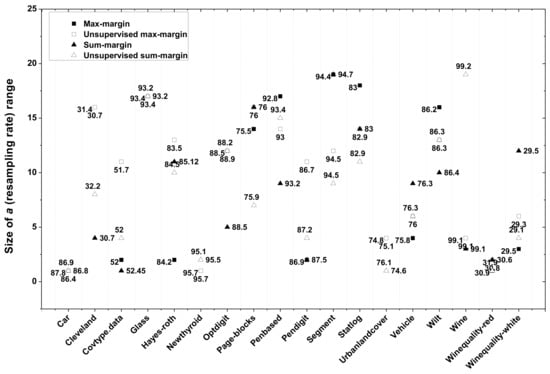
Figure 7.
F-measure with the optimal resampling rate a in margin based bagging involving four different margins for all the data sets.
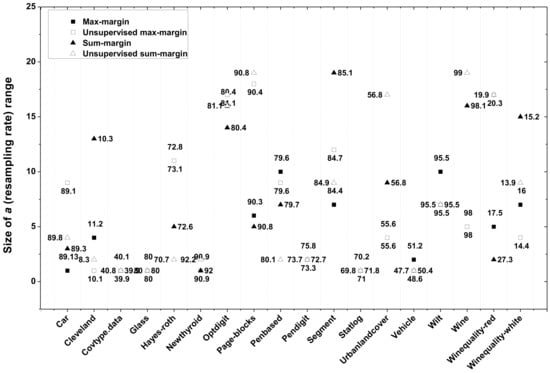
Figure 8.
Minimum accuracy per class with the optimal resampling rate a in margin based bagging involving four different margins for all the data sets.
Table 7, Table 8 and Table 9 respectively present the average accuracy, F-measure and minimum accuracy per class, achieved by our margin-based bagging algorithm using respectively max-margin, unsupervised max-margin, sum-margin and unsupervised sum-margin with optimal resampling ranges, on all the data sets. The exhibited results correspond to the classification results presented in Figure 6, Figure 7 and Figure 8. From these tables, we can see that sum margins obtain slightly better results compared with max margins in terms of the three metrics.

Table 7.
Average accuracy of margin-based bagging involving four margins with optimal resampling range.

Table 8.
F-measure of margin-based bagging involving four margins with optimal resampling range.

Table 9.
Minimum accuracy per class of margin-based bagging involving four margins with optimal resampling range.
6. Discussion
- Imbalanced classification can not be simply treated as a data redundancy problem. While our imbalance learning algorithm tries its utmost to achieve the main objective of imbalanced classification, improving a classifier’s recognition on minority class instances meanwhile keeping the accuracy of majority class from decreasing, it does not need to remove any instances from training set as in training data reduction algorithms.
- We have mentioned in the previous section that classic undersampling based ensemble approaches [56,77], such as UnderBagging [38], samples instances randomly from majority classes to achieve a balance ratio. However, in imbalance learning, not only the imbalance ratio needs to be considered, but also the quality of the sampled instances. Our method focuses more on class decision boundary and difficult instances (lower margin instances) which are more informative for imbalance learning while safe samples (higher margin instances) give less contribution.
- Most methods presented in the previous section such as [51,57] deal with binary imbalanced problems. Due to the difficult extension of these methods, class decomposition, such as One-vs-One (OVO) [48] or One-vs-All (OVA) [49], is the way to extend these methods to multi-class classification. However, those class decomposition based schemes are not suitable when a large number of classes is considered. The novel proposed method trains each base classifier with the most important instances selected from each class; hence, this method has better generalization ability for addressing both binary and multi-class imbalance problems.
- The change in ensemble diversity [78] depends on many factors, such as ensemble learning algorithm, size of training data set and training data complexity. Both the size and the distribution of the training set for constructing a base classifier are different in the margin ordering based bagging ensemble with respect to the original training set. Hence, our algorithm can result in increased diversity compared with the bagging built on original imbalanced data. Furthermore, under the condition of training base classifiers with a fixed amount of the training set, the employment of low margin instances can provide more diversity compared with random sampling involved in UnderBagging.
- Our algorithm selects important instances from each class according to their margin values and does not produce additional instances in the training process. Therefore, our method avoids the potential noise effect induced by new interpolated samples (SMOTE) which is difficultly addressed in SMOTEBagging [8].
7. Conclusions
Ensembles of classifiers have shown very good properties for addressing the problem of imbalanced classification. They work in line with baseline solutions for this task such as data preprocessing for an ensemble or for each classifier of the ensemble. However, selecting more informative instances should benefit ensemble construction and better handle multi class imbalanced classification. Our answer to this data selection problem consists of carrying out an estimation of instance importance which relies on the ensemble margin. More specifically, instances can be focused on or not by an ensemble of base classifiers according to their margin values. We consider the lowest margin instances as the most informative in classification tasks.
In this work, we have proposed a novel margin ordering and under sampling based bagging method for imbalanced classification. To evaluate the effectiveness of our approach, standard bagging as well as two state of the art imbalance learning ensemble methods UnderBagging and SMOTEBagging that inspired our method were used in comparative analysis. From this study, we have emphasized the superiority of the new proposed method, in handling the imbalance learning problem compared with bagging, UnderBagging and SMOTEBagging.
The performances of four margin definitions involved in our algorithm were also compared. The unsupervised margins achieve slightly better performance with respect to the supervised margins. The unsupervised max-margin generally outperforms other margins in terms of F-measure and minimum accuracy per class. In addition, the effectiveness of the new proposed margin in addressing the class imbalance problem is demonstrated. As future research we plan to extend the margin-based ensemble framework to an oversampling scheme, such as producing minority class instances by adopting the SMOTE procedure on the small margin instances.
References
Author Contributions
W.F. conceived and designed the experiments; W.F. performed the experiments and wrote the paper. W.F. revised the paper. J.R. and W.H. edited the manuscript. All authors reviewed and approved the final manuscript.
Acknowledgments
This work is supported by the Strategic Priority Research Program of the Chinese Academy of Sciences (XDA19080304), National Key R&D Program of China (2016YFB0501501), National Natural Science Foundation of China (61661136004), the STFC Newton Agritech Programme (ST/N006712/1), and the National Natural Science Foundation of China (61461003). We want to thank Samia Boukir, Bordeaux INP, G&E Lab, Pessac, France, for smoothing partial section of this paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Liu, Y.H.; Chen, Y.T. Total margin based adaptive fuzzy support vector machines for multiview face recognition. In Proceedings of the 2005 IEEE International Conference on Systems, Man and Cybernetics, Waikoloa, HI, USA, 10–12 October 2005; Volume 2, pp. 1704–1711. [Google Scholar]
- Munkhdalai, T.; Namsrai, O.E.; Ryu, K.H. Self-training in significance space of support vectors for imbalanced biomedical event data. BMC Bioinform. 2015, 16, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Siers, M.; Islam, M.Z. Software defect prediction using a cost sensitive decision forest and voting, and a potential solution to the class imbalance problem. Inf. Syst. 2015, 51, 62–71. [Google Scholar] [CrossRef]
- Sun, T.; Jiao, L.; Feng, J.; Liu, F.; Zhang, X. Imbalanced Hyperspectral Image Classification Based on Maximum Margin. IEEE Geosci. Remote Sens. Lett. 2015, 12, 522–526. [Google Scholar] [CrossRef]
- Galar, M.; Fernandez, A.; Barrenechea, E.; Bustince, H.; Herrera, F. A Review on Ensembles for the Class Imbalance Problem: Bagging-, Boosting-, and Hybrid-Based Approaches. IEEE Trans. Syst. Man Cybern. Part C Appl. Rev. 2012, 42, 463–484. [Google Scholar] [CrossRef]
- Hu, S.G.; Liang, Y.F.; Ma, L.T.; He, Y. MSMOTE: Improving Classification Performance When Training Data is Imbalanced. In Proceedings of the 2009 Second International Workshop on Computer Science and Engineering, WCSE ’09, Washington, DC, USA, 28–30 October 2009; Volume 2, pp. 13–17. [Google Scholar]
- Japkowicz, N.; Stephen, S. The Class Imbalance Problem: A Systematic Study. Intell. Data Anal. 2002, 6, 429–449. [Google Scholar]
- Wang, S.; Yao, X. Diversity analysis on imbalanced data sets by using ensemble models. In Proceedings of the IEEE Symposium on Computational Intelligence and Data Mining, Nashville, TN, USA, 30 March–2 April 2009; pp. 324–331. [Google Scholar]
- Krawczyk, B. Learning from imbalanced data: Open challenges and future directions. Prog. Artif. Intell. 2016, 5, 221–232. [Google Scholar] [CrossRef]
- Sáez, J.A.; Krawczyk, B.; Woźniak, M. Analyzing the oversampling of different classes and types of examples in multi-class imbalanced datasets. Pattern Recognit. 2016, 57, 164–178. [Google Scholar] [CrossRef]
- He, H.B.; Garcia, E.A. Learning from Imbalanced Data. IEEE Trans. Knowl. Data Eng. 2009, 21, 1263–1284. [Google Scholar]
- García, S.; Herrera, F. Evolutionary Undersampling for Classification with Imbalanced Datasets: Proposals and Taxonomy. Evol. Comput. 2009, 17, 275–306. [Google Scholar] [CrossRef] [PubMed]
- Ling, C.X.; Sheng, V.S. Cost-sensitive Learning and the Class Imbalanced Problem. In Encyclopedia of Machine Learning; Sammut, C., Ed.; Springer: Berlin, Germany, 2008. [Google Scholar]
- Ertekin, S.; Huang, J.; Bottou, L.; Giles, C.L. Learning on the border: Active learning in imbalanced data classification. In Proceedings of the Sixteenth ACM Conference on Conference on Information and Knowledge Management, Lisbon, Portugal, 6–10 November 2007; pp. 127–136. [Google Scholar]
- Zhou, Z.; Liu, X.Y. Training cost-sensitive neural networks with methods addressing the class imbalance problem. IEEE Trans. Knowl. Data Eng. 2006, 18, 63–77. [Google Scholar] [CrossRef]
- Sun, Y.; Kamel, M.S.; Wong, A.K.; Wang, Y. Cost-sensitive boosting for classification of imbalanced data. Pattern Recognit. 2007, 40, 3358–3378. [Google Scholar] [CrossRef]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer: New York, NY, USA, 1995. [Google Scholar]
- Ding, S.; Mirza, B.; Lin, Z.; Cao, J.; Lai, X.; Nguyen, T.V.; Sepulveda, J. Kernel based online learning for imbalance multiclass classification. Neurocomputing 2018, 277, 139–148. [Google Scholar] [CrossRef]
- Burges, C.J.C. A Tutorial on Support Vector Machines for Pattern Recognition. Data Min. Knowl. Discov. 1998, 2, 121–167. [Google Scholar] [CrossRef]
- Akbani, R.; Kwek, S.; Japkowicz, N. Applying Support Vector Machines to Imbalanced Datasets. In Machine Learning: ECML 2004: 15th European Conference on Machine Learning, Pisa, Italy, September 20–24, 2004, Proceedings; Boulicaut, J.F., Esposito, F., Giannotti, F., Pedreschi, D., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; pp. 39–50. [Google Scholar]
- Fan, X.N.; Tang, K.; Weise, T. Margin-Based Over-Sampling Method for Learning from Imbalanced Datasets. In Advances in Knowledge Discovery and Data Mining; Springer: Berlin/Heidelberg, Germany, 2011; Volume 6635, pp. 309–320. [Google Scholar]
- Qian, Y.; Liang, Y.; Li, M.; Feng, G.; Shi, X. A resampling ensemble algorithm for classification of imbalance problems. Neurocomputing 2014, 143, 57–67. [Google Scholar] [CrossRef]
- Liu, T.Y. EasyEnsemble and Feature Selection for Imbalance Data Sets. In Proceedings of the 2009 International Joint Conference on Bioinformatics, Systems Biology and Intelligent Computing, IJCBS ’09, Washington, DC, USA, 3–5 August 2009; pp. 517–520. [Google Scholar]
- Feng, W.; Bao, W. Weight-Based Rotation Forest for Hyperspectral Image Classification. IEEE Geosci. Remote Sens. Lett. 2017, 14, 2167–2171. [Google Scholar] [CrossRef]
- Khoshgoftaar, T.M.; Fazelpour, A.; Dittman, D.J.; Napolitano, A. Ensemble vs. Data Sampling: Which Option Is Best Suited to Improve Classification Performance of Imbalanced Bioinformatics Data? In Proceedings of the IEEE 27th International Conference on Tools with Artificial Intelligence (ICTAI), Vietri sul Mare, Italy, 9–11 November 2015; pp. 705–712. [Google Scholar]
- Blaszczyński, J.; Stefanowski, J. Neighbourhood sampling in bagging for imbalanced data. Neurocomputing 2015, 150, 529–542. [Google Scholar] [CrossRef]
- Schapire, R.E.; Freund, Y.; Bartlett, P.; Lee, W.S. Boosting the Margin: A New Explanation for the Effectiveness of Voting Methods. Ann. Stat. 1998, 26, 1651–2080. [Google Scholar] [CrossRef]
- Hu, Q.; Li, L.; Wu, X.; Schaefer, G.; Yu, D. Exploiting diversity for optimizing margin distribution in ensemble learning. Knowl. Based Syst. 2014, 67, 90–104. [Google Scholar] [CrossRef]
- Cantador, I.; Dorronsoro, J. Boosting Parallel Perceptrons for Label Noise Reduction in Classification Problems. In Artificial Intelligence and Knowledge Engineering Applications: A Bioinspired Approach; Springer: Berlin/Heidelberg, Germany, 2005; Volume 3562, pp. 586–593. [Google Scholar]
- Feng, W. Investigation of Training Data Issues in Ensemble Classification Based on Margin Concept: Application to Land Cover Mapping. Ph.D. Thesis, University of Bordeaux Montaigne, Pessac, France, 2017. [Google Scholar]
- Feng, W.; Boukir, S. Class noise removal and correction for image classification using ensemble margin. In Proceedings of the 2015 IEEE International Conference on Image Processing (ICIP), Quebec City, QC, Canada, 27–30 September 2015; pp. 4698–4702. [Google Scholar]
- Feng, W.; Boukir, S.; Guo, L. Identification and correction of mislabeled training data for land cover classification based on ensemble margin. In Proceedings of the IEEE International, Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 4991–4994. [Google Scholar]
- Marchiori, E. Class Conditional Nearest Neighbor for Large Margin Instance Selection. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 364–370. [Google Scholar] [CrossRef] [PubMed]
- Alshawabkeh, M. Hypothesis Margin Based Weighting for Feature Selection Using Boosting: Theory, Algorithms and Applications. Ph.D. Thesis, Northeastern University, Boston, MA, USA, 2013. [Google Scholar]
- Gao, W.; Zhou, Z.H. The kth, Median and Average Margin Bounds for AdaBoost. CoRR (Comput. Res. Repos.) arXiv, 2010; arXiv:abs/1009.3613. [Google Scholar]
- Li, L.J.; Zou, B.; Hu, Q.H.; Wu, X.Q.; Yu, D.R. Dynamic classifier ensemble using classification confidence. Neurocomputing 2013, 99, 581–591. [Google Scholar] [CrossRef]
- Xie, Z.X.; Xu, Y.; Hu, Q.H.; Zhu, P.F. Margin distribution based bagging pruning. Neurocomputing 2012, 85, 11–19. [Google Scholar] [CrossRef]
- Barandela, R.; Sánchez, J.S.; Valdovinos, R.M. New Applications of Ensembles of Classifiers. Pattern Anal. Appl. 2003, 6, 245–256. [Google Scholar] [CrossRef]
- Estabrooks, A.; Jo, T.; Japkowicz, N. A Multiple Resampling Method for Learning from Imbalanced Data Sets. Comput. Intell. 2004, 20, 18–36. [Google Scholar] [CrossRef]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic Minority Over-sampling Technique. J. Artif. Int. Res. 2002, 16, 321–357. [Google Scholar]
- Batista, G.E.A.P.A.; Prati, R.C.; Monard, M.C. A Study of the Behavior of Several Methods for Balancing Machine Learning Training Data. SIGKDD Explor. Newsl. 2004, 6, 20–29. [Google Scholar] [CrossRef]
- Fernández, A.; García, S.; Herrera, F. Addressing the Classification with Imbalanced Data: Open Problems and New Challenges on Class Distribution. In Hybrid Artificial Intelligent Systems: Proceedings of the HAIS 2011 6th International Conference, Wroclaw, Poland, 23–25 May 2011; Corchado, E., Kurzyński, M., Woźniak, M., Eds.; Springer: Berlin/Heidelberg, Germmany, 2011; Part I; pp. 1–10. [Google Scholar]
- Zhang, J.; Mani, I. KNN Approach to Unbalanced Data Distributions: A Case Study Involving Information Extraction. In Proceedings of the ICML’2003 Workshop on Learning from Imbalanced Datasets, Washington, DC, USA, 21 August 2003. [Google Scholar]
- Mease, D.; Wyner, A.J.; Buja, A. Boosted Classification Trees and Class Probability/Quantile Estimation. J. Mach. Learn. Res. 2007, 8, 409–439. [Google Scholar]
- Fernández, A.; López, V.; Galar, M.; del Jesus, M.J.; Herrera, F. Analysing the classification of imbalanced data-sets with multiple classes: Binarization techniques and ad-hoc approaches. Knowl. Based Syst. 2013, 42, 97–110. [Google Scholar] [CrossRef]
- Mellor, A.; Boukir, S.; Haywood, A.; Jones, S. Exploring issues of training data imbalance and mislabelling on random forest performance for large area land cover classification using the ensemble margin. J. Photogramm. Remote Sens. 2015, 105, 155–168. [Google Scholar] [CrossRef]
- Wang, S.; Yao, X. Multiclass Imbalance Problems: Analysis and Potential Solutions. IEEE Trans. Syst. Man Cybern. Part B (Cybern.) 2012, 42, 1119–1130. [Google Scholar] [CrossRef] [PubMed]
- Hastie, T.; Batista, G.E. Classification by pairwise coupling. Ann. Stat. 1998, 26, 451–471. [Google Scholar] [CrossRef]
- Rifkin, R.; Klautau, A. In Defense of One-Vs-All Classification. J. Mach. Learn. Res. 2004, 5, 101–141. [Google Scholar]
- Liu, X.Y.; Zhou, Z.H. Ensemble Methods for Class Imbalance Learning. In Imbalanced Learning: Foundations, Algorithms, and Applications; He, H., Ma, Y., Eds.; Wiley: New York, NY, USA, 2013; pp. 61–82. [Google Scholar]
- Chawla, N.V.; Lazarevic, A.; Hall, L.O.; Bowyer, K.W. SMOTEBoost: Improving Prediction of the Minority Class in Boosting. In Knowledge Discovery in Databases: PKDD 2003; Springer: Berlin/Heidelberg, 2003; Volume 2838, pp. 107–119. [Google Scholar]
- Thanathamathee, P.; Lursinsap, C. Handling imbalanced data sets with synthetic boundary data generation using bootstrap re-sampling and AdaBoost techniques. Pattern Recognit. Lett. 2013, 34, 1339–1347. [Google Scholar] [CrossRef]
- Wattanachon, U.; Lursinsap, C. SPSM: A new hybrid data clustering algorithm for nonlinear data analysis. Int. J. Pattern Recognit. Artif. Intell. 2009, 23, 1701–1737. [Google Scholar] [CrossRef]
- Efron, B.; Tibshirani, R. Bootstrap Methods for Standard Errors, Confidence Intervals, and Other Measures of Statistical Accuracy. Stat. Sci. 1986, 1, 54–75. [Google Scholar] [CrossRef]
- Haykin, S. Neural Networks: A Comprehensive Foundation, 2nd ed.; Prentice Hall PTR: Upper Saddle River, NJ, USA, 1998. [Google Scholar]
- Seiffert, C.; Khoshgoftaar, T.M.; Hulse, J.V.; Napolitano, A. RUSBoost: A Hybrid Approach to Alleviating Class Imbalance. IEEE Trans. Syst. Man Cybern. Part A Syst. Hum. 2010, 40, 185–197. [Google Scholar] [CrossRef]
- Díez-Pastor, J.; Rodríguez, J.; García-Osorio, C.; Kuncheva, L.I. Random Balance: Ensembles of variable priors classifiers for imbalanced data. Knowl. Based Syst. 2015, 85, 96–111. [Google Scholar] [CrossRef]
- Díez-Pastor, J.F.; Rodríguez, J.J.; García-Osorio, C.I.; Kuncheva, L.I. Diversity Techniques Improve the Performance of the Best Imbalance Learning Ensembles. Inf. Sci. 2015, 325, 98–117. [Google Scholar] [CrossRef]
- Galar, M.; Fernández, A.; Barrenechea, E.; Herrera, F. EUSBoost: Enhancing ensembles for highly imbalanced data-sets by evolutionary undersampling. Pattern Recognit. 2013, 46, 3460–3471. [Google Scholar] [CrossRef]
- Nikulin, V.; McLachlan, G.J.; Ng, S.K. Ensemble Approach for the Classification of Imbalanced Data. In AI 2009: Advances in Artificial Intelligence: Proceedings of the 22nd Australasian Joint Conference, Melbourne, Australia, 1–4 December 2009; Nicholson, A., Li, X., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 291–300. [Google Scholar]
- Jin, R.; Zhang, J. Multi-Class Learning by Smoothed Boosting. Mach. Learn. 2007, 67, 207–227. [Google Scholar] [CrossRef]
- Khoshgoftaar, T.M.; Hulse, J.V.; Napolitano, A. Comparing Boosting and Bagging Techniques with Noisy and Imbalanced Data. IEEE Trans. Syst. Man Cybern. Part A Syst. Hum. 2011, 41, 552–568. [Google Scholar] [CrossRef]
- Blaszczyński, J.; Stefanowski, J.; Idkowiak, L. Extending Bagging for Imbalanced Data. In Proceeding of the Eighth CORES (Core Ordering and Reporting Enterprise System), Springer Series on Advances in Intelligent Systems and Computing; Springer: Berlin/Heidelberg, Germany, 2013; Volume 226, pp. 269–278. [Google Scholar]
- Nejatian, S.; Parvin, H.; Faraji, E. Using sub-sampling and ensemble clustering techniques to improve performance of imbalanced classification. Neurocomputing 2018, 276, 55–66. [Google Scholar] [CrossRef]
- Hido, S.; Kashima, H.; Takahashi, Y. Roughly Balanced Bagging for Imbalanced Data. Stat. Anal. Data Min. 2009, 2, 412–426. [Google Scholar] [CrossRef]
- Nanni, L.; Fantozzi, C.; Lazzarini, N. Coupling different methods for overcoming the class imbalance problem. Neurocomputing 2015, 158, 48–61. [Google Scholar] [CrossRef]
- Park, Y.; Ghosh, J. Ensembles of (alpha)-Trees for Imbalanced Classification Problems. IEEE Trans. Knowl. Data Eng. 2014, 26, 131–143. [Google Scholar] [CrossRef]
- Crammer, K.; Gilad-bachrach, R.; Navot, A.; Tishby, N. Margin Analysis of the LVQ Algorithm. Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2002; pp. 462–469. [Google Scholar]
- Kapp, M.; Sabourin, R.; Maupin, P. An empirical study on diversity measures and margin theory for ensembles of classifiers. In Proceedings of the 10th International Conference on Information Fusion, Quebec City, QC, Canada, 9–12 July 2007; pp. 1–8. [Google Scholar]
- Guo, L.; Boukir, S. Margin-based ordered aggregation for ensemble pruning. Pattern Recognit. Lett. 2013, 34, 603–609. [Google Scholar] [CrossRef]
- Breiman, L. Bias, Variance, and Arcing Classifiers; Technical Report 460; Statistics Department, University of California at Berkeley: Berkeley, CA, USA, 1996. [Google Scholar]
- Davis, J.; Goadrich, M. The Relationship Between Precision-Recall and ROC Curves. In Proceedings of the 23rd International Conference on Machine Learning, ICML ’06, Pennsylvania, PA, USA, 25–29 June 2006; pp. 233–240. [Google Scholar]
- Kohavi, R.; Wolpert, D.H. Bias Plus Variance Decomposition for Zero-One Loss Functions. In Proceedings of the Thirteenth International on Machine Learning; Morgan Kaufmann Publishers: San Mateo, CA, USA, 1996; pp. 275–283. [Google Scholar]
- Demsar, J. Statistical comparisons of classifiers over multiple data sets. J. Mach. Learn. Res. 2006, 7, 1–30. [Google Scholar]
- Garcia, S.; Herrera, F. An Extension on “Statistical Comparisons of Classifiers over Multiple Data Sets” for all Pairwise Comparisons. J. Mach. Learn. Res. 2008, 9, 2677–2694. [Google Scholar]
- Karimi, H.A. (Ed.) Big Data: Techniques and Technologies in Geoinformatics; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Tahir, M.A.; Kittler, J.; Yan, F. Inverse random under sampling for class imbalance problem and its application to multi-label classification. Pattern Recognit. 2012, 45, 3738–3750. [Google Scholar] [CrossRef]
- Kuncheva, L.I.; Whitaker, C.J. Measures of Diversity in Classifier Ensembles and Their Relationship with the Ensemble Accuracy. Mach. Learn. 2003, 51, 181–207. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).