1. Introduction
Smart systems have been used in various fields of applied science for years. Civil engineering, however, is a relatively new area of application for such solutions [
1]. Nevertheless, many ongoing and recent research projects have focused on the investigation and implementation of smart technologies in the field of structural engineering [
2,
3,
4,
5].
Engineering structures, such as buildings or bridges, are subject to various actions, among which the most dangerous ones are accidental loads. It may be a challenge for an engineer to design a structure that would react to such accidental loading by modifying its own properties. It is possible with the use of smart technologies. Such intelligent technologies apply both to materials and structures. However, considering the immense costs of implementing smart materials into structural elements, the authors focus on structural smartness rather than the material one.
Smart structures can be defined as systems with the ability to sense and respond adaptively to changes in their environment [
6]. In contrast to standard, “traditional” structures, they adapt in a pre-designed manner to a functional need, by modifying their shape, stiffness or damping characteristics in order to minimize deflections and avoid potential damage.
Typically, the main idea of smart techniques is the integration of sensors, actuators and control mechanisms into one, fully-functional and coherent system that becomes an integral part of the structure. Such a system is able to sense changes in the environmental conditions and react to the stimulus in a predicted way, in real time or close to real time. However, neither the external devices installed on the structure, nor the applied intelligent technologies make the structure smart. The structure itself should have some special properties, referred to by the authors as “inherent”, which allow controlling it without any operation from the outside.
To the inherent properties of smart structures belong:
The tensegrity concept is a topic of particular interest in engineering sciences because of the possible smart structure applications. The term “tensegrity” was first introduced by Buckminster Fuller (see [
7] for historical details). Several definitions of this concept can be found in the literature [
7,
8,
9,
10,
11]. For the purpose of this paper, a tensegrity structure is defined as a pin-jointed system with a particular configuration of cables and struts that form a statically indeterminate structure in a stable equilibrium. Tensegrities consist of a discontinuous set of compressed elements inside a continuous net of tensioned members, which have no compressive stiffness. Infinitesimal mechanisms that occur in tensegrity structures are balanced with self-stress states [
12,
13,
14]. The occurrence of a self-stress state in a structure indicates that there is a certain set of internal forces in structural members, which are independent of external loading and boundary conditions because they are in self-equilibrium.
Tensegrity systems have many advantages, such as: large stiffness-to-mass ratio, deployability, reliability and controllability [
7,
8]. Moreover, tensegrities have some unique features that result from the infinitesimal mechanisms, which are stabilized by self-stress forces. It is possible to control their static and dynamic properties by adjusting the pre-stressing forces [
15,
16,
17,
18,
19,
20].
Smart uses of tensegrity structures have been an attractive area of scientific effort in recent years. A detailed description of the extreme softening/stiffening response of tensegrity modules can be found in [
21,
22] with a general view toward applications of smart extreme materials. A study of dynamic control problems can be found in [
23] and the references therein. Bridge engineering applications were recently presented in [
24,
25]. An interesting area of future applications is tensegrity-based metamaterials with unusual mechanical properties [
21,
26,
27].
Examples of the analyses presented in this paper prove that tensegrity modules and lattices have all four key elements of inherent smartness, that is: self-control, self-diagnosis, self-repair and self-adjustment (active control).
Self-control of tensegrity systems consists of self-stiffening of the structures under the applied load that causes displacements consistent with the infinitesimal mechanism mode. External loading acts similarly to the self-stress: it eliminates the singularity of the problem, additionally prestresses the structure and stiffens it.
Self-diagnosis refers to the possibility of damage detection and identification by measuring internal forces in active members. Damage of one structural element affects the distribution and level of self-stress in the whole structure.
Self-repair of tensegrity structures is realized by adjusting self-stress forces. A proper change of pre-stressing level can compensate the damaged element and restore the values of structural displacements from before damage.
Self-adjustment (active control) in regard to tensegrity systems is related to the ability of self-adjustment through self-stress forces. Both the pre-stressing of the whole structure and its part causes stiffening of the system and reduction of its displacements. Therefore, active control of tensegrities can be realized by adjusting the level of self-stress in only one selected part of the structure.
The above properties are especially found in tensegrity structures because of the infinitesimal mechanisms stabilized by the self-equilibrated forces. The presence of infinitesimal mechanisms makes tensegrities more sensitive for the control of their mechanical properties. This is the unique feature of tensegrities that distinguishes them from other structures under pre-stress.
The present paper discusses variable aspects of the structural control of smart systems with the focus on tensegrity structures. Analyses performed for this study prove that tensegrities have all of the above-mentioned properties, which they owe to infinitesimal mechanisms balanced with self-stress states. The presented examples of the analyses of different tensegrity modules and multi-module structures show that it is possible to control their properties by adjusting the pre-stressing forces.
After the above introduction, the second section of this paper is dedicated to the description of self-control of structures, from a simple two pin-joined cables, through a three-strut simplex single module to a plate-like multi-module tensegrity lattice. The influence of self-equilibrated forces, as well as additional self-stress due to geometrically non-linear properties on the response of the structures is analyzed. The possibility of self-diagnosis by monitoring of normal forces is presented in
Section 3. The analysis of the self-repair of plate-like tensegrity is described in detail in
Section 4. The aim of
Section 4 is to show how the self-stress of one module in the plate-like tensegrity can help in the active control of the response of the structure. The paper is summarized in
Section 5 with some potential technical/engineering applications proposed.
2. Self-Control: Geometrically Non-Linear Analysis
Due to the infinitesimal mechanisms that occur in tensegrity systems, it is possible to control their properties by adjusting the values of pre-stressing forces in structural members. However, the adjustment of self-stress is not the only method of changing the properties of these structures. Thanks to their inherent smart features, they are capable of self-control: they stiffen under the applied external load, which causes displacements that are consistent with the infinitesimal mechanism modes. In order to examine this unique property of tensegrities, a geometrically non-linear analysis has to be used. Analysis according to the second order theory, which includes self-stress, but neglects geometrical non-linearities, allows identifying infinitesimal mechanisms and determining self-stress states of the structure, but does not take into account self-stiffening of the structure. Therefore, the analyses presented in this section are performed according to the geometrically non-linear theory, referred to by the authors as the third order theory.
Three structures were analyzed:
Structure No. 1: a tensegrity-like structure consisting of two pin-jointed cables,
Structure No. 2: a typical tensegrity module, three-strut simplex,
Structure No. 3: a tensegrity plate-like structure built from fourteen three-strut simplex modules.
Structural members were chosen from the rod system Detan by Halfen [
28]. The following sections were used:
Structure No. 1: tension rods d = 30 mm made of steel S460N as cables,
Structure No. 2 and 3: tension rods d = 20 mm made of steel S460N as cables and compression rods D = 76.1 mm (outer diameter) and t = 2.9 mm (wall thickness) made of steel S355J2 as struts.
The calculations were performed in SOFiSTiK software (educational license), using the finite element method [
29,
30,
31,
32].
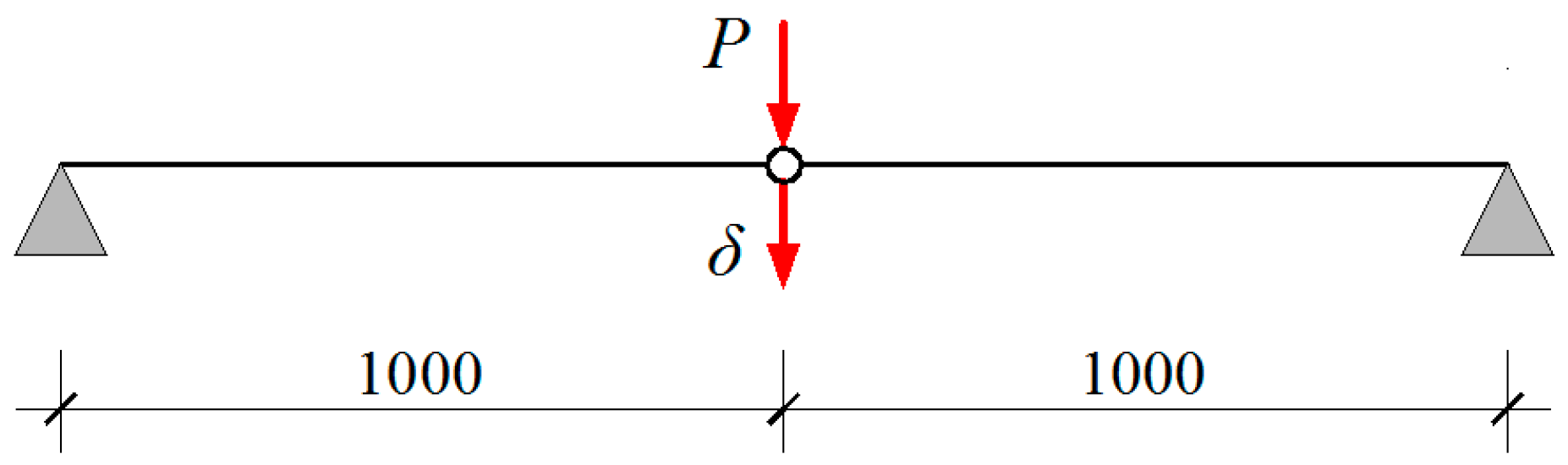
Structure No. 1 (
Figure 1), built from two pin-jointed cables of a length of 1 m each, was loaded with a concentrated force
P applied to the middle node. In order to eliminate the singularity of the problem, pre-stressing forces
S0 were introduced. The scope of the analysis was to evaluate the vertical displacement of the loaded node of the structure and the value of internal forces in cables.
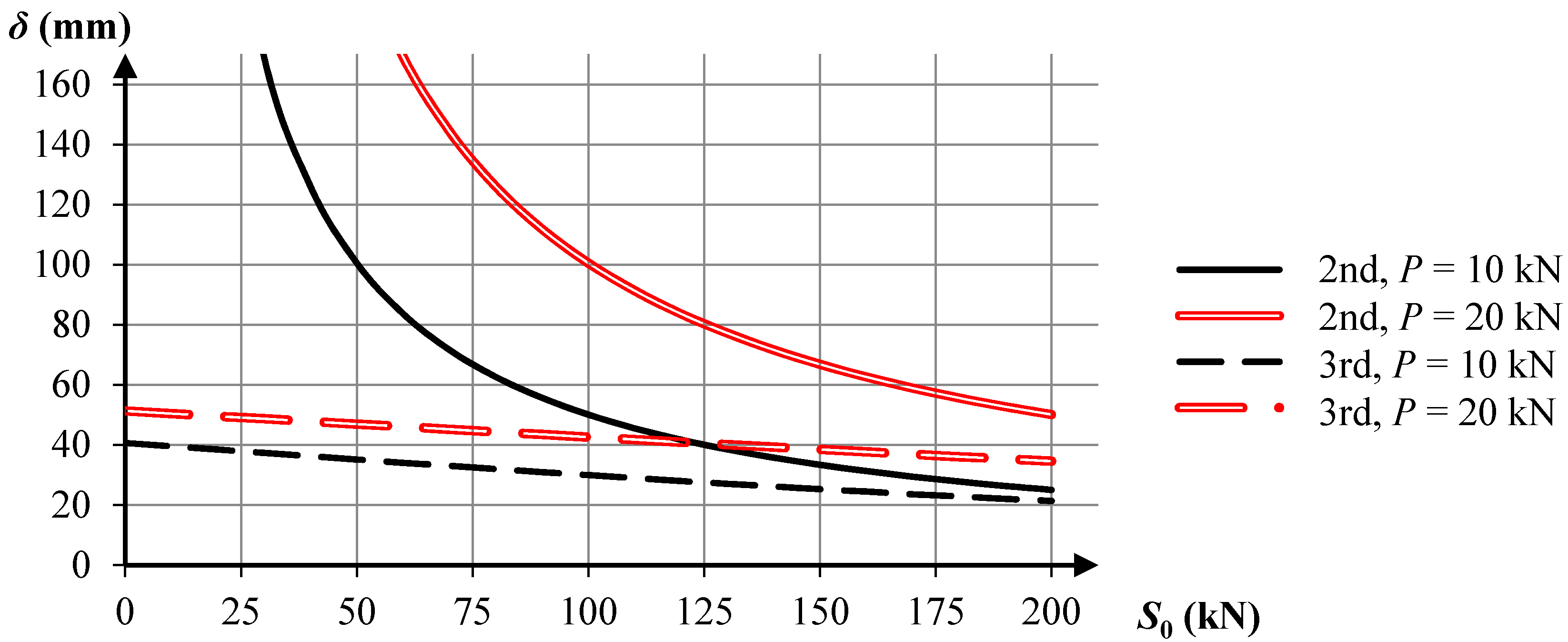
The diagram (
Figure 2) shows how self-stress forces (
S0) influence the analyzed displacement
δ, with two levels of loading:
P = 10 kN and
P = 20 kN are considered. The calculations were performed twice, according to the second and third order theory. When no self-stress is applied, the displacement determined with the use of the second order theory approaches infinity, which results from the infinitesimal geometrical instability of the system. Application of the geometrically non-linear analysis allows taking into account the self-stiffening of the structure under the applied external load.
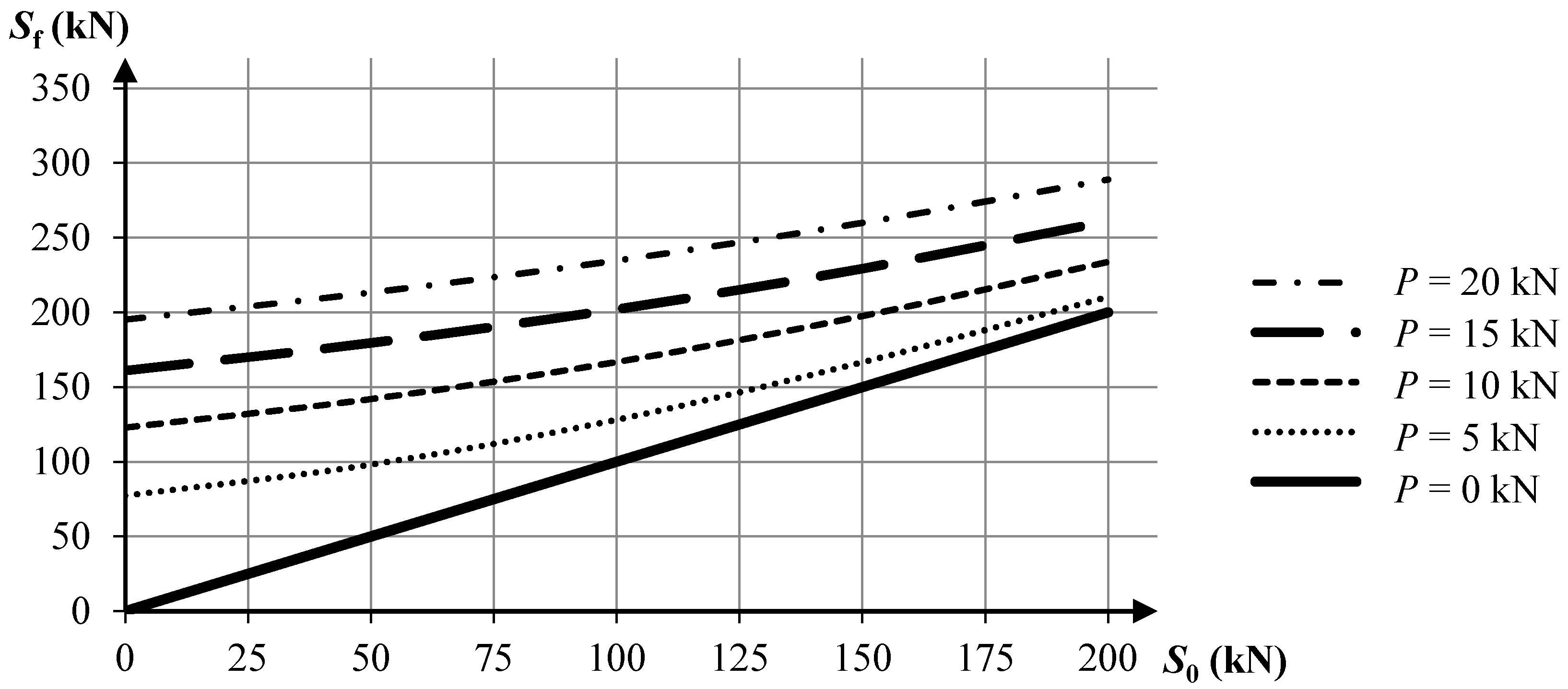
External load, similarly to self-stress, causes stiffening and pre-stressing of the structure. Its influence on the global stiffness of the system depends on the ratio between pre-stressing forces in cables and the forces caused by self-stiffening under the applied load. The diagram presented below (
Figure 3) shows the relation between the final internal force (
Sf) in the cable and the value of self-stress (
S0), with four levels of external load considered. The analysis was performed according to the geometrically non-linear theory. Comparison of the internal force in the cable with the pre-stressing force (curve obtained for
P = 0 kN) indicates that self-stress forces have a bigger influence on the global stiffness of the structure when the values of external forces
P are small. When
P increases, external loading starts to play an important role in self-stiffening and pre-stressing of the system.
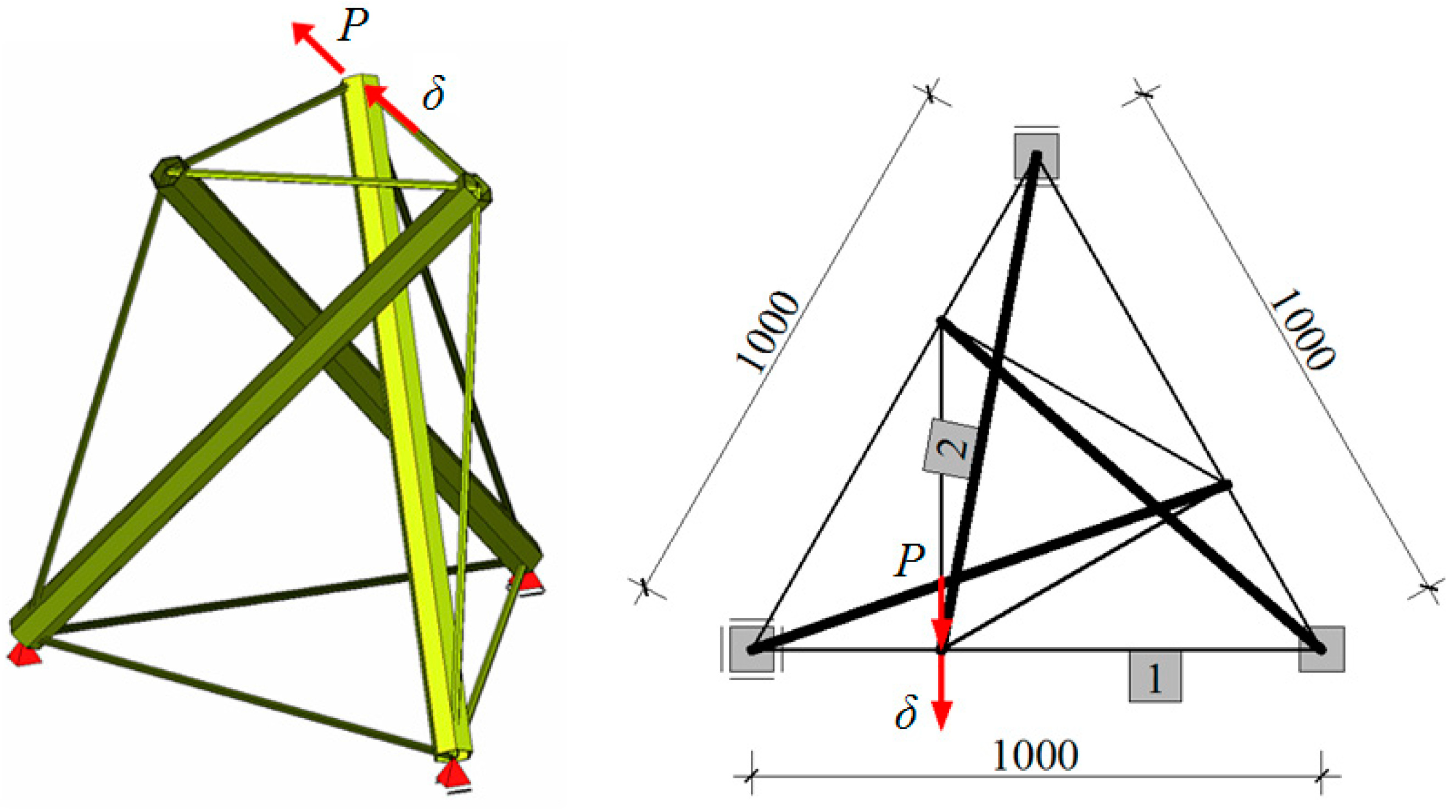
Similar analysis was performed for Structure No. 2: a three-strut simplex module (
Figure 4). The following values of self-stress were applied: −0.421637·
S0 (struts), 0.182574·
S0 (cables of the upper triangle), 0.333333·
S0 (diagonal cables), 0.105409·
S0 (cables of the lower triangle), where
S0 is a multiplier of the pre-stressing force.
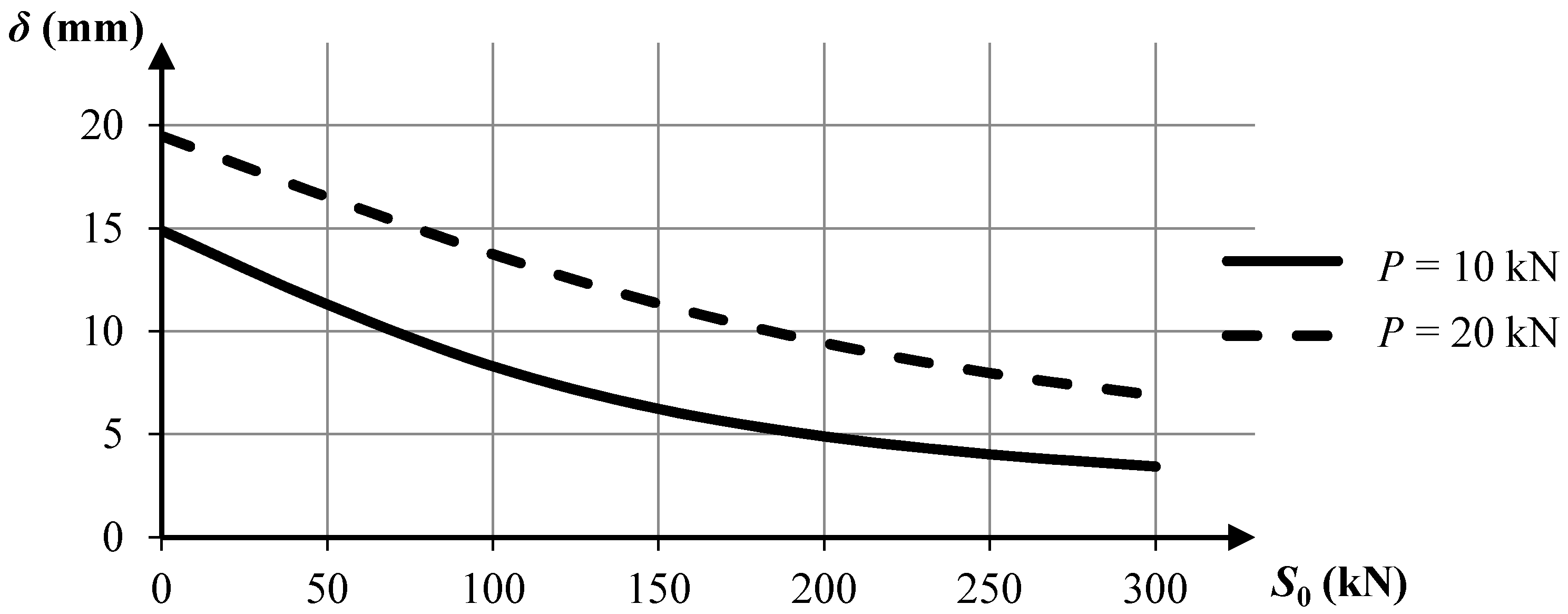
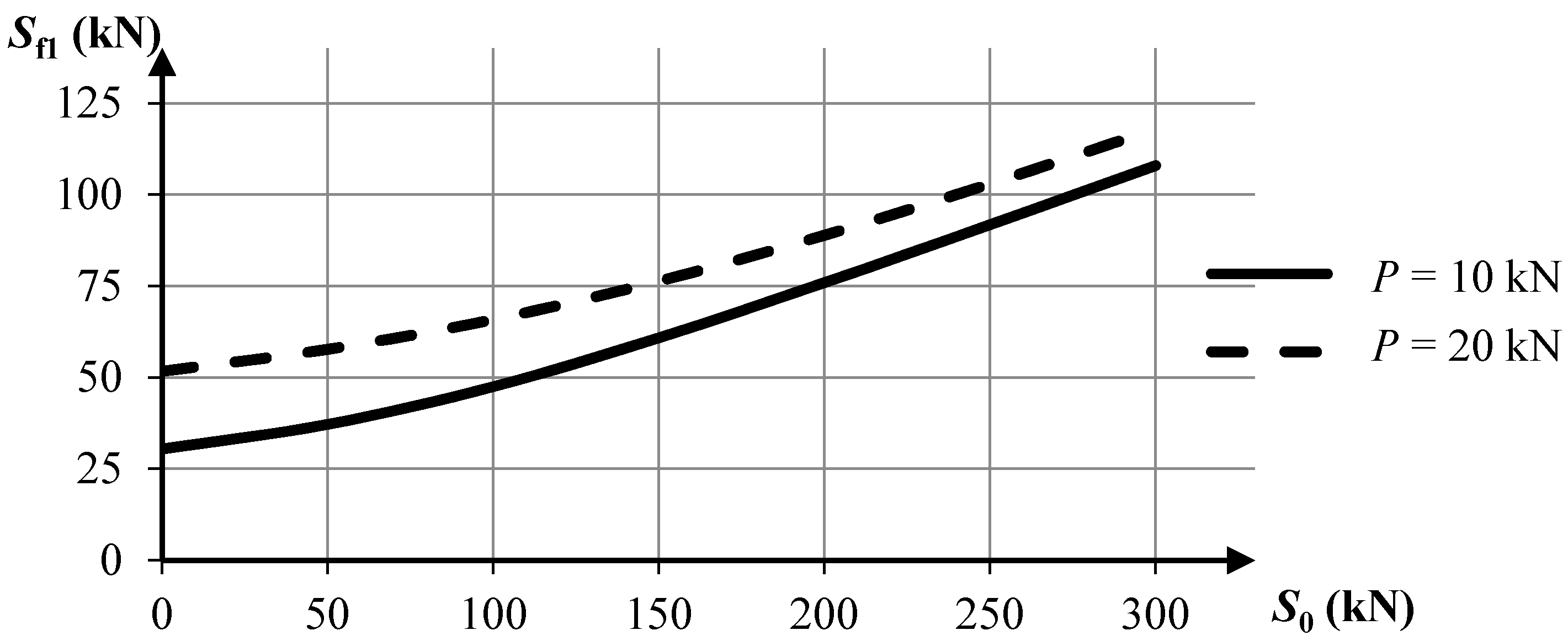
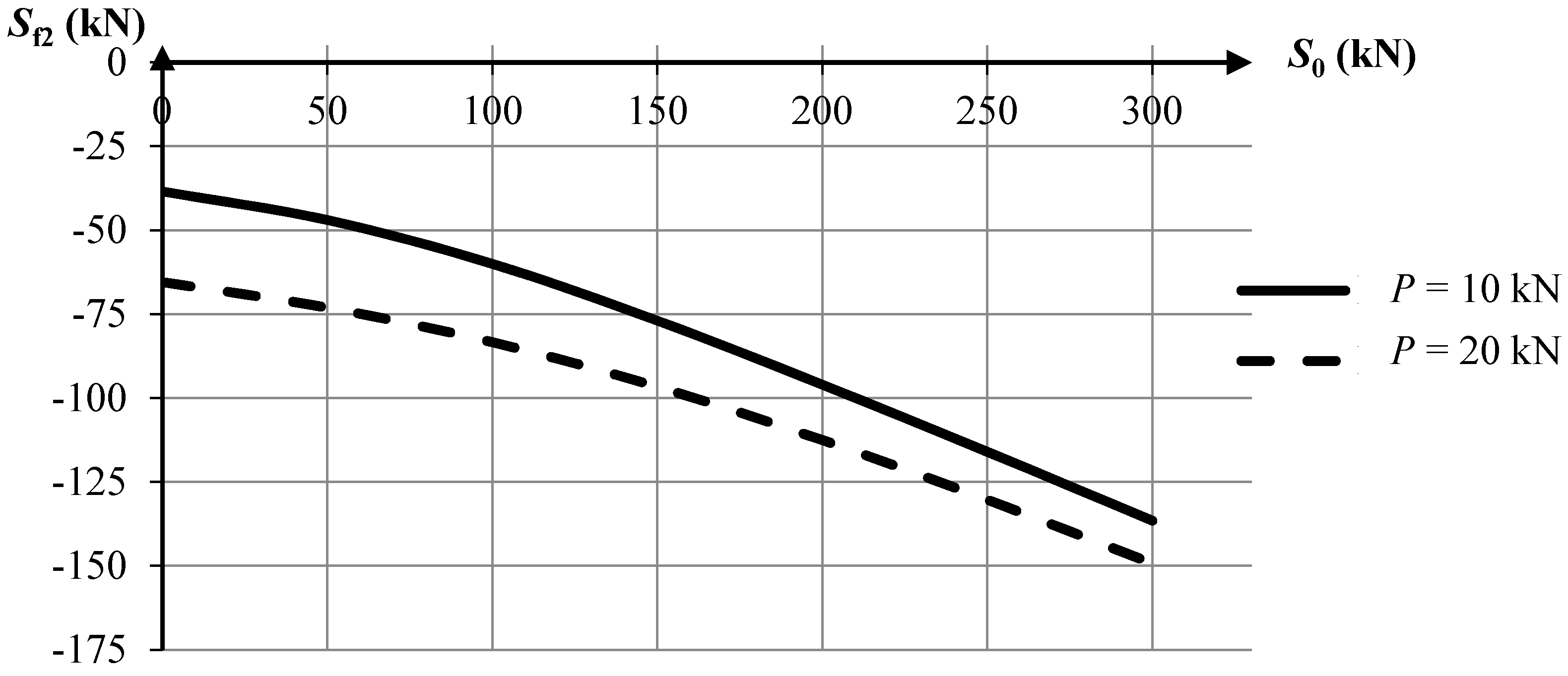
The diagrams presented below show the influence of external load
P on nodal displacement
δ (
Figure 5) and internal forces in two selected elements of the structure: a cable (
Sf1) (
Figure 6) and a strut (
Sf2) (
Figure 7). The calculations were performed according to the geometrically non-linear theory. The analyzed tensegrity module exhibits similar behavior as Structure No. 1. Both self-stress and external loading stiffen the structure, but the influence of external loading is bigger when the values of pre-stressing forces are small.
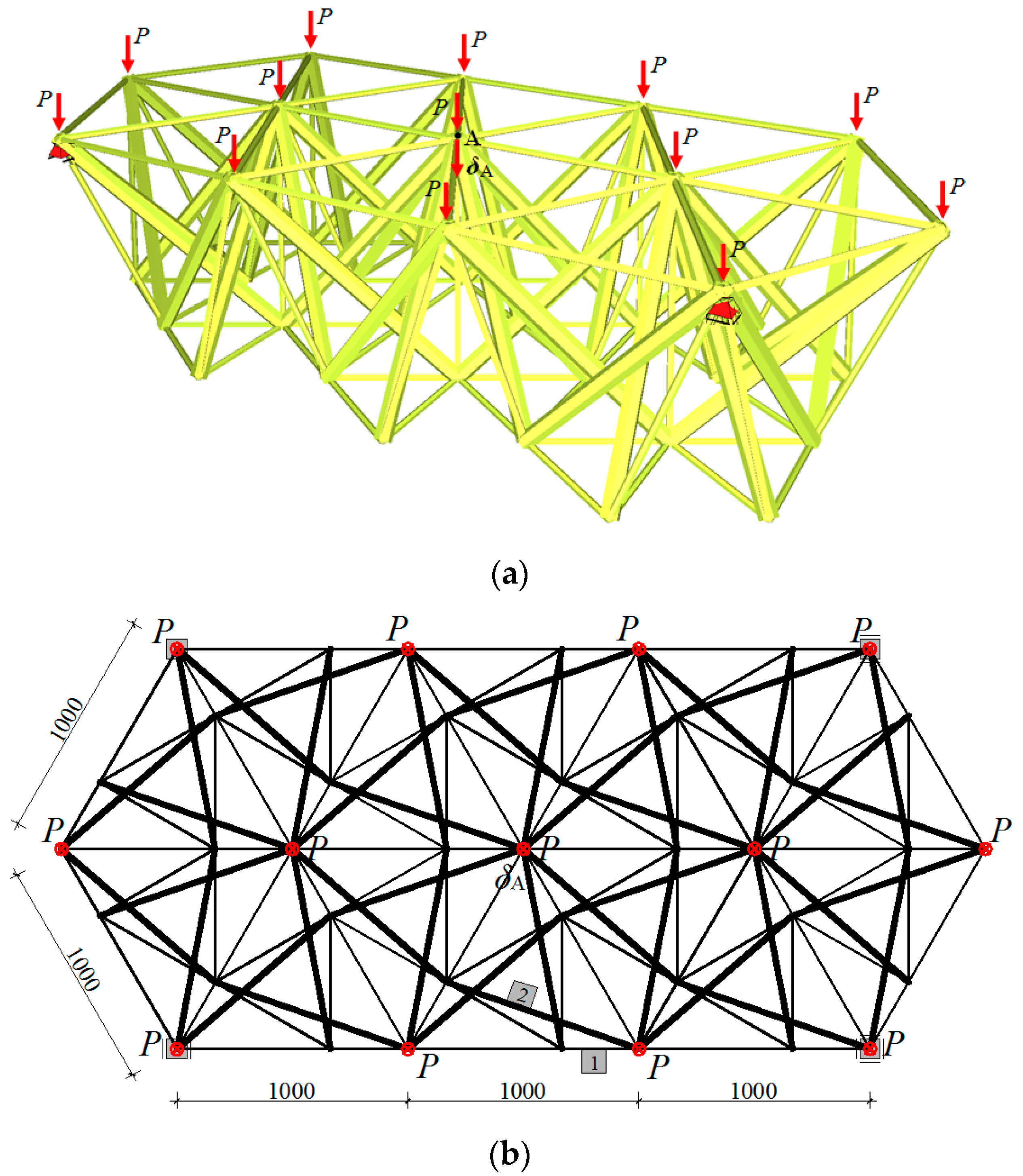
An analogous analysis was conducted for Structure No. 3, a tensegrity plate-like structure. The structure (
Figure 8) was built from fourteen three-strut simplex modules, rotated clockwise and counter-clockwise and connected together in nodes. The structure was loaded with concentrated forces
P applied to the nodes of the upper surface.
In the analysis, the same values of self-stress were applied as in the case of the three-strut simplex module. The diagrams presented below show the influence of external load
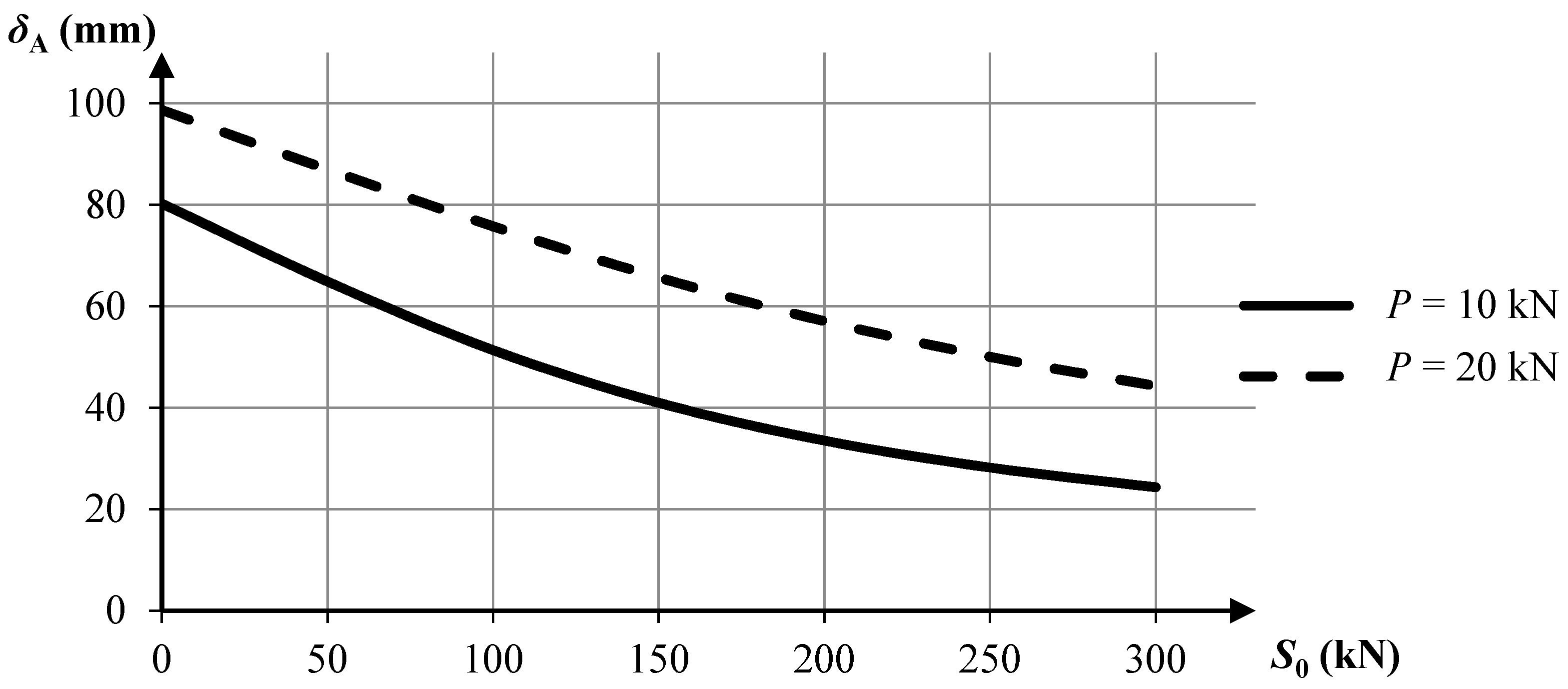
P on the displacement of the central upper node
δA (
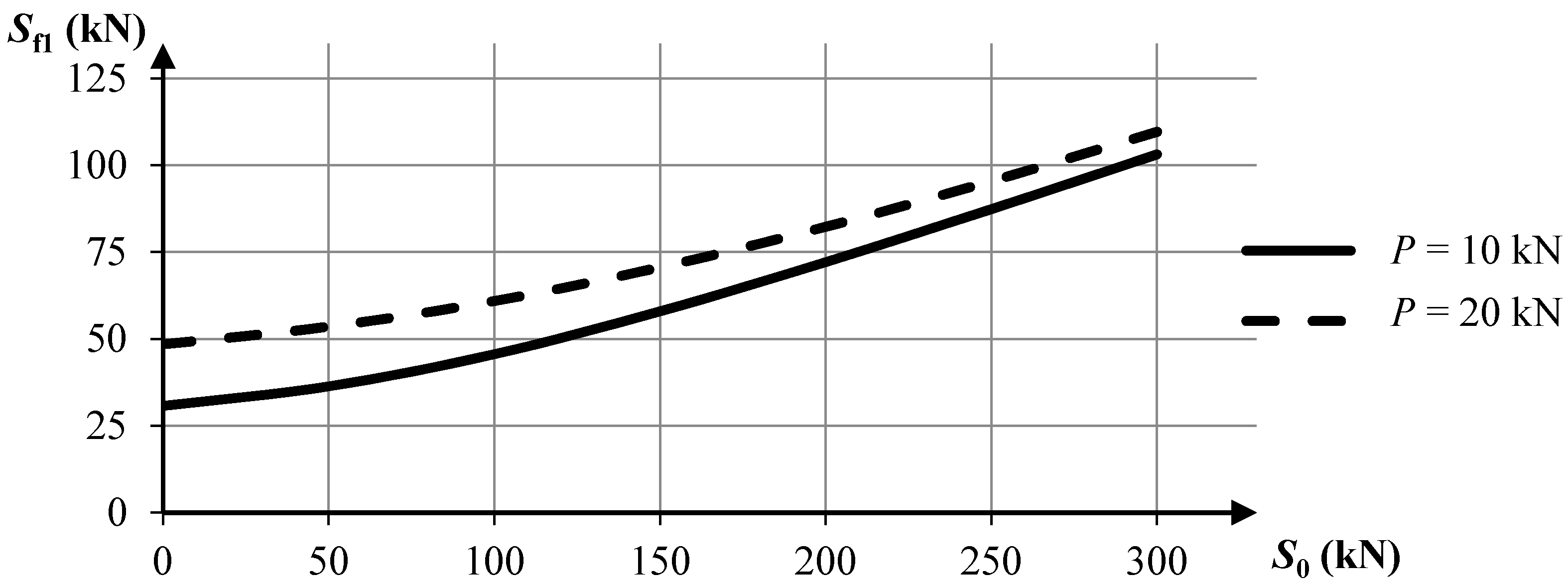
Figure 9) and internal forces in two selected elements of the structure: a cable (
Sf1) (
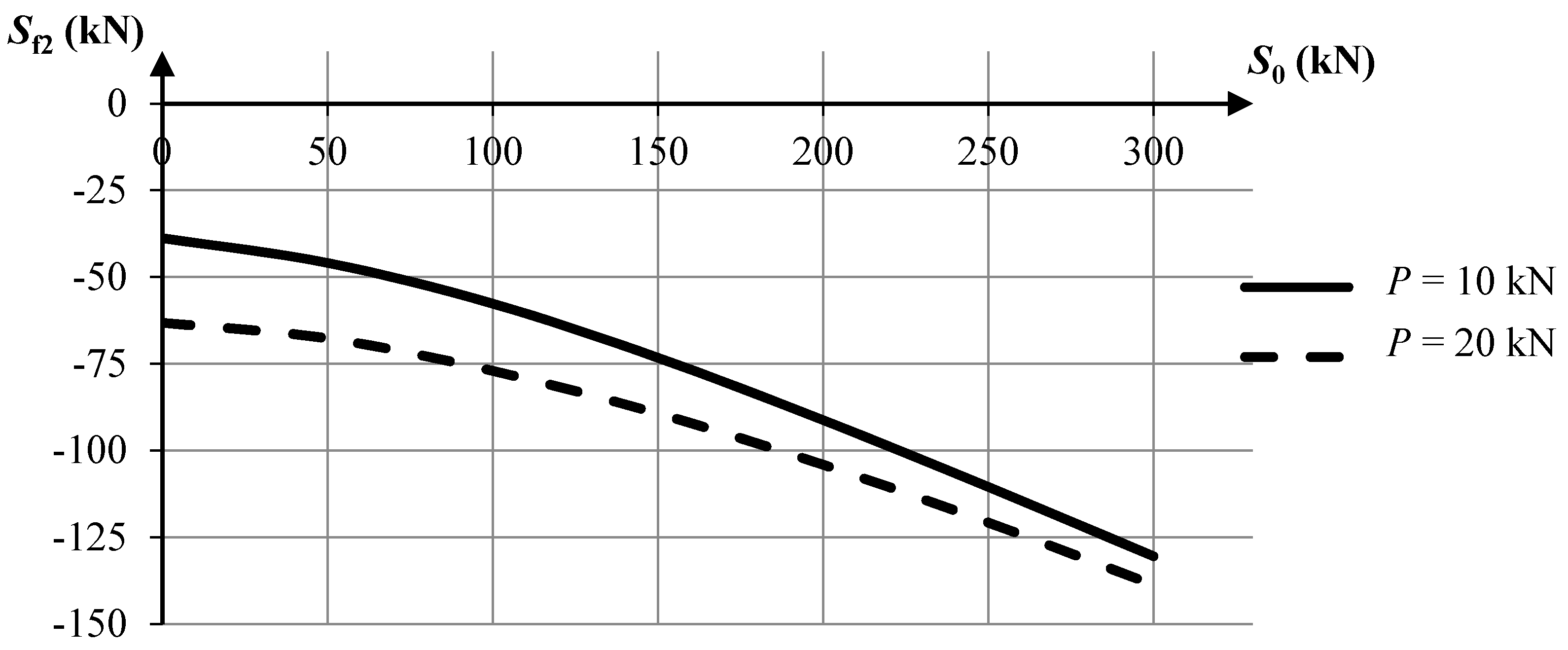
Figure 10) and a strut (
Sf2) (
Figure 11). The calculations were performed according to the geometrically non-linear theory. The analyzed tensegrity plate-like structure exhibits a similar behavior as two previously-presented structures. Both self-stress and external loading stiffen the structure, but the influence of external loading is bigger when the values of pre-stressing forces are small.
Similar analyses were performed for other tensegrity modules and more complex multi-module structures. All of them led to analogous results. All these analyses show that the properties of tensegrity structures do not depend only on self-stress. Tensegrities have the ability of self-control, which is realized by self-stiffening of the structure under the applied external load, which acts in the direction that is consistent with the infinitesimal mechanism mode. This feature is particularly important in the case of non-typical loading, which is hard to foresee.
3. Self-Diagnosis
One of the aims of the currently conducted research on structural health monitoring (SHM) is the development of the systems, which would allow detecting damage based on the analysis of data obtained from SHM [
33,
34]. Such a structural diagnosis is based on various smart technologies that include a series of external devices installed on the structure and is independent of the structural properties.
In the case of smart structures, the diagnosis of damages should be possible thanks to the special internal properties of the structure, not the smart devices with which the structure is equipped. Tensegrity structures are a good example. The analyses presented in the previous section proved that tensegrities are capable of self-control due to the infinitesimal mechanisms, which are balanced with self-stress states. This unique feature may be used not only for structural control, but also in the case of damage detection systems.
The failure of a random structural member causes the redistribution of nodal displacements and internal forces in cables and struts. In a single-module tensegrity structure, the failure of any member means the damage of the structure. In the case of multi-module structures, the failure of one element eliminates self-stress within the module(s) that contains it. It is not identical to the total damage of the structure. Therefore, identification of the damaged area can occur immediately if the member forces are controlled. Moreover, damage detection in tensegrity structures can be realized by measuring internal forces only in active cables and struts, as the failure of one random structural member causes the redistribution of pre-stressing forces within the whole structure. The number of active and controlled members can be limited. The possible, as well as most probable scenarios of failure can be simulated and included in the expert system for monitoring the structural health.
The analysis presented in the next section shows how the failure of one structural element influences the work of a whole tensegrity structure.
4. Self-Repair
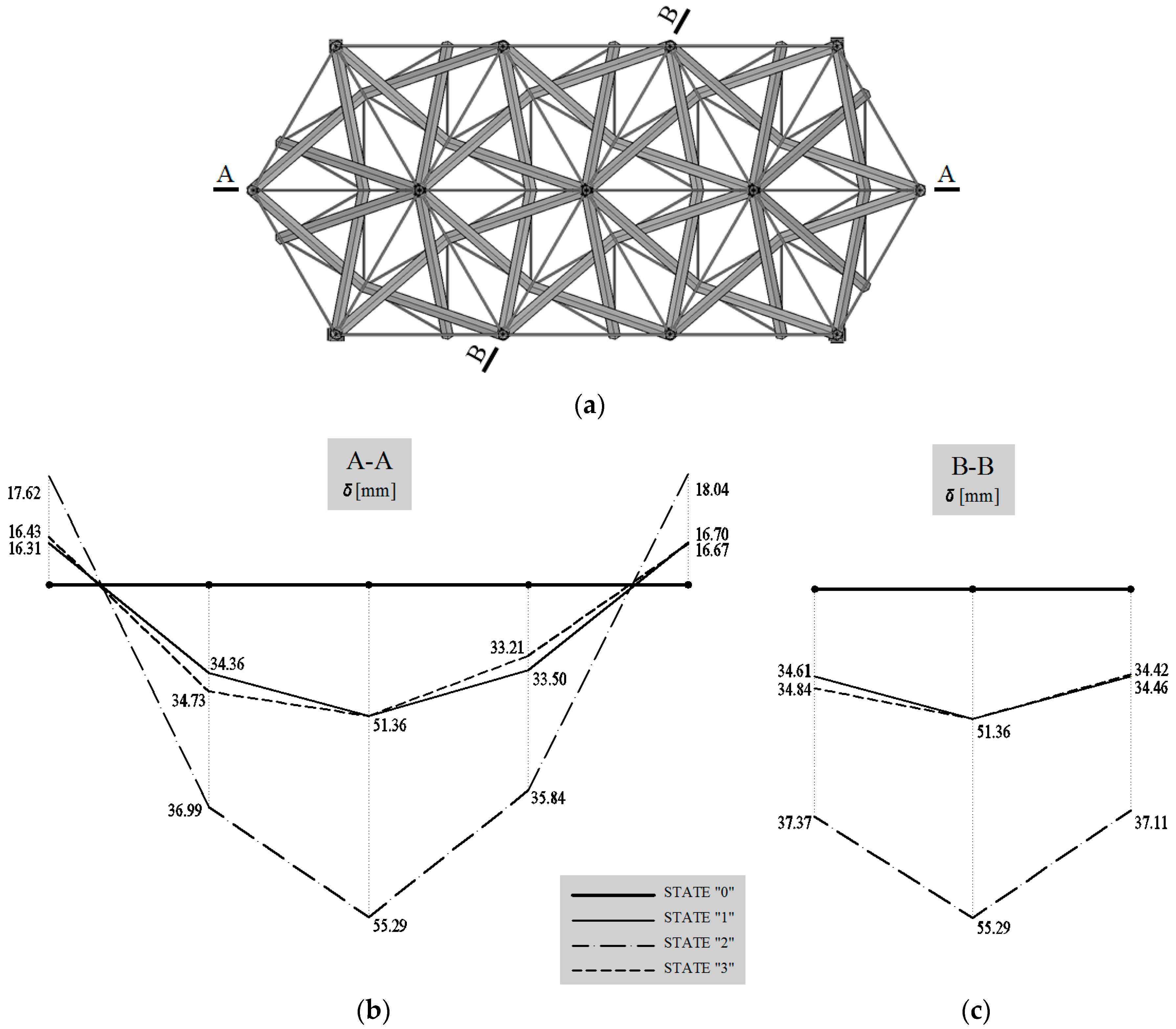
In order to prove that tensegrity systems are capable of self-repair, an analysis of a tensegrity plate-like structure was performed. In the analysis, the structure presented in
Figure 8 was considered, with the same materials, dimensions of the cross-sections, values of self-stress and loading as in the previous example.
The aim of the analysis was to examine the behavior of the structure in the case of a member loss and to verify the possibility of self-repair. The failure was modelled by removing one of the cables from the system, marked with the dashed red line in
Figure 12. The calculations were conducted in SOFiSTiK software, with the use of the finite element method, according to the geometrically non-linear theory.
One of the aims of the analysis was to verify the possibility of structural repair through an adjustment of self-stress in one selected module of the structure. Such a possibility would be particularly valuable from the practical point of view: it would allow one to significantly reduce the number of actuators installed on the active structural members. As is proven below, such a repair is possible in the case of the analyzed system.
The scope of the analysis was a vertical displacement of the central node of the upper surface of the plate-like structure, marked with letter A in
Figure 8 and
Figure 12. With the loading
P = 10 kN and self-stress
S0 = 100 kN, the value
δA = 51.36 mm was obtained. Removal of the cable caused changes in the structure of Module Nos. 3 and 10 (
Figure 12), so they could no longer be pre-stressed after the member loss. Self-stress on the level of
S0 = 100 kN was maintained in twelve undamaged modules. After damage, the value
δA = 55.29 mm was obtained.
The authors tried to simulate the repair of the structure, which is to reduce the value of
δA to the value from before damage, by adjusting the pre-stressing forces in single modules. Each time the level of self-stress within the considered module was changed, other modules were pre-stressed with the force
S0 = 100 kN.
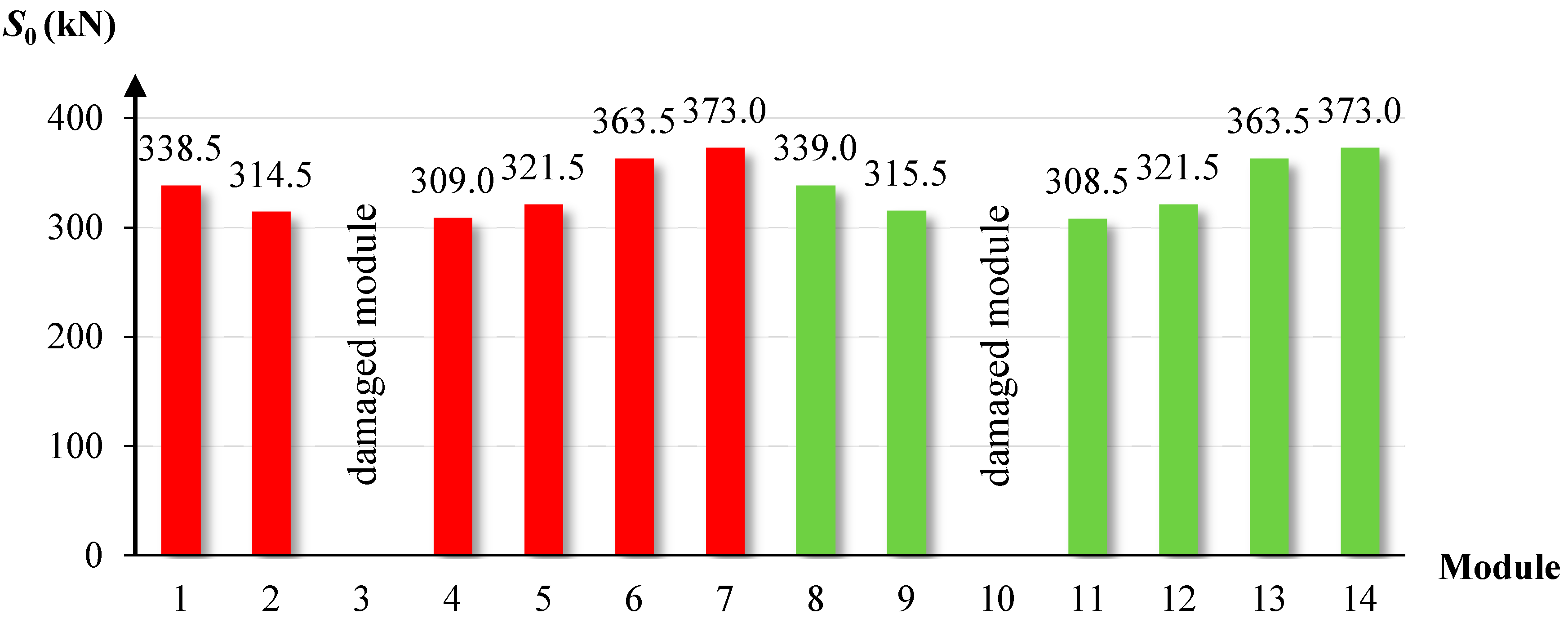
Figure 13 shows the levels of self-stress obtained for each module that allowed regaining the given value of
δA. The smallest values of pre-stressing forces that led to self-repair of the structure were obtained for Module No. 11.
The diagram presented below shows the distribution of the displacements of the upper structural nodes in two characteristic sections: A-A and B-B (
Figure 14). Four states were taken into account:
State “0”: structure before damage, the level of self-stress S0 = 100 kN, no external loading,
State “1”: structure before damage, the level of self-stress S0 = 100 kN, concentrated forces P = 10 kN applied to the upper nodes,
State “2”: structure after damage, the level of self-stress in undamaged modules S0 = 100 kN, concentrated forces P = 10 kN applied to the upper nodes,
State “3”: structure after repair, the level of self-stress in module 11 S0 = 308.5 kN and in other undamaged modules S0 = 100 kN, concentrated forces P = 10 kN applied to the upper nodes.
The presented example concerns only one damage scenario in one specific tensegrity structure and does not exhaust the problem of structural repair. However, the aim of the analysis was to show that tensegrities are capable of self-repair, not to investigate all possible cases of structural damage. Tensegrity structures owe this unique property of self-repair to infinitesimal mechanisms, which are balanced with self-stress states. Repair of these structures is possible through an adjustment of prestressing forces, without any operation from the outside.
5. Active Control: Self-Adjustment
The main point of an active control of smart structures is the possibility of adjusting their parameters by using their inherent properties. In the case of tensegrity systems, it is the ability of self-adjustment that allows one to actively control the properties of these structures.
The following example proves that tensegrities are prone to structural control through an adjustment of self-stress within both the whole structure and its selected part.
In the analysis, the plate-like structure presented in
Figure 8 was considered, with the same materials, dimensions of the cross-sections, values of self-stress and loading as in the previous examples. The calculations were performed in SOFiSTiK software (educational license), using the finite element method, according to the second order theory.
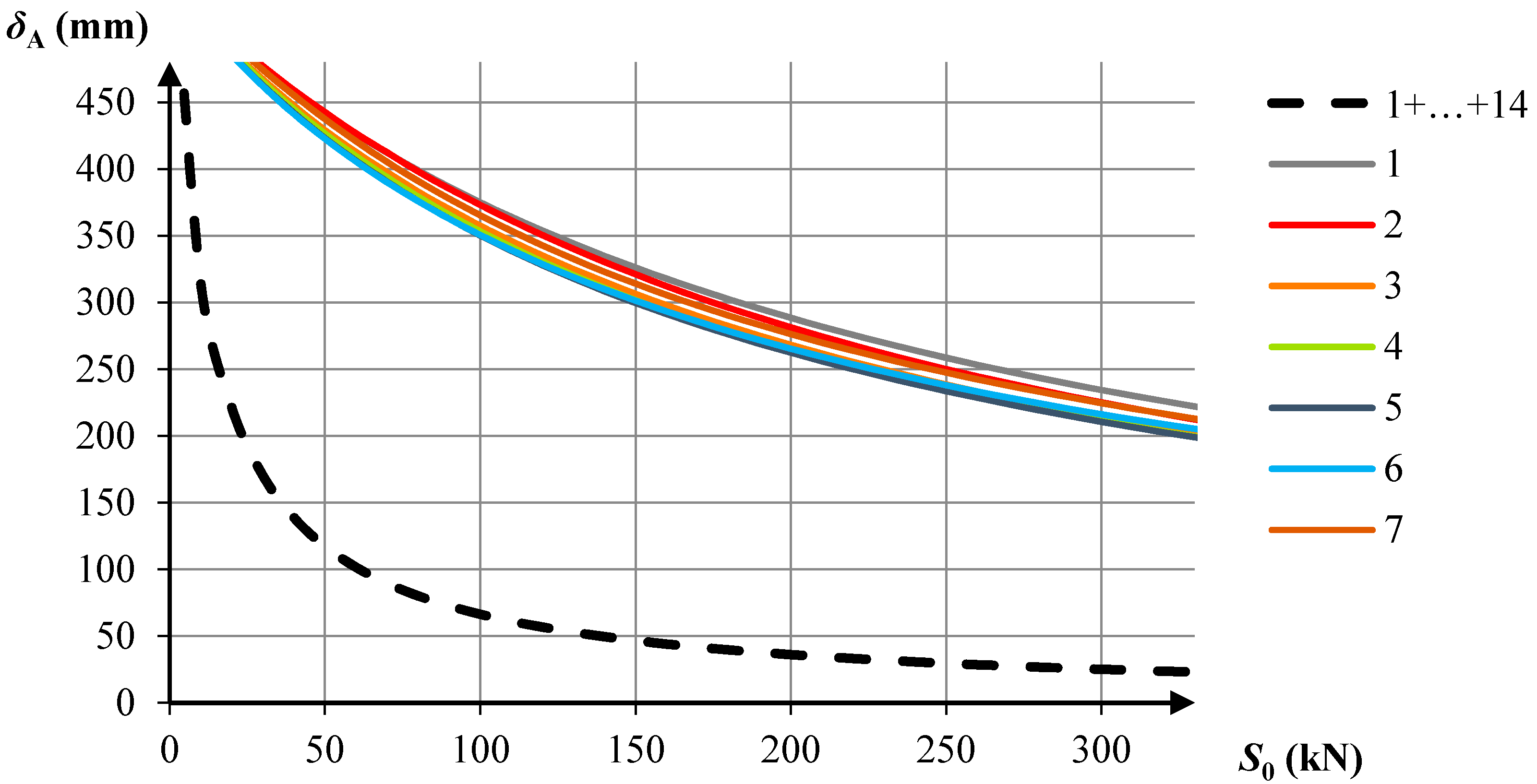
The aim of the analysis was to determine how the self-stress in a single module influences the displacement
δA of the structure, which was loaded with concentrated forces
P = 10 kN. Pre-stressing forces
S0 were introduced successively into Modules 1–7 (
Figure 12) and, for comparison purposes, into the whole system. When the considered module was pre-stressed, the others had no self-stress.
The diagrams (
Figure 15) show the influence of self-stress in single modules and in the whole structure on the considered displacement. It should be noticed that prestressing of a single module did not reduce the displacements to the same degree as self-stress applied to the whole structure did. However, it eliminated the infinitesimal mechanism and decreased the value of the considered displacement significantly. Depending on the module, the influence of self-stress on structural stiffness varies. The biggest reduction of the displacement
δA was obtained for the prestressing of Module No. 5, and the least effective was the pre-stressing of Module No. 1.
The results presented in
Figure 15 were obtained with the use of the second order theory. This theory is sufficient to show the differences in the influence of self-stress in single modules and in all modules together. The results within the third order theory show the same tendency of the results.
6. Conclusions
The study proves that tensegrity systems can be regarded as smart structures. They have some unique features that they owe to the infinitesimal mechanisms balanced with self-stress states.
According to the authors’ opinion, neither the external devices installed on the structure, nor the applied intelligent technologies make the structure smart. The structure itself should have some special properties, referred to by the authors as “inherent”, which allow controlling it without any operation from the outside. To the inherent properties of smart structures belong: self-control, self-diagnosis, self-repair and self-adjustment (active control).
The analyses presented in this paper prove that tensegrity structures have all of the defined inherent properties. Self-control is realized by self-stiffening of tensegrities under the applied external load that causes displacements consistent with the infinitesimal mechanism mode. Self-diagnosis relates to the possibility of damage detection and identification by measuring internal forces in active members. Self-repair of tensegrity structures is possible through an adjustment of self-stress forces: a proper change of pre-stressing level can compensate the damaged element and restore the values of structural displacements from before damage. Active control, on the other hand, is realized by adjusting the level of self-stress in only one selected part of the structure, hence affecting the properties of the whole system.
Another very significant conclusion that may be drawn from this study is that it is extremely important to choose a proper approach to the analysis of tensegrity systems. Analysis according to the second order theory, which includes self-stress, but neglects geometrical non-linearities, allows identifying infinitesimal mechanisms and determining self-stress states of the structure, but does not take into account self-stiffening of the structure. Therefore, in some cases, a geometrically non-linear theory must be applied.
According to the best knowledge of the authors, it is necessary to brake barriers in engineering design to allow the tensegrity structures to be introduced into common projects. The results presented in the paper should encourage engineers to design structures with non-standard inherent properties for potential technical/engineering applications with smart features. It is believed that smart structures will be more common in the near future, not only in aerospace engineering, but also in mechanical and civil engineering. Reliable results can be theoretically obtained with the use of fully-geometrically non-linear theory (third order) with a previous analysis of the properties of tensegrity structures (infinitesimal modes and self-equilibrated forces) within the second order theory. Experimental support is strongly recommended.
In future research, the authors plan to focus on two of the described properties of tensegrity structures: self-diagnosis and self-repair, as they seem to be particularly interesting from the point of view of engineering applications. Different tensegrity systems will be analyzed and various damage scenarios considered.