Vibrometry Assessment of the External Thermal Composite Insulation Systems Influence on the Façade Airborne Sound Insulation †
Abstract
:Featured Application
Abstract
1. Introduction
2. Experimental Approach
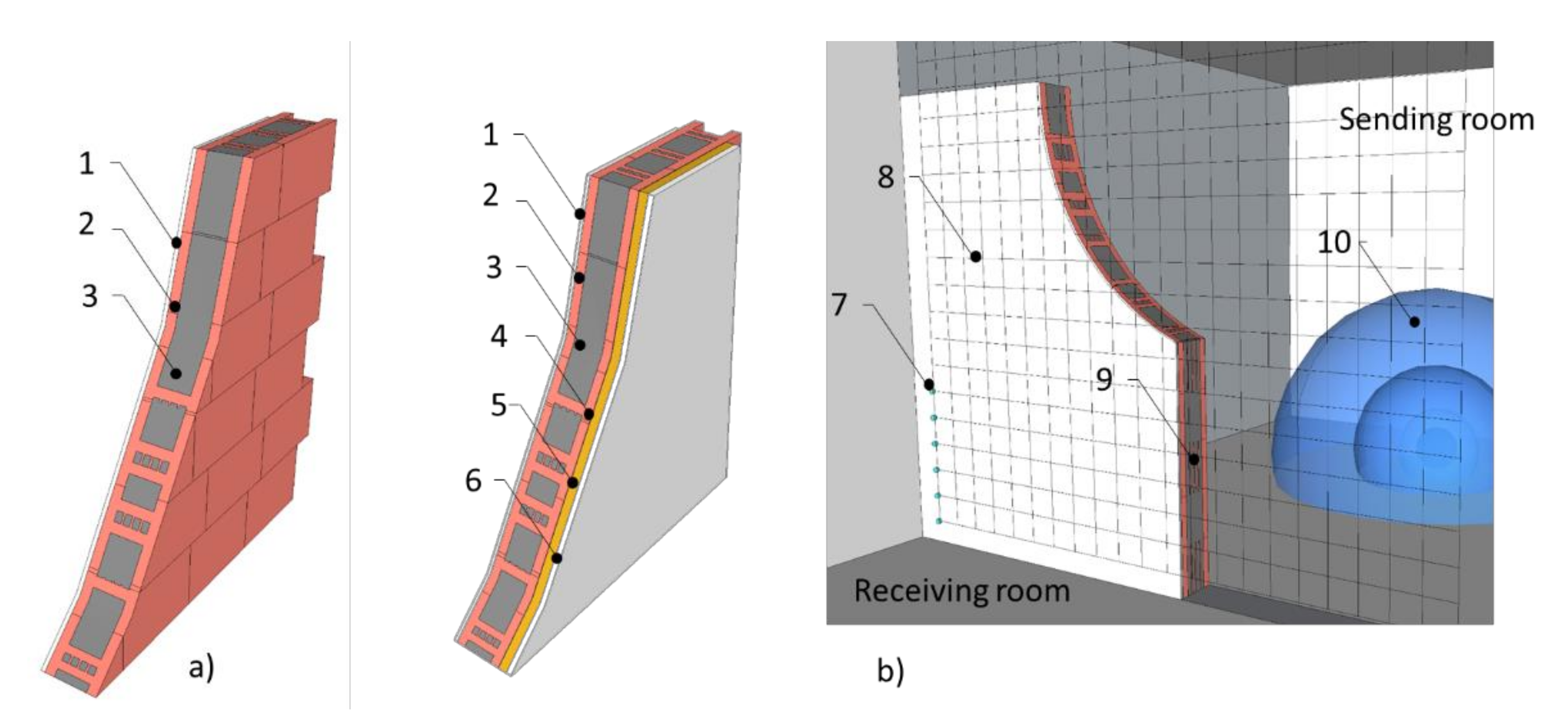
2.1. Determination of Airborne Sound Insulation Based on ISO 10140-2
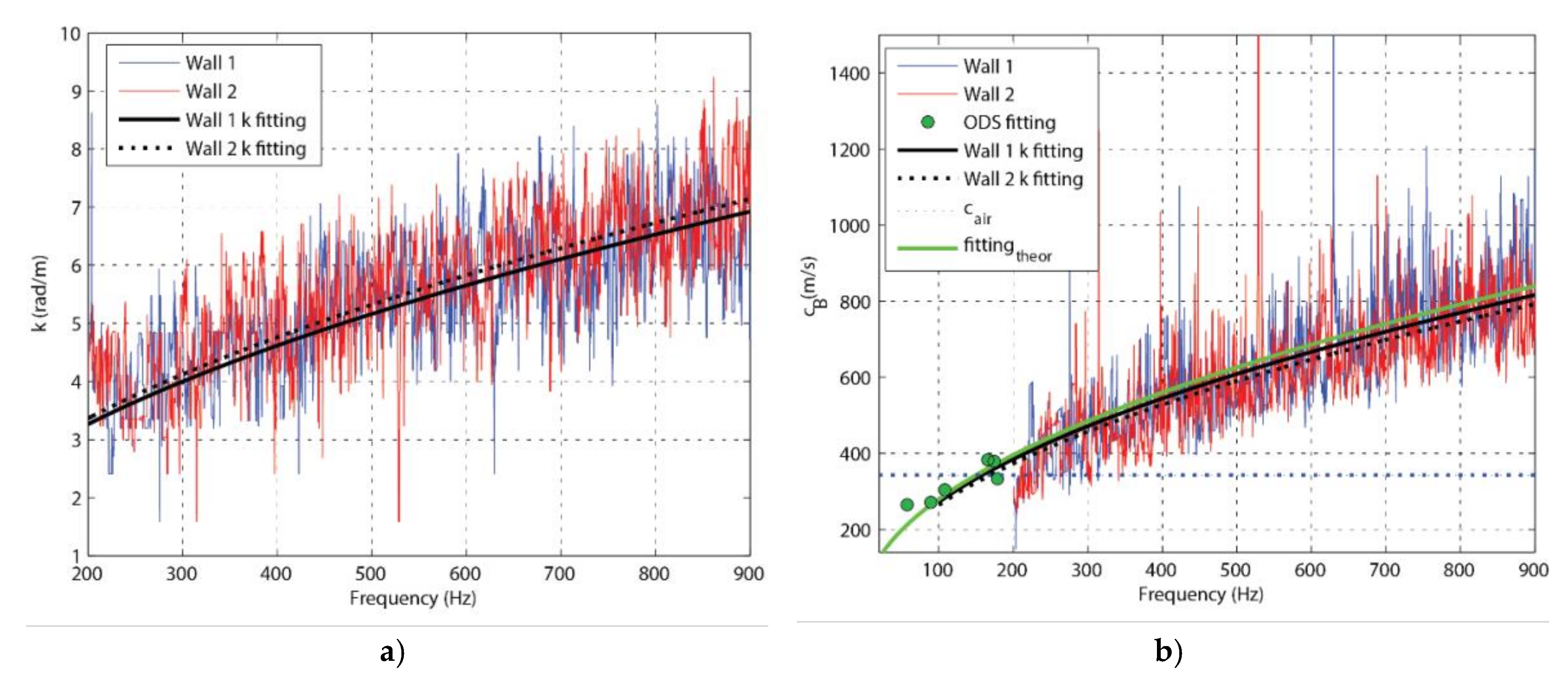
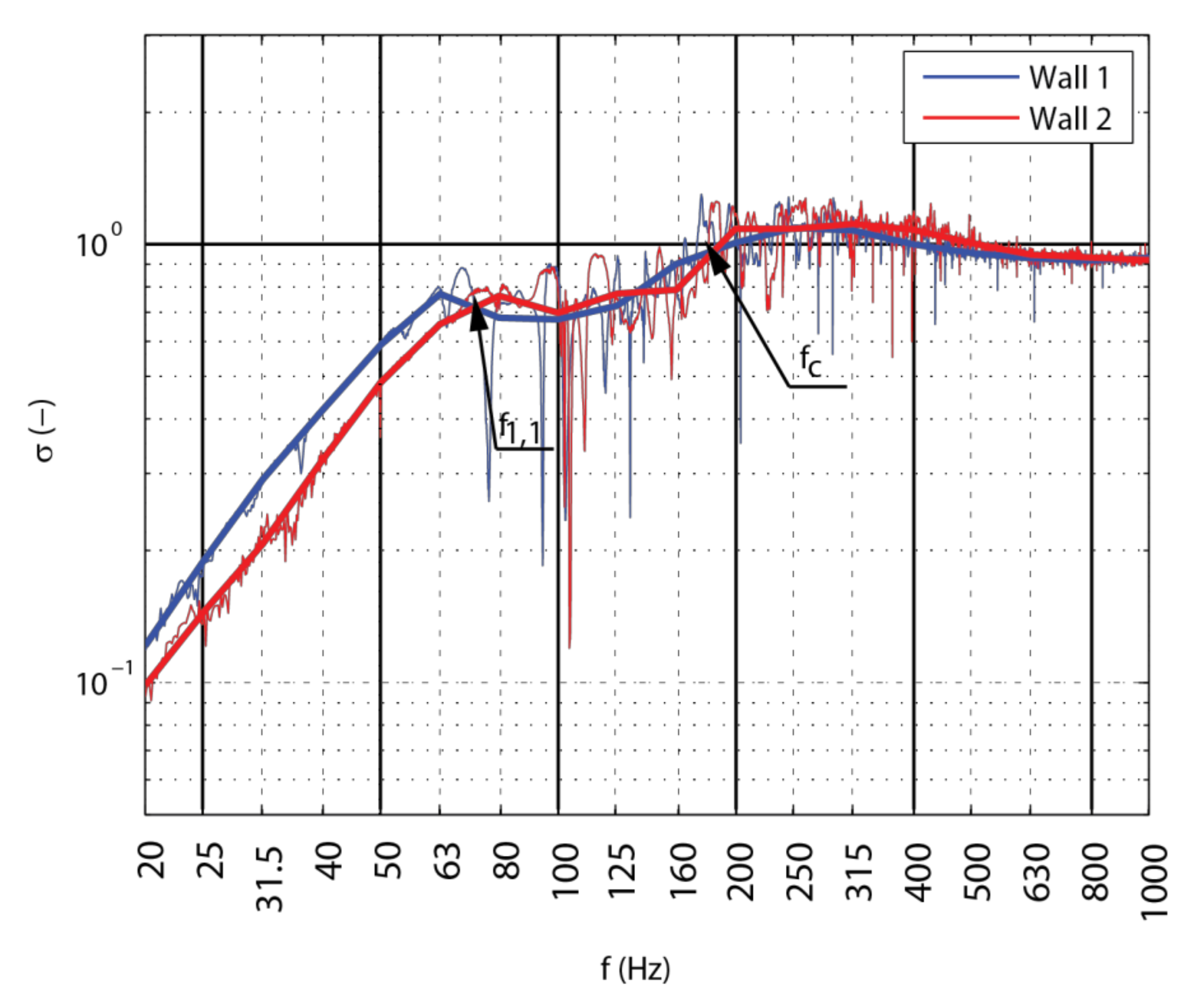
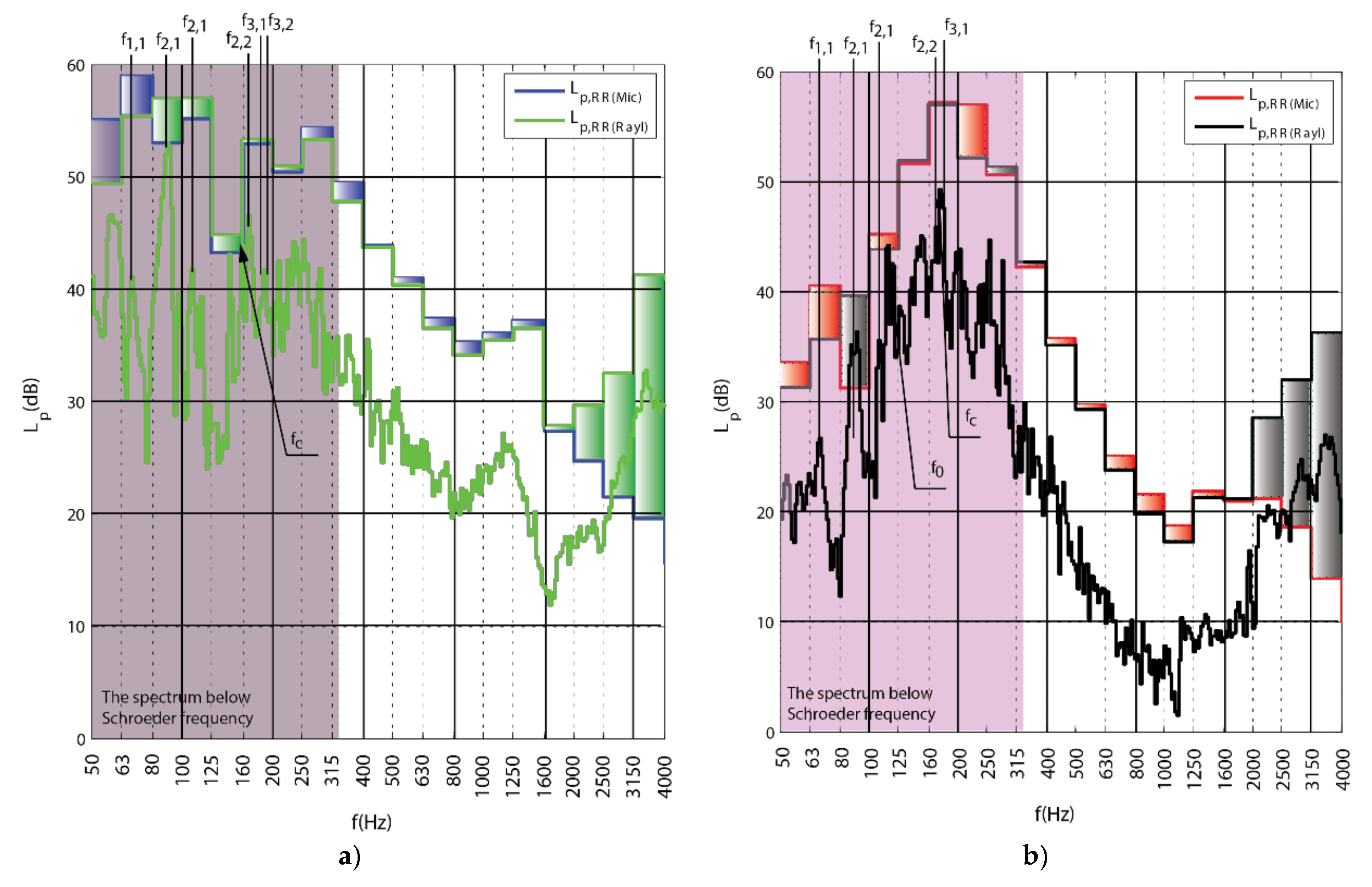
2.2. Determination of Airborne Sound Insulation Based on Vibrometry
2.3. Determination of ETICS Induced Weighted Sound Reduction Index Improvement
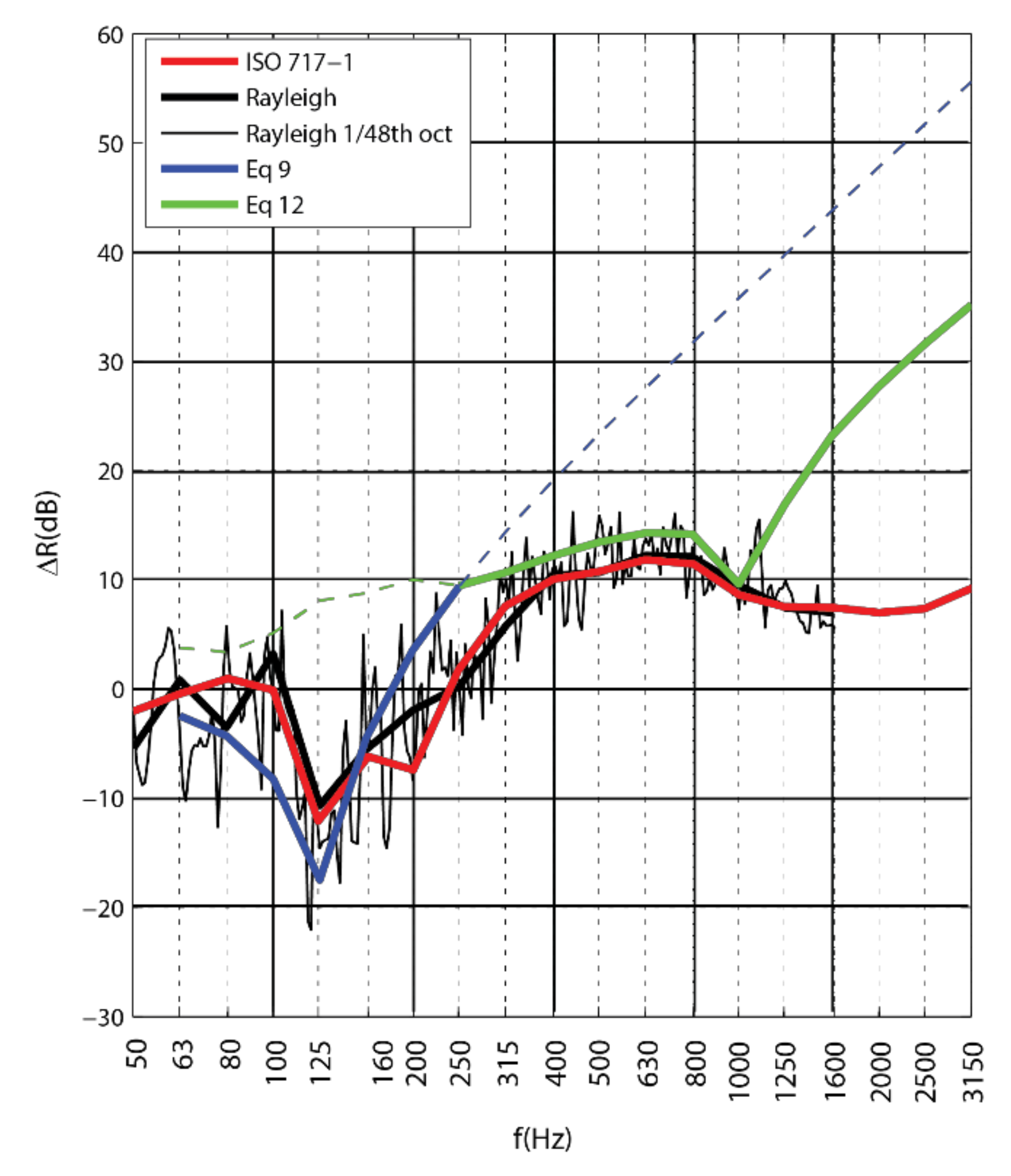
3. Results
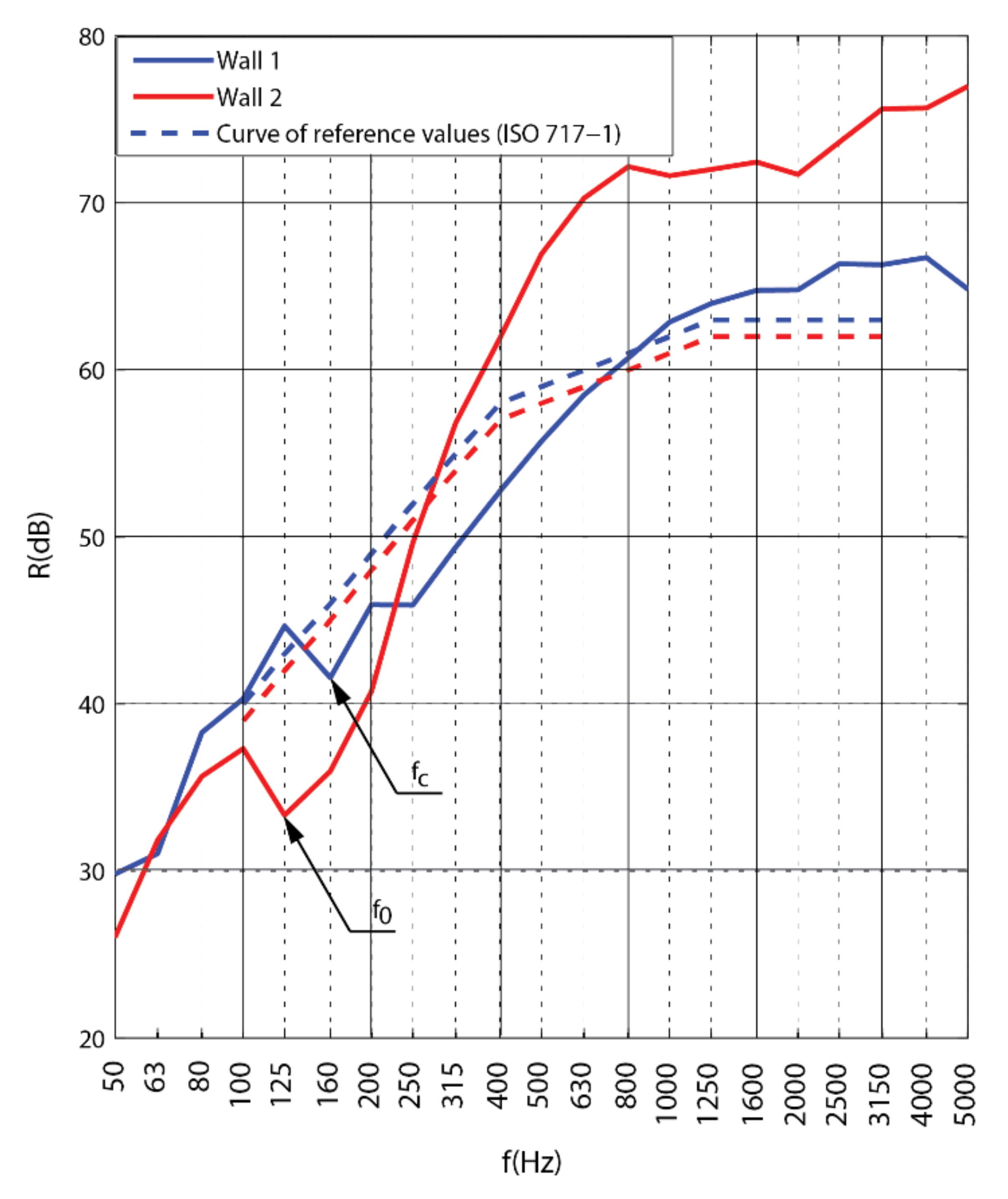
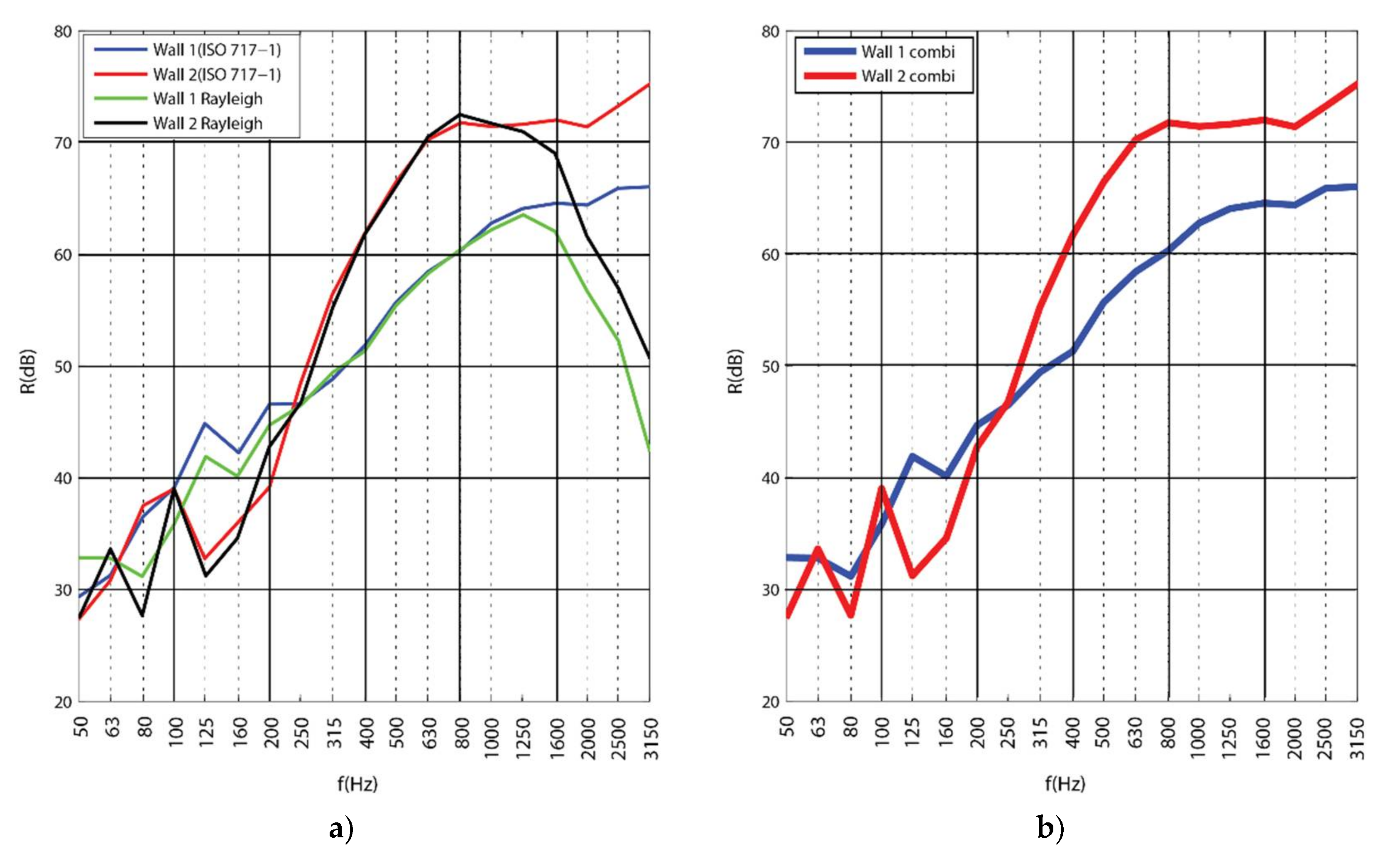
3.1. Assessment in Accordance to ISO 10140
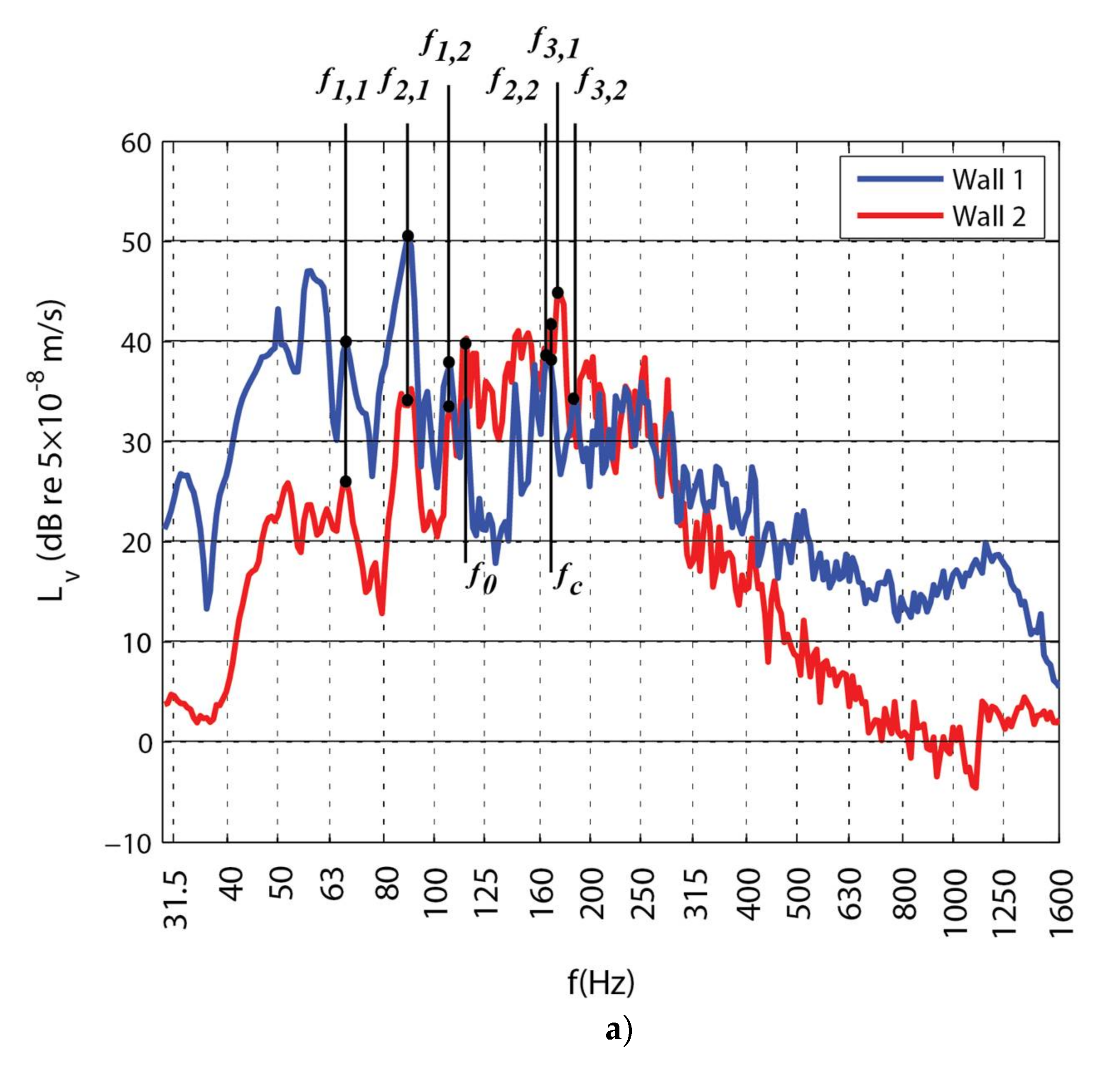
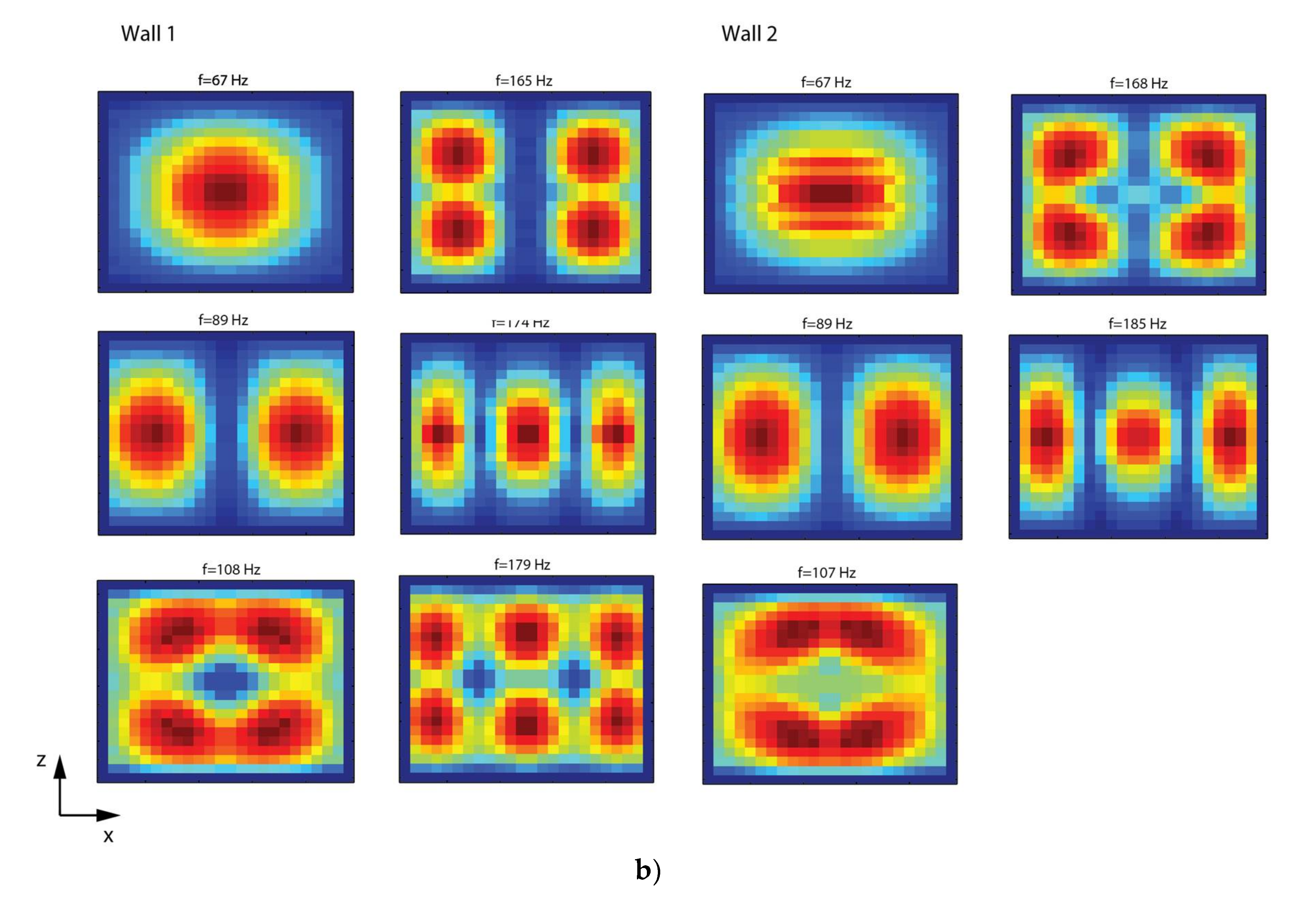
3.2. Assessment by Vibrometry Approach
3.3. Sound Reduction Improvement
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Gong, X.; Akashi, Y.; Sumiyoshi, D. Optimization of passive design measures for residential buildings in different Chinese areas. Build. Environ. 2012, 58, 46–57. [Google Scholar] [CrossRef]
- D’Orazio, M.; Cursio, G.; Graziani, L.; Aquilanti, L.; Osimani, A.; Clementi, F.; Yéprémian, C.; Lariccia, L.; Amoroso, S. Effects of water absorption and surface roughness on the bioreceptivity of ETICS compared to clay bricks. Build. Environ. 2014, 77, 20–28. [Google Scholar] [CrossRef]
- Barreira, E.; de Freitas, V.P. Experimental study of the hygrothermal behaviour of External Thermal Insulation Composite Systems (ETICS). Build. Environ. 2013, 63, 31–39. [Google Scholar] [CrossRef]
- Johansson, W.L.; Sandin, K. Estimation of mould growth levels on rendered façades based on surface relative humidity and surface temperature measurements. Build. Environ. 2010, 45, 1153–1160. [Google Scholar] [CrossRef]
- Al-Homoud, M.S. Performance characteristics and practical applications of common building thermal insulation materials. Build. Environ. 2005, 40, 353–366. [Google Scholar] [CrossRef]
- Thermal Protection of Buildings. Thermal Performance of Buildings and Components. Part 2: Functional Requirements; STN 73 0540-2/Z1; STN: Bratislava, Slovak, 2016.
- ISO. ISO 52003-1 Energy Performance of Buildings-Indicators, Requirements, Ratings and Certificates-Part 1: General Aspects and Application to the Overall Energy Performance; ISO: Geneva, Switzerland, 2017. [Google Scholar]
- Pietruschka, D.; Varga, E.; Drechsler, A.; Marin, R.; Eicker, U.; Fischer, H. Energetische und Akustische Sanierung von Wohngebäuden-vom Altbau zum Akustisch Optimierten Passivhaus; Forschungsbericht; Hochschule für Technik: Stuttgart, Germany, 2012. [Google Scholar]
- Nurzynski, J. The effect of additional thermal lining on the acoustic performance of a wall. In Proceedings of the Forum Acusticum 2008, Paris, France, 29 June–4 July 2008. [Google Scholar]
- Guigou-Carter, C.; Foret, R.; Villot, M.; Chene, J.B. Effect of thermal renovation on acoustic performance of buildings. In Proceedings of the Euronoise 2009, Edinburgh, UK, 26–28 October 2009. [Google Scholar]
- Magarini, A.; Scamoni, F.; Scrosati, C. Integrated acoustic and thermo-hygrometric performances of building walls, for more efficient refurbishment strategies: First evaluations. In Proceedings of the 21st International Congress on Sound and Vibration 2014, Beijing, China, 13–17 July 2014. [Google Scholar]
- Weber, L.; Kaltbeityel, B. Schalldämmung von Wärmedämm-Verbundsystemen mit Zweilagiger Dämmschicht; Fraunhofer IRB Verlag: Stuttgart, Germany, 2016. [Google Scholar]
- Weber, L.; Müller, S. Schallschutz bei Wärmedämm-Verbundsystemen; Fraunhofer IRB Verlag: Stuttgart, Germany, 2015. [Google Scholar]
- Weber, L.; Zhang, Y.; Brandstetter, D. Influence of Wall Construction on the Acoustical Behaviour of ETHICS. In Proceedings of the DAGA 2002, Bochum, Germany, 4–8 March 2002. [Google Scholar]
- Weber, L.; Buchele, A. Acoustic Refurbishment of Residential Buildings with Additional Linings and Additional Lining Constructions-Calculation, Design, and Optimization; Abridged Version of Research Report B-BA 2/2008; Fraunhofer Institute for Building Physics (IBP): Stuttgart, Germany.
- Weber, L. Effect of ETHICS on the flanking transmission of outer walls. In Proceedings of the Fortschritte der Akustik-DAGA, Strasbourg, France, 22–25 March 2004. [Google Scholar]
- Weber, L.; Brandstetter, D. Einheitliche Schalltechnische Bemessung von Wärmedämm-Verbundsystemen, -Ergänzung des Berechnungsverfahrens; IBP-Bericht B-BA 4/2005; Fraunhofer IRB Verlag: Stuttgart, Germany, 2002. [Google Scholar]
- Weber, L. Einheitliche Schalltechnische Bemessung von Wärmedämm-Verbundsystemen-Ergänzung des Berechnungsverfahrens; Fraunhofer IRB Verlag: Stuttgart, Germany, 2005. [Google Scholar]
- Scholl, W. Schalldämmung mit Wärmedämmverbundsystemen. Bauphysik 1999, 21, 20–28. [Google Scholar]
- ISO. ISO 717-1:2013. Acoustics-Rating of Sound Insulation in Buildings and of Building Elements-Part 1: Airborne Sound Insulation; ISO: Geneva, Switzerland, 2013. [Google Scholar]
- European Commission. Report from the Commission to the European Parliament and the Council on the Implementation of the Environmental Noise Directive in Accordance with Article 11 of Directive 2002/49/EC; European Commission: Belgium, 2017. [Google Scholar]
- Miedema, H.M.; Oudshoorn, C.G. Annoyance from transportation noise: Relationships with exposure metrics DNL and DENL and their confidence intervals. Environ. Health Perspect. 2001, 109, 409. [Google Scholar] [CrossRef] [PubMed]
- Muzet, A. Environmental noise, sleep and health. Sleep Med. Rev. 2007, 11, 135–142. [Google Scholar] [CrossRef] [PubMed]
- Lercher, P.; Evans, G.W.; Meis, M. Ambient noise and cognitive processes among primary schoolchildren. Environ. Behav. 2003, 35, 725–735. [Google Scholar] [CrossRef]
- Babisch, W.; Swart, W.; Houthuijs, D.; Selander, J.; Bluhm, G.; Pershagen, G.; Sourtzi, P. Exposure modifiers of the relationships of transportation noise with high blood pressure and noise annoyance. J. Acoust. Soc. Am. 2012, 132, 3788–3808. [Google Scholar] [CrossRef] [PubMed]
- ISO. ISO 10140-2:2010. Acoustics-Laboratory Measurement of Sound Insulation of Building Elements Part 2: Measurement of Airborne Sound Insulation; ISO: Geneva, Switzerland, 2010. [Google Scholar]
- ISO. ISO 10140-5:2010. Acoustics-Laboratory Measurement of Sound Insulation of Building Elements Part 5: Requirements for Test Facilities and Equipment; ISO: Geneva, Switzerland, 2010. [Google Scholar]
- Zaťko, P.; Urbán, D.; Tomašovič, P.; Rychtáriková, M. Acoustic Performance of the External Thermal Composite Insulation Systems Influence in Slovakia. In Proceedings of the Fortschritte der Akustik–DAGA 2016, Aachen, Germany, 14–17 March 2016. [Google Scholar]
- Foret, R.; Guigou-Carter, C.; Villot, M. Effect of thermal insulation systems on acoustic performances of ancient building construction elements. In Proceedings of the Internoise and Noise-on Institute of Noise Control Engineering, Portugal, 13–16 June 2010. [Google Scholar]
- Miskinis, K.; Dikavicius, V.; Buska, A. Acoustic and thermal properties of building envelope with ETICS. In Proceedings of the 23rd International Congress on Sound and Vibration, Athens, Greece, 10–14 July 2016. [Google Scholar]
- Guigou-Carter, C.; Foret, R.; Wetta, R.; Ducruet, P.; Villot, M. Comparison of measured and predicted sound insulation for a thermal retrofitted building. Noise Control Eng. J. 2011, 59, 278–289. [Google Scholar] [CrossRef]
- Santoni, A.; Bonfiglio, P.; Davy, J.L.; Fausti, P.; Pompoli, F.; Pagnoncelli, L. Sound transmission loss of ETICS cladding systems considering the structure-borne transmission via the mechanical fixings: Numerical prediction model and experimental evaluation. Appl. Acoust. 2017, 122, 88–97. [Google Scholar] [CrossRef]
- Allard, J.; Atalla, N. Propagation of Sound in Porous Media: Modelling Sound Absorbing Materials; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Fausti, P.; García, T.C.; Ingelaere, B.; Machimbarrena, M.; Monteiro, C.; Santoni, A.; Smith, S. Building Acoustics throughout Europe Volume 1: Towards a Common Framework in Building Acoustics Throughout Europe; COST Office and Authors, COST Action TU0901, COST Office: Brussels, Belgium, 2014. [Google Scholar]
- Wittstock, V. On the uncertainty of single-number quantities for rating airborne sound insulation. Acta Acust. United Acust. 2007, 93, 375–386. [Google Scholar]
- Buratti, C.; Belloni, E.; Moretti, E. Façade noise abatement prediction: New spectrum adaptation terms measured in field in different road and railway traffic conditions. Appl. Acoust. 2014, 76, 238–248. [Google Scholar] [CrossRef]
- Rasmussen, B.; Rindel, J.H. Concepts for evaluation of sound insulation of dwellings-from chaos to consensus. In Proceedings of the Forum Acusticum, Budapest, Hungary, 29 August–2 September 2005. [Google Scholar]
- Rasmussen, B. Sound insulation between dwellings–Requirements in building regulations in Europe. Appl. Acoust. 2010, 71, 373–385. [Google Scholar] [CrossRef]
- Rychtáriková, M.; Muellner, H.; Chmelík, V.; Roozen, N.B.; Urbán, D.; Garcia, D.P.; Glorieux, C. Perceived Loudness of Neighbour Sounds Heard Through Heavy and Light-Weight Walls with Equal Rw + C 50-5000. Acta Acust. United Acust. 2016, 102, 58–66. [Google Scholar] [CrossRef]
- Weber, L. Akustisches Berechnungsmodell für Wärmedämm-Verbundsysteme. In Proceedings of the DAGA 2005, Munich, Germany, 14–17 March 2005. [Google Scholar]
- Zaťko, P. Kontaktné zatepľovacie systémy a ich vplyv na akustické vlastnosti stavebných konštrukcií. Fyzikálne Faktory Prostredia 2014, 4, 21–24. [Google Scholar]
- ISO. ISO 12354-1. Building Acoustics—Estimation of Acoustic Performance of Buildings from the Performance of Elements-Part 1: Airborne Sound Insulation between Rooms; ISO: Geneva, Switzerland, 2017. [Google Scholar]
- De Salis, M.F.; Oldham, D.J.; Sharples, S. Noise control strategies for naturally ventilated buildings. Build. Environ. 2002, 37, 471–484. [Google Scholar] [CrossRef]
- Roozen, N.B.; Labelle, L.; Rychtáriková, M.; Glorieux, C. Determining radiated sound power of building structures by means of Laser Doppler vibrometry. J. Sound Vib. 2015, 346, 81–99. [Google Scholar] [CrossRef]
- Squicciarini, G.; Thompson, D.J.; Corradi, R. The effect of different combinations of boundary conditions on the average radiation efficiency of rectangular plates. J. Sound Vib. 2014, 333, 3931–3948. [Google Scholar] [CrossRef]
- Roozen, N.B.; Muellner, H.; Labelle, L.; Rychtáriková, M.; Glorieux, C. Influence of panel fastening on the acoustic performance of light-weight building elements: Study by sound transmission and laser scanning vibrometry. J. Sound Vib. 2015, 346, 100–116. [Google Scholar] [CrossRef]
- Villot, M.; Guigou, C.; Gagliardini, L. Predicting the acoustical radiation of finite size multi-layered structures by applying spatial windowing on infinite structures. J. Sound Vib. 2001, 245, 433–455. [Google Scholar] [CrossRef]
- Cheng, Z.; Fan, J.; Wang, B.; Tang, W. Radiation efficiency of submerged rectangular plates. Appl. Acoust. 2012, 73, 150–157. [Google Scholar] [CrossRef]
- Koopmann, G.H.; Benner, H. Method for Computing the Sound Power of Machines Based on the Helmholtz Integral. J. Acoust. Soc. Am. 1982, 71, 78–89. [Google Scholar] [CrossRef]
- Fahy, F. Sound and Structural Vibration: Radiation, Transmission and Response; Academic Press: London, UK, 1985. [Google Scholar]
- Lamancusa, J.S. Numerical optimization techniques for structuralacoustic design of rectangular panels. Comput. Struct. 1993, 48, 661–675. [Google Scholar] [CrossRef]
- Waterhouse, R.V. Interference patterns in reverberant sound fields. J. Acoust. Soc. Am. 1955, 27, 247–258. [Google Scholar] [CrossRef]
- Vorländer, M. Revised relation between the sound power and the average sound pressure level in rooms and consequences for acoustic measurements. Acta Acust. United Acust. 1995, 81, 332–343. [Google Scholar]
- ISO. ISO 3741. Acoustics-Determination of Sound Power Levels and Sound Energy Levels of Noise Sources Using Sound Pressure-Precision Methods for Reverberation Test Rooms; ISO: Geneva, Switzerland, 2010. [Google Scholar]
- Vernier. EN 29052-1. Acoustics. Determination of Dynamic Stiffness. Part 1: Materials Used under Floating Floors in Dwellings; Vernier: Geneva, Switzerland, 1992. [Google Scholar]
- Roozen, N.B.; Labelle, L.; Leclere, Q.; Ege, K.; Alvarado, S. Non-contact experimental assessment of apparent dynamic stiffness of constrained-layer damping sandwich plates in a broad frequency range using a Nd: YAG pump laser and a laser Doppler vibrometer. J. Sound Vib. 2017, 395, 90–101. [Google Scholar] [CrossRef]
- Williams, E.G. Fourier Acoustics, Sound Radiation and Nearfield Acoustical Holography; Academic Press: London, UK, 1999. [Google Scholar]
- Xie, G.; Thompson, D.J.; Jones, C.J.C. The radiation efficiency of baffled platesand strips. J. Sound Vib. 2005, 280, 181–209. [Google Scholar] [CrossRef]
- Cremer, L. Theorie der Schalldämmung dünner Wände bei schrägem Einfall. Akust. Z. 1942, 7, 81–104. [Google Scholar]
| Symbol | Wall 1 ISO | Wall 2 ISO | ΔRw, ISO |
|---|---|---|---|
| Rw (dB) | 59 | 58 | −1 |
| C (dB) | −2 | −3 | −1 |
| Ctr (dB) | −6 | −9 | −3 |
| C50–3150 (dB) | −3 | −4 | −1 |
| C50–5000 (dB) | −2 | −3 | −1 |
| C100–5000 (dB) | −1 | −3 | −2 |
| Ctr,50–3150 (dB) | −10 | −12 | −2 |
| Ctr,50–5000 (dB) | −10 | −12 | −2 |
| Ctr,100–5000 (dB) | −6 | −9 | −3 |
| Symbol | Wall 1 combi | Wall 2 combi | Wall 1 ISO | Wall 2 ISO | ΔRw, combi | ΔRw, ISO | ΔRw, Weber [13] |
|---|---|---|---|---|---|---|---|
| Rw (dB) | 58 | 58 | 59 | 58 | 0 | −1 | 8 (6) |
| C (dB) | −2 | −5 | −2 | −3 | −3 | −1 | 5 (3) |
| Ctr (dB) | −7 | −10 | −6 | −9 | −3 | −3 | 2 (0) |
| C50–3150 (dB) | −3 | −6 | −3 | −4 | −3 | −1 | - |
| C50–5000 (dB) | −2 | −5 | −2 | −3 | −3 | −1 | - |
| C100–5000 (dB) | −2 | −4 | −1 | −3 | −2 | −2 | - |
| Ctr,50–3150 (dB) | −11 | −14 | −10 | −12 | −3 | −2 | - |
| Ctr,50–5000 (dB) | −11 | −14 | −10 | −12 | −3 | −2 | - |
| Ctr,100–5000 (dB) | −7 | −10 | −6 | −9 | −3 | −3 | - |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Urbán, D.; Roozen, N.B.; Muellner, H.; Zaťko, P.; Niemczanowski, A.; Rychtáriková, M.; Glorieux, C. Vibrometry Assessment of the External Thermal Composite Insulation Systems Influence on the Façade Airborne Sound Insulation. Appl. Sci. 2018, 8, 703. https://doi.org/10.3390/app8050703
Urbán D, Roozen NB, Muellner H, Zaťko P, Niemczanowski A, Rychtáriková M, Glorieux C. Vibrometry Assessment of the External Thermal Composite Insulation Systems Influence on the Façade Airborne Sound Insulation. Applied Sciences. 2018; 8(5):703. https://doi.org/10.3390/app8050703
Chicago/Turabian StyleUrbán, Daniel, N.B. Roozen, Herbert Muellner, Peter Zaťko, Alexander Niemczanowski, Monika Rychtáriková, and Christ Glorieux. 2018. "Vibrometry Assessment of the External Thermal Composite Insulation Systems Influence on the Façade Airborne Sound Insulation" Applied Sciences 8, no. 5: 703. https://doi.org/10.3390/app8050703
APA StyleUrbán, D., Roozen, N. B., Muellner, H., Zaťko, P., Niemczanowski, A., Rychtáriková, M., & Glorieux, C. (2018). Vibrometry Assessment of the External Thermal Composite Insulation Systems Influence on the Façade Airborne Sound Insulation. Applied Sciences, 8(5), 703. https://doi.org/10.3390/app8050703





