Experimental Study on Dynamic Effects of a Long-span Railway Continuous Beam Bridge
Abstract
:1. Introduction
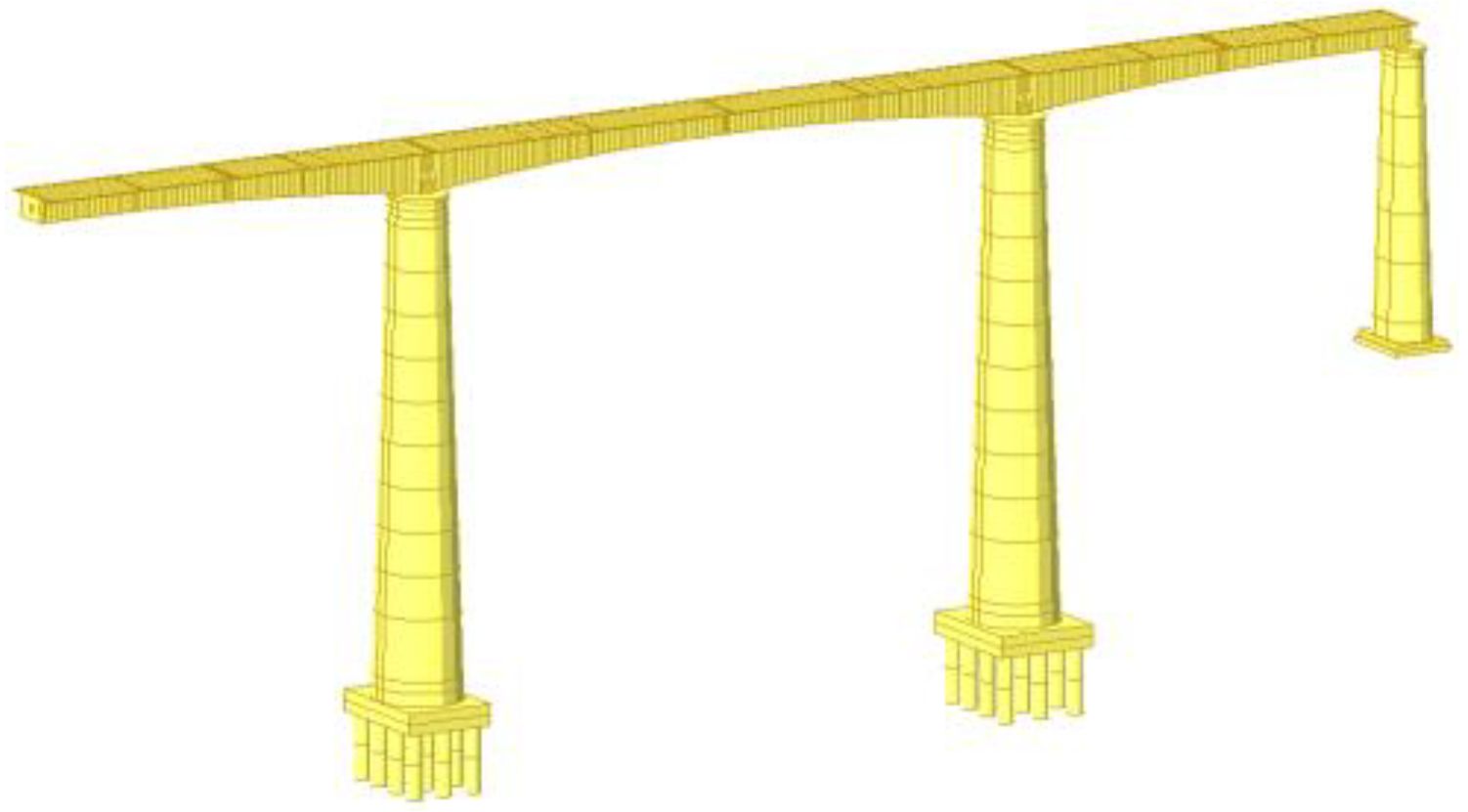
2. Description of the Bridge
3. Experiment Setup
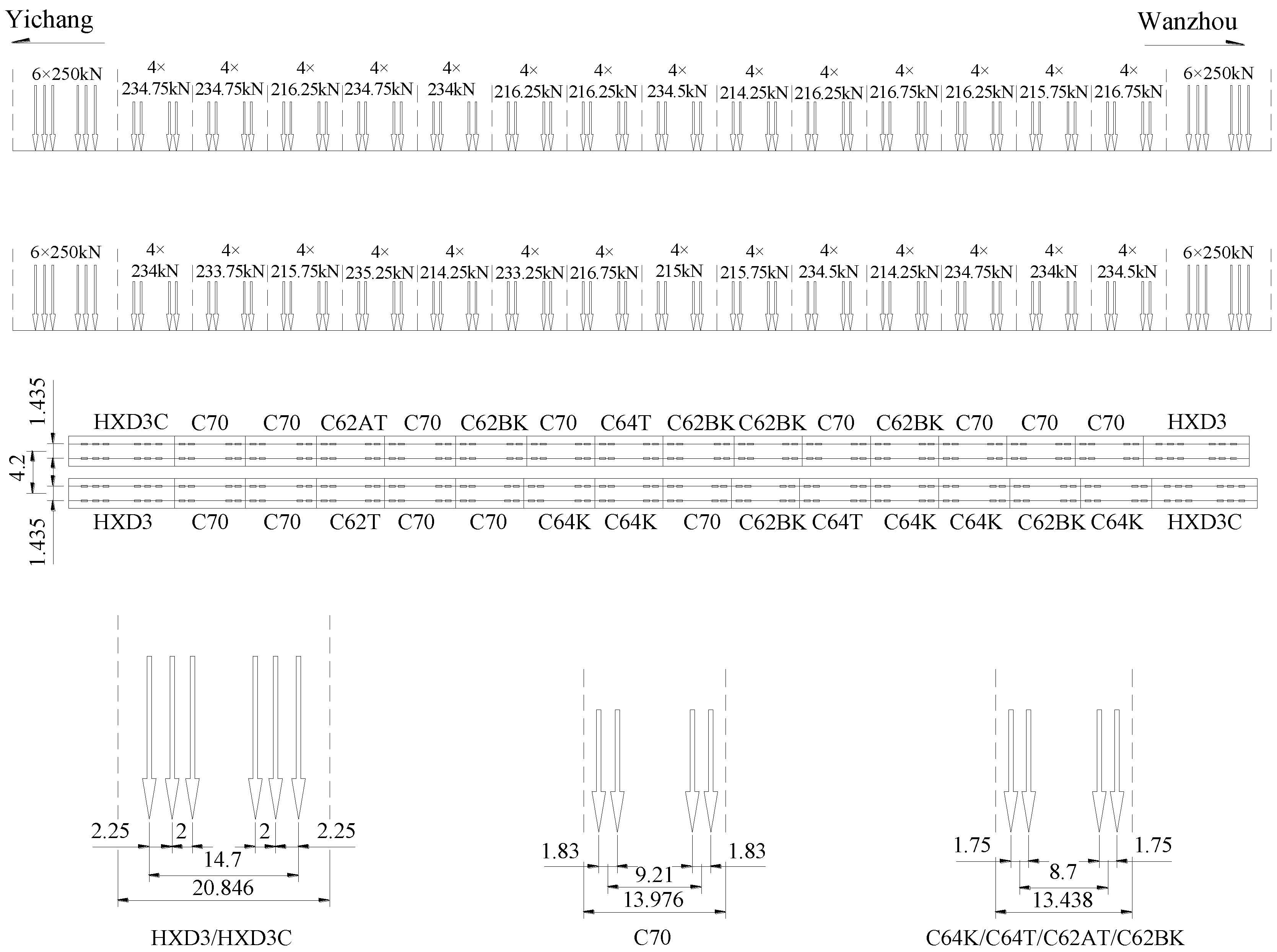
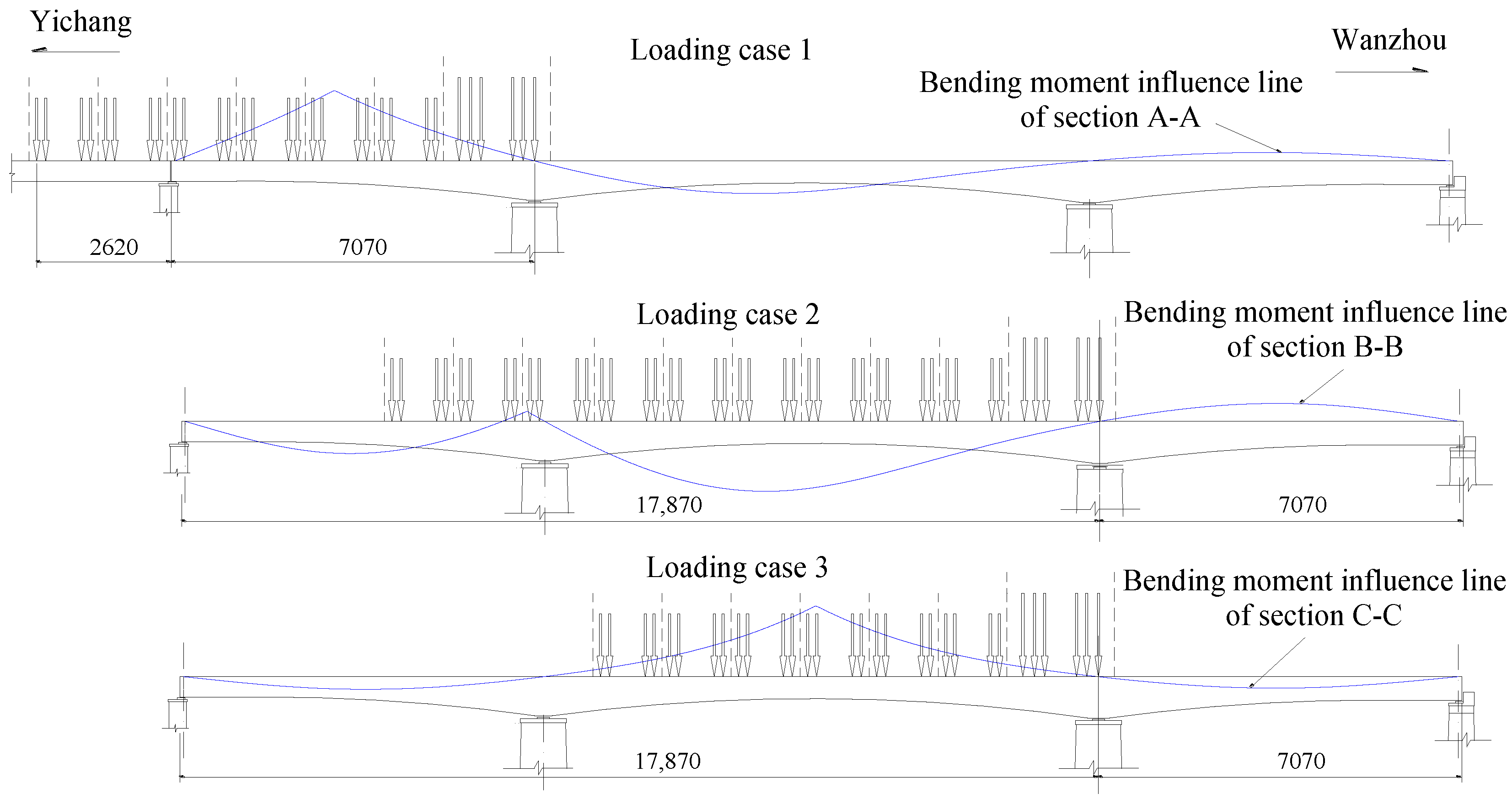
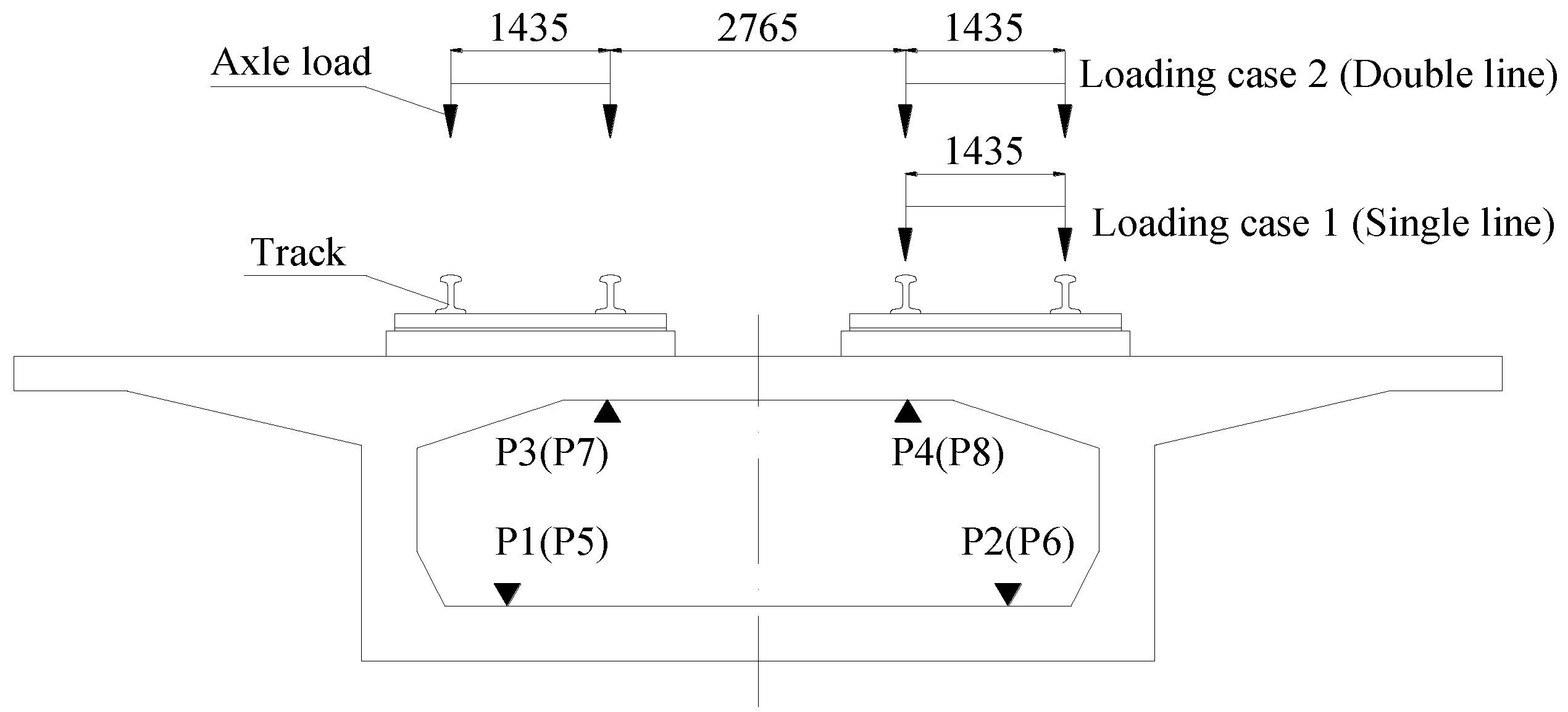
3.1. Loading Configurations
3.2. Instrumentation
4. Field Test Results
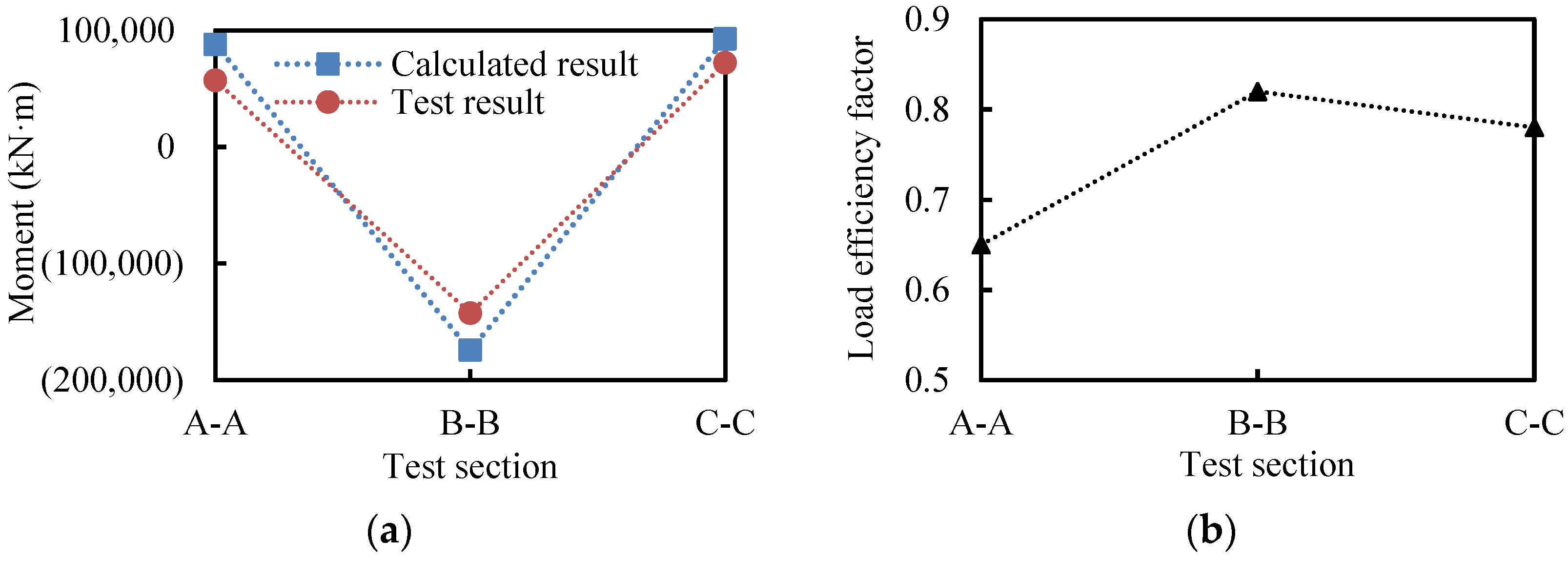
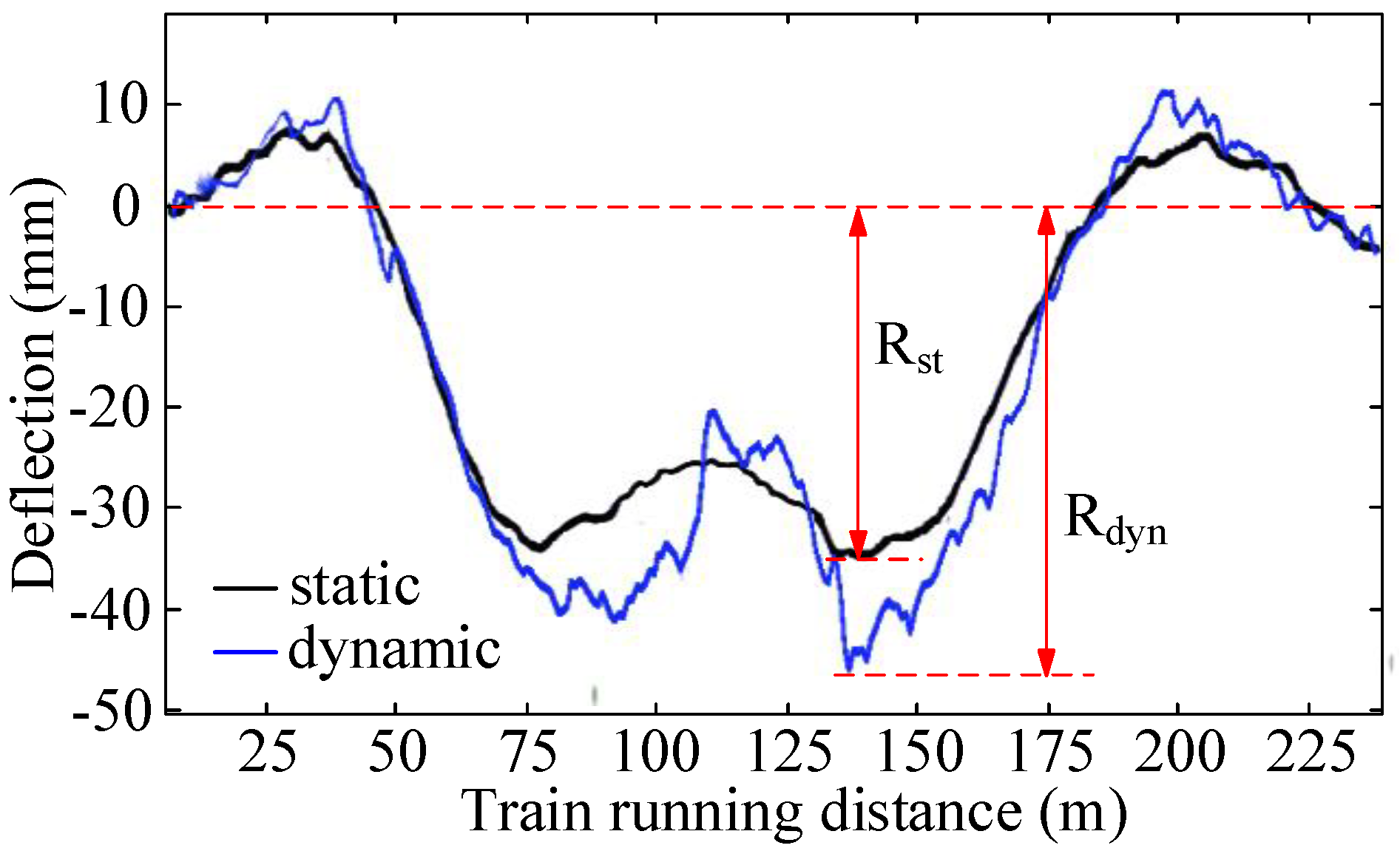
4.1. Static Test Results
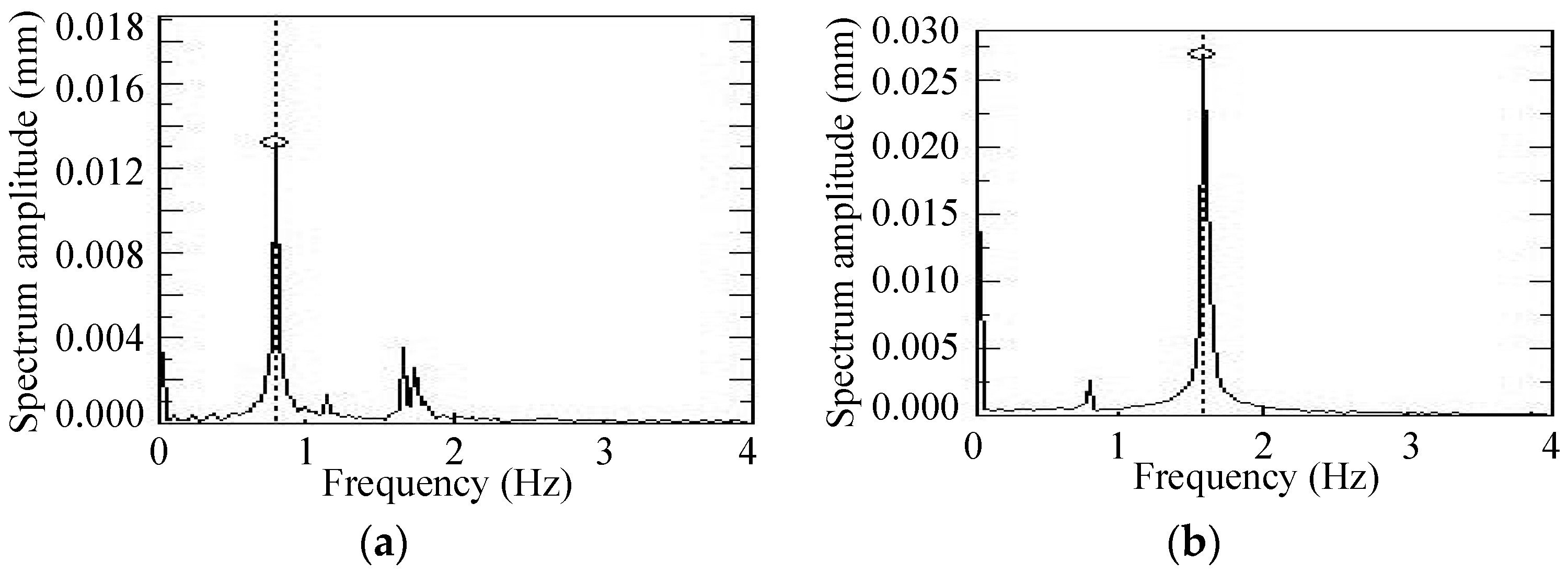
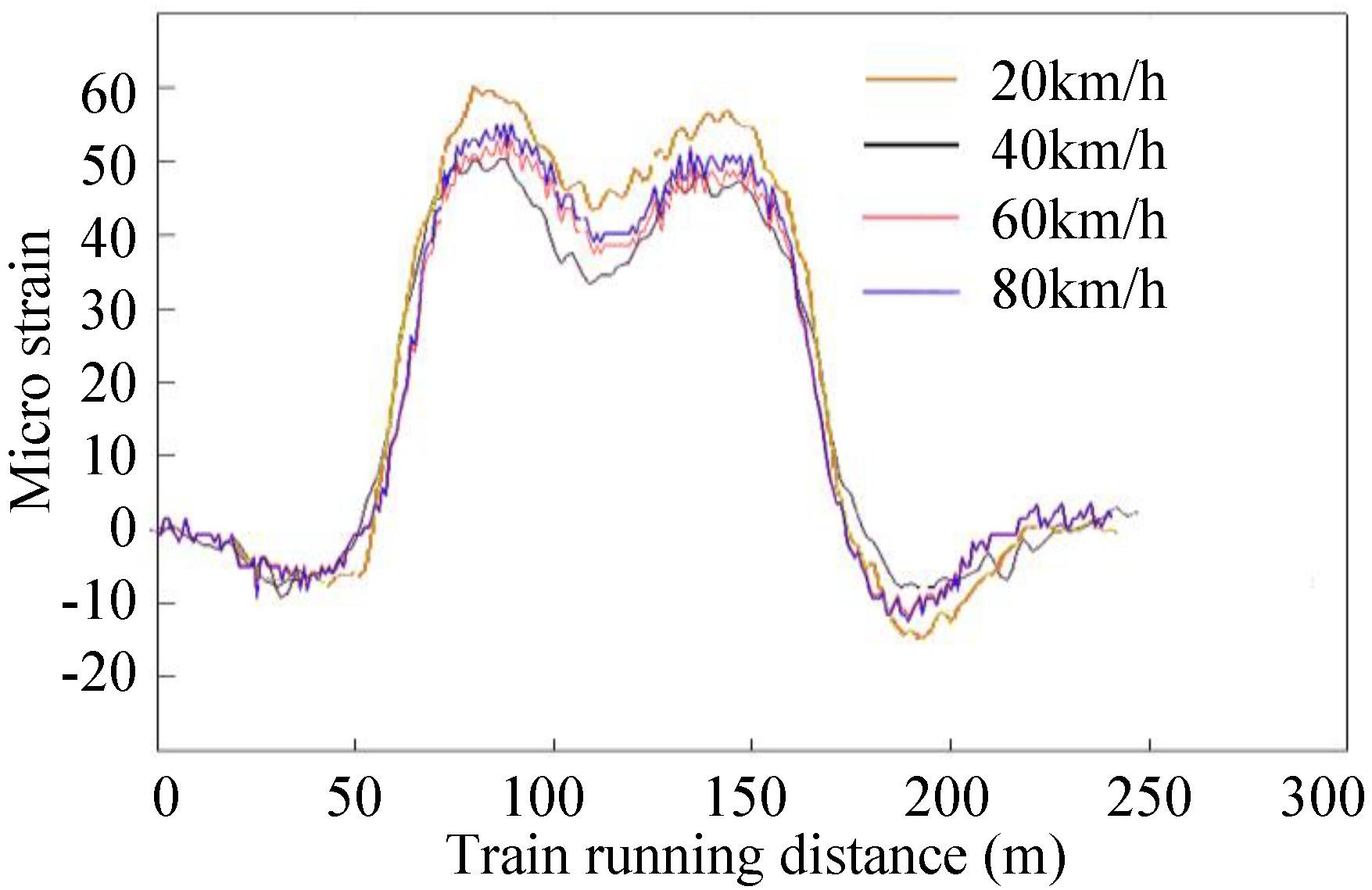
4.2. Dynamic Test Results
5. Analysis of Impact Factors
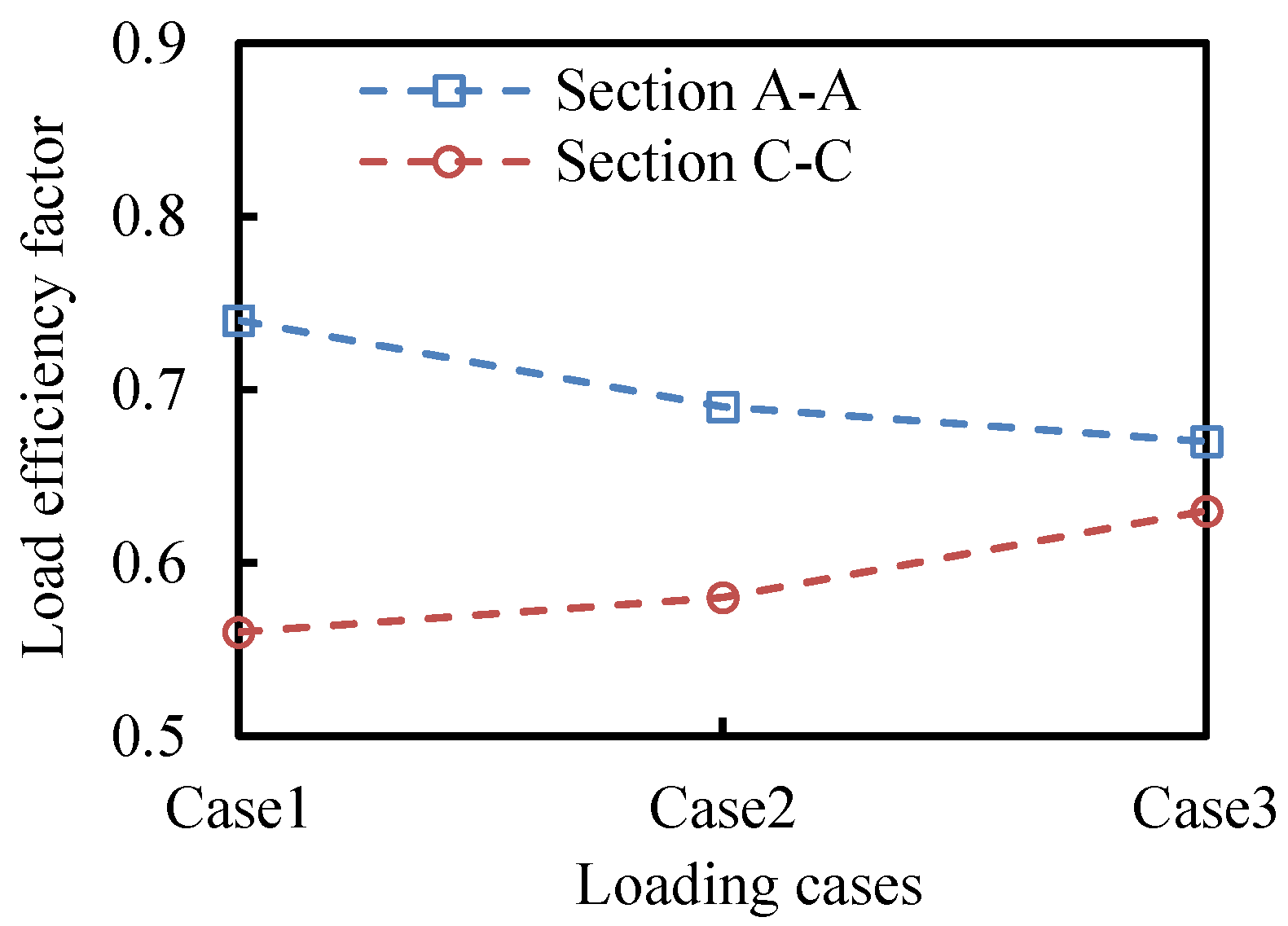
5.1. Definition of Impact Factor
5.2. Impact Factor Calcalated from Experrimental Deta
5.3. Comparison with the Bridge Design Code in China
6. Finite Element Model
6.1. Brideg Model
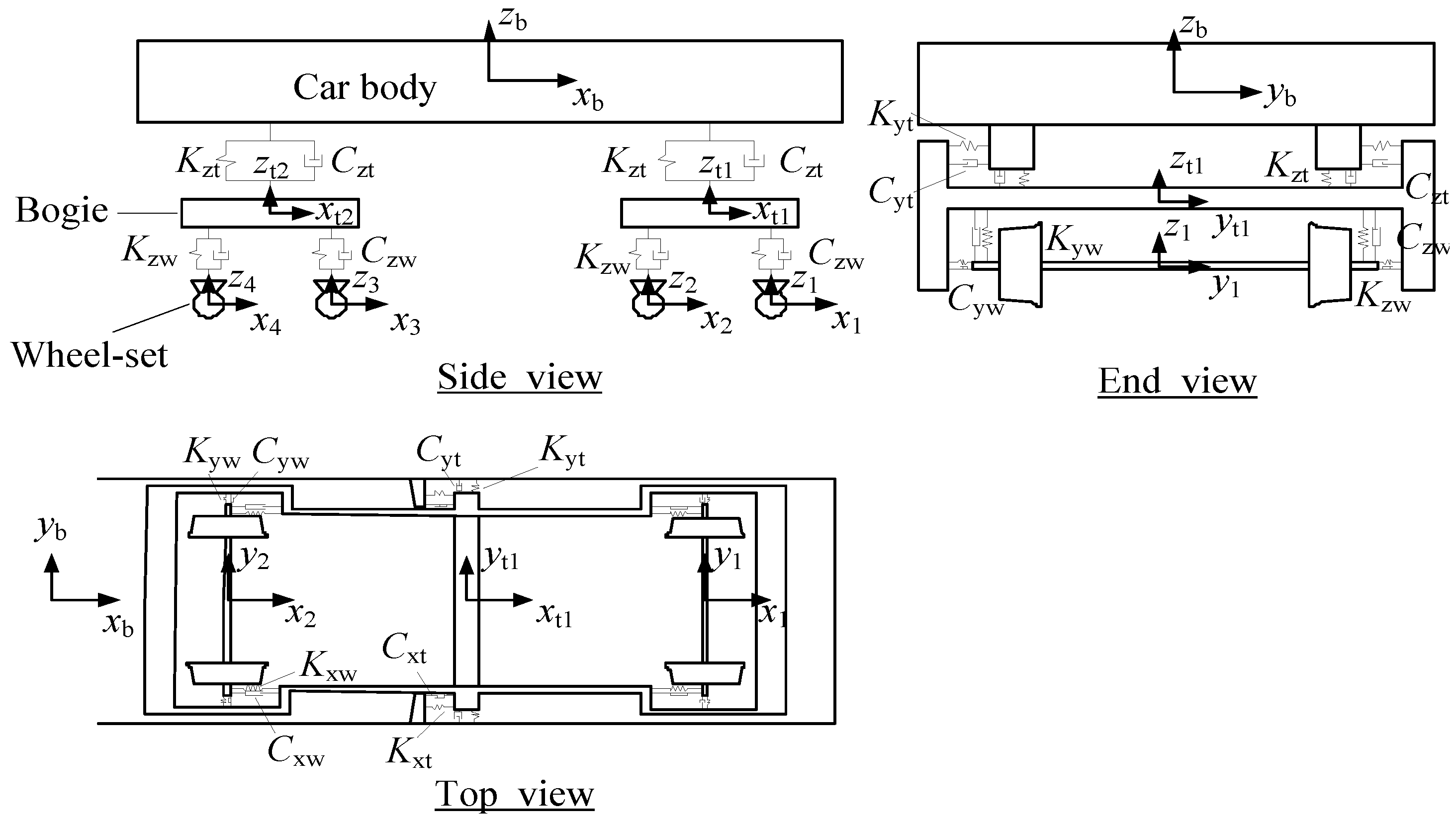
6.2. Vehicle Model
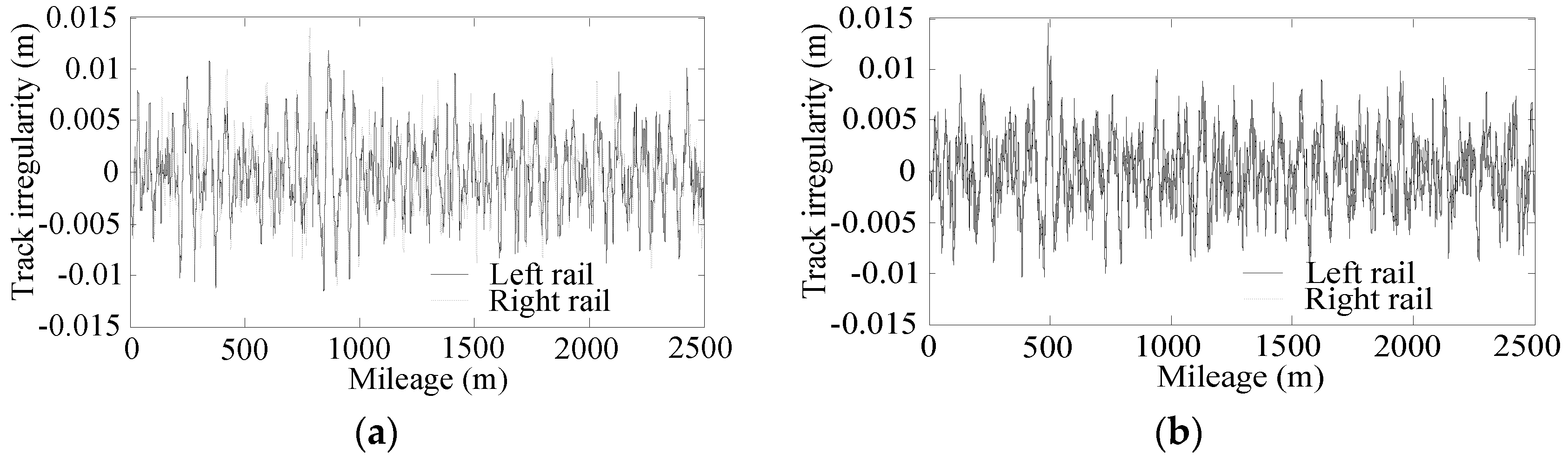
6.3. Track Irregularity
6.4. Train-Bridge Interation
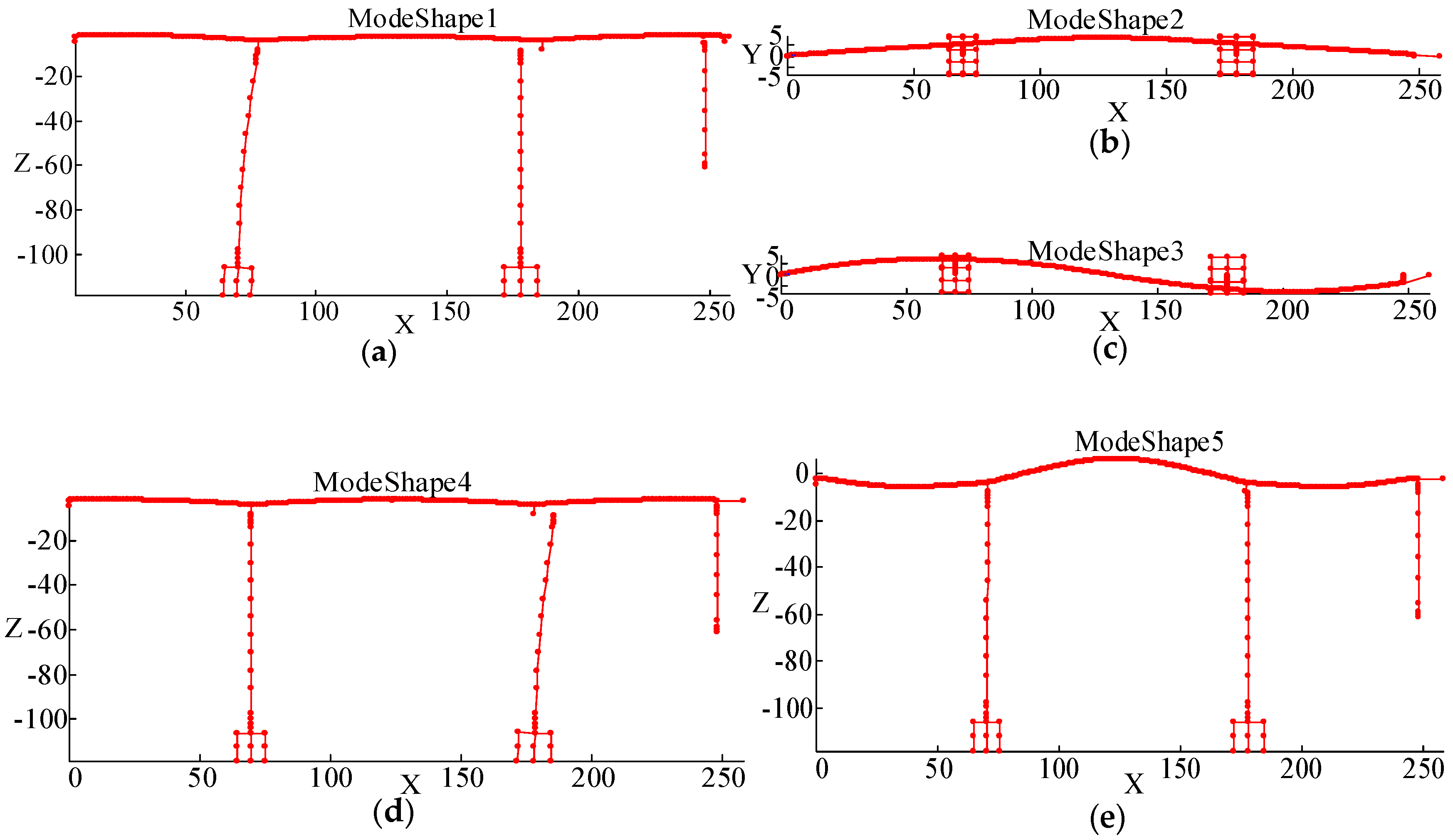
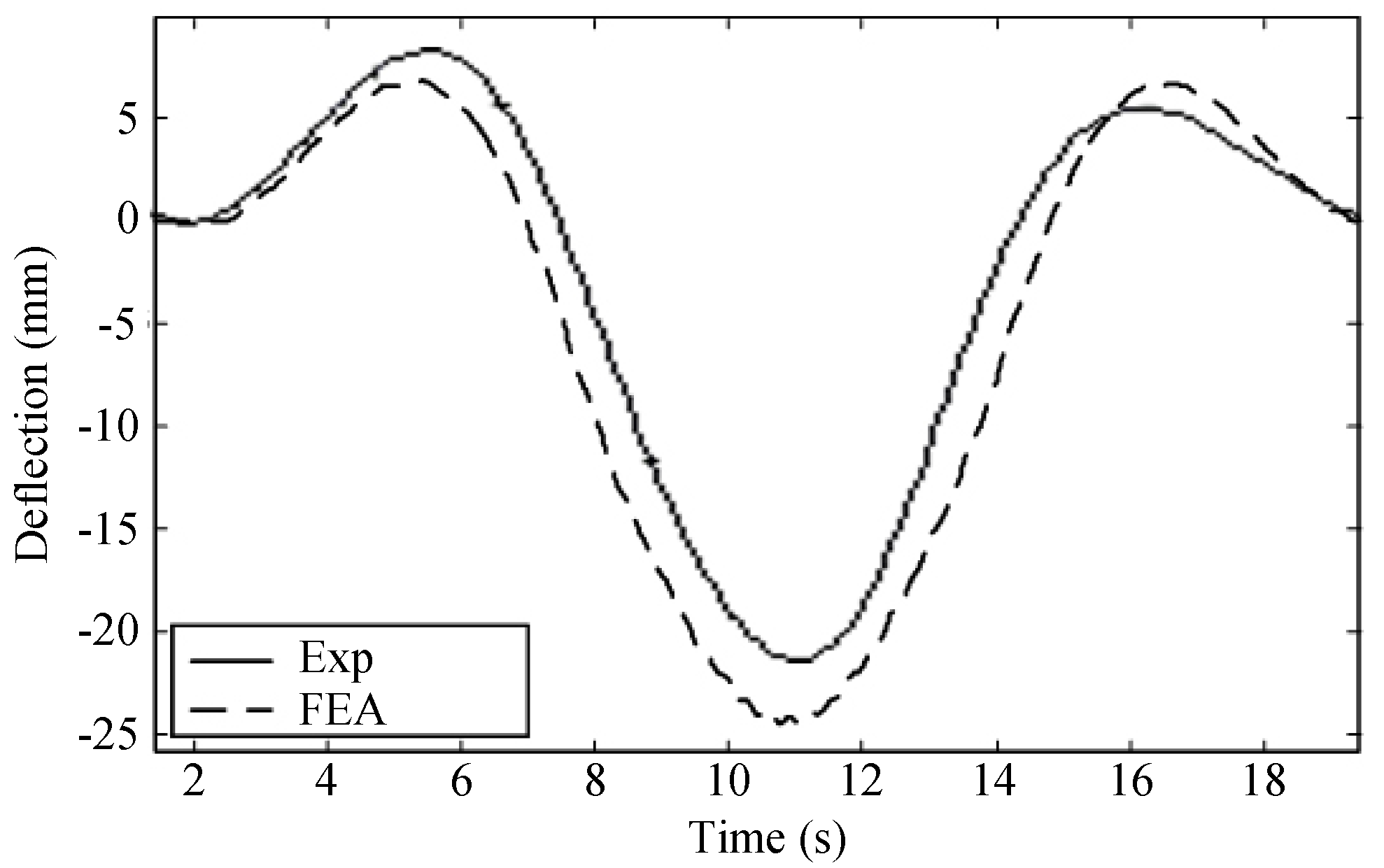
6.5. Model Validation
7. Analysis of Dynamic Effects of Train–Bridge System
8. Conclusions
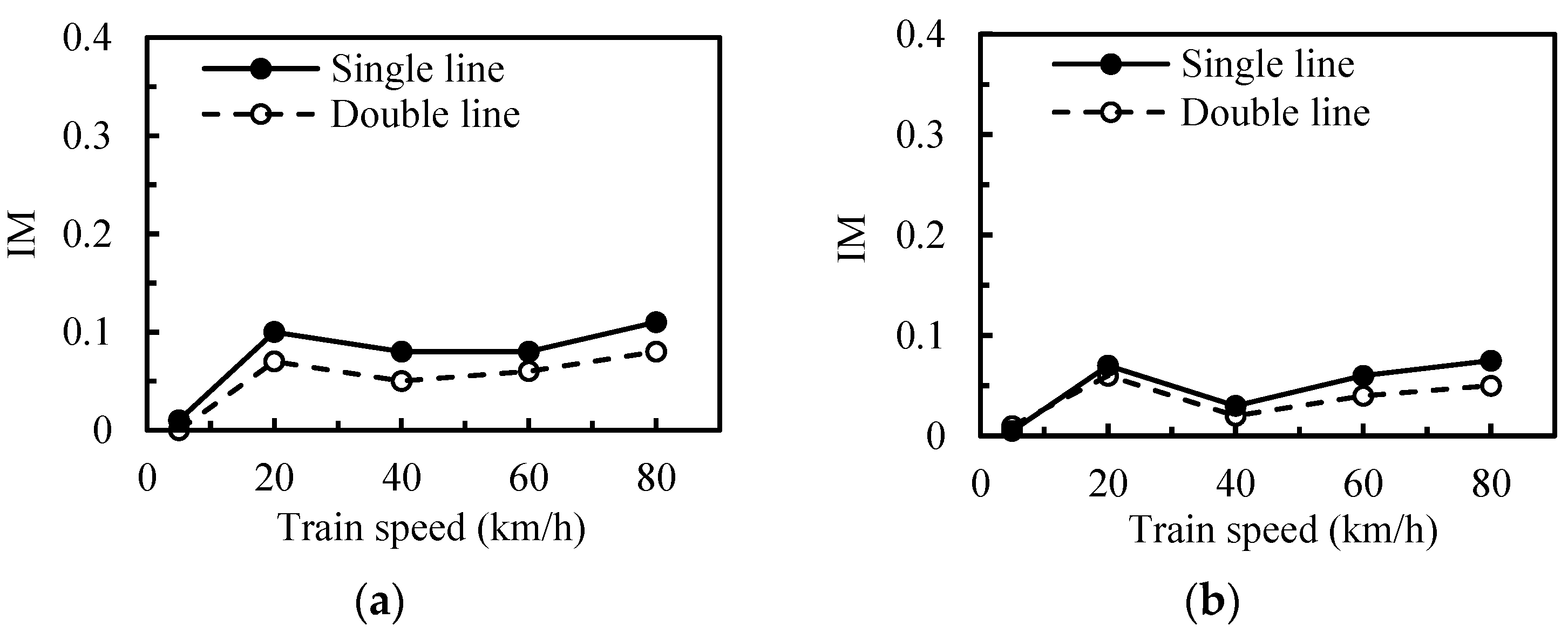
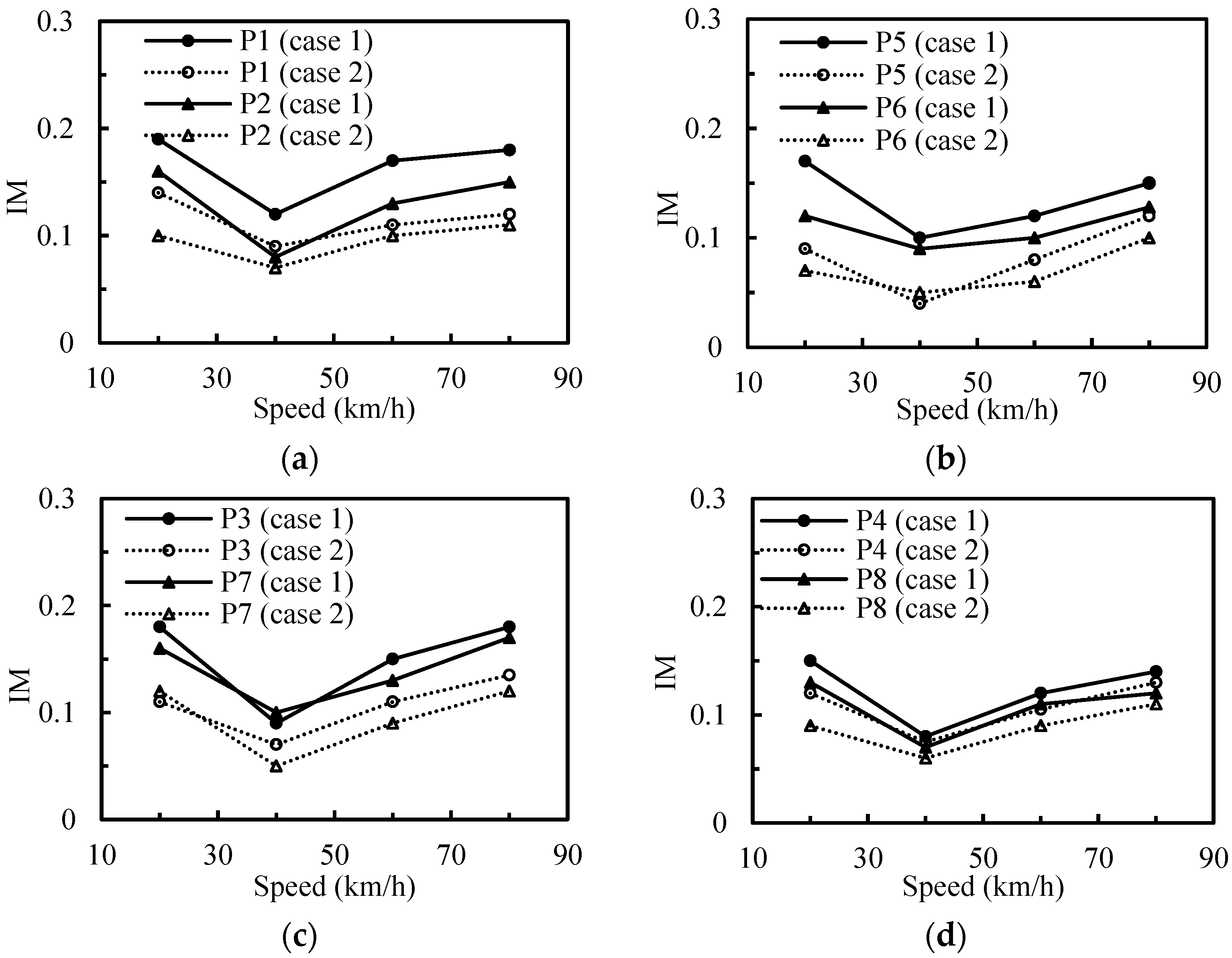
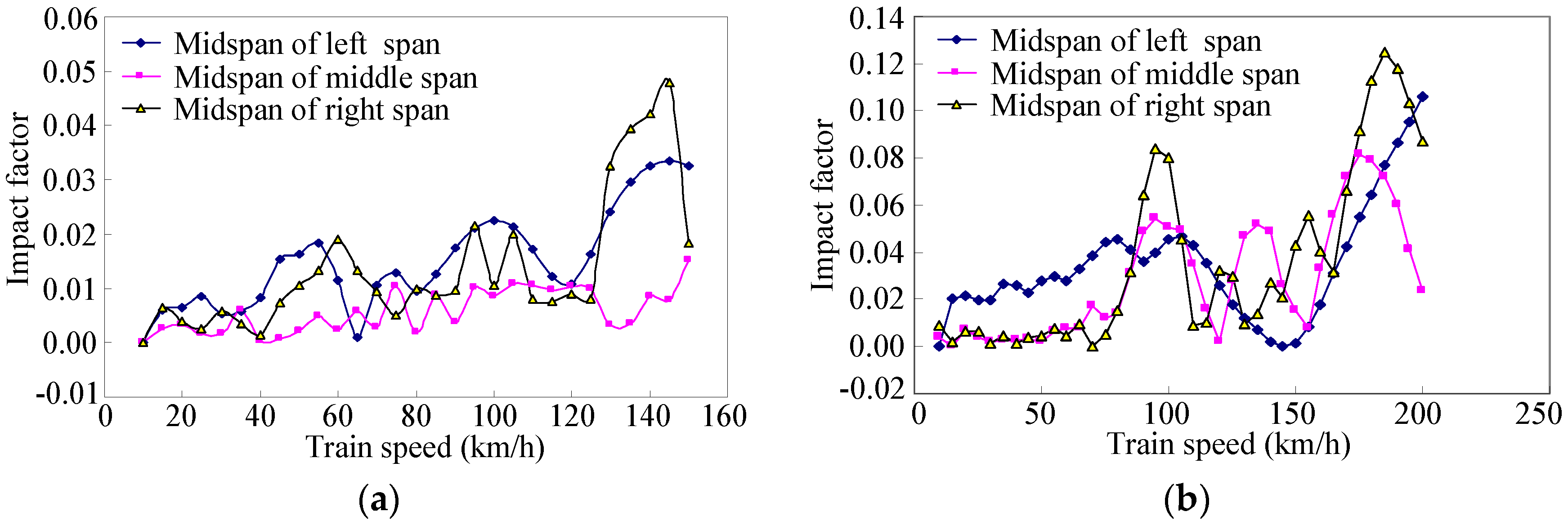
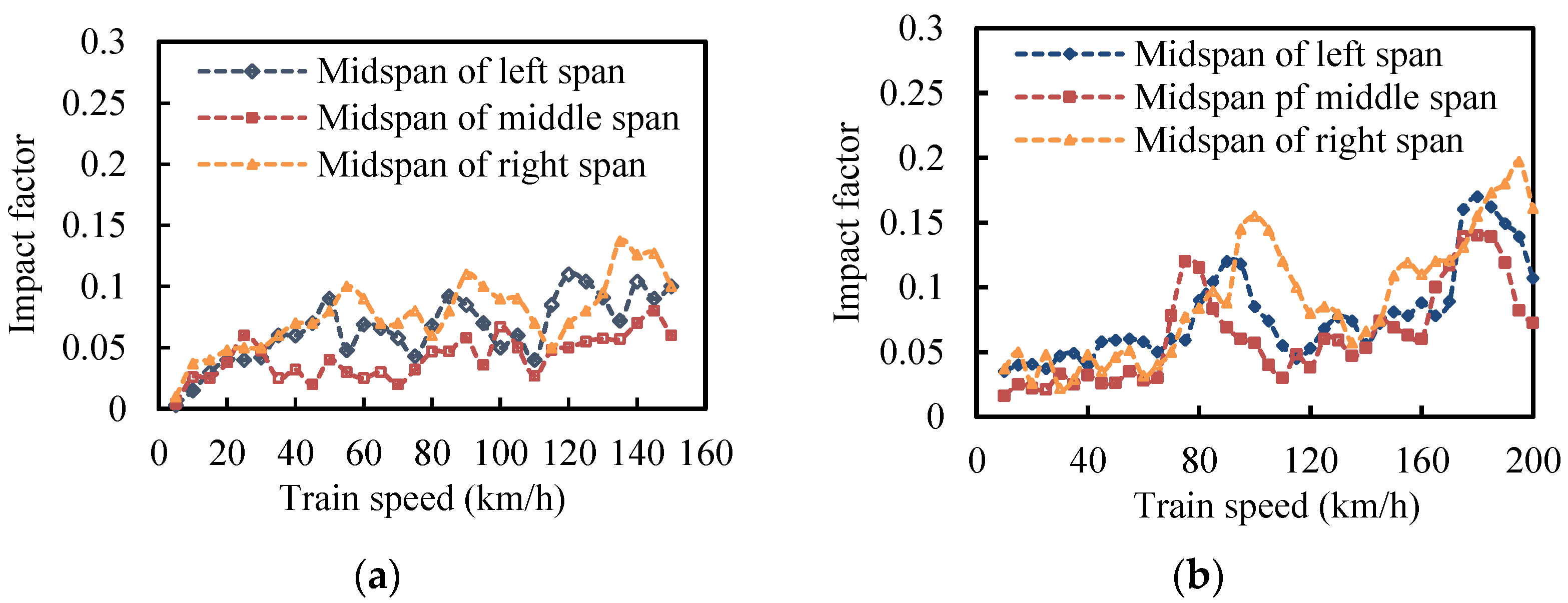
- The IMs from one train running on one track is greater than that from two trains running on two tracks. The average value of IMs of the central span is 0.15 under one running train condition and 0.11 under two running trains condition. A peak IM (0.19) occurred when one train travelled on the bridge at 20 km/h, which suggests that a resonance occurred. The IM is insensitive to the train speed. But from the overall development law, with the increase of train speed, the IM increases. The weight of vehicles has a significant influence on the IMs. The IM decreases with the increase of the weight of vehicles. Meanwhile, the IMs were found to depend strongly on the track irregularity, the track irregularity will greatly increase the IMs. Resonance may occur at multiple speeds, and will be affected by the track surface conditions. The IM calculated from deflections is smaller than the IM calculated from strains. So it is not reasonable to assign the same IM for different load effects. The IM calculated from strains reflects the local dynamic performance of the structure, and the IM calculated from deflections reflects the overall dynamic performance of the structure.
- The IMs obtained by experimental and numerical analysis are greater than the design value specified in the bridge code, which indicates that the bridge code underestimates the impact effect of the train on the bridge. Therefore, the authors recommend the design value of the IM should be properly improved in the bridge design. Because the long-term operation of the bridge will lead to the deterioration of the track surface conditions, and the train-bridge interaction will be more intense, which may seriously aggravate the impact of train on bridges. Thus maintaining good track surface conditions is very important for ensuring the safe operation of bridges. Moreover, when a component of bridge structures needs to be independently designed, the strain IM should be adopted.
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Xia, C.Y.; Lei, J.Q.; Zhang, N.; Xia, H.; Roeck, G.D. Dynamic analysis of a coupled high-speed train and bridge system subjected to collision load. J. Sound Vib. 2012, 331, 2334–2347. [Google Scholar] [CrossRef]
- Jung, H.; Kim, G.; Park, C. Impact factors of bridges based on natural frequency for various superstructure types. KSCE J. Civ. Eng. 2013, 17, 458–464. [Google Scholar] [CrossRef]
- Wang, L.B.; Jiang, P.W. Research on the computational method of vibration impact coefficient for the long-span bridge and its application in engineering. J. Vibroeng. 2016, 18, 394–407. [Google Scholar]
- Xu, T.; Castel, A. Modeling the dynamic stiffness of cracked reinforced concrete beams under low-amplitude vibration loads. J. Sound Vib. 2016, 368, 135–147. [Google Scholar] [CrossRef]
- Wei, K.; Myers, A.T.; Arwade, S.R. Dynamic effects in the response of offshore wind turbines supported by jackets under wave loading. Eng. Struct. 2017, 142, 36–45. [Google Scholar] [CrossRef]
- Gou, H.Y.; Wang, W.; Shi, X.Y.; Pu, Q.H.; Kang, R. Behavior of steel-concrete composite cable anchorage system. Steel Compos. Struct. 2018, 26, 115–123. [Google Scholar]
- Gao, Q.F.; Wang, Z.L.; Li, J.; Chen, C.; Jia, H.Y. Dynamic load allowance in different positions of the multi-span girder bridge with variable cross-section. J. Vibroeng. 2015, 17, 2025–2039. [Google Scholar]
- Gu, G.; Kapoor, A.; Lilley, D.M. Calculation of dynamic impact loads for railway bridges using a direct integration method. Proc. Inst. Mech. Eng. F -J. 2008, 222, 385–398. [Google Scholar] [CrossRef]
- Gou, H.Y.; Shi, X.Y.; Zhou, W.; Cui, K.; Pu, Q.H. Dynamic performance of continuous railway bridges: Numerical analyses and field tests. Proc. Inst. Mech. Eng. F -J. 2018, 232, 936–955. [Google Scholar] [CrossRef]
- Majka, M.; Hartnett, M. Effects of speed, load and damping on the dynamic response of railway bridges and vehicles. Comput. Struct. 2008, 86, 556–572. [Google Scholar] [CrossRef]
- Yin, C.; Wei, B. Numerical simulation of a bridge-subgrade transition zone due to moving vehicle in Shuohuang heavy haul railway. J. Vibroeng. 2013, 15, 1041–1047. [Google Scholar]
- Lee, H.H.; Jeon, J.C.; Kyung, K.S. Determination of a reasonable impact factor for fatigue investigation of simple steel plate girder railway bridges. Eng. Struct. 2012, 36, 316–324. [Google Scholar] [CrossRef]
- Hamidi, S.A.; Danshjoo, F. Determination of impact factor for steel railway bridges considering simultaneous effects of vehicle speed and axle distance to span length ratio. Eng. Struct. 2010, 32, 1369–1376. [Google Scholar] [CrossRef]
- Gou, H.Y.; Long, H.; Bao, Y.; Chen, G.D.; Pu, Q.H.; Kang, R. Experimental and numerical studies on stress distributions in girder-arch-pier connections of long-span continuous rigid frame arch railway bridge. J. Bridge Eng. 2018, in press. [Google Scholar] [CrossRef]
- Gou, H.Y.; He, Y.N.; Zhou, W.; Bao, Y.; Chen, G.D. Experimental and numerical investigations of the dynamic responses of an asymmetrical arch railway bridge. Proc. Inst. Mech. Eng. F -J. 2018. [Google Scholar] [CrossRef]
- Gou, H.Y.; Long, H.; Bao, Y.; Chen, G.D.; Pu, Q.H. Dynamic behavior of hybrid framed arch railway bridge under moving trains. Steel Compos. Struct. 2018, in press. [Google Scholar]
- Ding, Y.; Wang, G. Evaluation of dynamic load factors for a high-speed railway truss arch bridge. Shock Vib. 2016, 2016, 5310769. [Google Scholar]
- Kaloop, M.R.; Hu, J.W.; Elbeltagi, E. Evaluation of High-speed Railway Bridge based on Nondestructive Monitoring System. Appl. Sci. 2016, 6, 24. [Google Scholar] [CrossRef]
- Gou, H.Y.; Zhou, W.; Chen, G.D.; Bao, Y.; Pu, Q.H. In-situ test and dynamic analysis of a double-deck tied-arch bridge. Steel Compos. Struct. 2018, 27, 161–175. [Google Scholar]
- Flener, E.B.; Karoumi, R. Dynamic testing of a soil–steel composite railway bridge. Eng. Struct. 2009, 31, 2803–2811. [Google Scholar] [CrossRef]
- Khan, E.; Linzell, D.G.; Frankl, B.A.; Lobo, J.A.; Lozano, S. Field Measured Dynamic Effects and Load Distribution in a Prestressed Concrete Light Rail Bridge. In Proceedings of the Joint Rail Conference, Columbia, SC, USA, 12–15 April 2016. [Google Scholar]
- Research Institute of Highway Ministry. Test Method of Long Span Concrete Bridge; Research Institute of Highway Ministry: Beijing, China, 1982. (In Chinese) [Google Scholar]
- Chinese Railway Ministry. Fundamental Code for Design on Railway Bridge and Culvert; Chinese Railway Ministry: Beijing, China, 2005. (In Chinese)
- Senthilvasan, J.; Thambiratnam, D.P.; Brameld, G.H. Dynamic response of a curved bridge under moving truck load. Eng. Struct. 2002, 24, 1283–1293. [Google Scholar] [CrossRef]
- Aluri, S.; Jinka, C.; GangaRao, H.V. Dynamic response of three fiber reinforced polymer composite bridges. J. Bridge Eng. 2005, 10, 722–730. [Google Scholar] [CrossRef]
- Li, H.; Wekezer, J.; Kwasniewski, L. Dynamic response of a highway bridge subjected to moving vehicles. J. Bridge Eng. 2008, 13, 439–448. [Google Scholar] [CrossRef]
- Szurgott, P.; Wekezer, J.; Kwasniewski, L.; Siervogel, J.; Ansley, M. Experimental assessment of dynamic responses induced in concrete bridges by permit vehicles. J. Bridge Eng. 2011, 16, 108–116. [Google Scholar] [CrossRef]
- Ashebo, D.B.; Chan, T.H.T.; Yu, L. Evaluation of dynamic loads on a skew box girder continuous bridge Part II: Parametric study and dynamic load factor. Eng. Struct. 2007, 29, 1064–1073. [Google Scholar] [CrossRef]
- Huang, D. Dynamic and impact behavior of half-through arch bridges. J. Bridge Eng. 2005, 10, 133–141. [Google Scholar] [CrossRef]
- Moghimi, H.; Ronagh, H.R. Impact factors for a composite steel bridge using non-linear dynamic simulation. Int. J. Impact Eng. 2008, 35, 1228–1243. [Google Scholar] [CrossRef]
- Liu, C.L.; Yin, X.Q.; Lin, G.; Hu, Z.Q. Seismic response analysis of a time-varying high speed train-rail-bridge system based on ANSYS. J. Vib. Shock 2013, 32, 58–64. [Google Scholar]
- Johnson, K.L. Contact mechanics. J. Tribol. 1986, 108, 464. [Google Scholar] [CrossRef]
- Kaker, J.J. Three-Dimensional Elastic Bodies in Rolling Contact; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1990; Volume 2, p. 255. [Google Scholar]
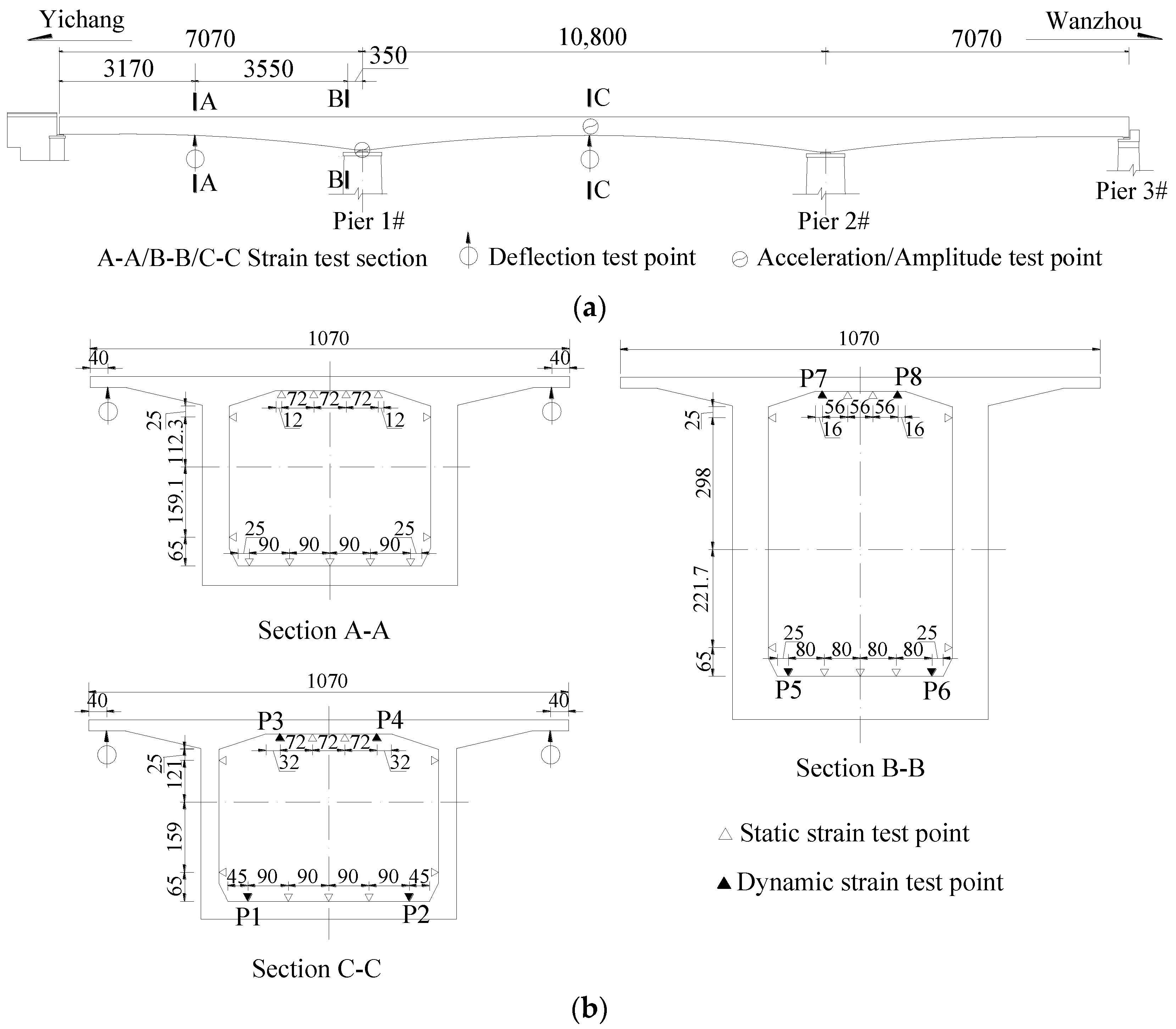
| Location | IM from Experimental Data | IM from Bridge Code | |
|---|---|---|---|
| Deflection IM | Strain IM | ||
| Section A-A | 0.110 | — | 0.087 |
| Section B-B | — | 0.17 | 0.087 |
| Section C-C | 0.070 | 0.19 | 0.087 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gou, H.; Zhou, W.; Bao, Y.; Li, X.; Pu, Q. Experimental Study on Dynamic Effects of a Long-span Railway Continuous Beam Bridge. Appl. Sci. 2018, 8, 669. https://doi.org/10.3390/app8050669
Gou H, Zhou W, Bao Y, Li X, Pu Q. Experimental Study on Dynamic Effects of a Long-span Railway Continuous Beam Bridge. Applied Sciences. 2018; 8(5):669. https://doi.org/10.3390/app8050669
Chicago/Turabian StyleGou, Hongye, Wen Zhou, Yi Bao, Xiaobin Li, and Qianhui Pu. 2018. "Experimental Study on Dynamic Effects of a Long-span Railway Continuous Beam Bridge" Applied Sciences 8, no. 5: 669. https://doi.org/10.3390/app8050669
APA StyleGou, H., Zhou, W., Bao, Y., Li, X., & Pu, Q. (2018). Experimental Study on Dynamic Effects of a Long-span Railway Continuous Beam Bridge. Applied Sciences, 8(5), 669. https://doi.org/10.3390/app8050669






