Abstract
The aim of this work was to introduce new ways to model the I-V characteristic of a photovoltaic (PV) cell or PV module using straight lines and Bézier curves. This is a complete novel approach, Bézier curves being previously used mainly for computer graphics. The I-V characteristic is divided into three sections, modeled with lines and a quadratic Bézier curve in the first case and with three cubic Bézier curves in the second case. The result proves to be accurate and relies on the fundamental points usually present in the PV cell datasheets: (the open circuit voltage), (the short circuit current), (the maximum power corresponding voltage) and (the maximum power corresponding current), and the parasitic resistances (shunt resistance at ) and (series resistance at ). The proposed algorithm completely defines all the implied control points and the error is analyzed. The temperature and irradiance influence is also analyzed. The model is also compared using the least squares fitting method. The final validation shows how to use Bézier cubic curves to accurately represent the I-V curves of an extensive range of PV cells and arrays.
1. Introduction
The forecast of the total photovoltaic (PV) installations, offered by Bloomberg New Energy Finance (BNEF) predicts an optimistic growth at 111 GW in 2018, rising to 121 GW in 2019, along with a polysilicon factory growth boom and module prices drop to US$ 0.30/W [1,2]. This robust growth explains the high interest in PV research, modeling, and simulation–along with design and development of PV equipment.
The electrical characteristics of the PV cell and PV modules have been of interest for several decades, and different models have been proposed. Phang and Chan [3] were among the first to propose a solution for PV cell parameter extraction. Garrido-Alzar [4] uses a double exponential model to extract the PV cell parameters using the experimental I-V curve. Villalva et al. [5] developed an algorithm to find the parameters defining the I-V characteristic for the single diode model of a PV cell, using the Newton-Raphson method and imposing a minimum error threshold for the maximum power point. Babu and Gurjar [6] introduced a simplified two-diode model for the PV module, while Cubas et al. [7] used the Lambert W-Function for finding the solar panel equivalent circuit parameters and also proposed an LTSpice model according to their findings. Temperature influence has been studied by Chander et al. [8]. Ishaque and Salam [9] use differential evolution to find the PV modules parameters.
Franzitta et al. provided extensive studies of the most widely used models both in single diode case [10] and for the double-diode version [11], introducing a criterion for rating the accuracy and usability of the analyzed models. In our previous paper [12], we proposed a complete SPICE model including all the parameters variation and selfheating. In a recent work, Cuce et al. [13] claim a good accuracy for their electrical model for a PV module and they also discuss energy and exergy efficiency as a reliable substitute for the fill factor. All the aforementioned works use an electrical model to describe the behavior of the circuit and rely on a specific circuit to generate the I-V characteristic of the PV cell or module.
This paper introduces a new approach. This time, the cell or module are not involved at the electrical level, being defined by just the specific points and by the parallel and series resistances and , specified at and , respectively. Careful inspection of the typical I-V characteristic of the PV module or PV cell (Figure 1a,b) shows a similar pattern in all curves. Our aim was to find a way to model it using smooth curves and the datasheet information currently available.
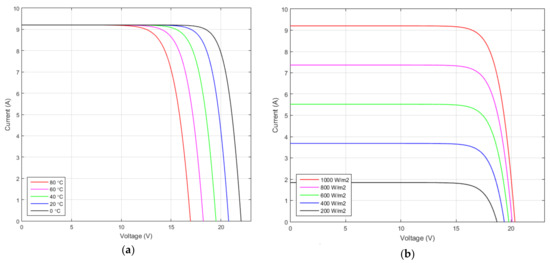
Figure 1.
Typical photovoltaic (PV) module I-V characteristics, with 30 cells connected in series. (a) at different temperatures (0–80 °C); (b) at different irradiances (200–1000 W/m2).
Bernstein polynomials have been studied since the beginning of the 20th century and they form the foundation for Bézier curves [14]. The core applications for graphics came first in 1959 when the French mathematician Paul de Casteljau developed an algorithm able to evaluate a family of specific curves at Citroën. In 1962 the French engineer Pierre Bézier also used them to design automobile bodies at Renault and afterwards they achieved wide acceptance [15].
Bézier curves are largely used in computer graphics [16,17] and also in the time domain for smoothing the trajectory of the robotic arms, for an accurate gluing or welding path or for trajectory generation [18]. Further development for shape representation was proposed by Jalba et al. [19].
The current proposal analyses the use of Bézier curves [20] in order to accurately represent the I-V characteristic of a PV cell or module. Although Bézier curves are commonly used as 2D curves (which are usually not functions) [21], our approach uses such curves to approximate an I-V characteristic (a function). A complete mathematical solution is provided, separately validated for a PV cell and a PV module and the error is analyzed. The results are also studied for different temperature and irradiances and finally compared with the ones offered by the least squares fitting method. In depth analysis of Bézier cubic curves fitting for 18 PV arrays and cells (from various manufacturers and different technologies) is also performed.
There are other possible approaches, for example spline fitting [22,23], well known Hermite interpolation, or spiral curve fitting [24]. Our aim was solely the Bézier curves.
The remainder of this paper is organized as follows: Section 2 briefly analyzes the definition of the quadratic and cubic Bézier curves and their equations, focusing on the basic knowledge needed in the subsequent paragraphs. Section 3 deals with the information usually provided by the PV cell or module manufacturers in their datasheets. The proposed models are covered in Section 4, with Section 4.1. introducing the approximation with two segments and one quadratic Bézier curve, while Section 4.2. deals with the better approximation based on three Bézier cubic curves. The models are rated at the reference temperature, 25 °C. The results are also compared with the least squares fitting method in Section 4.3. In Section 4.4. the influence of the external parameters is analyzed. The proposal is verified in Section 4.5. against a large range of PV cells and modules and the results show a good fit. Discussion and conclusions are provided in the next Sections.
2. Definition of the Bézier Curves
A quadratic Bézier curve (Figure 2) can be specified by three control points [15]: the curve goes through the ends and and approximates .
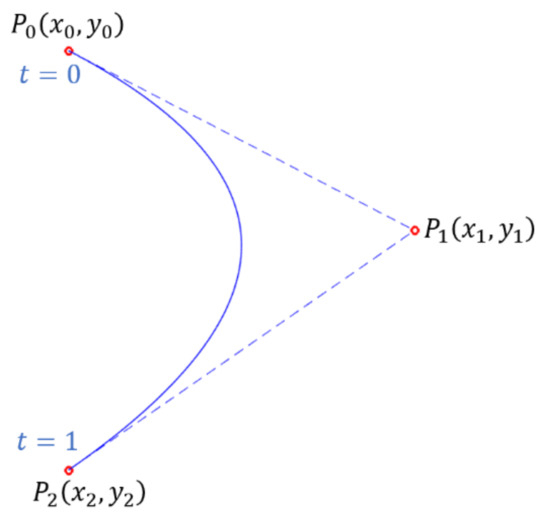
Figure 2.
A quadratic Bézier curve representation. and are the end points, the control point is approximated and the curve is tangent to and segments at and respectively.
The curve equation is as follows [20]:
where varies between 0 and 1. Equation (1) can be expressed for the and coordinates:
The derivative of (1) is:
At the end points, (3) becomes (4):
A cubic Bézier curve (Figure 3) can be specified by four control points [15]: the curve goes through the ends and and approximates and . The analytical expression of the curve is a cubic polynomial. The curve is tangent at to and at to .
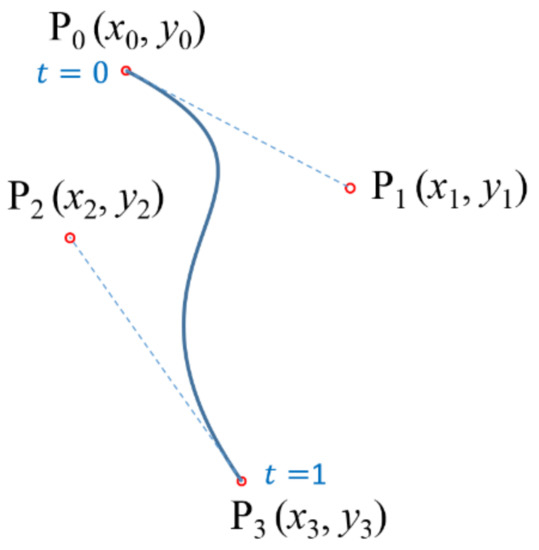
Figure 3.
A cubic Bézier curve representation. and are the end points, the control points and are approximated, and the curve is tangent to and segments at and respectively.
The equation for the Bézier cubic curve is [20]:
The previous equation can be expressed for the and coordinates:
The derivative of (5) is:
At the end points, (7) becomes (8):
3. Materials and Methods
The first PV cell used in our work is a high efficiency, silicon monocrystalline 156 × 156 mm2 cell [25] and has the main characteristics summarized in Table 1.

Table 1.
PV Cell main specifications on STC (1000 W/m2, AM 1.5, 25 °C).
The MSMD290AS-36_EU Monocrystalline PV module formerly manufactured by MünchenSolar Germany [26] has been well documented and studied by Cubas et al. [6]. Its main electrical data is listed in Table 2 and this information is used in Section 4.4. to evaluate the influence of the temperature and irradiance to our Bézier curves based model.

Table 2.
MSMD290AS-36_EU Module main specifications on STC (1000 W/m2, AM 1.5, 25 °C).
For studying and representing Bézier curves, an interesting application which allows draggable control points was developed by Mugnaini [27]. For computing the coordinates on the curves we used the Kronecker tensor product found as in [28]. An example for the Bézier least square fitting method is given in [29].
4. Results
It must be stressed that all the physical actual values involved in Section 4.1., Section 4.2., and Section 4.3. are specified at 25 °C, being reference values. The irradiance is also standard (1000 W/m2). As it is demonstrated in Section 4.4., the same method is suitable for different temperatures and irradiances.
4.1. I-V Characteristic Approximation with Two Segments and a Quadratic Bézier Curve
The first approximation implies five control points: and and is made of two segment lines and and one quadratic Bézier curve defined by the endpoints and and the control point (Figure 4).
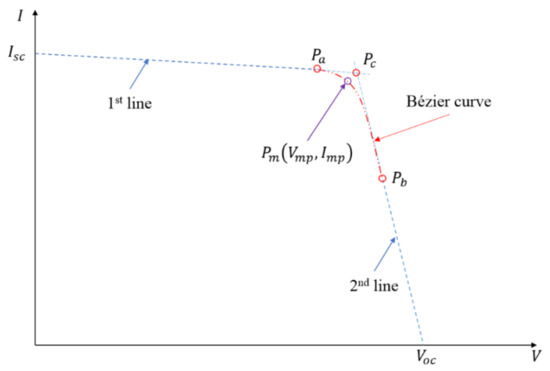
Figure 4.
Projected PV cell I-V characteristic approximation with two straight line segments and one quadratic Bézier curve.
It has already been proven [3] that the slopes of the lines can be written as (9) and (10):
Thus, the equation for first line is (11):
By choosing in the linear region (eg ), one can find from the above equation, so is completely defined.
For the second line, the next equation is valid (12):
The control point has therefore the coordinates defined by (13):
For , it must be emphasized that its position is on the end of the curve, a realistic value being . The maximum power point is positioned on the second curve, so solving (14) gives :
Replacing the positive solution for in (2) yields as in (15):
Now all the control points of the plot are completely defined. The results are summarized in Table 3. The application code written for the coordinate finding can be retrieved from [30].

Table 3.
The control point coordinates when using two lines and one quadratic Bézier curve.
The final plot is represented in Figure 5, where one can observe an excellent correspondence between the actual PV cell I-V characteristic, represented with black dots and the segment (blue line), a fair correlation for the second range, approximated by the Bézier quadratic curve (red line) and some modest results in the third region (magenta line).
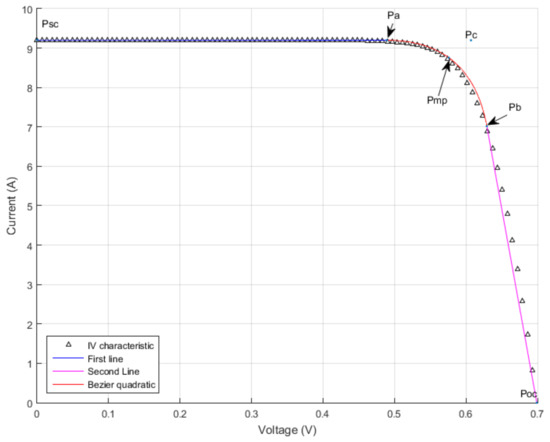
Figure 5.
PV cell I-V characteristic approximation with two straight lines and one quadratic Bézier curve—results.
The same conclusion arises from Figure 6, where the relative error has been plotted. It is worth mentioning that although the relative error is quite high above 0.64 V , the absolute error is in fact less than 0.7 A in a region where the cell normally should not operate.
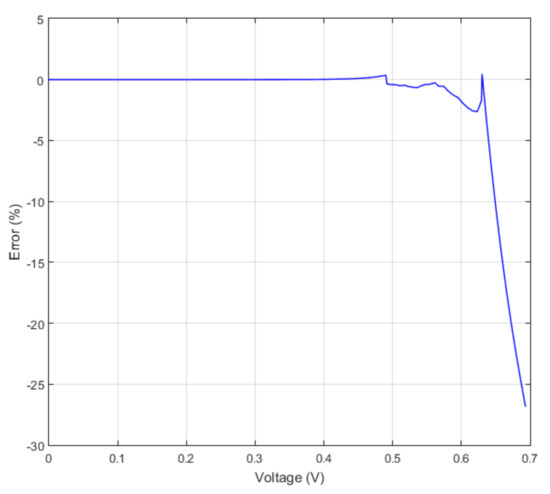
Figure 6.
Approximation errors are high over 0.64 V.
Looking for a more accurate model is the reason we came up with the second scenario, where the I-V characteristic is entirely modeled with cubic Bézier curves.
4.2. I-V Characteristic Approximation with Three Cubic Bézier Curves
In order to have a general solution, we analyzed the case where all three regions are covered with cubic Bézier curves. This implies 12 control points (Figure 7), i.e. 24 coordinates to be found.
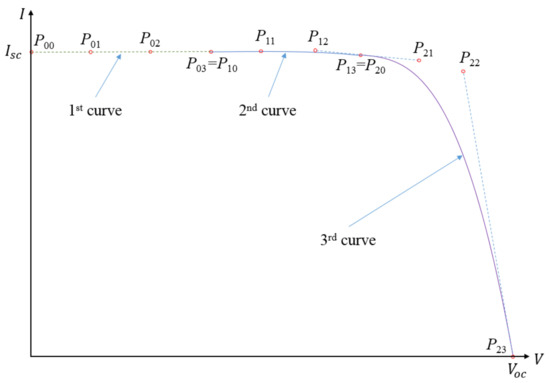
Figure 7.
Projected PV cell I-V characteristic approximation with three cubic Bézier curves.
The first curve, represented in Figure 8, is described by the control points and . It turns out that the linear approximation of the first region of the I-V curve has an error below 0.5% if . During various simulations we also discovered that all points can be evenly arranged, with . This leads to and . For the y coordinates, , with . Now the first curve is completely defined.
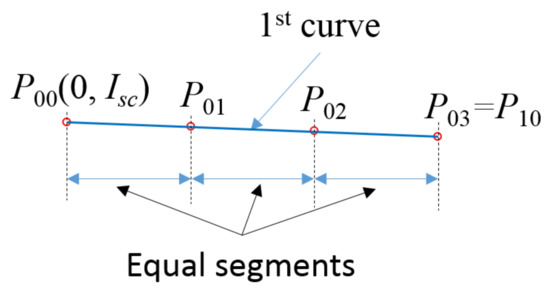
Figure 8.
First Bézier curve with the associated control points. The slope is exaggerated for a better understanding.
The second curve (Figure 7) is described by the control points and . We observed that offers a very good fit of the curve for this type of PV cell. With the same evenly arrangement for the x coordinates, , with . is also located in the linear region of the I-V curve, so . This leaves and as unknowns at this stage.
The third curve (Figure 7) is described by the control points and . Using the same assumptions as for the second curve, , with . It is obvious that and . The segment is tangent to the curve at the point , so . This leaves as an additional unknown at this step.
For continuity reasons, and segments belong to the same line. This implies that the derivatives of the second curve at and of the third curve at are equal (16):
Which means that:
The control point is placed on the second curve, so (18) can be written:
Solving the previous equation and keeping only the real solution for , (19) is also valid:
Finally, the graph also goes through the maximum power point , yielding Equation (20):
Keeping only the real solution for , (21) is also valid:
The linear system made of equations (17), (19), and (21) give the last three unknown coordinates , and . The results are summarized in Table 4. The application code written for coordinate finding can be retrieved from [30].

Table 4.
The control point coordinates when using three cubic Bézier curves.
Figure 9 shows the location of the control points with respect to the I-V characteristic of the PV cell. The control points and are collinear and with , are all placed on the I-V characteristic.
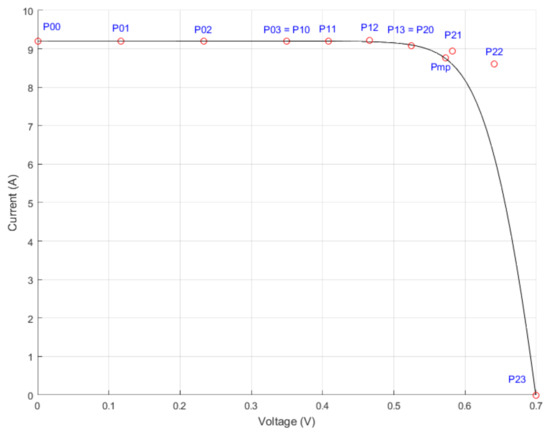
Figure 9.
PV cell I-V characteristic (black line, continuous) and the position of the 12 computed control points (red markers).
Figure 10 shows the modeled characteristic (red, green, and blue lines) overlapping in most areas with the practical I-V characteristic (black markers). The application code can also be retrieved from [30].
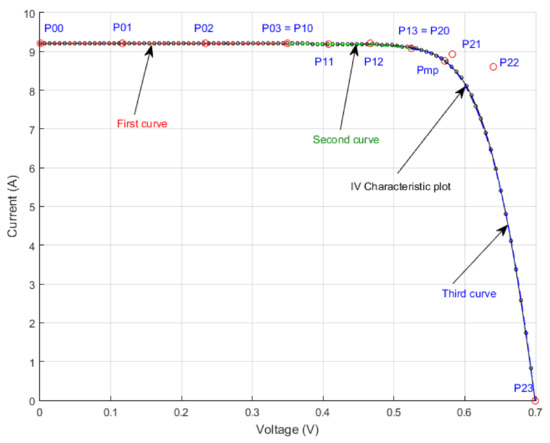
Figure 10.
I-V characteristic of a PV cell modeled with three cubic Bézier curves, defined by 12 control points.
The relative error of the Bézier modeled I-V characteristic against the actual data taken from [12] is shown in Figure 11. It must be emphasized that in the 0–0.94 range, the relative error is below 1%. Above 0.94 the absolute error is less than 72 mA, while the reference .
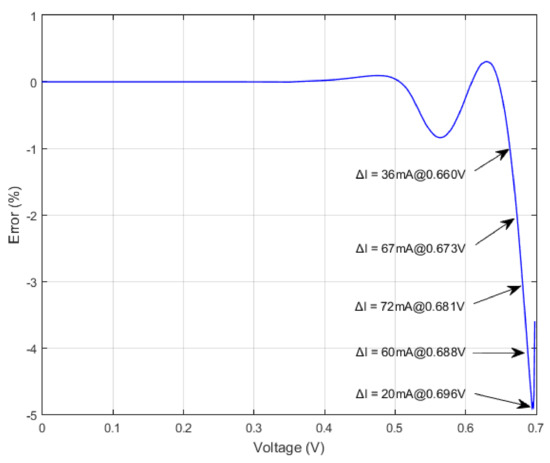
Figure 11.
The relative error of our model compared with the actual data. Good performance can be observed in the 0–0.5 V interval and near . Higher errors occur near for low output currents.
4.3. Data Fitting Using the Least Squares Method
Data fitting using the least squares method is a standard approach in data analysis [31,32]. A good overview of curve fitting using Bézier cubic curves in image processing is given by Shao et al. in [33], while Zhao et al. [34] extend this method using a genetic algorithm for parameter optimization for Bézier curve fitting. In Section 4.2. we have shown that for the studied PV cell, the best results arise when the coordinates of the middle end points are set at and respectively. A similar conclusion arises if the least squares method is used for the same cell modeling. Running the least squares method for the MSMD290AS-36_EU Monocrystalline PV module proved that the minimum error occurs when the control end points are set again at and respectively. Table 5 summarizes the data fitting results for the same PV cell used in Section 4.1. and Section 4.2., where the results from the two approaches are very close. The graphical representation of the date fitting is given in Figure 12, where only the endpoints are represented.

Table 5.
Control point coordinates comparison. On the left, the least squares method is used for computation, on the right the same values as in Table 4 are listed.
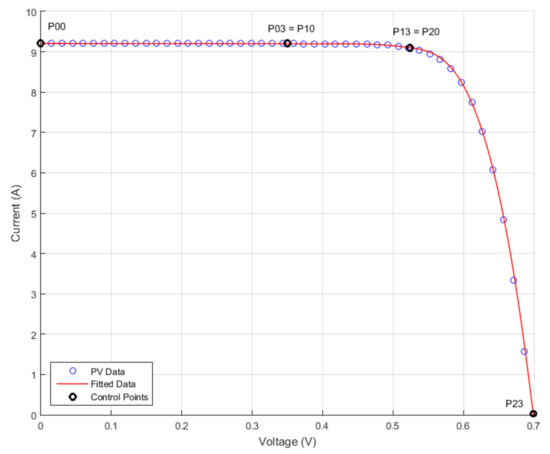
Figure 12.
Bézier approximation using the least squares method.
Figure 13 depicts the relative error of the modeled I-V characteristic compared with the actual data taken from our previous work [12]. In the range, the relative error is below 2%. Furthermore, above , the absolute error is less than 66 mA, while the reference short circuit current is 9.207 A.
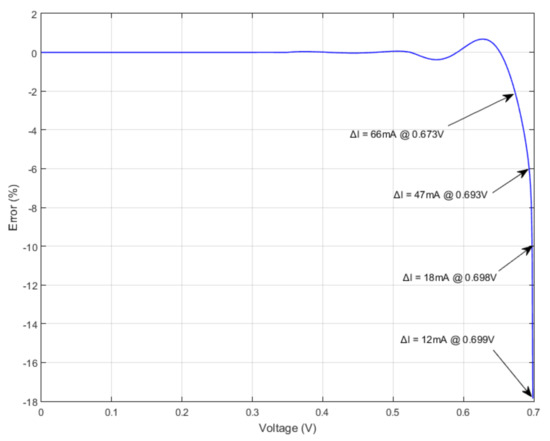
Figure 13.
The relative error of the least squares method Bézier based approximation compared with the actual data. The absolute error is also indicated.
4.4. Parameter Variation
In order to further validate the proposed method, in this section we analyze the temperature and irradiance influence for the MSMD290AS-36_EU Monocrystalline PV module. An extensive study of the parameter influence over the PV cell can be found in [12]. It is important to notice that the Bézier approximation is not related to any of the parameter variation, just to the specified points and the parasitic resistances and as already stated. The challenge becomes in this case the finding of the new position for the control points and the new values for the parasitic resistances.
Villalva et al. [5] accurately describe the short circuit current variation as in (22):
Ishaque and Salam [9] propose for the the following variation (23):
Equation (23) proved to be too conservative in this case, as larger variations were observed. A better approximation is the empirical law (24):
A possible way for defining behavior is suggested in [12], as in (25) with estimated as 8 for the best fit.
For , a linear variation law (26) is given in [12] with , again for the best fit:
Figure 14 shows the irradiance influence for the I-V module characteristic, where the approximated data using our proposed method is plotted with solid lines and the experimental data is represented with markers. and were computed using (22), (24–26) respectively.
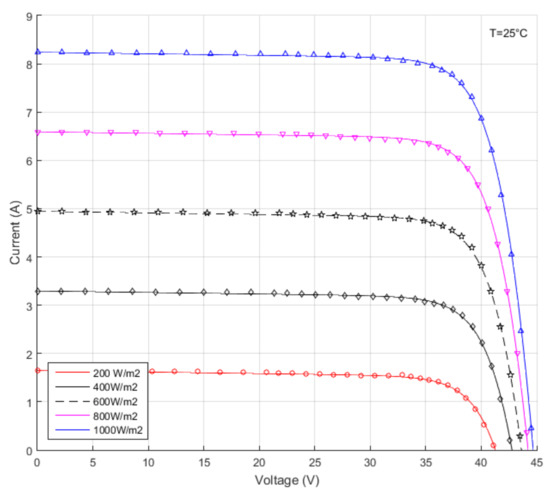
Figure 14.
Bézier approximation of the I-V irradiance dependent characteristics for the MSMD290AS-36_EU monocrystalline PV module. The lines represent the computed curves, whereas the markers represent the actual data.
The temperature dependent Bézier curves resulted from our algorithm compared with the actual data are introduced in Figure 15. Once again, the results show a very good correlation between the modeled data and the actual data.
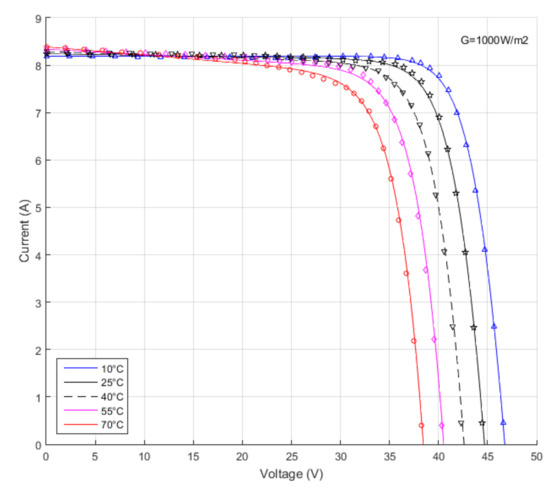
Figure 15.
Bézier approximation of the I-V temperature dependent characteristics for the MSMD290AS-36_EU Monocrystalline PV module. The lines represent the computed curves, whereas the markers represent the actual data.
4.5. Final Validation
In order to definitely test whether the proposed method is applicable to common PV cells and modules, a selection of 18 cases were analyzed at reference conditions, based on information found in their technical data [35,36,37,38,39,40,41,42,43,44,45,46,47,48,49], synthesized in Table 6. The selection includes three mono-crystalline PV arrays (1–3), nine poly-crystalline arrays (4–11 and 13) and one poly-crystalline PV cell (12), a thin-film array (14), one Heterojunction with Intrinsic Thin layer (HIT, 15) two amorphous silicon glass arrays (with different see-through degrees, respectively 10% and 30%, 16 and 17) and eventually an amorphous silicon cell (18).

Table 6.
Datasheet technical data for the analyzed 18 PV cells and modules [35,36,37,38,39,40,41,42,43,44,45,46,47,48,49].
Using the Villalva algorithm [5], the main parameters were computed and are listed in Table 7. For the last three cases, due to different technology, interesting values for the diode ideality factor occur.

Table 7.
Computed values for main parameters of the analyzed PV cells and modules.
Table 8 lists the control points computed for Bézier curve fitting, where in all cases the control end points are set at and respectively. Only two coordinates are presented, as the others are evenly spaced and can be easily computed. Selected plots of the PV devices are presented in Figure 16.

Table 8.
Control points coordinates of the analyzed PV cells and modules.
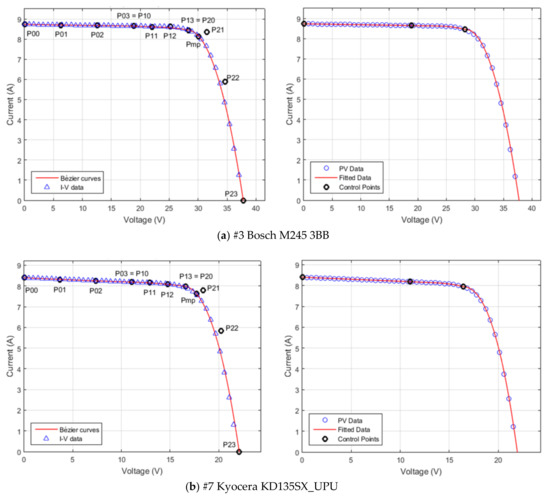
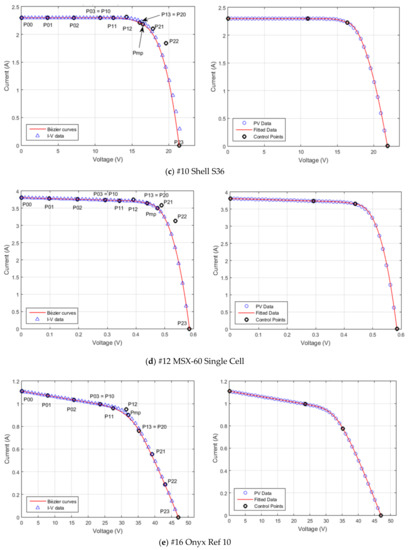
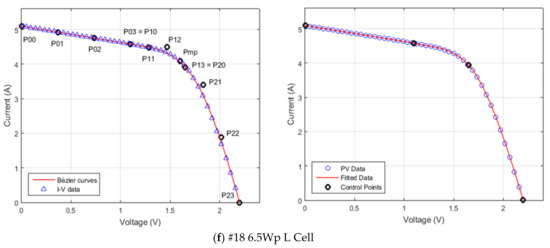
Figure 16.
Bézier approximation of the I-V curves using the proposed method (left) and the least squares method (right). The lines represent the computed curves, whereas the markers represent the actual data. Control points are represented with black dots. (a) Bosch M245 3BB Mono-Crystalline PV module; (b) Kyocera KD135SX_UPU Poly-Crystalline PV module; (c) Shell S36 Poly-Crystalline PV module; (d) Solarex MSX-60 Poly-Crystalline PV Cell; (e) Onyx Ref 10 amorphous Silicon PV Glass module; (f) 6.5Wp L amorphous Silicon PV Cell.
In the second column of Table 9, the average of the current () relative error is displayed in order to evaluate the fit quality. Maximum current error (absolute and relative, listed as positive values) is associated in each case with the coordinates where it appears. The maximum power point is also investigated as an absolute and relative error and finally the computed value is listed. The current () relative error is below 1.18% in all cases, and the relative error is even better (lower than 1%).

Table 9.
Computed errors for the analyzed PV cells and modules.
An additional plot of the relative error is introduced in Figure 17a,b for two of the analyzed PV devices. The same pattern arises as in Figure 11, with small errors up to . The curvature plots from Figure 17c,d were computed using the Herman and Klette method [50], with 20 forward and backward points, using an adapted script from [51].
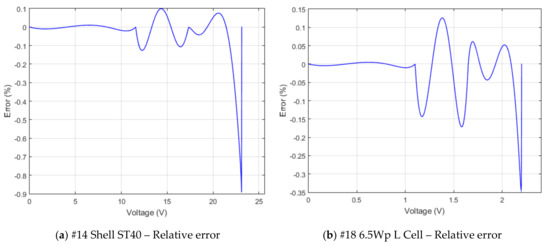
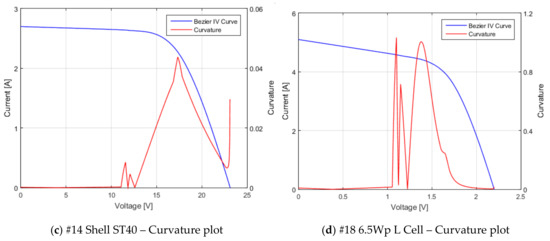
Figure 17.
Relative error (a,b) and curvature plots (c,d) for Shell ST40 Thin film PV module (a,c) and 6.5 Wp L amorphous Silicon PV Cell (b,d).
5. Discussion
In all studied cases, the coordinates can be evenly spaced. Both for the PV cells and for the PV modules, the first Bézier cubic curve was very close to a straight line and ended at , while the middle curve ended at . The relative error is less than or equal to 1.18% for all the studied PV devices, while neglecting the values in the region, where the absolute error is tens of mA and the relative error is misleading, (Figure 11 and Figure 17).
The differences between the results obtained with the proposed method and the least squares method are negligible (less than 1% for all coordinates). and can be easily derived from the manufacturer’s datasheet, using for example the method proposed by Vilallva et al. [5]. In most cases is close to (Table 7). Larger differences occur for the series parasitic resistance: for the same PV cell. For different irradiances and temperatures, Section 4.4 provides all the necessary formulae.
In most cases . The method was also valid for Onyx Ref 10, Onyx Ref 30, and 6.5 Wp L Cell, where the previous relation was not satisfied.
In relation to the Maximum Power Point Tracking (MPPT), it must be emphasized that the Bézier curves are inherently smooth. This reduces the risk for the algorithm of becoming stuck in some false area/minimum of the curve. Furthermore, as the generation of the Bézier curves is so easy, the MPPT simulation can be further simplified.
6. Conclusions
A novel method for modeling a PV cell or a PV module I-V characteristic was introduced. To the best of our knowledge, Bézier curves have not been used to model the I-V characteristic of PV devices before. The method proved high accuracy and was validated both in the case of a single PV cell and in the case of a whole PV module, for different technologies and manufacturers. The method was also used in the case of varying irradiance and temperature. The proposed method can be used for implementing hardware solar array simulators, for teaching or remote study. It is far easier to use the proposed method to find the I-V characteristic of a PV cell or module when compared with solving the exponential equations associated with the single or double diode model largely used today. A common microcontroller can compute the points on the I-V curve with a minimum of resources, inherently increasing the computing speed and the response of the system.
The advantage of our method relies on the ease of I-V characteristic generation: if we exclude and , only 10 different values (, , , , , , , , , ) have to be stored—SAS manufacturers usually use 1024 or more double points to accurately define the I-V characteristic. Alternate use is for any graphical plot of the I-V (and subsequently P-V) curves. Furthermore, little knowledge of the device itself is required, as only common data from the datasheet is needed.
As future work, fitting spiral segments will be investigated and compared with our current method.
Supplementary Files
Supplementary File 1Acknowledgments
This work was supported by both the Romanian National Authority for Scientific Research and Innovation, CNCS/CCCDI-UEFISCDI within PNCDI III, project number PN-III-P2-2.1-PED-2016-0074 and by the Politehnica University Timisoara, according to the Administration Board research policy.
Author Contributions
Both authors contributed to this research. Aurel Gontean conceived and designed the study and carried out the simulations. Roland Szabo analyzed the data. Aurel Gontean wrote the paper and reviewed the manuscript. Both authors read and approved the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Main Symbols | |
| Diode ideality factor | |
| Actual irradiance | |
| Reference irradiance, 1000 W/m2 | |
| Output current | |
| Output current at maximum power point | |
| Short circuit current | |
| Short circuit current 25 °C | |
| Boltzmann constant | |
| Current temperature coefficient, A/K | |
| Voltage temperature coefficient, V/K | |
| temperature exponent | |
| Number of series cells | |
| Maximum output power | |
| Electron charge | |
| Series resistance | |
| Series resistance at 25 °C | |
| Series resistance based on I-V characteristic slope close to | |
| Parallel (shunt) resistance | |
| Parallel (shunt) resistance, at 25 °C | |
| Parallel (shunt) resistance based on I-V characteristic slope close to | |
| Internal temperature, (K) | |
| Reference temperature 298.15 K | |
| Temperature difference | |
| Output voltage | |
| Open circuit voltage | |
| Open circuit reference voltage at 25 °C | |
| Solar cell open circuit voltage | |
| Solar cell open circuit reference voltage at 25 °C | |
| Output voltage at maximum power point | |
| Abbreviations | |
| AM | Air Mass |
| MPPT | Maximum Power Point Tracking |
| PV | Photovoltaic |
| SAS | Solar Array Simulator |
| STC | Standard Test Conditions (cell temp. 25 °C; irradiance 1000 W/m2; air mass 1.5) |
| Greek Symbols | |
| Series resistance temperature coefficient (linear law) |
References
- 4Q 2017 Frontier Power Market Outlook. Available online: https://about.bnef.com/blog/4q-2017-frontier-power-market-outlook/ (accessed on 3 January 2018).
- Solar PV 2018. Available online: https://www.pv-magazine.com/2017/12/01/solar-pv-2018-installs-of-111-gw-a-polysilicon-factory-boom-and-0-30w-for-modules-2/ (accessed on 3 January 2018).
- Phang, J.C.H.; Chan, D.S.H.; Phillips, J.R. Accurate Analytical Method for the Extraction of Solar Cell Model Parameters. Electron. Lett. 1984, 20, 406–408. [Google Scholar] [CrossRef]
- Garrido-Alzar, C.L. Algorithm for extraction of solar cell parameters from I–V curve using double exponential mode. Renew. Energy 1997, 10, 125–128. [Google Scholar] [CrossRef]
- Villalva, M.G.; Gazoli, J.R.; Filho, E.R. Comprehensive Approach to Modeling and Simulation of Photovoltaic Arrays. IEEE Trans. Power Electr. 2009, 24, 1198–1208. [Google Scholar] [CrossRef]
- Babu, B.C.; Gurjar, S. A novel simplified two-diode model of photovoltaic (PV) module. IEEE J. Photovolt. 2014, 4, 1156–1161. [Google Scholar] [CrossRef]
- Cubas, J.; Pindado, S.; de Manuel, C. Explicit Expressions for Solar Panel Equivalent Circuit Parameters Based on Analytical Formulation and the Lambert W-Function. Energies 2014, 7, 4098–4115. [Google Scholar] [CrossRef]
- Chander, S.; Purohit, A.; Sharma, A.; Nehra, S.P.; Dhaka, M.S. A study on photovoltaic parameters of mono-crystalline silicon solar cell with cell temperature. Energy Rep. 2015, 1, 104–109. [Google Scholar] [CrossRef]
- Ishaque, K.; Salam, Z. An improved modeling method to determine the model parameters of photovoltaic (PV) modules using differential evolution (DE). Sol. Energy 2011, 85, 2349–2359. [Google Scholar] [CrossRef]
- Franzitta, V.; Orioli, A.; Di Gangi, A. Assessment of the Usability and Accuracy of the Simplified One-Diode Models for Photovoltaic Modules. Energies 2016, 9, 1019. [Google Scholar] [CrossRef]
- Franzitta, V.; Orioli, A.; Gangi, A.D. Assessment of the Usability and Accuracy of Two-Diode Models for Photovoltaic Modules. Energies 2017, 10, 564. [Google Scholar] [CrossRef]
- Gontean, A.; Lica, S.; Bularka, S.; Szabo, R.; Lascu, D. A Novel High Accuracy PV Cell Model Including Self Heating and Parameter Variation. Energies 2018, 11, 36. [Google Scholar] [CrossRef]
- Cuce, E.; Cuce, P.M.; Karakas, I.H.; Bali, T. An accurate model for photovoltaic (PV) modules to determine electrical characteristics and thermodynamic performance parameters. Energy Convers. Manag. 2017, 146, 205–216. [Google Scholar] [CrossRef]
- Farin, G. A History of Curves and Surfaces in CAGD. In Handbook of Computer Aided Geometric Design; Farin, G.E., Hoschek, J., Kim, M.S., Eds.; Elsevier: Amsterdam, The Netherlands, 2002; pp. 1–22. ISBN 978-0-444-51104-1. [Google Scholar] [CrossRef]
- Farin, G. Curves and Surfaces for CAGD. A Practical Guide, 5th ed.; Academic Press: San Francisco, CA, USA, 2002; pp. 81–95. ISBN 1-55860-737-4. [Google Scholar] [CrossRef]
- Mortenson, M.E. Geometric Modeling, 3rd ed.; Industrial Press: South Norwalk, CT, USA, 2006; ISBN 978-0-831-13298-9. [Google Scholar]
- Farin, G. Shape Representation. In Wiley Encyclopedia of Electrical and Electronics Engineering; 13 July 2007; ISBN 978-0-471-34608-1. Available online: http://onlinelibrary.wiley.com/doi/10.1002/047134608X.W7525.pub2/full (accessed on 30 March 2018). [CrossRef]
- Tromba, D.; Munteanu, L.; Schneider, V.; Holzapfel, F. Approach trajectory generation using Bézier curves. In Proceedings of the 2015 IEEE International Conference on Aerospace Electronics and Remote Sensing Technology (ICARES), Bali, Indonesia, 3–5 December 2015. [Google Scholar] [CrossRef]
- Jalba, A.C.; Wilkinson, M.; Roerdink, J. Shape representation and recognition through morphological curvature scale spaces. IEEE Trans. Image Process. 2006, 15, 331–341. [Google Scholar] [CrossRef] [PubMed]
- Prautzsch, H.; Boehm, W.; Paluszny, M. Bézier and B-Spline Techniques; Spinger: Berlin, Germany, 2002; pp. 9–57. ISBN 3-540-43761-4. [Google Scholar]
- Farin, G. Class A Bézier curves. Comput. Aided Geom. Des. 2006, 23, 573–581. Available online: https://pdfs.semanticscholar.org/1412/bd2310c3f76a31e49129402895564b751e8d.pdf (accessed on 30 March 2018). [CrossRef]
- De Boor, C.; Rice, J.R. Least Squares Cubic Spline Approximation I-Fixed Knots; Dept. of Computer Sciences, Purdue University: West Lafayette, IN, USA, 1968; Available online: ftp://ftp.cs.wisc.edu/Approx/tr20.pdf (accessed on 30 March 2018).
- Levien, R.; Séquin, C. Interpolating Splines: Which is the fairest of them all? Comput. Aided Des. Appl. 2009, 6, 91–102. Available online: http://levien.com/phd/LevienSequinCAD09_014.pdf (accessed on 30 March 2018). [CrossRef]
- Bartoň, M.; Gershon, E. Spiral fat arcs—Bounding regions with cubic convergence. Graph. Models 2011, 73, 50–57. Available online: http://www.cs.technion.ac.il/~gershon/papers/SpiralFatArcs.pdf (accessed on 30 March 2018). [CrossRef]
- 156 mm Monocrystalline Mono Solar Cell 6x6. Available online: https://www.aliexpress.com/item/50pcs-lot-4-6W-156mm-mono-solar-cells-6x6-150feet-Tabbing-Wire-15feet-Busbar-Wire-1pc/1932804007.html (accessed on 21 September 2017).
- MünchenSolar. M Series Monocrystalline MSMDxxxAS-36.EU Datasheet. Available online: https://cdn.enf.com.cn/Product/pdf/Crystalline/559cd7e85436f.pdf (accessed on 31 January 2018).
- Mugnaini, D. Bézier Curve with Draggable Control Points. Draw, Manipulate and Reconstruct Bézier Curves, Version 1.11. Available online: https://www.mathworks.com/matlabcentral/fileexchange/51046-bézier-curve-with-draggable-control-points (accessed on 30 December 2017).
- Garrity, M. Bézier Curves and Kronecker’s Tensor Product. 13 October 2014. Available online: https://blogs.mathworks.com/graphics/2014/10/13/bézier-curves/ (accessed on 31 December 2017).
- Khan, M. Cubic Bézier Least Square Fitting, Version 1.4. Available online: https://www.mathworks.com/matlabcentral/fileexchange/15542-cubic-bézier-least-square-fitting (accessed on 30 December 2017).
- Thermo-Electric Hybrid Solar System (TESS), Grant PN-III-P2-2.1-PED-2016-0074. Available online: http://tess.upt.ro (accessed on 12 April 2018).
- Wolberg, J. Data Analysis Using the Method of Least Squares. Extracting the Most Information from Experiments; Springer: Berlin/Heidelberg, Germany, 2006; ISBN 978-3-540-25674-8. [Google Scholar] [CrossRef]
- Hansen, P.C.; Pereyra, V.; Scherer, G. Least Squares Data Fitting with Applications; JHU Press: Baltimore, ML, USA, 2013; ISBN 978-1-421-40786-9. [Google Scholar]
- Shao, L.; Zhou, H. Curve Fitting with Bézier Cubics. Graph.l Models Image Process. 1996, 58, 223–232. [Google Scholar] [CrossRef]
- Zhao, L.; Jiang, J.; Song, C.; Bao, L.; Gao, J. Parameter Optimization for Bézier Curve Fitting Based on Genetic Algorithm. In Advances in Swarm Intelligence; Tan, Y., Shi, Y., Mo, H., Eds.; Springer: Berlin, Germany, 2013; Volume 7928. [Google Scholar] [CrossRef]
- Shell SP70 Photovoltaic Solar Module, Product Information Sheet. Available online: http://www.solenerg.com.br/files/SP70.pdf (accessed on 15 March 2018).
- Isofoton I-150 InDach Solar Panel Specifications. Available online: http://www.posharp.com/i-150-indach-solar-panel-from-isofoton_p337595585d.aspx (accessed on 15 March 2018).
- Bosch Solar Module c-Si M 60 Model M245 3BB. Available online: http://www.bosch-solarenergy.de/media/us/alle_pdfs_1/technische_dokumente_3/datenblaetter_1/kristalline_module_6/p_60_eu30014_1/Bosch_Solar_Module_c_Si_M_60_EU30014_en_Europe.pdf (accessed on 16 March 2018).
- München Solarenergie GmbH MSP300AS-36.EU. Available online: http://www.secondsol.de/handelsplatz/herstellerdatenblatt/photovoltaikmodule/Polykristallin/M%C3%BCnchen%20Solarenergie%20GmbH/MSP300AS-36.EU.htm (accessed on 16 March 2018).
- Kyocera KC200GT. High Efficiency Multicrystal Photovoltaic Module. Available online: https://www.kyocerasolar.com/dealers/product-center/archives/spec-sheets/KC200GT.pdf (accessed on 16 March 2018).
- Kyocera KC85T. High Efficiency Multicrystal Photovoltaic Module. Available online: https://www.kyocerasolar.com/dealers/product-center/archives/spec-sheets/KC85T.pdf (accessed on 17 March 2018).
- Kyocera KD245GH-4FB2 High Efficiency Multi-Crystalline Photovoltaic Module. Available online: http://www.australiansolar.com.au/images/KD245GH-4FB2.pdf (accessed on 17 March 2018).
- Kyocera KD135SX_UPU Technical Data. Available online: http://www.datasheetspdf.com/pdf/846173/KYOCERA/KD135SX-UPU/1 (accessed on 17 March 2018).
- Sharp ND-224UC1 (224W) Solar Panel Technical Data. Available online: http://files.sharpusa.com/Downloads/Solar/Products/sol_dow_ND224UC1.pdf (accessed on 17 March 2018).
- Shell Solar Revised 2nd ed. Available online: http://www.efn-uk.org/l-street/renewables-lib/solar-reports/index_files/Shell-Solar.pdf (accessed on 18 March 2018).
- Solarex MSX-60 and MSX-64 Photovoltaic Modules Technical Data. Available online: https://www.solarelectricsupply.com/media/custom/upload/Solarex-MSX64.pdf (accessed on 18 March 2018).
- Amerisolar AS-6P Technical Data. Available online: https://www.acosolar.com/amfilerating/file/download/file_id/448/?___store=solar_all (accessed on 18 March 2018).
- Sanyo HIT-240 HDE4 Technical Data. Available online: http://future-energy-solutions.co.uk/wp-content/uploads/2014/10/Panasonic-Datasheet-HIT-240W.pdf (accessed on 18 March 2018).
- Onyx 1200x600 ref10 Technical Data. Available online: http://onyxsolardownloads.com/docs/ALL-YOU-NEED/Technical_Guide.pdf (accessed on 17 March 2018).
- 6.5Wp L Cell a-Si cell Technical Data. Available online: https://www.enfsolar.com/pv/cell-datasheet/1696 (accessed on 19 March 2018).
- Hermann, S.; Klette, R. Multigrid Analysis of Curvature Estimators. In Proceedings of the Image and Vision Computing ’03, Palmerston North, New Zealand, 26–28 November 2003; pp. 108–112. Available online: https://pdfs.semanticscholar.org/c7c4/d51563997009797bb83211a34687203c5e3c.pdf (accessed on 29 March 2018).
- Jianfei, P. Curvature Estimation. Available online: https://www.mathworks.com/matlabcentral/fileexchange/40920-curvature-estimation (accessed on 29 March 2018).
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).