A Novel Swarm Optimisation Algorithm Based on a Mixed-Distribution Model
Abstract
:1. Introduction
2. Introduction to Population Distribution Patterns
2.1. Random Distribution
2.2. Regular Distribution
2.3. Contagious Distribution
- The distance between a plant and its seeds (fruits) is limited due to gravity;
- The environment has spatial heterogeneity;
- There are interspecific relationships.
2.4. Overview of the Negative Binomial Distribution
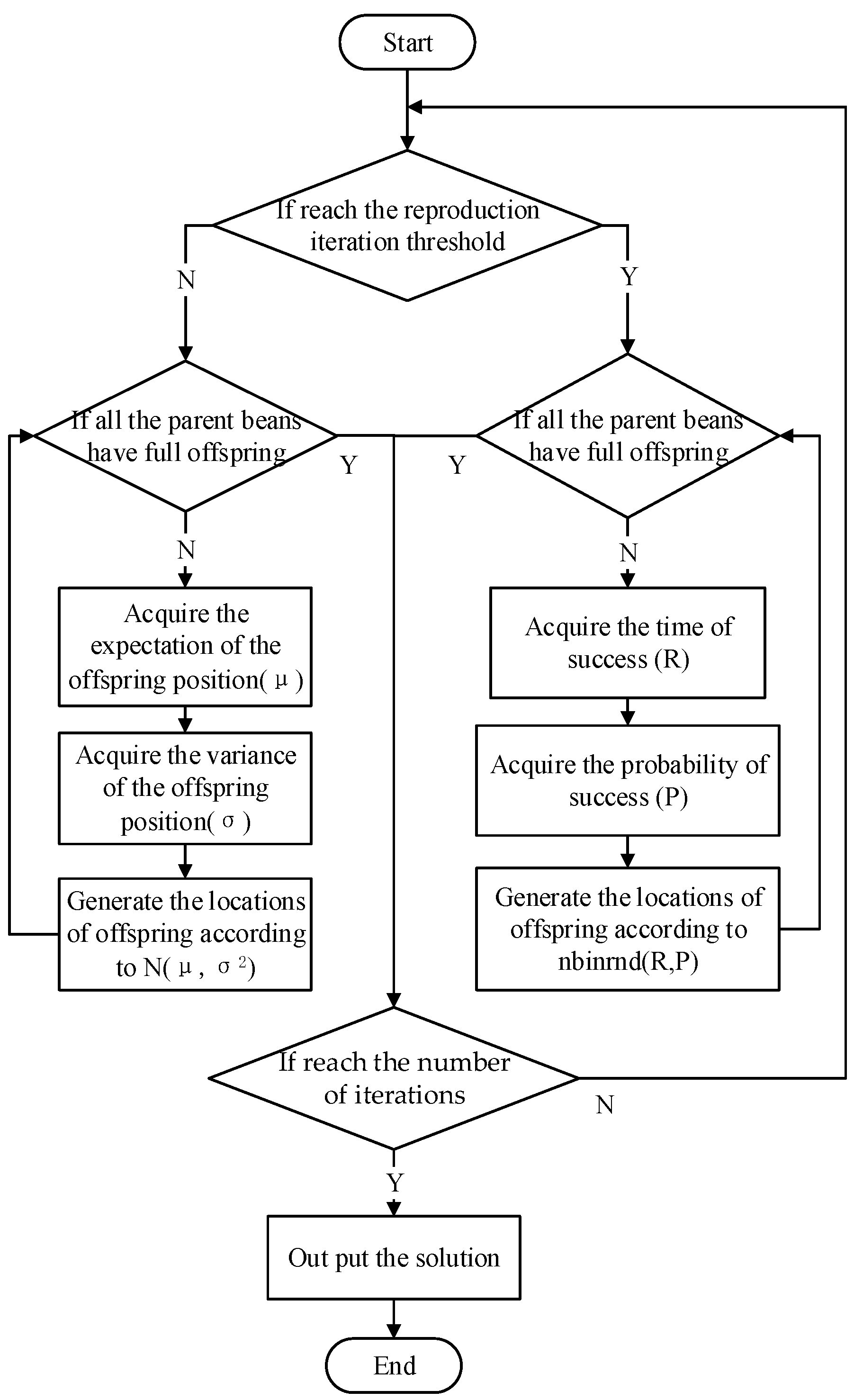
3. Population Distribution Model Based on a Mixed Distribution
4. Experiments and Analysis
4.1. Test Functions
4.2. Experimental Parameter Settings
4.3. Experimental Results
4.4. Experiment Analysis
4.4.1. Statistical Results
- Optimal Results
- Average Results
4.4.2. Analysis of Results
- 1. Unimodal Functions Optimisation Analysis
- (1)
- Because the population sizes of the four algorithms are same, the highest number of offspring dominated by parent beans occurred in algorithm NBOA-3. For example, the No. 1 parent bean in algorithm NBOA-3 dominated 70% of individual offspring and distributed them according to its wish. However, the No. 1 parent bean in algorithm NBOA-6 only dominated 30% of the offspring. Therefore, algorithm NBOA-3 can approximate the optimal solution (or the local optimal solution) more quickly in theory. This is largely consistent with the experimental results. Hence, better results appear to be given by algorithm NBOA-3.
- (2)
- Considering unimodal function optimisation, the mutation mechanism of individuals follows the method:
- (3)
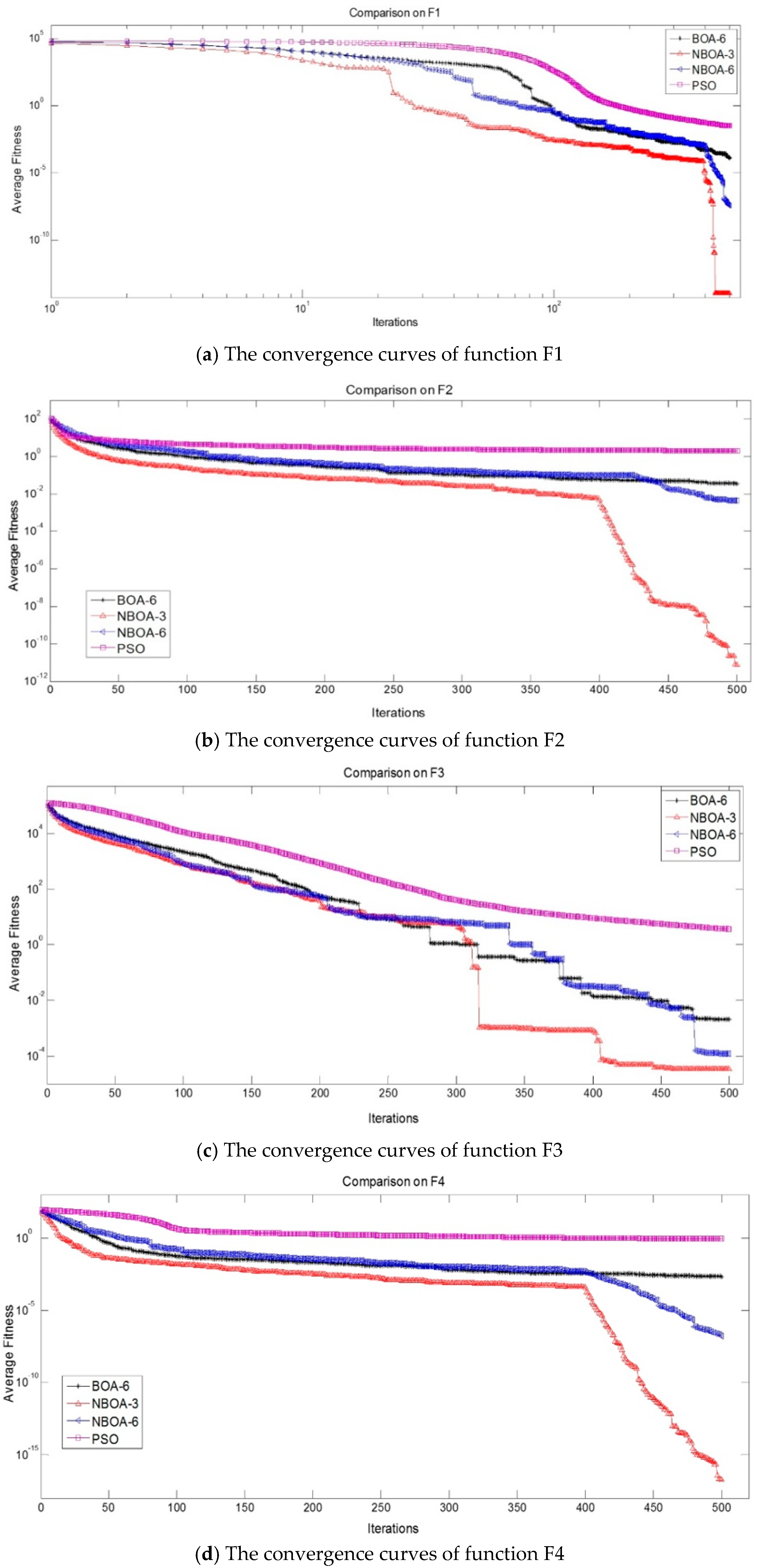
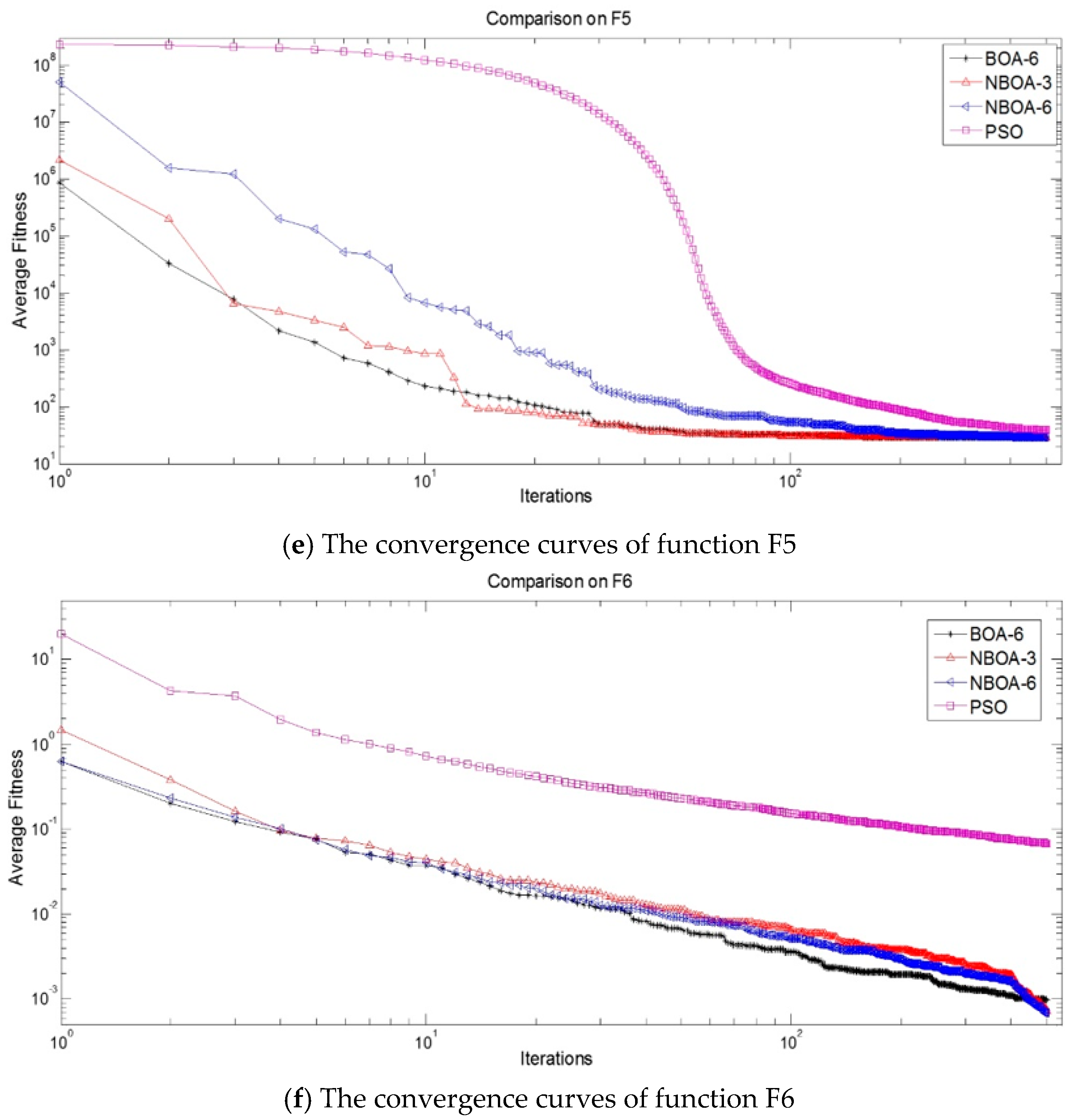
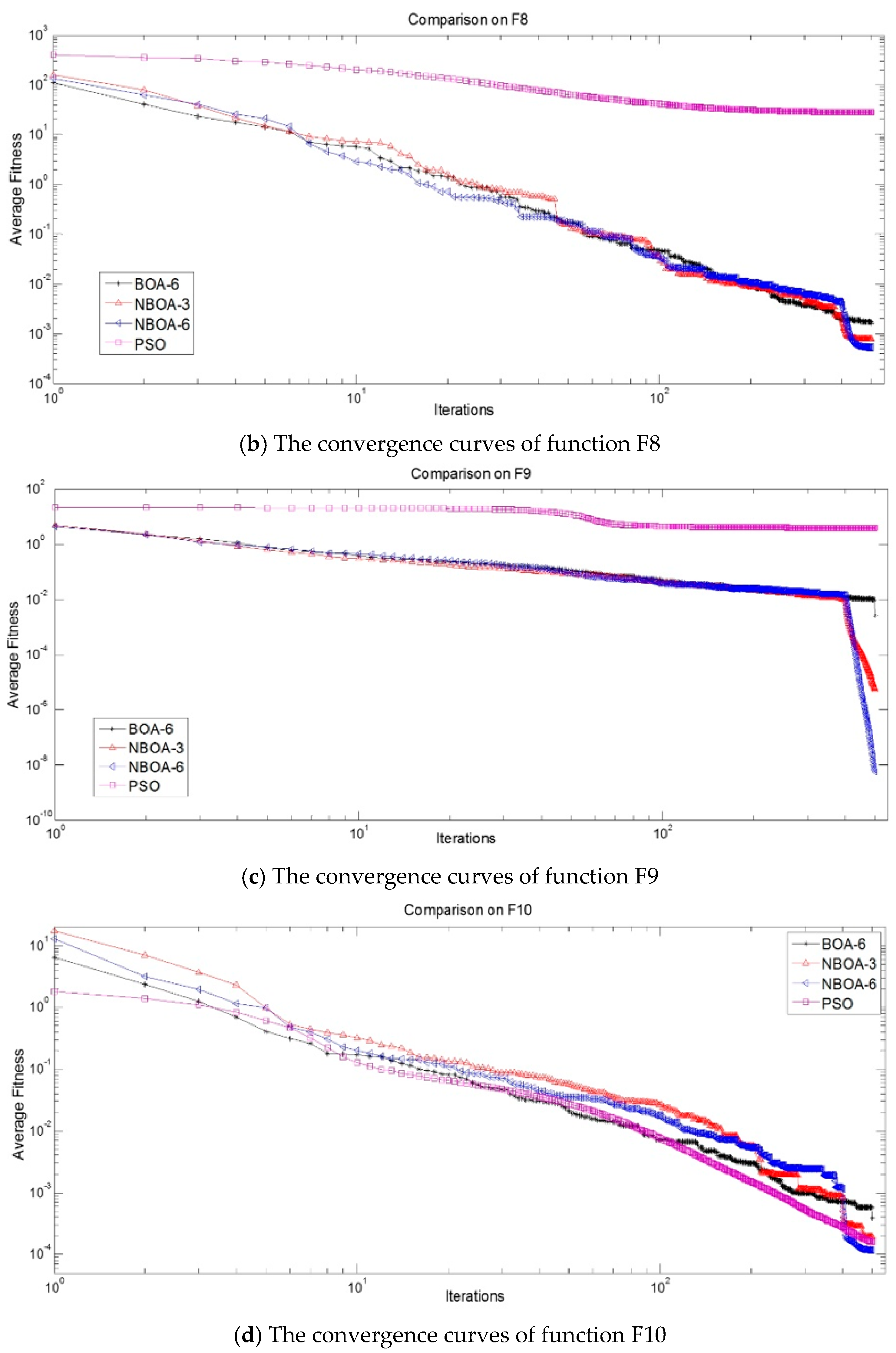
- The model based on the binomial distribution can effectively increase the optimisation ability of the algorithm. A decreasingly steep slope is evident in the comparative figures of algorithm convergence performance (Figure 2). It is the location of the steep slope that starts using the binomial distribution model in BOA. It is evident that the model based on the binomial distribution enhances the performance of NBOA-3 and NBOA-6.
- 2. Multimodal Functions Optimisation Analysis
- (1)
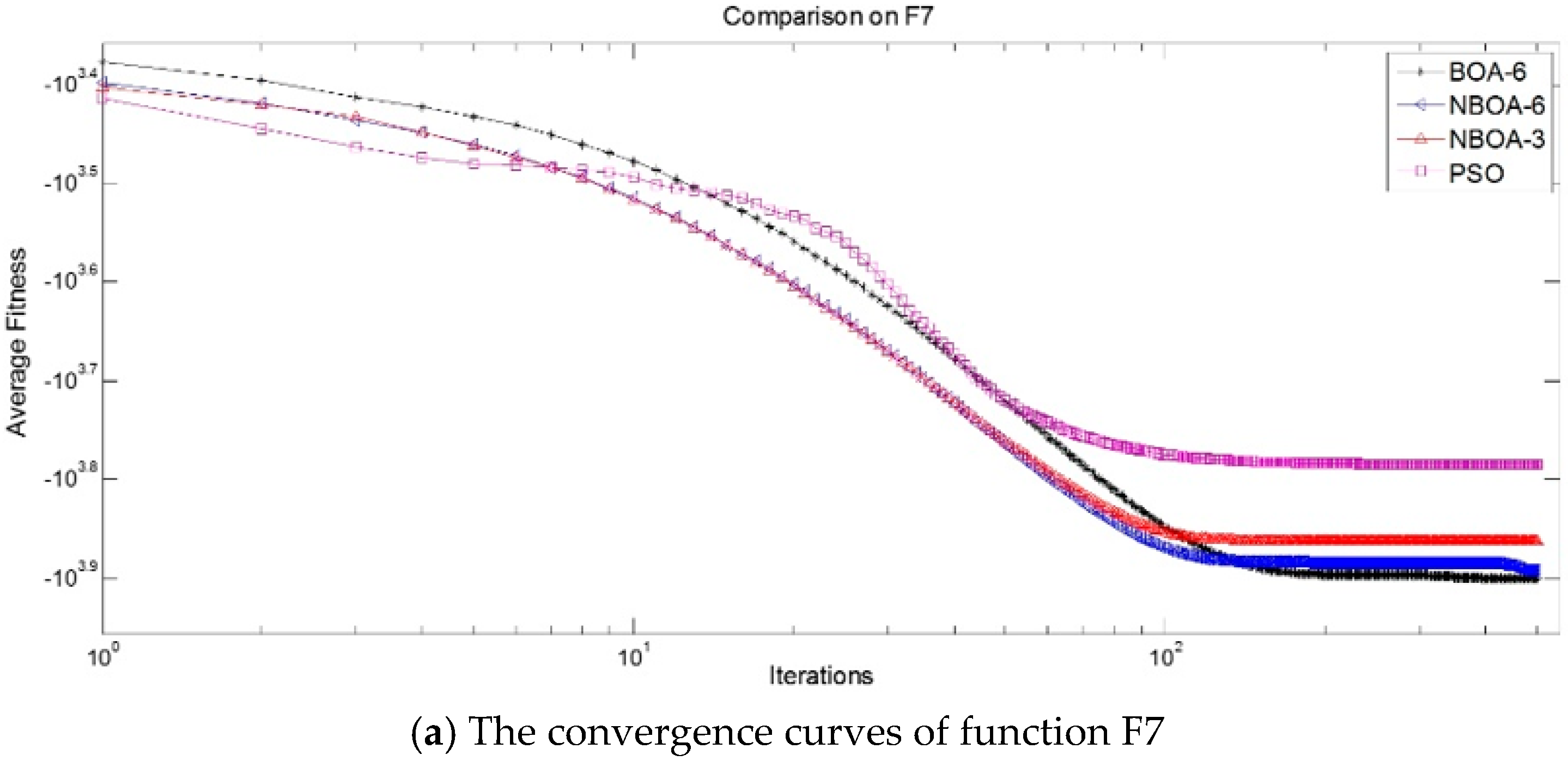
- Because the distances (Euclidean distances are used in the experiments) between the parent beans need to meet the threshold set before the experiments, the more parent beans there are, the more advantageously parent beans can explore the problem domain space. That is to say, there are more opportunities to quickly find better problem areas that effectively enhance the algorithm’s ability to achieve global optimisation.
- (2)
- For multimodal function optimisation, the mechanism of individual bean variation adopts the following method:pop(NumPop,:) = (rands(1,nn)) × (popmax − (popmax − popmin) × rand)
- (3)
- As mentioned above, because the model based on the negative binomial distribution is used in algorithm NBOA-6, its optimisation ability is better than that of algorithm BOA-6.
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Yang, B. Cooperative Control for Swarm Robots based on Bio-Inspired Intelligent Algorithms. Ph.D. Thesis, Donghua University, Shanghai, China, 2016. [Google Scholar]
- Bonyadi, M.R.; Michalewicz, Z. Particle Swarm Optimization for Single Objective Continuous Space Problems: A Review. Evolut. Comput. 2017, 25, 1–54. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Zhou, S.; Luo, J. A robust ant colony optimization for continuous functions. Expert Syst. Appl. 2017, 81, 309–320. [Google Scholar] [CrossRef]
- Zhu, X.; Ni, Z.; Cheng, M.; Li, J.; Jin, F.; Ni, L. Haze prediction method based on multi-fractal dimension and co-evolution discrete artificial fish swarm algorithm. Syst. Eng. Theory Pract. 2017, 37, 999–1010. [Google Scholar]
- Kalin, P. Free Search—Comparative analysis 100. Int. J. Metaheuristics 2014, 3, 118–132. [Google Scholar]
- Montiela, O.; Castillob, O.; Melinb, P.; Rodríguez Díazc, A.; Sepúlvedaa, R. Human evolutionary model: A new approach to optimization. Inf. Sci. 2007, 177, 2075–2098. [Google Scholar] [CrossRef]
- He, S.; Wu, Q.H.; Saunders, J.R. Group search optimizer: An optimization algorithm inspired by animal searching behavior. IEEE Trans. Evolut. Comput. 2009, 13, 973–990. [Google Scholar] [CrossRef]
- Hussein, W.A.; Sahran, S.; Abdullah, S.N.H.S. The variants of the Bees Algorithm (BA): A survey. Artif. Intell. Rev. 2017, 47, 67–121. [Google Scholar] [CrossRef]
- Yang, C.; Ji, J.; Liu, J.; Yin, B. Bacterial foraging optimization using novel chemotaxis and conjugation strategies. Inf. Sci. 2016, 363, 72–95. [Google Scholar] [CrossRef]
- Eusuff, M.; Lansey, K.; Pasha, F. Shuffled frog-leaping algorithm: A memetic meta-heuristic for discrete optimization. Eng. Optim. 2006, 38, 129–154. [Google Scholar] [CrossRef]
- Tan, Y.; Yu, C.; Zheng, S.; Ding, K. Introduction to Fireworks Algorithm. Int. J. Swarm Intell. Res. 2013, 4, 39–70. [Google Scholar] [CrossRef]
- Wang, G.G.; Tan, Y. Improving Metaheuristic Algorithms with Information Feedback Models. IEEE Trans. Cybern. 2017, 99, 1–14. [Google Scholar] [CrossRef]
- Wang, G.G.; Cai, X.; Cui, Z.; Min, G.; Chen, J. High Performance Computing for Cyber Physical Social Systems by Using Evolutionary Multi-Objective Optimization Algorithm. IEEE Trans. Emerg. Top. Comput. 2017. [Google Scholar] [CrossRef]
- Wang, G.G.; Guo, L.; Gandomi, A.H.; Hao, G.-S.; Wang, H. Chaotic Krill Herd algorithm. Inf. Sci. 2014, 274, 17–34. [Google Scholar] [CrossRef]
- Wang, G.G.; Gandomi, A.H.; Alavi, A.H.; Gong, D. A comprehensive review of krill herd algorithm: Variants, hybrids and applications. Artif. Intell. Rev. 2017. [Google Scholar] [CrossRef]
- Wang, G.G.; Gandomi, A.H.; Chu, H.C.; Zhao, X. Hybridizing harmony search algorithm with cuckoo search for global numerical optimization. Soft Comput. 2016, 20, 273–285. [Google Scholar] [CrossRef]
- Wang, G.G.; Deb, S.; Cui, Z. Monarch Butterfly Optimization. Neural Comput. Appl. 2015. [Google Scholar] [CrossRef]
- Wang, G.G. Moth search algorithm: A bio-inspired metaheuristic algorithm for global optimization problems. Memet. Comput. 2016. [Google Scholar] [CrossRef]
- Wang, G.G.; Deb, S.; Gandomi, A.H.; Zhang, Z.; Alavi, A.H. Chaotic cuckoo search. Soft Comput. 2016, 20, 3349–3362. [Google Scholar] [CrossRef]
- Eiben, A.E. In vivo veritas: Towards the evolution of things. Lect. Notes Comput. Sci. 2014, 8672, 24–39. [Google Scholar]
- Geng, J.C.; Cui, Z.; Gu, X.S. Scatter search based particle swarm optimization algorithm for earliness/tardiness flowshop scheduling with uncertainty. Int. J. Autom. Comput. 2016, 13, 285–295. [Google Scholar] [CrossRef]
- Lazzús, J.A.; Rivera, M.; López-Caraballo, C.H. Parameter estimation of Lorenz chaotic system using a hybrid swarm intelligence algorithm. Phys. Lett. A 2016, 380, 1164–1171. [Google Scholar] [CrossRef]
- Dadgar, M.; Jafari, S.; Hamzeh, A.A. PSO-based multi-robot cooperation method for target searching in unknown environments. Neurocomputing 2016, 177, 62–74. [Google Scholar] [CrossRef]
- Ghaemi, M.; Feizi-Derakhshi, M.R. Feature selection using Forest Optimization Algorithm. Pattern Recognit. 2016, 60, 121–129. [Google Scholar] [CrossRef]
- Garcia, M.A.P.; Montiel, O.; Castillo, O.; Melin, P. Path planning for autonomous mobile robot navigation with ant colony optimization and fuzzy cost function evaluation. Appl. Soft Comput. 2009, 9, 1102–1110. [Google Scholar] [CrossRef]
- Couceiro, M.S.; Figueiredo, C.M.; Rui, P.R.; Ferreira, N.M.F. Darwinian Swarm Exploration under Communication Constraints: Initial Deployment and Fault-Tolerance Assessment. Robot. Auton. Syst. 2014, 62, 528–544. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, R.; Song, L. A novel evolutionary algorithm—Seed optimization algorithm. Pattern Recognit. Artif. Intell. 2008, 21, 677–681. [Google Scholar]
- Zhang, X.; Sun, B.; Mei, T.; Wang, R. A novel evolutionary algorithm inspired by beans dispersal. Int. J. Comput. Intell. Syst. 2013, 6, 79–86. [Google Scholar] [CrossRef]
- Wang, P.; Cheng, Y. Relief supplies scheduling based on bean optimization algorithm. Econ. Res. Guide 2010, 8, 252–253. [Google Scholar]
- Zhang, X.; Sun, B.; Mei, T.; Wang, R. Post-disaster restoration based on fuzzy preference relation and bean optimization algorithm. In Proceedings of the 2010 IEEE Youth Conference on Information Computing and Telecommunications (YC-ICT), Beijing, China, 28–30 November 2010; pp. 253–256. [Google Scholar]
- Zhang, X.; Wang, H.; Sun, B.; Li, W.; Wang, R. The Markov model of bean optimization algorithm and its convergence analysis. Int. J. Comput. Intell. Syst. 2013, 6, 609–615. [Google Scholar] [CrossRef]
- Li, Y. Solving TSP by an ACO-and-BOA-based Hybrid Algorithm. In Proceedings of the 2010 International Conference on Computer Application and System Modeling, Taiyuan, China, 22–24 October 2010; pp. 189–192. [Google Scholar]
- Zhang, X.; Jiang, K.; Wang, H. An improved bean optimization algorithm for solving TSP. Lect. Notes Comput. Sci. 2012, 7331, 261–267. [Google Scholar]
- Feng, T. Study and Application of Bean Optimization Algorithm on Complex Problem. Master’s Thesis, University of Science and Technology of China, Hefei, China, 2017. [Google Scholar]
- Zhang, X.; Feng, T. Chaotic bean optimization algorithm. Soft Comput. 2018, 22, 67–77. [Google Scholar] [CrossRef]
- Guoyu, L.; Ruide, L. Brief introduction of spatial methods to distribution patterns of population. J. Northwest For. Univ. 2003, 18, 17–21. [Google Scholar]
- Hao-tao, L. Introduction to studies of the pattern of plant population. Chin. Bull. Bot. 1995, 12, 19–26. [Google Scholar]
- Fei, S.-M.; He, Y.-P.; Chen, X.-M.; Jiang, J.-M.; Guo, Z.-H. Quantitative features of populations of Pinus tabulaeformis and P. armandii regenerated following water damage at Qinling Mountain China. Chin. J. Plant Ecol. 2008, 32, 95–105. [Google Scholar]
- Feng, T.; Xie, Q.; Hu, H.; Song, L.; Cui, C.; Zhang, Z. Bean optimization algorithm based on negative Binomial Distribution. Lect. Notes Comput. Sci. 2015, 9140, 82–88. [Google Scholar]
| Parameters | |
| Support | |
| Mean | |
| Variance |
| Function Name | No. | Mathematical Representation (f(X)) | Initial Range | Best Objective Function Value |
|---|---|---|---|---|
| Sphere | F1 | [−100, 100]n | 0 | |
| Schwefel 2.22 | F2 | [−10, 10]n | 0 | |
| Schwefel 1.2 | F3 | [−100, 100]n | 0 | |
| Schwefel 2.21 | F4 | [−100, 100]n | 0 | |
| Rosenbrock | F5 | [−30, 30]n | 0 | |
| Quartic | F6 | [−1.28, 1.28]n | 0 | |
| Schwefel 2.26 | F7 | [−500, 500]n | −12,569.483 | |
| Rastrigin | F8 | [−5.12, 5.12]n | 0 | |
| Ackley | F9 | [−32, 32]n | 0 | |
| Griewank | F10 | [−600, 600]n | 0 |
| Experimental Algorithms | Population Size | Generations |
|---|---|---|
| NBOA-3 | 50 | 500 |
| NBOA-6 | ||
| BOA-6 | ||
| PSO |
| Experimental Functions | Distance Threshold |
|---|---|
| F1 | Di1 (0, 12]; Dj2 (0, 15]; Dk3 (0, 15]; Dm4 (0, 15]; D56 (0, 15]; |
| F2 | Di1 (0, 5]; Dj2 (0, 5]; Dk3 (0, 6]; Dm4 (0,6]; D56 (0, 6]; |
| F3 | Di1 (0, 10]; Dj2 (0, 10]; Dk3 (0, 12]; Dm4 (0, 12]; D56 (0, 12]; |
| F4 | Di1 (0, 10]; Dj2 (0, 10]; Dk3 (0, 12]; Dm4 (0, 12]; D56 (0, 12]; |
| F5 | Di1 (0, 6]; Dj2 (0, 6]; Dk3 (0, 9]; Dm4 (0, 9]; D56 (0, 9]; |
| F6 | Di1 (0, 4]; Dj2 (0, 4]; Dk3 (0, 5]; Dm4 (0, 5]; D56 (0, 5]; |
| F7 | Di1 (0, 30]; Dj2 (0, 30]; Dk3 (0, 35]; Dm4 (0, 35]; D56 (0, 35]; |
| F8 | Di1 (0, 3]; Dj2 (0, 3]; Dk3 (0, 5]; Dm4 (0, 5]; D56 (0, 5]; |
| F9 | Di1 (0, 12]; Dj2 (0, 12]; Dk3 (0, 15]; Dm4 (0, 15]; D56 (0, 15]; |
| F10 | Di1 (0, 60]; Dj2 (0, 60]; Dk3 (0, 80]; Dm4 (0, 80]; D56 (0, 80]; |
| Experimental Functions | [Vmax,Vmin] |
|---|---|
| F1 | [−1, 1] |
| F2 | [−1, 1] |
| F3 | [−1, 1] |
| F4 | [−1, 1] |
| F5 | [−0.5, 0.5] |
| F6 | [−1, 1] |
| F7 | [−30, 30] |
| F8 | [−0.5, 0.5] |
| F9 | [−1, 1] |
| F10 | [−15, 15] |
| Experimental Functions | Distance Threshold |
|---|---|
| F1 | D21 (0, 12]; D31 (0, 15]; D32 (0, 15]; |
| F2 | D21 (0, 5]; D31 (0, 6]; D32 (0, 6]; |
| F3 | D21 (0, 10]; D31 (0, 10]; D32 (0, 12]; |
| F4 | D21 (0, 10]; D31 (0, 10]; D32 (0, 12]; |
| F5 | D21 (0, 6]; D31 (0, 9]; D32 (0, 9]; |
| F6 | D21 (0, 4]; D31 (0, 5]; D32 (0, 5]; |
| F7 | D21 (0, 30]; D31 (0, 35]; D32 (0, 35]; |
| F8 | D21 (0, 3]; D31 (0, 5]; D32 (0, 5]; |
| F9 | D21 (0, 12]; D31 (0, 15]; D32 (0, 15]; |
| F10 | D21 (0, 60]; D31 (0, 80]; D32 (0, 80]; |
| Experimental Functions | Algorithms | Optimal Solutions | Average Results | SD |
|---|---|---|---|---|
| F1 | BOA-6 | 1.29 × 10−14 | 1.21 × 10−4 | 4.09 × 10−4 |
| NBOA-3 | 3.42 × 10−67 | 1.04 × 10−14 | 7.37 × 10−14 | |
| NBOA-6 | 1.31 × 10−33 | 3.84 × 10−8 | 2.18× 10−7 | |
| PSO | 6.97 × 10−3 | 3.09 × 10−2 | 1.88 × 10−2 | |
| F2 | BOA-6 | 2.42 × 10−12 | 3.45 × 10−4 | 2.01 × 10−3 |
| NBOA-3 | 5.21 × 10−68 | 8.44 × 10−17 | 5.97 × 10−16 | |
| NBOA-6 | 8.28 × 10−21 | 1.81 × 10−7 | 9.12 × 10−7 | |
| PSO | 5.99 × 10−1 | 1.99 | 1.04 | |
| F3 | BOA-6 | 2.39 × 10−12 | 2.10 × 10−3 | 4.01 × 10−3 |
| NBOA-3 | 3.89 × 10−48 | 3.49 × 10−5 | 2.47 × 10−4 | |
| NBOA-6 | 1.13 × 10−17 | 1.24 × 10−4 | 6.2 × 10−4 | |
| PSO | 9.34 × 10−1 | 3.67 | 1.74 | |
| F4 | BOA-6 | 4.28 × 10−9 | 2.16 × 10−3 | 3.55 × 10−3 |
| NBOA-3 | 2.25 × 10−36 | 1.88 × 10−17 | 1.33 × 10−16 | |
| NBOA-6 | 1.64 × 10−12 | 1.71 × 10−7 | 4.25 × 10−7 | |
| PSO | 3.39 × 10−1 | 8.77 × 10−1 | 4.81 × 10−1 | |
| F5 | BOA-6 | 2.88 × 10 | 2.89 × 10 | 8.89 × 10−2 |
| NBOA-3 | 2.86 × 10 | 2.89 × 10 | 1.31 × 10−1 | |
| NBOA-6 | 2.86 × 10 | 2.92 × 10 | 6.79 × 10−1 | |
| PSO | 2.28 × 10 | 3.92 × 10 | 2.93 × 10 | |
| F6 | BOA-6 | 4.79 × 10−5 | 9.89 × 10−4 | 6.63 × 10−4 |
| NBOA-3 | 1.19 × 10−5 | 7.15 × 10−4 | 6.22 × 10−4 | |
| NBOA-6 | 5.62 × 10−5 | 6.90 × 10−4 | 6.28 × 10−4 | |
| PSO | 2.64 × 10−2 | 6.82 × 10−2 | 3.38 × 10−2 |
| Experimental Functions | Algorithms | Optimal Solutions | Average Results | SD |
|---|---|---|---|---|
| F7 | BOA-6 | −9.091 × 103 | −7.94 × 103 | 6.41 × 102 |
| NBOA-3 | −8.99 × 103 | −7.28 × 103 | 7.04 × 102 | |
| NBOA-6 | −1.11 × 104 | −7.80 × 103 | 7.55 × 102 | |
| PSO | −7.69 × 103 | −6.09 × 103 | 6.39 × 102 | |
| F8 | BOA-6 | 1.61 × 10−8 | 1.62 × 10−3 | 3.07 × 10−3 |
| NBOA-3 | 2.11 × 10−7 | 8.04 × 10−4 | 1.97 × 10−3 | |
| NBOA-6 | 1.36 × 10−9 | 5.27 × 10−4 | 1.41 × 10−3 | |
| PSO | 9.63 | 2.79 × 10 | 8.74 | |
| F9 | BOA-6 | 7.71 × 10−6 | 2.58 × 10−3 | 4.37 × 10−3 |
| NBOA-3 | 1.15 × 10−13 | 5.32 × 10−6 | 3.76 × 10−5 | |
| NBOA-6 | 2.58 × 10−14 | 5.60 × 10−9 | 2.21 × 10−8 | |
| PSO | 2.02 | 3.89 | 8.18 × 10−1 | |
| F10 | BOA-6 | 7.01 × 10−8 | 3.90 × 10−4 | 8.64 × 10−4 |
| NBOA-3 | 1.52 × 10−8 | 1.94 × 10−4 | 4.57 × 10−4 | |
| NBOA-6 | 1.59 × 10−9 | 1.18 × 10−4 | 2.83 × 10−4 | |
| PSO | 4.31 × 10−5 | 1.65 × 10−4 | 8.35 × 10−5 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Feng, T.; Niu, Q.; Deng, X. A Novel Swarm Optimisation Algorithm Based on a Mixed-Distribution Model. Appl. Sci. 2018, 8, 632. https://doi.org/10.3390/app8040632
Zhang X, Feng T, Niu Q, Deng X. A Novel Swarm Optimisation Algorithm Based on a Mixed-Distribution Model. Applied Sciences. 2018; 8(4):632. https://doi.org/10.3390/app8040632
Chicago/Turabian StyleZhang, Xiaoming, Tinghao Feng, Qingsong Niu, and Xijin Deng. 2018. "A Novel Swarm Optimisation Algorithm Based on a Mixed-Distribution Model" Applied Sciences 8, no. 4: 632. https://doi.org/10.3390/app8040632
APA StyleZhang, X., Feng, T., Niu, Q., & Deng, X. (2018). A Novel Swarm Optimisation Algorithm Based on a Mixed-Distribution Model. Applied Sciences, 8(4), 632. https://doi.org/10.3390/app8040632





