1. Introduction
Automatic music transcription (AMT) is a process that aims to convert a music signal into a symbolic notation. It is a fundamental problem of music information retrieval and has many applications in related fields, such as music education and composition. AMT has been researched for decades [
1], and the transcription of polyphonic music remains to be unsolved [
2]. The concurrent notes overlap in the time domain and interact in the frequency domain so that the polyphonic signal is complex. Piano is a typical multi-pitch instrument and has a wide playing range of 88 pitches. As a challenging task in polyphonic AMT, piano transcription has been studied extensively [
3].
The note is the basic unit of music, as well as of notations. The main purpose of AMT is to figure out which notes are played and when they appear in the music, corresponding to a note-level transcription. The approaches to note extraction can be divided into frame-based methods and note-based methods. The frame-based approaches estimate pitches in each time frame and form frame-level results. The most straightforward solution is to analyze the time-frequency representation of audio and estimate pitches by detecting peaks in the spectrum [
4]. Short time Fourier transform (STFT) [
5,
6] and constant Q transform (CQT) [
7] are two widely-used time-frequency analysis methods. Spectrogram factorization techniques are also very popular in AMT, such as non-negative matrix factorization (NMF) [
8] and probabilistic latent component analysis (PLCA) [
9,
10]. The activations of factorization indicate which pitch is active at the given time frame. Recently, many deep neural networks have been used to identify pitches and provided satisfying performance [
11,
12,
13]. However, the frame-level notations do not strictly match note events, and an extra post-processing stage is needed to infer a note-level transcription from the frame-level notation.
The note-based transcription approaches directly estimate the notes without dividing them into fragments, which are more popular than frame-based methods currently. One solution is integrating the estimation of pitches and onsets into a single framework [
14,
15]. Kameoka used harmonic temporal structured clustering to estimate the attributes of notes simultaneously [
16]. Cogliati and Duan modeled the temporal evolution of piano notes through convolutional sparse coding [
17,
18]. Cheng proposed a method to model the attack and decay of notes in supervised NMF [
19]. Another solution is employing a separate onset detection stage and an additional pitch estimation stage. The approaches in this category often estimate the pitches using the segments between two successive onsets. Costantini detected the onsets and estimated the pitches at the note attack using SVM [
20]. Wang utilized two consecutive convolutional neural networks (CNN) to detect onsets and estimate the probabilities of pitches at each detected onset, respectively [
21]. In this category, the onset is detected with fairly high accuracy, which benefits the transcription greatly; whereas the complex interaction of notes limits the performance of pitch estimation, especially the recall. Therefore, there are some false negative notes that cause “blank onsets” in notations.
Models in the transcription methods mentioned above are analogous to the so-called acoustic models in speech recognition. In addition to a reliable acoustic model, a music language model (MLM) may potentially improve the performance of transcription since musical sequences exhibit structural regularity. Under the assumption that each pitch is independent, hidden Markov models (HMMs) were superposed on the outputs of a frame-level acoustic classifier [
22]. In [
22], each note class was modeled using a two-state, on/off, HMM. However, the concurrent notes appear in correlated patterns, so the pitch-specific HMM is not suitable for polyphonic music. To solve this problem, some neural networks have been applied to modeling musical sequences, since the inputs and outputs of networks can be high-dimensional vectors. Raczynski used a dynamic Bayesian network to estimate the probabilities of note combinations over adjacent time steps [
23]. With an internal memory, the recurrent neural network (RNN) is also an effective model to process musical sequential data. In [
24], Boulanger-Lewandowski used the restricted Boltzmann machine (RBM) to estimate the high-dimensional distribution of notes and combined the RBM with RNN to model music sequences. This model was further developed in [
25], where an input/output extension of the RNN-RBM was proposed. Sigtia et al. also used RNN-based MLMs to improve the transcription performance of a PLCA acoustic model [
26]. Similarly, they proposed a hybrid architecture to combine the RNN-based MLM with different frame-based acoustic models [
27]. In [
28], the RNN-based MLM was integrated with an end-to-end framework, and an efficient variant of beam search was used to decode the acoustic outputs at each frame.
To our knowledge, all the existing MLMs are frame-based models, which are superposed on frame-level acoustic outputs. Poliner indicated that the HMMs only enforced smoothing and duration constraints on the acoustic outputs [
22]. Sigtia also concluded that the frame-based MLM played a role of smoothing [
28]. This conclusion is consistent with that in [
29]. To evaluate the long short-term memory network (LSTM) MLM, Ycart and Benetos did the prediction experiments using different sample rates. Their experiments showed that a higher sample rate leads to a better prediction in music sequences, because self repetitions are more frequent. They also indicated that the system would repeat the previous notes when note changes had occurred. Therefore, the frame-based MLM is unable to model the note transitions in music. Besides, the existing MLMs could only be used along with frame-based acoustic models. The process of decoding over each frame costs much computing time and storage space. In general, the frame-based MLM is not optimal to model music sequences or improve the note-level transcription.
In this paper, we focus on the note-based MLM, which could be integrated with note-based transcription methods directly. In this case, the note event is the basic unit, so the note-based MLM could model how notes change in music. We explore the RNN, RNN-RBM and their LSTM variants as note-based MLMs in modeling high-dimensional temporal structure. In addition, we use a note-based integrated framework to incorporate information from the CNN-based acoustic model into the MLM. An inference algorithm is proposed in the testing stage, which repairs the thresholding transcription results using the note-based MLMs. Rather than decoding at the overall note sequence using the original outputs of the acoustic model, the inference algorithm predicts notes only at the blank onsets. The results show that the proposed inference algorithm achieves better performance than traditional beam search. We also observe that the RBM is proper to estimate a high-dimensional distribution, and the LSTM-RBM MLM improves the performance the most.
The outline of this paper is as follows.
Section 2 describes the neural network MLMs used in the experiments. The proposed framework and inference algorithm are presented in
Section 3.
Section 4 details the model evaluation and experimental results. Finally, conclusions are drawn in
Section 5.
3. Proposed Framework
In this section, we describe how to combine the note-based acoustic model with the MLM to improve the transcription performance. The note-based acoustic model is described first, followed by the integrated architecture. At last, an inference algorithm for the testing stage is introduced.
3.1. Acoustic Model
Apart from the MLM, the note-based acoustic model is another part of the proposed framework. The acoustic model is used to identify pitches in the current input. Given as the feature input at the n-th onset, the acoustic model can estimate the probability of pitches . Therefore, the note sequence can be obtained preliminarily through feeding a sequence of feature inputs to the acoustic model.
Here, we employ the hybrid note-based model in [
21], which contains an onset detection module and a pitch estimation module. As shown in
Figure 2, one CNN is used to detect onsets, and another CNN is used to estimate the probabilities of pitches at each detected onset.
We trained a CNN with one output unit as the onset detector, giving binary labels to distinguish onsets from non-onsets. The CNN takes a spectrogram slice of several frames as a single input, and each spectrogram excerpt centers on the frame to be detected. Feeding the spectrograms of the test signal to the network, we can obtain an onset activation function over time. The frame whose activation function is greater than the threshold is set as the detected onset.
The onset detector is followed by another CNN for multi-pitch estimation (MPE), which has the same architecture except for the output layer. Its input is a spectrogram slice centered at the onset frame. The CNN has 88 units in the output layer, corresponding to the 88 pitches of the piano. To make sure the multiple pitches can be estimated at the same time, all the outputs are transformed by a sigmoid function. In this case, a set of probabilities of 88 pitches at detected onsets is estimated through this network.
3.2. Integrated Architecture
The integrated architecture is constructed by applying the model in [
27,
28] to the note-level transcription. The model produces a posterior probability
, which can be represented using Bayes’ rule:
where
and
are the priors and
is the likelihood of the sequence of acoustic inputs
and corresponding transcriptions
. The likelihood can be factorized as follows:
Similarly to the assumptions in HMMs, the following independence assumptions are made:
Under these assumptions, the probability in Equation (
11) can be written as:
Based on Equations (10) and (14), the posterior probability produced by the integrated architecture can be reformulated as follows:
where
is prior statistics analyzed on the training data. In Equation (
15), the term
is obtained from the acoustic model, while the prior
can be calculated from the MLM using Equation (1). Therefore, the acoustic model and the MLM are combined directly in the integrated architecture.
3.3. Inference Algorithm
The integrated model can be trained by maximizing the posterior of training sequences. The process is easy because training of the acoustic model and the MLM is independent. In the test stage, we also aim to find the note sequence
maximizing the posterior
, which can be reformulated as a recursive form:
However, the test inference is rather complex. To estimate in the note sequence, we need to know the history and the acoustic output . Here, the history is not determined, and the possible configurations of are exponential in the number of pitches. Therefore, greedily searching for the best solution of is intractable.
Beam search is an algorithm for decoding, which is commonly used in speech recognition. There are two parameters when it scales to note sequences:
K is the branching factor, and
w is the width of the beam. The algorithm considers only
K most possible configurations of
according to the acoustic output
. At each inference step, no more than
w partial solutions are maintained for further search. As shown in Equation (
16), the
K candidates for
should be configurations maximizing
, and
w is the number of partial solutions maximizing
or
.
Similar to the frame-based inference in [
30], the beam search algorithm can be used to decode globally using the raw outputs of the note-based acoustic model and the MLM. This method will be referred to as global beam search (GBS). As described in Algorithm 1, the
K candidates at each onset are sampled from the posterior probability
. The simplified process is effective because the possible configurations of
can be easily enumerated through the independent acoustic outputs.
In the proposed inference algorithm (Algorithm 2), we adopt the beam search algorithm to repair the thresholding transcription results locally. Applying a proper threshold to the acoustic outputs, the note-based acoustic model produces a preliminary transcription. However, the fixed threshold leads to some false negative notes at the detected onset. Rather than decoding at each onset of the note sequence, the beam search algorithm is used to predict notes only at the blank onsets. At the non-blank onset, is determined through applying a threshold to the pitch probabilities . The determined notes without using MLM could avoid the accumulation of mistakes in a sequence over time. At each blank onset, we choose the top K candidates for maximizing . Under the rule of maximizing the posterior , notes at the blank onsets are predicted using the context information.
| Algorithm 1 Global beam search (GBS). |
Input: The acoustic model’s outputs at onset ;
The beam width w; the branching factor K. Output: The most likely note sequence . beam← new beam object beam.insert for to N do beam_tmp ← new beam object for in beam do for to K do -th_most_probable() with beam_tmp.insert end for end for beam_tmp ← min-priority queue of capacity beam ← beam_tmp end for return beam.pop() * Beam object is a queue of triple , where at onset n, l is the accumulated posterior probability , s is the partial candidate note sequence and stands for the music language model taking as the current input. A min-priority queue of fixed capacity w maintains at most w highest values.
|
| Algorithm 2 Local beam search (LBS). |
Input: The acoustic model’s outputs at onset ; The beam width w; The branching factor K; the threshold T applied to the acoustic outputs. Output: The most likely note sequence . beam← new beam object beam.insert for to N do beam_tmp ← new beam object for in beam do exceed the threshold T if isEmpty() then for to K do -th_probable() with beam_tmp.insert end for else with beam_tmp.insert end if end for beam_tmp ← min-priority queue of capacity beam ← beam_tmp end for return beam.pop() * Beam object is a queue of triple , where at onset n, l is the accumulated posterior probability , s is the partial candidate note sequence and stands for the music language model taking as the current input. A min-priority queue of fixed capacity w maintains at most w highest values.
|
5. Conclusions
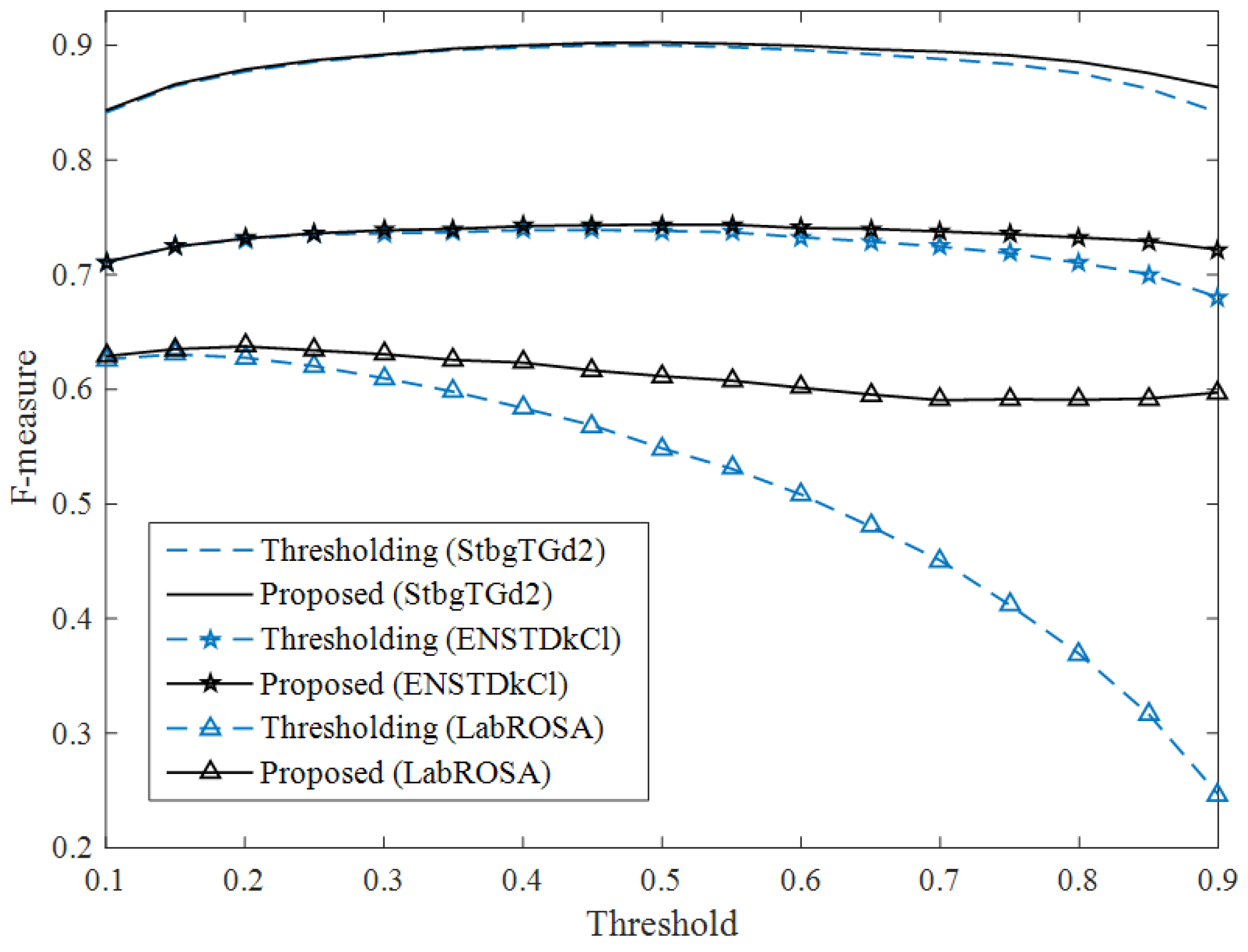
In this paper, we propose note-based MLMs for modeling note-level music structure. These note-based MLMs are trained to predict notes at the next onset, which is different from the smoothing operation of existing frame-based MLMs. An integrated architecture is used to combine the outputs of the MLM and the note-based acoustic model directly. We also propose an inference algorithm, which uses the note-based MLM to predict notes at the blank onsets in the thresholding transcription results. The experiments are conducted on the MAPS and LabROSA databases. Although the proposed algorithm only achieves an absolute 0.34% F-measure improvement on the synthetic data, it reaches absolute 0.77% and 2.39% improvements on two real piano test sets, respectively. We also observe that the combination of RBM and recurrent structure models the high-dimensional sequences better than a single RNN or LSTM does. Although the LSTM shows no superiority to other MLMs in transcribing the real piano, the LSTM-RBM always helps the system yield the best results regardless of the performance of acoustic models.
Overall, the improvement of the proposed algorithm over the thresholding method is small. One of the possible reasons is the limited training data. The MLMs are trained using only 161 pieces in the MAPS database, and the small amount of data may lead the neural networks to over-fitting. The abundance of musical scores can provide a way to solve the problem. Besides, the note sequences are indexed using the onset in the current system. Actually, the temporal structure of musical sequences should contain how the notes appear and last correlatively. Ignoring the note’s offset or duration time, the representation of musical sequences is partial. Therefore, the MLMs in this paper cannot model the temporal structure of note sequences completely. In the future, we will search for a proper way to represent the note-level musical sequences. One possible solution is to add a duration model to the current MLMs, such as an HMM.