Parameters Studies on Surface Initiated Rolling Contact Fatigue of Turnout Rails by Three-Level Unreplicated Saturated Factorial Design

Abstract

Surface initiated rolling contact fatigue (RCF), mainly characterized by cracks and material stripping, is a common type of damage to turnout rails, which can not only shorten service life of turnout but also lead to poor running safety of vehicle. The rail surface initiated RCF of turnouts is caused by a long-term accumulation, the size and distribution of which are related to the dynamic parameters of the complicated vehicle-turnout system. In order to simulate the accumulation of rail damage, some random samples of dynamic parameters significantly influencing it should be input. Based on the three-level unreplicated saturated factorial design, according to the evaluation methods of H, P and B statistic values, six dynamic parameters that influence the rail surface initiated RCF in turnouts, namely running speed of vehicle, axle load, wheel-rail profiles, integral vertical track stiffness and wheel-rail friction coefficient, are obtained by selecting 13 dynamic parameters significantly influencing the dynamic vehicle-turnout interaction as the analysis factors, considering four dynamic response results, i.e., the normal wheel-rail contact force, longitudinal creep force, lateral creep force and wheel-rail contact patch area as the observed parameters. In addition, the rail surface initiated RCF behavior in turnouts under different wheel-rail creep conditions is analyzed, considering the relative motion of stock/switch rails. The results show that the rail surface initiated RCF is mainly caused by the tangential stress being high under small creep conditions, the normal and tangential stresses being high under large creep conditions, and the normal stress being high under pure spin creep conditions.

1. Introduction

Turnouts are essential components of railway facilities. A turnout consists of a switch panel, a closure panel and a crossing panel [1]. In order to achieve vehicle transfer, the switch rail and point rail are designed as variable cross-section rails, transferring the wheels between the stock rail and switch rail and between the wing rail and nose rail. During this process, skipping wheel-rail contact points can cause strong dynamic wheel-rail interaction, which is also a main reason for wear, rolling contact fatigue (RCF) and accumulated plastic deformation [2,3,4] of turnout rail. The surface initiated RCF is mainly characterized by surface cracks (see Figure 1). These are caused by long-term accumulation and development of RCF under wheel loads, and the position and size of rail damage caused by each pass of vehicle wheels are related to the dynamic parameters of the vehicle-track system [1,3]. Therefore, it is necessary to analyze the RCF behaviors of turnout rails and the main parameters influencing the rail RCF in order to guide the simulation and prediction of rail damage in turnouts.

Figure 1. Surface cracks.

Wheel-rail RCF is a longstanding worldwide problem, and has been one of the research topics of international academic conferences such as the Conference on Contact Mechanics (CM) and the International Association for Vehicle System Dynamics (IAVSD). Researchers have presented many numerical and experimental studies on wheel-rail RCF in sectional lines, which form the basis for studying rail RCF in turnouts. However, considering the complicated structure of turnouts, the research is more difficult. Nicklisch et al. [5] presented a method for simulating the wear, RCF and plastic deformation of turnout switch/crossing panel rails, and used the method to evaluate the effects before and after the turnout geometric size and rails are optimized. Nielsen et al. [3] presented a numerical method for calculating the accumulated wear and RCF of turnout switch panel rails, for which, the random process of vehicle motion was simulated through discretizing the dynamic parameters of the vehicle-turnout system, the Archard model was used to predict the rail wear, and the rail RCF was predicted according to the Palmgren–Miner rule and a model deduced based on the Shakedown theory. In addition, they also evaluated the structural design of turnout switches based on this method. Markine, Wan and Wang et al. [6,7,8] optimized the track stiffness and rail profiles in order to reduce the dynamic wheel-rail interaction at turnout zones and solve problems such as rail wear and fatigue of turnout rails. Pletz et al. [9] presented a finite element model for crossing with a single running wheel according to the wheel-rail vibration, elastic wheel deformation and plastoelastic rail deformation, in order to calculate the dynamic wheel-rail interaction, then they also presented a simplified finite element model for calculating the dynamic wheel-crossing interaction [10], according to the influence of grid precision and calculation time, through setting appropriate grid sizes. Based on this model, they performed a contrast analysis on the properties of three materials used for crossings, Manganese steel, Hardox and Marage300 according to the generation and development of RCF cracks. Xin et al. [4] presented a finite element model with regard to crossing with a single running wheel-set in order to calculate the dynamic wheel-rail interaction, and studied the generation and fatigue process of RCF cracks of crossing rails based on their model. Researchers from Yanshan University of China [11,12,13] analyzed the wear and fatigue properties of high manganese steel/austenitic steel and bainitic steel materials used for crossings through material tests in order to realize good wear and fatigue resistance. At present, for the calculation of wheel-rail contact information of turnout switches, researchers usually consider a switch rail and a stock rail as a combined part. This paper presents a further study on the wheel-rail RCF behavior of turnout switches according to the relative motion of stock/switch rails.

In the early stages, the factorial design method was mainly adopted for determining active factors influencing the designs of products, and has been proven to be a feasible and effective method for selecting significant influence factors. The saturated factorial design method has been adopted widely in fields such as physics, biology and finance. However, the mutual influence among all factors must always be considered in this method and the calculation load is heavy if there are many active factors. In addition, many replicated tests will be required [14]. In response to this, unreplicated saturated factorial design methods can greatly shorten the test process and calculation time [15]. Hence, in the past 40 years, researchers have presented many unreplicated saturated factorial design methods, including normal or semi-normal probability graphs [16], Dong93 [17] and PSZ method [18]. Based on a given nominal layout of turnout, Kassa and Nielsen [1] used design of experiments methodology and a two-level fractional factorial screening design to select the most significant parameters related to the performance of railway turnout, including the axle load, wheel–rail friction coefficient, and wheel/rail profiles. Xu et al. [19] adopted a two-level unreplicated saturated factorial design method to select active factors that influence the wear performance of turnout rails. However, there have been few studies that use the three-level unreplicated saturated factorial design method for selecting active factors influencing the damage to turnout rails. Compared to the two-level factorial design method, the three-level unreplicated saturated factorial design method can be adopted to solve more complicated system factorial design problems such as multi-scale material and non-linear structure problems.

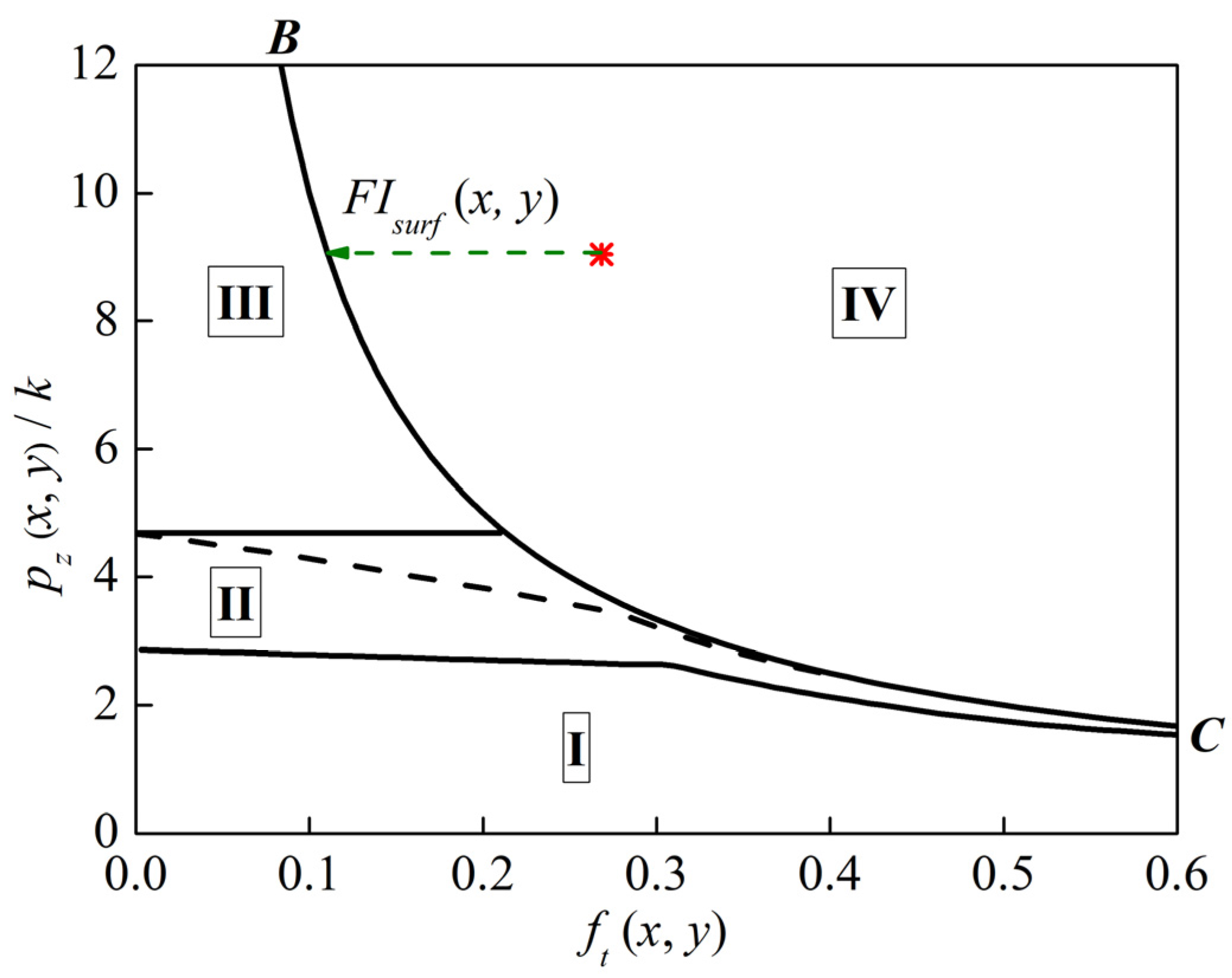
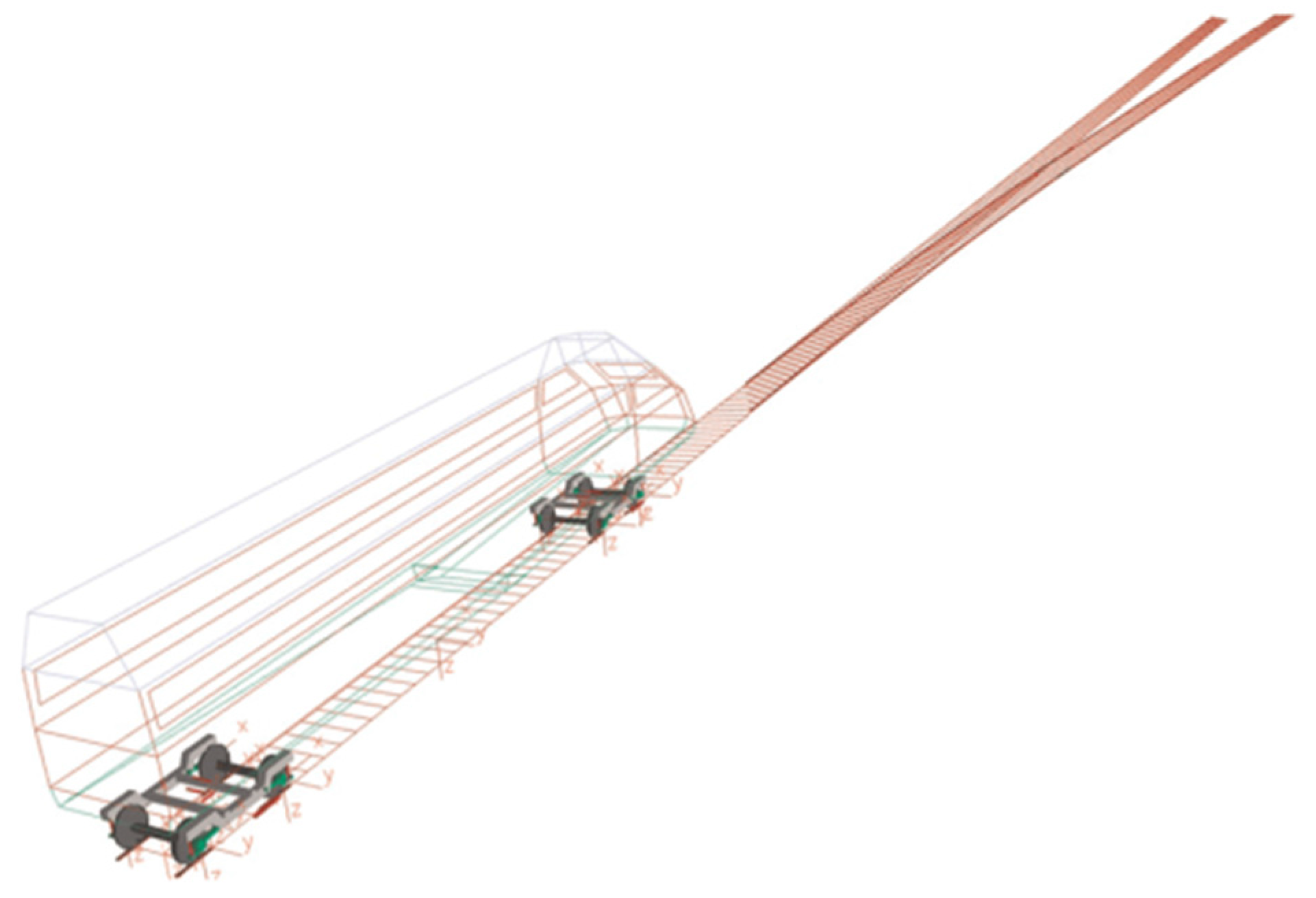
The wheel-rail contact mechanics in railway turnout is important for the investigation of rail damage. In this paper, firstly, a wheel-rail rolling contact calculation model considering the relative motion of stock/switch rails is established, and the surface initiated RCF behavior of turnout switch rail is studied under different wheel-rail creep conditions. Secondly, the dynamic parameters which can significantly influence the rail surface initiated RCF of turnouts are selected by the three-level unreplicated saturated factorial design method. The conclusions of this work can provide a theoretical guidance for the simulation and prediction of rail RCF in turnouts.

2. Simulation of Rail Surface Initiated RCF

According to the authors of [20,21], the prediction of surface initiated RCF is in direct relation to the wheel-rail rolling contact behavior, e.g., the normal and tangential wheel-rail contact stresses, wheel-rail contact patch positions and shapes etc. In this section, firstly, the prediction model of surface initiated RCF based on the Shakedown theory is introduced. Then, a wheel-rail rolling contact model of turnout switch panel considering the relative motion of stock/switch rails is built to calculate the wheel-rail contact information. Based on these two models, surface initiated RCF is performed at the section of switch rail with the head width 35 mm in a high-speed railway turnout called CN60-1100-1:18 under different wheel-rail creep conditions.

2.1. Surface Initiated Rolling Contact Fatigue

The surface initiated RCF is related to the surface material ratcheting effect and low cycle fatigue [21]. At present, the shakedown theory is adopted to quickly and correctly identify the relation between the load level and the surface initiated RCF factors such as the material ratcheting effect and low cycle fatigue. For the material shakedown map, see Figure 2. In this figure, the meanings of the abscissa and ordinate will be explained later, BC is the boundary line between the material shakedown region and ratcheting effect region. When entering into the ratcheting effect region from the shakedown region, the material will be subject to continuous accumulation of plastic deformation until cracks occur.

Figure 2. Shakedown map of wheel-rail material.

In the shakedown map, I is the elastic region where the material is not subject to contact fatigue, II is the elastic shakedown region where the rail material is subject to high cycle fatigue, III is the plastic shakedown region where the rail material is subject to low cycle fatigue, and IV is the ratcheting effect region where the rail material is subject to plastic deformation accumulation. When the plastic deformation accumulates to a certain degree, cracks will occur. The local creepages will be calculated in this paper, and thus the partial slip conditions would also be expected. Based on shakedown theory, an index for prediction of rolling contact load resulting in material ratchetting was introduced in reference [21]. This index was based on a full-slip contact approach. In addition, the fatigue index was always calculated for the total contact patch. If the distribution of partial shear stress in the wheel–rail contact patch is not full-slip, the case will be more complicated. A straight-forward approach in such a case would be to relate RCF damage to the local shear stress as [22,23]:

$$F{I}_{surf}(x,y)=f_t(x,y)-\frac{k}{p_z(x,y)}$$

(1)

where p_z is the normal wheel-rail contact stress, k is the shear yield strength of the material, and f_t is the traction coefficient calculated by Equation (2).

$$f_t(x,y)=\frac{\sqrt{{(p_x(x,y))}^2+(p_y{(x,y)}^2)}}{p_z(x,y)}$$

(2)

where p_x and p_y are the longitudinal and lateral wheel-rail tangential contact stresses respectively. Surface initiated RCF is predicted to occur if FI_surf > 0. The fatigue index values could be higher if partial slip is considered. Therefore, this index is only used to simulate and compare the surface initiated RCF of turnout rails but not as the observation parameter in factorial design. In addition, when the state of wheel-rail contact is full-slip conditions, the traction coefficient is equal to the wheel-rail friction coefficient, and when the state of wheel-rail contact is partial slip conditions, the traction coefficient is less than the wheel-rail friction coefficient. Therefore, this method considering the partial slip conditions is also matched to the full-slip shakedown diagram shown in Figure 2.

2.2. Wheel-Rail Rolling Contact Model

The structure of switch panel in railway turnout is shown in Figure 3, both the stock/switch rails are installed on the slide baseplate; the difference between them is that no part is set between the switch rail and slide baseplate, so the slide baseplate can offer a rigid support to the switch rail, and no vertical displacement will occur with the switch rail in relation to the slide baseplate under wheel loads. The stock rail is connected with the slide baseplate through the rubber pad of the fastener system and will experience vertical displacement in relation to the slide baseplate under wheel loads.

Figure 3. Combined structure of stock/switch rails.

Based on the relative spatial positions of stock/switch rails as well as the conditions of support provided to them from the slide baseplate, a wheel-rail contact calculation method considering the relative motion of stock/switch rails was presented in the previous work. This method mainly comprises three steps: (1) calculating the primary and secondary points between a wheel and the switch rail as well as between the wheel and the stock rail based on the trace line method; (2) analyzing the wheel-rail contact state according to the discriminant formula, i.e., the wheel is in contact with the stock rail only, the wheel is in contact with the switch rail only or the wheel is in contact with both the stock rail and switch rail; (3) calculating the distribution of the wheel-rail force on the switch rail and stock rail according to the coordinative relation between the displacement and forces with regard to the wheel, switch rail and stock rail, and finally calculating the wheel-rail contact information including the contact patch shape and distribution of normal and tangential wheel-rail contact stresses according to the ANALYN (normal contact) and FASTRIP (tangential contact) wheel-rail contact model [24,25,26]. For the detailed method, see Reference [27,28].

2.3. Surface Initiated RCF of Turnout Rail

In order to analyze the surface initiated RCF of turnout rail under different wheel-rail creep conditions, the calculations are presented at the section of switch rail with the head width 35 mm in a high-speed railway turnout called CN60-1100-1:18. The situation where the rail profiles contact with a new profile of LMA tread is analysed. The axle load applied on the wheel-set is 12 t, and the nominal wheel rolling radius is 430 mm. The assumed material properties of the wheel are the same as those of the rail, the elastic modulus, Poisson’s ratio and wheel-rail friction coefficient are 2.1 × 10¹¹ N/m², 0.3 and 0.3 [29], respectively, and the ultimate shear strength of the rail material is 350 MPa. When the lateral wheel-set displacement y_w results are 0 mm, 3 mm, 6 mm and 9 mm, respectively, the wheel-rail contact point positions of the selected section will be those as shown in Figure 4. In this figure, the coordinate zero point refers to the center of railway track, y and z refers to the lateral and vertical direction of railway line, respectively.

Figure 4. Wheel-rail contact point positions. (a) y_w = 0 mm; (b) y_w = 3 mm; (c) y_w = 6 mm; (d) y_w = 9 mm.

As shown in Figure 4, when the lateral wheel-set displacement is 9 mm, the wheel comes into contact with the switch rail and stock rail at the same time. Multi-point contact is one of the main characteristics of wheel-rail contact relations in turnout zones. Therefore, this paper studies the surface initiated RCF of turnout rails under different wheel-rail creep conditions, taking the lateral wheel-set displacement of 9 mm as an example.

2.3.1. Small Creep Conditions

Figure 5a shows the surface initiated RCF index of turnout rails within the wheel-rail contact patches when the longitudinal wheel-rail creep f_x, lateral creep f_y and spin creep fin are −5 × 10⁻⁴, −5 × 10⁻⁴ and 0, respectively. In this figure, the upper part refers to the wheel-stock rail contact region, and the lower part refers to the wheel-switch rail contact region. The black solid lines refer to the boundaries of the wheel-rail contact patch regions, and the colored region refers to the value of surface initiated RCF index if it greater than 0. The blank region means that the surface initiated RCF index of turnout rails is less than 0, namely no surface initiated RCF occurs. The coordinate zero point refers to the center of first contact patch, x and y refers to the longitudinal and lateral direction of railway line, respectively. Under the small wheel-rail creep conditions, the surface initiated RCF regions are small and located mainly at the trailing edge of the contact patches at the stock rail side along the rolling direction. The surface initiated RCF index within the wheel-switch rail contact patches are less than 0. The regions with surface initiated RCF account for 2.9% of the total contact patch area.

Figure 5. Small creep condition, f_x = −5 × 10⁻⁴, f_y = −5 × 10⁻⁴, fin = 0. (a) surface initiated rolling contact fatigue (RCF) index; (b) Shakedown map.

Figure 5b shows the stress state distribution of the rail surface material in the shakedown map. According to the shakedown map, most of the contact stress state positions within the wheel-rail contact patches are covered in the material shakedown region, while in the material ratcheting effect region, the proportion is relatively low. The tangential contact stress on this part of the rail surface material is high, while the normal stress is relatively low, therefore under the small creep conditions; the overly high tangential stress on the rail surface material is the main reason why the material is subject to a ratcheting effect.

2.3.2. Large Creep Conditions

Figure 6a shows the surface initiated RCF index of turnout rails within the wheel-rail contact patches when the longitudinal wheel-rail creep f_x, lateral creep f_y and spin creep fin are −3 × 10⁻³, −3 × 10⁻³ and 0, respectively. Under the large wheel-rail creep conditions, the surface initiated RCF regions are big and located mainly at the center of the contact patches at the wheel-stock rail contact patch side. The surface initiated RCF index within the wheel-switch rail contact patches are less than 0. The regions with surface initiated RCF account for 25.4% of the total contact patch area.

Figure 6. Large creep condition, f_x = −3 × 10⁻³, f_y =−3 × 10⁻³, fin = 0. (a) surface initiated RCF index; (b) Shakedown map.

Figure 6b shows the stress state distribution of the rail surface material in the shakedown map. According to the shakedown map, the proportion of the stress state positions within the wheel-rail contact patches in the material ratcheting effect region is high. Both the tangential and normal contact stresses on this part of rail surface material are high, therefore under large wheel-rail creep conditions, the overly high tangential and normal stresses on the rail surface material are the main reasons why the material is subject to a ratcheting effect.

2.3.3. Pure Spin Creep Conditions

Figure 7a shows the surface initiated RCF index of turnout rails within the wheel-rail contact patches when the longitudinal wheel-rail creep f_x, lateral creep f_y and spin creep fin are 0, 0 and −0.5 m⁻¹, respectively. Under the pure spin wheel-rail creep conditions, the surface initiated RCF regions are big and located mainly at the center of the contact patches at the wheel-stock rail contact patch side. The surface initiated RCF index within the wheel-switch rail contact patches are less than 0. The regions with surface initiated RCF account for 18.7% of the total contact patch area.

Figure 7. Pure spin creep condition, f_x = 0, f_y = 0, fin = −0.5 m⁻¹. (a) surface initiated RCF index; (b) Shakedown map.

Figure 7b shows the stress state distribution of the rail surface material in the shakedown map. According to the shakedown map, the proportion of the stress state positions within the wheel-rail contact patches in the material ratcheting effect region is high. The tangential stress on this part of the rail surface material is low, while the normal stress is high, therefore under pure spin wheel-rail creep conditions; the overly high normal stress on the rail surface material is the main reason why the material is subject to ratcheting effect.

3. Parameters Studies and Discussions

The rail surface initiated RCF of turnout is closely related to the dynamic vehicle-turnout response, while the latter is related to the dynamic parameters of the vehicle system, turnout track system and wheel-rail contact etc. However, many dynamic parameters of the vehicle-turnout system can be obtained, but their influence on the rail RCF in turnout is still unclear. Therefore, in this Section, the three-level unreplicated saturated factorial design method is adopted to select the dynamic parameters that significantly affect the rail surface initiated RCF in order to provide theoretical guidance for the simulation and prediction of turnout rail RCF. In this paper, the dynamic three-dimensional (3D) multi-body (Figure 8) vehicle-turnout system model is established using the commercial SIMPACK software, based on the Chinese CRH2 vehicle. The turnout model is an elastic track model (Figure 9) established according to a Chinese CN60-1100-1:18 high-speed railway turnout. For the detailed establishment of the models, see references [8,30].

Figure 8. Multi-body model of vehicle.

Figure 9. Elastic track foundation.

3.1. Three-Level Unreplicated Saturated Factorial Design Method

Chen et al. [31,32] presented a three-level unreplicated saturated factorial design method, in which the statistical model can be expressed as:

$$y=u+{\alpha }_i+{\beta }_j+\alpha {\beta }_{ij}+{\epsilon }_{ij}{,}^{}i,j=1,2,3$$

(3)

where, y = (y₁, y₂, …, y_n)^T is the observation vector, μ is the overall average, α_i is the main influence of the first factor, β_j is the main influence of the second factor, α_i and β_j shall satisfy the following constraint condition:

$$\{\begin{array}{l}{\displaystyle {\sum }_{i=1}^3{\alpha }_i}=0\\ {\displaystyle {\sum }_{j=1}^3{\beta }_j}=0\end{array}$$

(4)

αβ_ij is the mutual influence when the first factor is i level and the second factor is j level, the satisfying the following constraint condition:

$${\displaystyle {\sum }_{i=1}^3\alpha {\beta }_{ij}}=0{,}^{}j=1,2,3^{}{ \mathrm{and} }^{}{\displaystyle {\sum }_{j=1}^3\alpha {\beta }_{ij}}=0{,}^{}i=1,2,3$$

(5)

ε_ij is the experimental error, ε_ij is the independent normal distribution variable, and its mathematical expectation of normal distribution is 0, the variance is σ², which can be expressed by Equation (6).

$${\epsilon }_{ij}=N(0,{\sigma }^2)$$

(6)

Then the most active influence factors can be selected according to all observation values and the assumed conditions as shown in Equation (7).

$$\{\begin{array}{cc}{H}_0:{\alpha }_i,{\beta }_j,\alpha {\beta }_{ij}{,}^{}i,j=1,2,3\hfill & \hfill \mathrm{all} \mathrm{be} \mathrm{zero}\\ H_1:{\alpha }_i,{\beta }_j,\alpha {\beta }_{ij}{,}^{}i,j=1,2,3\hfill & \hfill \mathrm{not} \mathrm{all} \mathrm{be} \mathrm{zero}\end{array}$$

(7)

If H₀ is false, it is necessary to confirm which of α_i, β_j or αβ_ij is a non-zero value. When the deviation square and SS_i of the corresponding factors are considered in this method, the following can be adopted instead of the test assumptions of (7):

$$\{\begin{array}{l}{H}_0:\frac{EM{S}_1}{{\sigma }^2}=\frac{EM{S}_2}{{\sigma }^2}=\dots =\frac{EM{S}_m}{{\sigma }^2}=1\\ H_1:\frac{EM{S}_k}{{\sigma }^2},k=1,\dots ,m\hspace{1em}\hspace{1em}\mathrm{existing} \mathrm{results} \mathrm{greater} \mathrm{than} 1\end{array}$$

(8)

where, m is the total number of times the experiment has been conducted, EMS_i is the mathematical expectation of the mean square error. The equation for the mean square error MS_i is shown below [33,34]:

$$M{S}_i=S{S}_i/2$$

(9)

In the three-level unreplicated saturated factorial design method, three statistical methods, i.e., H/P/B statistical values, are adopted to select the significant influence factors.

3.1.1. H Statistical Value

The H statistical values were presented and adopted in the three-level unreplicated saturated factorial design method by Holms et al. [31,35], and can be expressed as:

$$H=\frac{(1+l)M{S}_k}{{\displaystyle {\sum }_{i=1}^{l}M{S}_{(i)}+M{S}_k}}{,}^{}k=1,2,\dots ,m$$

(10)

where, MS₍₁₎ ≤ MS₍₂₎ ≤ … ≤ MS_(m) is the permutation of MS_(i) statistical values from low to high. l is the maximum value of s and j. s is the minimum number of columns in the orthogonal table for evaluating the error variance, j is the maximum positive integer satisfying Equation (11).

$$M{S}_{(j)}/({\displaystyle {\sum }_{i=1}^j(M{S}_{(i)}/j)})<c_{pool}(\alpha ;j,m)$$

(11)

In Equation (11), the right part is the 1 − α quantile of the left part, α is the global significance level. When an H statistical value is adopted, the global significance level α and minimum number of columns in the orthogonal table s for evaluating the error variance should be given. If they satisfy Equation (12), then H₀ will be false, and those columns satisfying Equation (12) are considered to have a non-zero effect.

$$H>c^{(1)}(\alpha ;s,m)$$

(12)

During the testing process, some necessary critical values (c⁽¹⁾ (α; s, m)) and 1 − α quantiles (c_pool (α; j, m)) were listed in the appended Table A1.

3.1.2. P Statistical Value

The P statistical values are adopted for selecting key influence factors in the two-level unreplicated saturated factorial design method. The P statistic values were presented by Picard et al. [31,36], and can also be adopted in the three-level unreplicated saturated factorial design method, the expression of which is:

$$P=M{S}_k/({\displaystyle {\sum }_{i=1}^{l}M{S}_{(i)}}){,}^{}k=1,2,\dots ,m$$

(13)

where, l is the maximum positive integer less than or equal to 0.6 times m. When P statistical values are adopted, the global significance level α should be given first. If Equation (14) is satisfied, the H₀ will be false, and those columns satisfying Equation (15) are considered to have a non-zero effect.

$$M{S}_{(m)}/({\displaystyle {\sum }_{i=1}^{j}M{S}_{(i)}})>c_1^{(2)}(\alpha ,m)$$

(14)

$$P>c_2^{(2)}(\alpha ,m)$$

(15)

where, c₁⁽²⁾ (α, m) is the 1-α quantile of the left part of Equation (14), c₂⁽²⁾ (α, m) is the 1-α quantile of the left part of Equation (14). During the testing process, some necessary critical values (c₁⁽²⁾ (α,m)) and (c₂⁽²⁾ (α, m)) were listed in the appended Table A2.

3.1.3. B Statistical Value

The B statistical values were presented by Bartlett et al. [31,37], and their expression is shown below:

$$B=\ln (\frac{1}{k}{\displaystyle {\sum }_{i=1}^{k}M{S}_{(i)}})-\frac{1}{k}{\displaystyle {\sum }_{i=1}^k\ln M{S}_{(i)}}{,}^{}k=2,3,\dots ,m$$

(16)

The steps for adopting B values are shown below:

Step1: Give the global significance level α, let k = m, if Equation (17) is satisfied, go to Step 2, otherwise H₀ should be considered as a true value and the calculation should be ended;

$$B>c^{(3)}(\alpha ,k)$$

(17)

Step 2: Let k = k − 1, if k > 1, calculate the B statistical value and then go to Step 3, otherwise go to Step 4;

Step 3: If Equation (17) is satisfied, go to Step 2, otherwise go to Step 4;

Step 4: Check H₀ for being false and consider that column m-k with the maximum squared error has a non-zero effect.

During the testing process, some necessary critical values (c⁽³⁾ (α, k)) were listed in the appended Table A3.

3.2. Orthogonal Design Test

3.2.1. Analysis Factor and Observation Parameters

In this Section, 13 system parameters influencing the dynamic vehicle-turnout properties are selected as the analysis factors for studying in order to evaluate the degree of influence of the different analysis factors on the dynamic vehicle-turnout interaction and select those analysis factors significantly influencing the rail surface initiated RCF. The selected 13 analysis factors and their three-level values are shown in Table 1. The turnouts are subject to track irregularity due to asymmetric structures, therefore the influence of geometric track irregularity on the dynamic response of the vehicle-turnout system is not considered in the factor analysis.

Table 1. Analysis factors of turnout rail surface initiated RCF and their levels.

No.	Analysis Factor	Analysis Factor Levels
		Level 1	Level 2	Level 3
x1	Train speed/(km/h)	40	80	120
x2	Train axle load/(t)	12	14	16
x3	Nominal wheel rolling radius/(mm)	420	460	500
x4	Wheel profile	LMA	S1002CN	XP55
x5	Lateral stiffness of primary suspension/(kN/mm)	5.0	6.5	8.0
x6	Vertical stiffness of primary suspension/(kN/mm)	1.0	1.2	1.4
x7	Lateral stiffness of secondary suspension/(kN/mm)	0.10	0.15	0.20
x8	Vertical stiffness of secondary suspension/(kN/mm)	0.15	0.18	0.21
x9	Rail gauge/(mm)	1432	1435	1438
x10	Stock rail cant	0	1/40	1/20
x11	Integral lateral track stiffness/(kN/mm)	30	50	70
x12	Integral vertical track stiffness/(kN/mm)	80	100	120
x13	Wheel-rail friction coefficient	0.1	0.3	0.5

In Table 1, besides the wheel profile, the levels of analysis factors can be realized through adjusting the parameters. For wheel profiles, in this paper the one corresponding to Level 1 is a Chinese standard LMA wheel tread, the one corresponding to Level 2 is a Chinese standard S1002CN wheel tread, and the one corresponding to Level 3 is a Chinese standard XP55 wheel tread, see Figure 10 for the three-level wheel treads.

Figure 10. Three-level definition of wheel profile.

After the analysis factors and their levels are obtained, the observation parameters related to the rail surface initiated RCF should be ascertained. The fatigue index in Equations (1) and (2) have been used as a marker for RCF probability, but always qualitatively. Therefore, this index will not be used directly as the observation parameter in factorial design. According to the discussion results in Section 2.3, the parameters influencing the rail surface initiated RCF of railway turnout are the normal and tangential contact stresses, where the normal wheel contact stress is mainly related to the normal wheel-rail force and contact patch area. Therefore, in this paper, the normal wheel-rail contact force F_z and contact patch area A_c are selected for reflecting the normal wheel-rail contact stress level. Similarly, the tangential wheel-rail contact stress is mainly related to the tangential wheel-rail force and contact patch area. Therefore, in this paper the longitudinal wheel-rail creep force F_x, lateral creep force F_y and contact patch area A_c are selected for reflecting the tangential wheel-rail contact stress level. In conclusion, F_z, F_x, F_y and A_c are adopted as the observation parameters in the factorial design. In fact, these parameters are not independent markers for surface initiated RCF. The main purpose of this is to find out what is missing in the factorial design as the single parameter FI_surf cannot be used.

3.2.2. Orthogonal Test Plan

A total of 27 tests were conducted for the selected 13 analysis factors influencing the rail surface initiated RCF of turnouts using to the three-level unreplicated saturated factorial design based on the L₂₇ (3¹³) orthogonal table, see Table 2 for the detailed orthogonal test plan. In this Table, 1, 2 and 3 refer to the three levels. The simulation calculation for the tests of Table 2 is conducted according to the vehicle-turnout dynamic model. During the calculation, a vehicle passing the turnout in the diverging line with facing move is simulated. The dynamic response results of the obtained four observation parameters, i.e., F_z, F_x, F_y and A_c, are the observation vectors for the statistical analysis model, which, together with the 13 analysis factors selected according to H, P and B statistical values, are adopted to obtain the factors significantly influencing turnout rail RCF. It should be noted that the maximum dynamic wheel-rail response of the first wheel-set of vehicle at the switch rail sides is selected as the observation value. The calculated observation values are shown in Table 2.

Table 2. Twenty-seven experiment samples and the corresponding observation values.

No.	x1	x2	x3	x4	x5	x6	x7	x8	x9	x10	x11	x12	x13	Fz (kN)	Fx (kN)	Fy (kN)	Ac (mm2)
1	1	1	1	1	1	1	1	1	1	1	1	1	1	61.7	0.2	3.0	90.1
2	1	1	1	1	2	2	2	2	2	2	2	2	2	61.6	4.2	6.6	126.3
3	1	1	1	1	3	3	3	3	3	3	3	3	3	60.0	7.8	9.2	67.1
4	1	2	2	2	1	1	1	2	2	2	3	3	3	68.9	10.2	12.7	70.6
5	1	2	2	2	2	2	2	3	3	3	1	1	1	71.7	1.1	3.8	64.7
6	1	2	2	2	3	3	3	1	1	1	2	2	2	71.8	4.8	9.9	67.8
7	1	3	3	3	1	1	1	3	3	3	2	2	2	81.4	5.2	9.9	77.9
8	1	3	3	3	2	2	2	1	1	1	3	3	3	79.0	7.7	17.2	55.7
9	1	3	3	3	3	3	3	2	2	2	1	1	1	82.3	0.5	4.7	72.0
10	2	1	2	3	1	2	3	1	2	3	1	2	3	58.4	2.5	11.7	60.8
11	2	1	2	3	2	3	1	2	3	1	2	3	1	64.4	-0.2	3.8	50.3
12	2	1	2	3	3	1	2	3	1	2	3	1	2	65.0	3.9	9.0	53.3
13	2	2	3	1	1	2	3	2	3	1	3	1	2	74.9	4.1	8.7	120.1
14	2	2	3	1	2	3	1	3	1	2	1	2	3	72.9	9.7	13.1	163.6
15	2	2	3	1	3	1	2	1	2	3	2	3	1	74.3	0.7	3.9	83.0
16	2	3	1	2	1	2	3	3	1	2	2	3	1	84.4	0.9	4.1	75.5
17	2	3	1	2	2	3	1	1	2	3	3	1	2	83.0	7.3	9.4	69.5
18	2	3	1	2	3	1	2	2	3	1	1	2	3	81.1	11.4	14.0	78.6
19	3	1	3	2	1	3	2	1	3	2	1	3	2	66.9	4.0	8.6	78.6
20	3	1	3	2	2	1	3	2	1	3	2	1	3	65.3	9.1	13.5	72.5
21	3	1	3	2	3	2	1	3	2	1	3	2	1	67.6	0.2	3.4	68.8
22	3	2	1	3	1	3	2	2	1	3	3	2	1	77.3	0.5	4.4	68.5
23	3	2	1	3	2	1	3	3	2	1	1	3	2	77.7	3.7	10.8	51.6
24	3	2	1	3	3	2	1	1	3	2	2	1	3	75.8	7.8	15.6	59.2
25	3	3	2	1	1	3	2	3	2	1	2	1	3	84.8	10.0	15.1	129.8
26	3	3	2	1	2	1	3	1	3	2	3	2	1	86.1	1.0	3.8	146.0
27	3	3	2	1	3	2	1	2	1	3	1	3	2	87.2	6.0	10.7	98.6

3.2.3. Selection of Active Factors

The results calculated during the simulation for the observation parameters listed in Table 2 are adopted as observation vectors for Equation (3) for evaluation. Table 3 shows the mean square errors of analysis factors under different observation parameters.

Table 3. The mean square errors of 13 analysis factors for various observation objectives.

Factors	The Mean Square Errors
	Fz	Fx	Fy	Ac
x1	15.70742	0.02138	0.60160	44.53319
x2	196.36442	2.11052	2.69865	115.39593
x3	0.24615	0.13753	0.21154	69.21850
x4	0.05153	1.91301	1.04544	1557.16874
x5	0.24876	0.27282	0.08978	161.02762
x6	0.05817	0.88098	0.08544	13.81811
x7	0.02298	0.98206	0.25764	1.50246
x8	0.46019	0.61019	0.15663	16.25891
x9	0.22571	0.08459	0.41872	1.14816
x10	0.20981	0.02352	0.62467	219.01455
x11	0.09366	0.11422	0.12611	9.55418
x12	0.26766	0.12900	0.25309	320.33627
x13	4.48885	31.47385	47.28643	9.62576

(1) H statistic value

For the H statistic, in this paper, it is supposed that the effect is 0 for at least two columns of values in Table 2, i.e., s = 2. In addition, the given global significance level of this paper is α = 0.05. According to Equation (11) regarding calculation of l, the l values obtained corresponding to the four observation para meters are: l = 10 for F_z, l = 12 for F_x, l = 11 for F_y and l = 6 for A_c. Table 4 shows the H statistic values of all analysis factors calculated according to Equation (10).

Table 4. H statistic values of 13 analysis factors.

H Statistic Values								Critical Value
Factors	Fz	Factors	Fx	Factors	Fy	Factors	Ac
x7	0.06469	x1	0.02988	x6	0.17214	x9	0.14598	5.505
x4	0.14401	x10	0.03287	x5	0.18075	x7	0.18981	5.505
x6	0.16229	x9	0.11743	x11	0.25236	x11	1.05385	5.505
x11	0.25897	x11	0.15806	x8	0.31184	x13	1.06055	5.505
x10	0.56367	x12	0.17824	x3	0.41736	x6	1.42821	5.505
x9	0.60404	x3	0.18985	x12	0.49595	x8	1.62203	5.505
x3	0.65548	x5	0.37128	x7	0.50449	x1	3.16670	5.505
x5	0.66202	x8	0.80207	x9	0.79891	x3	3.93523	5.505
x12	0.70907	x6	1.12715	x1	1.11541	x2	4.77114	5.505
x8	1.16509	x7	1.24410	x10	1.15407	x5	5.24434	5.505
x13	5.89688	x4	2.22188	x4	1.81392	x10	5.61736	5.505
x1	8.81897	x2	2.40877	x2	3.77904	x12	5.99169	5.505
x2	10.78661	x13	10.03983	x13	10.67472	x4	6.76578	5.505

Figure 11 shows the H statistic positions of the observation parameters corresponding to different analysis factors in contrast with those of the critical value. As shown in Figure 12, for F_z, the H statistic values of 3 analysis factors are higher than the critical value, namely x₁, x₂ and x₁₃ are the significant influence factors of F_z. Similarly, x₁₃ is the significant influence factor of F_x and F_y, x₄, x₁₀ and x₁₂ are the significant influence factors of A_c.

Figure 11. Selection results of H statistic values.

Figure 12. Selection results of P statistic values.

(2) P statistic value

When the P statistic is adopted for selecting active factors, l = 7 is set according to the calculation principle of l in this paper. The given global significance level is α = 0.05. Table 5 shows the P statistic of all analysis factors calculated according to Equation (13).

Table 5. P statistic values of 13 analysis factors.

P statistic Values								Critical Value
Factors	Fz	Factors	Fx	Factors	Fy	Factors	Ac
x7	0.00790	x1	0.00768	x6	0.02687	x9	0.01166	1.310
x4	0.01772	x10	0.00845	x5	0.02823	x7	0.01526	1.310
x6	0.02000	x9	0.03039	x11	0.03965	x11	0.09706	1.310
x11	0.03221	x11	0.04104	x8	0.04925	x13	0.09778	1.310
x10	0.07215	x12	0.04635	x3	0.06652	x6	0.14037	1.310
x9	0.07762	x3	0.04942	x12	0.07958	x8	0.16516	1.310
x3	0.08465	x5	0.09803	x7	0.08101	x1	0.45239	1.310
x5	0.08554	x8	0.21925	x9	0.13166	x3	0.70315	1.310
x12	0.09204	x6	0.31655	x1	0.18917	x2	1.17224	1.310
x8	0.15825	x7	0.35287	x10	0.19642	x5	1.63578	1.310
x13	1.54362	x4	0.68738	x4	0.32873	x10	2.22484	1.310
x1	5.40143	x2	0.75835	x2	0.84857	x12	3.2541	1.310
x2	67.52536	x13	11.30908	x13	14.86887	x4	15.81833	1.310

Figure 12 shows the P statistic positions of the observation parameters corresponding to different analysis factors in contrast with those of the critical value. As shown in Figure 12, for F_z, the P statistic values of 3 analysis factors are higher than the critical value, namely x₁, x₂ and x₁₃ are the significant influence factors of F_z. Similarly, x₁₃ is the significant influence factor of F_x and F_y, x₄, x₅, x₁₀ and x₁₂ are the significant influence factors of A_c.

(3) B statistic value

According to Equation (16) and the B statistic calculation process, the B statistics of 13 analysis factors can be obtained, see Table 6. As shown in Table 6, for F_z, the B statistic values of 3 analysis factors are higher than the critical value, namely x₁, x₂ and x₁₃ are the significant influence factors of F_z. Similarly, x₁₃ is the significant influence factor of F_x and F_y, x₄, x₁₀ and x₁₂ are the significant influence factors of A_c.

Table 6. B statistic values of 13 analysis factors.

B Statistic Values								Critical Value
Factors	Fz	Factors	Fx	Factors	Fy	Factors	Ac
x7	-	x1	-	x6	-	x9	-	-
x4	-	x10	-	x5	-	x7	-	1.180
x6	-	x9	-	x11	-	x11	-	1.200
x11	-	x11	-	x8	-	x13	-	1.160
x10	-	x12	-	x3	-	x6	-	1.130
x9	-	x3	-	x12	-	x8	-	1.100
x3	-	x5	-	x7	-	x1	-	1.065
x5	-	x8	-	x9	-	x3	-	1.030
x12	-	x6	-	x1	-	x2	-	1.011
x8	0.3200	x7	-	x10	-	x5	0.9544	0.991
x13	1.1258	x4	-	x4	-	x10	1.0293	0.975
x1	1.9125	x2	0.9009	x2	0.5550	x12	1.1122	0.959
x2	3.6180	x13	2.1199	x13	2.1932	x4	1.6703	0.947

The blue markers mean B statistic values of factors are higher than the critical value.

According to the selected active factors of H/P/B statistical values, the factors significantly influencing turnout rail surface initiated RCF are x₁, x₂, x₄, x₁₀, x₁₂ and x₁₃, referring to train speed, axle load of vehicle, wheel profile, stock rail cant, integral vertical track stiffness and wheel-rail friction coefficient, respectively. In the previous work [1], Kassa and Nielsen presented axle load, wheel–rail friction coefficient, and wheel/rail profiles as the parameters which could affect the performance of railway turnout significantly. The results of this paper are basically the same with previous conclusions, and the previous results could be corroborated by this paper. In addition, the previous work is investigated based on an ordinary railway turnout which has a significant difference with the high-speed railway turnout, such as the structure, wheel/rail contact relationship and so on. Therefore, there are some different results, such as the integral vertical track stiffness. The outcome of this work could provide a theoretical guidance for the simulation and prediction of surface initiated RCF of high-speed railway turnouts.

4. Conclusions

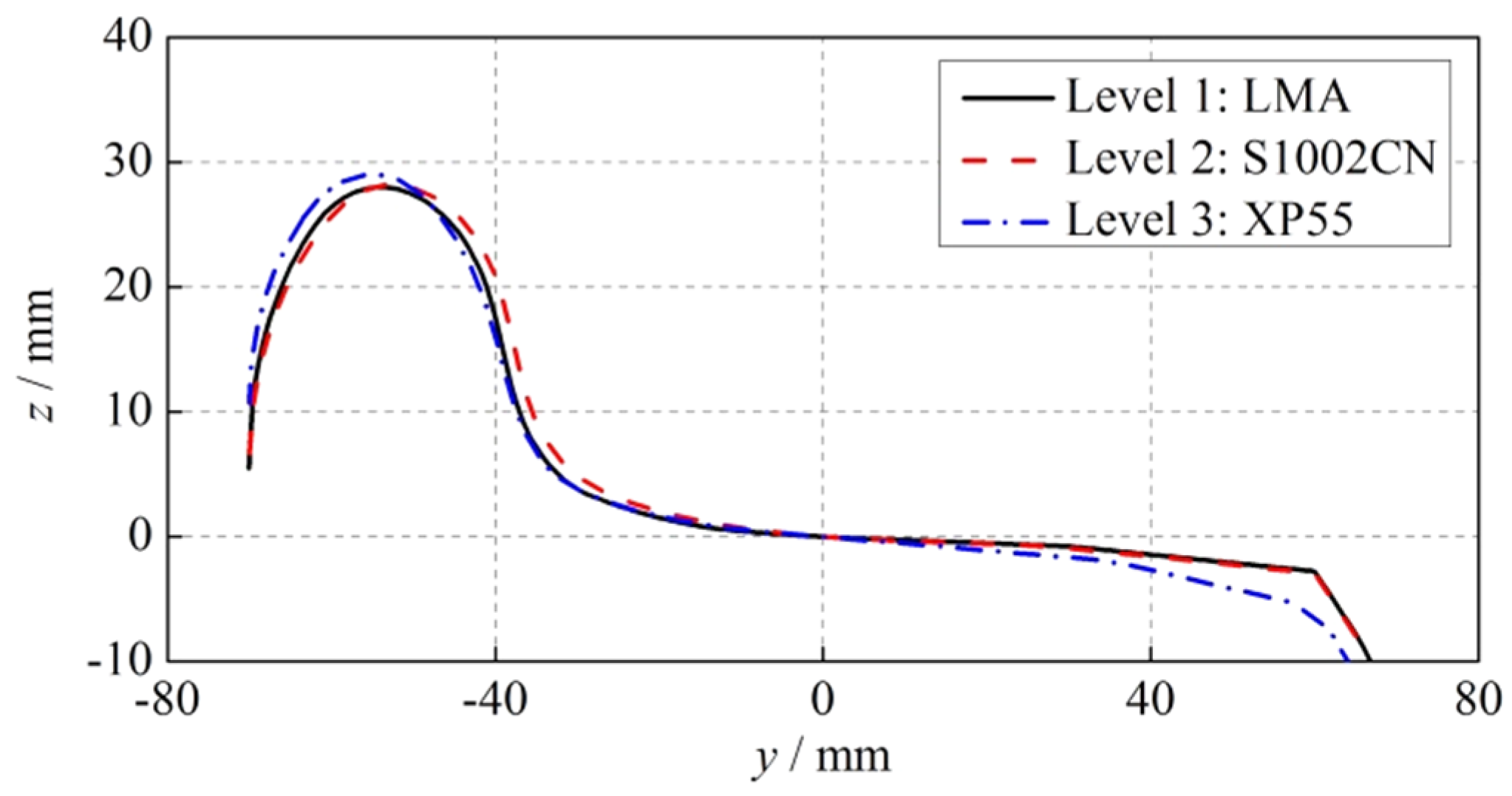
This paper, considering the relative motion of stock/switch rails, establishes a wheel-rail rolling contact model, simulates the rail surface initiated RCF behavior by taking a section of switch rail with the head width 35 mm in a high-speed railway turnout called CN60-1100-1:18 and a nominal LMA wheel profile as the objects of analysis, performs a contrast analysis on the rail surface initiated RCF of turnout under different wheel-rail creep conditions and finds that the material ratcheting effect is mainly caused by the overly high tangential stress on the rail surface material under low wheel-rail creep, overly high tangential stress and normal stress on the rail material under high wheel-rail creep and overly high normal stress on the rail under pure wheel-rail spin creep.

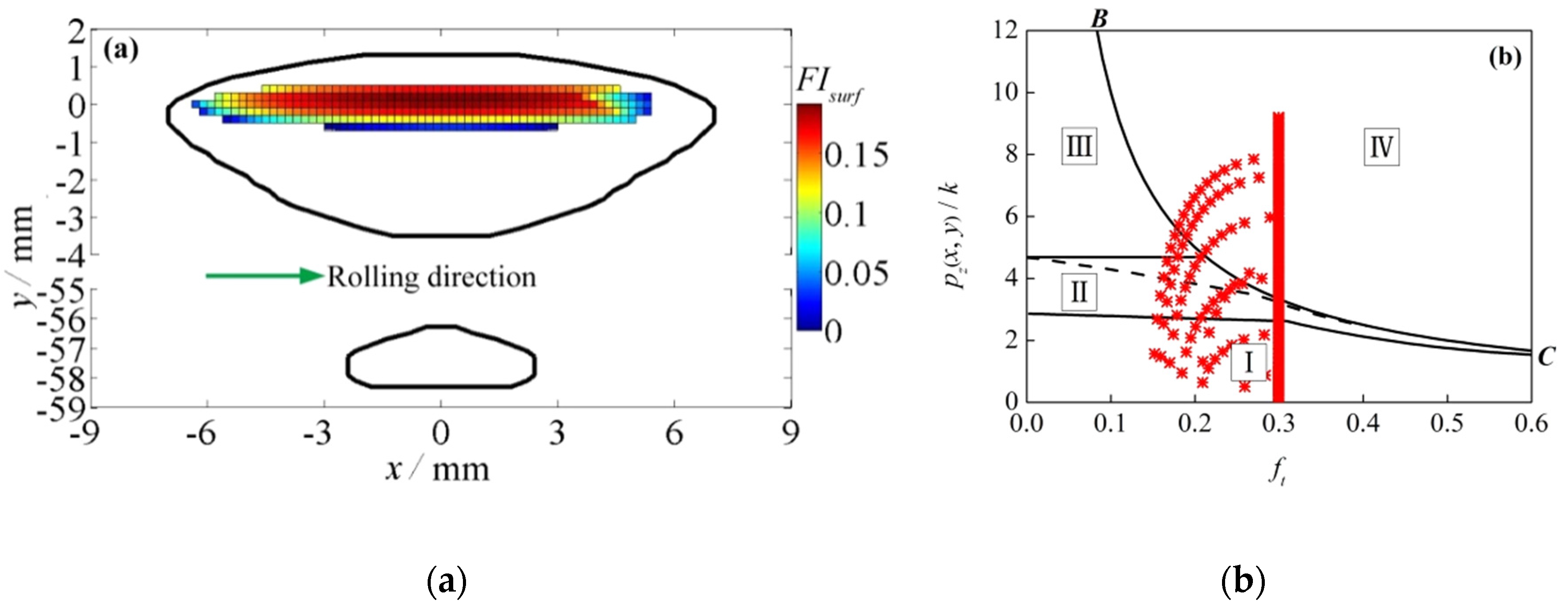
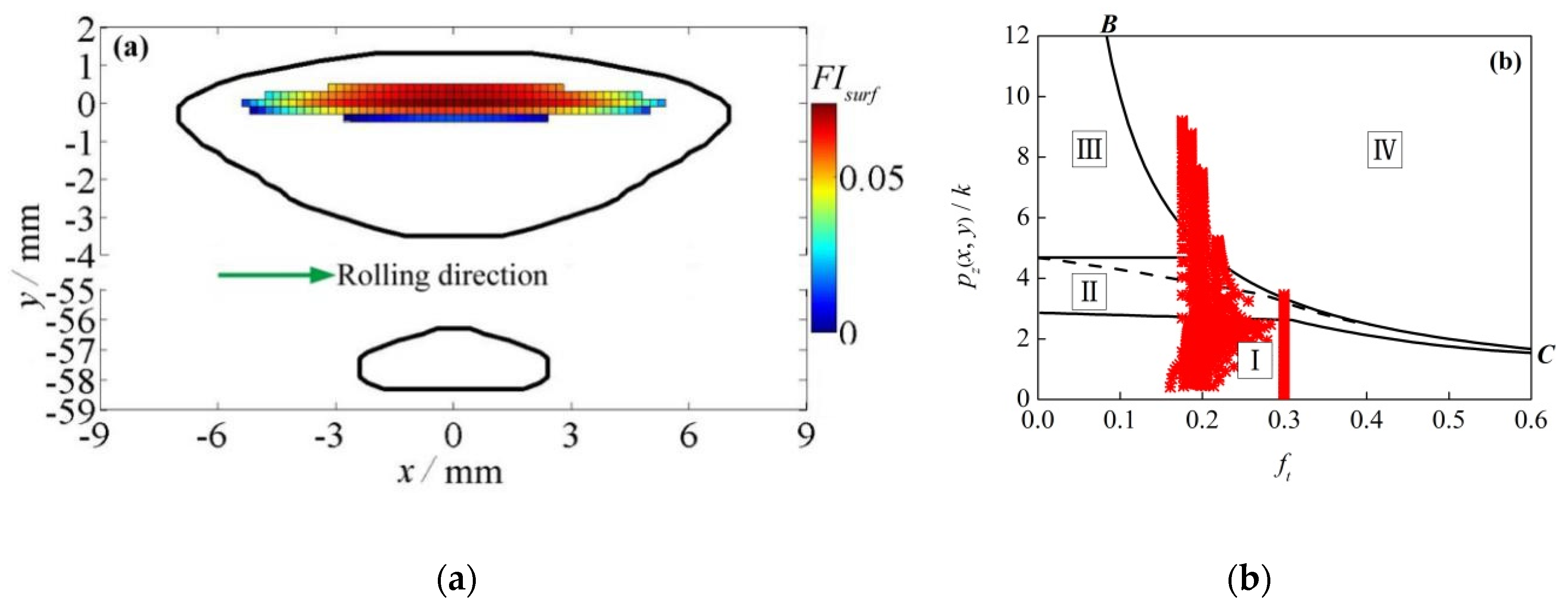
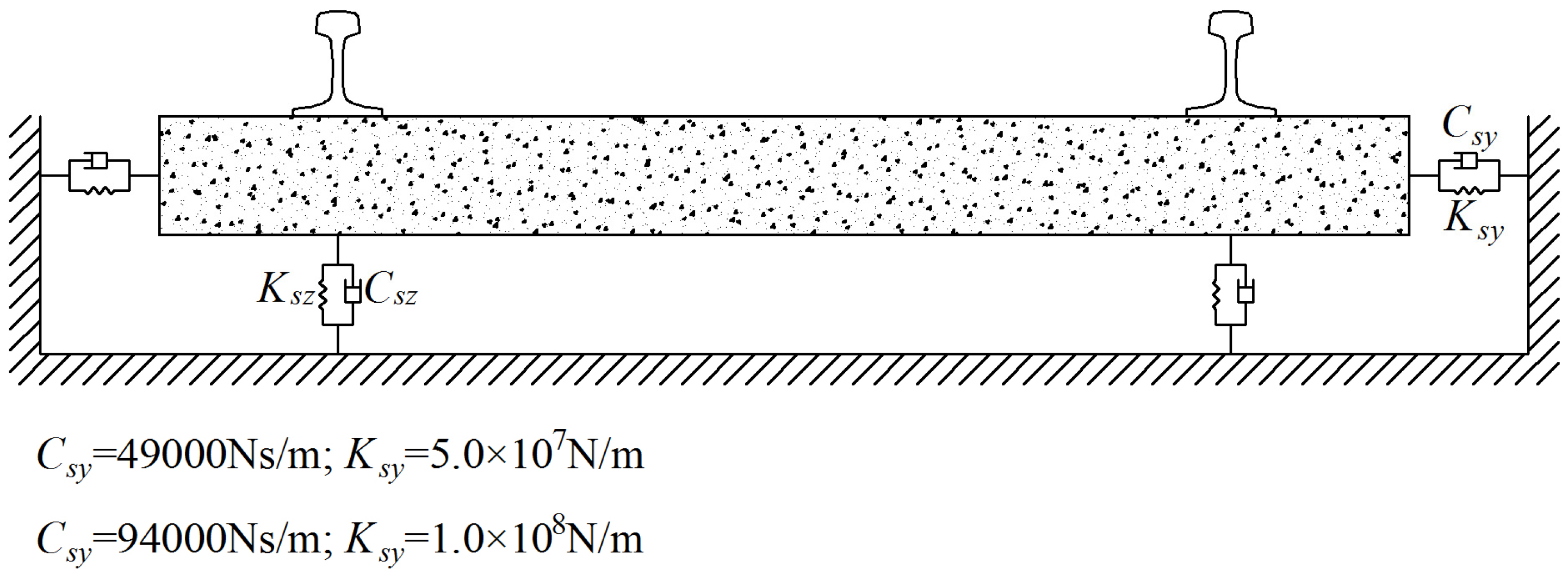
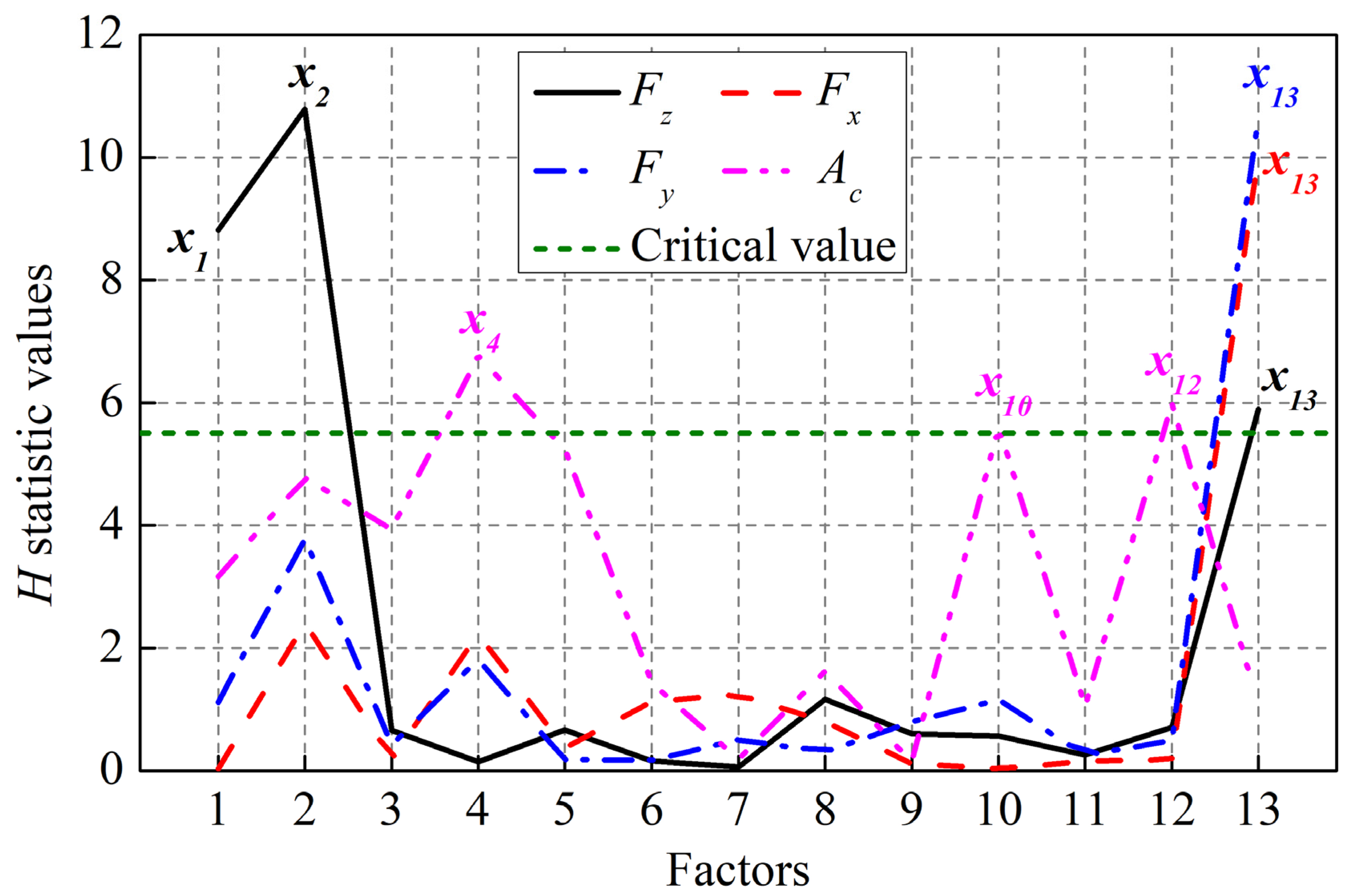
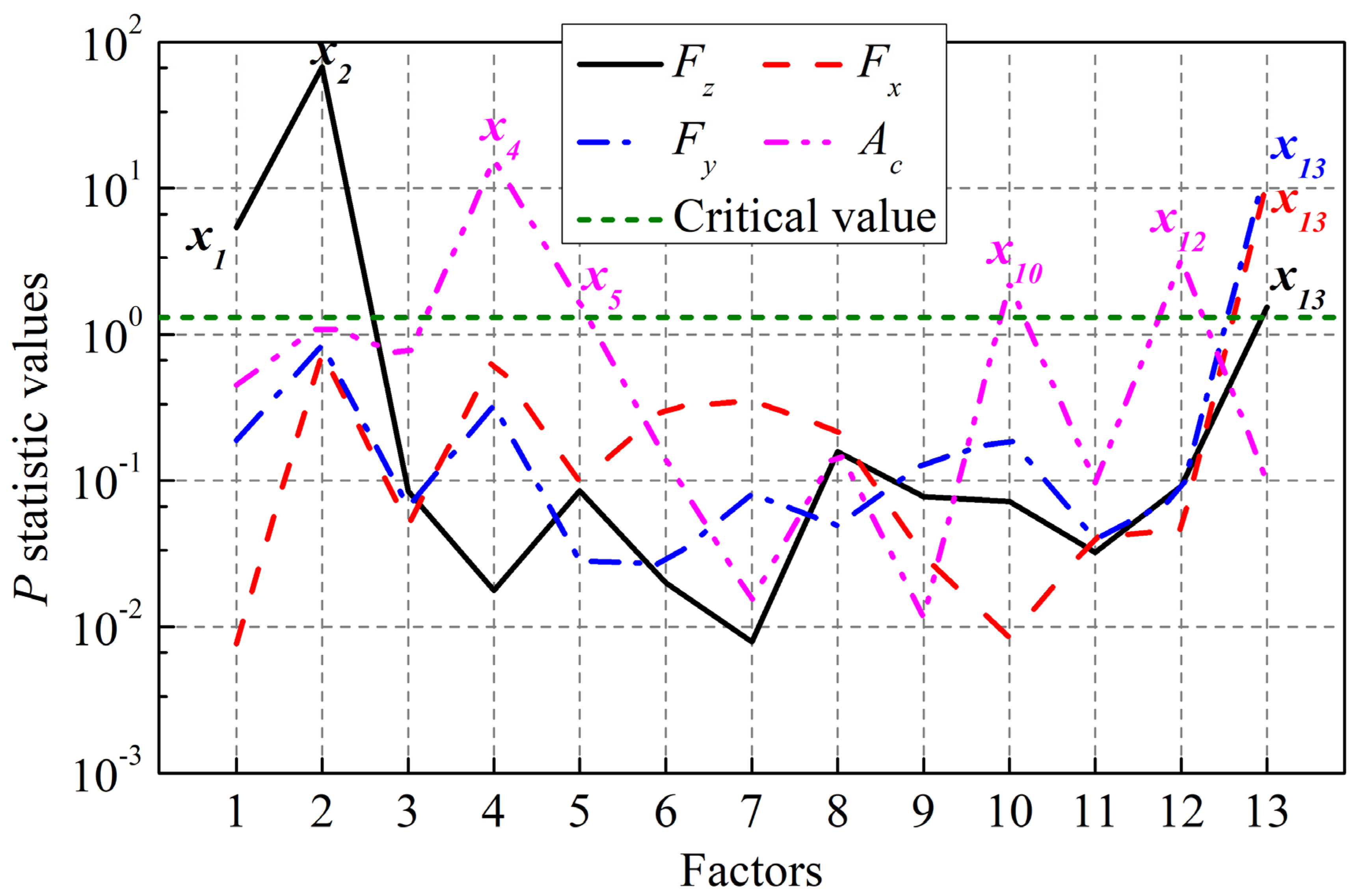
The dynamic parameters which can significantly influence turnout rail surface initiated RCF are selected according to the three-level unreplicated saturated factorial design method. The 13 dynamic parameters influencing the dynamic vehicle-turnout response are selected as the analysis factors first, then the normal wheel-rail force, longitudinal creep force, lateral creep force and contact patch area are selected as the observation parameters. The dynamic parameters influencing the rail surface initiated RCF of turnout are the train speed, train axle load, wheel-rail profile, integral vertical track stiffness and wheel-rail friction coefficient, respectively, which can be obtained according to the H/P/B statistic values. Based on a given nominal layout of ordinary turnout, axle load, wheel–rail friction coefficient, and wheel/rail profiles are selected as the parameters which could affect the performance of railway turnout significantly in the previous work. These conclusions could be corroborated by this paper. In addition, a high-speed railway turnout is used in the present work, and there are some different results, such as the integral vertical track stiffness.

This paper aims to provide guidance for the simulation and prediction of rail surface initiated RCF of turnout. This RCF is caused by a long-term accumulation and the influence of changing parameters of the vehicle-turnout system. Therefore, establishing a model for simulating and predicting this fatigue through generating random samples for dynamic parameters of the vehicle-turnout system and presenting a superimposition and accumulation method for rail surface initiated RCF damage is expected for further work. In addition, with the development of computer technology and finite element theory, some complicated wheel-rail rolling contact problems have been solved by the explicit finite element method [38,39]. Therefore, investigation of turnout rail surface initiated RCF behavior using this method is also the next step in the future works.