Real-Time Tomography of Gas-Jets with a Wollaston Interferometer
Abstract
:1. Introduction
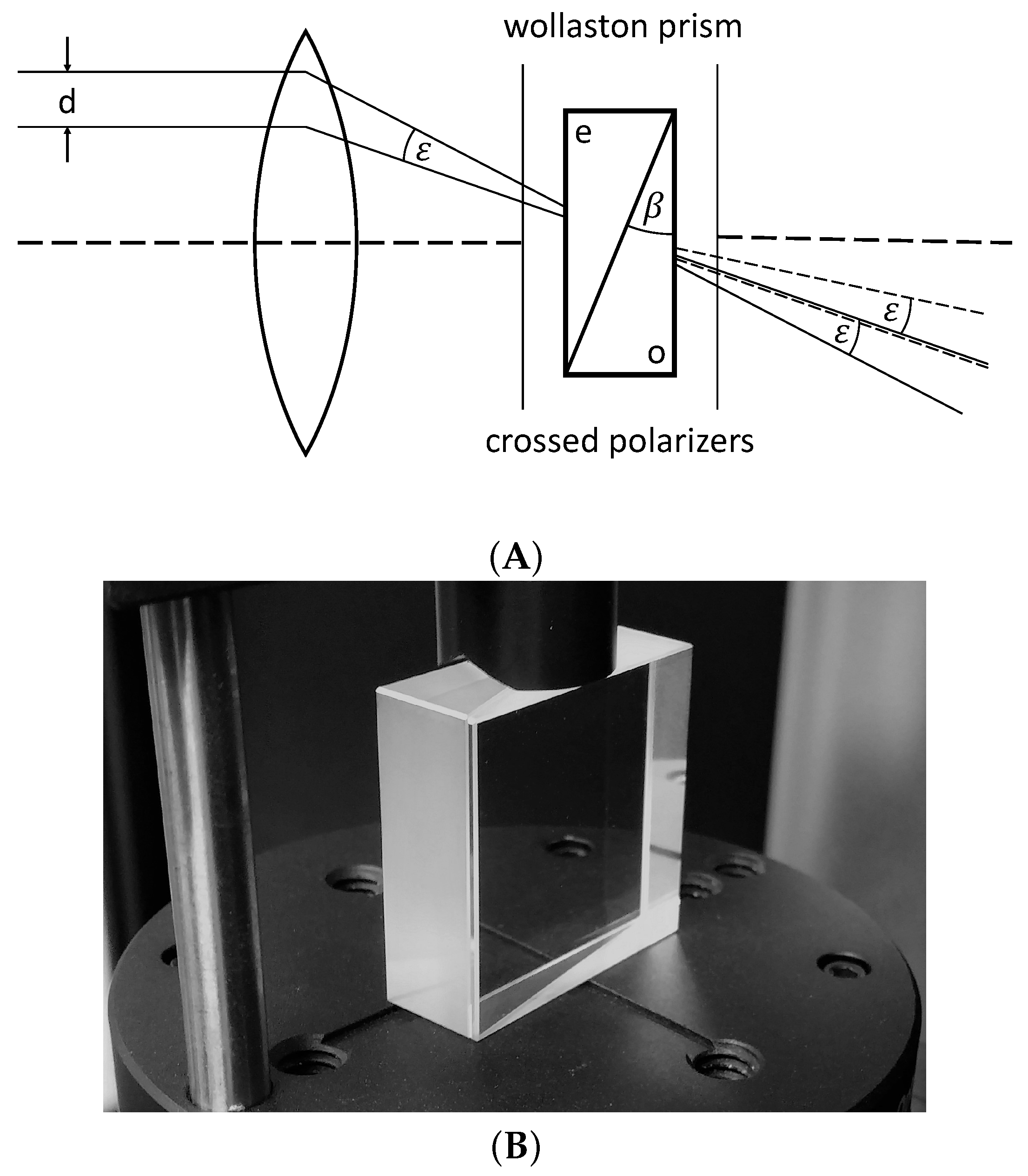
2. The Single Beam Wollaston Interferometer Setup
2.1. Theory
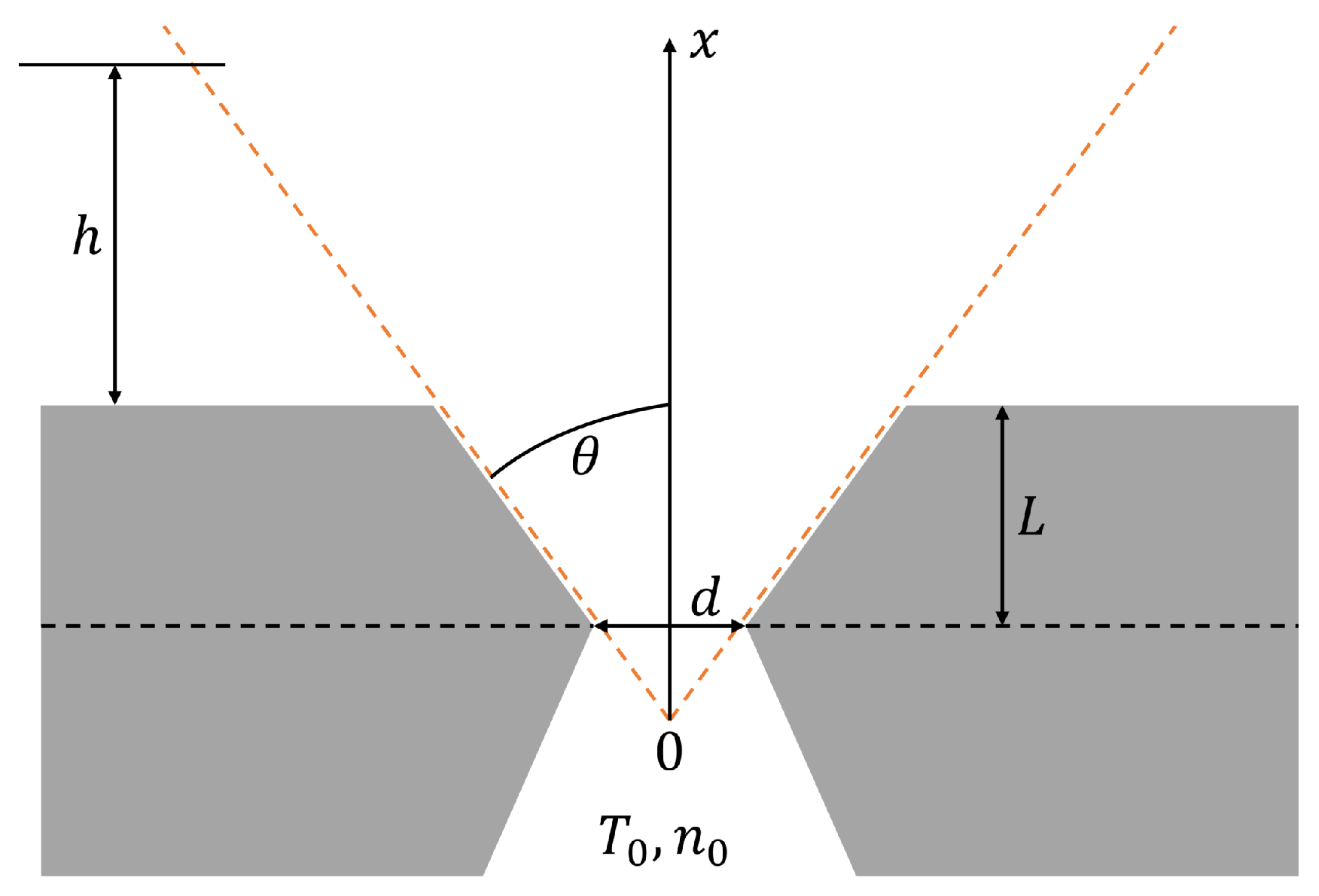
2.2. Estimation of Phase Shift Due to a Gas Jet Density Distribution
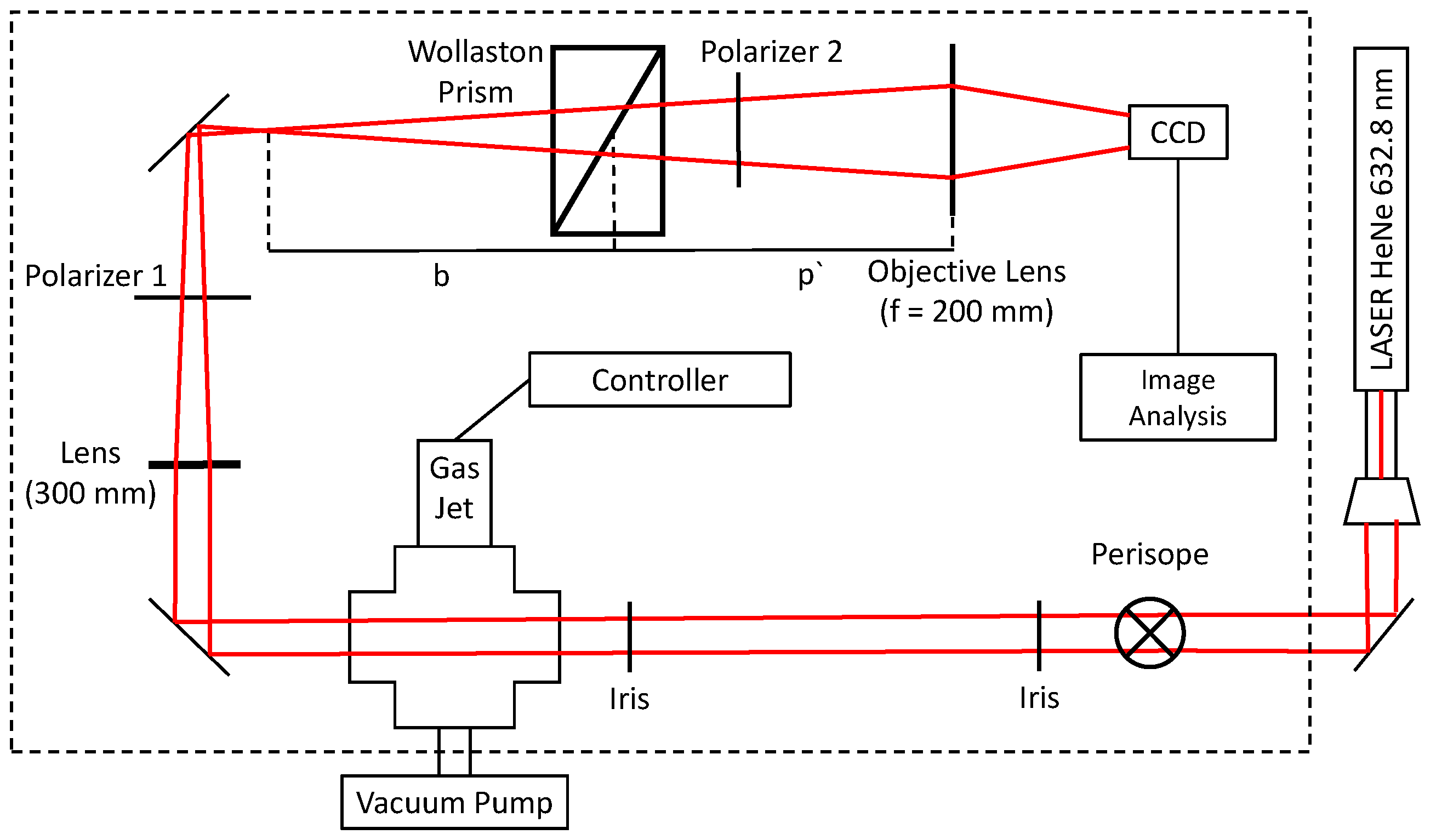
2.3. Experimental Setup for Gas Density Measurements
2.3.1. Wollaston Interferometer
2.4. Experimental Set-Up for Non-Rotational Measurements
3. Data Analysis for Interferometry and Real-Time Tomography
3.1. Numerical Tools
3.2. Tomographic Reconstruction
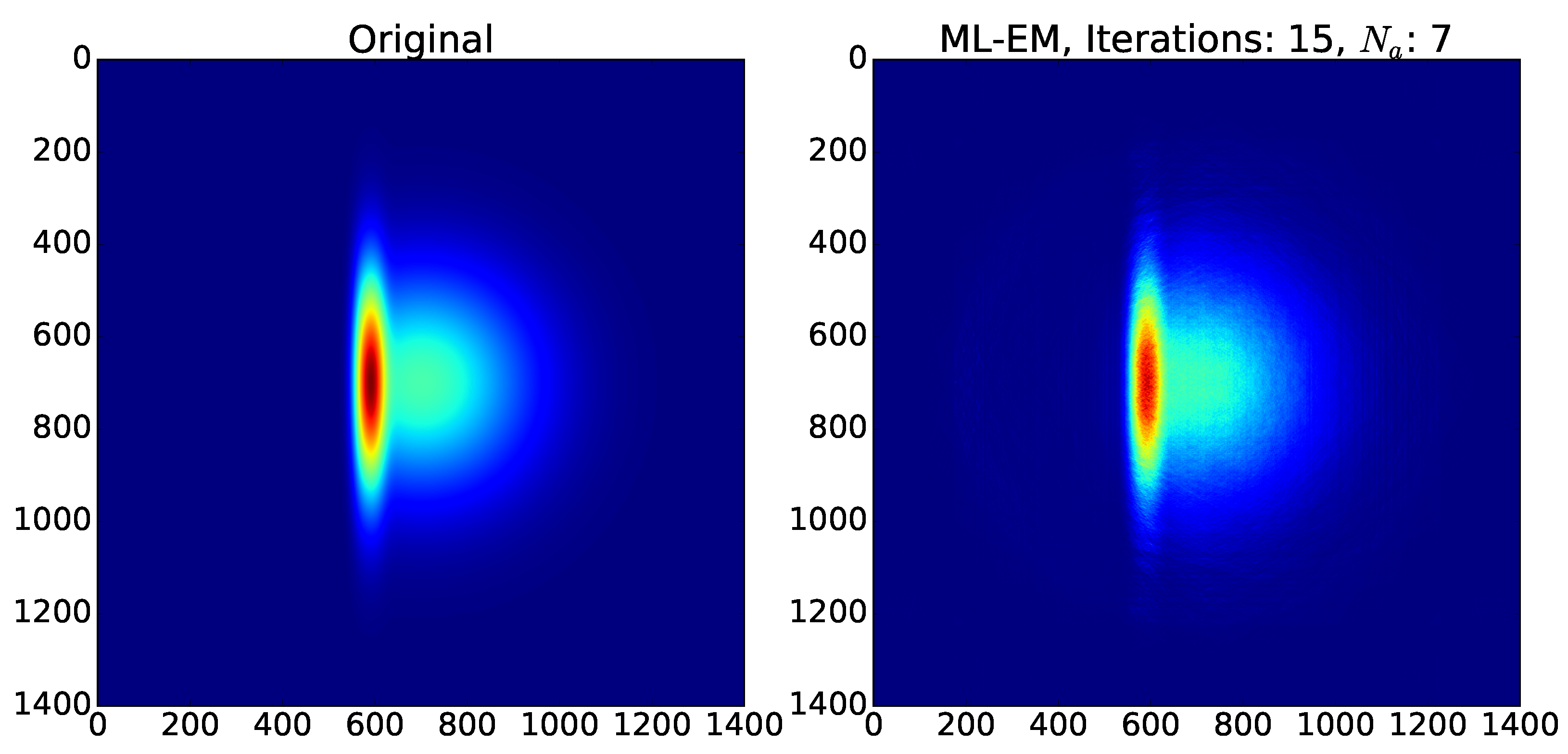
3.2.1. Maximum Likelihood-Expectation Maximization
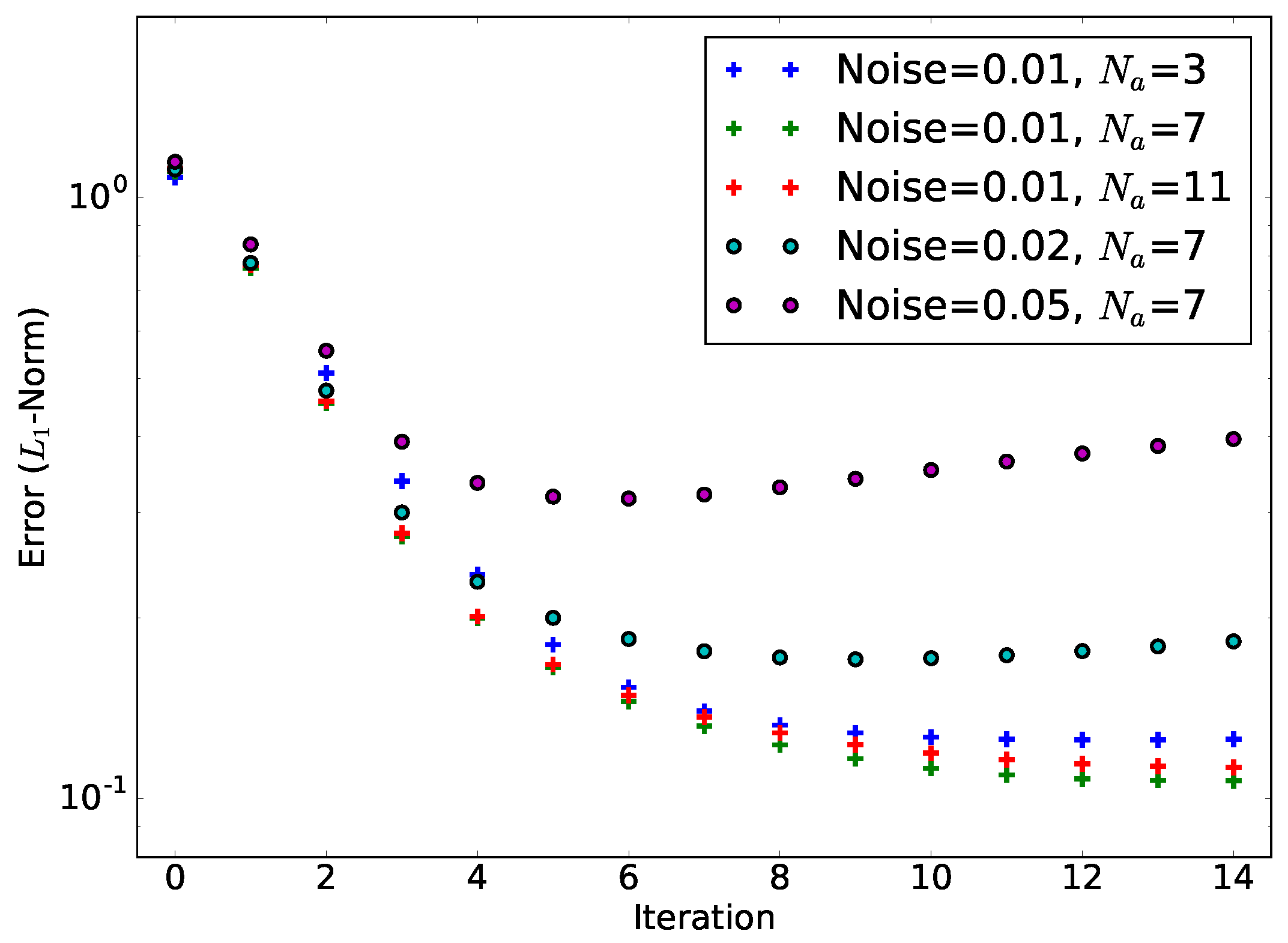
3.2.2. Convergence and Error Studies of ML-EM
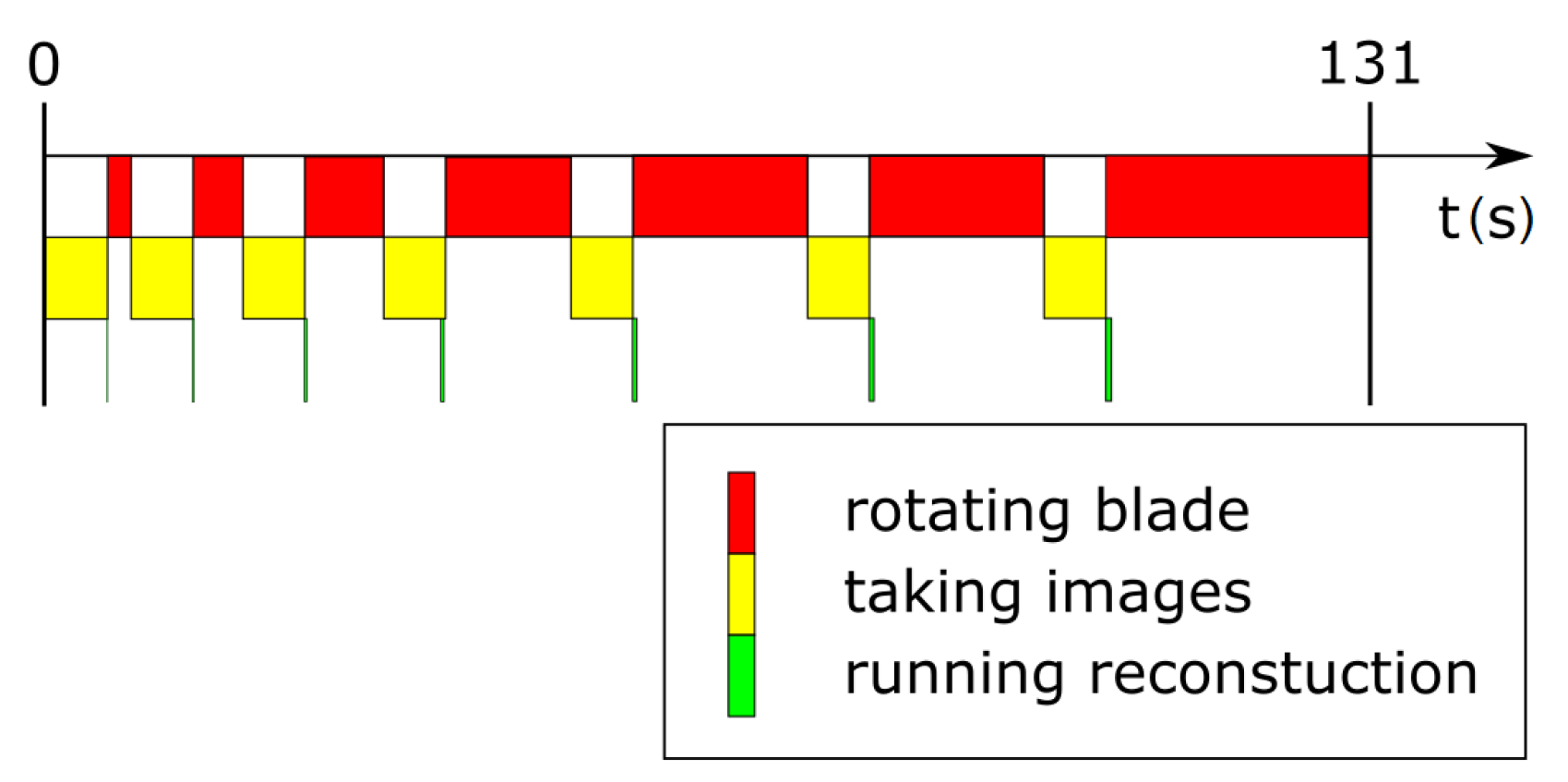
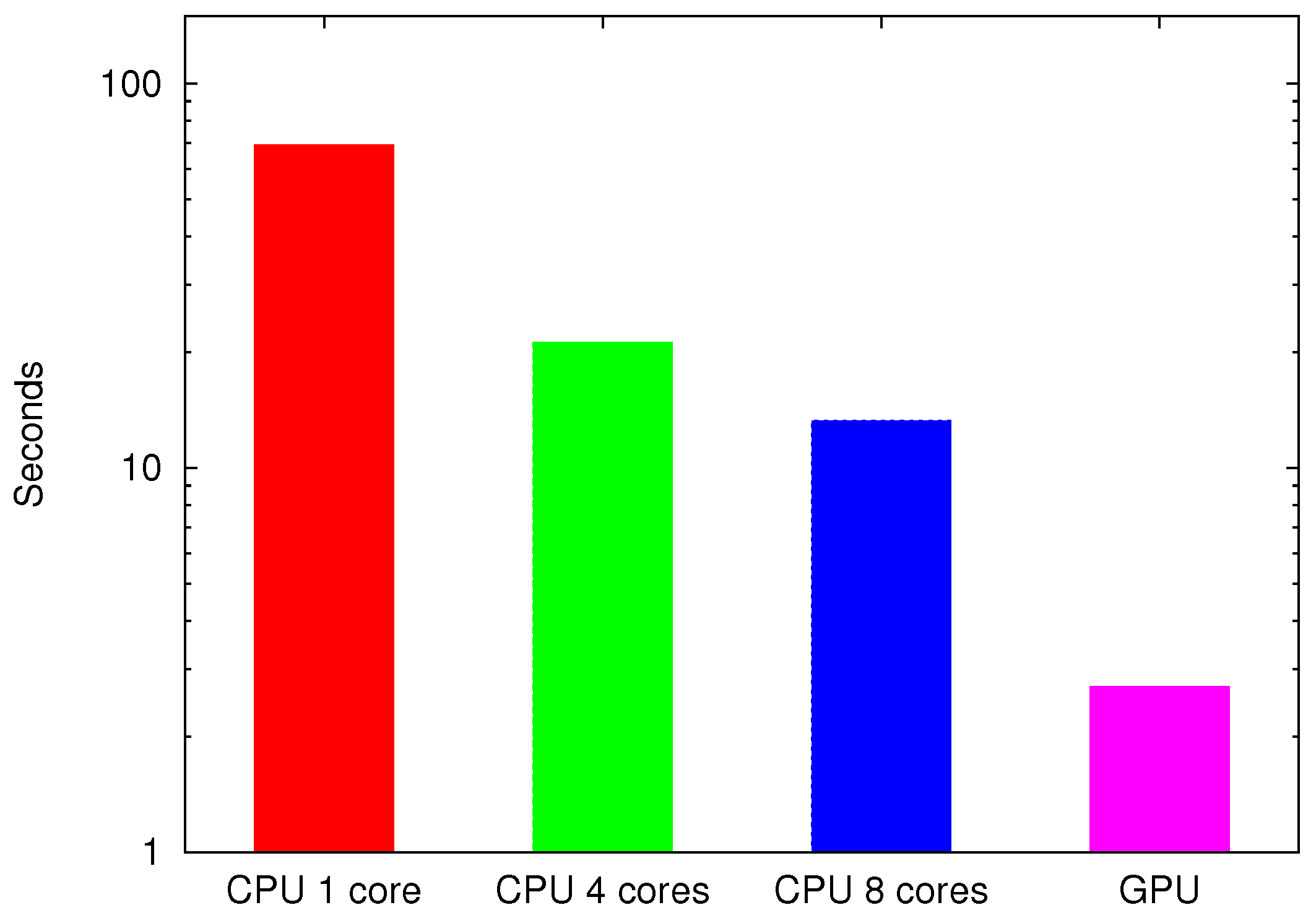
3.3. Real-Time Computation of the Density Reconstruction
4. Examples of Gas Jet Density Measurements
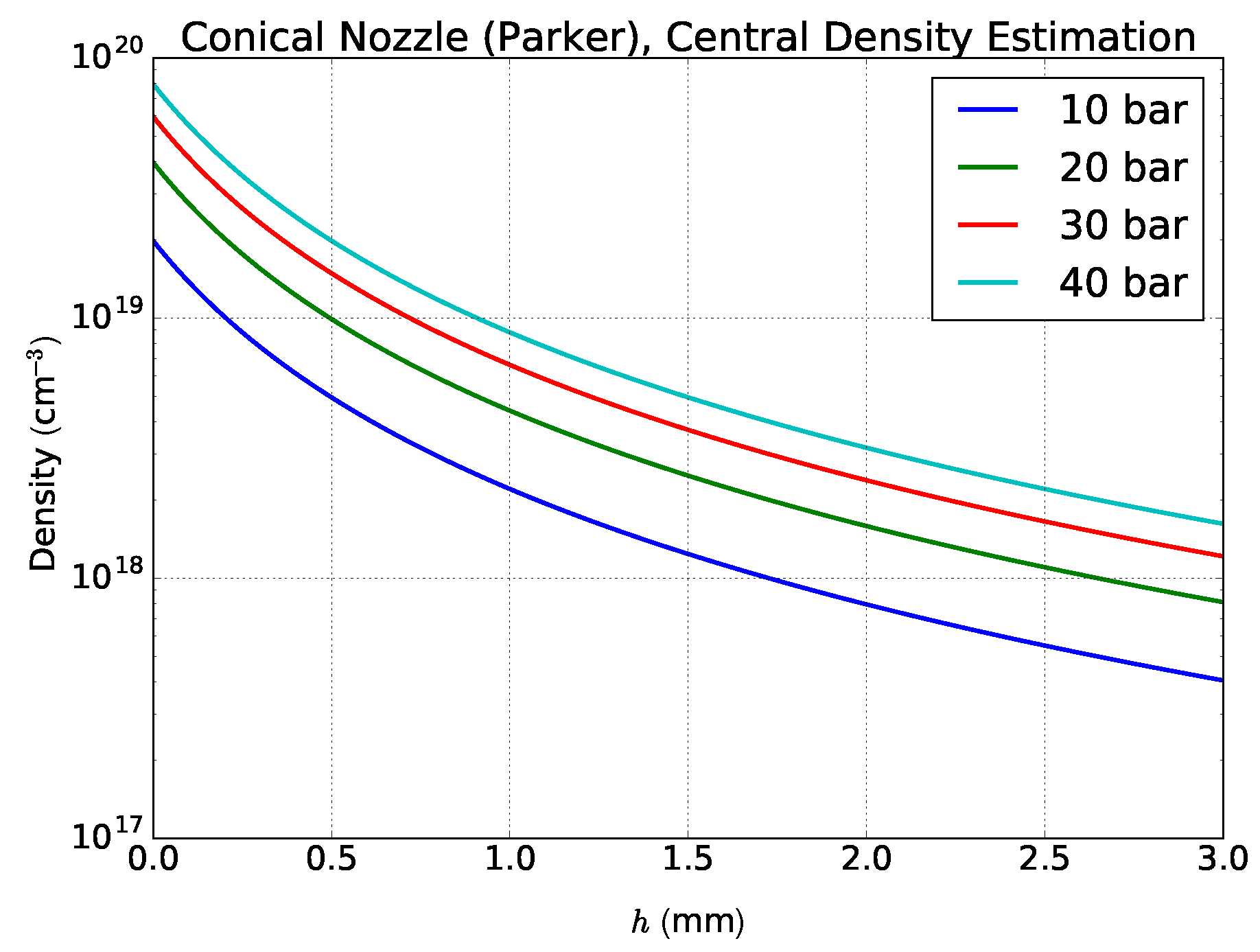
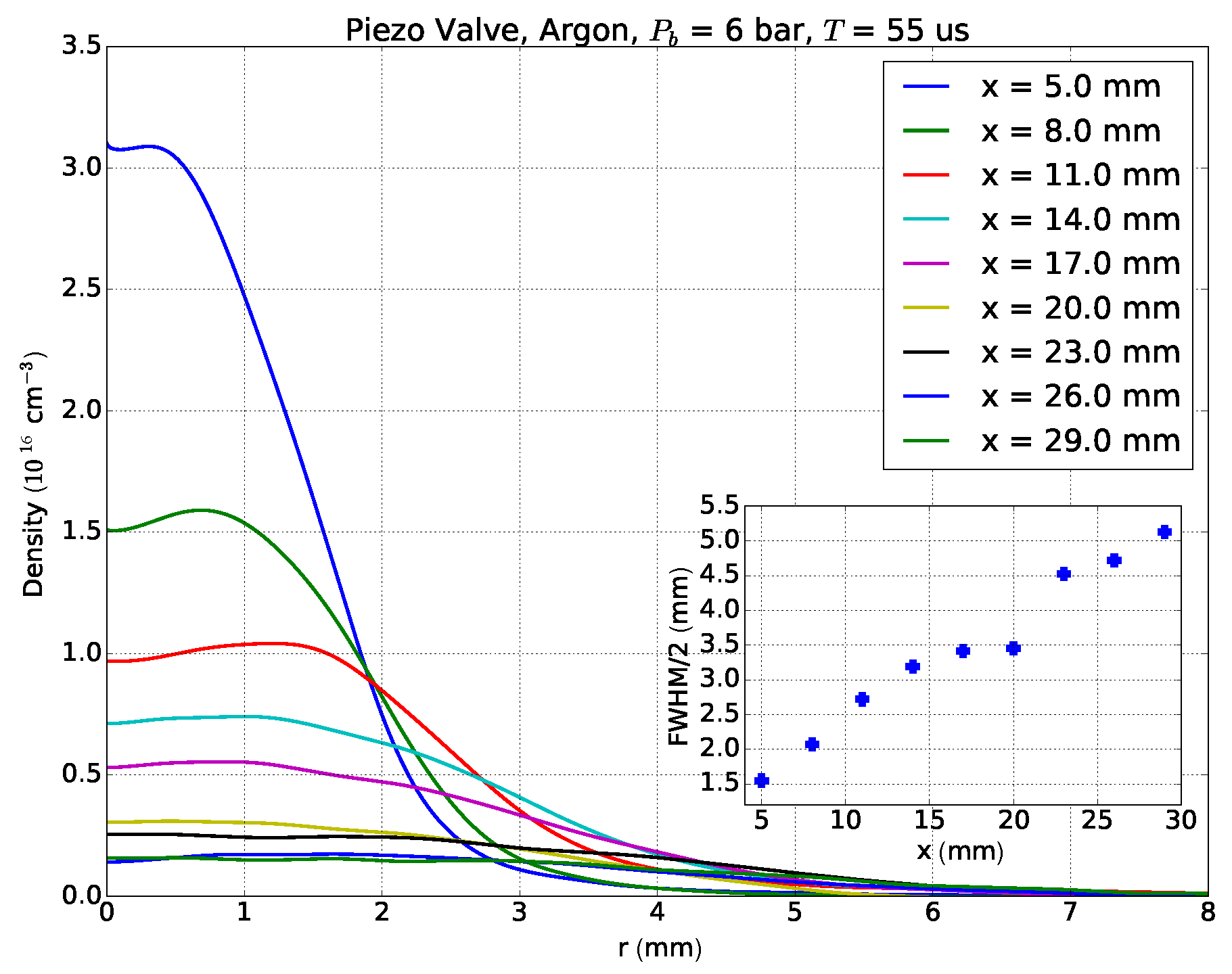
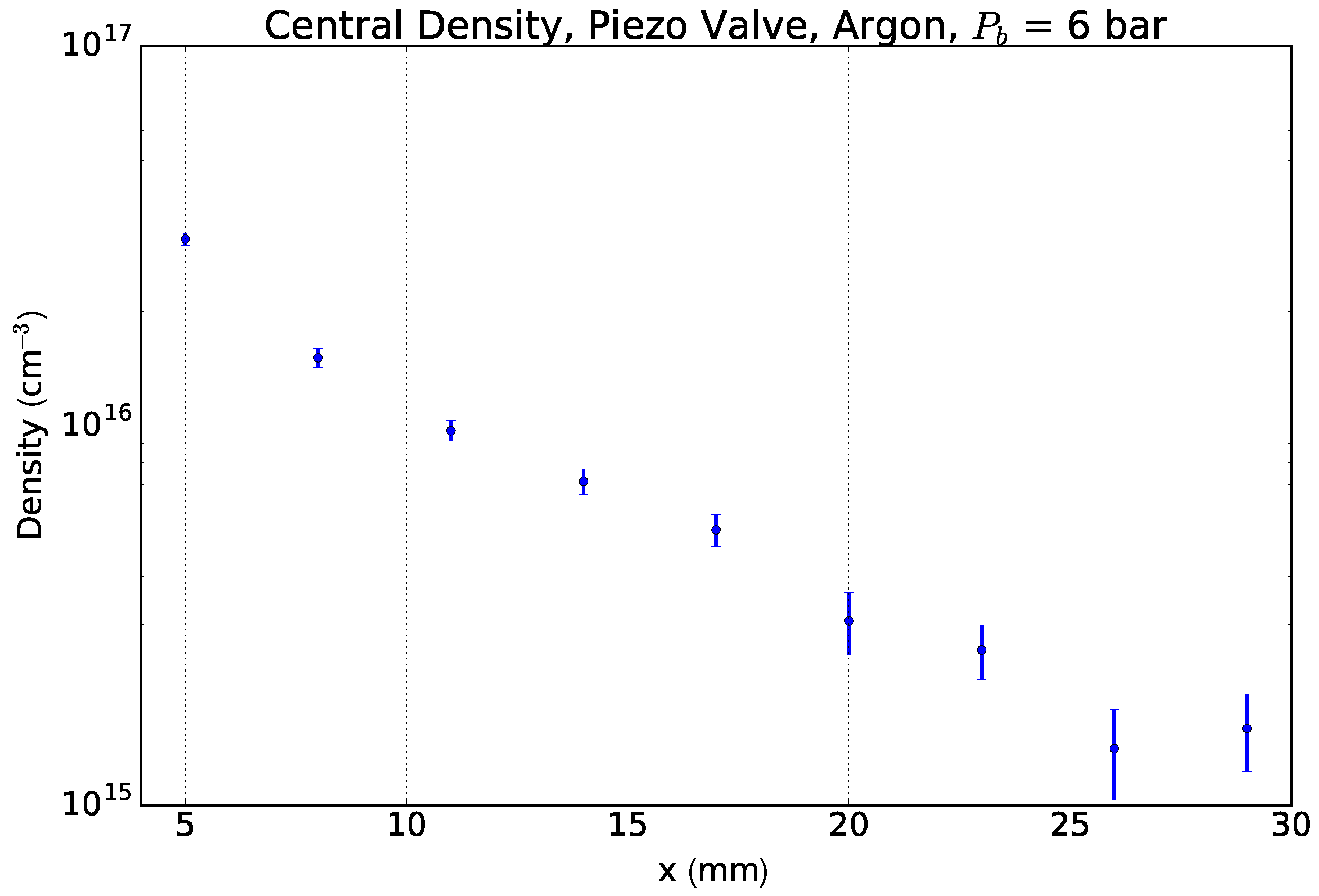
4.1. Piezo Gas Jet for Free Electron Laser Beam Instrumentation
4.2. Solenoid Gas Jet for LWFA
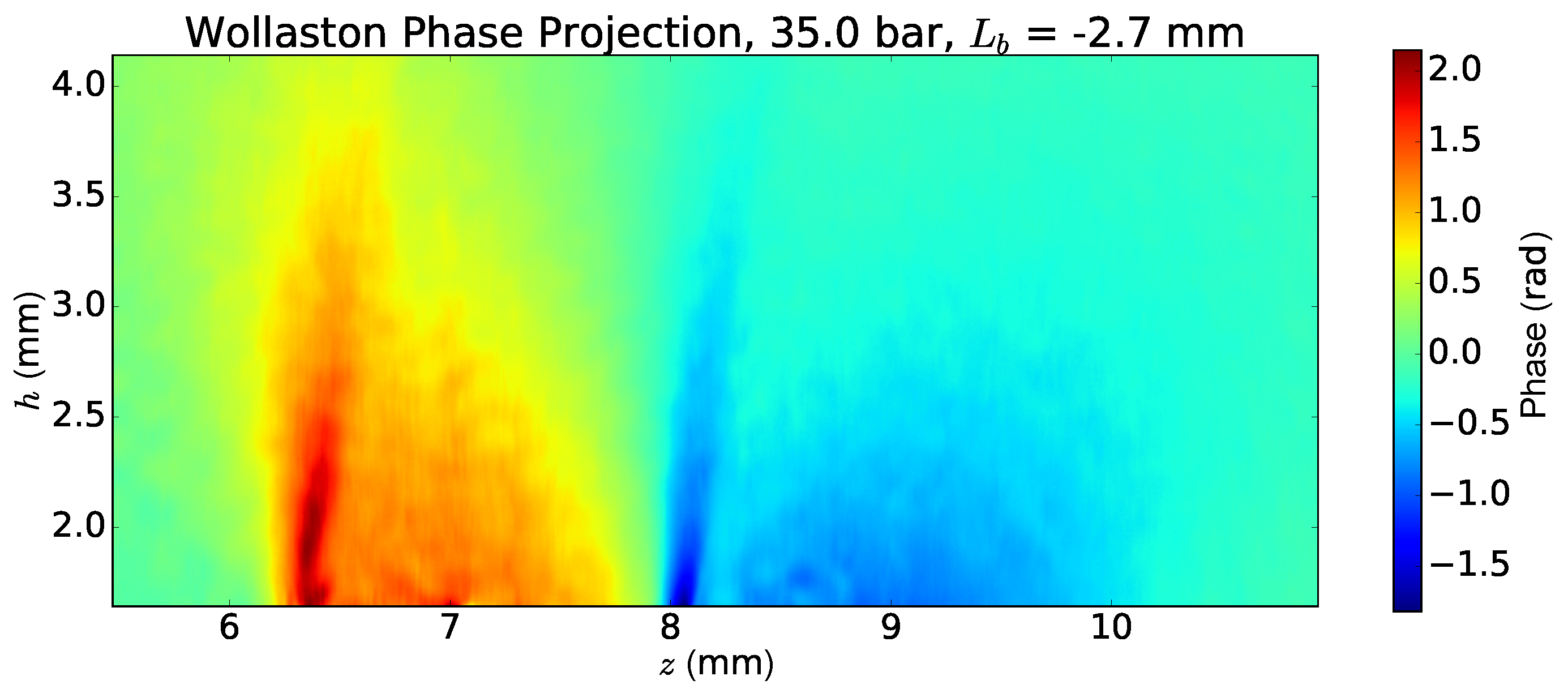
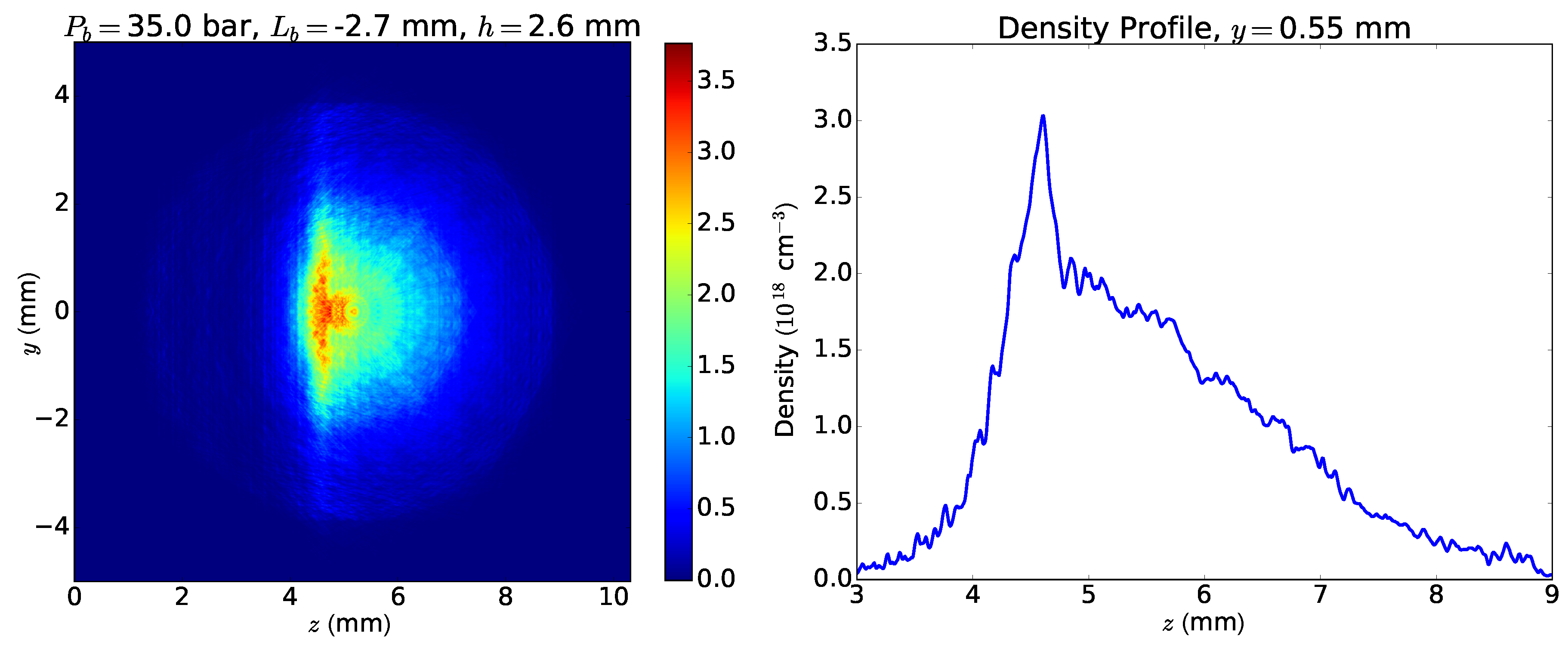
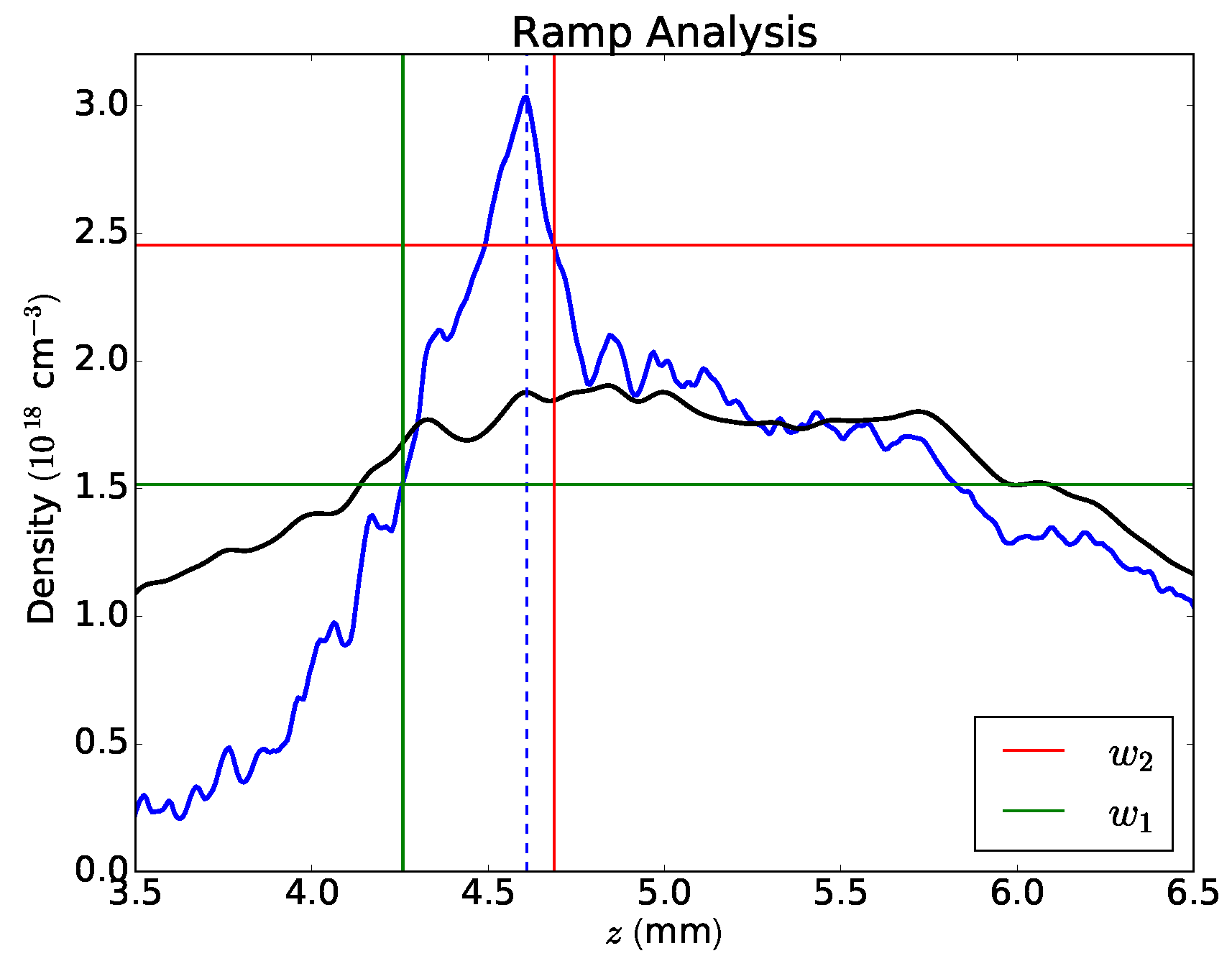
4.3. Shock Front Characterization in an LWFA
- Height of the shock front: density difference between ramped and undisturbed distribution at the ramp,
- Ramp factor r: ramped peak density divided by undisturbed peak density,
- : half-width (left) defined by the ramp peak density,
- : half-width (right) defined by the height .
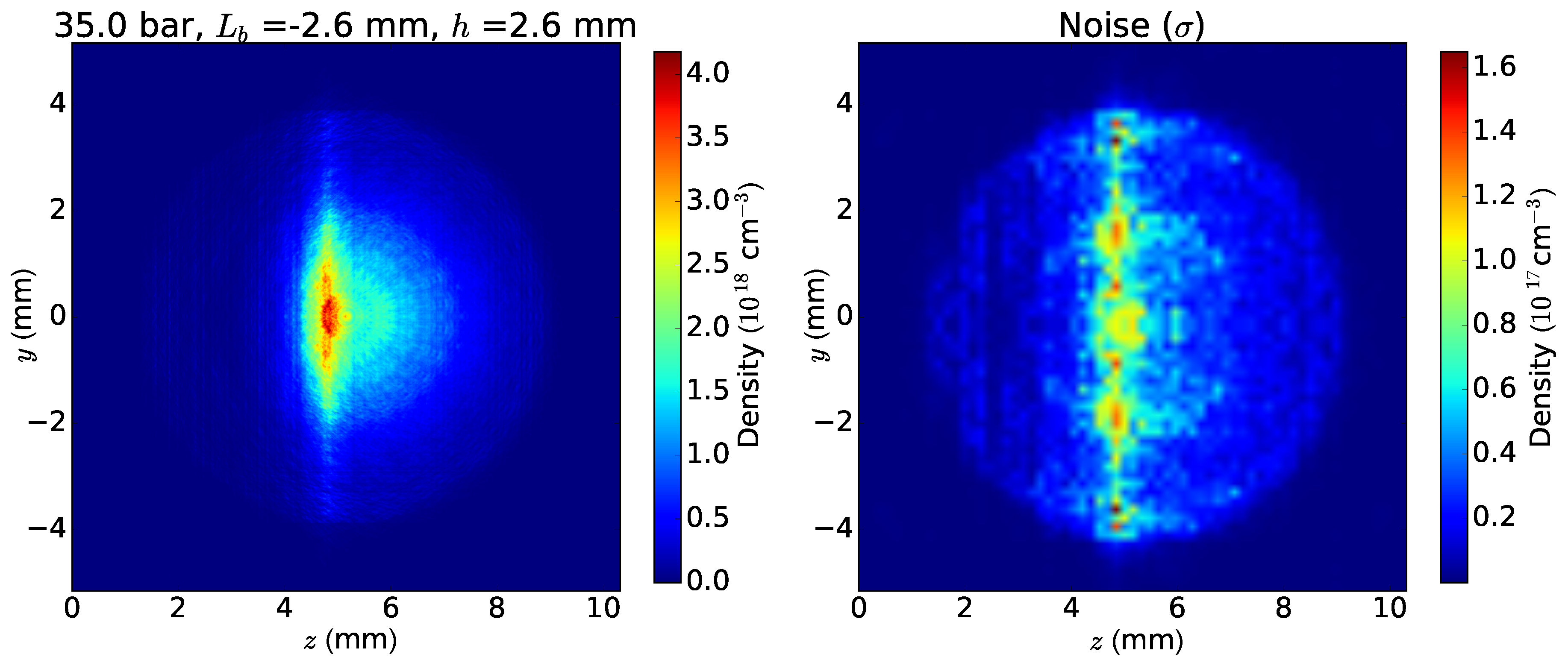
4.4. Error and Stability Analysis
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Bulanov, S.; Naumova, N.; Pegoraro, F.; Sakai, J. Particle injection into the wave acceleration phase due to nonlinear wake wave breaking. Phys. Rev. E 1998, 58, R5257–R5260. [Google Scholar] [CrossRef]
- Geddes, C.G.R.; Nakamura, K.; Plateau, G.R.; Toth, C.; Cormier-Michel, E.; Esarey, E.; Schroeder, C.B.; Cary, J.R.; Leemans, W.P. Plasma-density-gradient injection of low absolute-momentum-spread electron bunches. Phys. Rev. Lett. 2008, 100, 215004. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Li, J.; Sun, J.; Luo, X. Shock-wave-based density down ramp for electron injection. Phys. Rev. ST Accel. Beams 2012, 15, 020401. [Google Scholar] [CrossRef]
- Swanson, K.K.; Tsai, H.-E.; Barber, S.K.; Lehe, R.; Mao, H.-S.; Steinke, S.; van Tilborg, J.; Nakamura, K.; Geddes, C.G.R.; Schroeder, C.B.; et al. Control of tunable, monoenergetic laser-plasma-accelerated electron beams using a shock-induced density downramp injector. Phys. Rev. Accel. Beams 2017, 20, 051301. [Google Scholar] [CrossRef]
- Eckbreth, A.C. Laser Diagnostics for Combustion Temperature and Species; CRC Press: Boca Raton, FL, USA, 1996. [Google Scholar]
- Gizzi, L.A.; Giulietti, D.; Giulietti, A.; Afshar-Rad, T.; Biancalana, V.; Chessa, P.; Danson, C.; Schifano, E.; Viana, S.M.; Willi, O. Characterization of laser plasmas for interaction studies. Phys. Rev. E 1994, 49, 5628–5643. [Google Scholar] [CrossRef]
- Gizzi, L.A.; Giulietti, D.; Giulietti, A.; Afshar-Rad, T.; Biancalana, V.; Chessa, P.; Danson, C.; Schifano, E.; Viana, S.M.; Willi, O. Erratum: Characterization of laser plasmas for interaction studies. Phys. Rev. E 1994, 50, 4266. [Google Scholar] [CrossRef]
- Borghesi, M.; Giulietti, A.; Giulietti, D.; Gizzi, L.A.; Macchi, A.; Willi, O. Characterization of laser plasmas for interaction studies: Progress in time-resolved density mapping. Phys. Rev. E 1996, 54, 6769–6773. [Google Scholar] [CrossRef]
- Small, R.; Sernas, V.A.; Page, R.H. Single beam schlieren interferometer using a wollaston prism. Appl. Opt. 1972, 11, 858–862. [Google Scholar] [CrossRef] [PubMed]
- Biss, M.; Settles, G.S.; Staymates, M.E.; Sanderson, S.R. Differential schlieren-interferometry with a simple adjustable wollaston-like prism. Appl. Opt. 2008, 47, 328–335. [Google Scholar] [CrossRef] [PubMed]
- Benattar, R.; Popovics, C.; Sigel, R. Polarized light interferometer for laser fusion studies. Review Sci. Instrum. 1979. [Google Scholar] [CrossRef]
- Liu, Y.; Daum, P.H. Relationship of refractive index to mass density and self-consistency of mixing rules for multicomponent mixtures like ambient aerosols. J. Aerosol Sci. 2008, 39, 974–986. [Google Scholar] [CrossRef]
- Chen, G.; Geng, X.; Xu, H.; Mi, Y.; Zhang, X.; Wang, L.; Kim, D.E. Understanding of cluster size deviation by measuring the dimensions of cluster jet from conical nozzles. AIP Adv. 2013, 3, 032133. [Google Scholar] [CrossRef]
- Sauerwein, N. Design Study for Laser Plasma Wakefield Acceleration of Low Energy Electrons; ETH Zurich: Zurich, Switzerland; Paul Scherrer Institute: Villigen, Switzerland, 2016. [Google Scholar]
- McNaughton, G.D. Experimental Study of the Equation of State of Isochorically Heated Warm Dense Matter. Ph.D. Thesis, The University of Texas at Austin, Austin, TX, USA, 2007. [Google Scholar]
- Simons, S.; Yuan, Z.-G. The Filtered Abel Transform and Its Application in Combustion Diagnostics; NASA Technical Reports; NASA: Washington, DC, USA, 2003. Available online: http://ntrs.nasa.gov/search.jsp?R=20030031381 (accessed on 20 May 2016).
- Wikipedia. Abel Transform—Wikipedia, the Free Encyclopedia, 2015. Available online: https://en.wikipedia.org/w/index.php?title=Abel_transform&oldid=668868856 (accessed on 20 May 2016).
- Stults, J. FFT-Based Abel Inversion Tutorial, January 2010. Available online: http://www.variousconsequences.com/2010/01/fft-based-abel-inversion-tutorial.html (accessed on 25 May 2016).
- Zvolsky, M. Tomographic Image Reconstruction. An Introduction. DESY, University of Hamburg, 2014. Available online: http://www.desy.de/garutti/LECTURES/BioMedical/Lecture7_ImageReconstruction.pdf (accessed on 15 December 2016).
- Gürsoy, D.; de Carlo, F.; Xiao, X.; Jacobsen, C. Tomopy: A framework for the analysis of synchrotron tomographic data. J. Synchrotron Radiat. 2014, 21, 1188–1193. [Google Scholar] [CrossRef] [PubMed]
- Pelt, D.M.; Gürsoy, D.; Palenstijn, W.J.; Sijbers, J.; de Carlo, F.; Batenburg, K.J. Integration of tomopy and the astra toolbox for advanced processing and reconstruction of tomographic synchrotron data. J. Synchrotron Radiat. 2016, 23, 842–849. [Google Scholar] [CrossRef] [PubMed]
- Irimia, D.; Dobrikov, D.; Kortekaas, R.; Voet, H.; van den Ende, D.A.; Groen, W.A.; Janssen, M.H. A short pulse (7 μs fwhm) and high repetition rate (dc-5khz) cantilever piezovalve for pulsed atomic and molecular beams. Rev. Sci. Instrum. 2009, 80, 113303. [Google Scholar] [CrossRef] [PubMed]
- Juranić, P.N.; Stepanov, A.; Ischebeck, R.; Schlott, V.; Pradervand, C.; Patthey, L.; Radović, M.; Gorgisyan, I.; Rivkin, L.; Hauri, C.P.; et al. High-precision x-ray fel pulse arrival time measurements at sacla by a thz streak camera with xe clusters. Opt. Express 2014, 22, 30004–30012. [Google Scholar] [CrossRef] [PubMed]
- Frühling, U.; Wieland, M.; Gensch, M.; Gebert, T.; Schütte, B.; Krikunova, M.; Kalms, R.; Budzyn, F.; Grimm, O.; Rossbach, J.; et al. Single-shot terahertz-field-driven X-ray streak camera. Nat. Photonics 2009, 3, 523. [Google Scholar] [CrossRef]
- Gorgisyan, I.; Ischebeck, R.; Prat, E.; Reiche, S.; Rivkin, L.; Juranić, P. Simulation of FEL pulse length calculation with THz streaking method. J. Synchrotron Radiat. 2016, 23, 643–651. [Google Scholar] [CrossRef] [PubMed]
- Schmid, K.; Buck, A.; Sears, C.M.S.; Mikhailova, J.M.; Tautz, R.; Herrmann, D.; Geissler, M.; Krausz, F.; Veisz, L. Density-transition based electron injector for laser driven wake field accelerators. Phys. Rev. ST Accel. Beams 2010, 13, 091301. [Google Scholar] [CrossRef]
- Buck, A.; Wenz, J.; Xu, J.; Khrennikov, K.; Schmid, K.; Heigoldt, M.; Mikhailova, J.M.; Geissler, M.; Shen, B.; Krausz, F.; et al. Shock-front injector for high-quality laser-plasma acceleration. Phys. Rev. Lett. 2013, 110, 185006. [Google Scholar] [CrossRef] [PubMed]
- He, Z.H.; Hou, B.; Nees, J.A.; Easter, J.H.; Faure, J.; Krushelnick, K.; Thomas, A.G.R. High repetition-rate wake field electron source generated by few-millijoule, 30 fs laser pulses on a density downramp. New J. Phys. 2013, 15, 053016. [Google Scholar] [CrossRef]
- Savitzky, A.; Golay, M.J.E. Smoothing and differentiation of data by simplified least squares procedures. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
- Luo, J.; Ying, K.; Bai, J. Savitzky—Golay smoothing and differentiation filter for even number data. Signal Process. 2005, 85, 1429–1434. [Google Scholar] [CrossRef]



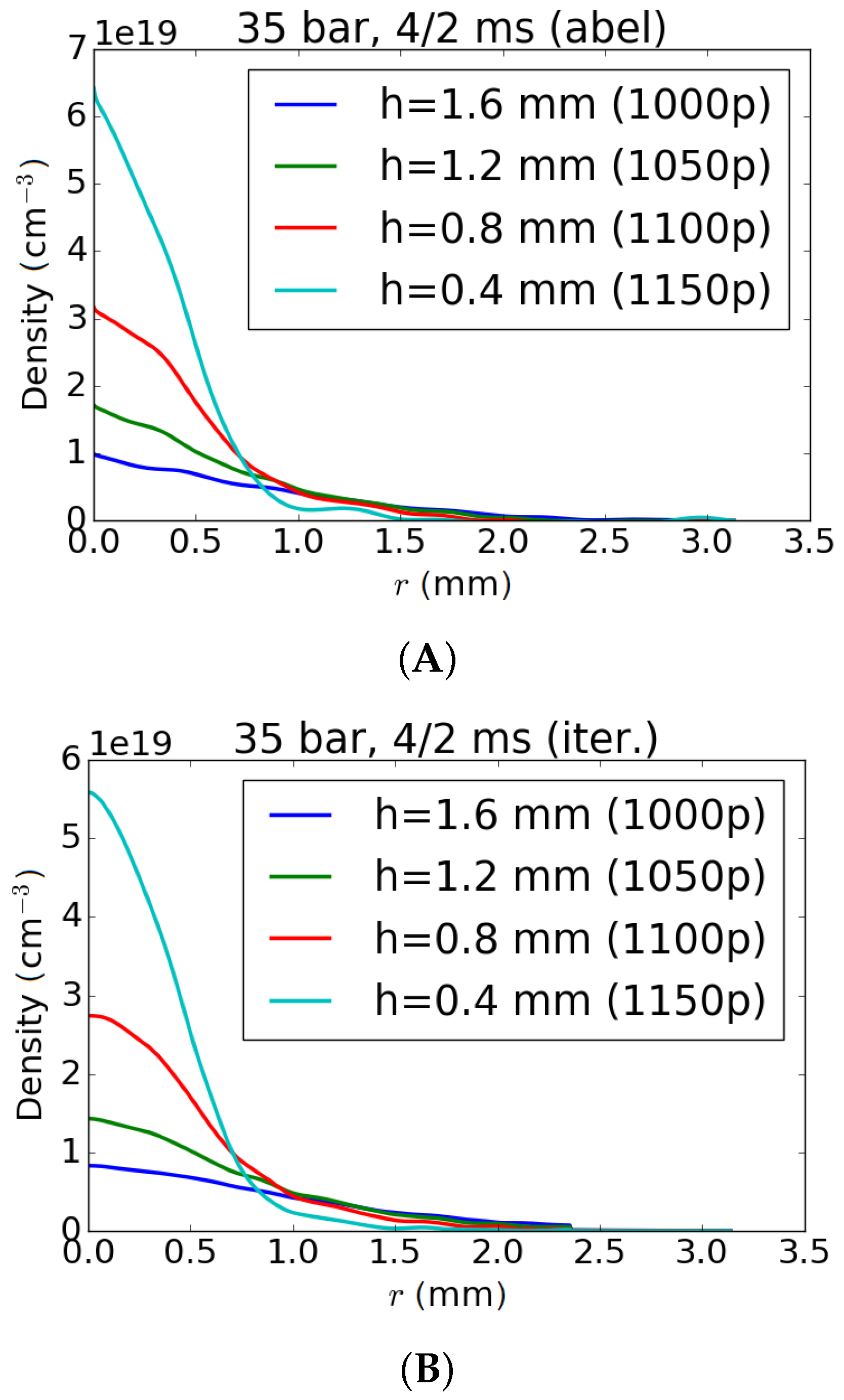


| (bar) | (mm) | h (mm) | h (pixel) | |
|---|---|---|---|---|
| min, max | 30.0, 40.0 | 1.8, 3.0 | 1200, 1050 | |
| step | 2.5 | 0.1 | 0.2 | 25 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Adelmann, A.; Hermann, B.; Ischebeck, R.; Kaluza, M.C.; Locans, U.; Sauerwein, N.; Tarkeshian, R. Real-Time Tomography of Gas-Jets with a Wollaston Interferometer. Appl. Sci. 2018, 8, 443. https://doi.org/10.3390/app8030443
Adelmann A, Hermann B, Ischebeck R, Kaluza MC, Locans U, Sauerwein N, Tarkeshian R. Real-Time Tomography of Gas-Jets with a Wollaston Interferometer. Applied Sciences. 2018; 8(3):443. https://doi.org/10.3390/app8030443
Chicago/Turabian StyleAdelmann, Andreas, Benedikt Hermann, Rasmus Ischebeck, Malte C. Kaluza, Uldis Locans, Nick Sauerwein, and Roxana Tarkeshian. 2018. "Real-Time Tomography of Gas-Jets with a Wollaston Interferometer" Applied Sciences 8, no. 3: 443. https://doi.org/10.3390/app8030443
APA StyleAdelmann, A., Hermann, B., Ischebeck, R., Kaluza, M. C., Locans, U., Sauerwein, N., & Tarkeshian, R. (2018). Real-Time Tomography of Gas-Jets with a Wollaston Interferometer. Applied Sciences, 8(3), 443. https://doi.org/10.3390/app8030443






