Capture Effect in the FSA-Based Networks under Rayleigh, Rician and Nakagami-m Fading Channels
Abstract
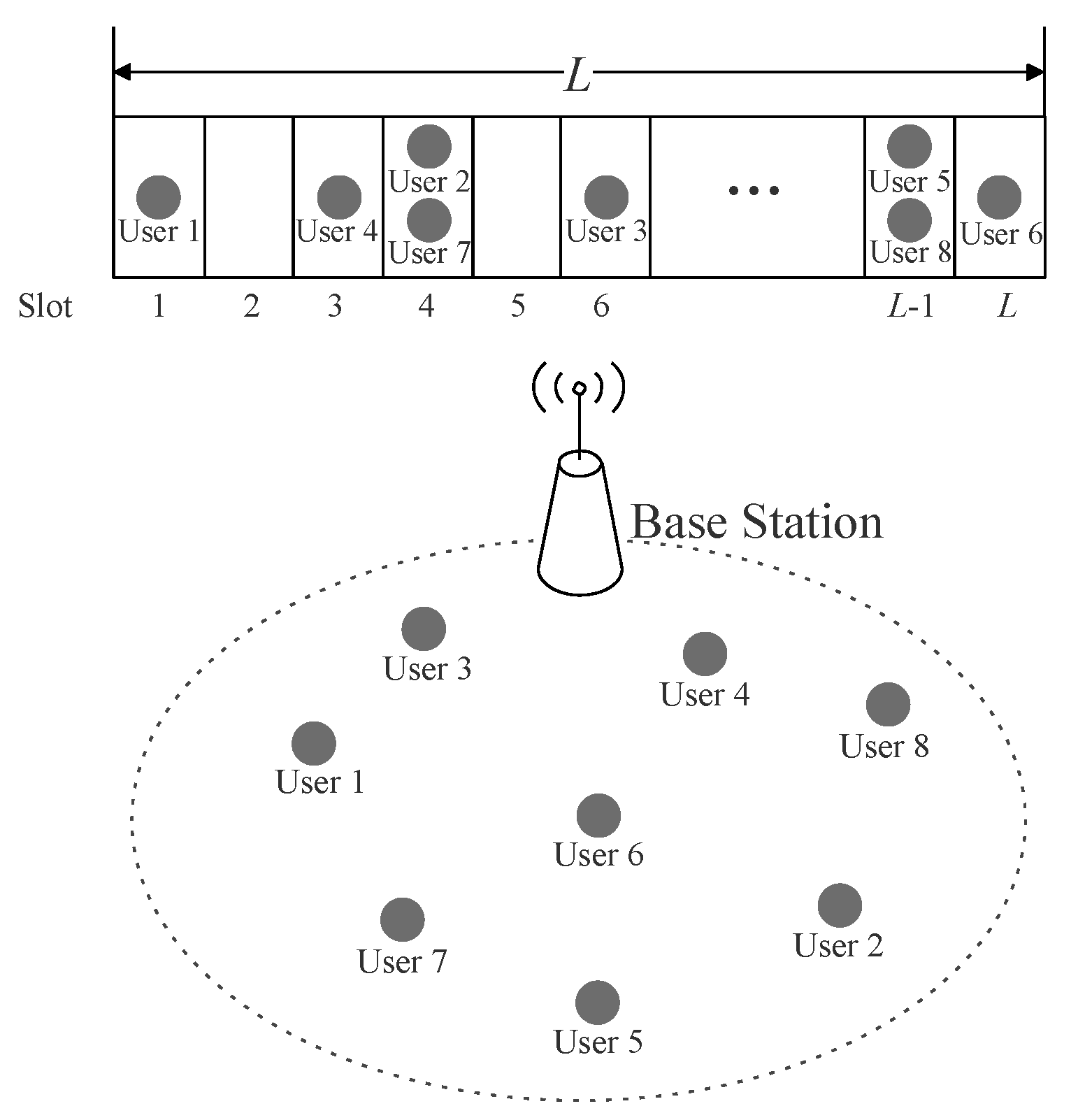
1. Introduction
2. Capture Probabilities Under Different Fading Channels
2.1. Rayleigh Fading Channel
2.2. Rician Fading Channel
2.3. Nakagami-m Fading Channel
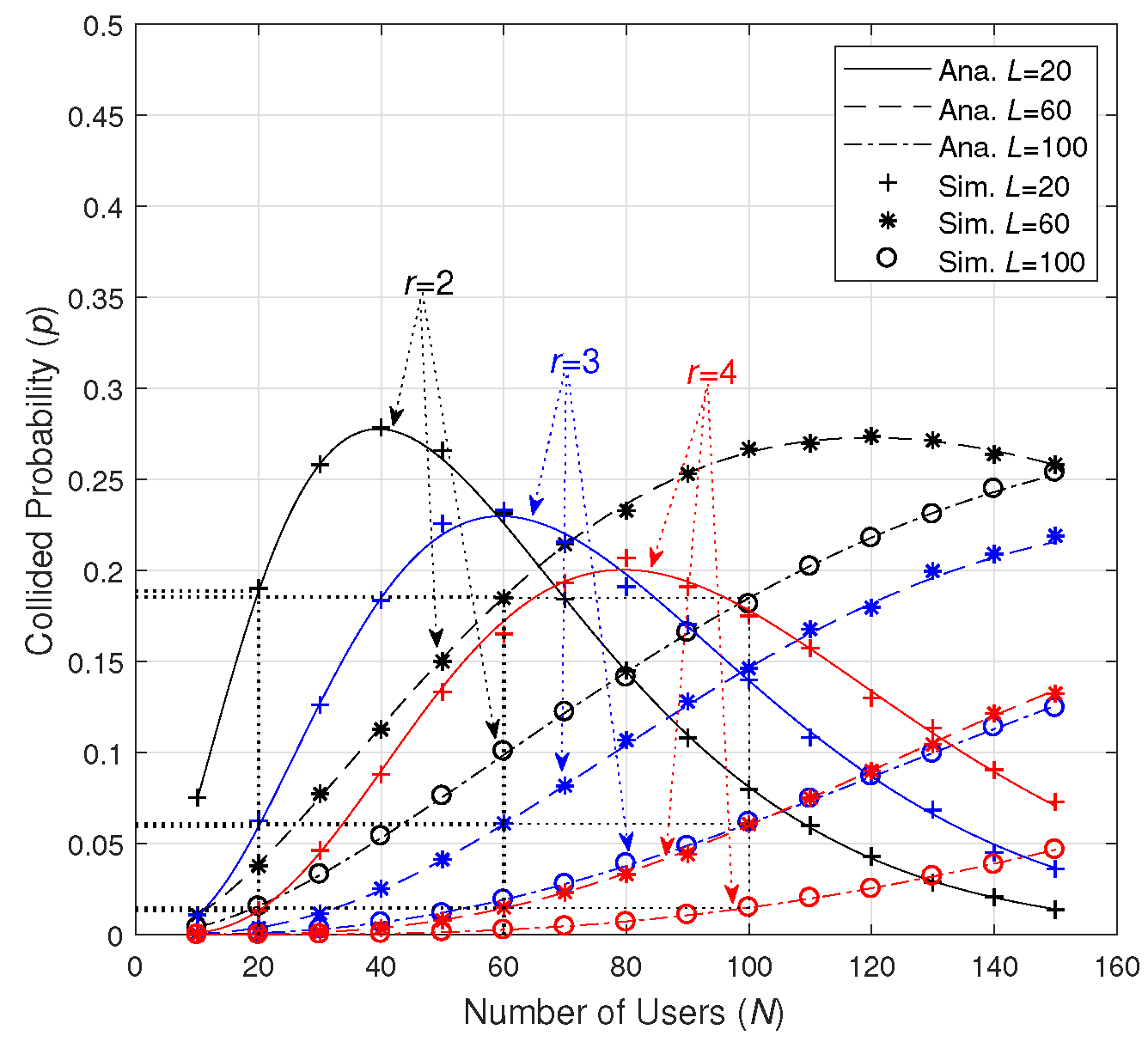
3. Optimal Frame Length and Maximum Channel Utilization
4. Numerical Results
4.1. Capture Probabilities
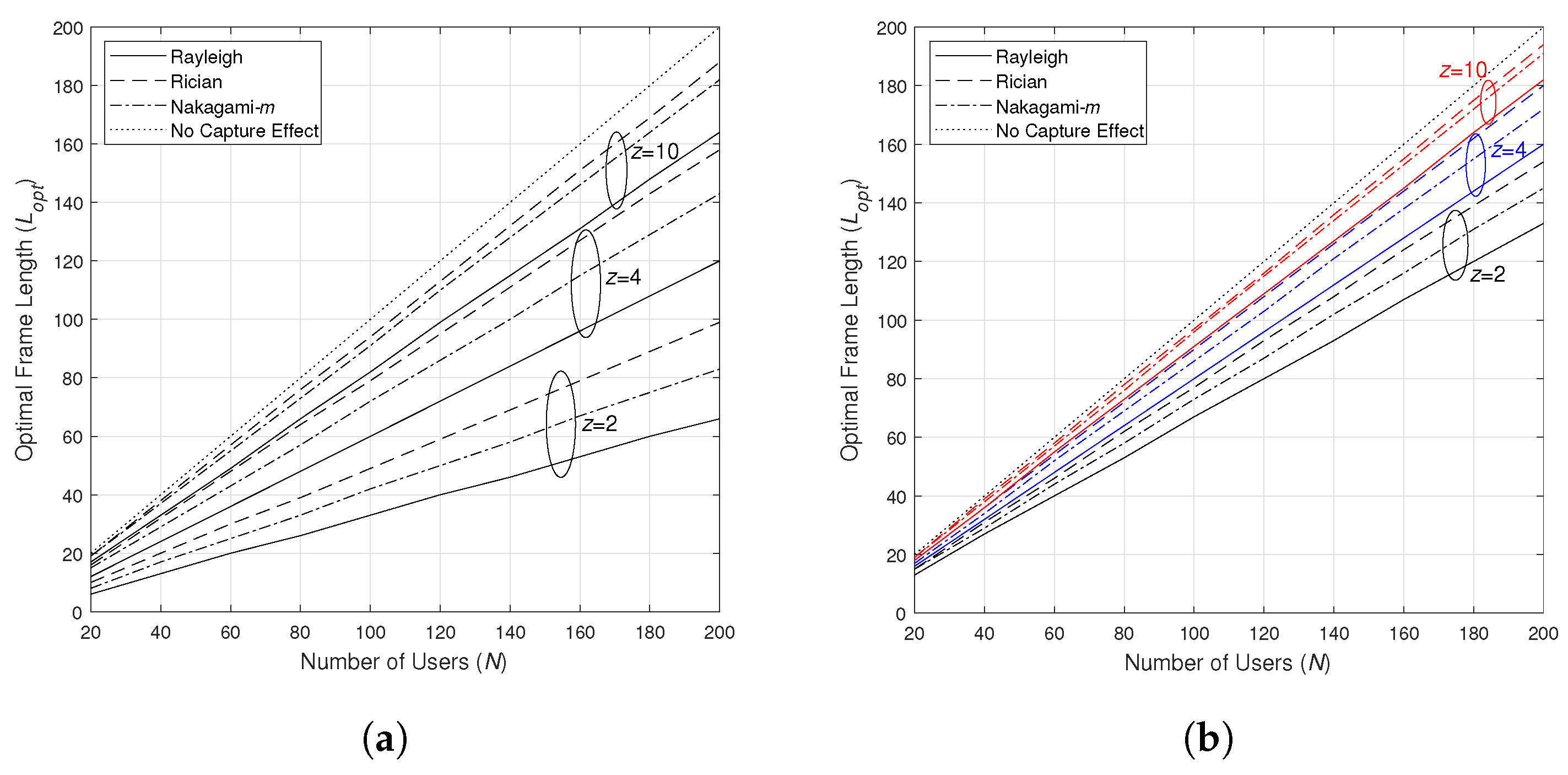
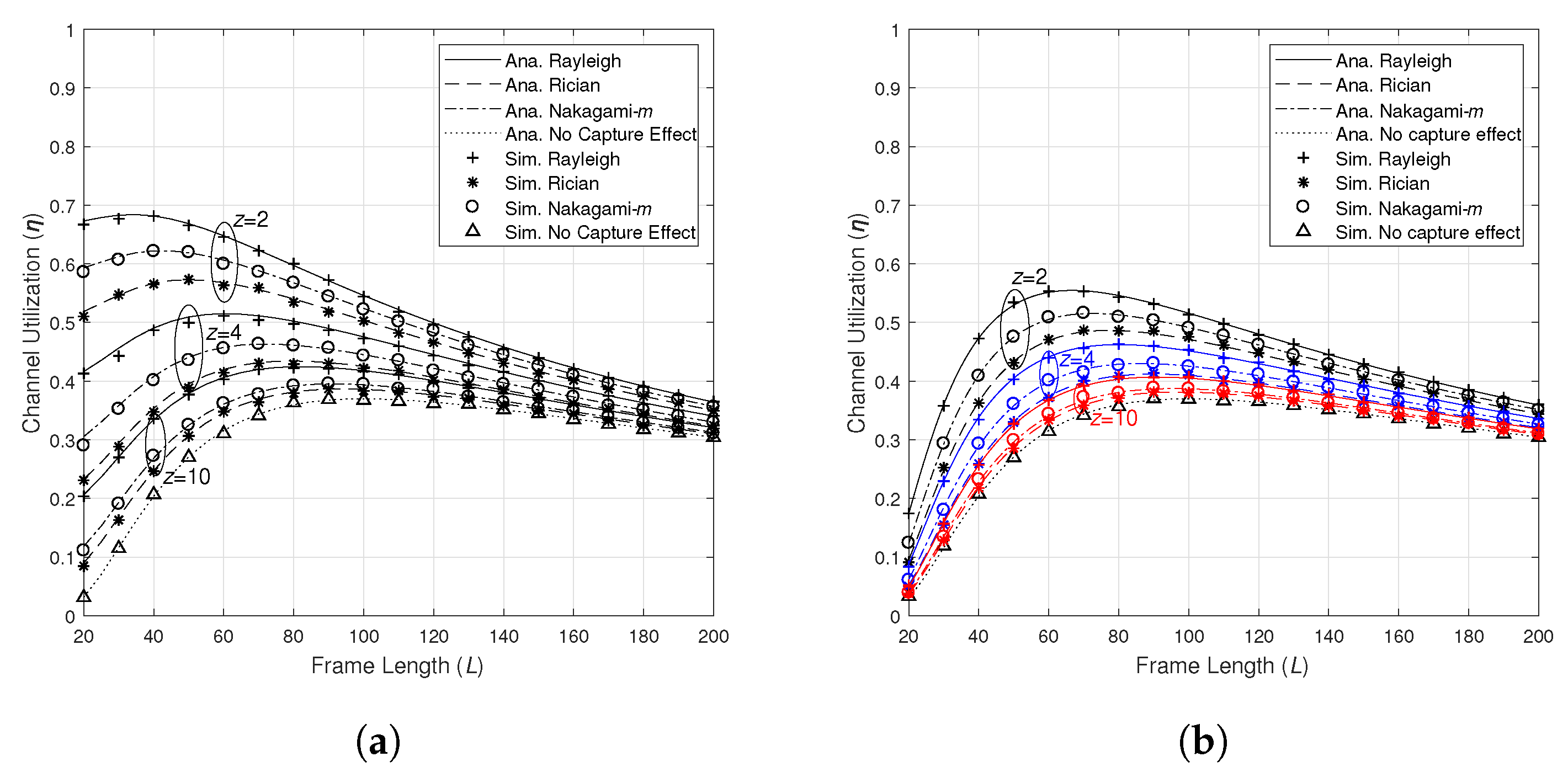
4.2. Optimal Frame Length
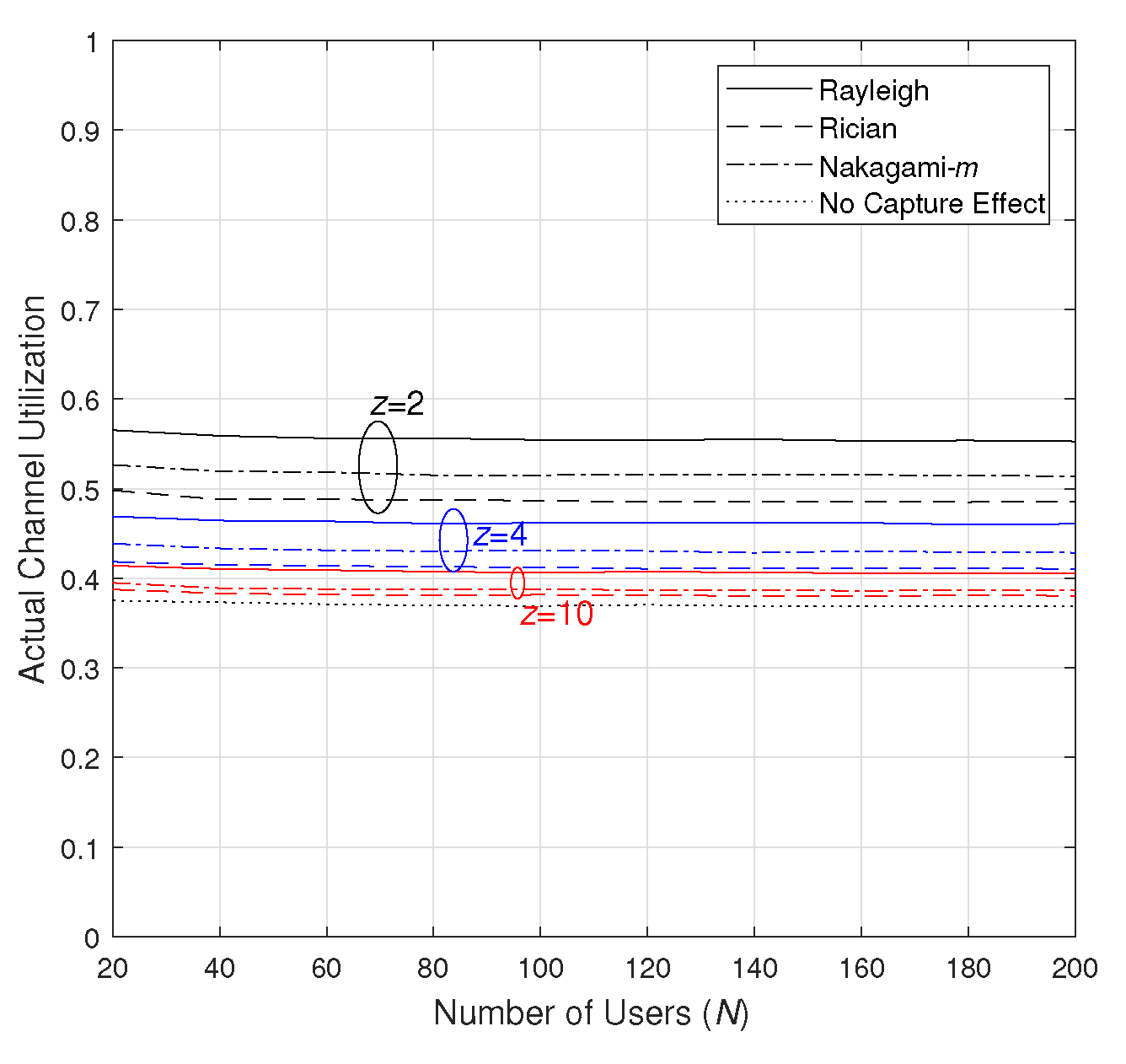
4.3. Channel Utilization
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Namislo, C. Analysis of mobile radio slotted ALOHA networks. IEEE J. Sel. Areas Commun. 1984, 2, 583–588. [Google Scholar] [CrossRef]
- Ma, R.T.; Misra, V.; Rubenstein, D. An analysis of generalized slotted-Aloha protocols. IEEE/ACM Trans. Netw. 2009, 17, 936–949. [Google Scholar]
- Tseng, S.M.; Lin, H.P.; Chen, C.H.; Wang, Y.C. Throughput analysis of DS CDMA/unslotted ALOHA wireless networks with fixed packet length in Rayleigh fading finite-state Markov channel model. Wirel. Pers. Commun. 2013, 71, 3091–3104. [Google Scholar] [CrossRef]
- Tseng, S.M.; Chiang, L.H.; Wang, Y.C. Throughput of coded DS CDMA/Unslotted ALOHA networks with variable length data traffic and two user classes in Rayleigh fading FSMC model. KSII Trans. Internet Inf. Syst. 2014, 8, 4324–4342. [Google Scholar]
- Liu, M.Y.; Wang, T.L.; Tseng, S.M. Throughput performance analysis of asynchronous optical CDMA networks with channel load sensing protocol. IEEE Photonics J. 2017, 9, 1–13. [Google Scholar] [CrossRef]
- Geraniotis, E.; Soroushnejad, M.; Yang, W.B. A multi-access scheme for voice/data integration in hybrid satellite/terrestrial packet radio networks. IEEE Trans. Commun. 1995, 43, 1756–1767. [Google Scholar] [CrossRef]
- Casini, E.; De Gaudenzi, R.; Herrero, O.D.R. Contention resolution diversity slotted ALOHA (CRDSA): An enhanced random access scheme for satellite access packet networks. IEEE Trans. Wirel. Commun. 2007, 6, 1408–1419. [Google Scholar] [CrossRef]
- Su, J.; Sheng, Z.; Hong, D.; Wen, G. An effective frame breaking policy for dynamic framed slotted Aloha in RFID. IEEE Commun. Lett. 2016, 20, 692–695. [Google Scholar] [CrossRef]
- Li, B.; Wang, J. Efficient anti-collision algorithm utilizing the capture effect for ISO 18000-6C RFID protocol. IEEE Commun. Lett. 2011, 15, 352–354. [Google Scholar]
- Salah, H.; Ahmed, H.A.; Robert, J.; Heuberger, A. A time and capture probability aware closed form frame slotted ALOHA frame length optimization. IEEE Commun. Lett. 2015, 19, 2009–2012. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, H.; Zeng, Y. Capture-aware estimation for large-scale RFID tags identification. IEEE Signal Process. Lett. 2015, 22, 1274–1277. [Google Scholar] [CrossRef]
- Espes, D.; Lagrange, X.; Suarez, L. A cross-layer MAC and routing protocol based on slotted Aloha for wireless sensor networks. Ann. Telecommun. 2015, 70, 159–169. [Google Scholar] [CrossRef][Green Version]
- Iannello, F.; Simeone, O.; Spagnolini, U. Medium access control protocols for wireless sensor networks with energy harvesting. IEEE Trans. Commun. 2012, 60, 1381–1389. [Google Scholar] [CrossRef]
- Ioo, Y.I.; Kim, S.T.; Kim, J.W. An efficient beacon scheduling scheme for multi-hop in vehicular environments. Wirel. Pers. Commun. 2015, 83, 1085–1099. [Google Scholar]
- Mao, Y.; Yan, F.; Shen, L. Multi-round elimination contention-based multi-channel MAC scheme for vehicular ad hoc networks. IET Commun. 2017, 11, 421–427. [Google Scholar] [CrossRef]
- Huang, J.; Li, Q.; Zhong, S.; Liu, L.; Zhong, P.; Wang, J.; Ye, J. Synthesizing existing CSMA and TDMA based MAC protocols for VANETs. Sensors 2017, 17, 338. [Google Scholar] [CrossRef] [PubMed]
- Madueno, G.C.; Pratas, N.K.; Stefanović, Č.; Popovski, P. Massive M2M access with reliability guarantees in LTE systems. In Proceedings of the 2015 IEEE International Conference on Communications (ICC), London, UK, 8–12 June 2015; pp. 2997–3002. [Google Scholar]
- Bello, L.M.; Mitchell, P.; Grace, D. Application of Q-learning for RACH access to support M2M traffic over a cellular network. In Proceedings of the 2014 20th European Wireless Conference, Barcelona, Spain, 14–16 May 2014; pp. 1–6. [Google Scholar]
- Durand, F.R.; Abrão, T. Energy efficient adaptive optical CDMA random access protocol based on particle swarm optimization. Photonic Netw. Commun. 2017, 33, 275–289. [Google Scholar] [CrossRef]
- Shoaie, M.A.; Khazraei, S.; Pakravan, M.R. Performance analysis of slotted ALOHA random access packet-switching optical CDMA networks using generalized optical orthogonal codes and M-ary overlapping PPM signaling. J. Opt. Commun. Netw. 2011, 3, 568–576. [Google Scholar] [CrossRef]
- Chen, W.T. An accurate tag estimate method for improving the performance of an RFID anticollision algorithm based on dynamic frame length ALOHA. IEEE Trans. Autom. Sci. Eng. 2009, 6, 9–15. [Google Scholar]
- Yang, L.; Zhang, G.; Lin, F.; Zheng, H. An efficient estimation method coping with the capture effect for RFID tags identification and application in remote learning. J. Intell. Fuzzy Syst. 2016, 31, 2707–2712. [Google Scholar] [CrossRef]
- Jun, J.; Yeon, S.; Kundu, T.; Agrawal, D.P.; Jeong, J. Caca: Link-based channel allocation exploiting capture effect for channel reuse in wireless sensor networks. In Proceedings of the 2016 IEEE 36th International Conference on In Distributed Computing Systems (ICDCS), Nara, Japan, 27–30 June 2016; pp. 600–608. [Google Scholar]
- Sheikh, A.U.; Yao, Y.D.; Wu, X. The ALOHA systems in shadowed mobile radio channels with slow or fast fading. IEEE Trans. Veh. Technol. 1990, 39, 289–298. [Google Scholar] [CrossRef][Green Version]
- Sanchez-Garcia, J.; Smith, D.R. Capture probability in Rician fading channels with power control in the transmitters. IEEE Trans. Commun. 2002, 50, 1889–1891. [Google Scholar] [CrossRef]
- Da Silva, A.P.T.R.; Brito, J.M.C. Analysis of adaptive modulation performance in networks with multiple access Slotted Aloha. In Proceedings of the 2017 31st International Conference on In Information Networking (ICOIN), Da Nang, Vietnam, 11–13 January 2017; pp. 210–215. [Google Scholar]
- Khoshnevis, B.; Khalaj, B.H. Optimum power selection algorithms in Aloha networks: Random and deterministic approaches. IEEE Trans. Wirel. Commun. 2007, 6, 3124–3136. [Google Scholar] [CrossRef]
- Hua, Y.; Wang, Y. On the saturate throughput of IEEE 802.11 DCF with capture effect in Rician fading channel. In Proceedings of the 2008 4th International Conference on Wireless Communications, Networking and Mobile Computing (WiCOM), Dalian, China, 19–21 September 2008; pp. 1–4. [Google Scholar]
- Hadzi-Velkov, Z.; Spasenovski, B. Capture effect in IEEE 802.11 basic service area under influence of Rayleigh fading and near/far effect. In Proceedings of the 2002 13th IEEE International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC), Lisboa, Portugal, 18 September 2002; pp. 172–176. [Google Scholar]
- Gradštejn, I.S.; Ryžik, I.M. Table of Integrals, Series, and Products; Elsevier/Academic: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Jameel, F.; Haider, M.A.A.; Butt, A.A. Performance analysis of VANETs under Rayleigh, Rician, Nakagami-m and Weibull fading. In Proceedings of the 2017 IEEE International Conference on Communication, Computing and Digital Systems (C-CODE), Islamabad, Pakistan, 8–9 March 2017; pp. 127–132. [Google Scholar]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables; Dover: New York, NY, USA, 1972. [Google Scholar]
- Simon, M.K.; Alouini, M.S. Digital Communication over Fading Channels; John Wiley & Sons: Hoboken, NJ, USA, 2005. [Google Scholar]
- Chen, W.T. Optimal frame length analysis and an efficient anti-collision algorithm with early adjustment of frame length for RFID systems. IEEE Trans. Veh. Technol. 2016, 65, 3342–3348. [Google Scholar] [CrossRef]
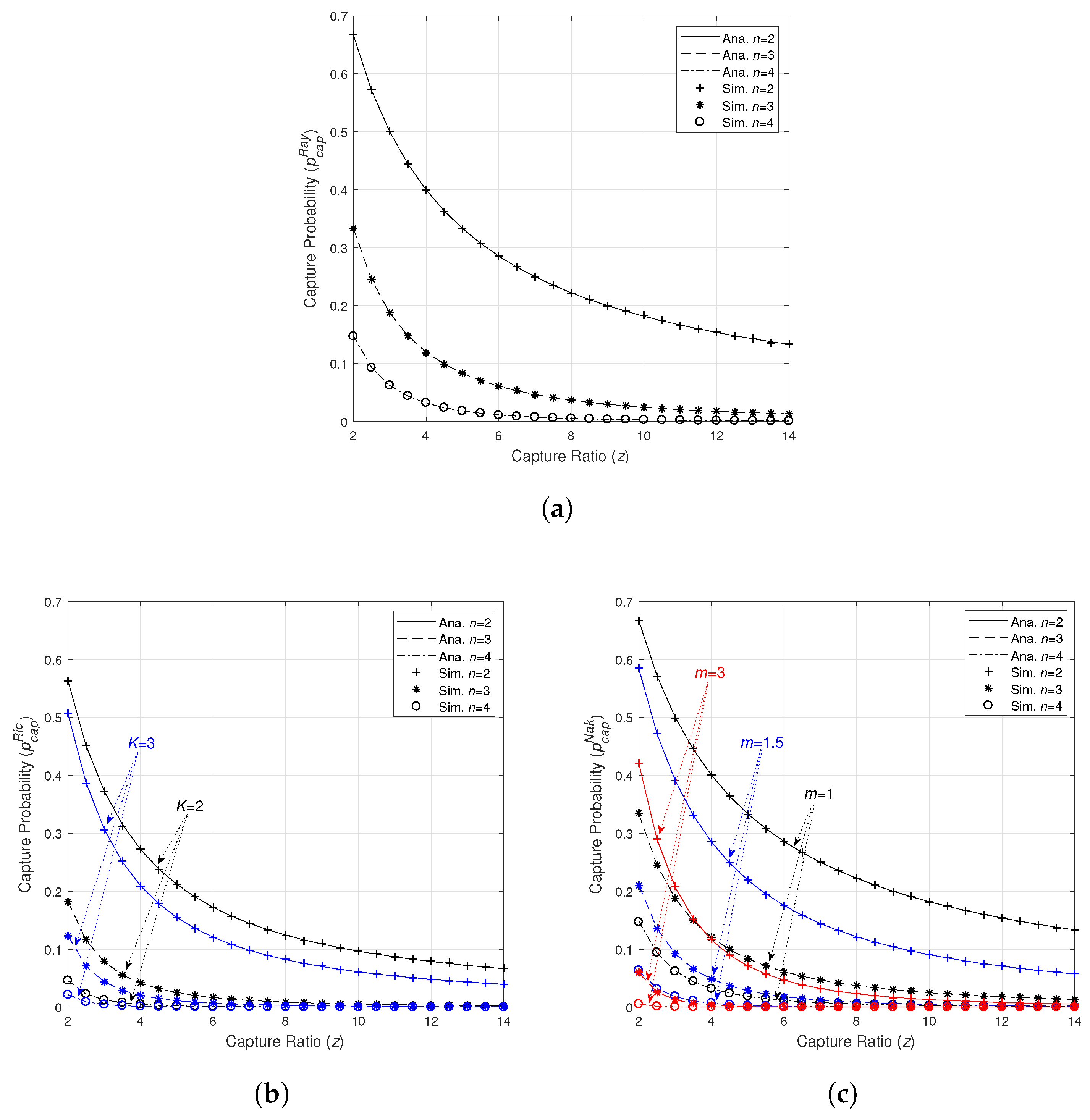
| 2*Fading | |||
|---|---|---|---|
| Rayleigh | 0.667 0.333 0.148 | 0.400 0.120 0.032 | 0.182 0.025 0.003 |
| Rician | 0.506 0.123 0.022 | 0.209 0.020 0.001 | 0.061 0.002 0.000 |
| Nakagami-m | 0.584 0.210 0.063 | 0.285 0.048 0.007 | 0.091 0.005 0.000 |
| Fading | |||
|---|---|---|---|
| Rayleigh | 0.56 | 0.46 | 0.41 |
| Rician | 0.49 | 0.41 | 0.38 |
| Nakagami-m | 0.52 | 0.43 | 0.39 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Shi, J.; Chen, L. Capture Effect in the FSA-Based Networks under Rayleigh, Rician and Nakagami-m Fading Channels. Appl. Sci. 2018, 8, 414. https://doi.org/10.3390/app8030414
Wang Y, Shi J, Chen L. Capture Effect in the FSA-Based Networks under Rayleigh, Rician and Nakagami-m Fading Channels. Applied Sciences. 2018; 8(3):414. https://doi.org/10.3390/app8030414
Chicago/Turabian StyleWang, Yang, Jianghong Shi, and Lingyu Chen. 2018. "Capture Effect in the FSA-Based Networks under Rayleigh, Rician and Nakagami-m Fading Channels" Applied Sciences 8, no. 3: 414. https://doi.org/10.3390/app8030414
APA StyleWang, Y., Shi, J., & Chen, L. (2018). Capture Effect in the FSA-Based Networks under Rayleigh, Rician and Nakagami-m Fading Channels. Applied Sciences, 8(3), 414. https://doi.org/10.3390/app8030414





