State-of-the-Art Mobile Intelligence: Enabling Robots to Move Like Humans by Estimating Mobility with Artificial Intelligence

Abstract

Mobility is a significant robotic task. It is the most important function when robotics is applied to domains such as autonomous cars, home service robots, and autonomous underwater vehicles. Despite extensive research on this topic, robots still suffer from difficulties when moving in complex environments, especially in practical applications. Therefore, the ability to have enough intelligence while moving is a key issue for the success of robots. Researchers have proposed a variety of methods and algorithms, including navigation and tracking. To help readers swiftly understand the recent advances in methodology and algorithms for robot movement, we present this survey, which provides a detailed review of the existing methods of navigation and tracking. In particular, this survey features a relation-based architecture that enables readers to easily grasp the key points of mobile intelligence. We first outline the key problems in robot systems and point out the relationship among robotics, navigation, and tracking. We then illustrate navigation using different sensors and the fusion methods and detail the state estimation and tracking models for target maneuvering. Finally, we address several issues of deep learning as well as the mobile intelligence of robots as suggested future research topics. The contributions of this survey are threefold. First, we review the literature of navigation according to the applied sensors and fusion method. Second, we detail the models for target maneuvering and the existing tracking based on estimation, such as the Kalman filter and its series developed form, according to their model-construction mechanisms: linear, nonlinear, and non-Gaussian white noise. Third, we illustrate the artificial intelligence approach—especially deep learning methods—and discuss its combination with the estimation method.

1. Introduction

Mobility is a basic feature of human intelligence. From the beginnings of robot technology, people have been imagining building a human-like machine. Smart movement is an obvious feature of a robot and an important manifestation of its intelligence. Self-moving of a robot mainly includes navigation and control, such as perceiving the surrounding environment, knowing where it wants to go and where it is at a given time, and further controlling its movement and adjusting the travel path to reach its destination. In this review, we focus only on the navigation, that is, the robot’s awareness of where it is in relation to the surrounding environment.

When we walk on the street, we can see that a car is moving and that the leaves on a tree are moving because of wind. Fortunately, we know that the house will not move. Although we see the house moving backward as our forward movement proceeds, we also know that the house is not moving. According to our position relative to that of the house, we also can judge our speed and that of the car, predict the location of the car, and determine whether we need to avoid the car.

For robots, the so-called mobile intelligence means that they can move in the same manner as human beings and exercise the same judgment. A robot on a road, for example, an autonomous car, needs to answer three questions constantly during movement: where am I, where am I going, and how do I go? It first needs to judge its movement relative to all other kinds of movement (cars, trees, and houses in the field of vision) and then has to avoid other cars. Among these tasks, the ability to understand surroundings is critical. The performance of an autonomous car heavily depends on the accuracy and reliability of its environmental perception technologies, including self-localization and perception of obstacles. For humans, these actions and judgments are dominated by human intelligence, but for machines, they are extremely complex processes.

We first define robotic mobile intelligence. When moving, a robot should have two basic capabilities: (1) to localize itself and navigate; and (2) to understand the environment. The core technologies enabling these capabilities are denoted as simultaneous localization and mapping (SLAM), tracking, and navigation. SLAM constructs or updates the map of an unknown environment while simultaneously keeping track of the robot’s location. It is a complex pipeline that consists of many computation-intensive stages, each performing a unique task. Tracking refers to the automatic estimation of the trajectory of a target as it moves. The tracking algorithms are based mainly on estimation theory. Here, the target is a general one, either the robot itself or others. When the robot wants to “track itself”, which means that the robot wants to know its own motion, called “navigation”, by which the robot determines its own position and direction of movement.

We now define foreground and background targets. We usually set the target to track as a foreground target, such as the cars. The house does not need to be tracked, nor do other stationary objects, so it is set as the background. Some mobile aspects that do not need to be tracked, such as the movement of leaves, are called background targets. The most difficult aspect of video tracking is to distinguish the difference between foreground and background targets.

In current navigation systems, researchers are trying to replicate such a complicated process by using a variety of sensors in combination with information processing. For example, vision sensors are commonly used sensors in robotic systems. In the video from a camera fixed on a robot moving on the street, the houses are moving, the cars are moving, and even the trees on the roof have their own motion because of the robot’s own movement. How to obtain the mobile relationship between the robot and foreground target from so many moving targets has always been an area of intense research interest. The optical flow method [1] is a widely used method to determine this relationship, which assumes that the apparent velocity of the brightness pattern varies smoothly almost everywhere in an image. Researchers have done much useful work in this area [2,3].

The disadvantage of the optical flow method is the large computational overhead. Moreover, it is difficult to find the correct optical flow mode when the robot is moving at a high speed. To overcome such a difficulty inherent in a visual sensor, other sensors have been introduced, for example, inertial measurement units (IMUs) and global positioning systems (GPSs), into the navigation system. GPSs are now widely used in cars [4]. In most cases, GPSs provide accuracy within approximately 10–30 m. For autonomous cars, however, this accuracy is insufficient.

IMUs have become smaller, lower cost, and consume less power thanks to miniaturization technologies, such as micro-electro-mechanical systems or nano-electro-mechanical systems. Because the measurements of the IMUs have unknown drift, it is difficult to use the acceleration and orientation measurements, to obtain the current position of a pedestrian in an indoor navigation system [5]. Combined with video sensors, IMUs have been used in indoor and outdoor seamless navigation connection, such as in unmanned aerial vehicles (UAVs) [6].

Other sensors, such as Wi-Fi [7,8], have been widely used in indoor navigation systems in recent years. Wi-Fi uses triangulation to locate a target, which can keep the indoor positioning error within tens of meters and effectively overcome the IMU position drift. Another sensor used for indoor positioning is ultra-wide-band (UWB) [9], which requires the user to place the receiver in the area of target activity.

Considering these factors, it is clear that the navigation systems are complex. In the process of movement, a robot must first perceive the surrounding environment firstly, and then need to know the way and speed of movement of itself and a target. It also needs to judge the movement of a foreground target and predict whether it will collide with it. Fortunately, some progress has been made in research on autonomous vehicles. Unmanned vehicles driving on roads can identify road signs, traffic conditions, and so on.

Robot navigation uses a tracking algorithm [10,11,12,13] to achieve maneuvering target estimation. Based on the known characteristics of the system noise, the estimation method extracts the estimated trajectory of a target from an uncertain signal. To obtain good estimation results, two models are crucial, namely, the process and measurement models. The process model, which describes the motion characteristics of maneuvering targets has been a hot topic in the field of target tracking. Based on a variety of different motion characteristics and using Newton’s law, many modeling methods for maneuvering models have been presented [14,15,16,17] that capture the characteristics of most moving targets.

However, at present, the research methods based on estimation still cannot deal with all the complicated situations in practical applications. The main reason is that it is difficult to obtain an accurate measurement model of a sensor used in different applications. For example, the drift of IMU data is still a subject that needs further study [18]. In visual tracking applications, the interference of light, sunlight, and flexible objects makes the target information obtained by the image-processing method less accurate and extremely computationally intensive [19,20].

The fact that we want robots to behave like human beings, and because a robot’s motion space and behaviors are increasingly complicated, brings great difficulties to the application of the traditional estimation-based tracking algorithms. We believe the reason that a robot system cannot cope with such a complex environment space and motion behavior, is that the information collected by sensors has a high degree of uncertainty because of the complexity of environment. In other words, we cannot accurately model the measurement model.

In our opinion, an estimation-based algorithm has a strong theoretical foundation and can obtain good kinematic analysis of moving targets. Therefore, these theories are still of great value for robotics in very complicated environments. However, in the face of increasingly complex environments and movements, the most important difficulty lies in the fact that a sensor cannot obtain the accurate information in response to the complex environment of the outside world. Therefore, a method of modeling the measurement sensor should be developed. Based on the traditional equation-based measurement model, a networked model representing the relationship among the various data should be considered to deal with these complex environments.

In this survey, we discuss the basic theory of a traditional tracking algorithm applied to a navigation system under the condition of analyzing the complex environments, as well as the factors affecting system performance in complex environments. In addition, we review the necessity, feasibility, and the method of using artificial intelligence method for navigation systems to achieve the mobile intelligence. Furthermore, we propose an the initial idea of how to apply a current artificial intelligence (AI) method to enhance the intelligence of a robot motion system.

2. Survey Organization

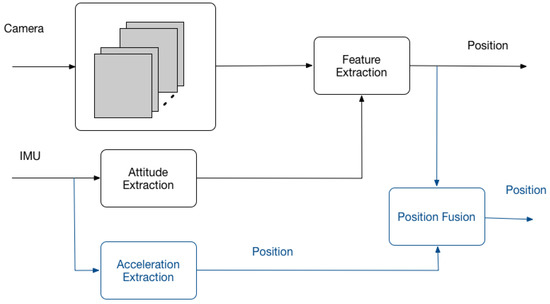
Figure 1 shows the organization of this survey. We first focus on robotics research, especially the mobile intelligence. Regarding navigation, Section 3.1 discusses the sensors applied in the robot system, such as video sensors, IMU, GPS, Wi-Fi, and UWB. In Section 3.2, we illustrate the methods for fusing information collected by multiple sensors, including GPS or vision, together with IMU. Section 3.2 also introduces other multi-sensor systems, such as IMU and Wi-Fi.

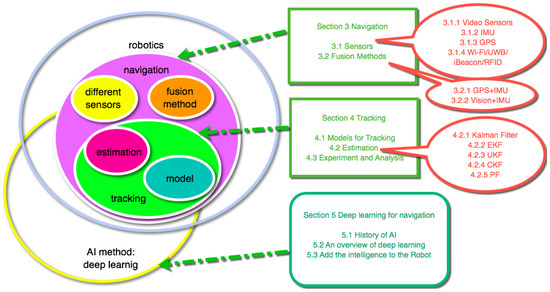
Figure 1. The organization of this survey.

As the basis algorithm of the navigation, tracking models and methods are very important. Section 4.1 discusses some representative models, including the Singer model, interacting multiple model (IMM), the adaptive model, etc., which are the most widely used models. In particular, we believe that the tracking methods are the most important part of navigation, so Section 4.2 details the estimation methods, including the extended Kalman Filter (EKF), unscented Kalman Filter (UKF), cubature Kalman Filter (CKF), and particle filter (PF).

Finally, as the most important part of this review, Section 5 introduces the deep learning applied to navigation. In addition to the typical network of deep learning, we also discussed how to combine deep learning with the estimation method to improve a robot’s mobile intelligence.

3. Navigation

In “robot navigation” that is based on the sensor measurements, the robot seeks to accomplish tasks such as constructing a map of its environment, locating itself in that map, and recognizing objects that should be avoided or sought. Learning and maintaining models of their environments are the first navigational problems of navigation for robots. Research on mobile robot navigation includes grid-based [21] and topological [22] studies.

DeSouza [23] surveyed the first 20 years of the area of vision for mobile robot navigation, in which the subject is divided on the basis of structured and unstructured environments. For indoor robots in structured environments, the cases of geometrical and topological models of space were considered separately. For unstructured environments, optical flow has been applied to navigation, using methods from the appearance-based paradigm and recognition of specific objects in the environment.

In the earlier robot navigation systems, sensors included the rotating ultrasonic range sensors, circular sonar sensors and cameras. Additional research also was done on multiple sensors. Kam et al. [24] presented a review of the techniques of sensor integration in robot navigation with complementary and redundant sensors, which divides integration techniques into two categories: low-level fusion is used for direct integration of sensory data, resulting in parameter and state estimates; and high-level fusion is used for indirect integration of sensory data in hierarchical architectures, through command arbitration and integration of control signals suggested by modules. Machine intelligence is also discussed as an effective method of integrating the multi-sensor signals, including rule-based techniques, behavior based algorithms, Dempster–Shafer reasoning, fuzzy logic, and neural networks.

We note that from the beginning of robot navigation research, multi-sensor fusion and machine intelligence is critical. Next, we will illustrate the state-the-art navigation elements, such as the sensors used, together with methodology.

3.1. Sensors

3.1.1. Video Sensors

Video sensors are one of the most popular sensors for robot navigation. Application systems include cars, small-size and low-cost airborne systems, and so on. There are two primary ways of placing a video image sensor. One is to fix the sensor in a certain position, which is generally used by the monitoring system. The other is to place the sensor on a moving target usually used by autonomous vehicles. This kind of system can be divided into a monocular camera system and a binocular camera system according to the number of sensors.

Regarding the binocular camera system, the position of the vehicle can be determined by comparing the measured image of two fixed cameras with the given distance relations, which is called the stereoscopic approach [25]. The principle of a binocular vision system obtaining the target distance is just like that of the human eye, which is the earliest research into a the visual system obtaining the target distance in the foreground.

In contrast, how a monocular vision system obtains the target of the distance is completely different. Two methods have been used for monocular vision. One is called landmark-based vision navigation, which determines position and attitude by calculating directions to landmarks from the measured image of the landmarks [26,27]. The principle of a monocular vision system is that the three-dimensional (3D) coordinates of each point in space have a one-to-one correspondence in two-dimensional (2D) images. This relationship is shown in Figure 2 [26], which depicts projected landmarks on the focal plane when the pinhole camera model is adopted. The $x_c$ axis of the camera frame is aligned with the optical plane when the pinhole camera model is adopted. The $y_c$ and $z_c$ axes are in the horizontal and vertical directions, respectively, of the focal plane f on the $x_c$ axis. The landmark k at the position of 3D space at $P_k^c(X_k^c,Y_k^c,Z_k^c)$ is projected onto the point $p_k^c(f,u_k,v_k)$ on the focal plane in the camera frame, where $u_k$ and $v_k$ are the location in the captured 2D image, respectively, and $u_k=f\frac{Y_k^c}{X_k^c}$ and $v_k=f\frac{Z_k^c}{X_k^c}$.

Figure 2. Landmark measurements in the vision navigation [26].

The other monocular vision method, visual odometry, determines the motion of the vehicle from successive images of the camera. This method was first proposed in Ref. [20], in which three steps were developed: feature detection, feature matching, and robust estimation. Its basic underlying principle is to use the difference between adjacent frame images to describe the motion characteristics of the motion camera. Although this approach, as proposed by the author, indicates that it can be used with binocular cameras, it is of even greater importance to monocular camera navigation systems such as those in autonomous car systems.

Visual odometry is a dead-reckoning algorithm and, therefore is prone to cumulative errors. The current pose of the platform is obtained from the previous pose by adding the last observed motion, which leads to a superlinear increment of the pose error over time. One solution to this problem is to compute visual odometry as a bundle adjustment (BA) algorithm [28]. BA imposes geometrical constraints over multiple frames, thus providing a global optimal estimate of all camera poses at once. However, the computational cost of BA algorithms increases with the cube of the number of frames used for computation [29], which uses the entire history of the tracked features at a cost of incurring a computational complexity that increases linearly with the number of tracked features and that is independent of the number of frames. A common approach, known as local BA, uses a small number of frames to limit the computational complexity [30]. The latest research on visual odometry includes online algorithms [31] and with the high-performance estimation of the feature points, as in convolutional neural networks [32].

3.1.2. IMU

An IMU can obtain the moving information of a target. Among dead-reckoning sensors, IMUs are widely used to construct inertial navigation systems (INSs). An IMU usually contains a set of three orthogonally installed accelerometers and three orthogonally installed gyros. An inertial navigation system is a real-time algorithm used to calculate the position, velocity, and attitude of the vehicle that carries the INS by integrating the acceleration and rotation rate signals from an IMU. The position is calculated by double integration of the sum of the the nongravitational acceleration from the three accelerometers. By integrating the rotation rate signals from the three gyros, we can determine the angular orientation of the three accelerometers is determined. Using this orientation information, the calculated acceleration, velocity and position are transformed into the desired navigation coordinate system by this orientation information [18].

Figure 3 shows the INS process. There are two main phases in INS operation: the initial condition alignment phase and the navigation phase. The alignment phase gives the the rotation matrix $C_b^n$, which transforms the measurement in the right-front-up (RFU) coordinate system form the carrier body frame (b-frame) to the East-North-up (ENU) geographic coordinate system in the navigation frame (n-frame),

$${[x_n,y_n,z_n]}^T=C_b^n{\left[x_b,y_b,z_b\right]}^T$$

(1)

where $x_n$ and $y_n$ represent the geographical coordinate systems of the East and North, respectively; $z_n$ points upward, toward the Earth’s surface, antiparallel to the surface’s outward normal. Meanwhile, $x_b$, $y_b$, and $z_b$ indicate the front, left, and upward, respectively, according to the movement of the body. The attitude transform matrix $C_b^n$ converts the acceleration in the body coordinate system b to the navigation coordinate system n. Kim and Golnaraghi [33] presented the definition and description of these two frames, as well as the method of computing the attitude transform matrix $C_b^n$; thus, some details are omitted here.

Figure 3. Inertial Navigation Systems (INS) process.

Then, for the navigation phase, we can obtain the acceleration of the navigation system f based on $C_b^n$, and the measured acceleration vectors $accX,accY$ and $accZ$ as follows:

$$f=C_b^n\times {\left[\begin{array}{ccc}accX& accY& accZ\end{array}\right]}^T-{\left[\begin{array}{ccc}0& 0& g\end{array}\right]}^T$$

(2)

where $accX$, $accY$ and $accZ$ are the accelerations of the body coordinates. f can be expressed as the vector ${\left[\begin{array}{ccc}{f}_{xn}& f_{yn}& f{}_{zn}\end{array}\right]}^T$, where $f_{xn}$ represents the acceleration of the $x_n$ axis, $f_{yn}$ represents the acceleration of $y_n$ axis, and $f_{zn}$ represents the acceleration of $z_n$ axis, respectively; and g is the gravitational acceleration. Based on the acceleration of the navigation system, we can obtain pedestrian location and speed information. Therefore, the accuracy of $C_b^n$, $accX$, $accY$, and $accZ$ are very important to navigation performance.

Any errors in either the alignment phase or the navigation phase will be integrated and will propagate over time. These errors greatly reduce the performance and navigational accuracy of the INS. Unfortunately, there is a serious drift in the measured data of an IMU, especially acceleration data, and the trajectory obtained by this method deviates significantly from the real trajectory. Therefore, to mitigate such problems in today’s IMU-based navigation systems, integration of multiple sensors is common. Section 3.2 introduces a specific system of this type.

3.1.3. GPS

Outdoor navigation systems are generally based on GPSs, which is based on satellite navigation system that provides access to accurate positioning information anywhere on the globe. At present, the accuracy of differential GPS technology has been significantly improved, but GPS accuracy is still not high enough because of the weather, buildings, and the current visible number of GPS satellites [34,35]. Moreover, GPS signals are not always available because they can be blocked by high buildings, canyons and forests, among others obstacles.

Today, the positioning error of the low-cost GPS systems in mobile terminals, such as the mobile phones and the car-mounted mobile terminals, is still a few meters or more. This can pose a great problem in certain situations, such as military maneuvers or even for emergency responders. Therefore, the data fusion method for GPS and IMU has become a hot research topic in navigation systems research, which is explored further in Section 3.2.

3.1.4. Wi-Fi, UWB, iBeacon, and Radio Frequency Identification

GPS receivers cannot perform well in indoor environments because of the absence of a line of sight to GPS satellites. Therefore, some other sensors are used in the indoor navigation systems, such as Wi-Fi, UWB, iBeacon and radio frequency identification (RFID).

Wi-Fi and UWB are protocol standards for short range wireless communications with low power consumption [36,37]. Wi-Fi requires access points (APs) in the area in which the target needs to be tracked. By UWB, an efficient indoor navigation system cannot be ensured because of antenna mismatch, low power emission, or possible external interference from other systems.

In RFID technology, position accuracy depends on the type of the tags used, which can be either active or passive, as well as the number of tags. Different than passive tags, active tags contain embedded batteries to develop position accuracy, but at high cost [38].

iBeacon is Apple Inc.’s (Cupertino, CA, USA) term used to describe its own implementation of Bluetooth Low Energy (BLE) beacon technology within iOS7. Moreover, the iBeacon protocol can be used in both iOS systems and Android ones, making this new approach portable [39]. Smart devices, such as iPhones or Android phones, can detect advertising signals sent by tiny, low-energy-consumption devices. Notifications will be pushed automatically to the user when a smart device with iBeacon apps enter come to certain areas. iBeacon has been used for the indoor location systems in hospitals [40] and museums [41]. A luggage tracking use case using iBeacon, with a evaluation of its possibilities and restrictions, is included in Ref. [42] .

The four kinds of sensors discussed in this subsection all use the received signal strength (RSS) from the APs to estimate the targets’ locations. We call this group of methods RSS-indicator (RSSI)-based approaches. The idea underlying RSSI-based approaches is to measure the received signal strength from multiple APs, which is related to the distances between the target and the APs, and to solve the target’s position by combining all of the constraints together as a nonlinear least-squares problem.

RSSI-based approaches work as follows. The distance $z_n\left(t_i\right)$ between the nth AP and the target at sampling time $t_i$ can be calculated by the RSSI nominal value $P_n(d,\varphi ,t_i)$ as follows:

$$z_n\left(t_i\right)=d_0{10}^{\frac{P_r\left(d_0\right)-P_n(d,\varphi ,t_i)}{10q}}$$

(3)

where $d_0$ is the close-in reference distance, $P_r\left(d_0\right)$ is the RSSI in dBm units with the reference distance $d_0$, and q is the path loss exponent. Let x and y be the target location along the horizontal and longitudinal axes. Assume that $d_n\left(t_i\right)$ is the actual distance between the nth AP and the target at sampling time $t_i$. By the measurement of the APs, it can be found that the actual distance $d_n\left(t_i\right)$ is a function of the state $x\left(t_i\right)$ as follows:

$$d_n\left(t_i\right)=\sqrt{{\left(x(t_i\right)-x_n^{}\left(0\right))}^2+{\left(y(t_i\right)-y_n^{}\left(0\right))}^2}$$

where $x_n^{}\left(0\right)$ and $y_n^{}\left(0\right)$ are the horizontal and longitudinal coordinates of the nth AP, while $x\left(t_i\right)$ and $y\left(t_i\right)$ denote the real location of the target in the 2D tracking space. In general, the measured distance $z_n\left(t_i\right)$ in Equation (3) and the actual distance $d_n\left(t_i\right)$ are not identical. The measurement error should be considered: $z_n\left(t_i\right)=d_n\left(t_i\right)+v_n\left(t_i\right)$, where $v_n\left(t_i\right)$ is the measurement noise of the nth AP at the sampling time $t_i$.

The measurement covariance of RFID satisfies

$$v_n\left(t_i\right)/d_n\left(t_i\right){}^{~}N(0,{\left(\frac{0.2303{\sigma }_p}{\gamma }\right)}^2)$$

where ${\sigma }_p$ is the standard deviation, $\gamma$ is the path loss exponent and ‘/’ denotes a division calculation. Therefore, the ratio of ranging error to the actual distance follows a normal distribution with a zero-mean and a standard deviation of ${\frac{0.2303{\sigma }_p}{\gamma }}^2$, where ${\sigma }_p$ can be fixed at 4 dB, which is the average reported standard deviation for wireless communications [43]. In addition, the path loss exponent $\gamma$ is usually between 1.6 and 6.5 based on actual measurements [44]. Because the RSSI depends not only on the distance but also on the environment, for example, the accuracy of RSSI through a wall decades significantly; thus, most RSSI based approaches only room level accuracy.

Noted that Wi-Fi-based localization can adopt other two methods to obtain the locations of targets, namely fingerprinting-based approaches [45] and angle of arrival (AoA)-based approaches [46]. Fingerprinting-based approaches first need to collect “fingerprints”, such as the vectors of RSSIs or channel state information (CSI) to all APs for all the cells on a map, and then they can locate the target by choosing the most similar vector in the map. This approach can realize the better performance than RSSI based approaches [36], but they require expensive and recurring fingerprinting operations when the environment changes (e.g., a door is opened or a chair is moved). The calibration task becomes tedious and time consuming for large scenarios, because the wireless signal must be measured in many different locations [47].

Typical computation of the AoA is done using the multiple signal classification algorithm. Assuming an antenna array of M antennas is equally spaced by a distance of d and a signal arriving at the antenna array through L propagation paths, the signal travels an additional distance of $d\times sin\theta$ by the signal to reach the second antenna of the array [48].

Unfortunately, all of the above approaches assume that the APs’ positions are known in advance to locate the target. The location performance mainly depends on the number of APs. Regarding the navigation system, the other information, such as the environmental information and movement direction, cannot be obtained.

3.2. Fusion Method

Unlike robots, humans can assimilate information from a scene, such as the traffic, and an experienced human driver functions well in dynamic traffic environments. However most state-of- the-art robotic perception systems function quite differently from the way a human driver understands traffic environments. A robotic car requires nearly 100% correct perception results for its autonomous driving. Thus, to develop high performance of the machine perception, it is necessary to fuse information from several different kinds of sensors to meet safety-critical requirements, because each type of sensor presents advantages and drawbacks, as described in the Section 3.1. For robots, the data from multiple sensors must be combined for increased reliability and safety. Therefore, we illustrate several information fusion methods here (see Table 1). The methods of integration, for example, Wi-Fi, RFID, and UWB, with IMU are similar to integrating GPS with IMU, which is widely used indoors when a GPS signal disappears. Therefore, we give only the details of GPS + IMU integration in Section 3.2.1. Furthermore, taking into account the particularity and complexity of the video image processing, we also give the details of Vision + IMU intergation in Section 3.2.2.

Table 1. Some references of navigation system.

Reference	Sensors
[18,49,50]	GPS, IMU
[19,51,52]	Camera, IMU
[36,53]	Wi-Fi, IMU
[54]	GPS, Digital Compass, IMU
[37,55,56]	UWB, IMU
[57,58]	RFID, IMU

3.2.1. GPS + IMU

The accuracy of GPS cannot meet a robot’s movement requirements. For example, parking requires the accuracy at the centimeter level, and the update frequency is approximately 100 Hz. In contrast, for routing and guidance, the required accuracy is reduced to the 10 to 100 m level and the update frequency is 0.1 Hz approximately. To address GPS measurements’ critical problems of low accuracy and susceptibility to interference, the combined use of inertial sensors and GPS will yield a high accuracy in the estimation of a robot’s location even when outdoor and indoor placements are mixed [59].

The approach to combine these two types of sensors is mainly based on the estimation method (see Section 4.2) and the tracking system models (see Section 4.1 for details). In Ref. [59], the constant acceleration model was adopted as the process model, along with the linear measurement models of the GPS that are used to obtain the position and those of the IMU that are used to obtain the acceleration—with the assumption that the system has zero-mean Gaussian white noise. By the covariance matrices of the GPS and IMU innovations, the validity domains of the GPS and IMU sensors are determined through the definition of contextual variables. Thresholds are defined considering the confidence level required. As shown in Figure 4, when covariance matrices less than the thresholds are reached, the data are accepted to estimate the trajectory.

Figure 4. Sensors validity domains of GPS + IMU [59].

Another model for the fusion of GPS and IMU is the state space representation of the error vector between the INS and GPS measurements [60,61]. The Kalman filter attitude correction approach achieves improved performance because of its ability to estimate the attitude errors and gyro bias states. The filter model is made up of two components, a linearized attitude error and gyro bias state model, and a nonlinear attitude quaternion error measurement model. The state model predicts when the attitude errors and gyro bias states will propagate based on input data from the gyros, and the measurement model corrects this prediction with the real world attitude error measurements obtained from an accelerometer.

Some of the main inadequacies in the Kalman filter approach for GPS/INS integration are a stochastic error model for every sensor used, which should be predefined, and values like correlation time, variance, and covariance, which should be known accurately. However, it is very difficult to obtain the accurate values of these parameters. Werries and Dolan [62] devised an adaptive Kalman filter that is able to adapt to different sensors and circumstances on its own, in which the covariance of the process noise is adapted based on the state-correction sequence and that of the measurement noise is adapted based on GPS receiver—reported standard deviation. However, GPS and IMU systems have different sampling frequencies, and, in Ref. [63], the so-called time-difference carrier phase (TDCP) problem was solved.

Recently, the AI-based techniques have been used to GPS/INS integration. In Ref. [64], the light detection and ranging (LIDAR) point clouds, GPS-IMU information, and Google drivingdirections were integrated by a fully convolutional neural network that jointly learned to carry out perception and path generation from real-world driving sequences.

In urban canyon environments, because of the possible operation of the GPS/IMU integrated system, there may be a variable delay between GPS measurement epochs, which makes it more difficult to model the system. Jaradat and Abdel-Hafez [65] proposed intelligent fusion architecture to take into account this delay. Bostanci et al. [66] investigated the vision-based estimates with measurements from other sensors, GPS, and IMU using fuzzy adaptive multiple models, the results of which exhibited improved accuracy and faster convergence of the fusion filter.

3.2.2. Vision + IMU Integration

Cameras have the advantage of providing an extensive amount of information while having a low weight, limited power consumption, low cost, and reasonable size. However, vision methods have their shortcomings, such as illumination change and distortion because of fast movement. Inertial sensors offer good signals with a high rate of measurement during fast motions, but they are sensitive to accumulated drift resulting from double integration during position estimation. In contrast, visual sensors provide precise ego-motion estimation with a low rate in the long term, but they suffer from blurred features under fast and unpredicted motions. The aim of inertial and vision sensor integration is to overcome these fundamental limitations of vision-only tracking and IMU-only tracking using the complementary properties of both methods.

The two main approaches are IMU-based and vision-based approaches. The IMU-based approach derives from the INS method, and the error model is used to describe the error of the position, velocity, and acceleration; in addition, the relationship between 3D and 2D video image is taken as the measurement data of the position to deduce the IMU drift error [19]. A nonlinear estimation method, such as EKF or UKF (see Section 4.2.2 and Section 4.2.3, respectively, for details) is used to obtain the estimated position [67,68].

The vision-based approach is shown in Figure 5. Natural landmarks, such as corridors, edges, doors, wall, and ceiling lights, are objects or features that are part of the environment. The choice of features is vital because it will determine the complexity of the feature description, detection, and matching. The attitude (roll, pitch, and yaw speed) is available as part of the image metadata. This facilitates acceleration of the localization algorithms, either by providing an initial guess of the attitude, or in closed form as direct contribution to the localization. The first part, shown by black arrows in the figure, depicts that the attitude extracted from the IMU helps the camera catch the more accurate feature points, which can result in the higher performance of the trajectory estimation [51,52]. The methods of feature detection include Integral Channel Image Patches (ICIMGP) [69], Scale Invariant Feature Transform (SIFT) [70], Features from Accelerated Segment Test (FAST) [71] and Speed Up Robust Features (SURF) [72]. The blue arrows in Figure 5 denote the position information of position obtained by the IMU being fused with that obtained by the camera to improve the accuracy of the trajectory estimation. Estimation of the fused weights of these two types of information was discussed by Spaenlehauer et al. [73].

Figure 5. Flow diagram of Vision+IMU integration algorithm.

4. Tracking

4.1. Models for Tracking

Target tracking has always been a hot topic in many application fields, and it is the basic algorithm in navigation systems. The displacement, velocity, acceleration, and other motion characteristics of the maneuvering target are estimated by using the data measured by the sensor.

In the 1970s, researchers were interested in target tracking technology [74], which had many military and civilian applications, such as missile defense, ocean surveillance, and so on.

In a tracking problem, two aspects are very important: the system models and the estimation method. The former includes the process model and the measurement model.

Accurate estimation requires accurate process models. For example, when radar tracks a target, the human action or control command of the driver at any time will make the target turn, dodge and execute other actions in the course of target movement. To obtain enough information about the trajectory tracking performance of the target, it is necessary to use the correct motion model of the maneuvering target to perform the estimation.

Some process models have been proposed for the tracking of a maneuvering target. The constant-velocity (CV) models emphasize that accelerations are very small with the so-called white-noise acceleration model. This model assumes that the target acceleration is an independent process (strictly white noise), such as $w_c\left(t\right){}^{~}N(0,{\sigma }^2)$, where $w_c\left(t\right)$ is the acceleration noise. The most attractive feature of this model is its simplicity.

The second simple model is the so-called constant-acceleration (CA) model or, more precisely, the “nearly-constant-acceleration model”. This model assumes that the derivative of acceleration is the Gaussion white-noise as $w_a\left(t\right){}^{~}N(0,{\sigma }^2)$, where $w_a\left(t\right)$ is the noise of the derivative of acceleration.

Since the Singer model was put forward in 1970 [14], researchers have advanced the “current” statistical model, and IMM, among other maneuvering target models. The Singer model models target acceleration as a first-order semi-Markovian process with zero mean, which is in essence an a priori model because it does not use online information for the target maneuvering, although it can be made adaptive through an adaptation of some parameters. Because of the complexity of the objectives of an actual track, any a priori model cannot be extremely effective for the diverse acceleration situations of actual target maneuvers. One of the main shortcomings of the Singer model is that the target acceleration has zero mean at any moment. Another shortcoming is that it cannot use online information.

An acceleration model, called the current statistical model [15] is, in essence, a Singer model with an adaptive mean—that is, a Singer model modified to have a nonzero mean of the acceleration. In this current model, the model can use online tracking information, and the priori (unconditional) probability density of the acceleration is replaced by a conditional density, (i.e., Rayleigh density). Clearly, this conditional density carries more accurate information and is better able to be used than the a priori density. We note that this conditional Rayleigh assumption was made for the sole purpose of obtaining the variance of the acceleration prediction.

Based on those models, there are many modified models for maneuvering target tracking, but all of them need a prior hypothesis. Because the tracking systems are of different types, the prior hypothesis is sometimes inappropriate. In general, we call the Singer model, the current statistical model, or the Jerk model as the ‘state’ model, and they have one common problem, that they all assume the maneuvering target possesses a particular set of movement characteristics. However, the noise characteristics of the actual maneuvering target will change, and the model that exhibits good tracking performance in the previous period may no longer maintain good performance.

The IMM models the change of the system dynamics as a Markovian parameter having a transition probability [16]. According to the filter results, the consistency between each model and the current actual maneuvering target is estimated, and then the estimated results are generated by weighting the estimation of each model, so that the tracking performance is better than that of any single model. However, when the maneuvering target exhibits complex motion, the IMM model suffers heavy computational burden. On the other hand, the limited number of the model can not still catch all the system dynamics feature.

Another model, called the adaptive model, assumes that no a prior information about the system noise is known, which must therefore be estimated based on the estimation of state [17]. Based on the basic idea that the model will effect the measurement data, and the measurement data contain the information of the model, the adaptive model describes system dynamics based on the measurement data on the condition that the system equation structure is given.

Most researchers agree that the disadvantage of the “state” model is the requirement of the given system parameter, which can not be known exactly. Although IMM and the adaptive model have tried the best to catch the maneuvering characteristics of a target, the model still seems to be insufficiently accurate in the practical system, especially when the system is complex.

The authors believed that the reasons are as follows: Firstly, the matrix form of the ‘state’ model can not contain enough parameters to describe the complex dynamics. For example, the process matrix of adaptive model [17] only has nine parameters, although they are adjusted each step online, the amount of information is insufficient.

Secondly, the structure of the model is too simple to describe the complex movement. The CV, CA, Singer model, the current statistical model as well as the Jerk model are all with a basic linear structure, and only the IMM and adaptive model have switched nonlinear structure between different models, but they still can not catch the complexity of the practical system. More complex network of non-linear structure is very necessary. In Section 5, we will explain why network-structured models can capture complex information and even make tremendous progress in pattern recognition.

4.2. Estimation

Estimation means that the desired state is obtained based on measurements undergoing the effects of noise, disturbance and, uncertainty. For a navigation system, many methods are used to estimate the state, including the Kalman filter, EKF, UKF, CKF, and PF. We introduce these methods in order, detail the relationship between them and their characteristics, and compare the performance of their algorithm. Owing to length considerations, the specific steps of the algorithms are listed in Appendix A Table A1, Table A2 and Table A3.

Even readers already familiar with these estimation methods will benefit from the information in this section; for newcomers to robot navigation research, this information should prove to be significant. Our focus is on the algorithm itself, and we succinctly explain the origin of the algorithm, while avoiding complex algorithmic deductions; the goal is to enable algorithmic engineers to quickly learn and use algorithmic processes.

4.2.1. Kalman Filter

A Kalman filter can estimate the state of a linear system based on the system model. First, we consider two system models: the measurement model and the process model. The measurement model describes the relationship between the desired state and the measurement. The linear measurement model is expressed as follows:

$$z\left(k\right)=C\left(k\right)x\left(k\right)+v\left(k\right)$$

(4)

where $z\left(k\right)$ is the measurement, $x\left(k\right)$ is the desired state, $C\left(k\right)$ is the measurement matrix, and $v\left(k\right)$ is the measured noise .

The estimated state is often variable, so it is necessary to consider the transfer mode of the state, which is called as the process model, which is generally expressed as the following with the linear transfer mode of the state

$$x(k+1)=A\left(k\right)x\left(k\right)+w\left(k\right)$$

(5)

where $A\left(k\right)$ is the process matrix and $w\left(k\right)$ is the process noise. It is clear that the characteristics of process noise and measurement noise play a crucial role in the performance of estimation methods. The simplest linear system is that the process noise $w\left(k\right)$ and measurement noise $v\left(k\right)$ are both Gaussian noise with a zero mean with a given covariance of $Q\left(k\right)$ and $R\left(k\right)$, respectively.

To obtain the estimated state for such systems, a Kalman filter [75] is one of the most widely used estimation methods. Theoretically, a Kalman filter is an estimator for what is called the linear-quadratic problem, which is the problem of estimating the state of a linear dynamic system. The resulting estimator is statistically optimal with respect to any quadratic function of estimation error [76,77]

According to these equations, details of the Kalman filter algorithm are presented in Figure 6, in which it is evident that it works in a two-step process from the initial value $\widehat{x}\left(0\right|0)$. In the first step, denoted the prediction step, the Kalman filter produces prediction estimates $\widehat{x}\left(k\right|k-1)$ along with their uncertainties from the last estimate $\widehat{x}(k-1|k-1)$. The second step is the update step. Once the outcome of the next measurement, $z\left(k\right)$, is obtained, the estimates $\widehat{x}\left(k\right|k)$ are updated using a filter gain $K\left(k\right)$ based on $\widehat{x}\left(k\right|k-1)$.

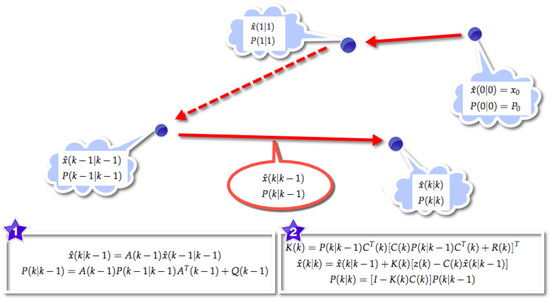
Figure 6. Illustration of Kalman filter. From an initial value $\widehat{x}\left(0\right|0)$, two steps are used to obtain the final estimate: (1) Prediction step. The Kalman filter produces prediction estimates $\widehat{x}\left(k\right|k-1)$ along with their uncertainties from the last estimate $\widehat{x}(k-1|k-1)$, where $A(k-1)$ is the process matrix and $Q(k-1)$ is the covariance of process noise. (2) Update step. The estimates $\widehat{x}\left(k\right|k)$ are updated using a filter gain $K\left(k\right)$ based on $\widehat{x}\left(k\right|k-1)$ and $z\left(k\right)$, where $C\left(k\right)$ is the measurement matrix and $R\left(k\right)$ is the covariance of measured noise.

4.2.2. EKF

The first nonlinear filtering algorithm, EKF, was developed on the basis of the theory of Kalman filtering. In this method, the Taylor expansion of a nonlinear function is used to retain the first-order linearization, and other high order terms are omitted to approximate the nonlinear function [78].

The details of the EKF algorithm are shown in Table A1, compared with a standard Kalman filter. The prediction and update of the state and covariance of both filters are listed. We can see the system to which the EKF is applied is nonlinear with the system models $f\left(x\right(k),w(k\left)\right)$ and $h\left(x\right(k),w(k\left)\right)$.

Owing to the Taylor expansion, EKF can deal with the nonlinear characteristics of the system and has been used in many applications. In Ref. [10], an extended Kalman filter was used to estimate the speed of a motor based on the measured quantities, such as stator currents and direct current link voltage. The estimated speed was used for vector control and overall speed control. To obtain the stable and convergent solutions, a weighted global iteration procedure with an objective function is proposed for stable estimation and is incorporated into the extended Kalman filter algorithm [79].

Regarding the navigation system, the EKF was designed for the online estimation of the speed and rotor position by only using measurements of the motor voltages and currents [80]. The EKF algorithms allow efficient computation compared with other nonlinear estimation methods. A quaternion based EKF was developed to determine the orientation of a rigid body from the outputs of IMUs [11].

An EKF is commonly applicable to the system with weak nonlinearity, because of the Taylor expansion only to the first order. If the nonlinearity of the system is strong, there will be a large difference between the approximate linear system of the Taylor expansion and the original nonlinear system. This leads to a decrease of estimation performance or even the filter divergence.

Because of its small amount of calculation, an EKF is apt for application in a practical system. Marins et al. [81] presented an extended Kalman filter for real-time estimation of rigid body orientation using an IMU. Different than the work in Ref. [11], the Gauss-Newton iteration algorithm was utilized in Ref. [81] to find the best quaternion that relates the measured accelerations and Earth’s magnetic field in the body coordinate frame to calculate values in the Earth’s coordinate frame. The best quaternion is used as part of the measurements for the Kalman filter. As a result, the measurement equations of the Kalman filter become linear, and the computational requirements are significantly reduced, making it possible to estimate the orientation in real time. Yang and Baum [82] presented a method of tracking an elliptical shape approximation of an extended object based on a varying number of spatially distributed measurements. Based on an explicit nonlinear measurement equation about the kinematic and shape parameters, an EKF was derived for a closed-form recursive measurement update.

4.2.3. UKF

To increase the nonlinear processing ability of estimation methods, Uhlmann and Julier proposed a UKF based on the idea of “approximating the probability density distribution of the system random variable to make the approximation of nonlinear function easier” [12,83]. According to the prior probability distribution of the state, a set of sigma points is determined and their corresponding weighted values are calculated. The sigma point is then taken as an independent variable to calculate the dependent variable of the known nonlinear function, and the mean and covariance are estimated by calculating the dependent variable. The UKF algorithm also inherits the Kalman filtering framework, and exhibits better nonlinear estimation performance than the EKF because the UKF does not need to calculate the Jacobi (Jacobian) matrix of a nonlinear system and reduces the difficulty of the calculation process.

However, in practical applications, UKF is widely used in systems with lower state dimensions. Once the system state reaches higher than three dimensions, the covariance matrix is obtained by an unscented transform (UT) to be a non-positive definite matrix, and the filter accuracy decreases rapidly.

Regarding the system model shown in Table A2, the UT selects 2n + 1 sigma points as the following:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill x^{\left(0\right)}=\overline{x}\hfill \\ \hfill x^{\left(i\right)}=\overline{x}+{\tilde{x}}^{\left(i\right)}\hfill & \hfill i=1,2\cdots 2n\\ \hfill {\tilde{x}}^{\left(i\right)}={{\left(\sqrt{(n+k)P}\right)}_i}^T\hfill & \hfill i=1,2\cdots n\\ \hfill {\tilde{x}}^{\left(i\right)}=-{{\left(\sqrt{(n+k)P}\right)}_i}^T\hfill & \hfill i=n+1,2\cdots 2n\end{array}\end{array}$$

(6)

where $\sqrt{P}{\sqrt{P}}^T=P$, and ${(\ast )}_i$ denotes the $i^{th}$ row of matrix *, and k is a constant [12].

The 2n + 1 weights are

$$\begin{array}{c}\hfill w^{\left(0\right)}=\frac{k}{n+k}\hfill \end{array}$$

(7)

$$\begin{array}{c}\hfill w^{\left(i\right)}=\frac{1}{2(n+k)}i=1,2\cdots 2n\hfill \end{array}$$

(8)

the nonlinear transfer by the nonlinear measurement equation is expressed as

$$z^{\left(i\right)}=h(x^{\left(i\right)})$$

(9)

and the mean and the covariance are expressed as

$$\begin{array}{c}\hfill \overline{z}=\sum _{i=0}^{2n}{w}^{\left(i\right)}{z}^{\left(i\right)}\hfill \end{array}$$

(10)

$$\begin{array}{c}\hfill P_z=\sum _{i=0}^{2n}{w}^{\left(i\right)}(z^{\left(i\right)}-\overline{z}){(z^{\left(i\right)}-\overline{z})}^T\hfill \end{array}$$

(11)

Table A2 details the UKF estimation method. The sigma points used for the prediction of the state with the weights, and the update of the state with the filter gain, are shown in this table. Finally, the prediction and update processes for the covariance are also listed.

4.2.4. CKF

The CKF was proposed by Simon Haykin and Ienkaran Arasaratnam [13]. This algorithm also inherits the Kalman filtering framework, and uses the numerical integration method of the spherical-radial cubature rule to approach the Gaussian integral. Similar to the UKF, the CKF also selects a set of point sets, and passes the selected point set through the nonlinear function, and then approximates the Gaussian integral in the filtering of the nonlinear system through a series of calculations. The CKF also avoids the large error caused by linearization of nonlinear functions by the EKF algorithm. It can handle any nonlinear system, and it does not depend on the specific equation of nonlinear function in the process of filtering. Unlike the UKF, the CKF algorithm used the spherical-radial cubature rule and Bayesian estimation to approximate the integral nonlinear Gaussian filter.

Regarding the system model shown in Table A3, the third-degree spherical-radial cubature rule selects 2n cubature points as follows:

$$\begin{array}{cc}\hfill x^{\left(i\right)}=\overline{x}+{\tilde{x}}^{\left(i\right)}\hfill & \hfill i=1,2\cdots 2n\\ \hfill {\tilde{x}}^{\left(i\right)}={{\left(\sqrt{P}\right)}_i}^T\hfill & \hfill i=1,2\cdots n\\ \hfill {\tilde{x}}^{\left(i\right)}=-{{\left(\sqrt{P}\right)}_i}^T\hfill & \hfill i=n+1,2\cdots 2n\end{array}$$

(12)

where $\sqrt{P}{\sqrt{P}}^T=P$, and ${(\ast )}_i$ means the ith row of matrix *, and the 2n weights are

$$\begin{array}{c}\hfill w^{\left(i\right)}=\frac{1}{2n}i=1,2\cdots 2n\end{array}$$

(13)

the nonlinear transfer by the nonlinear measurement equation is expressed as

$$z^{\left(i\right)}=h(x^{\left(i\right)})$$

(14)

and the mean and the covariance are expressed as

$$\begin{array}{c}\hfill \overline{z}=\sum _{i=1}^{2n}{w}^{\left(i\right)}{z}^{\left(i\right)}\hfill \end{array}$$

(15)

$$\begin{array}{c}\hfill P_z=\sum _{i=1}^{2n}{w}^{\left(i\right)}(z^{\left(i\right)}{z^{\left(i\right)}}^T)-\overline{z}\overline{z}+R\left(k\right)\hfill \end{array}$$

(16)

where $R\left(k\right)$ is the covariance of the measurement noise $v\left(k\right)$.

Until now, we have dealt with three filters to solve the estimation problem for nonlinear systems and determine which performs best. Much research has been done on the performance of these three nonlinear estimation filter. Hong-de et al. [84] considered an EKF, UKF, and CKF for the tracking of a ballistic target to estimate its position, velocity, and the ballistic coefficient, with the conclusion that the UKF and CKF both have higher accuracy and less computational cost than the EKF. Ding and Balaji [85] compared a UKF and a CKF for two radar tracking applications, namely, high-frequency surface wave radar (HFSWR) and passive coherent location (PCL) radar. The simulation showed that the UKF outperformed the CKF in both radar applications, using performance measures of root-mean-square error and normalized estimation error squared, and further concluded that the CKF is not as well suited as UKF to highly nonlinear systems, such as PCL radar. A similar conclusion was reached in Ref. [86] for bearings-only tracking (BOT) problem. Pesonen and Piché [87] compared a UKF and CKF using an extensive set of positioning benchmarks, including real and simulated data from GPS and mobile phone base stations, and resulting in conclusion that in tested scenarios no particular filter in this family is clearly superior.

Therefore, although the CKF was developed later than the UKF, we find that it does not have the obvious advantages of UKF. Recently, some developed nonlinear estimation methods have been proposed, but most are based on the fundamental principle of a UKF or CKF. For example, from the numerical-integration viewpoint, a sampling points set was derived by orthogonal transformation of the cubature points in Ref. [88]. By embedding these points into the UKF framework, a modified nonlinear filter, designated a transformed unscented Kalman filter (TUKF), is derived. The TUKF purportedly can address the nonlocal sampling problem inherent in the CKF while maintaining the virtue of numerical stability for high dimensional problems. Dunik et al. [89] pointed out that traditional filters providing local estimates of the state, such as the EKF, UKF, or CKF, are based on computationally efficient but approximate integral evaluations, and therefore proposed a general local filter that utilizes stochastic integration methods providing the asymptotically exact integral evaluation with computational complexity similar to the traditional filters.

From all of these research works, we conclude that the UKF and CKF are the popular estimation methods for the nonlinear systems, because they all have efficient computation speeds and nonlinear processing ability. However, for nonlinear highly complex problems, the performance of both filters still must be improved.

4.2.5. PF

All of the noted Kalman filters deal only deal with the Gaussian noise in the process model and measurement model. Another filter, the so-called PF, can handle the case of non-Gaussian noise [90]. The PF is a combination of the Monte Carlo integral sampling method and the Bayesian filtering algorithm, and its advantage is that it can be used to deal with any nonlinear and non-Gaussian estimation problem. It has been proven that the ideal estimation accuracy can be achieved as long as the number of particles is sufficient. Although the PF algorithm was proposed some time ago, it has not undergone substantive development because it has some problems, specifically the following: With increase of computational iterative PF algorithms, the PF has only one or a few particle weights close to 1, and most of its particle weights are almost 0, with the problem being the particles facing degradation. Moreover, to solve the particle degradation problem effectively, it is necessary to use the method of resampling—that is, the removal of particles of lower weight and the replicating of particles with higher weight [91,92,93].

However, this method destroys the diversity of particles, and makes the particle filter again face another important problem, namely, the lack of samples, which leads to a decrease of the filter’s estimation performance. Therefore, researchers have devised many solutions to these problems, including several variants of the particle filter (e.g., sampling importance resampling filter, auxiliary sampling importance resampling filter, and regularized particle filter) within a generic framework of the sequential importance sampling algorithm [94]. In Ref. [95], an enhanced particle swarm optimized particle filter was proposed together with a noninteracting multiple model, which can be efficiently applied in the modern radar maneuvering target tracking field efficiently.

Table 2 details the performance of all the Kalman filters and the PF, and it can be seen that the classical Kalman filter can be used only for a linear system with a Gaussian process and measurement noise, and, furthermore, that EKF, UKF, and CKF can deal with nonlinear systems accompanied by Gaussian noise. Moreover, the PK can be used in any system, although with high computational complexity.

Table 2. The difference of state estimation method.

Estimation Method	Linear	Nonlinear	Non-Gaussian Process/Measurement Noise	Computational Complexity
Kalman Filter	Yes	No	No	low
EKF	/	Yes	No	medium
UKF	/	Yes	No	medium
CKF	/	Yes	No	medium
PL	/	Yes	Yes	high

4.3. Experiment and Analysis

In this Section, we use experiments to show these two points: one is that the estimation method relies heavily on the accuracy of the models. If the model is not accurate enough, the estimating results can not get high performance. The other is that for the complex nonlinear system, none of the above mentioned filters, such as EKF, UKF, CKF and even PF, has outstanding advantage, and their performance still needs further improvement.

Here, the simulated 2D RFID tracking system developed in [43] was used as the experiment platform, which described a typical nonlinear estimation problem. The RFID readers were placed in the specific area and the measurement space of each reader with high detection rate were shown with circles (from inside to outside in contour map) in Figure 7. In the white area of the figure, the distance information of the target can only be obtained with low detection rate. The reference trajectory of the target is given with ‘black’ as terisk.

Figure 7. The measurement space of RFID readers and the reference trajectory. Note: The unit of each axes is meter.

The tracking covariance was defined as $Cov=\sqrt{X_{cov}^2+Y_{cov}^2}$, where $X_{cov}^{}$ and $Y_{cov}^{}$ are the estimation covariance of horizontal and longitudinal axes, respectively.

4.3.1. Case One

In this case, the CV, CA, Singer model, current model, IMM and the adaptive model were compared. The tracking covariance of each model with UKF estimation method is shown in Table 3.

Table 3. Comparison on tracking covariance of different models with UKF estimation method.

The Used Models	The Tracking Covariance $\mathit{Cov}$
CV	350.08
CA	290.76
Singer model	210.40
current model	178.98
IMM algorithm model	123.02
the adaptive model	120.75

It is noted that the covariances of the IMM and adaptive model are relatively small comparing with other models, and the CV model get the worst covariance. It is because that the trajectory generated by the simulated RFID tracking system has higher-order dynamic feature and complexity.

On the other hand, the covariances of the IMM and adaptive model obtained via the simulated system are much smaller than that in the practical system. This is because, on the one hand, the practical tracking case is more complex than the simulation, and, on the other hand, these models are based on given structures. If the structure is not in good accordance with the reality, the model will be impossible to grasp the characteristics of the actual movement, or correctly determine the relationship between the external environment and its own movement. This is the biggest obstacle to robot’s mobile intelligence.

4.3.2. Case Two

In this case, the EKF, UKF, CKF, and PF were used to track the trajectory in Figure 7, in which the adaptive model was used. The tracking covariances of each estimation methods are shown in Table 4.

Table 4. Comparison on tracking covariance of EKF, UKF, CKF and PF with adaptive model.

The Used Methods	The Tracking Covariance $\mathit{Cov}$
EKF	148.06
UKF	120.75
CKF	123.45
PF	122.29

It can be seen that the filters have similar performance. The estimated covariance of EKF is the largest, which shows the disadvantage of EKF when dealing with strong nonlinearity. UKF and CKF have the similar tracking covariance, the same conclusion has been gotten by other research works [84,85]: they both have higher accuracy than the EKF. A similar conclusion was reached in Ref. [86] for bearings-only tracking (BOT) problem. Pesonen and Piché [87] also compared a UKF and CKF using an extensive set of positioning benchmarks, including real and simulated data from GPS and mobile phone base stations, and resulting in conclusion that in tested scenarios no particular filter in this family is clearly superior. Therefore, although the CKF was developed later than the UKF, we find that it does not have the obvious advantages than UKF.

As to the PF, in this simulated system, it did not show superior performance because the Gaussian noise was used. In fact, for the practical system with non-Gaussian noise, PF can be much better than other methods based on accurate modeling of the noise, while the performance of PF depends heavily on the modeling methods in Section 4.1. It means that if we use the inaccurate model, the tracking performance will decrease greatly.

5. Deep Learning for Navigation

5.1. History of AI

AI technology has been interesting and attractive since its inception. For decades it has been one of the major technologies for robots. In this section, we briefly describe its development history, especially the technology that is closely related to the development of robot movement. From the development of these technologies, we will find that we are moving toward advanced mobile intelligence and getting closer and closer.

In 1956, the famous Dartmouth Conference proposed the assertion: “every aspect of learning or any other feature of intelligence can be so precisely described that a machine can be made to simulate it” [96]. Therefore, this conference was well acknowledged as the birth of AI. During the past 60 years, AI has experienced several different stages that divided based on their specific developmental features, as shown in Figure 8. In addition, because of certain criticisms and limitations, AI also encountered two winter periods. However, within all these years, researchers never stopped their works in related techniques, and breakthrough of various applications were also accompanied.

Figure 8. Development history of artificial intelligence (AI).

The first stage named as Inference Period (1956-1974) was considered as a golden period for AI development. The most important task in this period was to make the computers capable of logical inference. With the emerging intelligent techniques, people were experiencing various ‘unbelievable’ changes. For example, robot was able to both look and behave like human, or machine could learn to speak and communicate with people [97]. At that time, researchers all optimistically thought that AI could be easily achieved by logical inference. They even predicted that a fully intelligent machine would be built within the following 20 years. As a result, government agencies such as British government and United States National Research Council did invest large amount of money into this potential field. With the great financial aid, certain achievements were indeed obtained, such as the presentation of perceptron [98], which laid a significant foundation for AI.

However, AI failed to keep its development in 1970s. The optimism and confidence of AI researchers had raised extremely high expectations, and made them neglect the practical difficulties they faced, such as the limited computer power, intractability and combinatorial explosion, as well as the frame and qualification problems. Consequently, the financial support was eventually cut off for undirected research into AI. By 1974, almost no funding for AI projects was able to find. The first winter in AI development formally started.

When it came into the 1980s, knowledge engineering became the keyword of AI research, so we call the second stage as Knowledge Period (1980–1987). The significant development of technology in this period must be the combination of the multiple layer perceptron and back-propagation method. It needs to be pointed out that, in this period, the emphasis of AI research was changed from laboratory research to practical applications. A representative implementation of AI as expert systems was adopted by corporations around the world. For example, the so-called R1/XCON that designed for Digital Equipment Corporation (DEC) was a production-rule-based system, which could automatically select the computer system components based on the customer’s requirements. It was proven to save almost 25 million a year for the company [99].

With the commercialization of AI techniques, more and more expert systems, natural language processing systems and so on have entered the market. Accordingly, it has achieved great economic and social benefits, and demonstrated the broad prospect of AI applications. In short, with the development of intelligent robots and fifth-generation computers, AI research experienced a second boom and a prosperous age in this period. However, at the end of the 1980s, after more than a decade of prosperity and considerable progress in some fields, the AI research began to appear in crisis again. Generally speaking, there are mainly two problems: one is the so-called interaction problem, that is, the traditional AI method is hard to interact with the environment. The other is the poor generalization capability, that is, the traditional AI method is only suitable for the narrow domain expert system, and it was hard be extended to larger and wider complex systems. Thus far, the development of AI has entered a second dilemma.

After the short break in the second winter, AI began a new round of exploration since the early 1990s (Learning Period (1993–present)), when it was successfully applied throughout the technology industry. The impressive feature of this period is that computers should have certain self-learning ability with or without the aid of human. To achieve this purpose, massive data with abundant information was indispensable, and a core mission was to analyze the potential features and patterns submerged in the unstructured big data from multiple sources.

This mission brought a new challenge to the traditional AI methods. Instead of the old general research, it was fragmented into competing subfields focused on specific problems or approaches [97]. Deep learning was quite a representative example, and the most important event was the Deep Belief Network (DBN) proposed by Geoff Hinton et. al. in 2006 [100], which demonstrated how a multi-layered feedforward neural network could be effectively pre-trained with the large amount of known data. After several years development, deep learning has been successfully applied in image recognition and has become “superhuman”, producing more accurate results than human candidates in 2011 [101]. Another proof for the advantage of deep learning was the famous AlphaGo robot, which well learned the Go game and successfully beat different professional Go players [102]. The achievements mentioned above were all inseparable with the learning capability of AI developed in this period. It is never too late to learn for human beings, so as the development of AI. It is now a new era for AI research, and it will definitely bring more and more beneficial and promote the development of mobile intelligence.

5.2. An Overview of Deep Learning

Currently, many innovative learning algorithms and architectures are being developed for accelerating deep neural networks. These methods have dramatically improved the state-of-the-art in visual object recognition [103], motion detection [104] and many other domains such as autonomous navigation [105], medical diagnosis [106], etc. The first unsupervised learning procedures used Restricted Boltzmann Machines (RBM) to restrict the connectivity of the hidden units in order to make learning easier. The objective in maximum likelihood learning layer of feature detectors was to be able to model the import feature of raw inputs at a time greedily. By “pre-training” several layers of progressively more complex feature detectors, the weights of a deep network could be initialized to sensible values and the whole deep system could be fine-tuned using standard back-propagation [107]. This network and its improved version–deep belief network worked well in recognizing handwritten digits or for detecting pedestrians, especially when lack of sufficient labelled data [100].

There was another type of feedforward network that was much easier to train and generalized much better than networks with full connectivity between adjacent layers. This was the most common form of deep learning called the convolutional neural network (CNN). It achieved many practical successes since the breakthrough in 2012 ImageNet competition [108] achieved by AlexNet [109]—the first Deep Neural Network achieve better performance than traditional methods in this complex multi-class classification problem. It was made possible by the advent of three fundamental factors: the high-quality and large-scale benchmark database, fast graphics processing units and open-source computing platform (e.g., Tensorflow, Caffe2 , Pytorch, etc.), which promote deep learning framework that were convenient to program and allowed researchers to train networks 10 or 20 times faster. Some famous events revealed the heat of deep learning development as shown in Figure 9.

Figure 9. Some famous events revealed the heat of deep learning development.

Here, we omit the details of all the networks because there are many references about them. Alternatively, we give Figure 10 to show the comparison of the following deep learning models that have obtained the highest performance, in these four years, on the ImageNet and MSCOCO challenge: AlexNet [109], batch normalised Network In Network (BN-NIN) [110], ENet [111], GoogleNet [112], VGG-16 and -19 [113], ResNet-50, -101 and -152 [114], Inception-v3 [115], Inception-v4 [116], Densenet [117], YOLO9000 [118], SSD [119], Faster RCNN [120], Mask RCNN [121], MobileNet [122], ShuffleNet [123] and Mask${}^x$-RCNN [124]. Figure 10 shows one-crop accuracies of the most relevant entries submitted, from the AlexNet, on the bar left, to the Mask${}^x$-RCNN. We can see in the figure that the famous ResNet and Inception architectures surpass all other architectures by a significant margin of at least 7%.

Figure 10. Single-crop top-1 validation accuracies for top scoring single-model architectures.

As the most common form, CNNs have been applied with great success to the detection, segmentation and recognition of objects and regions in images. These were all tasks in which labelled data was relatively abundant at the pixel level, such as traffic sign recognition, the segmentation of biological images particularly for connectomics, and the detection of faces, text, pedestrians and human bodies in natural images. Essentially, CNNs are global image descriptor by using sliding filters and their outputs, known as feature maps, which involve not only the strength of the responses, but also their spatial positions. This indicates that the matching of visual objects should follow its spatial relationship and constraints. For instance, the region containing the head of human should be connected with torso region rather than feet.

However, for dynamic visual tasks or complex cross-modal tasks such as Visual Question Answering (VQA), the CNNs domain is usually represented only at a coarse frame level without explicitly revealing the temporal structure pertaining to a full-motion video or a textual element [125]. The hidden layers of a multilayer neural network learn to represent the network’s inputs in a way that makes it easy to predict the target outputs. This is nicely demonstrated by training a multilayer neural network to predict the next word or video in a sequence from a local context of earlier one.

The powerful dynamic system is another famous architecture of deep learning networks named Recurrent Neural Network(RNN), which takes its previous decisions back in current event and focuses on the connotative information about the history of all the past elements of the sequence. It was, nevertheless, proved that training RNNs is problematic because the back-propagated gradients either grow or shrink at each time step, so over many time steps they typically explode or vanish [126]. Thanks to advances in encoder–decoder architecture and ways of training them, RNNs have first been introduced mostly to predict the next text content in natural language processing and translate online speech-to-speech [127,128].

Although the main purpose of RNNs is to learn long-term dependencies, this architecture has trouble learning and storing temporal information for long periods. To correct for that, the long short-term memory (LSTM) network was first proposed by using special hidden units to remember long-time inputs [129]. This unit called the memory cell acts like an accumulator or a gated leaky neuron: it has a connection to itself at the next time step that has the same weight, so it copies its own real-valued state and accumulates the external signal, but this self-connection is multiplicatively gated by another unit that learns to decide when to clear the content of the memory. LSTM networks or related forms of gated units, such as Gated Recurrent Unit (GRU) [130], have currently proved to perform more effective than conventional RNNs. In recent years, some researchers have made different proposals to contract RNNs with a memory module or an attention module. Proposals include the Neural Turing Machine [131] and Attention Network [132], which have yielded excellent performance on standard question-answering and video-storying tasks [133,134].

The theoretical and empirical evidence shows that RNNs can be applied to regression problems and complex tasks. Together with CNN, it can model the series-relationship of signals and achieves a good application effect in the recognition of the video captioning model [135]. This method also has been successful in tasks such as classifying the type of the movement in videos [136].

We believe that the end-to-end systems in autonomous driving can benefit from the work in spatio-temporal deep network in video, that could be plausible proposals for localization of the textual elements and temporal characteristics of motion. A major recent practical success of the CNNs-RNNs combining is dynamic object detection and tracking in natural image for mobile robots or vehicle compared to conventional computer vision techniques. In recent years, companies such as Mobileye, NVIDIA and Google are using such methods in their real-time vision or autonomous navigation systems for smartphones, cameras, robots and self-driving cars [137]. A simple CNNs-RNNs technique has demonstrated advantages in pedestrian tracking and road identification task shown in the following Figure 11.

Figure 11. A CNNs-RNNs process in pedestrian tracking and road identification task.

We can see that the study of robots or self-driving cars has been involved in many steps. Firstly, abundant video and other multi-sensors data can be obtained and preprocessed as input of the intelligent perception system. Then, CNNs and RNNs will be alternate to extract the spatial and temporal motion or other features of different objects.

Those features maps will constitute representation and correlation between real events and abstract semantic information. At last, robot will understand the movement and relationship of all interesting targets in the environment as shown: an old man was walking on the road, a pedestrian was reading a book while walking, and a pedestrian wearing jeans was walking on the road as well. In our view, in addition to the current movement methods, navigation systems should incorporate the deep learning method to make the current robot as intelligent as humans.

Quantitative evaluations of the system are presented on the KITTI [138], and the results show a superior performance of the proposal [137] in terms of relative translational error when compared to other monocular systems. Caltagirone et al. [64] gave a system learned to carry out perception and path generation from real-world driving sequences based on a fully convolutional neural network. LIDAR point clouds, GPS coordinates, driving directions, and inertial measurements are the input of the network, and the output is a probability map of future vehicle positions. Yao et al. [139] gave a DeepSense learning framework that provided a general classification of time series inputs from sensors, such as accelerometers, gyroscopes, and magnetometers framework for three tasks: car tracking with motion sensors, heterogeneous human activity recognition, and user identification with biometric motion analysis.

5.3. Add the Intelligence to the Robot

As mentioned in Section 3, we can conclude that the study of robots movement has been investigated from many aspects; currently, however, robot movement is not as intelligent as human movement. The current research involves signal processing in the estimation approach mentioned in the Section 4.2. For example, the study of images mainly involves in finding the feature corners based on pixel points. As to other sensors, such as the IMU, the method is also point-to-point estimation of the measurement data. This is very different from human intelligence. Human beings first recognize the target they see and then judge their own speed and that of the target. Human judgment of distance haven’t high accuracy, but we can still clearly recognize the surrounding environment as we move. This is the biggest difference between the navigational system of robots and human movement. In our view, in addition to the current estimation methods, navigation systems should incorporate with an identification method just like human intelligence.

In terms of target recognition, especially image-based recognition, there have been tremendous advances in recent years. We can note that deep learning has progressed so rapidly that machines have been able to identify the target in a picture with very high accuracy based on CNN [140]. As an effective method of classifying images, a CNN extracts features from an image and pools new, smaller images, which intensify the features and make their position in the image less important. This makes the image less sensitive to translations, rotations and distortions.

Comparing with the classical estimation models, the CNN approach has quite different ways of extracting information: more parameters of the network are used, and the relationship of the parameters is more complicated. Moreover, there is also a unified structure that makes this web-based model easy to implement and much more similar to real systems.

There are five key ideas behind CNNs that take advantage of the properties of natural signals: local connections, shared weights, pooling, many flexible layers and complex loss function with optimization tricks. The architecture of a typical CNN is structured as a series of stages as shown in Figure 12.

Figure 12. The series of components and structural variants of typical convolutional neural network (CNN).

Firstly, the array data such as images or previous layers are slid by a convolutional filter to form the units of new feature maps, within which each unit is connected to local patches of the former layer through a set of weights called a filter bank. The result of this local weighted sum is then passed through a nonlinear activation function such as a rectified linear unit (ReLU) or exponential linear unit (ELU). All units in this new feature map share the same filter bank and different filter banks will detect corresponding feature maps.

Secondly, the pooling layer is to merge semantically similar features into one. Because the relative positions of the features forming a motif can vary somewhat, reliably detecting the motif can be done by coarse-graining the position of each feature. A typical pooling unit computes the maximum (max pooling) or average (average pooling) of a local patch of units in a few feature maps. Neighboring pooling units take input from patches that are shifted by more than one row or column, thereby reducing the dimension of the representation and creating an invariance to small shifts and distortions.

Once convolution, nonlinearization and pooling are stacked, more flexible layers such as batch-normalization, deconvolutional, dropout, embedding and merge layers are composited hierarchically to improve the operational and comprehensive capability of deep neural networks. After the previous operation, the remaining is just a fully-connected layers, which connects all the high-dimensional characteristics and exports the output value into classifier or loss function. Finally, back-propagating gradients optimized by mini-batch stochastic gradient descent (SGD), RMSprop, etc., through a CNN, will train and modify all the weights of all the filter banks in the whole deep network.

According to the research results obtained so far, this network structure has the following three advantages: First, when the image information is transformed, such as deformation and translation, the accurate feature information can still be obtained to identify the target. Secondly, when the target is disturbed by complex noises, it still can get enough accurate information to overcome the influence of noise. Finally, because the network model carries a large amount of information and there is no artificial priori knowledge interference, the model is more robust in the case of environmental changing.

RNN is another architecture of deep learning networks, which takes its previous decisions back in again and looks at sequences of events. Together with a CNN, a RNN can model the series relationship of signals and achieve a good application effect in the recognition of the movement mode [135]. This method has been successful in tasks such as classifying the type of the movement in videos [136]. It is possible that RNN could be used in autonomous driving systems online to obtain good effect for detection and movement recognition of the target.

In recent years, deep learning techniques have demonstrated advantages in object tracking compared with conventional computer vision techniques. Ref. [141] pointed out that they are widely used in object recognition tasks and discussed the autonomous driving architecture, including the three main stages (sensing, perception, and decision). In Ref. [142], a deep learning structure, YOLO9000 [118] was used as an object detector. The prior knowledge of the size of detected objects, such as depths and distances, was considered as a predefined prior of the Bayesian framework. Quantitative evaluations of this system are presented using the KITTI dataset [138], and the results show superior performance in terms of relative translational error when compared with other monocular systems. However, in our opinion, these methods are still somewhat complicated and it is not yet possible to run online. This is the biggest obstacle to use these methods for mobile intelligence.

Regarding a robot’s motion intelligence, the two most important aspects are the robot’s recognition of the environment and of the motion or non-motion of surrounding objects. As mentioned earlier, research in this area is currently focused on the use of deep learning for the detection of video images, and answers the question of “what is surrounding me?” [142]. Using the detected targets, a robot can recognize the road and predict its own future path [64].

This is not sufficient, however. In addition to knowing the surrounding objects, the robot must know which of the surrounding objects are moving and which are stationary, such as the background. That means robot must know exactly how fast it is moving and the speed of the moving objects around it. Using this information, robots can predict their own motion and that of other detected targets, including position, velocity, and acceleration, and avoid collisions with other targets.

In contrast to the former aspect, we consider that the study of extracting accurate moving data is the most important aspect for robots. As far as the current research is concerned, target recognition has been greatly developed due to the application of deep learning. However, the exact location of robot motion research is relatively more difficult to qualify. Although outdoor GPS can provide a relatively accurate location, overcoming the obstacle of missing GPS signals and overcoming GPS deficiencies in the indoor environment, will both require significant breakthroughs. In terms of the solutions to these problems, we assert that the estimation method is still the most important component of a solution, because it estimates the motion characteristics, in the presence of measurement noise.

As mentioned earlier, the problem inherent in any estimation method is that the model used for the estimation is not accurate enough because of the complexity of the real motion scenarios. In particular, there is a great deal of uncertainty in extracting motion information from various sensors, so we are sure that it is necessary to combine a deep learning method with the method of state estimation, instead of CNN plus RNN only. Using neural networks to capture the complex information in the environment can provide an accurate, reasonable and applicable model to compensate for the decrease in performance of the estimated motion features due to inaccurate models [143]. In this way, information from multiple sensors can be utilized to provide a more accurate robot motion characteristics and motion parameters. This is the most pivotal part of future robotics.

However, another method that has been widely used is mechanism-based modeling. In general, navigation can be considered to be a physical process, which is a sustained phenomenon marked by gradual changes through a series of states occurring in the physical world. Physicists and scientists attempt to model these processes in a principled way through analytic descriptions of the scientist’s prior knowledge of the underlying processes. This physical paradigm has been, and still is, the main framework for modeling complex natural phenomena [144], despite researchers warning that the modeling process are complex and sometimes cannot obtain accurate models. Bezenac et al. [144] proposed a CNN model that was based on the intuition gained from general background knowledge of sea surface temperature prediction, with the ability of additional prior knowledge-expressed as partial differential equations-to be incorporated in the model, by adding penalty terms in the loss function.

In agreement with Ref. [144], we also believe that the knowledge and techniques accumulated historically for modeling physical processes could be useful as a guideline to design efficient deep learning systems and conversely, that the machine learning paradigm could open new directions for modeling such complex processes in mobile intelligence. Researchers have acdtively explored the relevant research, for example, in Ref. [145], a novel Bayesian RNN encoder–decoder architecture was developed to predict odometry conditioned distributions over pedestrian trajectories and to capture epistemic and aleatoric uncertainty.

6. Conclusions

In this work, we have presented a survey of navigation and tracking for mobile intelligence of robot. The survey takes a relation-based organizational approach to reviewing the literature on robot navigation and tracking, as shown in Figure 1. By fusing different sensors, the navigation, such as location and SLAM, can be achieved with more accurate estimated trajectory and attitude. For the practical applications, however, due to the complexity of the surroundings, the perception of a moving target is disturbed by the complex environment-that is, the sensor measurement model becomes inaccurate. The inaccuracy of the model will significantly reduce the performance of the estimation method, which has led to very low mobile intelligence of robots in the real scenes, which has even been called “stupid” movement. Despite some progress in deep learning in recent years, several issues remain to be addressed in improving navigation in robotics system:

• As we have mentioned in Section 5, it is necessary to combine the estimation and AI methods. In essence, the estimation method is based on probability theory, while the AI method, especially the deep learning method, is based on statistical analysis. These methods have different theoretical foundations, and bringing them together requires in-depth research. These two methods are complementary. However, how to use deep learning methods to provide a more realistic model and how to use the estimation method to develop the prior knowledge of the deep neural network is an open field of study.
• Reinforcement learning has become a novel form, by which, for example, AlphaGo Zero has become its own teacher [146] to learning how to play go. The system starts off with a neural network that knows nothing about the game and then plays games against itself. Finally, the neural network is tuned and updated to predict moves, as well as the eventual winner of the games. The new player AlphaGo is obviously different from human chess players obviously. It may well be better than a human being because it is its own teacher and is not taught by a human being. Can we guess that a robot could have more intelligence than humans? How can we know if it will be able to move faster and be more flexible?
• End-to-end navigation with high intelligence should be executed on the hardware comprising the robot. If the deep learning method is used, current terminal hardware cannot achieve such a large amount of training. The current mechanisms are generally to train the network offline on high-performance hardware such as GPUs, and then online to give the model’s output. The estimation methods usually use a recursion solution form of the state equation; the calculation amount is small and can be executed on current terminal hardware. If combined with the AI method, controlling the total amount of calculating required by the entire system must be considered.

Appendix A.1. EKF

The details of the Standard Kalman Filter and EKF are shown in Table A1.

Appendix A.2. UKF

The details of UKF are shown in Table A2. The details of CKF are shown in Table A3.

Table A1. The details of the Standard Kalman Filter and EKF.

Different Parts of Filter	Standard Kalman Filter	EKF
System Model	$$\begin{array}{l}x(k+1)=A\left(k\right)x\left(k\right)+w\left(k\right)\\ z\left(k\right)=C\left(k\right)x\left(k\right)+v\left(k\right)\\ E\left[w\left(k\right)w^T\left(j\right)\right]=Q\left(k\right)\delta (k-j)\\ E\left[v\left(k\right)v^T\left(j\right)\right]=R\left(k\right)\delta (k-j)\\ E\left[w\left(k\right)v^T\left(j\right)\right]=0\end{array}$$	$$\begin{array}{l}x\left(k\right)=f\left(x\right(k-1),w(k-1\left)\right)\\ z\left(k\right)=h\left(x\right(k),v(k\left)\right)\\ E\left[w\left(k\right)w^T\left(j\right)\right]=Q\left(k\right)\delta (k-j)\\ E\left[v\left(k\right)v^T\left(j\right)\right]=R\left(k\right)\delta (k-j)\\ E\left[w\left(k\right)v^T\left(j\right)\right]=0\end{array}$$
Transformation	/	$$\begin{array}{c}\hfill \frac{\partial f}{\partial x}{|}_{\widehat{x}(k-1|k-1)}=F\left(k\right)\hfill \\ \hfill \frac{\partial f}{\partial w}{|}_{\widehat{x}(k-1|k-1)}=L\left(k\right)\hfill \\ \hfill \frac{\partial h}{\partial x}{|}_{x=\widehat{x}\left(k\right|k-1)}=H\left(k\right)\hfill \\ \hfill \frac{\partial h}{\partial v}{|}_{x=\widehat{x}\left(k\right|k-1)}=M\left(k\right)\hfill \end{array}$$
Prediction of the State	$\widehat{x}\left(k\right|k-1)=A(k-1)\widehat{x}(k-1|k-1)$	$\widehat{x}\left(k\right|k-1)=f(\widehat{x}(k-1|k-1),0)$
Updaton of the State	$\widehat{x}\left(k\right|k)=\widehat{x}\left(k\right|k-1)+K\left(k\right)\left(z\left(k\right)-C\left(k\right)\widehat{x}\left(k\right|k-1)\right)$	$\widehat{x}\left(k\right|k)=\widehat{x}\left(k\right|k-1)+K\left(k\right)(z\left(k\right)-h(\widehat{x}\left(k\right|k-1),0)$
Filter gain	$K\left(k\right)=P\left(k\right|k-1)C^T\left(k\right){(C\left(k\right)P\left(k\right|k-1)C^T\left(k\right)+R\left(k\right))}^{-1}$	$K\left(k\right)=P\left(k\right|k-1)H^T\left(k\right)(H\left(k\right)P\left(k\right|k-1)H^T\left(k\right)+M\left(k\right)R\left(k\right)M^T\left(k\right){)}^{-1}$
Prediction of the Covariance	$P\left(k\right|k-1)=A(k-1)P(k-1|k-1)A^T(k-1)+Q(k-1)$	$P\left(k\right|k-1)=F(k-1)P(k-1|k-1)F^T(k-1)+L(k-1)Q(k-1)L^T(k-1)$
Updaton of the Covariance	$P\left(k\right|k)=(I-K\left(k\right)C\left(k\right)\left)P\right(k|k-1)$	$P\left(k\right|k)=(I-K\left(k\right)H\left(k\right)P\left(k\right|k-1)$

Table A1. The details of the Standard Kalman Filter and EKF.

Different Parts of Filter	Standard Kalman Filter	EKF
System Model	$$\begin{array}{l}x(k+1)=A\left(k\right)x\left(k\right)+w\left(k\right)\\ z\left(k\right)=C\left(k\right)x\left(k\right)+v\left(k\right)\\ E\left[w\left(k\right)w^T\left(j\right)\right]=Q\left(k\right)\delta (k-j)\\ E\left[v\left(k\right)v^T\left(j\right)\right]=R\left(k\right)\delta (k-j)\\ E\left[w\left(k\right)v^T\left(j\right)\right]=0\end{array}$$	$$\begin{array}{l}x\left(k\right)=f\left(x\right(k-1),w(k-1\left)\right)\\ z\left(k\right)=h\left(x\right(k),v(k\left)\right)\\ E\left[w\left(k\right)w^T\left(j\right)\right]=Q\left(k\right)\delta (k-j)\\ E\left[v\left(k\right)v^T\left(j\right)\right]=R\left(k\right)\delta (k-j)\\ E\left[w\left(k\right)v^T\left(j\right)\right]=0\end{array}$$
Transformation	/	$$\begin{array}{c}\hfill \frac{\partial f}{\partial x}{|}_{\widehat{x}(k-1|k-1)}=F\left(k\right)\hfill \\ \hfill \frac{\partial f}{\partial w}{|}_{\widehat{x}(k-1|k-1)}=L\left(k\right)\hfill \\ \hfill \frac{\partial h}{\partial x}{|}_{x=\widehat{x}\left(k\right|k-1)}=H\left(k\right)\hfill \\ \hfill \frac{\partial h}{\partial v}{|}_{x=\widehat{x}\left(k\right|k-1)}=M\left(k\right)\hfill \end{array}$$
Prediction of the State	$\widehat{x}\left(k\right|k-1)=A(k-1)\widehat{x}(k-1|k-1)$	$\widehat{x}\left(k\right|k-1)=f(\widehat{x}(k-1|k-1),0)$
Updaton of the State	$\widehat{x}\left(k\right|k)=\widehat{x}\left(k\right|k-1)+K\left(k\right)\left(z\left(k\right)-C\left(k\right)\widehat{x}\left(k\right|k-1)\right)$	$\widehat{x}\left(k\right|k)=\widehat{x}\left(k\right|k-1)+K\left(k\right)(z\left(k\right)-h(\widehat{x}\left(k\right|k-1),0)$
Filter gain	$K\left(k\right)=P\left(k\right|k-1)C^T\left(k\right){(C\left(k\right)P\left(k\right|k-1)C^T\left(k\right)+R\left(k\right))}^{-1}$	$K\left(k\right)=P\left(k\right|k-1)H^T\left(k\right)(H\left(k\right)P\left(k\right|k-1)H^T\left(k\right)+M\left(k\right)R\left(k\right)M^T\left(k\right){)}^{-1}$
Prediction of the Covariance	$P\left(k\right|k-1)=A(k-1)P(k-1|k-1)A^T(k-1)+Q(k-1)$	$P\left(k\right|k-1)=F(k-1)P(k-1|k-1)F^T(k-1)+L(k-1)Q(k-1)L^T(k-1)$
Updaton of the Covariance	$P\left(k\right|k)=(I-K\left(k\right)C\left(k\right)\left)P\right(k|k-1)$	$P\left(k\right|k)=(I-K\left(k\right)H\left(k\right)P\left(k\right|k-1)$

Table A2. The details of UKF.

Different Parts of Filter	UKF
System Model	$$\begin{array}{l}x\left(k\right)=f\left(x\right(k-1\left)\right)+w(k-1)\\ z\left(k\right)=h\left(x\right(k\left)\right)+v\left(k\right)\\ E\left[w\left(k\right)w^T\left(j\right)\right]=Q\left(k\right)\delta (k-j)\\ E\left[v\left(k\right)v^T\left(j\right)\right]=R\left(k\right)\delta (k-j)\\ E\left[w\left(k\right)v^T\left(j\right)\right]=0\end{array}$$
Prediction of the State	${\widehat{x}}^{\left(0\right)}(k-1|k-1)=\widehat{x}(k-1|k-1)$ ${\widehat{x}}^{\left(i\right)}(k-1|k-1)=\widehat{x}(k-1|k-1)+{\tilde{x}}^{\left(i\right)}$ where ${\tilde{x}}^{\left(i\right)}={{\left(\sqrt{(n+k)P(k-1|k-1)}\right)}_i}^T,i=1,\cdots ,n$ ${\tilde{x}}^{\left(i\right)}=-{{\left(\sqrt{(n+k)P(k-1|k-1)}\right)}_i}^T$ $i=n+1,\cdots ,2n$ and ${\widehat{x}}^{\left(i\right)}\left(k\right|k-1)=f\left({\widehat{x}}^{\left(i\right)}(k-1|k-1)\right)$ $\widehat{x}\left(k\right|k-1)={\displaystyle \sum _{i=0}^{2n}}{w}^{\left(i\right)}{\widehat{x}}^{\left(i\right)}\left(k\right|k-1)$ with $w^{\left(0\right)}=\frac{k}{n+k}$ $w^{\left(i\right)}=\frac{1}{2(n+k)},i=1,2\cdots 2n$
Updation of the State	$$\begin{array}{l}{\widehat{x}}^{\left(0\right)}\left(k\right|k-1)=\widehat{x}\left(k\right|k-1)\\ {\widehat{x}}^{\left(i\right)}\left(k\right|k-1)=\widehat{x}\left(k\right|k-1)+{\tilde{x}}^{\left(i\right)},i=1,\cdots ,2n\\ {\tilde{x}}^{\left(i\right)}={{\left(\sqrt{(n+k)P\left(k\right|k-1)}\right)}_i}^T,i=1,\cdots ,n\\ {\tilde{x}}^{\left(i\right)}=-{{\left(\sqrt{(n+k)P\left(k\right|k-1)}\right)}_i}^T,i=n+1,\cdots ,2n\\ \\ {\widehat{z}}^{\left(i\right)}\left(k\right|k-1)=h({\widehat{x}}^{\left(i\right)}\left(k\right|k-1))\\ \widehat{z}\left(k\right|k-1)={\displaystyle \sum _{i=0}^{2n}}{w}^{\left(i\right)}{\widehat{z}}^{\left(i\right)}\left(k\right|k-1)\\ \widehat{x}\left(k\right|k)=\widehat{x}\left(k\right|k-1)+K\left(k\right)\left(z\left(k\right)-\widehat{z}\left(k\right|k-1)\right)\end{array}$$
Filter gain	$P_z={\displaystyle \sum _{i=0}^{2n}}{w}^{\left(i\right)}\left({\widehat{z}}^{\left(i\right)}\left(k\right|k-1)-\widehat{z}\left(k\right|k-1)\right)$ $$*{\left({\widehat{z}}^{\left(i\right)}\left(k\right|k-1)-\widehat{z}\left(k\right|k-1)\right)}^T+R\left(k\right)$$ $P_{xz}={\displaystyle \sum _{i=0}^{2n}}{w}^{\left(i\right)}\left({\widehat{x}}^{\left(i\right)}\left(k\right|k-1)-\widehat{x}\left(k\right|k-1)\right){\left({\widehat{z}}^{\left(i\right)}\left(k\right|k-1)-\widehat{z}\left(k\right|k-1)\right)}^T$ $K\left(k\right)=P_{xz}{P_z}^{-1}$
Prediction of the Covariance	$P\left(k\right|k-1)={\displaystyle \sum _{i=0}^{2n}}{w}^{\left(i\right)}\left({\widehat{x}}^{\left(i\right)}\left(k\right|k-1)-\widehat{x}\left(k\right|k-1)\right)$ $$*{\left({\widehat{x}}^{\left(i\right)}\left(k\right|k-1)-\widehat{x}\left(k\right|k-1)\right)}^T+Q(k-1)$$
Updation of the Covariance	$P(k+1|k+1)=P\left(k\right|k+1)-K\left(k\right)P_z{K}^T\left(k\right)$

Table A2. The details of UKF.

Different Parts of Filter	UKF
System Model	$$\begin{array}{l}x\left(k\right)=f\left(x\right(k-1\left)\right)+w(k-1)\\ z\left(k\right)=h\left(x\right(k\left)\right)+v\left(k\right)\\ E\left[w\left(k\right)w^T\left(j\right)\right]=Q\left(k\right)\delta (k-j)\\ E\left[v\left(k\right)v^T\left(j\right)\right]=R\left(k\right)\delta (k-j)\\ E\left[w\left(k\right)v^T\left(j\right)\right]=0\end{array}$$
Prediction of the State	${\widehat{x}}^{\left(0\right)}(k-1|k-1)=\widehat{x}(k-1|k-1)$ ${\widehat{x}}^{\left(i\right)}(k-1|k-1)=\widehat{x}(k-1|k-1)+{\tilde{x}}^{\left(i\right)}$ where ${\tilde{x}}^{\left(i\right)}={{\left(\sqrt{(n+k)P(k-1|k-1)}\right)}_i}^T,i=1,\cdots ,n$ ${\tilde{x}}^{\left(i\right)}=-{{\left(\sqrt{(n+k)P(k-1|k-1)}\right)}_i}^T$ $i=n+1,\cdots ,2n$ and ${\widehat{x}}^{\left(i\right)}\left(k\right|k-1)=f\left({\widehat{x}}^{\left(i\right)}(k-1|k-1)\right)$ $\widehat{x}\left(k\right|k-1)={\displaystyle \sum _{i=0}^{2n}}{w}^{\left(i\right)}{\widehat{x}}^{\left(i\right)}\left(k\right|k-1)$ with $w^{\left(0\right)}=\frac{k}{n+k}$ $w^{\left(i\right)}=\frac{1}{2(n+k)},i=1,2\cdots 2n$
Updation of the State	$$\begin{array}{l}{\widehat{x}}^{\left(0\right)}\left(k\right|k-1)=\widehat{x}\left(k\right|k-1)\\ {\widehat{x}}^{\left(i\right)}\left(k\right|k-1)=\widehat{x}\left(k\right|k-1)+{\tilde{x}}^{\left(i\right)},i=1,\cdots ,2n\\ {\tilde{x}}^{\left(i\right)}={{\left(\sqrt{(n+k)P\left(k\right|k-1)}\right)}_i}^T,i=1,\cdots ,n\\ {\tilde{x}}^{\left(i\right)}=-{{\left(\sqrt{(n+k)P\left(k\right|k-1)}\right)}_i}^T,i=n+1,\cdots ,2n\\ \\ {\widehat{z}}^{\left(i\right)}\left(k\right|k-1)=h({\widehat{x}}^{\left(i\right)}\left(k\right|k-1))\\ \widehat{z}\left(k\right|k-1)={\displaystyle \sum _{i=0}^{2n}}{w}^{\left(i\right)}{\widehat{z}}^{\left(i\right)}\left(k\right|k-1)\\ \widehat{x}\left(k\right|k)=\widehat{x}\left(k\right|k-1)+K\left(k\right)\left(z\left(k\right)-\widehat{z}\left(k\right|k-1)\right)\end{array}$$
Filter gain	$P_z={\displaystyle \sum _{i=0}^{2n}}{w}^{\left(i\right)}\left({\widehat{z}}^{\left(i\right)}\left(k\right|k-1)-\widehat{z}\left(k\right|k-1)\right)$ $$*{\left({\widehat{z}}^{\left(i\right)}\left(k\right|k-1)-\widehat{z}\left(k\right|k-1)\right)}^T+R\left(k\right)$$ $P_{xz}={\displaystyle \sum _{i=0}^{2n}}{w}^{\left(i\right)}\left({\widehat{x}}^{\left(i\right)}\left(k\right|k-1)-\widehat{x}\left(k\right|k-1)\right){\left({\widehat{z}}^{\left(i\right)}\left(k\right|k-1)-\widehat{z}\left(k\right|k-1)\right)}^T$ $K\left(k\right)=P_{xz}{P_z}^{-1}$
Prediction of the Covariance	$P\left(k\right|k-1)={\displaystyle \sum _{i=0}^{2n}}{w}^{\left(i\right)}\left({\widehat{x}}^{\left(i\right)}\left(k\right|k-1)-\widehat{x}\left(k\right|k-1)\right)$ $$*{\left({\widehat{x}}^{\left(i\right)}\left(k\right|k-1)-\widehat{x}\left(k\right|k-1)\right)}^T+Q(k-1)$$
Updation of the Covariance	$P(k+1|k+1)=P\left(k\right|k+1)-K\left(k\right)P_z{K}^T\left(k\right)$

Table A3. The details of CKF.

Different Parts of Filter	CKF
System Model	$$\begin{array}{l}x\left(k\right)=f\left(x\right(k-1\left)\right)+w(k-1)\\ z\left(k\right)=h\left(x\right(k\left)\right)+v\left(k\right)\\ E\left[w\left(k\right)w^T\left(j\right)\right]=Q\left(k\right)\delta (k-j)\\ E\left[v\left(k\right)v^T\left(j\right)\right]=R\left(k\right)\delta (k-j)\\ E\left[w\left(k\right)v^T\left(j\right)\right]=0\end{array}$$
Prediction of the State	${\widehat{x}}^{\left(i\right)}(k-1|k-1)=\widehat{x}(k-1|k-1)+{\tilde{x}}^{\left(i\right)}$ where ${\tilde{x}}^{\left(i\right)}={{\left(\sqrt{P(k-1|k-1)}\right)}_i}^T,i=1,\cdots ,n$ ${\tilde{x}}^{\left(i\right)}=-{{\left(\sqrt{P(k-1|k-1)}\right)}_i}^T,i=n+1,\cdots ,2n$ and ${\widehat{x}}^{\left(i\right)}\left(k\right|k-1)=f\left({\widehat{x}}^{\left(i\right)}(k-1|k-1)\right)$ $\widehat{x}\left(k\right|k-1)={\displaystyle \sum _{i=1}^{2n}}{w}^{\left(i\right)}{\widehat{x}}^{\left(i\right)}\left(k\right|k-1)$ with $w^{\left(i\right)}=\frac{1}{2n},i=1,2\cdots 2n$
Updaton of the State	$$\begin{array}{l}{\widehat{x}}^{\left(i\right)}\left(k\right|k-1)=\widehat{x}\left(k\right|k-1)+{\tilde{x}}^{\left(i\right)},i=1,\cdots ,2n\\ {\tilde{x}}^{\left(i\right)}={{\left(\sqrt{P\left(k\right|k-1)}\right)}_i}^T,i=1,\cdots ,n\\ {\tilde{x}}^{\left(i\right)}=-{{\left(\sqrt{P\left(k\right|k-1)}\right)}_i}^T,i=n+1,\cdots ,2n\\ \\ {\widehat{z}}^{\left(i\right)}\left(k\right|k-1)=h\left({\widehat{x}}^{\left(i\right)}\left(k\right|k-1)\right)\\ \widehat{z}\left(k\right|k-1)={\displaystyle \sum _{i=1}^{2n}}{w}^{\left(i\right)}{\widehat{z}}^{\left(i\right)}\left(k\right|k-1)\\ \widehat{x}\left(k\right|k)=\widehat{x}\left(k\right|k-1)+K\left(k\right)\left(z\left(k\right)-\widehat{z}\left(k\right|k-1)\right)\end{array}$$
Filter gain	$P_z={\displaystyle \sum _{i=1}^{2n}}{w}^{\left(i\right)}{\widehat{z}}^{\left(i\right)}\left(k\right|k-1){\widehat{z}}^{\left(i\right)}\left(k\right|k-1)$ $$-\widehat{z}\left(k\right|k-1)\widehat{z}{\left(k\right|k-1)}^T+R\left(k\right)$$ $P_{xz}={\displaystyle \sum _{i=1}^{2n}}{w}^{\left(i\right)}({\widehat{x}}^{\left(i\right)}\left(k\right|k-1){{\widehat{z}}^{\left(i\right)}\left(k\right|k-1))-\widehat{z}\left(k\right|k-1)\widehat{x}\left(k\right|k-1)}^T$ $K\left(k\right)=P_{xz}{P_z}^{-1}$
Prediction of the Covariance	$P\left(k\right|k-1)={\displaystyle \sum _{i=1}^{2n}}{w}^{\left(i\right)}\left({\widehat{x}}^{\left(i\right)}\left(k\right|k-1){\widehat{x}}^{\left(i\right)}\left(k\right|k-1)\right)$ $$-\widehat{x}{\left(k\right|k-1)}^T\widehat{x}\left(k\right|k-1)+Q(k-1)$$
Updaton of the Covariance	$P\left(k\right|k)=P\left(k\right|k-1)-K\left(k\right)P_z{K}^T\left(k\right)$

Table A3. The details of CKF.

Different Parts of Filter	CKF
System Model	$$\begin{array}{l}x\left(k\right)=f\left(x\right(k-1\left)\right)+w(k-1)\\ z\left(k\right)=h\left(x\right(k\left)\right)+v\left(k\right)\\ E\left[w\left(k\right)w^T\left(j\right)\right]=Q\left(k\right)\delta (k-j)\\ E\left[v\left(k\right)v^T\left(j\right)\right]=R\left(k\right)\delta (k-j)\\ E\left[w\left(k\right)v^T\left(j\right)\right]=0\end{array}$$
Prediction of the State	${\widehat{x}}^{\left(i\right)}(k-1|k-1)=\widehat{x}(k-1|k-1)+{\tilde{x}}^{\left(i\right)}$ where ${\tilde{x}}^{\left(i\right)}={{\left(\sqrt{P(k-1|k-1)}\right)}_i}^T,i=1,\cdots ,n$ ${\tilde{x}}^{\left(i\right)}=-{{\left(\sqrt{P(k-1|k-1)}\right)}_i}^T,i=n+1,\cdots ,2n$ and ${\widehat{x}}^{\left(i\right)}\left(k\right|k-1)=f\left({\widehat{x}}^{\left(i\right)}(k-1|k-1)\right)$ $\widehat{x}\left(k\right|k-1)={\displaystyle \sum _{i=1}^{2n}}{w}^{\left(i\right)}{\widehat{x}}^{\left(i\right)}\left(k\right|k-1)$ with $w^{\left(i\right)}=\frac{1}{2n},i=1,2\cdots 2n$
Updaton of the State	$$\begin{array}{l}{\widehat{x}}^{\left(i\right)}\left(k\right|k-1)=\widehat{x}\left(k\right|k-1)+{\tilde{x}}^{\left(i\right)},i=1,\cdots ,2n\\ {\tilde{x}}^{\left(i\right)}={{\left(\sqrt{P\left(k\right|k-1)}\right)}_i}^T,i=1,\cdots ,n\\ {\tilde{x}}^{\left(i\right)}=-{{\left(\sqrt{P\left(k\right|k-1)}\right)}_i}^T,i=n+1,\cdots ,2n\\ \\ {\widehat{z}}^{\left(i\right)}\left(k\right|k-1)=h\left({\widehat{x}}^{\left(i\right)}\left(k\right|k-1)\right)\\ \widehat{z}\left(k\right|k-1)={\displaystyle \sum _{i=1}^{2n}}{w}^{\left(i\right)}{\widehat{z}}^{\left(i\right)}\left(k\right|k-1)\\ \widehat{x}\left(k\right|k)=\widehat{x}\left(k\right|k-1)+K\left(k\right)\left(z\left(k\right)-\widehat{z}\left(k\right|k-1)\right)\end{array}$$
Filter gain	$P_z={\displaystyle \sum _{i=1}^{2n}}{w}^{\left(i\right)}{\widehat{z}}^{\left(i\right)}\left(k\right|k-1){\widehat{z}}^{\left(i\right)}\left(k\right|k-1)$ $$-\widehat{z}\left(k\right|k-1)\widehat{z}{\left(k\right|k-1)}^T+R\left(k\right)$$ $P_{xz}={\displaystyle \sum _{i=1}^{2n}}{w}^{\left(i\right)}({\widehat{x}}^{\left(i\right)}\left(k\right|k-1){{\widehat{z}}^{\left(i\right)}\left(k\right|k-1))-\widehat{z}\left(k\right|k-1)\widehat{x}\left(k\right|k-1)}^T$ $K\left(k\right)=P_{xz}{P_z}^{-1}$
Prediction of the Covariance	$P\left(k\right|k-1)={\displaystyle \sum _{i=1}^{2n}}{w}^{\left(i\right)}\left({\widehat{x}}^{\left(i\right)}\left(k\right|k-1){\widehat{x}}^{\left(i\right)}\left(k\right|k-1)\right)$ $$-\widehat{x}{\left(k\right|k-1)}^T\widehat{x}\left(k\right|k-1)+Q(k-1)$$
Updaton of the Covariance	$P\left(k\right|k)=P\left(k\right|k-1)-K\left(k\right)P_z{K}^T\left(k\right)$