1. Introduction
In 1991, Ophir et al. [
1] proposed a new ultrasound technique, quasi-static elastography, to visualize and quantify deformation of tissue to thus detect abnormalities (e.g., through the relatively stiffer breast and prostate tumors). In this technique, ultrasound radio frequency (RF) data are obtained prior to and after deformation of the target tissue. Deformation can be induced externally by the transducer or a vibrator, or internally by the heart or respiration. Several methods have been developed to estimate displacement or strain maps based on the acquired RF data [
2,
3,
4,
5,
6]. Conventionally, a template windows containing post-deformation RF-data is cross-correlated with a search window containing pre-deformation data. The position of the cross-correlation peak indicates the displacement of the template. To cope with relatively large displacements, coarse-to-fine cross-correlation methods were developed [
2]. In coarse-to-fine cross-correlation, multi-iterative cross-correlation is executed starting with relatively large windows analyzing the envelope signal and subsequently using finer windows of RF-signal in each subsequent iteration with the estimated displacements of the previous iteration as an offset. Finally, a least squares strain estimator can be used to reconstruct a strain map [
7].
The majority of current commercial ultrasound systems collect ultrasound RF data line-by-line using focused ultrasound transmit-and-receive sequences. Back in 1979, plane wave acquisitions were proposed as alternative to line-by-line sequences [
8,
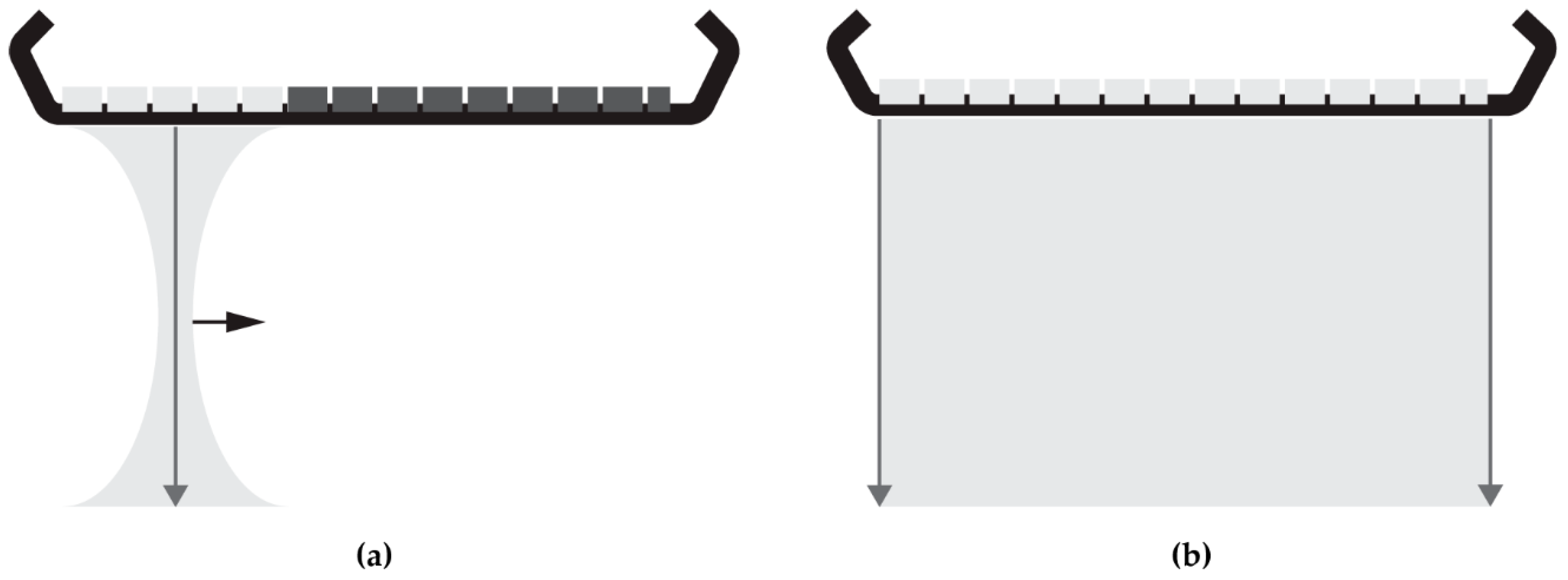
9]. This type of acquisition has been getting more attention since the mid-2000s when the computational power and data transfer rates had sufficiently increased to enable the processing of the data generated by plane-wave transmissions. In plane-wave imaging, the full transducer array is used to transmit one unfocussed plane-wave and receive the reflected signals (
Figure 1). In case of a 192-element array transducer, frame-rates can be increased by a factor of 192 compared to line-by-line scans. Consequently, ultrasound data can be collected with frame-rates over 10 kHz (theoretically limited by the two-way propagation of the ultrasound signal) and so fast deformations can also be quantified and visualized using quasi-static elastography. In the absence of focusing in transmit, plane-wave imaging requires software beam-forming to reconstruct RF-data from the obtained element data. In conventional ultrasound scanners, beam-forming is often applied in hardware. In this study, three software beam-forming strategies and their effect on displacement estimation were exploited: delay-and-sum (DaS) [
10] in the spatial-temporal domain originating from conventional focused ultrasound, and Lu’s-fk [
11,
12] and Stolt’s-fk [
13] beam-forming methods, both operating in the Fourier domain which are specifically developed for plane-wave acquisitions.
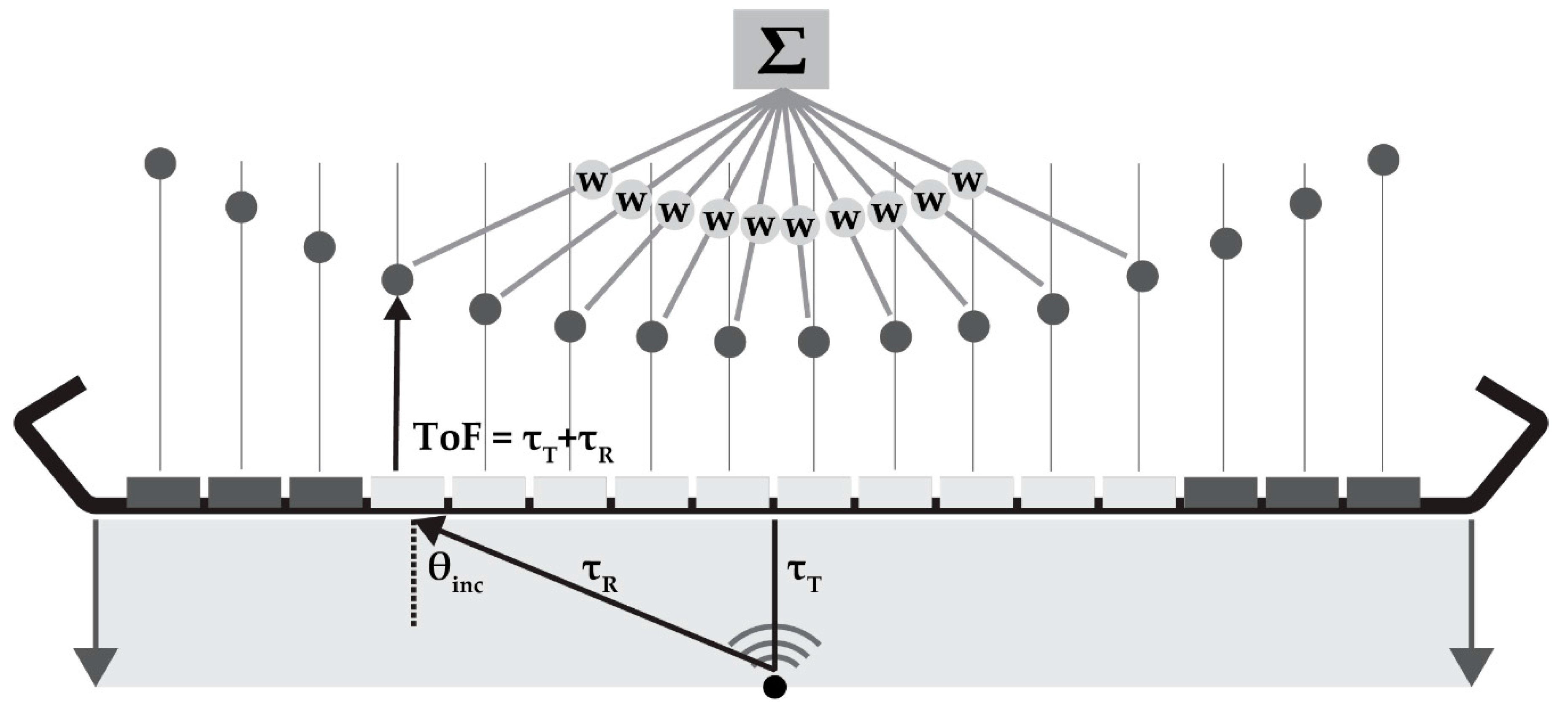
DaS is a beam-forming method based on delaying the element signal by the expected time-of-flight (ToF) and summation of the element data points (
Figure 2). For a certain point to be reconstructed, the ToF is calculated as the time of the plane-wave propagating to that point and the reflected or back-scattered signal to be received by the elements. The ToF is used to identify and sum the signals originating from each point in the element data. In dynamic focusing in receive, the F-number (F) dictates the number of elements (aperture) used for beam-forming:
where
d and
lapp are the depth of the reconstruction point and aperture width, respectively. Furthermore, apodization can be applied to weigh the signals (e.g., by Hamm or Hann function) to reconstruct each point and so expected angle sensitivity and back-scatter signal intensities can be incorporated. Apodization is often applied to increase contrast in B-mode images.
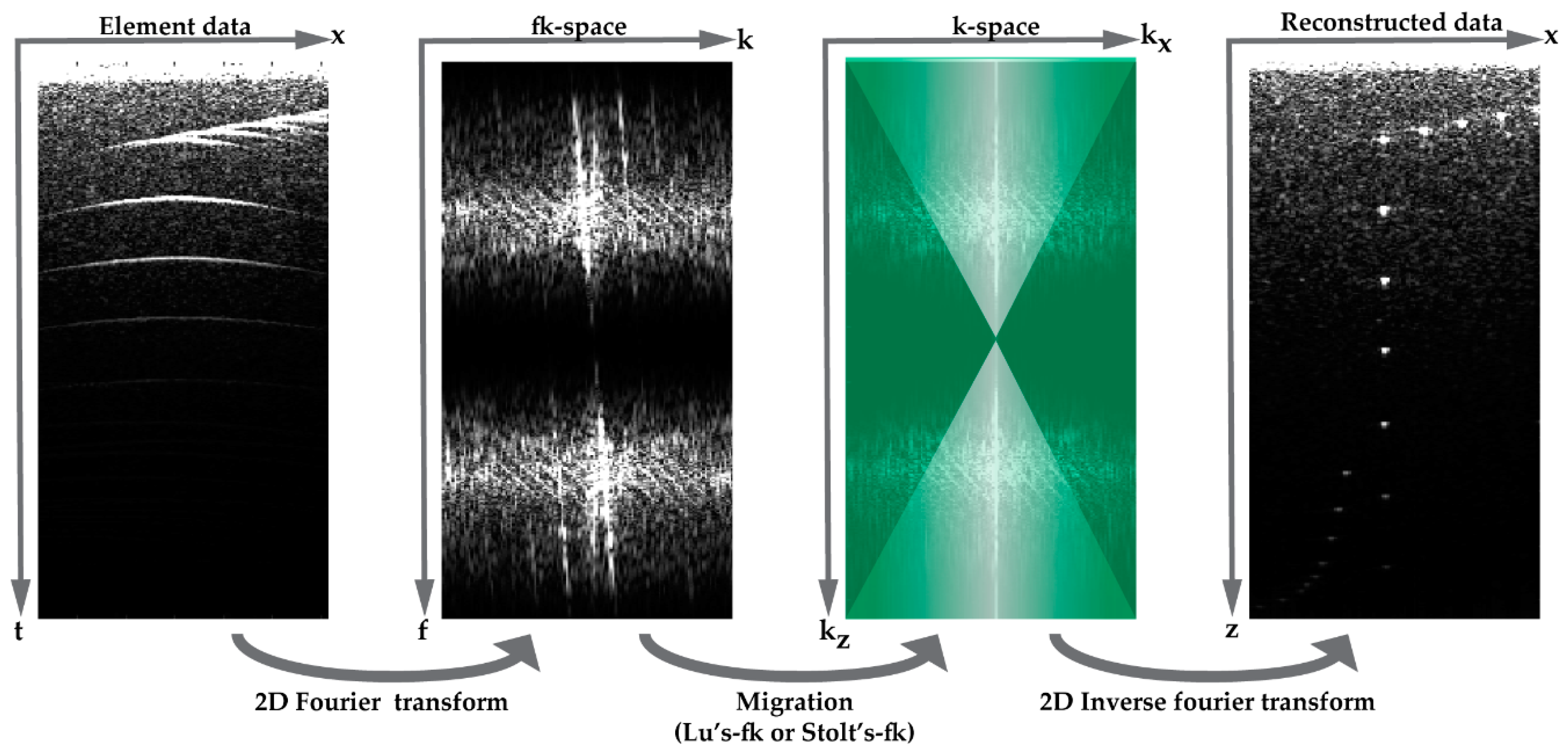
Another approach is beam-forming in the Fourier domain by Lu’s-fk or Stolt’s-fk which are computationally less expensive and can run around 25 times faster compared to DaS [
13]. In both methods, 2-D element data in the spatial-temporal domain are transformed to the fk-space. Next, a migration method is applied to transform the data into the complete k-space and finally the migrated data are transformed back into the spatial-temporal domain (
Figure 3). A migration method of plane-wave ultrasound was first carried out by Lu et al. from the analysis of limited diffraction beams [
11,
12]. Lu et al. introduced the mapping rule throughout the transmission–scattering–receiving process. More recently, Garcia et al. proposed another method by adapting Stolt’s-fk seismic wave migration to the plane wave ultrasound scenario [
13]. In this modification, the plane wave’s backscattering is fitted with waves spontaneously radiating from sources. Comparing Stolt’s-fk and Lu’s-fk, the two methods share a similar spectrum content at small angles, while their spectra differ more significantly in the mapping of large angles.
Similar to apodization in DaS, angular weighting can be applied in Fourier domain beam-forming to increase contrast in the final B-mode image [
14]. In this method, developed in our group, the Fourier spectrum after the migration (k-space) is multiplied with a template which is designed such that reflected waves originating from directions closely aligned with the plane-wave steering angle pass unaltered, whereas waves from wave directions deviating from the plane-wave propagation direction are attenuated according to a Hann function (
Figure 3). This template can be applied for both migration methods (Lu’s-fk and Stolt’s-fk).
Since the beam-forming in plane-wave imaging is executed using software, the design of the beam-forming reconstruction grid (USGrid) is more flexible compared to conventional focused line-by-line scanners in which beam-forming is executed by hardware. Consequently, more lines per pitch can be reconstructed, which might result in more accurate displacement estimates. For focused imaging, it has already been shown that more accurate lateral displacement estimates can be obtained when increasing the RF line density by interpolation [
15,
16].
Plane-wave imaging and displacement and strain imaging have been combined in multiple studies. Besides a paper from our group [
17] which investigated the effect of line density on displacement estimation for DaS, to our knowledge, the effects of different beam-forming strategies and line densities on displacement and strain estimation have not been explored. Therefore, the aim of this study was to investigate the effect of beam-forming strategies (DaS, Lu’s-fk and Stolt’s-fk) for plane-wave imaging on the accuracy of displacement estimates. Furthermore, the effect of the line density, apodization (in DaS) and angular weighting (in Lu’s-fk and Stolt’s-fk) were evaluated, and four different transducers were used with central frequencies varying between 5 and 21 MHz representing the whole range of clinically used linear array transducers. In this study, we evaluated the performance of displacement and strain estimation by using a rotating phantom. The advantage of a rotating phantom is that a displacement field is induced with axial and lateral displacements varying separately in magnitude instead of having pure axial or lateral displacements with same magnitude as obtained by linear translation of a phantom. Furthermore, the gradients of the axial and lateral displacement field were used to evaluate the accuracy of the displacement estimations because these gradients should be zero (see Materials and Methods section) without requiring exact knowledge of the reference displacement field. These gradients can also be considered as strains since strains are calculated the same way and are equal to their gradient.
2. Materials and Methods
To create a block phantom, gelatin (10% by weight; VMR International, Leuven, Belgium) was dissolved in demineralized water and heated to 90 °C and cooled to 35 °C while continuously stirring using a magnetic stirrer. During the cooling process, silica particles (2% by weight; silica gel 60, 0.015–0.040 mm; Merck KGaA, Darmstadt, Germany) were added, which act as scatterers. Next, the mixed solution was poured in an open container (200 × 100 × 100 mm) leaving a 20 mm space under the top surface. Finally, the phantom was placed in a fridge to consolidate for 24 h.
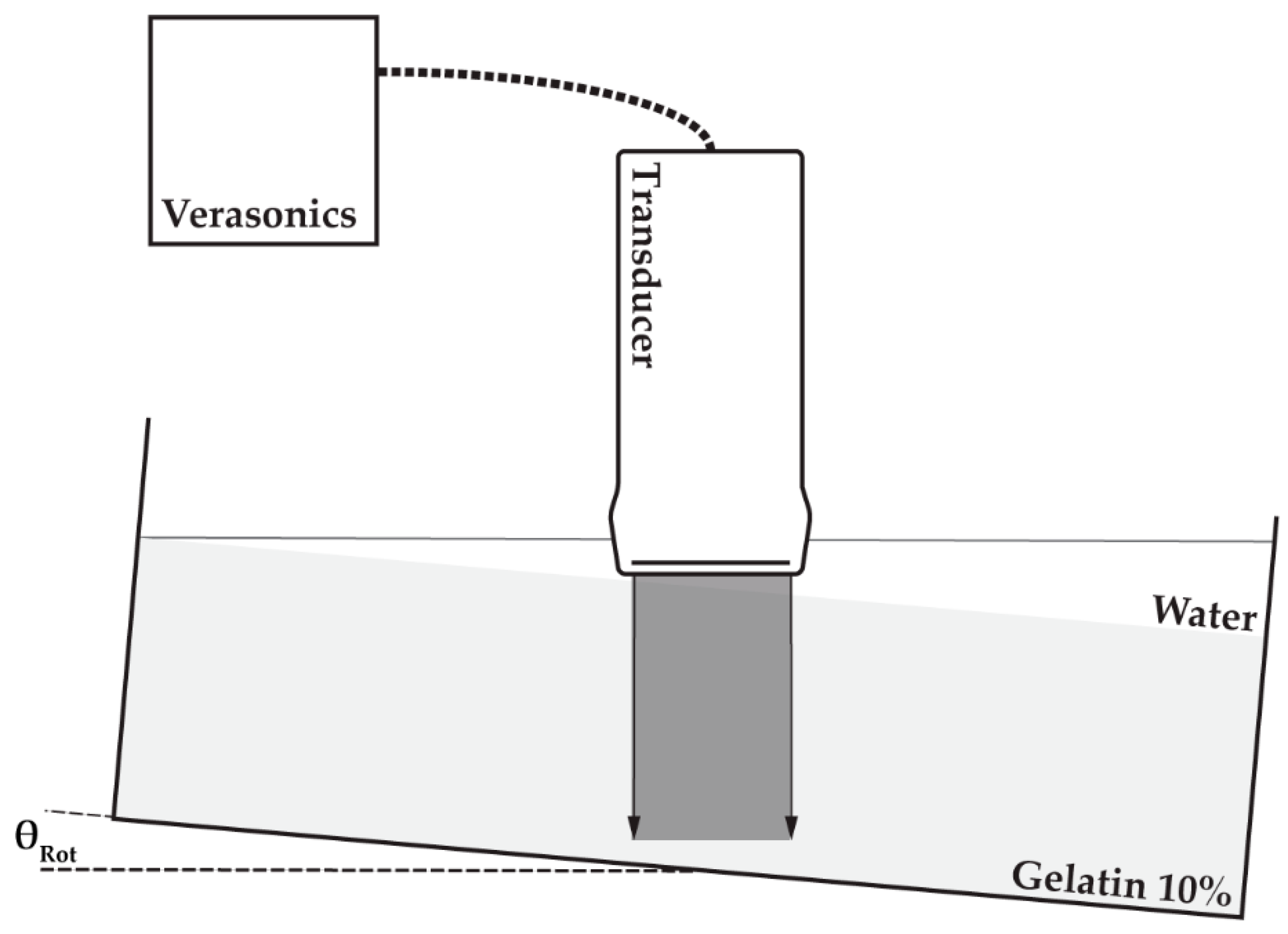
The phantom, including the container, was positioned on top of a seesaw to enable rotation of the phantom. One of the four different linear array transducers utilized in this study (
Table 1) was positioned above the phantom top surface such that the transducer footprint was unable to touch the phantom after rotation at the maximum angle of 10 degrees. Water was poured on the top surface of the phantom to fill the remaining 20 mm space and to ensure acoustic coupling between the transducer and phantom. The transducer was connected to a Verasonics V1 system (MS250 to Verasonics Vantage) to enable 0° plane-wave transmissions and element data collection using the center 128 elements of the transducer (MS250: all 256 elements). Element data were recorded prior to and after rotation (~2°) of the phantom. The experimental setup is also visualized in
Figure 4.
Element data were beam-formed using three different strategies: (1) Lu’s-fk [
11,
12], Stolt’s-fk [
13], and DaS [
10]; (2) with and without angular weighting (Lu’s-fk; Stolts-fk) [
14] or apodization by Hamm function (DaS); and (3) a beam-forming ultrasound grid (USGrid) with 8 samples per wave length and 1, 2, 3 and 4 lines per pitch. These strategies were implemented in Matlab (2016a; Mathworks Inc., Natick, MA, USA). Zero-padding was applied in the k-space to achieve higher line-densities for the fk-based strategies. Beam-forming settings were empirically determined: plane-wave element data were acquired in a multi-purpose phantom and beam-forming settings were tuned resulting in optimal contrast and resolution after beam-forming (see
Appendix A for more details). For all transducers, the F-number (DaS) and angle weighting range (Lu’s-fk; Stolts-fk) were set to 0.875 and ±20°, respectively.
Next, displacements were estimated by two step coarse-to-fine normalized cross correlation of pre- and post-rotation beam-formed ultrasound envelope and RF data in the first and second step respectively [
18,
19]. The cross-correlation peak was interpolated (2-D spline) after the final iteration to estimate sub-sample displacements. After each iteration, displacements were median filtered to remove outliers. Template and search windows, and other settings can be found in
Table 2.
The axial and lateral displacements (
uz and
ux) after rotation can be described as:
where
θ and (
x0,
z0) are the rotation angle and center coordinates, respectively. The gradient of
ux and
uz in the lateral (
x) and the axial (
z) directions can respectively be described as:
In this experiment, angle
θ can be considered small (~2°) and so it can be assumed that:
Consequently,
sxx and
szz in (Equations (4) and (5)) approximate zero, independently of the rotation angle and center. As these gradients (strains) yield 0 and the exact rotational angle and center were unknown in this experiment, we adopted the root-mean squared error (RMSE) of the gradients as a measure of the accuracy of the displacement estimates. The gradients of the displacements were calculated using a one-dimensional three-point least-squares strain estimator [
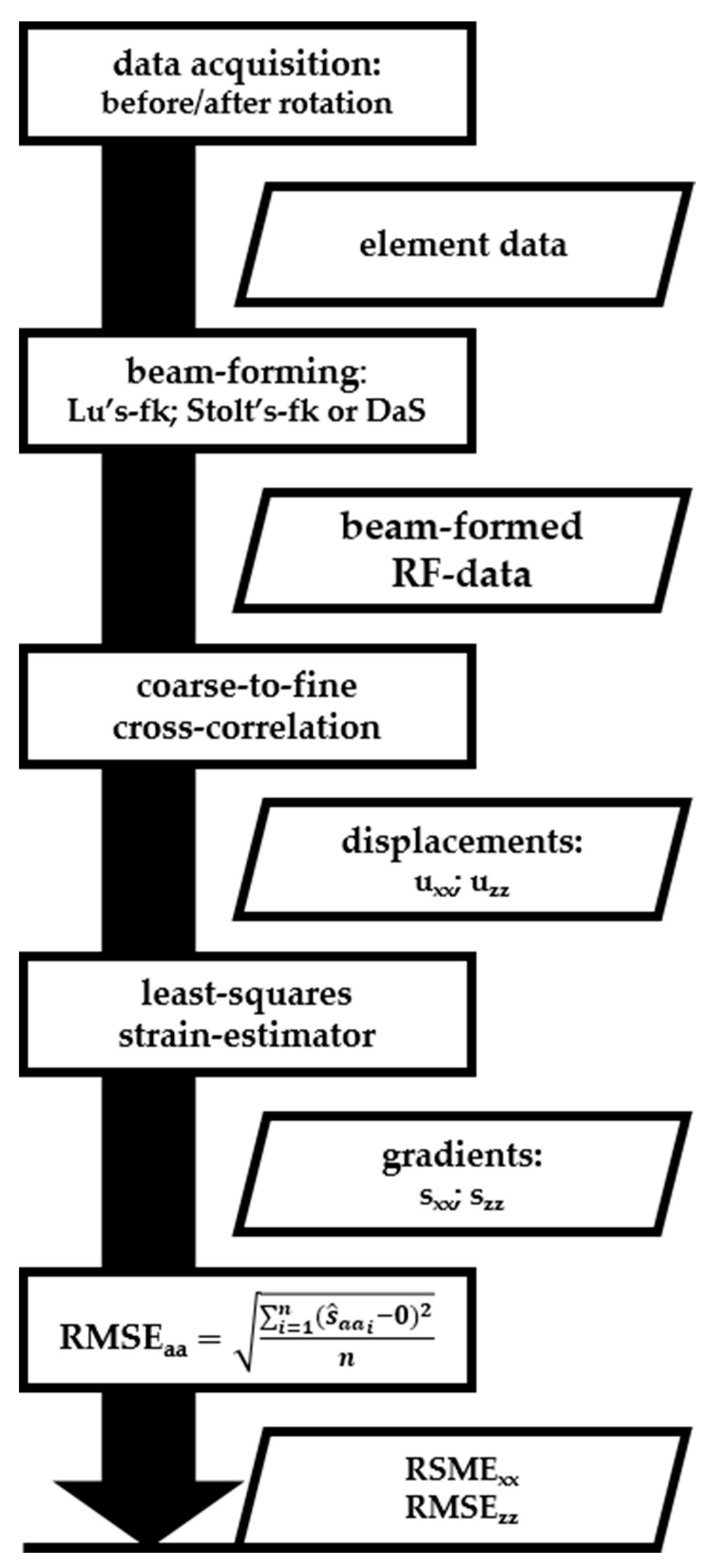
7]. Gradients were only calculated and evaluated within a field-of-view (FoV) measuring –10 to 10 mm laterally and 17.5 to 52.5 mm axially for all transducers. However, the FoV measurement of the MS250 transducer was –8 to 8 mm laterally, since the FoV was limited by the transducer footprint. The top 17.5-mm axial depth was measured through water and was therefore neglected for all transducers. All acquisition and processing steps and intermediate results are summarized in
Figure 5.
3. Results
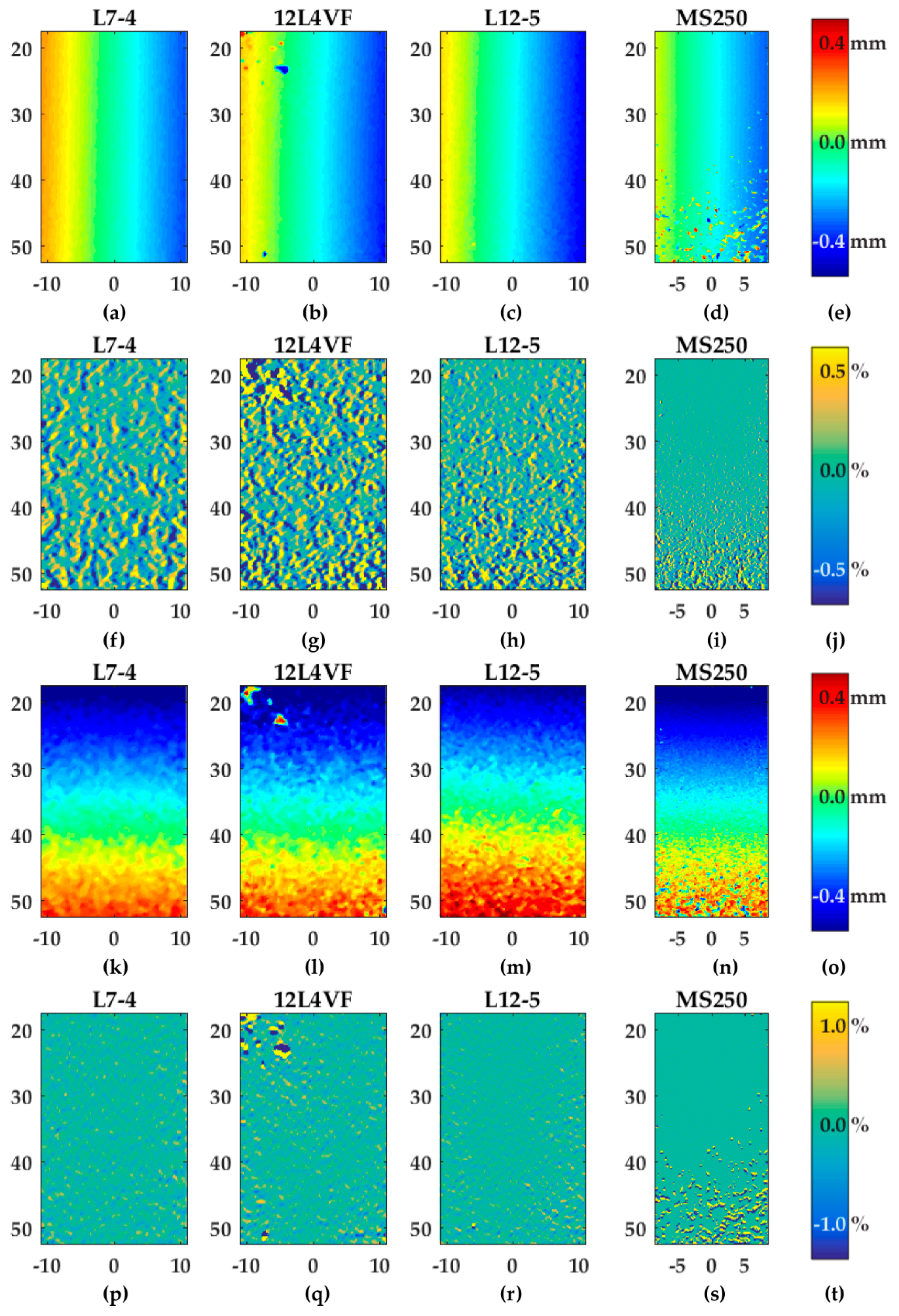
Figure 6 provides an overview of the estimated axial and lateral displacement and strain fields for all probes using Lu’s-fk beam-forming and a line density of two lines per pitch. As expected from Equations (2) to (6), the axial displacement fields (
Figure 6a–d) were constant in the axial direction and so the gradient of the axial displacements in axial directions (
szz) were approximately 0% (see
Figure 6f–i). For the 12L4VF transducer the results revealed some artifacts in the left top corner (
Figure 6b,g). These artifacts were visible for all beam-forming strategies and line densities. The MS250 transducer showed more outliers at lower depths (30–52.5 mm) which were probably caused by attenuation of the ultrasound signal at relatively large depths for this frequency.
The lateral displacement (
Figure 6k–n) and strain fields (
Figure 6p–s) resulted in similar observation as the axial results: constant displacement values in lateral direction and so approximately 0% gradient of lateral displacements in that direction (
sxx). Similar artefacts were also visible for the 12L4VF and MS250 transducers since the axial and lateral displacements were estimated using two-dimensional cross-correlations, which implies these estimations were coupled. Compared to the axial displacement and strain fields (
Figure 6a–j), the lateral fields (
Figure 6k–t) were noisier for all transducers, beam-forming strategies and line densities. In the case of two lines per pitch and Lu’s-fk beam-forming as shown in
Figure 6,
szz varied between ±0.5%, whereas
sxx varied between ±1%.
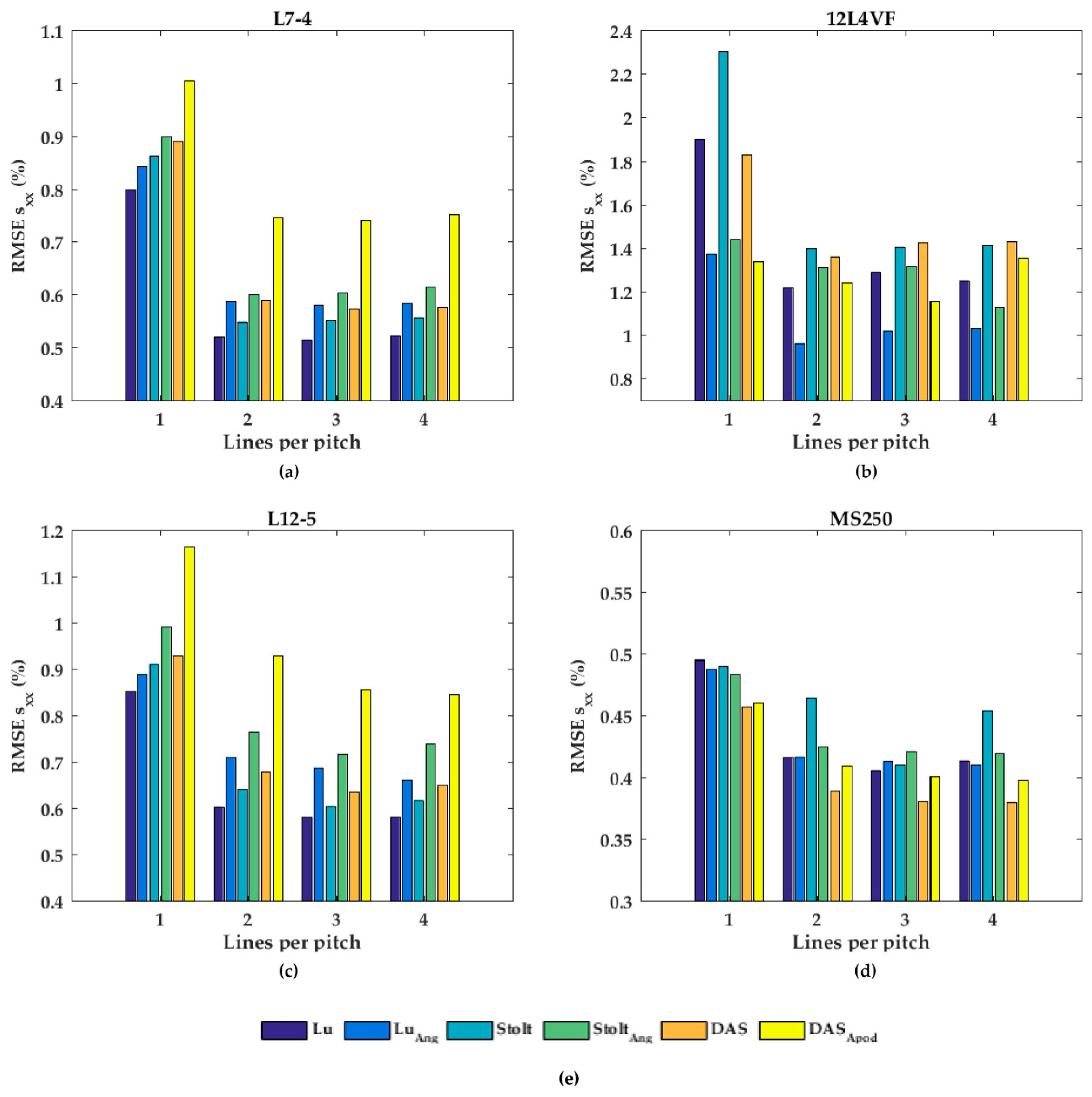
In
Figure 7, the performances of the axial displacement estimates are summarized for all transducers, beam-forming strategies (including angular weighting and apodization) and line densities. As can be noticed for L7-4 (
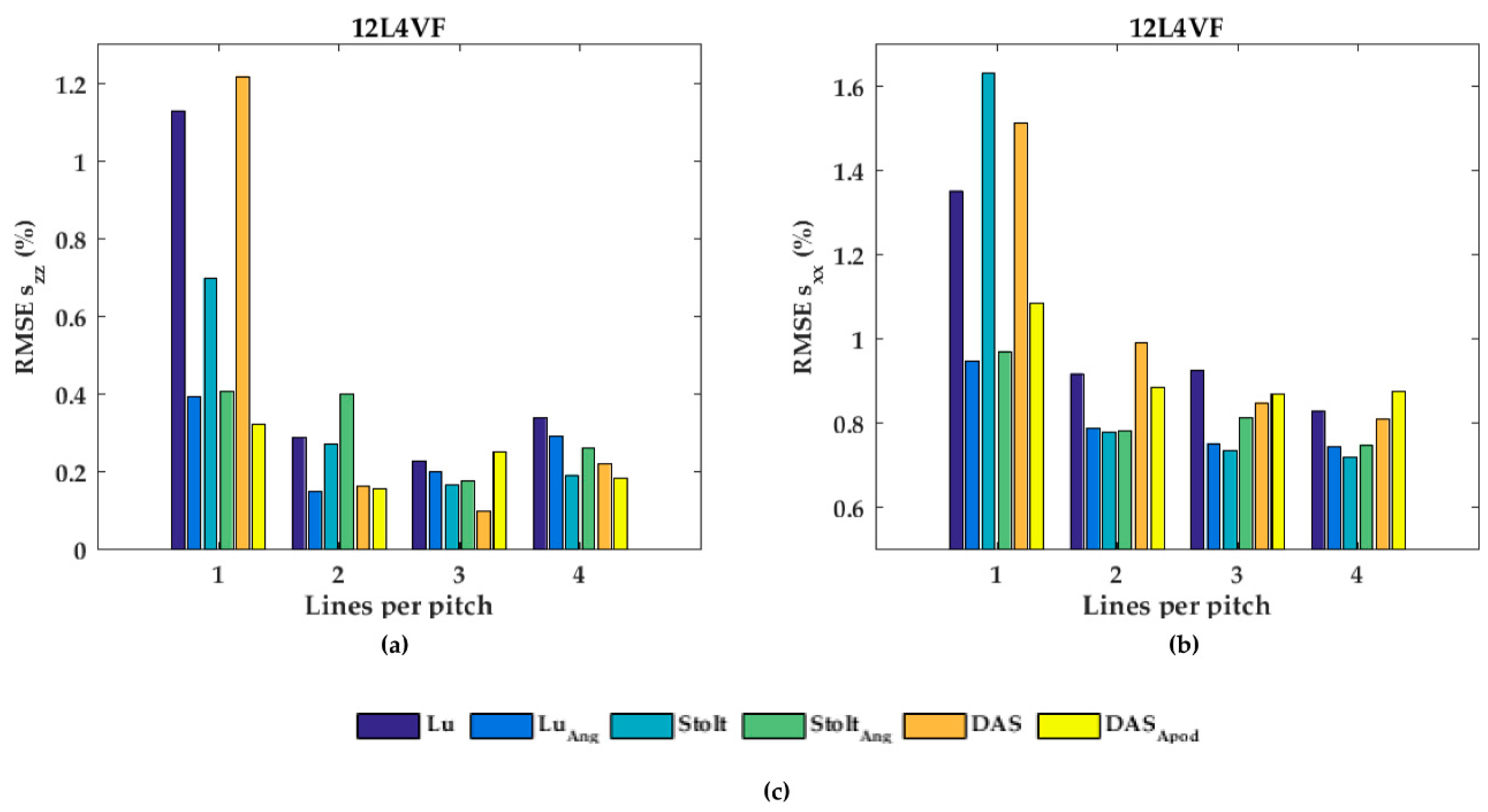
Figure 7a), the RMSE seemed to be almost constant for all beam-forming strategies and line-densities except DaS with one line per pitch, in which the RMSE increased. For the 12L4VF (
Figure 7b), three lines per pitch provided the lowest RMSE using Lu’s-fk, Stolt’s-fk or DaS, with apodization or angular weighting. Furthermore, apodization or angular weighting seemed to decrease the RMSE for this transducer. However, the opposite effect of weighting and apodization can be seen for both the L12-5 and MS250 (
Figure 7c,d) in which the RMSE increased. Multiple lines seemed to slightly increase the RMSE compared to one line per pitch for all strategies in these transducers. DaS or Lu’s-fk with one line per pitch resulted in the lowest RMSE in both L12-5 and MS250. The RMSE by the lateral displacements estimates (
Figure 8) decreased for each method and transducer using over 1 line per pitch.
The RMSE increased when applying angular weighting or apodization for all transducers except 12L4VF, for which the RMSE decreased. Lu’s-fk resulted in slightly decreased RMSE compared to other methods in both L7-4 and L12-5; Lu’s-fk with angular weighting in 12L4VF, and Lu’s-fk and DaS in MS250. For the 12L4VF, the RMSEs were recalculated neglecting the left top area (squared area; axial < 28 mm; lateral < 0 mm,
Figure 6g,q) including the artifact. The results are presented in
Figure 9. Although the overall RMSE values decreased, the observed results were similar to those for the full FoV (
Figure 7b and
Figure 8b). Line densities of two or three lines per pitch resulted in the lowest RMSE for all strategies. Apodization or weighting seemed to decrease RMSE values but less severely and at times even increased values. This artifact might be caused by a small number of damaged elements on the left side of the transducer, resulting in artifacts especially in the near-field as only a few elements were used for reconstruction in that area.
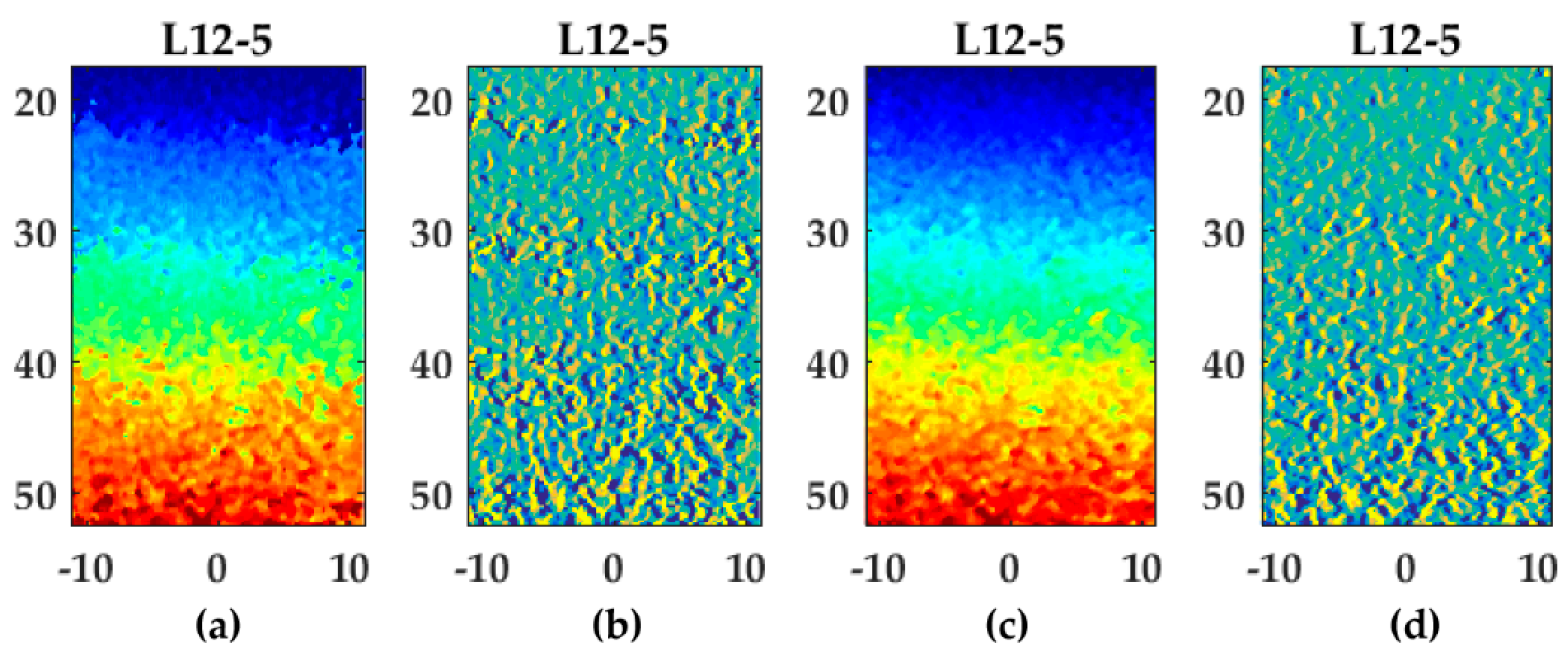
Examples of lateral displacement and strain fields (L12-5, Lu’s-fk) with a line density of one and two lines per pitch are shown in
Figure 10. In the gradient field at 1 line per pitch (
Figure 10b), bands with increased gradients are visible at axial positions of 20, 30, 40, and 50 cm. At these positions, the lateral displacements were approximately ±0.1 and ±0.3 mm, which were displacement at half-pitch positions. After beam-forming using two lines per pitch, these bands were decreased (
Figure 10c,d). These bands resulted in an increased RMSE for one compared to multiple lines per pitch (
Figure 10c). The appearance of these bands at sub-pitch displacements using one line per pitch were also observed for the other transducers and beam-forming methods.
4. Discussion
In this study, the effect of beam-forming strategies and line density on the accuracy of normalized cross-correlation-based displacement estimation was evaluated. Therefore, we designed a method to evaluate the accuracy by phantom rotation, which had two main advantages. First, displacement fields were induced with axial and lateral displacements separately varying within ±0.5 mm (
Figure 1a–d, i–l) instead of pure axial or lateral displacements. Second, the local displacement gradients are expected to be zero independent of the rotation center and angle in this case where the rotation angles was small (<<10°). Consequently, the error of the gradient (RMSE) was used as measure for the accuracy of displacement estimates.
Displacements were calculated by normalized cross-correlation and block-matching. Although other methods are available, only this method was used in the study since it is widely used in (shear) strain imaging. The effect of different methods on the accuracy of displacements was not the scope of this study and so not evaluated. Furthermore, a one dimensional, three-point least-square-strain estimator (LSQSE) was implemented to calculate the gradients for evaluation. Although not presented here, equal results were obtained for LSQSE sizes of 7 and 11 points.
The accuracy of displacement estimates, especially lateral, improved significantly using a line-density of multiple lines per pitch for all transducers except the high frequency transducer MS250 in which this improvement was minimal or the accuracy even slightly decreased for some beam-forming strategies. Improvement by higher line-densities was also observed by Konofagou et al. [
20] in which conventional focused ultrasound was used and RF-lines were interpolated (up to 64 lines per pitch) to gain higher line-densities to improve results. The accuracy of displacement estimates already improved by two or three lines per pitch in this study. However, interpolation of the cross-correlation peak after the final iteration was implemented in this study which also contributes to improved sub-sample displacement estimates [
2]. As can be seen in
Figure 10a,b, the performance of cross-correlation peak interpolation seemed to be decreased in displacements at half-pitch distances resulting in increased gradient bands (
Figure 10b). This effect seemed to disappear at a line density of two lines per pitch (
Figure 10c,d). The increased performance of sub-sample interpolation might be explained by the point spread function (PSF). According to Saris et al. [
17], beam-forming to a PSF-based USGrid results in a circular cross-correlation peak which improves the performance of two-dimensional spline peak interpolation. The optimal number lines should be between two or three lines according to the point spread function for all transducers. This line-density matched the optimal density found in this study.
For all transducers except the 12L4VF transducer, apodization or angular weighting seemed to decrease or minimally affect the accuracy of axial and lateral displacement estimates (
Figure 7 and
Figure 8). Weighting and apodization increased the lateral resolution of the beam-formed data (
Appendix A), which may explain the decreased accuracy of lateral estimates. In
Appendix A, the axial and lateral resolution and contrast-to-noise-ratios (CNR) of the beam-formed data by the different beam-forming, weighting and apodization methods were evaluated. The relation between lateral resolution and displacement estimation accuracy was also described previously by Luo et al. [
16]. Since lateral and axial displacement estimation was coupled, the accuracy of lateral displacement estimates also affected the accuracy of the axial estimates. For the 12L4VF transducer, the opposite effect can be noticed in the results with and without the top left artifact (
Figure 7b,
Figure 8b and
Figure 9). The increase in performance with apodization or angular weighting may be partially explained because weighting or apodization reduced artifacts in beam-formed data caused by broken elements in the left part of the transducer footprint. As can be observed in
Figure 9, the improvement in displacement estimation accuracy by weighting was less when neglecting the artifact. Another explanation might be related to the fact that side lobes are stronger for the 12L4VF compared to the other transducers given its increased element width-to-wavelength ratio. Weighting suppresses side lobes which might also explain the improved displacement estimates despite the worse lateral resolution. In this study, a homogenous phantom was used so the effect of improved contrast (
Appendix A) by weighting might be limited and has to be further investigated in an inhomogeneous phantom or in ex vivo tissue which can also be rotated. Furthermore, Lu’s-fk performed equally or outperformed DaS with optimal line density and for all transducers. This implied that the computationally more efficient Lu’s-fk method can be used as alternative for the widely applied DaS. Furthermore, Lu’s-fk often outperformed Stolt’s-fk method probably because Lu’s-fk resulted in an improved lateral resolution in the beam-formed data (
Appendix A).