Energy-Based Design Criterion of Dissipative Bracing Systems for the Seismic Retrofit of Frame Structures
Abstract
:Featured Application
Abstract
1. Introduction
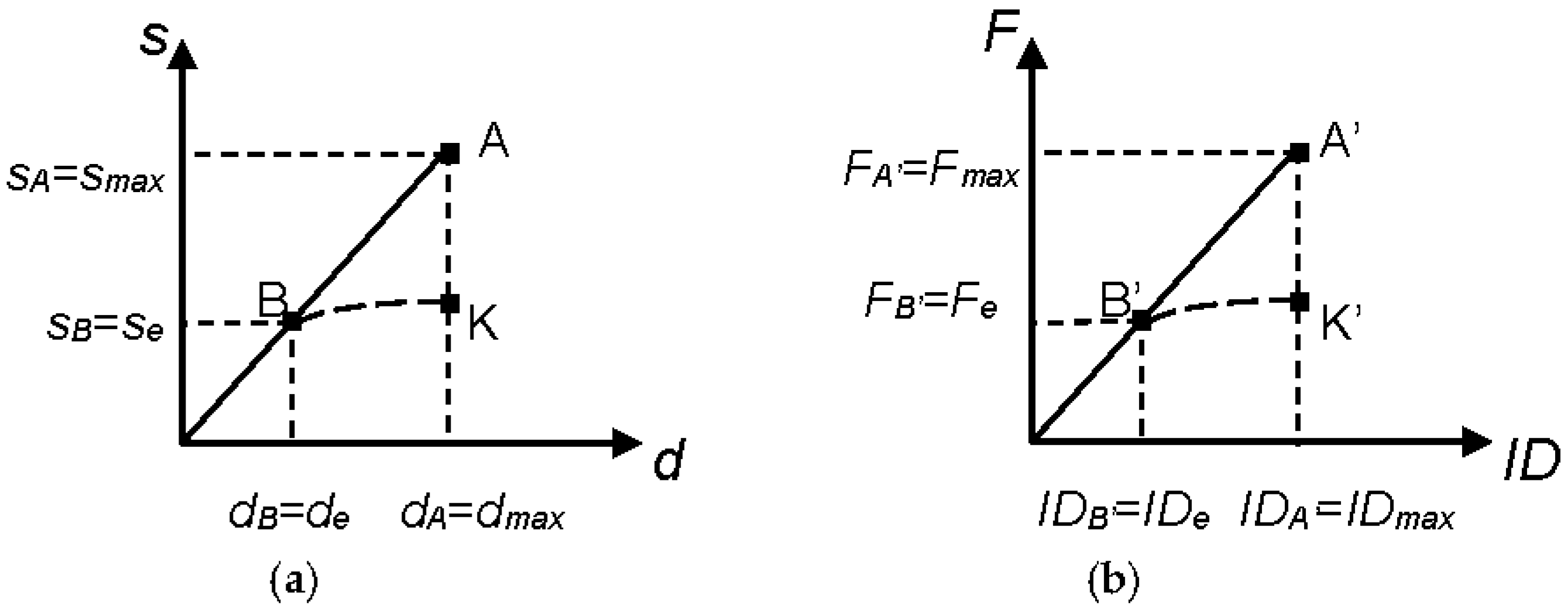
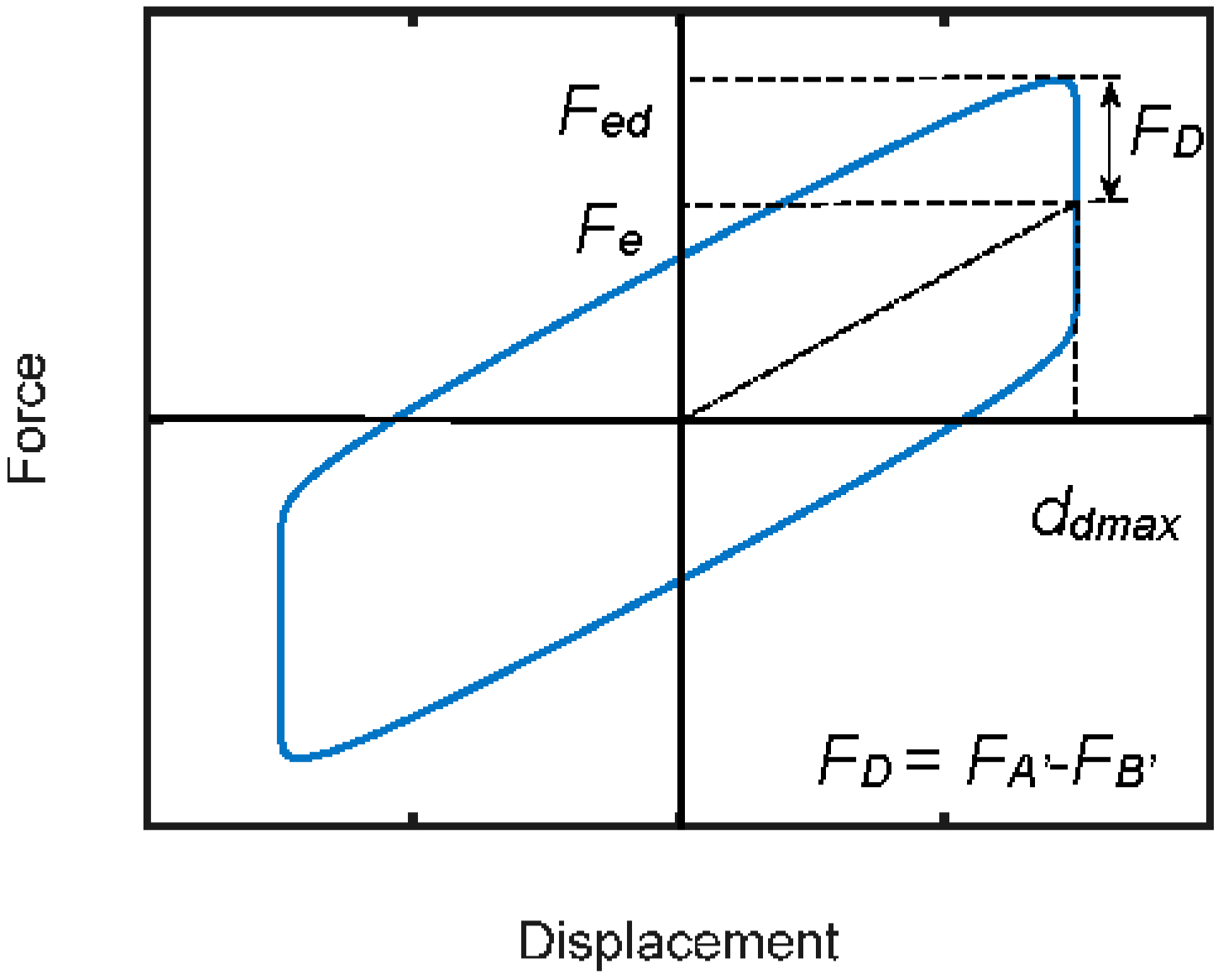
2. Design Procedure
2.1. Structures with Poor Shear or Bending Moment Strength of Constituting Members
2.2. Structures with Excessive InterStorey Drifts
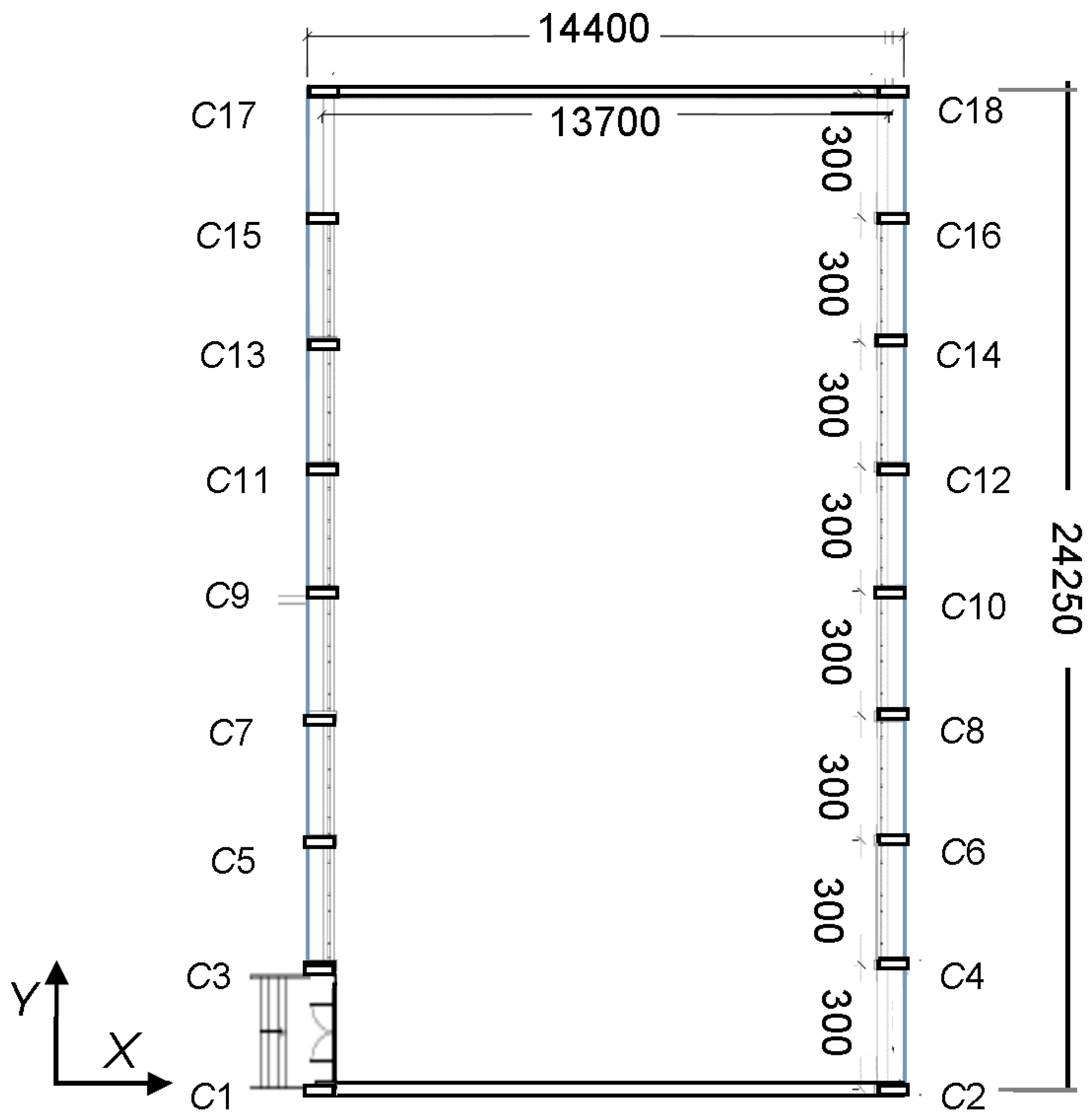
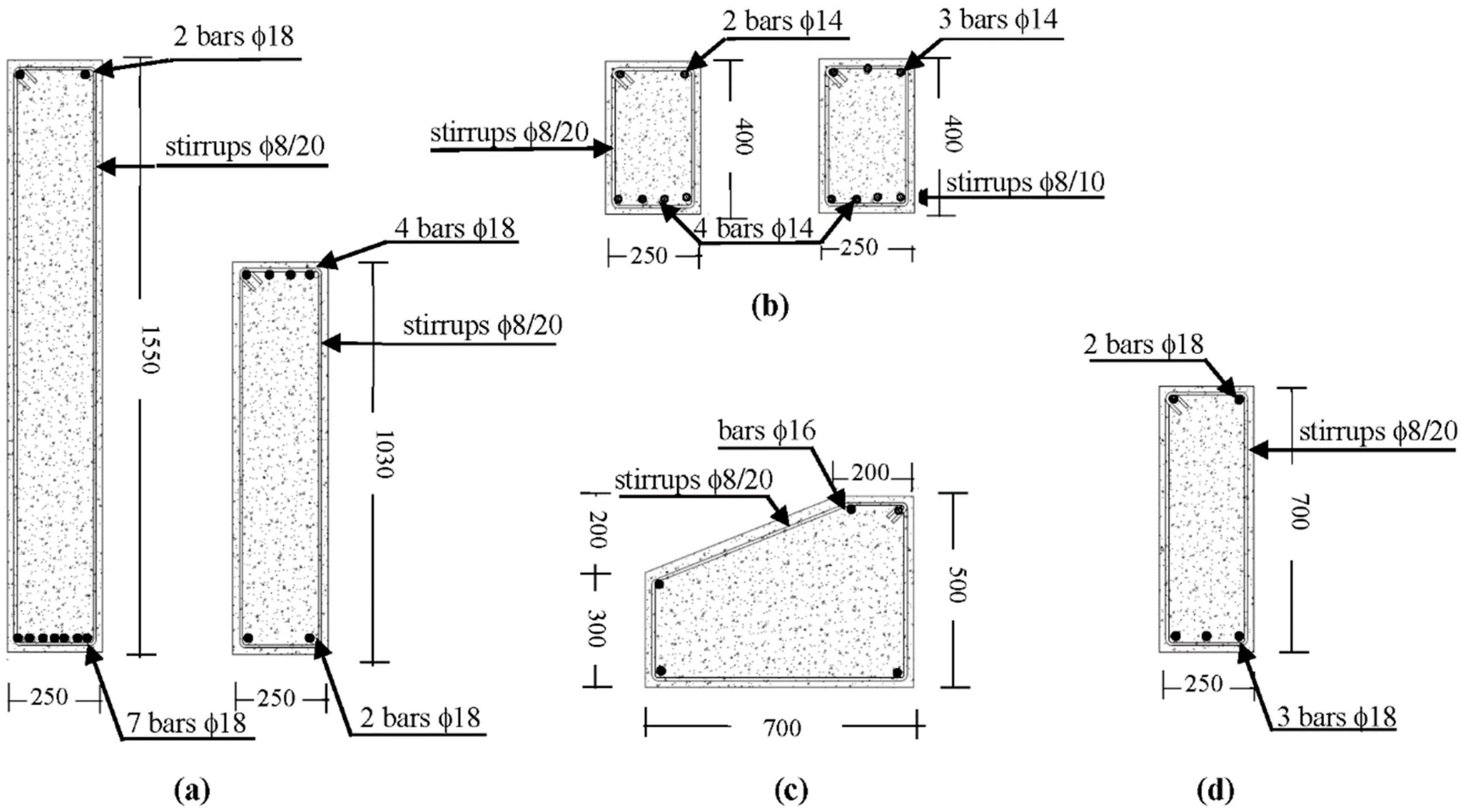
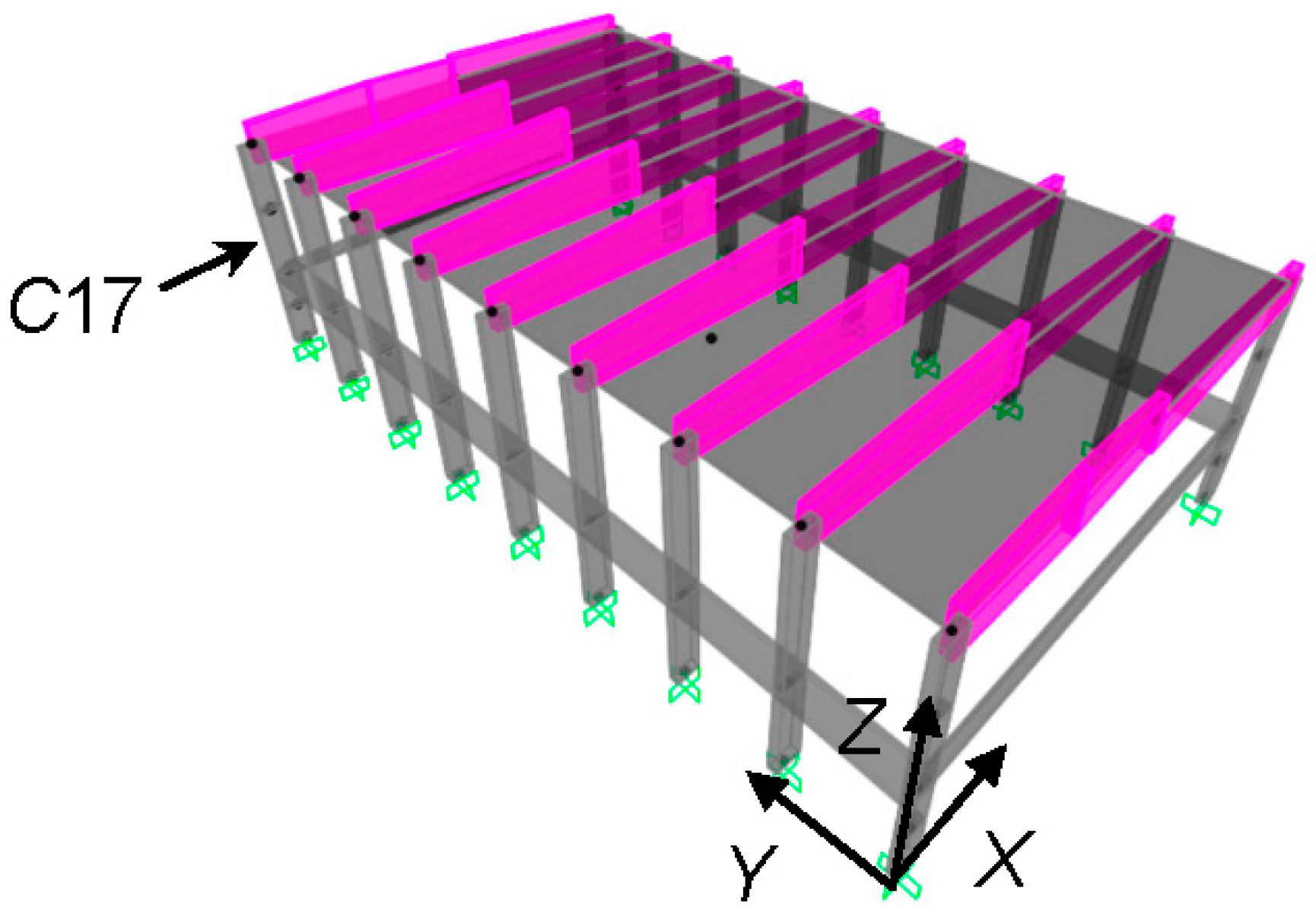
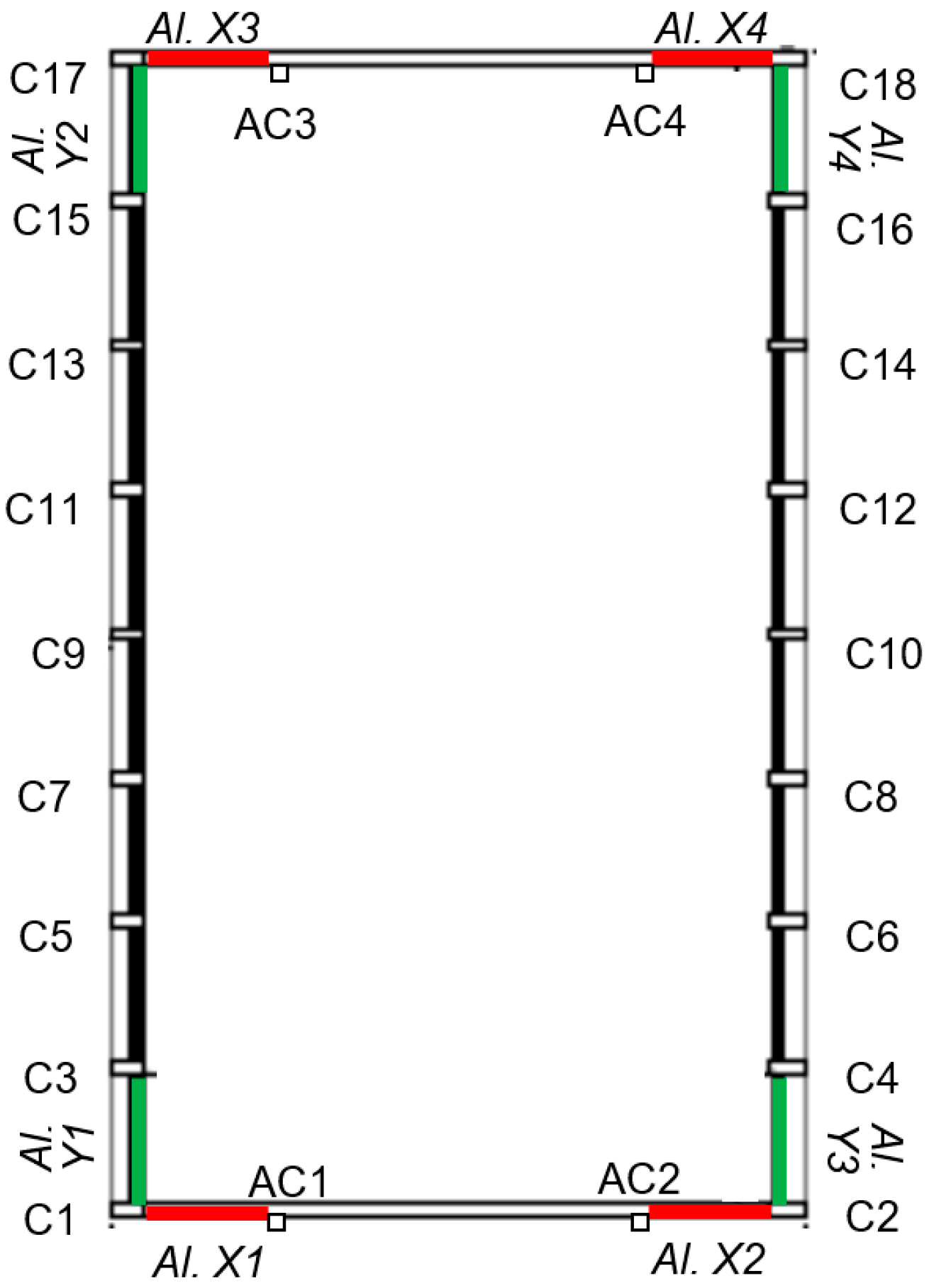
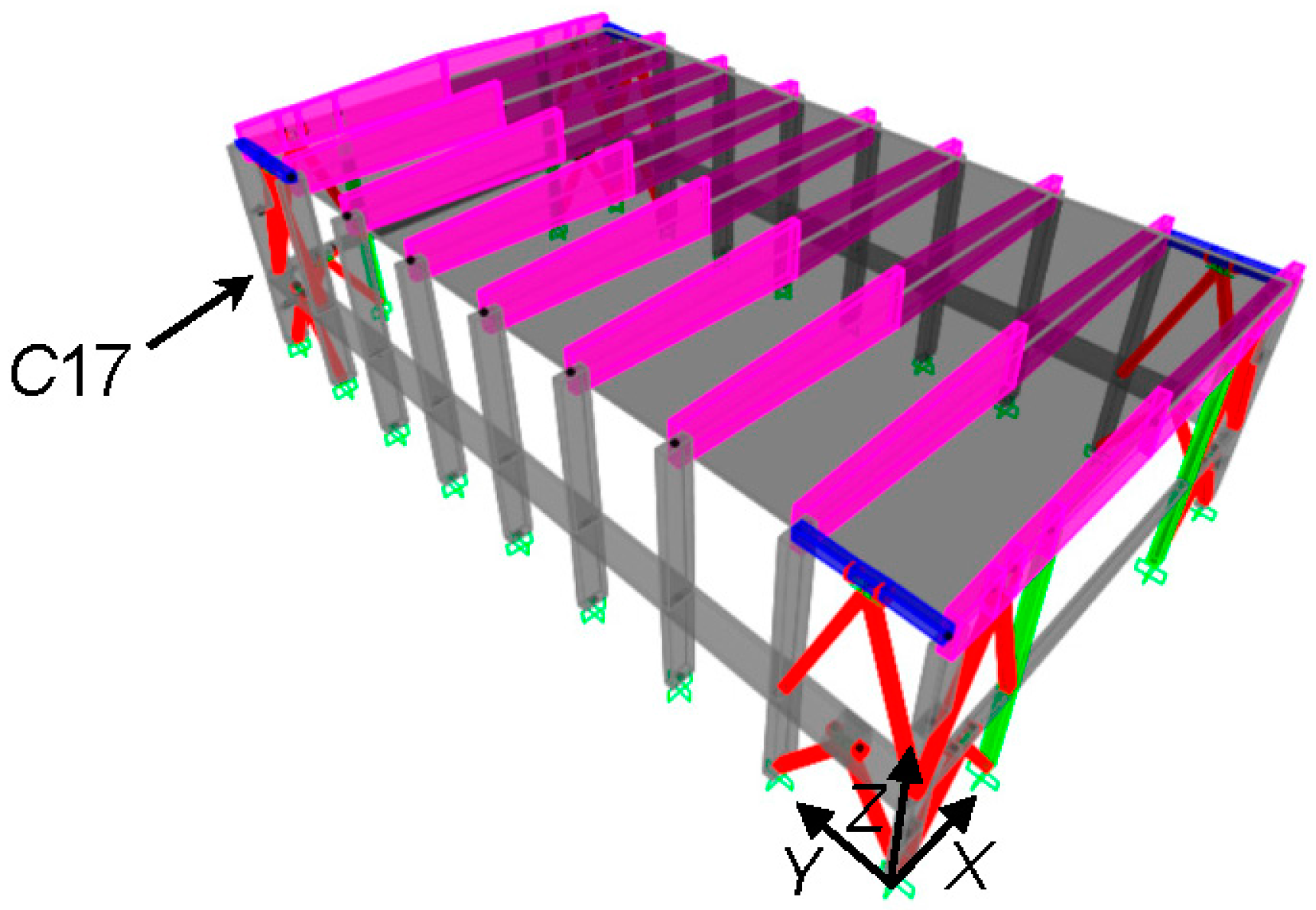
3. Geometrical and Structural Characteristics of the Case-Study Building
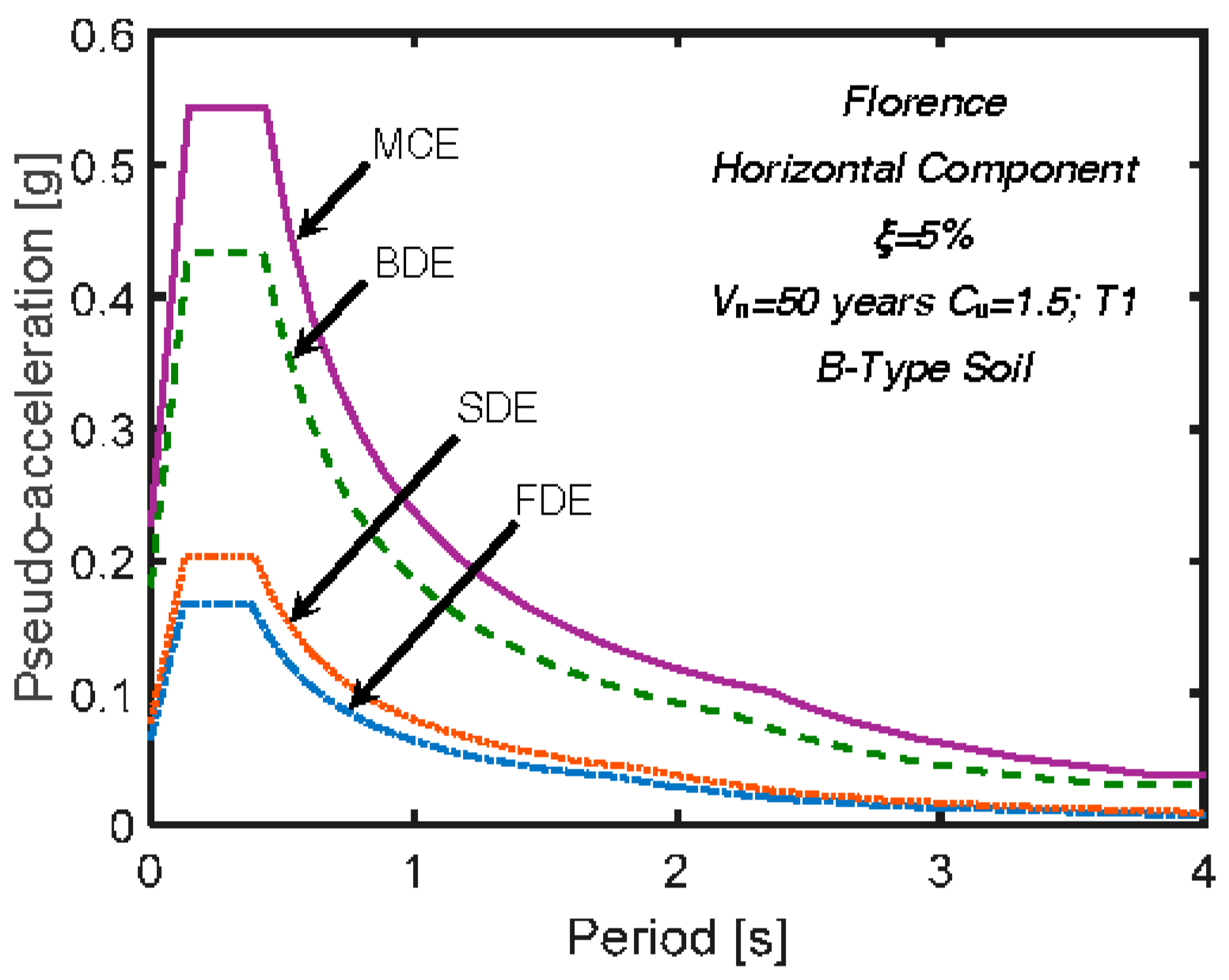
4. Verification Analysis in Current Conditions (Step 1 of the Design Procedure)
4.1. Modal Analysis
4.2. Time-History Verification and Performance Assessment Analysis
5. Dissipative Bracing Retrofit Solution
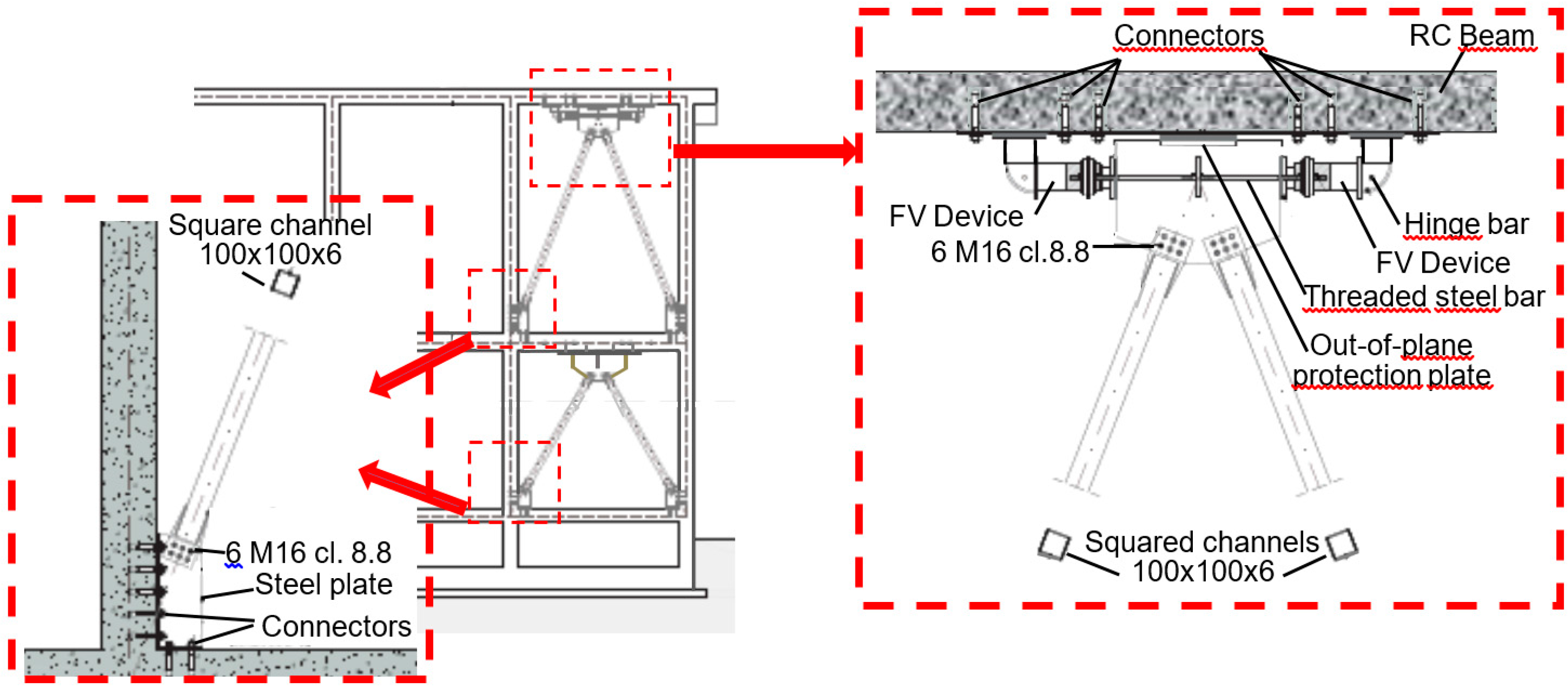
5.1. Characteristics of the Protective System
5.2. Application of the Design Method to the Case-Study Building
5.2.1. X Direction—Lack of Bending Moment Strength in the Columns
5.2.2. Y Direction—Lack of Bending Moment Strength in the Columns and Excessive Inter Level Drift
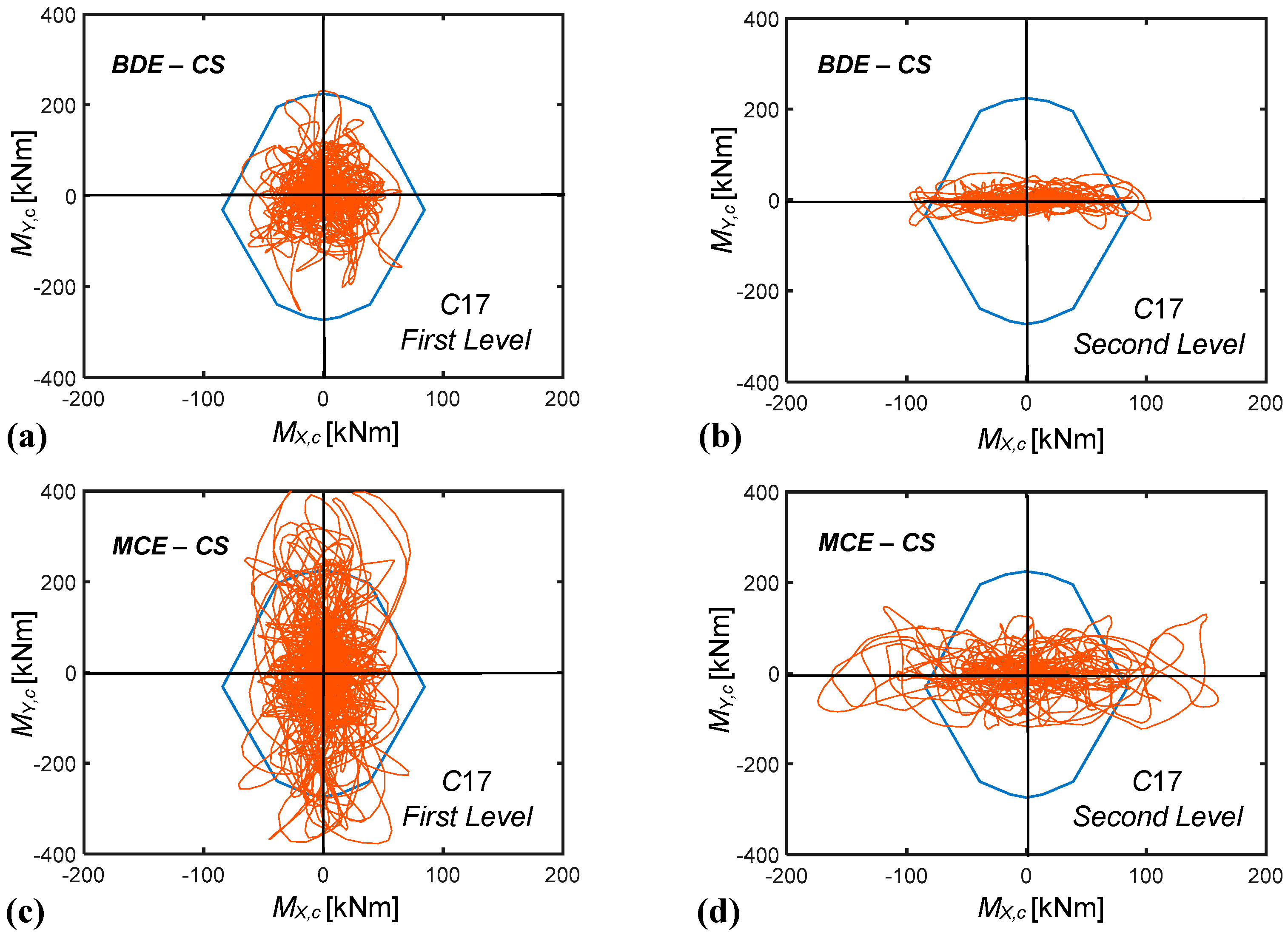
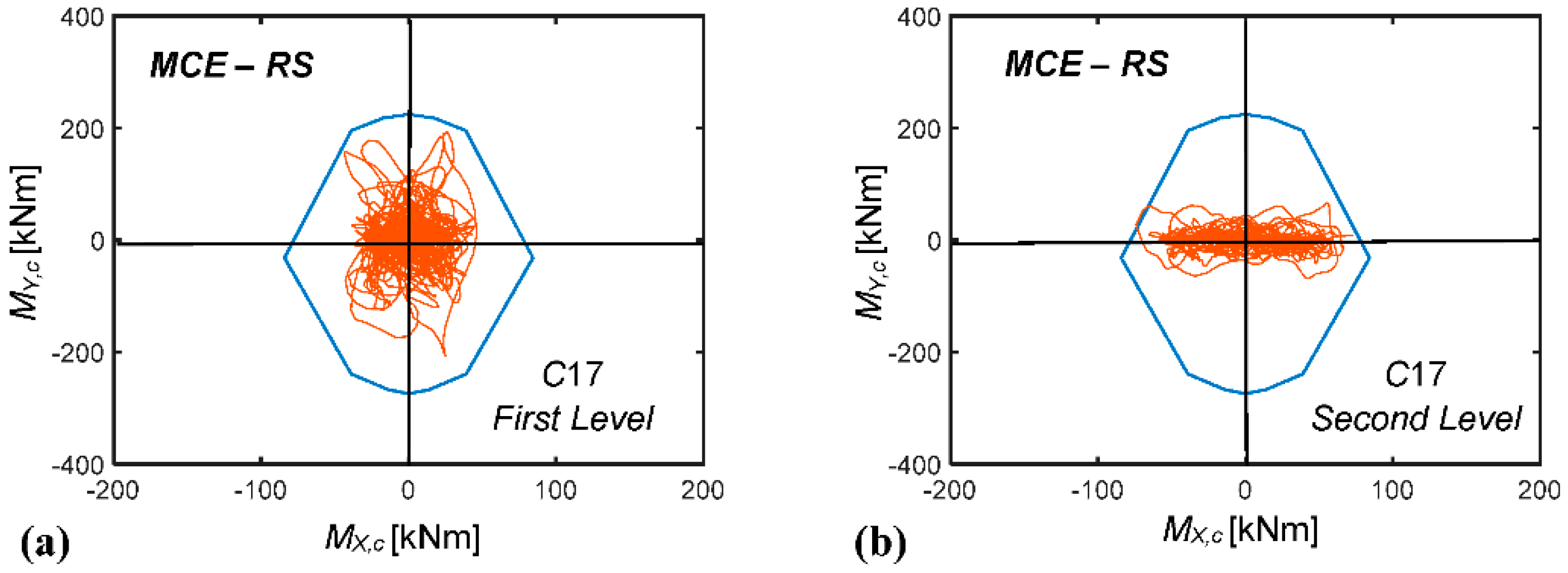
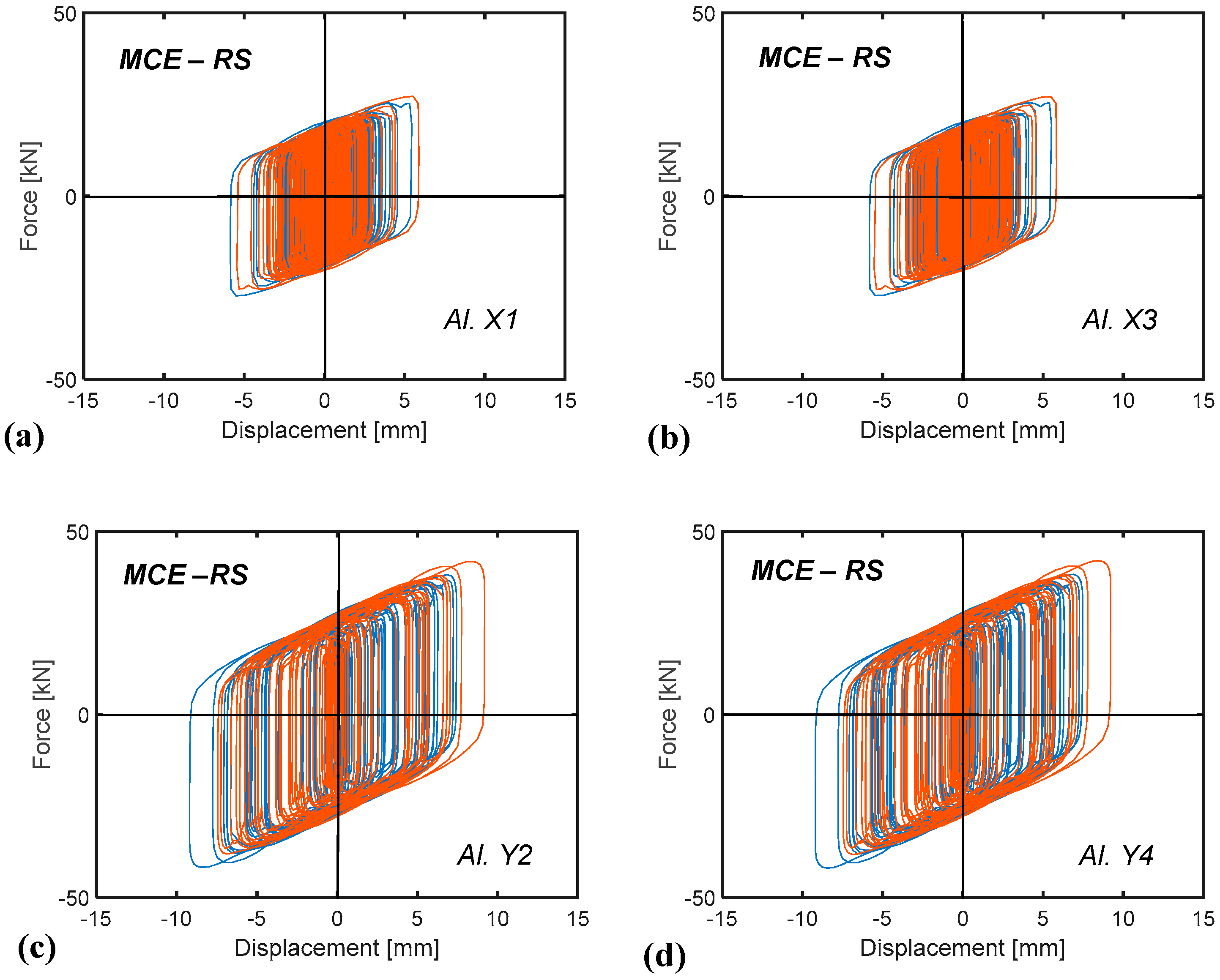
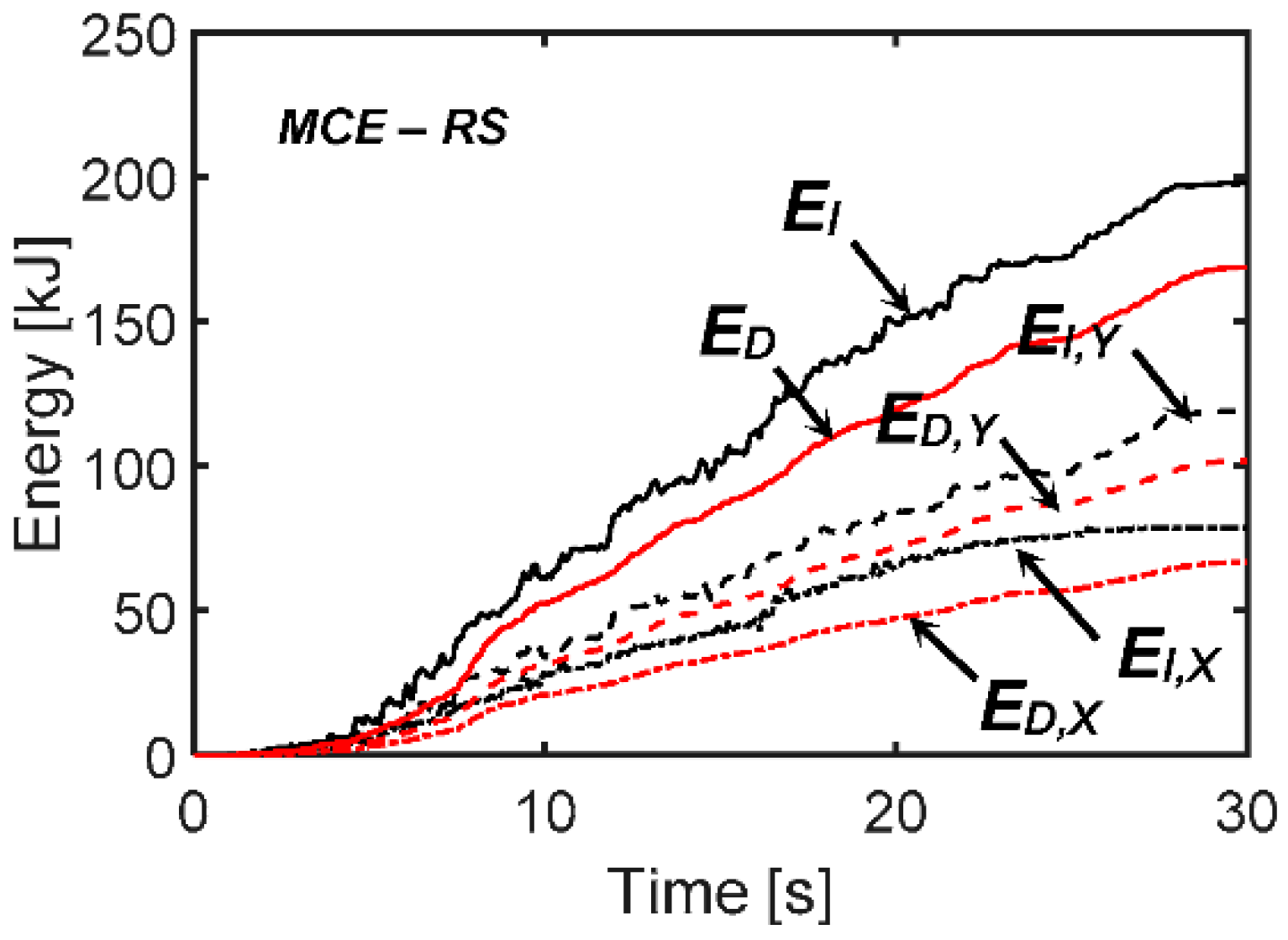
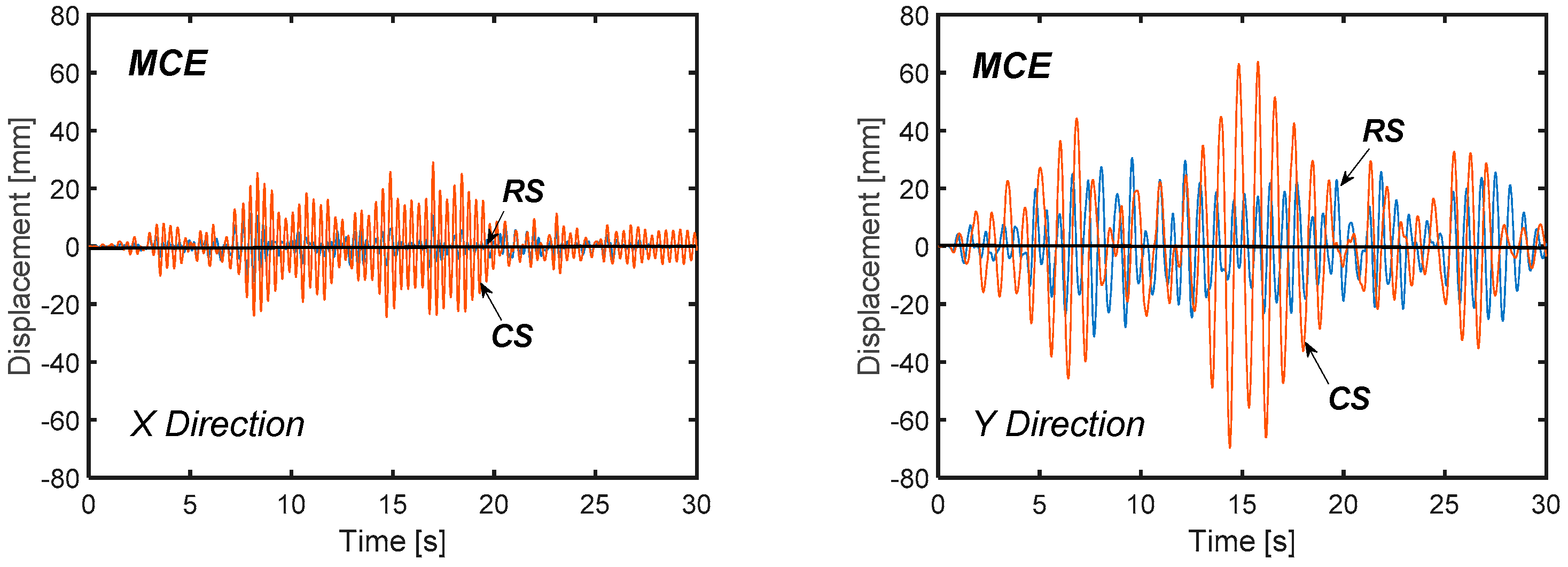
5.3. Numerical Verification of the Retrofit Solution
6. Conclusions
Acknowledgments
Conflicts of Interest
References
- Fenz, D.M.; Constantinou, M.C. Spherical sliding isolation bearings with adaptive behavior: Theory. Earthq. Eng. Struct. Dyn. 2008, 37, 163–183. [Google Scholar] [CrossRef]
- Fenz, D.M.; Constantinou, M.C. Spherical sliding isolation bearings with adaptive behavior: Experimental verification. Earthq. Eng. Struct. Dyn. 2008, 37, 185–205. [Google Scholar] [CrossRef]
- Quaglini, V.; Gandelli, E.; Dubini, P. Experimental investigation of the re-centring capability of curved surface sliders. Struct. Control Health Monit. 2017, 24. [Google Scholar] [CrossRef]
- Sorace, S.; Terenzi, G. Seismic performance assessment and base isolated floor-protection of statues exhibited in museum halls. Bull. Earthq. Eng. 2015, 13, 1873–1892. [Google Scholar] [CrossRef]
- Butterworth, J.W. Seismic response of a non-concentric rolling isolator system. Adv. Struct. Eng. 2006, 9, 39–54. [Google Scholar] [CrossRef]
- Guerreiro, L.; Azevedo, J.; Muhr, A.H. Seismic tests and numerical modeling of a rolling-ball isolation system. J. Earthq. Eng. 2007, 11, 49–66. [Google Scholar] [CrossRef]
- Foti, D.; Catalan Goni, A.; Vacca, S. On the dynamic response of rolling base isolation systems. Struct. Control Health Monit. 2013, 20, 639–648. [Google Scholar] [CrossRef]
- Mahmoudi, M.; Abdi, M.G. Evaluating response modification factors of TADAS frames. J. Constr. Steel Res. 2012, 71, 162–170. [Google Scholar] [CrossRef]
- Saeedi, F.; Shabakhty, N.; Mousavi, S.R. Seismic assessment of steel frames with triangular-plate added damping and stiffness devices. J. Constr. Steel Res. 2016, 125, 15–25. [Google Scholar] [CrossRef]
- Foti, D.; Diaferio, M.; Nobile, R. Optimal design of a new seismic passive protection device made in aluminium and steel. Int. J. Struct. Eng. Mech. 2010, 35, 119–122. [Google Scholar] [CrossRef]
- Foti, D.; Nobile, R. Optimum design of a new hysteretic dissipater. In Design Optimization of Active and Passive Structural Control Systems; Chapter 12; Lagaros, N.D., Plevris, V., Mitropoulou, C.C., Eds.; IGC Global: Hershey, PA, USA, 2012; pp. 274–299. [Google Scholar] [CrossRef]
- Sorace, S.; Terenzi, G.; Mori, C. Passive energy dissipation-based retrofit strategies for R/C frame water storage tanks. Eng. Struct. 2016, 106, 385–398. [Google Scholar] [CrossRef]
- Kang, T.H.-K.; Martin, R.D.; Park, H.-G.; Wilkerson, R.; Youssef, N. Tall building with steel plate shear walls subject to load reversal. Struct. Des. Tall Spec. Build. 2013, 22, 500–520. [Google Scholar] [CrossRef]
- Jain, S.; Rai, D.C.; Sahoo, D.R. Postyield cyclic buckling criteria for aluminum shear panels. J. Appl. Mech. Trans. ASME 2008, 75, 210151–210158. [Google Scholar] [CrossRef]
- Hamed, A.A.; Mofid, M. On the equivalent simple models of braced steel shear panels. Proc. Inst. Civil Eng. Struct. Build. 2015, 168, 570–577. [Google Scholar] [CrossRef]
- Hamed, A.A.; Mofid, M. On the experimental and numerical study of braced steel shear panels. Struct. Des. Tall Spec. Build. 2015, 24, 853–872. [Google Scholar] [CrossRef]
- De Matteis, G.; Brando, G.; Panico, S.; Mazzolani, F.M. Bracing type pure aluminium stiffened shear panels: An experimental study. Adv. Steel Constr. 2009, 5, 106–119. [Google Scholar]
- Zhang, C.; Zhu, J.; Wu, M.; Yu, J.; Zhao, J. The lightweight design of a seismic low-yield-strength steel shear panel damper. Materials 2016, 9, 424. [Google Scholar] [CrossRef] [PubMed]
- Vian, D.; Bruneau, M.; Purba, R. Special perforated steel plate shear walls with reduced beam section anchor beams. II: Analysis and design recommendations. J. Struct. Eng. 2009, 135, 221–228. [Google Scholar] [CrossRef]
- De Matteis, G.; Sarracco, G.; Brando, G. Experimental tests and optimization rules for steel perforated shear panels. J. Constr. Steel Res. 2016, 123, 41–52. [Google Scholar] [CrossRef]
- Valizadeh, H.; Sheidaii, M.; Showkati, H. Experimental investigation on cyclic behavior of perforated steel plate shear walls. J. Constr. Steel Res. 2012, 70, 308–316. [Google Scholar] [CrossRef]
- Chan, R.W.K.; Albermani, F.; Kitipornchai, S. Experimental study of perforated yielding shear panel device for passive energy dissipation. J. Constr. Steel Res. 2013, 91, 14–25. [Google Scholar] [CrossRef]
- Egorova, N.; Eatherton, M.R.; Maurya, A. Experimental study of ring-shaped steel plate shear walls. J. Constr. Steel Res. 2014, 103, 179–189. [Google Scholar] [CrossRef]
- Qu, B.; Liu, X.; Hou, H.; Qiu, C.; Hu, D. Testing of buckling-restrained braces with replaceable steel angle fuses. J. Struct. Eng. 2018, 144. [Google Scholar] [CrossRef]
- Lin, P.-C.; Tsai, K.-C.; Chang, C.-A.; Hsiao, Y.-Y.; Wu, A.-C. Seismic design and testing of buckling-restrained braces with a thin profile. Earthq. Eng. Struct. Dyn. 2016, 45, 339–358. [Google Scholar] [CrossRef]
- Deng, K.; Pan, P.; Li, W.; Xue, Y. Development of a buckling restrained shear panel damper. J. Constr. Steel Res. 2015, 106, 311–321. [Google Scholar] [CrossRef]
- Brando, G.; D’Agostino, F.; De Matteis, G. Experimental tests of a new hysteretic damper made of buckling inhibited shear panels. Mater. Struct. 2013, 46, 2121–2133. [Google Scholar] [CrossRef]
- Christopoulos, C.; Filiatrault, A. Principles of Passive Supplemental Damping and Seismic Isolation; IUSS Press: Pavia, Italy, 2006; ISBN 88-7358-037-8. [Google Scholar]
- Altieri, D.; Tubaldi, E.; Pratelli, E.; Dall’Asta, A. Assessment of optimal design methods of viscous dampers. Procedia Eng. 2017, 199, 1152–1157. [Google Scholar] [CrossRef]
- Lavan, O.; Dargush, G.F. Multi-objectve evolutionary seismic design with passive energy dissipation systems. J. Earthq. Eng. 2009, 13, 758–790. [Google Scholar] [CrossRef]
- Sorace, S.; Terenzi, G. Seismic protection of frame structures by fluid viscous damped braces. J. Struct. Eng. ASCE 2008, 134, 45–55. [Google Scholar] [CrossRef]
- Sorace, S.; Terenzi, G.; Fadi, F. Shaking table and numerical seismic performance evaluation of a fluid viscous-dissipative bracing system. Earthq. Spectra 2012, 28, 1619–1642. [Google Scholar] [CrossRef]
- Ramirez, O.M.; Costantinou, M.C.; Whittaker, A.S.; Kircher, C.A.; Chrysostomou, C.Z. Elastic and Inelastic Seismic Response of Buildings with Damping Systems. Earthq. Spectra 2002, 18, 531–547. [Google Scholar] [CrossRef]
- Soong, T.T.; Spencer, B.F. Supplemental energy dissipation: State-of-the-art and state-of-the-practice. Eng. Struct. 2002, 24, 243–259. [Google Scholar] [CrossRef]
- Whittaker, A.; Costantinou, M.; Ramirez, O.; Johnson, M.; Chrysostomou, C. Equivalent lateral force and modal analysis procedures for the 2000 NEHRP provisions for buildings with damping systems. Earthq. Spectra 2003, 19, 959–980. [Google Scholar] [CrossRef]
- ASCE/SEI 41-06. Seismic Rehabilitation of Existing Buildings; American Society of Civil Engineers—Structural Engineering Institute: Reston, VA, USA, 2006. [Google Scholar]
- ASCE 7-10. Minimum Design Loads for Buildings and Other Structures; American Society of Civil Engineers: Reston, VA, USA, 2010. [Google Scholar]
- Silvestri, S.; Gasparini, G.; Trombetti, T. A five-step procedure for the dimensioning of viscous dampers to be inserted in building structures. J. Earthq. Eng. 2010, 14, 417–447. [Google Scholar] [CrossRef]
- Palermo, M.; Muscio, M.; Silvestri, S.; Landi, L.; Trombetti, T. On the dimensioning of viscous dampers for the mitigation of the earthquake-induced effects in moment-resisting frame structures. Bull. Earthq. Eng. 2013, 11, 2429–2446. [Google Scholar] [CrossRef]
- Bergami, A.V.; Nuti, C. A design procedure of dissipative braces for seismic upgrading structures. Earthq. Struct. 2013, 4, 85–108. [Google Scholar] [CrossRef]
- Mazza, F.; Mazza, M.; Vulcano, A. Displacement-based seismic design of hysteretic damped braces for retrofitting in-elevation irregular r.c. framed structures. Soil Dyn. Earthq. Eng. 2015, 69, 115–124. [Google Scholar] [CrossRef]
- Mazza, F. Comparative study of the seismic response of RC framed buildings retrofitted using modern techniques. Earthq. Struct. 2015, 9, 29–48. [Google Scholar] [CrossRef]
- Levy, R.; Lavan, O. Fully stressed design of passive controllers in framed structures for seismic loading. Struct. Multidiscip. Optim. 2006, 32, 485–498. [Google Scholar] [CrossRef]
- Brando, G.; D’Agostino, F.; De Matteis, G. Seismic performance of MR frames protected by viscous or hysteretic dampers. Struct. Des. Tall Spec. Build. 2015, 24, 653–671. [Google Scholar] [CrossRef]
- Pollini, N.; Lavan, O.; Amir, O. Minimum-cost optimization of nonlinear fluid viscous dampers and their supporting members for seismic retrofitting. Earthq. Eng. Struct. Dyn. 2017, 46, 1941–1961. [Google Scholar] [CrossRef]
- EN 1998-4. Eurocode 8: Design of structures for earthquake resistance—Part 1: General seismic rules. In Seismic Actions and Rules for Buildings; European Committee for Standardisation: Brussels, Belgium, 2003. [Google Scholar]
- Italian Council of Public Works. Technical Standards on Constructions; Italian Council of Public Works: Rome, Italy, 2008. (In Italian) [Google Scholar]
- Jarret, S.L. Shock-Control Technologies. 2017. Available online: http://www.introini.info (accessed on 30 December 2017).
- Italian Council of Public Works. Commentary on the Technical Standards on Constructions; Italian Council of Public Works: Rome, Italy, 2009. (In Italian) [Google Scholar]
- Pieraccini, M.; Parrini, F.; Fratini, M.; Atzeni, C.; Spinelli, P.; Micheloni, M. Static and dynamic testing of bridges through microwave interferometry. NTD E Int. 2007, 40, 208–214. [Google Scholar] [CrossRef]
- Allend, D.E. Safety criteria for the evaluation of existing structures. In Proceedings of the IABSE Colloquium—Remaining Structural Capacity, Copenhagen, Denmark, 17–19 March 1993. [Google Scholar]
- SAP2000NL. Theoretical and Users’ Manual; Release 18.05; Computers & Structures Inc.: Berkeley, CA, USA, 2017. [Google Scholar]
- Vanmarcke, E.H.; Fenton, G.A.; Heredia-Zavoni, E. SIMQKE-II—Conditioned Earthquake Ground Motion Simulator: User’s Manual; Version 2.1; Princeton University: Princeton, NJ, USA, 1999; Available online: http://nisee.berkeley.edu/documents/SW/SIMQKE-II-V2-1.pdf (accessed on 23 November 2017).
- Terenzi, G. Effetti Dissipativi Nell’isolamento Sismico. Ph.D. Thesis, University of Florence, Florence, Italy, 1996. (In Italian). [Google Scholar]
- Terenzi, G. Dynamics of SDOF systems with nonlinear viscous damping. J. Eng. Mech. ASCE 1999, 125, 956–963. [Google Scholar] [CrossRef]
- Sorace, S.; Terenzi, G. Non-linear dynamic modelling and design procedure of FV spring-dampers for base isolation. Eng. Struct. 2001, 23, 1556–1567. [Google Scholar] [CrossRef]
- Sorace, S.; Terenzi, G. Motion control-based seismic retrofit solutions for a R/C school building designed with earlier Technical Standards. Bull. Earthq. Eng. 2014, 12, 2723–2744. [Google Scholar] [CrossRef]


© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Terenzi, G. Energy-Based Design Criterion of Dissipative Bracing Systems for the Seismic Retrofit of Frame Structures. Appl. Sci. 2018, 8, 268. https://doi.org/10.3390/app8020268
Terenzi G. Energy-Based Design Criterion of Dissipative Bracing Systems for the Seismic Retrofit of Frame Structures. Applied Sciences. 2018; 8(2):268. https://doi.org/10.3390/app8020268
Chicago/Turabian StyleTerenzi, Gloria. 2018. "Energy-Based Design Criterion of Dissipative Bracing Systems for the Seismic Retrofit of Frame Structures" Applied Sciences 8, no. 2: 268. https://doi.org/10.3390/app8020268
APA StyleTerenzi, G. (2018). Energy-Based Design Criterion of Dissipative Bracing Systems for the Seismic Retrofit of Frame Structures. Applied Sciences, 8(2), 268. https://doi.org/10.3390/app8020268




