1. Introduction
Comminution and especially grinding is one of the most important operations of the materials processing industry. For many decades, it has been the subject of intensive research in several industrial sectors including mineral processing [
1,
2], metallurgy [
3], cement, chemicals and ceramics production [
4,
5]. In addition, interest has been paid in recent years on the production of ultra-fine materials due to their improved physical and mechanical properties [
6]. It is also known that comminution is an energy intensive process and has low efficiency, due to the fact that most energy consumed is absorbed by the device and only a small share is used for size reduction [
7]. Considering these factors, it is deduced that improvement of process efficiency will definitely have a large impact on the operating cost of the mill, the environment and the conservation of resources.
Scientific research, aiming to improve grinding efficiency, was initiated with the empirical relationships of Rittinger, Kick, Bond as well as Walker and Shaw, which described the energy-particle size relationship [
8]. Later, theories which incorporated the concept of particle size distribution were developed [
9,
10], while recently research focused on the use of the mechanistic approach which is based on the recognition of physical events that take place during grinding [
11,
12,
13]. The mechanistic approach includes the matrix model, which considers grinding as a series of breakage events and the population balance model, which considers grinding as a continuous process. The population balance model considers first order kinetics and uses two functions, namely the breakage rate
Si and the breakage function
bi,j [
14,
15]. These functions generate the fundamental size-mass balance equation which is applied for fully mixed batch grinding operations. It is mentioned that many researchers have underlined the advantages of these functions [
16,
17], while the scale-up from laboratory to industrial mills has also been discussed in a number of studies [
18,
19,
20,
21].
The variation of breakage rate
Si (min
−1) as a function of particle size
xi (mm) has been considered by Austin [
15] and is expressed with Equation (1), which is accepted by many researchers [
22,
23,
24].
where,
xi (mm) is the upper size of class
i,
x0 is the standard size (1 mm),
αT (parameter that depends on milling conditions) is the breakage rate for size
xi = 1 mm and
α is a characteristic parameter depending on material properties.
Qi is a correction factor, which is 1 for small particles (normal breakage) and smaller than one for large particles that need to be nipped and fractured by the grinding media. In the abnormal breakage region, the material behaves as it consists of a soft and a harder fraction [
16].
Qi is calculated from Equation (2) [
15],
where,
µ is a parameter that depends on milling conditions and
Λ is a positive number that depends on material type and shows how rapidly the breakage rate decreases as size increases (
Λ ≥ 0). In addition, the particle size
xm for which the breakage rate reaches its maximum value is related with parameter
µ through the following equation [
25,
26],
Equation (3) shows that xm is directly proportional to μ since for the same material α and Λ are constants.
The physical and mechanical properties of a material play a crucial role in the design of a mineral processing circuit. The reliable determination of these properties enables the prediction of milling results and in this case no extensive milling tests that require large amounts of time and material are needed [
27]. In this respect, several researchers [
28,
29,
30,
31,
32,
33,
34,
35,
36] have attempted to identify the relationship between various material properties and P-wave velocity. These studies indicated that sound velocity is closely related to physico-mechanical properties such as uniaxial compressive strength, modulus of elasticity, hardness, effective porosity, water absorption and both saturated and dry density. P-wave velocity test is non-destructive, offers several advantages to researchers and can be easily applied both in laboratory and in situ. It is mentioned that P-wave velocity is related with the characteristics of the whole body of the material tested [
29].
The Schmidt hammer test is equally acceptable and used for estimating indirectly material hardness and strength, through the determined
RL value, which depends on the properties of the specimen. The operation of the device is based on the principle that the rebound of an elastic mass impacting on a surface depends on its hardness and thus the harder the surface the higher is the rebound distance [
37]. Several societies, including the International Society for Rock Mechanics [
38,
39] and the American Society for Testing and Materials [
40], have proposed test methods and standards, respectively, for the proper operation of the device [
41]. Other options for determining such material properties with the use of the Schmidt hammer have also been proposed [
42,
43,
44].
Breakage rate parameters depend on material properties, so it is very useful and practical from a laboratory and industrial point of view if correlations between them are established. In this regard, Deniz [
45] used limestone as test material and identified the relationship between Bond’s grindability and breakage rate parameters, while Aras [
46] established important correlations between the point load index and Bond’s grindability as well as breakage rate parameters. However, so far no correlations between other material properties such as uniaxial compressive strength or modulus of elasticity and breakage rate parameters have been established.
This study has a certain degree of novelty since it attempts to establish potential correlations between material properties derived from the application of destructive and non-destructive tests, and breakage rate parameters.
2. Materials and Methods
The materials used in the present experimental study were obtained from several Greek sites, namely quartz from Assiros, near Thessaloniki; marble from west Crete, Chania region; and quartzite and metasandstone from west Crete, Kissamos area. More than 100 kg of each material was sampled from several locations of the same site in order to obtain representative samples. Mineralogical analyses show that marble consists mainly of calcite, while quartzite and metasandstone of quartz and some mica. The quartz samples used in this study were of high purity white quartz. The main difference between quartzite and metasandstone is the degree of transformation. Quartzite, due to dynamic re-crystallization, consists of fine crystalline and elongated quartz grains, which are well oriented; due to the mechanical strain imposed, individual quartz crystals are present. However, metasandstone consists of a fine crystalline matrix with individual quartz crystals, which exhibit lack of orientation due to the lower degree of transformation compared to quartzite. In addition, large gaps are observed between its grains due to the high porosity.
Table 1 presents the porosity and density of each raw material, as determined with the use of Archimedes method [
47]; all measurements were carried out in triplicate and average values are shown. The standard deviation of porosity and density was 0.002 and 0.005 respectively, for all materials tested.
Cylindrical cores of representative samples with NX size (diameter 54.7 mm) were used to determine the physico-mechanical properties of each material. Both ends of the core specimens were cut flat and polished using a cut-off and a special polishing machine, respectively. The height to diameter ratio of all specimens was kept equal to 2 in order to minimize the size effect. From each material type 6–8 specimens were cored (
Figure 1a,b). Specimens exhibiting cracks, discontinuities, or alteration phenomena as a result of coring were not used in tests and replaced with new specimens.
In this study, the non-destructive P-wave velocity and Schmidt hammer rebound tests were carried out. The P-wave velocity test was performed using the PUNDIT 6 (Portable Ultrasonic Non-destructive Digital Indicating Tester) device (CNS Farnell, London, UK) at a frequency of 1 MHz. According to the procedure, two transducers were placed opposite the two parallel surfaces of the core samples (
Figure 2a,b) and the travel time of the ultrasonic waves, from one transducer to the other, was recorded. By taking into account that the distance between the two surfaces of each specimen is known, the velocity of the ultrasonic waves can be calculated [
48]. It is known that the ultrasonic velocity depends on density and the elastic properties of each material and is higher when the sample has adequate density, uniformity and homogeneity [
49].
The Schmidt hammer rebound test was performed using an L-type hammer with impact energy 0.735 Nm. Core specimens were tested in a V-shaped cradle block with an approximate weight of 23 kg. Prior to test execution the circular ends of each specimen were divided into eight equal arcs, from the ends of which eight straight parallel lines along their longitudinal axis were drawn (
Figure 3). The test was performed by placing the core specimens in the cradle and impacting the hammer vertically along the drawn lines, starting from line No1 (
Figure 4). In this manner, five individual impacts were conducted at equal spacing and consequently five rebound values
RL were recorded along the first line drawn. Then, the same procedure was repeated by rotating the specimen 45°. In total, depending on the number of the specimens used, 40 rebound values for each specimen and 240 or 280 for each material were recorded. The rebound values given in this study for each material are the average of all recorded values.
After the execution of non-destructive tests, the cylindrical specimens were used for the determination of their uniaxial compressive strength (
UCS) and tangent modulus of elasticity (
Et). The uniaxial compression tests were performed using a 1600 KN hydraulic device, manufactured by MTS (Mechanical Testing System) corporation (Kalamazoo, MI, USA). According to the procedure, the cylindrical specimens were subjected to a load acting on both ends (
Figure 5a), using a loading rate 0.01 mm/s under displacement control mode; the failure of specimens occurred in less than 5 min. The peak stress value and the tangent modulus of elasticity of each specimen were calculated from the complete stress-strain curve (
Figure 5b).
For the determination of the breakage rate parameters, experiments were performed in a laboratory-scale ball mill with a volume of 5423 cm
3 (
Table 2) operating at a constant speed of
Ν = 66 rpm (1.1 Hz), which is 70% of its critical speed. The core samples as well as other materials with the same properties (porosity, density, mineralogy etc.) were crushed and prepared for the grinding tests. The mill charge consisted of 25.4 mm (1 inch) stainless steel balls with density
ρb = 7.85 g/cm
3. The parameters
J (ball filling volume) and
fc (material filling volume), were calculated from Equations (4) and (5), respectively.
where,
ε is the bed porosity of balls and material (assumed to be 40%) [
15].
The material filling volume
fc was kept constant at 4%, corresponding to 345.0 g, 351.5 g, 342.5 g and 273.3 g of quartz, marble, quartzite and metasandstone, respectively. The fraction of the space between the balls at rest that is filled with material (interstitial filling,
U) was calculated from Equation (6); in this study,
U was kept constant at 0.5.
Four mono-size fractions of each material (−3.35 + 2.36 mm), (−1.7 + 1.18 mm), (−0.850 + 0.600 mm) and (−0.425 + 0.300 mm) were ground in a laboratory ball mill for various grinding times
t (0.5, 1, 2, 4 min). The products obtained after each grinding time
t were wet sieved using a series of screens with a ratio of
for the determination of particle size distribution. It should be noted that fresh feed was used in each test and the mill was loaded using successive layers of balls and feed [
50].
4. Conclusions
In this study, the correlation between the properties of four materials, namely quartz, marble, quartzite and metasandstone, and breakage rate parameters have been established. The properties of the materials that were taken into account were P-wave velocity, Schmidt rebound values, uniaxial compressive strength and tangent modulus of elasticity. The breakage rate parameters that were determined through batch grinding experiments were breakage rate Si, parameter αT, parameter α, maximum breakage rate Sm and optimum particle size xm. The results can be summarized as follows:
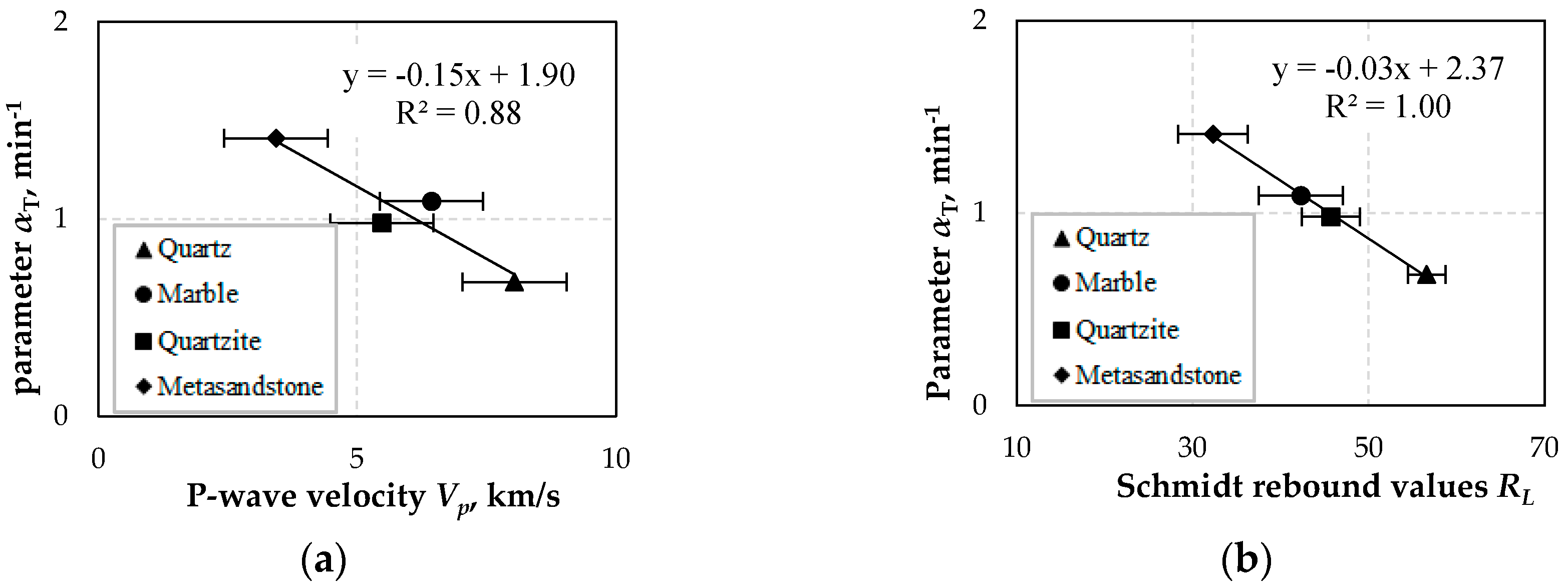
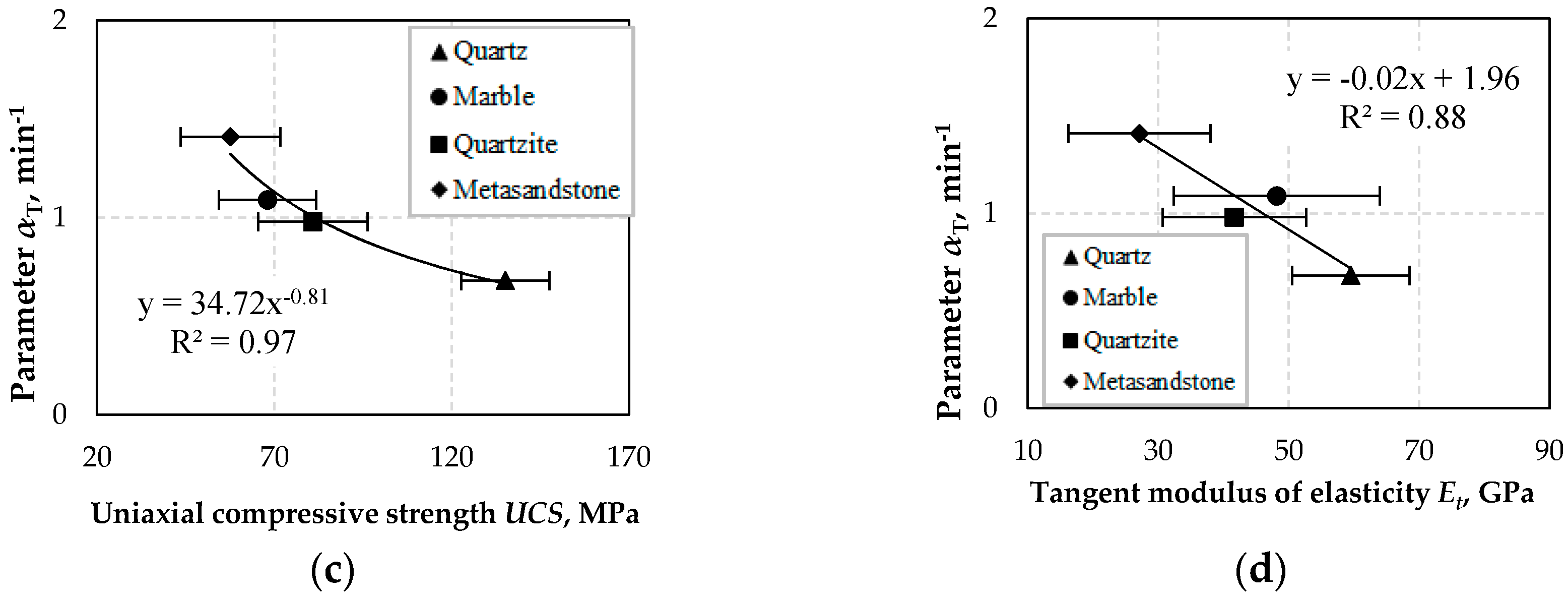
Breakage rate Si or parameter αΤ increase with decreasing uniaxial compressive strength (UCS) and tangent modulus of elasticity (Et). Therefore, it is deduced that as the strength or stiffness of a material is reduced this will be ground faster in a mill. Similar results can be obtained from the P-wave velocity (Vp) and Schmidt rebound values (RL), which are widely considered for the indirect estimation of material’s hardness and strength. The properties of the tested materials can be used for an accurate prediction of Si or αΤ of the ground materials since the obtained correlation coefficients are high.
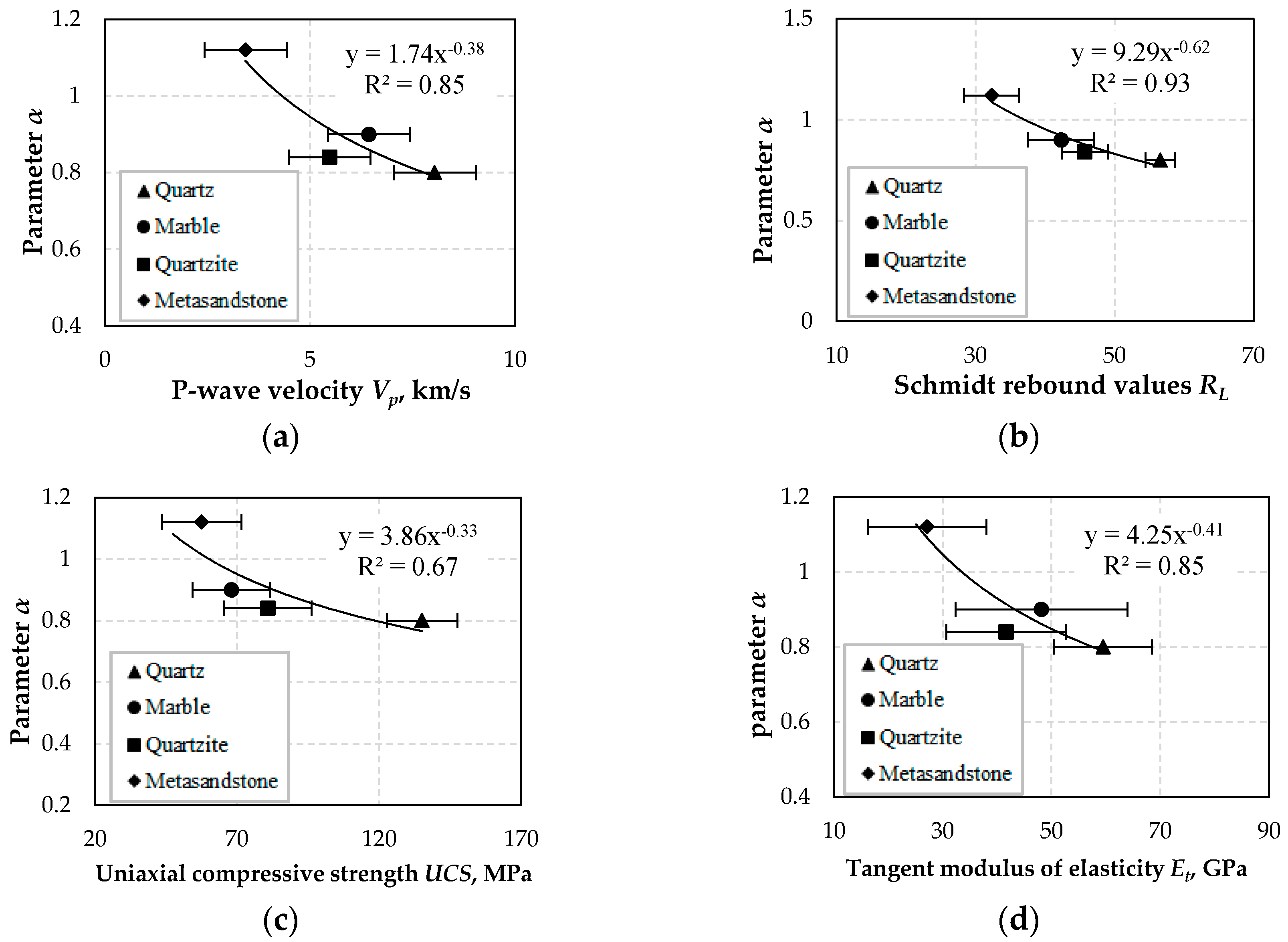
Parameter α which is constant for the same material and independent of grinding conditions is well correlated with Vp, RL and Et when inverse exponential functions are used. However, the results showed that α has a moderate correlation with UCS (R2 = 0.67) and therefore the results of the functions derived are not very reliable.
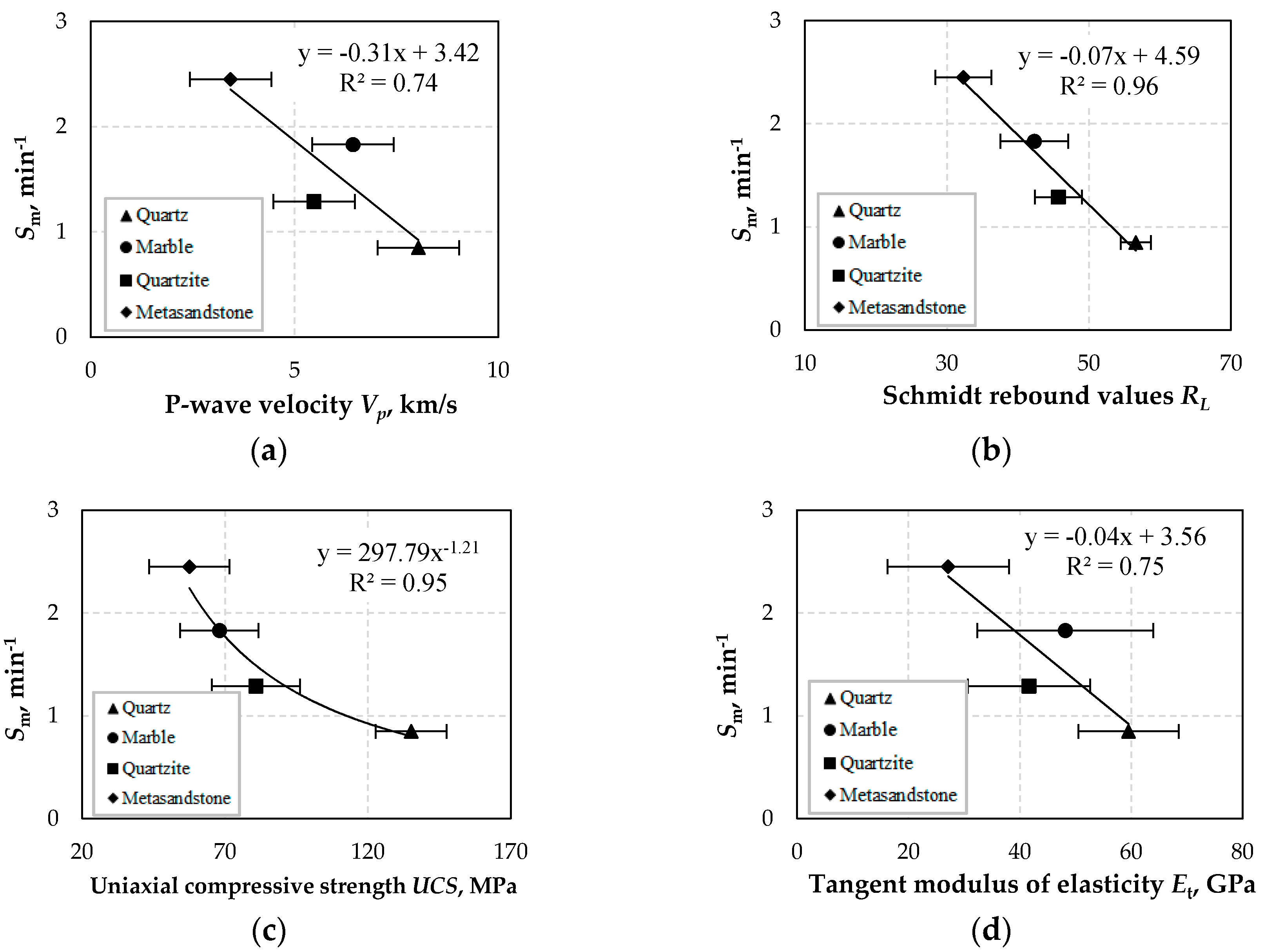
Maximum breakage rate Sm is strongly correlated with RL and UCS using inverse functions and therefore either RL or UCS values can be used to predict the maximum breakage rate of each tested material during grinding. However, the prediction of Sm from Vp or Et is not fully reliable due to the moderate correlations between these parameters.
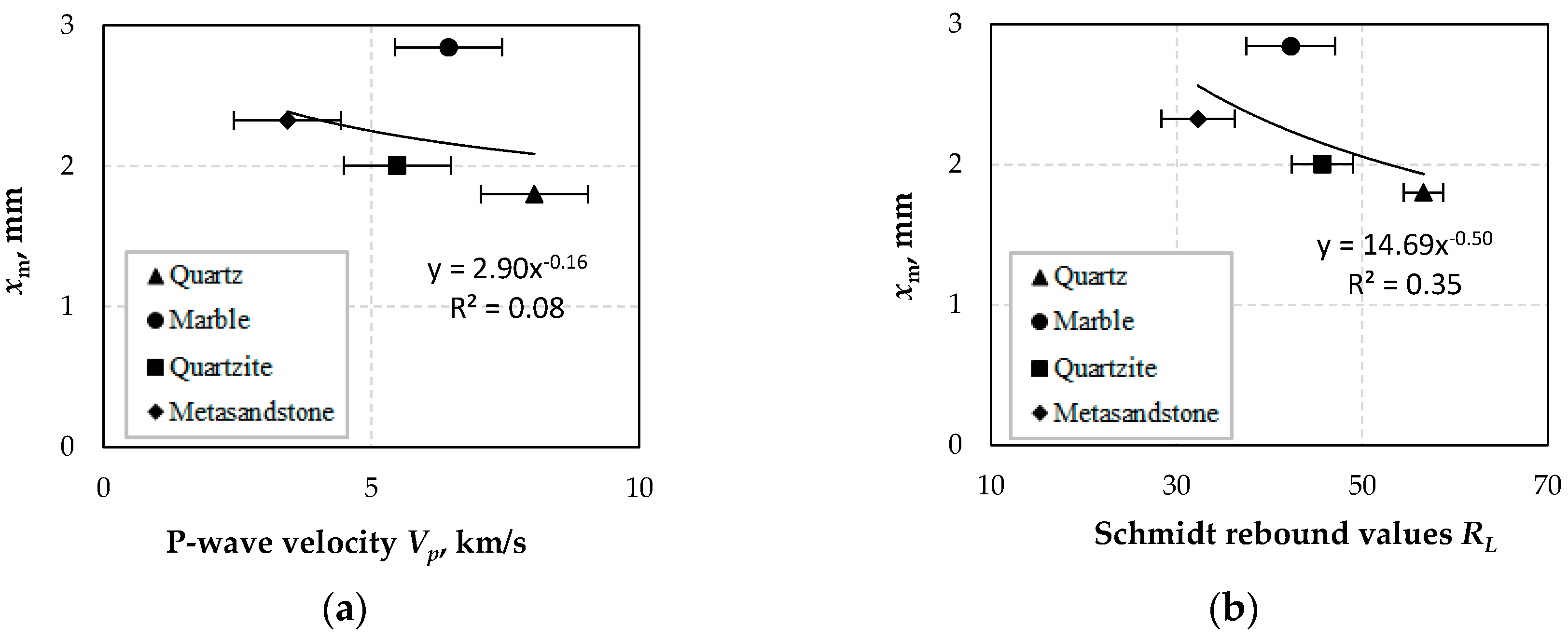
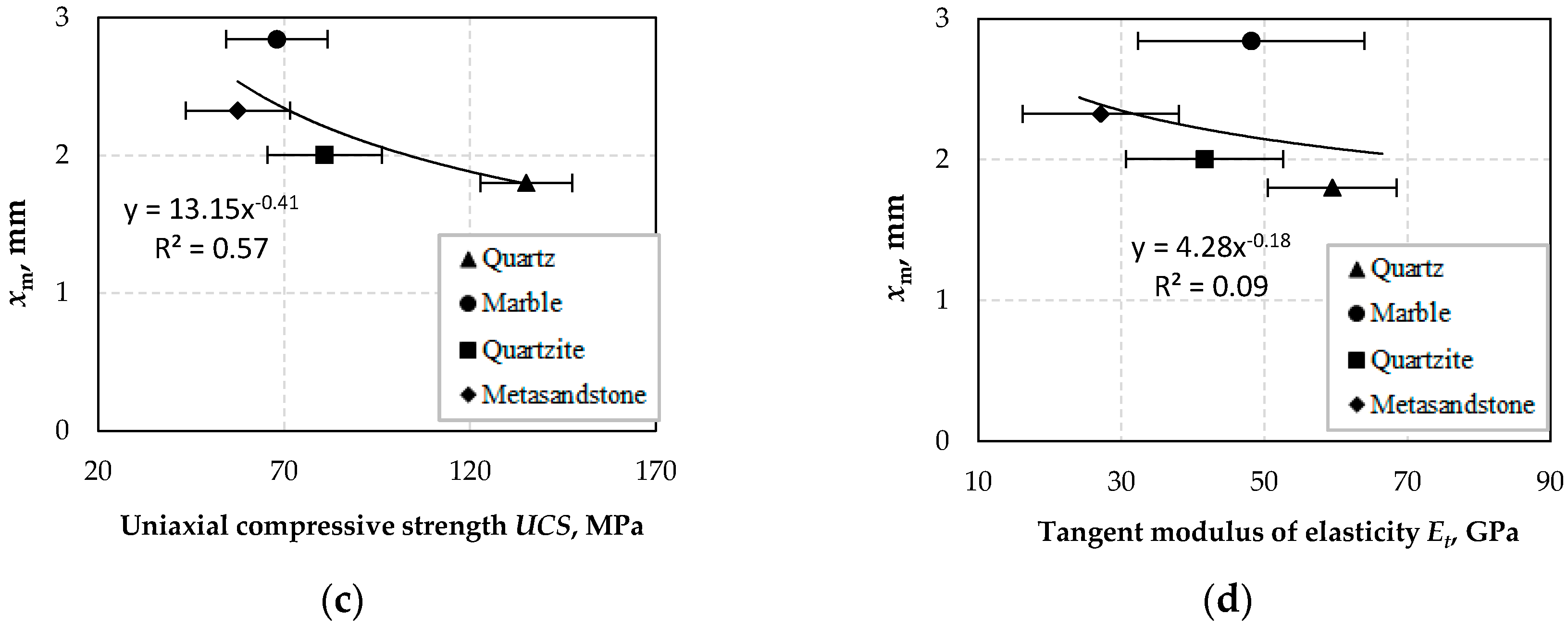
As far as optimum size xm is concerned, the results showed that optimum size xm increases with decreasing P-wave velocity, Schmidt rebound value, uniaxial compressive strength and tangent modulus of elasticity. However, marble seems to deviate from this tendency and further research is required, by considering its properties and other aspects including the presence of twinning planes and the production of ultra-fine material during grinding, to elucidate its behavior. It is mentioned that the behavior of mixed materials and the effect of each material type on the overall breakage rate is now under investigation.