Control Requirements for Future Gas Turbine-Powered Unmanned Drones: JetQuads
Abstract
:1. Introduction
- The energy density measures energy storage in a unit mass. The JetQuad uses diesel fuel with an energy density of 40 MJ/kg, whereas electrical drones use solid lithium-based batteries that at most have an energy density of 1 MJ/kg. Thus, for the same on-board mass of fuel (or battery) storage, the JetQuad stores 40 times more energy than the equivalent electrical drone. Although jet engines are heavier than electrical motors, they have much higher power-to-weight ratios, so this penalty is insignificant. The U.S. Department of Energy (DOE) has recently initiated a five-year research project to develop next-generation battery technology. The DOE targets an energy density achievement of 3 MJ/kg energy density. This is still 1/10 of the energy density of diesel. As a result, the JetQuad will remain competitive for many years to come [13].
- The power-to-weight ratio determines how much power a given engine outputs for a given mass of that engine. Electrical drones have a large penalty in this regard. A brushless electrical motor, on its own, has a very large power-to-weight ratio. However, when added to the weight of propeller, electronic speed controllers, and batteries, this ratio is greatly decreased. Turbine-based engines, such as jet engines, do not suffer from this problem. More specifically, the JetQuad uses microturbines that have an ultrahigh rotation rate and lead to vast amounts of power produced from a small engine. In addition, electrical drones must limit current flow to prevent the overheating of electronics that support smooth motor operation. In contrast, fuel flow rate is the limiting factor for turbine-based engines. It gives jet-engine designers the flexibility to extract much more power from smaller motors [13].
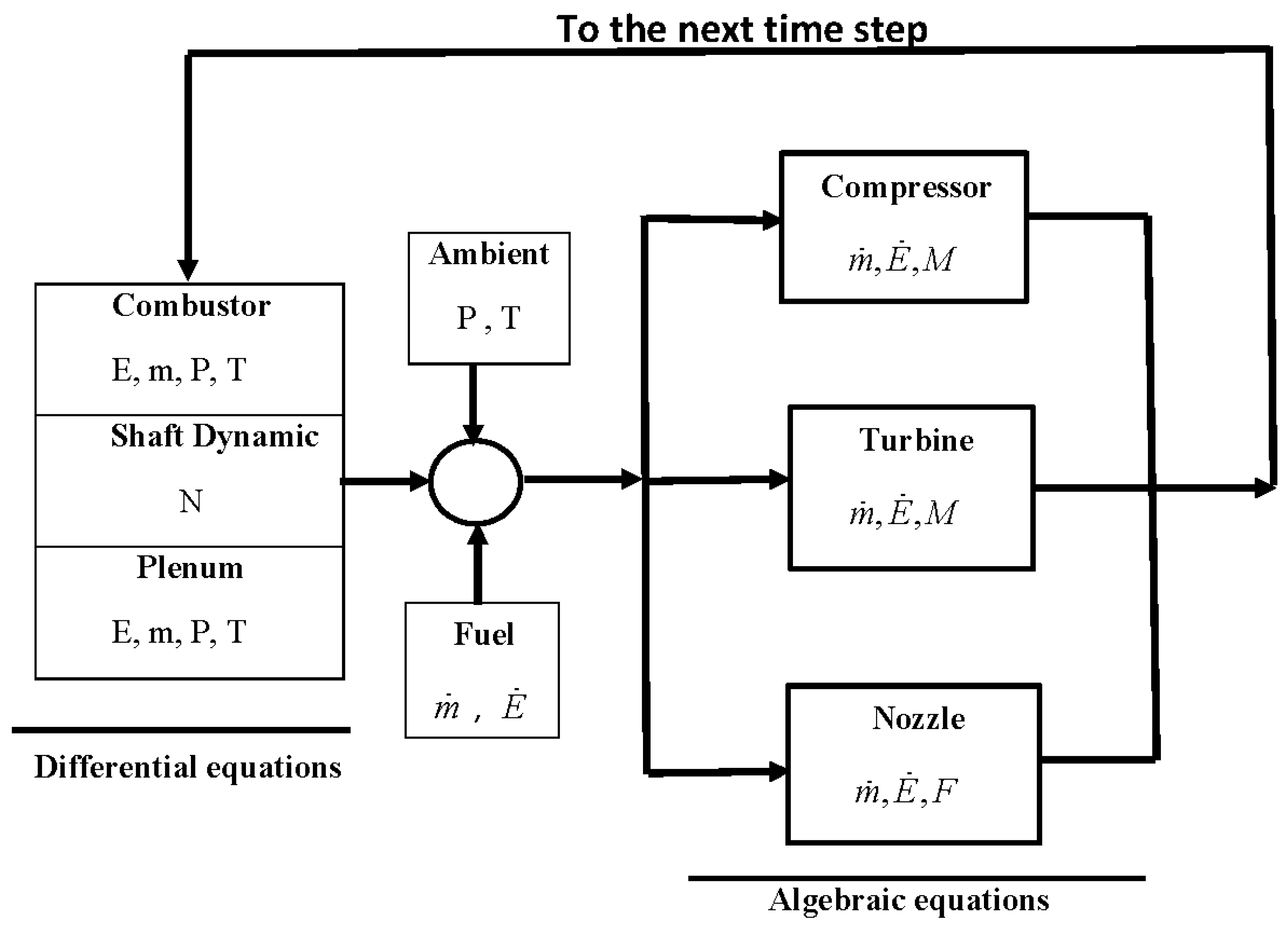
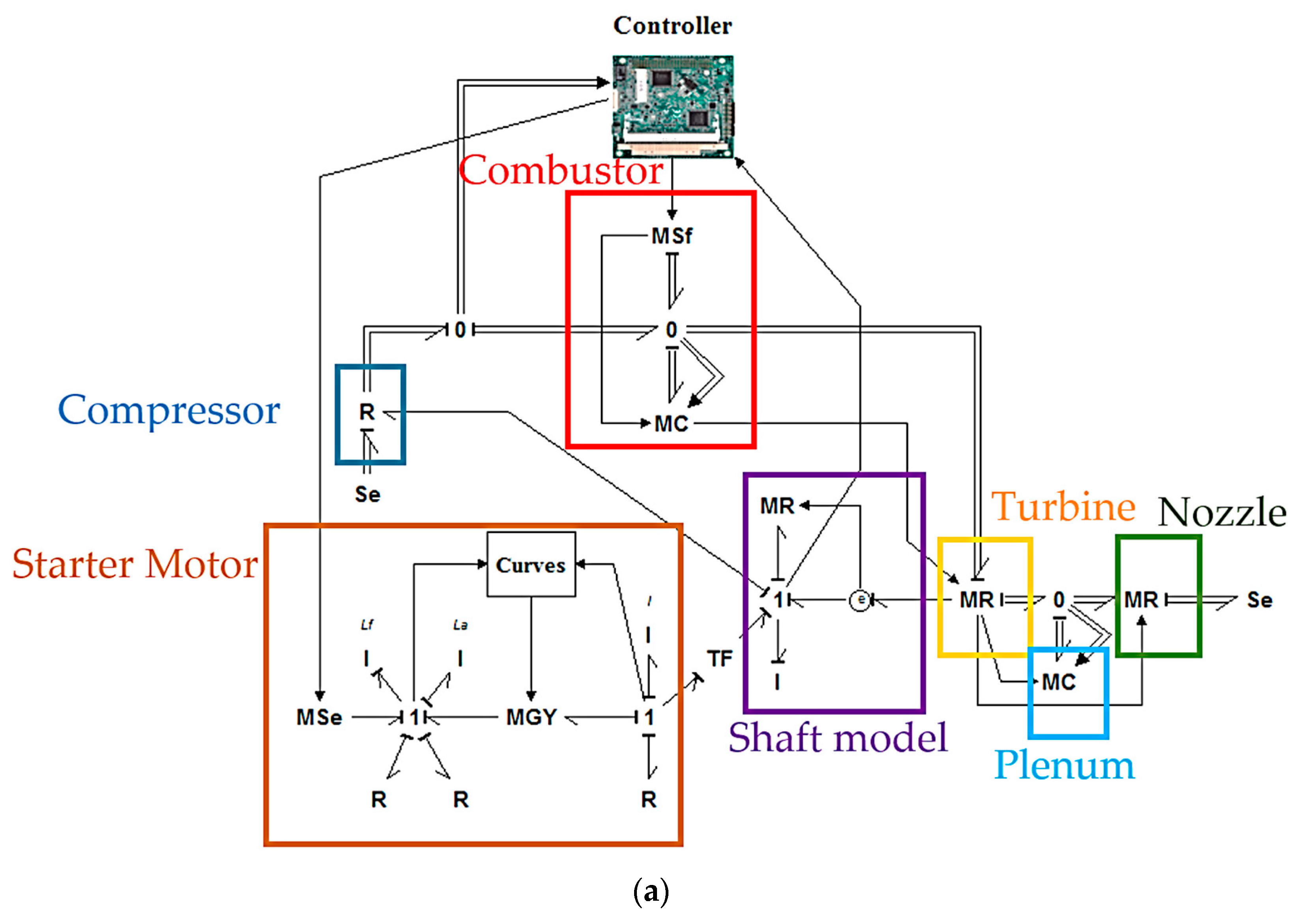
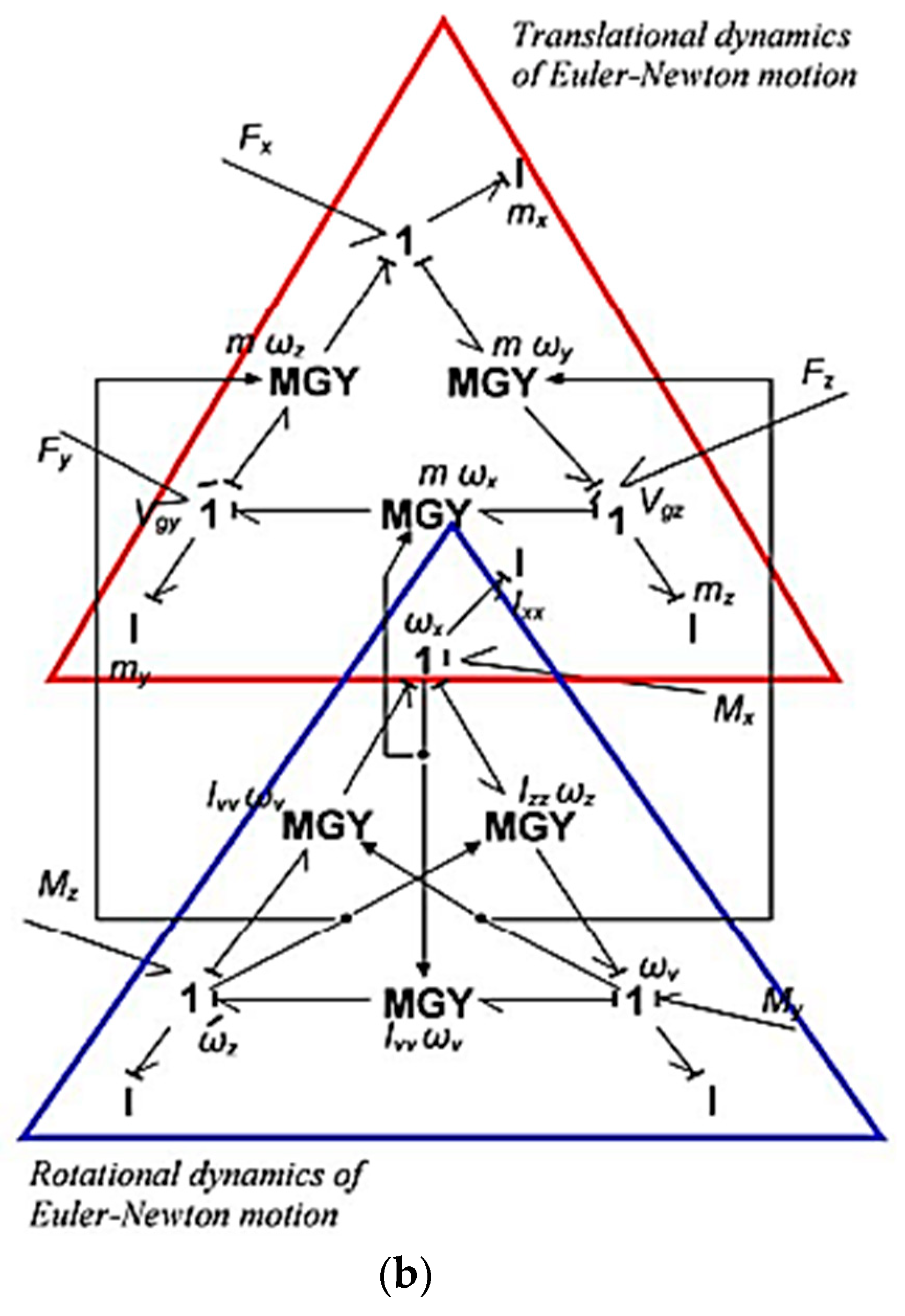
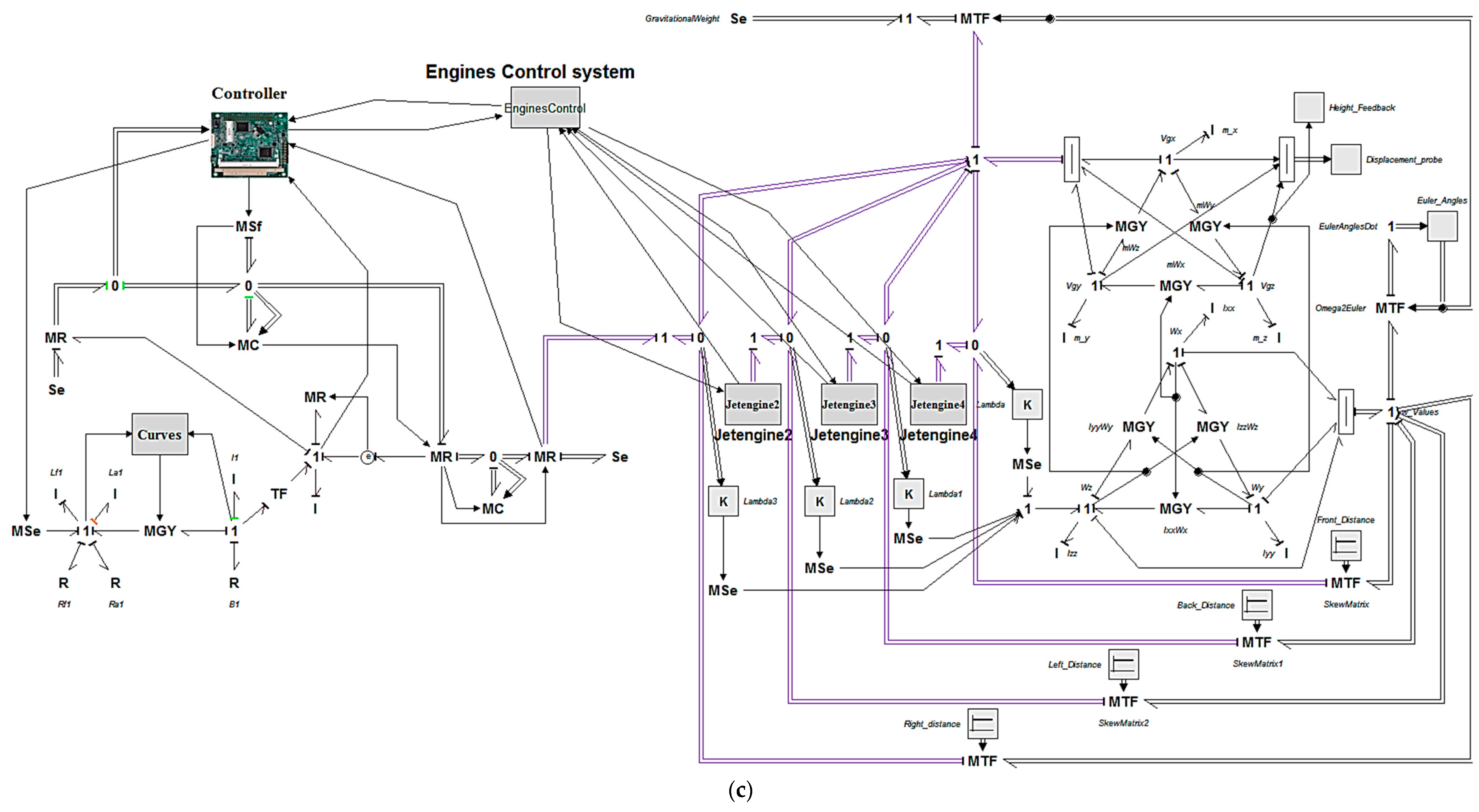
2. JetQuad Modeling
- Heat loss in components is negligible.
- Inlet pressure drop is negligible.
- The compressor mass flow rate is constant.
- The turbine mass flow rate is constant and has no effect on energy storage.
- The nozzle mass flow rate is constant, with no effect on energy storage.
3. JetQuad Simulation Results
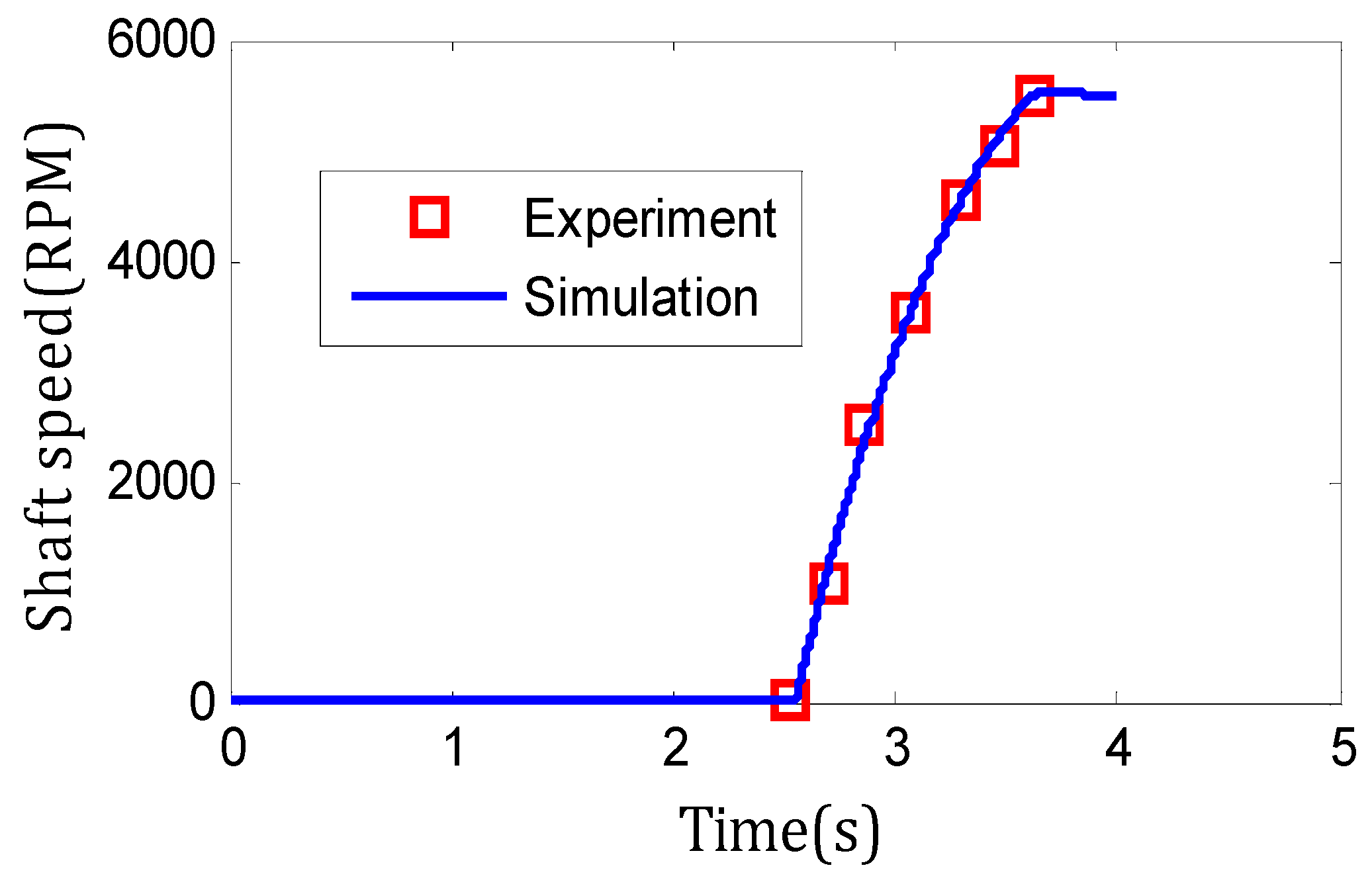
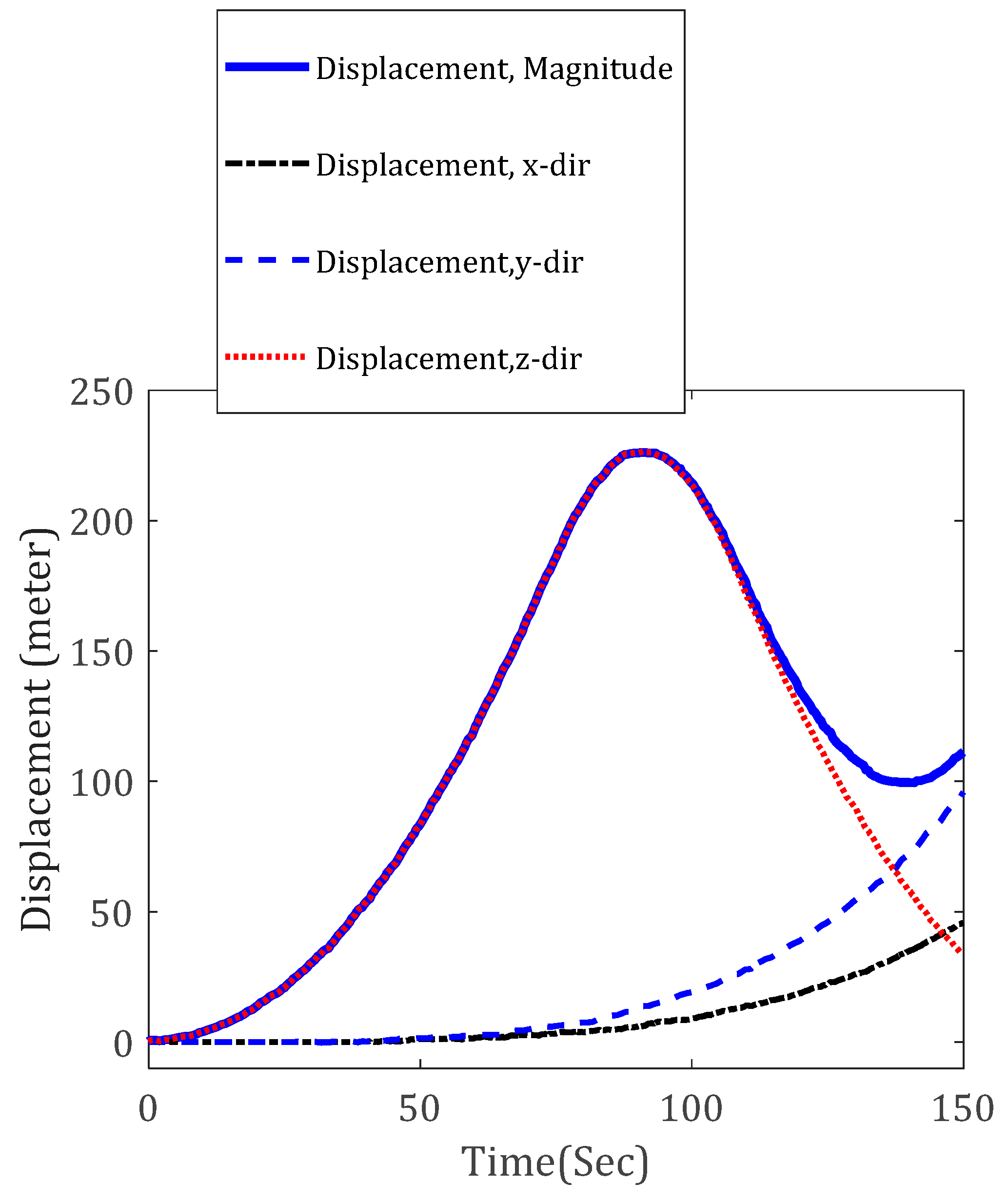
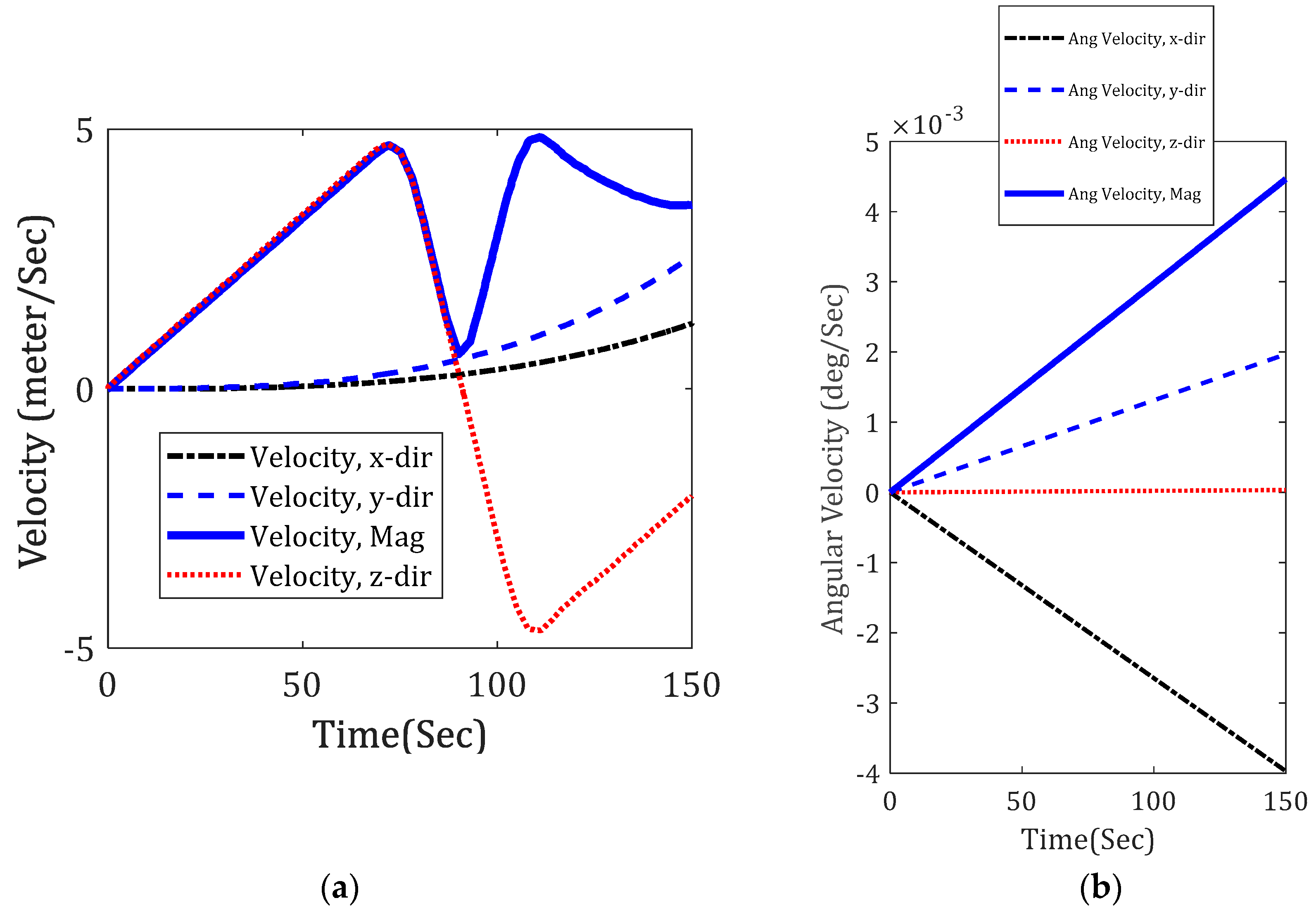
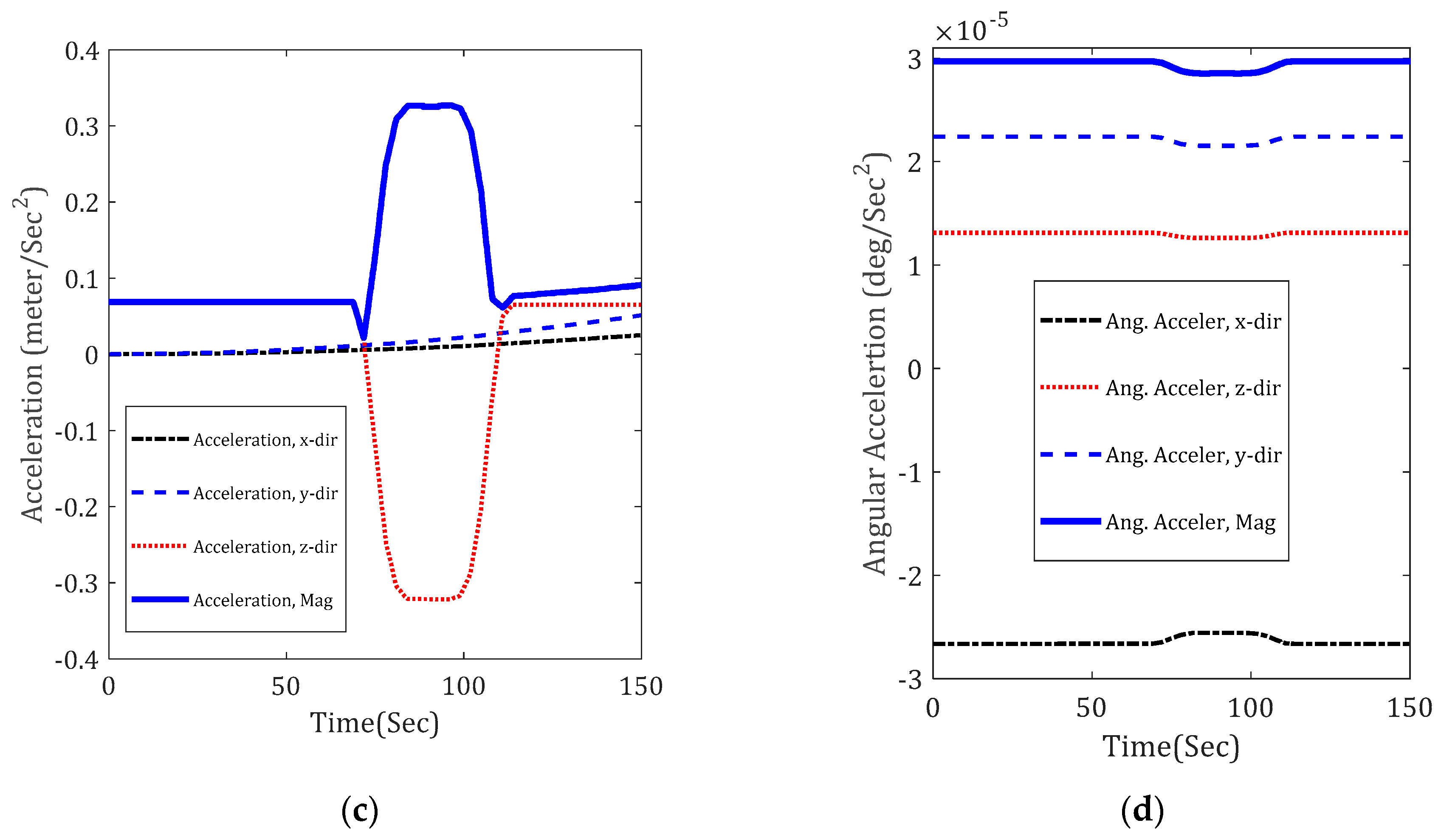
3.1. Scenario (i): Compatibility Test
3.2. Discussion of Scenario (i) Results
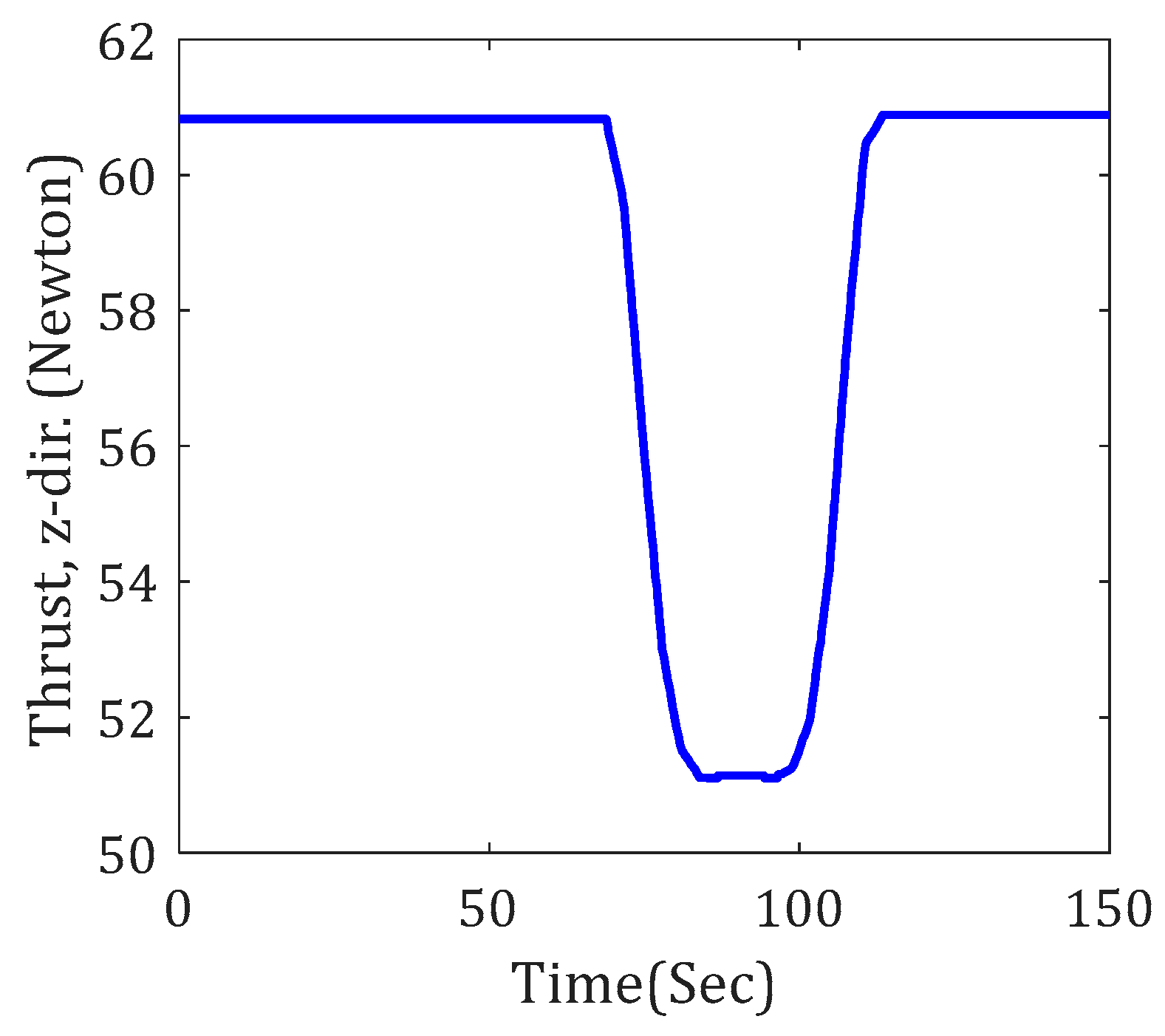
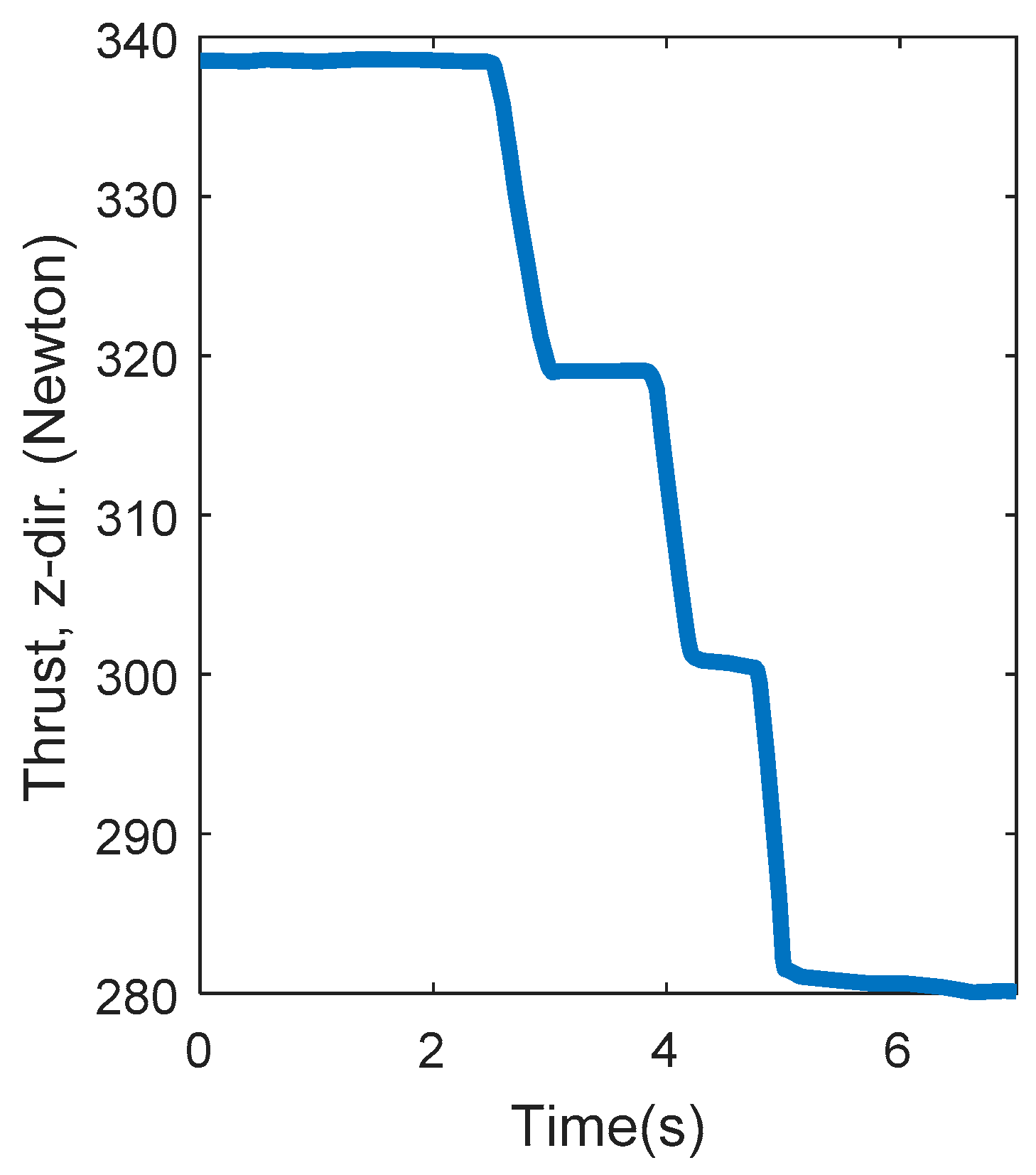
3.3. Scenario (ii): Robustness Test
3.4. Discussion of Scenario (ii) Results
4. JetQuad Control Requirements
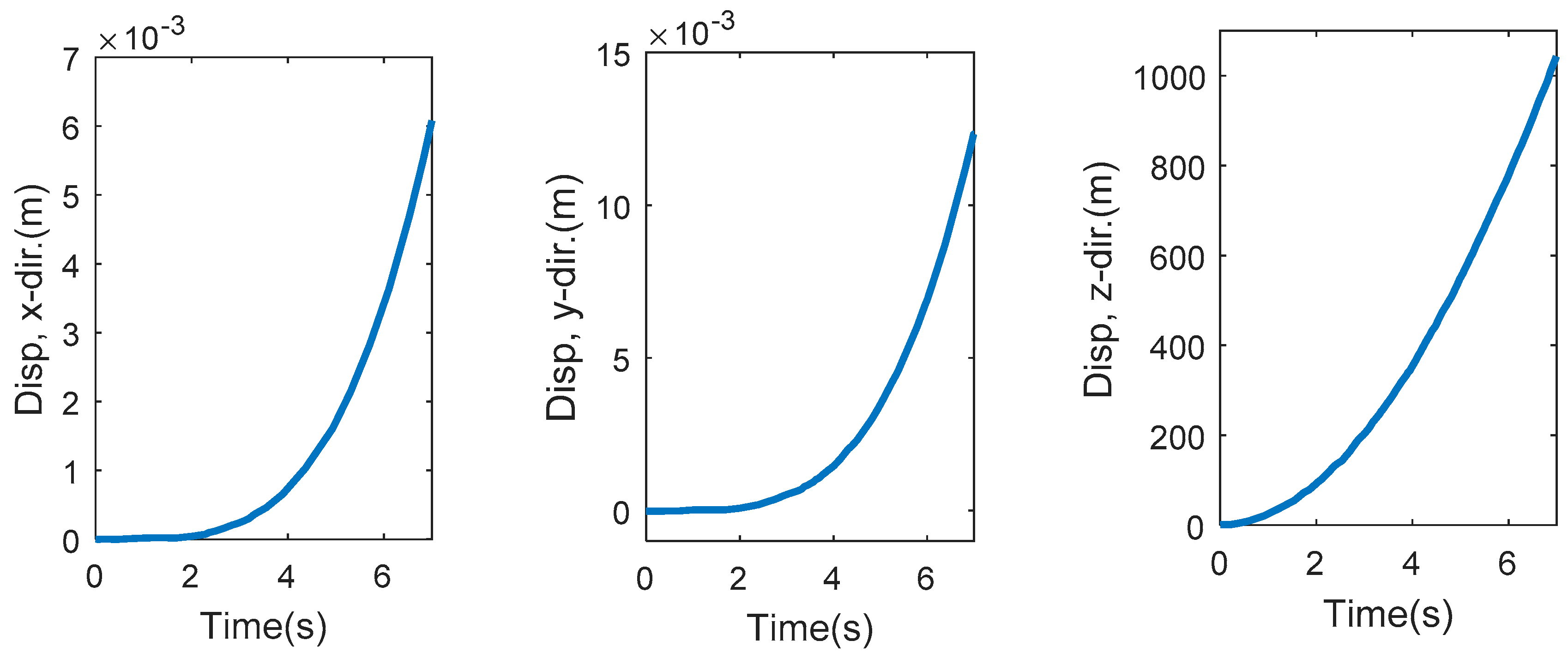
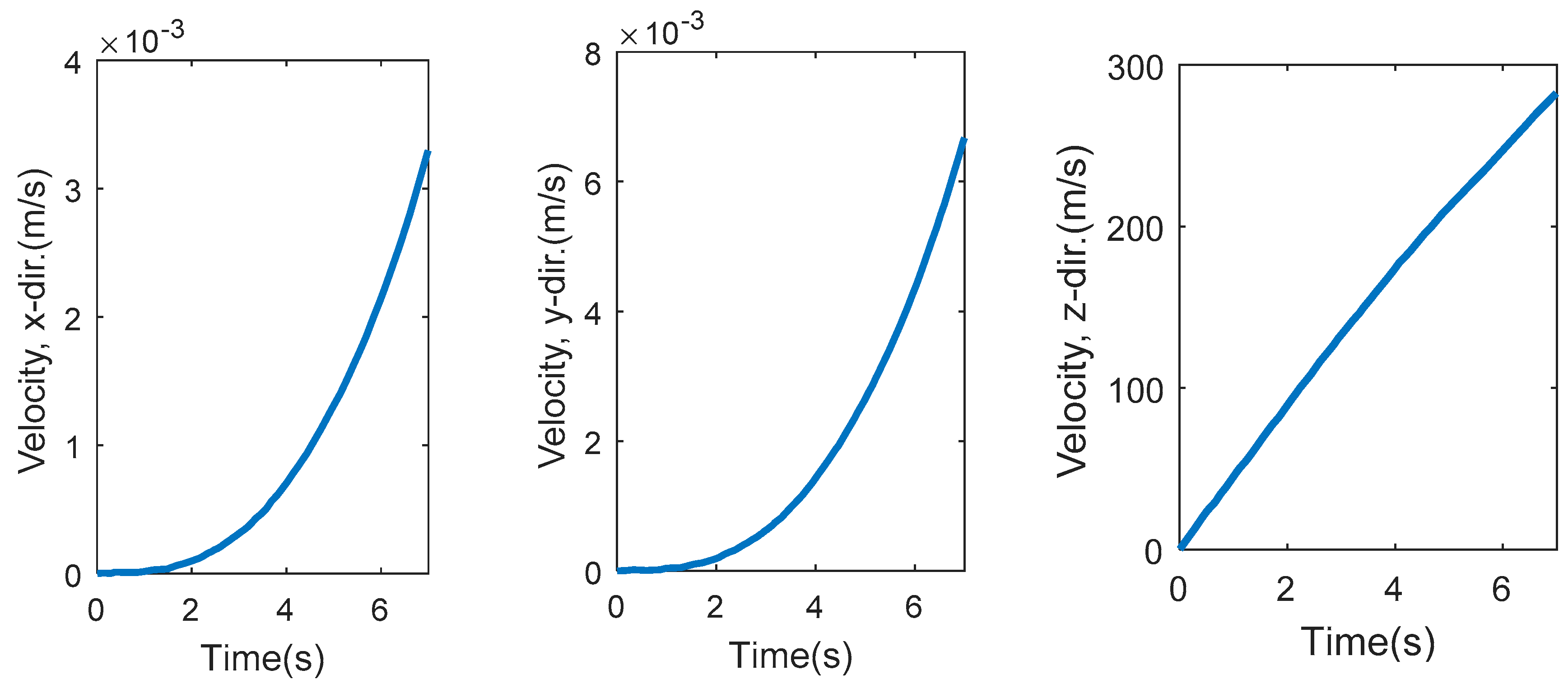
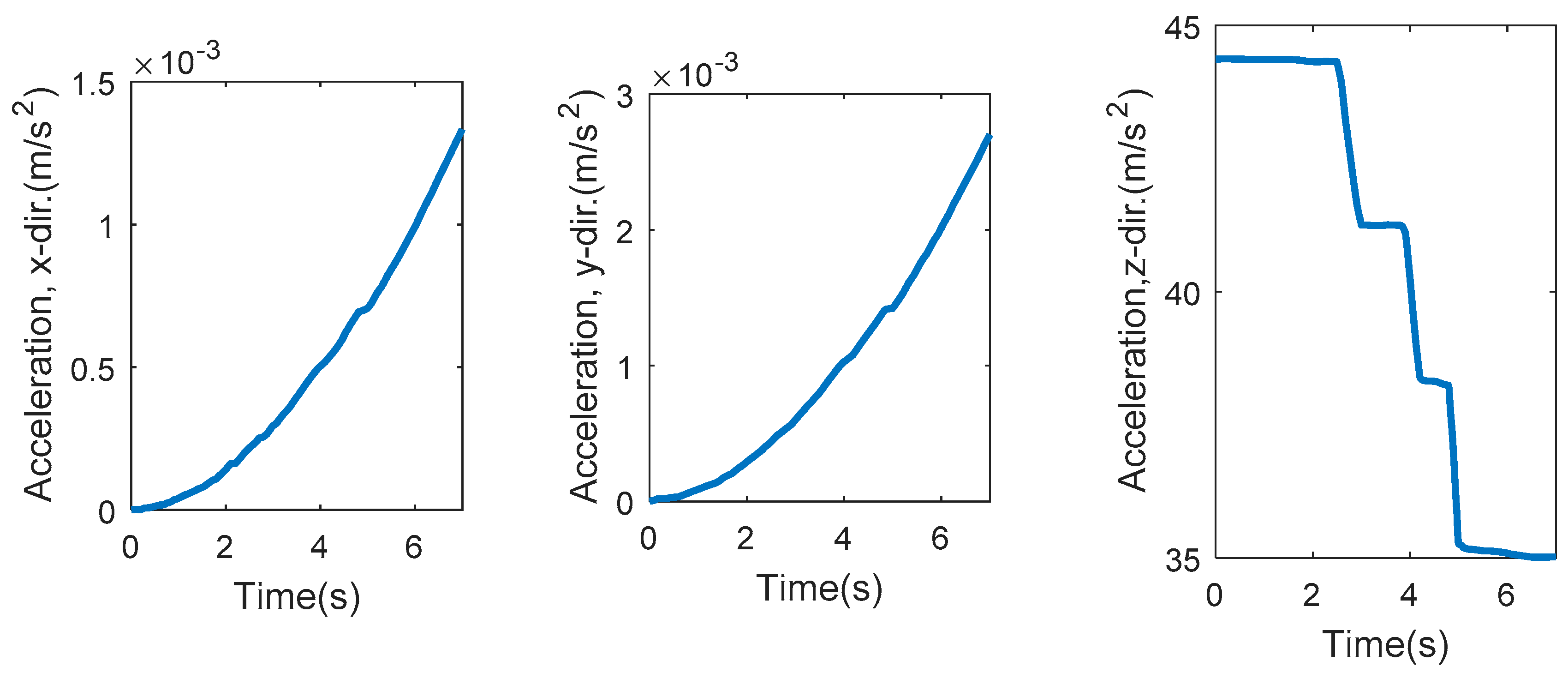
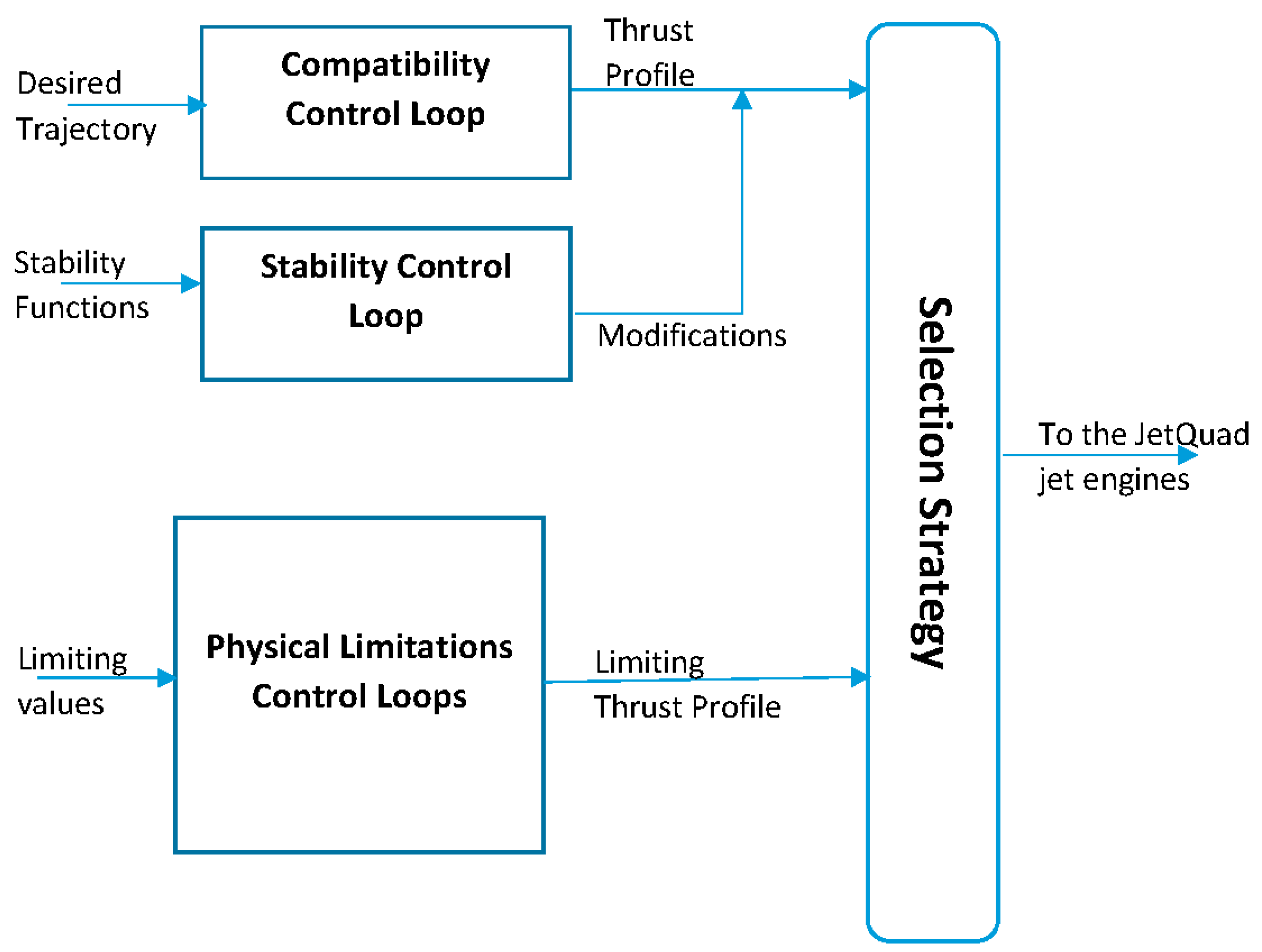
- The compatibility test showed that a control loop is required to provide a compatible motion for the JQ with respect to a predefined thrust profile. The input of this control loop would be a predefined displacement (trajectory) for the JQ, and the output would be the thrust profile for each jet engine as a function of time.
- The criteria for testing the compatibility control mode would be the value of displacement, velocity, and acceleration of the JQ in different directions. For instance, if the target is a vertical movement, the value of the displacements and velocities on the x and y axes should be zero (or negligible).
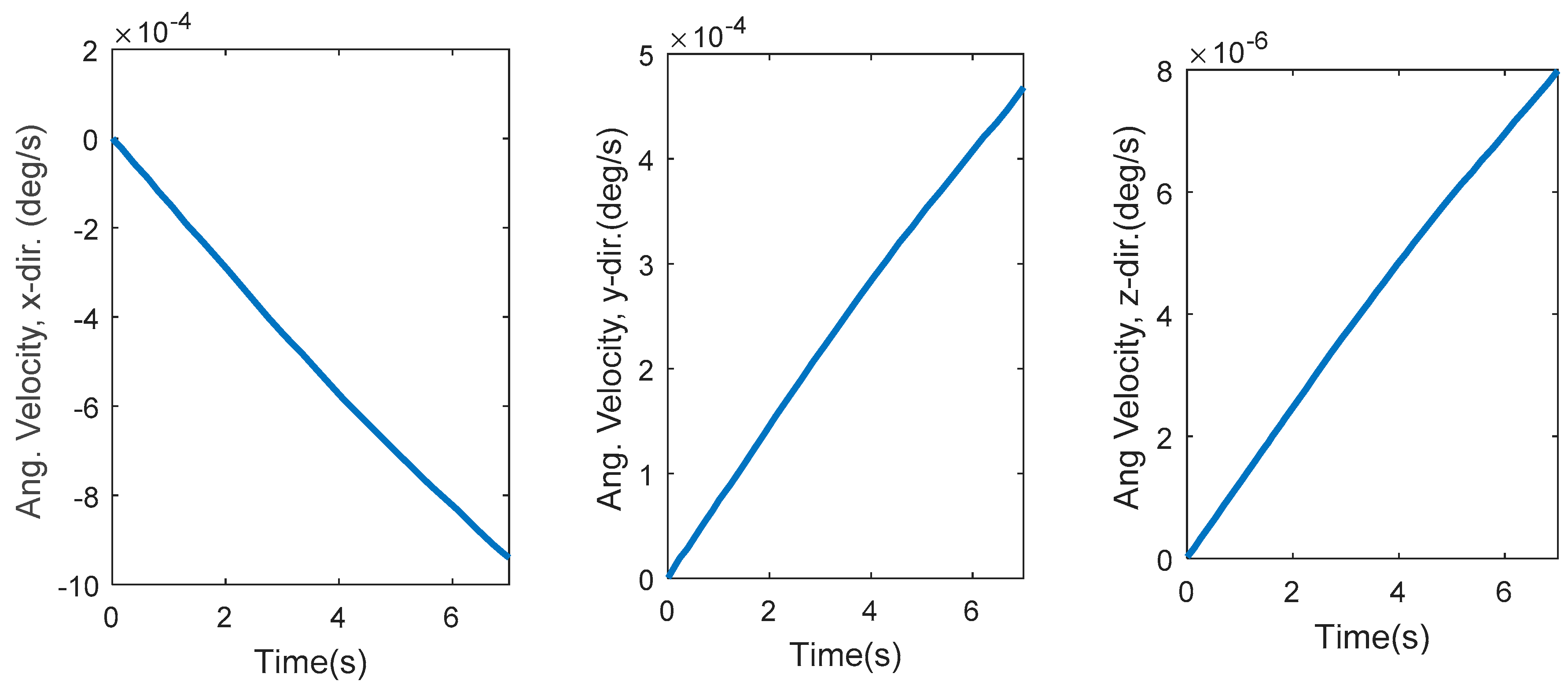
- A stability control mode should also be considered for the JQ. However, with respect to the values of angular velocity and acceleration in the compatibility test, it could be considered to be a lower priority than the compatibility control mode.
- The necessity of the stability control mode depends on the application of the JQ. Thus, a control loop could be designed in this regard with a predefined angular velocity and acceleration profile as the input and the modification of the thrust profile as the output of the controller.
- The robustness test showed that the structure of the JQ was robust and performed well even with severe changes in thrust profile. Thus, the robustness control mode is not a “must” in the first version of the JQ controller.
- The robustness test also showed that there is a vital need for a physical limitation control mode to protect the JQ from overspeed and other malfunctions. The inputs of this control loop would be the maximum and minimum allowable values for the velocity and acceleration of the JQ, and the outputs of this loop should be compared to the compatibility control loop as constraints.
- First, the compatibility control loop calculates the appropriate thrust profile for each jet engine to minimize the error between the desired and actual trajectory of the JQ.
- The stability control loop then calculates the required modifications on the thrust profiles to minimize the instability parameters.
- The compatibility and stability control loops work together and have mutual effects on each other.
- The physical limitation control loops (e.g., maximum speed, maximum acceleration, and minimum speed) calculate the limitations for the thrust profile to protect the engine from malfunctions.
- The outputs of the physical limitation control loops are compared to the outputs of the compatibility control loop (modified by the stability control loop) in a selection mechanism, and an appropriate and safe thrust profile for each jet engine is generated as the final output of the controller.
- These thrust profiles satisfy all JQ control modes simultaneously (e.g., compatibility, stability, and physical limitations).
5. Conclusions
- Compatibility control loop;
- Stability control loop;
- Physical limitation control loops.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| constant pressure specific heat | |
| constant volume specific heat | |
| E | effort sensor |
| energy flow | |
| Fuel-to-air ratio | |
| GY | gyrator |
| enthalpy | |
| H | height |
| I | current of the voltage source |
| I | rotor inertia |
| La, Lf | the self-inductance coefficients of the armature and field windings |
| MGY | modulated gyrator |
| MSE | modulated source of effort |
| mass | |
| compressor torque | |
| mass flow rate | |
| rotational speed | |
| pressure | |
| R | the mechanical loss |
| Ra, Rf | the resistances of the armature and field |
| Se | source of effort |
| Temperature | |
| U | average velocity |
| V | voltage source |
| specific heat ratio | |
| Θ | nondimensional compressor inlet total temperature |
| Δ | nondimensional compressor inlet total pressure |
| efficiency | |
| Π | pressure ratio |
Subscripts
| C | compressor |
| D | downstream |
| Fric | friction |
| In | inlet |
| Is | isentropic |
| Mech | mechanical |
| Out | outlet |
| Ref | standard value (of pressure or temperature) |
| T | turbine |
| U | upstream |
References
- Prime Air. 2018. Available online: https://www.amazon.com/Amazon-Prime-Air/b?ie=UTF8&node=8037720011 (accessed on 18 December 2018).
- Best Robot Toys. 2016. Available online: http://bestrobotictoys.com/ (accessed on 18 December 2018).
- Omari, S.; Gohi, P.; Burri, M. Visual Industrial Inspection Using Aerial Robots. In Proceedings of the 2014 3rd International Conference on Applied Robotics for the Power Industry, Foz do Iguassu, Brazil, 14–16 October 2014. [Google Scholar] [CrossRef]
- Gohl, P.; Burri, M.; Omari, S.; Achtelik, M.; Siegwart, R. Towards Autonomous Mine Inspection. In Proceedings of the International Conference on Applied Robotics for the Power Industry (CARPI), Foz do Iguassu, Brazil, 14–16 October 2014. [Google Scholar]
- Nikolic, J.; Burri, M.; Rehder, J.; Leutenegger, S.; Huerzeler, C.; Siegwart, R. A UAV system for inspection of industrial facilities. In Proceedings of the IEEE Aerospace Conference, Big Sky, MT, USA, 2–9 March 2013. [Google Scholar]
- Le, P.H.; Wang, Z.; Hirai, S. Origami structure toward floating aerial robot. In Proceedings of the 2015 IEEE International Conference on Advanced Intelligent Mechatronics (AIM), Busan, Korea, 7–11 July 2015. [Google Scholar]
- Jimenez-Cano, A.E.; Martin, J.; Heredia, G.; Ollero, A.; Cano, R. Control of an aerial robot with multi-link arm for assembly tasks. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation (ICRA), Karlsruhe, Germany, 6–10 May 2013. [Google Scholar]
- Hossain, M.R.; Rideout, D.G.; Krouglicof, D.N. Bond graph dynamic modeling and stabilization of a quad-rotor helicopter. In Proceedings of the 2010 Spring Simulation Multiconference, Orlando, FL, USA, 11–15 April 2010. [Google Scholar]
- Hossain, M.R.; Krouglicof, N. Multi-body dynamics modeling & control of quadrotor helicopter using bond graph. In Proceedings of the International Conference on Bond Graph Modeling and Simulation, Montreal, QC, Canada, 24–27 July 2016. [Google Scholar]
- Granda, J.J.; Montgomery, R.C. Automated Modeling and Simulation Using the Bond Graph Method for the Aerospace Industry; NASA: Washington, DC, USA, 2003.
- Mohammadi, V.; Ghaemi, S.; Kharrati, H. PSO tuned FLC for full autopilot control of quadrotor to tackle wind disturbance using bond graph approach. Appl. Soft Comput. 2018, 65, 184–195. [Google Scholar] [CrossRef]
- Chikhaoui, Z.; Gomand, J.; Malburet, F.; Pavel, M.; Barre, P. Towards an energetic modeling of rotorcraft using Bond-Graphs. In Proceedings of the AHS 69th Annual Forum, Phoenix, AR, USA, 21–23 May 2013. [Google Scholar]
- AB4 JetQuad. 2017. Available online: http://fusionflight.com/jetquad/ (accessed on 18 December 2018).
- Fashandi, S.A. l Montazeri-gh M. Modeling and simulation of JetQuad aerial robot. In Proceedings of the 2017 IEEE 4th International Conference on Knowledge-Based Engineering and Innovation (KBEI), Tehran, Iran, 22 December 2017; pp. 753–762. [Google Scholar] [CrossRef]
- Montazeri-Gh, M.; Fashandi, S.A.M. Application of Bond Graph approach in dynamic modelling of industrial gas turbine. Mech. Ind. 2017, 18, 410. [Google Scholar] [CrossRef]
- Montazeri-Gh, M.; Miran-F, S.A. Bond graph modeling of a jet engine with electric starter. Proc. Inst. Mech. Eng. Part G J. Aeros. Eng. 2018. [Google Scholar] [CrossRef]
- Paynter, H.M. ; The, M.I.T. Analysis and Design of Engineering Systems; The M.I.T. Press: Cambridge, MA, USA, 1961; ISBN 0-262-16004-8. [Google Scholar]
- Borutzky, W. Bond Graph Modelling of Engineering Systems; Springer: Berlin/Heidelberg, Germany, 2011; ISBN1 9783319474342 (online). ISBN2 9783319474342 (print). [Google Scholar]
- Montazeri-Gh, M.; Miran-F, S.A. Modeling and simulation of a two-shaft gas turbine propulsion system containing a frictional plate–type clutch. Proc. Inst. Mech. Eng. Part M J. Eng. Marit. Environ. 2018. [Google Scholar] [CrossRef]
- Montazeri-Gh, M.; Miran-F, S.A.; Abyaneh, S. Real-Time Simulation Test-bed For an Industrial Gas Turbine Engine’s Controller. Mech. Ind. 2018. [Google Scholar] [CrossRef]
- Montazeri-Gh, M.; Miran-F, S.A. Application of Bond-Graph Method in Microjet Engine Cold Start Modeling to Investigate the Idea of Injecting Compressed Air. Appl. Mech. Mater. 2015, 788–800, 890–894. [Google Scholar] [CrossRef]
- Krikelis, N.; Papadakis, F. Gas turbine modelling using pseudo-bond graphs. Int. J. Syst. Sci. 1988, 19, 537–550. [Google Scholar] [CrossRef]
- Movaghar, A.S.; Novinzadeh, A. Ideal Turbo charger Modeling and Simulation using Bond Graph Approach. In Proceedings of the ASME 2011 Turbo Expo: Turbine Technical Conference and Exposition: American Society of Mechanical Engineers, Vancouver, BC, Canada, 6–10 June 2011; pp. 871–879. [Google Scholar]
- Sanei, A.; Novinzadeh, A.; Habibi, M. Addition of momentum and kinetic energy effects in supersonic compressible flow using pseudo bond graph approach. Math. Comput. Model. Dyn. Syst. 2014, 20, 491–503. [Google Scholar] [CrossRef]
- Shoureshi, R.; Brackney, L. Applications of Active Adaptive Noise Control to Jet Engines; Technical Report; NASA: Washington, DC, USA, 1993.
- Diston, D.J. Unified Modelling of Aerospace Systems: A Bond Graph Approach; University of Glasgow: Glasgow, Scotland, 1999. [Google Scholar]
- Uddin, N.; Gravdahl, J.T. Bond graph modeling of centrifugal compression systems. Simulation 2015, 91, 998–1013. [Google Scholar] [CrossRef] [Green Version]
- Munari, E.; Morini, M.; Pinelli, M.; Spin, P.R. Experimental Investigation and Modeling of Surge in a Multistage Compressor. Energy Procedia 2017, 105, 1751–1756. [Google Scholar] [CrossRef]
- Uddin, N.; Gravdahl, J.T. Active compressor surge control system by using piston actuation: Implementation and experimental results. IFAC-PapersOnLine 2016, 49, 347–352. [Google Scholar] [CrossRef]
- Jafari, S.; Montazeri-Gh, M. Evolutionary optimization for gain tuning of jet engine min-max fuel controller. J. Propul. Power 2011, 27, 1015–1023. [Google Scholar] [CrossRef]
- Montazeri-Gh, M.; Fashandi, S.A.M.; Jafari, S. Theoretical and Experimental Study of a Micro Jet Engine Start-Up Behaviour. Tehnički Vjesnik 2018, 25, 839–845. [Google Scholar] [CrossRef]
- Montazeri-Gh, M.; Jafari, S.; Ilkhani, M.R. Application of particle swarm optimization in gas turbine engine fuel controller gain tuning. Eng. Optim. 2012, 44, 225–240. [Google Scholar] [CrossRef]

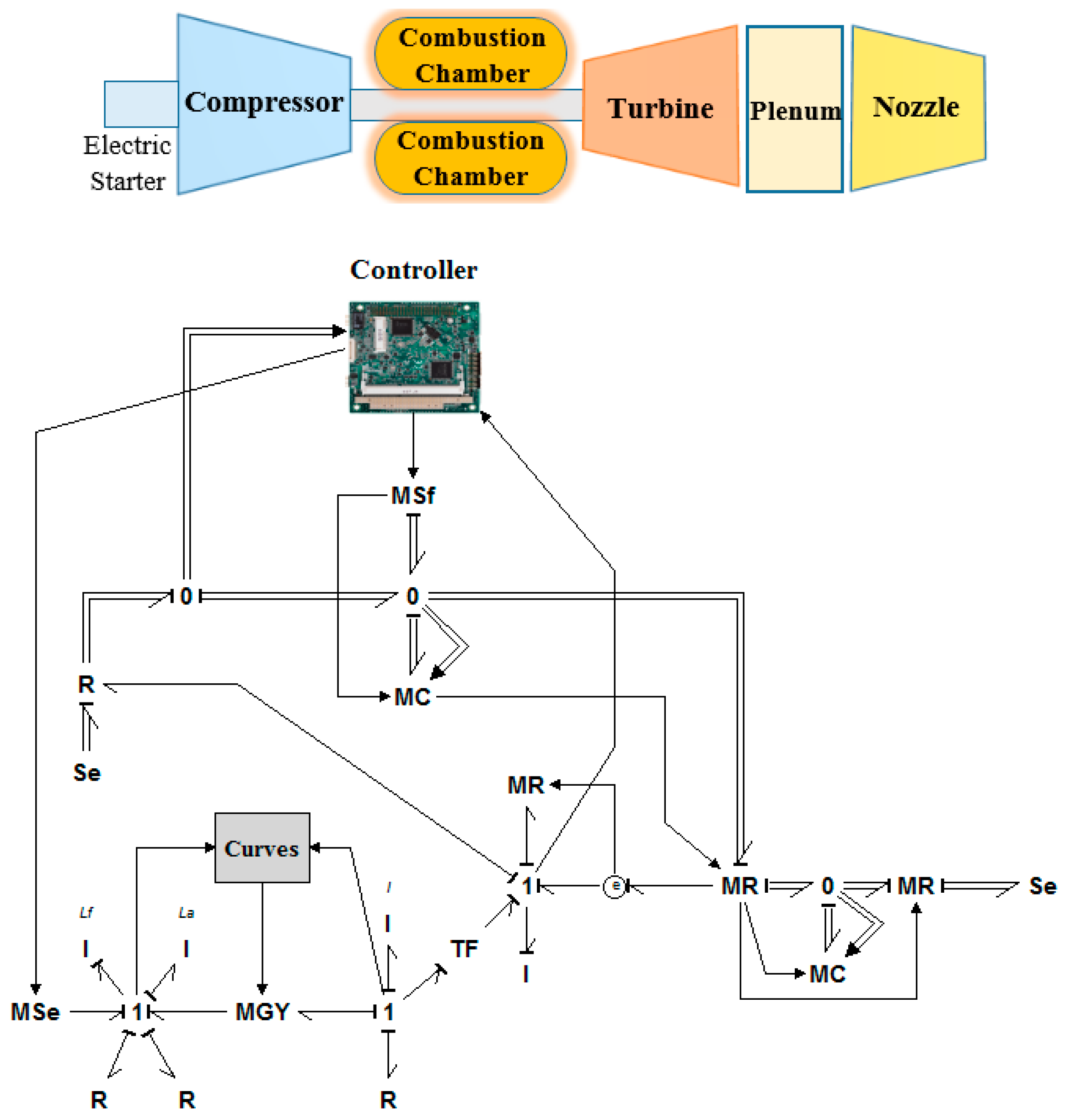
| Main Characteristics of the AB4 JetQuad | ||
|---|---|---|
| 1 | Propulsion | Four identical microturbines each generate 25 horsepower. |
| 2 | Payload | Up to 30 lb. |
| 3 | Performance | With a 30-lb payload, the drone has an endurance of 8 min. |
| 4 | Geometry | Under 2 feet in diameter and about 2 feet tall. |
| Quantity | Value |
|---|---|
| Inlet air temperature (k) | 288 |
| Inlet air pressure (bar) | 1.01325 |
| Lower heating value (LHV) (KJ·Kg−1) | 43,323 |
| Compressor exhaust temperature (k) | 379.85 |
| Compressor isentropic efficiency | 0.76 |
| Turbine isentropic efficiency | 0.80 |
| Compressor pressure ratio | 3.78 |
| Turbine inlet gas temperature (k) | 1158.5 |
| Turbine pressure ratio | 2.024 |
| Turbine exhaust gas temperature (k) | 1015.9 |
| Combustion efficiency | 0.68 |
| Mechanical shaft efficiency | 0.99 |
| Component | Equations |
|---|---|
| Compressor equations | |
| Combustion chamber model equations | |
| Turbine model equations | |
| Plenum model equations | |
| Nozzle equations | |
| Shaft model |
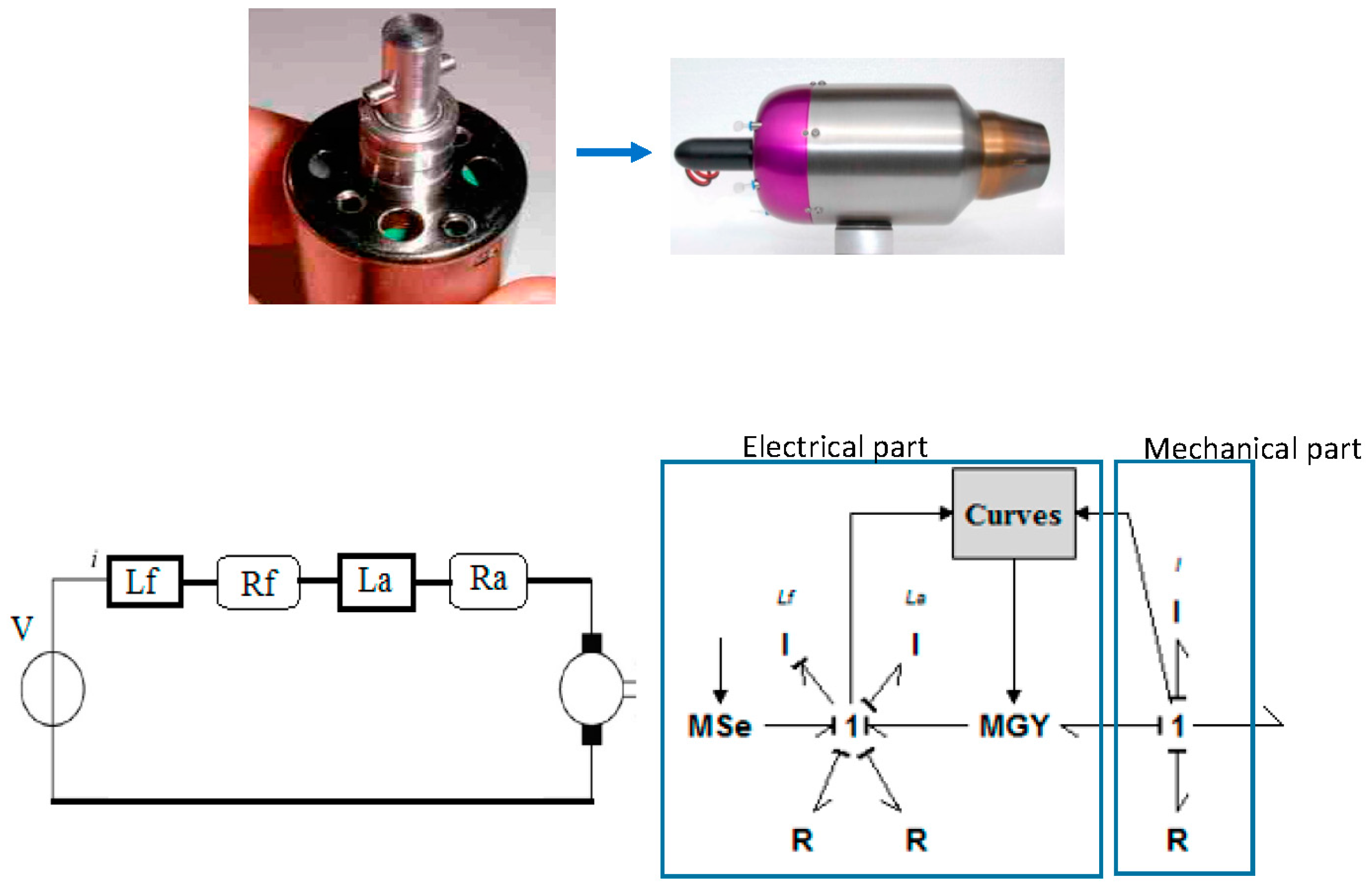
| Quantity | Value |
|---|---|
| Power | 60 W |
| Efficiency | 67.6 |
| Laf | 0.002 H |
| Torque | 0.0955 N·m |
| V | 12 V |
| Ra | 0.3 ohm |
| La | 0.0005 H |
| Rf | 0.1 ohm |
| Lf | 0.001 H |
| J | 0.000015 kg·m2 |
| B | 0.00001 kg·m·s |
| I | 6.9 A |
| Nominal speed | 6000 rpm |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jafari, S.; Miran Fashandi, S.A.; Nikolaidis, T. Control Requirements for Future Gas Turbine-Powered Unmanned Drones: JetQuads. Appl. Sci. 2018, 8, 2675. https://doi.org/10.3390/app8122675
Jafari S, Miran Fashandi SA, Nikolaidis T. Control Requirements for Future Gas Turbine-Powered Unmanned Drones: JetQuads. Applied Sciences. 2018; 8(12):2675. https://doi.org/10.3390/app8122675
Chicago/Turabian StyleJafari, Soheil, Seyed Alireza Miran Fashandi, and Theoklis Nikolaidis. 2018. "Control Requirements for Future Gas Turbine-Powered Unmanned Drones: JetQuads" Applied Sciences 8, no. 12: 2675. https://doi.org/10.3390/app8122675
APA StyleJafari, S., Miran Fashandi, S. A., & Nikolaidis, T. (2018). Control Requirements for Future Gas Turbine-Powered Unmanned Drones: JetQuads. Applied Sciences, 8(12), 2675. https://doi.org/10.3390/app8122675







