Semi-Supervised Ridge Regression with Adaptive Graph-Based Label Propagation
Abstract
1. Introduction
2. Related Works
2.1. Least Square Regression
2.2. Ridge Regression
2.3. Label Propagation
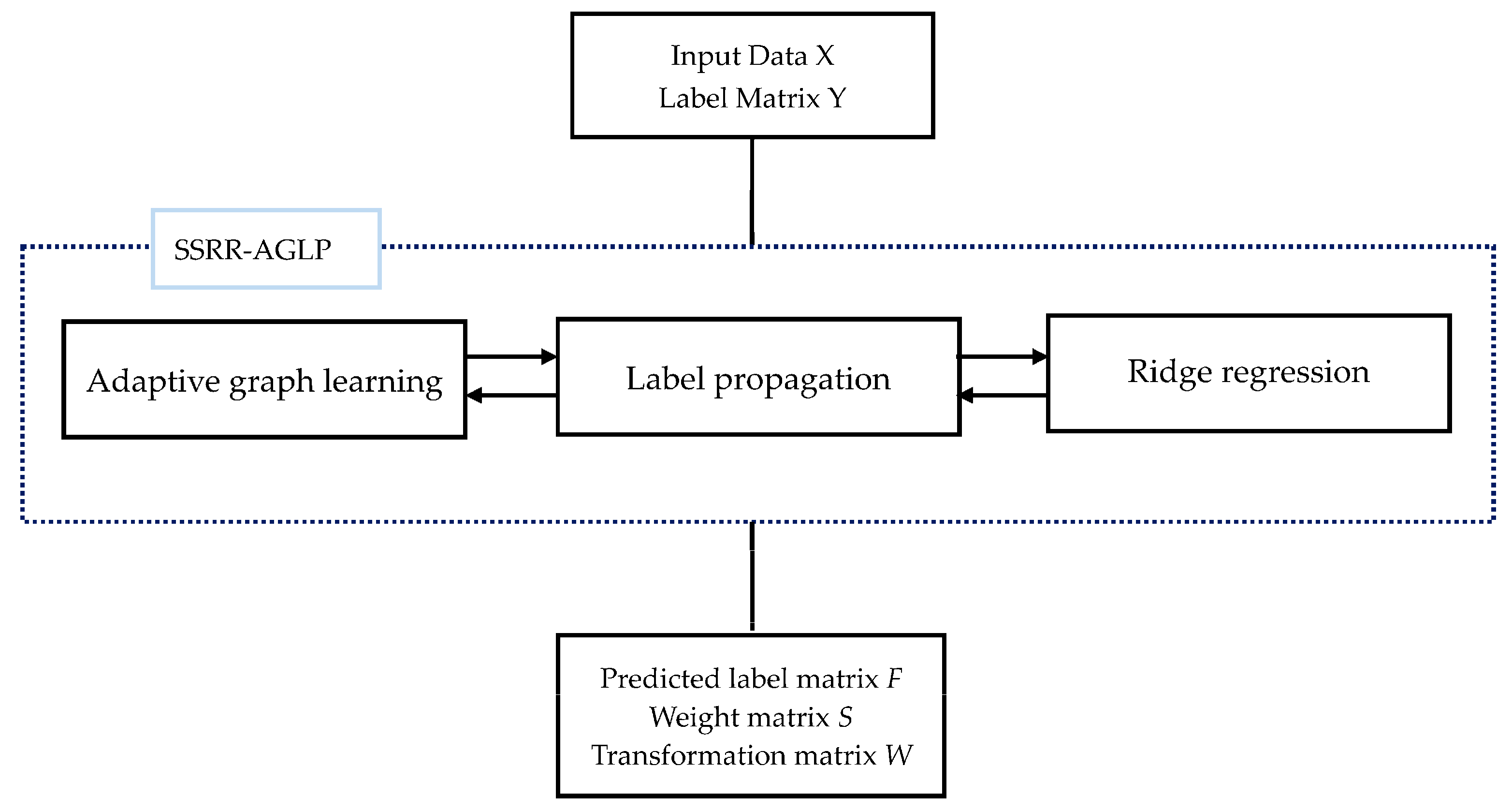
3. The Proposed Method
3.1. Objective Function of SSRR-AGLP
3.2. Optimization Solution
3.2.1. Fix Transformation Matrix W and Prediction Label Matrix F to Solve Weight Matrix S
3.2.2. Fix Weight Matrix S and Transformation Matrix W to Solve Prediction Label Matrix F
3.2.3. Fix Weight Matrix S and Prediction Label Matrix F to Solve Transformation Matrix W
3.2.4. The Optimization Algorithm
| Algorithm 1. The algorithm to solve the objective function of SSRR-AGLP |
| Input: the training set , the label matrix of training set 1: Initialization: parameters , matrices are an arbitrary nonnegative matrix, t = 0 2: According to Equations (11) and (15), the diagonal matrices and are calculated respectively. 3: Repeat steps 3–9 until convergence conditions 4: According to , calculate , and then calculate matrix where 5: According to , calculate where 6: Update to 7: Update to 8: Update to 9: Update |
| Output: Predicted label matrix F, weight matrix S and transformation matrix W |
3.3. Classification Criterion
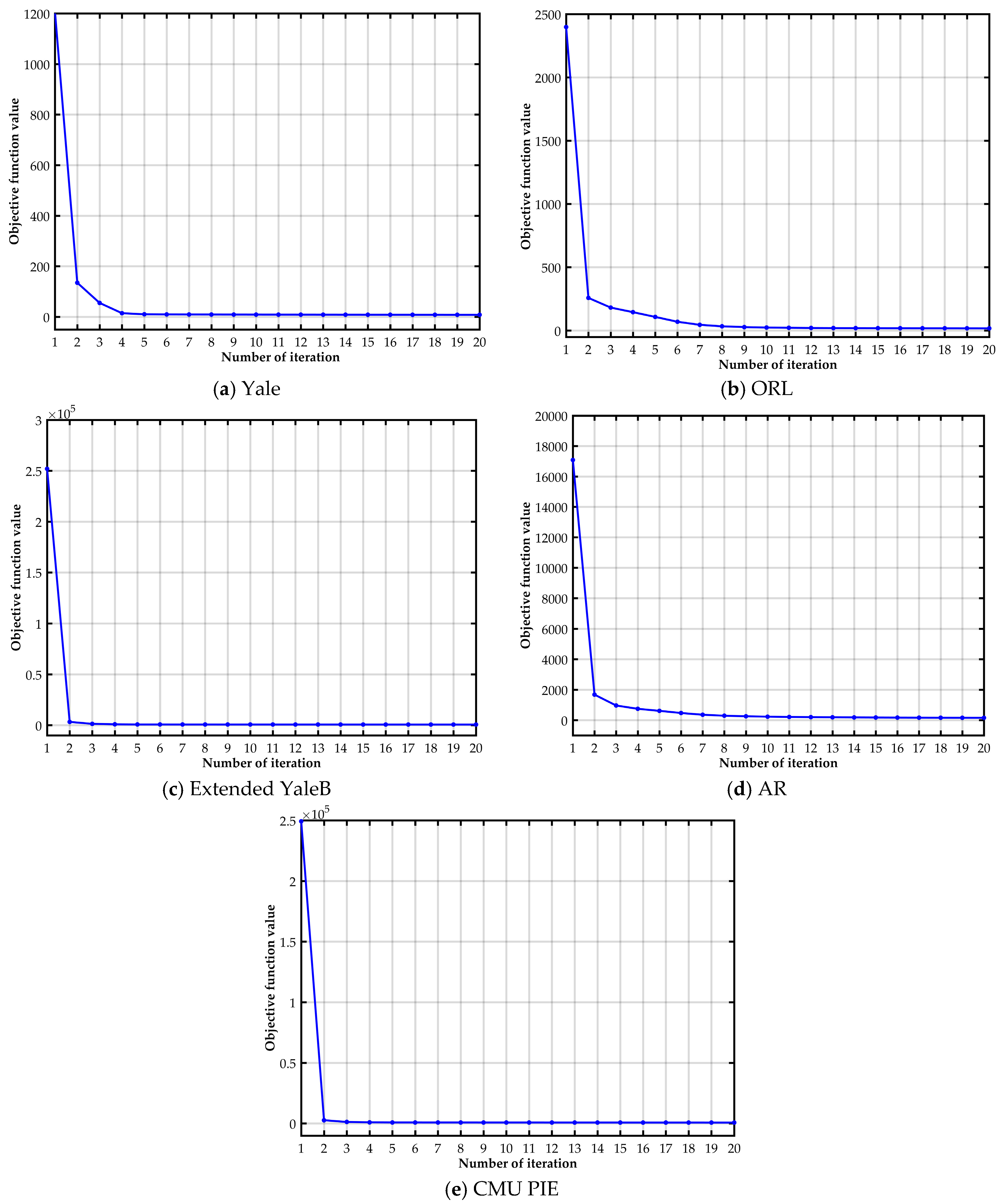
3.4. Convergence Analysis
4. Experiment and Analysis
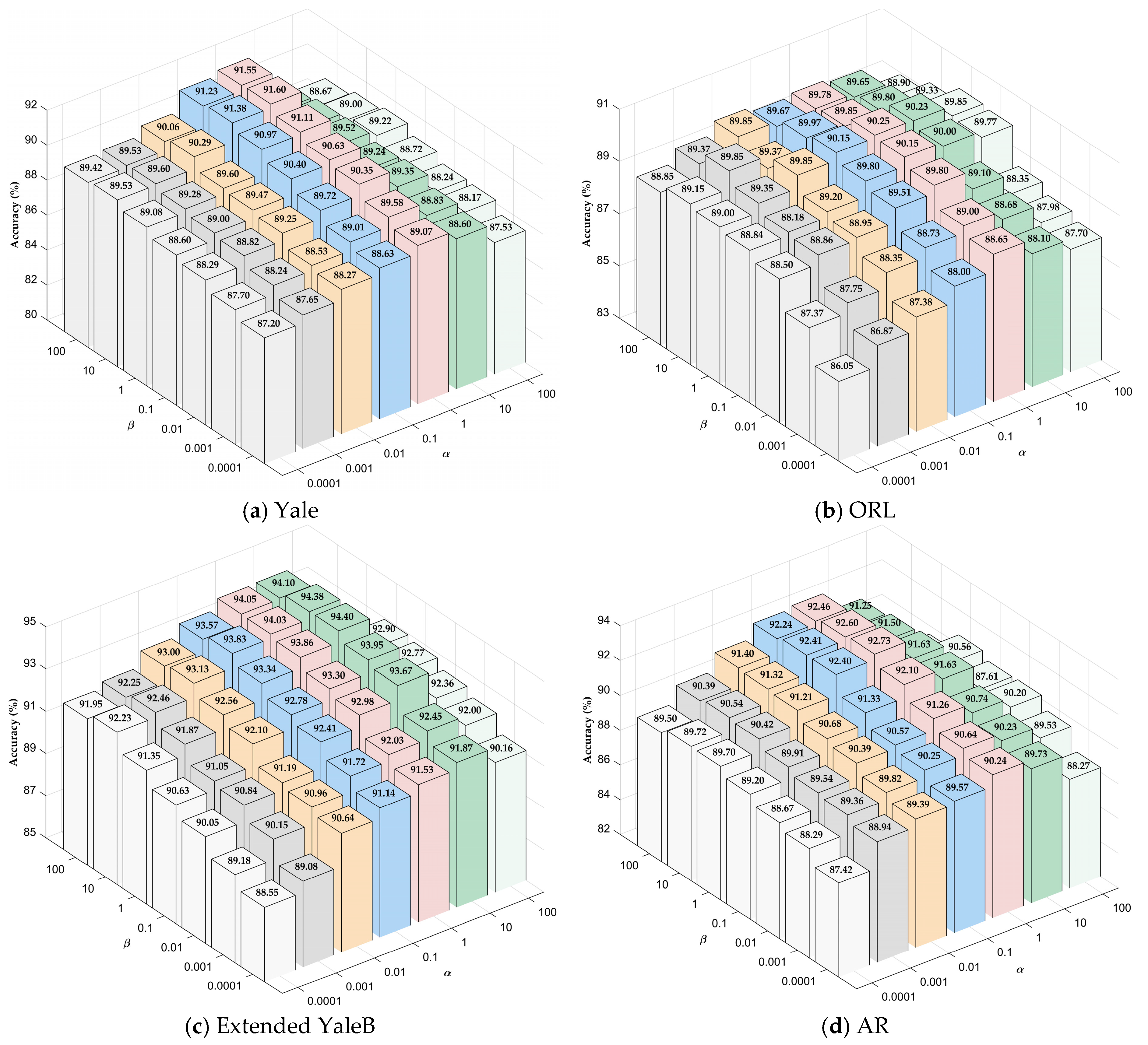
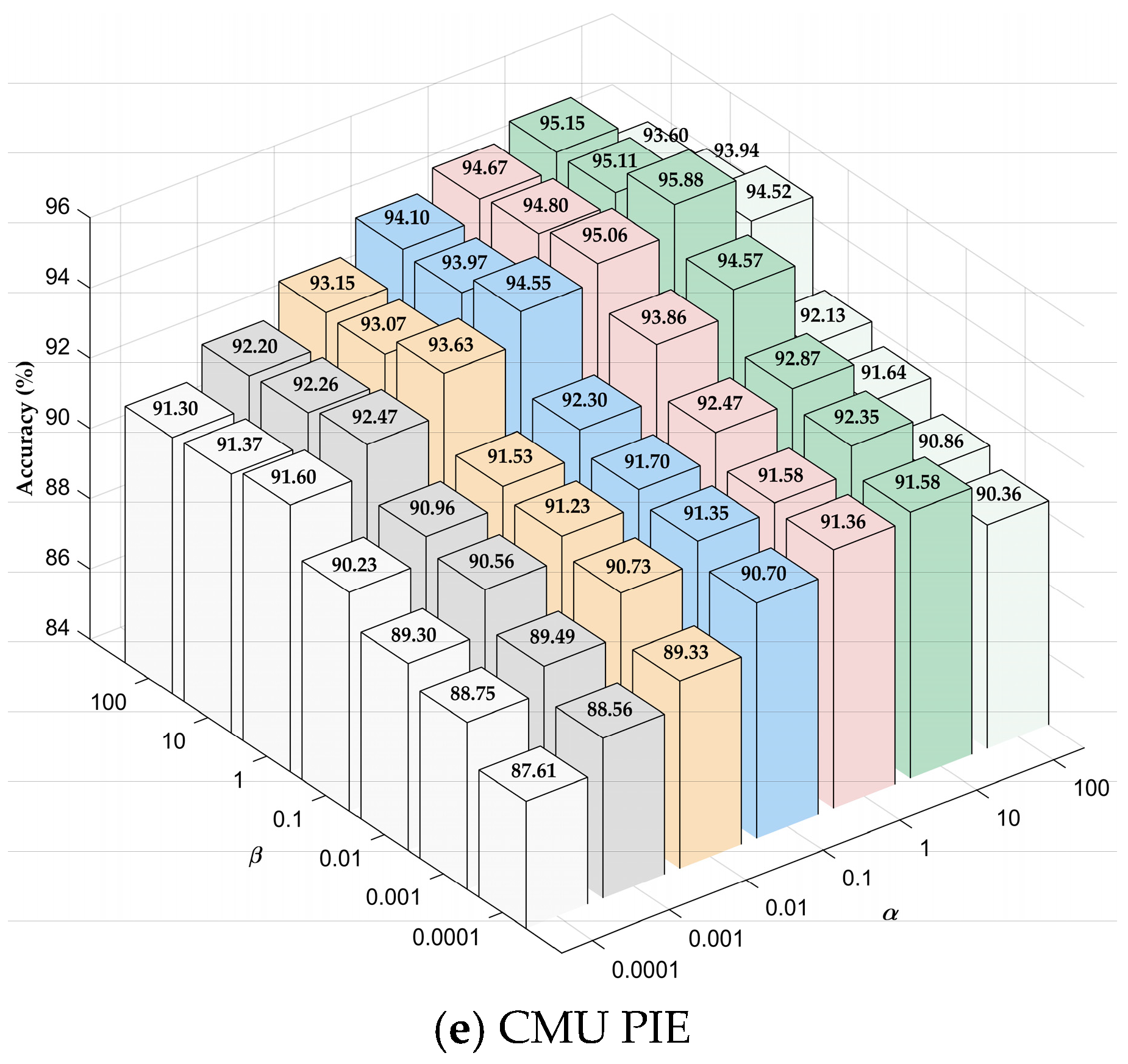
4.1. Parameter Setting
4.2. Experimental Results and Analysis
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Strutz, T. Data Fitting and Uncertainty: A Practical Introduction to Weighted Least Squares and Beyond; Vieweg: Wiesbaden, Germany, 2010. [Google Scholar]
- Krishnan, A.; Williams, L.J.; McIntosh, A.R.; Abdi, H. Partial Least Squares (PLS) methods for neuroimaging: A tutorial and review. Neuroimage 2011, 56, 455–475. [Google Scholar] [CrossRef] [PubMed]
- Ruppert, D.; Sheather, S.J.; Wand, M.P. An effective bandwidth selector for local least squares regression. J. Am. Statist. Assoc. 1995, 90, 1257–1270. [Google Scholar] [CrossRef]
- Gao, J.; Shi, D.; Liu, X. Significant vector learning to construct sparse kernel regression models. Neural Netw. 2007, 20, 791–798. [Google Scholar] [CrossRef] [PubMed]
- Gold, C.; Sollich, P. Model selection for support vector machine classification. Neurocomputing 2003, 55, 221–249. [Google Scholar] [CrossRef]
- Kim, H.; Park, H. Nonnegative matrix factorization based on alternating nonnegativity constrained least squares and active set method. SIAM J. Matrix Anal. Appl. 2008, 30, 713–730. [Google Scholar] [CrossRef]
- Li, Y.; Ngom, A. Nonnegative least-squares methods for the classification of high-dimensional biological data. IEEE/ACM Trans. Comput. Biol. Bioinform. (TCBB) 2013, 10, 447–456. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Pan, C. Groupwise retargeted least-squares regression. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 1352–1358. [Google Scholar] [CrossRef]
- Zhang, L.; Valaee, S.; Xu, Y.; Vedadi, F. Graph-based semi-supervised learning for indoor localization using crowdsourced data. Appl. Sci. 2017, 7, 467. [Google Scholar] [CrossRef]
- Zhang, Z.; Lai, Z.; Xu, Y.; Shao, L.; Wu, J.; Xie, G.S. Discriminative elastic-net regularized linear regression. IEEE Trans. Image Process. 2017, 26, 1466–1481. [Google Scholar] [CrossRef]
- Peng, Y.; Kong, W.; Yang, B. Orthogonal extreme learning machine for image classification. Neurocomputing 2017, 266, 458–464. [Google Scholar] [CrossRef]
- Yuan, H.; Zheng, J.; Lai, L.L.; Tang, Y.Y. A constrained least squares regression model. Inf. Sci. 2018, 429, 247–259. [Google Scholar] [CrossRef]
- Yuan, H.; Zheng, J.; Lai, L.L.; Tang, Y.Y. Semi-supervised graph-based retargeted least squares regression. Signal Proces. 2018, 142, 188–193. [Google Scholar] [CrossRef]
- Ruppert, D.; Wand, M.P. Multivariate locally weighted least squares regression. Ann. Stat. 1994, 22, 1346–1370. [Google Scholar] [CrossRef]
- Xiang, S.; Nie, F.; Meng, G.; Pan, C.; Zhang, C. Discriminative least squares regression for multiclass classification and feature selection. IEEE Trans. Neural Netw. Learn. Syst. 2012, 23, 1738–1754. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.Y.; Wang, L.; Xiang, S.; Liu, C.L. Retargeted least squares regression algorithm. IEEE Trans. Neural Netw. Learn. Syst. 2015, 26, 2206–2213. [Google Scholar] [CrossRef] [PubMed]
- De la Torre, F. A least-squares framework for component analysis. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 1041–1055. [Google Scholar] [CrossRef]
- Wen, J.; Xu, Y.; Li, Z.; Ma, Z.; Xu, Y. Inter-class sparsity based discriminative least square regression. Neural Netw. 2018, 102, 36–47. [Google Scholar] [CrossRef]
- Jolliffe, I. Principal Component Analysis, International Encyclopedia of Statistical Science; Springer: Berlin/Heidelberg, Germany, 2011; pp. 1094–1096. [Google Scholar]
- Bandos, T.V.; Bruzzone, L.; Camps-Valls, G. Classification of hyperspectral images with regularized linear discriminant analysis. IEEE Trans. Geosci. Remote Sens. 2009, 47, 862–873. [Google Scholar] [CrossRef]
- Lu, J.; Tan, Y.P. Regularized locality preserving projections and its extensions for face recognition. IEEE Trans. Syst. Man Cybern. Part B 2010, 40, 958–963. [Google Scholar]
- Brown, P.J.; Zidek, J.V. Adaptive multivariate ridge regression. Ann. Stat. 1980, 8, 64–74. [Google Scholar] [CrossRef]
- McDonald, G.C. Ridge regression. Wiley Interdiscip. Rev. Comput. Stat. 2009, 1, 93–100. [Google Scholar] [CrossRef]
- Işik, H.; Sezgin, E.; Avunduk, M.C. A new software program for pathological data analysis. Comput. Biol. Med. 2010, 40, 715–722. [Google Scholar] [CrossRef] [PubMed]
- Bashir, Y.; Aslam, A.; Kamran, M.; Qureshi, M.I.; Jahangir, A.; Rafiq, M.; Bibi, N.; Muhammad, N. On forgotten topological indices of some dendrimers structure. Molecules 2017, 22, 867. [Google Scholar] [CrossRef] [PubMed]
- Mahmood, Z.; Muhammad, N.; Bibi, N.; Ali, T. A review on state-of-the-art face recognition approaches. Fractals 2017, 25, 1750025. [Google Scholar] [CrossRef]
- Muhammad, N.; Bibi, N.; Qasim, I.; Jahangir, A.; Mahmood, Z. Digital watermarking using Hall property image decomposition method. Pattern Anal. Appl. 2018, 21, 997–1012. [Google Scholar] [CrossRef]
- Muhammad, N.; Bibi, N.; Wahab, A.; Mahmood, Z.; Akram, T.; Naqvi, S.; Sook, H.; Kim, D.-G. RImage de-noising with subband replacement and fusion process using bayes estimators. Comput. Electron. Eng. 2018, 70, 413–427. [Google Scholar] [CrossRef]
- Saunders, C.; Gammerman, A.; Vovk, V. Ridge Regression Learning Algorithm in Dual Variables; University of London: London, UK, 1998. [Google Scholar]
- Xue, H.; Zhu, Y.; Chen, S. Local ridge regression for face recognition. Neurocomputing 2009, 72, 1342–1346. [Google Scholar] [CrossRef]
- Huang, G.B.; Zhou, H.; Ding, X.; Zhang, R. Extreme learning machine for regression and multiclass classification. IEEE Trans. Syst. Man Cybern. Part B 2012, 42, 513–529. [Google Scholar] [CrossRef]
- Zhang, Y.; Wainwright, M.J.; Duchi, J.C. Communication-efficient algorithms for statistical optimization. Adv. Neural Inf. Process. Syst. 2012, 1502–1510. [Google Scholar] [CrossRef]
- An, S.; Liu, W.; Venkatesh, S. Face recognition using kernel ridge regression. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Minneapolis, MN, USA, 17–22 June 2007; pp. 1–7. [Google Scholar]
- Liu, E.; Song, Y.; Liang, J. An accelerator for kernel ridge regression algorithms based on data partition. J. Univ. Sci. Technol. China 2018, 48, 284–289. [Google Scholar]
- Li, Z.; Lai, Z.; Xu, Y.; Zhang, D. A locality-constrained and label embedding dictionary learning algorithm for image classification. IEEE Trans. Neural Netw. Learn. Syst. 2017, 28, 278–293. [Google Scholar] [CrossRef] [PubMed]
- Yi, Y.; Shi, Y.; Zhang, H.; Wang, J.; Kong, J. Label propagation based semi-supervised non-negative matrix factorization for feature extraction. Neurocomputing 2015, 149, 1021–1037. [Google Scholar] [CrossRef]
- Yi, Y.; Bi, C.; Li, X.; Wang, J.; Kong, J. Semi-supervised local ridge regression for local matching based face recognition. Neurocomputing 2015, 167, 132–146. [Google Scholar] [CrossRef]
- Yi, Y.; Qiao, S.; Zhou, W.; Zheng, C.; Liu, Q.; Wang, J. Adaptive multiple graph regularized semi-supervised extreme learning machine. Soft Comput. 2018, 22, 3545–3562. [Google Scholar] [CrossRef]
- Rwebangira, M.R.; Lafferty, J. Local Linear Semi-Supervised Regression; School of Computer Science Carnegie Mellon University: Pittsburgh, PA, USA, 2009; p. 15213. [Google Scholar]
- Chang, X.; Lin, S.B.; Zhou, D.X. Distributed semi-supervised learning with kernel ridge regression. J. Mach. Learn. Res. 2017, 18, 1–22. [Google Scholar]
- Zhu, X.; Ghahramani, Z. Learning from Labeled and Unlabeled Data with Label Propagation. 2002. Available online: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.14.3864&rep=rep1&type=pdf (accessed on 14 December 2018).
- Wang, F.; Zhang, C. Label propagation through linear neighborhoods. IEEE Trans. Knowl. Data Eng. 2008, 20, 55–67. [Google Scholar] [CrossRef]
- Zhu, X.; Ghahramani, Z.; Lafferty, J.D. Semi-supervised learning using gaussian fields and harmonic functions. In Proceedings of the 20th International conference on Machine learning (ICML-03), Washington, DC, USA, 21–24 August 2003; pp. 912–919. [Google Scholar]
- Zhou, D.; Bousquet, O.; Lal, T.N.; Weston, J.; Schölkopf, B. Learning with local and global consistency. Adv. Neural Inf. Process. Syst. 2004, 321–328. [Google Scholar] [CrossRef]
- Qiao, L.; Zhang, L.; Chen, S.; Shen, D. Data-driven Graph Construction and Graph Learning: A. Review. Neurocomputing 2018, 312, 336–351. [Google Scholar] [CrossRef]
- Cheng, B.; Yang, J.; Yan, S.; Fu, Y.; Huang, TS. Learning With l1-Graph for Image Analysis. IEEE Trans. Image Process. 2010, 19, 858–866. [Google Scholar] [CrossRef]
- Rohban, M.H.; Rabiee, H.R. Supervised neighborhood graph construction for semi-supervised classification. Pattern Recognit. 2012, 45, 1363–1372. [Google Scholar] [CrossRef]
- Wright, J.; Yang, A.Y.; Ganesh, A.; Sastry, S.S.; Ma, Y. Robust face recognition via sparse representation. IEEE Trans. Pattern Anal. Mach. Intell. 2009, 31, 210–227. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Xu, Y.; Yang, J.; Li, X.; Zhang, D. A survey of sparse representation: Algorithms and applications. IEEE Access 2015, 3, 490–530. [Google Scholar] [CrossRef]
- Nasrabadi, N.M. Pattern recognition and machine learning. J. Electron. Imaging 2007, 16, 049901. [Google Scholar]
- Cai, D.; He, X.; Han, J.; Huang, T.S. Graph regularized nonnegative matrix factorization for data representation. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 33, 1548–1560. [Google Scholar] [PubMed]
- Georghiades, A.; Belhumeur, P.; Kriegman, D. Yale Face Database. Center for Computational Vision and Control at Yale University. 1997, 2, p. 6. Available online: http://cvc.yale.edu/projects/yalefaces/yalefa (accessed on 10 December 2002).
- Samaria, F.S.; Harter, A.C. Parameterisation of a stochastic model for human face identification. In Proceedings of the Second IEEE Workshop on Applications of Computer Vision, Sarasota, FL, USA, 5–7 December 1994; pp. 138–142. [Google Scholar]
- Lee, K.C.; Ho, J.; Kriegman, D.J. Acquiring linear subspaces for face recognition under variable lighting. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 5, 684–698. [Google Scholar]
- Martinez, A.M. The AR Face Database; CVC Technical Report24; The Ohio State University: Columbus, OH, USA, 1998 June. [Google Scholar]
- Baker, S.; Bsat, M. The CMU Pose, Illumination, and Expression Database. IEEE Trans. Pattern Anal. Mach. Intell. 2003, 25, 1615. [Google Scholar]
- Duda, R.O.; Hart, P.E.; Stork, D.G. Pattern Classification; John Wiley & Sons: New York, NY, USA, 2012. [Google Scholar]

| Database | Size | Samples | Classes | Per Class |
|---|---|---|---|---|
| Yale | 32 × 32 | 165 | 15 | 11 |
| ORL | 32 × 32 | 400 | 40 | 10 |
| Extended YaleB | 32 × 32 | 2432 | 38 | 64 |
| AR | 32 × 32 | 1400 | 100 | 14 |
| CMU PIE | 32 × 32 | 1632 | 68 | 24 |
| Database | Training Sample Size | Test Sample Size | |
|---|---|---|---|
| Labeled Samples | Unlabeled Samples | ||
| Yale | 3 | 3 | 5 |
| ORL | 3 | 2 | 5 |
| Extended YaleB | 18 | 14 | 32 |
| AR | 4 | 3 | 7 |
| CMU PIE | 6 | 6 | 12 |
| Database | Yale | ORL | Extended YaleB | AR | CMU PIE |
|---|---|---|---|---|---|
| γ = 0.0001 | 89.61 ± 5.20 | 88.73 ± 4.68 | 92.08 ± 5.69 | 91.00 ± 4.39 | 92.96 ± 3.57 |
| γ = 0.001 | 91.27 ± 5.79 | 90.00 ± 3.16 | 94.22 ± 6.72 | 92.66 ± 5.45 | 95.51 ± 3.41 |
| γ = 0.01 | 91.60 ± 5.83 | 90.25 ± 3.75 | 94.40 ± 6.87 | 92.73 ± 5.06 | 95.88 ± 3.55 |
| γ = 0.1 | 91.00 ± 4.80 | 89.95 ± 3.18 | 94.24 ± 5.18 | 91.93 ± 4.86 | 95.37 + 3.87 |
| γ = 1 | 90.52 ± 4.69 | 88.76 ± 3.87 | 93.13 ± 5.60 | 91.00 ± 4.24 | 94.19 + 3.46 |
| γ = 10 | 89.87 ± 5.64 | 87.54 ± 3.25 | 92.16 ± 5.09 | 90.54 ± 3.69 | 93.27 ± 3.23 |
| γ = 100 | 88.76 ± 5.78 | 86.90 ± 3.63 | 91.40 ± 4.28 | 89.79 ± 4.50 | 92.35 ± 3.08 |
| Method | Yale | ORL | Extended YaleB | AR | CMU PIE |
|---|---|---|---|---|---|
| KNN | 84.93 ± 7.20 | 73.05 ± 2.68 | 75.42 ± 6.98 | 69.04 ± 6.93 | 90.07 ± 6.51 |
| LSR | 88.27 ± 7.97 | 84.75 ± 1.60 | 87.51 ± 7.22 | 82.66 ± 6.70 | 91.57 ± 5.41 |
| RR | 89.07 ± 7.82 | 85.75 ± 2.30 | 88.33 ± 9.23 | 86.77 ± 4.72 | 92.44 ± 5.03 |
| ICS_DLSR | 90.00 ± 2.45 | 87.60 ± 1.98 | 92.04 ± 0.81 | 90.93 ± 1.44 | 92.71 + 0.75 |
| LCLE_DL | 90.40 ± 3.00 | 87.65 ± 3.11 | 91.93 ± 0.62 | 90.91 ± 1.14 | 93.91 + 1.34 |
| SSRR-AGLP | 91.60 ± 5.83 | 90.25 ± 3.75 | 94.40 ± 6.87 | 92.73 ± 5.06 | 95.88 ± 3.55 |
| Database | Accuracy (%) | ||
|---|---|---|---|
| Yale | 88.80 ± 5.56(2/4) | 91.60 ± 5.83(3/3) | 95.20 ± 4.88(4/2) |
| ORL | 83.25±2.92(2/3) | 90.25 ± 3.75(3/2) | 92.35 ± 2.16(4/1) |
| Extended YaleB | 92.07 ± 4.20(12/20) | 92.38 ± 4.23(16/16) | 94.40 ± 6.87(18/14) |
| AR | 90.37 ± 8.07(3/4) | 92.73 ± 5.06(4/3) | 94.27 ± 4.93(5/2) |
| CMU PIE | 85.78 ± 7.95(4/8) | 95.88 ± 3.55(6/6) | 93.82 ± 4.58(8/4) |
| Database | LP | SSRR-AGLP |
|---|---|---|
| Yale | 89.56 ± 5.89 | 97.33 ± 2.30 |
| ORL | 88.13 ± 2.38 | 90.25 ± 3.81 |
| Extended YaleB | 77.39 ± 8.30 | 95.55 ± 5.15 |
| AR | 78.00 ± 9.27 | 97.63 ± 3.40 |
| CMU PIE | 88.55 ± 9.75 | 91.74 ± 6.83 |
| Database | RR | LP + RR | SSRR-AGLP |
|---|---|---|---|
| Yale | 89.07 ± 7.82 | 89.20 ± 6.89 | 91.60 ± 5.83 |
| ORL | 85.75 ± 2.30 | 87.55 ± 2.34 | 90.25 ± 3.75 |
| Extended YaleB | 88.33 ± 9.23 | 91.89 ± 7.89 | 94.40 ± 6.87 |
| AR | 86.77 ± 4.72 | 88.44 ± 4.07 | 92.73 ± 5.06 |
| CMU PIE | 92.44 ± 5.03 | 92.95 ± 5.18 | 95.88 ± 3.55 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yi, Y.; Chen, Y.; Dai, J.; Gui, X.; Chen, C.; Lei, G.; Wang, W. Semi-Supervised Ridge Regression with Adaptive Graph-Based Label Propagation. Appl. Sci. 2018, 8, 2636. https://doi.org/10.3390/app8122636
Yi Y, Chen Y, Dai J, Gui X, Chen C, Lei G, Wang W. Semi-Supervised Ridge Regression with Adaptive Graph-Based Label Propagation. Applied Sciences. 2018; 8(12):2636. https://doi.org/10.3390/app8122636
Chicago/Turabian StyleYi, Yugen, Yuqi Chen, Jiangyan Dai, Xiaolin Gui, Chunlei Chen, Gang Lei, and Wenle Wang. 2018. "Semi-Supervised Ridge Regression with Adaptive Graph-Based Label Propagation" Applied Sciences 8, no. 12: 2636. https://doi.org/10.3390/app8122636
APA StyleYi, Y., Chen, Y., Dai, J., Gui, X., Chen, C., Lei, G., & Wang, W. (2018). Semi-Supervised Ridge Regression with Adaptive Graph-Based Label Propagation. Applied Sciences, 8(12), 2636. https://doi.org/10.3390/app8122636





