Multi-Channel Electrical Impedance-Based Crack Localization of Fiber-Reinforced Cementitious Composites under Bending Conditions
Abstract
1. Introduction
2. FRCCs-Based Electrical Impedance Acquisition System and Crack Localization Algorithm
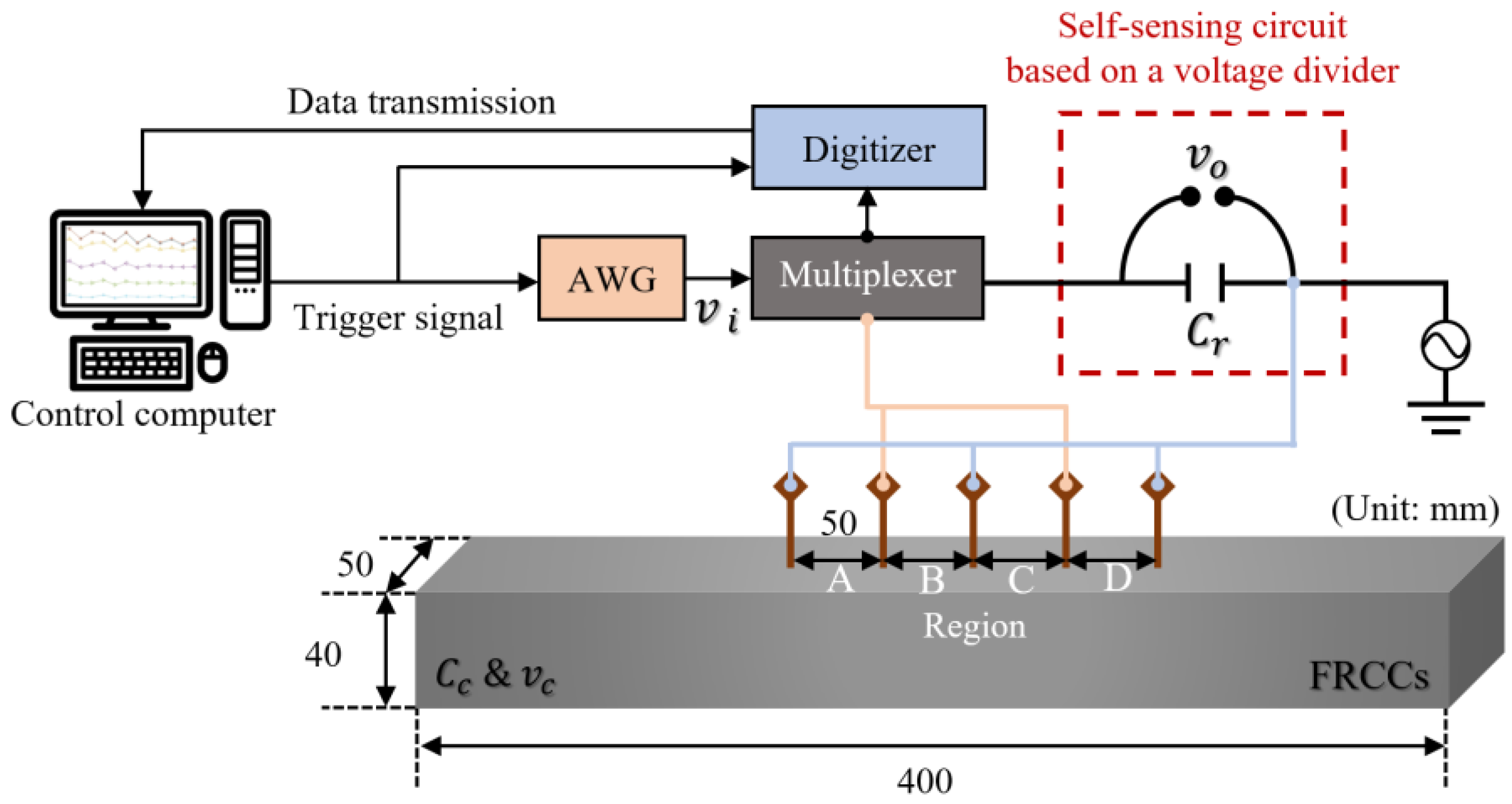
2.1. Instantaneous Multi-Channel Electrical Impedance Acquisition System
2.2. Preparation of Fiber-Reinforced Cementitious Composites
2.3. Crack Localization Algorithm
3. Experimental Validation
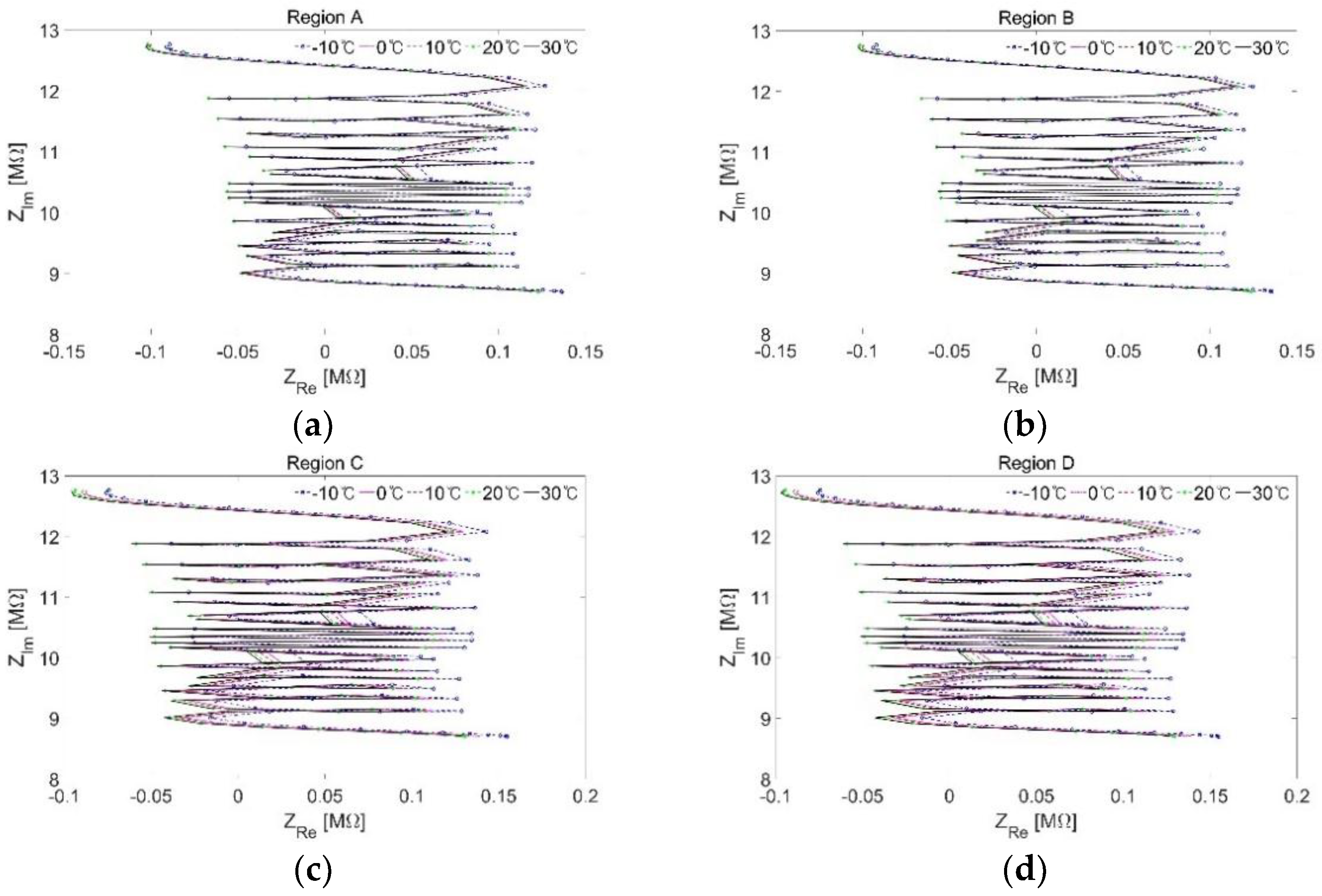
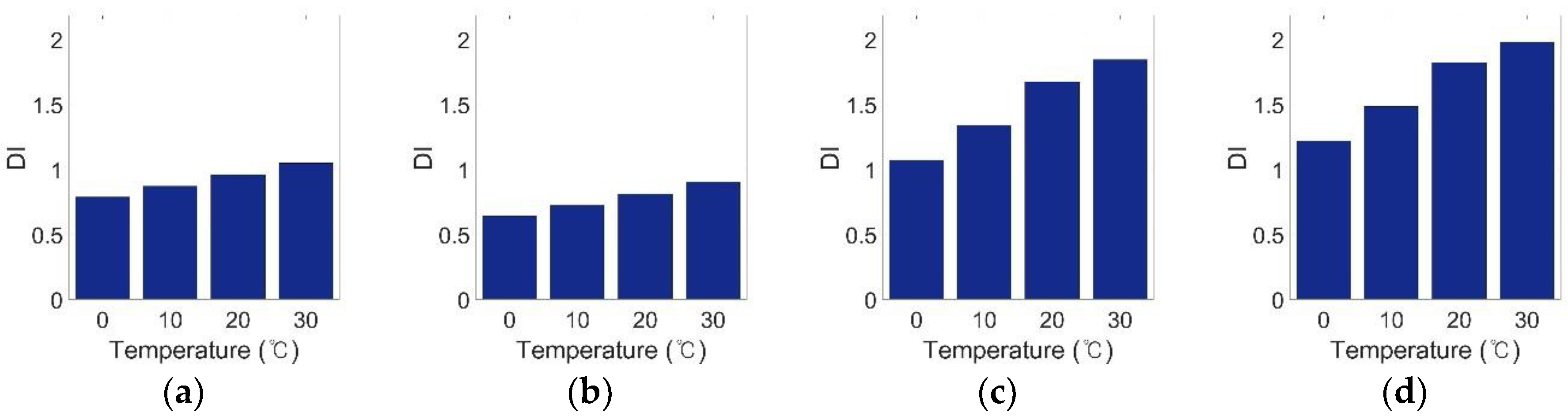
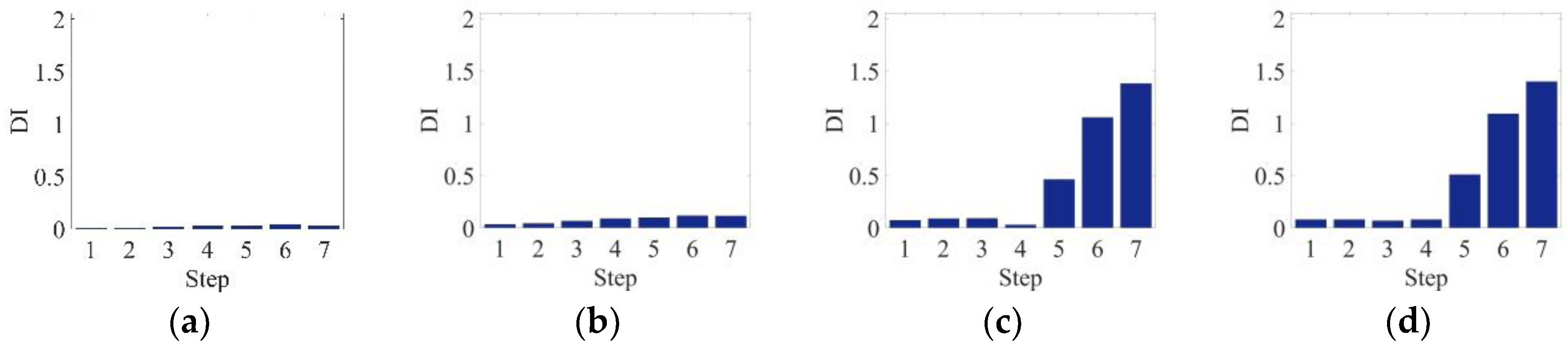
3.1. Investigation of Temperature Variation Effects
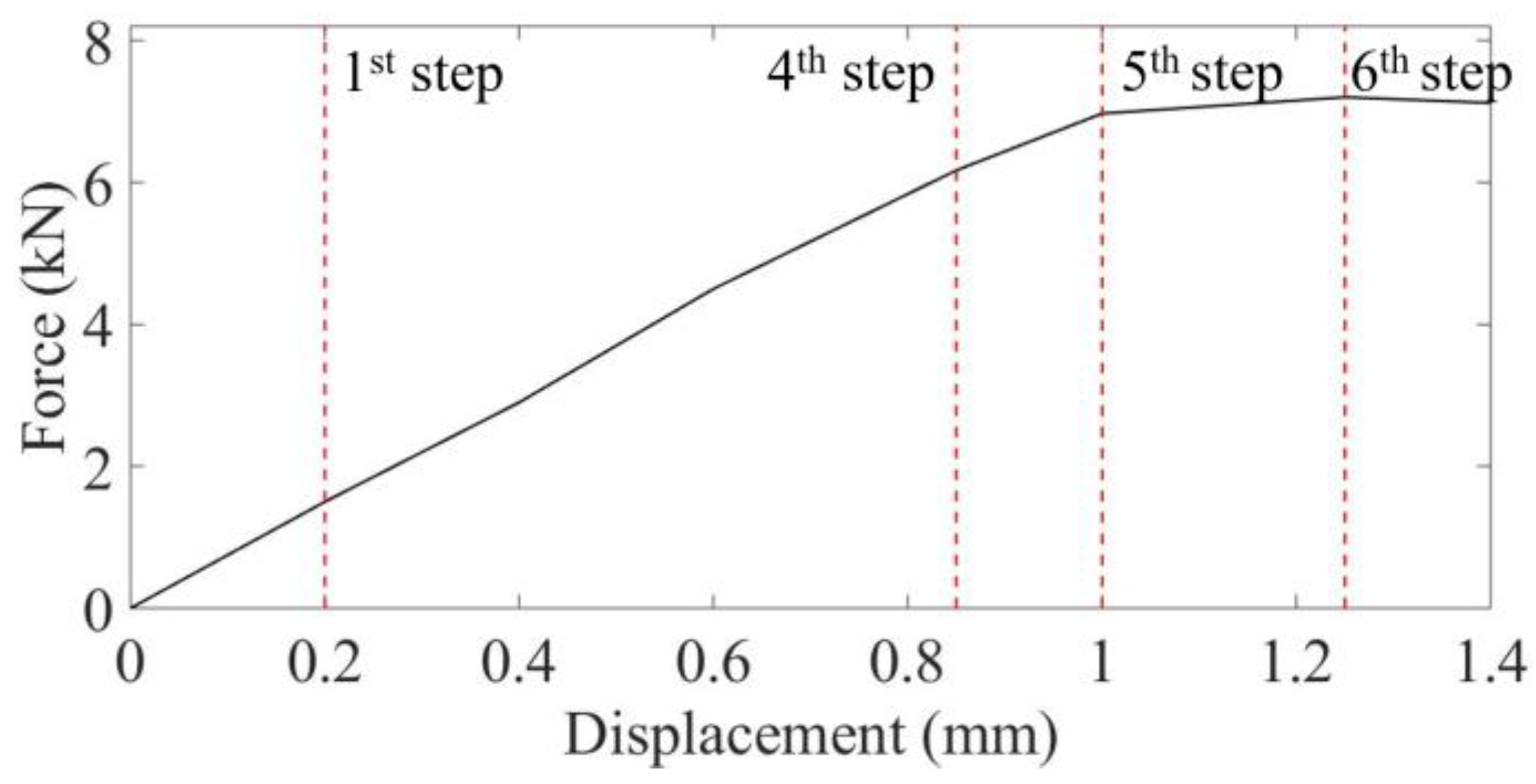
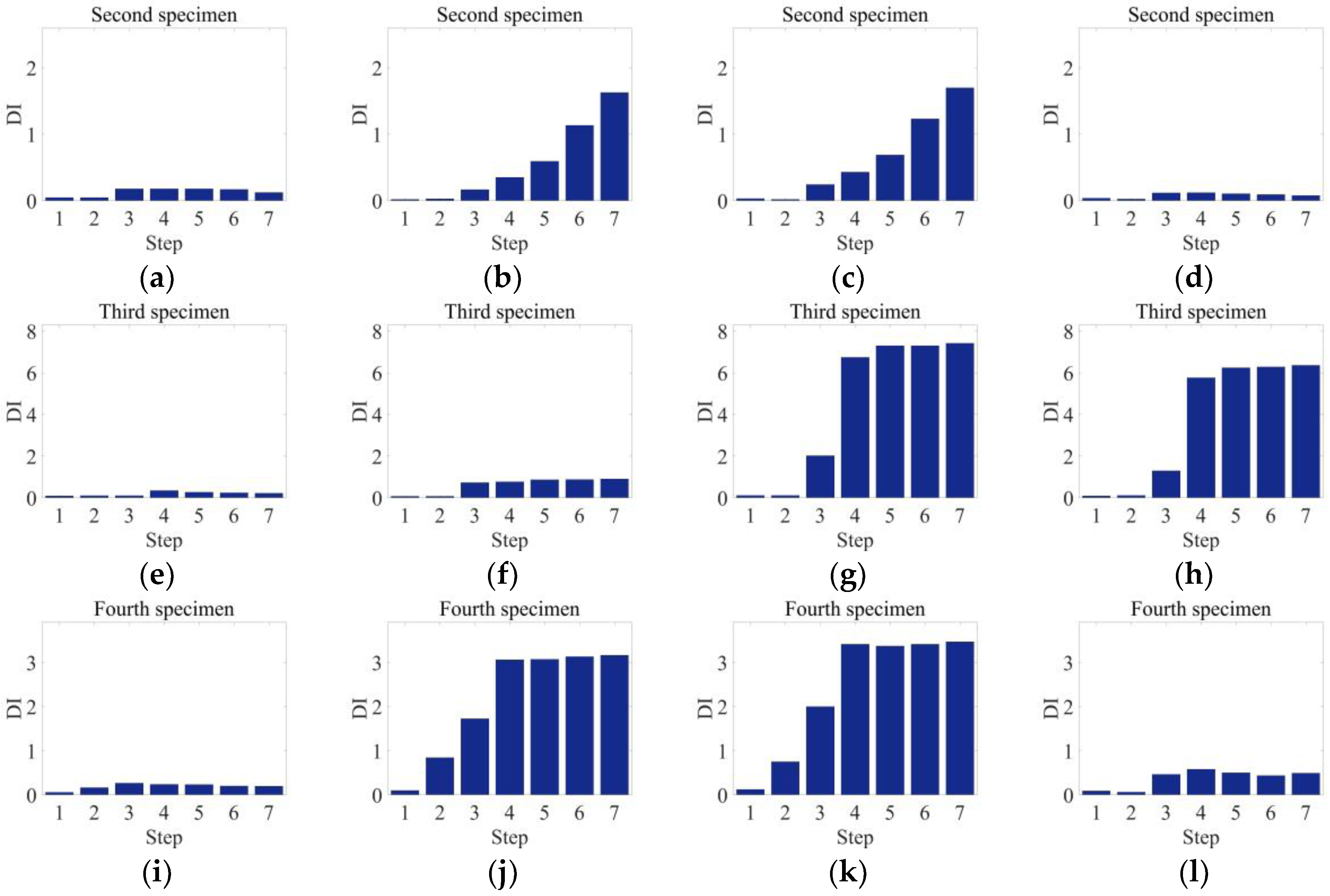
3.2. The Three-Point Bending Load Tests
4. Discussion
Author Contributions
Funding
Conflicts of Interest
References
- Lomborg, B. The Skeptical Environmentalist: Measuring the Real State of the World; Cambridge University Press: Cambridge, UK, 1998; p. 138. ISBN 978-0-521-80447-9. [Google Scholar]
- Neild, S.A.; Williams, M.S.; Mcfadden, P.D. Development of vibrating wire strain gauge for measuring small strains in concrete bemas. Strain 2005, 41, 3–9. [Google Scholar] [CrossRef]
- Kageyama, K.; Murayama, H.; Ohsawa, I.; Kanai, M.; Nagata, K.; Machijima, Y.; Matsumura, F. Acoustic emission monitoring of a reinforced concrete structure by applying new fiber-optic sensors. Smart Mater. Struct. 2005, 14, S52–S59. [Google Scholar] [CrossRef]
- Verstrynge, E.; Pfeiffer, H.; Wevers, M. A novel technique for acoustic emission monitoring in civil structures with global fiber optic sensors. Smart Mater. Struct. 2014, 23, 1–9. [Google Scholar] [CrossRef]
- Paul, S.C.; Pirskawetz, S.; Zijl, G.P.A.G.; Schmidt, W. Acoustic emission for characterizing the crack propagation in strain-hardening cement-based composites. Cem. Concr. Res. 2015, 69, 19–24. [Google Scholar] [CrossRef]
- Pimentel, R.; Guedes, T.; Melo, L.; Ferreira, G.; Goncalves, M. Damage detection assessment in reinforced concrete slabs using impact tests. Procedia Eng. 2017, 199, 1976–1981. [Google Scholar] [CrossRef]
- Ribolla, E.L.M.; Hajidehi, M.R.; Rizzo, P.; Scimemi, G.F.; Spada, A.; Giambanco, G. Ultrasonic inspection for the detection of debonding in CFRP-reinforced concrete. Struct. Infrastruct. Eng. 2018, 14, 807–816. [Google Scholar] [CrossRef]
- Voutetaki, M.E.; Papadopoulos, N.A.; Angeli, G.M.; Providakis, C.P. Investigation of a new experimental method for damage assessment of RC beams falling in shear using piezoelectric transducers. Eng. Struct. 2016, 114, 226–240. [Google Scholar] [CrossRef]
- Yang, Y.; Hu, Y.; Lu, Y. Sensitivity of PZT impedance sensors for damage detection of concrete structures. Sensors 2008, 8, 327–346. [Google Scholar] [CrossRef] [PubMed]
- Providakis, C.P.; Stefanaki, K.D.; Voutetaki, M.E.; Tsompanakis, Y.; Stavroulaki, M. Damage detection in concrete structures using a simultaneously activated multi-mode PZT active sensing system: Numerical modelling. Struct. Infrastruct. Eng. 2014, 10, 1451–1468. [Google Scholar] [CrossRef]
- Ai, D.; Luo, H.; Wang, C.; Zhu, H. Monitoring of the load-induced RC beam structural tension/compression stress and damage using piezoelectric transducers. Eng. Struct. 2018, 38–51. [Google Scholar] [CrossRef]
- Rucka, M.; Wilde, K. Experimental study on ultrasonic monitoring of splitting failure in reinforced concrete. J. Nondestruct. Eval. 2013, 32, 372–383. [Google Scholar] [CrossRef]
- Song, F.; Huang, G.L.; Kim, J.H.; Haran, S. On the study of surface wave propagation in concrete structures using a piezoelectric actuator/sensor system. Smart Mater. Struct. 2008, 17, 1–8. [Google Scholar] [CrossRef]
- Divsholi, B.S.; Yang, Y. Combined embedded and surface-bonded piezoelectric transducers for monitoring of concrete structures. NDT E Int. 2014, 65, 28–34. [Google Scholar] [CrossRef]
- Genenko, Y.A.; Glaum, J.; Hoffmann, M.J.; Albe, K. Mechanisms of aging and fatigue in ferroelectrics. Mater. Sci. Eng. B 2015, 192, 52–82. [Google Scholar] [CrossRef]
- An, Y.K.; Lim, H.J.; Kim, M.K.; Yang, J.Y.; Sohn, H.; Lee, C.G. Application of local reference-free damage detection techniques to in situ bridges. J. Struct. Eng. 2014, 140. [Google Scholar] [CrossRef]
- An, Y.K.; Park, B.J.; Sohn, H. Complete noncontact laser ultrasonic imaging for automated crack visualization in a plate. Smart Mater. Struct. 2013, 22, 1–10. [Google Scholar] [CrossRef]
- Barazzetti, L.; Scaioni, M. Crack measurement: Development, testing and applications of an automatic image-based algorithm. ISPRS J. Photogramm. 2009, 64, 285–296. [Google Scholar] [CrossRef]
- Nguyen, H.N.; Kam, T.Y.; Cheng, P.Y. An automatic approach for accurate edge detection of concrete crack utilizing 2D geometric features of crack. J. Signal Process. Syst. 2014, 77, 221–240. [Google Scholar] [CrossRef]
- Talab, A.M.A.; Huang, Z.; Xi, F.; Liu, H. Detection crack in image using Otsu method and multiple filtering in image processing techniques. Optik 2016, 127, 1030–1033. [Google Scholar] [CrossRef]
- Giri, P.; Kharkovsky, S. Detection of surface crack in concrete using measurement technique with laser displacement sensor. IEEE Trans. Instrum. Meas. 2016, 65, 1951–1953. [Google Scholar] [CrossRef]
- Sham, F.C.; Chen, N.; Long, L. Surface crack detection by flash thermography on concrete surface. Insight 2008, 50, 240–243. [Google Scholar] [CrossRef]
- Milovanovic, B.; Pecur, I.B. Review of active IR thermography for detection and characterization of defects in reinforced concrete. J. Imaging 2016, 2, 11. [Google Scholar] [CrossRef]
- Henriques, M.J.; Roque, D. Unmanned aerial vehicles (UAV) as a support to visual inspections of concrete dams. In Proceedings of the Second International Dam World Conference, Lisbon, Portugal, 21–24 April 2015. [Google Scholar]
- Kim, H.J.; Lee, J.H.; Ahn, E.J.; Cho, S.J.; Shin, M.S.; Sim, S.H. Concrete crack identification using a UAV incorporating hybrid image processing. Sensors 2017, 17, 2052. [Google Scholar] [CrossRef] [PubMed]
- Pereira, F.C.; Pereira, C.E. Embedded image processing systems for automatic recognition of cracks using UAVs. IFAC-PapersOnLine 2015, 48, 16–21. [Google Scholar] [CrossRef]
- Jang, K.Y.; An, Y.K. Multiple crack evaluation on concrete using a line laser thermography scanning system. Smart Struct. Syst. 2018, 22, 201–207. [Google Scholar] [CrossRef]
- Jang, K.Y.; Kim, N.G.; An, Y.K. Deep learning-based autonomous concrete crack evaluation through hybrid image scanning. Struct. Health Monit. 2018, (in press).
- Laskar, A.; Gu, H.; Mo, Y.L.; Song, G. Progressive collapse of a two-story reinforced concrete frame with embedded smart aggregates. Smart Mater. Strut. 2009, 18, 1–10. [Google Scholar] [CrossRef]
- Mangat, P.S. Tensile strength of steel fiber reinforced concrete. Cem. Concr. Res. 1976, 6, 245–252. [Google Scholar] [CrossRef]
- Song, P.S.; Hwang, S. Mechanical properties of high-strength steel fiber-reinforced concrete. Constr. Build. Mater. 2004, 18, 669–673. [Google Scholar] [CrossRef]
- An, Y.K.; Kim, M.K.; Sohn, H. Airplane hot spot monitoring using integrated impedance and guided wave measurements. Struct. Control. Health Monit. 2012, 19, 592–604. [Google Scholar] [CrossRef]
- You, I.; Yoo, D.Y.; Kim, S.; Kim, M.J.; Zi, G. Electrical and self-sensing properties of ultra-high-performance fiber-reinforced concrete with carbon nanotubes. Sensors 2017, 17, 2481. [Google Scholar] [CrossRef] [PubMed]
- Chung, D.D.L. Carbon materials for structural self-sensing, electromagnetic shielding and thermal interfacing. Carbon 2012, 50, 3342–3353. [Google Scholar] [CrossRef]
- Luo, J.L.; Duan, Z.D.; Zhao, T.J.; Li, Q.Y. Self-sensing property of cementitious nanocomposites hybrid with nanophase carbon nanotube and carbon black. Adv. Mater. Res. 2010, 143–144, 644–647. [Google Scholar] [CrossRef]
- Vaidya, S.; Allouche, E.N. Experimental evaluation of electrical conductivity of carbon fiber reinforced fly-ash based geopolymer. Smart Struct. Syst. 2011, 7, 27–40. [Google Scholar] [CrossRef]
- Park, J.M.; Kwon, D.J.; Wang, Z.J.; Devries, L. Review of self-sensing of damage and interfacial evaluation using electrical resistance measurements in nano/micro carbon materials-reinforced composites. Adv. Compos. Mater. 2015, 24, 197–219. [Google Scholar] [CrossRef]
- Qiao, G.; Guo, B.; Li, Z.; Ou, J.; He, Z. Corrosion behavior of a steel bar embedded in a cement-based conductive composite. Constr. Build. Mater. 2017, 134, 388–396. [Google Scholar] [CrossRef]
- Han, B.; Ding, S.; Yu, X. Intrinsic self-sensing concrete and structures: A review. Measurement 2015, 59, 110–128. [Google Scholar] [CrossRef]
- Hou, T.C.; Lynch, J.P. Electrical impedance tomographic methods for sensing strain fields and crack damage in cementitious structures. J. Intell. Mater. Syst. Struct. 2009, 20, 1363–1379. [Google Scholar] [CrossRef]
- Downey, A.; D’Alessandro, A.; Baquera, M.; Garcia-Macias, E.; Rolfes, D.; Ubertini, F.; Laflamme, S.; Castro-Triguero, R. Damage detection, localization and quantification in conductive smart concrete structures using a resistor mesh model. Eng. Struct. 2017, 148, 924–935. [Google Scholar] [CrossRef]
- Downey, A.; D’Alessandro, A.; Ubertini, F.; Laflamme, S.; Geiger, R. Biphasic DC measurement approach for enhanced measurement stability and multi-channel sampling of self-sensing multi-functional structural materials doped with carbon-based additives. Smart Mater. Struct. 2017, 26, 1–11. [Google Scholar] [CrossRef]
- Zhou, X.; Bhat, P.; Ouyang, H.; Yu, J. Localization of cracks in cementitious materials under uniaxial tension with electrical resistance tomography. Constr. Build. Mater. 2017, 138, 45–55. [Google Scholar] [CrossRef]
- Kang, M.S.; An, Y.K.; Kim, D.J. Electrical impedance-based crack detection of SFRC under varying environmental conditions. Smart Struct. Syst. 2018, 22, 1–11. [Google Scholar] [CrossRef]
- An, Y.K.; Sohn, H. Integrated impedance and guided wave based damage detection. Mech. Syst. Signal Process. 2012, 28, 50–62. [Google Scholar] [CrossRef]
- Nguyen, D.L.; Song, J.; Manathamsombat, C.; Kim, D.J. Comparative electromechanical damage-sensing behaviors of six strain-hardening. Compos. Part B Eng. 2015, 69, 159–168. [Google Scholar] [CrossRef]





| Water (kg/m3) | Cement (kg/m3) | Sand (kg/m3) | Superplasticizer (kg/m3) | Steel Fiber | |
|---|---|---|---|---|---|
| Long (kg/m3) | Short (kg/m3) | ||||
| 390 | 867.5 | 694 | 1.74 | 108.44 | 108.44 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kang, M.-S.; Lee, H.; Yim, H.J.; An, Y.-K.; Kim, D.J. Multi-Channel Electrical Impedance-Based Crack Localization of Fiber-Reinforced Cementitious Composites under Bending Conditions. Appl. Sci. 2018, 8, 2582. https://doi.org/10.3390/app8122582
Kang M-S, Lee H, Yim HJ, An Y-K, Kim DJ. Multi-Channel Electrical Impedance-Based Crack Localization of Fiber-Reinforced Cementitious Composites under Bending Conditions. Applied Sciences. 2018; 8(12):2582. https://doi.org/10.3390/app8122582
Chicago/Turabian StyleKang, Man-Sung, Hanju Lee, Hong Jae Yim, Yun-Kyu An, and Dong Joo Kim. 2018. "Multi-Channel Electrical Impedance-Based Crack Localization of Fiber-Reinforced Cementitious Composites under Bending Conditions" Applied Sciences 8, no. 12: 2582. https://doi.org/10.3390/app8122582
APA StyleKang, M.-S., Lee, H., Yim, H. J., An, Y.-K., & Kim, D. J. (2018). Multi-Channel Electrical Impedance-Based Crack Localization of Fiber-Reinforced Cementitious Composites under Bending Conditions. Applied Sciences, 8(12), 2582. https://doi.org/10.3390/app8122582






