An Adaptive Neural Non-Singular Fast-Terminal Sliding-Mode Control for Industrial Robotic Manipulators
Abstract
:Featured Application
Abstract
1. Introduction
- The inheritance of NFTSMC advantages in terms of non-singularity, finite-time convergence, fast transient response, low steady-state errors, and high position tracking accuracy.
- The achievement of smooth control inputs with chattering behavior elimination.
- The removal of demand for an exact dynamic model by applying an adaptive radial basis function neural network to approximate an unknown robot function.
- Better tracking performance and less impact by disturbances and uncertainties compared to classic SMC and other control methods based on TSMC.
- Improved robustness and stability of the robot system, as demonstrated by Lyapunov theory.
2. Problem Statements
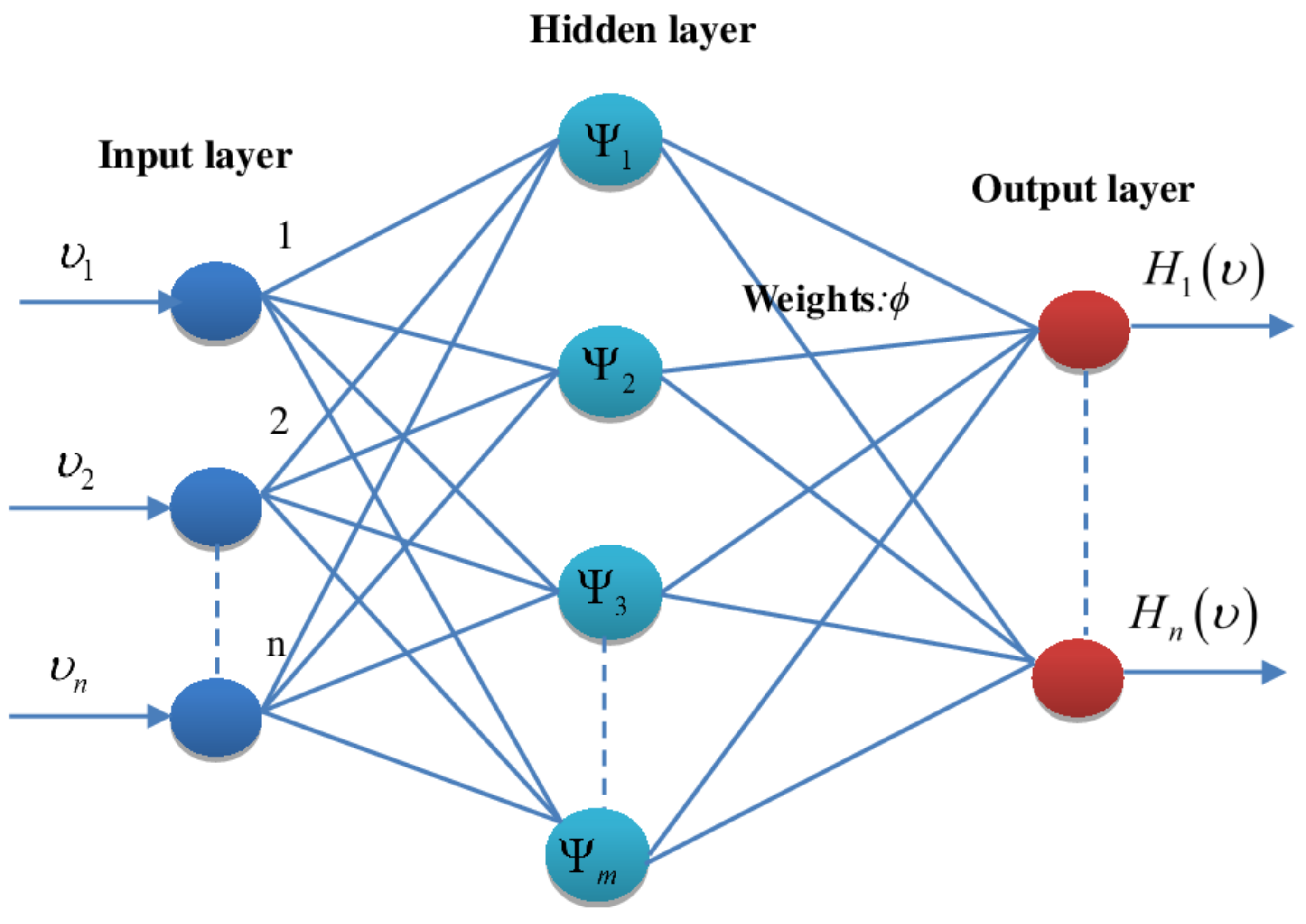
2.1. Radial Basis Function Neural Network
2.2. Dynamic Model of the Robot Manipulator
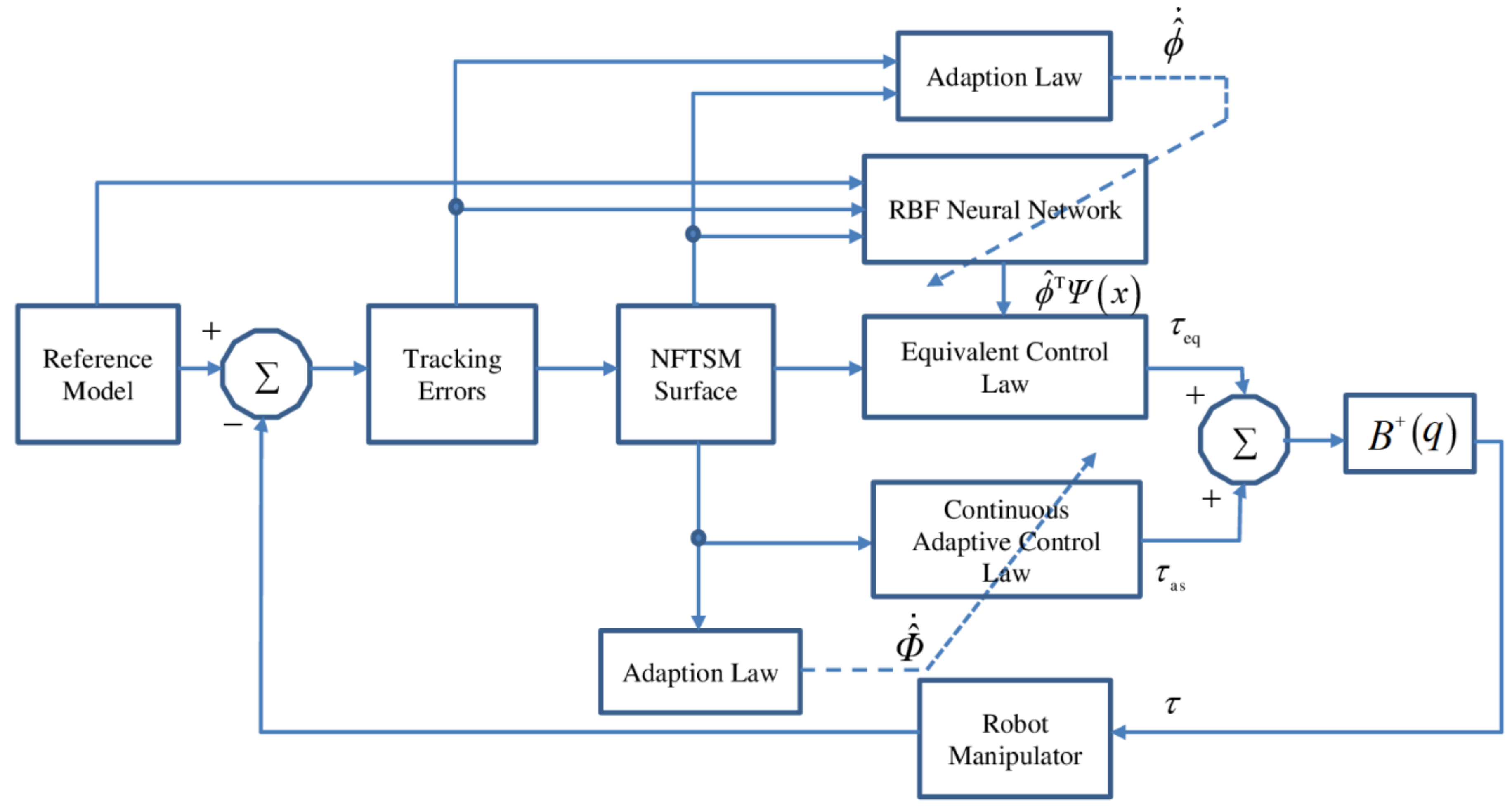
3. Design Procedure for a Control Strategy
3.1. Design Non-Singular Fast-Terminal Sliding Variable
3.2. Design an Adaptive Neural Non-Singular Fast-Terminal Sliding-Mode Control for Robotic Manipulators
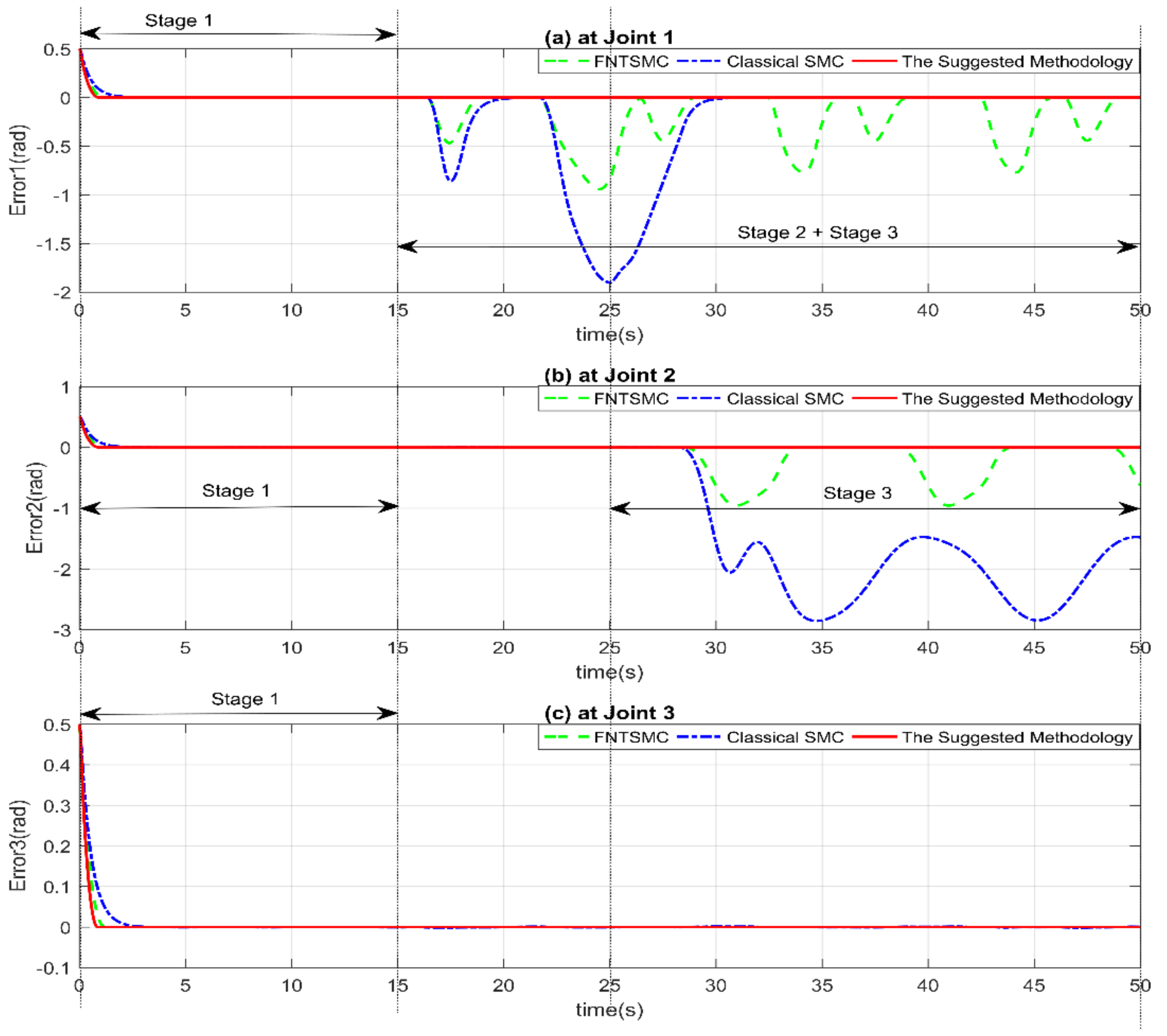
4. Simulation Analyses
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Yang, C.; Huang, Q.; Jiang, H.; Peter, O.O.; Han, J. PD control with gravity compensation for hydraulic 6-DOF parallel manipulator. Mech. Mach. Theory 2010, 45, 666–677. [Google Scholar] [CrossRef]
- Ouyang, P.R.; Zhang, W.-J.; Wu, F.-X. Nonlinear PD control for trajectory tracking with consideration of the design for control methodology. In Proceedings of the IEEE International Conference on Robotics and Automation, ICRA’02, Washington, DC, USA, 10–17 May 2002; Volume 4, pp. 4126–4131. [Google Scholar]
- Arimoto, S. Stability and robustness of PID feedback control for robot manipulators of sensory capability. In Proceedings of the Robotics Research: The First International Symposium, Bretton Woods, NH, USA, 25 August–2 September 1983; pp. 783–799. [Google Scholar]
- Su, Y.; Müller, P.C.; Zheng, C. Global Asymptotic Saturated PID Control for Robot Manipulators. IEEE Trans. Control Syst. Technol. 2010, 18, 1280–1288. [Google Scholar] [CrossRef]
- Guo, Y.; Woo, P.-Y. An adaptive fuzzy sliding mode controller for robotic manipulators. IEEE Tran. Syst. Man Cybern.-Part A Syst. Hum. 2003, 33, 149–159. [Google Scholar]
- Tran, X.-T.; Kang, H.-J. TS fuzzy model-based robust finite time control for uncertain nonlinear systems. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2015, 229, 2174–2186. [Google Scholar] [CrossRef]
- Vo, A.T.; Kang, H.-J.; Le, T.D. An Adaptive Fuzzy Terminal Sliding Mode Control Methodology for Uncertain Nonlinear Second-Order Systems. In Proceedings of the International Conference on Intelligent Computing, Wuhan, China, 15–18 August 2018; pp. 123–135. [Google Scholar]
- Sanger, T.D. Neural network learning control of robot manipulators using gradually increasing task difficulty. IEEE Trans. Robot. Autom. 1994, 10, 323–333. [Google Scholar] [CrossRef]
- Hsia, T.C.; Jung, S. A simple alternative to neural network control scheme for robot manipulators. IEEE Trans. Ind. Electron. 1995, 42, 414–416. [Google Scholar] [CrossRef]
- Vo, A.T.; Kang, H.-J.; Nguyen, V.-C. An output feedback tracking control based on neural sliding mode and high order sliding mode observer. In Proceedings of the 2017 10th International Conference on Human System Interactions (HSI), Ulsan, Korea, 17–19 July 2017; pp. 161–165. [Google Scholar]
- Van, M.; Kang, H.-J.; Suh, Y.-S.; Shin, K.-S. A robust fault diagnosis and accommodation scheme for robot manipulators. Int. J. Control Autom. Syst. 2013, 11, 377–388. [Google Scholar] [CrossRef]
- Shang, W.; Cong, S. Nonlinear computed torque control for a high-speed planar parallel manipulator. Mechatronics 2009, 19, 987–992. [Google Scholar] [CrossRef]
- Zhihong, M.; O’day, M.; Yu, X. A robust adaptive terminal sliding mode control for rigid robotic manipulators. J. Intell. Robot. Syst. 1999, 24, 23–41. [Google Scholar] [CrossRef]
- Moreno, J.A.; Negrete, D.Y.; Torres-González, V.; Fridman, L. Adaptive continuous twisting algorithm. Int. J. Control 2016. [Google Scholar] [CrossRef]
- Lim, K.; Eslami, M. Robust adaptive controller designs for robot manipulator systems. IEEE J. Robot. Autom. 1987, 3, 54–66. [Google Scholar] [CrossRef]
- Utkin, V.I. Sliding Modes in Control and Optimization; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]
- Edwards, C.; Spurgeon, S. Sliding Mode Control: Theory and Applications; Crc Press: Boca Raton, FL, USA, 1998. [Google Scholar]
- Eker, I. Sliding mode control with PID sliding surface and experimental application to an electromechanical plant. ISA Trans. 2006, 45, 109–118. [Google Scholar] [CrossRef]
- Kamal, S.; Moreno, J.A.; Chalanga, A.; Bandyopadhyay, B.; Fridman, L.M. Continuous terminal sliding-mode controller. Automatica 2016. [Google Scholar] [CrossRef]
- Xiao, B.; Hu, Q.; Zhang, Y. Adaptive sliding mode fault tolerant attitude tracking control for flexible spacecraft under actuator saturation. IEEE Trans. Control Syst. Technol. 2012, 20, 1605–1612. [Google Scholar] [CrossRef]
- Man, Z.; Paplinski, A.P.; Wu, H.R. A robust MIMO terminal sliding mode control scheme for rigid robotic manipulators. IEEE Trans. Autom. Control 1994, 39, 2464–2469. [Google Scholar] [CrossRef]
- Wu, Y.; Yu, X.; Man, Z. Terminal sliding mode control design for uncertain dynamic systems. Syst. Control Lett. 1998, 34, 281–287. [Google Scholar] [CrossRef]
- Tang, Y. Terminal sliding mode control for rigid robots. Automatica 1998, 34, 51–56. [Google Scholar] [CrossRef]
- Yu, X.; Zhihong, M. Fast terminal sliding-mode control design for nonlinear dynamical systems. Circuits Syst. I Fundam. Theory 2002, 49, 261–264. [Google Scholar] [CrossRef]
- Mobayen, S. Fast terminal sliding mode controller design for nonlinear second-order systems with time-varying uncertainties. Complexity 2015, 21, 239–244. [Google Scholar] [CrossRef]
- Madani, T.; Daachi, B.; Djouani, K. Modular-controller-design-based fast terminal sliding mode for articulated exoskeleton systems. IEEE Trans. Control Syst. Technol. 2017, 25, 1133–1140. [Google Scholar] [CrossRef]
- Eshghi, S.; Varatharajoo, R. Nonsingular terminal sliding mode control technique for attitude tracking problem of a small satellite with combined energy and attitude control system (CEACS). Aerosp. Sci. Technol. 2018, 76, 14–26. [Google Scholar] [CrossRef]
- Safa, A.; Abdolmalaki, R.Y.; Shafiee, S.; Sadeghi, B. Adaptive nonsingular terminal sliding mode controller for micro/nanopositioning systems driven by linear piezoelectric ceramic motors. ISA Trans. 2018. [Google Scholar] [CrossRef] [PubMed]
- Lin, C.-K. Nonsingular terminal sliding mode control of robot manipulators using fuzzy wavelet networks. IEEE Trans. Fuzzy Syst. 2006, 14, 849–859. [Google Scholar] [CrossRef]
- Su, Y.; Zheng, C.; Mercorelli, P. Global finite-time stabilization of planar linear systems with actuator saturation. IEEE Trans. Circuits Syst. II Express Briefs 2017, 64, 947–951. [Google Scholar] [CrossRef]
- Su, Y.; Zheng, C. Robust finite-time output feedback control of perturbed double integrator. Automatica 2015, 60, 86–91. [Google Scholar] [CrossRef]
- Xu, S.S.-D.; Chen, C.-C.; Wu, Z.-L. Study of nonsingular fast terminal sliding-mode fault-tolerant control. IEEE Trans. Ind. Electron. 2015, 62, 3906–3913. [Google Scholar] [CrossRef]
- Yang, L.; Yang, J. Nonsingular fast terminal sliding-mode control for nonlinear dynamical systems. Int. J. Robust Nonlinear Control 2011, 21, 1865–1879. [Google Scholar] [CrossRef]
- Chen, G.; Jin, B.; Chen, Y. Nonsingular fast terminal sliding mode posture control for six-legged walking robots with redundant actuation. Mechatronics 2018, 50, 1–15. [Google Scholar] [CrossRef]
- Utkin, V. Discussion aspects of high-order sliding mode control. IEEE Trans. Autom. Control 2016, 61, 829–833. [Google Scholar] [CrossRef]
- Feng, Y.; Zhou, M.; Zheng, X.; Han, F.; Yu, X. Full-order terminal sliding-mode control of MIMO systems with unmatched uncertainties. J. Frankl. Inst. 2018, 355, 653–674. [Google Scholar] [CrossRef]
- Feng, Y.; Han, F.; Yu, X. Chattering free full-order sliding-mode control. Automatica 2014, 50, 1310–1314. [Google Scholar] [CrossRef]
- Rubio-Astorga, G.; Sánchez-Torres, J.D.; Cañedo, J.; Loukianov, A.G. High-order sliding mode block control of single-phase induction motor. IEEE Trans. Control Syst. Technol. 2014, 22, 1828–1836. [Google Scholar] [CrossRef]
- Nentwig, M.; Mercorelli, P. Throttle valve control using an inverse local linear model tree based on a fuzzy neural network. In Proceedings of the 7th IEEE International Conference on Cybernetic Intelligent Systems, London, UK, 9–10 September 2008; pp. 1–6. [Google Scholar]
- Li, X.-J.; Yang, G.-H. Neural-network-based adaptive decentralized fault-tolerant control for a class of interconnected nonlinear systems. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 144–155. [Google Scholar] [CrossRef] [PubMed]
- Sun, R.; Wang, J.; Zhang, D.; Shao, X. Neural network-based sliding mode control for atmospheric-actuated spacecraft formation using switching strategy. Adv. Space Res. 2018, 61, 914–926. [Google Scholar] [CrossRef]
- Shen, Q.; Jiang, B.; Cocquempot, V. Adaptive fuzzy observer-based active fault-tolerant dynamic surface control for a class of nonlinear systems with actuator faults. IEEE Trans. Fuzzy Syst. 2014, 22, 338–349. [Google Scholar] [CrossRef]
- Huo, B.; Xia, Y.; Yin, L.; Fu, M. Fuzzy adaptive fault-tolerant output feedback attitude-tracking control of rigid spacecraft. IEEE Trans. Syst. Man Cybern. Syst. 2017, 47, 1898–1908. [Google Scholar] [CrossRef]
- Wang, S.-Y.; Liu, F.-Y.; Chou, J.-H. Adaptive TSK fuzzy sliding mode control design for switched reluctance motor DTC drive systems with torque sensorless strategy. Appl. Soft Comput. 2018, 66, 278–291. [Google Scholar] [CrossRef]
- Spong, M.W.; Vidyasagar, M. Robot Dynamics and Control; John Willey & Sons: New York, NY, USA, 1989. [Google Scholar]
- Islam, S.; Liu, X.P. Robust sliding mode control for robot manipulators. IEEE Trans. Ind. Electron. 2011, 58, 2444–2453. [Google Scholar] [CrossRef]
- Polyakov, A.; Fridman, L. Stability notions and Lyapunov functions for sliding mode control systems. J. Frankl. Inst. 2014, 351, 1831–1865. [Google Scholar] [CrossRef]
- Bhat, S.P.; Bernstein, D.S. Finite-time stability of continuous autonomous systems. SIAM J. Control Opt. 2000, 38, 751–766. [Google Scholar] [CrossRef]
- Yu, S.; Yu, X.; Shirinzadeh, B.; Man, Z. Continuous finite-time control for robotic manipulators with terminal sliding mode. Automatica 2005, 41, 1957–1964. [Google Scholar] [CrossRef]
- Feng, Y.; Yu, X.; Man, Z. Non-singular terminal sliding mode control of rigid manipulators. Automatica 2002, 38, 2159–2167. [Google Scholar] [CrossRef]
- Armstrong, B.; Khatib, O.; Burdick, J. The explicit dynamic model and inertial parameters of the PUMA 560 arm. In Proceedings of the 1986 IEEE International Conference on Robotics and Automation, San Francisco, CA, USA, 7–10 April 1986; Volume 3, pp. 510–518. [Google Scholar]



| Control Strategy | Control Parameters | Parameter Value |
|---|---|---|
| Classical SMC | 2, 9.9, 1 | |
| NFTSMC | 5, 3, 2 | |
| 9.9, 1, 0.1 | ||
| Proposed Control Strategy (ANNFTSMC) | ||
| 0.5, 0.1, 0.01, 0.1 |
| Error Control Strategy | |||
|---|---|---|---|
| SMC | |||
| NFTSMC | |||
| ANNFTSMC |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vo, A.T.; Kang, H.-J. An Adaptive Neural Non-Singular Fast-Terminal Sliding-Mode Control for Industrial Robotic Manipulators. Appl. Sci. 2018, 8, 2562. https://doi.org/10.3390/app8122562
Vo AT, Kang H-J. An Adaptive Neural Non-Singular Fast-Terminal Sliding-Mode Control for Industrial Robotic Manipulators. Applied Sciences. 2018; 8(12):2562. https://doi.org/10.3390/app8122562
Chicago/Turabian StyleVo, Anh Tuan, and Hee-Jun Kang. 2018. "An Adaptive Neural Non-Singular Fast-Terminal Sliding-Mode Control for Industrial Robotic Manipulators" Applied Sciences 8, no. 12: 2562. https://doi.org/10.3390/app8122562
APA StyleVo, A. T., & Kang, H.-J. (2018). An Adaptive Neural Non-Singular Fast-Terminal Sliding-Mode Control for Industrial Robotic Manipulators. Applied Sciences, 8(12), 2562. https://doi.org/10.3390/app8122562






