Online Streaming Feature Selection via Conditional Independence
Abstract
1. Introduction
2. Related Work
3. Framework for Streaming Features Filtering
3.1. Notations, Definitions, and Formalizations
3.1.1. Notation Mathematical Meanings
3.1.2. Definitions
3.1.3. Formalization of Online Feature Selection with Streaming Features
3.2. Framework for Filtering Conditional Independence
3.2.1. Filtering of Null-Conditional Independence
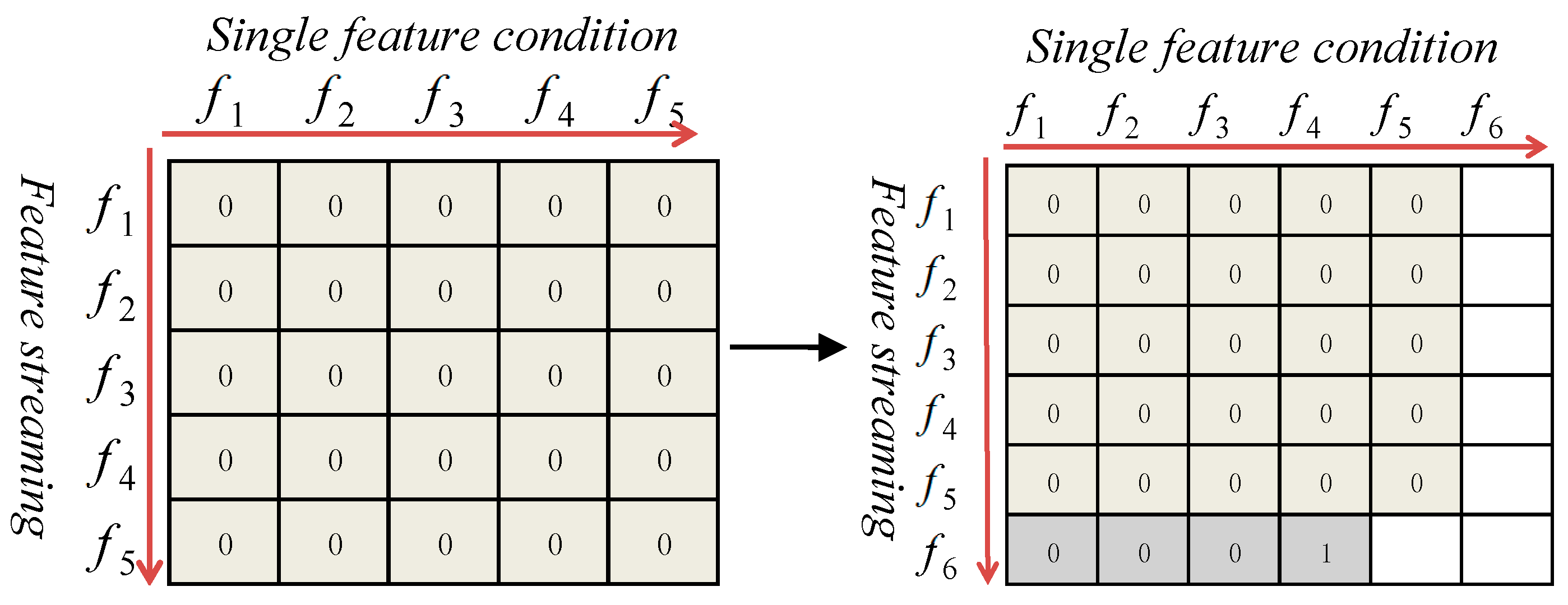
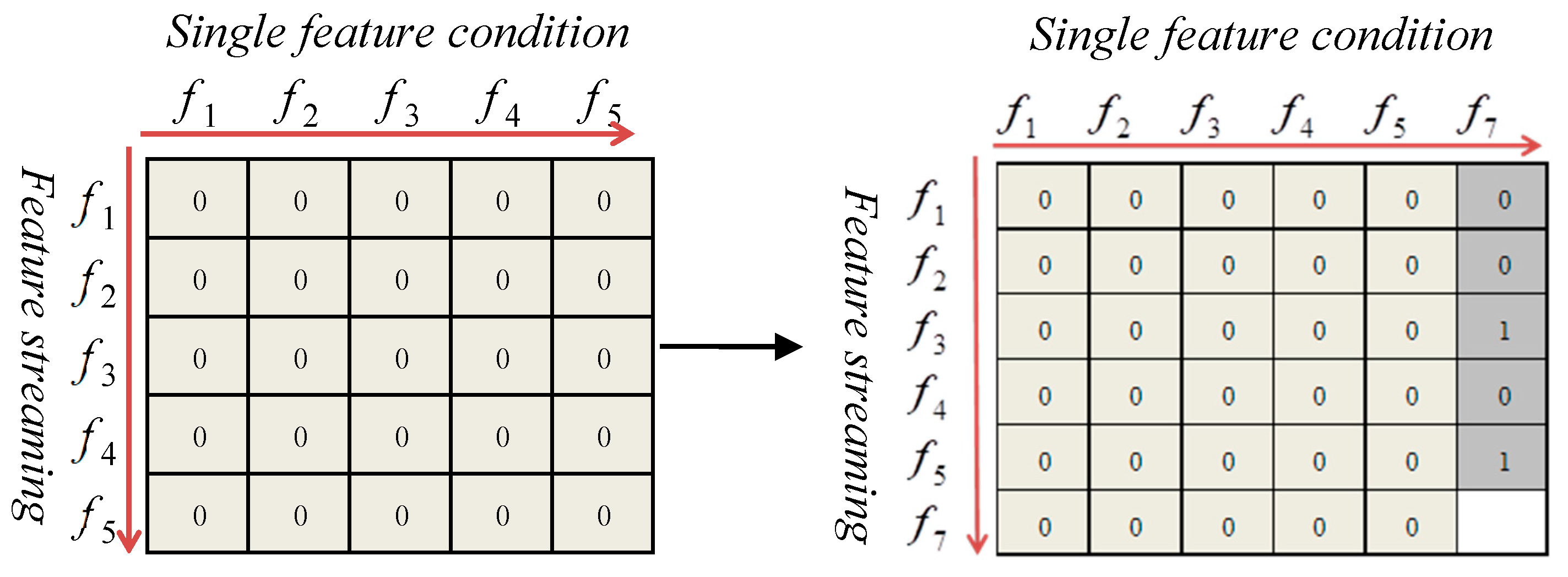
3.2.2. Filtering of Single-Conditional Independence
- Step (1): Let CFS = {f1, f2, f3, f4, f5}; C is a class attribute, and f6 is a new feature.
- Step (2): For each fi ∈CFS, (i = 1, 2, …, 5), if ∃ fi, s.t. f6 C|[ fi,], then discard f6.
- Step (3): Else CFS = CFS {f6}.
- Step (4): Return CFS.
- Step (1): Let CFS = {f1, f2, f3, f4, f5, f7}, C is a class attribute, and f7 is a new feature that is already added in the CFS through the filtering of single-conditional independence 1.
- Step (2): For each fi (i = 1, 2, …, 5), if ∃ fi, s.t. fi C|f7, then CFS = CFS/{fi}.
- Step (3): Return CFS.
3.2.3. Filtering of Multi-Conditional Independence
- Step (1): C is a class attribute; for each f ∈ CFS, Si CFS/{f},
- if ∃ Si, s.t. f C|Si, then CFS = CFS/{f}.
- Step (2): If f ∈ CFS, Si CFS/{f}, s.t. f C|Si, return CFS.
4. Online Streaming Feature Selection Algorithms
4.1. The ConInd Algorithm and Analysis
- Filtering of single-conditional independence 1: For each feature in the CFS, we determine the conditional independence with the class attribute C. If , then discard , because it is a redundant feature. Next, jump to Step 3 and continue to determine the next new feature . On the contrary, if , then feature is non-redundant with the class attribute C. The feature is then included in the CFS. It is validated through the filtering of single-conditional independence 2.
- During the filtering of single-conditional independence 2: For the new feature , the conditional independence of each feature in the CFS expected for is determined one feature at a time. If , discard f from CFS and jump to Step 3. The reason is that f and C are conditionally independent under the condition of . Therefore, the feature f is unnecessary if ∈ CFS. On the contrary, if , , the feature is kept in the CFS. Then, we continue filtering for multi-conditional independence.
4.2. The Time Complexity of ConInd
4.3. Analysis of Approximate Markov Blankets of ConInd
5. Experiments and Analysis
5.1. Experimental Setup
5.2. Number of Features through Filtering of Conditional Dependence in the ConInd Algorithm
5.3. Comparison of ConInd with Two Online Algorithms
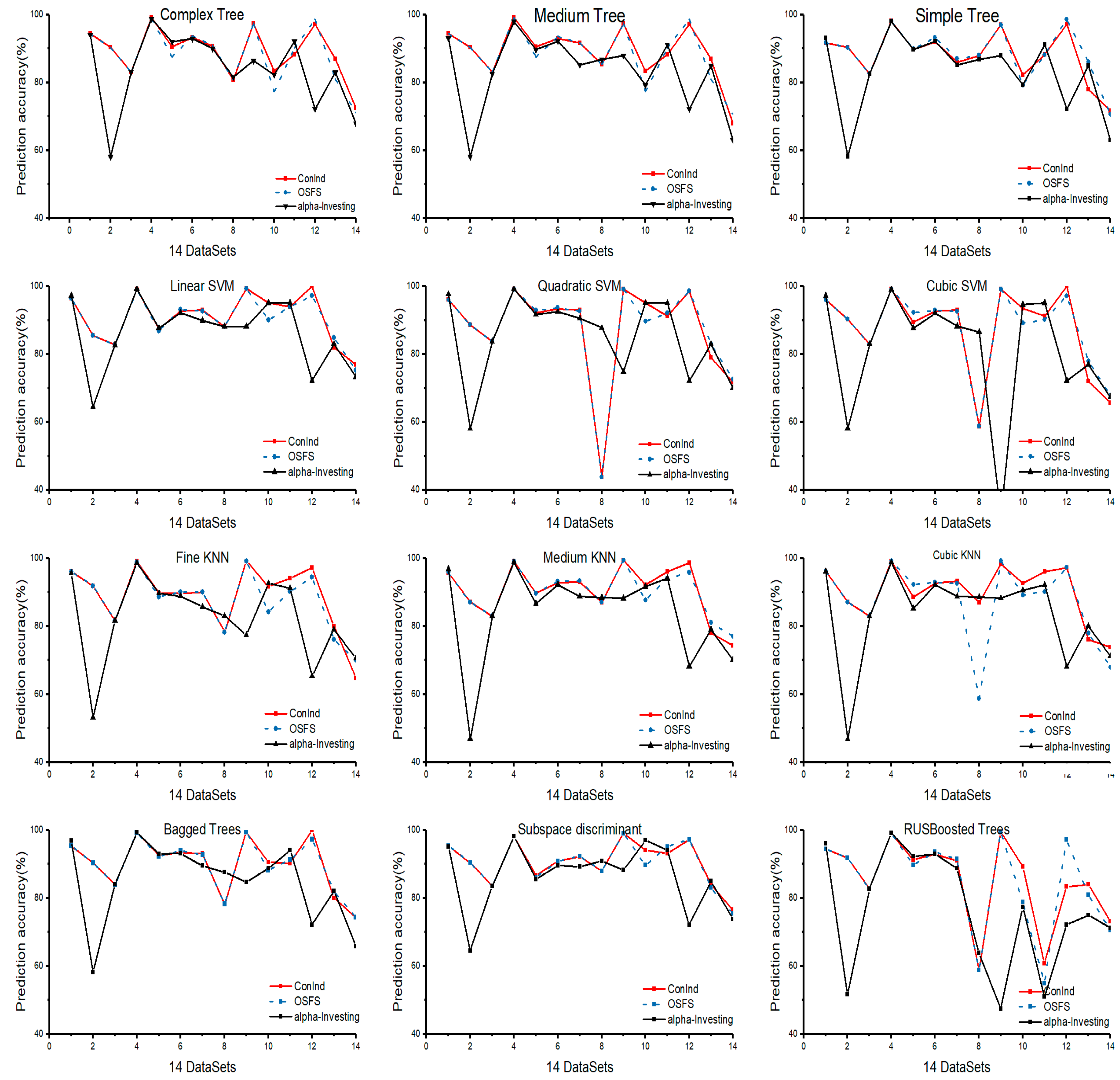
5.3.1. Prediction Accuracy
5.3.2. The Number of Selected Features and Running Time
- (a)
- The predictive accuracy of Alpha-investing is low. This means that a part of the elements in Markov blanket cannot be obtained.
- (b)
- For the OSFS algorithm, during the redundant feature analysis phase, it is possible that non-redundant features are discarded under the condition of redundant features, resulting in low predictive accuracy and fewer features being selected.
- (c)
- For the ConInd algorithm, there are two aspects that account for the large number of selected features. On the one hand, ConInd significantly outperforms OSFS and Alpha-investing in mining the elements in the Markov blanket. It can find many more elements than OSFS in the Markov blanket. On the other hand, the number of #SIC is much smaller than the number of #NIC, as presented in Table 4. This also means that the size of the feature subset for the #SIC condition is smaller than the subset of #NIC. Therefore, there is a low possibility that the feature can be discarded.
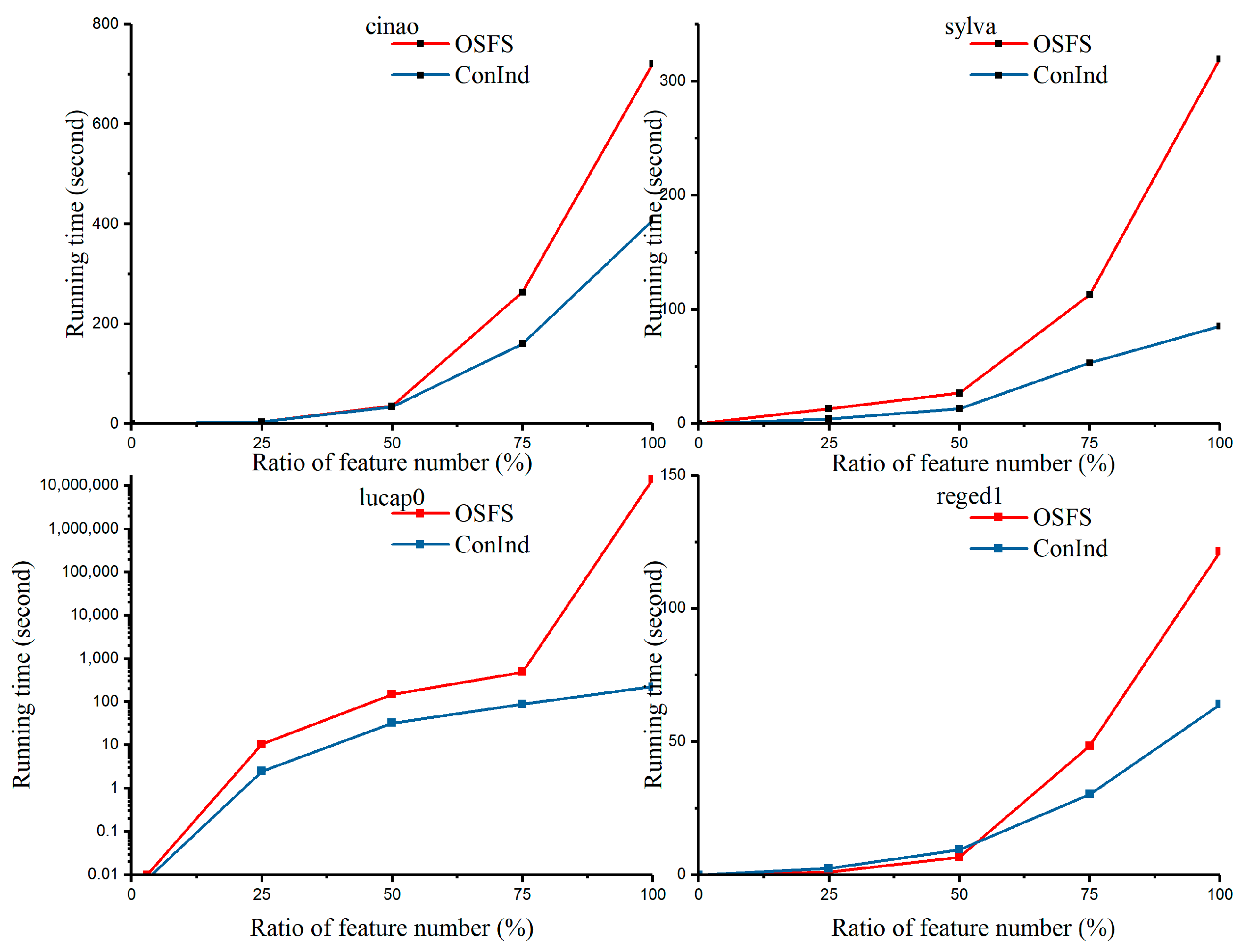
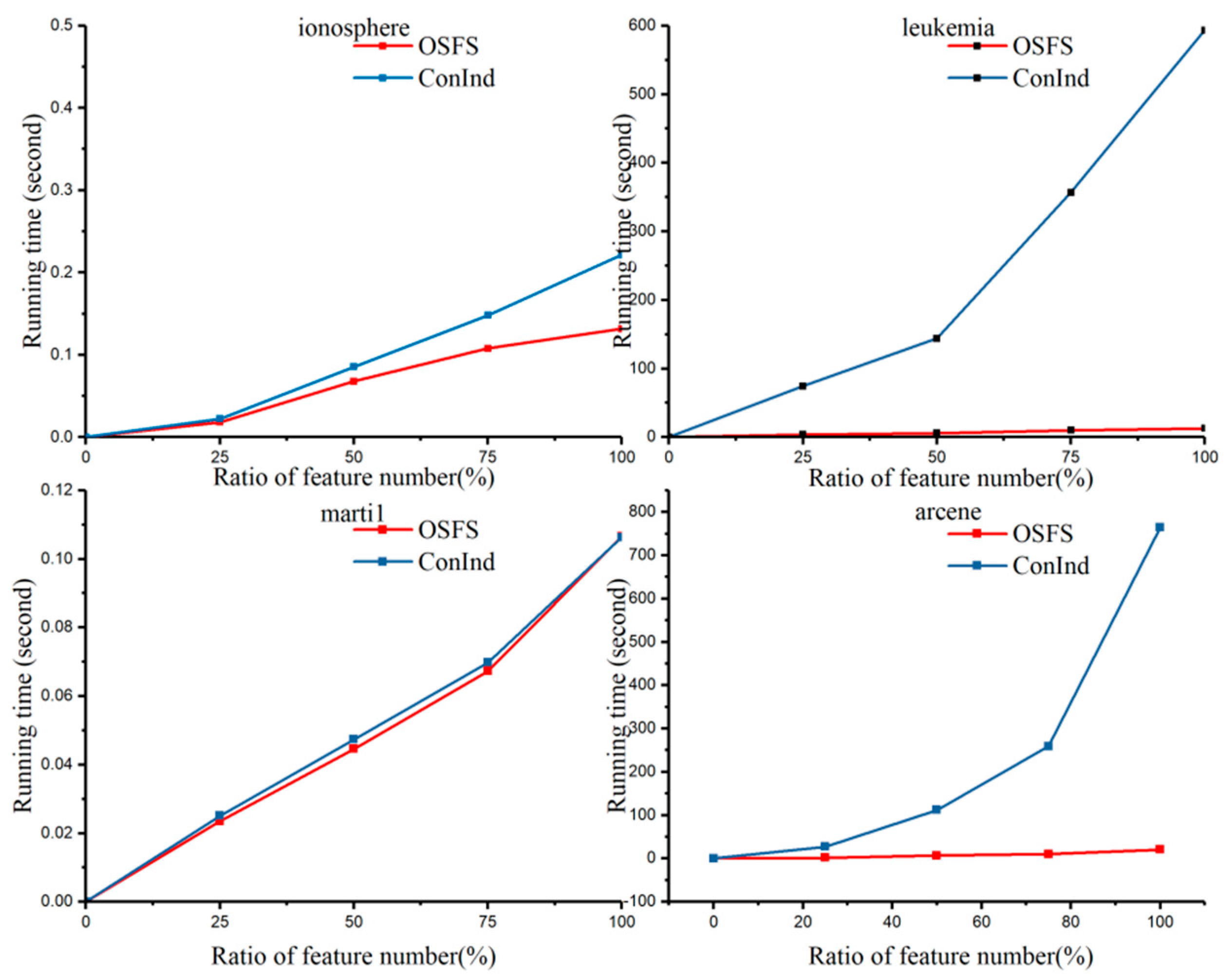
5.3.3. Variation in the Number of Features and Running Time with the Increase of Feature Ratio
5.4. Comparison of ConInd with Two Markov Blanket Algorithms
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Datasets | HITON_MB | OSFS | ConInd |
|---|---|---|---|
| wdbc | 12 22 23 27 28 | 22 23 28 | 22 23 28 |
| colon | 513 765 1582 | 765 1582 1993 | 765 1423 1582 |
| lucas0 | 1 5 9 10 11 | 1 5 9 11 | 1 5 9 11 |
| sylva | 6 8 13 14 16 18 19 20 21 24 28 29 30 37 39 42 46 49 50 52 54 60 62 65 67 71 78 81 85 88 89 93 95 99 100 102 107 110 111 116 117 121 126 133 136 141 152 170 171 173 175 176 180 181 183 186 188 189 193 195 198 202 209 216 | 21 42 46 50 52 65 85 89 93 100 111 171 173 183 193 198 202 216 | 21 42 46 50 52 65 69 85 89 93 99 100 111 116 134 138 171 173 183 186 193 198 202 216 |
| ionosphere | 1 3 5 8 17 34 | 1 3 5 8 | 1 3 5 7 8 |
| cina0 | 2 3 6 9 10 12 13 14 16 17 18 20 21 23 24 25 27 30 32 34 35 36 37 39 40 41 45 46 48 51 52 59 60 61 62 63 68 69 72 74 76 78 79 81 87 88 90 91 94 95 96 97 99 100 103 105 109 110 113 114 115 121 122 125 127 128 | 9 12 13 18 21 25 39 40 41 52 60 63 68 69 76 79 88 90 96 110 121 125 | 9 12 13 18 25 35 39 40 41 49 52 53 60 63 68 69 76 77 79 88 90 93 96 100 107 110 121 123 124 125 |
| lucap0 | 2 3 4 6 8 9 11 13 14 18 19 20 22 24 25 26 28 30 31 35 38 42 44 45 50 51 52 53 54 56 59 62 63 64 66 67 69 70 71 73 74 75 77 78 79 80 84 85 86 88 91 93 94 96 101 105 108 112 113 114 116 117 119 120 121 122 123 124 125 126 132 133 134 135 136 137 139 140 143 | 2 6 8 22 24 26 38 42 44 45 51 52 54 59 63 64 69 70 73 78 79 84 85 91 93 94 113 116 117 120 123 124 133 137 139 143 | 2 6 8 13 18 22 24 26 27 38 41 42 44 45 51 52 54 59 63 64 69 70 73 78 79 84 85 91 93 94 113 116 117 120 123 124 133 137 139 143 |
| marti1 | 997 998 999 | 998 | 998 |
| reged1 | 26 83 251 312 321 335 344 409 421 425 453 454 503 516 561 593 594 739 780 825 904 930 939 983 | 83 251 321 344 409 425 453 593 594 739 825 930 939 | 83 251 321 344 409 425 453 593 594 739 825 930 939 |
| Lung | 39 93 132 249 277 322 368 436 486 491 498 499 510 524 588 614 628 641 704 748 755 777 792 883 892 930 936 1043 1063 1074 1111 1137 1152 1206 1273 1274 1293 1296 1333 1358 1385 1405 1414 1421 1457 1464 1471 1548 1558 1562 1575 1687 1728 1765 1767 1882 1934 1946 1957 1974 1984 1987 2027 2033 2045 2186 2223 2248 2271 2308 2311 2331 2342 2349 2369 2495 2513 2649 2682 2701 2750 2759 2826 2873 2879 2988 2997 3014 3016 3028 3074 3083 3089 3178 3190 3238 3246 | 776 1405 1534 1982 2045 2342 2548 2660 2856 2949 3244 | 368 776 786 792 1266 1328 1405 1534 1615 1791 1820 1836 1871 1957 1982 2045 2090 2294 2342 2428 2430 2513 2548 2551 2621 2660 2760 2772 2949 2988 3091 3226 3244 3279 3302 |
| prosate_GE | 2586 2935 4960 4978 5279 5599 | 2586 4960 4978 | 2586 4163 4960 5599 |
| leukemia | 1300 1528 1536 4378 4542 4866 | 1528 1536 4378 | 1516 1528 1536 4378 4853 4866 6360 6652 |
| arcene | 312 1184 1208 1552 3319 4290 4352 5144 | 1184 4352 9868 9970 10,000 | 1552 3319 4352 5144 9234 |
| Smk_can_187 | 1240 2658 3224 4736 5702 8890 11,564 16,877 17,072 19,653 19,821 | 5702 16,877 17,072 19,170 | 5702 10,082 11,564 13,492 14,552 16,877 16,878 17,072 19,653 |
References
- Tang, J.; Alelyani, S.; Liu, H. Feature selection for classification: A review. Data Classif. Algorithms Appl. 2014, 37. [Google Scholar] [CrossRef]
- Kumar, V. Feature selection: A literature review. Smart Comput. Rev. 2014, 4. [Google Scholar] [CrossRef]
- Li, J.; Cheng, K.; Wang, S.; Morstatter, F.; Trevino, R.P.; Tang, J.; Liu, H. Feature selection: A data perspective. ACM Comput. Surv. (CSUR) 2017, 50, 94. [Google Scholar] [CrossRef]
- Cai, J.; Luo, J.; Wang, S.; Yang, S. Feature selection in machine learning: A new perspective. Neurocomputing 2018, 300, 70–79. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhang, P.; Long, G.; Ding, W.; Zhang, C.; Wu, X. Online learning from trapezoidal data streams. IEEE Trans. Knowl. Data Eng. 2016, 28, 2709–2723. [Google Scholar] [CrossRef]
- Wu, X.; Yu, K.; Ding, W.; Wang, H.; Zhu, X. Online feature selection with streaming features. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1178–1192. [Google Scholar] [PubMed]
- Li, Y.; Li, T.; Liu, H. Recent advances in feature selection and its applications. Knowl. Inf. Syst. 2017, 53, 551–577. [Google Scholar] [CrossRef]
- Yu, K.; Ding, W.; Simovici, D.A.; Wang, H.; Pei, J.; Wu, X. Classification with streaming features: An emerging-pattern mining approach. ACM Trans. Knowl. Discov. Data 2015, 9, 30. [Google Scholar] [CrossRef]
- Mairal, J.; Bach, F.; Ponce, J.; Sapiro, G. Online learning for matrix factorization and sparse coding. J. Mach. Learn. Res. 2010, 11, 19–60. [Google Scholar]
- Wang, J.; Zhao, P.; Hoi, S.C.; Jin, R. Online feature selection and its applications. IEEE Trans. Knowl. Data Eng. 2014, 26, 698–710. [Google Scholar] [CrossRef]
- Jia, X.; Kuo, B.-C.; Crawford, M.M. Feature mining for hyperspectral image classification. Proc. IEEE 2013, 101, 676–697. [Google Scholar] [CrossRef]
- Xie, W.; Zhu, F.; Jiang, J.; Lim, E.-P.; Wang, K. Topicsketch: Real-time bursty topic detection from twitter. IEEE Trans. Knowl. Data Eng. 2016, 28, 2216–2229. [Google Scholar] [CrossRef]
- Ashfaq, R.A.R.; Wang, X.-Z.; Huang, J.Z.; Abbas, H.; He, Y.-L. Fuzziness based semi-supervised learning approach for intrusion detection system. Inf. Sci. 2017, 378, 484–497. [Google Scholar] [CrossRef]
- Medhat, F.; Chesmore, D.; Robinson, J. Automatic classification of music genre using masked conditional neural networks. IEEE Int. Conf. Data Min. 2017, 979–984. [Google Scholar] [CrossRef]
- Wu, X.; Zhu, X.; Wu, G.-Q.; Ding, W. Data mining with big data. IEEE Trans. Knowl. Data Eng. 2014, 26, 97–107. [Google Scholar]
- Hu, X.G.; Zhou, P.; Li, P.P.; Wang, J.; Wu, X.D. A survey on online feature selection with streaming features. Front. Comput. Sci. 2018, 12, 479–493. [Google Scholar] [CrossRef]
- Ni, J.; Fei, H.; Fan, W.; Zhang, X. Automated medical diagnosis by ranking clusters across the symptom-disease network. In Proceedings of the 2017 IEEE International Conference on Data Mining (ICDM), New Orleans, LA, USA, 18–21 November 2017; pp. 1009–1014. [Google Scholar]
- Zhou, J.; Foster, D.; Stine, R.; Ungar, L. Streaming feature selection using alpha-investing. In Proceedings of the Eleventh ACM SIGKDD International Conference on Knowledge Discovery in Data Mining, Chicago, IL, USA, 21–24 August 2005; ACM: New York, NY, USA, 2005; pp. 384–393. [Google Scholar]
- Yu, K.; Wu, X.; Ding, W.; Pei, J. Scalable and accurate online feature selection for big data. ACM Trans. Knowl. Discov. Data 2016, 11, 16. [Google Scholar] [CrossRef]
- Aliferis, C.F.; Statnikov, A.; Tsamardinos, I.; Mani, S.; Koutsoukos, X.D. Local causal and markov blanket induction for causal discovery and feature selection for classification part i: Algorithms and empirical evaluation. J. Mach. Learn. Res. 2010, 11, 171–234. [Google Scholar]
- Yu, K.; Wu, X.; Zhang, Z.; Mu, Y.; Wang, H.; Ding, W. Markov blanket feature selection with non-faithful data distributions. In Proceedings of the 2013 IEEE 13th International Conference on Data Mining, Dallas, TX, USA, 7–10 December 2013; pp. 857–866. [Google Scholar]
- Yu, K.; Wu, X.; Ding, W.; Mu, Y.; Wang, H. Markov blanket feature selection using representative sets. IEEE Trans. Neural Netw. Learn. Syst. 2017, 28, 2775–2788. [Google Scholar] [CrossRef]
- Izmailov, R.; Lindqvist, B.; Lin, P. Feature selection in learning using privileged information. In Proceedings of the 2017 IEEE International Conference on Data Mining Workshops (ICDMW), New Orleans, LA, USA, 18–21 November 2017; pp. 957–963. [Google Scholar]
- Kaul, A.; Maheshwary, S.; Pudi, V. Autolearn—Automated feature generation and selection. In Proceedings of the 2017 IEEE International Conference on Data Mining (ICDM), New Orleans, LA, USA, 18–21 November 2017; pp. 217–226. [Google Scholar]
- Gheyas, I.A.; Smith, L.S. Feature subset selection in large dimensionality domains. Pattern Recognit. 2010, 43, 5–13. [Google Scholar] [CrossRef]
- Lin, Y.; Hu, Q.; Zhang, J.; Wu, X. Multi-label feature selection with streaming labels. Inf. Sci. 2016, 372, 256–275. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhang, P.; Long, G.; Ding, W.; Zhang, C.; Wu, X. Towards mining trapezoidal data streams. In Proceedings of the 2015 IEEE International Conference on Data Mining, Atlantic City, NJ, USA, 14–17 November 2015; pp. 1111–1116. [Google Scholar]
- Perkins, S.; Theiler, J. Online feature selection using grafting. In Proceedings of the 20th International Conference on Machine Learning (ICML-03), Washington, DC, USA, 21–24 August 2003; pp. 592–599. [Google Scholar]
- Wang, J.; Wang, M.; Li, P.; Liu, L.; Zhao, Z.; Hu, X.; Wu, X. Online feature selection with group structure analysis. IEEE Trans. Knowl. Data Eng. 2015, 27, 3029–3041. [Google Scholar] [CrossRef]
- Tsamardinos, I.; Aliferis, C.F. Towards principled feature selection: Relevancy, filters and wrappers. In Proceedings of the Ninth International Workshop on Artificial Intelligence & Statistics, Key West, FL, USA, 3–6 January 2003. [Google Scholar]
- Aliferis, C.F.; Tsamardinos, I.; Statnikov, A.R.; Brown, L.E. Causal explorer: A causal probabilistic network learning toolkit for biomedical discovery. In Proceedings of the International Conference on Mathematics and Engineering Techniques in Medicine and Biological Scienes, Las Vegas, NV, USA, 23–26 June 2003; pp. 371–376. [Google Scholar]
- Aliferis, C.F.; Tsamardinos, I.; Statnikov, A. Hiton: A novel markov blanket algorithm for optimal variable selection. AMIA Ann. Symp. Proc. 2003, 2003, 21. [Google Scholar]
- Tsamardinos, I.; Aliferis, C.F.; Statnikov, A. Time and sample efficient discovery of markov blankets and direct causal relations. In Proceedings of the Ninth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Washington, DC, USA, 24–27 August 2003; ACM: New York, NY, USA, 2003; pp. 673–678. [Google Scholar]
- Statnikov, A.; Lytkin, N.I.; Lemeire, J.; Aliferis, C.F. Algorithms for discovery of multiple markov boundaries. J. Mach. Learn. Res. 2013, 14, 499–566. [Google Scholar] [PubMed]
- Yu, K.; Wu, X.; Wang, H.; Ding, W. Causal discovery from streaming features. In Proceedings of the 2010 IEEE 10th International Conference on Data Mining, Sydney, Australia, 13–17 December 2010; pp. 1163–1168. [Google Scholar]
- Pellet, J.-P.; Elisseeff, A. Using markov blankets for causal structure learning. J. Mach. Learn. Res. 2008, 9, 1295–1342. [Google Scholar]
- Lim, Y.; Kang, U. Time-weighted counting for recently frequent pattern mining in data streams. Knowl. Inf. Syst. 2017, 53, 391–422. [Google Scholar] [CrossRef]
- Chen, C.-C.; Shuai, H.-H.; Chen, M.-S. Distributed and scalable sequential pattern mining through stream processing. Knowl. Inf. Syst. 2017, 53, 365–390. [Google Scholar] [CrossRef]
- Yu, K.; Ding, W.; Wu, X. Lofs: A library of online streaming feature selection. Knowl.-Based Syst. 2016, 113, 1–3. [Google Scholar] [CrossRef]
- Polson, N.G.; Sokolov, V. Deep learning: A bayesian perspective. Bayesian Anal. 2017, 12, 1275–1304. [Google Scholar] [CrossRef]


| Framework: The ConInd Framework |
| 1. Initialization: class attribute C; candidate feature set: CFS; selected feature set ; 2. Get a new feature, , at time ti. 3. Filtering of null-conditional independence: If is an irrelevant feature, discard ; if not, enter Step 4. 4. Filtering of single-conditional independence: Remove part of redundant features. 4.1 If is a redundant feature in the filtering of single-conditional independence 1 condition, discard ; if not, , enter Step 4.2. 4.2 If x ∈ CFS is a redundant feature in the filtering of single-conditional independence 2 condition, discard x from CFS; if not, enter Step 5. 5. Filtering of multi-conditional independence: Further remove redundant features in CFS in the filtering of the multi-conditional independence condition. 6. Repeat Steps 2–5 until there are no new features or the stopping criterion is met. 7. When SF = CFS, output the selected features, SF. |

| Notation | Mathematical Meanings |
|---|---|
| Xi | the data set at time ti, denoted as Xi = [x1, x2, ..., xn]T ∈ Rn×i |
| S | the set of feature space under the streaming features |
| f | a feature, f ∈ S |
| ti | a time point of the ith arriving feature |
| fi | the ith arriving feature at time ti |
| CFS | candidate feature set at current time |
| C | class attribute (target variable) |
| P(x) | event probability of feature x |
| P(.|.) | conditional probability |
| ρ | a threshold |
| α | significance levels of 0.05 or 0.01 in statistics |
| MB(C) | Markov blanket of C |
| a ⊥ b | a is independent of b |
| Phase of Filtering | Cost |
|---|---|
| null-conditional independence | O(|N|) |
| single-conditional independence | O((|N| − |Ni|)|CFS|) |
| multi-conditional independence | O(|M||CFS|2|CFS|) |
| Datasets | # | Size | Dataset | # | Size |
|---|---|---|---|---|---|
| wdbc | 30 | 569 | marti1 | 1024 | 500 |
| colon | 2000 | 62 | reged1 | 999 | 500 |
| lucas0 | 11 | 2000 | lung | 3312 | 203 |
| sylva | 216 | 13,086 | prosate_GE | 5966 | 102 |
| ionosphere | 34 | 351 | leukemia | 7066 | 72 |
| cina0 | 132 | 16,033 | arcene | 10,000 | 100 |
| lucap0 | 143 | 2000 | Smk_can_187 | 19,993 | 187 |
| Datasets | Number of Features (#) | |||
|---|---|---|---|---|
| #IFS | #NIC | #SIC | #MIC (SF) | |
| wdbc | 30 | 24 | 6 | 3 |
| colon | 2000 | 359 | 5 | 3 |
| lucas0 | 11 | 9 | 4 | 4 |
| sylva | 216 | 77 | 52 | 24 |
| ionosphere | 34 | 25 | 7 | 5 |
| cina0 | 132 | 106 | 57 | 30 |
| lucap0 | 143 | 94 | 49 | 40 |
| marti1 | 1024 | 1 | 1 | 1 |
| reged1 | 999 | 541 | 16 | 13 |
| Lung | 3312 | 2318 | 212 | 35 |
| prosate_GE | 5966 | 3182 | 24 | 4 |
| leukemia | 7066 | 2019 | 47 | 8 |
| arcene | 10,000 | 2666 | 13 | 6 |
| Smk_can_187 | 19,993 | 4924 | 55 | 9 |
| Algorithms | Average Accuracy for Classifiers in 14 the Datasets (%) | Average Accuracy (%) | |||||
|---|---|---|---|---|---|---|---|
| Alpha-investing | Complex Tree | Medium Tree | Simple Tree | Linear SVM | Quadratic SVM | Cubic SVM | 83.33 |
| 83.89 | 84.14 | 83.18 | 86.34 | 85.13 | 80.78 | ||
| Decision Tree average: 83.74 | SVM average: 84.08 | ||||||
| Fine KNN | Medium KNN | Cubic KNN | Bagged Trees | Subspace discriminant | RUSBoosted Trees | ||
| 82.31 | 83.75 | 83.54 | 84.91 | 86.19 | 75.81 | ||
| KNN average: 83.2 | ENSEMBLE average: 82.3 | ||||||
| OSFS | Complex Tree | Medium Tree | Simple Tree | Linear SVM | Quadratic SVM | Cubic SVM | 88.44 |
| 88.22 | 88.58 | 88.62 | 90.44 | 87.60 | 87.64 | ||
| Decision Tree average: 88.47 | SVM average: 88.56 | ||||||
| Fine KNN | Medium KNN | Cubic KNN | Bagged Trees | Subspace discriminant | RUSBoosted Trees | ||
| 87.83 | 90.22 | 87.41 | 89.89 | 90.27 | 84.54 | ||
| KNN: 88.49 | ENSEMBLE: 88.23 | ||||||
| ConInd | Complex Tree | Medium Tree | Simple Tree | Linear SVM | QuadraticSVM | Cubic SVM | 88.95 |
| 89.14 | 89.19 | 88.05 | 90.94 | 87.50 | 87.46 | ||
| Decision Tree average: 88.79 | SVM average: 88.63 | ||||||
| Fine KNN | Medium KNN | Cubic KNN | Bagged Trees | Subspace discriminant | RUSBoosted Trees | ||
| 88.79 | 90.42 | 90.07 | 90.05 | 90.63 | 85.14 | ||
| KNN average: 89.76 | ENSEMBLE average: 88.61 | ||||||
| Datasets | Algorithms | |||||
|---|---|---|---|---|---|---|
| Alpha-investing | OSFS | ConInd | ||||
| # | Time | # | Time | # | Time | |
| wdbc | 20 | 0.0138 | 3 | 0.1577 | 3 | 0.2201 |
| colon | 1 | 0.0663 | 3 | 0.6778 | 3 | 8.6637 |
| lucas0 | 4 | 0.0008 | 4 | 0.0142 | 4 | 0.0304 |
| sylva | 70 | 1.6717 | 18 | 247.9366 | 24 | 189.8111 |
| ionosphere | 10 | 0.0147 | 4 | 0.1315 | 5 | 0.2215 |
| cina0 | 8 | 0.1046 | 22 | 721.3638 | 30 | 407.7689 |
| lucap0 | 10 | 0.0197 | 36 | 1.67 × 103 | 40 | 225.7368 |
| marti1 | 28 | 0.116 | 1 | 0.1081 | 1 | 0.1063 |
| reged1 | 1 | 0.0417 | 13 | 121.2839 | 13 | 63.9082 |
| lung | 45 | 0.7523 | 11 | 420.5678 | 35 | 3.48 × 104 |
| prosate_GE | 12 | 0.4308 | 3 | 7.7915 | 4 | 4.72 × 104 |
| leukemia | 1 | 0.4346 | 3 | 12.7647 | 8 | 593.3249 |
| arcene | 8 | 1.4139 | 5 | 20.8445 | 6 | 764.5764 |
| Smk_can_187 | 6 | 2.7929 | 4 | 42.8323 | 9 | 327.1579 |
| the ratio of average features number: = 242% | ||||||
| Datasets | Running Time | |||
|---|---|---|---|---|
| TA | TC | |||
| sylva | 247.9366 | 189.8111 | −0.2344 | −0.5356 |
| cina0 | 721.3638 | 407.7689 | −0.4347 | |
| lucap0 | 1.43 × 107 | 225.7368 | −0.9998 | |
| reged1 | 121.2839 | 63.9082 | −0.4731 | |
| Dataset | Ratio | # | Time | ||||
|---|---|---|---|---|---|---|---|
| ConInd | OSFS | ConInd | OSFS | ||||
| #NIC | #SIC | SF | SF | ||||
| ionosphere | 25% | 8 | 5 | 5 | 4 | 0.0222 | 0.0184 |
| 50% | 15 | 6 | 5 | 4 | 0.0855 | 0.0678 | |
| 75% | 21 | 6 | 5 | 4 | 0.148 | 0.1078 | |
| 100% | 25 | 7 | 5 | 4 | 0.2215 | 0.1315 | |
| marti1 | 25% | 0 | 0 | 0 | 0 | 0.0235 | 0.0251 |
| 50% | 0 | 0 | 0 | 0 | 0.0446 | 0.0474 | |
| 75% | 0 | 0 | 0 | 0 | 0.0673 | 0.0698 | |
| 100% | 1 | 1 | 1 | 1 | 0.1063 | 0.1081 | |
| leukemia | 25% | 488 | 21 | 5 | 3 | 74.3909 | 3.6738 |
| 50% | 914 | 28 | 6 | 3 | 143.903 | 5.8859 | |
| 75% | 1521 | 35 | 8 | 4 | 356.6957 | 9.9276 | |
| 100% | 2019 | 47 | 9 | 3 | 593.3249 | 12.7647 | |
| arcene | 25% | 670 | 3 | 3 | 4 | 26.9589 | 1.6326 |
| 50% | 1354 | 8 | 5 | 4 | 111.864 | 6.8246 | |
| 75% | 2017 | 11 | 6 | 3 | 259.0335 | 10.2471 | |
| 100% | 2666 | 13 | 6 | 5 | 764.5764 | 20.8445 | |
| cina0 | 25% | 24 | 17 | 12 | 10 | 3.6124 | 3.8368 |
| 50% | 52 | 30 | 17 | 14 | 34.372 | 35.8382 | |
| 75% | 81 | 47 | 28 | 23 | 157.9134 | 263.1822 | |
| 100% | 106 | 57 | 30 | 22 | 407.7689 | 721.3638 | |
| sylva | 25% | 22 | 17 | 12 | 10 | 4.3963 | 12.7006 |
| 50% | 36 | 24 | 15 | 13 | 13.3102 | 27.0316 | |
| 75% | 55 | 39 | 22 | 18 | 53.8118 | 115.1798 | |
| 100% | 77 | 52 | 24 | 18 | 189.8111 | 247.9366 | |
| lucap0 | 25% | 24 | 18 | 16 | 15 | 2.4505 | 10.5797 |
| 50% | 50 | 38 | 32 | 26 | 32.2265 | 147.5867 | |
| 75% | 68 | 44 | 36 | 30 | 88.2781 | 416.6544 | |
| 100% | 94 | 49 | 40 | 36 | 225.7368 | 1.43 × 107 | |
| reged1 | 25% | 6 | 1 | 1 | 2 | 0.0282 | 0.0299 |
| 50% | 15 | 3 | 3 | 4 | 0.0791 | 0.103 | |
| 75% | 22 | 5 | 5 | 6 | 0.1639 | 0.2067 | |
| 100% | 541 | 16 | 13 | 13 | 63.9082 | 121.2839 | |
| Dataset | HITON_MB | OSFS | ConInd |
|---|---|---|---|
| wdbc | 5 | 3 | 3 |
| colon | 3 | 3 | 3 |
| lucas0 | 5 | 4 | 4 |
| sylva | 64 | 18 | 24 |
| ionosphere | 6 | 4 | 5 |
| cina0 | 66 | 22 | 30 |
| lucap0 | 79 | 36 | 40 |
| marti1 | 3 | 1 | 1 |
| reged1 | 24 | 13 | 13 |
| lung | 97 | 11 | 35 |
| prosate_GE | 6 | 3 | 4 |
| leukemia | 7 | 3 | 8 |
| arcene | 8 | 5 | 6 |
| Smk_can_187 | 11 | 4 | 9 |
| Algorithms | Average Accuracy for Classifiers in the 14 Datasets (%) | Average Accuracy (%) | |||||
|---|---|---|---|---|---|---|---|
| HITON_MB | Complex Tree | Medium Tree | Simple Tree | Linear SVM | Quadratic SVM | Cubic SVM | 89.51 |
| 88.54 | 88.74 | 88.80 | 92.76 | 91.78 | 87.59 | ||
| Decision Tree average: 88.69 | SVM average: 90.71 | ||||||
| Fine KNN | Medium KNN | Cubic KNN | Bagged Trees | Subspace discriminant | RUSBoosted Trees | ||
| 89.11 | 90.98 | 90.56 | 88.61 | 91.61 | 85.00 | ||
| KNN average: 90.22 | ENSEMBLE average: 88.41 | ||||||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
You, D.; Wu, X.; Shen, L.; He, Y.; Yuan, X.; Chen, Z.; Deng, S.; Ma, C. Online Streaming Feature Selection via Conditional Independence. Appl. Sci. 2018, 8, 2548. https://doi.org/10.3390/app8122548
You D, Wu X, Shen L, He Y, Yuan X, Chen Z, Deng S, Ma C. Online Streaming Feature Selection via Conditional Independence. Applied Sciences. 2018; 8(12):2548. https://doi.org/10.3390/app8122548
Chicago/Turabian StyleYou, Dianlong, Xindong Wu, Limin Shen, Yi He, Xu Yuan, Zhen Chen, Song Deng, and Chuan Ma. 2018. "Online Streaming Feature Selection via Conditional Independence" Applied Sciences 8, no. 12: 2548. https://doi.org/10.3390/app8122548
APA StyleYou, D., Wu, X., Shen, L., He, Y., Yuan, X., Chen, Z., Deng, S., & Ma, C. (2018). Online Streaming Feature Selection via Conditional Independence. Applied Sciences, 8(12), 2548. https://doi.org/10.3390/app8122548




