A Robust Maximum Power Point Tracking Control Method for a PEM Fuel Cell Power System
Abstract
:1. Introduction
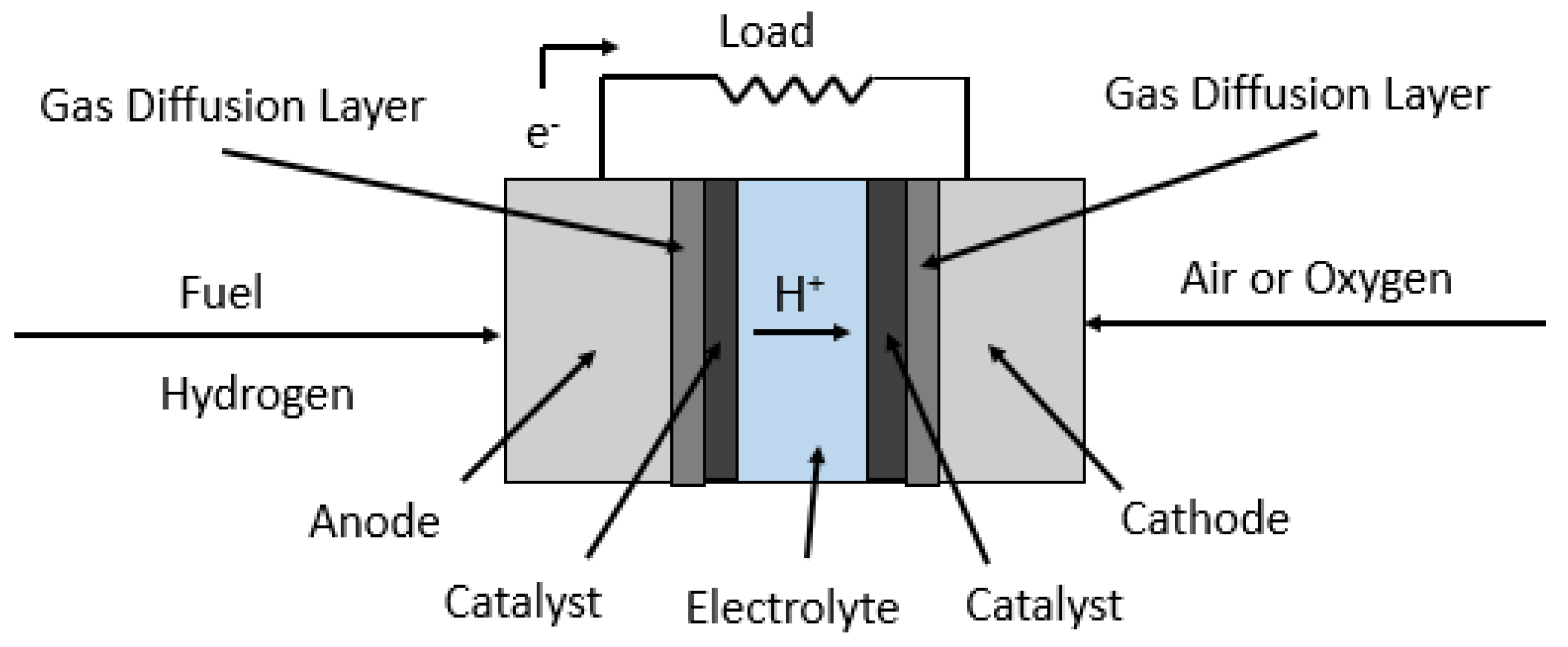
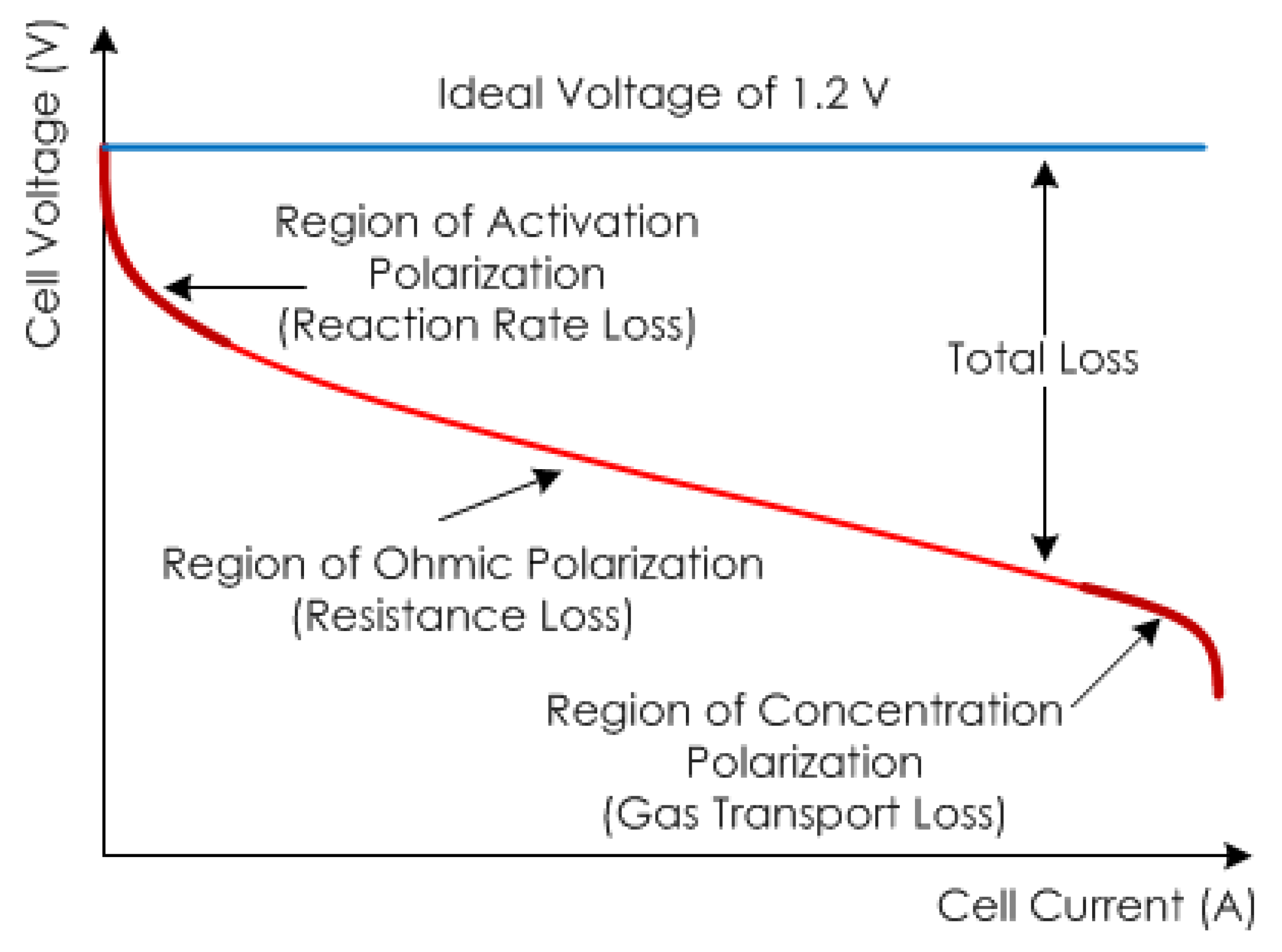
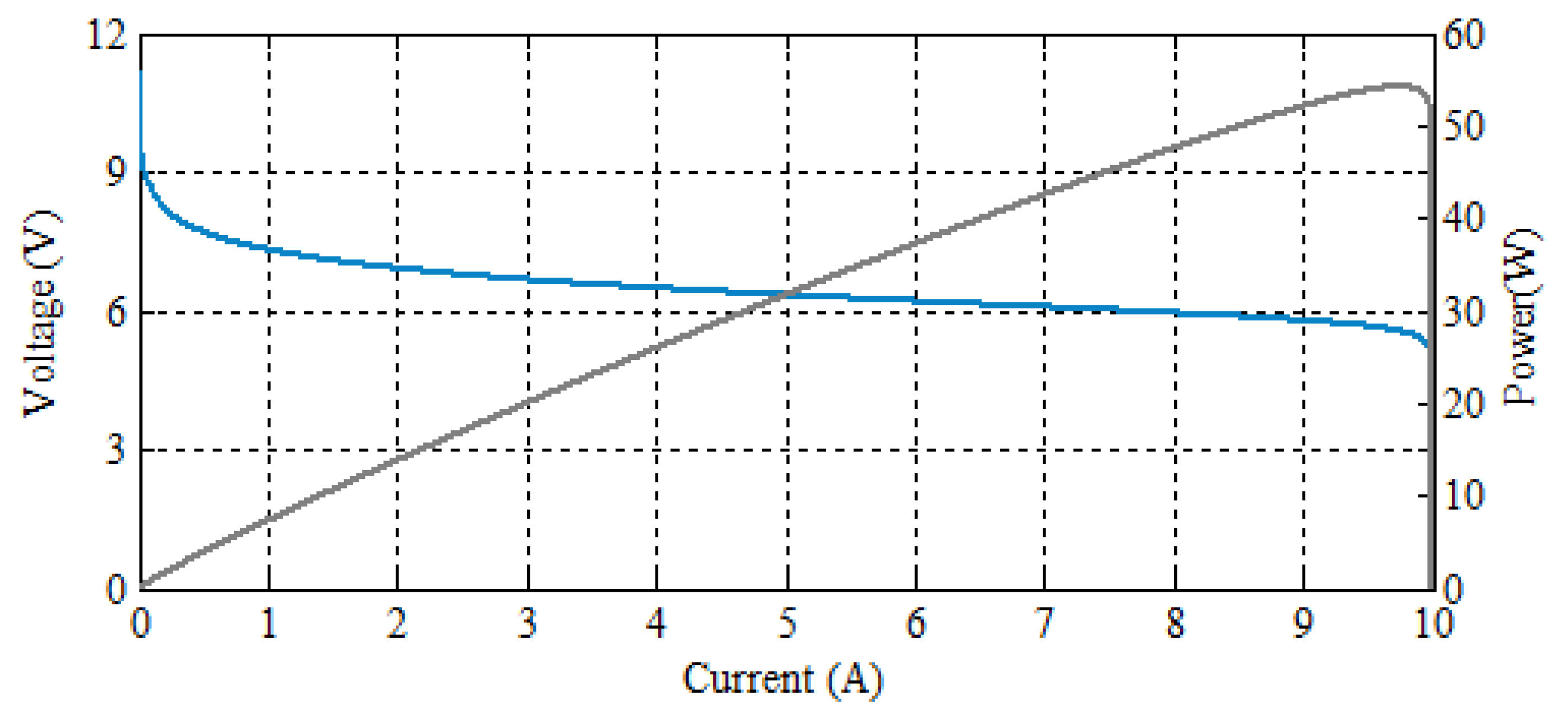
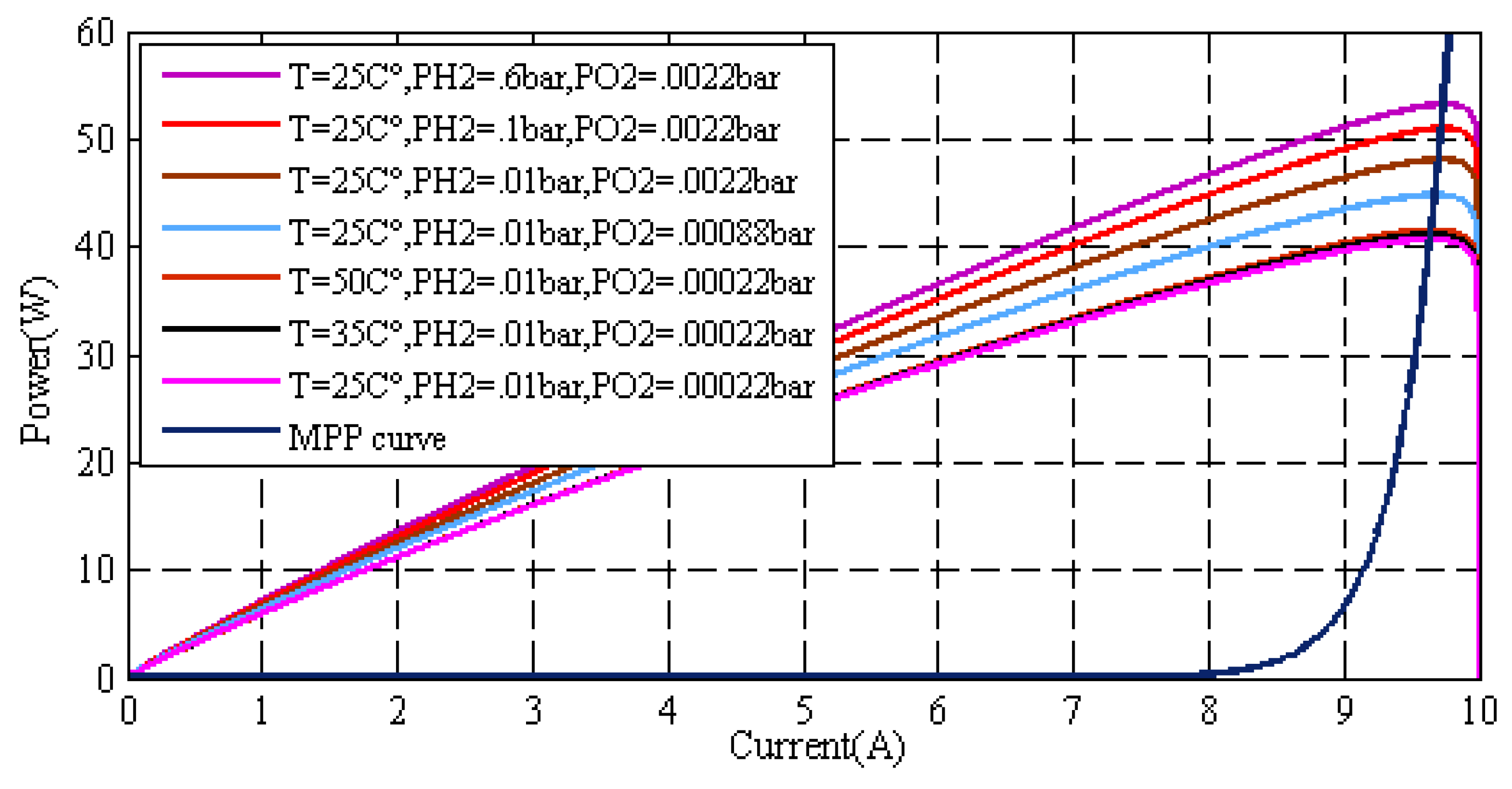
2. PEM Fuel Cell
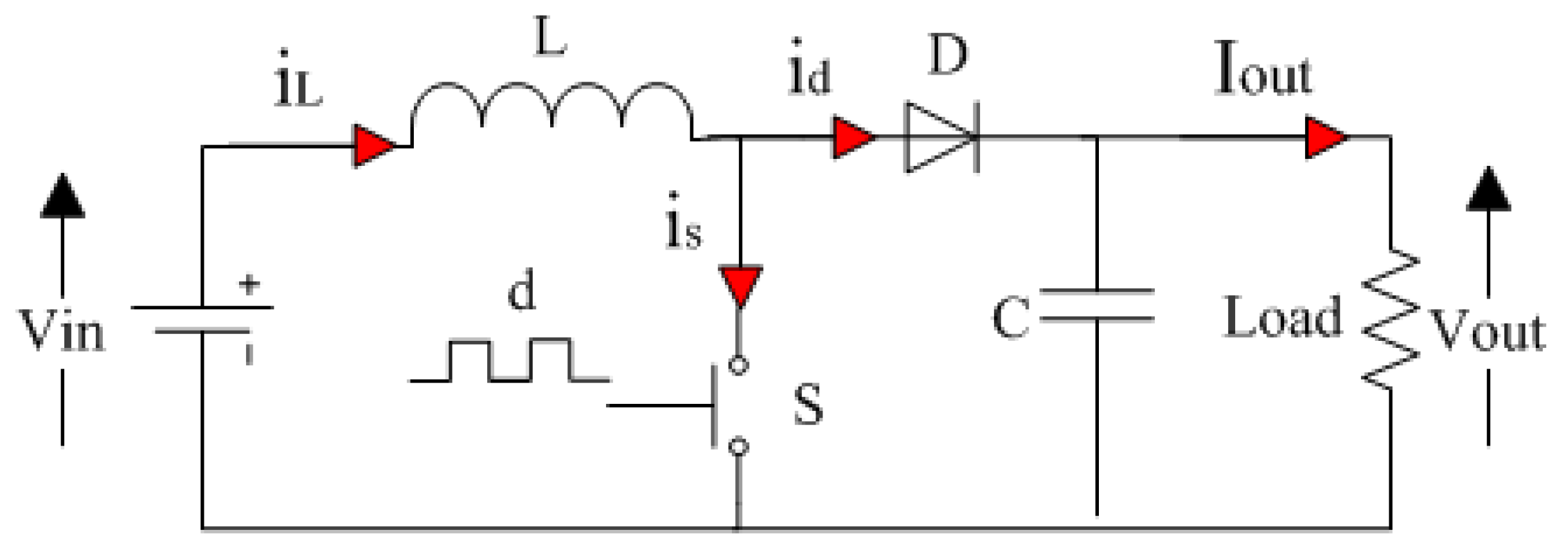
3. DC–DC Boost Converter
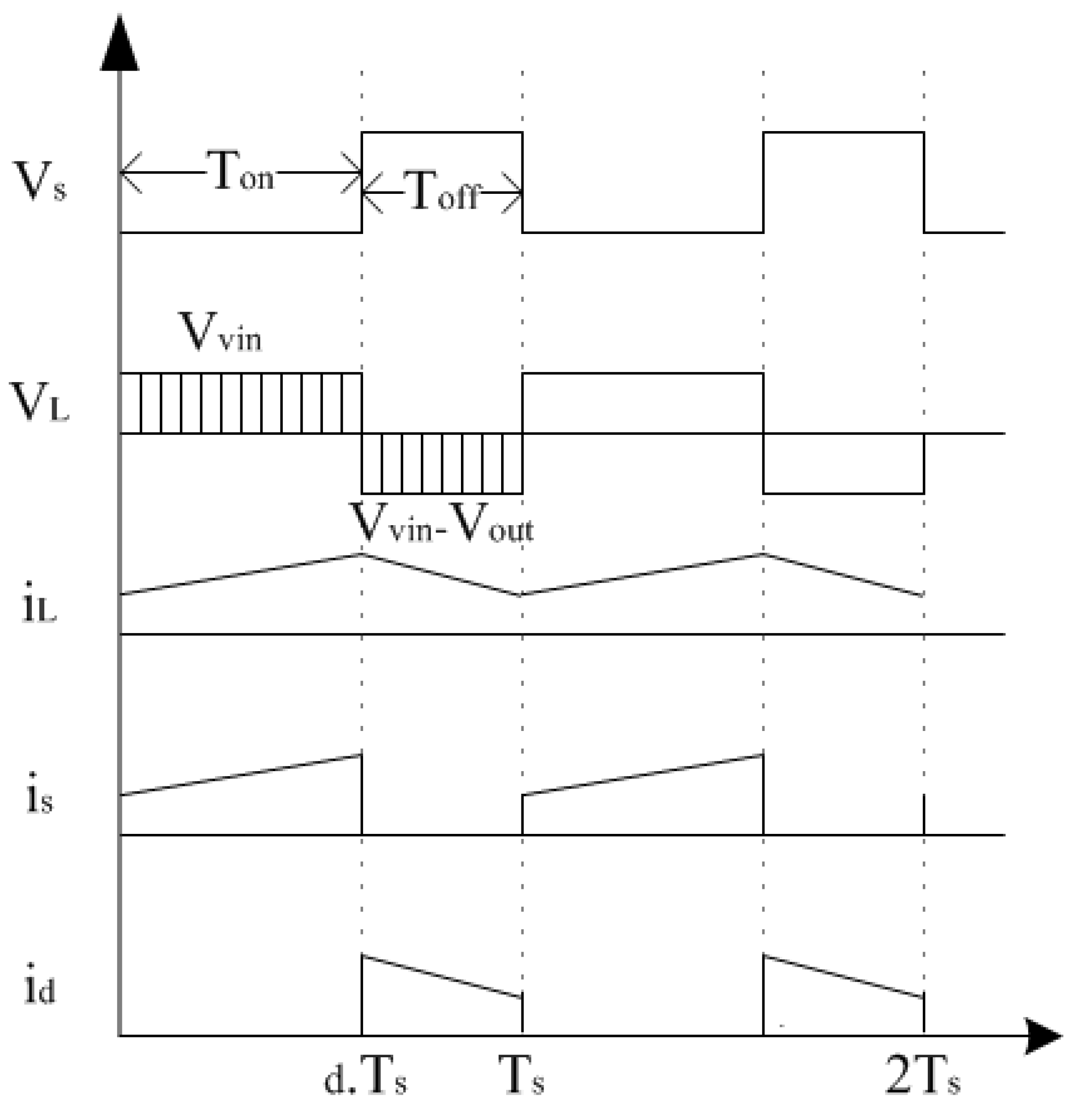
- The ON state: When the switch S turns ON, the inductor L connects to the DC source voltage. Therefore, the current moves across the inductor L and the transistor switch s, which results in an increase in the magnitude of and , while is approximately equal to the input voltage . On the other hand, during this state, the capacitor C discharges through the load R. The obtained differential equations of the inductor current and the output voltage are expressed as follows:
- The OFF state: When the switch S turns OFF, the inductor L connects to the capacitor C and the load R. Therefore, the current moves across the inductor L, the diode D, the capacitor C, and the load R, which results in a decrease in the magnitude of and (discharging of the inductor L into the load R and the capacitor C). During this state, is approximately equal to . The obtained differential equations of the inductor current and the output voltage are expressed as follows:
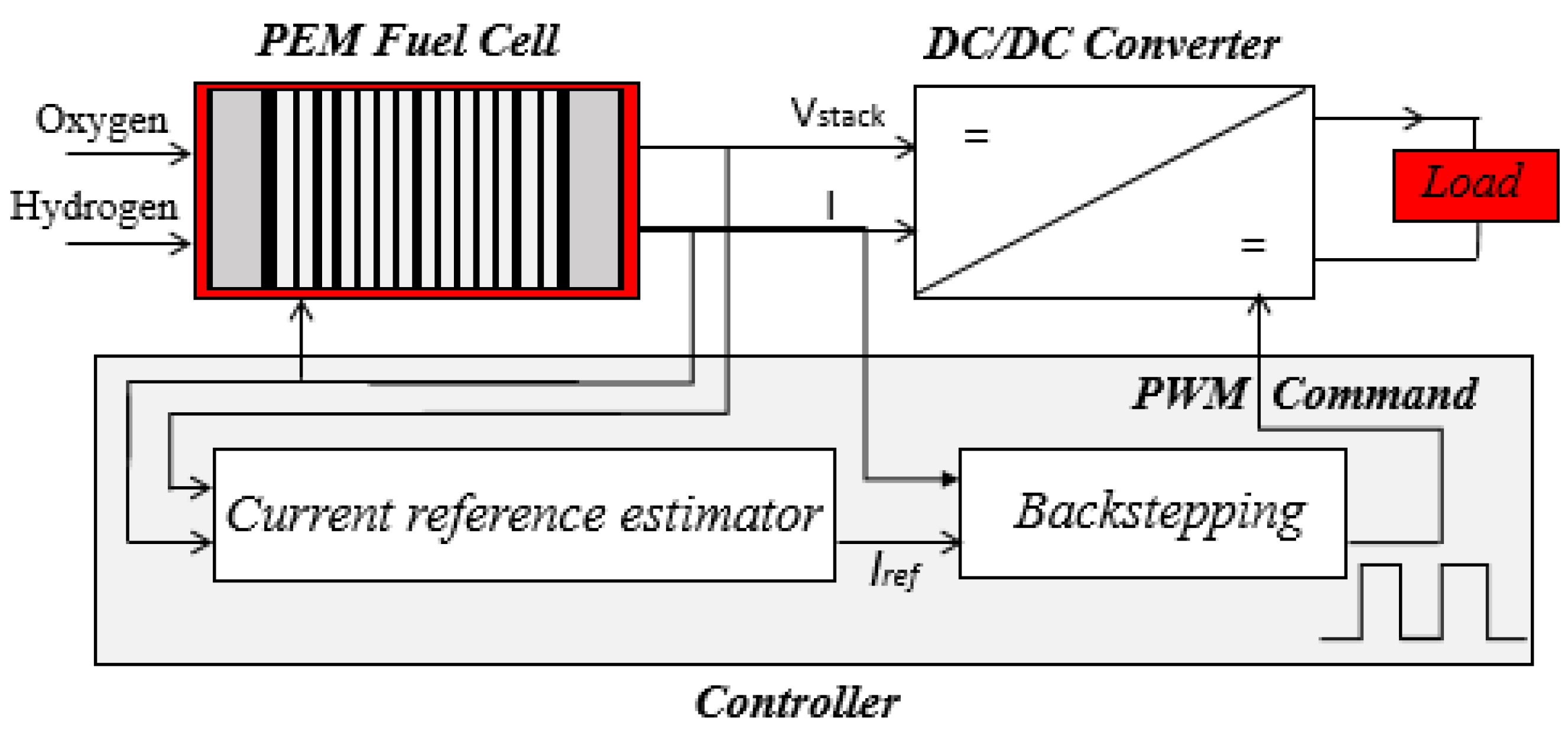
4. MPPT Control Design
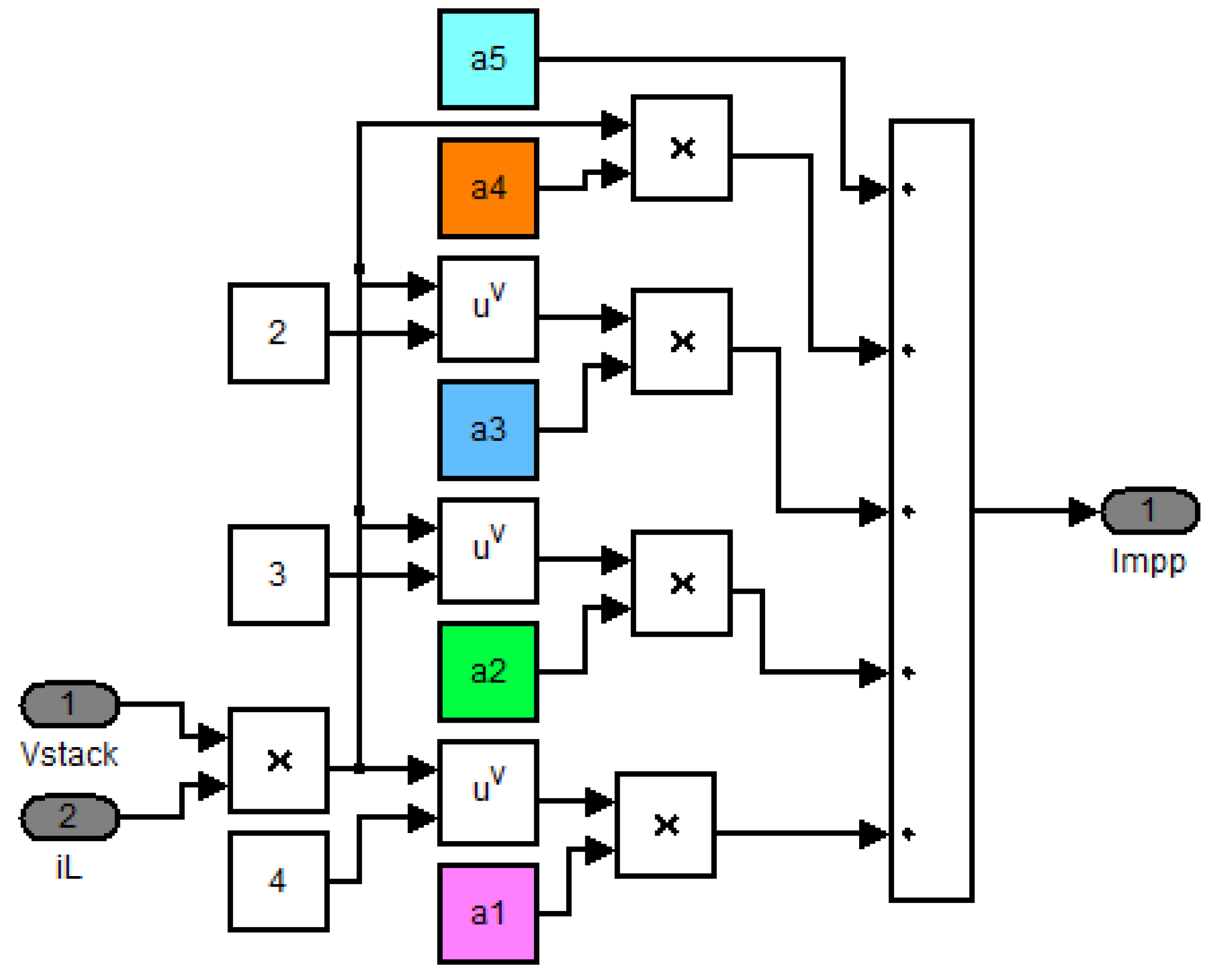
4.1. Current Reference Estimator
4.2. Current Regulation
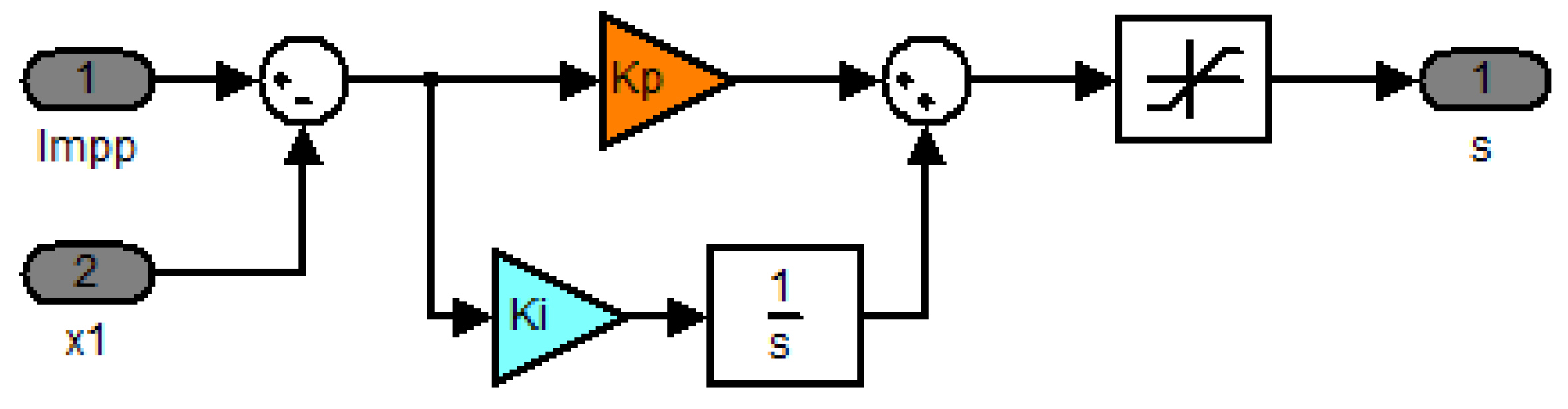
4.2.1. PI Controller
- The first step is to switch off the integral and derivative gains ( and ).
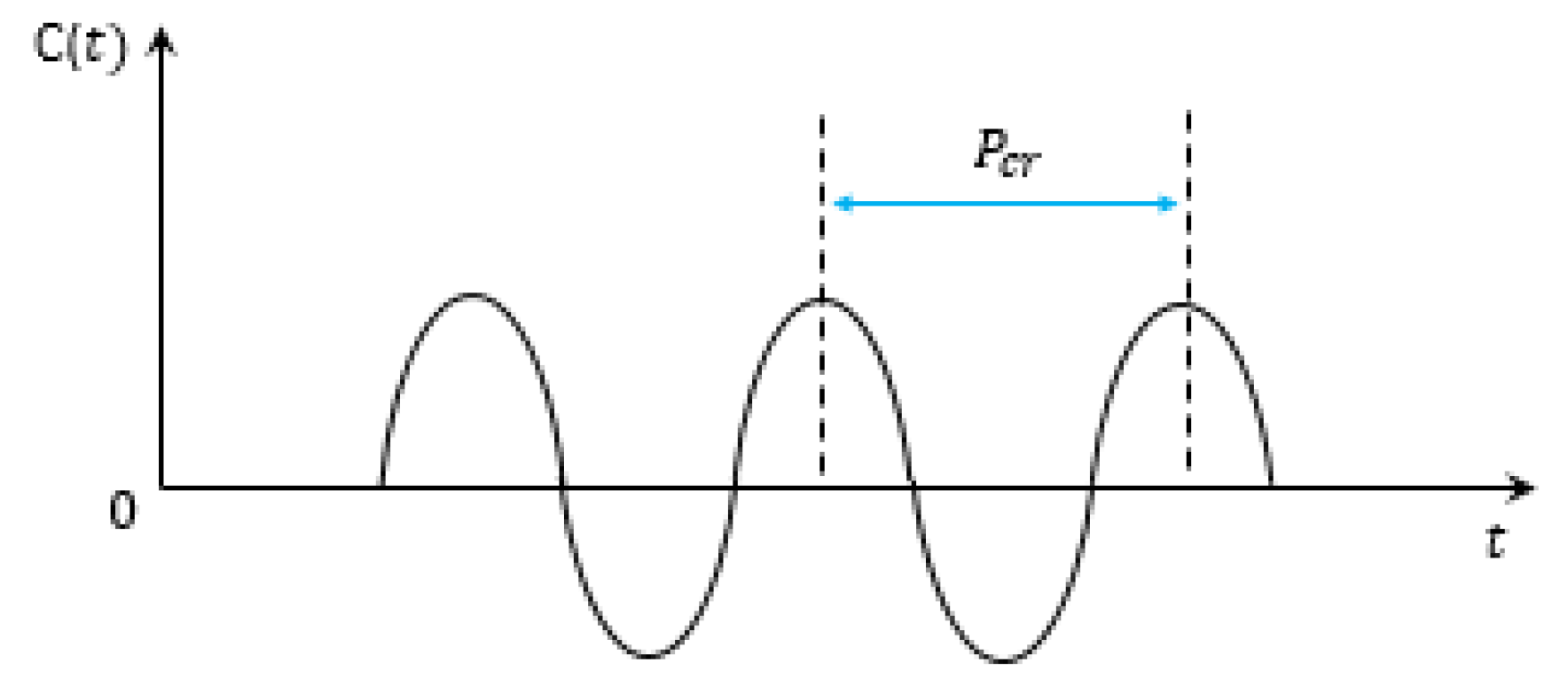
- The second step is to increase the gain from a low/zero value until the first sustained oscillation occurs (Figure 11). The reached gain at the sustained oscillation is noted as a critical value , while the period of these oscillations is measured as .
- Finally, taking into account the type of the used controller, and can be calculated using the formula given in Table 2.
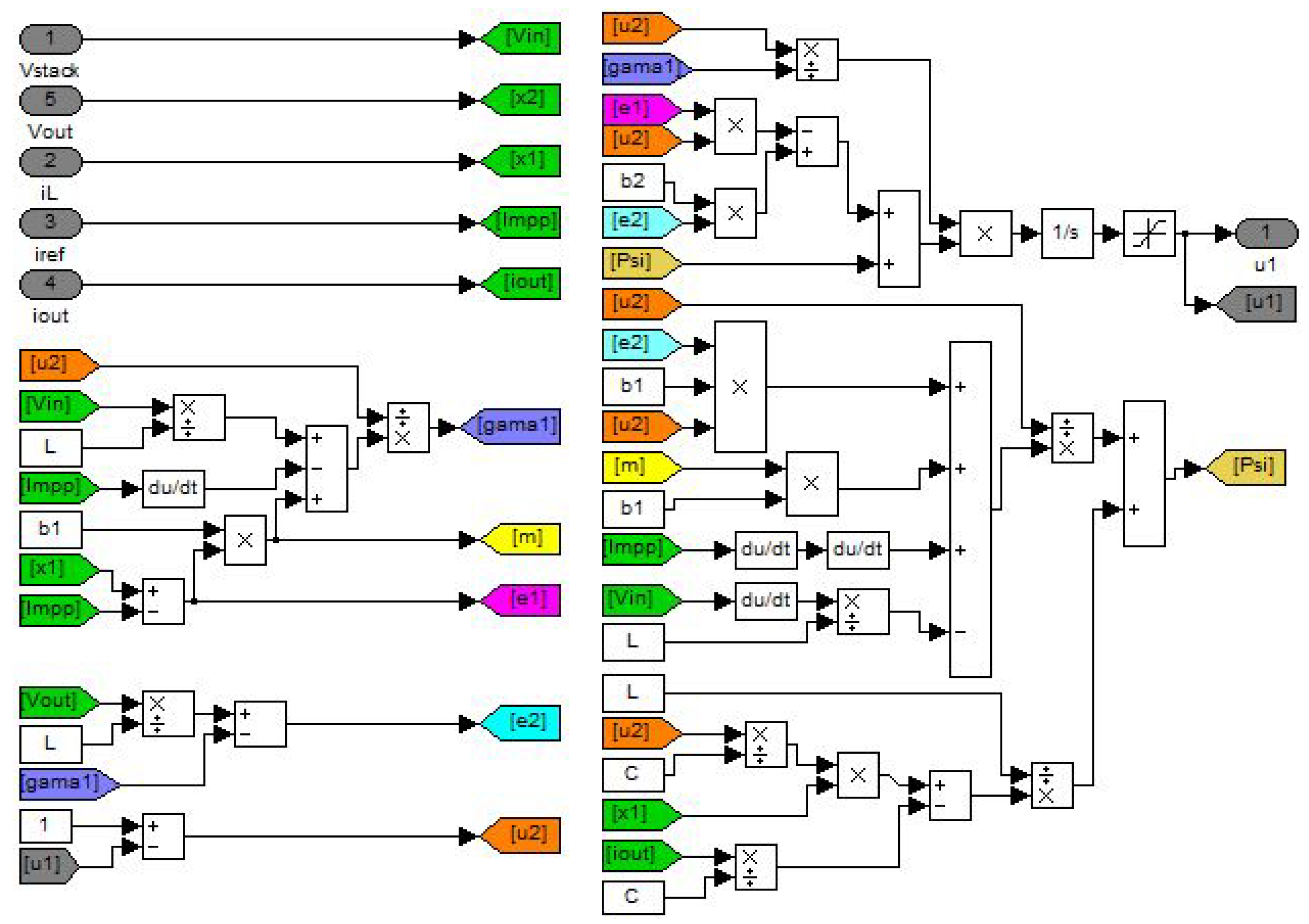
4.2.2. Backstepping Algorithm
- Step 1. First, we define the tracking current error asIn order to achieve the tracking objective, it is needed to enforce to vanish. Therefore, the dynamics of must be clearly defined. By placing Equation (18) into Equation (21), the time derivative of can be written aswhere the quantity is a virtual variable. In order to stabilize the virtual error , a Lyapunov function is considered:Using the equations mentioned above, the time derivative of can be represented asEquation (24) shows that can be adjusted to zero () if , where the stabilizing function is defined by Equation (25):where is a positive constant parameter. Since is a virtual variable and not the actual input of the controller, then a second tracking error variable is given by Equation (26):Using Equations (25) and (26), Equation (22) can be written asTherefore, the Lyapunov function given in Equation (24) can also be rewritten as
- Step 2. The aim of this step is to enforce the errors to vanish. For this reason, first of all, the dynamics of must be determined. Using Equations (18), (25) and (27), the time-derivative of can be obtained aswhereIn order to obtain a stabilizing control law for the whole system, the following Lyapunov function candidate is proposed:The time derivative of the above Lyapunov function is obtained by combining Equations (28) and (29):It can be easily determined that the global asymptotic stability of the equilibrium is achieved only if the time derivative of the error variable is chosen aswhere is a positive design parameter. Finally, by combining Equations (29) and (34), the following control law can be obtained:
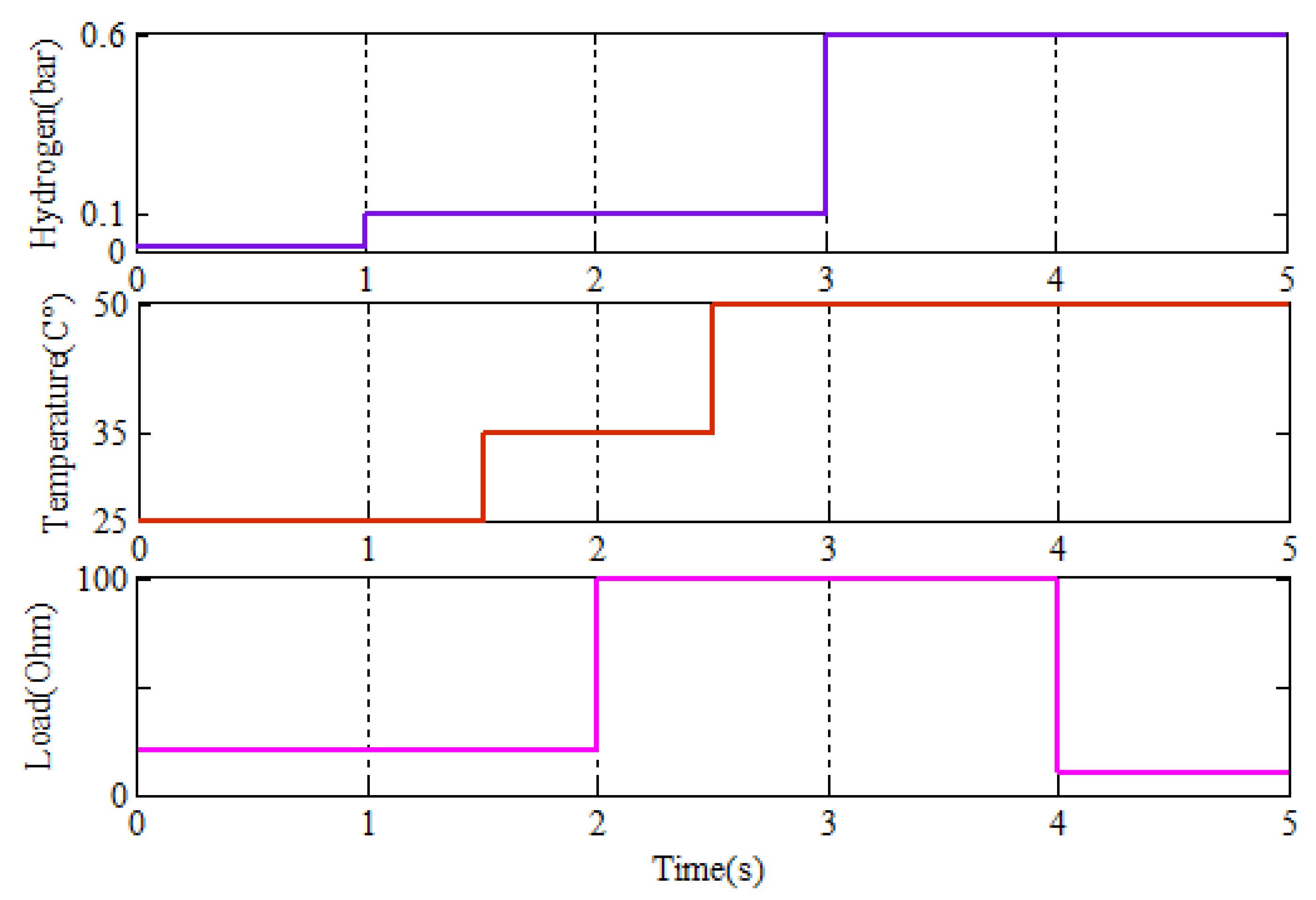
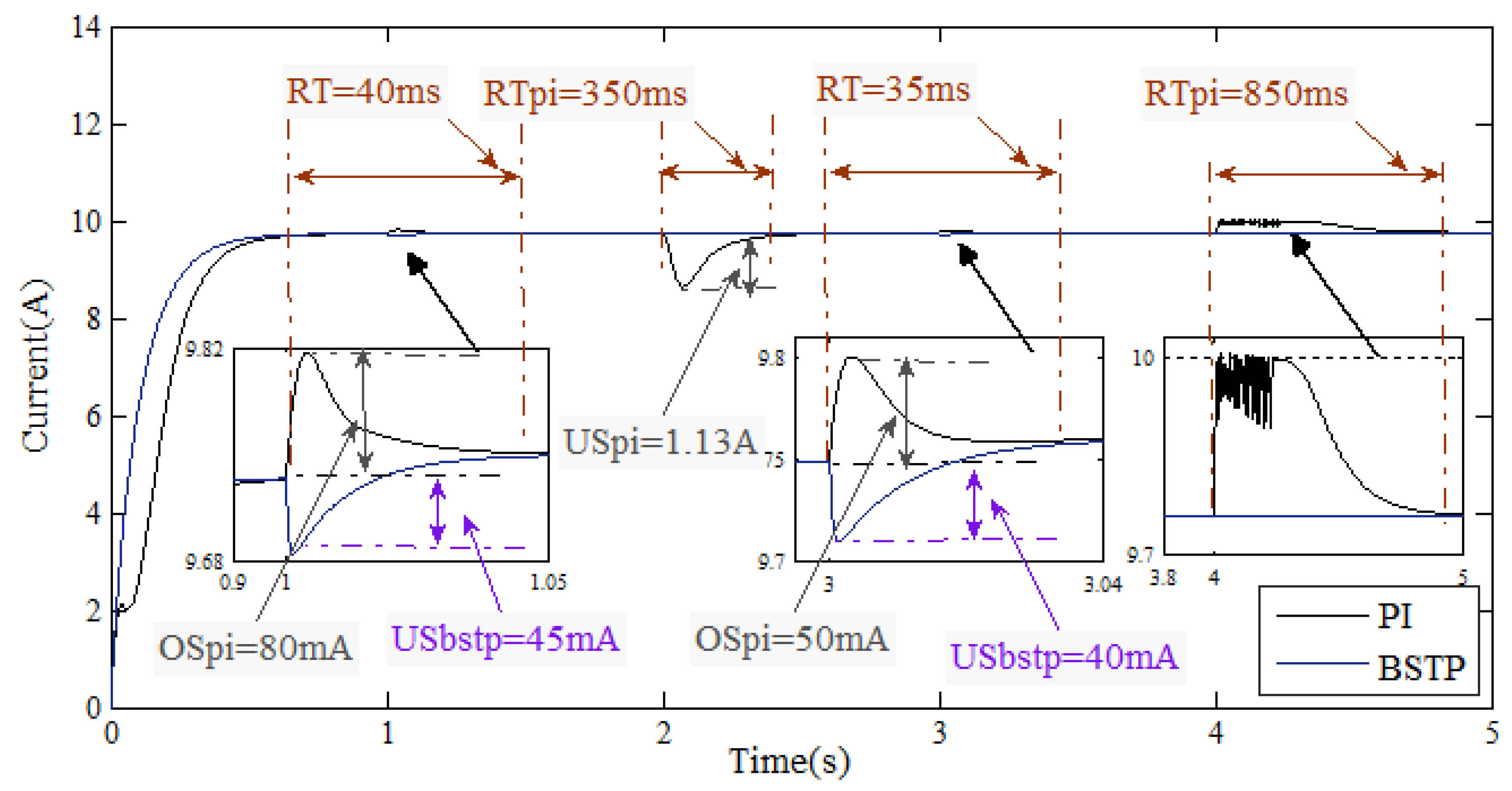
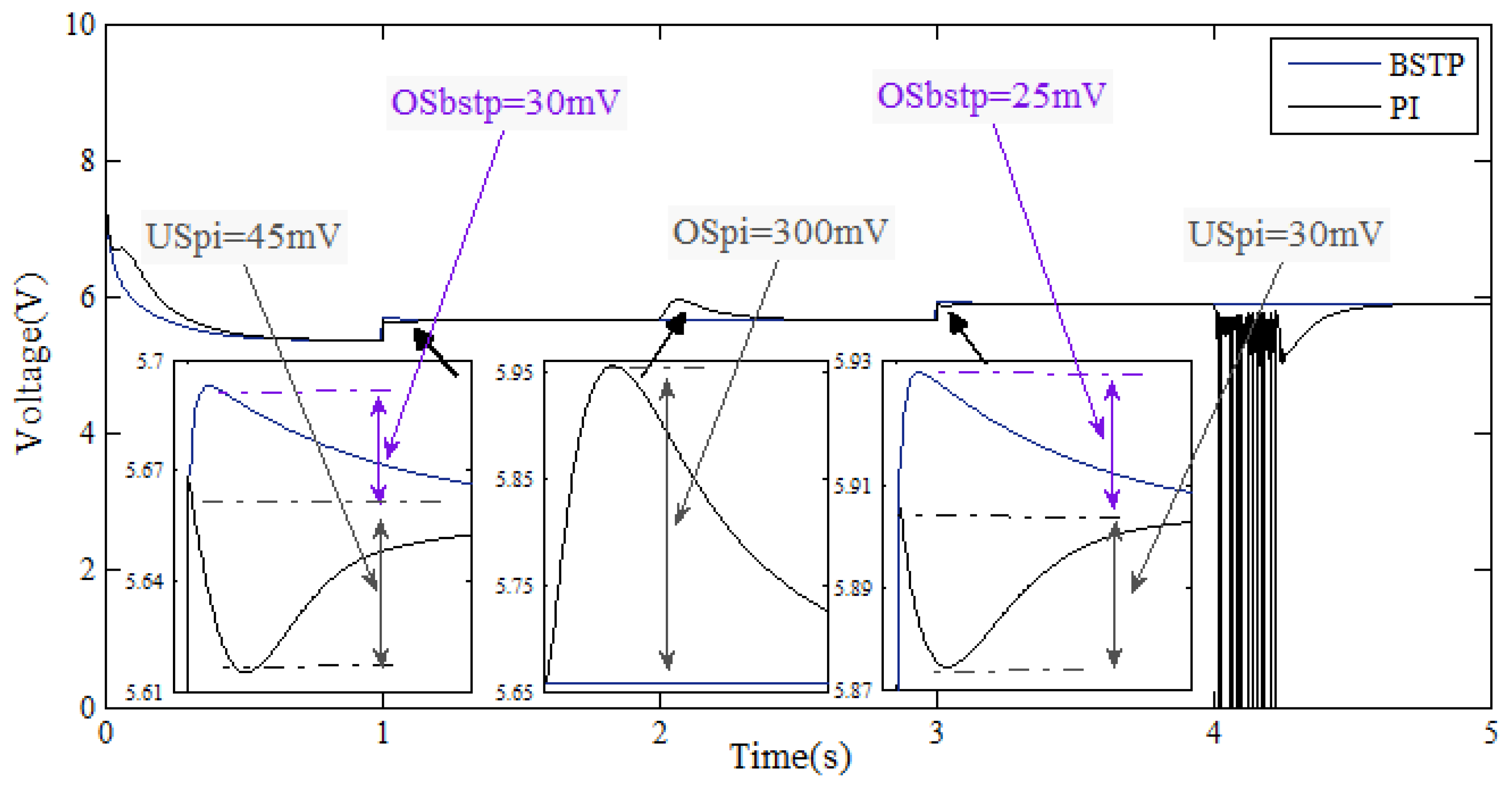
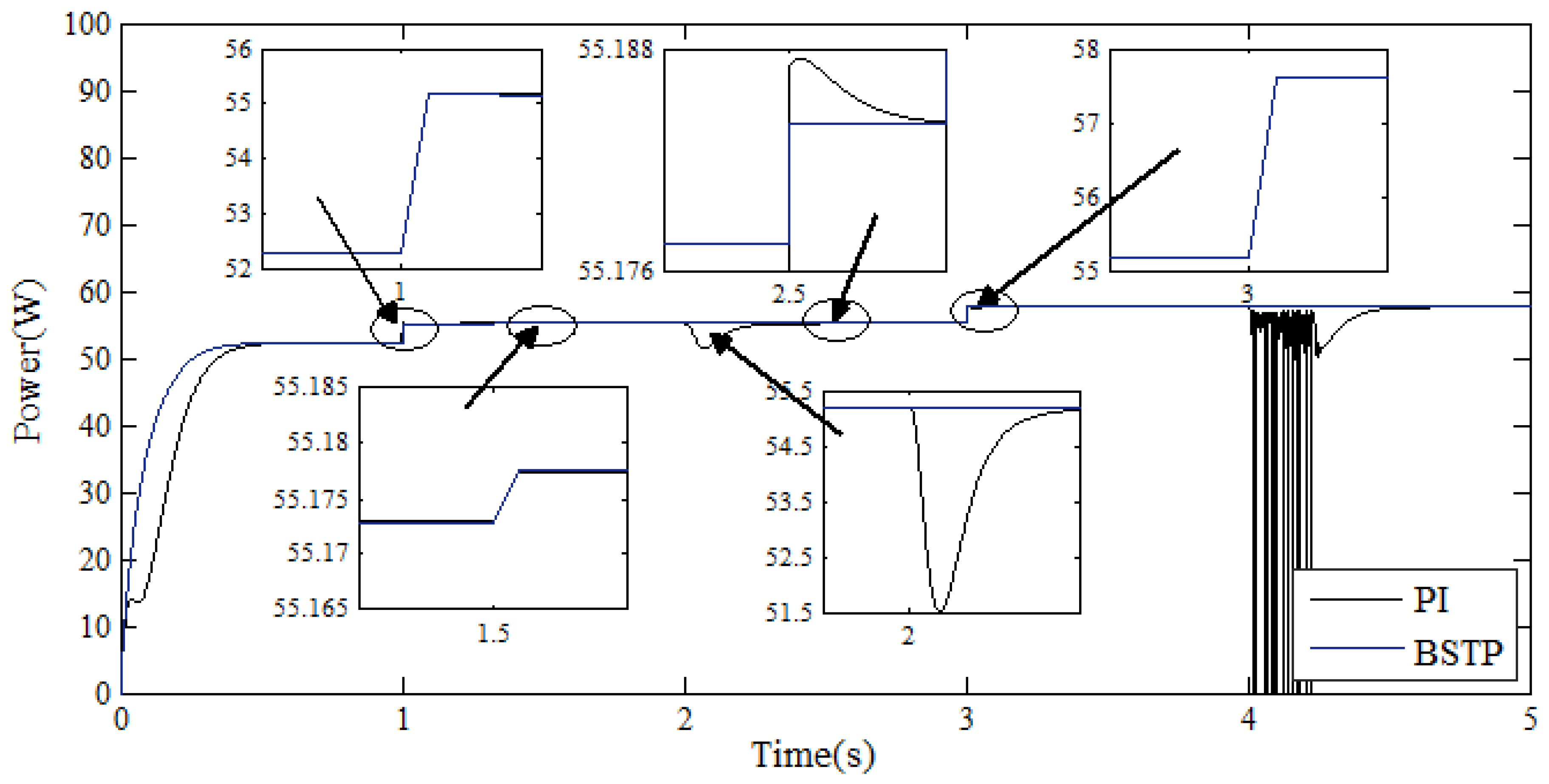
5. Simulation Results
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| MPP | Maximum Power Point |
| MPPT | Maximum Power Point Tracker |
| PEMFCs | proton exchange membrane Fuel Cell systems |
| FSC | Fractional Short Circuit |
| P&O | Perturb and Observation |
| FOC | Fractional Open Circuit |
| Inc-Cond | Incremental Conductance |
| ESC | Extremum Seeking Control |
| SMC | Sliding Mode Control |
| CS | Current Sweep |
| FLC | Fuzzy Logic Control |
| ESC | Eagle Strategy Control |
| PSO | Particle Swarm Optimization |
| NNC | Neural Network Control |
| GA | Genetic Algorithms |
| VSIR | Variable Step-size Incremental Resistance algorithm |
| RCC | Ripple Correlation Control |
| CL | Catalyst Layer |
| GDL | Gas Diffusion Layer |
| CCM | Continuous Conduction Mode |
References
- Martin, S.S.; Chebak, A. Concept of educational renewable energy laboratory integrating wind, solar and biodiesel energies. Int. J. Hydrog. Energy 2016, 41, 21036–21046. [Google Scholar] [CrossRef]
- Roumila, Z.; Rekioua, D.; Rekioua, T. Energy management based fuzzy logic controller of hybrid system wind/photovoltaic/diesel with storage battery. Int. J. Hydrog. Energy 2017, 42, 19525–19535. [Google Scholar] [CrossRef]
- Simari, C.; Potsi, G.; Policicchio, A.; Perrotta, I.; Nicotera, I. Clay–Carbon Nanotubes Hybrid Materials for Nanocomposite Membranes: Advantages of Branched Structure for Proton Transport under Low Humidity Conditions in PEMFCs. J. Phys. Chem. C 2016, 120, 2574–2584. [Google Scholar] [CrossRef]
- Rosli, R.; Sulong, A.; Daud, W.; Zulkifley, M.; Husaini, T.; Rosli, M.; Majlan, E.; Haque, M. A review of high-temperature proton exchange membrane fuel cell (HT-PEMFC) system. Int. J. Hydrog. Energy 2017, 42, 9293–9314. [Google Scholar] [CrossRef]
- Torki, W.; Derbeli, M. Modeling and control of a stand-alone PEMFC for AC load-PMSM application. In Proceedings of the 2017 International Conference on Green Energy Conversion Systems (GECS), Hammamet, Tunisia, 23–25 March 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Headley, A.; Yu, V.; Borduin, R.; Chen, D.; Li, W. Development and Experimental Validation of a Physics-Based PEM Fuel Cell Model for Cathode Humidity Control Design. IEEE/ASME Trans. Mech. 2016, 21, 1775–1782. [Google Scholar] [CrossRef]
- Sher, H.A.; Murtaza, A.F.; Noman, A.; Addoweesh, K.E.; Al-Haddad, K.; Chiaberge, M. A new sensorless hybrid MPPT algorithm based on fractional short-circuit current measurement and P&O MPPT. IEEE Trans. Sustain. Energy 2015, 6, 1426–1434. [Google Scholar] [CrossRef]
- Bharath, K.; Suresh, E. Design and Implementation of Improved Fractional Open Circuit Voltage Based Maximum Power Point Tracking Algorithm for Photovoltaic Applications. Int. J. Renew. Energy Res. (IJRER) 2017, 7, 1108–1113. [Google Scholar]
- Gosumbonggot, J. Maximum power point tracking method using perturb and observe algorithm for small scale DC voltage converter. Proc. Comput. Sci. 2016, 86, 421–424. [Google Scholar] [CrossRef]
- Derbeli, M.; Sbita, L.; Farhat, M.; Barambones, O. Proton exchange membrane fuel cell—A smart drive algorithm. In Proceedings of the 2017 International Conference on Green Energy Conversion Systems (GECS), Hammamet, Tunisia, 23–25 March 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Serrano-Guerrero, X.; González-Romero, J.; Cárdenas-Carangui, X.; Escrivá-Escrivá, G. Improved variable step size P&O MPPT algorithm for PV systems. In Proceedings of the 2016 51st International Universities Power Engineering Conference (UPEC), Coimbra, Portugal, 6–9 September 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Sarvi, M.; Barati, M. Voltage and current based MPPT of fuel cells under variable temperature conditions. In Proceedings of the 2010 45th International Universities Power Engineering Conference (UPEC), Cardiff, UK, 31 August–3 September 2010; pp. 1–4. [Google Scholar]
- Chen, P.Y.; Yu, K.N.; Yau, H.T.; Li, J.T.; Liao, C.K. A novel variable step size fractional order incremental conductance algorithm to maximize power tracking of fuel cells. Appl. Math. Model. 2017, 45, 1067–1075. [Google Scholar] [CrossRef]
- Harrag, A.; Messalti, S. Variable Step Size IC MPPT Controller for PEMFC Power System Improving Static and Dynamic Performances. Fuel Cells 2017, 17, 816–824. [Google Scholar] [CrossRef]
- Cecati, C.; Khalid, H.A.; Tinari, M.; Adinolfi, G.; Graditi, G. DC nanogrid for renewable sources with modular DC/DC LLC converter building block. IET Power Electron. 2016, 10, 536–544. [Google Scholar] [CrossRef]
- Bizon, N.; Thounthong, P.; Raducu, M.; Constantinescu, L.M. Designing and modelling of the asymptotic perturbed extremum seeking control scheme for tracking the global extreme. Int. J. Hydrog. Energy 2017, 42, 17632–17644. [Google Scholar] [CrossRef]
- Bizon, N. Energy optimization of fuel cell system by using global extremum seeking algorithm. Appl. Energy 2017, 206, 458–474. [Google Scholar] [CrossRef]
- Jiao, J.; Cui, X. A real-time tracking control of fuel cell power systems for maximum power point. J. Comput. Inf. Syst. 2013, 9, 1933–1941. [Google Scholar]
- Liu, J.; Zhao, T.; Chen, Y. Maximum power point tracking of proton exchange membrane fuel cell with fractional order filter and extremum seeking control. In Proceedings of the ASME 2015 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Houston, TX, USA, 13–19 November 2015. [Google Scholar] [CrossRef]
- Derbeli, M.; Sbita, L.; Farhat, M.; Barambones, O. PEM fuel cell green energy generation—SMC efficiency optimization. In Proceedings of the 2017 International Conference on Green Energy Conversion Systems (GECS), Hammamet, Tunisia, 23–25 March 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Mrad, I.; Derheli, M.; Shita, L.; Barhot, J.P.; Farhat, M.; Baramhones, O. Sensorless and robust PEMFEC power system drive based on Z (Tn) observability. In Proceedings of the 2017 International Conference on Green Energy Conversion Systems (GECS), Hammamet, Tunisia, 23–25 March 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Hahm, J.; Kang, H.; Baek, J.; Lee, H.; Park, M. Design of incremental conductance sliding mode MPPT control applied by integrated photovoltaic and proton exchange membrane fuel cell system under various operating conditions for BLDC motor. Int. J. Photoenergy 2015, 2015. [Google Scholar] [CrossRef]
- Fang, Y.; Zhu, Y.; Fei, J. Adaptive Intelligent Sliding Mode Control of a Photovoltaic Grid-Connected Inverter. Appl. Sci. 2018, 8, 1756. [Google Scholar] [CrossRef]
- Tsang, K.; Chan, W. Maximum power point tracking for PV systems under partial shading conditions using current sweeping. Energy Convers. Manag. 2015, 93, 249–258. [Google Scholar] [CrossRef]
- Derbeli, M.; Mrad, I.; Sbita, L.; Barambones, O. PEM fuel cell efficiency boosting—Robust MPP tracking. In Proceedings of the 2018 9th International Renewable Energy Congress (IREC), Hammamet, Tunisia, 20–22 March 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Benchouia, N.E.; Derghal, A.; Mahmah, B.; Madi, B.; Khochemane, L.; Aoul, E.H. An adaptive fuzzy logic controller (AFLC) for PEMFC fuel cell. Int. J. Hydrog. Energy 2015, 40, 13806–13819. [Google Scholar] [CrossRef]
- Robles Algarín, C.; Taborda Giraldo, J.; Rodríguez Álvarez, O. Fuzzy logic based MPPT controller for a PV system. Energies 2017, 10, 2036. [Google Scholar] [CrossRef]
- Na, W.; Chen, P.; Kim, J. An improvement of a Fuzzy Logic-Controlled maximum power point tracking algorithm for photovoltic applications. Appl. Sci. 2017, 7, 326. [Google Scholar] [CrossRef]
- Macaulay, J.; Zhou, Z. A Fuzzy Logical-Based Variable Step Size P&O MPPT Algorithm for Photovoltaic System. Energies 2018, 11, 1340. [Google Scholar] [CrossRef]
- Rezoug, M.R.; Chenni, R.; Taibi, D. Fuzzy Logic-Based Perturb and Observe Algorithm with Variable Step of a Reference Voltage for Solar Permanent Magnet Synchronous Motor Drive System Fed by Direct-Connected Photovoltaic Array. Energies 2018, 11, 462. [Google Scholar] [CrossRef]
- Avanaki, I.N.; Sarvi, M. A new maximum power point tracking method for PEM fuel cells based on water cycle algorithm. J. Renew. Energy Environ. 2016, 3, 35. [Google Scholar]
- Fathabadi, H. Novel highly accurate universal maximum power point tracker for maximum power extraction from hybrid fuel cell/photovoltaic/wind power generation systems. Energy 2016, 116, 402–416. [Google Scholar] [CrossRef]
- Mohapatra, A.; Nayak, B.; Das, P.; Mohanty, K.B. A review on MPPT techniques of PV system under partial shading condition. Renew. Sustain. Energy Rev. 2017, 80, 854–867. [Google Scholar] [CrossRef]
- Karami, N.; Moubayed, N.; Outbib, R. General review and classification of different MPPT Techniques. Renew. Sustain. Energy Rev. 2017, 68, 1–18. [Google Scholar] [CrossRef]
- Sarvi, M.; Parpaei, M.; Soltani, I.; Taghikhani, M. Eagle strategy based maximum power point tracker for fuel cell system. Int. J. Eng.-Trans. A Basics 2015, 28, 529–536. [Google Scholar]
- Kim, M.K. Optimal control and operation strategy for wind turbines contributing to grid primary frequency regulation. Appl. Sci. 2017, 7, 927. [Google Scholar] [CrossRef]
- Kalaiarasi, N.; Dash, S.S.; Padmanaban, S.; Paramasivam, S.; Morati, P.K. Maximum Power Point Tracking Implementation by Dspace Controller Integrated Through Z-Source Inverter Using Particle Swarm Optimization Technique for Photovoltaic Applications. Appl. Sci. 2018, 8, 145. [Google Scholar] [CrossRef]
- Pohjoranta, A.; Sorrentino, M.; Pianese, C.; Amatruda, F.; Hottinen, T. Validation of neural network-based fault diagnosis for multi-stack fuel cell systems: Stack voltage deviation detection. Energy Procedia 2015, 81, 173–181. [Google Scholar] [CrossRef]
- Bicer, Y.; Dincer, I.; Aydin, M. Maximizing performance of fuel cell using artificial neural network approach for smart grid applications. Energy 2016, 116, 1205–1217. [Google Scholar] [CrossRef]
- Chen, M.; Ma, S.; Wu, J.; Huang, L. Analysis of MPPT failure and development of an augmented nonlinear controller for MPPT of photovoltaic systems under partial shading conditions. Appl. Sci. 2017, 7, 95. [Google Scholar] [CrossRef]
- Hadji, S.; Gaubert, J.P.; Krim, F. Real-Time Genetic Algorithms-Based MPPT: Study and Comparison (Theoretical an Experimental) with Conventional Methods. Energies 2018, 11, 459. [Google Scholar] [CrossRef]
- Adinolfi, G.; Graditi, G.; Siano, P.; Piccolo, A. Multiobjective optimal design of photovoltaic synchronous boost converters assessing efficiency, reliability, and cost savings. IEEE Trans. Ind. Inform. 2015, 11, 1038–1048. [Google Scholar] [CrossRef]
- Xiao, W.; Dunford, W.G.; Palmer, P.R.; Capel, A. Application of centered differentiation and steepest descent to maximum power point tracking. IEEE Trans. Ind. Electron. 2007, 54, 2539–2549. [Google Scholar] [CrossRef]
- Tolentino, L.K.S.; Cruz, F.R.G.; Garcia, R.G.; Chung, W.Y. Maximum power point tracking controller IC based on ripple correlation control algorithm. In Proceedings of the 2015 International Conference on Humanoid, Nanotechnology, Information Technology, Communication and Control, Environment and Management (HNICEM), Cebu City, Philippines, 9–12 December 2015; pp. 1–6. [Google Scholar] [CrossRef]
- Ferdous, S.; Shafiullah, G.; Oninda, M.A.M.; Shoeb, M.A.; Jamal, T. Close loop compensation technique for high performance MPPT using ripple correlation control. In Proceedings of the 2017 Australasian Universities Power Engineering Conference (AUPEC), Melbourne, Australia, 19–22 November 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Hammami, M.; Grandi, G. A Single-Phase Multilevel PV Generation System with an Improved Ripple Correlation Control MPPT Algorithm. Energies 2017, 10, 2037. [Google Scholar] [CrossRef]
- Benhalima, S.; Miloud, R.; Chandra, A. Real-Time Implementation of Robust Control Strategies Based on Sliding Mode Control for Standalone Microgrids Supplying Non-Linear Loads. Energies 2018, 11, 2590. [Google Scholar] [CrossRef]
- Martin, A.D.; Cano, J.; Silva, J.F.A.; Vázquez, J.R. Backstepping control of smart grid-connected distributed photovoltaic power supplies for telecom equipment. IEEE Trans. Energy Convers. 2015, 30, 1496–1504. [Google Scholar] [CrossRef]
- Patra, S.; Ankur Narayana, M.; Mohanty, S.R.; Kishor, N. Power quality improvement in grid-connected photovoltaic—Fuel cell based hybrid system using robust maximum power point tracking controller. Electr. Power Compon. Syst. 2015, 43, 2235–2250. [Google Scholar] [CrossRef]
- Taouni, A.; Abbou, A.; Akherraz, M.; Ouchatti, A.; Majdoul, R. MPPT design for photovoltaic system using backstepping control with boost converter. In Proceedings of the 2016 International Renewable and Sustainable Energy Conference (IRSEC), Marrakech, Morocco, 14–17 November 2016; pp. 469–475. [Google Scholar] [CrossRef]
- Reddak, M.; Berdai, A.; Gourma, A.; Belfqih, A. Integral backstepping control based maximum power point tracking strategy for wind turbine systems driven DFIG. In Proceedings of the 2016 International Conference on Electrical and Information Technologies (ICEIT), Paris, France, 17–18 March 2016; pp. 84–88. [Google Scholar] [CrossRef]
- Wu, D.; Chen, M.; Gong, H.; Wu, Q. Robust Backstepping Control of Wing Rock Using Disturbance Observer. Appl. Sci. 2017, 7, 219. [Google Scholar] [CrossRef]
- Chen, L.H.; Peng, C.C. Extended backstepping sliding controller design for chattering attenuation and its application for servo motor control. Appl. Sci. 2017, 7, 220. [Google Scholar] [CrossRef]
- Lee, K.U.; Choi, Y.H.; Park, J.B. Backstepping Based Formation Control of Quadrotors with the State Transformation Technique. Appl. Sci. 2017, 7, 1170. [Google Scholar] [CrossRef]
- Nafaa, H.; Farhat, M.; Lassaad, S. A PV water desalination system using backstepping approach. In Proceedings of the 2017 International Conference on Green Energy Conversion Systems (GECS), Hammamet, Tunisia, 23–25 March 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Guo, Q.; Liu, Y.; Jiang, D.; Wang, Q.; Xiong, W.; Liu, J.; Li, X. Prescribed Performance Constraint Regulation of Electrohydraulic Control Based on Backstepping with Dynamic Surface. Appl. Sci. 2018, 8, 76. [Google Scholar] [CrossRef]
- Duan, K.; Fong, S.; Zhuang, Y.; Song, W. Artificial Neural Networks in Coordinated Control of Multiple Hovercrafts with Unmodeled Terms. Appl. Sci. 2018, 8, 862. [Google Scholar] [CrossRef]
- Wang, S.; Wang, L.; Qiao, Z.; Li, F. Optimal Robust Control of Path Following and Rudder Roll Reduction for a Container Ship in Heavy Waves. Appl. Sci. 2018, 8, 1631. [Google Scholar] [CrossRef]
- Arsalan, M.; Iftikhar, R.; Ahmad, I.; Hasan, A.; Sabahat, K.; Javeria, A. MPPT for photovoltaic system using nonlinear backstepping controller with integral action. Sol. Energy 2018, 170, 192–200. [Google Scholar] [CrossRef]
- Wilberforce, T.; El-Hassan, Z.; Khatib, F.; Al Makky, A.; Baroutaji, A.; Carton, J.G.; Thompson, J.; Olabi, A.G. Modelling and simulation of Proton Exchange Membrane fuel cell with serpentine bipolar plate using MATLAB. Int. J. Hydrog. Energy 2017, 42, 25639–25662. [Google Scholar] [CrossRef]
- Rismanchi, B.; Akbari, M. Performance prediction of proton exchange membrane fuel cells using a three-dimensional model. Int. J. Hydrog. Energy 2008, 33, 439–448. [Google Scholar] [CrossRef]
- Handbook, F.C. US Department of Energy, Office of Fossil Energy, and National Energy Technology Laboratory, EG&G Technical Services; Science Application International Corporation: Reston, VA, USA, 2002. [Google Scholar]
- Larminie, J.; Dicks, A. Fuel Cell Systems Explained; John willey & Sons, Ltd.: West Sussex, UK, 2000. [Google Scholar]
- Derbeli, M.; Farhat, M.; Barambones, O.; Sbita, L. Control of PEM fuel cell power system using sliding mode and super-twisting algorithms. Int. J. Hydrog. Energy 2017, 42, 8833–8844. [Google Scholar] [CrossRef]
- Kolli, A.; Gaillard, A.; De Bernardinis, A.; Bethoux, O.; Hissel, D.; Khatir, Z. A review on DC/DC converter architectures for power fuel cell applications. Energy Convers. Manag. 2015, 105, 716–730. [Google Scholar] [CrossRef]
- Boukrich, N.; Derbeli, M.; Farhat, M.; Sbita, L. Smart auto-tuned regulators in electric vehicule PMSM drives. In Proceedings of the 2017 International Conference on Green Energy Conversion Systems (GECS), Hammamet, Tunisia, 23–25 March 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Harahap, C.R.; Hanamoto, T. Fictitious Reference Iterative Tuning-Based Two-Degrees-of-Freedom Method for Permanent Magnet Synchronous Motor Speed Control Using FPGA for a High-Frequency SiC MOSFET InverterMOSFET Inverter. Appl. Sci. 2016, 6, 387. [Google Scholar] [CrossRef]
- Espíndola-López, E.; Gómez-Espinosa, A.; Carrillo-Serrano, R.V.; Jáuregui-Correa, J.C. Fourier series learning control for torque ripple minimization in permanent magnet synchronous motors. Appl. Sci. 2016, 6, 254. [Google Scholar] [CrossRef]
- Chen, J.H.; Yau, H.T.; Lu, J.H. Implementation of FPGA-based charge control for a self-sufficient solar tracking power supply system. Appl. Sci. 2016, 6, 41. [Google Scholar] [CrossRef]
- Rosyadi, M.; Muyeen, S.; Takahashi, R.; Tamura, J. A design fuzzy logic controller for a permanent magnet wind generator to enhance the dynamic stability of wind farms. Appl. Sci. 2012, 2, 780–800. [Google Scholar] [CrossRef]
- Ho, T.J.; Chang, C.H. Robust Speed Tracking of Induction Motors: An Arduino-Implemented Intelligent Control Approach. Appl. Sci. 2018, 8, 159. [Google Scholar] [CrossRef]

| Parameter | Symbole | Value |
|---|---|---|
| Cell operating temperature | T | [K] |
| Cell standard temperature | 298.15 [K] | |
| Cell operating current | I | [A] |
| Universal constant of the gases | R | 83.143 [JmolK] |
| Constant of Faraday | F | 96,485.309 [Cmol] |
| Maximum current density | 0.062 A cm | |
| Current density | J | [Acm] |
| Change in the free Gibbs energy | [Jmol] | |
| Change of entropy | [Jmol] | |
| Enthalpy of formation | −285.84 kJmol | |
| Change in the Gibbs free energy at standard condition | [Jmol] | |
| Change of entropy at standard condition | [Jmol] | |
| Electrochemical thermodynamics potential | E | [V] |
| Standard potential of the fuel cell | 1.229 [V] | |
| Membrane active area | A | [162 cm] |
| Hydrogen and oxygen partial pressures | , | [atm] |
| Oxygen concentration | [molcm] | |
| Fuel cell voltage | [V] | |
| Activation losses | [V] | |
| Ohmic losses | [V] | |
| Concentration losses | [V] | |
| Constant parameters | 0.1 [V] | |
| Electric charge | Q | [coulombs] |
| Equivalent resistance of the electron flow | ||
| Proton resistance | ||
| Parametric coefficients | , , , |
| Type of Controller | |||
|---|---|---|---|
| P | /2 | ∞ | 0 |
| PI | /2.2 | /1.2 | 0 |
| PID | /1.7 | /2 | /8 |
| Ideal DC–DC Boost Converter | PI Controller | Backstepping | |||||
|---|---|---|---|---|---|---|---|
| Parameter | R | L | C | ||||
| Value | 20 | H | F | 9 | 220 | ||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Derbeli, M.; Barambones, O.; Sbita, L. A Robust Maximum Power Point Tracking Control Method for a PEM Fuel Cell Power System. Appl. Sci. 2018, 8, 2449. https://doi.org/10.3390/app8122449
Derbeli M, Barambones O, Sbita L. A Robust Maximum Power Point Tracking Control Method for a PEM Fuel Cell Power System. Applied Sciences. 2018; 8(12):2449. https://doi.org/10.3390/app8122449
Chicago/Turabian StyleDerbeli, Mohamed, Oscar Barambones, and Lassaad Sbita. 2018. "A Robust Maximum Power Point Tracking Control Method for a PEM Fuel Cell Power System" Applied Sciences 8, no. 12: 2449. https://doi.org/10.3390/app8122449
APA StyleDerbeli, M., Barambones, O., & Sbita, L. (2018). A Robust Maximum Power Point Tracking Control Method for a PEM Fuel Cell Power System. Applied Sciences, 8(12), 2449. https://doi.org/10.3390/app8122449







