Combustion State Recognition of Flame Images Using Radial Chebyshev Moment Invariants Coupled with an IFA-WSVM Model
Abstract
:1. Introduction
2. Feature Selection Using Radial Chebyshev Moment Invariants
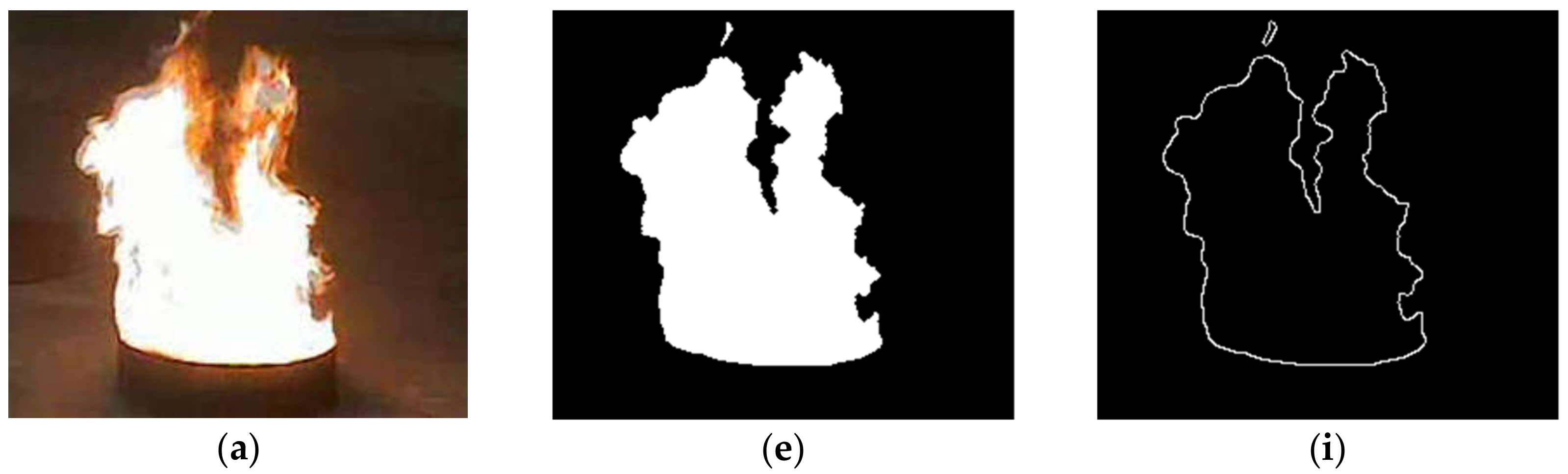
2.1. Pre-Processing of Candidate Image
2.2. Radial Chebyshev Moments
2.3. Radial Chebyshev Moment Invariants
2.4. Feature Selection
3. Improved Firefly Algorithm-Wavelet Support Vector Machine
3.1. Wavelet Support Vector Machine (WSVM)
3.2. Firefly Algorithm
3.3. Improved Firefly Algorithm
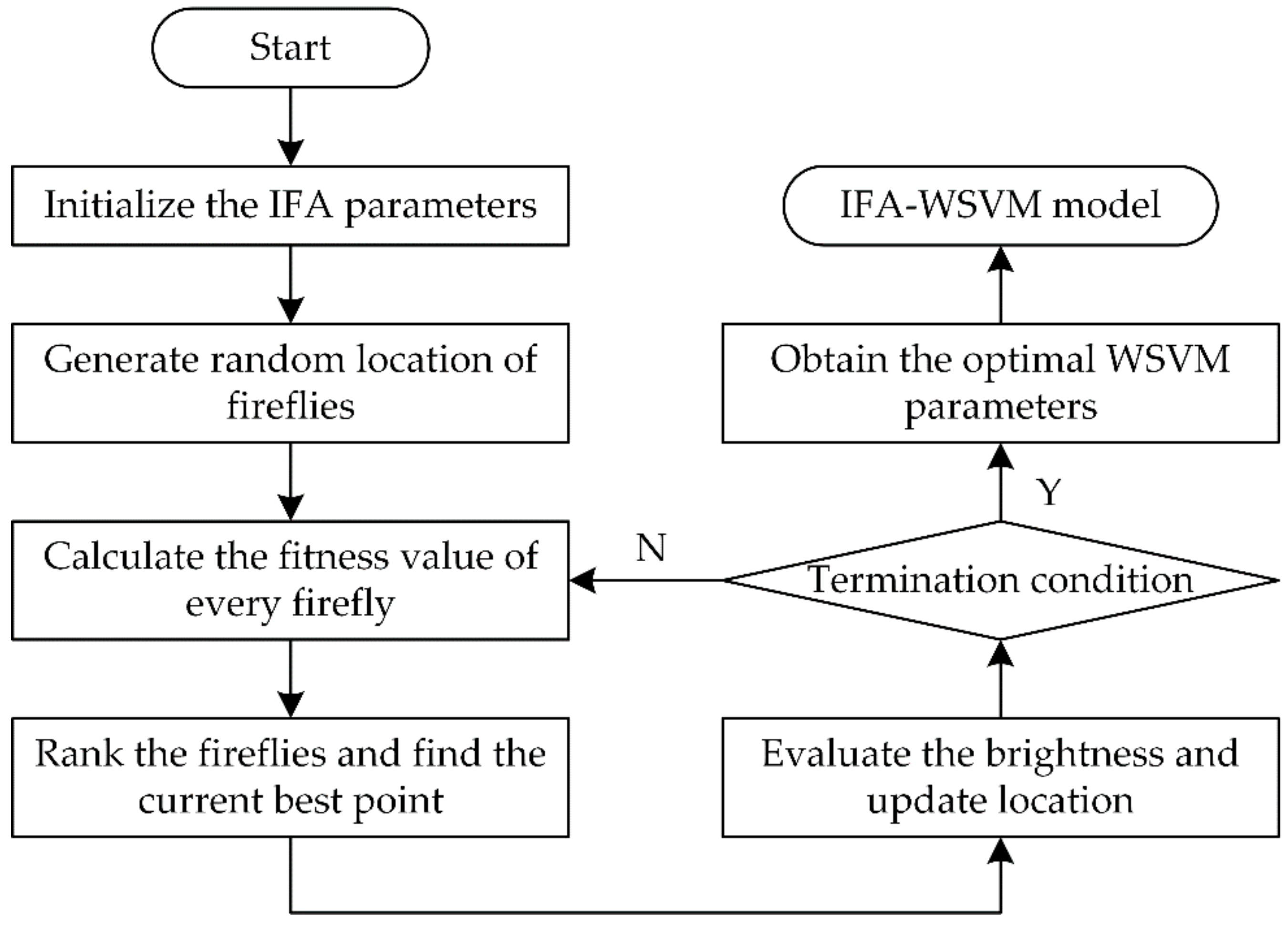
3.4. WSVM Parameter Optimization Based on Improved Firefly Algorithm
- Step 1.
- Initialize the improved firefly algorithm, and set up the parameters, including the number of fireflies , initial and final randomization parameters and , maximum iterations , attractiveness , basic attractiveness and light absorption coefficient .
- Step 2.
- Generate the initial locations of fireflies at random as , every firefly is composed of the WSVM parameters and .
- Step 3.
- Calculate the fitness value of every firefly to determine or update its brightness.
- Step 4.
- Rank the fireflies by their brightness and regard the firefly with minimum brightness as the global-best point.
- Step 5.
- Evaluate the brightness of every current firefly and compare the brightness of any two fireflies and . If , calculate the distance to obtain the improved attractiveness . Then, move firefly towards in all dimensions using Equation (28). The randomization parameter is updated by Equation (26).
- Step 6.
- Check termination condition. If the maximum iteration limit is reached, stop the optimization process and output the values of optimal parameters and . Otherwise, return to Step 3.
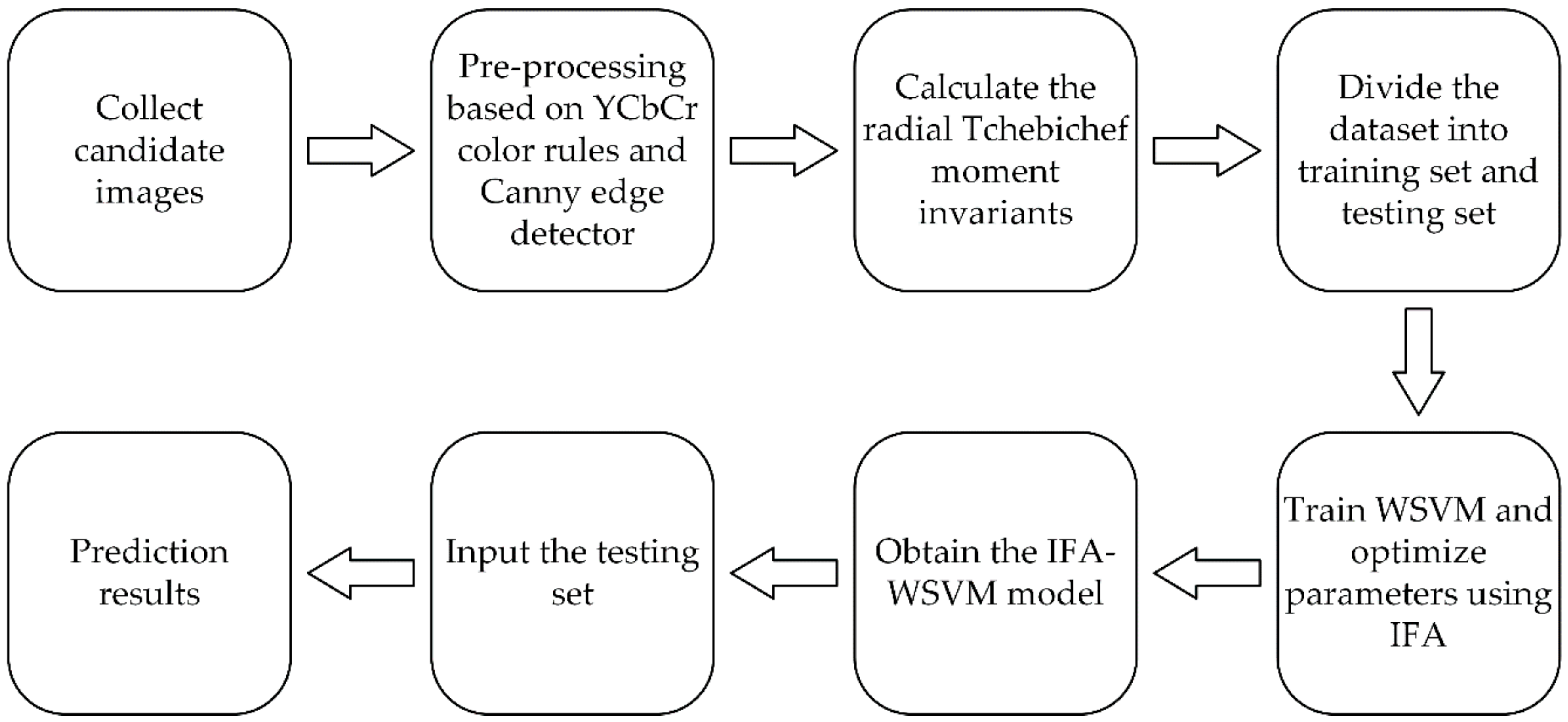
4. Combustion State Recognition Based on IFA-WSVM Model
- Step 1.
- Apply a video camera to collect a series of candidate images. Then, the pre-processed and edge images are obtained by pre-processing the candidate images.
- Step 2.
- Calculate the radial Chebyshev moment invariants of every pre-processed and edge image. Select the region and contour moment invariants to construct the corresponding feature vector . The dataset is composed of all the feature vectors and their labels.
- Step 3.
- Divide the dataset into training set and testing set. The former is employed to construct model, and the latter is used for validating the IFA-WSVM model.
- Step 4.
- Train the WSVM with the feature vectors of training set, and apply IFA to determine the penalty factor and the dilation parameter . When the termination condition is met, the optimal parameters are obtained.
- Step 5.
- Input the training data into the WSVM with optimal parameters once again, rebuilding the IFA-WSVM model. The features vectors of testing set are input into the IFA-WSVM model to predict their belonging labels, achieving the combustion state recognition.
5. Case Studies
5.1. Study Setup
5.2. Results and Discussion
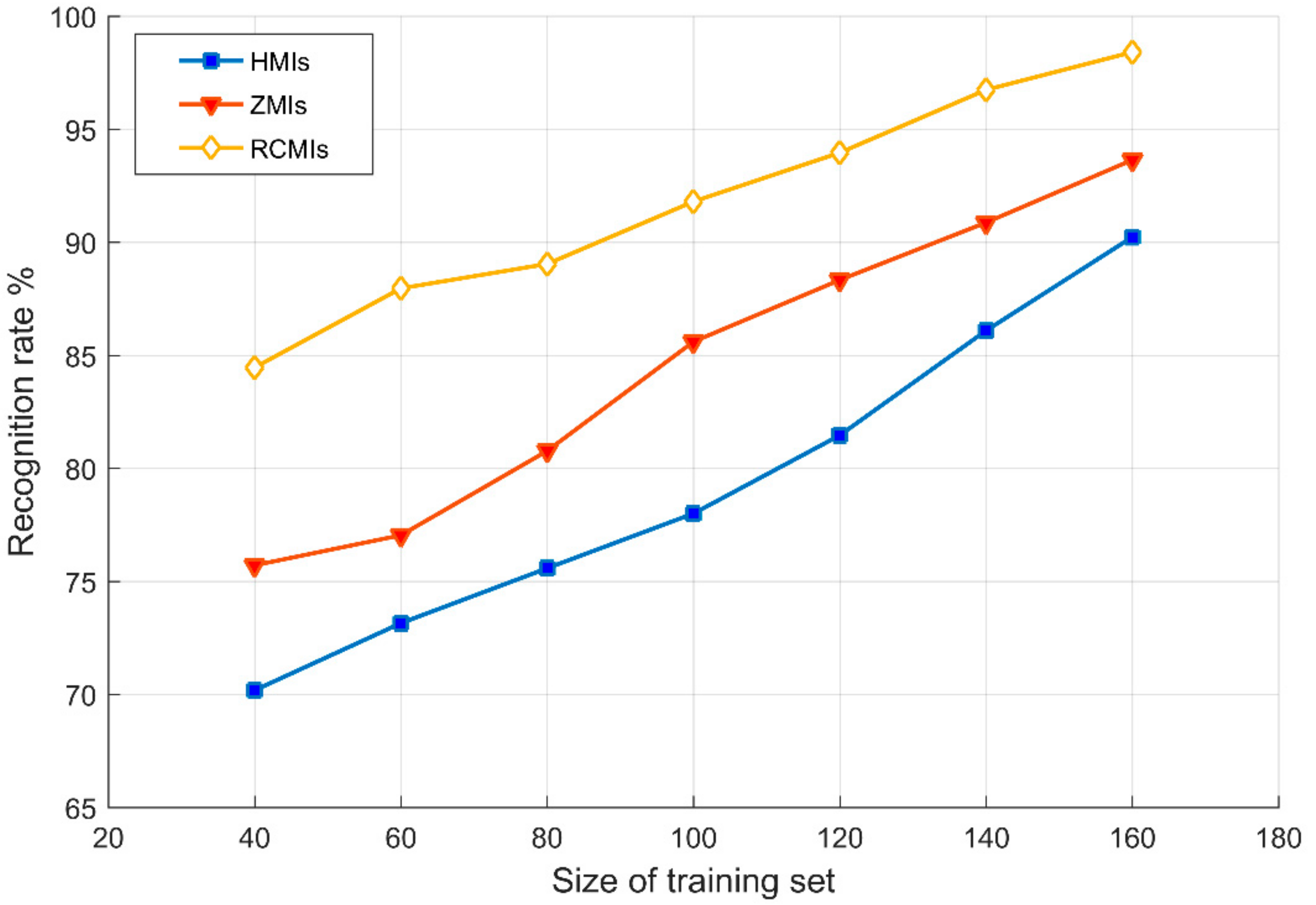
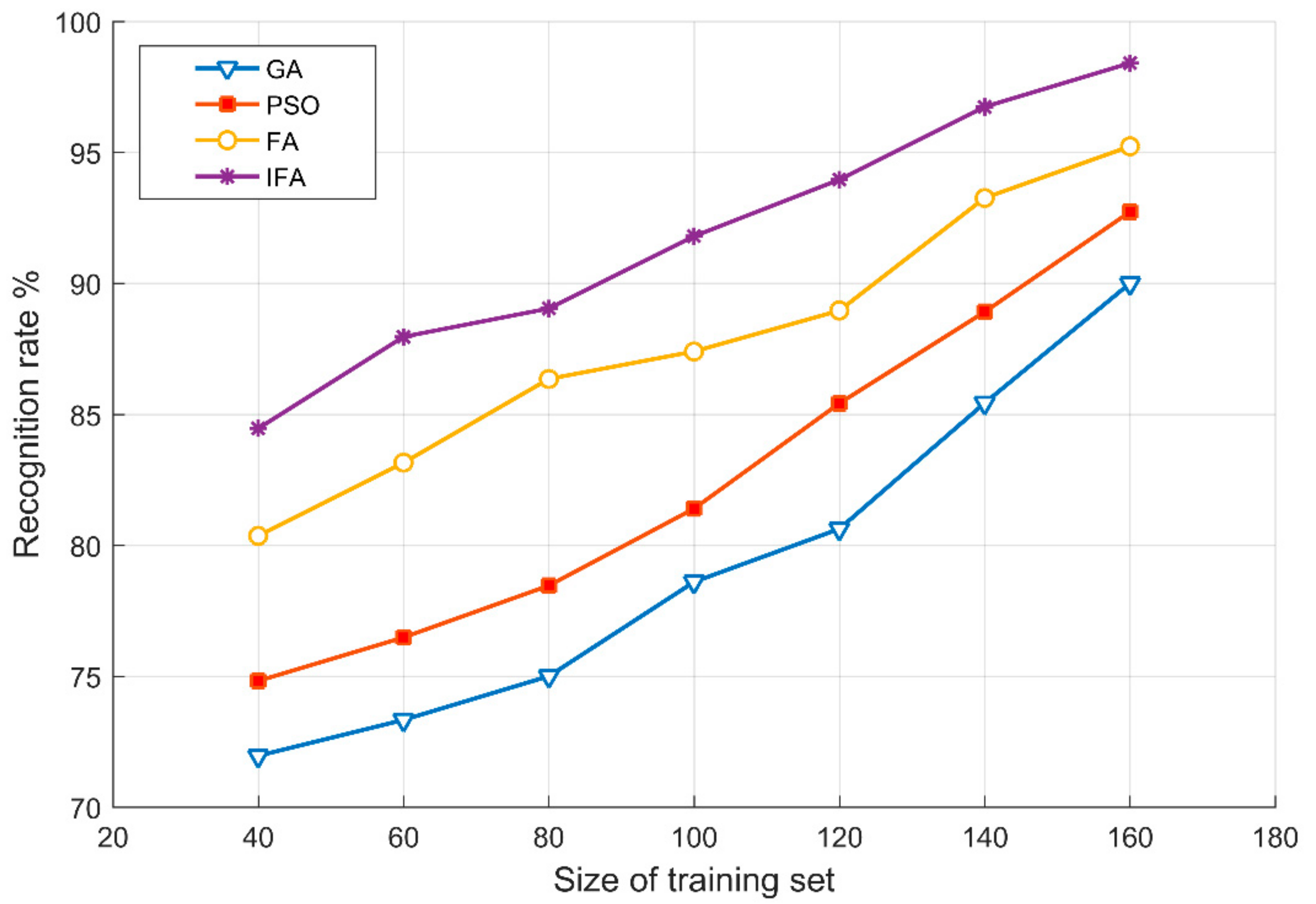
5.2.1. Results for the First Case Study and Comparison
5.2.2. Results for the Second Case Study and Comparison
5.2.3. Results for the Third Case Study and Comparison
5.2.4. Results for the Fourth Case Study and Comparison
5.2.5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Duong, H.D.; Tinh, D.T. An efficient method for vision-based fire detection using SVM classification. In Proceedings of the International Conference on Soft Computing and Pattern Recognition (SoCPaR), Hanoi, Vietnam, 15–18 December 2013. [Google Scholar]
- Hasan, M.M.; Razzak, M.A. An automatic fire detection and warning system under home video surveillance. In Proceedings of the IEEE 12th International Colloquium on Signal Processing & ITS Applications (CSPA), Malacca, Malaysia, 4–6 March 2016. [Google Scholar]
- Jayashree, D.; Pavithra, S.; Vaishali, G.; Vidhya, J. System to detect fire under surveillanced area. In Proceedings of the Third International Conference on Science Technology Engineering & Management (ICONSTEM), Chennai, India, 23–24 March 2017. [Google Scholar]
- Lascio, R.D.; Greco, A.; Saggese, A.; Vento, M. Improving fire detection reliability by a combination of videoanalytics. In Proceedings of the 11th International Conference on Image Analysis and Recognition (ICIAR), Vilamoura, Portugal, 22–24 October 2014. [Google Scholar]
- Zhang, Z.J.; Shen, T.; Zou, J.H. An Improved Probabilistic Approach for Fire Detection in Videos. Fire Technol. 2014, 50, 745–752. [Google Scholar] [CrossRef]
- Duong, H.D.; Tinh, D.T. A new approach to vision-based fire detection using statistical features and Bayes classifier. In Proceedings of the 9th International Conference on Simulated Evolution and Learning (SEAL), Hanoi, Vietnam, 16–19 December 2012. [Google Scholar]
- Shao, L.S.; Guo, Y.C. Flame recognition algorithm based on Codebook in video. J. Comput. Appl. 2015, 35, 1483–1487. [Google Scholar]
- Sandhu, H.S.; Singh, K.J.; Kapoor, D.S. Automatic edge detection algorithm and area calculation for flame and fire images. In Proceedings of the 6th International Conference-Cloud System and Big Data Engineering (Confluence), Noida, India, 14–15 January 2016. [Google Scholar]
- Wang, Y.K.; Wu, A.G.; Zhang, J.; Zhao, M.; Li, W.S.; Dong, N. Fire smoke detection based on texture features and optical flow vector of contour. In Proceedings of the 12th World Congress on Intelligent Control and Automation (WCICA), Guilin, China, 12–15 June 2016. [Google Scholar]
- Maksymiv, O.; Rak, T.; Peleshko, D. Real-time fire detection method combining AdaBoost, LBP and convolutional neural network in video sequence. In Proceedings of the 14th International Conference the Experience of Designing and Application of Cad Systems in Microelectronics (CADSM), Lviv, Ukraine, 21–25 February 2017. [Google Scholar]
- Russo, A.U.; Deb, K.; Tista, S.C.; Islam, A. Smoke Detection Method Based on LBP and SVM from Surveillance Camera. In Proceedings of the International Conference on Computer, Communication, Chemical, Material and Electronic Engineering (IC4ME2), Rajshahi, Bangladesh, 8–9 February 2018. [Google Scholar]
- Wang, D.; Cui, X.N.; Park, E.; Jin, C.L.; Kim, H. Adaptive flame detection using randomness testing and robust features. Fire Saf. J. 2013, 55, 116–125. [Google Scholar] [CrossRef]
- Zhong, Z.; Wang, M.J.; Shi, Y.K.; Gao, W.L. A convolutional neural network-based flame detection method in video sequence. Signal Image Video Process. 2018, 12, 1619–1627. [Google Scholar] [CrossRef]
- Lin, Y.J.; Chai, L.; Zhang, J.X.; Zhou, X.J. On-line burning state recognition for sintering process using SSIM index of flame images. In Proceedings of the 11th World Congress on Intelligent Control and Automation, Shenyang, China, 29 June–4 July 2014. [Google Scholar]
- Cheng, Y.; Sheng, Y.X.; Chai, L. Burning state recognition using CW-SSIM index evaluation of color flame images. In Proceedings of the 27th Chinese Control and Decision Conference (CCDC), Qingdao, China, 23–25 May 2015. [Google Scholar]
- Prema, C.E.; Vinsley, S.S.; Suresh, S. Multi Feature Analysis of Smoke in YUV Color Space for Early Forest Fire Detection. Fire Technol. 2016, 52, 1–24. [Google Scholar]
- Shi, L.F.; Long, F.; Zhan, Y.J.; Lin, C.H. Video-based fire detection with spatio-temporal SURF and color features. In Proceedings of the 12th World Congress on Intelligent Control and Automation (WCICA), Guilin, China, 12–15 June 2016. [Google Scholar]
- Yan, X.F.; Cheng, H.; Zhao, Y.D.; Yu, W.H.; Huang, H.; Zheng, X.L. Real-Time Identification of Smoldering and Flaming Combustion Phases in Forest Using a Wireless Sensor Network-Based Multi-Sensor System and Artificial Neural Network. Sensors 2016, 16, 1228. [Google Scholar] [CrossRef] [PubMed]
- Chauhan, A.; Semwal, S.; Chawhan, R. Artificial neural network-based forest fire detection system using wireless sensor network. In Proceedings of the Annual IEEE India Conference (INDICON), Mumbai, India, 13–15 December 2013. [Google Scholar]
- Ghorbani, M.A.; Shamshirband, S.; Zare Haghi, D.; Azani, A.; Bonakdari, H.; Ebtehaj, I. Application of firefly algorithm-based support vector machines for prediction of field capacity and permanent wilting point. Soil Tillage Res. 2017, 172, 32–38. [Google Scholar] [CrossRef]
- Vapnik, V. The Nature of Statistical Learning Theory, 2nd ed.; Springer: New York, NY, USA, 1999. [Google Scholar]
- Niu, X.; Yang, C.; Wang, H.; Wang, Y. Investigation of ANN and SVM based on limited samples for performance and emissions prediction of CRDI-assisted marine diesel engine. Appl. Ther. Eng. 2016, 111, 1353–1364. [Google Scholar] [CrossRef]
- Sung, A.H.; Mukkamala, S. Identifying important features for intrusion detection using support vector machines and neural networks. In Proceedings of the Symposium on Applications and the Internet, Orlando, FL, USA, 27–31 January 2003. [Google Scholar]
- Motamedi, S.; Shamshirband, S.; Ch, S.; Hashim, R.; Arif, M. Soft computing approaches for forecasting reference evapotranspiration. Comput. Electron. Agric. 2015, 113, 164–173. [Google Scholar]
- Jiang, M.L.; Jiang, L.; Jiang, D.D.; Xiong, J.P.; Shen, J.G.; Ahmed, H.S.; Luo, J.Y.; Song, H.B. Dynamic Measurement Errors Prediction for Sensors Based on Firefly Algorithm Optimize Support Vector Machine. Sustain. Cities Soc. 2017, 35, 250–256. [Google Scholar] [CrossRef]
- Li, Y.F.; Chen, M.N.; Lu, X.D.; Zhao, W.Z. Research on optimized GA-SVM vehicle speed prediction model based on driver-vehicle-road-traffic system. Sci. China Technol. Sci. 2018, 61, 782–790. [Google Scholar] [CrossRef]
- Liu, X.; Gang, C.; Gao, W.; Zhang, K. GA-AdaBoostSVM classifier empowered wireless network diagnosis. Eurasip J. Wirel. Commun. Netw. 2018, 77, 1–18. [Google Scholar] [CrossRef]
- Ding, S.; Hang, J.; Wei, B.; Wang, Q. Modelling of supercapacitors based on SVM and PSO algorithms. IET Electr. Power Appl. 2018, 12, 502–507. [Google Scholar] [CrossRef]
- Ma, Z.; Dong, Y.; Liu, H.; Shao, X.; Wang, C. Method of Forecasting Non-Equal Interval Track Irregularity Based on Improved Grey Model and PSO-SVM. IEEE Access. 2018, 6, 34812–34818. [Google Scholar] [CrossRef]
- Yang, X.S. Firefly Algorithm, Stochastic Test Functions and Design Optimisation. Int. J. Bio-Inspired Comput. 2010, 2, 78–84. [Google Scholar] [CrossRef]
- Celik, T.; Ozkaramanlt, H.; Demirel, H. Fire Pixel Classification using Fuzzy Logic and Statistical Color Model. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, Honolulu, HI, USA, 15–20 April 2007. [Google Scholar]
- Jia, Y.; Wang, H.; Yan, H.U.; Dang, B. Flame detection algorithm based on improved hierarchical cluster and support vector machines. Comput. Eng. Appl. 2014, 50, 165–168. [Google Scholar]
- BT. 601: Studio Encoding Parameters of Digital Television for Standard 4:3 and Wide Screen 16:9 Aspect Ratios. Available online: https://www.itu.int/rec/R-REC-BT.601-7-201103-I/en (accessed on 1 November 2018).
- Canny, J. A Computational Approach to Edge Detection. IEEE Trans. Pattern Anal. Mach. Intell. 1986, 8, 679–698. [Google Scholar] [CrossRef] [PubMed]
- Flusser, J.; Zitova, B.; Suk, T. Moments and Moment Invariants in Pattern Recognition, 1st ed.; Wiley & Sons Ltd.: West Sussex, UK, 2009. [Google Scholar]
- Nikiforov, A.F.; Uvarov, V.B.; Suslov, S.K. Classical Orthogonal Polynomials of a Discrete Variable; Springer: New York, NY, USA, 1991. [Google Scholar]
- Mukundan, R. Radial Tchebichef Invariants for Pattern Recognition. In Proceedings of the Tencon 2005 IEEE Region 10 Conference, Melbourne, Australia, 21–24 November 2005. [Google Scholar]
- Zhong, W.; Zhuang, Y.; Sun, J.; Gu, J.J. A load prediction model for cloud computing using PSO-based weighted wavelet support vector machine. Appl. Intell. 2018, 48, 4072–4083. [Google Scholar] [CrossRef]
- Du, P.; Tan, K.; Xing, X. Wavelet SVM in Reproducing Kernel Hilbert Space for hyperspectral remote sensing image classification. Opt. Commun. 2010, 283, 4978–4984. [Google Scholar] [CrossRef]
- Kang, S.; Cho, S.; Kang, P. Constructing a multi-class classifier using one-against-one approach with different binary classifiers. Neurocomputing 2015, 149, 677–682. [Google Scholar] [CrossRef]
- Galar, M.; Ndez, A.; Barrenechea, E.; Bustince, H.; Herrera, F. An overview of ensemble methods for binary classifiers in multi-class problems: Experimental study on one-vs-one and one-vs-all schemes. Pattern Recognit. 2011, 44, 1761–1776. [Google Scholar] [CrossRef]




| Stable burning state | 0.05764 | 0.1434 | 0.06644 | 0.07413 | 0.05933 | 0.1205 | 0.07037 | 0.05952 |
| Extinguishing state | 0.09043 | 0.1052 | 0.07653 | 0.06037 | 0.04384 | 0.1627 | 0.09681 | 0.04934 |
| Final extinguished state | 0.1105 | 0.1751 | 0.05140 | 0.04476 | 0.03403 | 0.06471 | 0.05474 | 0.1346 |
| Non-flame state | 0.1022 | 0.1882 | 0.2518 | 0.1948 | 0.2879 | 0.3698 | 0.2118 | 0.2461 |
| Coefficient of variation | 25.73% | 24.18% | 84.35% | 73.34% | 114.36% | 74.18% | 65.54% | 74.19% |
| Stable burning state | 0.2231 | 0.2069 | 0.2632 | 0.2318 | 0.2162 | 0.5859 | 0.3427 | 0.3169 |
| Extinguishing state | 0.2418 | 0.2789 | 0.3329 | 0.2783 | 0.2824 | 0.4407 | 0.4145 | 0.4081 |
| Final extinguished state | 0.5374 | 0.7651 | 0.2971 | 0.2147 | 0.3470 | 0.7293 | 0.4514 | 0.4533 |
| Non-flame state | 0.2017 | 0.4388 | 0.3742 | 0.2721 | 0.2329 | 0.5646 | 0.3281 | 0.4908 |
| Coefficient of variation | 52.63% | 58.74% | 15.04% | 12.40% | 21.78% | 20.39% | 15.25% | 17.97% |
| Parameter | Value | Range | Description |
|---|---|---|---|
| 10 | — | Number of fireflies | |
| 0.5 | — | Initial randomization parameters | |
| — | Final randomization parameters | ||
| 50 | — | Maximum number of iterations | |
| 1 | — | Attractiveness | |
| 0.2 | — | Basic attractiveness | |
| 1 | — | Light absorption coefficient | |
| — | Penalty factor of WSVM | ||
| — | Dilation parameter of WSVM |
| Parameter | Region Moments | Region and Contour Moments | ||||
|---|---|---|---|---|---|---|
| Hu | Zernike | Radial-Chebyshev | Hu | Zernike | Radial-Chebyshev | |
| Recognition amount | 1751 | 1808 | 1875 | 1796 | 1844 | 1916 |
| Recognition rate | 90.54% | 93.49% | 96.95% | 92.86% | 95.35% | 99.07% |
| Average operating time of a single image | 32.19 ms | 103.54 ms | 41.07 ms | 66.16 ms | 205.79 ms | 83.38 ms |
| (a) | 0.05444 | 0.07434 | 0.04488 | 0.03860 | 0.07514 | 0.2510 | 0.08892 | 0.07073 |
| (b) | 0.06002 | 0.07957 | 0.04718 | 0.03732 | 0.07636 | 0.2244 | 0.08912 | 0.07578 |
| (c) | 0.05684 | 0.07554 | 0.04697 | 0.03652 | 0.07114 | 0.2494 | 0.09563 | 0.06927 |
| (d) | 0.05888 | 0.07493 | 0.04831 | 0.03963 | 0.08176 | 0.2232 | 0.09072 | 0.07867 |
| (e) | 0.05713 | 0.07609 | 0.04288 | 0.03778 | 0.07301 | 0.2431 | 0.08103 | 0.07241 |
| (f) | 0.05563 | 0.07076 | 0.04622 | 0.03576 | 0.07406 | 0.2499 | 0.08882 | 0.07744 |
| (g) | 0.05484 | 0.07380 | 0.04410 | 0.03947 | 0.07741 | 0.2507 | 0.09012 | 0.07114 |
| (h) | 0.05863 | 0.07114 | 0.04512 | 0.03465 | 0.07286 | 0.2206 | 0.09840 | 0.07812 |
| (i) | 0.05261 | 0.07264 | 0.04923 | 0.04097 | 0.08093 | 0.2646 | 0.08392 | 0.08116 |
| Coefficient of variation | 4.24% | 3.64% | 4.43% | 5.34% | 4.81% | 6.39% | 5.88% | 5.59% |
| Parameter | Region Moments | Region and Contour Moments | ||||
|---|---|---|---|---|---|---|
| Hu | Zernike | Radial-Chebyshev | Hu | Zernike | Radial-Chebyshev | |
| Recognition amount | 376 | 391 | 419 | 397 | 412 | 433 |
| Recognition rate | 85.45% | 88.86% | 95.23% | 90.23% | 93.64% | 98.41% |
| Average operating time of a single image | 33.39 ms | 100.90 ms | 46.37 ms | 67.84 ms | 198.16 ms | 90.42 ms |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, M.; Bian, Y.; Yang, J.; Liu, G. Combustion State Recognition of Flame Images Using Radial Chebyshev Moment Invariants Coupled with an IFA-WSVM Model. Appl. Sci. 2018, 8, 2331. https://doi.org/10.3390/app8112331
Yang M, Bian Y, Yang J, Liu G. Combustion State Recognition of Flame Images Using Radial Chebyshev Moment Invariants Coupled with an IFA-WSVM Model. Applied Sciences. 2018; 8(11):2331. https://doi.org/10.3390/app8112331
Chicago/Turabian StyleYang, Meng, Yongming Bian, Jixiang Yang, and Guangjun Liu. 2018. "Combustion State Recognition of Flame Images Using Radial Chebyshev Moment Invariants Coupled with an IFA-WSVM Model" Applied Sciences 8, no. 11: 2331. https://doi.org/10.3390/app8112331
APA StyleYang, M., Bian, Y., Yang, J., & Liu, G. (2018). Combustion State Recognition of Flame Images Using Radial Chebyshev Moment Invariants Coupled with an IFA-WSVM Model. Applied Sciences, 8(11), 2331. https://doi.org/10.3390/app8112331





