1. Introduction
Lithium batteries are widely used in electronic products as they are highly energy-dense electrochemical cells. There are two kinds of lithium battery: the primary lithium battery, also called a lithium metal battery, and the secondary lithium battery, also called a lithium-ion battery. Primary lithium batteries have lithium metal or lithium compounds as the anode. By comparison, the lithium-ion battery is a member of the rechargeable battery family. Primary lithium batteries are commonly used in portable consumer electronic devices and in electric vehicles, ranging from full sized vehicles to radio controlled toys. The most widely used primary lithium battery is the lithium/manganese dioxide (MnO2) couple. Lithium-ion batteries are common in consumer electronics. They are one of the most popular types of rechargeable battery for portable electronics, with one of the best energy densities, no memory effect, and only a slow loss of charge when not in use. In addition to consumer electronics, lithium-ion batteries are growing in popularity for military, electric vehicle, and aerospace applications. The mostly popular lithium-ion batteries are based on lithium cobalt oxide (LCO), lithium iron phosphate (LFP), lithium manganese oxide (LMO), and lithium nickel manganese cobalt oxide (NMC).
All lithium batteries contain highly flammable organic solvents and potentially explosive components [
1]. Many fire and explosion lithium battery accidents have occurred in the past and knowledge of appropriate fire protection agents has not kept pace with the industrial use of lithium batteries, which has grown substantially over the past few years [
2,
3]. Many past studies focused on the safety aspects of lithium batteries in relation to their components, such as electrode materials, the separator, the component of electrolyte, and its additives; to the structure of battery; and the manufacturing process [
4,
5,
6]. Studies on other hazards of lithium batteries have been conducted on the overcharge, nail penetration, crush, and internal short circuit [
7,
8,
9]. Fire behaviors of primary lithium and lithium-ion batteries have been more recently investigated [
10,
11]. The thermal runaway is thought to be the main cause of fire and explosion in lithium-ion batteries [
12,
13,
14]. The burning of lithium batteries produces toxic gases such as HF, CO, and SO
2, which threaten health [
15,
16]. Ribiere et al. studied the combustion of a single 2.9 Ah LiMn
2O
4 battery to investigate the process of battery fire, and found that the state of charge (SOC) significantly affected the burning behavior [
17]. Ping et al. performed similar fire research to evaluate the safety of a large lithium-iron phosphate/graphite battery with 50 Ah capacity and significant fire hazards were also observed [
18]. Larsson et al. conducted fire tests on commercial lithium iron phosphate batteries [
19]. Fu et al. conducted an experimental study on the burning behaviors of 18,650 lithium-ion batteries, and evaluated the effects of SOC on burning behaviors of lithium-ion batteries [
20]. According to their studies, SOC is the main factor affecting the thermal runaway and sustained fire. The SOC of a lithium-ion battery can significantly affect the burning behaviors, and it is generally thought that batteries with larger SOC have a greater ability to burn or explode [
21,
22,
23,
24]. Normally, higher SOC batteries produce higher heat release rate peaks and higher total HF emission than lower SOC batteries.
Batteries are rarely stored and transported as single batteries, and the burning behavior of a pile of multiple batteries can be drastically different from that of a single one. When lithium batteries catch fire, especially during air transport and storage, they can be extraordinarily hazardous. International Air Transport Association Dangerous Goods Regulations (IATA DGR) had introduced special rules about lithium battery transport for the prevention of fire and explosion. Federal Aviation Administration (FAA) had completed a series of tests to determine the flammability characteristics of primary lithium batteries and the dangers associated with shipping them in bulk on commercial transport category aircraft [
25]. Scholars have conducted experimental and theoretical investigations to analyze the thermal runaway and fire behaviors of multiple lithium batteries. Feng et al. studied a three-dimensional (3D) thermal runaway propagation model for a large format lithium-ion battery module and presented four recommendations to postpone or prevent thermal runaway propagation [
26,
27]. Larsson predicted cell-to-cell fire propagation in a five lithium-ion battery pack by simulating the temperature distribution in neighboring cells, which is important for designing and validating safe systems [
28]. Ouyang et al. found that the higher the number of batteries the worse the battery pack fire, and thermal failure appeared earlier for packs with more heaters [
29]. Electric vehicles and plug-in hybrid electric vehicles use large batteries pack to store energy. The energy flows into the battery pack as it is charged, either from regenerative braking or from the grid, and discharges from the pack to power the vehicle. The charging and discharging current causes heating in the batteries; the higher the current the greater the heating effect. The performance of lithium battery is greatly impacted by its temperature, which can lead to thermal runaway. Special cooling systems may be required to prevent damage or even fire during charging and discharging [
30,
31,
32,
33].
In order to develop reliable fire protection strategies for the mass storage and transport of lithium batteries, more studies are needed to understand the fire behaviors of multiple lithium batteries. However, studying large-scale lithium battery fires with experiments is costly. A simulation method is needed to calculate the magnitude of fires for multiple large batteries in order to provide awareness and recommendations for safety protection. In this study, experiments and simulations were conducted to investigate the burning behaviors of different numbers of lithium batteries. The purpose was to establish a baseline set of analyses that characterize specific quantities of primary lithium batteries involved in an unsuppressed fire.
2. Experimental Description
The batteries used in this research are Panasonic (Osaka Prefecture, Japan) CR123A type lithium cells and
Figure 1 shows the appearance and physical size parameters of the batteries (diameter 17 mm, height 34.2 mm). The specifications of the battery obtained from the product brochure were: nominal voltage 3 V, nominal capacity 1550 mAh, and these batteries can be used from −40 °C to 85 °C. Panasonic CR123A is one of the most common lithium primary batteries using lithium as the anode and manganese dioxide (MnO
2) as the cathode. This battery is popular in cameras, game counters, photo equipment, medical equipment, tactical flashlights, and home security systems. This kind of battery has a wide operating temperature range, long shelf life, and is low cost. They are not normally used in large quantities together, but are often packaged together for transportation and storage. There is a large fire risk during these processes, especially during air transport.
The most important parameter for defining fire hazard in this research is heat release rate (HRR). To cater to the current need, an in-situ calorimeter was constructed, which consisted of a burning chamber, an exhaust system, and a katharometer system. A detailed diagram of the in-situ calorimeter and experimental setup is shown in
Figure 2. The dimensions of the burning chamber were 1.2 × 1.2 × 1.2 m. The chamber had a 0.15 m gap at the bottom to allow the intake of fresh air. The gases were collected and removed by an exhaust pump with a volumetric flow rate of 0.18 m
3 s
−1. In general, heater choices for test apparatuses have included gas-fired panels, electric resistance heaters, and flames. Gas-fired panels or flames affect the measurement of HRR. In this study, a 2 kW electric radiation heater coil twined by the electric resistance was used and placed under the batteries at a vertical distance of 10 mm. The batteries were placed on top of the wire net. The heat flux at the bottom of the battery specimen above the center of the heater was measured as 20 ± 0.3 kW m
−2. Under this thermal radiation, lithium batteries can be easily ignited. When the battery caught fire and released gases, the combustion gas escaped from the combustion chamber via the pipe and then was ejected outside by the exhaust pump. Part of the combustion gas was collected, sampled, filtered, and dried at the back of the exhaust pipe, and analyzed in a Servomex 4100 gas analyzer (Servomex, Egham, UK), which was designed to provide 3 simultaneous gas stream measurements of oxygen, carbon dioxide, and carbon monoxide. The HRR measurement by the in situ calorimeter is based on the oxygen consumption principle [
34,
35].
Six groups of experiments were designed to study fire scenarios and examine the effects of different numbers of batteries (1, 2, 4, 9, 36, and 100 batteries) on the primary lithium battery fire behavior. In this study, the samples were heated with a constant power using a heater. Therefore, the heating rate for every experimental configuration was the same. The simulation enabled the creation of a heat release rate curve for primary lithium batteries based on t2 fire model and MATLAB software (version 2014, MathWorks, Natick, MA, USA) mathematical curve construction. The simulation results were also compared with the experimental results to verify the rationality and accuracy of the simulation results.
3. Results and Discussion
In 1980, Huggett introduced a method to estimate HRR based on oxygen consumption measurements [
36]. After a combustion process has been completed, the HRR can be estimated by:
where
is the heat release rate,
and
are the mass flow rates of oxygen from the entrained air, and
E is the energy released per mass unit of O
2 consumed for a given fuel. Huggett validated the constant net heat release per unit mass of oxygen consumed for organic solids and obtained an average value of 13.1 kJ g
−1 ± 5% for the constant. Considering incomplete combustion, the CO
2 and CO consumption are also needed for correcting the HRR result.
The final form of the equation for HRR is then given by [
37]:
with oxygen depletion factor:
where
E = 13.1 kJ/g is the heat release per mass unit of oxygen consumed;
ECO = 17.6 kJ/g is the heat release for the conversion from CO to CO
2;
= 1.105 is the volumetric expansion factor;
= 32 g/mol and
= 29 g/mol are the molecular weights of oxygen and air, respectively;
and
are measured mole fraction of O
2 and CO
2, respectively;
,
, and
are the mole fraction of O
2, CO
2, and CO in the incoming air, respectively; and
is the mole fraction of water in the incoming air.
According to the oxygen consumption principle and experimental method, the HRR of a lithium battery can be obtained.
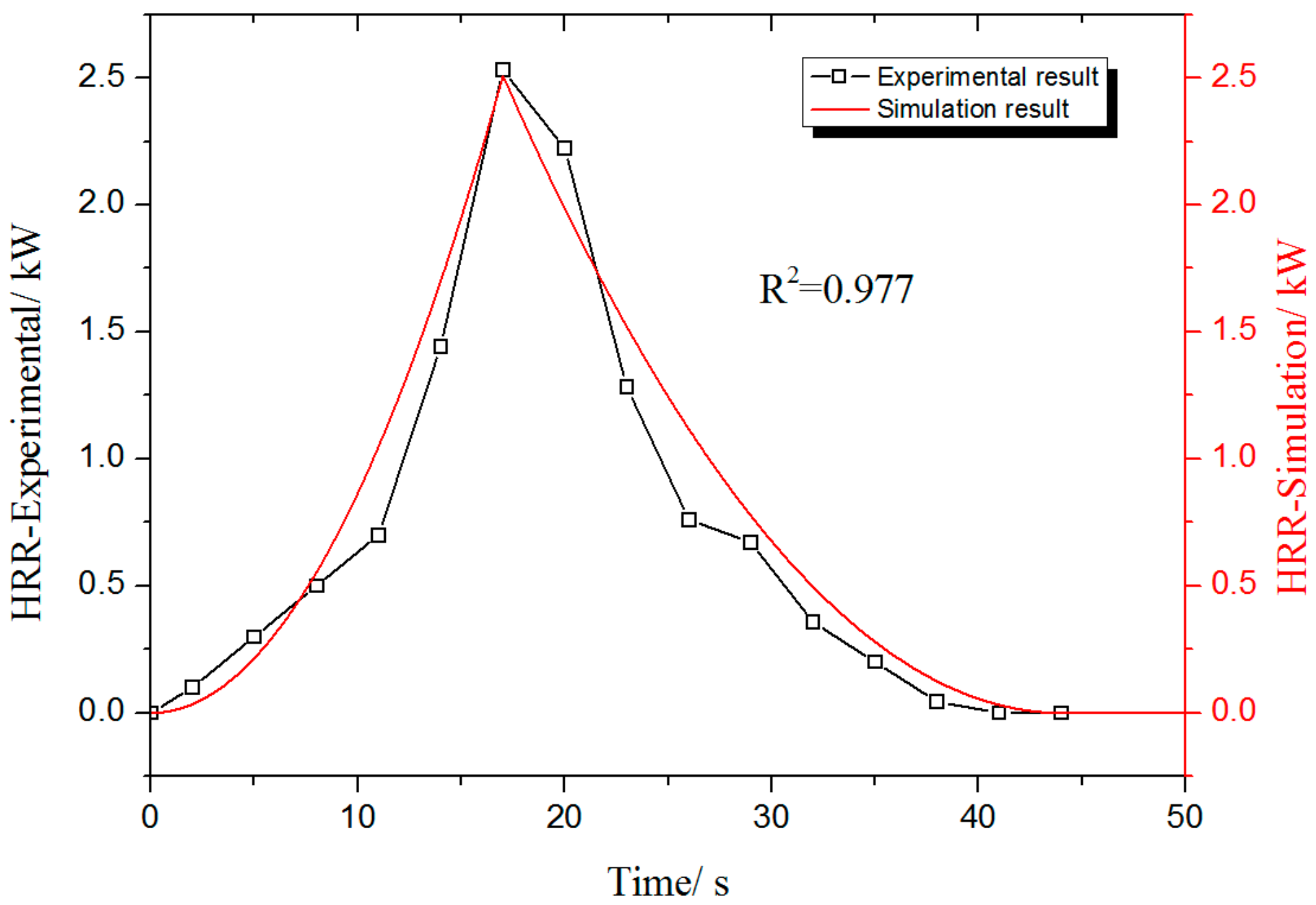
Figure 3 shows the HRR data of one Panasonic CR123A battery. The maximum HRR value is 2.51 kW. The energy is released within a very short time, which may entail the potential risk of explosion. The integration of the HRR curve is the totally released heat (THR) of the lithium batteries fire.
The detailed maximum HRR and THR data are shown in
Table 1. The discussed methodology to create the designed lithium battery fire and criteria for selection of input data are, at best, based on a generalization of fire experimental data and statistics. Performing an analysis to determine a plausible designed lithium battery fire scenario for predicting fire growth was our objective. The t
2 fire model was used to create the designed lithium battery fire, and the required data were based on the experiment results in
Table 1.
Experimental research has shown that the HRR changes with time. For a wide range of fires, the fire growth can be accurately represented with a power law relation:
where
is the heat release rate of the fire,
b is the fire intensity coefficient, and
t is time. National Institute of Standards and Technology (NIST) developed this model that is used in Consolidate Fire and Smoke Transport (CFAST), which is simulation software for fire and smoke spreading in multi-room buildings [
38]. According to the combustion behavior and the HRR curve, lithium battery fires are quite fast, involving a jetting fuel process, which is suitable for the
t2 fire model. The complete
t2 fire model of a specific fire can be built by presetting the fire growth phase, maximum heat release rate, and fire attenuation phase. Its mathematical description is:
where
b1 is the fire growth rate coefficient,
is the maximum HRR,
b2 is the fire attenuation rate coefficient,
t1 is the maximum HRR time, and
t2 is the fire end time. The fire of single lithium battery was designed according to the specific
t1,
t2, and maximum HRR values listed in
Table 1.
The designed fire for one lithium battery is shown in
Figure 3. The designed lithium battery fire data were compared with the experimental result with a correlation coefficient of 0.977, which supports a good statistical relationships between the two data values. The designed lithium battery fire was assumed the same
t1, maximum HRR, and
t2. The difference was the calculated released heat, which was 32.4 kJ for the experiment and 33.6 kJ for the designed simulation, and the margin of error was about 3.7%. The simulation can be used as a fundamental element for fire prediction of multiple batteries and bundled packs.
The energy released in the combustion process should increase in proportion to the amount of fuel, which has a certain combustion efficiency. Unlike normal combustion, lithium battery fire is a fast and jetting fuel process. The released energy is correlated with the complete degree of the combustion. Previous discussion indicated that the energy released is not proportionally related to the battery numbers (
n) of a simple cell [
10]. It can be assumed that an exponential relationship between thermal energy released and the number of batteries is:
where
n is the battery number,
is the energy released from
n batteries, and
is the energy released from one battery. The fitting result by Chen et al. was
Q1 = 31.77 kJ,
a = 1.26, and fitting coefficient of 0. 997. The equation should be added into the simulation of a multiple lithium battery fire. The most difficult problem is that the ignition time of each battery in the bundle is random. Even in the same external environment and with the same heating power, batteries do not always ignite at the same time. We observed that the time of ignition was quite random or varied significantly under the same external heating condition. The non-simultaneous ignition of batteries resulted in differences in heat release rate data.
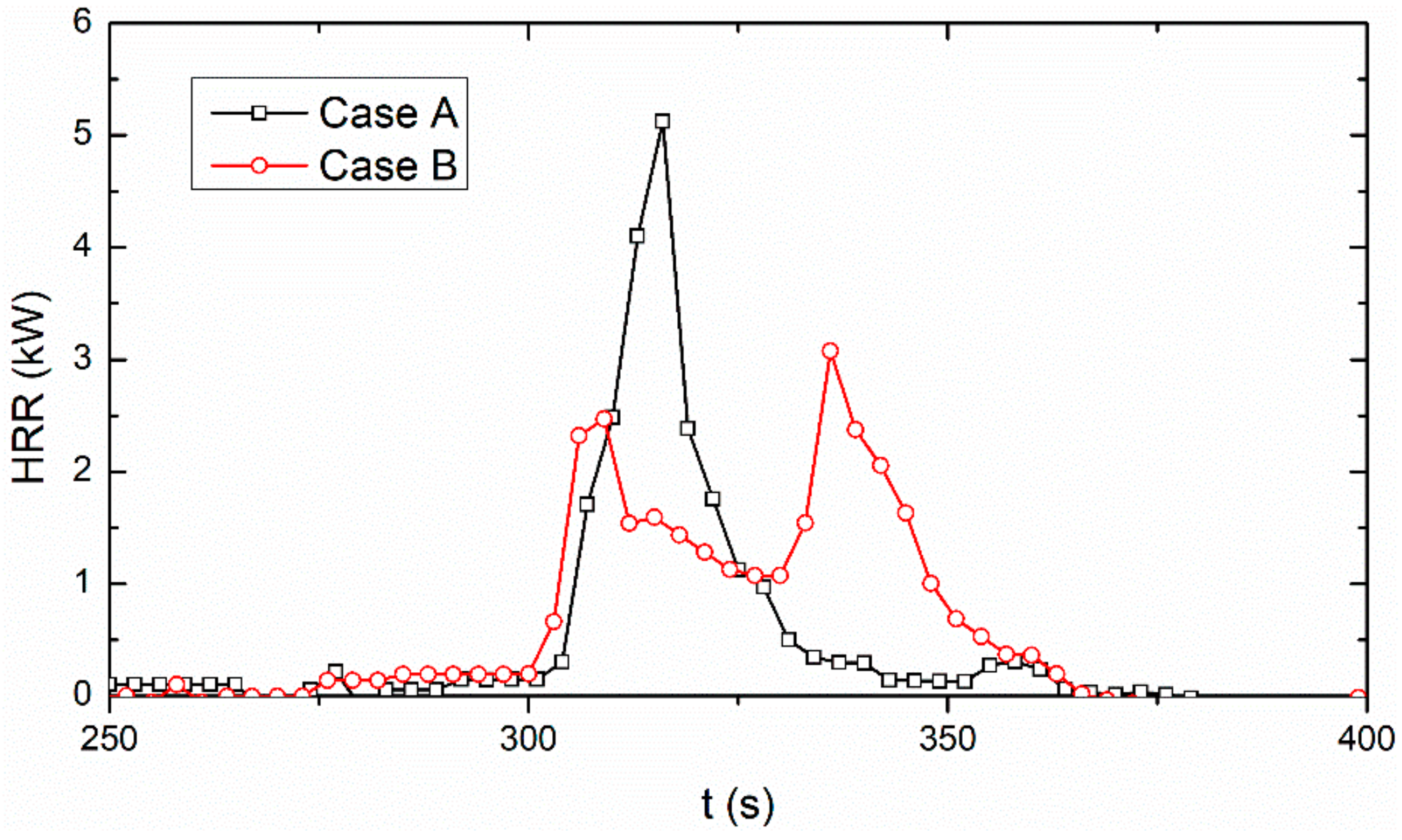
Figure 4 shows the two different experiment results of two batteries under the same heating condition. The two batteries ignited at the same time in Case A and separately in Case B. The time gap in Case B was about 19 s. Given the sporadic ignition of individual batteries in a multi-cell bundle, the maximum heat release rate of the bundle is not equal to the product of the single battery maximum heat release rate multiplied by the number of batteries in the bundle. The time gap in ignitions should be considered in the mathematical calculation process. A time random variable could be added into the HRR simulation for bundled batteries. The ignition gap of two batteries cannot exceed 30 s according to the experiment results:
Considering the exponential relationship of energy, Equation (5) can be written as:
By introducing a time variable and combining the t
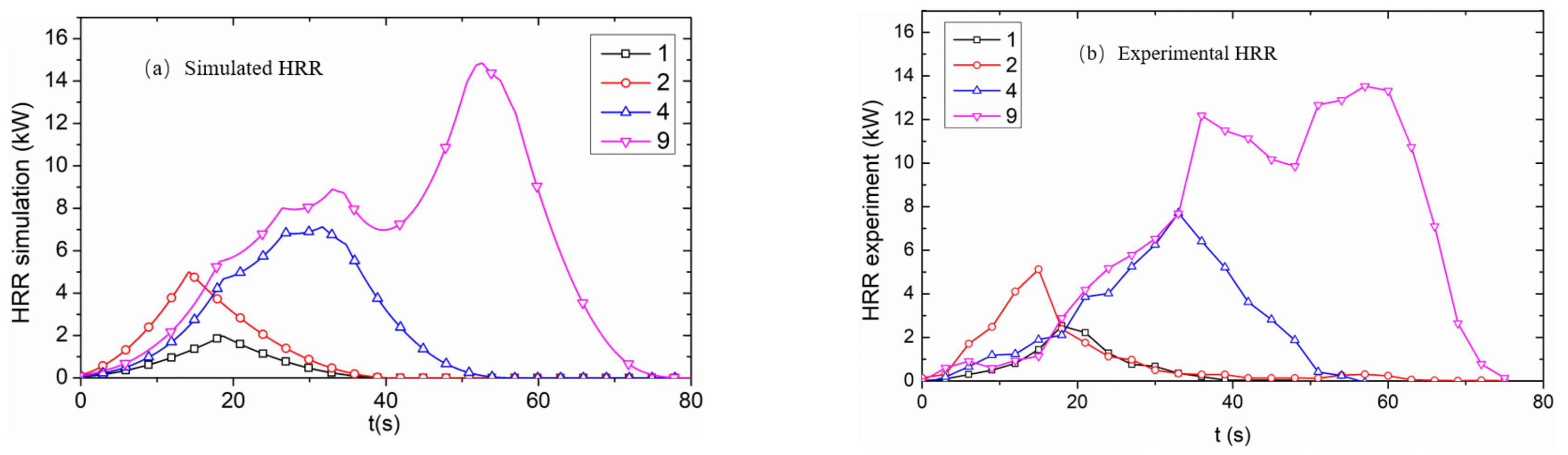
2 fire model and the heat release rate growth model, the HRRs of one, two, four, and nine batteries were simulated and compared with the experimental results, as shown in
Figure 5. The ignition time gap was random so the HRR curve was not unique. The battery combustion curve in the experiment was also not unique. The calculation results were close to the experimental results under the same ignition time gap condition. According to the results, the overall simulation trend was close to the experimental results, and the values of maximum HRR and total heat release (THR) were close to each other, as shown in
Table 2. Therefore, this simulation can be used as a preliminary analysis to simulate the scale of a lithium battery fire, providing a reference for the simulation of foreseeable disasters.
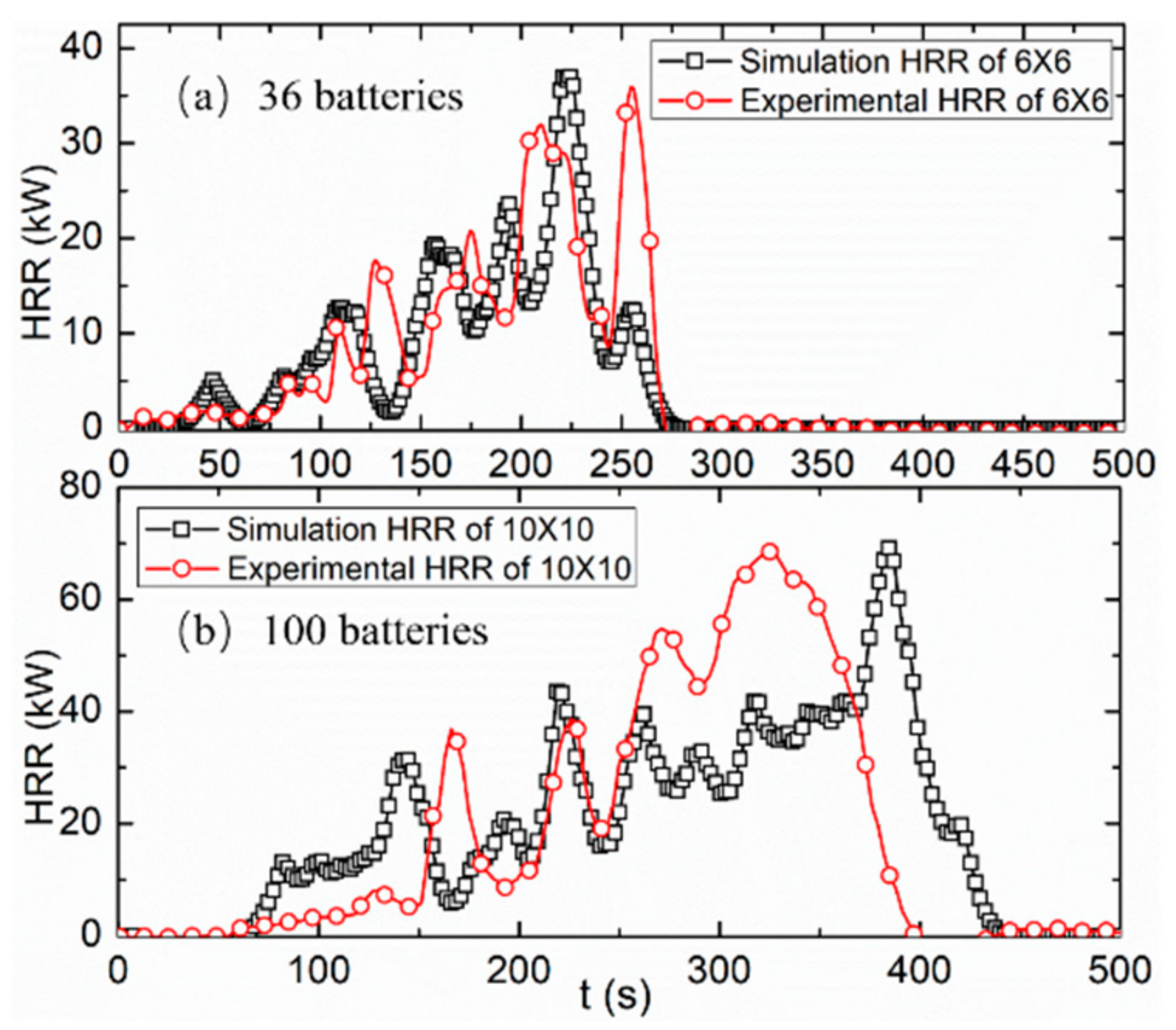
When a large number of batteries burned, as the combustion scale increased, several batteries ignited at the same time. This process is more likely to occur after the flame increases. It is necessary to assume that several batteries ignite simultaneously at a certain time when simulating a large number of batteries burning. The ignition gap at this time is not simply between two batteries, but the ignition interval of the battery pack. Applying the simulation analysis to a fire with more batteries, the comparison results of a 6 × 6 and 10 × 10 test are shown in
Figure 6. The changing trends in the simulation curves are consistent with the experimental curves. Obtained by the figure, the simulation THR data from 6 × 6 and 10 × 10 were calculated as 2802 kJ and 10,388 kJ, respectively. The energies of the three groups of 6 × 6 experiments were 2925 kJ, 2800 kJ, and 2834 kJ; and 10,080 kJ, 9985 kJ, and 10,290 kJ for 10 × 10 tests. These results feasibly aligned with the fitting line. There was a small difference in reaction time between simulation and experimental results for the 10 × 10 test. The reason for this difference is that both the reaction time of the experiment and simulation were not a fixed value. These simulation curves conformed well to the experimental ones. As a result, this HRR simulation analysis is suitable for simulation of CR123A battery fires.
Based on the analysis methodology, primary lithium battery fire could be predicted. Firstly, the curve of the HRR for a single primary lithium battery was plotted. The curve provides a simplified analysis to create the heat release rate curve of a primary lithium battery based on t
2 fire model in Equations (5)–(8) and using MATLAB software for mathematical curve construction. The required data for t
2 fire were obtained experimentally (
Table 1). Secondly, the individual curves of the single battery were integrated into one curve for predicting the HRR curve of a primary lithium battery pack; that is, the combustion of each battery in the pack was added up to form a whole pack fire. The most important factors for predicting the HRR curve of a primary lithium battery pack are the HRR growth model in Equation (11) and the hypothetical time horizon for sporadic ignition of individual batteries in a multi-cell bundle in Equation (10). The methodology to select the input data was based on a generalization of fire experiment data and statistics. Thirdly, the HRR curve of a specific number of primary lithium battery packs can be plotted within a given range. The drawn curve will be different from the experimental curve mainly because of the uncertainty in battery ignition time in the reality.
4. Conclusions
The combustion properties of 1, 2, 4, 9, 36, and 100 primary lithium batteries were experimentally examined in this paper. Based on the t2 fire principle and total heat release results from the experiments, a simplified analysis was further developed to predict the fire hazard, and especially the heat release rate of primary lithium batteries. An exponential relationship between thermal energy released and the number of batteries was added into the simulation of a fire of multiple lithium batteries. The most difficult problem for simulation was that the ignition time of each battery in the bundle is random. Even in the same external environment and under the same heating power, the batteries did not always ignite at the same time. The ignition time difference parameter was introduced into the simulation to achieve similar results to the heat release rate of the multiple battery combustion. By comparing the experimental and simulation results, the heat release rate curves based on the oxygen consumption measurements of 1, 2, 4, 9, 36, and 100 primary lithium batteries agreed well with the simulation. The overall trend and curve shape were similar to the experimental results, and the values of maximum HRR and THR were close to each other.
The experiments and simulations with different numbers of batteries in the current study provide some insights into the fire hazards of primary lithium batteries and indicate the possibility of predicting their heat release rate with a more accurate and simplified model. This prediction analysis is applicable to primary lithium batteries that are smaller than or equal to the dimensions used in this study. The results cannot be directly extrapolated to larger or even industrial scale batteries unless further validation is conducted.