Target Speaker Localization Based on the Complex Watson Mixture Model and Time-Frequency Selection Neural Network
Abstract
:1. Introduction
2. Statistical Model
2.1. Directional Statistics
2.2. Complex Watson Distribution
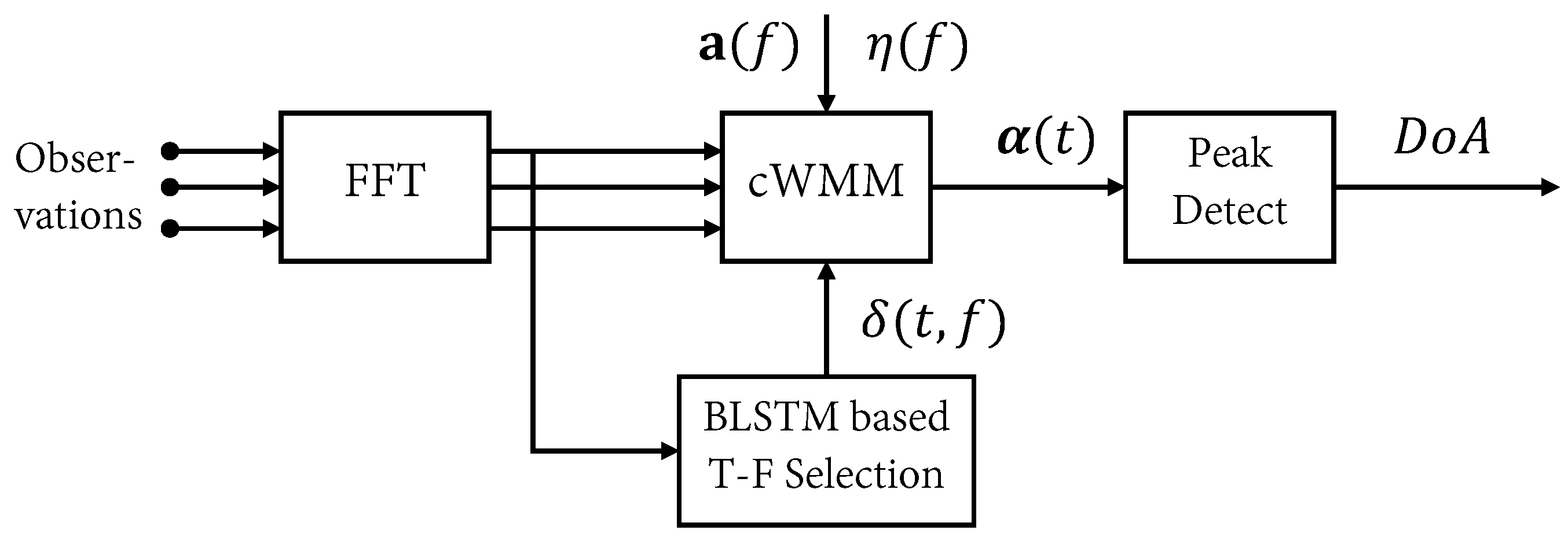
3. Proposed Method
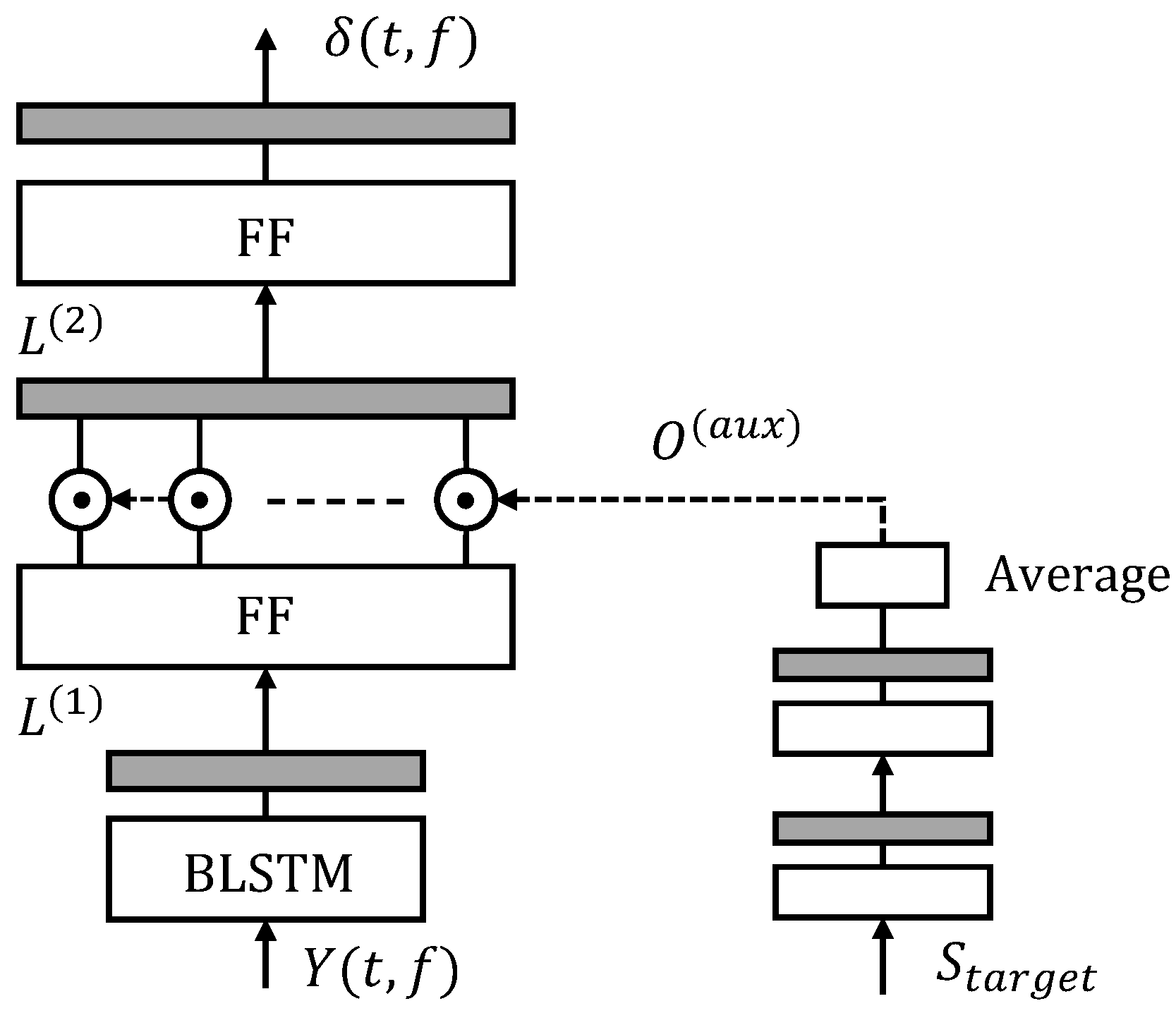
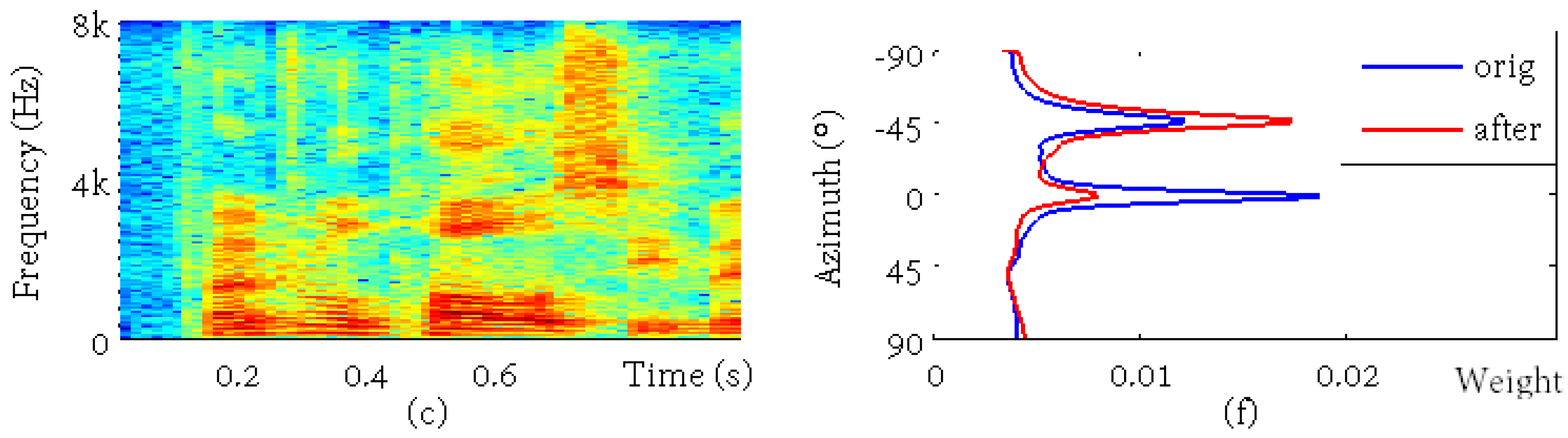
3.1. Time-Frequency Selection
3.2. Weight Parameter Estimation
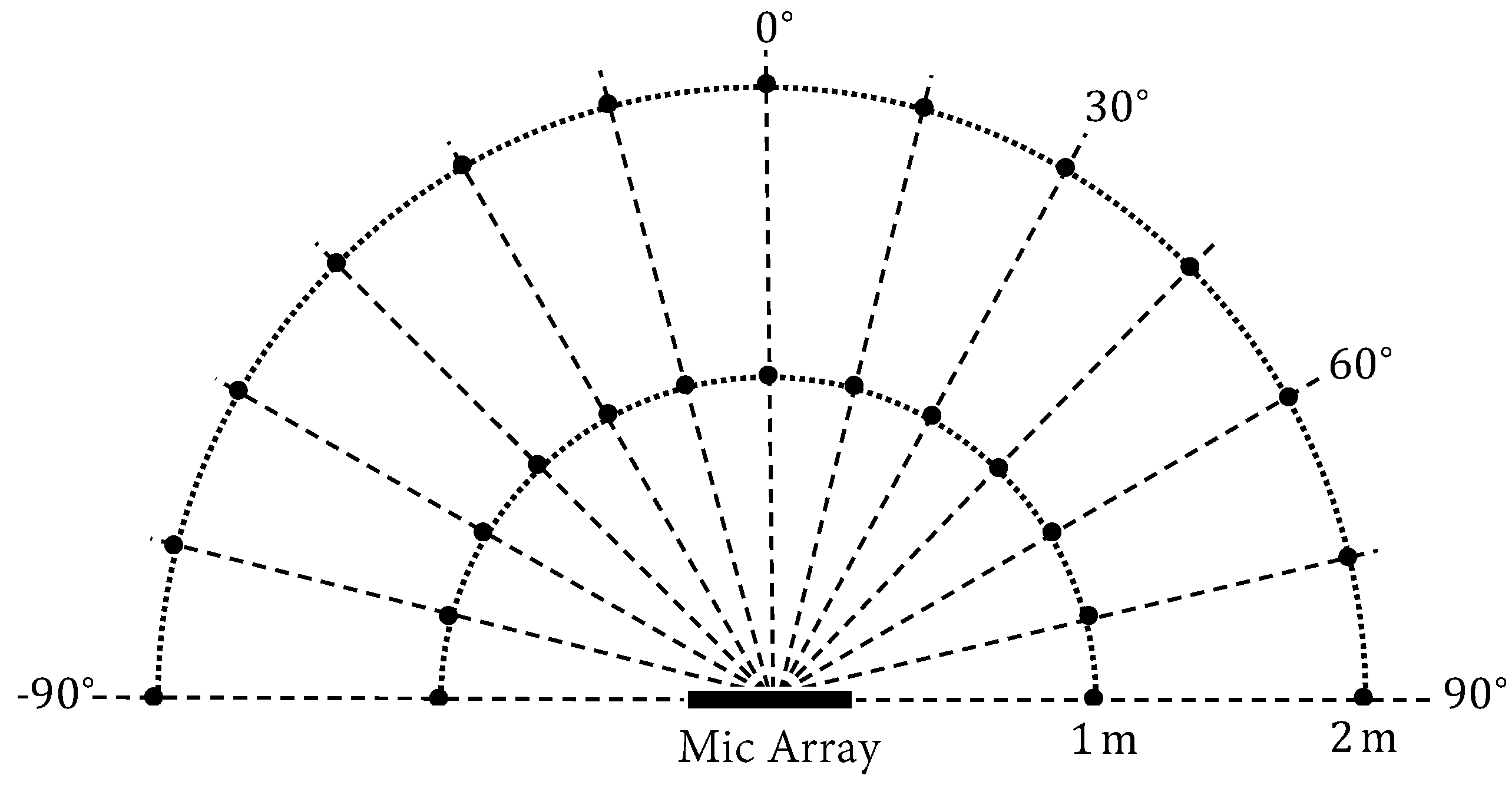
4. Experiments
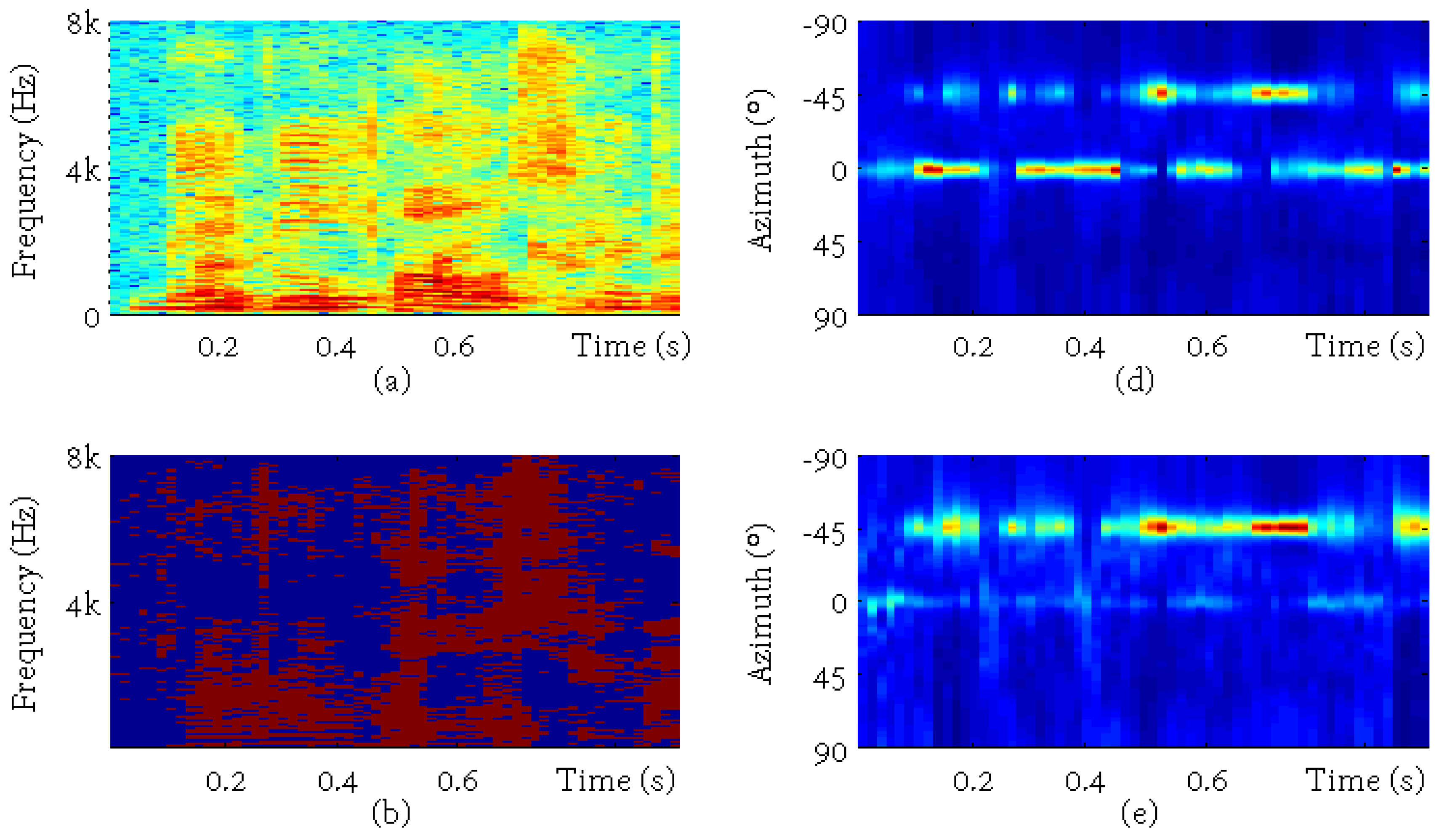
4.1. Oracle Investigation
4.2. Performance with Competing Speakers
4.3. Performance with Competing Noises
4.4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| cWMM | Complex Watson Mixture Model |
| DNN | Deep Neural Network |
| DoA | Direction of Arrival |
| FF | Feed-Forward layer |
| GCC-PHAT | Generalized Cross-Correlation with Phase Transform |
| GER | Gross Error Rate |
| LHUC | Learning Hidden Unit Contribution |
| LSTM | Long Short-Term Memory |
| MAE | Mean Absolute Error |
| ML | Maximum Likelihood |
| MUSIC | Multiple Signal Classification |
| RIR | Room Impulse Response |
| SIR | Signal-to-Interference Ratio |
| SNR | Signal-to-Noise ratio |
| SRP | Steered Response Power |
| SSL | Sound Source Localization |
| STFT | Short Time Fourier Transform |
| TSL | Target Speaker Localization |
References
- Argentieri, S.; Danès, P.; Souères, P. A survey on sound source localization in robotics: From binaural to array processing methods. Comput. Speech Lang. 2015, 34, 87–112. [Google Scholar] [CrossRef]
- Huang, Y.; Benesty, J.; Elko, G.W. Passive acoustic source localization for video camera steering. In Proceedings of the 2000 IEEE International Conference on Acoustics, Speech, and Signal Processing, Istanbul, Turkey, 5–9 June 2000; Volume 2, pp. II909–II912. [Google Scholar]
- Crocco, M.; Trucco, A. Design of robust superdirective arrays with a tunable tradeoff between directivity and frequency-invariance. IEEE Trans. Signal Process. 2011, 59, 2169–2181. [Google Scholar] [CrossRef]
- May, T.; van de Par, S.; Kohlrausch, A. A binaural scene analyzer for joint localization and recognition of speakers in the presence of interfering noise sources and reverberation. IEEE Trans. Audio Speech Lang. Process. 2012, 20, 2016–2030. [Google Scholar] [CrossRef]
- Busso, C.; Hernanz, S.; Chu, C.W.; Kwon, S.i.; Lee, S.; Georgiou, P.G.; Cohen, I.; Narayanan, S. Smart room: Participant and speaker localization and identification. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP ’05), Philadelphia, PA, USA, 23 March 2005; Volume 2. [Google Scholar]
- Knapp, C.; Carter, G. The generalized correlation method for estimation of time delay. IEEE Trans. Acoust. Speech Signal Process. 1976, 24, 320–327. [Google Scholar] [CrossRef]
- DiBiase, J.H.; Silverman, H.F.; Brandstein, M.S. Robust localization in reverberant rooms. In Microphone Arrays; Springer: Berlin/Heidelberg, Germany, 2001; pp. 157–180. [Google Scholar]
- Schmidt, R. Multiple emitter location and signal parameter estimation. IEEE Trans. Antennas Propag. 1986, 34, 276–280. [Google Scholar] [CrossRef]
- Brendel, A.; Huang, C.; Kellermann, W. STFT Bin Selection for Localization Algorithms based on the Sparsity of Speech Signal Spectra. ratio 2018, 2, 6. [Google Scholar]
- Araki, S.; Nakatani, T.; Sawada, H.; Makino, S. Blind sparse source separation for unknown number of sources using Gaussian mixture model fitting with Dirichlet prior. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, Taipei, Taiwan, 19–24 April 2009; pp. 33–36. [Google Scholar]
- Braun, S.; Zhou, W.; Habets, E.A. Narrowband direction-of-arrival estimation for binaural hearing aids using relative transfer functions. In Proceedings of the IEEE Workshop on Applications of Signal Processing to Audio and Acoustics (WASPAA), New Paltz, NY, USA, 18–21 October 2015; pp. 1–5. [Google Scholar]
- Taseska, M.; Lamani, G.; Habets, E.A. Online clustering of narrowband position estimates with application to multi-speaker detection and tracking. In Advances in Machine Learning and Signal Processing; Springer: Berlin/Heidelberg, Germany, 2016; pp. 59–69. [Google Scholar]
- Yilmaz, O.; Rickard, S. Blind separation of speech mixtures via time-frequency masking. IEEE Trans. Signal Process. 2004, 52, 1830–1847. [Google Scholar] [CrossRef]
- Ying, D.; Zhou, R.; Li, J.; Yan, Y. Window-dominant signal subspace methods for multiple short-term speech source localization. IEEE/ACM Trans. Audio Speech Lang. Process. 2017, 25, 731–744. [Google Scholar] [CrossRef]
- Woodruff, J.; Wang, D. Binaural localization of multiple sources in reverberant and noisy environments. IEEE Trans. Audio Speech Lang. Process. 2012, 20, 1503–1512. [Google Scholar] [CrossRef]
- Wang, D.; Brown, G.J. Computational Auditory Scene Analysis: Principles, Algorithms, and Applications; Wiley-IEEE Press: Hoboken, NJ, USA, 2006. [Google Scholar]
- Pertilä, P.; Cakir, E. Robust direction estimation with convolutional neural networks based steered response power. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), New Orleans, LA, USA, 5–9 March 2017; pp. 6125–6129. [Google Scholar]
- Xu, C.; Xiao, X.; Sun, S.; Rao, W.; Chng, E.S.; Li, H. Weighted Spatial Covariance Matrix Estimation for MUSIC based TDOA Estimation of Speech Source. In Proceedings of the Interspeech 2017, Stockholm, Sweden, 20–24 August 2017; pp. 1894–1898. [Google Scholar]
- Wang, Z.Q.; Zhang, X.; Wang, D. Robust TDOA Estimation Based on Time-Frequency Masking and Deep Neural Networks. In Proceedings of the Interspeech 2018, Hyderabad, India, 2–6 September 2018. [Google Scholar]
- Wang, D.; Chen, J. Supervised speech separation based on deep learning: An overview. IEEE/ACM Trans. Audio Speech Lang. Process. 2018, 26, 1702–1726. [Google Scholar] [CrossRef]
- Xiao, X.; Zhao, S.; Zhong, X.; Jones, D.L.; Chng, E.S.; Li, H. A learning-based approach to direction of arrival estimation in noisy and reverberant environments. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brisbane, Australia, 19–24 April 2015; pp. 2814–2818. [Google Scholar]
- Takeda, R.; Komatani, K. Discriminative multiple sound source localization based on deep neural networks using independent location model. In Proceedings of the IEEE Spoken Language Technology Workshop (SLT), San Diego, CA, USA, 13–16 December 2016; pp. 603–609. [Google Scholar]
- Li, X.; Girin, L.; Horaud, R.; Gannot, S. Multiple-speaker localization based on direct-path features and likelihood maximization with spatial sparsity regularization. IEEE/ACM Trans. Audio Speech Lang. Process. 2017, 25, 1997–2012. [Google Scholar] [CrossRef]
- Sivasankaran, S.; Vincent, E.; Fohr, D. Keyword-based speaker localization: Localizing a target speaker in a multi-speaker environment. In Proceedings of the Interspeech, Hyderabad, India, 2–6 September 2018. [Google Scholar]
- Vu, D.H.T.; Haeb-Umbach, R. Blind speech separation employing directional statistics in an expectation maximization framework. In Proceedings of the IEEE International Conference on Acoustics Speech and Signal Processing (ICASSP), Dallas, TX, USA, 14–19 March 2010; pp. 241–244. [Google Scholar]
- Ito, N.; Araki, S.; Delcroix, M.; Nakatani, T. Probabilistic spatial dictionary based online adaptive beamforming for meeting recognition in noisy and reverberant environments. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), New Orleans, LA, USA, 5–9 March 2017; pp. 681–685. [Google Scholar]
- Drude, L.; Jacob, F.; Haeb-Umbach, R. DOA-estimation based on a complex watson kernel method. In Proceedings of the 23rd European Signal Processing Conference (EUSIPCO), Nice, France, 31 August–4 September 2015; pp. 255–259. [Google Scholar]
- Drude, L.; Chinaev, A.; Vu, D.H.T.; Haeb-Umbach, R. Source counting in speech mixtures using a variational EM approach for complex Watson mixture models. In Proceedings of the 2014 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Florence, Italy, 4–9 May 2014; pp. 6834–6838. [Google Scholar]
- Mardia, K.; Dryden, I. The complex Watson distribution and shape analysis. J. R. Stat. Soc. Ser. B Stat. Methodol. 1999, 61, 913–926. [Google Scholar] [CrossRef]
- Ito, N.; Araki, S.; Nakatani, T. Permutation-free convolutive blind source separation via full-band clustering based on frequency-independent source presence priors. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013; pp. 3238–3242. [Google Scholar]
- Swietojanski, P.; Li, J.; Renals, S. Learning hidden unit contributions for unsupervised acoustic model adaptation. IEEE/ACM Trans. Audio Speech Lang. Process. 2016, 24, 1450–1463. [Google Scholar] [CrossRef]
- Žmolíková, K.; Delcroix, M.; Kinoshita, K.; Higuchi, T.; Ogawa, A.; Nakatani, T. Learning speaker representation for neural network based multichannel speaker extraction. In Proceedings of the IEEE Automatic Speech Recognition and Understanding Workshop (ASRU), Okinawa, Japan, 16–20 December 2017; pp. 8–15. [Google Scholar]
- Ito, N.; Araki, S.; Nakatani, T. Data-driven and physical model-based designs of probabilistic spatial dictionary for online meeting diarization and adaptive beamforming. In Proceedings of the European Signal Processing Conference (EUSIPCO), Kos, Greece, 28 August–2 September 2017; pp. 1165–1169. [Google Scholar]
- Paul, D.B.; Baker, J.M. The design for the Wall Street Journal-based CSR corpus. In Proceedings of the workshop on Speech and Natural Language, Harriman, NY, USA, 23–26 February 1992; pp. 357–362. [Google Scholar]
- Wang, Z.Q.; Le Roux, J.; Hershey, J.R. Multi-Channel Deep Clustering: Discriminative Spectral and Spatial Embeddings for Speaker-Independent Speech Separation. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, Calgary, AB, Canada, 15–20 April 2018. [Google Scholar]
- Allen, J.B.; Berkley, D.A. Image method for efficiently simulating small-room acoustics. J. Acoust. Soc. Am. 1979, 65, 943–950. [Google Scholar] [CrossRef]
- Veselỳ, K.; Watanabe, S.; Žmolíková, K.; Karafiát, M.; Burget, L.; Černockỳ, J.H. Sequence summarizing neural network for speaker adaptation. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Shanghai, China, 20–25 March 2016; pp. 5315–5319. [Google Scholar]
| Noise Type | N0 | N1 | |||||
|---|---|---|---|---|---|---|---|
| SIR | −5 | 0 | 5 | −5 | 0 | 5 | |
| 160 ms | SRP-PHAT | 0.90 | 0.56 | 0.30 | 0.82 | 0.64 | 0.28 |
| cWMM | 0.76 | 0.48 | 0.28 | 0.74 | 0.59 | 0.28 | |
| cWMM-TF | 0.43 | 0.24 | 0.15 | 0.48 | 0.25 | 0.14 | |
| cWMM-ORC | 0.09 | 0.08 | 0.07 | 0.07 | 0.10 | 0.05 | |
| 360 ms | SRP-PHAT | 0.83 | 0.47 | 0.34 | 0.82 | 0.51 | 0.34 |
| cWMM | 0.75 | 0.47 | 0.37 | 0.75 | 0.51 | 0.33 | |
| cWMM-TF | 0.42 | 0.34 | 0.18 | 0.42 | 0.28 | 0.16 | |
| cWMM-ORC | 0.08 | 0.06 | 0.09 | 0.06 | 0.07 | 0.10 | |
| 610 ms | SRP-PHAT | 0.78 | 0.56 | 0.29 | 0.82 | 0.62 | 0.25 |
| cWMM | 0.70 | 0.54 | 0.28 | 0.73 | 0.57 | 0.28 | |
| cWMM-TF | 0.48 | 0.22 | 0.15 | 0.52 | 0.23 | 0.13 | |
| cWMM-ORC | 0.11 | 0.08 | 0.07 | 0.08 | 0.10 | 0.08 | |
| Noise Type | N0 | N1 | |||||
|---|---|---|---|---|---|---|---|
| SIR | −5 | 0 | 5 | −5 | 0 | 5 | |
| 160 ms | SRP-PHAT | 62.49 | 34.38 | 13.14 | 54.82 | 36.32 | 12.86 |
| cWMM | 55.42 | 32.14 | 16.54 | 49.46 | 39.92 | 17.65 | |
| cWMM-TF | 28.26 | 12.62 | 5.71 | 30.23 | 13.16 | 5.17 | |
| cWMM-ORC | 1.82 | 1.69 | 1.71 | 1.55 | 1.92 | 1.55 | |
| 360 ms | SRP-PHAT | 58.43 | 28.98 | 18.26 | 51.80 | 31.41 | 17.53 |
| cWMM | 53.26 | 29.55 | 23.38 | 47.47 | 32.62 | 19.71 | |
| cWMM-TF | 28.99 | 19.71 | 7.40 | 24.67 | 14.56 | 8.70 | |
| cWMM-ORC | 2.54 | 1.53 | 1.59 | 1.70 | 1.75 | 1.85 | |
| 610 ms | SRP-PHAT | 50.92 | 37.30 | 15.28 | 58.21 | 36.51 | 13.65 |
| cWMM | 45.59 | 37.82 | 15.57 | 52.91 | 37.79 | 17.87 | |
| cWMM-TF | 31.73 | 11.97 | 7.85 | 33.56 | 15.71 | 8.19 | |
| cWMM-ORC | 2.97 | 1.87 | 1.61 | 1.87 | 2.06 | 2.07 | |
| Noise Type | N0 | N1 | N2 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| SNR | 0 | 5 | 10 | 0 | 5 | 10 | 0 | 5 | 10 | |
| 360 ms | SRP-PHAT | 3.94 | 3.92 | 3.22 | 16.01 | 7.65 | 6.28 | 59.53 | 46.04 | 23.22 |
| cWMM | 2.70 | 1.84 | 1.30 | 28.08 | 10.28 | 5.55 | 53.41 | 38.65 | 24.03 | |
| cWMM-TF | 2.18 | 1.97 | 1.52 | 10.22 | 6.01 | 3.95 | 23.81 | 12.97 | 10.12 | |
| cWMM-ORC | 1.94 | 1.92 | 1.50 | 5.32 | 2.83 | 2.51 | 2.09 | 2.02 | 1.66 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Li, J.; Yan, Y. Target Speaker Localization Based on the Complex Watson Mixture Model and Time-Frequency Selection Neural Network. Appl. Sci. 2018, 8, 2326. https://doi.org/10.3390/app8112326
Wang Z, Li J, Yan Y. Target Speaker Localization Based on the Complex Watson Mixture Model and Time-Frequency Selection Neural Network. Applied Sciences. 2018; 8(11):2326. https://doi.org/10.3390/app8112326
Chicago/Turabian StyleWang, Ziteng, Junfeng Li, and Yonghong Yan. 2018. "Target Speaker Localization Based on the Complex Watson Mixture Model and Time-Frequency Selection Neural Network" Applied Sciences 8, no. 11: 2326. https://doi.org/10.3390/app8112326
APA StyleWang, Z., Li, J., & Yan, Y. (2018). Target Speaker Localization Based on the Complex Watson Mixture Model and Time-Frequency Selection Neural Network. Applied Sciences, 8(11), 2326. https://doi.org/10.3390/app8112326




