Internal Mechanism and Improvement Criteria for the Runaway Oscillation Stability of a Pump-Turbine
Abstract
1. Introduction
2. Numerical Models and Schemes
2.1. Pump-Turbine Model
2.2. Turbulence Model and Boundary Conditions
2.3. Control Method of Varying Angular Speed
2.4. Time Step and Numerical Scheme
3. Results and Analysis
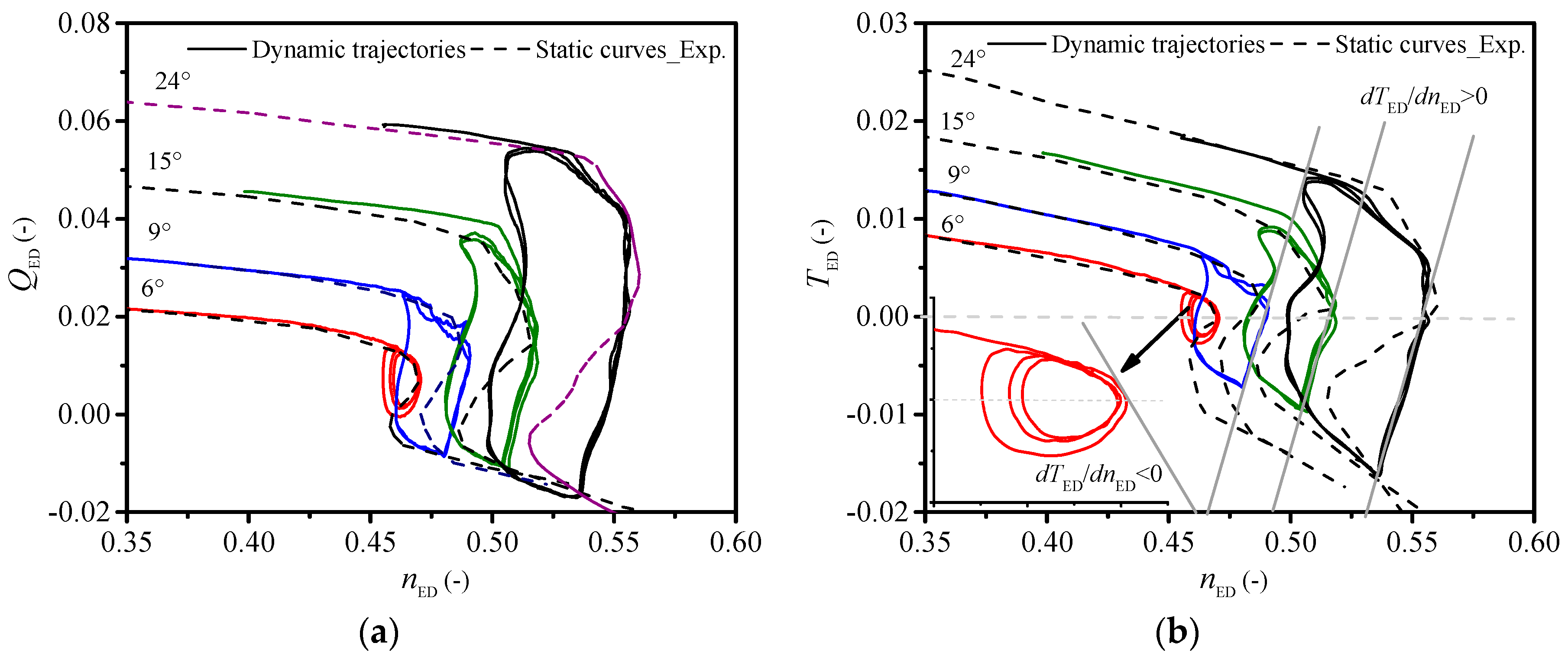
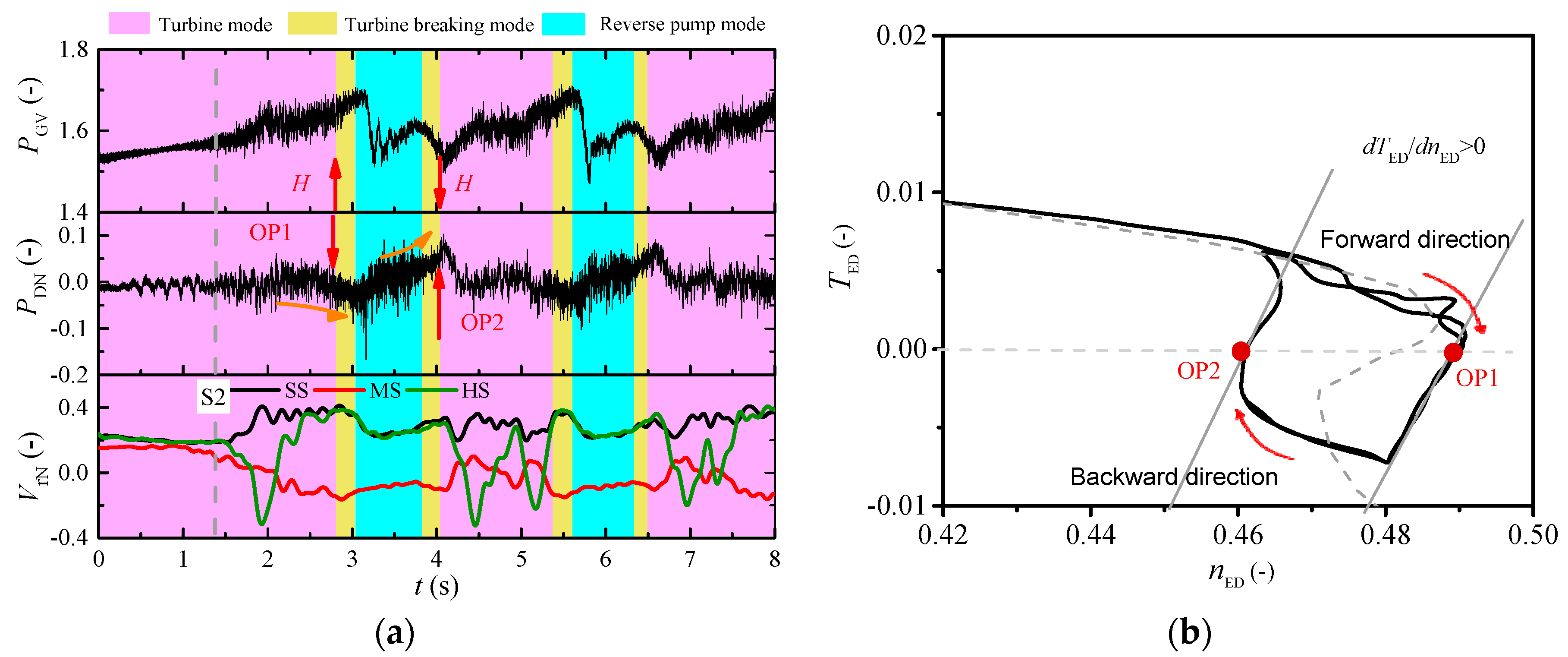
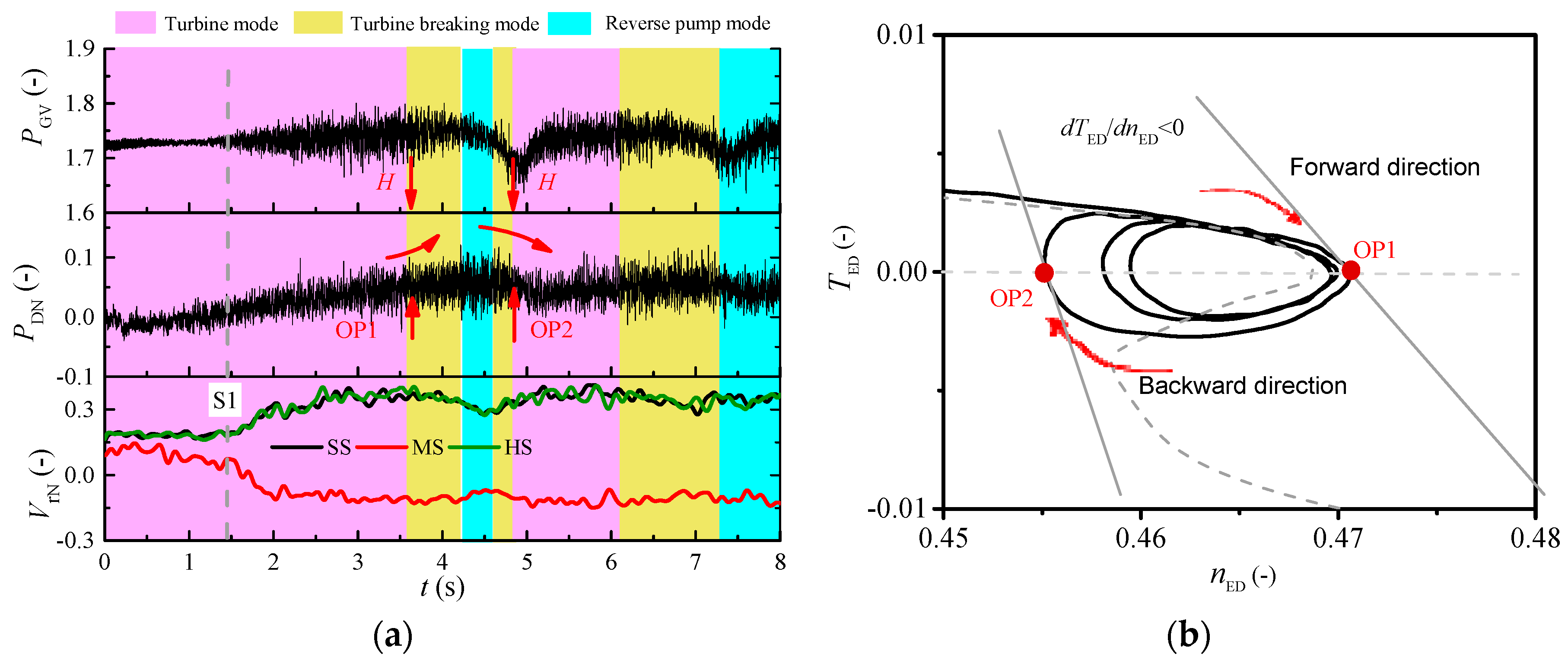
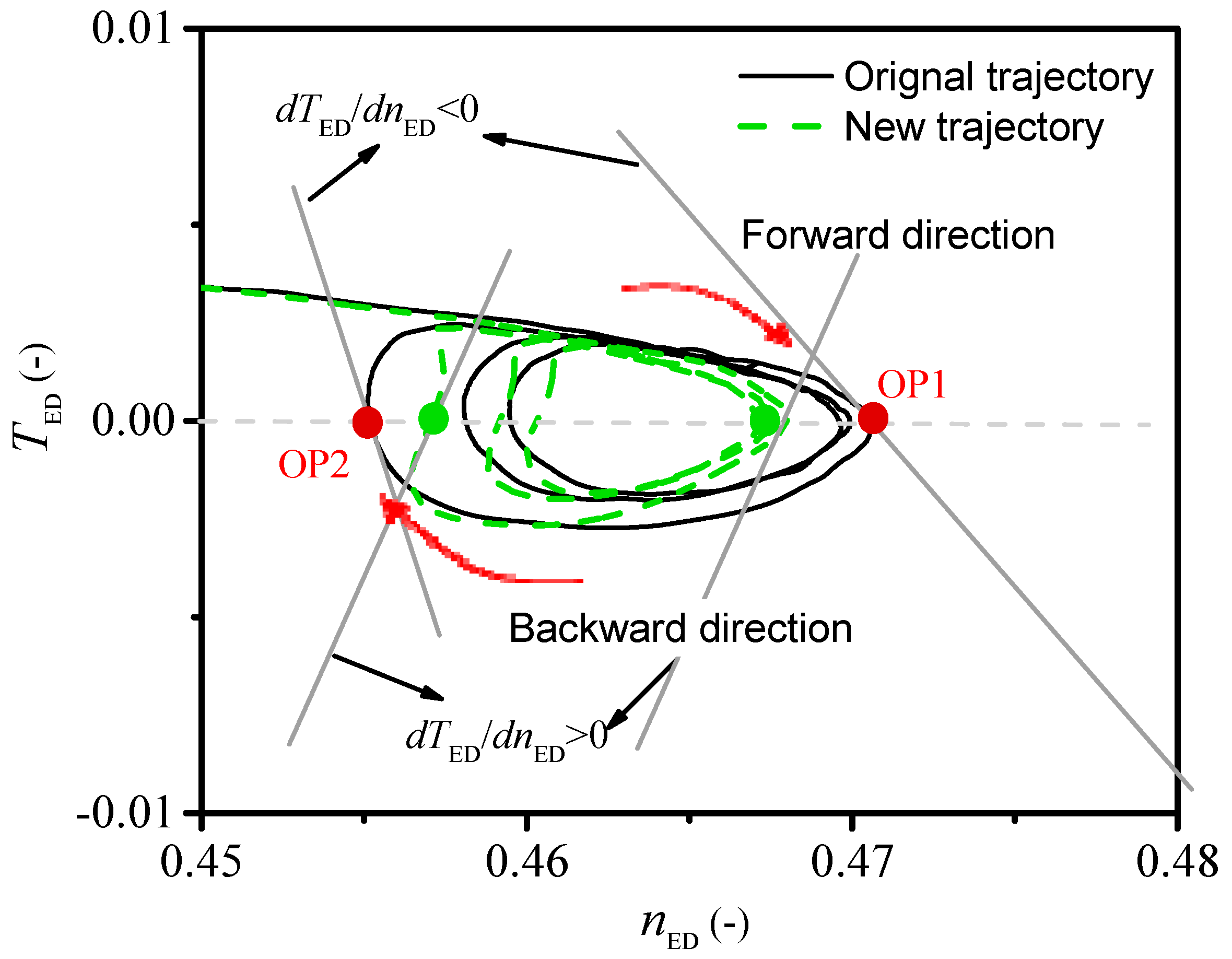
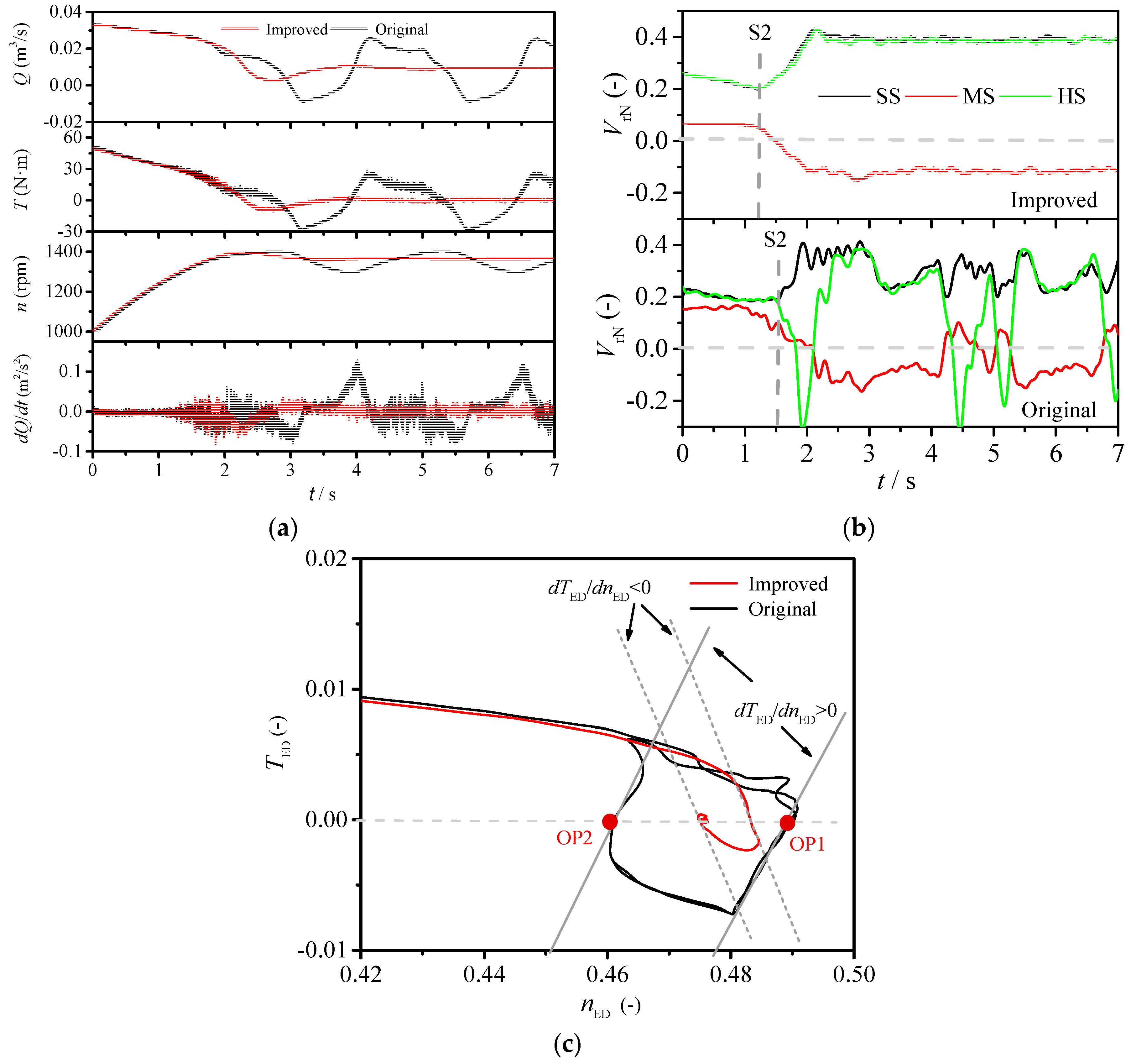
3.1. Dynamic Trajectories at Different GVOs
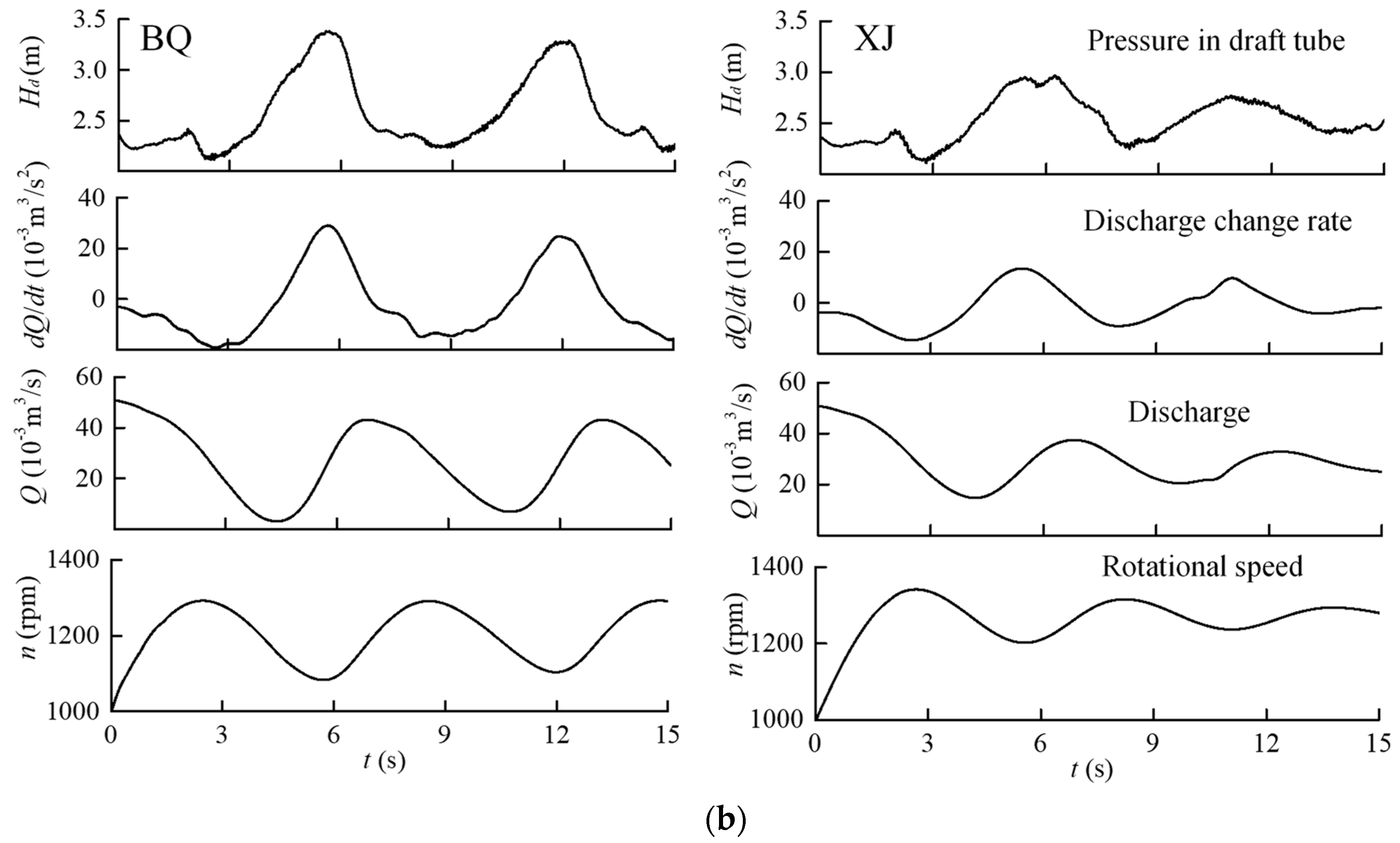
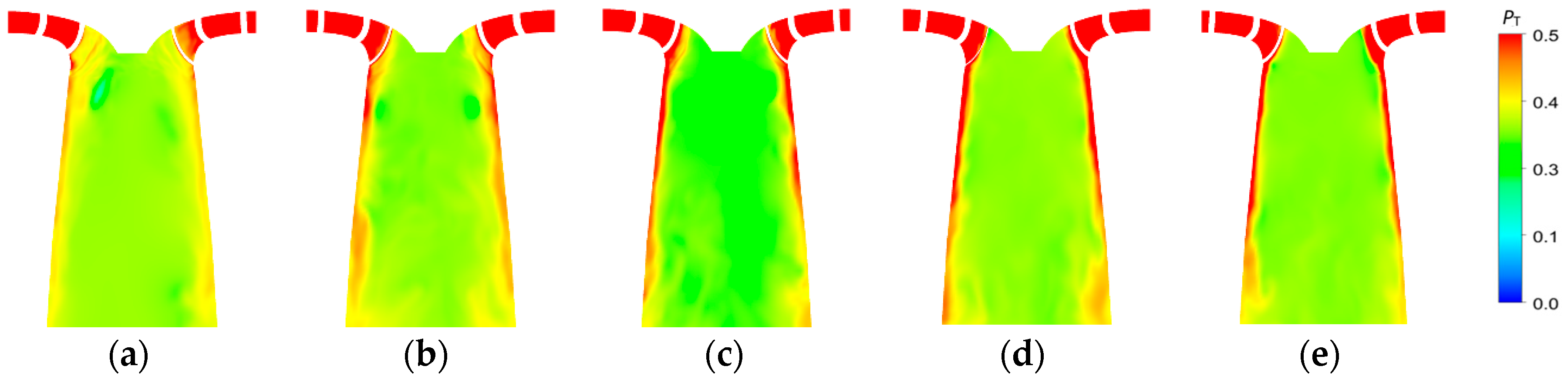
3.2. Influence of Pressure Fluctuations and Flow Changes on Dynamic Trajectories
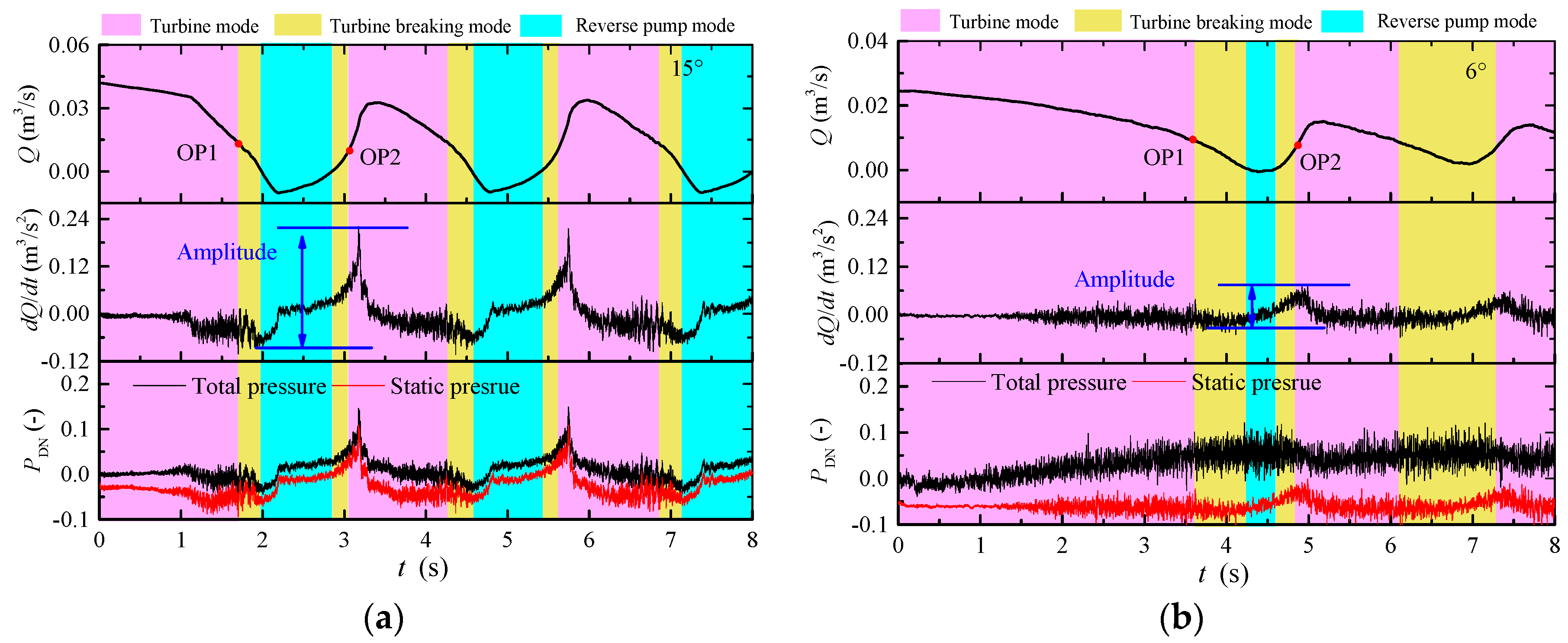
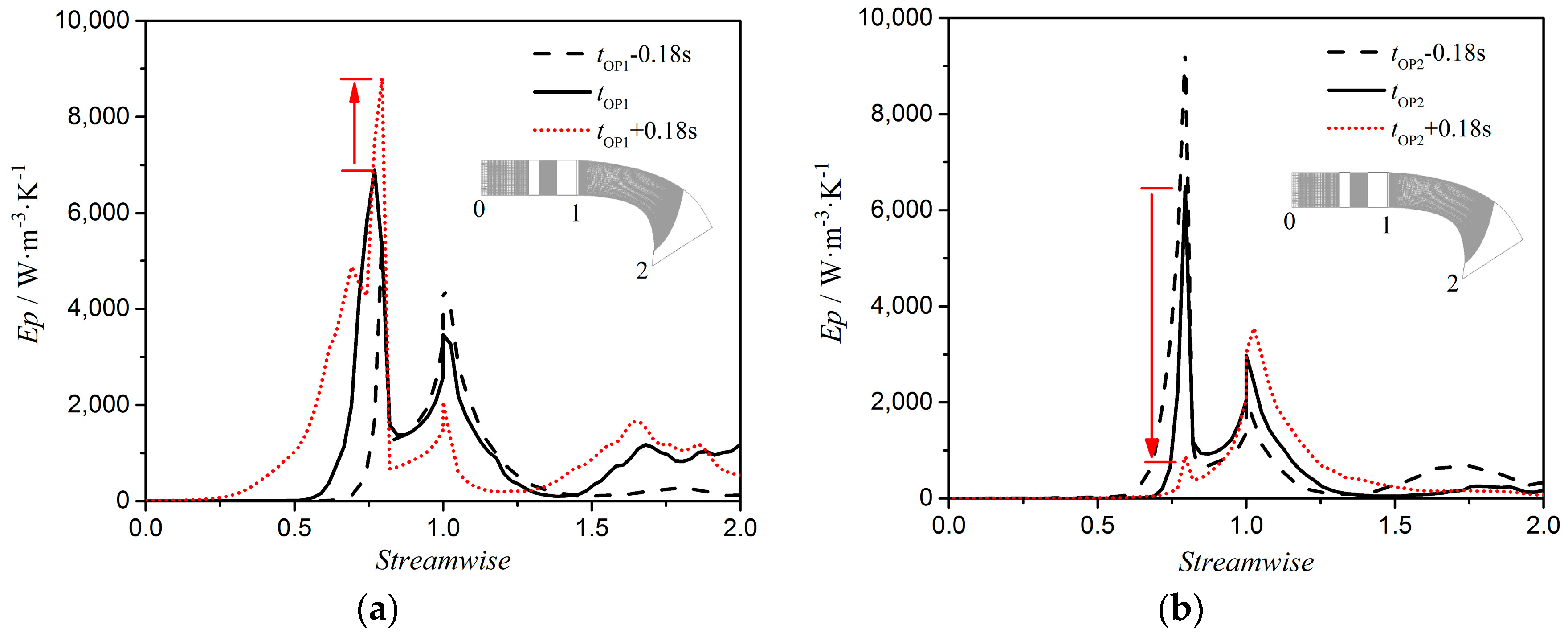
3.3. Influence of Discharge Change Rate on Runaway Stability
3.4. Influence of Flow Transitions on Discharge Change Rate
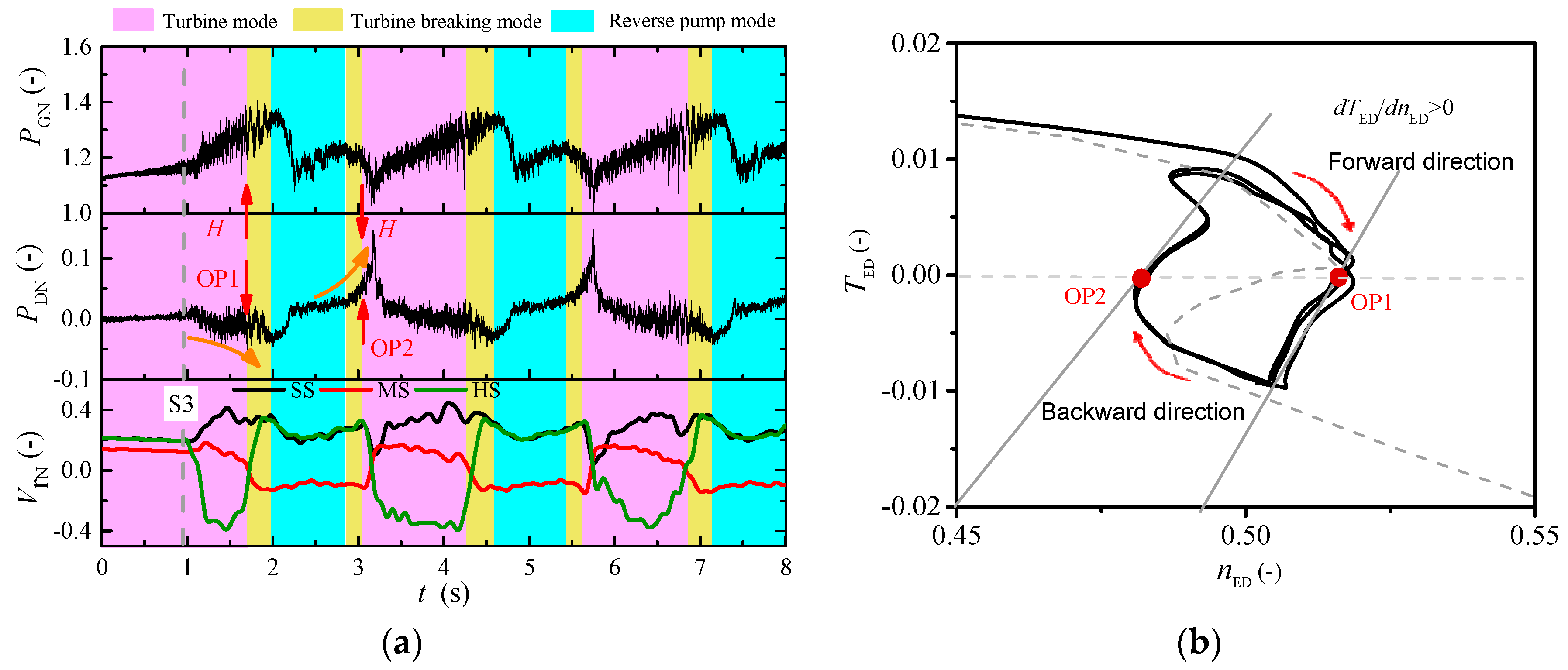
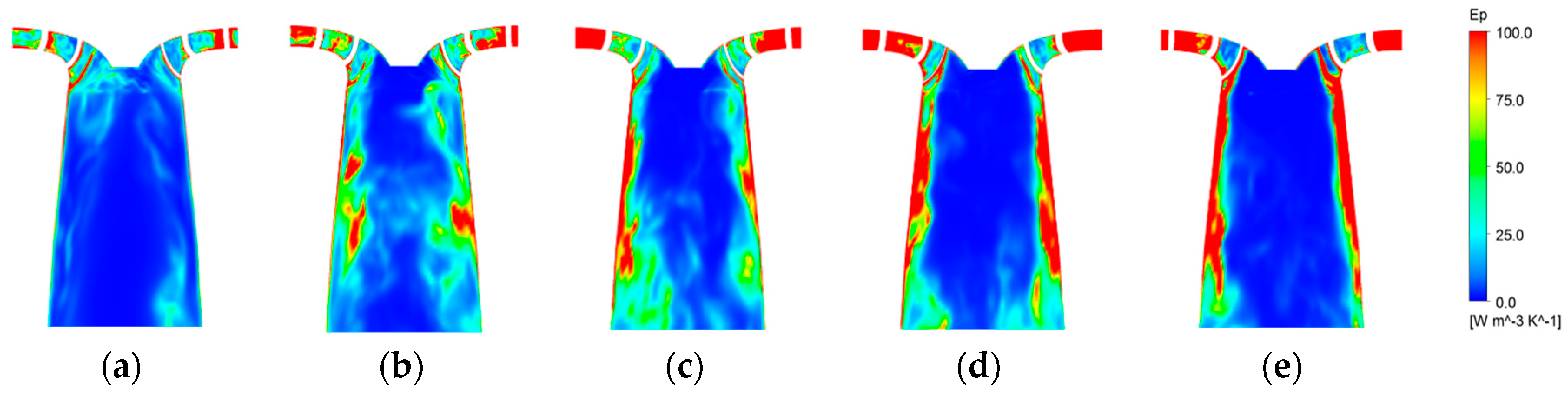
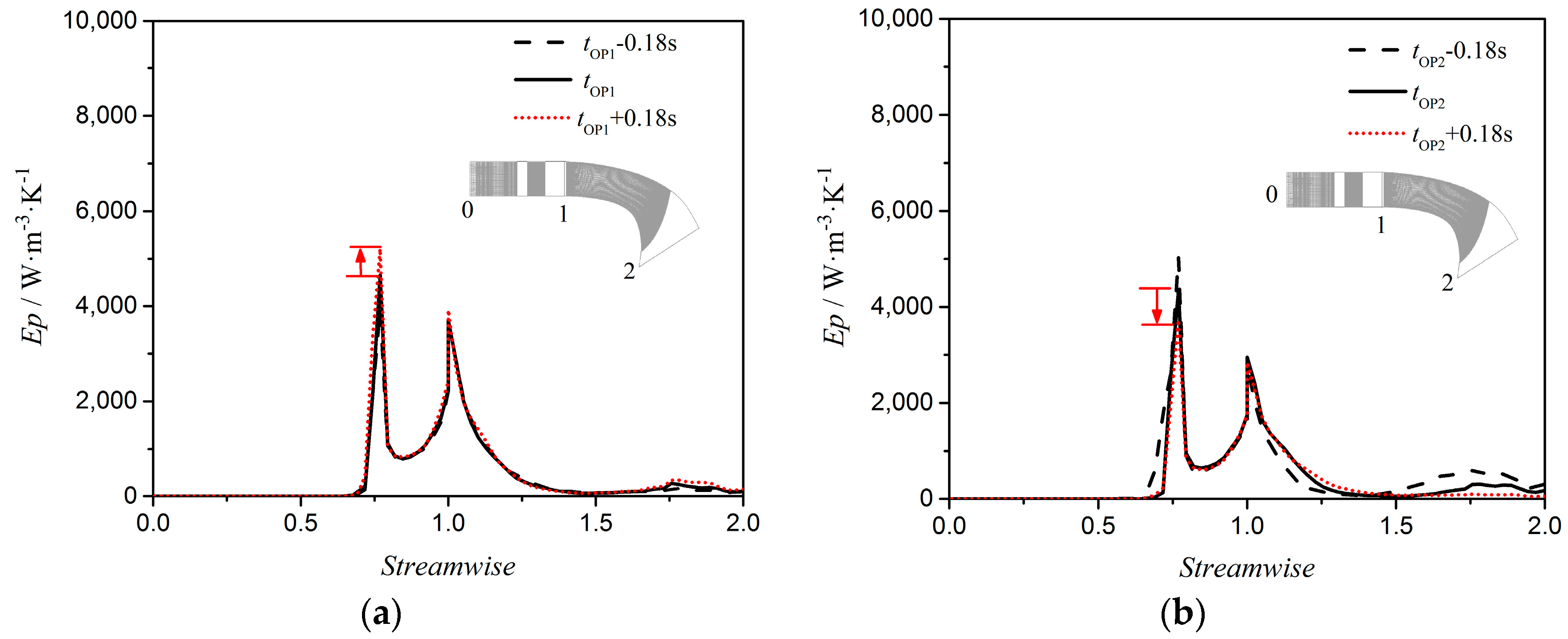
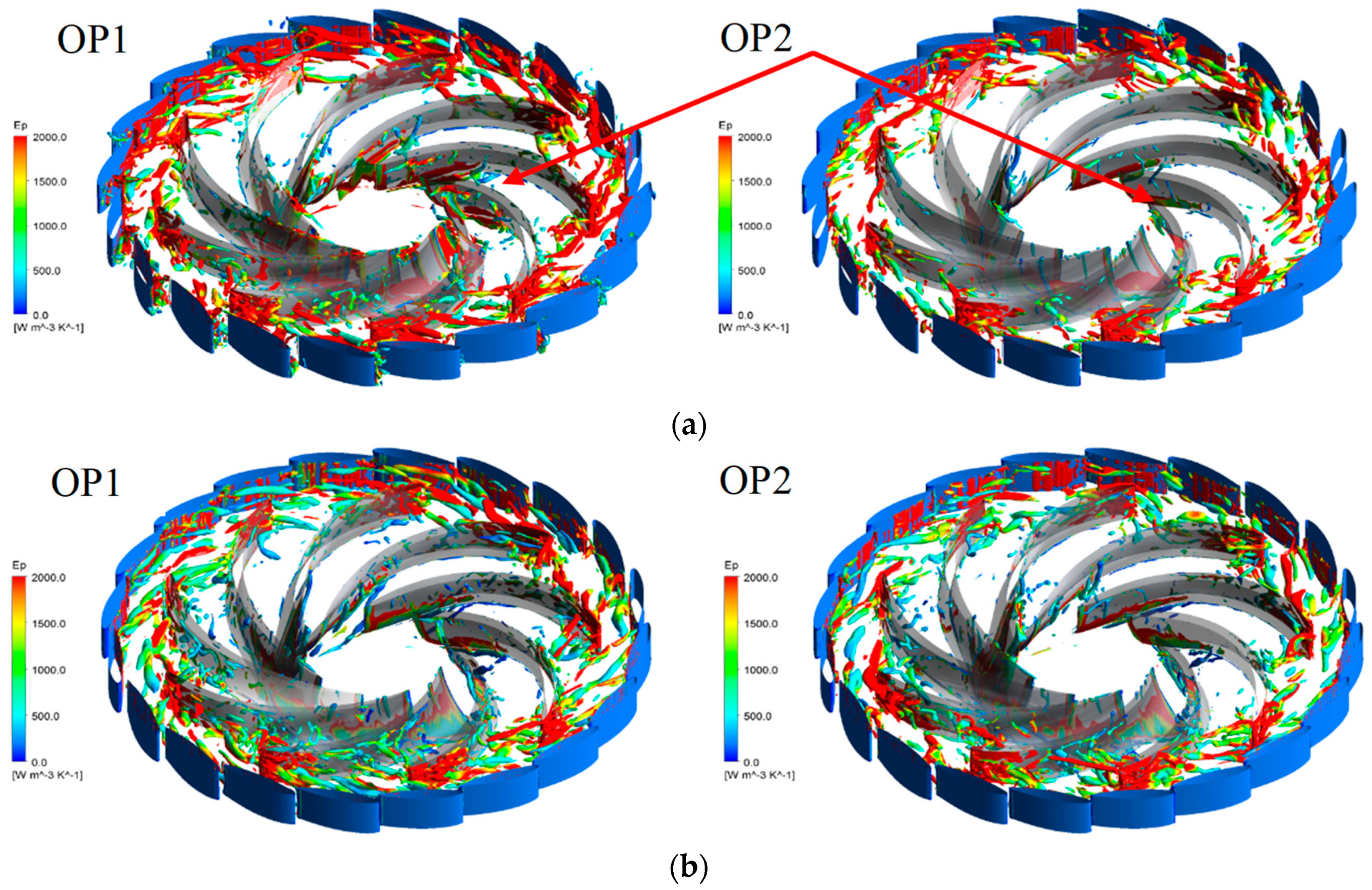
3.5. Improvement of the Runaway Oscilation Stability
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| T | Torque (N·m) |
| n | Rotational speed (rpm) |
| Q | Rotational inertia (kg·m2) |
| g | Gravitational acceleration (m·s−2) |
| D1 | Runner inlet diameter (m) |
| H | Water head (m) |
| Water density (kg·m−3) | |
| t | Time (s) |
| Speed factor () | |
| Discharge factor () | |
| Torque factor () | |
| PT | Total pressure (Pa) |
| PN | Pressure coefficient (P/0.5ρ (πnD1/60)2) |
| GVO | Guide vane opening |
| ns | Specific speed nQ0.5/H0.75 |
| BFVS | Backflow vortex structure |
| Radial velocity (m·s−1) | |
| Normalized radial velocity () |
References
- Rehman, S.; Al-Hadhrami, L.; Alam, M. Pumped hydro energy storage system: A technological review. Renew. Sustain. Energy Rev. 2015, 44, 586–598. [Google Scholar] [CrossRef]
- Spänhoff, B. Current status and future prospects of hydropower in Saxony (Germany) compared to trends in Germany, the European Union and the World. Renew. Sustain. Energy Rev. 2014, 30, 518–525. [Google Scholar] [CrossRef]
- Pérez-Sánchez, M.; Sánchez-Romero, F.; Ramos, H.; López-Jiménez, P. Energy recovery in existing water networks: Towards greater sustainability. Water 2017, 9, 97. [Google Scholar] [CrossRef]
- Paish, O. Micro-hydropower: Status and prospects. Proc. Inst. Mech. Eng. A J. Power Energy 2002, 216, 31–40. [Google Scholar] [CrossRef]
- Trivedi, C.; Cervantes, M.; Gandhi, B.; Dahlhaug, O. Transient pressure measurements on a high head model Francis turbine during emergency shutdown, total load rejection, and runaway. J. Fluids Eng. 2014, 136, 121107. [Google Scholar] [CrossRef]
- Zuo, Z.; Fan, H.; Liu, S.; Wu, Y. S-Shaped Characteristics on the Performance Curves of Pump-Turbines in Turbine Mode—A Review. Renew. Sustain. Energy Rev. 2016, 60, 836–851. [Google Scholar] [CrossRef]
- Zhang, X.; Cheng, Y.; Xia, L.; Yang, J.; Qian, Z. Looping Dynamic Characteristics of a Pump-Turbine in the S-Shaped Region during Runaway. J. Fluids Eng. 2016, 138, 091102. [Google Scholar] [CrossRef]
- Zuo, Z.; Liu, S.; Sun, Y.; Wu, Y. Pressure fluctuations in the vaneless space of High-head pump-turbines—A review. Renew. Sustain. Energy Rev. 2015, 41, 965–974. [Google Scholar] [CrossRef]
- Cavazzini, G.; Covi, A.; Pavesi, G. Analysis of the unstable behavior of a pump-turbine in turbine mode: Fluid-dynamical and spectral characterization of the S-Shape characteristic. J. Fluids Eng. 2016, 138, 021105. [Google Scholar] [CrossRef]
- Liu, L.; Zhu, B.; Bai, L.; Liu, X.; Zhao, Y. Parametric Design of an Ultrahigh-Head Pump-Turbine Runner Based on Multi objective Optimization. Energies 2017, 10, 1169. [Google Scholar] [CrossRef]
- Xia, L.; Cheng, Y.; You, J.; Zhang, X.; Yang, J.; Qian, Z. Mechanism of the S-Shaped Characteristics and the Runaway Instability of Pump-Turbines. J. Fluids Eng. 2017, 139, 031101. [Google Scholar] [CrossRef]
- Rezghi, A.; Riasi, A. Sensitivity analysis of transient flow of two parallel pump-turbines operating at runaway. Renew. Energy 2016, 86, 611–622. [Google Scholar] [CrossRef]
- Zhang, H.; Chen, D.; Wu, C.; Wang, X.; Lee, J.; Jung, K. Dynamic Modeling and Dynamical Analysis of Pump-Turbines in S-shaped Regions during Runaway Operation. Energy Convers. Manag. 2017, 138, 375–382. [Google Scholar] [CrossRef]
- Zhou, J.; Karney, B.; Hu, M.; Xu, J. Analytical study on possible self-excited oscillation in S-shaped regions of pump-turbines. Proc. Inst. Mech. Eng. A J. Power Energy 2011, 225, 1132–1142. [Google Scholar] [CrossRef]
- Zeng, W.; Yang, J.; Guo, W. Runaway instability of pump-turbines in S-shaped regions considering water compressibility. J. Fluids Eng. 2015, 137, 051401. [Google Scholar] [CrossRef]
- Dörfler, P.; Engineer, A.; Pendse, R. Stable operation achieved on a single-stage reversible pump-turbine showing instability at no load. In Proceedings of the 19th IAHR Symposium on Hydraulic Machinery and Cavitation, Singapore, 9–11 September 1998. [Google Scholar]
- Xiao, Y.; Zhu, W.; Wang, Z.; Zhang, J.; Ahn, S.-H.; Zeng, C.; Luo, Y. Numerical Analysis of the Effect of Misaligned Guide Vanes on Improving S-Shaped Characteristics for a Pump-Turbine. J. Fluids Eng. 2018, 140, 031102. [Google Scholar]
- Staubli, T.; Senn, F.; Sallaberger, M. Instability of Pump-Turbines during Start-up in Turbine Mode. In Proceedings of the Hydro 2008, Ljubljana, Slovenia, 6–8 October 2008. [Google Scholar]
- Gentner, C.; Sallaberger, M.; Widmer, C.; Braun, O.; Staubli, T. Numerical and experimental analysis of instability phenomena in pump turbines. IOP Conf. Ser. Earth Env. Sci. 2012, 15, 032042. [Google Scholar] [CrossRef]
- Zeng, W.; Yang, J.; Hu, J. Pumped storage system model and experimental investigations on s-induced issues during transients. Mech. Syst. Signal Process. 2017, 90, 350–364. [Google Scholar] [CrossRef]
- Widmer, C.; Staubli, T.; Ledergerber, N. Unstable characteristics and rotating stall in turbine braking operation of pump-turbines. J. Fluids Eng. 2011, 133, 041101. [Google Scholar] [CrossRef]
- Pacot, O.; Kato, C.; Guo, Y.; Yamade, Y.; Avellan, F. Large eddy simulation of the rotating stall in a pump-turbine operated in pumping mode at a part-load condition. J. Fluids Eng. 2016, 13, 111102. [Google Scholar] [CrossRef]
- Xia, L.; Cheng, Y.; Yang, Z.; You, J.; Yang, J.; Qian, Z. Evolutions of Pressure Fluctuations and Runner Loads during Runaway Processes of a Pump-Turbine. J. Fluids Eng. 2017, 139, 091101. [Google Scholar] [CrossRef]
- Xia, L.; Cheng, Y.; Yang, J.; Cai, F. Evolution of flow structures and pressure fluctuations in the S-shaped region of a pump-turbine. J. Hydraul. Res. 2018, 1–15. [Google Scholar] [CrossRef]
- Wang, Z.; Zhu, B.; Wang, X.; Qin, D. Pressure fluctuations in the S-shaped region of a reversible pump-turbine. Energies 2017, 10, 96. [Google Scholar] [CrossRef]
- Martin, C. Stability of pump-turbines during transient operation. In Proceedings of the 5th Conference on Pressure Surges, BHRA, Hannover, Germany, 22–24 September 1986. [Google Scholar]
- Martin, C. Instability of pump-turbines with S-shaped characteristics. In Proceedings of the 20th IAHR Symposium on Hydraulic Machinery and Systems, Charlotte, NC, USA, 6–9 August 2000. [Google Scholar]
- Zhao, X.; Xiao, Y.; Wang, Z.; Luo, H.; Ahn, S.-H.; Yao, Y.; Fan, H. Numerical analysis of non-axisymmetric flow characteristic for a pump-turbine impeller at pump off-design condition. Renew. Energy 2018, 115, 1075–1085. [Google Scholar]
- Menter, F.; Egorov, Y. The scale-adaptive simulation method for unsteady turbulent flow predictions. Part 1: Theory and model description. Flow Turbul. Combust. 2010, 85, 113–138. [Google Scholar] [CrossRef]
- Herwig, H.; Gloss, D.; Wenterodt, T. A new approach to understanding and modelling the influence of wall roughness on friction factors for pipe and channel flows. J. Fluid Mech. 2008, 613, 35–53. [Google Scholar] [CrossRef]
- Li, D.; Wang, H.; Qin, Y.; Han, L.; Wei, X.; Qin, D. Entropy production analysis of hysteresis characteristic of a pump-turbine model. Energy Convers. Manag. 2017, 149, 175–191. [Google Scholar] [CrossRef]
- Saqr, K.; Shehata, A.; Taha, A.; ElAzm, M. CFD modelling of entropy generation in turbulent pipe flow: Effects of temperature difference and swirl intensity. Appl. Therm. Eng. 2016, 100, 999–1006. [Google Scholar] [CrossRef]
- Kock, F.; Herwig, H. Local entropy production in turbulent shear flows: A high-Reynolds number model with wall functions. Int. J. Heat Mass Transf. 2004, 47, 2205–2215. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, K.; Xian, H.; Du, X. A review of methods for vortex identification in hydro turbines. Renew. Sustain. Energy Rev. 2018, 81, 1269–1285. [Google Scholar] [CrossRef]



| Parameter | Value |
|---|---|
| Specific speed | 29.17 |
| Runner inlet diameter D1 | 0.280 m |
| Runner outlet diameter D2 | 0.1409 m |
| Number of runner blades zb | 9 |
| Number of stay vanes nsv | 20 |
| Number of guide vanes ngv | 20 |
| Rated rotational speed n0 | 1000 r/min |
| Guide-vane openings α | 6°, 9°, 15°, 24° |
| Spiral-Case | Guide/Stay Vane (6°) | Guide/Stay Vane (9°) | Guide/Stay Vane (15°) | Guide/Stay Vane (24°) | Runner | Draft-Tube with Extension |
|---|---|---|---|---|---|---|
| 1.01 | 2.06 | 1.98 | 2.42 | 1.96 | 2.45 | 2.34 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Q.; Xia, L.; Zhang, C. Internal Mechanism and Improvement Criteria for the Runaway Oscillation Stability of a Pump-Turbine. Appl. Sci. 2018, 8, 2193. https://doi.org/10.3390/app8112193
Zhou Q, Xia L, Zhang C. Internal Mechanism and Improvement Criteria for the Runaway Oscillation Stability of a Pump-Turbine. Applied Sciences. 2018; 8(11):2193. https://doi.org/10.3390/app8112193
Chicago/Turabian StyleZhou, Qin, Linsheng Xia, and Chunze Zhang. 2018. "Internal Mechanism and Improvement Criteria for the Runaway Oscillation Stability of a Pump-Turbine" Applied Sciences 8, no. 11: 2193. https://doi.org/10.3390/app8112193
APA StyleZhou, Q., Xia, L., & Zhang, C. (2018). Internal Mechanism and Improvement Criteria for the Runaway Oscillation Stability of a Pump-Turbine. Applied Sciences, 8(11), 2193. https://doi.org/10.3390/app8112193




