Abstract
As researches on the quantum computer have progressed immensely, interests in post-quantum cryptography have greatly increased. NTRU is one of the well-known algorithms due to its practical key sizes and fast performance along with the resistance against the quantum adversary. Although NTRU has withstood various algebraic attacks, its side-channel resistance must also be considered for secure implementation. In this paper, we proposed the first single trace attack on NTRU. Previous side-channel attacks on NTRU used numerous power traces, which increase the attack complexity and limit the target algorithm. There are two versions of NTRU implementation published in succession. We demonstrated our attack on both implementations using a single power consumption trace obtained in the decryption phase. Furthermore, we propose a countermeasure to prevent the proposed attacks. Our countermeasure does not degrade in terms of performance.
1. Introduction
The currently used public key cryptography (PKC) such as RSA and Elliptic Curve Cryptography (ECC) are no longer secure if the quantum computer is developed running the Shor algorithm [1,2,3]. Due to the recent advances in quantum computing, post-quantum cryptography (PQC) is an active area of research. Moreover, the national institute of standards and technology (NIST) announced a project to define new standards for the PKC [4]. There are five categories studied for PQC: lattice-based cryptography, multivariate-based cryptography, hash-based cryptography, code-based cryptography, and isogeny-based cryptography. Among those categories, lattice-based cryptography is one of the prominent candidates due to the fast performance with a practical key size. In the same context, the largest number of candidates submitted to NIST project belong to the lattice-based cryptography. One of the well known lattice-based cryptography is NTRU, which is an abbreviation of N-th degree truncated polynomial ring.
NTRU proposed in 1996 by Hoffstein et al. [5] is an encryption algorithm based on the shortest vector problem. NTRU has attracted much attention to the researchers due to the faster speed than classical cryptosystems by more than two orders of magnitude on the same security level. Regarding the implementation, only the encryption code was open to the public until 2017. After the patent release in 2017, all of the source code was available. Currently, two kinds of implementation are proposed in the literature, one released on GitHub in 2017 and the other submitted on NIST standardization project. We distinguish the prior one as NTRU Open Source and the latter as NTRUEncrypt, and also the algorithm itself as NTRU. Although NTRU has withstood various mathematical attacks, the security of its implementation is an open question.
After the proposal of the side channel analysis (SCA) by Kocher et al. [6] in 1996, most of the cryptosystems consider a SCA as a de facto standard in nowadays. Additionally, since the resistance of a SCA is included as a requirement in FIPS140-2 (Federal Information Processing Standard publication 140-2), NTRU should consider the resistance against SCA to substitute the RSA and ECC. Moreover, the NIST standardization project suggests a resistance to SCA for the submitted candidates. The SCA is an attack using additional information such as time, sound, and power consumption during the operation of a cryptographic device. Among these methods, power analysis attack such as the differential power analysis (DPA) and simple power analysis (SPA) is known to be the most practical method. The SPA performs by analyzing a single power consumption trace of the device. The DPA is a statistical approach by exploiting a number of power traces related to secret data. Even though the cryptographic algorithm is theoretically safe, the private key or secret message can be exposed by the side-channel leakage when executing the algorithm. In this regard, there are previous studies on SCA on NTRU by Lee et al. [7] and Zheng et al. [8]. They performed DPA on NTRU and revealed the secret key. However, whether other types of power analysis can be performed has not been analyzed so far.
1.1. Our Contribution
In this paper, we propose the first single trace side channel analysis (STA) against on both NTRU Open Source and NTRUEncrypt with experimental results, and propose a countermeasure. Previous SCA on NTRU [7,8,9] targeted the polynomial multiplication between the cipher-text and the secret key. However, since NTRU was patented until 2017, existing SCAs on NTRU are based on the assumption that publicized polynomial multiplications are used in the decryption process. In this paper, we performed STA on the decryption algorithm used in [10] and on the version submitted in NIST standardization project [11].
Based on the proposed analysis, every NTRU based cryptosystem can be vulnerable to our attack. Moreover, as the PKC is mostly used to exchange the session key between two parties, there might be the case where power consumption trace can only be obtained by one execution of the algorithm. Since we recover with a single power consumption trace, our attack is indeed a threat to these implementations whereas existing DPA cannot be applied in this circumstances. We implement the algorithm on the ATmega128 8-bit processor of the KLA-SCARF AVR [12] and applied the proposed attack. The details of our attack are presented in Section 3.
We propose two versions of countermeasure against the proposed analysis. Although the previous DPA target the different implementation, their method can still be applied on NTRU Open Source and NTRUEncrypt. In this paper, we propose a countermeasure that prevents not only our proposed attack but also the DPA. The proposed countermeasure on NTRU Open Source does not increase the computational cost. Furthermore, the proposed countermeasure on NTRUEncrypt reduces the computational cost approximately by half. The description of our countermeasure is presented in Section 4.
1.2. Organization
This paper is organized as follows. In Section 2, we describe NTRU and its implementation. Also, previous SCAs on NTRU are described. In Section 3, we propose our single trace attack and show experimental results. Next, proposed countermeasures and computation comparisons are in Section 4. We make our conclusion in Section 5.
2. Background
2.1. Algorithm of NTRU
The NTRU is a PKC based on the shortest vector problem whose computational complexity is exponential even in the presence of a quantum computer. The encryption and decryption scheme use polynomial rings in , which consist of all polynomials with degree less than N and coefficients in . Thus, an element can be written as . The polynomial multiplication in is denoted as ·, and is performed as in Equation (1).
Let be a set of with coefficients equal to 1 and coefficients to and let be a set of with coefficients equal to 1 and , where and are fixed parameter. We express the polynomials in and as a trinary polynomial because they consist of only three number of coefficient. The modulus values of integers p and q are used and they satisfy the conditions and . We define as a polynomial in obtained by reducing the coefficients of modulo p. The inverse of in is denoted as . The and are defined in the same manner.
Key Generation
The private key f is a trinary polynomial selected from and the public key h satisfies . The public key is used in the data encryption and private key is used in the data decryption.
Encryption
The purpose of encryption is to transport the data by converting a message using the public key of the receiver. Then only an owner of proper private key can decrypt the message. To encrypt a plain-text , we first choose a random polynomial r in and compute the cipher-text e as Equation (2).
The modulus q in the above equation means that each coefficient in a polynomial is reduced modulo q.
Decryption
Decryption is used to recover the message from sender. The received data is usually called as cipher-text. The cipher-text e is decrypted by computing the following equations.
Note that by choosing the private key f as where , then is equal to 1 so that the Equation (4) can be omitted [13]. Both target of this paper (NTRUEncrypt, NTRU Open Source) use this optimization.
2.2. Side Channel Analysis and Related Work
Although an algorithm is mathematically secure, naive implementation can make cryptosystem vulnerable to various attacks. The most important considerations in implementation are random number generator and leakage of the secret information. In most cryptosystems, the quality of the random numbers used directly determines the security of the system. Therefore, a predictable random value (i.e., low entropy source) may weaken the system. The studies for the randomness have done in the respect of entropy [14,15,16,17,18,19]. However, the analysis herein discusses the implementation in the side of SCA.
The SCA is first introduced by Kocher et al. in 1996 [6]. Subsequently, power analysis attacks such as the simple power analysis (SPA), differential power analysis (DPA), and correlation power analysis (CPA) [20,21] have been proposed. Nowadays, any attack that exploits information gained from the implementation is considered as SCA. This includes cache attack, EM analysis, and attacks that exploit hardware vulnerabilities [22,23,24,25]. However, we mainly focus on the power analysis attack. The power analysis attacks rely on the dependency between the power consumption of the device and the operated data during the execution of an algorithm. The SCA is an actual threat since it can recover the private key of the cryptosystem in practical time. To prevent these type of attack, masking and hiding are studied [26]. Masking refers to a method of computing secret information with random values, so that the actual value is unused during the encryption and decryption. Hiding removes the relationship between power consumption and the data. Hiding is one of the hardware level countermeasure which is focused on the security during the operation.
Additionally, the Internet of Things (IoT) devices are advanced nowadays, the security against low-power design is essential [27]. However, the conventional PKC is difficult to implement on the resource-constrained environment. Therefore, there is a research on the physical unclonable function (PUF) as a light-weight authentication security primitive. For example, side-channel resistant PUF was intensively studied in [28].
2.3. Previous Side Channel Analysis on NTRU
The first studied SCA on the NTRU was timing attacks in 2007 [29]. In 2010, Lee et al. introduced a SPA and CPA on NTRU and proposed a countermeasure against the attack [7]. The idea behind the proposed SPA in [7] is that there exists a difference in the power consumption when adding non-zero with zero values and non-zero with non-zero values. They also performed CPA on the multiplication using 1000 traces. Also, a second order CPA is proposed in [7] using 10,000 traces. For the description of the attack, please refer to [7]. To prevent the SPA, they proposed to initialize the temporary buffer with a non-zero value and to randomize the order of computation and data. They also provided countermeasures against CPA such as masking and shuffling.
In 2013, a first-order collision attack was proposed in [8] with the purpose of incapacitating the countermeasure proposed in [7]. Their attack against the first-order countermeasure is an improvement in [8] since the attack is performed with 5,000 traces. The target of the attack was when the same registers are loaded during the multiplication. Overall, the decryption code used for the analysis in [7] and [8] was not an official implementation. Although the proposed attacks can be applied to official implementation, the attack environment is restricted to the case where multiple executions of NTRU with the same key is possible.
3. Proposed Single Trace Side Channel Analysis on NTRU Implementation
In this section, we propose our STA on the two cases of NTRU implementation. For each case, we first describe the implementation and then suggest our STA. Lastly, we present the experimental results on our attack. The purpose of our attack is to recover the private key. Therefore, only the implementation of decryption is introduced in this paper.
3.1. NTRU Open Source
The integral parts of NTRU implementation are the way to store polynomials and a polynomial multiplication.
Representing Polynomials
To store a polynomial f of the private key, NTRU Open Source stores the degree of indeterminant x whose coefficient is or . Because the addition is computed according to the degree of and , it is possible to operate without the degree of . Thus, the private key array first stores all the degree whose coefficient is and then it stores all the degree where its coefficient is in an array. For example, if , then the array of f would be . The polynomial in general, is stored such that the coefficient of the xth degree is the xth element in an array. For example, the polynomial represent as .
Polynomial Multiplication
For efficiency, the private key is set as and F is divided into three trinary polynomials . The advantage of splitting F, is that it lowers the hamming weight of polynomials so that the multiplication could be speed up [13,30]. Consequently, the decryption of NTRU Open Source performs as in Equation (7) considering the order of multiplication.
Computation of Equation (7) is represented in Algorithm 1 and algorithm for polynomial multiplication is in Algorithm 2.
| Algorithm 1 Decryption in NTRU Open Source |
|
The input b of Algorithm 2 is formed in a way such that the degree having coefficient is stored in ascending order and then degree having is stored. The polynomial multiplication starts with the smallest degree where its coefficient equals to and add cipher-text to the initialized array. Since the result must be reduced modulo , this implementation performs the addition from the beginning to and restarts for the th element in an array when the degree exceeds N. After the modular operation, the sign is reversed and the same steps are repeated on for the degree having coefficient . Lastly, the (mod operation is performed by AND(∧) since the q is set as power of .
| Algorithm 2 Polynomial Multiplication during NTRU Open Source Decryption |
|
3.1.1. Proposed Method
The idea behind the attack is that the correlation between power consumption traces obtained when performing the same operations is higher than the power consumption trace obtained when performing different operations. Let the power trace obtained during the addition operation be taken as a reference trace R. Let O be the subtraces of the power consumption trace in Algorithm 2. When calculating the correlation between R and O, the correlation coefficient will be obtained when computing Algorithm 2. When plotting the gained coefficients values, then a graph appear like Figure 1. There are peaks, called as high peak herein, which signify the affinity between R and O. Then, we recover the private key polynomial by calculating the distance between the high peaks.
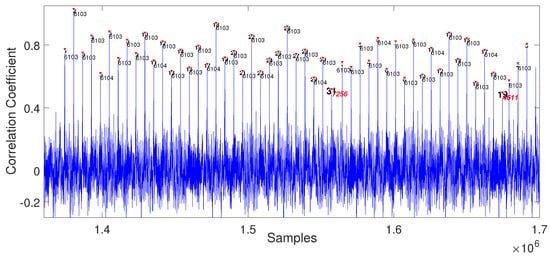
Figure 1.
Result: High peaks of the addition and a distance value between the peaks.
As in Algorithm 2, the additions in steps 4 to 12 and steps 16 to 24 depend on the private value. For example, suppose and let be the smallest degree when its coefficient equals to . Then the steps 6 to 8 are repeated 6 times and steps 9 to 11 are repeated 5 times. Note that, there is a moment when the loop passes to the next loop, then the distance between high peaks is different at that moment. Thus, if the real value is x, so that the interval between th and th high peak is different from the others. Therefore, we can recover the whole value by applying the same steps for the coefficients and .
3.1.2. Experiment
Figure 2 is a full trace of the NTRU Open Source porting on an KLA-SCARF AVR, captured in Lecroy HDO6104A oscilloscope with 250 M sampling rate [12,31]. The parameters for the experiment are N = , = , = , = and the private key is as follows.
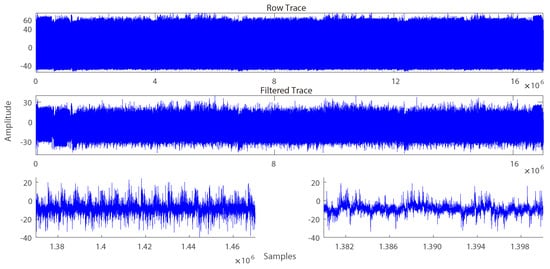
Figure 2.
Full trace of NTRU Open Source: The top figure is a raw trace, the middle figure is a filtered trace, and the bottom two are enlarged figure of the filtered trace.
We choose these values as we considered them to be suitable in the experimental environment. The first 16 entries of b represent , the next 16 values represent and the rest of the values represent .
The first step for analysis is discovering a reference trace R by SPA (Figure 3). The length of R is calculated by dividing the full trace length by the total number of operations. After that, the correlation coefficient can be calculated from the trace using the reference. Figure 1 is a part of the result containing the high peaks and the following intervals. There are two indices tagged on each peak, one represents an order of the high peak and the other is a distance between the previous high peak. The th peak has different distance than others, so the first degree where coefficient is is . With this process, we can recover and the private key.
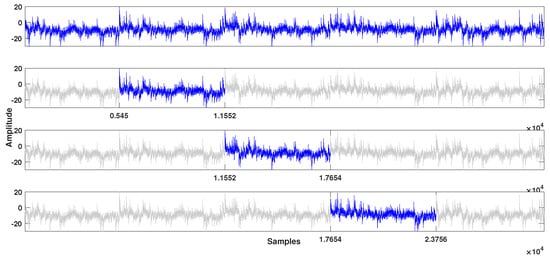
Figure 3.
Figuring the reference trace: The three set of an addition operation.
3.2. NTRUEncrypt
Representing Polynomials
In the NTRUEncrypt, the polynomial is represented as the coefficients in order. For example, stored as F = . Before the polynomial multiplication of cipher-text and private key, there are steps to compute .
Polynomial Multiplication
The the Equation (3) operates using the grade school multiplication. Unlike NTRU Open Source, the polynomial multiplication operates separately. These steps are described in Algorithm 3.
| Algorithm 3 Decryption in NTRUEncrypt |
|
3.2.1. Proposed Method
The proposed method exploits the power consumption of steps 1 to 3 and steps 5 to 13 in Algorithm 3 to recover the trinary polynomial F. When F get recovered, the private key polynomial f is computed by , where p is a public value. The relative order of coefficients is discovered by analyzing the steps 1 to 3 operation. Because F is a trinary polynomial, a constant value p is multiplied by three values . Since most of the processor apply 2’s complement method to express negative value, a hamming weight of is bigger than others. Thus we can observe the high peaks in the power consumption trace when the is operated. Note that, the proposed analysis depends on the operation of the processor. Thus, if the processor uses another method to represent negative value, the proposed analysis should consider such circumstances.
The next step, the relative orders of the coefficient are known from 5 to 13 steps which are the polynomial multiplication of cipher-text e and private key f. The power consumption when calculating the coefficient of the cipher-text and 0 will be lower than other calculation processes. This portion where the power consumption is low is referred to as low peak. Therefore, after finding the relative position from to , and combining this result with the information of s then F is completed recovered. Finally, we can get f by computing .
3.2.2. Experiment
Figure 4a is a full trace of the NTRUEncrypt porting on the KLA-SCARF AVR and is captured with a Lecroy HDO6104A oscilloscope at a 250 M sampling rate [12,31]. The parameters for the experiment are N = , p = , q = , and a private key is as follows.
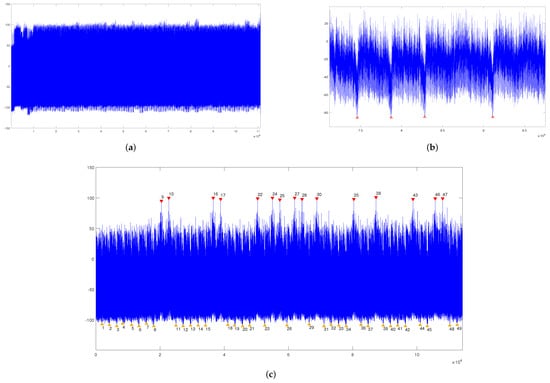
Figure 4.
(a) Full trace of NTRUEncrypt; (b) Enlarged Low Peaks; (c) Result of SPA against .
The p and q follow the proposed parameter but N is smaller than the standard because of the experimental environment.
Figure 4c depicts the power consumption of steps 1 to 3 in Algorithm 3. As mentioned above, the high peaks represent the moment when p is multiplied by . Also, in the Figure 4c, there are the low peaks related to the coefficient and . Thus the relative orders of and others can be recovered by analyzing Figure 4c.
The following process is to recover the coefficients . For each coefficient of the cipher-text, there are N multiplications with the private key. During the N operations, the operation of the private key appears in the same order, so the low peaks appear regularly on the whole power trace (Figure 4a). To recover the degree, we should classify a set of multiplications by SPA among the trace. The multiplication between cipher-text and private key occurs after computing , and the total recovered number of multiplications is . To reduce the noise, one can average multiple power consumption trace. Figure 5 illustrates the average of 10 traces. Figure 4b is an enlarged plot of four low peaks to deduce that peaks are identified. Lastly, with the three coefficients recovered from the analysis, the private key f is obtained.
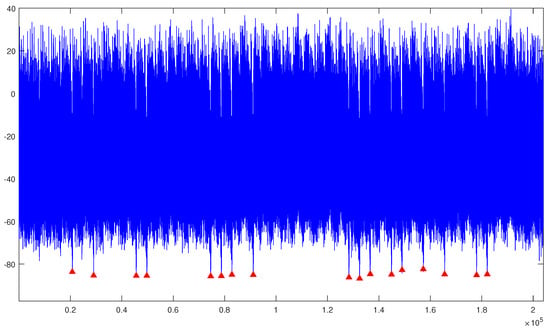
Figure 5.
The Average of 10 Power Consumption Traces of Polynomial Multiplication using Grace School Multiplication Method.
4. Countermeasure
In this section, we propose a countermeasure for each of the two implementations. The proposed analysis on NTRU Open Source and NTRUEncrypt does not depend on the data information. Since we used a single power consumption trace, countermeasures to prevent DPA such as adding dummy operation and shuffling cannot prevent our attack.
4.1. Countermeasure against NTRU Open Source Implementation
Since the advantage of the original implementation is that computes both modular reduction and polynomial multiplication, simultaneously, the countermeasure we propose also process both of the operation at the same time. Furthermore, the modified implementation has the same number of polynomial coefficient addition as the original implementation. The Algorithm 4 is a countermeasure for the polynomial multiplications described in Algorithm 2.
The Algorithm 4 is a method that precomputes the index i, where the cipher-text polynomial will be added. For example, let be the degree of the polynomial and let be a coefficient of degree , then the original cipher-text polynomial coefficient addition performs as in Figure 6a. During the original iteration, the additions when operate with different loop when . However, the addition in the proposed method operates in the same loop so there is no leakage for side channel analysis. The proposed method first finds the index of cipher-text which is added to the middle index of the result array, then the addition operates simultaneously as in Figure 6b.

Figure 6.
Iteration of Addition.
| Algorithm 4 Countermeasure of NTRU Open Source Proeject |
|
4.2. Countermeasure against NTRUEncrypt Implementation
The proposed countermeasure in this paper uses three tables initialized with a random number. The countermeasure prevents not only proposed attack in this paper but also the other previous attacks with a decreased number of computations compared to the submitted implementation. The NTRUEncrypt first calculates the private key then multiplies . However, the proposed countermeasure uses a trinary polynomial F, and computes and adds e to decrypt the cipher-text. This is expressed in Equation (8).
To compute , the proposed countermeasure first computes and temporarily save the value. After that, it updates the output of computation in the three tables according to from the trinary polynomial F. Then the table of the coefficient is subtracted from the table of the coefficient . During the accumulation, a start index is sought by to process at the same time for increased efficiency.
For the side channel resistance, by encoding the trinary polynomial of the private key at the storage step, it relieves the difference in power consumption coming from loading and . The encoding function is chosen by considering the physical property. The proposed countermeasure uses an encoding function as , to have the same hamming weight. Then the trinary polynomial would be represented with at the proposed algorithm. Algorithm 5 describes the above procedure.
| Algorithm 5 Countermeasure Applied Decryption of NTRUEncrypt |
|
At the final step 13, a subtraction of and , an addition of e and could be processed at once. Since q is a power of 2 in the proposed parameters, can be operated as AND (∧). In Algorithm 5, different tables are accessed according to the coefficient of F. However, since the same operation is performed regardless of the coefficients, it can be considered that there is no difference in the power consumption which depends on . Furthermore, as the three tables are initialized with the same random number (steps 3 to 5), the algorithm also prevents SPA and CPA proposed in [7]. SPA can be prevented by initializing the array to hold the result with non-zero values and removing the operations that add zero and non-zero values. Also, choosing the non-zero value for initial as random, the algorithm is protected from CPA because the intermediate value cannot be guessed. When three tables initialized with the same random non-zero value, the random values can be removed without additional computation, as in step 13.
4.3. Implementation of Countermeasure
4.3.1. Comparison of the NTRUEncrypt
The computational cost of the proposed countermeasure on NTRU Open Source is similar to the unprotected version, only with additional precomputations. Moreover, it is hard to compare the NTRU Open Source and NTRUEncrypt because of the different process of the private key multiplication. Thus, we only compare the computational cost and memory of the protected and unprotected version of NTRUEncrypt. Table 1 includes the number of initialization, addition, and multiplication costs when the degree is N. Since the computational cost of subtraction is similar to that of the addition, we include both the numbers of subtractions and the numbers of additions. The computation to find the start degree is not included.

Table 1.
Comparison of Operation between Unprotected and Protected NTRUEncrypt.
As shown in Table 1, the total number of computational steps necessary to calculate is reduced when applying our countermeasure. Moreover, the number of multiplications is reduced to square root of the original. Also, the comparison of the memory usage is presented in Table 2. Since NTRUEncrypt use 16 bit as a word size, Table 2 refers to the multiplication of a word size and the number of used arrays.

Table 2.
Comparison of the Memory Usage between Unprotected and Protected NTRUEncrypt.
Although the number of used arrays is doubled compared to that used in the unprotected NTRUEncrypt, the total computational cost(number of computational steps) is reduced from to , where N is at least . Consequently, considering the computational costs and the memory size, Algorithm 5 is more efficient compared to Algorithm 3 and has side channel resistance.
4.3.2. Result of the Countermeasure Implementation
Figure 7a is the full trace of the Algorithm 5 implemented in the same environment as the analyzed traces. Since the countermeasure uses a table for all coefficients in the private key, the power consumption difference depending on the private key is not exposed and this is observed in Figure 7b.
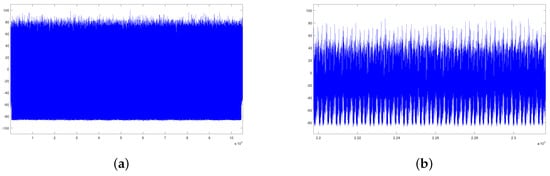
Figure 7.
Iteration of Addition. (a) Full Trace of Countermeasure; (b) Enlarged Trace of Countermeasure.
5. Conclusions
Although the cryptosystem is proven to be secure, the security of its implementation must be considered as the devices may expose side channel leakages. Since PQC cryptosystems are implemented in classical computers, side channel must be considered. In this paper, we analyzed the two versions of NTRU implementation – NTRUEncrypt and NTRU Open Source. By using a single power consumption obtained in the decryption, we were able to recover the private key on both implementations. Our attack is practical and powerful since it can be applied without constraints of the environment. We also proposed countermeasures for our attack. Our countermeasures not only prevent our proposed attack but also prevents the previous attack. Moreover, our countermeasures do not degrade its performance. In addition, as the NIST standardization project is still in process, every algorithm including NTRU may provide an updated optimized implementation. The proposed analysis is based on the implementation up to now but more optimized version might appear in the future.
Author Contributions
All authors have contributed to this work. Soojung An and Suhri Kim analyzed the algorithm and drafted and revised the manuscript. Soojung An and Sunghyun Jin performed the experiment and analyzed the result. Soojung An, Suhri Kim, Sunghyun Jin, and HanBit Kim devised the countermeasure and HeeSeok Kim verified the analytical methods and supervised this work.
Acknowledgments
This research was supported by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Science and ICT (NRF-2017R1C1B2004583).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Shor, P.W. Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer. SIAM Rev. 1999, 41, 303–332. [Google Scholar] [CrossRef]
- Rivest, R.L.; Shamir, A.; Adleman, L. A method for obtaining digital signatures and public-key cryptosystems. Commun. ACM 1978, 21, 120–126. [Google Scholar] [CrossRef]
- Koblitz, N. Elliptic curve cryptosystems. Math. Comput. 1987, 48, 203–209. [Google Scholar] [CrossRef]
- Chen, L.; Chen, L.; Jordan, S.; Liu, Y.K.; Moody, D.; Peralta, R.; Perlner, R.; Smith-Tone, D. Report on Post-Quantum Cryptography; US Department of Commerce, National Institute of Standards and Technology: Gaithersburg, MD, USA, 2016.
- Hoffstein, J.; Pipher, J.; Silverman, J.H. NTRU: A ring-based public key cryptosystem. In Algorithmic Number Theory, Proceedings of the Third International Symposiun, ANTS-III, Portland, OR, USA, 21–25 June 1998; Springer: Berlin, Germany, 1998; Volume 1423, pp. 267–288. [Google Scholar]
- Kocher, P.C. Timing attacks on implementations of Diffie-Hellman, RSA, DSS, and other systems. In Advances in Cryptology—CRYPTO ’96, Proceedings of the 16th Annual International Cryptology Conference, Santa Barbara, CA, USA, 18–22 August 1996; Springer: Berlin, Germany, 1996; Volume 1109, pp. 104–113. [Google Scholar]
- Lee, M.K.; Song, J.E.; Choi, D.; Han, D.G. Countermeasures against power analysis attacks for the NTRU public key cryptosystem. IEICE Trans. Fundam. Electron. Commun. Comput. Sci. 2010, 93, 153–163. [Google Scholar] [CrossRef]
- Zheng, X.; Wang, A.; Wei, W. First-order collision attack on protected NTRU cryptosystem. Microprocess. Microsyst. 2013, 37, 601–609. [Google Scholar] [CrossRef]
- Song, J.E.; Han, D.G.; Lee, M.K.; Choi, D.H. Power analysis attacks against NTRU and their countermeasures. J. Korea Inst. Inf. Secur. Cryptol. 2009, 19, 11–21. [Google Scholar]
- Whyte, W.; Etzel, M. NTRU Open Source. 2017. Available online: https://github.com/NTRUOpenSourceProject/ntru-crypto (accessed on 19 October 2018).
- Zhang, Z.; Chen, C.; Hoffstein, J.; Whyte, W. NTRUEncrypt. 2017. Available online: https://csrc.nist.gov/Projects/Post-Quantum-Cryptography/Round-1-Submissions (accessed on 19 October 2018).
- Choi, Y.; Choi, D.; Ryou, J. Implementing Side Channel Analysis Evaluation Boards of KLA-SCARF system. J. Korea Insti. Inf. Secur. Cryptol. 2014, 24, 229–240. [Google Scholar] [CrossRef]
- Hoffstein, J.; Silverman, J. Optimizations for NTRU. In Public-Key Cryptography and Computational Number Theory; Walter de Gruyter: Warsaw, Poland, 2001; pp. 77–88. [Google Scholar]
- Guariglia, E. Entropy and fractal antennas. Entropy 2016, 18, 84. [Google Scholar] [CrossRef]
- Zmeskal, O.; Dzik, P.; Vesely, M. Entropy of fractal systems. Comput. Math. Appl. 2013, 66, 135–146. [Google Scholar] [CrossRef]
- Zanette, D.H. Generalized Kolmogorov entropy in the dynamics of multifractal generation. Phys. Stat. Mech. Its Appl. 1996, 223, 87–98. [Google Scholar] [CrossRef]
- Guariglia, E. Harmonic Sierpinski Gasket and Applications. Entropy 2018, 20, 714. [Google Scholar] [CrossRef]
- Berry, M.V.; Lewis, Z.; Nye, J.F. On the Weierstrass-Mandelbrot fractal function. Proc. R. Soc. Lond. A 1980, 370, 459–484. [Google Scholar] [CrossRef]
- Guariglia, E. Spectral analysis of the Weierstrass-Mandelbrot function. In Proceedings of the 2017 2nd International Multidisciplinary Conference on Computer and Energy Science (SpliTech), Split, Croatia, 12–14 July 2017; pp. 1–6. [Google Scholar]
- Brier, E.; Clavier, C.; Olivier, F. Correlation power analysis with a leakage model. In Cryptographic Hardware and Embedded Systems—CHES 2004, Proceedingds of the 6th International Workshop, Cambridge, MA, USA, 11–13 August 2004; Springer: Berlin, Germany, 2004; Volume 3156, pp. 16–29. [Google Scholar]
- Kocher, P.; Jaffe, J.; Jun, B. Differential power analysis. In Advances in Cryptology—CRYPTO’ 99, Proceedingds of the 19th Annual International Cryptology Conference, Santa Barbara, CA, USA, 15–19 August 1999; Springer: Berlin, Germany, 1999; Volume 1666, pp. 388–397. [Google Scholar]
- Yarom, Y.; Falkner, K. FLUSH+ RELOAD: A High Resolution, Low Noise, L3 Cache Side-Channel Attack. In Proceedings of the 23rd USENIX Security Symposium, San Diego, CA, USA, 20–22 August 2014; Volume 1, pp. 22–25. [Google Scholar]
- Inci, M.S.; Gulmezoglu, B.; Irazoqui, G.; Eisenbarth, T.; Sunar, B. Cache attacks enable bulk key recovery on the cloud. In Cryptographic Hardware and Embedded Systems—CHES 2016, Proceedings of the 18th International Conference, Santa Barbara, CA, USA, 17–19 August 2016; Springer: Berlin, Germany, 2016; Volume 9813, pp. 368–388. [Google Scholar]
- Martinasek, Z.; Zeman, V.; Trasy, K. Simple electromagnetic analysis in cryptography. Int. J. Adv. Telecommun. Electrotech. Signals Syst. 2012, 1, 13–19. [Google Scholar] [CrossRef]
- Rooney, C.; Seeam, A.; Bellekens, X. Creation and Detection of Hardware Trojans Using Non-Invasive Off-The-Shelf Technologies. Electronics 2018, 7, 124. [Google Scholar] [CrossRef]
- Coron, J.S.; Goubin, L. On boolean and arithmetic masking against differential power analysis. In Cryptographic Hardware and Embedded Systems—CHES 2000, Proceedings of the Second International Workshop, Worcester, MA, USA, 17–18 August 2000; Springer: Berlin, Germany, 2000; Volume 1965, pp. 231–237. [Google Scholar]
- Yuan, J.S.; Lin, J.; Alasad, Q.; Taheri, S. Ultra-Low-Power Design and Hardware Security Using Emerging Technologies for Internet of Things. Electronics 2017, 6, 67. [Google Scholar] [CrossRef]
- Cao, Y.; Zhao, X.; Ye, W.; Han, Q.; Pan, X. A Compact and Low Power RO PUF with High Resilience to the EM Side-Channel Attack and the SVM Modelling Attack of Wireless Sensor Networks. Sensors 2018, 18, 322. [Google Scholar] [CrossRef] [PubMed]
- Silverman, J.H.; Whyte, W. Timing attacks on NTRUEncrypt via variation in the number of hash calls. In Topics in Cryptology—CT-RSA 2007, Proceedings of the Cryptographers’ Track at the RSA Conference 2007, San Francisco, CA, USA, 5–9 February 2007; Springer: Berlin, Germany, 2007; Volume 4377, pp. 208–224. [Google Scholar]
- Howgrave-Graham, N.; Silverman, J.H.; Singer, A.; Whyte, W. NAEP: Provable Security in the Presence of Decryption Failures. IACR Cryptol. ePrint Arch. 2003, 2003, 172. [Google Scholar]
- LeCroy, T. HDO6000A High Definition. Available online: http://cdn.teledynelecroy.com/files/pdf/hdo6000a-oscilloscopes-datasheet.pdf (accessed on 11 October 2018).
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).