A Brief Review of Specialty Optical Fibers for Brillouin-Scattering-Based Distributed Sensors
Abstract
1. Introduction
2. The Waveguide
3. The Material
4. Fiber Configurations
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Bao, X.; Chen, L. Recent Progress in Distributed Fiber Optic Sensors. Sensors 2012, 12, 8601–8639. [Google Scholar] [CrossRef] [PubMed]
- Photonic Sensor Consortium Market Survey Report. 2018 Distributed and Single Point Fiber Optic Sensing Systems Forecast; Information Gatekeepers, Inc.: Winchester, UK, May 2018. [Google Scholar]
- Iribas, H.; Urricelqui, J.; Mariñelarena, J.; Sagues, M.; Loayssa, A. Cost-Effective Brillouin Optical Time-Domain Analysis Sensor Using a Single Optical Source and Passive Optical Filtering. J. Sens. 2016, 7, 8243269. [Google Scholar] [CrossRef]
- Mizuno, Y.; Zou, W.; He, Z.; Hotate, K. Proposal of Brillouin optical correlation-domain reflectometry (BOCDR). Opt. Express 2008, 16, 12148–12153. [Google Scholar] [CrossRef] [PubMed]
- Hayashi, N.; Mizuno, Y.; Nakamura, K. Simplified Configuration of Brillouin Optical Correlation-Domain Reflectometry. IEEE Photonics J. 2014, 6, 6802807I. [Google Scholar] [CrossRef]
- Horiguchi, T.; Shimizu, K.; Kurashima, T.; Tateda, M.; Koyamada, Y. Development of a Distributed Sensing Technique Using Brillouin Scattering. J. Lightwave Technol. 1995, 13, 1296–1302. [Google Scholar] [CrossRef]
- Lee, B. Review of the present status of optical fiber sensors. Opt. Fiber Technol. 2003, 9, 57–79. [Google Scholar] [CrossRef]
- Ukil, A.; Braendle, H.; Krippner, P. Distributed Temperature Sensing: Review of Technology and Applications. IEEE Sens. J. 2012, 12, 885–892. [Google Scholar] [CrossRef]
- Bao, X.; Chen, L. Recent Progress in Brillouin Scattering Based Fiber Sensors. Sensors 2011, 11, 4152–4187. [Google Scholar] [CrossRef] [PubMed]
- Thévenaz, L. Brillouin distributed time-domain sensing in optical fibers: State of the art and perspectives. Front. Optoelectron. China 2010, 3, 13–21. [Google Scholar] [CrossRef]
- Barrias, A.; Casas, J.R.; Villalba, S. A Review of Distributed Optical Fiber Sensors for Civil Engineering Applications. Sensors 2016, 16, 748. [Google Scholar] [CrossRef] [PubMed]
- Grattan, K.T.V.; Sun, T. Fiber optic sensor technology: An overview. Sens. Actuators A 2000, 82, 40–61. [Google Scholar] [CrossRef]
- Galindez-Jamioy, C.A.; López-Higuera, J.M. Brillouin Distributed Fiber Sensors: An Overview and Applications. J. Sens. 2012, 2012, 204121. [Google Scholar] [CrossRef]
- Selker, J.S.; Thévenaz, L.; Hurwald, H.; Mallet, A.; Luxemburg, W.; van de Giesen, N.; Stejskal, M.; Zeman, J.; Westhoff, M.; Parlange, M.B. Distributed fiber-optic temperature sensing for hydrologic systems. Water Resour. Res. 2006, 42, W12203. [Google Scholar] [CrossRef]
- Motil, A.; Bergman, A.; Tur, M. State of the art of Brillouin fiber-optic distributed sensing. Opt. Laser Technol. 2016, 78, 81–103. [Google Scholar] [CrossRef]
- Beugnot, J.-C.; Sylvestre, T.; Alasia, D.; Maillotte, H.; Laude, V.; Monteville, A.; Provino, L.; Traynor, N.; Mafang, S.F.; Thévenaz, L. Complete experimental characterization of stimulated Brillouin scattering in photonic crystal fiber. Opt. Express 2007, 15, 15517–15522. [Google Scholar] [CrossRef] [PubMed]
- Zou, L.; Bao, X.; Chen, L. Brillouin scattering spectrum in photonic crystal fiber with a partially germanium-doped core. Opt. Lett. 2003, 28, 2022–2024. [Google Scholar] [CrossRef] [PubMed]
- McElhenny, J.E.; Pattnaik, R.K.; Toulouse, J.; Saitoh, K.; Koshiba, M. Uniqu characteristic features of stimulated Brillouin scattering in small-core photonic crystal fibers. J. Opt. Soc. Am. B 2008, 25, 582–593. [Google Scholar] [CrossRef]
- Dong, Y.; Bao, X.; Chen, L. Distributed temperature sensing based on birefringence effect on transient Brillouin grating in a polarization-maintaining photonic crystal fiber. Opt. Lett. 2009, 34, 2590–2592. [Google Scholar] [CrossRef] [PubMed]
- Zou, L.; Bao, X.; Afshar, V.S.; Chen, L. Dependence of the Brillouin frequency shift on strain and temperature in a photonic crystal fiber. Opt. Lett. 2004, 29, 1485–1487. [Google Scholar] [CrossRef] [PubMed]
- Lee, Y.W.; Urbanek, K.E.; Digonnet, M.J.F.; Byer, R.L.; Jiang, S. Measurement of the stimulated Brillouin scattering gain coefficient of a phosphate fiber. Proc. SPIE 2007, 6469, 64690L. [Google Scholar] [CrossRef]
- Qin, G.; Sotobayashi, H.; Tsuchiya, M.; Mori, A.; Suzuki, T.; Ohishi, Y. Stimulated Brillouin Scattering in a Single-Mode Tellurite Fiber for Amplification, Lasing, and Slow Light Generation. J. Lightwave Technol. 2008, 26, 492–498. [Google Scholar] [CrossRef]
- Lambin-Iezzi, V.; Loranger, S.; Saad, M.; Kashyap, R. Stimulated Brillouin scattering in SM ZBLAN fiber. J. Non-Cryst. Solids 2013, 359, 65–68. [Google Scholar] [CrossRef]
- Abedin, K.S. Observation of strong stimulated Brillouin scattering in single-mode As2Se3 chalcogenide fiber. Opt. Express 2005, 13, 10266–10271. [Google Scholar] [CrossRef] [PubMed]
- Bashkansky, M.; Dutton, Z.; Sanghera, J.; Pureza, P.; Aggarwal, I. Stimulated Brillouin scattering in single-mode As2S3 and As2Se3 chalcogenide fibers. Opt. Express 2006, 14, 12063–12070. [Google Scholar]
- Ballato, J.; Dragic, P. Glass: The Carrier of Light—A Brief History of Optical Fiber. Int. J. Appl. Glass Sci. 2016, 7, 413–422. [Google Scholar] [CrossRef]
- Gloge, D. Dispersion in Weakly Guiding Fibers. Appl. Opt. 1971, 10, 2442–2445. [Google Scholar] [CrossRef] [PubMed]
- Tamura, Y.; Sakuma, H.; Morita, K.; Suzuki, M.; Yamamoto, Y.; Shimada, K.; Honma, Y.; Sohma, K.; Fujii, T.; Hasegawa, T. The First 0.14-dB/km Loss Optical Fiber and its Impact on Submarine Transmission. J. Lightwave Technol. 2018, 36, 44–49. [Google Scholar] [CrossRef]
- Kao, K.C.; Hockham, G.A. Dielectric-fibre surface waveguides for optical frequencies. Proc. Inst. Electr. Eng. 1966, 113, 1151–1158. [Google Scholar] [CrossRef]
- Snitzer, E. Cylindrical Dielectric Waveguide Modes. J. Opt. Soc. Am. 1961, 51, 491–498. [Google Scholar] [CrossRef]
- Herstrøm, S.; Grüner-Nielsen, L.; Pálsdóttir, B. Acoustic index of Ge-doped optical fibers. Opt. Lett. 2009, 34, 3689–3691. [Google Scholar] [CrossRef] [PubMed]
- Jen, C.K. Similarities and Differences between Fiber Acoustics and Fiber Optics. In Proceedings of the IEEE 1985 Ultrasonics Symposium, San Francisco, CA, USA, 16–18 October 1985; Volume 2, pp. 1128–1133. [Google Scholar]
- Mangognia, A.; Kucera, C.; Guerrier, J.; Furtick, J.; Hawkins, T.; Dragic, P.D.; Ballato, J. Spinel-derived single mode optical fiber. Opt. Mater. Express 2013, 3, 511–518. [Google Scholar] [CrossRef]
- Dragic, P.D.; Ryan, C.; Kucera, C.J.; Cavillon, M.; Tuggle, M.; Jones, M.; Hawkins, T.W.; Yablon, A.D.; Stolen, R.; Ballato, J. Single- and few-moded lithium aluminosilicate optical fiber for athermal Brillouin strain sensing. Opt. Lett. 2015, 40, 5030–5033. [Google Scholar] [CrossRef] [PubMed]
- Dragic, P.D.; Cavillon, M.; Ballato, A.; Ballato, J. A unified materials approach to mitigating optical nonlinearities in optical fiber. II. B. The optical fiber, material additivity and the nonlinear coefficients. Int. J. Appl. Glass Sci. 2018, 9, 307–318. [Google Scholar] [CrossRef]
- Auld, B.A. Acoustic Fields and Waves in Solids; John Wiley: Hoboken, NY, USA, 1973. [Google Scholar]
- Mason, W.P. Physical Acoustics and the Properties of Solids; Van Nostrand: Princeton, NJ, USA, 1958. [Google Scholar]
- Thomas, P.J.; Rowell, N.L.; van Driel, H.M.; Stegeman, G.I. Normal acoustic modes and Brillouin scattering in single-mode optical fibers. Phys. Rev. B 1979, 19, 4986–4998. [Google Scholar] [CrossRef]
- Jen, C.-K.; Safaai-Jazi, A.; Farnell, G.W. Leaky Modes in Weakly Guiding Fiber Acoustic Waveguides. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1986, 33, 634–643. [Google Scholar]
- Jen, C.-K.; Goto, N. Backward Collinear Guided-Wave-Acousto-Optic Interactions in Single-Mode Fibers. J. Lightwave Technol. 1989, 7, 2018–2023. [Google Scholar] [CrossRef]
- Jen, C.-K.; Oliveira, J.E.B.; Goto, N.; Abe, K. Role of Guided Acoustic Wave Properties in Single-Mode Optical Fiber Design. Electron. Lett. 1988, 24, 1419–1420. [Google Scholar] [CrossRef]
- Shibata, N.; Azuma, Y.; Horiguchi, T.; Tateda, M. Identification of longitudinal acoustic modes guided in the core region of a single-mode optical fiber by Brillouin gain spectra measurements. Opt. Lett. 1988, 13, 595–597. [Google Scholar] [CrossRef] [PubMed]
- Shibata, N.; Okamoto, K.; Azuma, Y. Longitudinal acoustic modes and Brillouin-gain spectra for GeO2-doped-core single-mode fibers. J. Opt. Soc. Am. B 1989, 6, 6–1167. [Google Scholar] [CrossRef]
- Dragic, P.D. Novel dual-Brillouin-frequency optical fiber for distributed temperature sensing. Proc. SPIE 2009, 7197, 719710. [Google Scholar]
- Koyamada, Y.; Sato, S.; Nakamura, S.; Sotobayashi, H.; Chujo, W. Simulating and Designing Brillouin Gain Spectrum in Single-Mode Fibers. J. Lightwave Technol. 2004, 22, 631–639. [Google Scholar] [CrossRef]
- Dong, L. Limits of Stimulated Brillouin Scattering Suppression in Optical Fibers with Transverse Acoustic Waveguide Designs. J. Lightwave Technol. 2010, 28, 3156–3161. [Google Scholar]
- Tuggle, M.; Kucera, C.; Hawkins, T.; Sligh, D.; Runge, A.F.J.; Peacock, A.C.; Dragic, P.; Ballato, J. Highly nonlinear yttrium-aluminosilicate optical fiber with a high intrinsic stimulated Brillouin scattering threshold. Opt. Lett. 2017, 42, 4849–4852. [Google Scholar] [CrossRef] [PubMed]
- Mermelstein, M.D.; Ramachandran, S.; Fini, J.M.; Ghalmi, S. SBS gain efficiency measurements and modeling in a 1714 μm2 effective area LP08 higher-order mode optical fiber. Opt. Express 2007, 15, 15952–15963. [Google Scholar] [CrossRef] [PubMed]
- Agrawal, G.P. Nonlinear Fiber Optics, 2nd ed.; Academic Press: San Diego, CA, USA, 1995. [Google Scholar]
- Fleming, J.W. Dispersion in GeO2-SiO2 glasses. Appl. Opt. 1984, 23, 4486–4493. [Google Scholar] [CrossRef] [PubMed]
- Haake, S.J.; Patterson, E.A. The dispersion of birefringence in photoelastic materials. Strain 1993, 29, 3–7. [Google Scholar] [CrossRef]
- Dragic, P.D.; Ballato, J.; Morris, S.; Hawkins, T. Pockels’ coefficients of alumina in aluminosilicate optical fiber. J. Opt. Soc. Am. B 2013, 30, 244–250. [Google Scholar] [CrossRef]
- Jog, E.S.; Krishnan, R.S. Dispersion of the Photoelastic Constants of Fused Silica. Nature 1957, 179, 540–541. [Google Scholar] [CrossRef]
- Jen, C.K.; Neron, C.; Bussiere, J.F.; Abe, K.; Li, L.; Lowe, R.; Kushibiki, J. Acoustic Microscopy of Cladded Optical Fibrers. In Proceedings of the IEEE Ultrasonics Symposium, Montreal, QC, Canada, 3–6 October 1989; pp. 831–835. [Google Scholar]
- Jen, C.-K.; Neron, C.; Shang, A.; Abe, K.; Bonnell, L.; Kushibiki, J. Acoustic Characterization of Silica Glass. J. Am. Ceram. Soc. 1993, 76, 712–716. [Google Scholar] [CrossRef]
- Ohmori, Y.; Okazawi, H.; Hatakeyama, I.; Takata, H. Very Low OH Content P2O5-Doped Silica Fibres. Electron. Lett. 1979, 15, 616–618. [Google Scholar] [CrossRef]
- Niklès, M.; Thevenaz, L.; Robert, P.A. Brillouin Gain Spectrum Characterization in Single-Mode Optical Fibers. J. Lightwave Technol. 1997, 15, 1842–1851. [Google Scholar] [CrossRef]
- Lagakos, N.; Bucaro, J.A.; Hughes, R. Acoustic sensitivity predictions of single-mode optical fibers using Brillouin scattering. Appl. Opt. 1980, 19, 3668–3670. [Google Scholar] [CrossRef] [PubMed]
- Shiraki, K.; Ohashi, M. Sound Velocity Measurement Based on Guided Acoustic-Wave Brillouin Scattering. IEEE Photonics Technol. Lett. 1992, 4, 1177–1180. [Google Scholar] [CrossRef]
- Zou, W.; He, Z.; Hotate, K. Experimental study of Brillouin scattering in fluorine-doped single-mode optical fibers. Opt. Express 2008, 16, 18804–18812. [Google Scholar] [CrossRef] [PubMed]
- Xiao, H.; Ren, G.; Dong, Y.; Li, H.; Xiao, S.; Wu, B.; Jian, S. A numerical analysis of GeO2-doped multi-step index single-mode fiber for stimulated Brillouin scattering. J. Opt. 2018, 20, 065701. [Google Scholar] [CrossRef]
- Xu, Y.; Ren, M.; Lu, Y.; Lu, P.; Lu, P.; Bao, X.; Wang, L.; Messaddeq, Y.; LaRochelle, S. Multi-parameter sensor based on stimulated Brillouin scattering in inverse-parabolic graded-index fiber. Opt. Lett. 2016, 41, 1138–1141. [Google Scholar] [CrossRef] [PubMed]
- Winkelmann, A.; Schott, O. On the elasticity and the tensile and compressive strength of several new glasses in their dependence on the chemical composition. Ann. Phys. Chem. 1894, 51, 697–730. [Google Scholar] [CrossRef]
- Dragic, P.; Ballato, J. 120 Years of Optical Glass Science. Opt. Photonics News 2014, 25, 44–51. [Google Scholar] [CrossRef]
- Dragic, P.D. Brillouin spectroscopy of Nd-Ge co-doped silica fibers. J. Non-Cryst. Solids 2009, 355, 403–413. [Google Scholar] [CrossRef]
- Bloss, F.D. Relationship between Density and Composition in Mol Per Cent for Some Solid Solution Series. Am. Mineral. 1952, 37, 966–981. [Google Scholar]
- Dragic, P.D. The Acoustic Velocity of Ge-Doped Silica Fibers: A Comparison of Two Models. Int. J. Appl. Glass Sci. 2010, 1, 330–337. [Google Scholar] [CrossRef]
- Dragic, P.D. Simplified model for effect of Ge doping on silica fibre acoustic properties. Electron. Lett. 2009, 45, 256–257. [Google Scholar] [CrossRef]
- Dragic, P.; Law, P.-C.; Ballato, J.; Hawkins, T.; Foy, P. Brillouin spectroscopy of YAG-derived optical fibers. Opt. Express 2010, 18, 10055–10067. [Google Scholar] [CrossRef] [PubMed]
- Cavillon, M.; Furtick, J.; Kucera, C.J.; Ryan, C.; Tuggle, M.; Jones, M.; Hawkins, T.W.; Dragic, P.; Ballato, J. Brillouin Properties of a Novel Strontium Aluminosilicate Glass Optical Fiber. J. Lightwave Technol. 2016, 34, 1435–1441. [Google Scholar] [CrossRef]
- Dragic, P.; Kucera, C.; Furtick, J.; Guerrier, J.; Hawkins, T.; Ballato, J. Brillouin spectroscopy of a novel baria-doped silica glass optical fiber. Opt. Express 2013, 21, 10924–10941. [Google Scholar] [CrossRef] [PubMed]
- Dragic, P.D.; Ballato, J.; Morris, S.; Hawkins, T. The Brillouin gain coefficient of Yb-doped aluminosilicate glass optical fibers. Opt. Mater. 2013, 35, 1627–1632. [Google Scholar] [CrossRef]
- Dragic, P.D.; Kucera, C.; Ballato, J.; Litzkendorf, D.; Dellith, J.; Schuster, K. Brillouin scattering properties of lanthano-aluminosilicate optical fiber. Appl. Opt. 2014, 53, 5660–5671. [Google Scholar] [CrossRef] [PubMed]
- Dragic, P.D.; Pamato, M.G.; Iordache, V.; Bass, J.D.; Kucera, C.J.; Jones, M.; Hawkins, T.W.; Ballato, J. Athermal distributed Brillouin sensors utilizing all-glass optical fibers fabricated from rare earth garnets: LuAG. New J. Phys. 2016, 18, 015004. [Google Scholar] [CrossRef]
- Dragic, P.D. Brillouin Gain Reduction Via B2O3 Doping. J. Lightwave Technol. 2011, 29, 967–973. [Google Scholar] [CrossRef]
- Dragic, P.; Ballato, J.; Ballato, A.; Morris, S.; Hawkins, T.; Law, P.-C.; Ghosh, S.; Paul, M.C. Mass density and the Brillouin spectroscopy of aluminosilicate optical fibers. Opt. Mater. Express 2012, 2, 1641–1654. [Google Scholar] [CrossRef]
- Guerette, M.; Ackerson, M.R.; Thomas, J.; Yuan, F.; Watson, E.B.; Walker, D.; Huang, L. Structure and Properties of Silica Glass Densified in Cold Compression and Hot Compression. Sci. Rep. 2015, 5, 15343. [Google Scholar] [CrossRef] [PubMed]
- Burkhard, D.J.M. Elastic Properties of Alkali Silicate Glasses with Iron Oxide: Relation to Glass Structure. Sol. State Commun. 1997, 101, 903–907. [Google Scholar] [CrossRef]
- Jabraoui, H.; Vaills, Y.; Hasnaoui, A.; Badawi, M.; Ouaskit, S. Effect of Sodium Oxide Modifier on Structural and Elastic Properties of Silicate Glass. J. Phys. Chem. B 2016, 120, 13193–13205. [Google Scholar] [CrossRef] [PubMed]
- Trejo, R.; Lara-Curzio, E.; Shyam, A.; Kirkham, M.J.; Garcia-Negron, V.; Wang, Y. Physical and Mechanical Properties of Barium Alkali Silicate Glasses for SOFC Sealing Applications. In. J. Appl. Glass Sci. 2012, 3, 369–379. [Google Scholar] [CrossRef]
- Vasantharani, P.; Neelayathashi alias Vichitra, S. Structural and Elastic Studies of Strontium Doped Manganese Borate Glasses. IOSR J. Appl. Phys. 2017, 9, 44–49. [Google Scholar] [CrossRef]
- Gerlich, D.; Wolf, M.; Yaacov, I.; Nissensen, B. Thermelastic Properties of ULE® Titanium Silicate Glass. J. Non-Cryst. Solids 1976, 21, 243–249. [Google Scholar] [CrossRef]
- Weigel, C.; Le Losq, C.; Vialla, R.; Dupas, C.; Clément, S.; Neuville, D.R.; Rufflé, B. Elastic moduli of XAlSiO4 aluminosilicate glasses: Effects of charge-balancing cations. J. Non-Cryst. Solids 2016, 447, 267–272. [Google Scholar] [CrossRef]
- Huang, Y.Y.; Hunt, J.L.; Stevens, J.R. Determination of elastic constants in isotropic silicate glasses by Brillouin scattering. J. Appl. Phys. 1973, 44, 3589–3592. [Google Scholar] [CrossRef]
- Yablon, A.D. Optical and Mechanical Effects of Frozen-in Stresses and Strains in Optical Fibers. IEEE J. Sel. Top. Quantum Electron. 2004, 10, 300–311. [Google Scholar] [CrossRef]
- Zou, W.; He, Z.; Yablon, A.D.; Hotate, K. Effect of draw-induced residual elastic and inelastic strains on Brillouin frequency shift in optical fibers. In Proceedings of the OFC/NFOEC 2007—2007 Conference on Optical Fiber Communication and the National Fiber Optic Engineers Conference, Anaheim, CA, USA, 25–29 March 2007. Paper OTuC3. [Google Scholar]
- Gulistan, A.; Rahman, M.M.; Ghosh, S.; Rahman, B.M.A. Tailoring light-sound interactions in a single mode fiber for the high-power transmission or sensing applications. In Proceedings of the Third International Conference on Photonic Solutions, Pattaya, Thailand, 5 March 2018; Volume 10714, p. 1071403. [Google Scholar]
- Ward, B.; Spring, J. Finite element analysis of Brillouin gain in SBS-suppressing optical fibers with non-uniform acoustic velocity profiles. Opt. Express 2009, 17, 15685–15699. [Google Scholar] [CrossRef] [PubMed]
- Sriratanavaree, S.; Azizur Rahman, B.M.; Leung, D.M.H.; Kejalakshmy, N.; Grattan, K.T.V. Full-Vectorial Finite-Element Analysis of Acoustic Modes in Silica Waveguides. IEEE J. Quantum Electron. 2014, 50, 1006–1013. [Google Scholar] [CrossRef]
- Zou, W.; He, Z.; Hotate, K. Two-Dimensional Finite-Element Modal Analysis of Brillouin Gain Spectra in Optical Fibers. IEEE Photonics Technol. Lett. 2006, 18, 2487–2489. [Google Scholar] [CrossRef]
- Mamdem, Y.S.; Phéron, X.; Taillade, F.; Jaoüen, Y.; Gabet, R.; Lanticq, V.; Moreau, G.; Boukenter, A.; Ouerdane, Y.; Lesoille, S.; et al. Two-dimensional FEM Analysis of Brillouin Gain Spectra in Acoustic Guiding and Antiguiding Single Mode Optical Fibers. In Proceedings of the COMSOL Conference, Paris, France, 17–19 November 2010. [Google Scholar]
- Zervas, M.N.; Codemard, C.A. High Power Fiber Lasers: A Review. IEEE J. Sel. Top. Quantum Electron. 2014, 20, 0904123. [Google Scholar] [CrossRef]
- Dragic, P.D.; Ward, B.G. Accurate Modeling of the Intrinsic Brillouin Linewidth via Finite-Element Analysis. IEEE Photonics Technol. Lett. 2010, 22, 1698–1700. [Google Scholar] [CrossRef]
- Law, P.-C.; Liu, Y.-S.; Croteau, A.; Dragic, P. Acoustic coefficients of P2O5-doped silica fiber: Acoustic velocity, acoustic attenuation, and thermo-acoustic coefficient. Opt. Mater. Express 2011, 1, 686–699. [Google Scholar] [CrossRef]
- Ballato, J.; Dragic, P. Rethinking Optical Fiber: New Demands, Old Glasses. J. Am. Ceram. Soc. 2013, 96, 2675–2692. [Google Scholar] [CrossRef]
- Anan’ev, A.V.; Bogdanov, V.N.; Champagnon, B.; Ferrari, M.; Karapetyan, G.O.; Maksimov, L.V.; Smerdin, S.N.; Solovyev, V.A. Origin of Rayleigh scattering and anomaly of elastic properties in vitreous and molten GeO2. J. Non-Cryst. Solids 2008, 354, 3049–3058. [Google Scholar] [CrossRef]
- Law, P.-C.; Croteau, A.; Dragic, P.D. Acoustic coefficients of P2O5-doped silica fiber: The strain-optic and strain-acoustic coefficients. Opt. Mater. Express 2012, 2, 391–404. [Google Scholar] [CrossRef]
- Ballato, J.; Cavillon, M.; Dragic, P. A unified materials approach to mitigating optical nonlinearities in optical fiber. I. Thermodynamics of optical scattering. Int. J. Appl. Glass Sci. 2018, 9, 263–277. [Google Scholar] [CrossRef]
- Dragic, P.D.; Cavillon, M.; Ballato, A.; Ballato, J. A unified materials approach to mitigating optical nonlinearities in optical fiber. II. A. Material additivity models and basic glass properties. Int. J. Appl. Glass Sci. 2018, 9, 278–287. [Google Scholar] [CrossRef]
- Cavillon, M.; Kucera, C.; Hawkins, T.; Dawson, J.; Dragic, P.D.; Ballato, J. A unified materials approach to mitigating optical nonlinearities in optical fiber. III. Canonical examples and materials road map. Int. J. Appl. Glass Sci. 2018, 9, 447–470. [Google Scholar] [CrossRef]
- Krischer, C. Optical Measurements of Ultrasonic Attenuation and Reflection Losses in Fused Silica. J. Acoust. Soc. Am. 1970, 48, 1086–1092. [Google Scholar] [CrossRef]
- Law, P.-C.; Dragic, P.D. Wavelength dependence of the Brillouin spectral width of boron doped germanosilicate optical fibers. Opt. Express 2010, 18, 18852–18865. [Google Scholar] [CrossRef] [PubMed]
- Dragic, P.; Hawkins, T.; Foy, P.; Morris, S.; Ballato, J. Sapphire-derived all-glass optical fibres. Nat. Photonics 2012, 6, 627–633. [Google Scholar] [CrossRef]
- Prod’homme, L. A new approach to the thermal change in the refractive index of glasses. Phys. Chem. Glasses 1960, 1, 119–122. [Google Scholar]
- Kishida, K.; Yamauchi, Y.; Guzik, A. Study of Optical Fibers Strain-Temperature Sensitivities Using Hybrid Brillouin-Rayleigh System. Photonics Sens. 2014, 4, 1–11. [Google Scholar] [CrossRef]
- Lu, X.; Soto, M.A.; Thévenaz, L. Impact of the Fiber Coating on the Temperature Response of Distributed Optical Fiber Sensors at Cryogenic Ranges. J. Lighwave Technol. 2018, 36, 961–967. [Google Scholar] [CrossRef]
- Gu, H.; Dong, H.; Zhang, G.; He, J.; Pan, H. Effects of Polymer Coatings on Temperature Sensitivity of Brillouin Frequency Shift Within Double-Coated Fiber. IEEE Sens. J. 2013, 13, 864–869. [Google Scholar] [CrossRef]
- Peselnick, L.; Meister, R.; Wilson, W.H. Pressure Derivatives of Elastic Moduli of Fused Quartz to 10 kb. J. Phys. Chem. Solids 1967, 28, 635–639. [Google Scholar] [CrossRef]
- Gerlich, D.; Kennedy, G.C. Second Pressure Derivatives of the Elastic Moduli of Fused Quartz. J. Phys. Chem. Solids 1978, 39, 1189–1191. [Google Scholar] [CrossRef]
- Tielbürger, D.; Merz, R.; Ehrenƒels, R.; Hunklinger, S. Thermally Activated Relaxation Processes in Vitreous Silica: An Investigation by Brillouin Scattering at High Pressures. Phys. Rev. B 1992, 45, 2750–2760. [Google Scholar] [CrossRef]
- Pine, A.S. Brillouin Scattering Study of Acoustic Attenuation in Fused Quartz. Phys. Rev. 1969, 185, 1187–1193. [Google Scholar] [CrossRef]
- Masnik, J.E.; Kieffer, J.; Bass, J.D. The complex mechanical modulus as a structural probe: The case of alkali borate liquids and glasses. J. Chem. Phys. 1995, 103, 9907–9917. [Google Scholar] [CrossRef]
- Hertling, J.; Baeβler, S.; Rau, S.; Kasper, G.; Hunklinger, S. Internal friction and hypersonic velocity in vitreous germania under high pressure. J. Non-Cryst. Sol. 1998, 226, 129–137. [Google Scholar] [CrossRef]
- Parker, T.R.; Farhadiroushan, M.; Handerek, V.A.; Rogers, A.J. A Fully Distributed Simultaneous Strain and Temperature Sensor using Spontaneous Brillouin Backscatter. IEEE Photonics Technol. Lett. 1997, 9, 979–981. [Google Scholar] [CrossRef]
- Kee, H.H.; Lees, G.P.; Newson, T.P. All-fiber system for simultaneous interrogation of distributed strain and temperature sensing by spontaneous Brillouin scattering. Opt. Lett. 2000, 25, 695–697. [Google Scholar] [CrossRef] [PubMed]
- Maughan, S.M.; Kee, H.H.; Newson, T.P. Simultaneous distributed fibre temperature and strain sensor using microwave coherent detection of spontaneous Brillouin backscatter. Meas. Sci. Technol. 2001, 12, 834–842. [Google Scholar] [CrossRef]
- Bao, X.; Webb, D.J.; Jackson, D.A. Combined distributed temperature and strain sensor based on Brillouin loss in an optical fiber. Opt. Lett. 1994, 19, 141–143. [Google Scholar] [CrossRef] [PubMed]
- Zou, W.; He, Z.; Hotate, K. Complete discrimination of strain and temperature using Brillouin frequency shift and birefringence in a polarization-maintaining fiber. Opt. Express 2009, 17, 1248–1255. [Google Scholar] [CrossRef] [PubMed]
- Zou, W.; He, Z.; Hotate, K. Demonstration of Brillouin Distributed Discrimination of Strain and Temperature Using a Polarization-Maintaining Optical Fiber. IEEE Photonics Technol. Lett. 2010, 22, 526–528. [Google Scholar] [CrossRef]
- Dong, Y.; Chen, L.; Bao, X. High-Spatial-Resolution Time-Domain Simultaneous Strain and Temperature Sensor Using Brillouin Scattering and Birefringence in a Polarization-Maintaining Fiber. IEEE Photonics Technol. Lett. 2010, 22, 1364–1366. [Google Scholar] [CrossRef]
- Ding, M.; Mizuno, Y.; Nakamura, K. Discriminative strain and temperature measurement using Brillouin scattering and fluorescence in erbium-doped optical fiber. Opt. Express 2014, 22, 24706–24712. [Google Scholar] [CrossRef] [PubMed]
- Li, M.-J.; Li, S.; Derick, J.A.; Stone, J.S.; Chow, B.C.; Bennett, K.W.; Sutherlin, D.M. Dual Core Optical Fiber for Distributed Brillouin Fiber Sensors. In Proceedings of the Asia Communications and Photonics Conference, Shanghai, China, 11–14 November 2014. [Google Scholar]
- Zaghloul, M.A.S.; Wang, M.; Milione, G.; Li, M.-J.; Li, S.; Huang, Y.-K.; Wang, T.; Chen, K.P. Discrimination of Temperature and Strain in Brillouin Optical Time Domain Analysis Using a Multicore Optical Fiber. Sensors 2018, 18, 1176. [Google Scholar] [CrossRef] [PubMed]
- Mizuno, Y.; Hayashi, N.; Tanaka, H.; Wada, Y.; Nakamura, K. Brillouin scattering in multi-core optical fibers for sensing applications. Sci. Rep. 2015, 5, 11388. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Z.; Soto, M.A.; Tang, M.; Thévenaz, L. Distributed shape sensing using Brillouin scattering in multi-core fibers. Opt. Express 2016, 24, 25211–25223. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Z.; Soto, M.A.; Tang, M.; Thévenaz, L. Demonstration of distributed shape sensing based on Brillouin scattering in multi-core fibers. Proc. SPIE 2017, 10323, 1032393. [Google Scholar]
- Li, A.; Wang, Y.; Fang, J.; Li, M.-J.; Kim, B.Y.; Shieh, W. Few-mode fiber multi-parameter sensor with distributed temperature and strain discrimination. Opt. Lett. 2015, 40, 1488–1491. [Google Scholar] [CrossRef] [PubMed]
- Weng, Y.; Ip, E.; Pan, Z.; Wang, T. Single-end simultaneous temperature and strain sensing techniques based on Brillouin optical time domain reflectometry in few-mode fibers. Opt. Express 2015, 23, 9024–9039. [Google Scholar] [CrossRef] [PubMed]
- Pradhan, P.; Sengupta, D.; Wang, L.; Tremblay, C.; LaRochelle, S.; Ung, B. The Brillouin gain of vector modes in few-mode fiber. Sci. Rep. 2017, 7, 1552. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.-J.; Gao, H.-L.; Fu, X.-H.; Tian, Y.-S. Characterization of Brillouin scattering in a few-mode fiber. Acta Phys. Sin. 2017, 66, 024207. [Google Scholar]
- Xu, Y.; Ren, M.; Lu, Y.; Lu, P.; Bao, X.; LaRochelle, S. Multi-parameter sensing based on the stimulated Brillouin scattering of higher-order acoustic modes in OAM fiber. Proc. SPIE 2015, 9634, 96340L. [Google Scholar]
- Wu, H.; Tang, M.; Wang, M.; Zhao, C.; Zhao, Z.; Wang, R.; Liao, R.; Fu, S.; Yang, C.; Tong, W.; et al. Few-mode optical fiber based simultaneously distributed curvature and temperature sensing. Opt. Express 2017, 25, 12722–12732. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.C.; Chiang, P.W.; Chi, S. Utilization of a Dispersion-Shifted Fiber for Simultaneous Measurement of Distributed Strain and Temperature Through Brillouin Frequency Shift. IEEE Photonics Technol. Lett. 2001, 12, 1094–1096. [Google Scholar] [CrossRef]
- Liu, X.; Bao, X. Brillouin Spectrum in LEAF and Simultaneous Temperature and Strain Measurement. J. Lightwave Technol. 2012, 30, 1053–1059. [Google Scholar] [CrossRef]
- Li, M.-J.; Li, S.; Stone, J.S. Novel Optical Fibers for Distributed Sensor Applications. Proc. SPIE 2017, 10323, 103231C. [Google Scholar]
- Zou, W.; He, Z.; Kishi, M.; Hotate, K. Stimulated Brillouin scattering and its dependences on strain and temperature in a high-delta optical fiber with F-doped depressed inner cladding. Opt. Lett. 2007, 32, 600–602. [Google Scholar] [CrossRef] [PubMed]
- Zou, W.; He, Z.; Hotate, K. Acoustic modal analysis and control in w-shaped triple-layer optical fibers with highly-germanium-doped core and F-doped cladding. Opt. Express 2008, 16, 10006–10017. [Google Scholar] [CrossRef] [PubMed]
- Dragic, P.D. Distributed temperature sensing via Brillouin-tailored optical fiber. Proc. SPIE 2009, 7316, 731605. [Google Scholar]
- Dragic, P.; Cavillon, M.; Ballato, J. On the thermo-optic coefficient of P2O5 in SiO2. Opt. Mater. Express 2017, 7, 3654–3661. [Google Scholar] [CrossRef]
- Li, H.-L.; Zhang, W.; Huang, Y.-D.; Peng, J.-D. Acoustical longitudinal mode coupling in w-shaped Al/Ge Co-doped fibre. Chin. Phys. B 2011, 20, 104211. [Google Scholar] [CrossRef]
- Xiao, S.; Dong, Y.; Xiao, H.; Ren, G.; Jen, S. SMFs with a Ge/F Co-Doped Inner Core for SBS-Based Discriminative Sensing of Temperature and Strain. IEEE Sens. J. 2018, 18, 1087–1093. [Google Scholar] [CrossRef]
- Hotate, K.; Zou, W.; Yamashita, R.K.; He, Z. Distributed Discrimination of Strain and Temperature Based on Brillouin Dynamic Grating in an Optical Fiber. Photonics Sens. 2013, 3, 332–344. [Google Scholar] [CrossRef]
- Lu, Y.; Qin, Z.; Lu, P.; Zhou, D.; Chen, L.; Bao, X. Distributed Strain and Temperature Measurement by Brillouin Beat Spectrum. IEEE Photonics Technol. Lett. 2013, 25, 1050–1053. [Google Scholar] [CrossRef]
- Shiraki, K.; Ohashi, M.; Tateda, M. Performance of Strain-Free Stimulated Brillouin Scattering Suppression Fiber. J. Lightwave Technol. 1996, 14, 549–554. [Google Scholar] [CrossRef]
- Ohashi, M.; Tateda, M. Design of Strain-Free-Fiber with Nonuniform Dopant Concentration for Stimulated Brillouin Scattering Suppression. J. Lightwave Technol. 1993, 11, 1941–1945. [Google Scholar] [CrossRef]
- Evert, A.; James, A.; Hawkins, T.; Foy, P.; Stolen, R.; Dragic, P.; Dong, L.; Rice, R.; Ballato, J. Longitudinally-graded optical fibers. Opt. Express 2012, 20, 17393–17401. [Google Scholar] [CrossRef] [PubMed]
- Dragic, P.D.; Mangognia, A.; Ballato, J. Chirped fiber Brillouin frequency-domain distributed sensing. Opt. Eng. 2014, 53, 056117. [Google Scholar] [CrossRef]
- Dragic, P.D.; Ryan, C.; Kucera, C.J.; Cavillon, M.; Tuggle, M.; Jones, M.; Hawkins, T.W.; Yablon, A.D.; Stolen, R.; Ballato, J. Lithium Aluminosilicate Optical Fiber for Brillouin-Based Distributed Sensing. In Proceedings of the Advanced Photonics Congress, Vancouver, BC, Canada, 18–20 July 2016. Paper SeM2D. [Google Scholar]
- Mizuno, Y.; Nakamura, K. Brillouin Scattering in Polymer Optical Fibers: Fundamental Properties and Potential Use in Sensors. Polymers 2011, 3, 886–898. [Google Scholar] [CrossRef]
- Dragic, P.D.; Martin, S.W.; Ballato, A.; Ballato, J. On the Anomalously Strong Dependence of the Acoustic Velocity of Alumina on Temperature in Aluminosilicate Glass Optical Fibers—Part I: Material Modeling and Experimental Validation. Int. J. Appl. Glass Sci. 2016, 7, 3–10. [Google Scholar] [CrossRef]
- Ballato, A.; Dragic, P.D.; Martin, S.W.; Ballato, J. On the Anomalously Strong Dependence of the Acoustic Velocity of Alumina on Temperature in Aluminosilicate Glass Optical Fibers—Part II: Acoustic Properties of Alumina and Silica Polymorphs, and Approximations of the Glassy State. Int. J. Appl. Glass Sci. 2016, 7, 11–26. [Google Scholar] [CrossRef]
- Cavillon, M.; Dragic, P.D.; Ballato, J. Additivity of the coefficient of thermal expansion in silicate optical fibers. Opt. Lett. 2017, 42, 3650–3653. [Google Scholar] [CrossRef] [PubMed]
- Tao, G.; Abouraddy, A.F.; Stolyarov, A.M. Multimaterial Fibers. Int. J. Appl. Glass Sci. 2012, 3, 349–368. [Google Scholar] [CrossRef]
- Ballato, J.; Ebendorff-Heidepriem, H.; Zhao, J.; Petit, L.; Troles, J. Glass and Process Development for the Next Generation of Optical Fibers. Fibers 2017, 5, 11. [Google Scholar] [CrossRef]
- Morris, S.; Ballato, J. Molten-core fabrication of novel optical fibers. Am. Ceram. Soc. Bull. 2013, 92, 24–29. [Google Scholar]
- Wu, F.; Machewirth, D.; Snitzer, E.; Sigel, G.H. An efficient single-mode Nd3+ fiber laser prepared by the sol-gel method. J. Mater. Res. 1994, 9, 2703–2705. [Google Scholar] [CrossRef]
- Halder, A.; Bhadra, S.K.; Bysakh, S.; Paul, M.C.; Das, S. Strong and Broad Visible Emission of Bismuth Doped Nano-Phase Separated Ytteria-alumina-silica Optical Fibers. Curr. Nanosci. 2016, 12, 309–315. [Google Scholar] [CrossRef]
- Schuster, K.; Unger, S.; Aichele, C.; Lindner, F.; Grimm, S.; Litzkendorf, D.; Kobelke, J.; Bierlich, J.; Wondraczek, K.; Bartelt, H. Material and technology trends in fiber optics. Adv. Opt. Technol. 2014, 3, 447–468. [Google Scholar] [CrossRef]
- Geng, J.; Staines, S.; Blake, M.; Jiang, S. Distributed fiber temperature and strain sensor using coherent radio-frequency detection of spontaneous Brillouin scattering. Appl. Opt. 2007, 46, 5928–5932. [Google Scholar] [CrossRef] [PubMed]
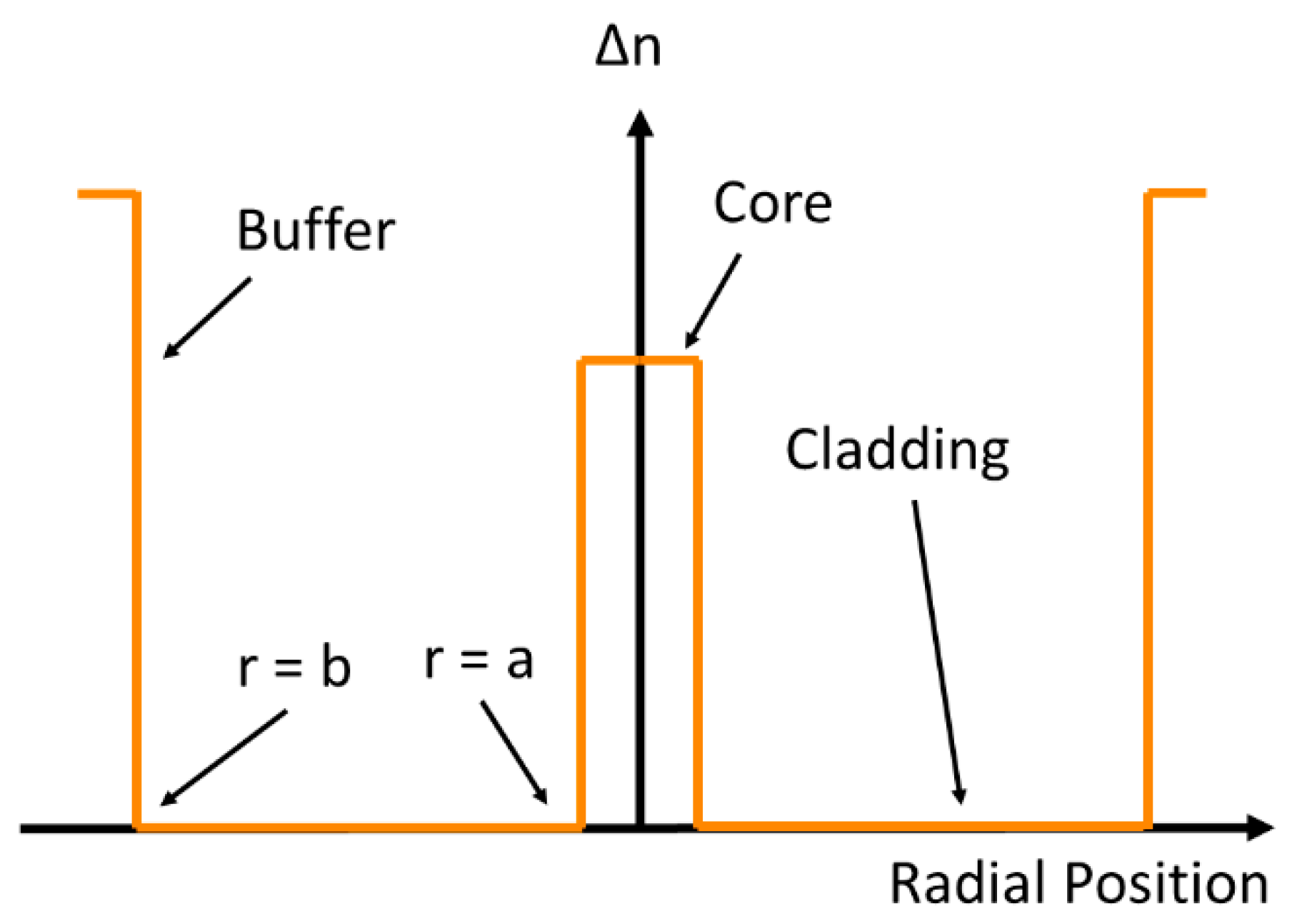
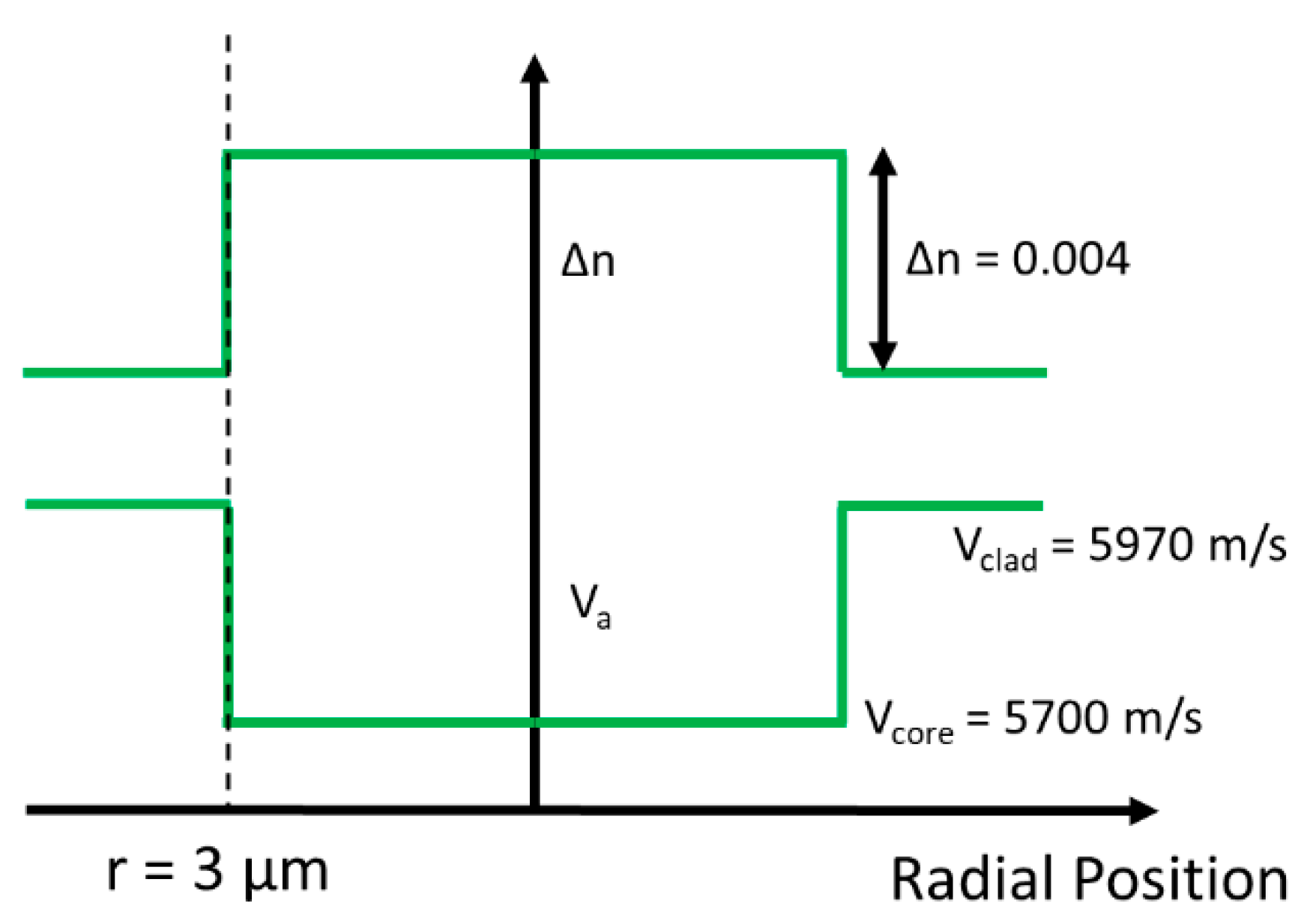
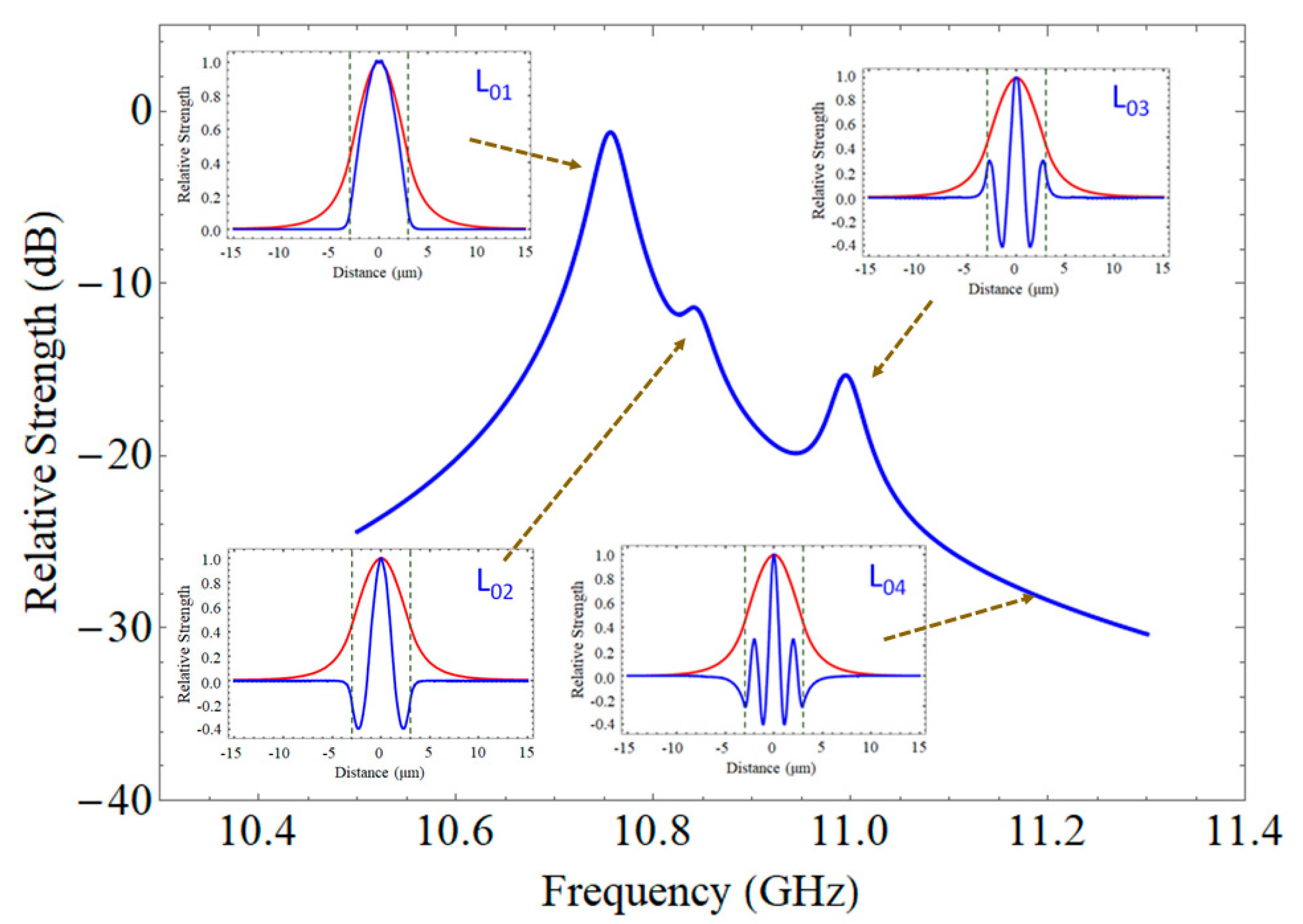
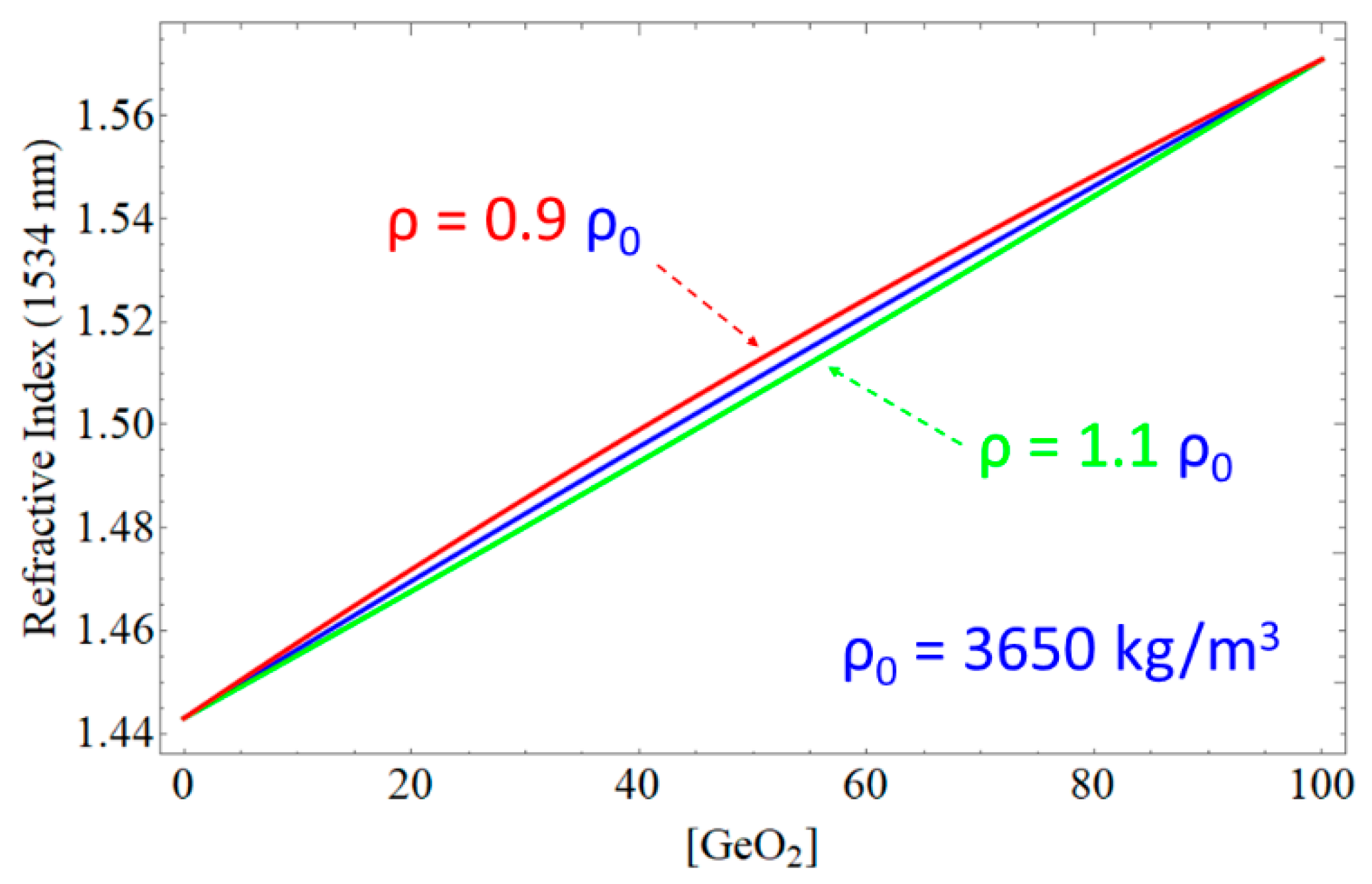

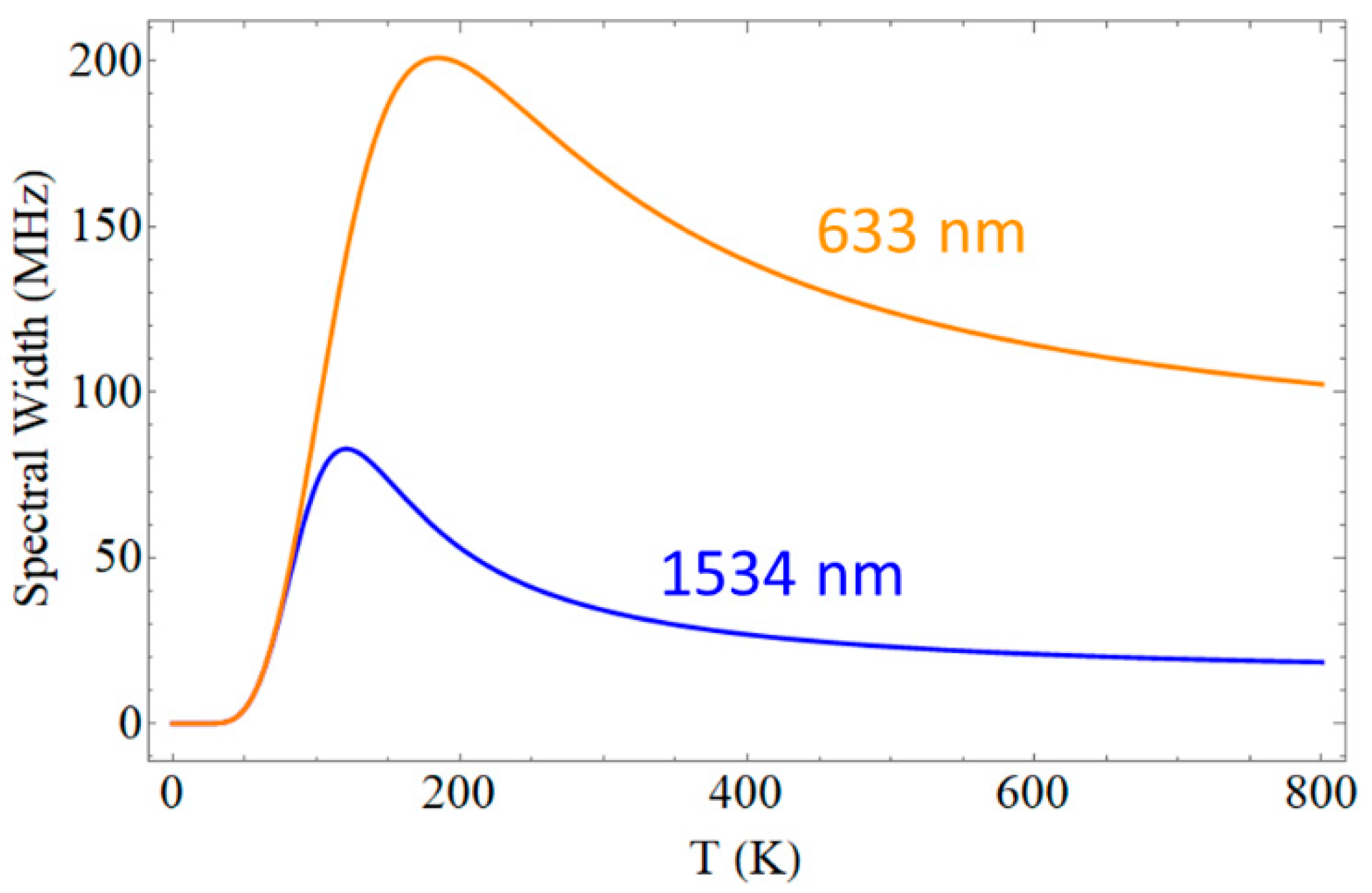
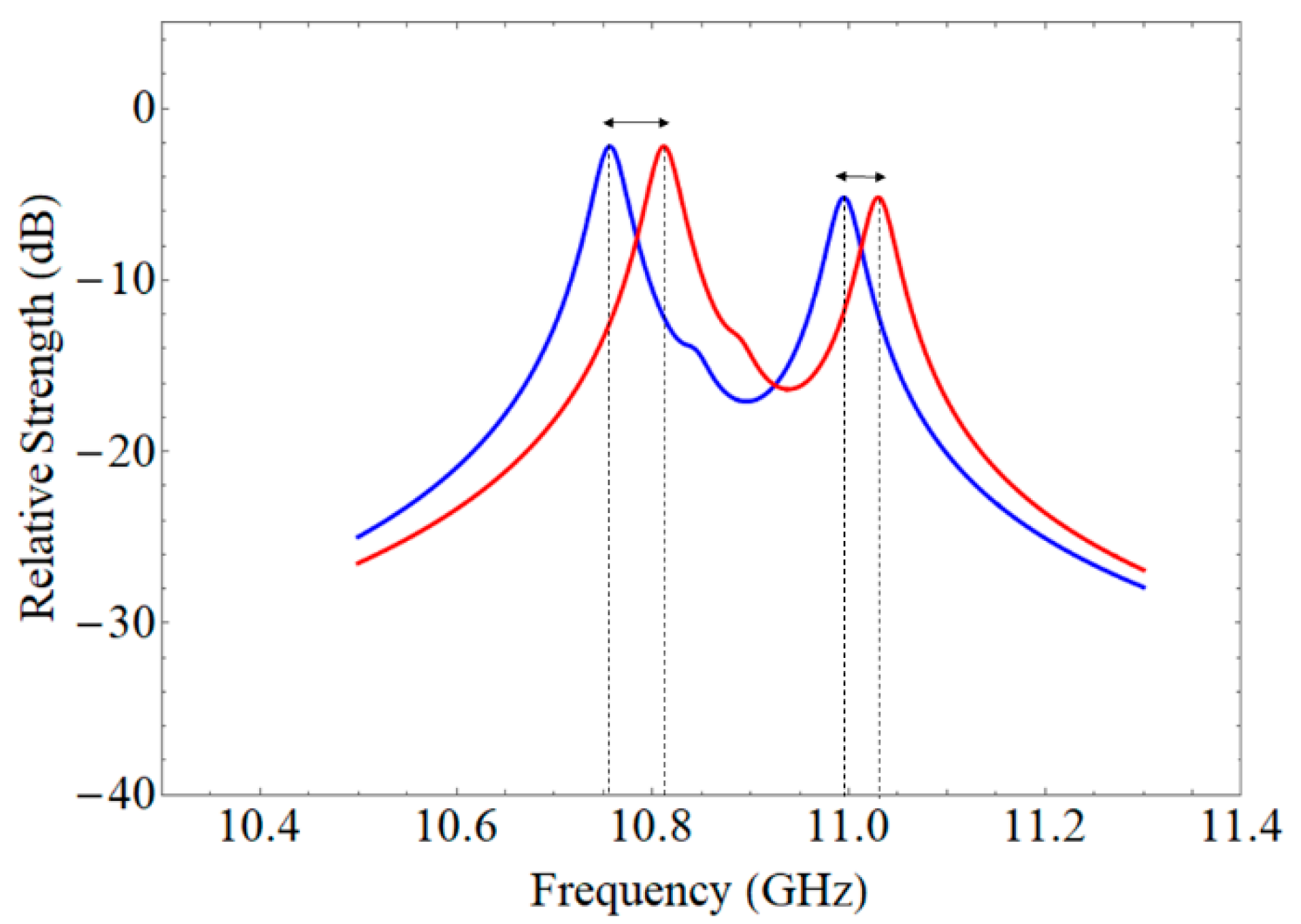
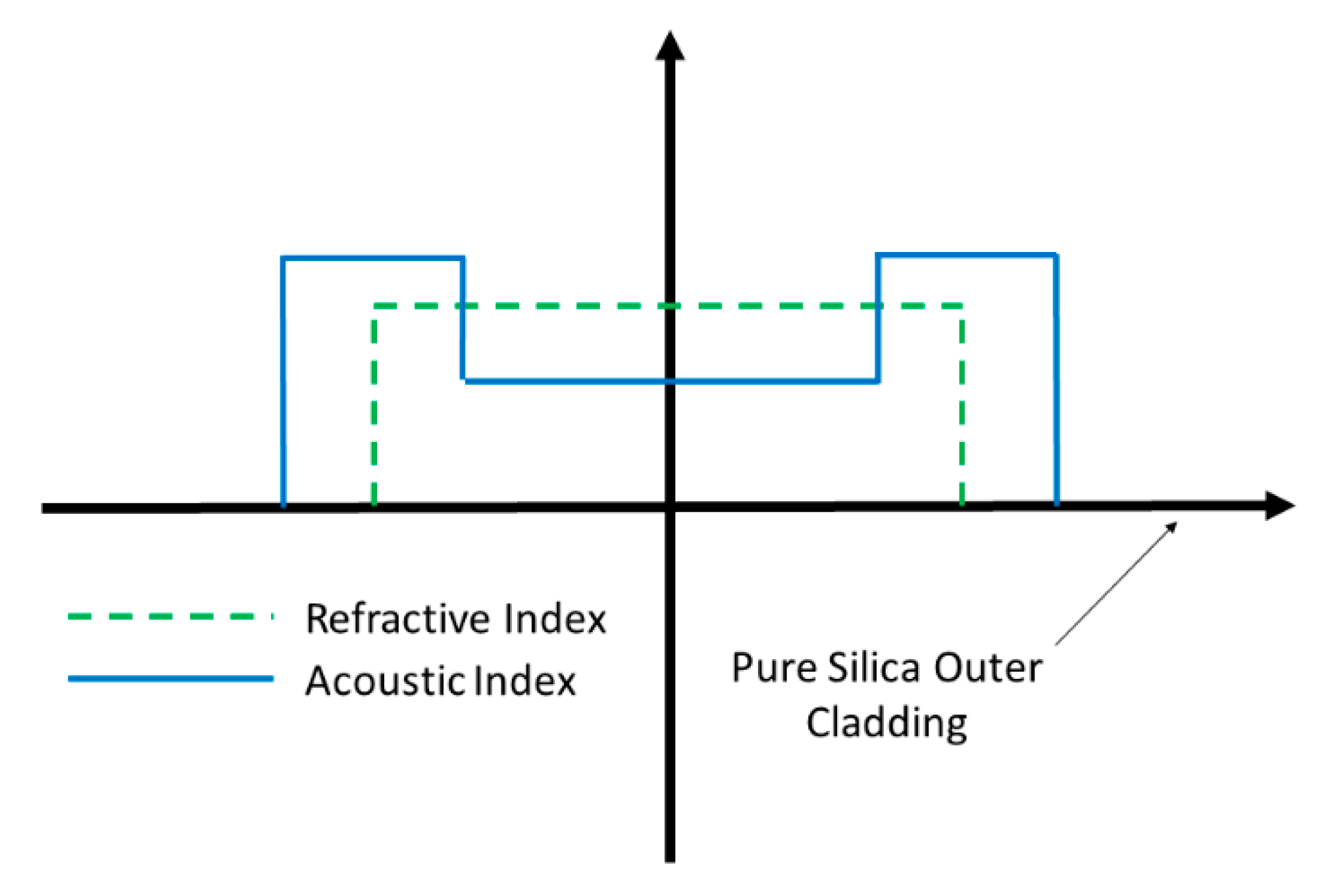
| GeO2 | P2O5 | TiO2 | B2O3 | F | Al2O3 | Y2O3 | RE2O3 | |
|---|---|---|---|---|---|---|---|---|
| no | ↑ | ↑ | ↑ | ↓ | ↓ | ↑ | ↑ | ↑ |
| na | ↑ | ↑ | ↑ | ↑ | ↑ | ↓ | ↓ | ↑ |
| Dopant | Δn (%/wt%) | ΔVS (%/wt%) | ΔVL (%/wt%) |
|---|---|---|---|
| GeO2 | +0.056 | −0.49 | −0.47 |
| P2O5 | +0.020 | −0.41 | −0.31 |
| F | −0.31 | −3.1 | −3.6 |
| TiO2 | +0.23 | −0.45 | −0.59 |
| Al2O3 | +0.063 | +0.21 | +0.42 |
| B2O3 | −0.033 | −1.18 | −1.23 |
| n | VL (m/s) | ρ (kg/m3) | p12 | ΔνB (MHz @ 11 GHz) | |
|---|---|---|---|---|---|
| SiO2 | 1.444 | 5970 | 2204 | 0.252 | 17.0 |
| P2O5 | 1.488 | 3936 | 2390 | 0.226 | 176.8 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dragic, P.; Ballato, J. A Brief Review of Specialty Optical Fibers for Brillouin-Scattering-Based Distributed Sensors. Appl. Sci. 2018, 8, 1996. https://doi.org/10.3390/app8101996
Dragic P, Ballato J. A Brief Review of Specialty Optical Fibers for Brillouin-Scattering-Based Distributed Sensors. Applied Sciences. 2018; 8(10):1996. https://doi.org/10.3390/app8101996
Chicago/Turabian StyleDragic, Peter, and John Ballato. 2018. "A Brief Review of Specialty Optical Fibers for Brillouin-Scattering-Based Distributed Sensors" Applied Sciences 8, no. 10: 1996. https://doi.org/10.3390/app8101996
APA StyleDragic, P., & Ballato, J. (2018). A Brief Review of Specialty Optical Fibers for Brillouin-Scattering-Based Distributed Sensors. Applied Sciences, 8(10), 1996. https://doi.org/10.3390/app8101996




