Effective Implementation of Edge-Preserving Filtering on CPU Microarchitectures
Abstract
1. Introduction
2. Edge-Preserving Filters
3. Floating Point Numbers and Denormalized Numbers in IEEE Standard 754
4. CPU Microarchitectures and SIMD Instruction Sets
5. Proposed Methods for the Prevention of Denormalized Numbers
6. Effective Implementation of Edge-Preserving Filtering
- RCSC: range computing spatial computing; range and spatial kernels are directly and separately computed.
- MC: merged computing; range and spatial kernels are merged and directly computed.
- RCSL: range computing spatial LUT; the range kernel is directly computed, and LUTs are used for the spatial kernel.
- RLSC: range LUT spatial computing; LUTs are used for the range kernel, and the spatial kernel is directly computed.
- RLSL: range LUT spatial LUT; LUTs are used for both range and spatial kernels.
- ML: merged LUT; LUTs are used for the merged range and spatial kernels;
- RqLSL, RLSqL: range (quantized) LUT spatial (quantized) LUT; LUTs are quantized for each range and spatial LUT in RLSL
- MqL: merged quantized LUT; range and spatial kernels are merged, and then, the LUTs are quantized.
- RC: range computing; the range kernel is directly computed.
- RL: range LUT; LUTs are used for the range kernel.
- RqL: range quantized LUT; quantized LUTs are used for the range kernel.
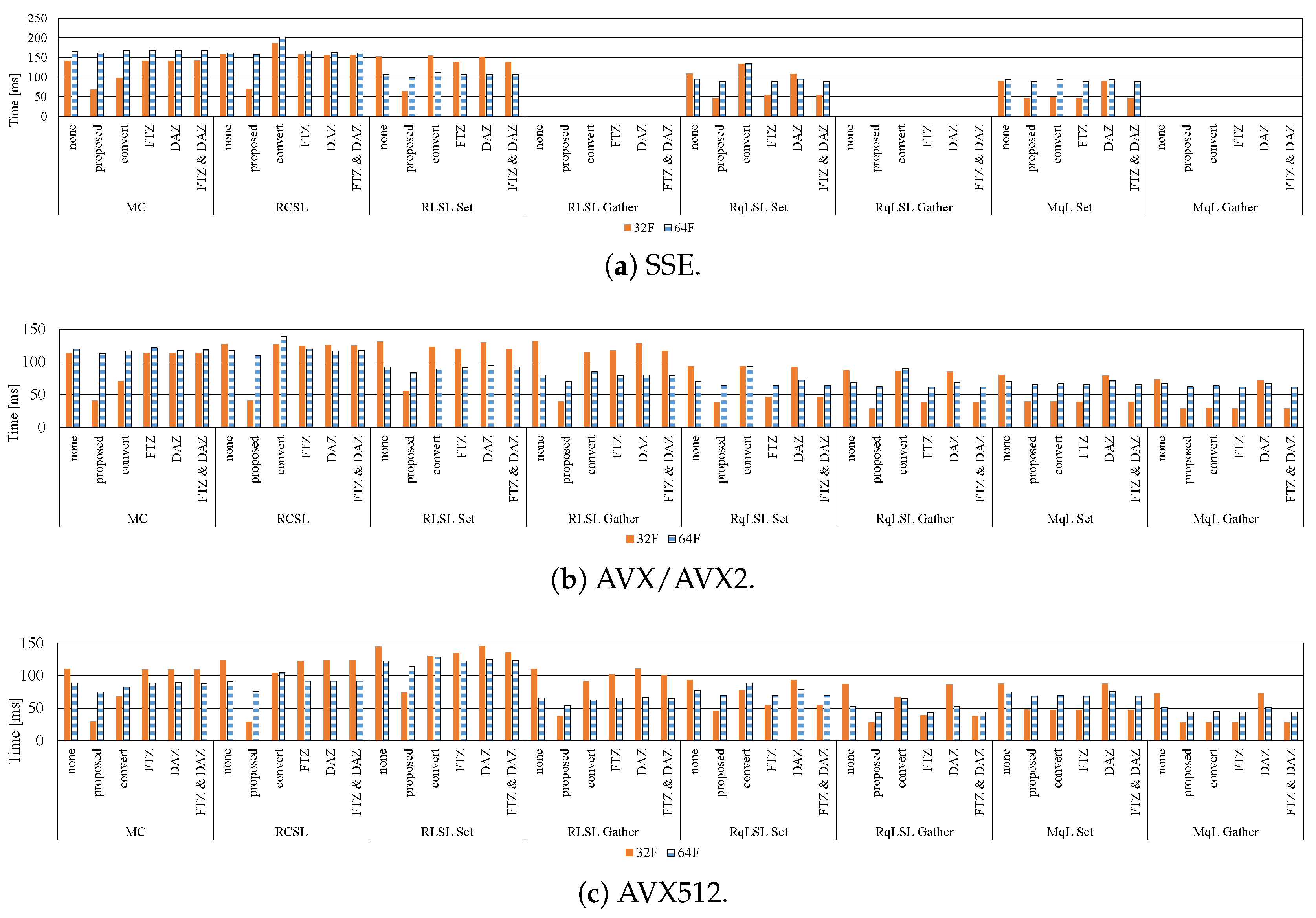
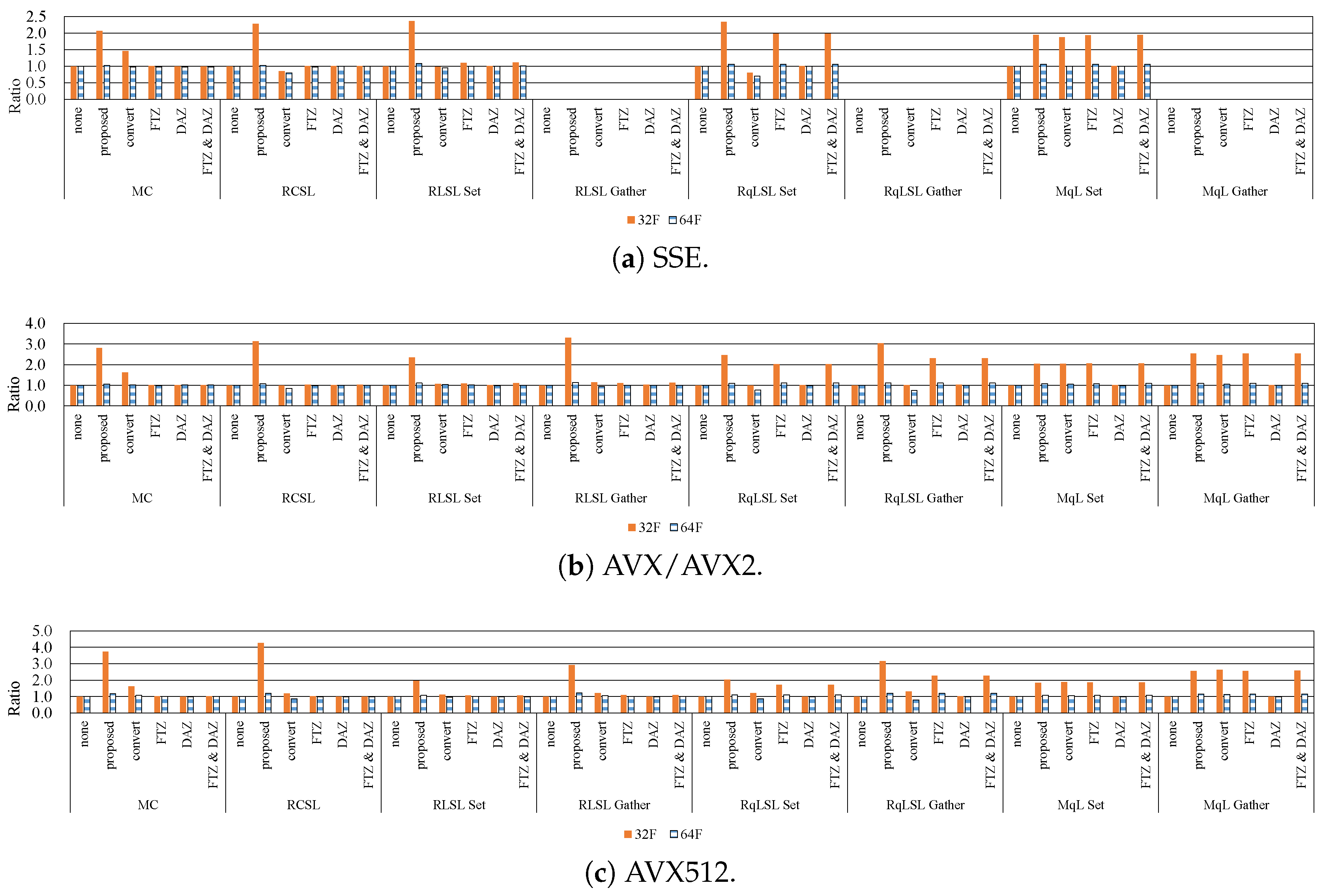
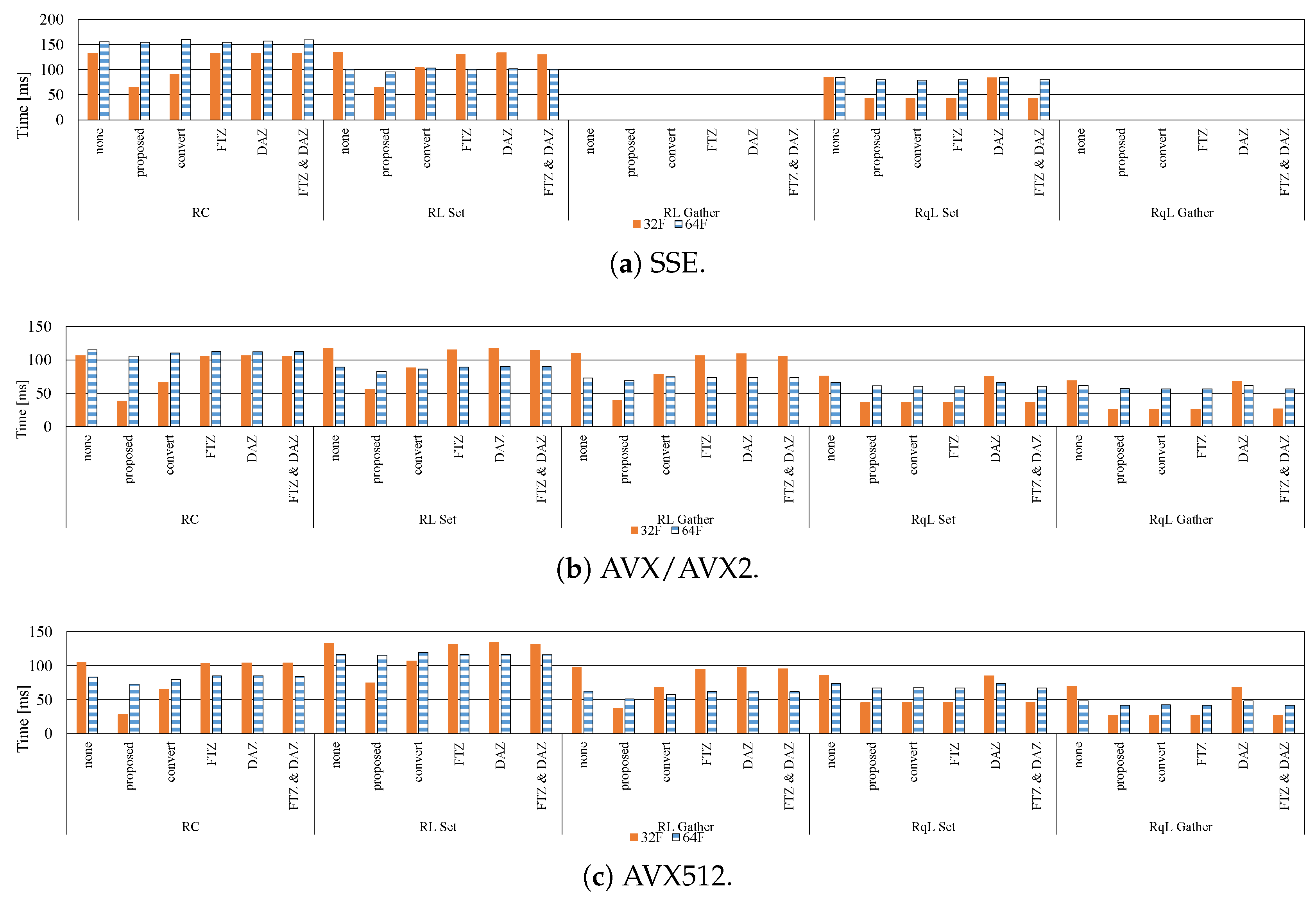
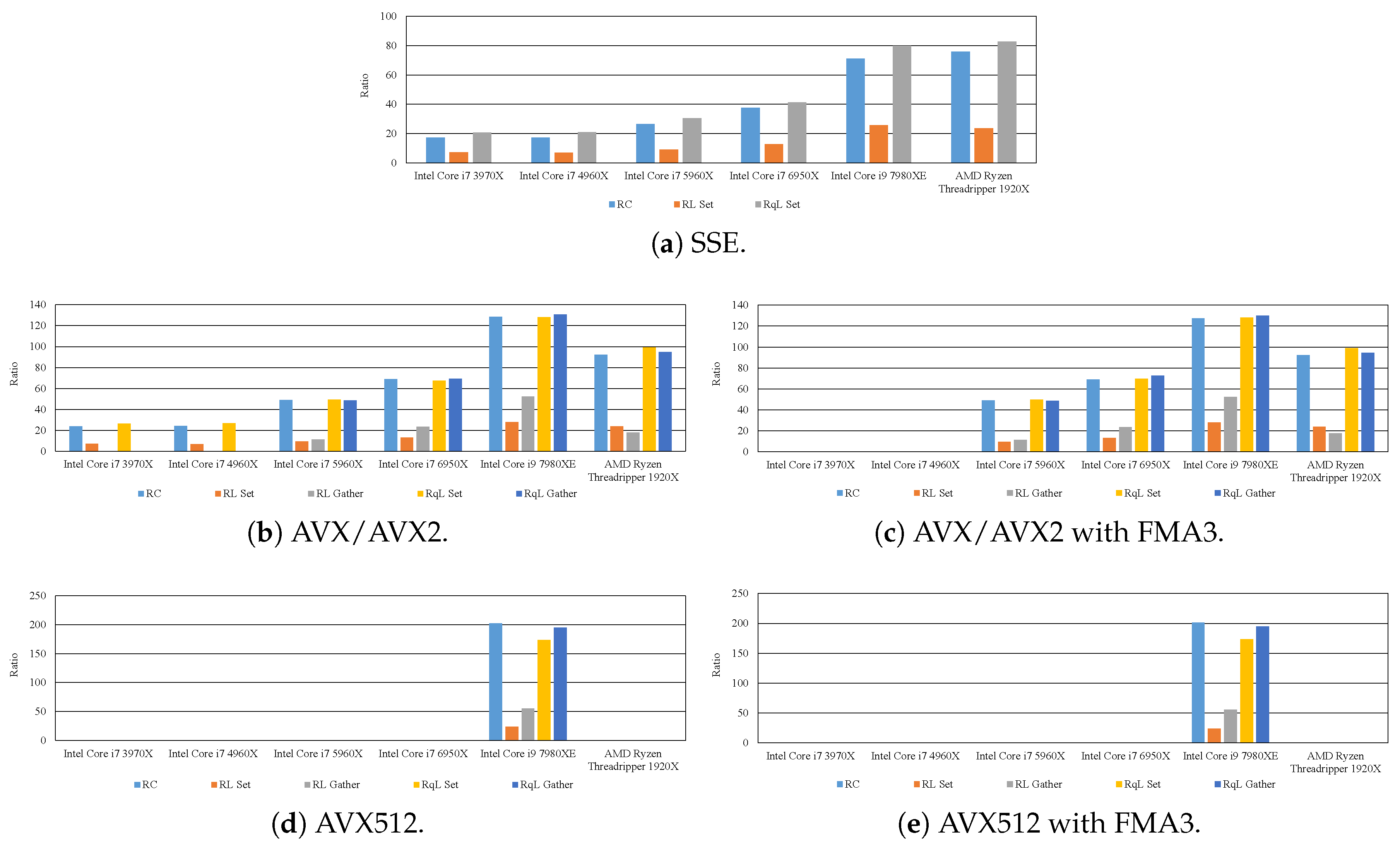
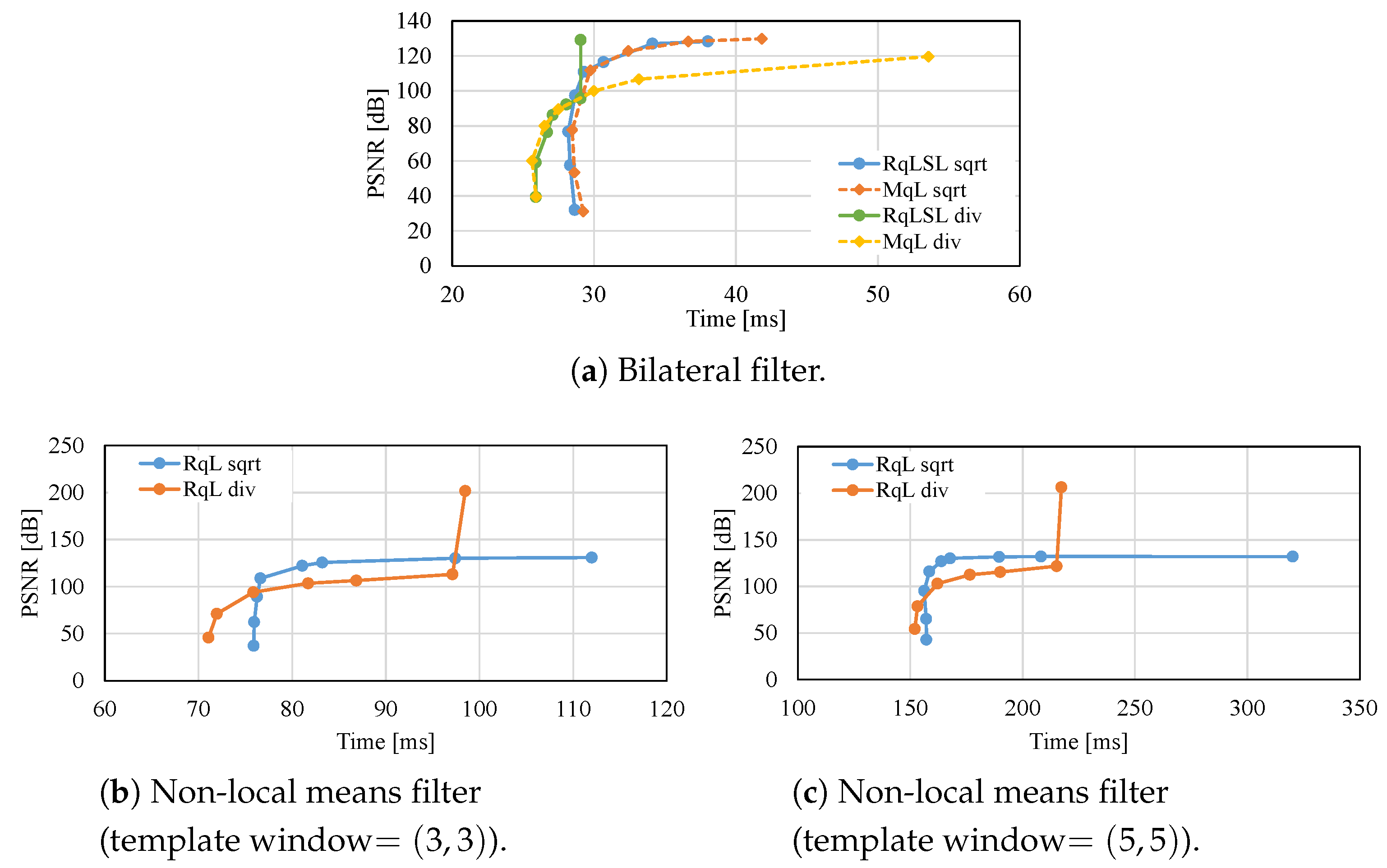
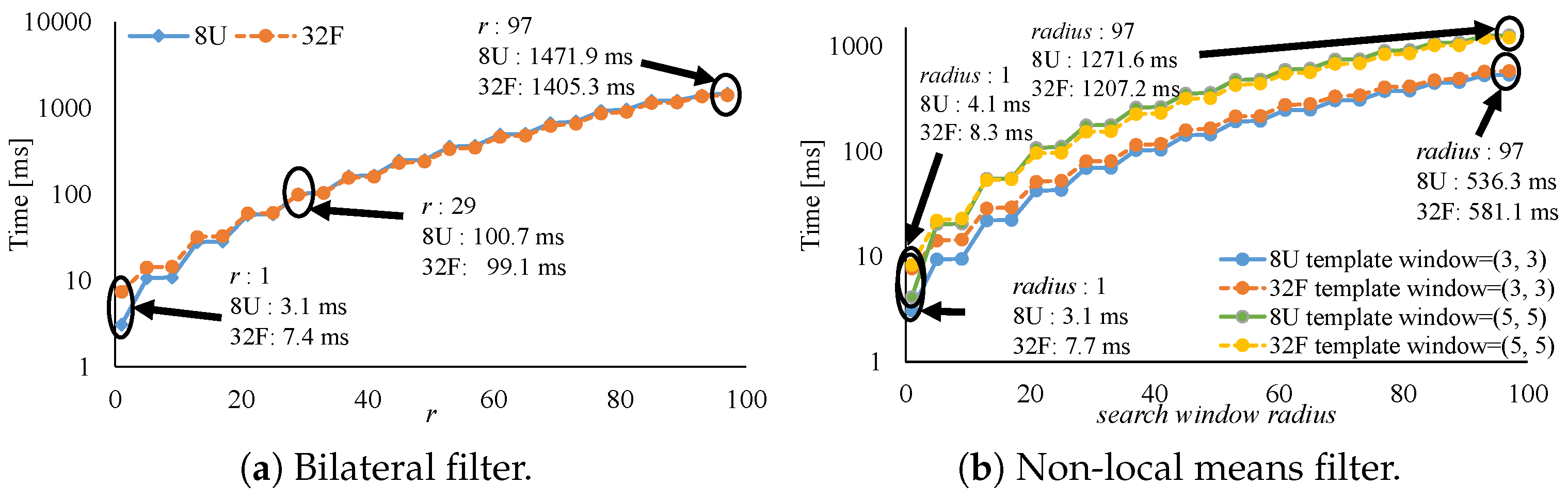
7. Experimental Results
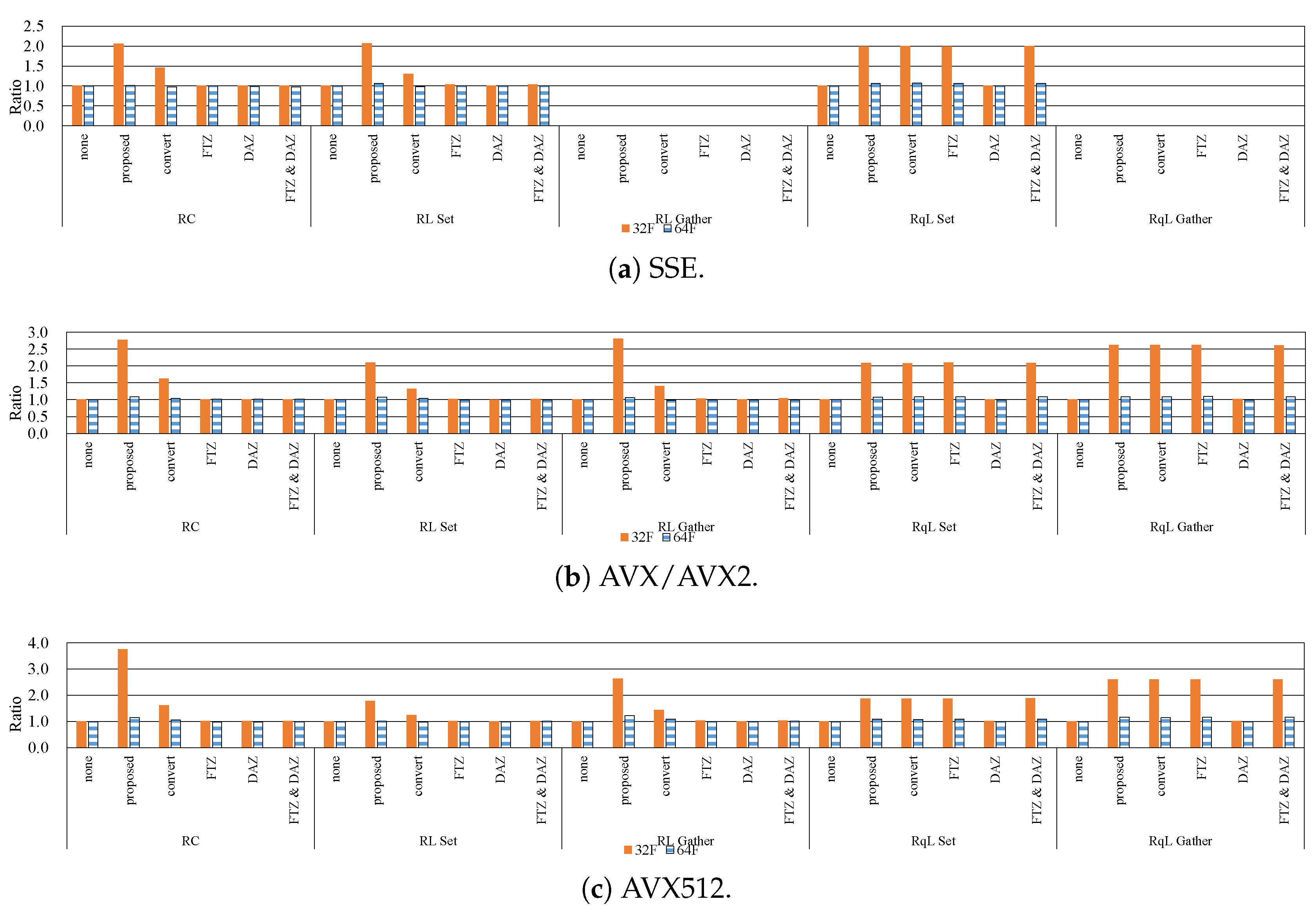
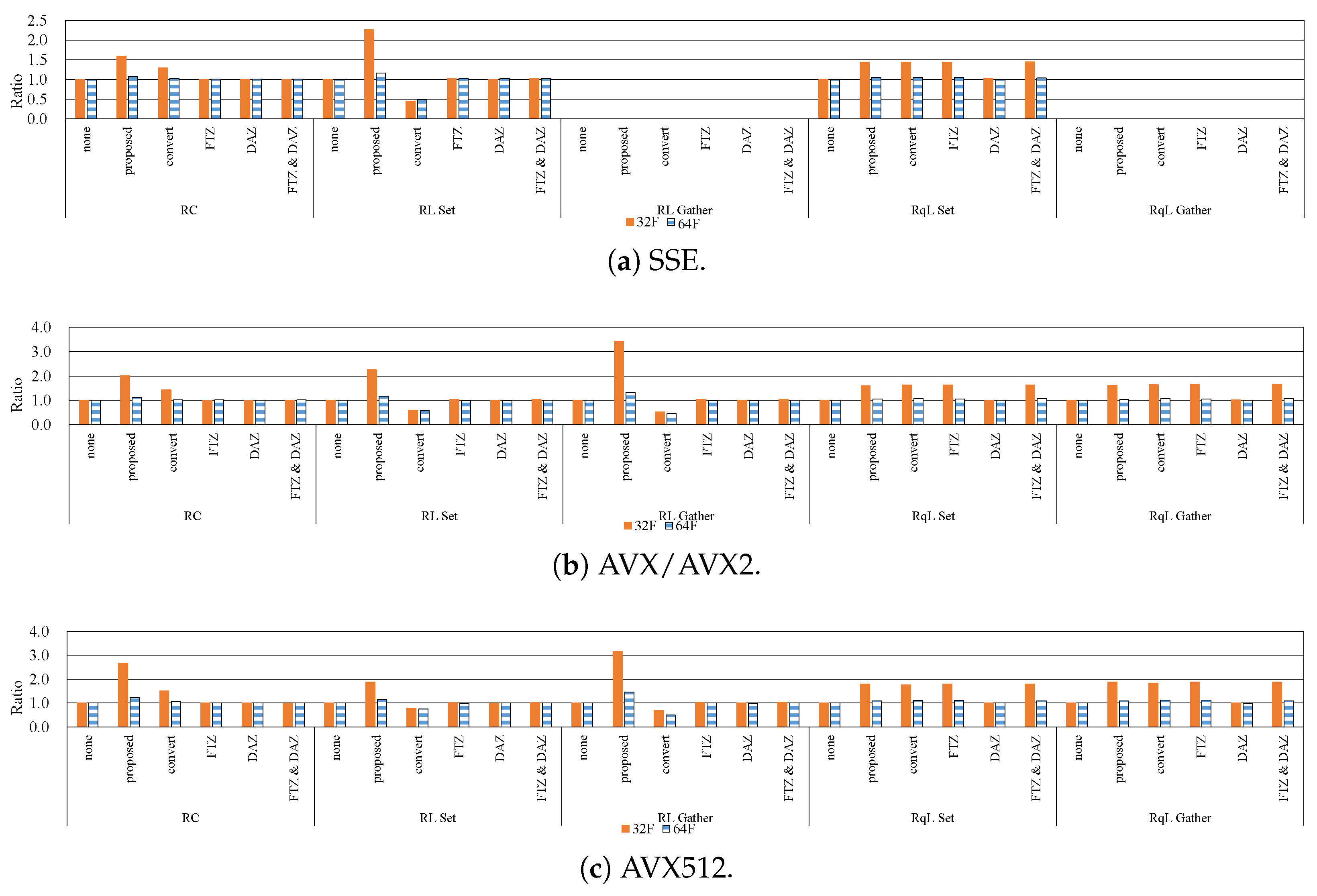
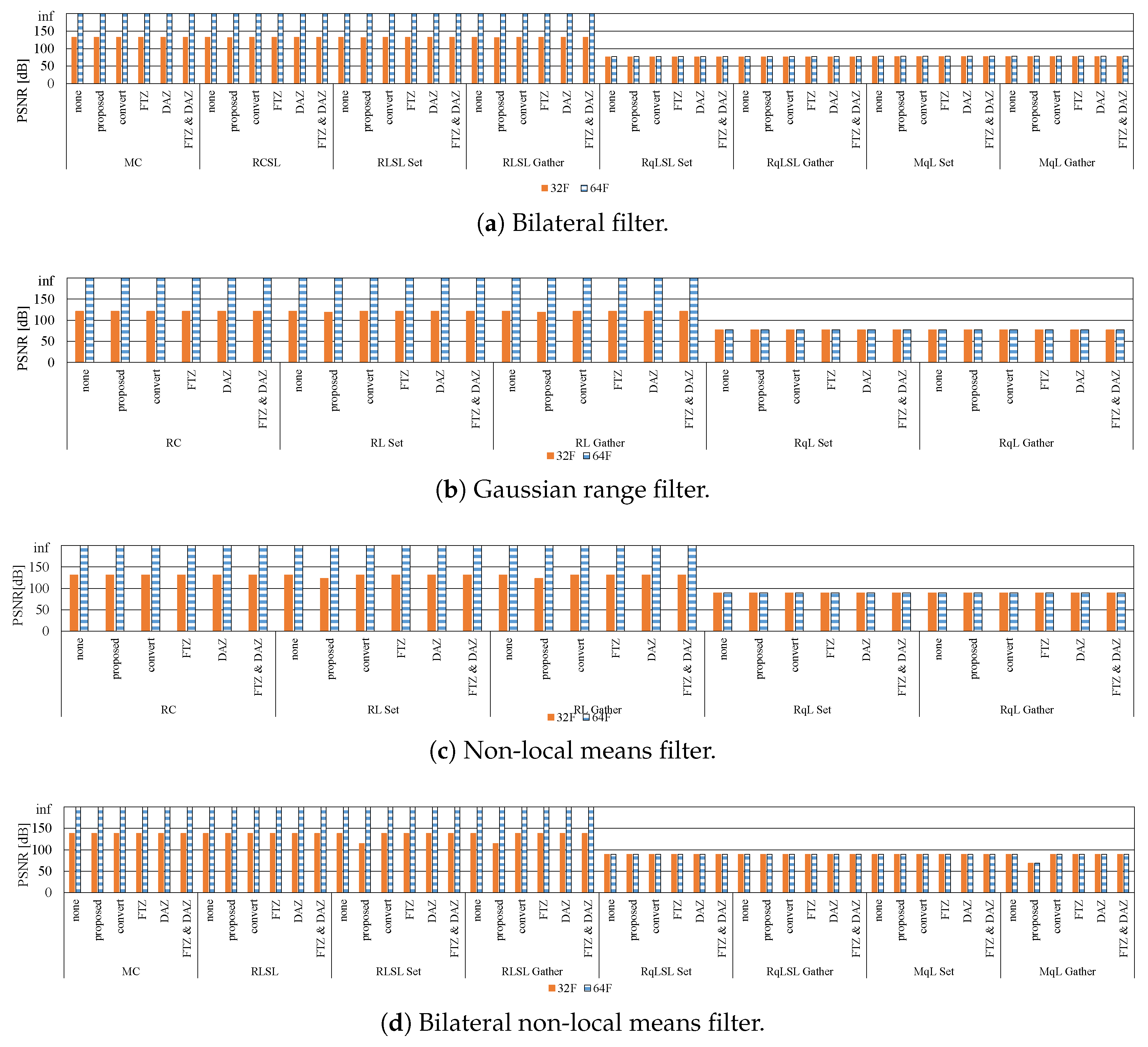
7.1. Influence of Denormalized Numbers
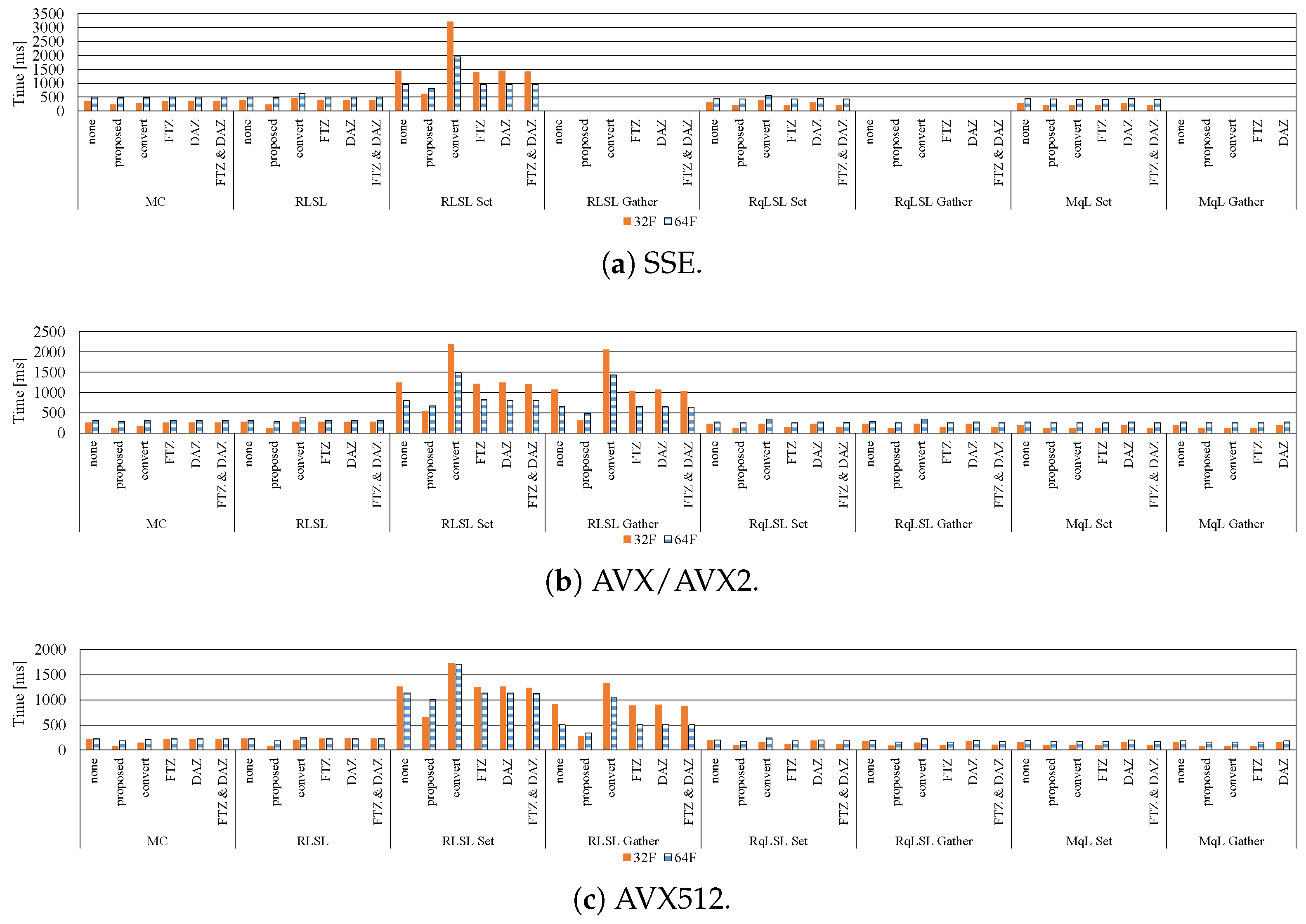
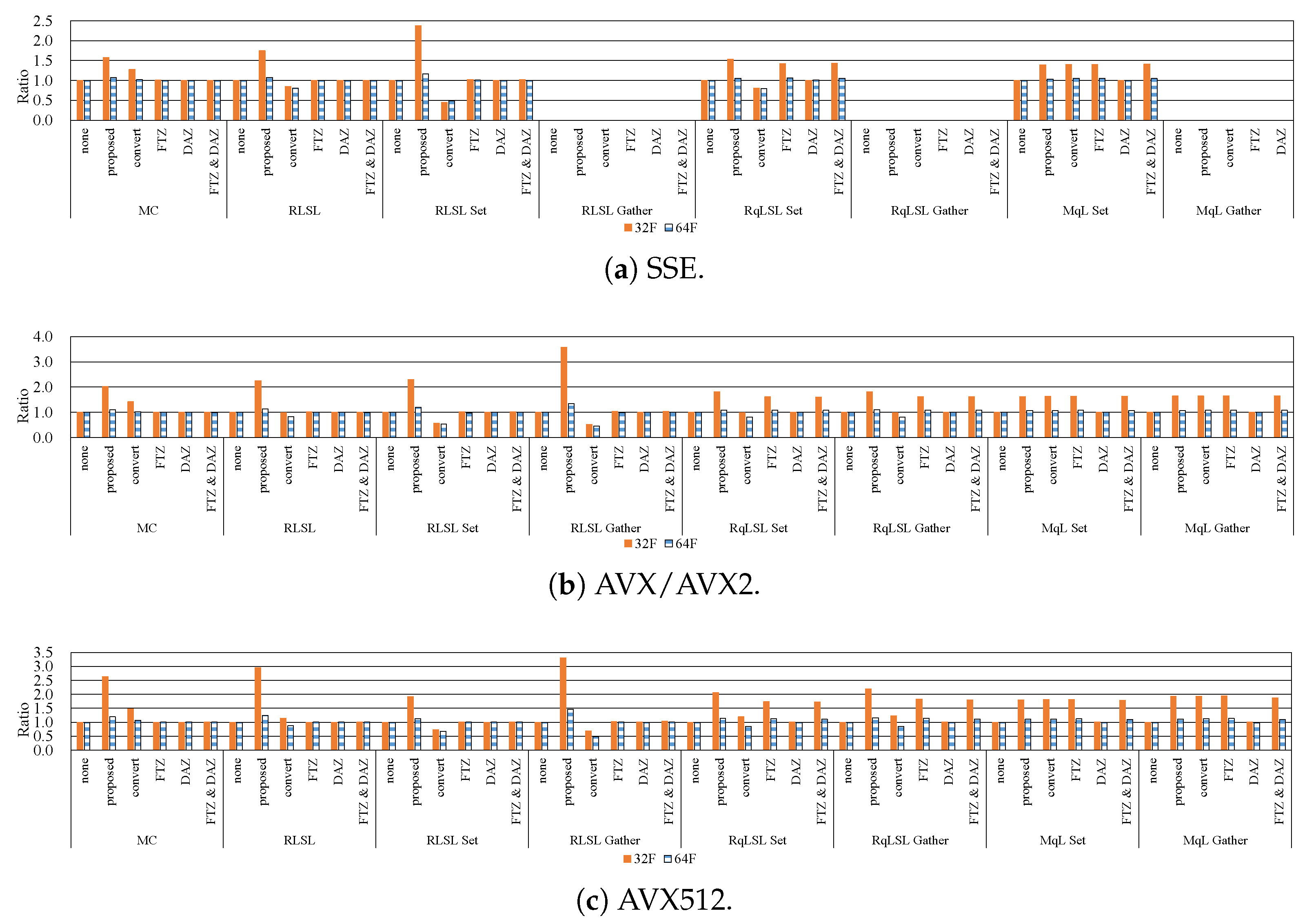
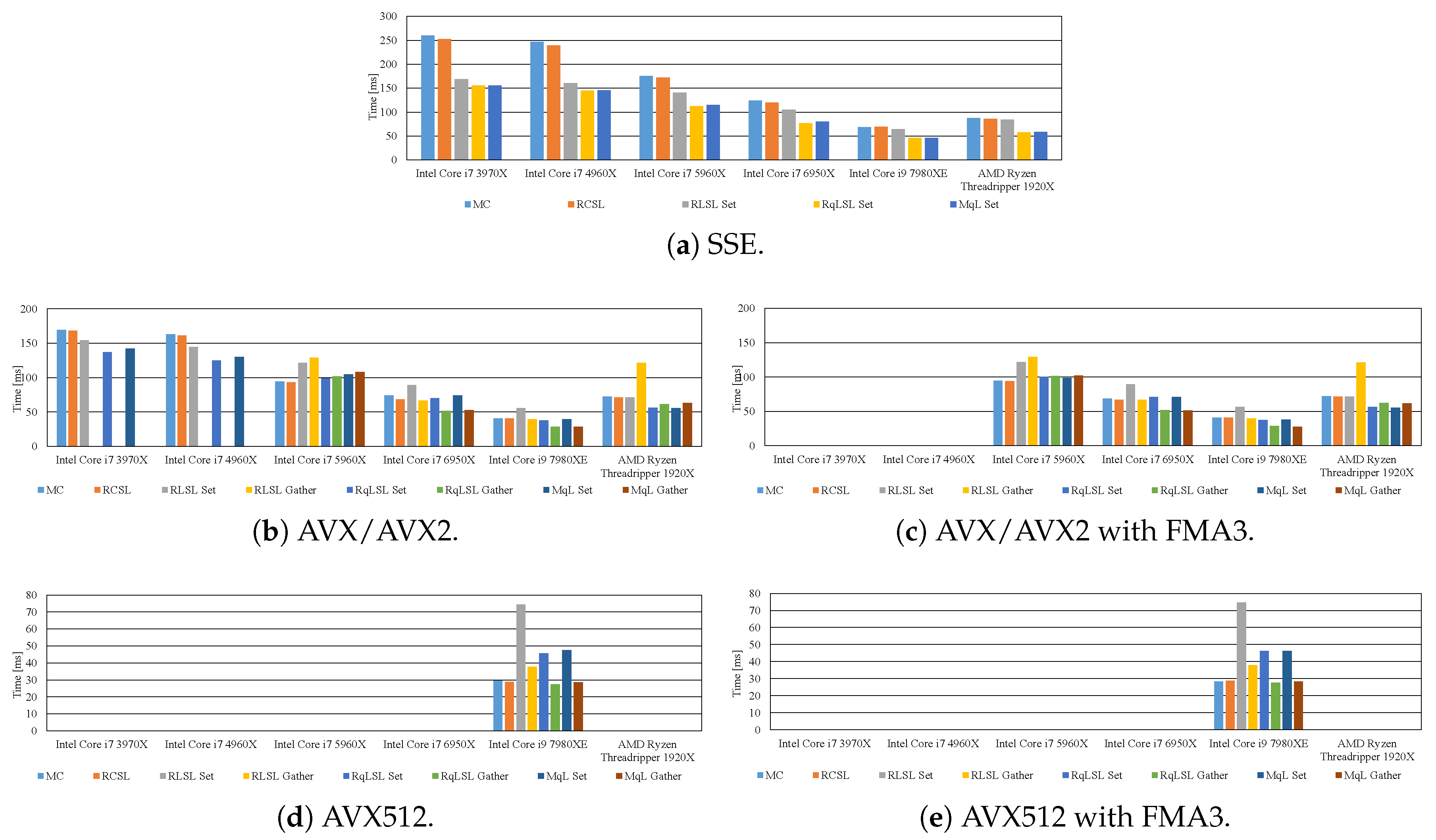
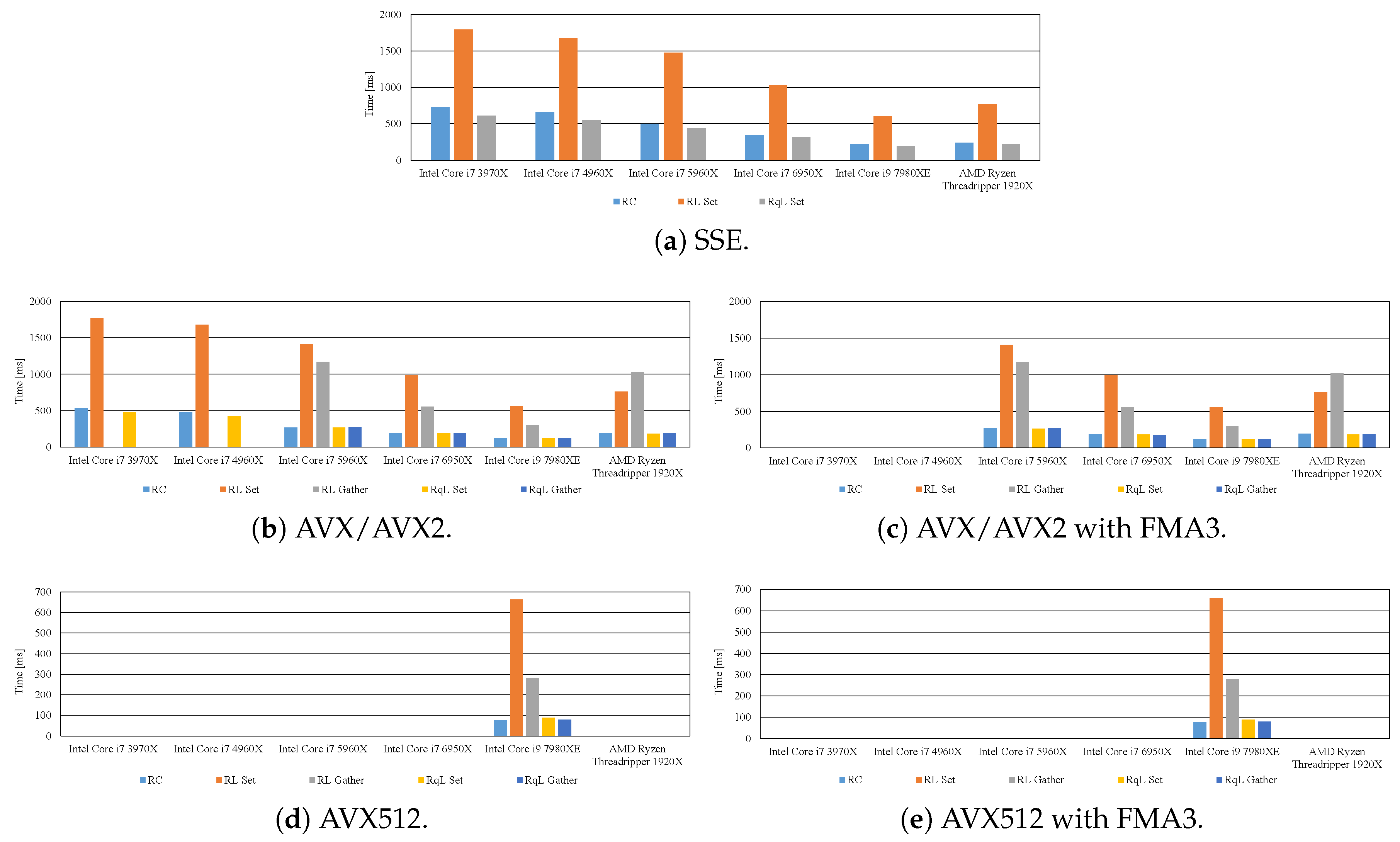
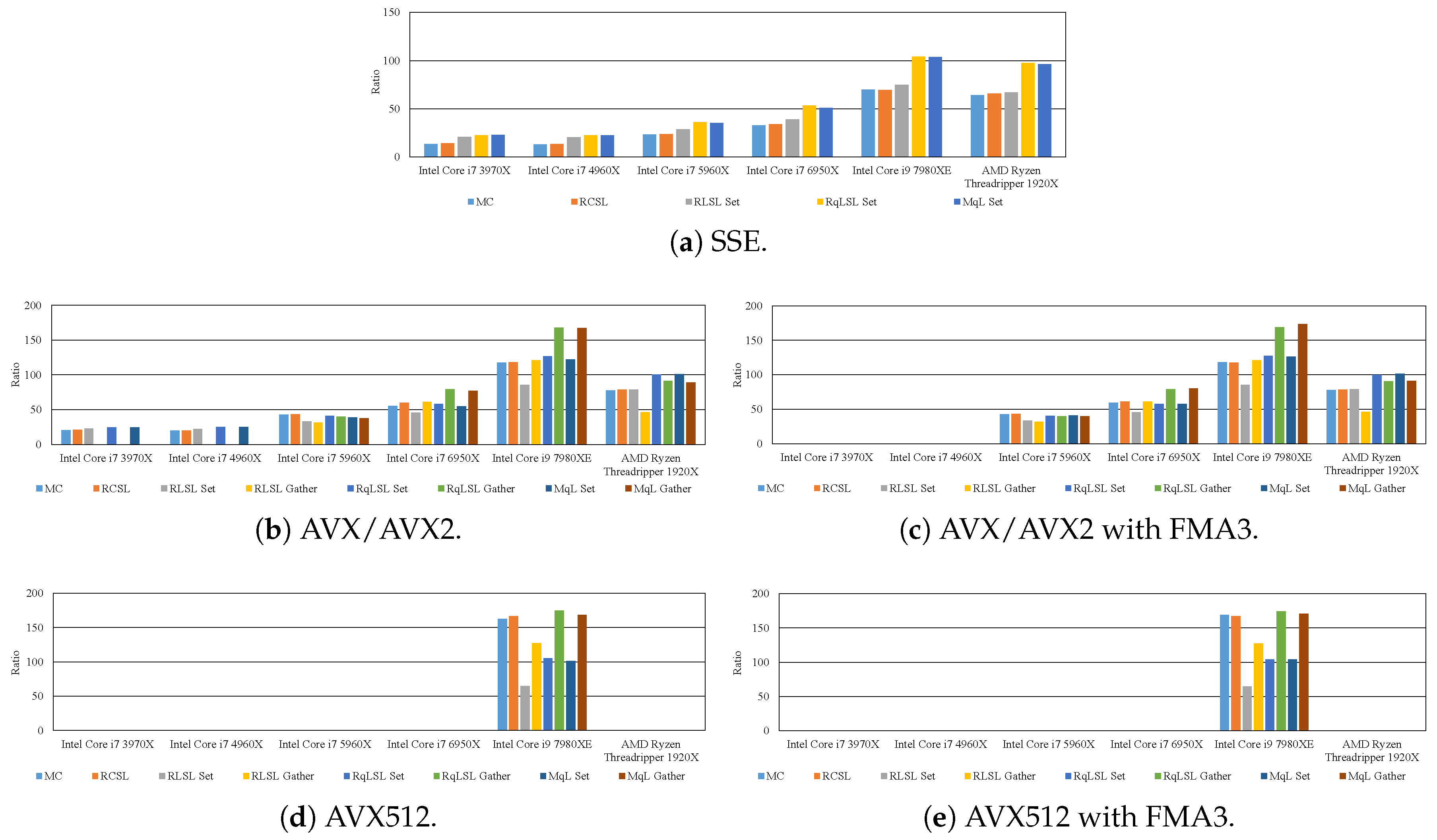
7.2. Effective Implementation on CPU Microarchitectures
8. Conclusions
- The proposed methods are up to five-times faster than the implementation without preventing the occurrence of denormalized numbers.
- In modern CPU microarchitectures, the gather instruction in the SIMD instruction set is effective for loading weights from the LUTs.
- By reducing the LUT size through quantization, the filtering can be accelerated while maintaining high accuracy. Moreover, the optimum quantization function and the quantization LUT size depends on the required accuracy and computational time.
- When the kernel size is small, the 8U implementation is faster than the 32F implementation. By contrast, in the case of the large kernel, the 32F implementation is faster than the 8U implementation.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Tomasi, C.; Manduchi, R. Bilateral Filtering for Gray and Color Images. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Bombay, India, 4–7 January 1998; pp. 839–846. [Google Scholar]
- Paris, S.; Kornprobst, P.; Tumblin, J.; Durand, F. Bilateral Filtering: Theory and Applications; Now Publishers Inc.: Delft, The Netherlands, 2009. [Google Scholar]
- Buades, A.; Coll, B.; Morel, J.M. A Non-Local Algorithm for Image Denoising. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), San Diego, CA, USA, 20–25 June 2005; pp. 60–65. [Google Scholar]
- He, K.; Sun, J.; Tang, X. Guided Image Filtering. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1397–1409. [Google Scholar] [CrossRef] [PubMed]
- He, K.; Sun, J.; Tang, X. Guided Image Filtering. In Proceedings of the European Conference on Computer Vision (ECCV), Crete, Greece, 5–11 Septembe 2010. [Google Scholar]
- Fukushima, N.; Sugimoto, K.; Kamata, S. Guided Image Filtering with Arbitrary Window Function. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Calgary, AB, Canada, 15–20 April 2018. [Google Scholar]
- Kang, W.; Yu, S.; Seo, D.; Jeong, J.; Paik, J. Push-Broom-Type Very High-Resolution Satellite Sensor Data Correction Using Combined Wavelet-Fourier and Multiscale Non-Local Means Filtering. Sensors 2015, 15, 22826–22853. [Google Scholar] [CrossRef] [PubMed]
- Durand, F.; Dorsey, J. Fast Bilateral Filtering for the Display of High-Dynamic-Range Images. ACM Trans. Graph. 2002, 21, 257–266. [Google Scholar] [CrossRef]
- Bae, S.; Paris, S.; Durand, F. Two-Scale Tone Management for Photographic Look. ACM Trans. Graph. 2006, 25, 637–645. [Google Scholar] [CrossRef]
- Fattal, R.; Agrawala, M.; Rusinkiewicz, S. Multiscale Shape and Detail Enhancement from Multi-Light Image Collections. ACM Trans. Graph. 2007, 26, 51. [Google Scholar] [CrossRef]
- Li, L.; Si, Y.; Jia, Z. Remote Sensing Image Enhancement Based on Non-Local Means Filter in NSCT Domain. Algorithms 2017, 10, 116. [Google Scholar] [CrossRef]
- Mori, Y.; Fukushima, N.; Yendo, T.; Fujii, T.; Tanimoto, M. View Generation with 3D Warping using Depth Information for FTV. Signal Process. Image Commun. 2009, 24, 65–72. [Google Scholar] [CrossRef]
- Petschnigg, G.; Agrawala, M.; Hoppe, H.; Szeliski, R.; Cohen, M.; Toyama, K. Digital Photography with Flash and No-Flash Image Pairs. ACM Trans. Graph. 2004, 23, 664–672. [Google Scholar] [CrossRef]
- Eisemann, E.; Durand, F. Flash Photography Enhancement via Intrinsic Relighting. ACM Trans. Graph. 2004, 23, 673–678. [Google Scholar] [CrossRef]
- Kopf, J.; Cohen, M.; Lischinski, D.; Uyttendaele, M. Joint Bilateral Upsampling. ACM Trans. Graph. 2007, 26, 96. [Google Scholar] [CrossRef]
- Zhou, D.; Wang, R.; Lu, J.; Zhang, Q. Depth Image Super Resolution Based on Edge-Guided Method. Appl. Sci. 2018, 8, 298. [Google Scholar] [CrossRef]
- Kodera, N.; Fukushima, N.; Ishibashi, Y. Filter Based Alpha Matting for Depth Image Based Rendering. In Proceedings of the Visual Communications and Image Processing (VCIP), Kuching, Malaysia, 17–20 November 2013. [Google Scholar]
- He, K.; Sun, J.; Tang, X. Single Image Haze Removal using Dark Channel Prior. In Proceedings of the Computer Vision and Pattern Recognition (CVPR), Miami, FL, USA, 20–24 June 2009. [Google Scholar]
- Hosni, A.; Rhemann, C.; Bleyer, M.; Rother, C.; Gelautz, M. Fast Cost-Volume Filtering for Visual Correspondence and Beyond. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 504–511. [Google Scholar] [CrossRef] [PubMed]
- Matsuo, T.; Fukushima, N.; Ishibashi, Y. Weighted Joint Bilateral Filter with Slope Depth Compensation Filter for Depth Map Refinement. In Proceedings of the International Conference on Computer Vision Theory and Applications (VISAPP), Barcelona, Spain, 21–24 February 2013; pp. 300–309. [Google Scholar]
- Le, A.V.; Jung, S.W.; Won, C.S. Directional Joint Bilateral Filter for Depth Images. Sensors 2014, 14, 11362–11378. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.; Lai, P.; Tian, D.; Chen, C.W. New Depth Coding Techniques with Utilization of Corresponding Video. IEEE Trans. Broadcast. 2011, 57, 551–561. [Google Scholar] [CrossRef]
- Fukushima, N.; Inoue, T.; Ishibashi, Y. Removing Depth Map Coding Distortion by Using Post Filter Set. In Proceedings of the International Conference on Multimedia and Expo (ICME), San Jose, CA, USA, 15–19 July 2013. [Google Scholar]
- Fukushima, N.; Fujita, S.; Ishibashi, Y. Switching Dual Kernels for Separable Edge-Preserving Filtering. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brisbane, Australia, 19–24 April 2015. [Google Scholar]
- Pham, T.Q.; Vliet, L.J.V. Separable Bilateral Filtering for Fast Video Preprocessing. In Proceedings of the International Conference on Multimedia and Expo (ICME), Amsterdam, The Netherlands, 6–9 July 2005. [Google Scholar]
- Chen, J.; Paris, S.; Durand, F. Real-Time Edge-Aware Image Processing with the Bilateral Grid. ACM Trans. Graph. 2007, 26, 103. [Google Scholar] [CrossRef]
- Sugimoto, K.; Fukushima, N.; Kamata, S. Fast Bilateral Filter for Multichannel Images via Soft-assignment Coding. In Proceedings of the APSIPA ASC, Jeju, Korea, 13–16 December 2016. [Google Scholar]
- Sugimoto, K.; Kamata, S. Compressive Bilateral Filtering. IEEE Trans. Image Process. 2015, 24, 3357–3369. [Google Scholar] [CrossRef] [PubMed]
- Paris, S.; Durand, F. A Fast Approximation of the Bilateral Filter using a Signal Processing Approach. Int. J. Comput. Vis. 2009, 81, 24–52. [Google Scholar] [CrossRef]
- Chaudhury, K.N. Acceleration of the Shiftable O(1) Algorithm for Bilateral Filtering and Nonlocal Means. IEEE Trans. Image Process. 2013, 22, 1291–1300. [Google Scholar] [CrossRef] [PubMed]
- Chaudhury, K. Constant-Time Filtering Using Shiftable Kernels. IEEE Signal Process. Lett. 2011, 18, 651–654. [Google Scholar] [CrossRef]
- Chaudhury, K.; Sage, D.; Unser, M. Fast O(1) Bilateral Filtering Using Trigonometric Range Kernels. IEEE Trans. Image Process. 2011, 20, 3376–3382. [Google Scholar] [CrossRef] [PubMed]
- Adams, A.; Gelfand, N.; Dolson, J.; Levoy, M. Gaussian KD-trees for fast high-dimensional filtering. ACM Trans. Graph. 2009, 28. [Google Scholar] [CrossRef]
- Adams, A.; Baek, J.; Davis, M.A. Fast High-Dimensional Filtering Using the Permutohedral Lattice. Comput. Graph. Forum 2010, 29, 753–762. [Google Scholar] [CrossRef]
- Porikli, F. Constant Time O(1) Bilateral Filtering. In Proceedings of the Computer Vision and Pattern Recognition (CVPR), Anchorage, AK, USA, 23–28 June 2008. [Google Scholar]
- Yang, Q.; Tan, K.H.; Ahuja, N. Real-time O(1) bilateral filtering. In Proceedings of the Computer Vision and Pattern Recognition (CVPR), Miami, FL, USA, 20–24 June 2009; pp. 557–564. [Google Scholar]
- IEEE. IEEE Standard for Floating-Point Arithmetic; IEEE Std 754-2008; IEEE: Piscataway, NJ, USA, 2008; pp. 1–70. [Google Scholar] [CrossRef]
- Schwarz, E.M.; Schmookler, M.; Trong, S.D. FPU Implementations with Denormalized Numbers. IEEE Trans. Comput. 2005, 54, 825–836. [Google Scholar] [CrossRef]
- Schwarz, E.M.; Schmookler, M.; Trong, S.D. Hardware Implementations of Denormalized Numbers. In Proceedings of the IEEE Symposium on Computer Arithmetic, Santiago de Compostela, Spain, 15–18 June 2003; pp. 70–78. [Google Scholar] [CrossRef]
- Zheng, L.; Hu, H.; Yihe, S. Floating-Point Unit Processing Denormalized Numbers. In Proceedings of the International Conference on ASIC, Shanghai, China, 24–27 October 2005; Volume 1, pp. 6–9. [Google Scholar] [CrossRef]
- Flynn, M.J. Some Computer Organizations and Their Effectiveness. IEEE Trans. Comput. 1972, 100, 948–960. [Google Scholar] [CrossRef]
- Hughes, C.J. Single-Instruction Multiple-Data Execution. Synth. Lect. Comput. Archit. 2015, 10, 1–121. [Google Scholar] [CrossRef]
- Kim, Y.S.; Lim, H.; Choi, O.; Lee, K.; Kim, J.D.K.; Kim, J. Separable Bilateral Nonlocal Means. In Proceedings of the International Conference on Image Processing (ICIP), Brussels, Belgium, 11–14 September 2011; pp. 1513–1516. [Google Scholar]
- Moore, G.E. Cramming more components onto integrated circuits, Reprinted from Electronics, volume 38, number 8, April 19, 1965, pp.114 ff. IEEE Solid-State Circuits Soc. Newsl. 2006, 11, 33–35. [Google Scholar] [CrossRef]
- Rotem, E.; Ginosar, R.; Mendelson, A.; Weiser, U.C. Power and thermal constraints of modern system-on-a-chip computer. In Proceedings of the International Workshop on Thermal Investigations of ICs and Systems (THERMINIC), Berlin, Germany, 25–27 September 2013; pp. 141–146. [Google Scholar] [CrossRef]
- Intel Architecture Instruction Set Extensions and Future Features Programming Reference. Available online: https://software.intel.com/sites/default/files/managed/c5/15/architecture-instruction-set-extensions-programming-reference.pdf (accessed on 1 October 2018).
- Ercegovac, M.D.; Lang, T. Digital Arithmetic, 1st ed.; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 2003. [Google Scholar]
- Williams, S.; Waterman, A.; Patterson, D. Roofline: An Insightful Visual Performance Model for Multicore Architectures. Commun. ACM 2009, 52, 65–76. [Google Scholar] [CrossRef]
- Bradski, G.; Kaehler, A. Learning OpenCV: Computer Vision with the OpenCV Library; O’Reilly Media, Inc.: Sevvan, CA, USA, 2008. [Google Scholar]
- Maeda, Y.; Fukushima, N.; Matsuo, H. Taxonomy of Vectorization Patterns of Programming for FIR Image Filters Using Kernel Subsampling and New One. Appl. Sci. 2018, 8, 1235. [Google Scholar] [CrossRef]
- Telegraph, I.; Committee, T.C. CCITT Recommendation T.81: Terminal Equipment and Protocols for Telematic Services: Information Technology–Digital Compression and Coding of Continuous-tone Still Images–Requirements and Guidelines; International Telecommunication Union: Geneva, Switzerland, 1993. [Google Scholar]
- Domanski, M.; Rakowski, K. Near-Lossless Color Image Compression with No Error Accumulation in Multiple Coding Cycles; Lecture Notes in Computer Science; CAIP; Springer: Berlin, Germany, 2001; Volume 2124, pp. 85–91. [Google Scholar]


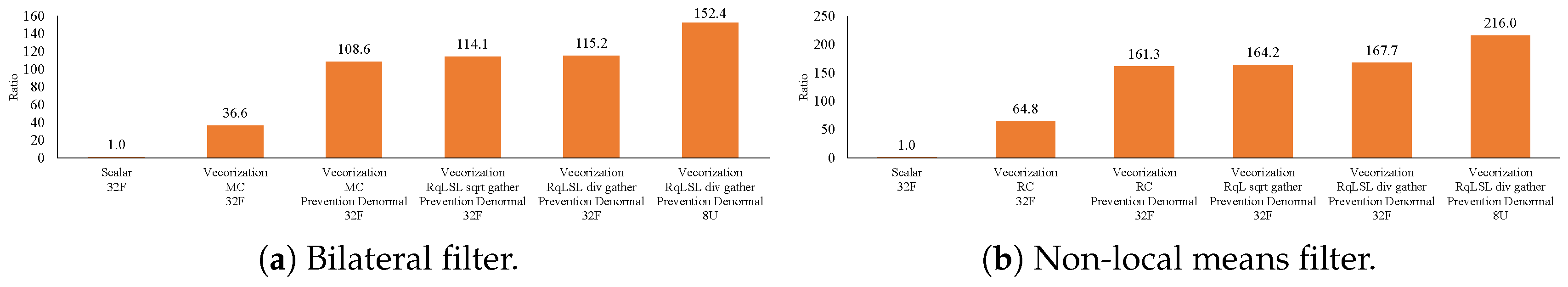
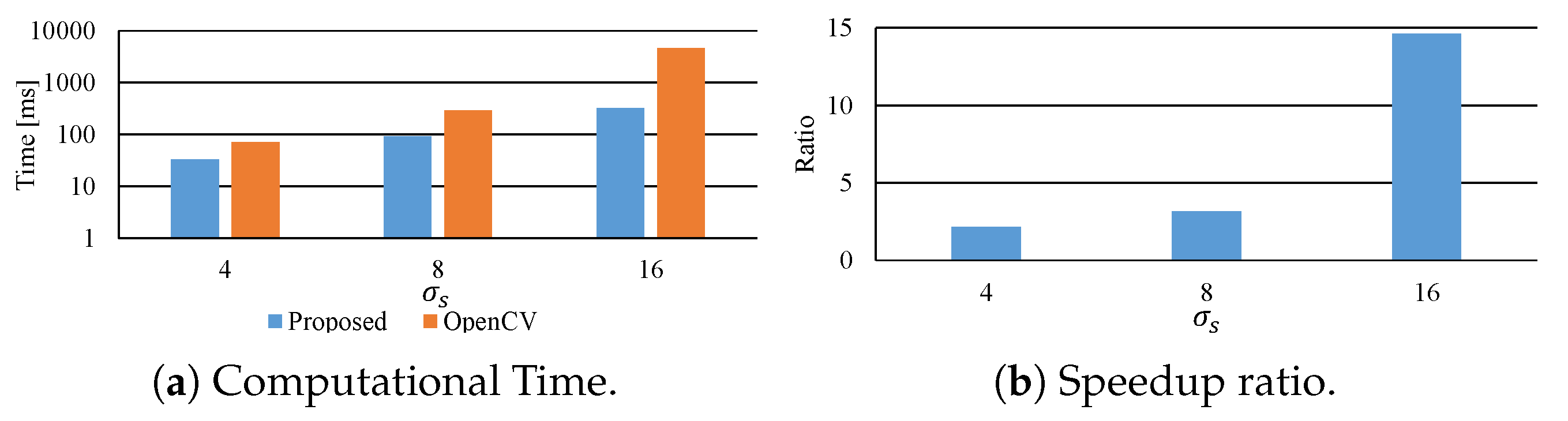
| Generation | 1st | 2nd | 3rd | 4th | 5th | 6th |
|---|---|---|---|---|---|---|
| codename | Gulftown | Sandy Bridge | Ivy Bridge | Haswell | Broadwell | Skylake |
| model | 990X | 3970X | 4960X | 5960X | 6950X | 7980XE |
| launch date | Q1’11 | Q4’12 | Q3’13 | Q3’14 | Q2’16 | Q3’17 |
| lithography | 32 nm | 32 nm | 22 nm | 22 nm | 14 nm | 14 nm |
| base frequency [GHz] | 3.46 | 3.50 | 3.60 | 3.00 | 3.00 | 2.60 |
| max turbo frequency [GHz] | 3.73 | 4.00 | 4.00 | 3.50 | 3.50 | 4.20 |
| number of cores | 6 | 6 | 6 | 8 | 10 | 18 |
| L1 cache (×number of cores) | 64 KB (data cache 32 KB, instruction cache 32 KB) | |||||
| L2 cache (×number of cores) | 256 KB | 256 KB | 25 6KB | 256 KB | 256 KB | 1 MB |
| L3 cache | 12 MB | 15 MB | 15 MB | 20 MB | 25 MB | 24.75 MB |
| memory types | DDR3-1066 | DDR3-1600 | DDR3-1866 | DDR4-2133 | DDR4-2133 | DDR4-2666 |
| max number of memory channels | 3 | 4 | 4 | 4 | 4 | 4 |
| SIMD instruction sets | SSE4.2 | SSE4.2 AVX | SSE4.2 AVX | SSE4.2 AVX/AVX2 FMA3 | SSE4.2 AVX/AVX2 FMA3 | SSE4.2 VX/AVX2 AVX512 FMA3 |
| CPU | Intel Core i7 3970X | Intel Core i7 4960X | Intel Core i7 5960X | Intel Core i7 6950X | Intel Core i9 7980XE | AMD Ryzen Threadripper 1920X |
|---|---|---|---|---|---|---|
| memory | DDR3-1600 6 GBytes | DDR3-1866 16 GBytes | DDR4-2133 32 GBytes | DDR4-2400 32 GBytes | DDR4-2400 16 GBytes | DDR4-2400 16 GBytes |
| SIMD instruction sets | SSE4.2 AVX | SSE4.2 AVX | SSE4.2 AVX/AVX2 FMA3 | SSE4.2 AVX/AVX2 FMA3 | SSE4.2 AVX/AVX2 AVX512F FMA3 | SSE4.2 AVX/AVX2 FMA3 |
| (a) | (b) | (c) | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| σr | 4 | 8 | 16 | σr | 4 | 8 | 16 | σr | 4 | 8 | 16 | |||||
| σs | σs | σs | ||||||||||||||
| 4 | 17.48 | 17.57 | 17.63 | 4 | 66.48 | 51.36 | 50.24 | 4 | 3.80 | 2.92 | 2.85 | |||||
| 8 | 43.96 | 43.86 | 43.73 | 8 | 217.55 | 194.94 | 192.96 | 8 | 4.95 | 4.45 | 4.41 | |||||
| 16 | 147.76 | 147.58 | 147.50 | 16 | 763.87 | 755.56 | 719.00 | 16 | 5.17 | 5.12 | 4.87 | |||||
| (a) | (b) | (c) | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| σr | 4 | 8 | 16 | σr | 4 | 8 | 16 | σr | 4 | 8 | 16 | |||||
| r | r | r | ||||||||||||||
| 12 | 16.76 | 16.83 | 16.85 | 12 | 63.95 | 48.69 | 48.09 | 12 | 3.82 | 2.89 | 2.85 | |||||
| 24 | 42.53 | 42.40 | 42.39 | 24 | 207.54 | 185.16 | 181.40 | 24 | 4.88 | 4.37 | 4.28 | |||||
| 48 | 143.24 | 143.01 | 142.58 | 48 | 741.42 | 717.41 | 685.18 | 48 | 5.18 | 5.02 | 4.81 | |||||
| (a) | (b) | (c) | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| h | 4 | 8 | 16 | h | 4 | 8 | 16 | h | 4 | 8 | 16 | |||||
| Search Window | Search Window | Search Window | ||||||||||||||
| (25, 25) | 40.31 | 39.80 | 39.64 | (25, 25) | 98.91 | 82.84 | 80.66 | (25, 25) | 2.45 | 2.08 | 2.03 | |||||
| (49, 49) | 128.90 | 128.90 | 128.90 | (49, 49) | 332.88 | 307.58 | 300.00 | (49, 49) | 2.58 | 2.39 | 2.33 | |||||
| (97, 97) | 485.88 | 485.88 | 485.36 | (97, 97) | 1148.48 | 1158.53 | 1134.93 | (97, 97) | 2.36 | 2.38 | 2.34 | |||||
| (a) | (b) | (c) | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| h | 4 | 8 | 16 | h | 4 | 8 | 16 | h | 4 | 8 | 16 | |||||
| σs | σs | σs | ||||||||||||||
| 4 | 40.20 | 40.05 | 39.92 | 4 | 99.14 | 84.85 | 82.85 | 4 | 2.47 | 2.12 | 2.08 | |||||
| 8 | 133.61 | 133.02 | 132.85 | 8 | 340.29 | 311.72 | 301.38 | 8 | 2.55 | 2.34 | 2.27 | |||||
| 16 | 496.86 | 496.57 | 495.89 | 16 | 1166.17 | 1191.36 | 1163.34 | 16 | 2.35 | 2.40 | 2.35 | |||||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maeda, Y.; Fukushima, N.; Matsuo, H. Effective Implementation of Edge-Preserving Filtering on CPU Microarchitectures. Appl. Sci. 2018, 8, 1985. https://doi.org/10.3390/app8101985
Maeda Y, Fukushima N, Matsuo H. Effective Implementation of Edge-Preserving Filtering on CPU Microarchitectures. Applied Sciences. 2018; 8(10):1985. https://doi.org/10.3390/app8101985
Chicago/Turabian StyleMaeda, Yoshihiro, Norishige Fukushima, and Hiroshi Matsuo. 2018. "Effective Implementation of Edge-Preserving Filtering on CPU Microarchitectures" Applied Sciences 8, no. 10: 1985. https://doi.org/10.3390/app8101985
APA StyleMaeda, Y., Fukushima, N., & Matsuo, H. (2018). Effective Implementation of Edge-Preserving Filtering on CPU Microarchitectures. Applied Sciences, 8(10), 1985. https://doi.org/10.3390/app8101985





