Establishing an ANN-Based Risk Model for Ground Subsidence Along Railways
Abstract
1. Introduction
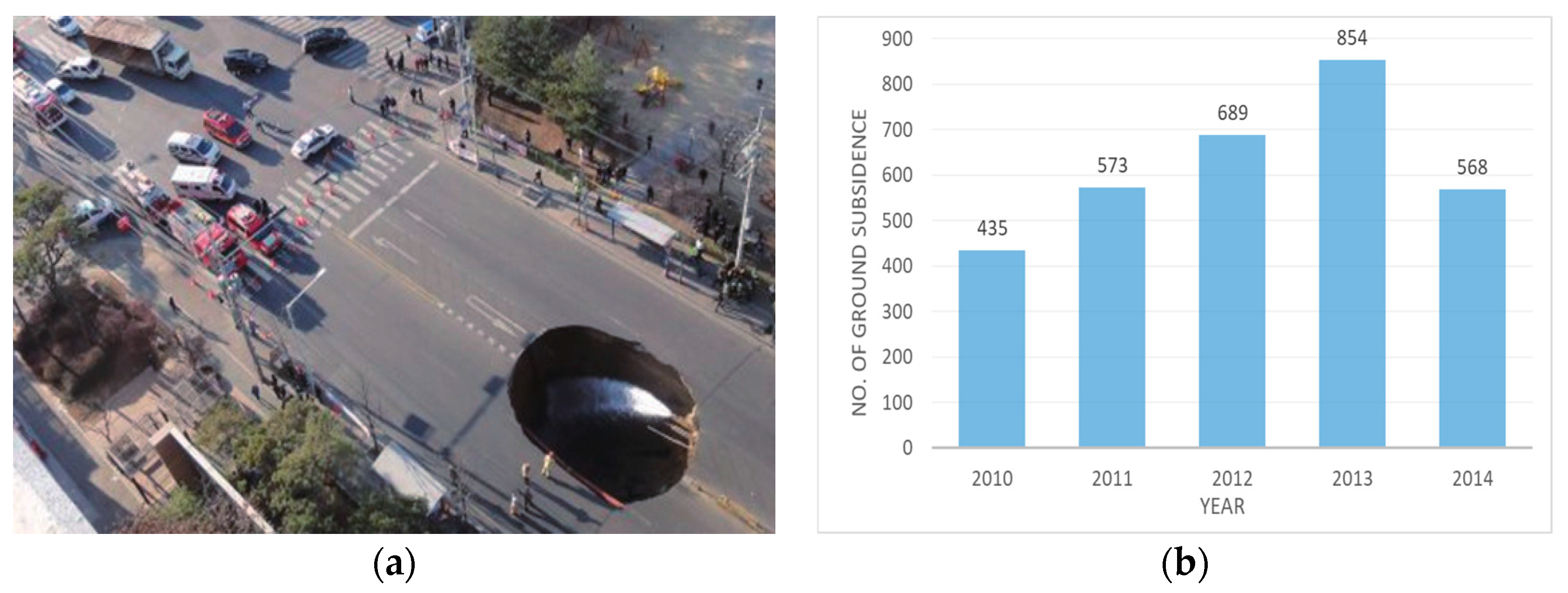
- Since 2010, around 600 ground subsidences have mainly taken place annually in roadways, sidewalks, and vicinities of underground construction areas.
- Around 40 percent of events occurred during the summer season (June to August), which has frequent heavy rainfalls ranging from 50~100 mm/h.
- The causes of the events have been categorized as:
- (1)
- Damage to water and sewage utilities, which allows surrounding soil loss through the holes made;
- (2)
- Inappropriate backfill compaction during excavation activities that include open-cut construction and installation of underground utilities;
- (3)
- Drop in the ground water table due to pumping activities or damage to sheet pile wall.
2. Establishing of Database
3. Risk Model
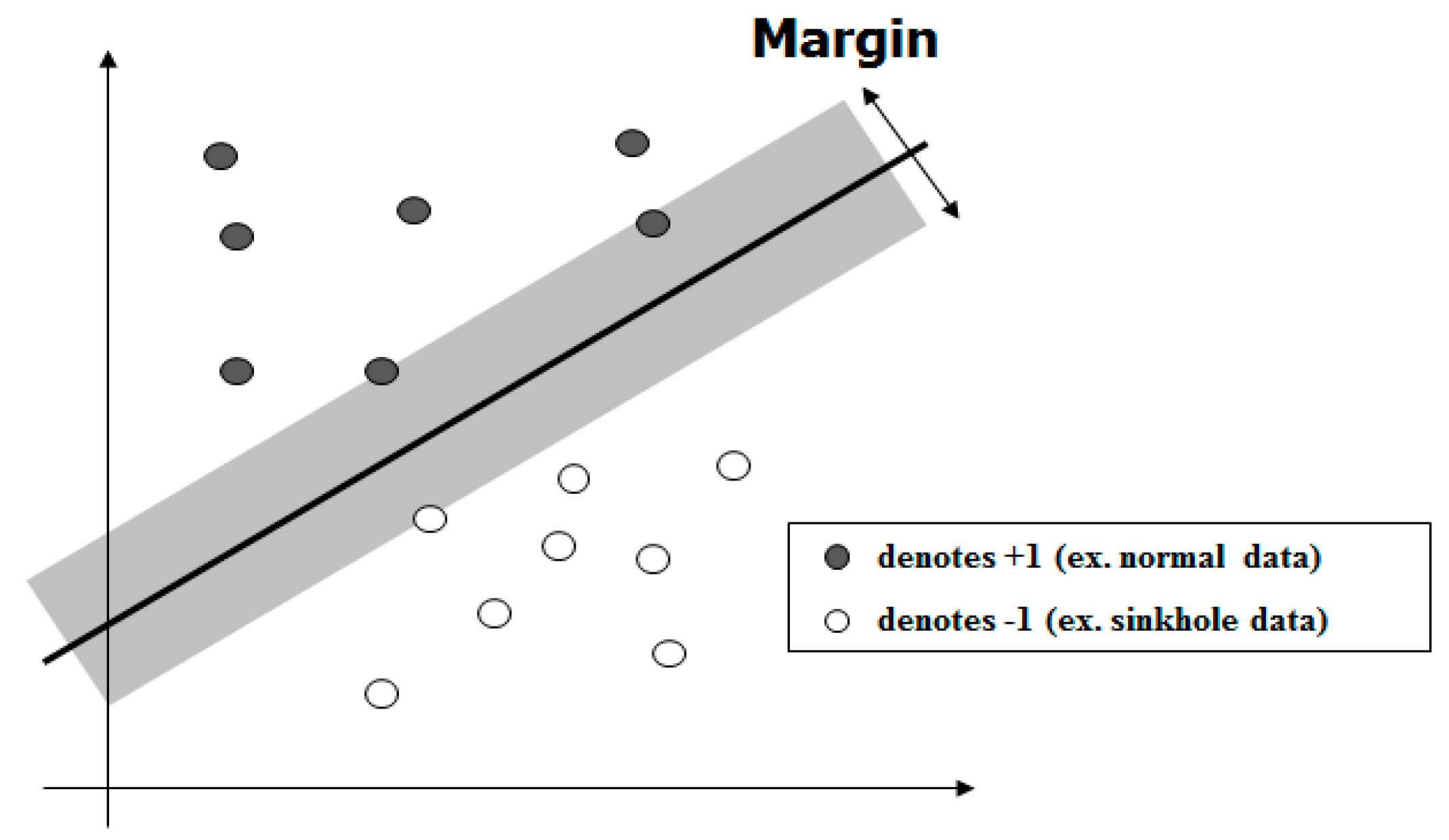
3.1. Support Vector Machine (SVM)
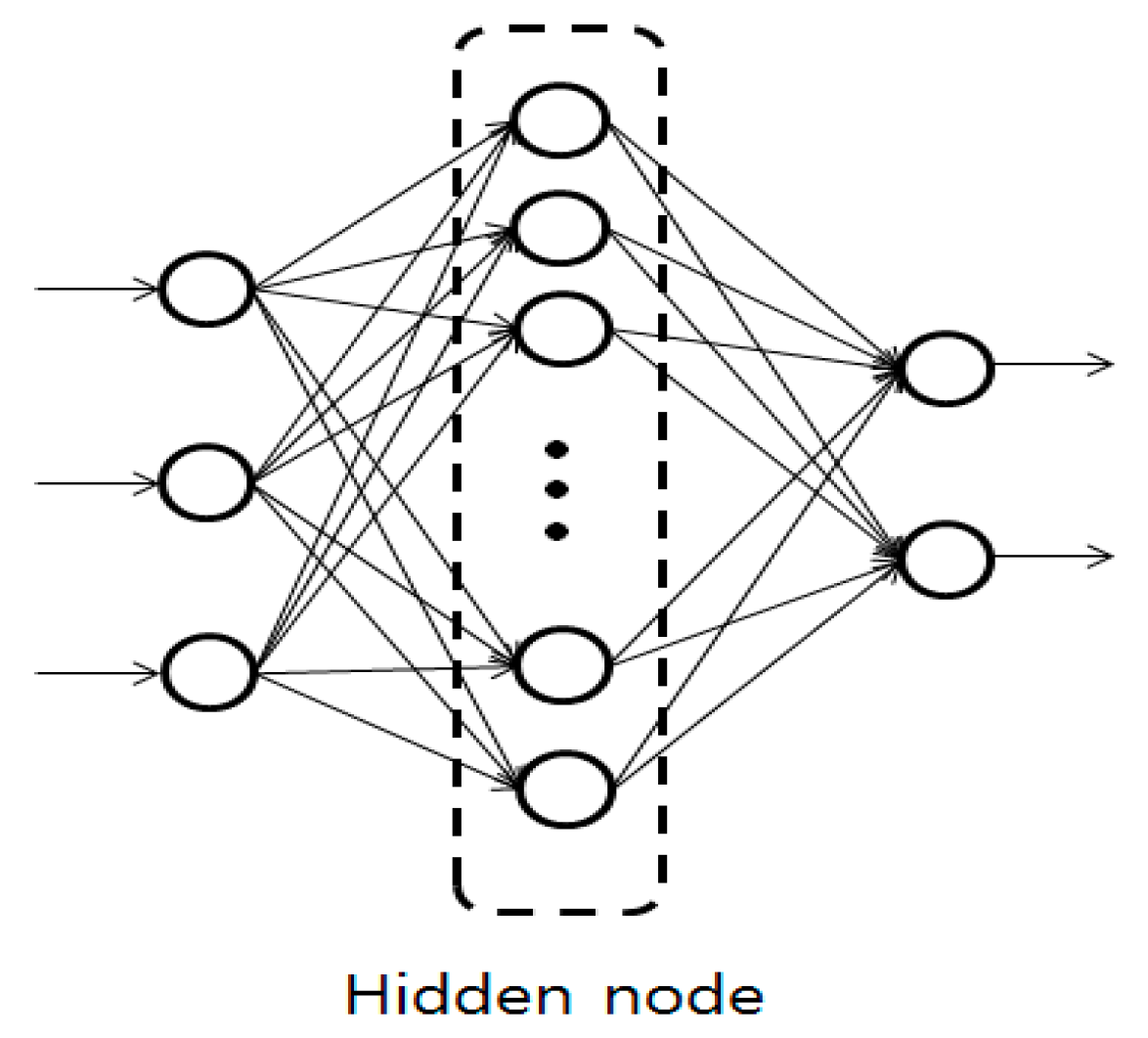
3.2. Multi-Layer Perceptron (MLP)
3.3. Evaluation of Risk Model
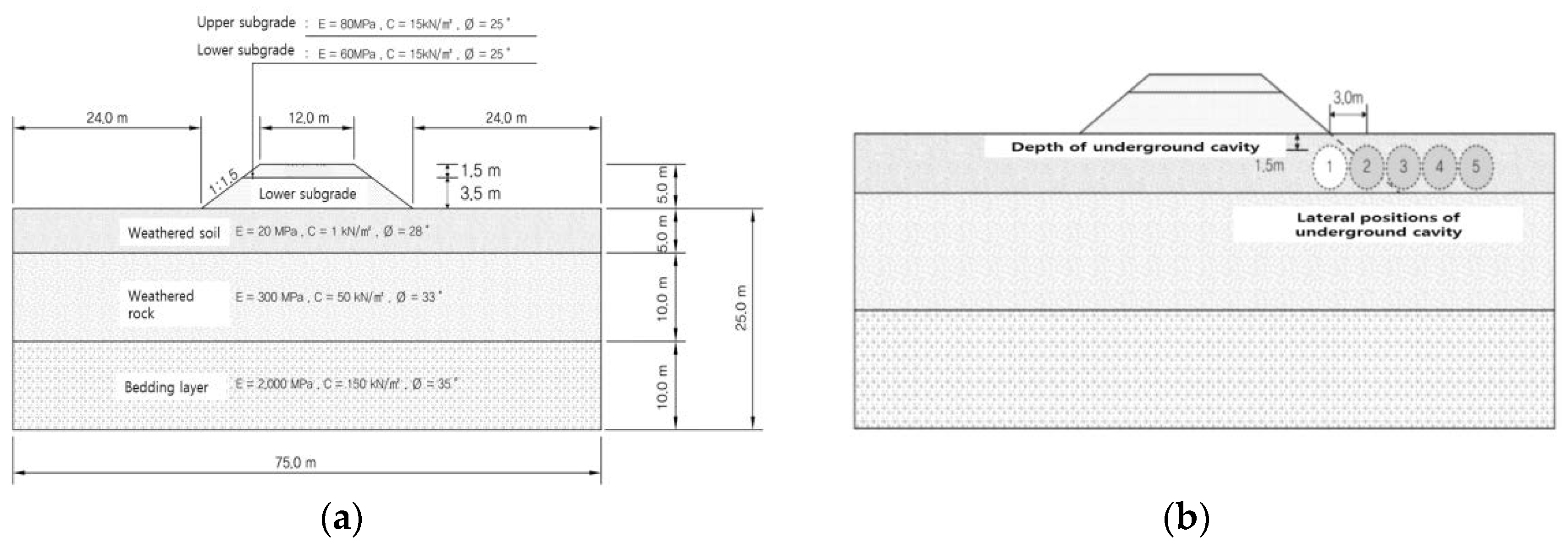
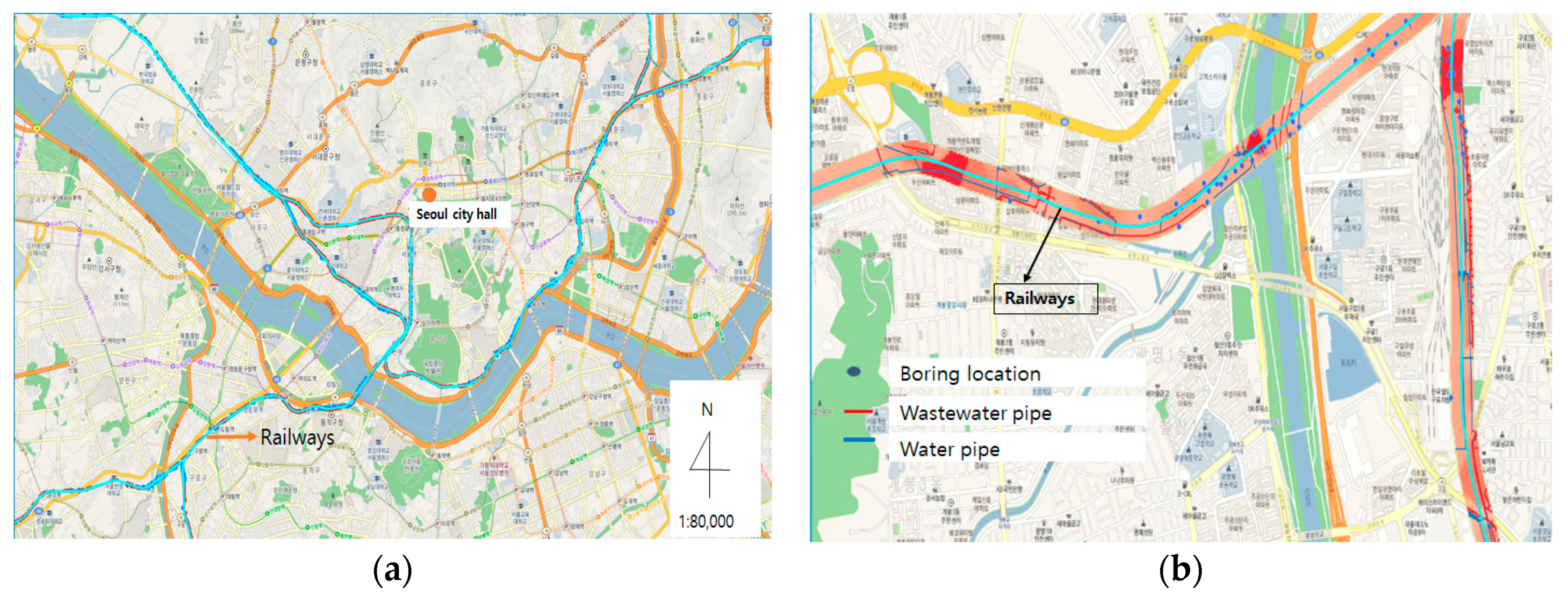
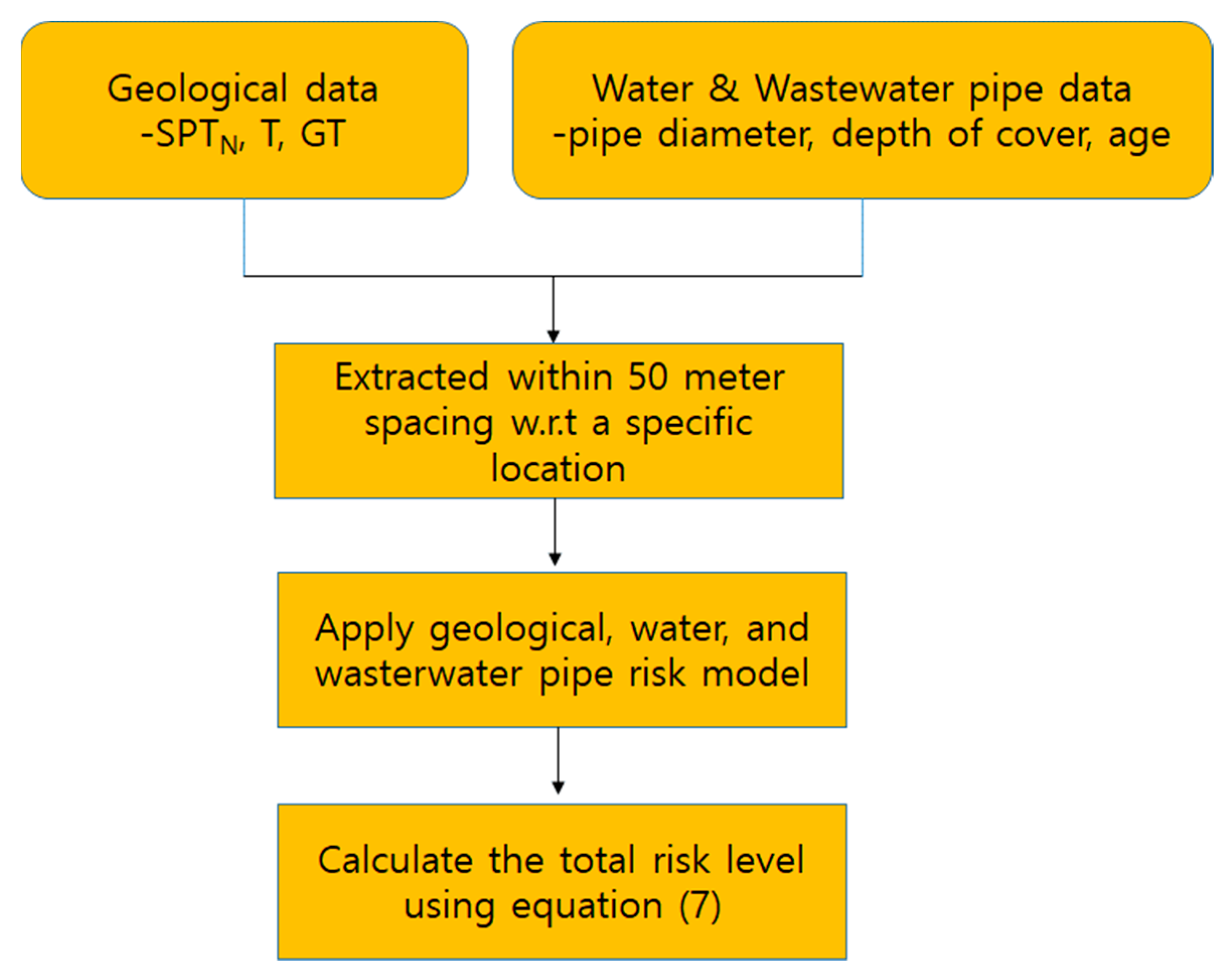
4. Field Evaluation of Risk Model
5. Concluding Remarks
- (1)
- Between the two approaches (i.e., SVM and MLP) employed in this study to develop a risk model, the MLP approach was found to be more efficient by improving the classification accuracy of the presence of ground subsidence.
- (2)
- The number of hidden nodes played a significant role in determining overall accuracy of the risk model. Considering the number of input data for water and wastewater pipes (564 for water and 929 for wastewater pipes), it was deemed appropriate to have more hidden nodes than inputs to ensure the reliability of the risk model. A previous study recommended that the number of hidden nodes be 1.5 times the number of parameters in the input layer [17].
- (3)
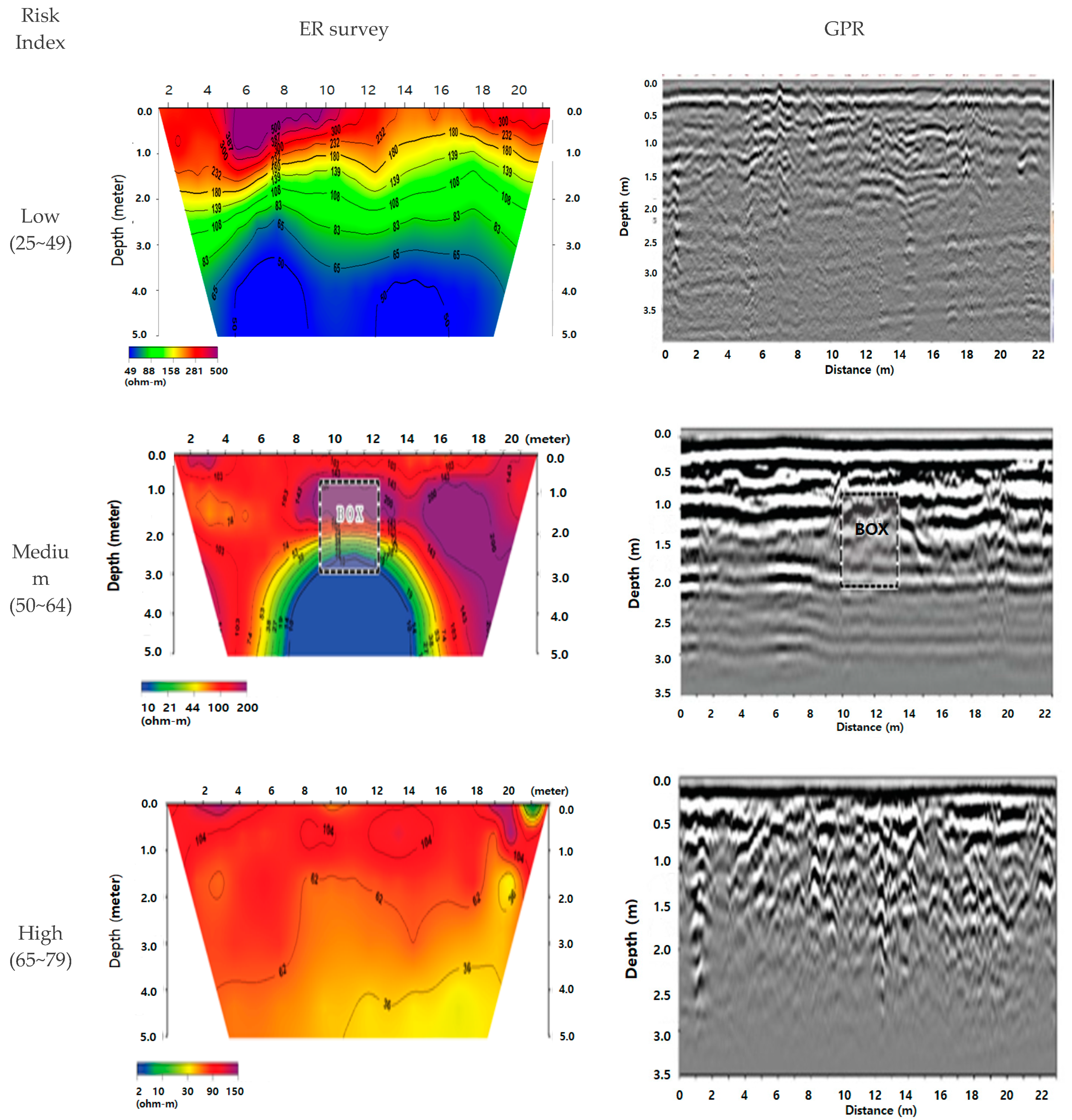
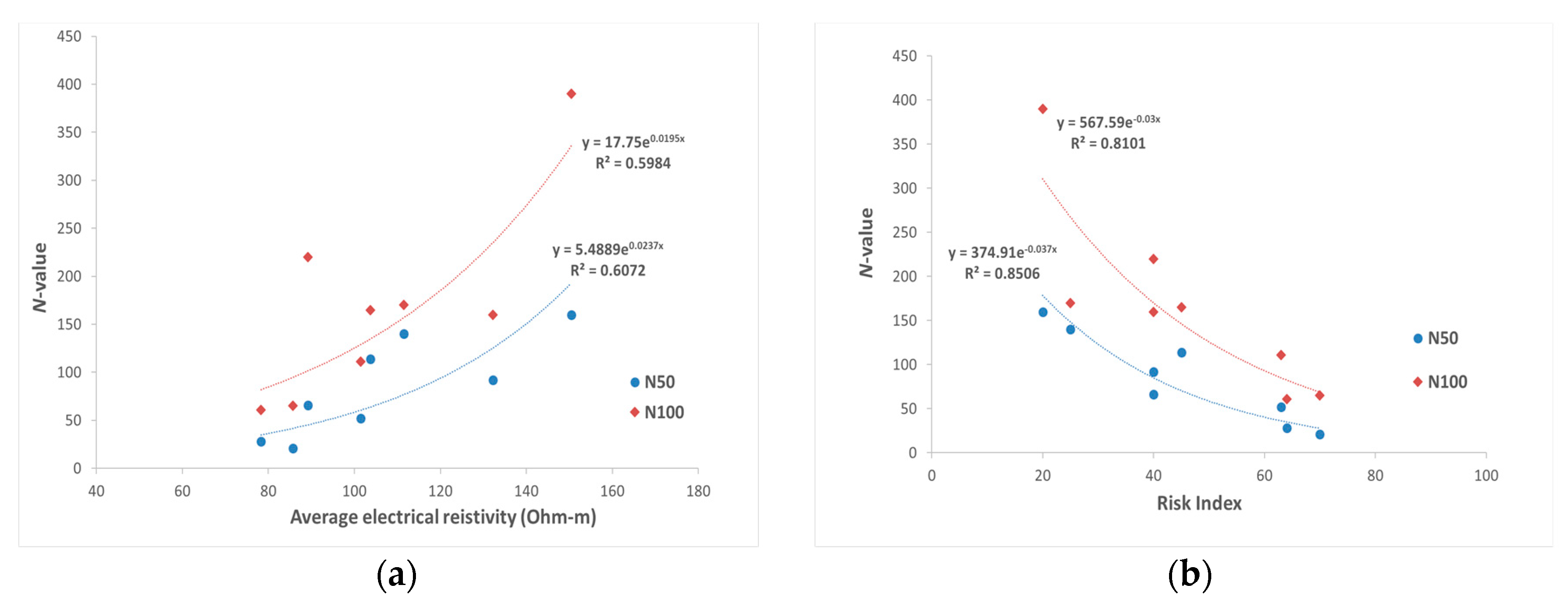
- A series of field experimental programs using GPR, ER survey, and PCP tests exhibited that the correlations between measurements seemed to be promising in the assessment of the risk index with respect to ground subsidence in spite of limited field validations. It is strongly recommended that further investigation needs to be done to verify this finding in the near future. Ground penetrating radar survey is useful to visually detect underground utilities and underground homogeneity. Electrical resistance survey gives the variation of electrical resistance, which can be quantified for the tested section. Pneumatic cone penetration testing provides bearing capacity of tested ground, which is associated with risk index and ER values. Consequently, the use of hazard map systems in conjunction with field investigation is recommended as a proactive approach to mitigate the progress of ground subsidence along railways.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Seoul Metropolitan Government. Investigation of Underground Cavity Mechanism; Research Report; Seoul Metropolitan Government: Seoul, Korea, 2015.
- Al-Kouri, O.; Al-Fugara, A.; Al-Rawashdeh, S.; Sadoun, B.; Pradhan, B. Geospatial Modeling for Sinkholes Hazard Map based on GIS&RS Data. J. Geog. Inf. Syst. 2013, 5, 584–592. [Google Scholar]
- Klimchouk, A. Morphogenesis of hypogenic caves. Geomorphol. 2009, 106, 100–117. [Google Scholar] [CrossRef]
- USGS. Available online: https://www.usgs.gov/faqs/what-difference-between-a-sinkhole-and-land-subsidence?qt-news_science_products=0#qt-news_science_products (accessed on 20 September 2018).
- Galve, J.P.; Remondo, J.; Gutierrez, F. Improving sinkhole hazard models incorporating magnitude–frequency relationships and nearest neighbor analysis. Geomorphol. 2011, 134, 157–170. [Google Scholar] [CrossRef]
- Galve, J.P.; Gutierrez, F.; Lucha, P.; Bonachea, J.; Remondo, J.; Cendrero, A.; Gutierrez, M.; Gimeno, M.J.; Pardo, G.; Sanchez, J.A. Sinkholes in the Salt-bearing evaporate karst of the Ebro River valley upstream of Zaragoza city (NE Spain) Geomorphological mapping and analysis as a basis for risk management. Geomorphology 2009, 108, 145–158. [Google Scholar] [CrossRef]
- Zhao, A.; Tang, A. Land subsidence risk assessment and protection in mined-out regions. Proc. IAHS 2015, 372, 145–150. [Google Scholar] [CrossRef]
- Park, J.K.; Cho, D.H.; Hossain, M.S.; Oh, J. Assessment of Settlement Profile Caused by Underground Box Structure Installation with an Artificial Neural Network Model. J. Transp. Res. Board 2018. [Google Scholar] [CrossRef]
- Park, H.I. Study for Application of Artificial Neural Networks in Geotechnical Problems. In Artificial Neural Networks-Application; IntechOpen: Rijeka, Croatia, 2011. [Google Scholar]
- Lee, H.; Kim, E. Genetic outlier detection for a robust support vector machine. Int. J. Fuzzy Log. Intell. Syst. 2015, 15, 96–101. [Google Scholar] [CrossRef]
- Lee, H.; Hong, S.; Kim, E. A new genetic feature selection with neural network ensemble. Int. J. Comput. Math. 2009, 1105–1117. [Google Scholar]
- Oh, J.; Kim, J.; Choi, J.; Kim, K. Smart Evaluation of Railroad Roadbed with Respect to the Ground Subsidence; Final Research Report No. 2017-50102-002; Korea Rail Network Authority: Daejeon, Korea, 2016. [Google Scholar]
- Yoo, H.; Oh, J. Mechanical and chemical reinforcements for the installation of underground utilities to mitigate underground cavity. J. Korean Soc. Hazard Mitig. 2017, 17, 257–268. [Google Scholar] [CrossRef]
- Oh, K.; Lee, H.; Hong, S.; Kim, E. Side view face recognition as an aid to gait recognition. In Proceedings of the Joint 3rd International Conference on Soft Computing and Intelligent Systems and 7th International Symposium on Advanced Intelligent Systems, Japan Society for Fuzzy Theory and Intelligent Informatics, Tokyo, Japan, 20–24 September 2006; pp. 490–495. [Google Scholar]
- Hagan, M.T.; Demuth, H.B.; Beale, H. Neural Network Design; PWS Publishing Company: Boston, MA, USA, 1995. [Google Scholar]
- Suen, C.Y.; Nadal, C.; Mai, T.; Legaulr, R.; Lam, L. Recognition of handwritten numerals based on the concept of multiple experts, In Proceedings of the 1st International Workshop on Frontiers Handwriting Recognition: Montreal, QC, Canada, 2–3 April 1990; pp. 131–144. [Google Scholar]
- Mamaqani, B. Numerical Modeling of Ground Movements Associated with Trenchless Box Jacking Technique. Ph.D. Thesis, The University of Texas, Arlington, TX, USA, 2014. [Google Scholar]
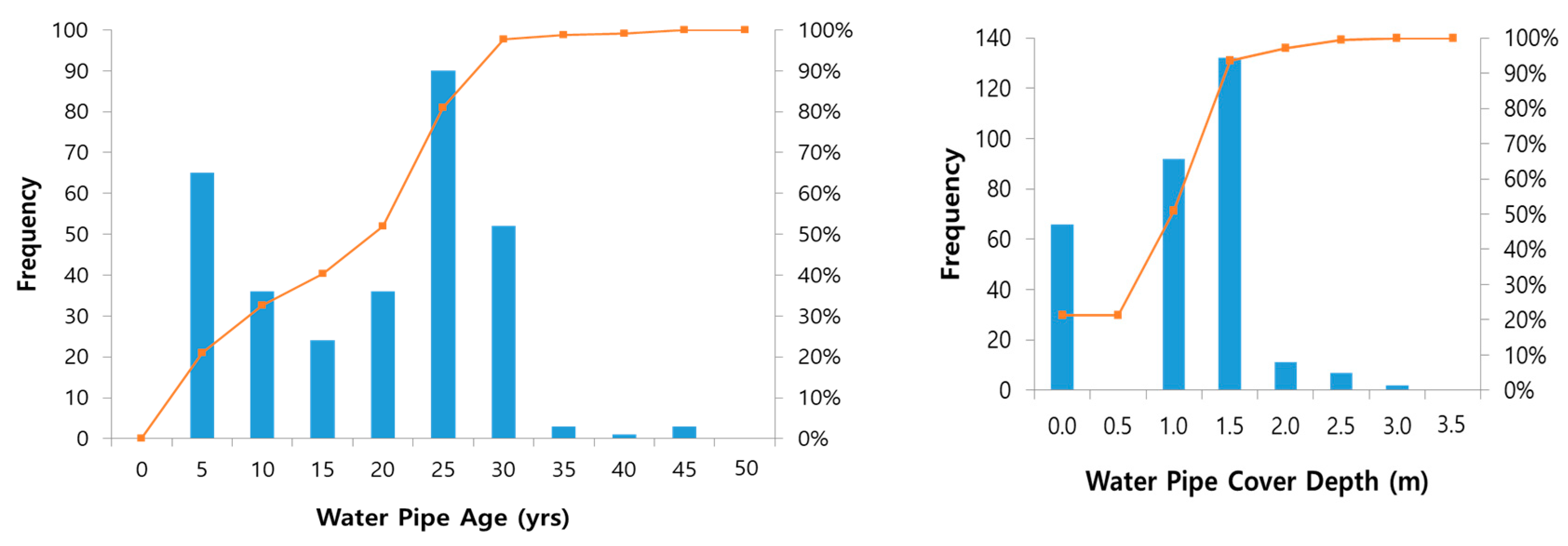
| Pipe Type | Installation Date | Diameter (m) | Length (m) | Average Depth (m) |
|---|---|---|---|---|
| Water | 19 October 2011 | 1.00 | 14.62 | 1.10 |
| Wastewater | 1 January 1997 | 4.50 | 59.09 | 2.00 |
| Wastewater | 1 January 1989 | 7.00 | 4.01 | 5.00 |
| Water Supply Risk Prediction | Indicator of Event | No. of Event | Classification Accuracy (%) | Overall Accuracy (%) | |
|---|---|---|---|---|---|
| 0.00 | 1.00 | ||||
| Polynomial kernel | 0.00 | 99 | 55 | 64.3 | 81.5 |
| 1.00 | 31 | 279 | 90.0 | ||
| Radial basis function (RBF) kernel | 0.00 | 112 | 42 | 72.7 | 86.6 |
| 1.00 | 20 | 290 | 93.5 | ||
| Water Supply Risk Prediction | Indicator of Event | No. of Event | Classification Accuracy (%) | Overall Accuracy (%) | |
|---|---|---|---|---|---|
| 0.00 | 1.00 | ||||
| Hidden node: 100 | 0.00 | 126 | 28 | 81.8 | 89.9 |
| 1.00 | 19 | 291 | 93.9 | ||
| Hidden node: 300 | 0.00 | 132 | 22 | 85.7 | 92.2 |
| 1.00 | 14 | 296 | 95.5 | ||
| Hidden node: 500 | 0.00 | 127 | 27 | 82.5 | 90.3 |
| 1.00 | 18 | 292 | 94.2 | ||
| Hidden node: 700 | 0.00 | 135 | 19 | 87.7 | 92.7 |
| 1.00 | 15 | 295 | 95.2 | ||
| Wastewater Supply Risk Prediction | Indicator of Event | No. of Event | Classification Accuracy (%) | Overall Accuracy (%) | |
|---|---|---|---|---|---|
| 0.00 | 1.00 | ||||
| Polynomial kernel | 0.00 | 827 | 1 | 99.9 | 89.6 |
| 1.00 | 96 | 5 | 5.0 | ||
| RBF kernel | 0.00 | 818 | 10 | 98.8 | 90.3 |
| 1.00 | 80 | 21 | 20.1 | ||
| Wastewater Supply Risk Prediction | Indicator of Event | No. of Event | Classification Accuracy (%) | Overall Accuracy (%) | |
|---|---|---|---|---|---|
| 0.00 | 1.00 | ||||
| Hidden node: 100 | 0.00 | 799 | 29 | 96.5 | 89.3 |
| 1.00 | 37 | 64 | 36.6 | ||
| Hidden node: 300 | 0.00 | 810 | 18 | 97.8 | 91.6 |
| 1.00 | 60 | 41 | 40.6 | ||
| Hidden node: 500 | 0.00 | 809 | 19 | 97.7 | 92.8 |
| 1.00 | 48 | 53 | 52.5 | ||
| Hidden node: 700 | 0.00 | 807 | 21 | 97.5 | 93.3 |
| 1.00 | 41 | 60 | 59.4 | ||
| Total Risk Index (%) | Description |
|---|---|
| 80~100 | Very high risk requires closing the line for repair |
| 65~79 | High risk requires immediate maintenance action |
| 50~64 | Medium risk requires periodic maintenance action |
| 25~49 | Low risk requires a maintenance plan |
| <25 | Very low risk requires no maintenance action |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, H.; Oh, J. Establishing an ANN-Based Risk Model for Ground Subsidence Along Railways. Appl. Sci. 2018, 8, 1936. https://doi.org/10.3390/app8101936
Lee H, Oh J. Establishing an ANN-Based Risk Model for Ground Subsidence Along Railways. Applied Sciences. 2018; 8(10):1936. https://doi.org/10.3390/app8101936
Chicago/Turabian StyleLee, Heesung, and Jeongho Oh. 2018. "Establishing an ANN-Based Risk Model for Ground Subsidence Along Railways" Applied Sciences 8, no. 10: 1936. https://doi.org/10.3390/app8101936
APA StyleLee, H., & Oh, J. (2018). Establishing an ANN-Based Risk Model for Ground Subsidence Along Railways. Applied Sciences, 8(10), 1936. https://doi.org/10.3390/app8101936





