Abstract
Most methods for singular points detection usually depend on the orientation fields of fingerprints, which cannot achieve reliable and accurate detection of poor quality fingerprints. In this study, a new method for fingerprint singular points detection based on Faster-RCNN (Faster Region-based Convolutional Network method) is proposed, which is a two-step process, and an orientation constraint is added in Faster-RCNN to obtain orientation information of singular points. Besides, we designed a convolutional neural network (ConvNet) for singular points detection according to the characteristics of fingerprint images and the existing works. Specifically, the proposed method could extract singular points directly from raw fingerprint images without traditional preprocessing. Experimental results demonstrate the effectiveness of the proposed method. In comparison with other detection algorithms, our method achieves 96.03% detection rate for core points and 98.33% detection rate for delta points on FVC2002 DB1 dataset while 90.75% for core points and 94.87% on NIST SD4 dataset, which outperform other algorithms.
1. Introduction
Of all biological characteristics, fingerprints have become one of the most describable biometric traits and used for biometric verification and identification tasks [1]. Nevertheless, with explosive growth in fingerprint databases (e.g., ID Card fingerprints), automatic recognition system has become increasingly more difficult than ever. As a global feature of fingerprint, singular points (shown in Figure 1) [1] could be used in fingerprint pattern classification [2], which could reduce the matched templates so as to reduce matching time in large databases during identification tasks. Moreover, since the fingerprint alignment according to minutiae is usually not so satisfactory, singular points are used as reference points for alignment in fingerprint minutiae matching [3]. In [4], a robust fingerprint matching system is proposed by extracting region of interest (ROI) centered at the core points and align two fingerprints by maximizing their orientation correlation.

Figure 1.
Fingerprint singular points: (a) core points, (b) delta point.
In [5], Kawagoe et al. proposed a Poincare index approach to obtain singular regions for fingerprint classification. By calculating the cumulative changes along a counter-clockwise closed contour in fingerprint orientation field, Zhou et al. [6] proposed an improved method based on Poincare index to judge whether there exist singular points. However, almost the methods based on Poincare index are fully depended on fingerprint orientation field Then, algorithms are affected by noise easily. To solve this problem, the Zero-pole Model and Hough Transform (HT) are combined to detect singular points in [7] and the Poincare index is used to refine positions of the candidate singular points. Contrary to orientation field generation, detection of singular points is simplified to determine the parameters of the Zero-pole Model. Obviously, the performance of these conventional algorithms for singular points detection is limited by the accuracy of the Poincare index.
Nowadays, the progress on the development of deep convolutional neural networks (CNNs) [8] has significantly advanced the state-of-the-art performance on a wide variety of computer vision tasks (e.g., face recognition [9,10], video recognition [11]). In object detection tasks, Faster-RCNN [12] obtained an excellent performance and a Region Proposal Network (RPN) was introduced to simultaneously predict object bounds and corresponding scores at each position. Finally, locations of objects could be determined according to corresponding scores. Furthermore, Izadpanahkakhk et al. [13] proposed a novel approach for palmprint verification by using deep region of interest (ROI) and feature extraction models.
Due to the outstanding learning behavior, CNNs are also used in fingerprint fields. Wang et al. [14] achieved an outstanding effect in fingerprint classification tasks based on the depth neural network method. In [15], deep learning technique also shows good performance in partial fingerprint matching. Labati et al. [16] proposed a two-step CNN method to extract the coordinates of the sweat pores from fingerprint images, which perform first the detection of candidate regions and Then, the extraction of the points of interest in the second step. Besides, Qin et al. [17] used fully convolutional networks (FCN) [18] to detect fingerprint singular points. Nevertheless, this method only predict location information and obtain poor performance on some specific fingerprint images, such as the issue that two core points are very close.
In this study, we propose a new method for singular points detection based on Faster-RCNN [12] and an orientation constraint is introduced to obtain orientation information of singular points, which is usually used for fingerprint alignment. Besides, since not all fingerprint images have delta points, on the other hand, fingerprint alignment can be achieved only by orientations of up-core points, Then, we only estimate that of up-core points. By studying the characteristics of fingerprint images, we design a convolutional neural network for singular points detection. Moreover, a two-step strategy is chosen to achieve this task. In the first step, some candidate patches where there might exist singular points are generated and the network could calculate cursory locations of the probable singular points. In the second step, singular points will be extracted by another network from all candidate patches, including the location and orientation of singular points. Furthermore, because it is a fully feed-forward step and does not need to process those complex steps (e.g., orientation field calculation), the proposed method could achieve a very fast speed for detection tasks.
2. Proposed Method
In this section, we present a fast and exact scheme for singular points detection based on Faster-RCNN by analyzing the differences between singular points and generic objects in details. Figure 2 shows the overall flowchart of the proposed method: Generating proposals in pixel level (Step 1): a raw fingerprint image is input into the networks to extract features and the shared feature map is used to generate corresponding features of each grid cell to predict the probability whether there might exist a singular point or not and calculate coarse location information of the singular point through classification and regression tasks. Thus, proposals will be generated by ranking the probability and the coarse location information; Classifying the candidate patches generated by the proposals, refining the location and calculating the orientation information (Step 2): this is regarded as a singular point extractor, which is applied on all candidate patches to detect singular points. Section 2.1 and Section 2.2 describe the two processes in detail.
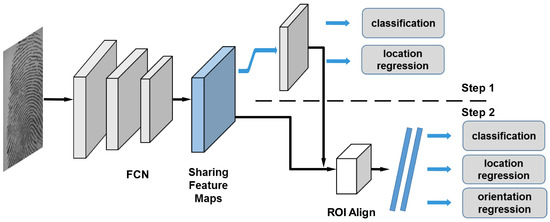
Figure 2.
The overall flowchart of our proposed method. Each thin rectangle denotes a fully-connected layer.
2.1. Generating Proposals
For generic object detection task in Faster-RCNN [12], deep FCN (e.g., VGG model [19]) usually needs to extract objects which are often from more than 10 different subject classes in natural images. Different objects in images usually contain different features, such as color, shape and size. The mixture of these features often makes the detection tasks more difficult. As for fingerprint images, they are usually gray scale images and not as complex as natural images. Moreover, the elements that make up fingerprints are ridges which are represented by dark lines in fingerprint images, Then, the structures of singular points are much more simple than generic objects so that this detection task can be achieved by a shallow and wide FCN, which ensures that network can process any images with different sizes.
Inspired by the success of object detection on natural images, singular points detection could be regarded as a point detection problem. As shown in Figure 3, the proposed FCN is composed of three convolutional blocks, four additional convolutional layers (three (Conv, 256, 3) and one (Conv, 3, 3)) and an up-sample layer. Each convolutional block is connected by a max-pooling layer and consists of two convolutional layers, followed by batch normalization (BN) layer [20] and exponential linear unit (ELU) layer [21]. In our study, the filter size of all convolutional layers is set to , while that of all max-pooling layers is fixed to .
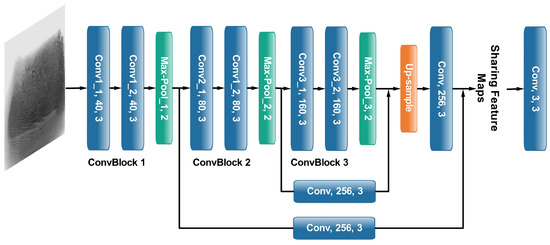
Figure 3.
The proposed FCN architecture.
Figure 3 shows that the network extracts features from raw fingerprint images. Instead of only using the features extracted by final layer, a more effective backbone named Feature Pyramid Network (FPN) [22] is explored. In FPN, a top-down architecture with lateral connections is used to build an in-network feature pyramid from a single-scale input. In addition, the operation in FPN could upsample the features of high levels to get the same size of features in bottom level and combine high-level and low-level features, which could make extracted features contain more corresponding information for detection tasks. As shown in Figure 3, three feature maps from different convolutional blocks are added into sharing feature maps where the same features are used extracted from raw fingerprint images in both steps.
The network is used to map raw fingerprint to point-score map, namely the output of the network. Specially, each value is a probability measured whether there might exist a singular point in a patch from the raw fingerprints. Besides, a raw fingerprint image includes at most four singular points (up-core, down-core, left-delta, right-delta) and these points are not often close in image each other. Therefore, it is hardly to exist two singular points in one box with small size in a raw fingerprint image. In our study, we divide the input image into a gird which is designed to have the same size as the shared feature map and each grid cell is set to a pixel box. The shared feature map is used to generate corresponding features of each grid cell and the network will use the features to process classification and regression tasks and train the network in order to predict the probability that there is a singular point and calculate coarse location of the singular point. In concrete terms, when there might exist singular points in the corresponding region, a high score (probability) could be gotten. In order to get more accurate locations, a multi-task loss (location regression and classification) (see Figure 2) is used to train the network to refine the locations of singular points. Section 2.3 will describe this process in detail. Thus, proposals will be generated according to the probability and the coarse location information.
2.2. Fine Single Point Extractor
From Section 2.1, large numbers of proposals without orientation information are generated by the network. To generate candidate patches which are big enough for detection task, we choose pixel patches and choose top-100 patches ranked by the probabilities (after non-maximum suppression) as the candidate patches. The number of the candidate patches is set to be larger than the number of true singular points in a single fingerprint image (at most four singular points) so that our method can ensure the efficiency of the second step. As we choose more candidate patches than true singular points in each fingerprint images and the patches are different from the gird cells in size and location, the patches also need to be classified to predict the probability whether there exists a singular point in each patch. Moreover, this network will use the shared feature map to extract corresponding features of each patch so that the running time will be reduced. Then, in the second step, candidate patches expanded by these proposals will be reclassified and their orientations will be calculated based on corresponding regions.
As these patches are centering on the predicted coarse locations of the singular points, it is necessary to extract the features of the corresponding region for precise prediction. A RoIAlign [23] operation is used to extract features of each patch, which uses bilinear interpolation to compute the exact values of features and will keep location information of each patch. In order to obtain orientation information, an orientation constraint is added in the network (see Figure 2). Then, the corresponding regions centering at proposals are used to train the network with another multi-task loss consisting of location classification, location regression and orientation regression. Finally, location information will be refined and orientation information will be calculated, while the probability (score) will be predicted according to whether the candidate patches exist singular points. Thus, we can get the corresponding regions centering at singular points and the center coordinates of the regions are the coordinates of singular points according to the location information and probability. Combining with the orientation information, singular points will be detected. Furthermore, the same features, which are extracted from raw fingerprint images in the first step, are used from sharing feature maps; thus, singular points extracting speed could be accelerated.
2.3. Loss Definition and Training
To train the network, we assign a positive label to a grid cell with a singular point, while these grid cells will be labeled by a negative label if its neighborhood does not contain a singular point. Thus, this can ensure that the grid cells without singular points but close to any singular point are not used to train the network. Moreover, we use all positive grid cells and the same number of negative grid cells in the training to keep the sampled positive and negative cells balanced. As described in Section 2.1 and Section 2.2, a two-step strategy is chosen to achieve this detection task.
In the first step, the network generates a large number of proposals without orientation information. Specifically, a raw fingerprint image is input into the networks and divided into a grid. These labeled grid cells are used for classification and regression tasks to train the network. Then, the network predicts the probability that there is a singular point and calculate coarse location of the singular point so that proposals will be generated according to the probability and the coarse location information. In order to get more accurate locations, the network is trained under a multi-task loss (location classification and regression ) to refine the locations of singular points. For the location classification, we chose the categorical cross-entropy loss. It takes the formulation
where is the truth label of class i, is the predicted probability that there exists a singular point. n is the number of subject classes. Because a raw fingerprint image consists of at most four kinds of singular points, Then, the number of classes n is 5 (the background is regarded as a subject class) in our works.
For the location regression , we used the smooth loss with the Euclidean distance between the ground truth location and the predicted location. The location regression is formulated as
where , are the location coordinates of the center of the regions where there might exist singular points and ground-truth singular points, is the output of the network. We regress to the difference between the center coordinates and the singular points coordinates instead of the location of the singular points. is the function of the smooth loss and expressed as
Then, the loss function for the first step is a joint loss function combined with the categorical cross-entropy loss (Equation (1)) and the regression loss (Equation (2)) and takes the formulation
where is the number of all samples and scalar is used as a weight for balancing the two loss functions. Since only regions in which there might exist singular points are used for location regression, Then, mean of is used in , here label is ranged from 0 to 4 and means that object belongs to background.
In the second step, candidate patches generated by the proposals are chosen to train the network to calculate orientation information of singular points and refine the location. As candidate patches expanded by proposals are different from these proposals, the patches will be reclassified and regressed to refine the location and orientation information. All patch samples that are generated from a candidate proposal have the same label. We regard these samples, which are generated from background and get high predicted scores in the first step, as hard samples. When training the network, hard samples will be used to improve detection performance. In our works, patch samples and hard samples are selected by a ratio of 1:2. Similar to the location regression, an orientation constraint using the smooth loss is added in multi-task loss proposed in the first step to learn the proposal network to predict orientations of singular points. In order to learn orientation information more easily, orientation is normalized to . The orientation constraint can be expressed as
where refer to the predicted orientation and correspond to the ground-truth orientation after normalization. In the right of Equation (5), and are used to measure the distance between the predicted and the ground truth orientation. Thus, the multi-task loss for this stage is defined as follows:
Similar to scalar in Equation (4), scalar and are used as weights to balance the loss functions. Finally, we adopt an end-to-end approach combining with a joint loss in two steps, where scalar is also used as a weight.
In this study, scalar , and is fixed to 0.5, 200, 1 respectively. Then, the network is learned through minimizing the loss using stochastic gradient descent (SGD) with the standard back-propagation. To avoid border effects during training, all the convolutional layers have no padding operations.
3. Experimental Results
In this section, the experimental results are shown to evaluate the proposed method and its comparison with others. In concrete terms, we firstly presented the experimental setups including datasets, and parameter setups. Secondly, we compared the proposed method with other algorithms in terms of singular points detection performance on fingerprint public datasets FVC2002 DB1 and NIST DB4.
3.1. Experimental Setup
The experimental evaluation of the proposed method and its comparison with other algorithms are performed on FVC2002 (800 images) [24], NIST sd04 (4000 images) [25] and Ten-Finger Card dataset (62,655 images) from a laboratory database. Specifically, we randomly choose data from Ten-Finger Card dataset as training data and the residual data are used for testing. The FVC2002 DB1 and NIST sd04 datasets are randomly sampled for training and testing respectively. Meanwhile, we randomly selected images from training data to generate the validation data to validate the performance of network during training. Obviously, singular points location and orientation (only up-core) of fingerprint images should be marked out artificially for training. However, it is extremely difficult to achieve because it is a time-consuming and labor-intensive work. Thus, we choose the singular points detection algorithm [7] to automatically extract the singular points information of Ten-Finger Card fingerprints, while the singular points of FVC2002 and NIST sd04 fingerprints are manually labeled beforehand as the ground truth labels. Besides, neither enhancement nor segmentation are carried out on all fingerprint images.
In our works, the weights of each layer are initialized by drawing randomly from a Gaussian distribution with zero mean and standard deviation and biases are set to 0. A weight decay with the coefficient is used to prevent overfitting. The learning rate is initialized to 0.001 and changed with iteration steps by an exponent drop.
The Tensorflow (https://www.tensorflow.org/) (version 1.4.1) [26] framework is used to implement the proposed method and the experiments are run on the machine with an Intel Core i7-6700 CPU at 3.4 GHz, 16 GB RAM, and a NVIDIA GeForce GTX 1060 GPU. Moreover, when testing the proposed method, we can even use a CPU to achieve the process.
3.2. Singular Points Detection Performance
In this subsection, we compare the detection performance on FVC2002 DB1 and NIST sd04 public datasets to demonstrate the effect of the proposed deep learning detection method with conventional detection algorithms [6,7,27] and deep learning detection method [17]. The detection rate and false alarm rate are chosen as the indicators measured.
Figure 4 shows some illustrations of the performance of our method on the Ten-Finger Card fingerprint dataset. From Figure 4, it can be shown that our method could extract the singular points accurately, including the location and orientation information of singular points. In addition, our method could also achieve good performance on poor quality images.
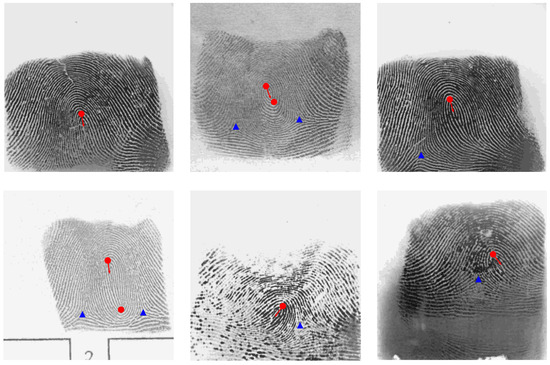
Figure 4.
Illustrations of of the performance of our method over the Ten-Finger Card fingerprint dataset. Red dots and blue triangles denote the core points and delta points respectively, while the red arrows represent the orientations of up-core points.
Specially, an extracted singular point by our method will be regarded as a truth singular point if the difference between the predicted location coordinates and the ground truth location is less than 10 pixels, while the difference between the predicted orientation and the ground truth is less than . It takes the formulation
We compare our proposed algorithm with other algorithms in terms of singular point detection performance on FVC2002 DB1 and NIST sd04 datasets. Table 1 and Table 2 describe the detection rate and false alarm rate comparisons with existing detection algorithms on FVC2002 DB1 and NIST sd04 respectively. We note that our method outperforms other detection algorithms on detection performance on the two datasets. In addition, the detection speed of our method is about 95 milliseconds on a GPU averagely. Figure 5 shows some illustrations over the two methods in [7,17] and our method. As shown in Figure 5, our method and the method of Qin et al. [17] could achieve better effect than the method of Fan et al. [7] on poor quality images for location information of singular points. For some special issues (e.g., arch fingerprint images), our method could perform better than the two methods. Furthermore, our method could obtain orientation information compared with the two methods.

Table 1.
The performance comparisons with different algorithms on FVC2002 DB1 dataset.

Table 2.
The performance comparisons with different algorithms on NIST sd04 dataset.
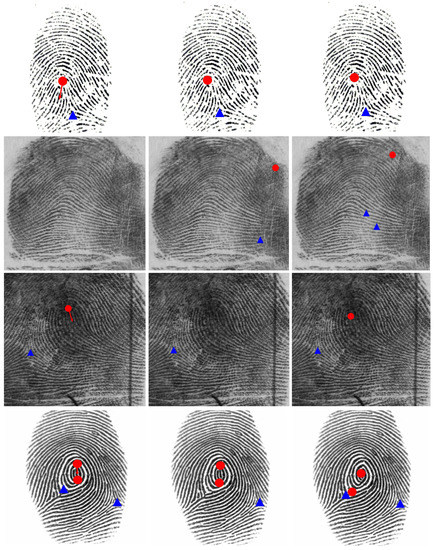
Figure 5.
Illustrations of singular points detection over our method, the method of Fan et al. [7], the method of Qin et al. [17] from left to right. Red dots and blue triangles denote the core points and delta points respectively, while the red arrows represent the orientations of up-core points.
4. Conclusions and Future Lines
This paper presents an end-to-end method for singular points detection and a shallow and wide fully convolutional network, which ensures that a network can process any images with different sizes to generate candidate patches from raw fingerprint images. By setting a default threshold, the network will predict the probability which there exists a singular point in the patch, so location coordinates (center coordinates of the patches) and orientation of a singular point will be calculated after ranking the probabilities. Experimental results show that the proposed method achieves a better performance than other detection algorithms for detection tasks. Moreover, the proposed method is a fully feed-forward step and does not need to process complex preprocessing (e.g., orientation field calculation). Besides, we believe that our method will perform better if using more accurate data (e.g., artificially marked totally) to train the network. In future work, we plan to continue to improve the proposed FCN to generate more precise candidate patches to improve the detection performance. Meanwhile, we will change the training and detection strategies to achieve fingerprint minutiae extraction.
Author Contributions
Y.L. wrote and modified the paper. Y.L. and B.Z. achieved the algorithm and performed the experiments. C.H. supplied the resources of the work. T.G. performed the project administration. C.H. and T.G. supervised the research. J.Q. designed the algorithm.
Funding
This research was funded by State Key Program of National Natural Science Foundation of China grant number 11731013 and 11331012, and funded by National Natural Science Foundation of China grant number 11571014.
Acknowledgments
All authors thank the two anonymous reviewers and editors for their comments and proofreading.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Maltoni, D.; Maio, D.; Jain, A.K.; Prabhakar, S. Handbook of Fingerprint Recognition; Springer: New York, NY, USA, 2009. [Google Scholar]
- Guo, J.; Liu, Y.; Chang, J.; Lee, J. Fingerprint classification based on decision tree from singular points and orientation field. Expert Syst. Appl. 2014, 41, 752–764. [Google Scholar] [CrossRef]
- Jiang, X.; Yau, W. Fingerprint minutiae matching based on the local and global structures. In Proceedings of the IEEE International Conference on Pattern Recognition (ICPR), Barcelona, Spain, 3–7 September 2000; pp. 1038–1041. [Google Scholar]
- Kumar, R.; Chandra, P.; Hanmandlu, M. A robust fingerprint matching system using orientation features. J. Inf. Process. Syst. 2016, 12, 83–89. [Google Scholar]
- Kawagoe, M.; Tojo, A. Fingerprint pattern classification. Pattern Recognit. 1984, 17, 295–303. [Google Scholar] [CrossRef]
- Zhou, J.; Chen, F.; Gu, J. A novel algorithm for detecting singular points from fingerprint images. IEEE Trans. Pattern Anal. Mach. Intell. (TPAMI) 2009, 31, 1239–1250. [Google Scholar] [CrossRef] [PubMed]
- Fan, L.; Wang, S.; Wang, H.; Guo, T. Singular points detection based on zero-pole model in fingerprint images. IEEE Trans. Pattern Anal. Mach. Intell. (TPAMI) 2008, 30, 929–940. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. In Proceedings of the Advances in Neural Information Processing Systems (NIPS), Lake Tahoe, NV, USA, 3–8 December 2012; pp. 1097–1105. [Google Scholar]
- Sun, Y.; Chen, Y.; Wang, X.; Tang, X. Deep learning face representation by joint identification-verification. In Proceedings of the Advances in Neural Information Processing Systems (NIPS), Montreal, QC, Canada, 8–13 December 2014; pp. 1988–1996. [Google Scholar]
- Liu, W.; Wen, Y.; Yu, Z.; Li, M.; Raj, B.; Song, L. Sphereface: Deep hypersphere embedding for face recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 212–220. [Google Scholar]
- Zhu, X.; Xiong, Y.; Dai, J.; Yuan, L.; Wei, Y. Deep feature flow for video recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 2349–2358. [Google Scholar]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster r-cnn: Towards real-time object detection with region proposal networks. In Proceedings of the Advances in Neural Information Processing Systems (NIPS), Montreal, QC, Canada, 7–12 December 2015; pp. 91–99. [Google Scholar]
- Izadpanahkakhk, M.; Razavi, S.M.; Taghipour-Gorjikolaie, M.; Zahiri, S.H.; Uncini, A. Deep Region of Interest and Feature Extraction Models for Palmprint Verification Using Convolutional Neural Networks Transfer Learning. Appl. Sci. 2018, 8, 1210. [Google Scholar] [CrossRef]
- Wang, R.; Han, C.; Guo, T. A novel fingerprint classification method based on deep learning. In Proceedings of the IEEE International Conference on Pattern Recognition (ICPR), Cancún, Mexico, 4–8 December 2016; pp. 931–936. [Google Scholar]
- Qin, J.; Tang, S.; Han, C.; Guo, T. Partial fingerprint matching via phase-only correlation and deep convolutional neural network. In Proceedings of the International Conference on Neural Information Processing (ICONIP), Guangzhou, China, 14–18 November 2017; pp. 602–611. [Google Scholar]
- Labati, R.D.; Genovese, A.; Muñoz, E.; Piuri, V.; Scotti, F. A novel pore extraction method for heterogeneous fingerprint images using Convolutional Neural Networks. Pattern Recognit. Lett. 2017. [Google Scholar] [CrossRef]
- Qin, J.; Han, C.; Bai, C.; Guo, T. Multi-scaling detection of singular points based on fully convolutional networks in fingerprint images. In Proceedings of the Chinese Conference on Biometric Recognition (CCBR), Shenzhen, China, 28–29 October 2017; pp. 221–230. [Google Scholar]
- Long, J.; Shelha, E. Fully convolutional networks for semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 3431–3440. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv, 2014; arXiv:1409.1556. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In Proceedings of the International Conference on International Conference on Machine Learning (ICML), Lille, France, 6–11 July 2015; pp. 448–456. [Google Scholar]
- Clevert, D.A.; Unterthiner, T.; Hochreiter, S. Fast and Accurate Deep Network Learning by Exponential Linear Units (ELUs). arXiv, 2015; arXiv:1511.07289. [Google Scholar]
- Lin, T.; Dollár, P.; Girshick, R.; He, K.; Hariharan, B.; Belongie, S. Feature pyramid networks for object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 936–944. [Google Scholar]
- He, K.; Gkioxari, G.; Dollár, P.; Girshick, R. Mask r-cnn. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 2980–2988. [Google Scholar]
- Maio, D.; Maltoni, D.; Cappelli, R.; Wayman, J.L.; Jain, A.K. FVC2002: Second fingerprint verification competition. In Proceedings of the IEEE International Conference on Pattern Recognition (ICPR), Quebec City, QC, Canada, 11–15 August 2002; pp. 811–814. [Google Scholar]
- Watson, C.; Wilson, C. Nist Special Database 4; Fingerprint Database; National Institute of Standards and Technology: Gaithersburg, MD, USA, 1992; Volume 17, p. 77. [Google Scholar]
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; et al. TensorFlow: Large-scale machine learning on heterogeneous systems. arXiv, 2016; arXiv:1605.08695. [Google Scholar]
- Chikkerur, S.; Ratha, N. Impact of singular point detection on fingerprint matching performance. In Proceedings of the Fourth IEEE Workshop on Automatic Identification Advanced Technologies (AutoID’05), Buffalo, NY, USA, 17–18 October 2005; pp. 207–212. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).