On the Contribution of Wind Farms in Automatic Generation Control: Review and New Control Approach
Abstract
:1. Introduction
- (1)
- Wind farms contribution to frequency regulation of power systems is studied.
- (2)
- Review on application of wind farms in AGC is presented.
- (3)
- The FOPID controller is applied to variable speed wind turbine.
- (4)
- Performance of FOPID controller for variable speed wind turbine-based wind farm is compared to classical controller.
- (5)
- Frequency variation effect of different penetration levels of wind farms in power systems is investigated.
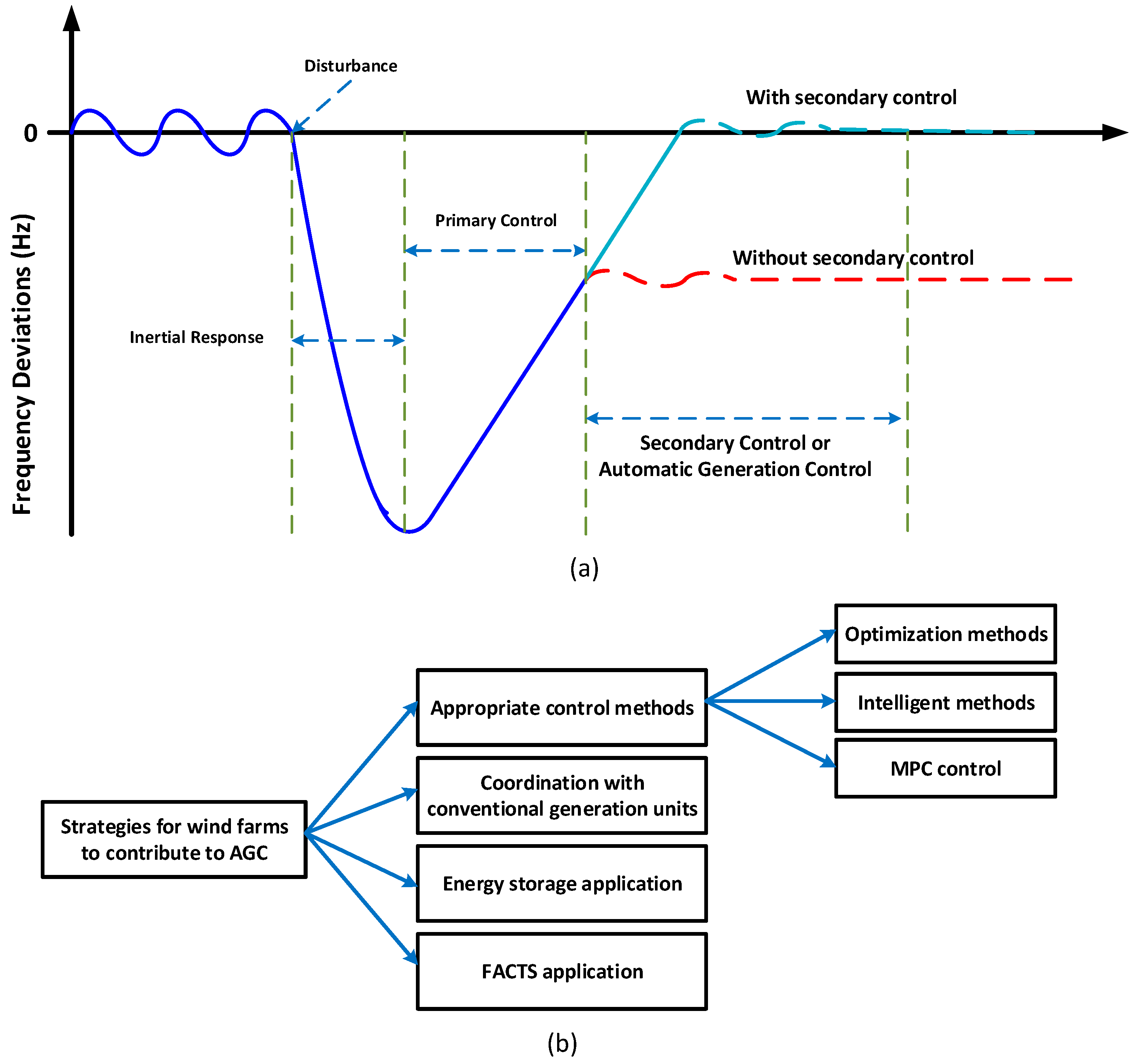
2. Wind Farm Contribution in Frequency Regulation
3. Wind Farms Contribution in AGC
3.1. Applied Control Methods
3.2. BESS and FACTS Integration with Wind Farm
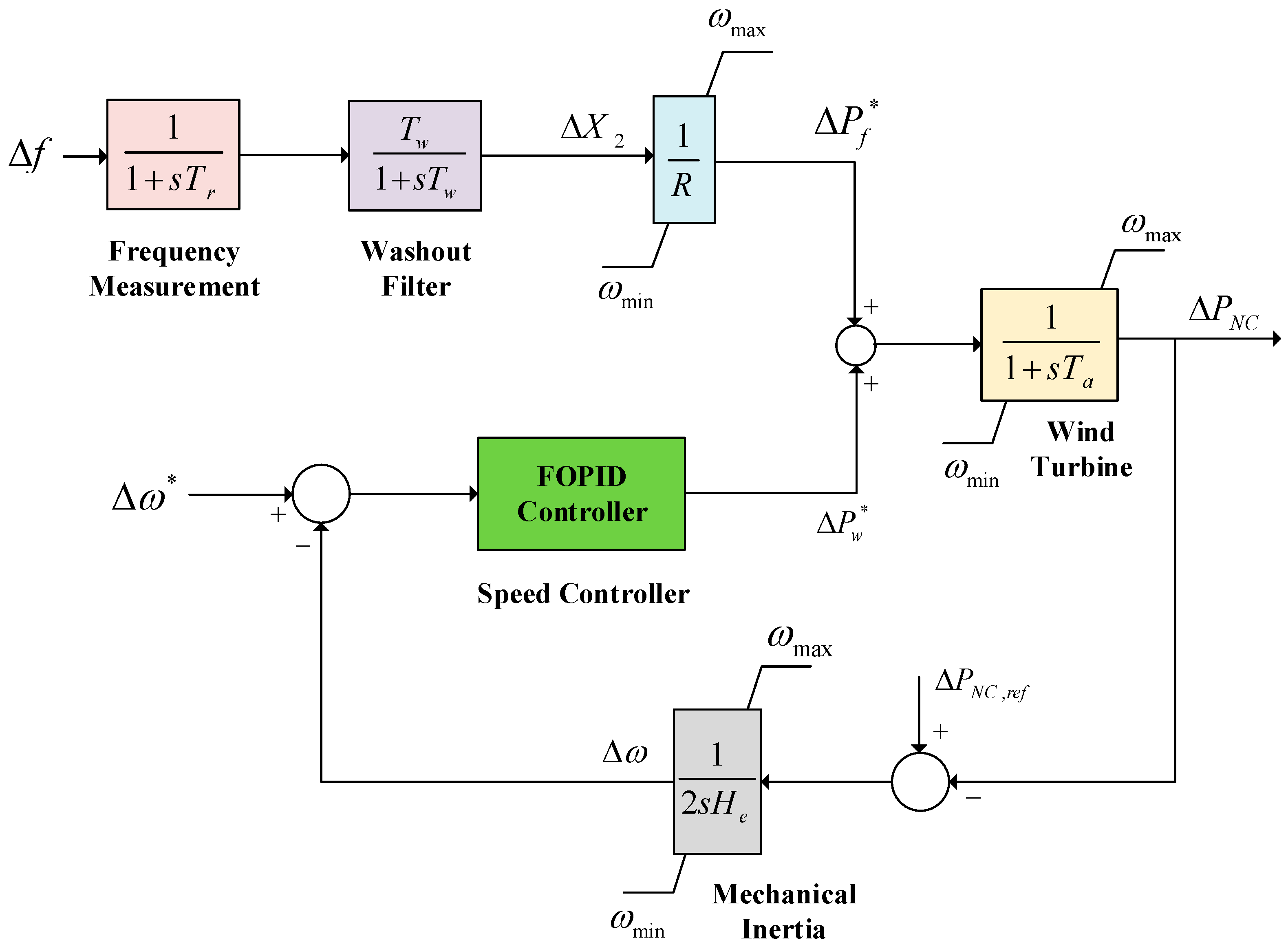
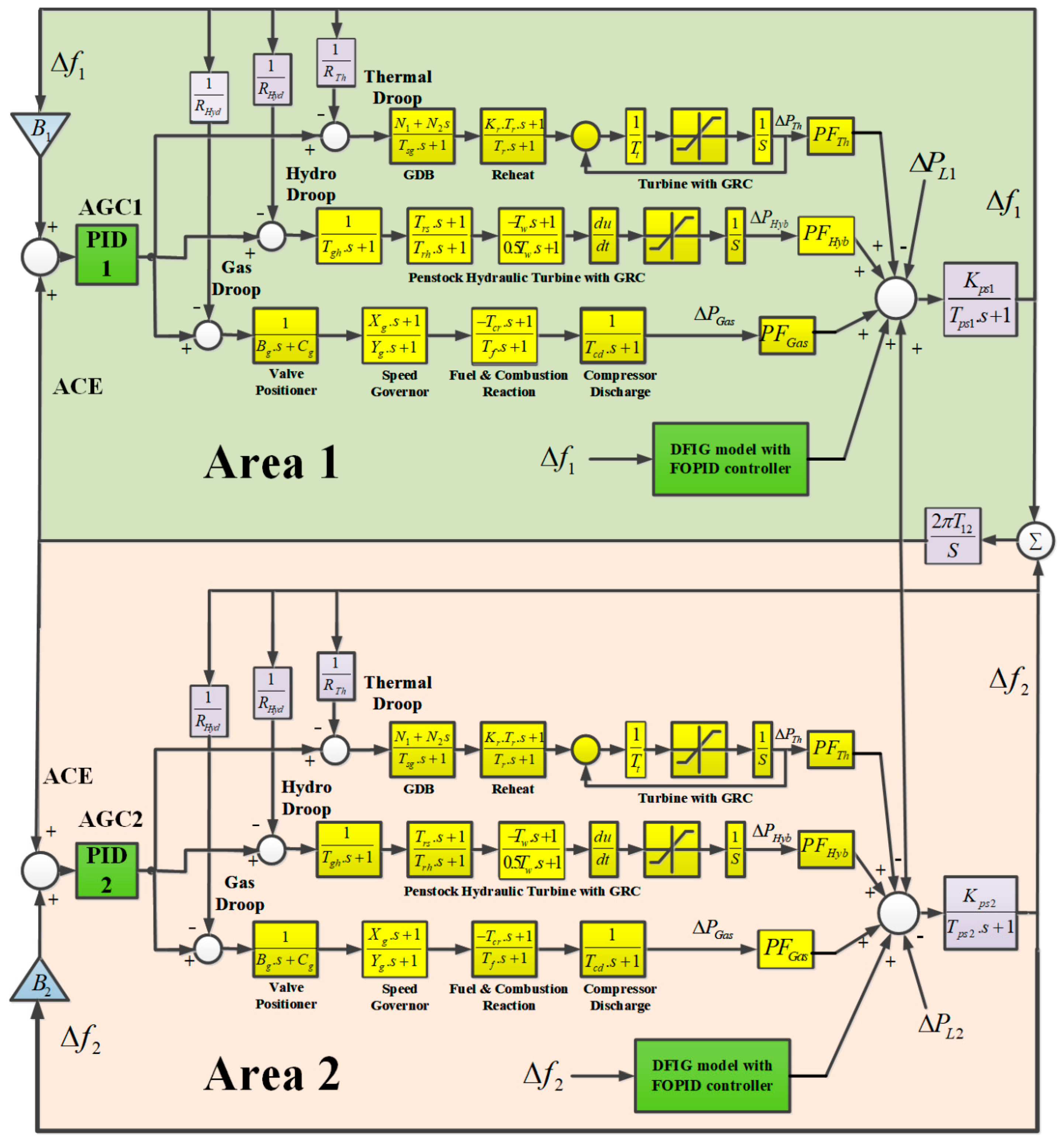
4. Proposed Wind Farm Control Technique in AGC
4.1. Wind Turbine Modeling in AGC
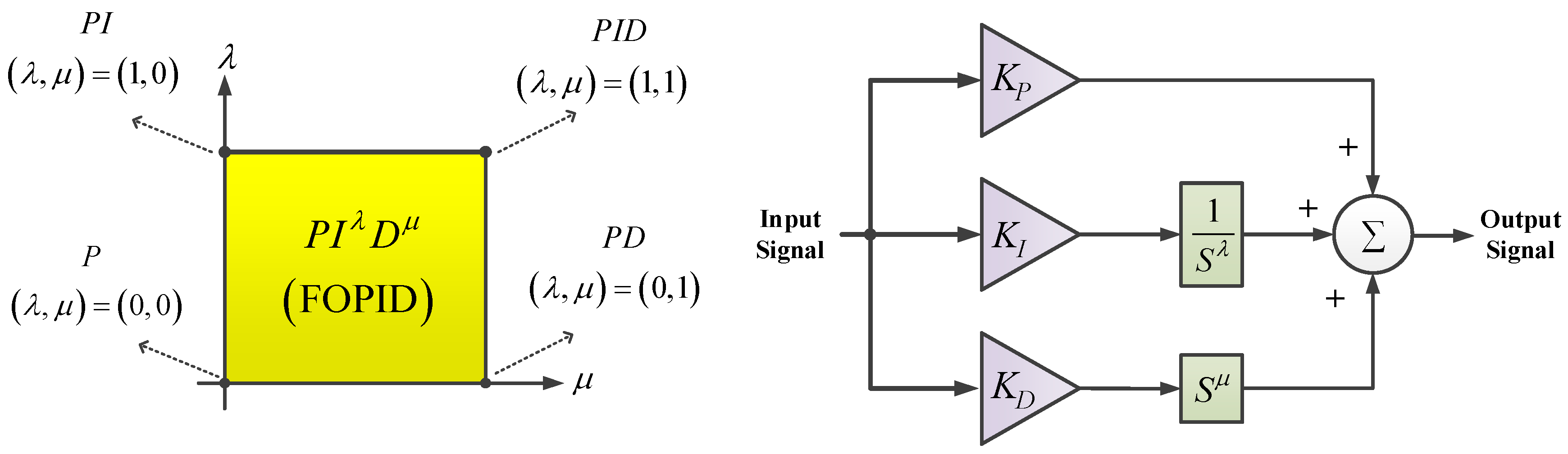
4.2. Design Procedure of SCA-Based FOPID Controller
4.2.1. Fractional Order PID Controller
4.2.2. Objective Function Formulation and Employed Optimization Algorithm
4.2.3. Sine-Cosine Algorithm
5. Simulation Results
5.1. First Scenario: Step Load Change
5.2. Second Scenario: Comparison of Results in Different Level of Wind Penetration
5.3. Third Scenario: Sinusoidal Load Change
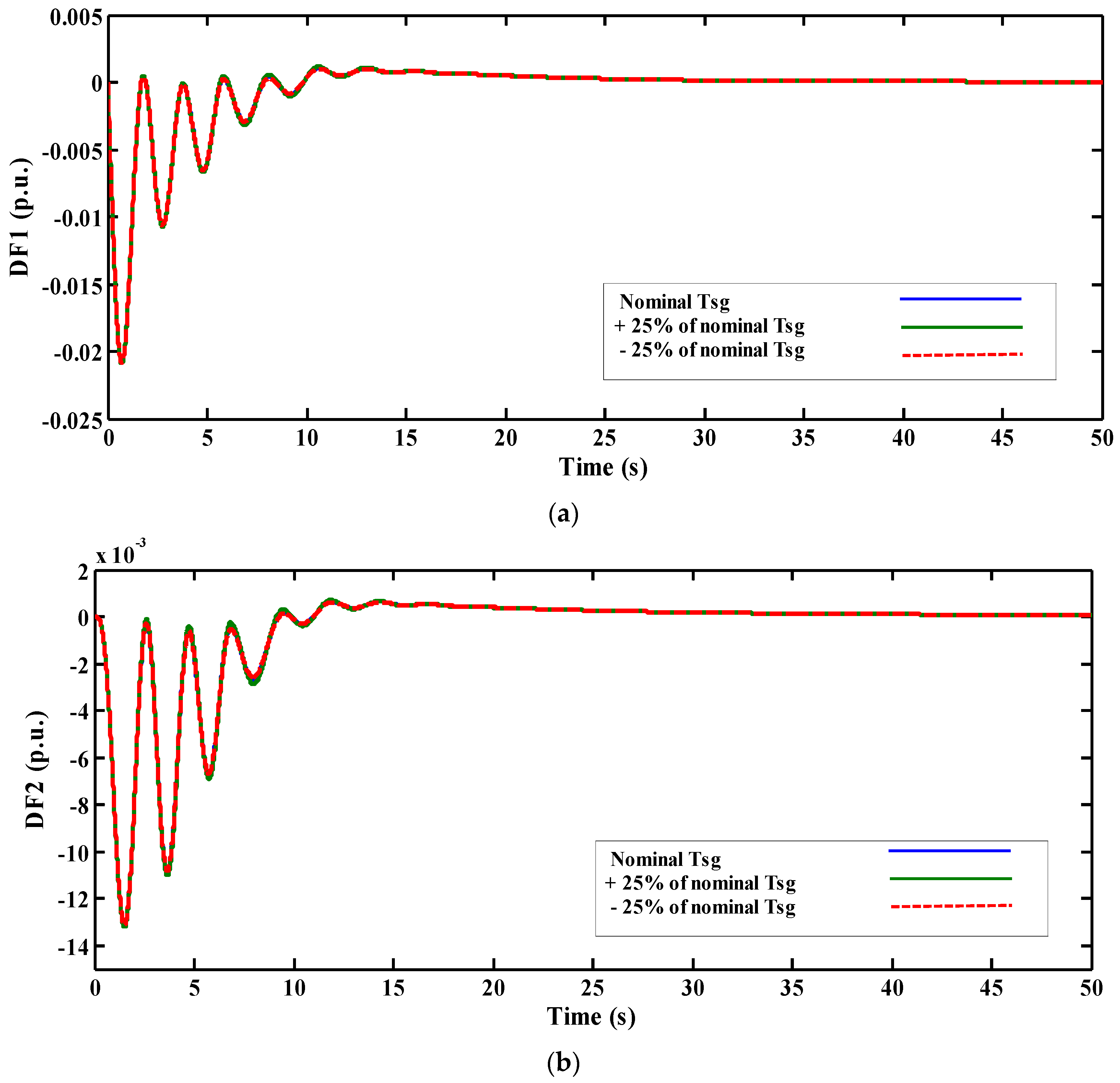
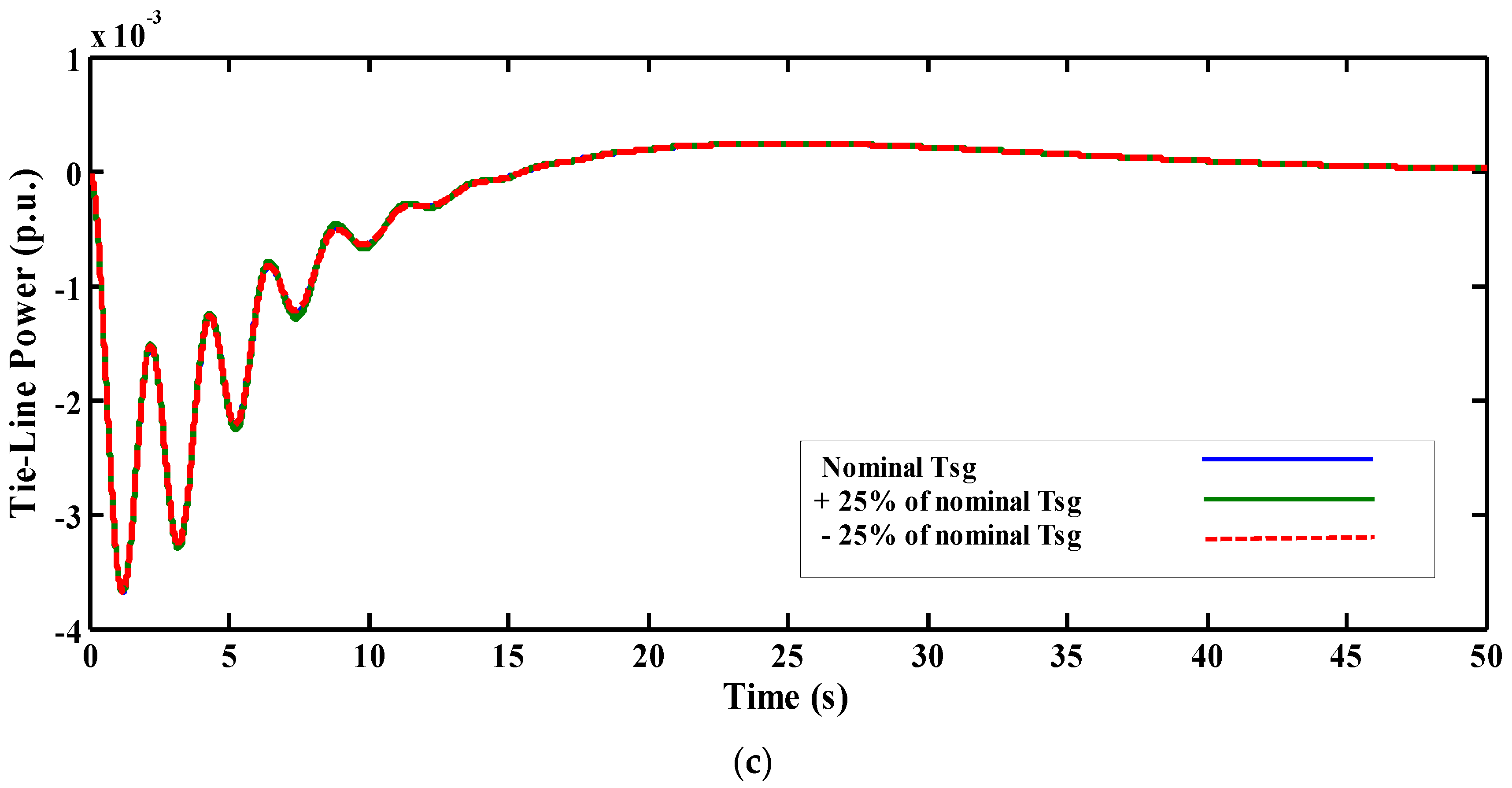
5.4. Fourth Scenario: Sensitivity Analysis
6. Conclusions and Future Directions
Author Contributions
Funding
Conflicts of Interest
References
- GWEC Report 2017. Available online: http://www.gwec.net/publications/global-wind-report-2/global-wind-report-2017-annual-market-update/ (accessed on 25 April 2017).
- Blaabjerg, F.; Ma, K. Wind energy systems. Proc. IEEE 2017, 105, 2116–2131. [Google Scholar]
- Li, H.; Chen, Zh. Overview of different wind generator systems and their comparisons. IET Renew. Power Gener. 2009, 2, 123–138. [Google Scholar] [CrossRef]
- Torkaman, H.; Keyhani, A. A review of design consideration for Doubly Fed Induction Generator based wind energy system. Electr. Power Syst. Res. 2018, 160, 128–141. [Google Scholar] [CrossRef]
- Khezri, R.; Bevrani, H. Voltage performance enhancement of DFIG-based wind farms integrated in large-scale power systems: Coordinated AVR and PSS. Int. J. Electr. Power Energy Syst. 2015, 73, 400–410. [Google Scholar] [CrossRef]
- Oshnoei, A.; Khezri, R.; Hagh, M.T.; Techato, K.; Muyeen, S.M.; Sadeghian, O. Direct probabilistic load flow in radial distribution systems including wind farms: An approach based on data clustering. Energies 2018, 11, 310. [Google Scholar] [CrossRef]
- Bousseau, P.; Belhomme, R.; Monnot, E.; Laverdure, N.; Boeda, D.; Roye, D.; Bacha, S. Contribution of wind farms to ancillary services. CIGRE 2006, 21, 1–11. [Google Scholar]
- Kayikci, M.; Milanovic, J.V. Reactive power control strategies for DFIG-based plants. IEEE Trans. Energy Convers. 2007, 22, 389–396. [Google Scholar]
- Gabash, A.; Li, P. On variable reverse power flow-part I: Active-reactive optimal power flow with reactive power of wind stations. Energies 2016, 9, 121. [Google Scholar] [CrossRef]
- Muyeen, S.M.; Tamura, J.; Murata, T. Stability Augmentation of a Grid-Connected wind Farm; Springer: Berlin, Germany, 2008. [Google Scholar]
- Golkhandan, K.R.; Aghaebrahimi, M.R.; Farshad, M. Control strategies for enhancing frequency stability by DFIGs in a power system with high percentage of wind power penetration. Appl. Sci. 2017, 7, 1140. [Google Scholar] [CrossRef]
- Jalali, M. DFIG Based Wind Turbine Contribution to System Frequency Control. Master’s Thesis, University of Waterloo, Waterloo, ON, Canada, 2010; pp. 1–92. [Google Scholar]
- Tang, Y.; He, H.; Wen, J.; Liu, J. Power system stability control for a wind farm based on adaptive dynamic programming. IEEE Trans. Smart Grid 2015, 6, 166–177. [Google Scholar] [CrossRef]
- Hazari, M.R.; Mannan, M.A.; Muyeen, S.M.; Umemura, A.; Takahashi, R.; Tamura, J. Stability augmentation of a grid-connected wind farm by fuzzy-logic-controlled DFIG-based wind turbines. Appl. Sci. 2018, 8, 20. [Google Scholar] [CrossRef]
- Mishra, A.; Tripathi, P.M.; Chatterjee, K. A review of harmonic elimination techniques in grid connected doubly fed induction generator based wind energy system. Renew. Sustain. Energy Rev. 2018, 89, 1–15. [Google Scholar] [CrossRef]
- Liu, Y.; Garcia, J.R.; King, T.J.; Liu, Y. Frequency regulation and oscillation damping contributions of variable-speed wind generators in the U.S. eastern interconnection (EI). IEEE Trans. Sustain. Energy 2015, 6, 951–958. [Google Scholar] [CrossRef]
- Ma, H.; Chowdhury, B. Working towards frequency regulation with wind plants: Combined control approaches. IET Renew. Power Gener. 2010, 4, 308–316. [Google Scholar] [CrossRef]
- Yingcheng, X.; Nengling, T. Review of contribution to frequency control through variable speed wind turbine. Renew. Energy 2011, 36, 1671–1677. [Google Scholar] [CrossRef]
- Kim, M.-K. Optimal Control and Operation Strategy for Wind Turbines Contributing to Grid Primary Frequency Regulation. Appl. Sci. 2017, 7, 927. [Google Scholar] [CrossRef]
- Sun, Y.; Zhang, Z.; Li, G.; Lin, J. Review on frequency control of power systems with wind power penetration. In Proceedings of the 2010 International Conference on Power System Technology (POWERCON), Hangzhou, China, 24–28 October 2010; pp. 1–8. [Google Scholar]
- Khezri, R.; Golshannavaz, S.; Vakili, R.; Memar-Esfahani, B. Multi-layer under frequency load shedding in back-pressure smart industrial microgrids. Energy 2017, 132, 96–105. [Google Scholar] [CrossRef]
- Bevrani, H. Robust Power System Frequency Control, 2nd ed.; Springer: Berlin, Germany, 2014. [Google Scholar]
- Golshannavaz, S.; Khezri, R.; Esmaeeli, M.; Siano, P.L. A two-stage robust-intelligent controller design for efficient LFC based on Kharitonov theorem and fuzzy logic. J. Ambient Intell. Hum. Comput. 2017, 9, 1445–1454. [Google Scholar] [CrossRef]
- Mohamed, TH.; Bevrani, H.; Hassan, A.; Hiyama, T. Decentralized model predictive based load frequency control in an interconnected power system. Energy Convers. Manag. 2011, 16, 1208–1214. [Google Scholar] [CrossRef]
- Khezri, R.; Golshannavaz, S.; Shokoohi, S.; Bevrani, H. Fuzzy Logic Based Fine-tuning Approach for Robust Load Frequency Control in a Multi-area Power System. Electr. Power Compon. Syst. 2016, 44, 2073–2083. [Google Scholar] [CrossRef]
- Oshnoei, A.; Hagh, M.T.; Khezri, R.; Mohammadi-Ivatloo, B. Application of IPSO and fuzzy logic methods in electrical vehicles for efficient frequency control of multi-area power systems. In Proceedings of the 2017 Iranian Conference on Electrical Engineering (ICEE), Tehran, Iran, 2–4 May 2017; pp. 1349–1354. [Google Scholar]
- Cam, E.; Gorel, G.; Mamur, H. Use of the Genetic Algorithm-Based Fuzzy Logic Controller for Load-Frequency Control in a Two Area Interconnected Power System. Appl. Sci. 2017, 7, 308. [Google Scholar] [CrossRef]
- Khezri, R.; Oshnoei, A.; Tarafdar Hagh, M.; Muyeen, S.M. Coordination of Heat Pumps, Electric Vehicles and AGC for Efficient LFC in a Smart Hybrid Power System via SCA-Based Optimized FOPID Controllers. Energies 2018, 11, 420. [Google Scholar] [CrossRef]
- Chang-Chien, L.; Chih-Che, S.; Yu-Ju, Y. Modeling of wind farm participation in AGC. IEEE Trans. Power Syst. 2014, 29, 1204–1211. [Google Scholar] [CrossRef]
- Chang-Chien, L.R.; Lin, W.T.; Yin, Y.C. Enhancing frequency response control by DFIGs in the high wind penetrated power systems. IEEE Trans. Power Syst. 2011, 26, 710–718. [Google Scholar] [CrossRef]
- Mauricio, J.M.; Marano, A.; Gómez-Expósito, A.; Ramos, J.L.M. Frequency regulation through variable-speed wind energy conversion systems. IEEE Trans. Power Syst. 2009, 24, 173–180. [Google Scholar] [CrossRef]
- Hazari, R.M.; Mannan, M.A.; Muyeen, S.M.; Umemura, A.; Takahashi, R.; Tamura, J. Transient Stability Augmentation of Hybrid Power System Based on Synthetic Inertia Control of DFIG. In Proceedings of the Australasian Universities Power Engineering Conference 2017 (AUPEC2017), Melbourne, Australia, 19–22 November 2017; pp. 1–6. [Google Scholar]
- Wang, Y.; Meng, J.; Zhang, X.; Xu, L. Control of PMSG-Based wind turbines for system inertial response and power oscillation damping. IEEE Trans. Sustain. Energy 2015, 6, 565–574. [Google Scholar] [CrossRef]
- Ataee, S.; Khezri, R.; Feizi, M.R.; Bevrani, H. Investigating the impacts of wind power contribution on the short-term frequency performance. In Proceedings of the Smart Grid Conference (SGC), Tehran, Iran, 9–10 December 2014; pp. 1–6. [Google Scholar]
- Zhang, Z.S.; Sun, Y.Z.; Lin, J.; Li, G.J. Coordinated frequency regulation by doubly fed induction generator based wind power plants. IET Renew. Power Gen. 2010, 6, 38–47. [Google Scholar] [CrossRef]
- Kleftakis, V.; Rigas, A.; Papadimitriou, C.; Katsoulakos, N.; Moutis, P.; Hatziargyriou, N. Contribution to frequency control by a PMSG wind turbine in a Diesel-Wind Turbine microgrid for rural electrification. In Proceedings of the 9th Mediterranean Conference on Power Generation, Transmission Distribution and Energy Conversion (MedPower 2014), Athens, Greece, 2–5 November 2014; pp. 1–5. [Google Scholar]
- Vidyanandan, K.V.; Senroy, N. Primary frequency regulation by deloaded wind turbines using variable droop. IEEE Trans. Power Syst. 2013, 28, 837–846. [Google Scholar] [CrossRef]
- Yingcheng, X.; Nengling, T. System frequency regulation in doubly fed induction generators. Int. J. Electr. Power Energy Syst. 2012, 43, 977–983. [Google Scholar] [CrossRef]
- Ataee, S.; Khezri, R.; Feizi, M.R.; Bevrani, H. Impacts of wind and conventional power coordination on the short-term frequency performance. In Proceedings of the 23rd Iranian Conference on Electrical Engineering (ICEE), Tehran, Iran, 10–14 May 2015; pp. 1–6. [Google Scholar]
- Ataee, S.; Bevrani, H. Improvement of primary frequency control by inertial response: Coordination between wind and conventional power plants. Int. Trans. Electr. Energy Syst. 2017, 27, e2340. [Google Scholar] [CrossRef]
- Verma, Y.P.; Kumar, A. Dynamic contribution of variable-speed wind energy conversion system in system frequency regulation. Front. Energy 2012, 3, 184–192. [Google Scholar] [CrossRef]
- Badmasti, B.; Bevrani, H. On contribution of DFIG wind turbines in the secondary frequency control. In Proceedings of the 1st Conference on New Research Achievements in Electrical and Computer Engineering, Tehran, Iran, 12 May 2016; pp. 1–7. [Google Scholar]
- Jalali, M.; Bhattacharya, K. Frequency regulation and AGC in isolated systems with DFIG-based wind turbines. In Proceedings of the IEEE Power & Energy Society General Meeting, Vancouver, BC, Canada, 21–25 July 2013; pp. 1–5. [Google Scholar]
- Aziz, A.; Shafiullah, G.M.; Stojcevski, A.; Amanullah, M.T.O. Participation of DFIG based wind energy system in load frequency control of interconnected multi-generation power system. In Proceedings of the Australasian Universities Power Engineering Conference (AUPEC), Perth, Australia, 28 September–1 October 2014; pp. 1–6. [Google Scholar]
- Ibraheem; Niazi, K.R.; Sharma, G. Study on dynamic participation of wind turbines in automatic generation control of power systems. Electr. Power Compon. Syst. 2015, 43, 44–55. [Google Scholar]
- Abo-Elyousr, F.K. Load frequency controller design for two-area interconnected power system with DFIG-based wind turbine via ant colony algorithm. In Proceedings of the Eighteenth International Middle East Power Systems Conference (MEPCON), Cairo, Egypt, 27–29 December 2016; pp. 1–8. [Google Scholar]
- Bhatt, P.; Roy, R.; Ghoshal, S.P. Dynamic participation of doubly fed induction generator in automatic generation control. Renew. Energy 2011, 36, 1203–1213. [Google Scholar] [CrossRef]
- Oshnoei, A.; Khezri, R.; Ghaderzadeh, M.; Parang, H.; Oshnoei, S.; Kheradmandi, M. Application of IPSO algorithm in DFIG-based wind turbines for efficient frequency control of multi-area power systems. In Proceedings of the Smart Grids Conference (SGC), Tehran, Iran, 20–21 December 2017; pp. 1–6. [Google Scholar]
- Preeti; Sharma, V.; Naresh, R.; Pulluri, H. Automatic generation control of multi-source interconnected power system including DFIG wind turbine. In Proceedings of the 1st IEEE International Conference on Power Electronics, Intelligent Control and Energy Systems (ICPEICES), Delhi, India, 4–6 July 2016; pp. 1–6. [Google Scholar]
- Pappachen, A.; Fathima, A.P. Genetic algorithm based PID controller for a two-area deregulated power system along with DFIG units. In Proceedings of the IEEE Sponsored 2nd International Conference on Innovations in Information, Embedded and Communication systems (ICIIECS), Coimbatore, India, 19–20 March 2015; pp. 1–6. [Google Scholar]
- Chaine, S.; Tripathy, M.; Satpathy, S. NSGA-II based optimal control scheme of wind thermal power system for improvement of frequency regulation characteristics. Ain Shams Eng. J. 2015, 6, 851–863. [Google Scholar] [CrossRef]
- Chaine, S.; Tripathy, M.; Jain, D. Non dominated Cuckoo search algorithm optimized controllers to improve the frequency regulation characteristics of wind thermal power system. Eng. Sci. Technol. Int. J. 2017, 20, 1092–1105. [Google Scholar] [CrossRef]
- Sahu, P.C.; Prusty, R.C.; Panda, S. ALO optimized NCTF controller in multi-area AGC system integrated with WECS based DFIG system. In Proceedings of the International Conference on Circuits Power and Computing Technologies (ICCPCT), Paris, France, 21–22 September 2017; pp. 1–6. [Google Scholar]
- Kumar, A.; Sathans. Impact study of DFIG based wind power penetration on LFC of a multi-area power system. In Proceedings of the Annual IEEE India Conference (INDICON), New Delhi, India, 17–20 December 2015; pp. 1–6. [Google Scholar]
- Azizipanah-Abarghooee, R.; Malekpour, M.; Zare, M.; Terzija, V. A new inertia emulator and fuzzy-based LFC to support inertial and governor responses using Jaya algorithm. In Proceedings of the IEEE Power & Energy Society General Meeting (PESGM), Boston, MA, USA, 17–21 July 2016; pp. 1–5. [Google Scholar]
- Sharma, G.; Niazi, K.R.; Ibraheem. Recurrent ANN based AGC of a two-area power system with DFIG based wind turbines considering asynchronous tie-lines. In Proceedings of the IEEE International Conference on Advances in Engineering & Technology Research (ICAETR), Unnao, India, 1–2 August 2014; pp. 1–5. [Google Scholar]
- Sharma, G.; Niazi, K.R.; Ibraheem; Bansal, R.C. LS-SVM based AGC of power system with dynamic participation from DFIG based wind turbines. In Proceedings of the 3rd Renewable Power Generation Conference (RPG), Naples, Italy, 24–25 September 2014; pp. 1–6. [Google Scholar]
- Qudaih, Y.S.; Bernard, M.; Mitani, Y.; Mohamed, T.H. Model predictive based load frequency control design in the presence of DFIG wind turbine. In Proceedings of the 2nd International Conference on Electric Power and Energy Conversion Systems (EPECS), Sharjah, The United Arab Emirates, 15–17 November 2012; pp. 1–6. [Google Scholar]
- Mohamed, T.H.; Morel, J.; Bevrani, H.; Hiyama, T. Model predictive based load frequency control design concerning wind turbines. Int. J. Electr. Power Energy Syst. 2012, 43, 859–867. [Google Scholar] [CrossRef]
- Ma, M.; Liu, X.; Zhang, C. LFC for multi-area interconnected power system concerning wind turbines based on DMPC. IET Gen. Transm. Distrib. 2017, 11, 2689–2696. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, X.; Qu, B. Distributed model predictive load frequency control of multi-area power system with DFIGs. IEEE/CAA J. Autom. Sin. 2017, 4, 125–135. [Google Scholar] [CrossRef]
- Kawakami, N.; Iijima, Y.; Fukuhara, M.; Bando, M.; Sakanaka, Y.; Ogawa, K.; Matsuda, T. Development and field experiences of stabilization system using 34MW NAS batteries for a 51 MW wind farm. In Proceedings of the IEEE International Symposium on Industrial Electronics, Istanbul, Turkey, 1–4 June 2014; pp. 2371–2376. [Google Scholar]
- Hui, W.; Wen, T. Load frequency control of power systems with wind turbines through flywheels. In Proceedings of the 27th Chinese Control and Decision Conference (CCDC), Qingdao, China, 23–25 May 2015; pp. 1–5. [Google Scholar]
- Bhatt, P.; Roy, R.; Ghoshal, S.P. Dynamic contribution of DFIG along with SMES for load frequency control of interconnected restructured power systems. In Proceedings of the 10th International Conference on Environment and Electrical Engineering, Rome, Italy, 8–11 May 2011; pp. 1–6. [Google Scholar]
- Kouba, N.Y.; Menaa, M.; Hasni, M.; Boudour, M. LFC enhancement concerning large wind power integration using new optimised PID controller and RFBs. IET Gen. Transm. Distrib. 2016, 10, 4065–4077. [Google Scholar] [CrossRef]
- Bhatt, P.; Ghoshal, S.P.; Roy, R. Coordinated control of TCPS and SMES for frequency regulation of interconnected restructured power systems with dynamic participation from DFIG based wind farm. Renew. Energy 2012, 40, 40–50. [Google Scholar] [CrossRef]
- Kumar, A.; Suhag, S. Effect of TCPS, SMES, and DFIG on load frequency control of a multi-area multi-source power system using multi-verse optimized fuzzy-PID controller with derivative filter. J. Vib. Control 2017. [Google Scholar] [CrossRef]
- Dhundhara, S.; Verma, Y.P. Evaluation of CES and DFIG unit in AGC of realistic multisource deregulated power system. Int. Trans. Electr. Energy Syst. 2017, 27, e2304. [Google Scholar] [CrossRef]
- Shankar, R.; Pradhan, R.; Sahoo, S.B.; Chatterjee, K. GA based improved frequency regulation characteristics for thermal-hydro-gas & DFIG model in coordination with FACTS and energy storage system. In Proceedings of the 3rd Int’l Conf. on Recent Advances in Information Technology, Dhanbad, India, 3–5 March 2016; pp. 1–6. [Google Scholar]
- Pan, I.; Das, S. Fractional order AGC for distributed energy resources using robust optimization. IEEE Trans. Smart Grid 2015, 7, 2175–2186. [Google Scholar] [CrossRef]
- Mirjalili, S. SCA: A sine cosine algorithm for solving optimization problems. Knowl.-Based Syst. 2016, 96, 120–133. [Google Scholar] [CrossRef]
- Dahiya, P.; Sharma, V.; Sharma, R.N. Optimal generation control of interconnected power system including DFIG-based wind turbine. IETE J. Res. 2015, 61, 285–300. [Google Scholar] [CrossRef]
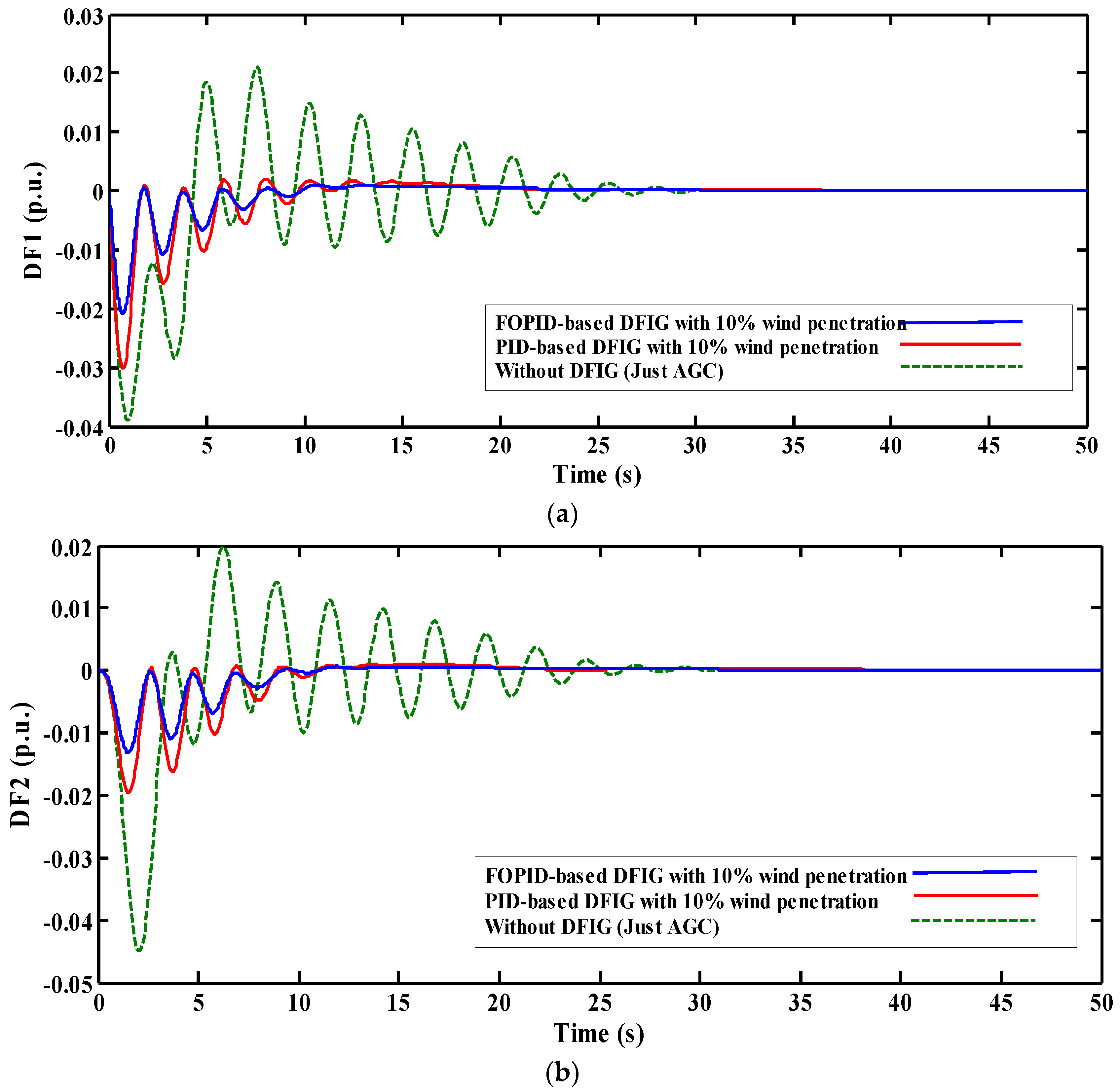

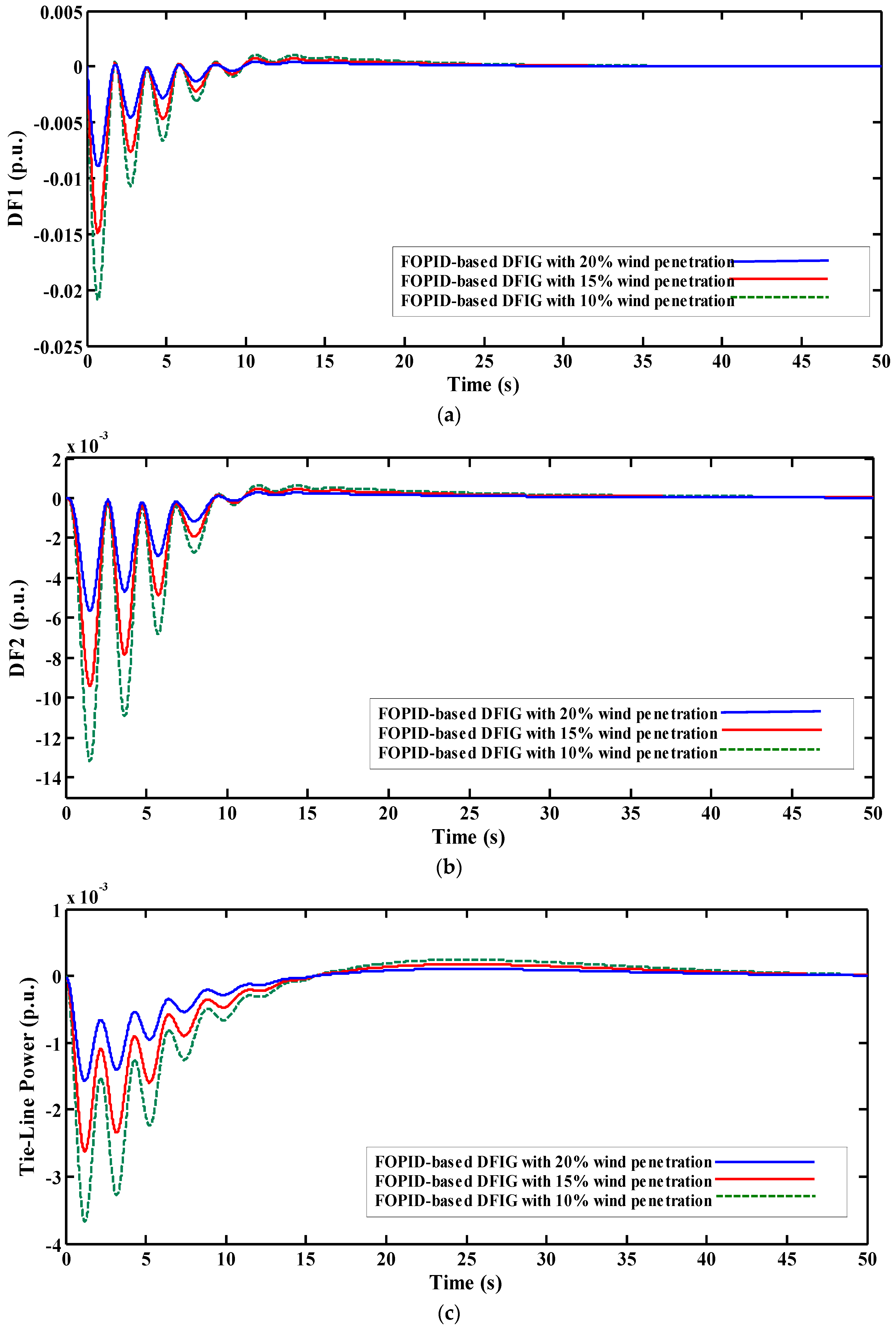
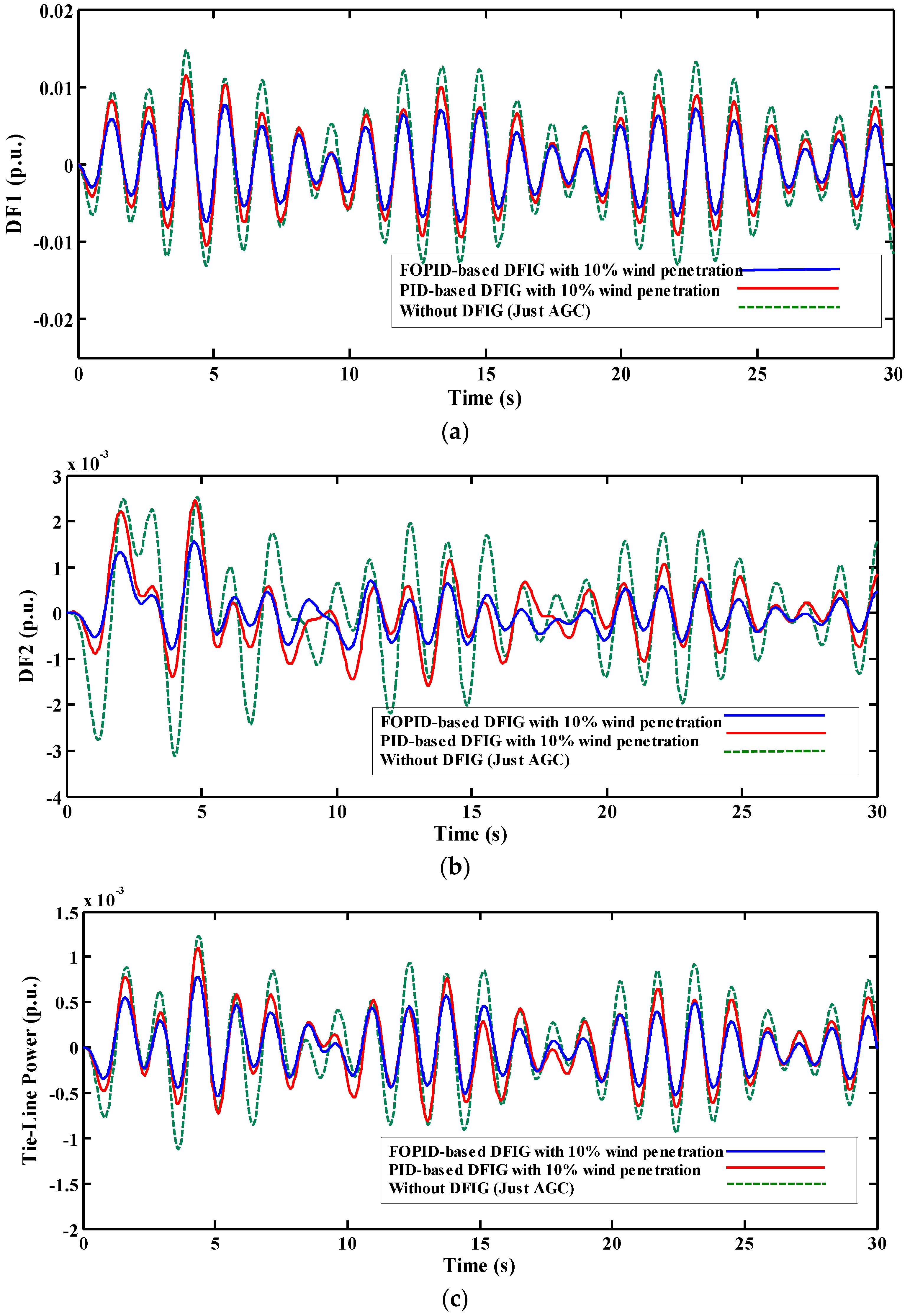

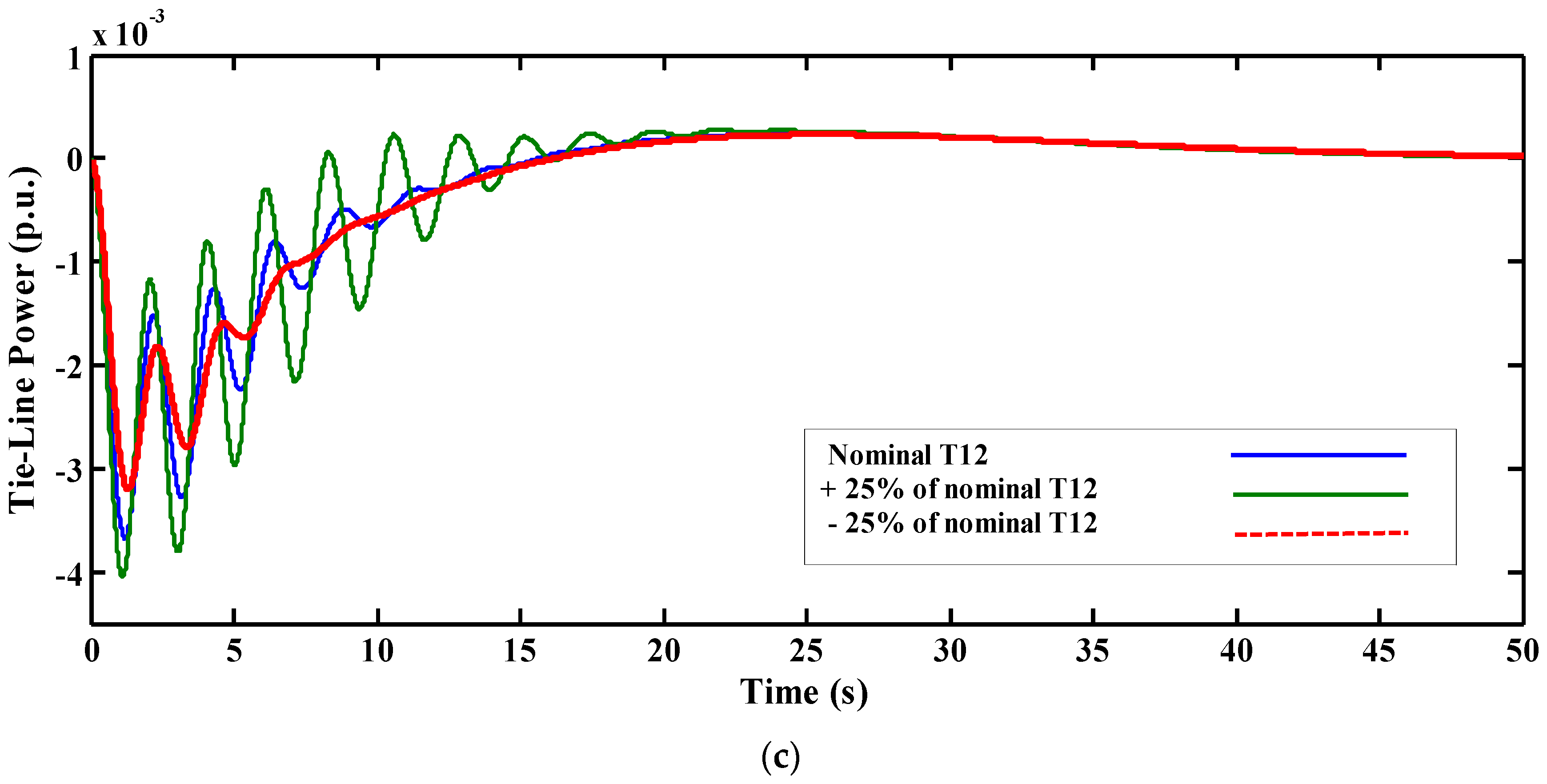
| Ref. | Generation Unit | System Configuration | Control Approach (AGC) | Optimization Techniques | |||
|---|---|---|---|---|---|---|---|
| Wind | Thermal | Gas | Hydro | ||||
| [43] | √ | √ | Single area power system | Integral controller | _ | ||
| [44] | √ | √ | √ | √ | Three area power system | Integral controller | _ |
| [45] | √ | √ | Two area power system | Integral controller | _ | ||
| [46] | √ | √ | Two area power system | PI controller | ACO | ||
| [47] | √ | √ | √ | Two area power system | Integral controller | CRPSO | |
| [48] | √ | √ | Three area power system | PI controller | IPSO | ||
| [49] | √ | √ | √ | √ | Four area power system | PID controller | OGSA |
| [50] | √ | √ | √ | Deregulated two area power system | PI controller | GA | |
| [51] | √ | √ | Two area power system | Integral controller | NSGAII | ||
| [52] | √ | √ | Two area power system | Integral controller | NSCS | ||
| [53] | √ | √ | Two area power system | Integral controller | ALO | ||
| [54] | √ | √ | Two area power system | Fuzzy logic-PI controller | _ | ||
| [55] | √ | √ | Three area power system | Fuzzy logic-PID controller | JA | ||
| [56] | √ | √ | Two area power system | Non-linear recurrent ANN | _ | ||
| [57] | √ | √ | Two area power system | Least squares vector machines | _ | ||
| [58] | √ | √ | Single area power system | MPC | _ | ||
| [59] | √ | √ | Two area power system | MPC | _ | ||
| [60] | √ | √ | Three area power system | DMPC | _ | ||
| [61] | √ | √ | Four area power system | DMPC | _ | ||
| [62] | √ | √ | Two area power system with flywheel | PID controller | _ | ||
| [63] | √ | √ | √ | Deregulated two area power system with SMES | Integral controller | CRPSO | |
| [64] | √ | √ | √ | Two area power system with RFB | PID controller | Grey Wolf Optimizer (GWO) | |
| [65] | √ | √ | √ | Deregulated two area power system with SMES and TCPS | Integral controller | CRPSO | |
| [66] | √ | √ | √ | Two area power system with SMES and TCPS | Fuzzy logic-PID with derivative filter controller | Multi-Verse Optimizer (MVO) | |
| [67] | √ | √ | √ | √ | Deregulated two area power system with CES and TCPS | Integral controller | _ |
| [68] | √ | √ | √ | √ | Two area power system with RFB and SSSC | Integral controller | GA |
| Controller Type | Areas | λ | μ | |||
|---|---|---|---|---|---|---|
| FOPID-DFIG | Area 1 | 0.2104 | −0.2002 | 0.7112 | 0.4704 | 0.6387 |
| PID-DFIG | Area 1 | 0.1509 | −0.1807 | 0.7409 | - | - |
| PID-AGC | Area 1 | 0.8544 | 0.2979 | 0.5840 | - | - |
| FOPID-DFIG | Area 2 | 0.2194 | −0.2233 | 0.2901 | 0.4418 | 0.5794 |
| PID-DFIG | Area 2 | 0.1644 | −0.1907 | 0.6987 | - | - |
| PID-AGC | Area 2 | 0.4811 | 0.2977 | 0.5133 | - | - |
| Controller Type | Signal | MDR | PO | PT | ST | ITSE |
|---|---|---|---|---|---|---|
| FOPID-based DFIG & AGC | 0.1910 | 0.0208 | 0.6997 | 14.1210 | 0.0026 | |
| 0.0131 | 1.5054 | 14.8400 | ||||
| 0.0036 | 1.1957 | 21.0161 | ||||
| PID-based DFIG & AGC | 0.0658 | 0.0301 | 0.7311 | 17.0812 | 0.0041 | |
| 0.0194 | 1.5536 | 18.3103 | ||||
| 0.0053 | 1.2089 | 23.4412 | ||||
| Without DFIG (Just AGC) | 0.0498 | 0.0389 | 0.9309 | 28.1927 | 0.0333 | |
| 0.0449 | 2.0776 | 27.1289 | ||||
| 0.0073 | 1.3934 | 32.5925 |
| FOPID-based DFIG & AGC | Signal | MDR | PO | PT (s) | ST (s) | ITSE |
|---|---|---|---|---|---|---|
| 0.0537 | 0.0201 | 0.6765 | 19.2995 | 0.0053 | ||
| 0.0146 | 1.4438 | 19.0713 | ||||
| 0.0040 | 1.1106 | 21.2130 | ||||
| 0.1096 | 0.0217 | 0.7285 | 14.9600 | 0.0023 | ||
| 0.0112 | 1.5874 | 13.8402 | ||||
| 0.0031 | 1.3164 | 20.9504 | ||||
| 0.0745 | 0.0209 | 0.6997 | 15.0300 | 0.0027 | ||
| 0.0132 | 1.5054 | 14.9200 | ||||
| 0.0036 | 1.1957 | 21.0041 | ||||
| 0.0815 | 0.0208 | 0.6997 | 14.5210 | 0.0026 | ||
| 0.0131 | 1.5054 | 14.4467 | ||||
| 0.0036 | 1.1957 | 20.2161 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oshnoei, A.; Khezri, R.; Muyeen, S.; Blaabjerg, F. On the Contribution of Wind Farms in Automatic Generation Control: Review and New Control Approach. Appl. Sci. 2018, 8, 1848. https://doi.org/10.3390/app8101848
Oshnoei A, Khezri R, Muyeen S, Blaabjerg F. On the Contribution of Wind Farms in Automatic Generation Control: Review and New Control Approach. Applied Sciences. 2018; 8(10):1848. https://doi.org/10.3390/app8101848
Chicago/Turabian StyleOshnoei, Arman, Rahmat Khezri, SM Muyeen, and Frede Blaabjerg. 2018. "On the Contribution of Wind Farms in Automatic Generation Control: Review and New Control Approach" Applied Sciences 8, no. 10: 1848. https://doi.org/10.3390/app8101848
APA StyleOshnoei, A., Khezri, R., Muyeen, S., & Blaabjerg, F. (2018). On the Contribution of Wind Farms in Automatic Generation Control: Review and New Control Approach. Applied Sciences, 8(10), 1848. https://doi.org/10.3390/app8101848








