One-Dimensional Fluid–Structure Interaction Models in Pressurized Fluid-Filled Pipes: A Review
Abstract
Featured Application
Abstract
1. Introduction
2. Definitions and Basic Concepts
2.1. Fluid–Structure Interaction
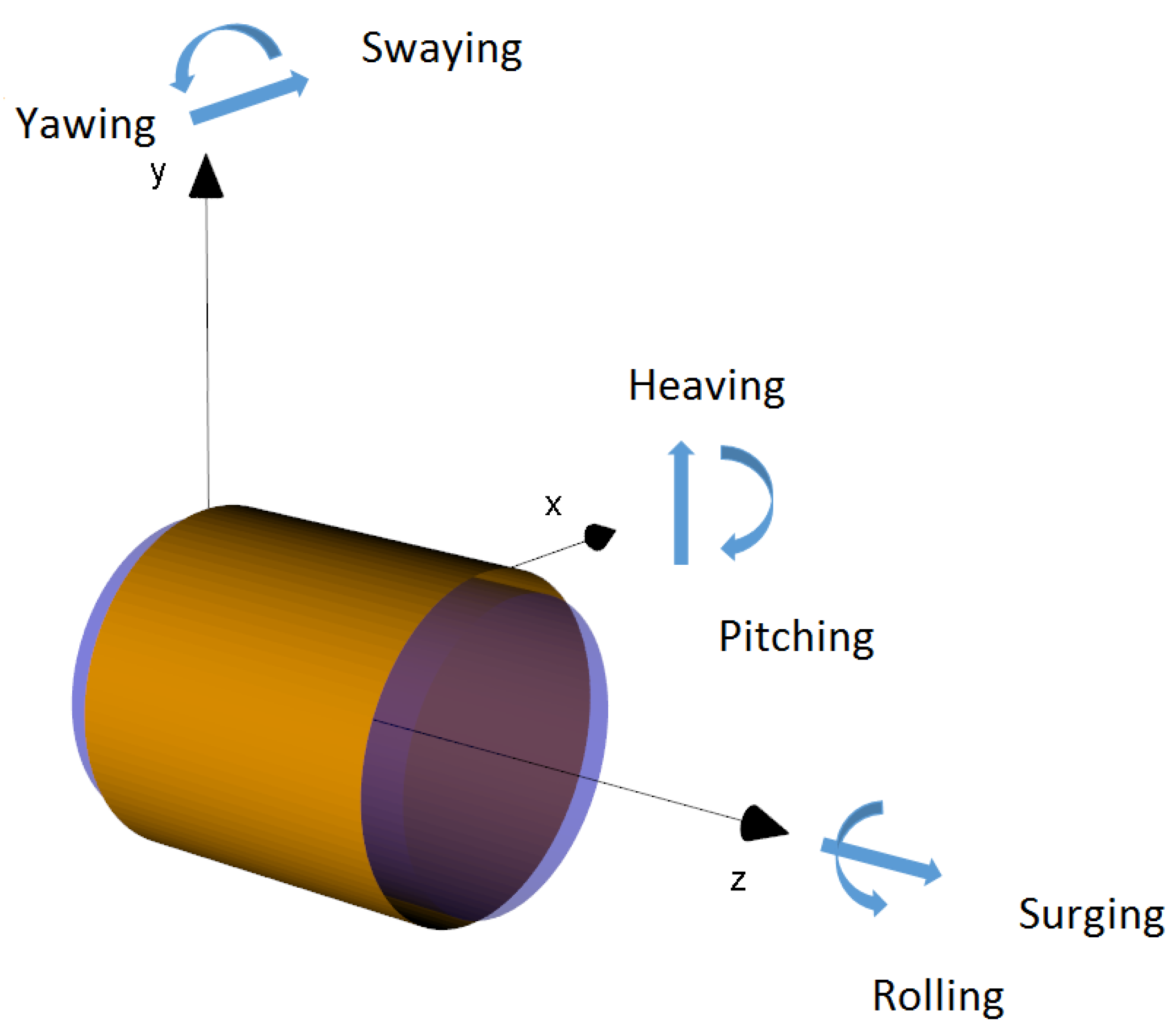
2.2. Degrees-of-Freedom in Fluid-Filled Pipes
- 1-DOF (fluid surging): only the axial fluid transient event is described.
- 2-DOF (breathing): radial inertia of the fluid and the pipe are taken into account.
- 3-DOF (solid surging): refers to the axial movement of the pipe.
- 4-DOF (swaying): includes the effect of horizontal displacement of the pipe.
- 5-DOF (heaving): includes the effect of vertical displacement of the pipe.
- 6-DOF (yawing): includes the rotation of the pipe in the plane.
- 7-DOF (pitching): includes the rotation of the pipe in the plane.
- 8-DOF (rolling): includes the rotation of the pipe on the plane.
2.3. Fundamental Formulae
2.4. Coupling Mechanisms and Modelling Approaches
3. Numerical and Experimental Research
3.1. Introduction
3.2. One Degree-of-Freedom Models
3.3. Two Degree-of-Freedom Models
3.4. Three Degree-of-Freedom Models
3.5. Four Degree-of-Freedom Models
3.6. Seven Degree-of-Freedom Models
3.7. Other FSI Mechanisms
4. Engineering Applications
4.1. FSI Consideration in Codes and Standards
4.2. Anchor and Support Forces
4.3. Vibration Damping and Noise Reduction
4.4. Earthquake Engineering
4.5. Aerospace Engineering
4.6. Biomechanics
4.7. Accidents and Post-Accident Analyses
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| fluid cross-sectional area (m) | p | fluid pressure (Pa) | |
| pressure wave speed (ms) | r | radius of the pipe-wall (m) | |
| pipe-wall cross-sectional area (m) | R | rotational velocity (rad s) | |
| acoustic speed of the i-DOF (ms) | bend radius of curvature (m) | ||
| D | pipe inner diameter (m) | t | time (s) |
| E | pipe-wall Young’s modulus (Pa) | U | pipe-wall velocity (ms) |
| e | pipe-wall thickness (m) | V | fluid mean velocity (ms) |
| G | shear modulus (Pa) | W | pipe-wall radial velocity (ms) |
| I | second moment of area (m) | Poisson’s ratio (–) | |
| J | polar second moment of area (m) | fluid density (kgm) | |
| K | bulk modulus of compressibility (Pa) | pipe density (kgm) | |
| L | pipe length (m) | pipe-wall stress (Pa) | |
| M | moment (N m) | strain (–) |
Appendix A. Summary Tables of Experimental and Numerical Research
| DOF | Method | References |
|---|---|---|
| 1 & 3 | MOC-MOC | [51,57,93,98,106,107,109,158,200]. |
| 1 & 3 | FDM-FDM | [47,49]. |
| 1 & 3 | FEM-FEM | [52]. |
| 1 & 3 | MOC-FEM | [48,51]. |
| 1 & 3 | FVM-FVM | [55]. |
| 1 & 3 | Analytical solution | [12,54,56,112]. |
| 1, 2 & 3 | MOC-MOC | [5,47]. |
| 1, 2 & 3 | MOC-FEM | [58]. |
| 1, 2 & 3 | MOC-FDM | [59]. |
| 1, 3 & 4, 6 or 5, 7 | MOC-MOC | [64,65,66,67]. |
| 1, 3 & 4, 6 or 5, 7 | FVM-FVM | [68]. |
| 1, 3, 4, 5, 6, 7 & 8 | MOC-MOC | [7,8,126]. |
| 1, 3, 4, 5, 6, 7 & 8 | MOC-FEM | [51,70,71,72,73,74]. |
| Location | Description and references |
|---|---|
| City University London, U.K. | Aluminium alloy straight pipe. Experimental evidence of precursor waves is depicted [84] |
| University of Dundee, U.K. | Suspended pipe rigs excited by the impact of a solid rod aiming at isolating FSI effects [53,94,95,96,97,201]. |
| University of Karlsruhe, Germany | Physical data from diverse case-studies: subterranean salt cavern, water-main bridge andtank-ship loading line. The aim was the development and validation of a four-equation model [10,50,85,88,89,90,91,92]. |
| Delft Hydraulics, The Netherlands | Complex apparatus held by suspension wires and specially designed for FSI tests. Used for the development and verification of the FLUSTRIN code [69,127,128]. |
| Michigan State University, U.S.A. | U-bend and multi-plane copper pipe aiming at validating a fourteen-equation model [48,120,125]. |
| Stanford Research Institute, U.S.A. | Straight pipe extensively equipped with pressure and strain gauges in order to analyse pipe flexure during the transient events generated by a pulse gun [30,61,63,176]. |
| University of Berkeley, U.S.A. | Conduit excited by firing steel spheres onto the pipe ends with the goal to study axial stress waves. [202,203]. |
| University of Kentucky, U.S.A. | Rigidly supported straight pipe terminated by a spring-mass device. [204,205] |
| IST, University of Lisbon, Portugal; and EPFL, Switzerland | Straight copper pipe rig, copper coil and polyethylene coil [57,99,109,110,158]. |
| University of Guanajuato, Mexico; and IST University of Lisbon, Portugal | Pipe-rig assembled by concentric elbows aiming at validation of a CFD model [40,124] |
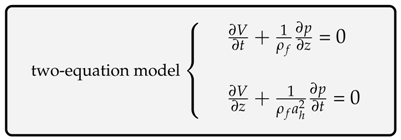
Appendix B. Two-Equation Model
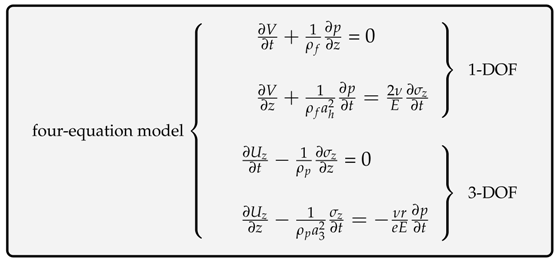
Appendix C. Four-Equation Model
Appendix C.1. Continuity in 1-DOF
Appendix C.2. Continuity in 3-DOF
References
- Korteweg, D. Ueber die Fortpflanzungsgeschwindigkeit des Schalles in elastischen Röhren. Annalen der Physik 1878, 241, 525–542. [Google Scholar] [CrossRef]
- Helmholtz, H. Report on theoretical acoustics concerning works of the years 1848 and 1849. Gesammelte wissenschaftliche Abhandlungen 1882, 1, 233–255. [Google Scholar]
- Skalak, R. An Extension of the Theory of Water Hammer. Ph.D. Thesis, Department of Civil Engineering and Engineering Mechanics Columbia Univiversity, New York, NY, USA, 1955. [Google Scholar]
- Wilkinson, D. The Dynamic Response of Pipework Systems to Water Hammer; Central Electricity Generating Board: London, UK, 1977. [Google Scholar]
- Walker, J.; Phillips, J. Pulse propagation in fluid-filled tubes. J. Appl. Mech. 1977, 44, 31–35. [Google Scholar] [CrossRef]
- Valentin, R.A.; Phillips, J.W.; Walker, J.S. Reflection and Transmission of Fluid Transients at an Elbow; Technical Report; Argonne National Lab.: Chicago, IL, USA, 1979.
- Wiggert, D.; Hatfield, F.; Stuckenbruck, S. Analysis of liquid and structural transients in piping by the method of characteristics. J. Fluids Eng. 1985, 109, 161–165. [Google Scholar] [CrossRef]
- Wiggert, D. Coupled transient flow and structural motion in liquid-filled piping systems: A survey. In Proceedings of the ASME Pressure Vessels and Piping Conference, Chicago, IL, USA, 20–24 July 1986. [Google Scholar]
- Joung, I.B.; Shin, Y. A new model on transient wave propagation in fluid-filled tubes. J. Press. Vessel Technol. 1987, 109, 88–93. [Google Scholar] [CrossRef]
- Bürmann, W.; Thielen, H. Measurement and computation of dynamic reactive forces on pipes containing flow. 3R Int. 1988, 27, 434–440. [Google Scholar]
- Wiggert, D.C.; Tijsseling, A.S. Fluid transients and Fluid-Structure Interaction in flexible liquid-filled piping. Appl. Mech. Rev. 2001, 54, 455–481. [Google Scholar] [CrossRef]
- Tijsseling, A. Exact solution of linear hyperbolic four-equation system in axial liquid-pipe vibration. J. Fluids Struct. 2003, 18, 179–196. [Google Scholar] [CrossRef]
- Wood, F.M. History of Water–Hammer; Number 65; Department of Civil Engineering, Queen’s University: Kingston, ON, Canada, 1970. [Google Scholar]
- Thorley, A. A survey of investigations into pressure surge phenomena. In Research Memorandum ML83; City University, Department of Mechanical Engineering: London, UK, 1976. [Google Scholar]
- Anderson, A. Menabrea’s note on waterhammer: 1858. J. Hydraul. Div. 1976, 102, 29–39. [Google Scholar]
- Tijsseling, A.S.; Anderson, A. Johannes von Kries and the history of water hammer. J. Hydraul. Eng. 2007, 133, 1–8. [Google Scholar] [CrossRef]
- Tijsseling, A.S.; Anderson, A. Thomas Young’s research on fluid transients: 200 years on. In Proceedings of the BHR Group 2008 Conference on Pressure Surges, Edinburgh, UK, 14–16 May 2008; pp. 21–33. [Google Scholar]
- Tijsseling, A.; Anderson, A. A. Isebree Moens and D.J. Korteweg: On the speed of propagation of waves in elastic tubes. In Proceedings of the 11th International Conference on Pressure Surges, Lisbon, Portugal, 24–26 October 2012; pp. 227–245. [Google Scholar]
- Boulanger, A. Étude Sur la Propagation des Ondes Liquides Dans Les Tuyaux Élastiques; Tallandier: Paris, France, 1913; Volume 2. [Google Scholar]
- Lambossy, P. Paper historique et critique sur le probleme de la propagation des ondes dans un liquide compressible enferme dans un tube elastique. Helv. Physiol. Pharmacol. Acta 1950, 8, 209–227. [Google Scholar] [PubMed]
- Stecki, J.; Davis, D. Fluid transmission lines distributed parameter models part 1: A review of the state of the art. J. Power Energy 1986, 200, 215–228. [Google Scholar] [CrossRef]
- Ghidaoui, M.S.; Zhao, M.; McInnis, D.A.; Axworthy, D.H. A review of water hammer theory and practice. Appl. Mech. Rev. 2005, 58, 49–76. [Google Scholar] [CrossRef]
- Tijsseling, A. Fluid-Structure Interaction in liquid-filled pipe systems: A review. J. Fluids Struct. 1996, 10, 109–146. [Google Scholar] [CrossRef]
- Li, S.; Karney, B.W.; Liu, G. FSI research in pipeline systems—A review of the literature. J. Fluids Struct. 2015, 57, 277–297. [Google Scholar] [CrossRef]
- Giannopapa, C.G. Fluid Structure Interaction in Flexible Vessels. Ph.D. Thesis, University of London, King’s College, London, UK, 2004. [Google Scholar]
- Sinha, A. Vibration of Mechanical Systems; Cambridge University Press: Cambridge, UK, 2010; ISBN 13 978-1107694170. [Google Scholar]
- Tijsseling, A.S.; Vardy, A.E. What is wave speed? In Proceedings of the 12th International Conference on Pressure Surges, Dublin, Ireland, 18–20 November 2015; pp. 343–360. [Google Scholar]
- Ware, A.; Williamson, R. BLAZER: A RELAP5/MODI post processor to generate force-time history input data for structural computer codes. In Proceedings of the ASME Pressure Vessel and Piping Conference, Orlando, FL, USA, 27 June–1 July 1982; Volume 64. [Google Scholar]
- Belytschko, T.; Karabin, M.; Lin, J. Fluid-Structure Interaction in waterhammer response of flexible piping. J. Press. Vessel Technol. 1986, 108, 249–255. [Google Scholar] [CrossRef]
- A-Moneim, M.; Chang, Y. Comparison of Icepel code predictions with straight flexible pipe experiments. Nucl. Eng. Des. 1978, 49, 187–196. [Google Scholar] [CrossRef]
- Romander, C.; Schwer, L.; Cagliostro, D. Response of water-filled thin-walled pipes to pressure pulses: Experiments and analysis. J. Press. Vessel Technol. 1980, 102, 56–61. [Google Scholar] [CrossRef]
- Kulak, R. Some Aspects of Fluid–Structure Coupling; Technical Report; Argonne National Laboratory: Argonne, IL, USA, 1982.
- Kulak, R. Three-dimensional fluid–structure coupling in transient analysis. Comput. Struct. 1985, 21, 529–542. [Google Scholar] [CrossRef]
- Erath, W.; Nowotny, B.; Maetz, J. Simultaneous coupling of the calculation of pressure waves and pipe oscillations. 3R Int. 1998, 37, 501–508. [Google Scholar]
- Erath, W.; Nowotny, B.; Maetz, J. Modelling the fluid structure interaction produced by a waterhammer during shutdown of high-pressure pumps. Nucl. Eng. Des. 1999, 193, 283–296. [Google Scholar] [CrossRef]
- Bietenbeck, F.; Petruschke, W.; Wuennenberg, H. Piping response due to blowdown significant parameters for a comparison of experimental and analytical results. In Proceedings of the 8th International Conference on Structural Mechanics in Reactor Technology, Brussels, Belgium, 19–23 August 1985. [Google Scholar]
- Mueller, W. Uncoupled and coupled analysis of a large HDR pipe. In Proceedings of the Transactions of the 9th International Conference on Structural Mechanics in Reactor Technology, Lausanne, Switzerland, 17–21 August 1987. [Google Scholar]
- Casadei, F.; Halleux, J.; Sala, A.; Chille, F. Transient fluid—Structure interaction algorithms for large industrial applications. Comput. Methods Appl. Mech. Eng. 2001, 190, 3081–3110. [Google Scholar] [CrossRef]
- Simão, M.; Mora, J.; Ramos, H.M. Fluid–structure interaction with different coupled models to analyse an accident occurring in a water supply system. Res. Technol. Aqua 2015, 64, 302–315. [Google Scholar] [CrossRef]
- Simão, M.; Mora-Rodriguez, J.; Ramos, H.M. Interaction between hydraulic transient events and structure vibration. In Proceedings of the 12th International Conference on Pressure Surges, Dublin, Ireland, 18–20 November 2015; pp. 273–286. [Google Scholar]
- Menabrea, L.F. Note sur les effects de choc de l’eau dans les conduites. Comptes Rendus Hebd. Seances de L’Academie des Sci. 1858, 47, 221–224. [Google Scholar]
- Von Kries, J. Ueber die Beziehungen zwischen Druck und Geschwindigkeit, welche bei der Wellenbewegung in elastischen Schlaff fluchen bestehen. On the relations between pressure and velocity, which exist in the wavelike motion in elastic tubes. Festschrift der 1883, 56, 67–88. [Google Scholar]
- Frizell, J. Pressures resulting from changes of velocity of water in pipes. Trans. Am. Soc. Civ. Eng. 1898, 39, 1–7. [Google Scholar]
- Allievi, L. Teoria Generale Del Moto Perturbato Dell’acqua Nei Tubi in Pressione (Colpo D’ariete). Translated into English by EE Halmos (1925); American Society of Civil Engineers: Reston, VA, USA, 1902. [Google Scholar]
- Joukowsky, N. On the hydraulic hammer in water supply pipes. Proc. Am. Water Works Assoc. 1904, 24, 341–424. [Google Scholar]
- Halliwell, A. Velocity of a water–hammer wave in an elastic pipe. J. Hydraul. Div. 1963, 89, 1–21. [Google Scholar]
- Schwarz, W. Druckstoßberechnung unter Berücksichtigung der Radial-und Längsverschiebungen der Rohrwandung. Ph.D. Thesis, Universität Stuttgart, Institut fuür Wasserbau, Mitteilungen, Heft 43, Stuttgart, Germany, 1978. ISSN 0343-1150. [Google Scholar]
- Wiggert, D. Fluid-Structure Interaction in piping systems. In Proceedings of the Druckstoßberechnung von Rohrleitungssystemen, Haus der Technik, Essen, Germany, December 1983. [Google Scholar]
- Kojima, E.; Shinada, M. Dynamic behavior of a finite length straight pipe subject to water–hammer (2nd report, for a very thin-walled pipe). Trans. Jpn. Soc. Mech. Eng. Ser. B 1988, 54, 3346–3353. [Google Scholar] [CrossRef]
- Bürmann, W.; Thielen, H. Untersuchung der Bewegung des Befüllstrangs einer Salzkaverne. (Study on the motion of the filling string of a saline cavern.). 3R Int. 1988, 27, 275–281. [Google Scholar]
- Lavooij, C.; Tijsseling, A.S. Fluid-Structure Interaction in liquid-filled piping systems. J. Fluids Struct. 1991, 5, 573–595. [Google Scholar] [CrossRef]
- Zhang, X.; Huang, S.; Wang, Y. The FEM of fluid structure interaction in piping pressure transients. In Proceedings of the First International Conference on Flow Interaction, Hong Kong, 5–9 September 1994; pp. 532–535. [Google Scholar]
- Vardy, A.; Fan, D.; Tijsseling, A. Fluid-Structure Interaction in a T-piece pipe. J. Fluids Struct. 1996, 10, 763–786. [Google Scholar] [CrossRef]
- Li, Q.; Yang, K.; Zhang, L. Analytical solution for Fluid-Structure Interaction in liquid-filled pipes subjected to impact-induced water hammer. J. Eng. Mech. 2003, 129, 1408–1417. [Google Scholar] [CrossRef]
- Gale, J.; Tiselj, I. Applicability of the Godunov’s method for fundamental four-equation FSI model. In Proceedings of the International Conference on Nuclear Energy for New Europe, Bled, Slovenia, 5–8 September 2005. [Google Scholar]
- Loh, K.; Tijsseling, A.S. Water Hammer (With FSI): Exact Solution Parallelization and Application. In Proceedings of the ASME 2014 Pressure Vessels and Piping Conference; American Society of Mechanical Engineers: New York, NY, USA, 2014; p. V005T11A016. [Google Scholar]
- Ferras, D.; Manso, P.A.; Schleiss, A.J.; Covas, D.I. Fluid-structure interaction in straight pipelines with different anchoring conditions. J. Sound Vib. 2017, 394, 348–365. [Google Scholar] [CrossRef]
- Kellner, A.; Voss, J.; Schoenfelder, C. Fluid-Structure Interaction in piping systems: Experiment and theory. In Proceedings of the 7th International Conference on Structural Mechanics in Reactor Technology, Chicago, IL, USA, 22–26 August 1983; Volume B. [Google Scholar]
- Gorman, D.; Reese, J.; Zhang, Y. Vibration of a flexible pipe conveying viscous pulsating fluid flow. J. Sound Vib. 2000, 230, 379–392. [Google Scholar] [CrossRef]
- Tijsseling, A. Water hammer with fluid–structure interaction in thick-walled pipes. Comput. Struct. 2007, 85, 844–851. [Google Scholar] [CrossRef]
- Regetz, J. An Experimental Determination of the Dynamic Response of a Long Hydraulic Line; Technical Note; National Aeronautics and Space Administration (NASA): Washington, DC, USA, 1960.
- Wood, D.J.; Chao, S. Effect of pipeline junctions on water hammer surges. Trans. Eng. J. 1971, 97, 441–457. [Google Scholar]
- A-Moneim, M.; Chang, Y. Comparison of ICEPEL predictions with single-elbow flexible piping system experiment. J. Press. Vessel Technol. 1979, 101, 142–148. [Google Scholar] [CrossRef]
- Hu, C.K.; Phillips, J. Pulse propagation in fluid-filled elastic curved tubes. J. Press. Vessel Technol. 1981, 103, 43–49. [Google Scholar] [CrossRef]
- Tijsseling, A.; Fan, D.; Vardy, A. Transient Fluid-Structure Interaction and cavitation in a single-elbow pipe system. In Proceedings of the First International Conference on Flow Interaction, Hong Kong, 5–9 September 1994; pp. 346–349. [Google Scholar]
- Tijsseling, A.; Vardy, A.; Fan, D. Fluid-Structure Interaction and cavitation in a single-elbow pipe system. J. Fluids Struct. 1996, 10, 395–420. [Google Scholar] [CrossRef]
- Tijsseling, A.; Heinsbroek, A. The influence of bend motion on waterhammer pressures and pipe stresses. In Proceedings of the 3rd ASME & JSME Joint Fluids Engineering Conference, Symposium S-290 Water Hammer, San Francisco, CA, USA, July 1999; Volume 248, pp. 1–7. [Google Scholar]
- Gale, J.; Tiselj, I. Eight equation model for arbitrary shaped pipe conveying fluid. In Proceedings of the International Conference on Nuclear Energy for New Europe, Portoroz, Slovenia, 18–21 September 2006. [Google Scholar]
- Weijde, P. Prediction of pressure surges and dynamic forces in pipeline systems, influence of system vibrations on pressures and dynamic forces (fluid–structure interaction). In Proceedings of the Symposium on Pipelines, Utrecht, The Netherlands, November 1985; pp. 327–335. [Google Scholar]
- Tijsseling, A.; Lavooij, C. Waterhammer with Fluid-Structure Interaction. Appl. Sci. Res. 1990, 47, 273–285. [Google Scholar] [CrossRef]
- Lavooij, C.; Tijsseling, A.S. Fluid-Structure Interaction in compliant piping systems. In Proceedings of the 6th International Conference on Pressure Surges, Cambridge, UK, 4–6 October 1989; pp. 85–100. [Google Scholar]
- Kruisbrink, A. Modelling of safety and relief valves in waterhammer computer codes. In Proceedings of the 3rd International Conference on Developments in Valves and Actuators for Fluid Control, BHRA, Bournemouth, UK, 27–29 March 1990; pp. 137–149. [Google Scholar]
- Bettinali, F.; Molinaro, P.; Ciccotelli, M.; Micelotta, A. Transient analysis in piping networks including Fluid-Structure Interaction and cavitation effects. Trans. SMiRT 1991, 11, 565–570. [Google Scholar]
- Heinsbroek, A. Fluid-Structure Interaction in non-rigid pipeline systems. Nucl. Eng. Des. 1997, 172, 123–135. [Google Scholar] [CrossRef]
- Young, T. Hydraulic investigations, subservient to an intended Croonian lecture on the motion of the blood. Philos. Trans. R. Soc. Lond. 1808, 98, 164–186. [Google Scholar] [CrossRef]
- Weber, W. Theory of waves propagating in water or other incompressible liquids contained in elastic pipes. Math. Phys. 1866, 18, 353–357. [Google Scholar]
- Resal, H. Note on the small motions of incompressible fluids in an elastic tube. J. Math. Pures Appl. 1876, 3, 342–344. [Google Scholar]
- Moens, A. The Pulsation; Brill: Leiden, The Netherlands, 1878. [Google Scholar]
- Ghidaoui, M.S. On the fundamental equations of water hammer. Urban Water J. 2004, 1, 71–83. [Google Scholar] [CrossRef]
- Chaudhry, M.H. Applied Hydraulic Transients; Springer: New York, NY, USA, 2014; ISBN 978-1-4614-8537-7. [Google Scholar]
- Vardy, A.E.; Tijsseling, A.S. Method of characteristics: (Why) is it so good? In Proceedings of the 12th International Conference on Pressure Surges, Dublin, Ireland, 18–20 November 2015; pp. 327–341. [Google Scholar]
- Gromeka, I. On the velocity of propagation of wave-like motion of fluids in elastic tubes. Phys. Math. Sect. Sci. Soc. 1883, 5, 1–19. [Google Scholar]
- Lamb, H. On the velocity of sound in a tube, as affected by the elasticity of the walls. Manch. Mem. 1898, 42, 1–16. [Google Scholar]
- Thorley, A. Pressure transients in hydraulic pipelines. J. Basic Eng. 1969, 91, 453–460. [Google Scholar] [CrossRef]
- Bürmann, W. Druckstossmessungen an koaxialen Rohren. (Water hammer measurements on coaxial pipes.). 3R Int. 1979, 18, 624–628. [Google Scholar]
- Thielen, H.; Bürmann, W. Calculation and protection of pipe lines laid in the open against undue internal pressure and reactive forces resulting from water hammer. 3R Int. 1980, 19, 622–628. [Google Scholar]
- Tijsseling, A.S.; Lambert, M.F.; Simpson, A.R.; Stephens, M.L.; Vítkovskỳ, J.P.; Bergant, A. Skalak’s extended theory of water hammer. J. Sound Vib. 2008, 310, 718–728. [Google Scholar] [CrossRef]
- Bürmann, W. Water hammer in coaxial pipe systems. J. Hydraul. Div. 1975, 101, 699–715. [Google Scholar]
- Bürmann, W.; Feser, G.; Janson, H.; Thielen, H. Mathematical simulation of the dynamics of pipelines laid in the open in case of unsteady flows. In Report on the Measurements and Numerical Simulation of the Measurements on the Neckar Bridge; Bericht Nr. 623; Universität Karlsruhe, Institut fur Hydromechanik: Karlsruhe, Germany, 1985. [Google Scholar]
- Bürmann, W.; Feser, G.; Janson, H.; Thielen, H. Mathematical simulation of the dynamics of pipelines laid in the open in case of unsteady flows. In Report on the Second Measurements and Numerical Simulation; Bericht Nr. 64; Universität Karlsruhe, Institut fur Hydromechanik: Karlsruhe, Germany, 1986. [Google Scholar]
- Bürmann, W.; Feser, G.; Janson, H.; Thielen, H. Pressure and acceleration measurements on the pipe bridge of a long-distance water main to study the piping dynamics in case of unsteady flow. 3R Int. 1987, 26, 638–646. [Google Scholar]
- Bürmann, W.; Feser, G.; Janson, H.; Thielen, H. Mathematical simulation of the dynamics of pipelines laid in the open in case of unsteady flows. In Report on the Measurements and Numerical Simulation of the Measurements on the Jade Transhipment Station; Bericht Nr. 622; Universität Karlsruhe, Institut fur Hydromechanik: Karlsruhe, Germany, 1986. [Google Scholar]
- Vardy, A.; Alsarraj, A. Method of characteristics analysis of one-dimensional members. J. Sound Vib. 1989, 129, 477–487. [Google Scholar] [CrossRef]
- Vardy, A.; Fan, D. Water hammer in a closed tube. In Proceedings of the 5th International Conference on Pressure Surges, Hanover, Germany, 22–24 September 1986. [Google Scholar]
- Vardy, A.; Fan, D. Constitutive factors in transient internal flows. In Proceedings of the International Conference on Numerical Methods in Engineering: Theory and Applications (NUMETA 87), Swansea, UK, 6–10 July 1987; Volume 2. [Google Scholar]
- Vardy, A.; Fan, D. Flexural waves in a closed tube. In Proceedings of the 6th International Conference on Pressure Surges, BHRA, Cambridge, UK, 4–6 October 1989; pp. 43–57. [Google Scholar]
- Fan, D. Fluid-Structure Interaction in Internal Flows. Ph.D. Thesis, University of Dundee, Department of Civil Engineering, Dundee, UK, 1989. [Google Scholar]
- Ellis, J. A study of pipe-liquid interaction following pump trip and check-valve closure in a pumping station. In Proceedings of the 3rd International Conference on Pressure Surges, Canterbury, UK, 25–27 March 1980; Volume 1. [Google Scholar]
- Ferràs, D.; Manso, P.A.; Schleiss, A.J.; Covas, D.I. Experimental distinction of damping mechanisms during hydraulic transients in pipe flow. J. Fluids Struct. 2016, 66, 424–446. [Google Scholar] [CrossRef]
- Elansary, A.; Contractor, D. Minimization of stresses and pressure surges. J. Press. Vessel Technol. 1990, 112, 311–316. [Google Scholar] [CrossRef]
- Elansary, A.; Contractor, D. Valve closure: Method for controlling transients. J. Press. Vessel Technol. 1994, 116, 437–442. [Google Scholar] [CrossRef]
- Elansary, A.S.; Chaudhry, M.H.; Silva, W. Numerical and experimental investigation of transient pipe flow. J. Hydraul. Res. 1994, 32, 689–706. [Google Scholar] [CrossRef]
- Budny, D.D.; Wiggert, D.; Hatfield, F. The influence of structural damping on internal pressure during a transient pipe flow. J. Fluids Eng. 1991, 113, 424–429. [Google Scholar] [CrossRef]
- Goldberg, D.E. Characteristics method using time-line interpolations. J. Hydraul. Eng. 1983, 109, 670–683. [Google Scholar] [CrossRef]
- Forsythe, G.E.; Wasow, W.R. Finite-Difference Methods for Partial Differential Equations; Wiley: Hoboken, NJ, USA, 1960; ISBN 13: 9780471266976. [Google Scholar]
- Bouabdallah, S.; Massouh, F. Fluid-Structure Interaction in Hydraulic Networks; Aerospace Division Newsletter; American Society of Mechanical Engineers: New York, NY, USA, 1997; Volume AD-53-2, pp. 543–548. [Google Scholar]
- Ghodhbani, A.; Hadj-Taïeb, E. Numerical Coupled Modeling of Water Hammer in Quasi-rigid Thin Pipes. In Design and Modeling of Mechanical Systems; Springer: Berlin, Germany, 2013; pp. 253–264. ISBN 978-3-642-37142-4. [Google Scholar]
- Khalighi, F.; Ahmadi, A.; Keramat, A. Investigation of Fluid-structure Interaction by Explicit Central Finite Difference Methods. Int. J. Eng. Trans. B Appl. 2016, 29, 590–598. [Google Scholar]
- Ferras, D.; Manso, P.; Covas, D.; Schleiss, A. Fluid–structure interaction in pipe coils during hydraulic transients. J. Hydraul. Res. 2017, 55, 491–505. [Google Scholar] [CrossRef]
- Ferràs, D.; Covas, D.I.; Schleiss, A.J. Stress–strain analysis of a toric pipe for inner pressure loads. J. Fluids Struct. 2014, 51, 68–84. [Google Scholar] [CrossRef]
- Keramat, A.; Tijsseling, A. Waterhammer with column separation, Fluid-Structure Interaction and unsteady friction in a viscoelastic pipe. In Proceedings of the International Conference on Pressure Surges, Lisbon, Portugal, 24–26 October 2012. [Google Scholar]
- Tijsseling, A.S. Exact computation of the axial vibration of two coupled liquid-filled pipes. In Proceedings of the ASME 2009 Pressure Vessels and Piping Conference, Prague, Czech Republic, 26–30 July 2009. [Google Scholar]
- Xu, Y.; Jiao, Z. Exact solution of axial liquid-pipe vibration with time-line interpolation. J. Fluids Struct. 2017, 70, 500–518. [Google Scholar] [CrossRef]
- Ferràs, D. Fluid-Structure Interaction During Hydraulic Transients in Pressurized Pipes: Experimental and Numerical Analyses. Ph.D. Thesis, École Polytechnique Fédérale de Lausanne EPFL, Lausanne, Switzerland, 2016. [Google Scholar]
- Tijsseling, A. Poisson-coupling beat in extended waterhammer theory. In Proceedings of the 4th International Symposium on Fluid–Structure Interactions, Aeroelasticity, Flow-Induced Vibration and Noise, At Dallas, TX, USA, November 1997; Volume 53-2, pp. 529–532. [Google Scholar]
- Borzi, A.; Propst, G. Numerical investigation of the Liebau phenomenon. Z. für Angew. Math. Physik ZAMP 2003, 54, 1050–1072. [Google Scholar] [CrossRef]
- Tijsseling, A.S. An Overview of Fluid-Structure Interaction Experiments in Single-Elbow Pipe Systems; CASA-Report 1616; TUE: Eindhoven, The Netherlands, 2016. [Google Scholar]
- Swaffield, J. The influence of bends on fluid transients propagated in incompressible pipe flow. Proc. Inst. Mech. Eng. 1968, 183, 603–614. [Google Scholar] [CrossRef]
- Otwell, R. The Effect of Elbow Restraint on Pressure Transients. Ph.D. Thesis, Michigan State University, Department of Civil and Sanitary Engineering, East Lansing, NI, USA, 1984. [Google Scholar]
- Wiggert, D.; Otwell, R.; Hatfield, F. The effect of elbow restraint on pressure transients. J. Fluids Eng. 1985, 107, 402–406. [Google Scholar] [CrossRef]
- Tijsseling, A.; Vaugrante, P. FSI in L-shaped and T-shaped pipe systems. In Proceedings of the 10th International Meeting of the IAHR Work Group on the Behaviour of Hydraulic Machinery under Steady Oscillatory Conditions, Trondheim, Norway, 26–28 June 2001. [Google Scholar]
- Steens, N.; Pan, J. Transient vibration in a simple fluid carrying pipe system. Acoust. Aust. 2008, 36, 15–21. [Google Scholar]
- Altstadt, E.; Carl, H.; Prasser, H.; WeiB, R. Fluid-Structure Interaction during artificially induced water hammers in a tube with a bend–Experiments and analyses. Multiph. Sci. Technol. 2008, 20, 213–238. [Google Scholar] [CrossRef]
- Simão, M.; Mora-Rodriguez, J.; Ramos, H.M. Mechanical Interaction in Pressurized Pipe Systems: Experiments and Numerical Models. Water 2015, 7, 6321–6350. [Google Scholar] [CrossRef]
- Lesmez, M.W.; Wiggert, D.; Hatfield, F. Modal analysis of vibrations in liquid-filled piping systems. J. Fluids Eng. 1990, 112, 311–318. [Google Scholar] [CrossRef]
- Obradović, P. Fluid-Structure Interactions: An accident which has demonstrated the necessity for FSI analysis. In Proceedings of the 15th IAHR Symposium on Hydraulic Machinery and Cavitation, Belgrade, Yugoslavia, 14 September 1990. [Google Scholar]
- Kruisbrink, A.; Heinsbroek, A. Fluid-Structure Interaction in non-rigid pipeline systems—Large scale validation tests. In Proceedings of the International Conference on Pipeline Systems, Manchester, UK, 1992; pp. 151–164. [Google Scholar]
- Heinsbroek, A.; Kruisbrink, A. Fluid-Structure Interaction in non-rigid pipeline systems-large scale validation experiments. In Proceedings of the 12th International Conference on Structural Mechanics in Reactor Technology (SMiRT), Stuttgart, Germany, 15–20 August 1993. [Google Scholar]
- Lavooij, C. FLUSTRIN: Benchmark Problems; Delft Hydraulics: Delft, The Netherlands, 1987. [Google Scholar]
- Ahmadi, A.; Keramat, A. Investigation of fluid–structure interaction with various types of junction coupling. J. Fluids Struct. 2010, 26, 1123–1141. [Google Scholar] [CrossRef]
- Keramat, A.; Tijsseling, A.; Hou, Q.; Ahmadi, A. Fluid–Structure Interaction with Pipe-Wall Viscoelasticity During Water Hammer; Elsevier: Amsterdam, The Netherlands, 2012; Volume 28, pp. 434–455. [Google Scholar]
- Kochupillai, J.; Ganesan, N.; Padmanabhan, C. A new finite element formulation based on the velocity of flow for water hammer problems. Int. J. Press. Vessels Pip. 2005, 82, 1–14. [Google Scholar] [CrossRef]
- Hatfield, F.; Wiggert, D. Harmonic analysis of coupled fluid and piping. In Proceedings of the ASCE Engineering Mechanics Speciality Conference, West Lafayette, IN, USA, 23–25 May 1983; pp. 180–192. [Google Scholar]
- Davidson, L.; Samsury, D. Liquid-structure coupling in curved pipes-I. Shock Vib. Bull. 1969, 40, 197–207. [Google Scholar]
- Davidson, L.; Samsury, D. Liquid-structure coupling in curved pipes-II. Shock Vib. Bull. 1972, 43, 123–135. [Google Scholar]
- Clark, R.; Reissner, E. Deformations and stresses in Bourdon tubes. J. Appl. Phys. 1950, 21, 1340–1341. [Google Scholar] [CrossRef]
- Reissner, E.; Clark, R.; Gilroy, R. Stresses and Deformations of Torsional Shells of an Elliptical Cross Section with Applications to the Problems of Bending of Curved Tubes and the Bourdon Gage. Trans. ASME J. Appl. Mech. 1952, 37–48. [Google Scholar]
- Bathe, K.; Almeida, C. A simple and effective pipe elbow element-linear analysis. J. Appl. Mech. 1980, 47, 93–100. [Google Scholar] [CrossRef]
- Bathe, K.; Almeida, C. A simple and effective pipe elbow element-interaction effects. J. Appl. Mech. 1982, 49, 165–171. [Google Scholar] [CrossRef]
- Tentarelli, S. Propagation of Noise and Vibration in Complex Hydraulic Tubing Systems. Ph.D. Thesis, Lehigh University, Department of Mechanical Engineering, Bethlehem, PA, USA, 1990. [Google Scholar]
- Brown, F.T.; Tentarelli, S.C. Dynamic behavior of complex fluid-filled tubing systems, Part 1: Tubing analysis. J. Dyn. Syst. Meas. Control 2001, 123, 71–77. [Google Scholar] [CrossRef]
- Tentarelli, S.C.; Brown, F.T. Dynamic behavior of complex fluid-filled tubing systems—Part 2: System analysis. J. Dyn. Syst. Meas. Control 2001, 123, 78–84. [Google Scholar] [CrossRef]
- Budny, D.; Hatfield, F.; Wiggert, D. An experimental study on the influence of structural damping on internal fluid pressure during a transient flow. J. Press. Vessel Technol. 1990, 112, 284–290. [Google Scholar] [CrossRef]
- Housner, G. Bending vibrations of a pipe line containing flowing fluid. J. Appl. Mech. Trans. ASME 1952, 19, 205–208. [Google Scholar]
- Gregory, R.; Païdoussis, M. Unstable oscillation of tubular cantilevers conveying fluid. In Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences, London, UK, 23 August 1966; Volume 293, pp. 512–527. [Google Scholar]
- Païdoussis, M.P.; Issid, N. Dynamic stability of pipes conveying fluid. J. Sound Vib. 1974, 33, 267–294. [Google Scholar] [CrossRef]
- Païdoussis, M.; Laithier, B. Dynamics of Timoshenko beams conveying fluid. J. Mech. Eng. Sci. 1976, 18, 210–220. [Google Scholar] [CrossRef]
- Jendrzejczyk, J.; Chen, S. Experiments on tubes conveying fluid. Thin Walled Struct. 1985, 3, 109–134. [Google Scholar] [CrossRef]
- Païdoussis, M.P. Fluid–Structure Interactions: Slender Structures and Axial Flow; Academic Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Leslie, D.; Vardy, A. Practical guidelines for fluid–structure interaction in pipelines: A review. In Proceedings of the 10th International Meeting of the Work Group on the Behaviour of Hydraulic Machinery under Steady Oscillatory Conditions, Trondheim, Norway, 26–28 June 2001. [Google Scholar]
- Moussou, P.; Lafon, P.; Potapov, S.; Paulhiac, L.; Tijsseling, A. Industrial cases of FSI due to internal flows. In Proceedings of the 9th International Conference on Pressure Surges, Chester, UK, 24–26 March 2004; Volume 1, pp. 13–31. [Google Scholar]
- Almeida, A.; Pinto, A. A special case of transient forces on pipeline supports due to water hammer effects. In Proceedings of the 5th International Conference on Pressure Surges, Hanover, Germany, 22–24 September 1986; Volome 2224, p. 2734. [Google Scholar]
- Hamilton, M.; Taylor, G. Pressure surge—Case studies. In Proceedings of the 7th International Conference on Pressure Surges and Fluid Transients in Pipelines and Open Channels, Harrogate, UK, 16–18 April 1994; pp. 15–27. [Google Scholar]
- Hamilton, M.; Taylor, G. Pressure surge—Criteria for acceptability. In Proceedings of the 7th International Conference on Pressure Surges and Fluid Transients in Pipelines and Open Channels, Harrogate, UK, 16–18 April 1994; pp. 343–362. [Google Scholar]
- Locher, F.; Huntamer, J.; O’Sullivan, J. Caution: Pressure surges in process and industrial systems may be fatal. In Proceedings of the BHR Group Conference Series; Professional Engineering Publishing: Bury St. Edmunds, UK, 2000; Volume 39, pp. 3–18. [Google Scholar]
- Heinsbroek, A.; Tijsseling, A. The influence of support rigidity on waterhammer pressures and pipe stresses. In Proceedings of the 2nd International Conference on Water Pipeline Systems, Scotland, UK, 24–26 May 1994; pp. 17–30. [Google Scholar]
- Tijsseling, A.; Vardy, A. Axial modelling and testing of a pipe rack. In Proceedings of the BHR Group Conference Series Publication, Harrogate, UK, 16–18 April 1996; Volume 19, pp. 363–384. [Google Scholar]
- Ferràs, D.; Manso, P.A.; Schleiss, A.J.; Covas, D.I. Fluid-Structure Interaction in straight pipelines: Friction coupling mechanisms. Comput. Struct. 2016, 175, 74–90. [Google Scholar] [CrossRef]
- Zanganeh, R.; Ahmadi, A.; Keramat, A. Fluid–structure interaction with viscoelastic supports during waterhammer in a pipeline. J. Fluids Struct. 2015, 54, 215–234. [Google Scholar] [CrossRef]
- Wu, J.S.; Shih, P.Y. The dynamic analysis of a multispan fluid-conveying pipe subjected to external load. J. Sound Vib. 2001, 239, 201–215. [Google Scholar] [CrossRef]
- Yang, K.; Li, Q.; Zhang, L. Longitudinal vibration analysis of multi-span liquid-filled pipelines with rigid constraints. J. Sound Vib. 2004, 273, 125–147. [Google Scholar] [CrossRef]
- Moser, M.; Heckl, M.; Ginters, K.H. On Wave Propagation of Fluid-Filled Circular Cylindrical Tubes. Acustica 1986, 60, 34–44. [Google Scholar]
- Kwong, A.; Edge, K. Structure-borne noise prediction in liquid-conveying pipe systems. J. Syst. Control Eng. 1996, 210, 189–200. [Google Scholar] [CrossRef]
- Kwong, A.; Edge, K. A method to reduce noise in hydraulic systems by optimizing pipe clamp locations. J. Syst. Control Eng. 1998, 212, 267–280. [Google Scholar] [CrossRef]
- De Jong, C. Analysis of Pulsations and Vibrations in Fluid-Filled Pipe Systems. Ph.D. Thesis, Technische Universiteit Eindhoven, Eindhoven, The Netherlands, 1994. [Google Scholar]
- Janssens, M.; Verheij, J.; Thompson, D. The use of an equivalent forces method for the experimental quantification of structural sound transmission in ships. J. Sound Vib. 1999, 226, 305–328. [Google Scholar] [CrossRef]
- Chen, C.C. Noise and vibration in complex hydraulic tubing systemss. In Continuum Mechanics—Progress in Fundamentals and Engineering Applications; Gan, Y., Ed.; Intech Open Access Publisher: London, UK, 2012; ISBN 978-953-51- 0447-6. [Google Scholar]
- Tijsseling, A.; Vardy, A. On the suppression of coupled liquid/pipe vibrations. In Hydraulic Machinery and Cavitation; Springer: Berlin, Germany, 1996; pp. 945–954. [Google Scholar]
- Hachem, F.E.; Schleiss, A.J. Effect of drop in pipe wall stiffness on water–hammer speed and attenuation. J. Hydraul. Res. 2012, 50, 218–227. [Google Scholar] [CrossRef]
- Koo, G.; Park, Y. Vibration reduction by using periodic supports in a piping system. J. Sound Vib. 1998, 210, 53–68. [Google Scholar] [CrossRef]
- Young, F.; Hunter, S. Hydraulic Transients in Liquid-Filled Pipelines During Earthquakes. In Lifeline Earthquake Engineering Buried Pipelines, Seismic Risk and Instrumentation; American Society of Mechanical Engineers: New York, NY, USA, 1979. [Google Scholar]
- Lo Frano, R.; Forasassi, G. Preliminary assessment of the Fluid-Structure Interaction effects in a GEN IV LMR. In Proceedings of the International Conference on Heat Transfer, Fluid Mechanics and Thermodynamics, Malta, 16–18 July 2012. [Google Scholar]
- Mitsume, N.; Yoshimura, S.; Murotani, K.; Yamada, T. Improved MPS-FE Fluid-Structure Interaction coupled method with MPS polygon wall boundary model. Comput. Model. Eng. Sci. 2014, 101, 229–247. [Google Scholar]
- Hara, F. Seismic vibration analysis of Fluid-Structure Interaction in LMFBR piping systems. J. Press. Vessel Technol. 1988, 110, 177–181. [Google Scholar] [CrossRef]
- Hatfield, F.; Wiggert, D. Seismic pressure surges in liquid-filled pipelines. J. Press. Vessel Technol. 1990, 112, 279–283. [Google Scholar] [CrossRef]
- Blade, R.J.; Lewis, W.; Goodykoontz, J.H. Study of a Sinusoidally Perturbed Flow in a Line Including a 90 Degree Elbow with Flexible Supports; National Aeronautics and Space Administration (NASA), Lewis Research Center: Cleveland, OH, USA, 1962.
- Steelant, J. Multi-phase fluid-hammer in aerospace applications. In Proceedings of the 12th International Conference on Pressure Surges, Dublin, Ireland, 18–20 November 2015; pp. 21–31. [Google Scholar]
- Bombardieri, C.; Traudt, T.; Manfletti, C. Experimental and Numerical Analysis of Water Hammer During the Filling Process of Pipelines. In Proceedings of the Space Propulsion Conference, Cologne, Germany, 18–22 May 2014. [Google Scholar]
- McDonald, D.A. Blood Flow in Arteries; Williams & Wilkins: Baltimore, MD, USA, 1974; ISBN 13 9780713142136. [Google Scholar]
- Nakoryakov, V.; Sobolev, V.; Shrieber, I.; Shtivel’Man, B.Y. Water hammer and propagation of perturbations in elastic fluid-filled pipes. Fluid Dyn. 1976, 11, 493–498. [Google Scholar] [CrossRef]
- Anderson, A.; Johnson, G. Effect of Tube Ovalling on Pressure Wave Propagation Speed. J. Eng. Med. 1990, 204, 245–251. [Google Scholar] [CrossRef] [PubMed]
- Sherwin, S.; Franke, V.; Peiró, J.; Parker, K. One-dimensional modelling of a vascular network in space-time variables. J. Eng. Math. 2003, 47, 217–250. [Google Scholar] [CrossRef]
- Van de Vosse, F.N.; Stergiopulos, N. Pulse wave propagation in the arterial tree. Annu. Rev. Fluid Mech. 2011, 43, 467–499. [Google Scholar] [CrossRef]
- Nichols, W.; O’Rourke, M.; Vlachopoulos, C. McDonald’s Blood Flow in Arteries: Theoretical, Experimental and Clinical Principles; CRC Press: Boca Raton, FL, USA, 2011; ISBN 9780340985014. [Google Scholar]
- Alastruey, J.; Parker, K.H.; Sherwin, S.J. Arterial pulse wave haemodynamics. In Proceedings of the 11th International Conference on Pressure Surges, Lisbon, Portugal, 24–26 October 2012; pp. 401–442. [Google Scholar]
- Wathen, A.; Galdi, G.; Rannacher, R.; Robertson, A.; Turek, S. Hemodynamical Flows: Modeling, Analysis and Simulation; Springer: Berlin, Germany, 2009; ISBN 978-3-7643-7805-9. [Google Scholar]
- Janela, J.; Moura, A.; Sequeira, A. A 3D non-Newtonian fluid–structure interaction model for blood flow in arteries. J. Comput. Appl. Math. 2010, 234, 2783–2791. [Google Scholar] [CrossRef]
- Simão, M.; Ferreira, J.; Mora-Rodriguez, J.; Ramos, H. Identification of DVT diseases using numerical simulations. Med. Biol. Eng. Comput. 2016, 54, 1591–1609. [Google Scholar] [CrossRef] [PubMed]
- Jaeger, C.; Kerr, L.; Wylie, E. Water hammer effects in power conduits. Civ. Eng. Public Works Rev. 1948, 23, 500–503. [Google Scholar]
- Bergant, A.; Simpson, A.R.; Tijsseling, A.S. Water hammer with column separation: A review of research in the twentieth century. J. Fluids Struct. 2006, 22, 135–171. [Google Scholar] [CrossRef]
- Wang, C.; Pizzica, P.; Gvildys, J.; Spencer, B. Analysis of Fluid-Structure Interaction and Structural Response of Chernobyl-4 Reactor; Technical Report; Argonne National Lab.: Argonn, IL, USA, 1989.
- Simão, M.; Mora-Rodriguez, J.; Ramos, H.M. Dynamic response behind an accident occurred in a main WSS. Eur. J. Environ. Civ. Eng. 2016, 22, 267–287. [Google Scholar] [CrossRef]
- Leishear, R.A. Nuclear power plant fires and explosions, IV, water hammer explosions mechanisms. In Proceedings of the ASME 2017 Pressure Vessels and Piping Conference, Waikoloa, HI, USA, 16–20 July 2017. [Google Scholar]
- Bonin, C. Water-hammer damage to Oigawa power station. J. Eng. Power 1960, 82, 111–116. [Google Scholar] [CrossRef]
- Trenkle, C.J. Failure of Riveted and Forge-Welded Penstock. J. Energy Div. 1979, 105, 93–102. [Google Scholar]
- Almeida, A.; Ramos, H. Water supply operation: Diagnosis and reliability analysis in a Lisbon pumping system. J. Water Suppl. Res. Technol. Aqua 2010, 59, 66–78. [Google Scholar] [CrossRef]
- Vecchio, R.S.; Sinha, S.K.; Bruck, P.M.; Esselman, T.C.; Zysk, G. The 2007 New York City steam explosion: Post-accident analysis. In Proceedings of the 12th International Conference on Pressure Surges, Dublin, Ireland, 18–20 November 2015; pp. 7–17. [Google Scholar]
- Adamkowski, A. Case study: Lapino powerplant penstock failure. J. Hydraul. Eng. 2001, 127, 547–555. [Google Scholar] [CrossRef]
- Meserve, R.A. Safety Issues at the Defense Production Reactors: A Report to the US Department of Energy; National Academies: Washington, DC, USA, 1987; ISBN-13 9780000001542. [Google Scholar]
- Vardy, A.; Alsarraj, A. Coupled axial and flexural vibration of 1-D members. J. Sound Vib. 1991, 148, 25–39. [Google Scholar] [CrossRef]
- Fan, D.; Vardy, A. Waterhammer including Fluid-Structure Interactions. In Proceedings of the First International Conference on Flow Interaction, Hong Kong, 5–9 September 1994; pp. 439–442. [Google Scholar]
- Krause, N.; Goldsmith, W.; Sackman, J. Transients in tubes containing liquids. Int. J. Mech. Sci. 1977, 19, 53–68. [Google Scholar] [CrossRef]
- Barez, F.; Goldsmith, W.; Sackman, J. Longitudinal waves in liquid-filled tubes I: Theory. Int. J. Mech. Sci. 1979, 21, 213–221. [Google Scholar] [CrossRef]
- Wood, D.J. A study of the response of coupled liquid flow-structural systems subjected to periodic disturbances. J. Basic Eng. 1968, 90, 532–540. [Google Scholar] [CrossRef]
- Wood, D.J. Influence of line motion on waterhammer pressures. J. Hydraul. Div. 1969, 95, 941–960. [Google Scholar]

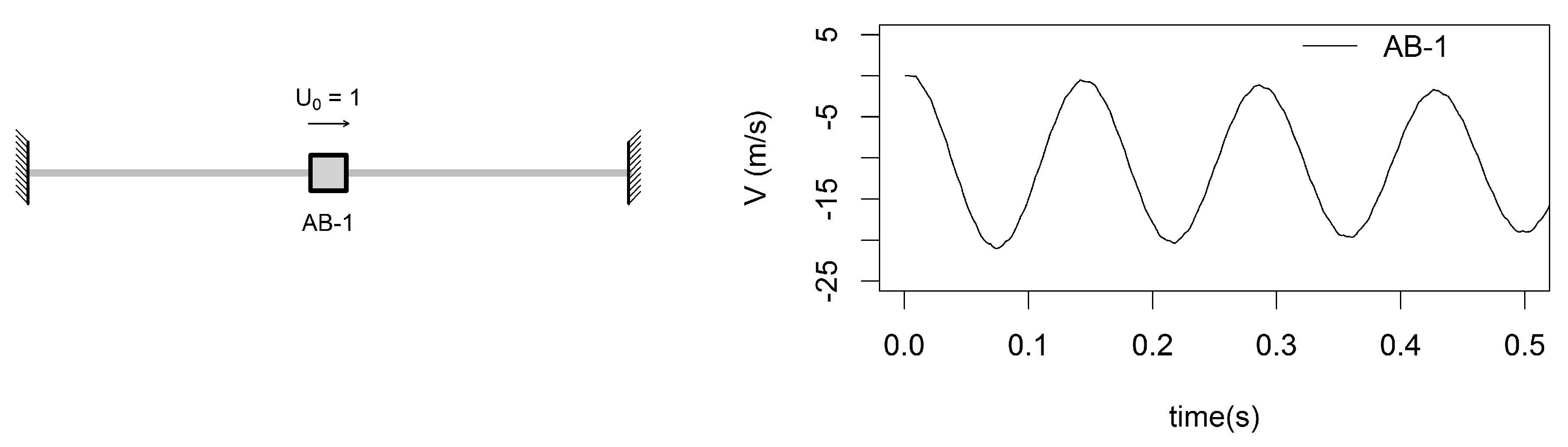
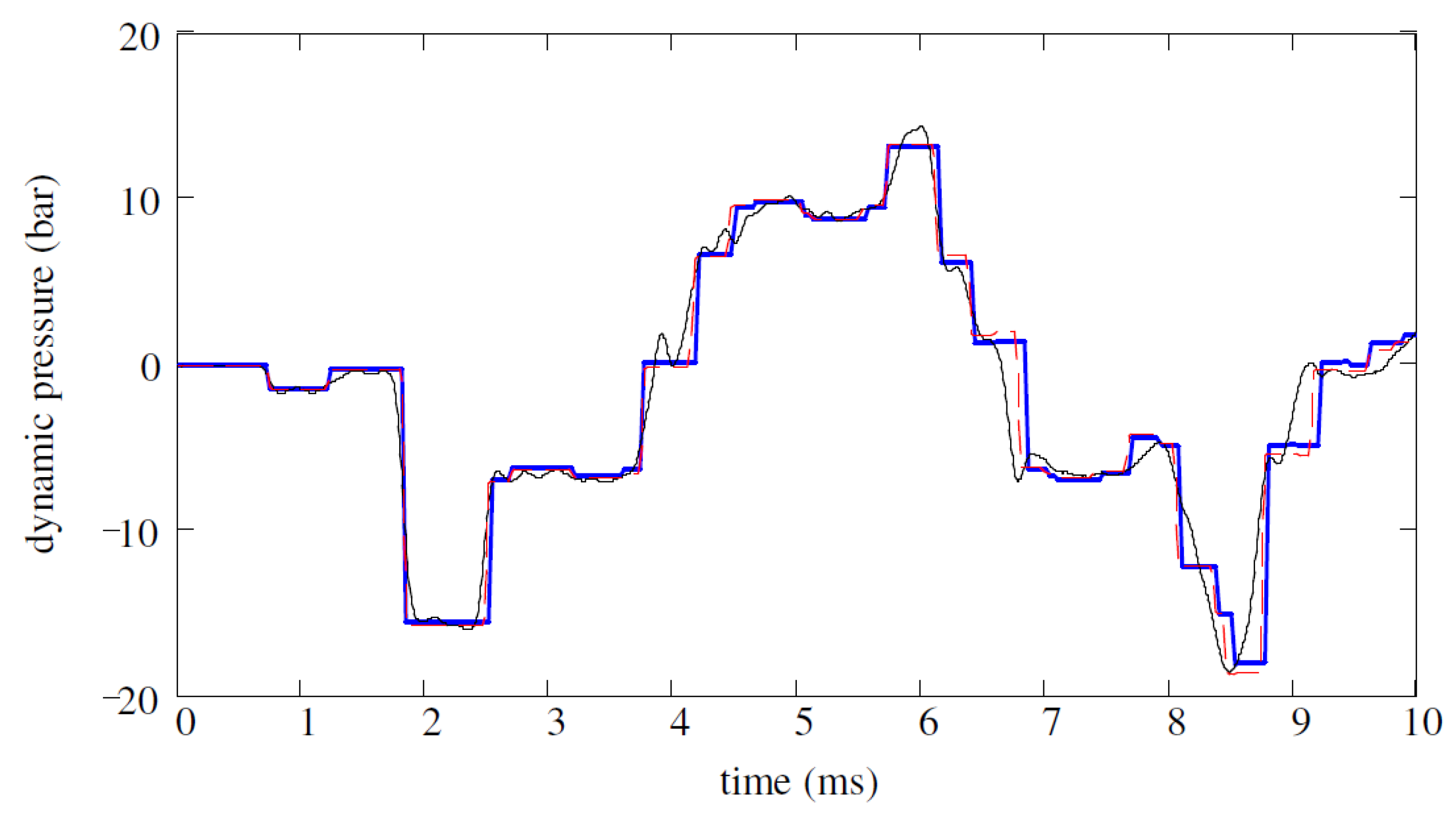

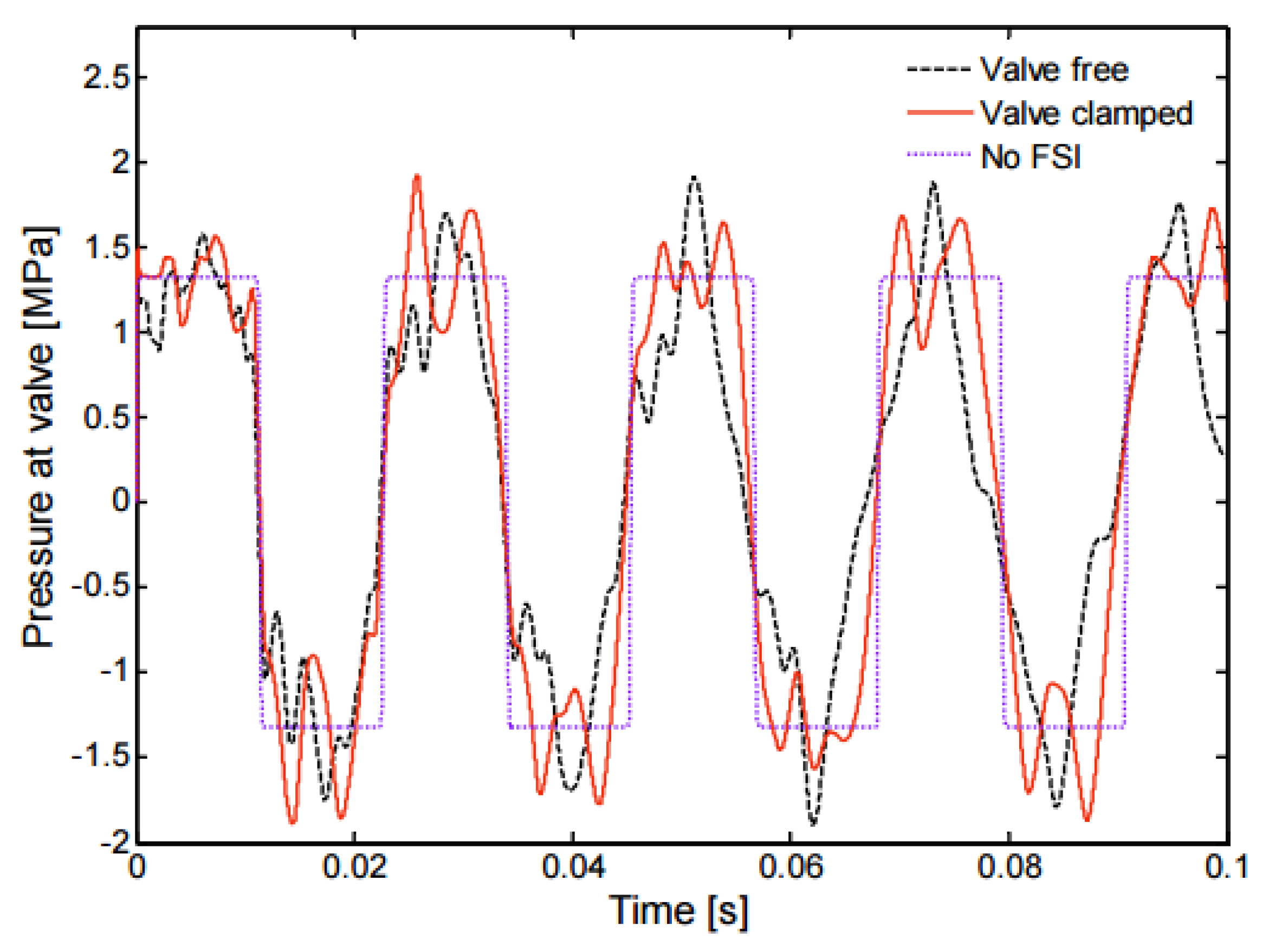
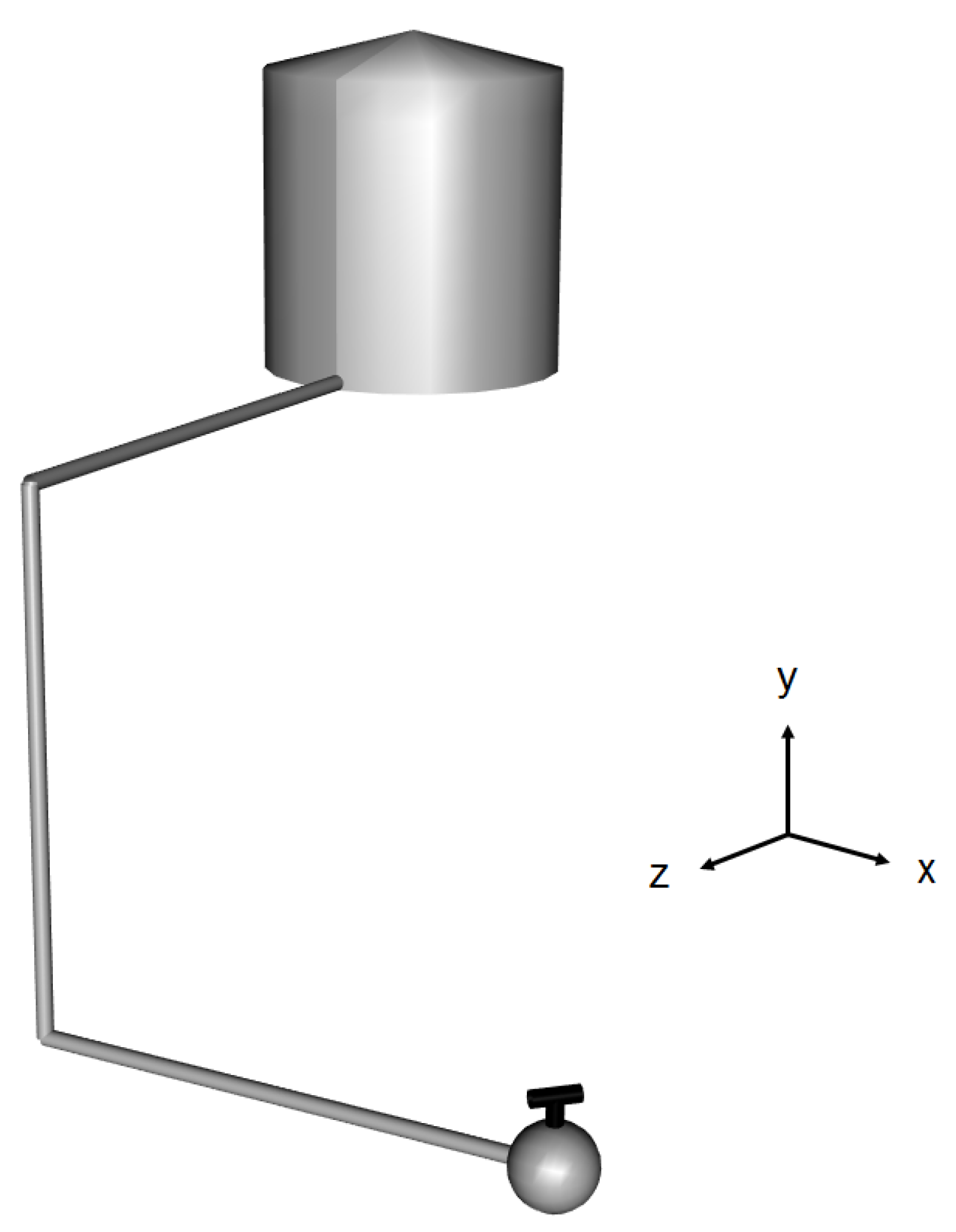
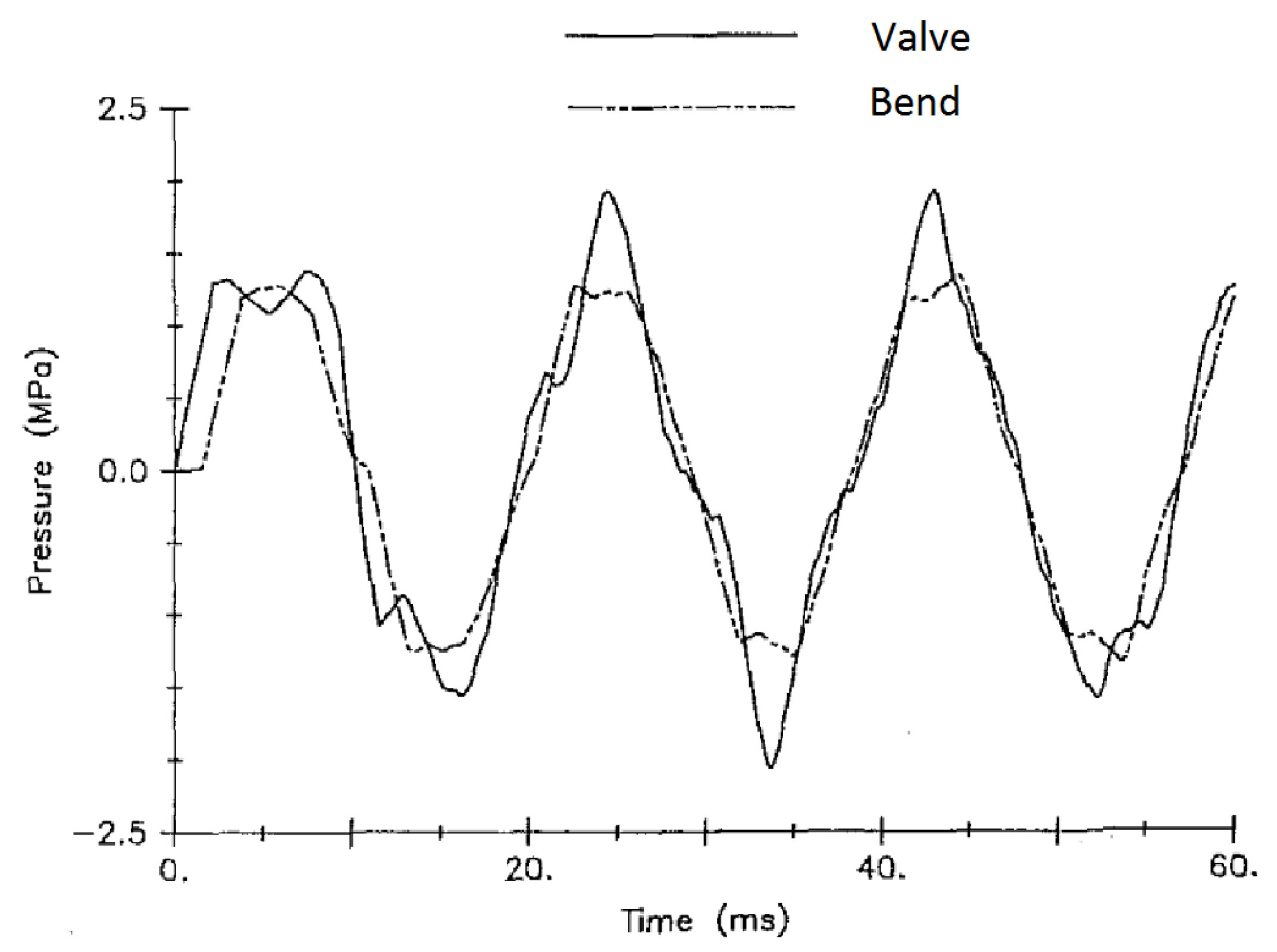
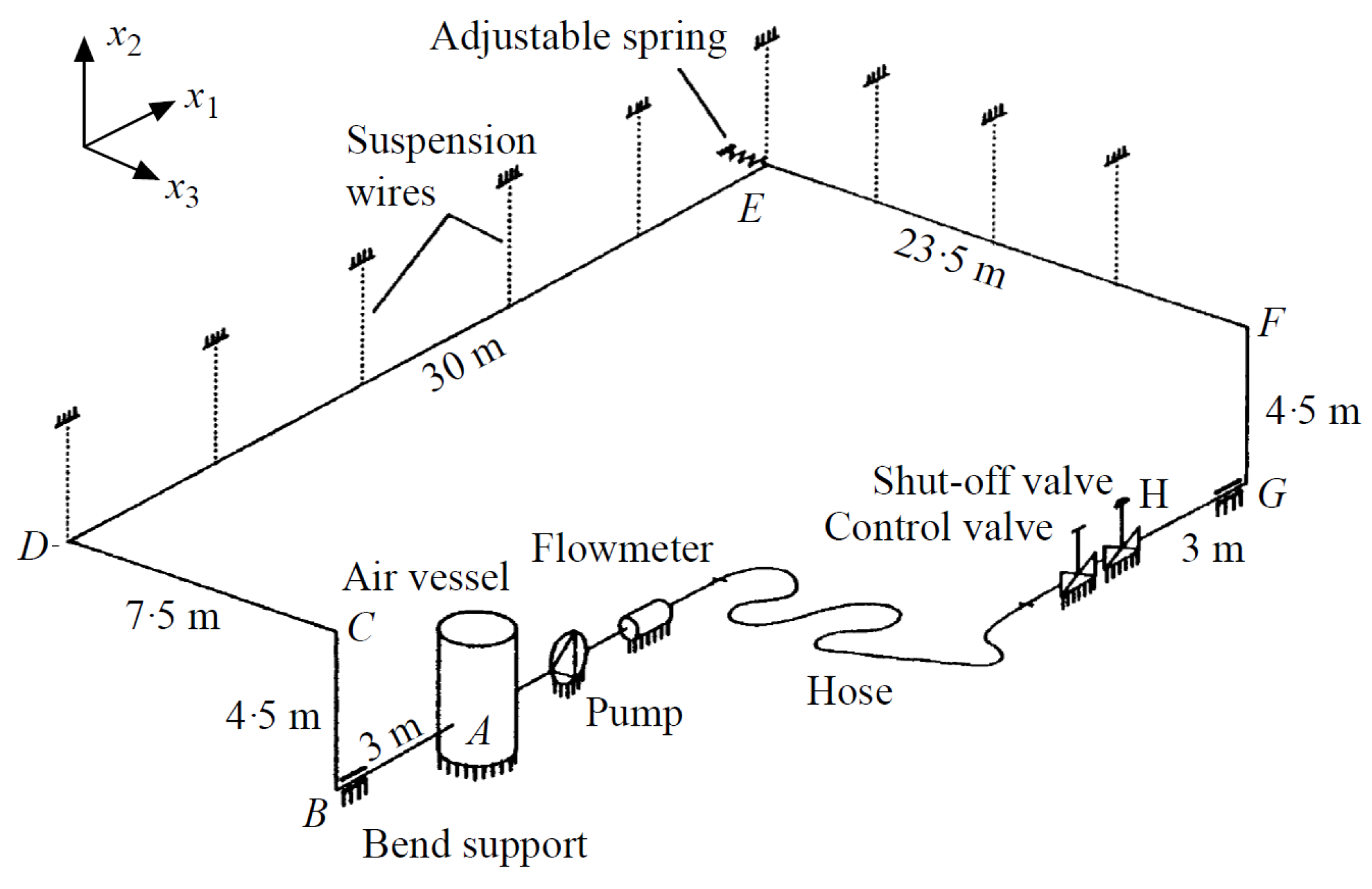
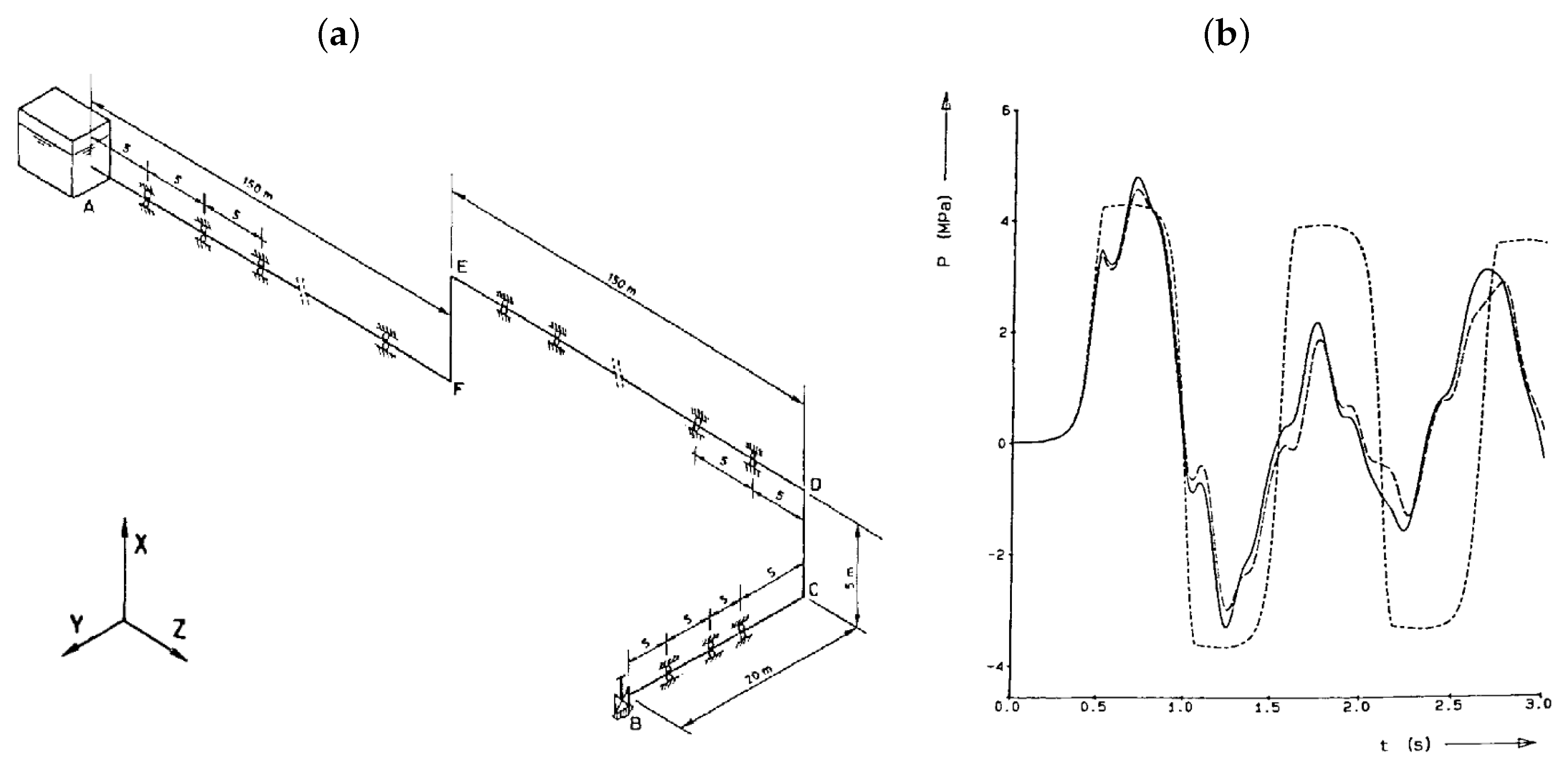
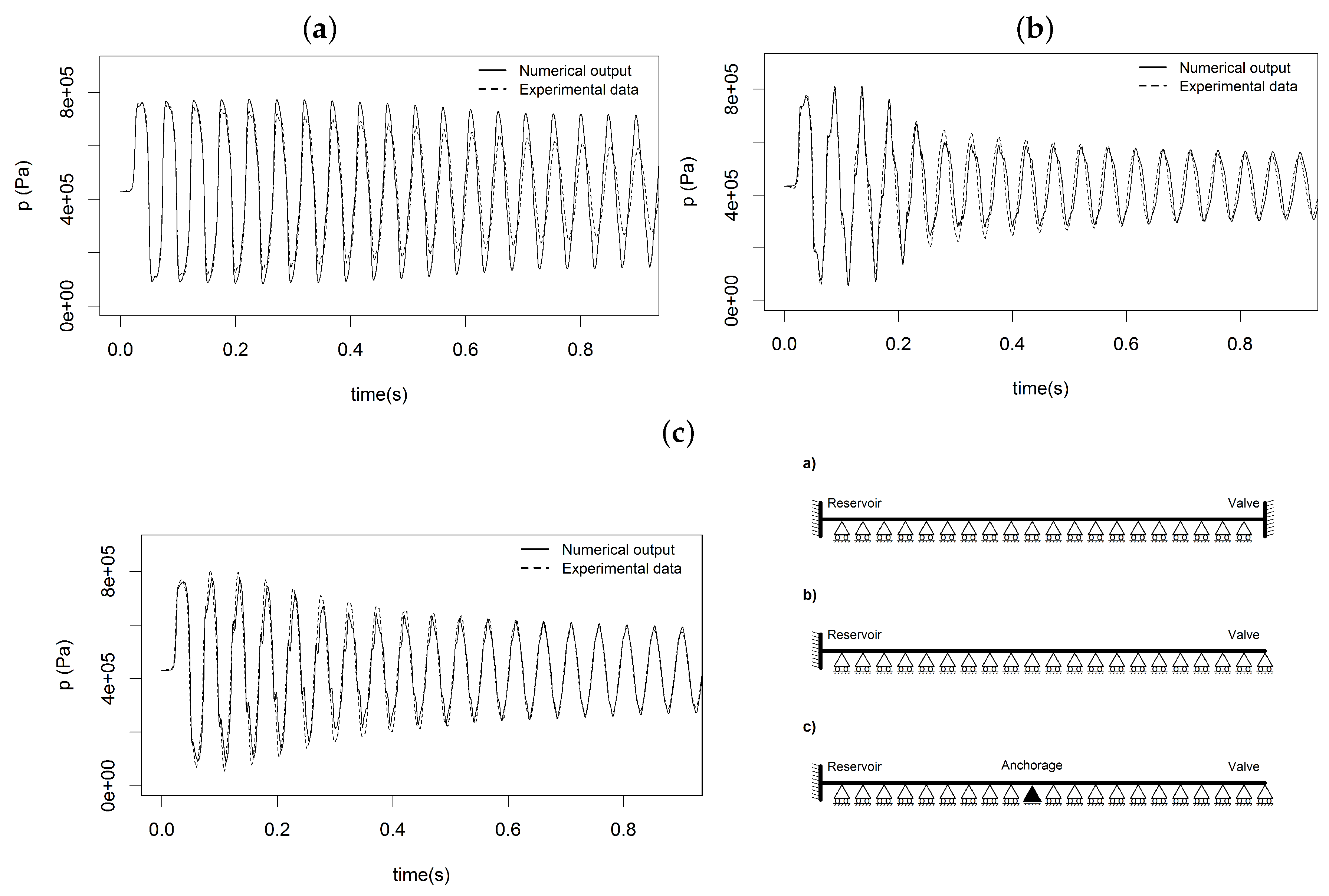
| DOF | Description | Main Contributions |
|---|---|---|
| 1 | Only the fluid transient is described. Equations solved: (1), (2) | [1,41,42,43,44,45,46] |
| 1,3 | Solid surging is coupled with the fluid. Equations solved: (1), (2), (5), (6) | [12,47,48,49,50,51,52,53,54,55,56,57] |
| 1,2,3 | Fluid, breathing and solid surging interact. Equations solved: (1), (2), (3), (4), (5), (6) | [5,47,58,59,60] |
| 1,3 and 4,6 or 5,7 | Fluid and solid surging, and either swaying and yawing or heaving and pitching are taken into account. Equations solved: (1), (2), (5), (6) and (7), (8), (11), (12) or (9), (10), (13), (14) | [40,53,61,62,63,64,65,66,67,68] |
| 1,3,4,5,6,7,8 | Fluid and solid surging, swaying, heaving, yawing, pitching and rolling are coupled. Equations solved: (1), (2), (5), (6), (7), (8), (9), (10), (11), (12), (13), (14), (15), (16) | [51,69,70,71,72,73,74] |
| Reference | Experimental Setup | Transient Test |
|---|---|---|
| [118] | 45–180, hor. mitre, hor. curved bends , rigid (2 jacks) | valve closure: 2–5 ms initial flow vel.: 0.6–2.4 m/s |
| [62] | 30–150, hor. mitre, rigid and free | valve closure: 2 ms initial flow vel.: 2–3 m/s |
| [63] | hor. 114.3 mm, mm, , rigid | gun: 150 bar pulse 3 |
| [64] | pellet impact 0.2 m/s | |
| [119] [120] | hor. | valve closure: 4 ms initial flow vel.: 1.2 m/s |
| [66] [121] | hor. 0.88 kg | rod impact 0.15 m/s |
| [122] | hor. | impact hammer pulse 1–2 ms |
| [123] | vert. elbow | valve opening: 20–200 ms initial flow vel.: 2–17 m/s |
| Industry | Application | International Standards |
|---|---|---|
| Hydropower energy | penstocks | ASME-B31.3 DIN-19704-1 ASCE MOP 79 CECT-1979 |
| Nuclear/Thermal energy | cooling systems | ASME-BPV NS-G-1.9 |
| Oil/Gas transportation | oil/gas mains | ASME-B31.2 ASME-B31.4 ISO-13628 |
| Water distribution | water pipes | ANSI/ASSE-1010 PDI-WH 201 |
| Aerospace | fuel pipes | ISO/FDIS-8575 NASA-STD-8719 |
| Location | Facility | Description and Citations |
|---|---|---|
| Oigawa, Japan | Penstock | A water–hammer wave, caused by a fast valve-closure, split the penstock open and produced the pipe collapse upstream [194]. |
| Big Creek, U.S.A. | Penstock | Burst turbine inlet valve caused by a fast closure [195]. |
| Azambuja, Portugal | Pump station | Collapse of water column separation causing the burst of the pump casing [80]. |
| Lütschinen, Switzerland | Penstock | Penstock failure during draining due to the buckling produced by a frozen vent at the upstream end [80]. |
| Arequipa, Peru | Penstock | The clogging of the control system of a valve resulted in buckling and the failure of the welding seams of the penstock due to fatigue [80]. |
| Ok, Papua New Guinea | Power house | The draft tube access doors were damaged and the power house flooded due to column separation in the system [80]. |
| Lisbon, Portugal | Water main | Rupture of concrete support blocks during the slow closure of an isolation valve installed in a large suction pipe [192,196]. |
| New York, U.S.A. | Steam pipe | Condensation-induced water–hammer caused the rupture of the steam pipe [197]. |
| Lapino, Poland | Penstock | Burst of the penstock caused by a rapid cut-off and low quality of the facility [198]. |
| Chernobyl, Ukraine | Nuclear reactor | Fuel pin failure, fuel-coolant interaction and Fluid–Structure Interaction were involved in the failure of the nuclear reactor [191]. |
| New York, U.S.A | Nuclear reactor | Circumferential weld failure in one of the feedwater lines due to a steam generator water–hammer [199]. |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ferras, D.; Manso, P.A.; Schleiss, A.J.; Covas, D.I.C. One-Dimensional Fluid–Structure Interaction Models in Pressurized Fluid-Filled Pipes: A Review. Appl. Sci. 2018, 8, 1844. https://doi.org/10.3390/app8101844
Ferras D, Manso PA, Schleiss AJ, Covas DIC. One-Dimensional Fluid–Structure Interaction Models in Pressurized Fluid-Filled Pipes: A Review. Applied Sciences. 2018; 8(10):1844. https://doi.org/10.3390/app8101844
Chicago/Turabian StyleFerras, David, Pedro A. Manso, Anton J. Schleiss, and Dídia I. C. Covas. 2018. "One-Dimensional Fluid–Structure Interaction Models in Pressurized Fluid-Filled Pipes: A Review" Applied Sciences 8, no. 10: 1844. https://doi.org/10.3390/app8101844
APA StyleFerras, D., Manso, P. A., Schleiss, A. J., & Covas, D. I. C. (2018). One-Dimensional Fluid–Structure Interaction Models in Pressurized Fluid-Filled Pipes: A Review. Applied Sciences, 8(10), 1844. https://doi.org/10.3390/app8101844