Image Reconstruction of Internal Defects in Wood Based on Segmented Propagation Rays of Stress Waves

Abstract

In order to detect the size and shape of defects inside wood, an image reconstruction method based on segmented propagation rays of stress waves is proposed. The method uses sensors to obtain the stress wave velocity data by hanging around the timber equally, visualizes those data, and reconstructs the image of internal defects with the visualized propagation rays. The basis of the algorithm is precisely segmenting the rays to benefit the spatial interpolation. First, a ray segmentation algorithm using the elliptical neighborhood technique is proposed, which can be used to segment the rays and estimate the velocity values of segmented rays by the nearby original rays using elliptical zones. Second, a spatial interpolation algorithm utilizing a segmented ellipse according to the segmented rays is also proposed, which can be used to estimate the velocity value of a grid cell by the segmented ellipses corresponding to the nearby segmented rays. Then, the image of the internal defect inside the wood is reconstructed. Both simulation and experimental data were used to evaluate the proposed method, and the area and shape of the imaging results were analyzed. The comparison results show that the proposed method can produce high quality reconstructions with clear edges and high accuracy.

1. Introduction

It is important to detect wood internal defects which can endanger the health of trees. Different from other non-destructive testing technologies, such as X-ray [1,2,3], the stress wave method has become the mainstream technology in wood non-destructive testing because of its low cost, portability, and harmlessness [4,5,6]. So far, the wave propagation mechanism for standing trees or wood is not fully understood, and the precise physics model of sound’s interaction with defect is very difficult to establish [7,8]. Using stress wave timing instruments, researchers can measure the transmission time of a manually produced sound impulse (stress wave). Therefore, many researchers use this testing method to analyze whether there are any defects in wood [9,10,11,12]. The concept of detecting defects using this method is based on the observation that stress wave propagation is sensitive to the presence of degradation in wood [13]. Stress wave velocity is directly related to the physical and mechanical properties of the wood, and defects result in a decrease in wood density or mass [14]. In general, stress waves travel slower in decayed or deteriorated wood than in sound wood, and they also travel around hollows, increasing the transmission time between two testing points [13,15,16,17]. Based on this fundamental conclusion and signal acquisition of stress wave propagation velocity in wood cross sections, the horizontal distribution of the stress wave velocity in wood can be analyzed and images of wood internal defects can also be reconstructed [18,19,20].

The image reconstruction algorithm is the key step of stress wave nondestructive testing technology. Feng et al. [21] proposed an image reconstruction method for detecting wood internal decay. The method uses the Kriging interpolation algorithm, which estimates the velocity values of the unknown grid cells based on the surrounding information. Schubert et al. [22] visualized the elastic waves that propagate in a trunk during a tomographic measurement by numerical simulations. The numerical model enabled investigation of the influence of decay on tomographic measurements while neglecting the heterogeneity of wood. Lin et al. [23] analyzed the envelope peak value of the first arrival wave in the stress wave signal, determined the location of the defect, drew the general outline of the cavity, and verified the reliability of the method by experiments on camphor trees. Zhan et al. [24] collected stress wave velocity signals of tree cross-sections using professional equipment, and proposed a stress wave imaging algorithm named IABLE, which calculated the grid distribution of wave velocity in tree faults by an iterative inversion method. Du et al. [25] proposed a stress save tomography method of wood internal defects using ellipse-based spatial interpolation and velocity compensation. The algorithm is good at processing the regions near the sensors and can resist signal interference.

Image reconstruction for stress wave tomography is a nonlinear problem, and the signals for imaging algorithms are usually sparse. Therefore, the solutions for stress wave tomography are not unique [26,27]. Although several image reconstruction methods for stress wave tomography have been proposed, the accuracy of imaging is still not satisfactory. For example, when an internal defect is present in the tree trunk, the existing stress wave tomography methods tend to overestimate its size [28,29]. In addition, the quality of images taken near the sensor is significantly lower than those taken in the middle part of a trunk using stress wave velocity and the tomography method [30].

The objective of this study is to improve the quality of reconstructed imaging of internal defects in wood using stress wave technology. We propose a novel image reconstruction algorithm using segmented propagation rays of stress waves. Then, the algorithm is applied to detect the size and shape of defects inside wood. To verify the feasibility of the proposed approach, eight specimens with defects of different size and position were tested, and the area and shape of the imaging results were analyzed.

2. Materials and Methods

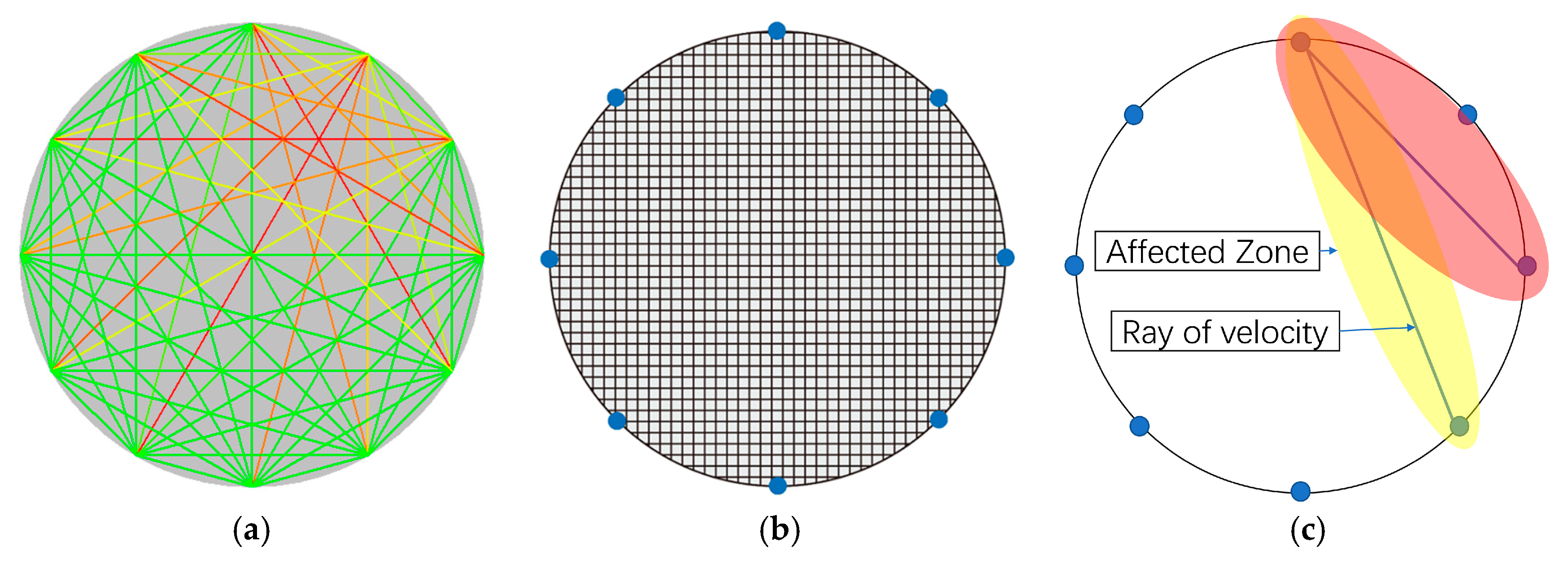
2.1. Ellipse-Based Spatial Interpolation and Image Reconstruction

Assuming that stress wave propagation in wood follows a straight path, a certain propagation ray can represent the velocity and path of a stress wave between a pair of sensors. As shown in Figure 1a, after the acquisition of stress wave velocity signals, the velocity matrix which records the propagation velocity between any pair of sensors can be visualized as a graph of propagation rays. The red ray indicates that the wave velocity is slow, which means that the stress wave passes through the defect area. In contrast, the green ray indicates that the wave velocity is fast, which means that the stress wave passes through a healthy area. Figure 1b shows the gridding of the imaging area, which is commonly applied in existing image reconstruction algorithms for stress wave tomography. The quality of the reconstructed image depends on the correct estimation of grid values. Based on the visualization of propagation rays and the grid graph, an ellipse-based spatial interpolation (EBSI for short) method for image reconstruction has been developed in recent years [25,31,32]. As shown in Figure 1c, each ray affects the surrounding area (called affected zone) and the shape of the affected zone is elliptical. Then, the value of the grid cells in the affected zone is equal to the value of the corresponding ray. If a certain grid cell is in several affected zones simultaneously, the value of this grid cell will be determined by the value of those affected zones using different strategies.

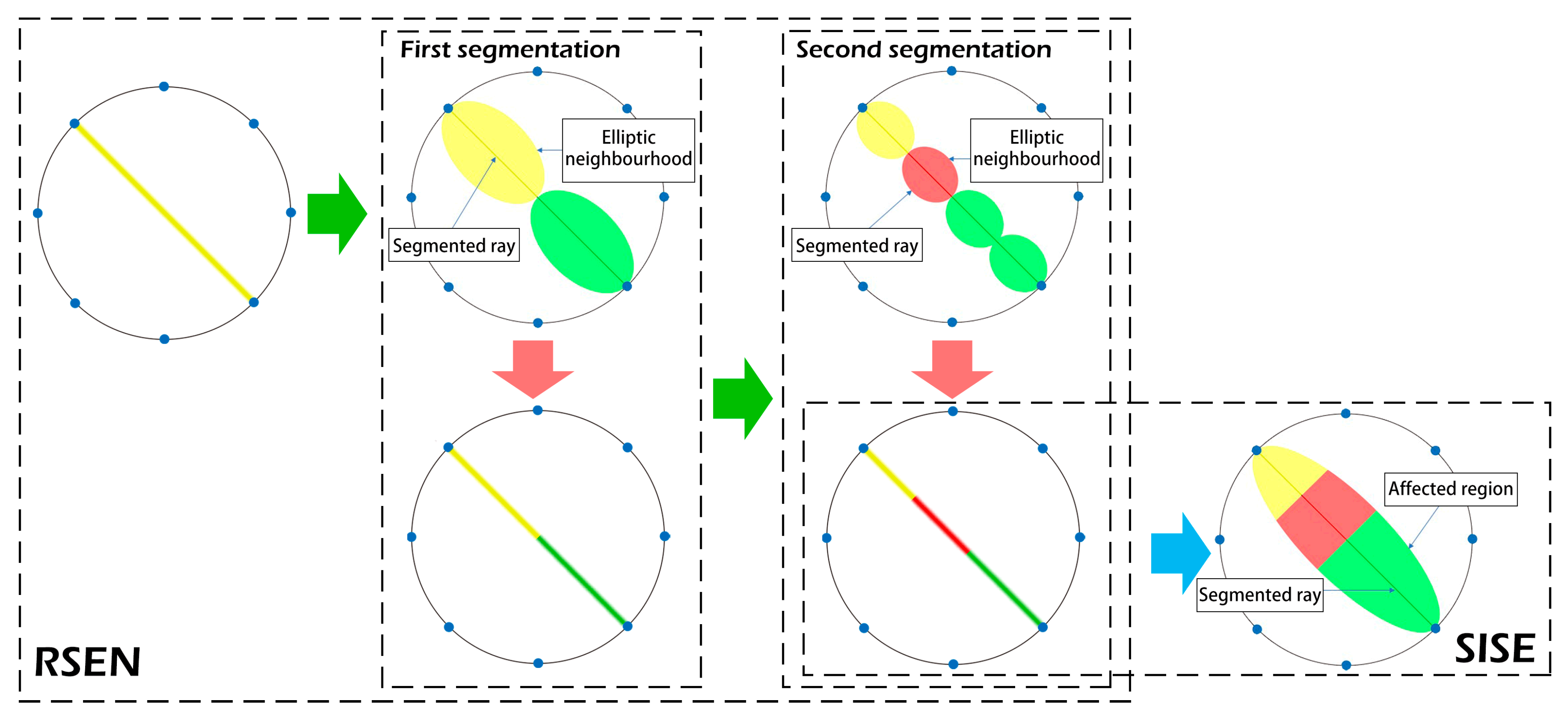
2.2. Modified Image Reconstruction Algorithm

In addition to the algorithm itself, the input signal can also improve the accuracy of imaging [33,34]. In this field, the rays graph can be regarded as the input of spatial interpolation algorithm. The color and length are two basic graphic features of a certain propagation ray. For red rays which pass through the defective area, compared with longer rays, the ellipse corresponding to a shorter ray is more likely to overlap the defect area. Du et al. [25] increased the weight of shorter rays, and achieved better imaging results than that of equivalent weight strategy, especially improving the image quality near the sensor, because the rays between adjacent sensors are usually the shortest. Therefore, making full use of the graphic elements in the graph of propagation rays is helpful to improve the accuracy of the spatial interpolation algorithm. By considering this issue, a modified image reconstruction method is presented in this paper. The basis of the proposed method is to segment long rays into short rays in order to make every propagation ray more precise and more conducive to subsequent spatial interpolation. As shown in Figure 2, the algorithm consists of two parts: ray segmentation by elliptical neighborhood (RSEN for short) and corresponding spatial interpolation by segmented ellipse (SISE for short). In the RSEN algorithm, each original ray is segmented several times by iteration. At each iteration, a certain ray is divided into two rays with equal length, and the velocity determined for that ray is calculated by the elliptical neighborhood corresponding to the ray. In the SISE algorithm, based on a group of segmented rays, a segmented ellipse is constructed to estimate the value of surrounding grid cells.

Estimating the new value of the segmented ray is the key step in the RSEN method, and an ellipse is used to define the neighborhood range. As shown in Figure 3a, those propagation rays passing through the gray ellipse, such as L1 and L2, can be used to calculate the value of segmented ray. The long axis of the ellipse is the segmented ray, and the shape of the elliptical neighborhood can be expressed as,

$$c_1=b_1/a_1$$

(1)

where a₁ is the long axis of the ellipse, and b₁ is the short axis of the ellipse. Therefore, c₁ is the control coefficient of the elliptical shape. For convenience of calculation, each original ray is discretized into a set of points. If any point of a certain ray is in the range of the ellipse, it indicates that the ray passes through the ellipse. Whether a certain point is in the elliptical zone can be identified as follows,

$$f(x,y)=\{\begin{array}{c}1\hspace{1em}{D}^2{}_{x{b}_1}/a_1{}^{2\hspace{1em}}+D^2{}_{y{a}_1}/b_1{}^2\le 1\\ 0\hspace{1em}{D}^2{}_{x{b}_1}/a_1{}^{2\hspace{1em}}+D^2{}_{y{a}_1}/b_1{}^2>1\end{array}$$

(2)

where D_xb1 is the distance between a certain discretized point and the short axis of the ellipse, and D_ya1 is the distance between a certain discretized point and the long axis of the ellipse. If f(x,y) = 1, it means that the point is within the ellipse. Then, the original ray that the point belongs to is recorded. When all the rays have been identified, the estimated value of the segmented ray can be calculated as

$$v={\displaystyle \sum _{k=1}^M{v}_{R_k}}/M$$

(3)

where v is the estimated value of the segmented ray, v_Rk is the velocity value of a certain ray in the elliptical neighborhood, and M is the total number of the recorded rays. An original ray will be segmented many times to get a more precise rays graph for spatial interpolation, and the termination condition for iterative segmentation can be given as,

$$l_{Ri}\le (l_{\min }/2)$$

(4)

where l_Ri is the length of a certain ray after segmentation, and l_min is the shortest length of all original propagation rays. Therefore, each ray has the opportunity to be segmented and optimized.

When the RSEN algorithm is finished, a modified graph of rays which is different from conventional rays graph is generated. In order to fit the segmented rays, a modified spatial interpolation algorithm is proposed. An ellipse is used again to define the affected zone, and the shape of the ellipse can be expressed as,

$$c_2=b_2/a_2$$

(5)

where a₂ is the long axis of the ellipse, and b₂ is the short axis of the ellipse. Therefore, c₂ is the control coefficient of the second ellipse for interpolation.

$$h(x,y)=\{\begin{array}{c}1\hspace{1em}{D}^2{}_{x{b}_2}/a_2{}^{2\hspace{1em}}+D^2{}_{y{a}_2}/b_2{}^2\le 1\\ 0\hspace{1em}{D}^2{}_{x{b}_2}/a_2{}^{2\hspace{1em}}+D^2{}_{y{a}_2}/b_2{}^2>1\end{array}$$

(6)

The strategy for selection of affected regions according to the segmented rays is shown in Figure 3b. After recording all grid cells in the elliptical region by Equation (6) that is similar to Equation (2), whether a certain grid cell is in a segmented area of the ellipse can be identified as follows,

$$g(x,y)=\{\begin{array}{c}1\hspace{1em}\theta \le \pi /2\\ 0\hspace{1em}\theta >\pi /2\end{array}$$

(7)

where θ is the angle between L_SE (point start to point end) and L_PE (a certain point in ellipse to point end). If g(x,y) = 1, it means that the grid cell is within a segmented area of the ellipse. Then, the grid cells in one ellipse can be can be divided into different affected zones. When all ellipses are segmented, if a grid cell is in several affected zones at the same time, the value of the grid cell is determined as follows,

$$v^{\prime }{}_{xy}={\displaystyle \sum _{k=1}^N{v}^{\prime }{}_k}/N$$

(8)

where v’_xy is the estimated velocity value of a certain grid cell, v’_k is the value of a certain zone that affects the specific grid cell, and N is the total number of zones that affect the specific grid cell, simultaneously.

In summary, the steps of image reconstruction method using segmented propagation rays of stress wave are as follows:

Step 1:

Normalizing all collected values of velocity rays with respect to the range of velocity values, visualizing them, and generating the grid graph.

Step 2:

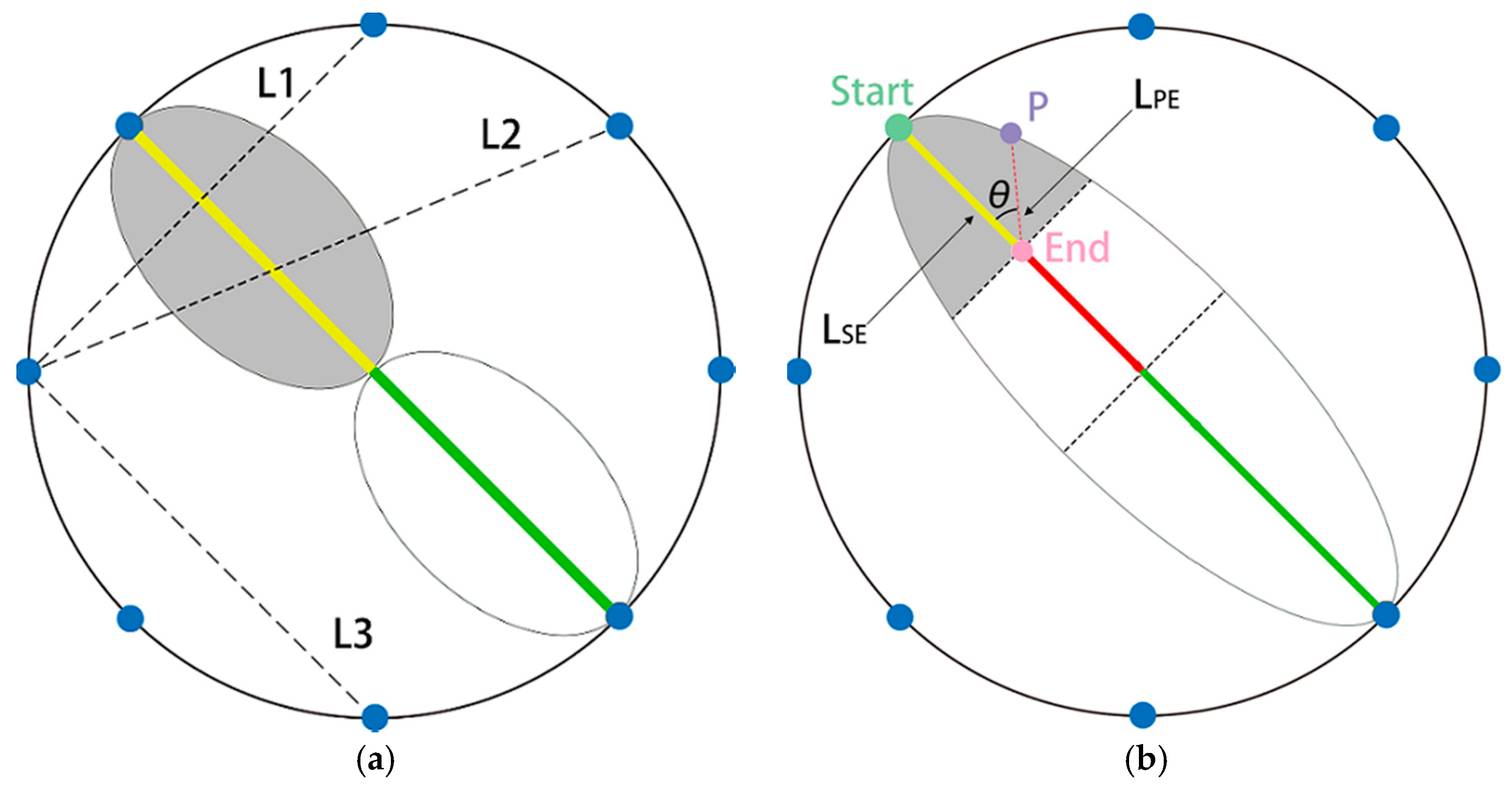
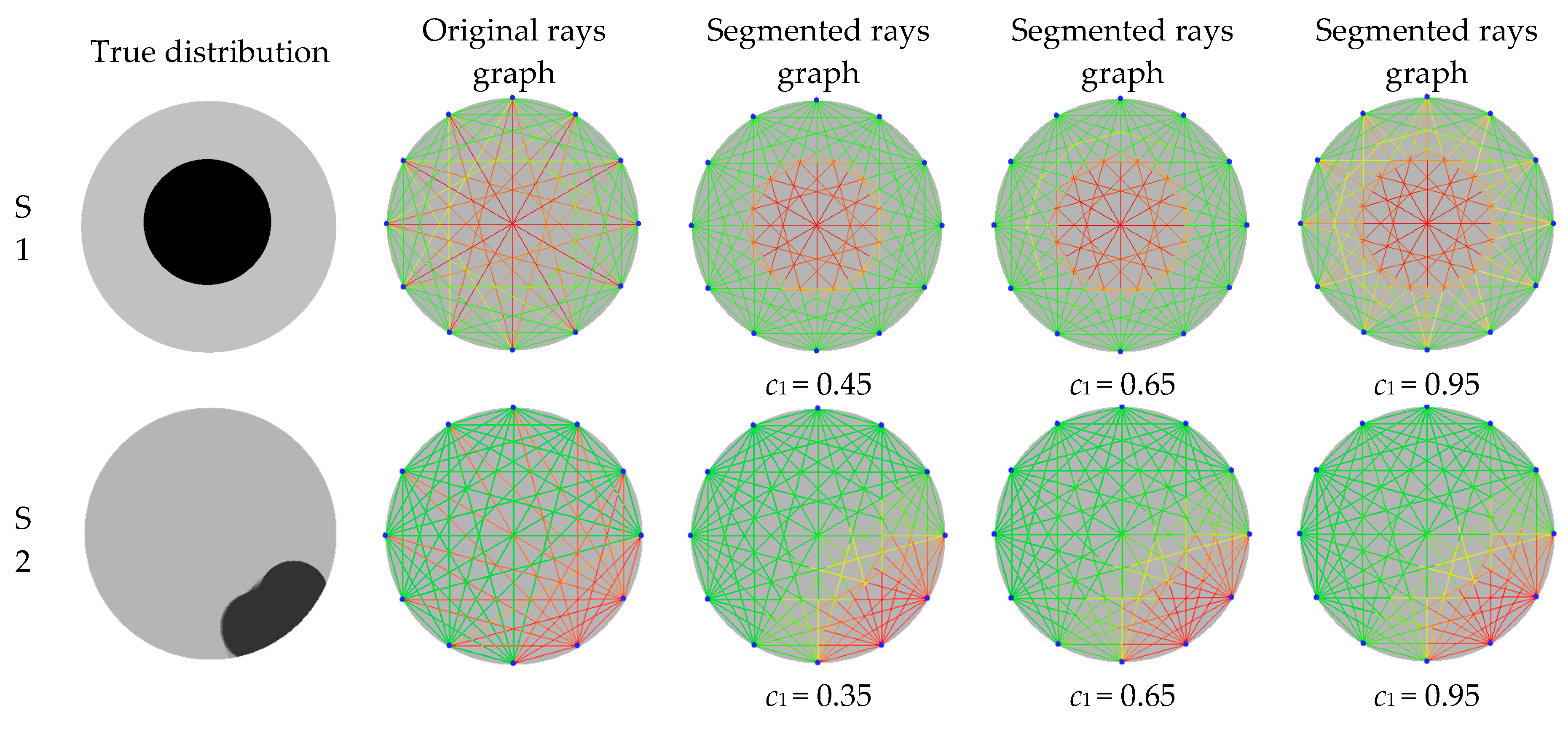
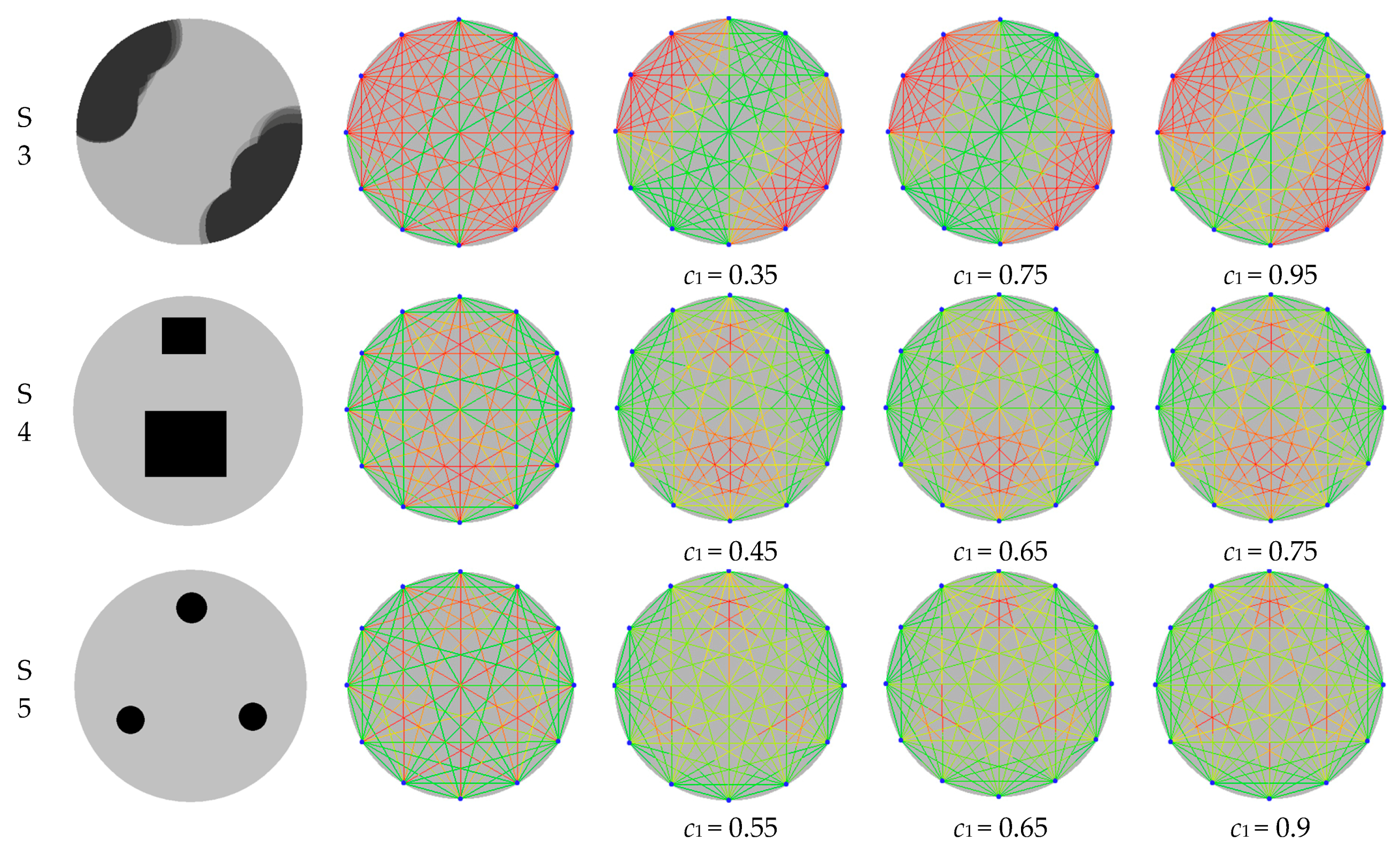
Segmenting a certain ray repeatedly, constructing elliptical neighborhood of segmented rays with Equation (2), and estimating the values of segmented rays with Equation (3), until the termination condition (Equation (4)) is reached.

Step 3:

Repeating Step 2 until every original ray has been processed, and generating the modified rays graph.

Step 4:

Constructing all of the elliptical affected zones with Equations (6), and estimating the values of a certain grid cell with Equations (7) and (8).

Step 5:

Repeating Step 4 until every grid cell has been processed.

Step 6:

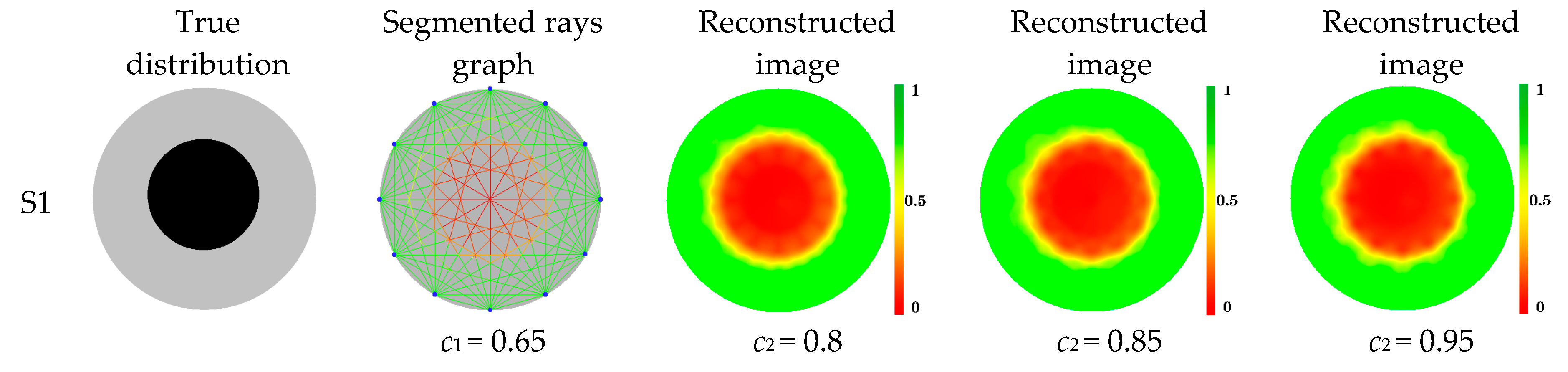
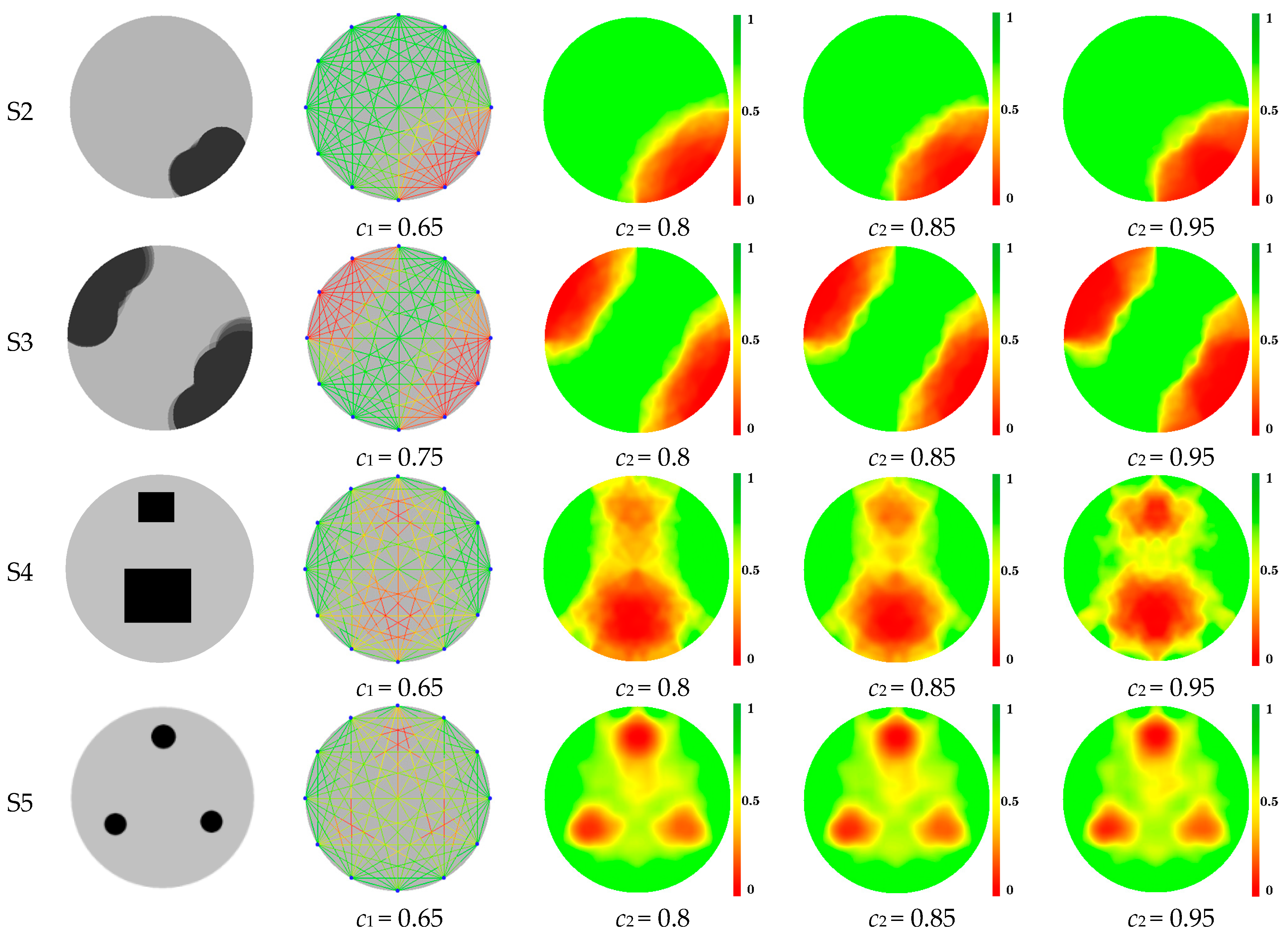
Reconstructing the image of internal defects in wood using the estimated values of grid cells with a certain color scale.

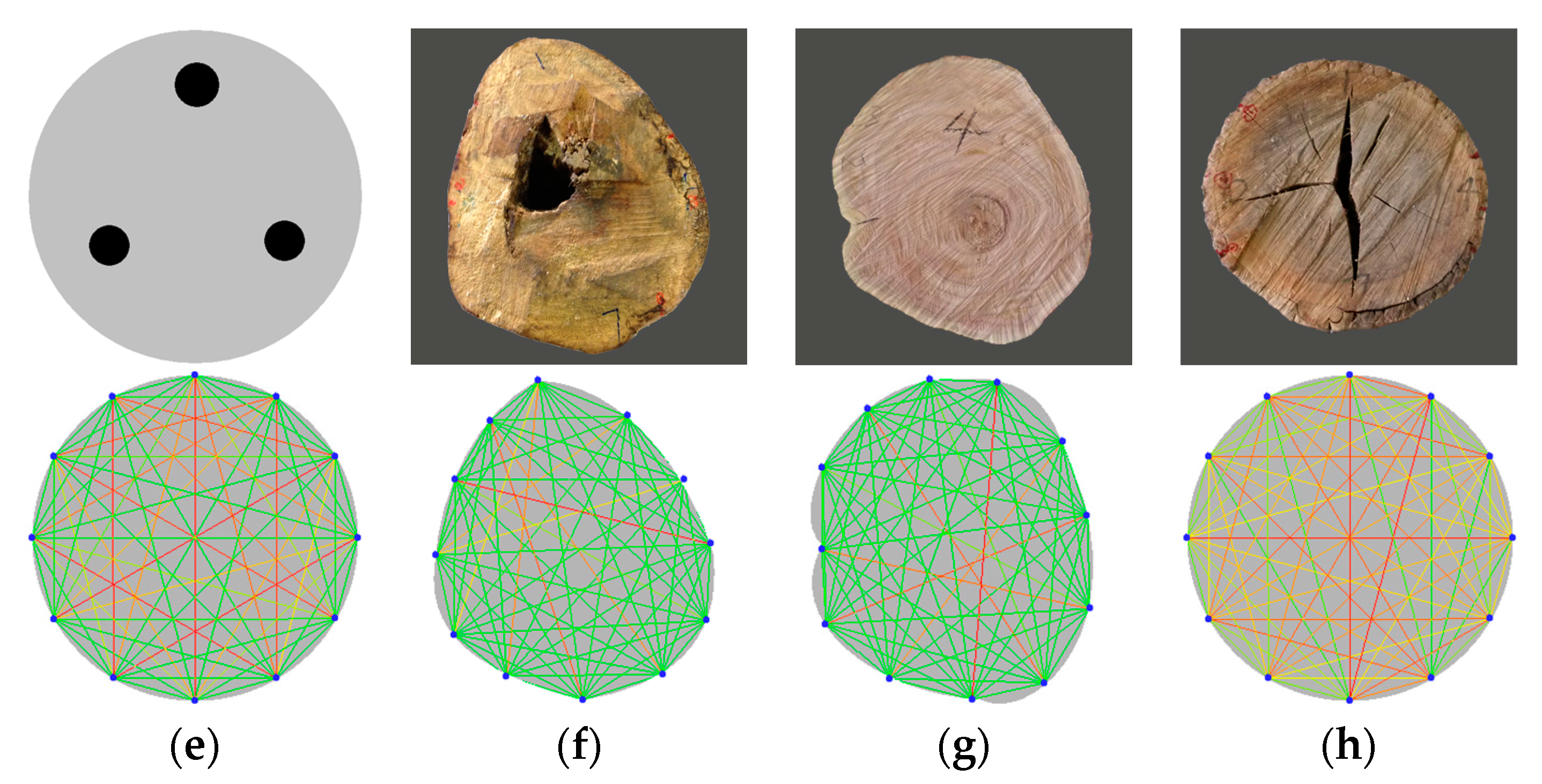
2.3. Materials and Data Acquisition

In order to evaluate the effectiveness of the proposed method, both simulation data and experimental data are used for image reconstructions. In simulation, five defect distributions are designed to evaluate the reconstruction results. The simulation data contains graph of defect distribution and graph of rays. The graph of defect distribution is manually designed and shows the size and shape of virtual defects, and is the expected output result of the proposed image reconstruction algorithm. The graph of rays is manually generated based on the corresponding graph of defect distribution, and is the input of the proposed method. Figure 4 illustrates these corresponding normalized defect distributions, including single circle distribution, single edge distribution, two-edge distribution, two-rectangle distribution, and three-circle distribution. In addition, three test samples are utilized in the experiments. The graph of rays in a real experiment is generated by the collected velocity data. Figure 4 also illustrates these real samples, including Chinaberry timber with hole defects, Firmiana timber with knot defects, and Pecan timber with crack defects.

This study uses the self-developed portable timber tomographic imaging instrument. As shown in Figure 5, this instrument contains a stress wave signal processor box, several data wires, and 12 stress wave sensors. To detect a timber sample, sensors are equally fixed around the cross-section of a trunk section. When a sensor is knocked by the electronic hammer, all remaining sensors will receive the stress wave signal. Then, the signal processor analyzes the signals with DSP (digital signal processing) technology in order to obtain the stress wave transmission time. This paper focuses on the image reconstruction algorithm, and the details of how to collect the transmission time with the instrument have been reported in our previous work [18,35,36].

In order to achieve complete data, it is necessary to knock each sensor one by one until the propagation time of the stress wave between any two sensors is obtained. The distance between sensors is known, so the propagation velocity of the stress waves between any two sensors can also be calculated as follows,

$$\mathrm{S}=\left[\begin{array}{cccc}{s}_{11}& s_{12}& \dots & s_{1J}\\ s_{21}& s_{22}& \dots & s_{2J}\\ \dots & \dots & \dots & \dots \\ {\mathrm{s}}_{J1}& s_{J2}& \dots & s_{JJ}\end{array}\right]=\left[\begin{array}{cccc}null& d_{12}/t_{12}& \dots & d_{1J}/t_{1J}\\ d_{21}/t_{21}& null& \dots & d_{2J}/t_{2J}\\ \dots & \dots & \dots & \dots \\ d_{J1}/t_{J1}& d_{J2}/t_{J2}& \dots & null\end{array}\right],$$

(9)

where d_ij represents the measured distance between sensor number i and sensor number j. t_ij represents the acquired propagation time from sensor number i to sensor number j. Therefore, S_ij represents the velocity from sensor number i to sensor number j. J is the total number of sensors. The velocities are the entries of the matrix S, and matrix S is the input for the proposed method.

The only difference between the simulation experiment and the real experiment is the input data. The input data of the real experiment is collected by the self-developed instrument, and the input data of the simulation experiment is generated manually.

Table 1. The simulation input data of sample (a).

Sensor	1	2	3	4	5	6	7	8	9	10	11	12
1	null	0.80	0.80	0.70	0.56	0.40	0.22	0.35	0.52	0.67	0.78	0.80
2	0.80	null	0.80	0.80	0.71	0.57	0.41	0.23	0.35	0.53	0.67	0.79
3	0.80	0.80	null	0.80	0.80	0.72	0.57	0.41	0.22	0.36	0.54	0.69
4	0.70	0.80	0.80	null	0.80	0.80	0.72	0.57	0.40	0.21	0.38	0.55
5	0.56	0.71	0.80	0.80	null	0.80	0.80	0.71	0.56	0.38	0.20	0.39
6	0.40	0.57	0.72	0.80	0.80	null	0.80	0.80	0.70	0.54	0.37	0.22
7	0.22	0.41	0.57	0.72	0.80	0.80	null	0.80	0.80	0.68	0.53	0.36
8	0.35	0.23	0.41	0.57	0.71	0.80	0.80	null	0.80	0.79	0.67	0.52
9	0.52	0.35	0.22	0.40	0.56	0.70	0.80	0.80	null	0.80	0.78	0.66
10	0.67	0.53	0.36	0.21	0.38	0.54	0.68	0.79	0.80	null	0.80	0.77
11	0.78	0.67	0.54	0.38	0.20	0.37	0.53	0.67	0.78	0.80	null	0.80
12	0.80	0.79	0.69	0.55	0.39	0.22	0.36	0.52	0.66	0.77	0.80	null

shows an example of simulated input data. Sensor No. 1 is at 12 o’clock, sensor No. 4 is at 3 o’clock, sensor No. 7 is at 6 o’clock, and sensor No. 10 is at 9 o’clock. The virtual velocity values in the matrix are designed as relative values.

3. Results and Discussion

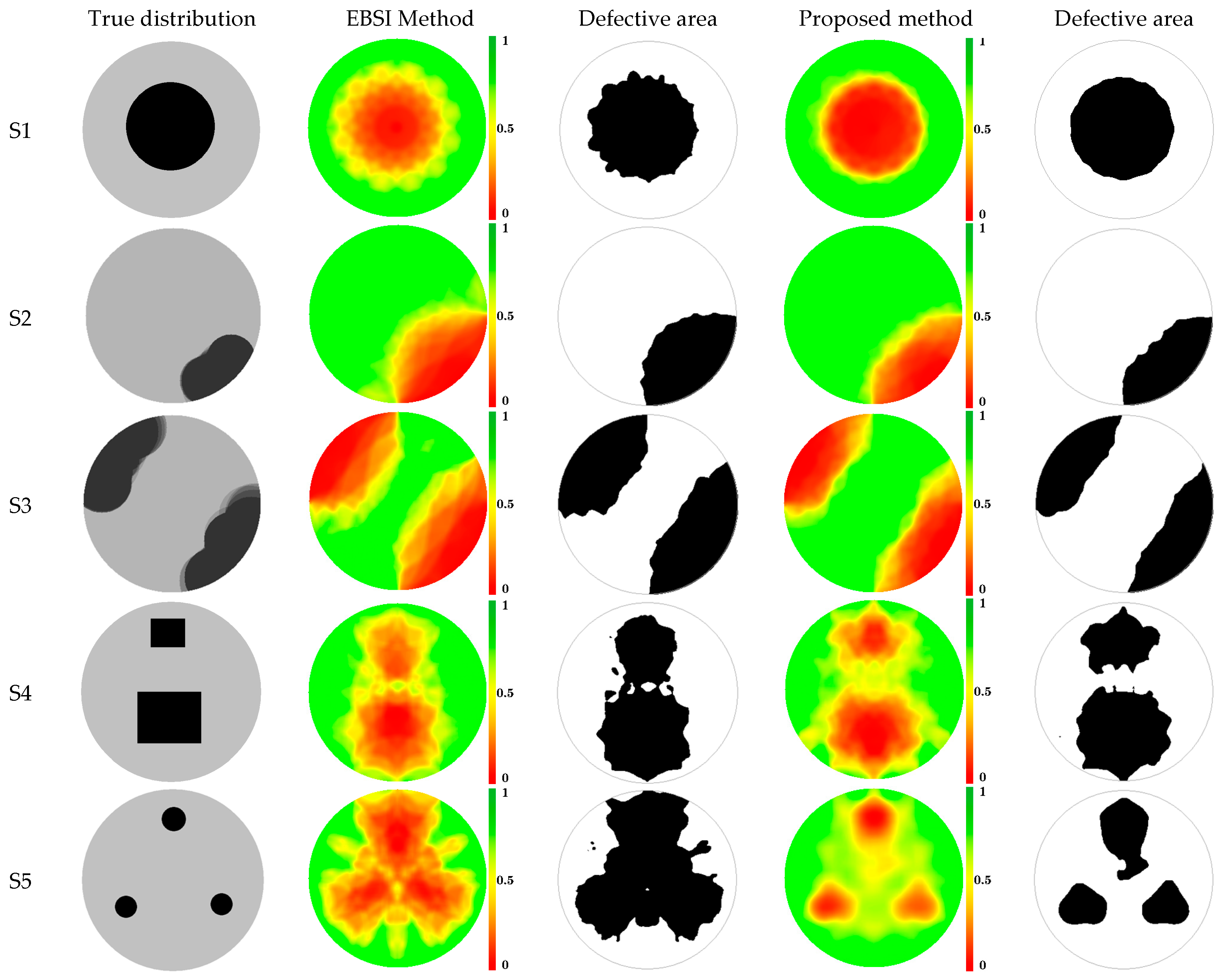
3.1. Results Based on Simulation Data

To unify the imaging conditions, 12 sensors are used to acquire enough data for both numerical simulation and experimental study. The number of pixels in each cell is 1 pixel, and the resolution of reconstructed image is 300 × 300 pixels. The resolution of the simulation defects image is also 300 × 300 pixels, and the proportion of the reconstructed image size to the simulation data is 1:1. To express the appropriate visual effects for the rays graph and the reconstructed image, red is used to represent the lowest velocity values, yellow is used to represent low velocity values, and green is used to represents high velocity values. Besides, c₁ is the control coefficient of the elliptical shape in RSEN algorithm, and c₂ is the control coefficient of the ellipse for interpolation in the SISE algorithm.

In order to show the results of the proposed method more comprehensively, the result of the RSEN algorithm and the result of the SISE algorithm are both displayed in this section. The original rays graph and segmented rays graph using the RSEN method from the simulation data with different control coefficients are shown in Figure 6. It was found that the RSEN algorithm significantly improved the original rays graph. Compared with the original graph of rays, the segmented graph of rays can reflect the spatial distribution of defects better. The approximate regions of defects are even reflected clearly in the segmented rays graph.

On the other hand, all the possible values of the control coefficient c₁ have been studied (that is, from 0 to 1). To clearly display the results, we selected three representative values of c₁ for each sample (min, mid, and max). When c₁ is less than min or more than max for each sample, the corresponding rays graph begins to become worse. Value mid is the optimal choice of the value of the parameter c₁. For samples 1–3, the difference between the results of the RSEN method with different control coefficients is not obvious. It indicates that the algorithm is not sensitive to the control coefficient for defect patterns with single circle distribution or edge distribution. In addition, for samples 4 and 5, when the control coefficient is greater than 0.75, the results begin to become worse. Overall, the coefficient c₁ with a value in the range of 0.65–0.75 is suggested for ray segmentation.

The results of image reconstruction using the SISE method from simulation data with different control coefficients are shown in Figure 7. All values of ray velocity are normalized in the first step of our algorithm, so the scales of the false colors in Figure 7 range from 0 to 1. It can be seen that the reconstructed images reflect the size and shape of defects inside the wood. Once again, for samples 1–3, the difference between the results of the SISE method with different control coefficients c₂ is not obvious. For sample 4, when the control coefficient is less than 0.9, the result begins to become worse. In general, the coefficient c₂ with a value in the range of 0.85–0.95 is suggested for image reconstruction.

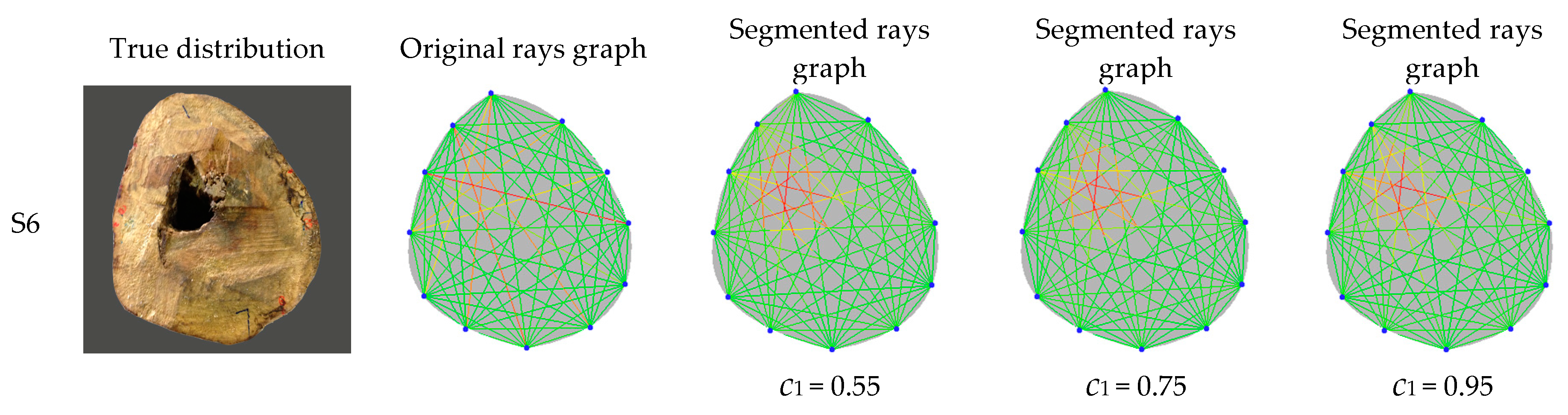
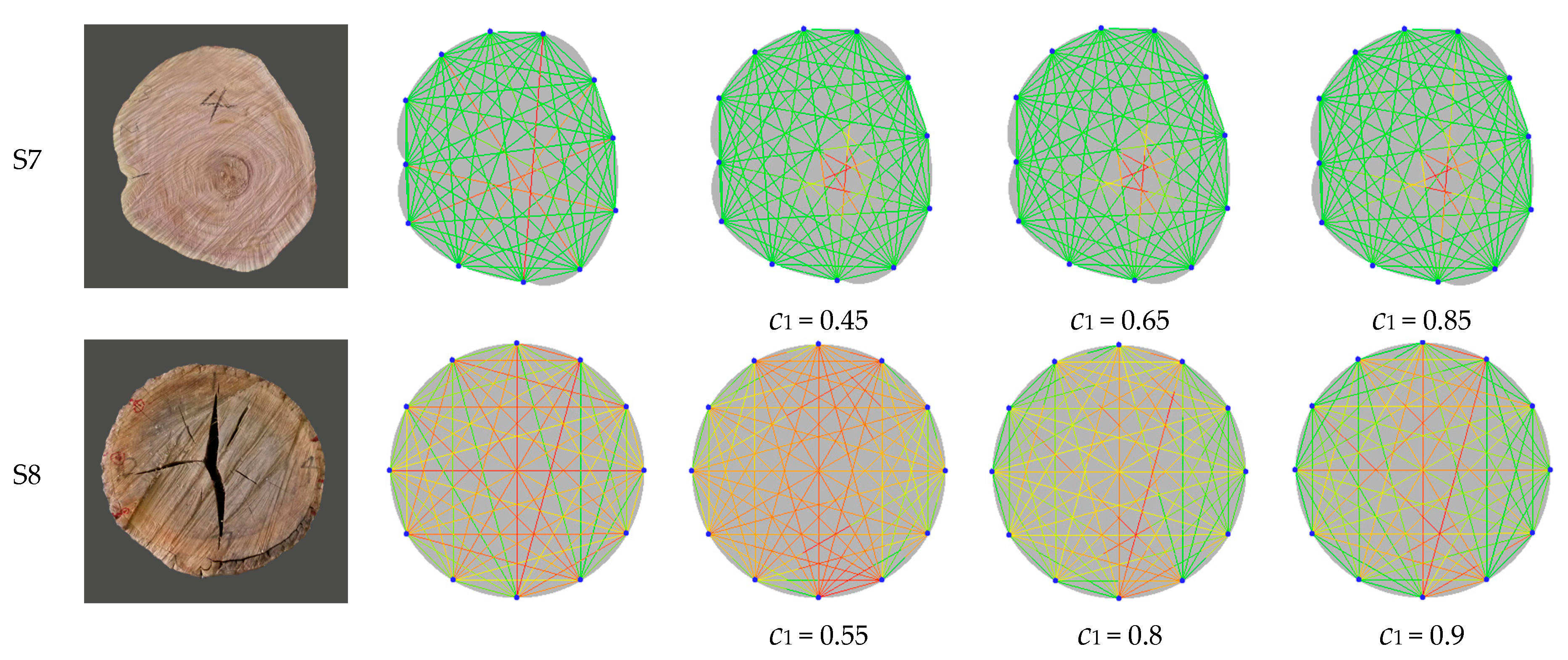
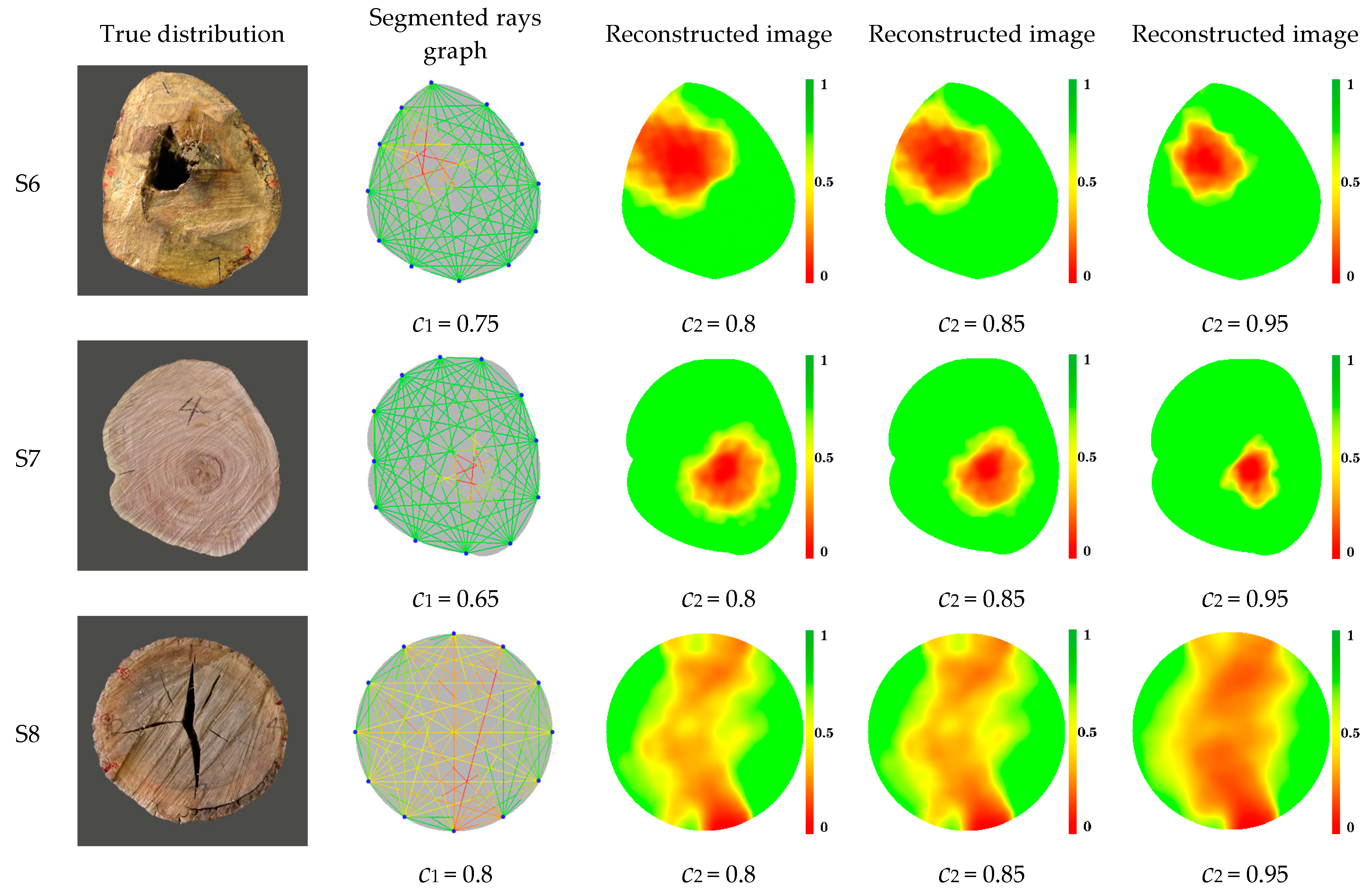
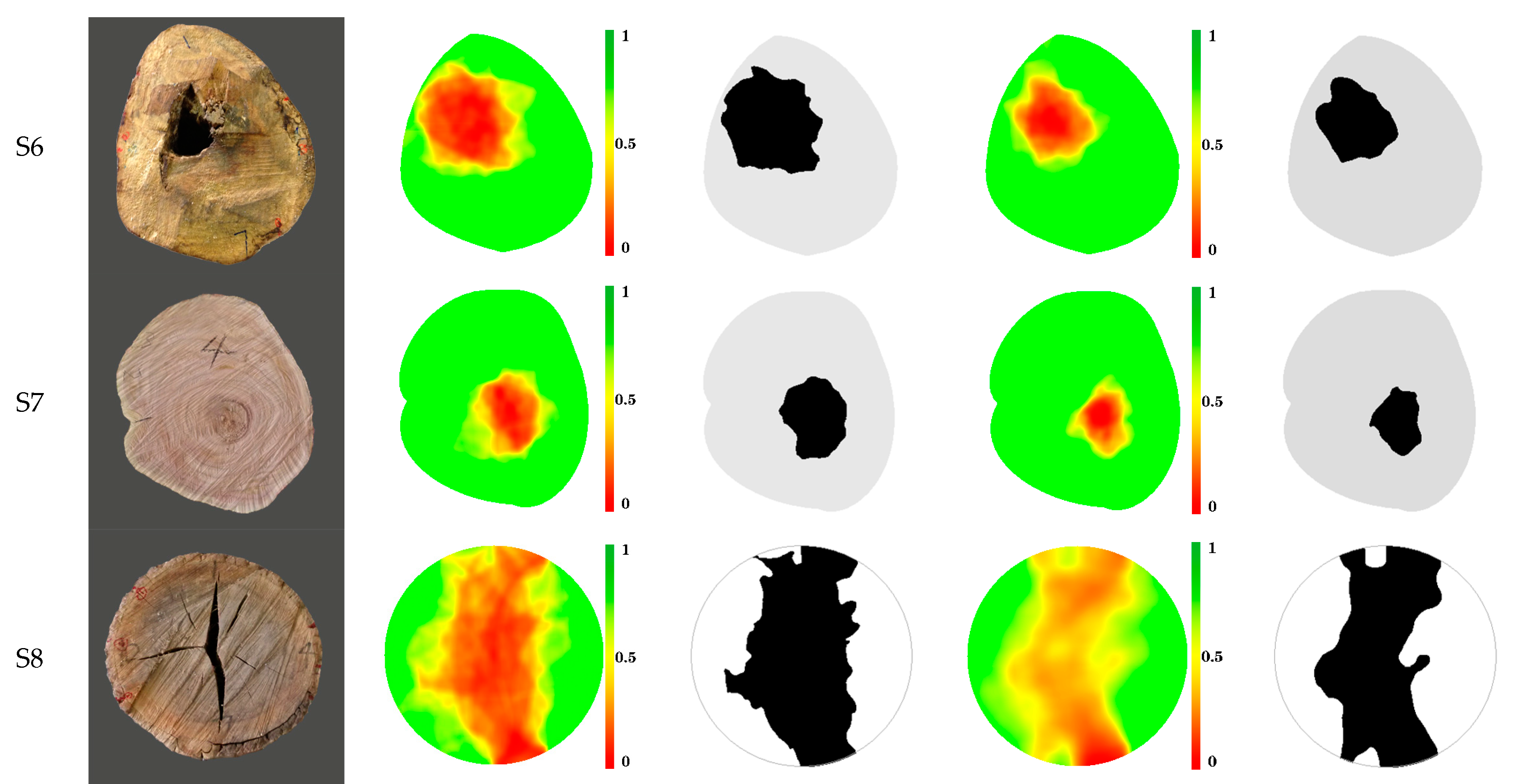
3.2. Results Based on Experiment Data

To obtain stable stress wave signals, an electronic hammer was used to knock the sensors. In addition, all sensors were knocked several times in order to get the average value of velocity for image reconstruction. The hole defect is located at the upper left of the cross section of the wood sample, the knot defect is located at the lower right of the cross section of the wood sample, and the long crack defect is located at the center of the cross section of the wood sample. Especially, the shape of crack defects is not conducive to the acquisition of velocity signals.

Like simulation experiments, the number of pixels in each cell is 1 pixel, and the resolution of reconstructed image is 300 × 300 pixels (actual size is about 6.1 cm × 6.1 cm). The actual diameter of S6 is about 35 cm, so the proportion of the reconstructed image size to the sample 6 is about 1:33. The actual diameter of S7 is about 33 cm, so the proportion of the reconstructed image size to the sample 7 is about 1:29. The actual diameter of S8 is about 28 cm, so the proportion of the reconstructed image size to the sample 8 is about 1:21. The results of the segmented rays graphs and reconstructed images with different control coefficients from the real data are shown in Figure 8 and Figure 9.

As shown in Figure 8, the original rays graphs are all improved significantly. Especially for sample 8, the RSEN algorithm helps to reflect the potential spatial distribution of defects. The coefficient c₁ with a value in the range of 0.65–0.8 is suggested. The experimental results, as shown in Figure 9 (the scales of the false colors range from 0 to 1), prove that the improvement of the rays graph is beneficial to the subsequent interpolation algorithm. Hole defects and knot defects are clearly shown in reconstructed images, and even the complex crack defects can be approximately reflected. The coefficient c₂ with a value in the range of 0.85–0.95 is suggested for the SISE algorithm.

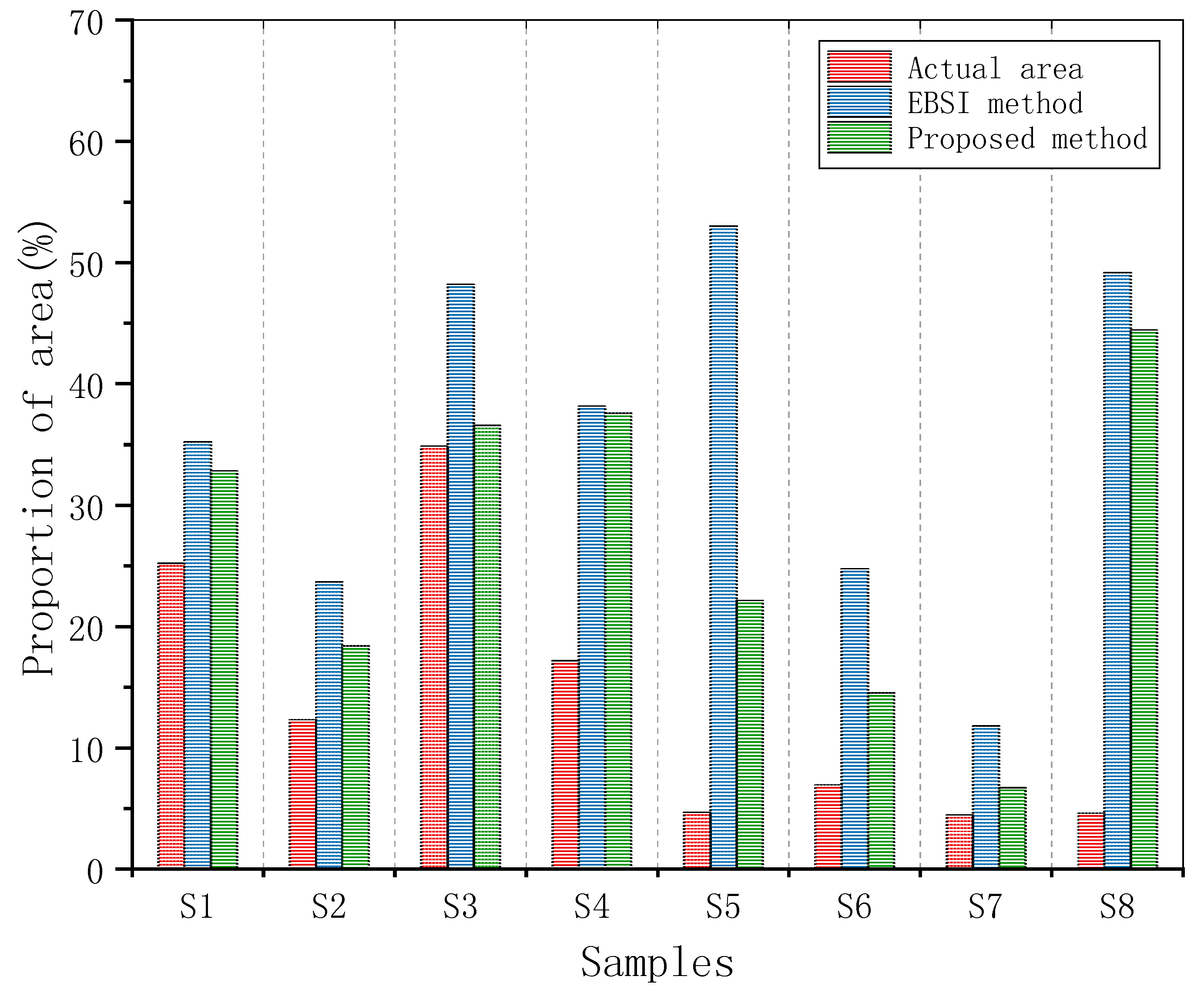
3.3. Defect Area Analysis

In order to compare the experimental results with other algorithms, we repeated the stress wave tomography method using the EBSI method [25]. The comparison results of imaging are shown in Figure 10. Furthermore, to evaluate the proposed method quantitatively, image segmentation technology was used to obtain the area of defective regions in the reconstructed images. The comparison results of defective area are also shown in Figure 10, and the parameters of the proposed algorithm for each sample are shown in

Table 2. The parameters of the proposed algorithm for each sample.

	S1	S2	S3	S4	S5	S6	S7	S8
c1	0.65	0.65	0.75	0.65	0.65	0.75	0.65	0.8
c2	0.85	0.85	0.85	0.95	0.95	0.95	0.95	0.85

.

The comparison results show that the reconstructed images from the proposed algorithm are significantly better than those using the basic ellipse interpolation for all of the given samples. For defect patterns with two-rectangle distribution, the reconstructed image using the EBSI method seems to be connected. For defect patterns with three-circle distribution and crack, the reconstructed images using EBSI are distorted. This indicates that the basic ellipse interpolation method cannot deal with complicated samples. By contrast, reconstructed images using the proposed method are closer to the real distributions for all samples.

Compared with the actual defective area, the data of the defective areas from the reconstructed images using the two methods for all samples are shown in Figure 11. The results indicate that both methods overestimate the size of the real defects. This is because the input signal of stress wave technology is relatively sparse, which is consistent with the conclusion of Wang et al. [28]. It can be seen that the data from the proposed method is closer to the data of the real area than that from EBSI. In general, qualitative imaging results and quantitative defective area analysis demonstrate the effectiveness of the proposed method.

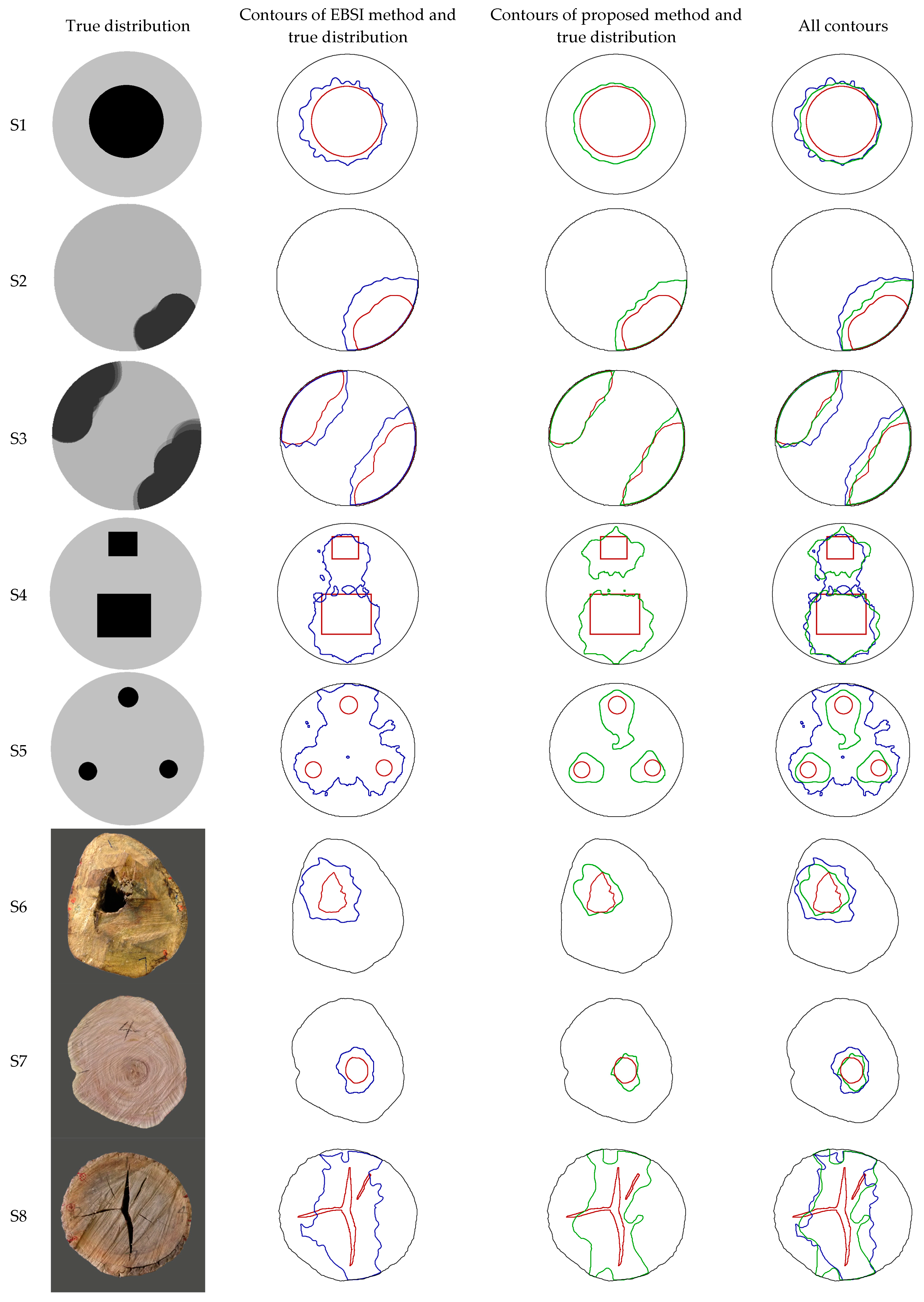
3.4. Defect Shape Analysis

To further analyze the results of reconstructed images, we extracted the contour of defects from the reconstructed images using the two methods and the real contour of defects. Then, all contours were put into one image together for comparison. The comparison results of the defect shape are shown in Figure 12.

As shown in Figure 12, the red line represents the actual contour, the blue line represents the contour extracted from the EBSI result, and the green line represents the contour extracted from the result of the proposed method. The comparison results clearly show that the blue contour is always much larger than the red contour, but the green contour is always closer to the red contour. It reflects that the contour extracted from the reconstructed image using the proposed method is much more similar to the actual contour. In order to quantitatively calculate the imaging accuracy of the proposed algorithm, a confusion matrix is introduced to evaluate the quality of reconstructed image [37]. The confusion matrix contains information about the actual and predicted classification done by an imaging algorithm. As shown in

Table 3. Four kinds of classification in confusion matrix. TP indicates the area is correctly predicted as defects. FN indicates the area is incorrectly predicted as normal wood. FP indicates the area is incorrectly predicted defects. TN indicates the area is correctly predicted as normal wood.

	Predict Defects	Predict Wood
Real defects	TP	FN
Real wood	FP	TN

, TP indicates the area is correctly predicted as defects. FN indicates the area is incorrectly predicted as normal wood. FP indicates the area is incorrectly predicted defects. TN indicates the area is correctly predicted as normal wood.

As shown in Figure 13, the confusion matrix can effectively represent the overlap of two figures. Statistical characteristics such as accuracy, precision, and recall can be calculated as follows:

$$\mathrm{Accuracy}=\frac{\mathrm{TP}+\mathrm{TN}}{\mathrm{TP}+\mathrm{TN}+\mathrm{FP}+\mathrm{FN}}$$

(10)

$$\mathrm{Precision}=\frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FP}}$$

(11)

$$\mathrm{Recall}=\frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FN}}$$

(12)

Accuracy, precision, and recall of EBSI and the proposed method for all of the given samples are shown in Figure 14. The recall of the two algorithms is close to 100%. It indicates that both of the algorithms can detect the location of internal wood defects, and the contours of the reconstructed images using the two algorithms can cover the true defective contour. Therefore, compared with recall, accuracy and precision are able to reflect the quality of the reconstructed images better in this field. It can be found that the accuracy of the proposed algorithm is higher than that of the EBSI algorithm for each sample. Especially for sample 5, the accuracy of the proposed algorithm is 30% higher than that of EBSI algorithm. It indicates that the proposed algorithm has more advantages in dealing with complex defects. The average accuracy of the proposed algorithm is 86.9%, while the average accuracy of EBSI algorithm is only 78.0%. In addition, the precision of the proposed algorithm is also higher than that of the EBSI algorithm for each sample. The precision of the two algorithms is low when dealing with sample 5 or sample 8. It indicates that both of the methods overestimate the size of real defects, especially for complicated defects, and this result is consistent with the results of defect area analysis in the previous paper. In general, the accuracy and precision show the high quality of the reconstructed images using the proposed algorithm.

4. Conclusions

In this paper, a modified image reconstruction method for detecting the internal defects in wood using segmented propagation rays of stress wave was proposed. To verify the feasibility of the proposed method, both simulation data and experimental data were used for image reconstructions. Eight specimens with defects differing in size and position were tested, and the area and shape of the imaging results were analyzed. The presented experiments support the following conclusions:

(1)

The original rays graphs are all improved significantly by the RSEN (ray segmentation by elliptical neighborhood) algorithm. Compared with the original graph of rays, the segmented graph of rays can better reflect the potential spatial distribution of defects and benefits the subsequent spatial interpolation. In addition, the RSEN algorithm is not sensitive to control coefficient c₁ for defect patterns with single circle distribution or edge distribution. For other defects, when c₁ is less than 0.65 or more than 0.85, the corresponding results of rays graphs begin to become worse. The coefficient c₁ with a value in the range of 0.65–0.8 is suggested.

(2)

The images reconstructed by the SISE (spatial interpolation by segmented ellipse) algorithm can reflect the size and shape of defects inside wood. In addition, the SISE algorithm is also not sensitive to control coefficient c₂ for defect patterns with single circle distribution or edge distribution. For other defects, when c₂ is less than 0.85, the corresponding results of reconstructed images begin to become worse. The coefficient c₂ with a value in the range of 0.85–0.95 is suggested.

(3)

The defective area proportion from the reconstructed image using the proposed method is closer to the actual defective area, and the contour extracted from the reconstructed image using the proposed method is much more similar to the actual contour.

(4)

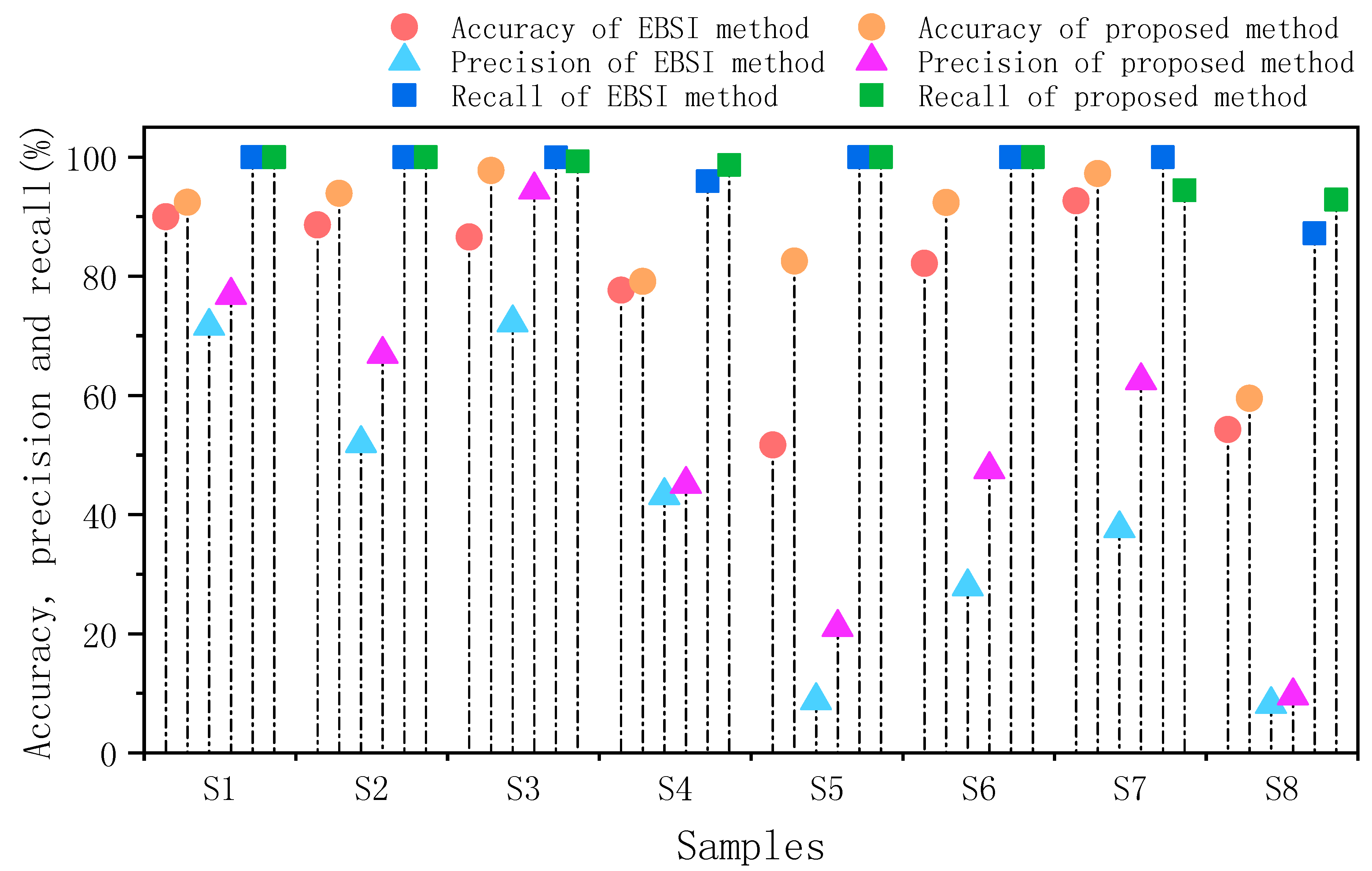
The average accuracy of the proposed algorithm is 8.9% higher than that of the EBSI (ellipse based spatial interpolation) algorithm, and the average precision of the proposed algorithm is 12.8% higher than that of the EBSI algorithm.

In general, compared with the results of the EBSI algorithm, the proposed algorithm not only can better reflect internal wood defects qualitatively and quantitatively, but also has a high quality of reconstructed images. However, the method overestimates the size of real defects, especially for complicated samples. We can further improve the method in future work.